Сколько законов кирхгофа существует: Законы Кирхгофа — это… Что такое Законы Кирхгофа? — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Законы Кирхгофа — это… Что такое Законы Кирхгофа?

Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.^[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.

Формулировка

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений

для переменных напряжений

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

Особенности составления уравнений для расчёта токов

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме;
- положительные направления обхода контуров для составления уравнений по второму закону.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.

При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники.

Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.^{[источник не указан 912 дней]}

Закон излучения

Закон излучения Кирхгофа — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Примечания

Литература

Матвеев А. Н. Электричество и магнетизм — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи — 11-е издание. — М.: Гардарики, 2007.

Законы Кирхгофа

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или , между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома.

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.

Разветвлённая цепь.

В узле А цепь разветвляется на четыре ветви, которые сходятся в узел В.

Обозначим токи в неразветвленной части цепи — I, а в ветвях соответственно

, I2, I3, I4.

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквой I.
Силу тока в отдельных ветвях соответственно I1, I2, I3 и I4.
Напряжение между точками A и B — U.
Общее сопротивление между этими точками — R.

По закону Ома напишем:

I = U/R; I1 = U/R1; I2 = U/R2; I3 = U/R3; I4 = U/R4;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4; или U/R = U/R1+U/R2+U/R3+U/R4.

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4, что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2, то можно написать равенство:

1/R =1/R1+1/R2;

Из этого равенства найдем сопротивление R, которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.
Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2.
Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1—Е2.

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»

Скачать можно здесь

(Подробно и доходчиво в видеокурсе «В мир электричества — как в первый раз!»)

Законы Кирхгофа простыми словами — Юридическая помощь

Первый закон Кирхгофа

Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.

Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.

Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.

Согласно первому закону Кирхгофа

Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.

1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.

Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.

Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:

I₁ — I₂ — I₃ = 0.

Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.

Закон кирхгофа для конденсаторов

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7.
Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с.

Общие понятия и описание первого закона Кирхгофа

Первый закон Кирхгофа показывает связь токов и узлов электрической цепи. Формула связи очень проста. Это правило гласит, что сумма токов всех ветвей, которые сходятся в один узел электроцепи, равняется нулю (речь идёт об алгебраических значениях).

При этом накопление электрических зарядов в одной точке замкнутой электроцепи невозможно.
При суммировании токов принято брать положительный знак, если электроток идёт по направлению к узлу, и отрицательный знак, если ток идёт в противоположную от узла сторону. Для описания понятной аналогии для этого случая, уместны сравнения с течениями воды в соединенных между собой трубопроводах.

Пример вышеописанной формулы первого закона:

Закон Ома — первый кит электротехники

А когда Георг Симон Ом, изучая гальванические, как тогда называли, цепи, вывел своё простейшее соотношение, этого понять не мог никто, кроме немногих посвящённых. Просто потому, что обыденный мозг тогда сразу упирался в нечто невообразимое, а значит, непреодолимое: что это за течение такое, ток частиц, которых не то что пощупать, но и представить нельзя ввиду абсолютно исчезающей малости. Да ещё «текущих» в металле, твёрдом предмете. Уж не то, что попытаться составлять какие-либо точные формулы.

Теперь это соотношение кажется простым и ясным, как удар молнии. Видимо, он сумел почувствовать это явление — электрическое напряжение.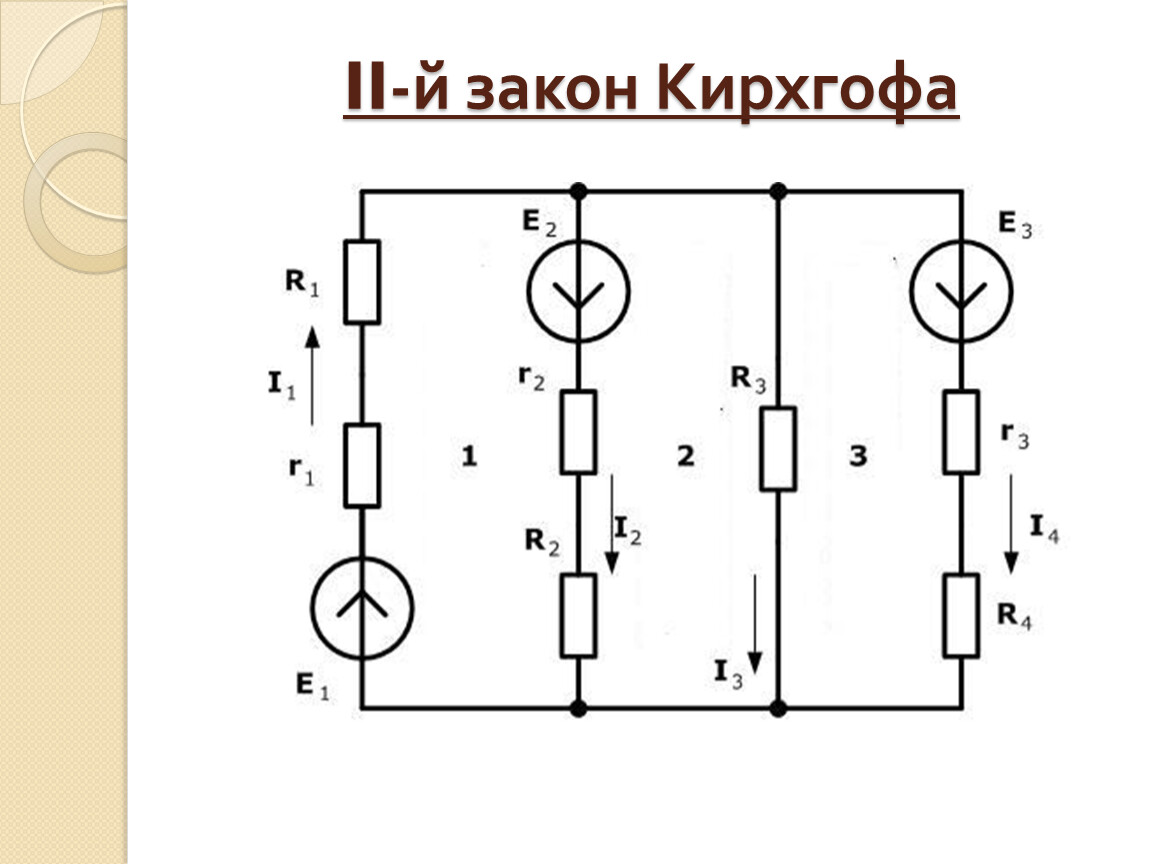 Если цепь разомкнута, то тока ещё никакого нет, ничего не нагревается и не пузырится (как вода под током), а напряжение вот оно — попробуй, тронь! Видимо, как-то сумел гений потрогать и попробовать.

Собственно, вся любая электрическая цепь и описана законом Ома. Источник, дающий напряжение и нагрузка, подставляющая напряжению своё тело, отчего получается электрический ток. Соотношение простейшее — чем больше напряжение, тем больше ток. А конкретно каким он получится, определяет пропускная способность нагрузки, G, или проводимость.

I=U*G

Удобнее и нагляднее оказалось вместо проводимости пользоваться понятием сопротивления, R, величиной обратной проводимости (R=1/G).

И обозначения на первой электросхеме самые простейшие: прямоугольничек — нагрузка, две линии поперёк тока — батарейка.

Самая первая электрическая схема

Видимо, и подключали поначалу что-то одно к чему-то одному. Но вот и эта схема «под напором реальности» усложняется. Во-первых, сама батарейка имеет сопротивление.

Как это изобразить, вот так?

Некрасиво.

Лучше располагать рядом так:

Есть искушение поставить этот прямоугольничек на другую сторону, рядом с нагрузкой, а нельзя, всё-таки батарейка и её внутреннее сопротивление — одно нераздельное физическое устройство.

Чтобы видеть действие тока, лучше в качестве нагрузки использовать лампочку. Понятно, с выключателем.

Мы получили последовательную цепочку.

Ток во всех её частях обязан быть одним и тем же, то есть одинаковый везде.

Это логично, и если включить выключатель, лампочка сразу загорится.

При этом никто и не задумывается, что если у нас через лампочку течёт ток всего в один ампер, то это значит, что каждую секунду через неё пробегает:

6 квинтиллионов 241 квадриллион 509 триллионов 125 миллиардов 493 миллиона 690 тысяч с небольшим электронов.

И все они вышли из небольшой батареечки и в неё же и вернутся с другой стороны.

Если поставить вместо одной лампочки две одинаковых, то они загорятся вполнакала, то есть ток I, протекающей последовательно из батарейки через выключатель сначала в лампочку Л1, потом в лампочку Л2 и снова в батарейку, станет меньше, чем был, когда стояла одна лампочка.

Это значит, что сопротивление стало больше: было R у одной лампочки, стало R+R, то есть 2R.

Токи и напряжения в сети

Точную величину тока можно подсчитать, если применить закон Ома ко всей нашей цепи, общее сопротивление которой есть сумма сопротивлений всех её нагрузок.

(1) А если оставить в формуле сопротивление только одной лампочки, то, зная, что ток у нас везде один и тот же, можно вычислить напряжение Uл конкретно для этого потребителя, лампочки.

Это напряжение, которое падает именно на нашу лампочку, так и называется «падение напряжения». Оно примерно вдвое меньше нашего напряжения питания U. Примерно — потому что в формуле (1) среди сопротивлений есть ещё небольшой довесок в виде r, внутреннего сопротивления нашей батареи. Что делать, она не идеальна, и вместе со всеми остальными потребляет энергию (свою же собственную) и даже греется от этого. Хотя сопротивление её достаточно малое.

А теперь взглянем на нашу цепь как на единый контур, который можно обходить по часовой или против часовой стрелки. Ток наш идёт, как нарисовано, против часовой стрелки. Двинемся по этому направлению с любого места и пройдём всё, складываем падения напряжения на всех попадающихся по дороге приборах.

Для токов — узлы, для напряжений — контуры

Получится:

Последним напряжением добавлено то, которое вырабатывается батареей, только со знаком минус, так как оно работает не на потребление, а наоборот, вырабатывается и поставляется в сеть нашей героической батареей. И что у нас получилось?

Правило Кирхгофа для напряжений (2й закон)

А получилось ровно 0. Потому что вся энергия от батареи потребляется лампочками + внутреннее сопротивление батареи. И понятно, это есть высшая справедливость природы. То есть второй закон Кирхгофа в действии.

И вдруг у нас случился… прорыв.

Правило Кирхгофа для токов (1й закон)

К нам в двух точках — А и B — подключились неизвестные, скорее всего, инопланетяне.

И начали качать от нас энергию. И теперь мы знаем, что ток I3 и ток I4 — не наши, они инопланетянские. И наша схема может быть безнадёжно испорчена.

Но!

А обойдём ка мы контур снова. Может быть, не всё ещё потеряно. И вот:

Ur=I1*r

Uл1=I2*R=Uл2

И, наконец:

U=Uг+Uл1+Uл2.

Потому что I1=I2+I3. И I1=I2+I4.

То есть сколько току вытекло в качестве тока I3 в точке А, столько его и вернулось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А помогло нам при этом здравое рассуждение, о том, что в любой точке цепи, где электрическая сеть разветвляется, общее количество тока, вытекающего из узла, то есть этой точки, равно количеству тока, втекающего в этот узел. Поэтому смело рисуем схему, зная, что нам помог уже первый, а не второй закон Кирхгофа:

Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.

Ох уж эти выдумки инопланетянские! С нашей стороны осталось только в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин) в противоположное направление. Потому что мы сначала подумали, что инопланетяне плохие, а они оказались хорошими.

Расчёт цепи по законам Кирхгофа интуитивно понятен — правила позволяют рассчитывать электрические цепи, то есть определять все неизвестные параметры — токи, напряжения — любой, сколь угодно замысловатой цепи.

Законы Кирхгофа простыми словами ⋆ diodov.net

Два закона Кирхгофа вместе с законом Ома составляют тройку законов, с помощью которых можно определить параметры электрической цепи любой сложности.

Законы Кирхгофа мы будем проверять на примерах простейших электрических схем, собрать которые не составит никакого труда.

Для этого понадобится несколько резисторов, пара источников питания, в качестве которых подойдут гальванические элементы (батарейки) и мультиметр.

Первый закон Кирхгофа

Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.

Согласно первому закону Кирхгофа

I1 — I2 — I3 = 0.

Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.

Второй закон Кирхгофа

Второй закон Кирхгофа воспринимается начинающими радиолюбителями гораздо сложнее, нежели первый. Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.

Упрощенно 2 закон Кирхгофа говорит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений

ΣE = ΣIR

Самый простой случай данного закона разберем на примере батарейки 1,5 В и одного резистора.

Поскольку резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.

Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, то есть по 0,75 В.

Если возьмем три резистора снова одинакового номинала, например по 1 кОм, то падение напряжения на них будет по 0,5 В.

Формулой это будет записано следующим образом:

Рассмотрим условно более сложный пример. Добавим в последнюю схему еще один источник питания E2, напряжением 4,5 В.

Обратите внимание, что оба источника соединены последовательно и согласно, то есть плюс одной батарейки соединяется с минусом другой батарейки или наоборот. При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:

И последний отличительный вариант, который мы рассмотрим в данной статье, предполагает последовательное встречное соединение гальванических элементов. При таком соединении источников питания из большей ЭДС отнимается значение меньшей ЭДС. Следовательно к резисторам R1…R3 будет приложена разница E1 – E2, то есть 4,5 – 1,5 = 3 В, — по одному вольту на каждый резистор.

Второй закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, а также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить соответствующие измерения с помощью мультиметра.

Законы Кирхгофа действуют как для постоянного, так и для переменного тока.

Источник: https://diodov.net/zakony-kirhgofa-prostymi-slovami/

Первый и второй закон Кирхгофа — доступное объяснение

Первый закон Кирхгофа

Определение первого закона звучит так: «Алгебраическая сума токов, протекающих через узел, равна нулю». Можно сказать немного в другой форме: «Сколько токов втекло в узел, столько же и вытекло, что говорит о постоянстве тока».

Узлом цепи называют точку соединения трех и больше ветвей. Токи в таком случае распределяются пропорционально сопротивлениям каждой ветви.

I₁=I₂+I₃

Такая форма записи справедлива для цепей постоянного тока. Если использовать первый закон Кирхгофа для цепи переменного тока, то используются мгновенные значения напряжений, обозначаются буквой İ и записывается в комплексной форме, а метод расчета остаётся прежним:

Комплексная форма учитывает и активную и реактивную составляющие.

Законы Кирхгофа — формулы и примеры использования

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».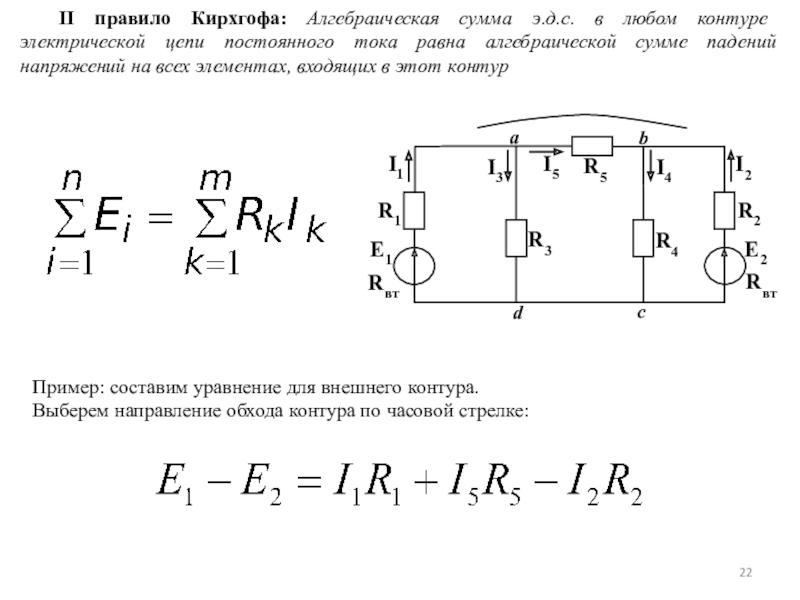

Первый закон Кирхгофа

Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.

Согласно первому закону Кирхгофа

Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.

I₁ — I₂ — I₃ = 0.

Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.

Законы и уравнения Кирхгофа

Содержание:

Законы и уравнения Кирхгофа

Первый закон Кирхгофа: алгебраическая сумма токов ветвей, соединенных одним узлом, равна нулю.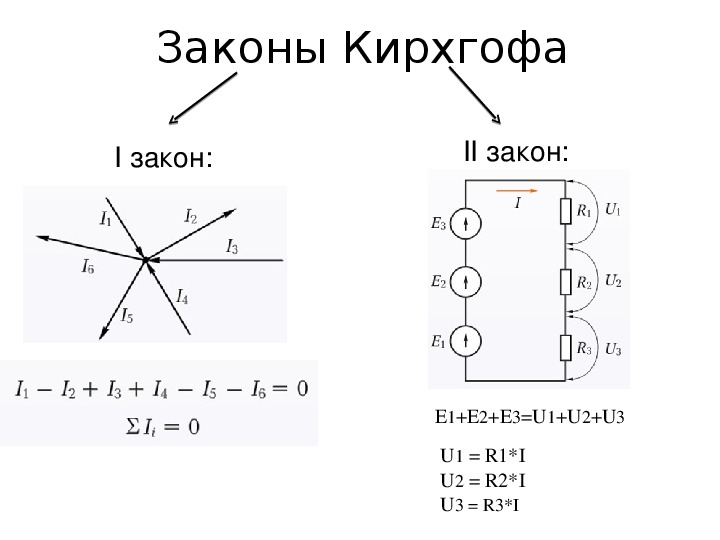 Форма уравнения, составленная в соответствии с этим законом: (1.1) ток из узла (исходящий) входит в уравнение с положительным знаком, а ток в узел (входящий) имеет отрицательный знак.

Второй закон Кирхгофа: алгебраическая сумма напряжений ветвления вдоль контура равна нулю. Уравнение, составленное по второму закону Кирхгофа, имеет вид (1.2), а напряжение, соответствующее направлению обхода схемы, принимается с положительным знаком, противоположным направлению обхода схемы. Направленное напряжение берется с отрицательным знаком.

Уравнения или правила Кирхгофа относятся к основным законам электрических цепей.

Они подчиняются основным законам, таким как закон сохранения заряда и вихревая природа электростатических полей. Это когда-то было описано уравнениями Максвелла. Уравнение Кирхгофа часто используется для его универсальности, пригодности для решения многих задач в теории электротехники, в том числе связанных с расчетом сложных электрических цепей, и практичности.

Применяя правило Кирхгофа к линейной электрической цепи, вы можете получить систему линейных уравнений, из которой вы можете найти значения тока для всех ветвей цепи и для всех узловых напряжений.

Правила Кирхгофа применяют концепцию электрических цепей, таких как узлы, ветви и цепи. Участок электрической цепи с одинаковым током называется ответвлением.

Например, в сегментах с 1 по 4 на рисунке 1 течет ток i1, и существует ветвь.

Точка, соединяющая три или более ветвей, называется узлом. Например, точки 1, 2, 3 и 4 на рисунке 1 являются узлами. Замкнутый путь через несколько ветвей и узлов разветвленной электрической цепи называется цепью.

Начиная с определенного узла в цепочке, проходя через несколько ветвей и узлов и возвращаясь к исходному узлу, он проходит по пути, называемому закрытым. Ветви и узлы, проходящие во время таких обходов, обычно называют принадлежащими этой цепи, и необходимо учитывать, что ветви и узлы могут принадлежать нескольким контурам одновременно.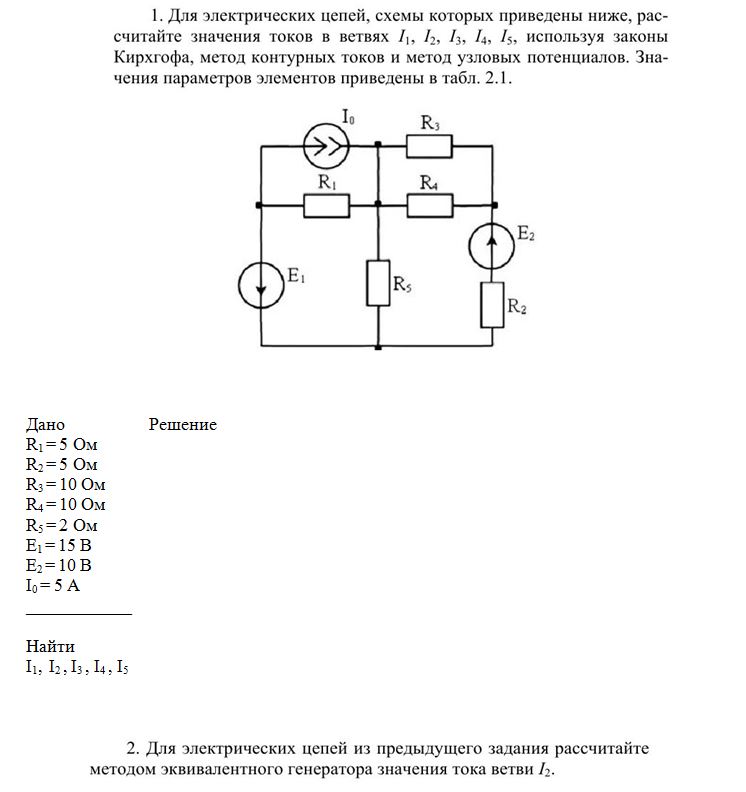

Первое правило Кирхгофа основано на заявлении о непрерывности тока любого узла в электрической цепи или замкнутом контуре.

Первое правило Кирхгофа интерпретирует алгебраическую сумму токов ветвления для любого узла или замкнутого участка электрической цепи как ноль.

Алгебраическая сумма узловых токов равна нулю. Первый закон Кирхгофа

Выше указано, что заряд на узле (например, S2 на фиг.1) или поперечном сечении (например, S14 на фиг.1) не может накапливаться ни в одной электрической цепи. Другими словами, количество тока, протекающего через узел, и количество тока, протекающего от узла.

Второе правило Кирхгофа основано на утверждении, что электрические цепи являются потенциальными и что работа движущегося заряда в замкнутой цепи равна нулю.

Работа с замкнутым циклом

Где U — работа (напряжение), а k — количество источников, выполняющих работу.

Рассмотрим схему, показанную на рисунке 1, образованную биполярными элементами, в которых ответвительные ветви образуют узлы 1, 2, 3 и 4, и направления напряжения и тока ответвления совпадают. Произвольно выберите узел S2, замкнутый участок S14 («несколько узлов») и замкнутый контур 1, чтобы скомпилировать уравнения Кирхгофа. На рисунке 1 показано направление обхода.

Если ток, генерируемый из сечения и узла, является положительным, а ток притока считается отрицательным, то уравнение, составленное по первому правилу Кирхгофа, имеет вид

Первый закон Кирхгофа

Чтобы построить уравнение в соответствии со вторым правилом Кирхгофа, учтите, что напряжение, соответствующее направлению обхода схемы, является положительным, а не отрицательным. В этом случае уравнение принимает вид:

Общее напряжение при обходе замкнутого контура

Рассмотрим второе правило Кирхгофа с более конкретным примером (см. Рисунок 2 ниже) и более простой интерпретацией для практического понимания. Эта схема

Второй закон Кирхгофа

Где k — количество источников ЭДС. m — количество ветвей в замкнутом цикле. Ii, Ri-i ветви тока и сопротивления.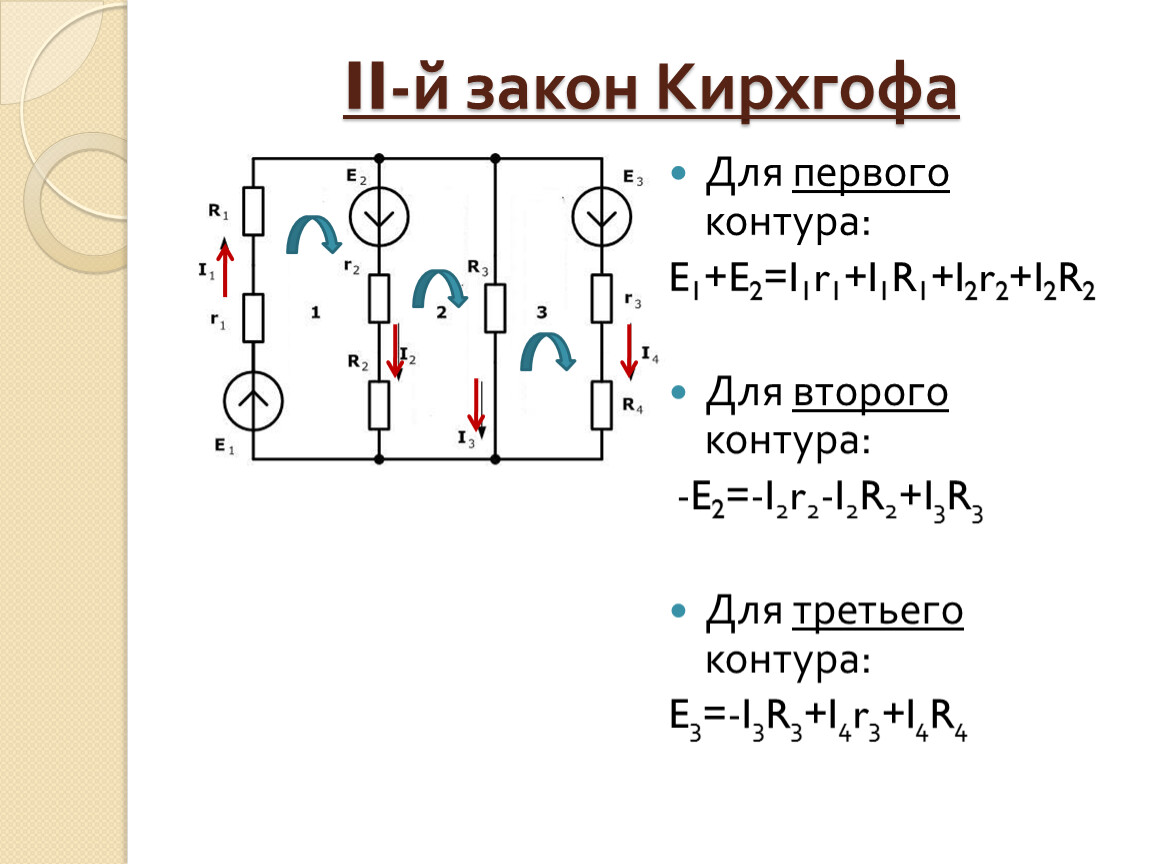

Замкнутая цепь с некоторым ЭДС
Примените второе правило Кирхгофа, чтобы создать уравнение контура замкнутой цепи.

Уравнения замкнутой цепи на основе закона Кирхгофа
При составлении результирующего уравнения знак учитывался следующим образом:
-EMF (E) положительна, если его направление совпадает с произвольно выбранным направлением обхода цепи.
-Падение напряжения (IR) резистора является положительным, если направление тока резистора совпадает с направлением байпаса.
Мы рассмотрели применение правил Кирхгофа на простом примере.

Смотрите также:

Кирхгоф закон излучения — Справочник химика 21

Кирхгофа закон излучения [c.360]

Закон Кирхгофа. Закон устанавливает численное равенство спектральных величин коэффициентов теплового излучения и поглощения [c.195]

На основании закона Кирхгофа излучение продуктов сгорания в пламени (независимо от их природы и длины волны), если они характеризуются локальным равновесием, может быть описано законами излучения, полученными для абсолютно черного тела с учетом коэффициента излучения (их излучательной способности). Спектральное распределение энергии излучения пламени типичного осветительного состава (в сравнении с абсолютно черным телом) показано на рис. 1.5. [c.22]

Проделав множество опытов. Прево высказал предположение о том, что всякое тело непрерывно испускает тепловые лучи, а взамен получает теплоту благодаря лучеиспусканию окружающих тел. Строго этот закон излучения был сформулирован только в 1859 г. немецким физиком Г. Р. Кирхгофом. В соответствии с законом Кирхгофа, излу-чательная способность любого тела пропорциональна его способности поглощать излучение. Это означает, что чем сильнее тело поглощает излучение от внешнего источника, тем в большей степени оно само способно к лучеиспусканию. Сильнее всего поглощает излучение (в любой области спектра-ультрафиолетовой, видимой или инфракрасной) так называемое абсолютно черное тело -этот термин тоже ввел в употребление Кирхгоф. Такое тело поглощает все падающие на него лучи и ничего не отражает.

Коэффициент поглощения абсолютно черного тела при любой температуре равен единице (е= 1). [c.156]

Тепловое излучение имеет сплошной спектр. В соответствии с законом Кирхгофа отношение испускательной способности тела к его поглощательной способности при данной температуре есть универсальная функция частоты V и абсолютной температуры [c.92]

В 1860 г. Кирхгоф установил, что излучательная а и поглощательная а способности при тепловом равновесии должны быть равны для поверхностей серых и абсолютно черных. Это закон иллюстрирует обратимость процессов излучения и поглощения излучения из него также следует, что отдельная частица внутри изотермической излучающей полости не может быть нагрета излучением до большей температуры, чем температура полости. Поскольку температуры равны, частица должна терять при излучении столько же энергии, сколько она приобретает при поглощении. Для несерых тел закон Кирхгофа выполняется лишь при сопоставлении спектральных величин. [c.193]

Закон Кирхгофа. Соотношение между лучеиспускательной и поглощательной способностями тел устанавливается законом Кирхгофа. Это соотношение может быть получено пз рассмотрения процесса обмена лучистой энергии между двумя телами абсолютно черным п серым (рис. 6-2). Поверхности тел параллельны и расположены на расстоянии, при котором излучение каждого из тел попадает на другое. Левое — абсолютно черное тело имеет температуру лучеиспускательную способность Е(, и поглощательную Лд = 1, правое — серое тело соответственно Т, Е и А, при этом Г > Г д. Излучение Е попадает на абсолютно черное тело и целиком поглощается им. Излучение попадает на серое тело, при этом часть его, [c.128]

Для расшифровки состава природных органических соединений нефти и нефтепродуктов и характеристики их свойств применяются оптические методы. Сюда относятся инфракрасная и ультрафиолетовая спектрометрия, метод комбинационного рассеяния света, определения показателя преломления и оптической активности.

Вещество, через которое проходит излучение, поглощает лучи только определенной длины волны (частоты), и по закону Кирхгофа само вещество излучает только те лучи, которые оно в данных условиях поглощает. Каждый ион, атом, молекула дают характерные частоты в спектре поглощения, спектре испускания и спектре комбинационного рассеяния. Задачей спектрального анализа является определение этих характеристических частот, зная которые, можно определить качественный состав углеводородной смеси. Для этого существуют таблицы характеристических частот индивидуальных углеводородов. Для количественного анализа еще необходима оценка интенсивности излучения. [c.228]

Во многих случаях вопрос о коэффициенте поглощения значительно упрощается, так как часто можно принять, что местные коэффициенты а-), не зависят от длины волны. Тела, у которых ах не зависят от длины волны, называются серыми. В этих случаях средний коэффициент поглощения а не будет зависеть от распределения энергии в спектре, т. е. от температуры источника излучения. Следовательно, а будет зависеть только от температуры поглощающего тела (применимость закона Кирхгофа). [c.300]

Под поглощательной способностью тела обычно понимают его поглощательную способность по отношению к излучению абсолютно черного тела. В этом случае поглощательная способность любого тела определяется в долях от поглощательной способности абсолютно черного тела, принимаемой за единицу. Однако для соблюдения закона Кирхгофа поглощательная способность любого тела должна определяться при условии, что его температура равна температуре абсолютно черного источника излучения. [c.14]

В 1859 г. Кирхгоф пришел к выводу, что если температура стенок и содержимого полости поддерживается неизменной, то поток излучения в каком-либо направлении должен быть таким же, как и в любом другом направлении кроме того, он должен быть одним и тем же в любой точке источника и не зависеть от материала стенок. Если бы это было не так, то нарушался бы второй закон термодинамики. [c.18]

Для того чтобы определить вид функции /(ЯГ), необходимо было рассмотреть механизм излучения. Так как Кирхгоф показал, что природа стенок, а следовательно, и излучателя в изотермическом источнике не имеет никакого значения, можно было избрать любую разумную модель. Вин выбрал осцилляторы молекулярного размера и применил к ним законы классической электромагнитной теории. В результате он вывел уравнение [c.19]

Конечно, реальное тело не является абсолютно черным, но можно показать (закон Кирхгофа), что интенсивность излучения абсолютно черного тела является верхним пре делом для интенсивности излучения любого тела при за данной температуре. [c.315]

Коэффициент поглощения газового объема А не является физической характеристикой газа. Он зависит от спектра падающего излучения и различен при различных температурах окружающих газ стенок. Лишь при условии лучистого равновесия (температуры газа и стенок одинаковы) в соответствии с законом Кирхгофа коэффициент поглощения и коэффициент излучения газового объема равны А = е. Для коэффициента поглощения изотермического объема газа с температурой Гг по отношению к излучению абсолютно черной оболочки с температурой Тс были получены следующие эмпирические зависимости [96] для СО2 [c.203]

В природе не существует абсолютно черных тел, однако их свойства довольно точно можно воспроизвести искусственным путем. Закон Кирхгофа гласит, что тело, которое поглощает все падающее излучение, само излучает, как абсолютно черное тело. Поэтому мы можем создать подобие абсолютно черного тела в виде полости с небольшим отверстием (рис. 13-6). Стенки полости должны иметь повсюду одинаковую температуру. Луч, попадающий в полость через отверстие, отразится от стенок полости не- [c.447]

СКОЛЬКО раз, Прежде чем он снова выи рет через отверстие. Если поверхность полости обладает большой поглощательной способностью, то при каждом отражении большая часть энергии луча окажется поглощенной и поэтому после нескольких отражений вся энергия луча будет поглощена стенками. Таким образом, отверстие в Поло.м теле ведет себя подобно абсолютно черной поверхности. Уменьшая отверстие, можно воспроизвести свойства абсолютно черного тела с желаемой точностью. Если стенки полости разогреть, то согласно закону Кирхгофа отверстие будет испускать излучение абсолютно черного тела. [c.448]

По закону Кирхгофа полную поглощательную способность газа можно точно определить только для падающего излучения, испускаемого абсолютно черным телом, обладающим температурой, равной температуре газа. Выше было показано, что поглощательные способности, вычисленные при помощи уравнения (13-4), справедливы с хорошим приближением для обмена излучением газа с абсолютно черной поверхностью, пока температура таза выше температуры поверхности излучающего тела. [c.474]

В отношении тел, непрозрачных для тепловых лучей, справедливо равенство (13-2), а для теплового излучения вообще справедлив закон Кирхгофа з = А.

Выразив в последнем уравнении через поглощательную способность А , получим [c.492]

Это уравнение можно теперь написать для того случая, когда две стенки и заключенный между ними газ имеют одинаковую температуру. Из закона Кирхгофа известно, что в замкнутом пространстве с одинаковой температурой поток излучения через любую произвольную плоскость равен потоку излучения, исходящему от черной поверхности, и что чистая потеря тепла благодаря излучению стенки 1 равна нулю. [c.505]

Температуру пламени или излучающих газов чаще всего измеряют . методом обращенных спектральных лини й. Этот метод основан на законе Кирхгофа. Путе.м добавления очень малого количества натрия газ делают светящимся в желаемом месте. Если на газ смотреть при помощи спектроскопа, можно наблюдать ярко-желтые линии натрия. Поместив с одной стороны окрашенного натрием пламени абсолютно черное тело и наблюдая с помощью спектроскопа, установленного с другой стороны пламени, черное тело, будем видеть непрерывный-спектр излучения. На фоне этого спектра в случае, когда температура пламени выше температуры черного тела, линия натрия в спектре будет более светлой, чем фон и, наоборот, более темной, чем фон, если температура черного тела выше. Когда температура газа и чер.ного тела одинакова, линии исчезают, так как в этом случае 526 [c.526]

Закономерности теплового излучения (радиации) описываются законами Стефана — Больцмана, Кирхгофа и Ламберта. В невидимой инфракрасной области с длиной волн 0,8…40 мкм может передаваться большое количество теплоты. Интенсивность теплового излучения возрастает с повышением температуры тела, а при температурах выше 600 °С теплообмен между твердыми телами и газами осуществляется путем лучеиспускания. [c.721]

Полученные соотношения показывают, что отношение энергии излучения к энергии поглощения не зависит от природы тел и равно излучающей способности абсолютно черного тела при той же температуре это положение носит название закона Кирхгофа (1882 г. ). Из сопоставления формулы (VI.72) и соотношения (б) следует г = А, т. е. степень черноты тела равна его поглощательной способности. [c.307]

Коэффициент излучения. Законы Кирхгофа, Стефана-Больцмана и Вина. Ламбертовский излучатель. [c.376]

Согласно закону Кирхгофа, излучательная и поглощательная способности тел совпадают. Это, в частности, означает, что если реальное тело излучает некоторую определенную долю лучистой энергии по отношению к черному телу, то оно и поглощает такую же долю падающего на него внешнего излучения. Остальную долю (1 — ) излучения такое тело отражает в окру- [c.245]

Кирхгоф (Kir hhof) Густав Роберт (1824—1887) — немецкий химик, ин. ч.-к. Петерб. АН. Совместно с Р. Бунзеном заложил основы спектрального анализа, открыл цезий и рубидий. Ввел понятие абсолютно черного тела и открыл закон излучения, названный его именем 199, 202 и сл., 220, 232, 235, 237 Клаирот (Klaproth) Мартин Генрих (1743—1817) — немецкий химик, сторонник Лавуазье. Занимался неорганической и минералогической химией. Открыл четыре новых элемента — уран, цирконий, титан и церий получил новые данные об элементах и соединениях, уже найденных другими экспериментаторами, в том числе о те-плуре, церитовой и стронциевой землях. Прославился скрупулезной точностью своих исследований [c.283]

По закону Кирхгофа абсолютно черное тело обладает маюсимальной способностью Излучать энергию, поэтому оно является как бы эталоном, с которым можно сравнивать излучательную спосо бность д р угих тел. Оановиые законы излучения выведены для абсолютно черных тел. [c.49]

Известно, что при прохождении через вещество лучей от источника излучения. это вещество поглощает лучи только определенной длины волны (частоты), и по закону Кирхгофа само вещество излучает только те лучи, которые оно в данных условиях поглощает. В результате этого калчдая молекула, каждый атом или ион дают характерные частоты в спектре поглощения, спектре испускания или спектре комбинационного рассеяния. Спектр — это распределение энергии излучения, испускаемого (поглощаемого) телом по частотам или длинам волн. Задача качественного спектрального анализа заключается в обнаружении этих харак-тсрнстичоских частот и сравнении их с частотами индивидуальных веществ. Для количественного анализа требуется еще оценка интенсивности излучения. [c.90]

Для реальных тел, отличающихся от абсолютно черного, в соответствии с законом Кирхгофа (5.4) в расчетах надо учитывать их спектральные или интегральные поглощательные способности, которые всегда меньще единицы. По характеру излучения нечерные тела делятся на тела с селективным и серым излучением. Распределение энергии в спектре для трех типов излучателей (черного, серого и селективного) показано на рис. 5.1. Серыми излучателями являются твердые тела с шероховатыми поверхностями, а селективными — с полосовым спектром излучения-газы и непрерывным — металлы и оксиды. [c.93]

Кд+Кй)/. Слагаемое, соответствующее излучаемой энергии, при наличии локального термодинамического равновесия находят, используя закон Кирхгофа. Если термодинамическое состояние частиц или молекул можно характеризовать температурой Т, то для излучаемой энергии получим Кд/ь(х, Т). При полном термодинамическом равновесии /=/ь и потери —к 1 в точности компенсируются испусканием излучения Уравнение переноса для нерассеивающей среды в состоянии локального термодинамического равновесия нредегавим в виде [c.485]

Лучеиспускание газов. Излучение газов существенно отличается от излучения твердых тел. Одноатомные газы (Не, Аг и др.), а также многие двухатомные газы (На, Оз, N3 и т. д.) прозрачны для тепловых лучей, т. е. являются диатермичными. Вместе с тем ряд имеющих важное техническое значение многоатомных газов и паров (СОа, ЗОз, ЫИд, И, О и др.) могут поглощать лучистую энергию в определенных интервалах длин волн. В соответствии с законом Кирхгофа эти газы обладают излу-чательной способностью в тех же интервалах длин волн. Кроме того. [c.274]

Конечно, реальное тело не является абсолютно черным, но можно показать (закон Кирхгофа), что интенеивность излучения [c.234]

Резонансное поглощение. Вследствие пространственного расширения возбужденной плазмы и существующего в ней градиента температур внутри плазмы может происходить обратное поглощение спектральных линий (закон инверсии испускания и поглощения Кирхгофа). Это явление самопогло-щения наблюдается преимущественно для резонансных линий и искажает связь между интенсивностью и числом частиц. Так как во внешних более холодных зонах плазмы допплеровское уширение меньше, чем в более горячей центральной зоне, то поглощаются преимущественно центры линий. В предельном случае интенсивность центра линий становится пренебрежимо малой по сравнению с интенсивностью обоих крыльев линии (самообраш -ние линий). Линии, отличающиеся склонностью к самопоглощению и само-обращению, в спектральных атласах приводят с индексом R (от reversal — обратный ход). Наблюдая резонансное поглощение в сложном спектре, можно найти, какие линии соответствуют переходам на основной уровень. Резонансное поглощение наблюдается также в случае прохождения резонансной линии от внешнего источника излучения через диссоциированный до атомов пар соответствующего простого вещества. Интенсивность первичного светового потока ослабляется при этом соответственно уравнению [c.186]

По закону Кирхгофа, если газ поглощает лучи определенной длины волны, тс. он должен и испускать такие же лучи, причем если в каких-либо пределах длин волнь газ поглотает все лучи, то его излучение в этой части спектра является черным . [c.296]

Метод отражения. Предназиачеп для определения спектрального коэффициента направленного теплового излучения зеркально отражающих поверхностей. На основе закона Кирхгофа для непрозрачных тел [c.461]

Это название обязано своим происхождением тому, что поверхность, поглощающая асе свето1вые лучи, воаприни-мается глазом, как черная. Однако поверхность может поглотить практически, все тепловое излучение, не поглощая всех Световых лучей, и по этому на взгляд не покажется черной. Например, побеленная стена является почти черной для инфракрасного излучения. Абсолютно черных поверхностей не существует в природе, так как определенный процент падающего излучения всегда отражается, но существуют такие поверхности, которые отражают лишь очень малую часть падающего излучения. Поверхностью почти абсолютно черной для инфракрасного излучения является снег, поглощательная способность которого равна 0,985 для теплового излучения тела, температура которого не слишком высока. Хотя в природе нет абсолютно черных поверхностей, понятие о черном теле очень полезно, так как законы, управляющие его излучением, сравнительно просты и, кроме того, это понятие дает возможность доказать, что в природе не существует таких поверхностей, которые Излучают больше тепла, чем черная. Это и есть содержание закона Кирхгофа. [c.438]

Все твердые и жидкие тела отражают часть падающего теплового излучения, а поэтому соглаоно закону Кирхгофа они излучают меньше тепловой энергии, чем абсолютно черное тело. В отношении свойств теплового излучения между электрическими проводниками и непроводниками в области инфракрасных длин волн существует принципиальная разница. [c.455]

Эту величину можно вычислить, если будут известньь монохроматическая поглощательная способность и температура Гг. Для нечерного излучения величины могут значительно отличаться друг от друга. Из сравнения уравнений (13-19) и (13-20) видно, что закон Кирхгофа [см. уравнение (13-4)] неверен для полных поглощательной и излучательной способностей поверхности. Только в том случае, когда падающее излучение испускается черным телом и когда его температура равна температуре поглощающей поверхности, уравнение (13-19) становится идентичным уравнениям (13-20) и (13-21). Интегралы в вышеуказанных уравнениях обычно определяются численно или графически. Для получения поглощательной способности падающего излучения черного тела, например, надо каждую ординату кривой 1а рис. 13-5, взятой для данной температуры, умножить на соответствующую поглощательную способность (полученную, например, из рис. 13-9). Площадь, ограниченную получившейся кривой, необходимо затем разделить на площадь, ограниченную соответствующей кривой графика (рис. 13-5). Определенные таким образом В. Зибером значения поглощательной и отражательной способностей различных материалов представлены графически на рис. 13-10. Эти кривые наглядно показывают различие в поведении проводников (представленных алюминием) и непроводников. Поглощательная способность непроводников падает с повышением температуры для проводников картина обратная. Технические излучатели обладают температурой 280—2 780° К. При таком лучеиспускании поглощательная способность непроводников намного превышает поглощательную способность проводников. Солнце обладает температурой 5 500° К. При такой температуре непроводники с белой поверхностью поглощают меньше лучистой энергии, чем металлические поверхности. Лишь немногие металлы, например серебро, обладают [c.459]

Излучение газов существенно отличается от излучения твердых тел. Газы являются проницаемыми в широких пределах длин волн и обладают заметным поглощением или излучением только в отдельных частях спектра, т. е. газы имеют линейчатый спектр, поглощая лучи только определенной длины волны, в то время как твердые тела имеют сплошной спектр поглощения, поскольку поглощают все падающие на них лучи любой длины. Одно-и двухатомные газы (воздух, Nj, О,, Hj и др.) практически луче-прозрачны (диатермичны). Ряд многоатомных газов и паров могут поглощать лучистую энергию в определенных интервалах длин волн (СО2, SO2, Nh4, пары воды и др.). В соответствии с законом Кирхгофа эти газы излучают теплоту в тех же интервалах длин волн. Кроме того, в отличие от твердых тел, газы поглощают лучи всем объемом. Поэтому излучательная способность газов зависит еще и от формы сосуда, в котором они находятся, его толщины. И, наконец, излучательная способность газов нестрого подчиняется закону Стефана-Больцмана. Например, излучательная способность СО2 пропорциональна температуре в степени 3,5 (а не 4). Однако в технических расчетах принимают = 5,67 8 (7/100)» , учитывая получаемую при этом неточность в расчетах степени черноты газа е , которую находят по справочникам. [c.276]

Закон Кирхгофа устанавливает, что в точке поверхности теплового излучателя при любых температуре и длине волны спектральный коэффициент излучения для заданного направления равен спектральному коэффициенту поглощения для противоположно направленного неполяризо-ванного излучения. Практически, этот закон устанавливает простое численное соответствие между коэффициентами поглощения и излучения тел [c.186]

Сценарий открытого урока по электротехнике «Законы Кирхгофа»

Сценарий проведения открытого урока

на региональном конкурсе профессионального мастерства

«Преподаватель года-2015»

Разработчик: Кольцова Галина Александровна, преподаватель Смоленского областного государственного бюджетного профессионального образовательного учреждения «Вяземский политехнический техникум»

Дисциплина: ОП 02. Электротехника и электроника

Тема занятия: Законы Кирхгофа

Вид занятия: комбинированный урок

Цель: изучить законы Кирхгофа.

План занятия:

— организационный момент -3 мин;

— актуализация опорных знаний – 7 мин;

— объяснение нового материала – 15 мин;

— актуализация полученных знаний – 5 мин;

— формирование умений применения законов Кирхгофа – 8 мин:

— рефлексия – 5 мин;

— итог занятия – 5 мин;

— домашнее задание – 2 мин.

1 Организационный момент

Здравствуйте. Садитесь, приготовьтесь к занятию. Проверим ваше присутствие. …

(СЛАЙД : тема занятия: законы Кирхгофа)

2 Актуализация опорных знаний

Тема нашего занятия- законы Кирхгофа.

Цель нашего занятия: (СЛАЙД)

— выяснить, как можно использовать законы Кирхгофа на практике;

— как законы Кирхгофа связаны с другими фундаментальными науками;

— познакомиться с формулировками и составлением уравнений по законам Кирхгофа.

Сегодня у нас очень интересная и актуальная тема. Мы рассмотрим законы Кирхгофа, которые вам обязательно пригодятся не только в вашей деятельности, но и в повседневной жизни.

Вы — будущие электрики, и ваша деятельность будет связана с электрическими сетями, и поэтому вам необходимо знать те процессы и явления, которые в них происходят. Вы уже знакомы с законами Ома, Кулона, знаете, как возникает электрический ток, и другие явления. Законы Кирхгофа являются одними из основных законов электротехники, наряду с другими законами. Они сформулированы очень давно, но не утратили своей актуальности.

Итак, кто же такой Кирхгоф? (СЛАЙД)

Густав Роберт Кирхгоф – немецкий ученый, родился в 1824 году, член Берлинской АН, помимо того, он являлся также и членом — корреспондентом Петербургской АН, а свой законы сформулировал в возрасте 21 года.

Что же представляют собой законы Кирхгофа? ( СЛАЙД)

Зако́ны Кирхго́фа — два правила, основанные на законах сохранения заряда и энергии, которые применимы к цепям электрического тока. Какие элементы электрической цепи выделялись для их формулировки? (СЛАЙД)

Для формулировки законов Кирхгофа в электрической цепи выделяются узлы и контуры. Законов Кирхгофа два: первый рассматривает токи в узле электрической цепи, а второй – напряжения в контуре. Но для того, чтобы непосредственно перейти к изучению этих законов, нам необходимо вспомнить уже пройденное вами, а именно: что является узлом электрической цепи, ветвью, контуром, что такое электрическая схема, как обозначаются на схеме ее элементы, а также вспомнить законы Ома.

Я предлагаю следующее задание. (СЛАЙД). На слайде представлена таблица, в которой заданы понятия и их определения. Вам нужно найти соответствие между понятием и его правильным определением. Соответствия укажите стрелками. (Раздаю проверочный материал). На это задание время – 2 минуты.

А теперь проверим, правильно ли вы выполнили задание. Поднимите руку те, кто знает ответ. Отвечать можно, не вставая.

Что такое электрическая схема?

Что называется ветвью электрической цепи?

Что называется узлом электрической цепи?

Что называется контуром электрической цепи?

Ребята, все согласны с ответами? Теперь проверьте правильность соответствия на слайде , если есть ошибки, то исправьте. (СЛАЙД).

А теперь поднимите руку те, кто правильно ответил на все вопросы. Молодцы.

3 Объяснение нового материала

(СЛАЙД). Рассмотрим схему электрической цепи, представленную на экране. Кто может назвать, какие контуры и узлы она содержит? Поднимите руку, кто хочет ответить. ( Отвечают ). Ребята, правильно ли были названы узлы и контуры? Молодцы!

А теперь – первый закон Кирхгофа. (СЛАЙД)

Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю. Обратите внимание, сумма – алгебраическая, а не арифметическая, поэтому нельзя определить значение результирующего тока простым сложением значений токов. Необходимо учитывать знак тока, исходя из его направления по отношению к узлу. Для этого существует правило знаков: (СЛАЙД).

Рассмотрим узел. В нем сходятся четыре ветви, в них протекают токи, направление которых указано стрелками. Правило знаков такое: токи, входящие в узел считаются положительными, а токи, выходящие из узла – отрицательные.

С учетом этого правила запишем: (СЛАЙД)

Преобразуем это выражение (СЛАЙД).

А теперь попробуйте сами составить уравнения для узла, который представлен в следующем задании: (СЛАЙД)

Уравнения составьте по образцу, как в объяснении. Что у вас получилось? Кто хочет ответить ? (Отвечает ). У всех такой результат? Молодцы! Какой вывод можно сделать из второго уравнения? Кто может ответить? (Отвечает ).

Правильно, сумма токов, входящих в узел, равна сумме токов, выходящих из узла. Так почему же все-таки ток в узле равен нулю?

Вспомним закон сохранения заряда. Кто помнит, поднимите руку. Так,________отвечает. Правильно, молодец.

Вспомним теперь, что ток – это направленное движение зарядов. Если бы значение заряда, приносимого входящими в узел токами не совпадало бы с зарядом, уносимым токами, выходящими из узла, то закон сохранения зарядов был бы нарушен. Этим и объясняется физический смысл первого закона Кирхгофа. (СЛАЙД).

Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.

Речь шла о токах в узле, но можно привести аналогию, сравнивая ток в ветви с потоком воды в трубе. Сколько воды притекает в место соединения труб, столько же и вытекает по другим отходящим трубам. (СЛАЙД). Итак, с первым законом Кирхгофа вы познакомились, теперь перейдем ко второму закону Кирхгофа. (СЛАЙД).

Алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура:

Здесь опять говорится об алгебраической сумме составляющих уравнения, и опять действует правило знаков для напряжений и ЭДС. (СЛАЙД).

Перед записью уравнения по второму закону Кирхгофа выбирают направление обхода по замкнутому контуру (по часовой стрелке или против). Здесь так же принято правило знаков: слагаемые, в которых ток и ЭДС совпадают по направлению с выбранным направлением обхода контура, берутся со знаком плюс «+», в противном случае берутся со знаком минус «-«.

Здесь представлены источники ЭДС и резисторы, по которым протекает ток.

Вспомним, как направлена ЭДС внутри источника. Кто хочет ответить?( )

Правильно.

Видим, что в левой части рисунка знаки положительны, а в правой части – отрицательны.

Вернемся к нашей схеме. (СЛАЙД). Запишем уравнения.

для контура abcda:
-E₁-E₂ = U₁+U₂
для контура adefa:
E₂+E₃ = -U₂+U₃для контура abcdefa:
-E₁+E₃ = U₁+U₃

где

U₁ = I₁R₁

U₂ = I₂R₂

U₃ = I₃R₃

по закону Ома

Теперь давайте подумаем, что явилось основанием для таких выводов?

Вспомним, в начале урока было сказано, что зако́ны Кирхго́фа — два правила, основанные на законах сохранения заряда и энергии, которые применимы к цепям электрического тока. Вспомним закон сохранения энергии. Кто желает его озвучить? (Ответ ). Правильно. Энергетической характеристикой электрической энергии является потенциал. Для определенной точки электрической цепи он имеет постоянное значение. При перемещении по контуру потенциал изменяется, но доходя до начальной точки контура он принимает свое первоначальное значение. (СЛАЙД).

Итак, законы Кирхгофа рассмотрены, и возникает вопрос: для каких цепей эти законы справедливы? Изучая классификацию цепей на предыдущих занятиях, мы выяснили, что цепи могут быть линейными и нелинейными. Кто может вспомнить эти понятия? (Ответ ). Молодец!

Так вот: Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

С понятийной точки зрения законы Кирхгофа можно назвать правилами. Почему? Потому, что не являются фундаментальными. Вспомним, что они формировались на основании других законов – законов сохранения заряда и энергии. (СЛАЙД).

Где же нашли применение эти законы?(СЛАЙД). В расчетах электрических цепей.

И сейчас мы проверим, как вы поняли, о чем мы сегодня говорили на уроке. Для этого вам предлагается такое задание: вам нужно составить для предлагаемой в варианте схемы составить узловое уравнение и контурное. Номер узла и контур также заданы по вариантам. (СЛАЙД). Работаем парами, номер варианта соответствует номеру стола. (Раздаточный материал). Дается на решение 2 минуты.

А теперь проведем взаимопроверку. Второй стол проверяет первый, третий –второй и т д. (СЛАЙД). На слайде приведены правильные решения. У кого найдены ошибки? Какие? В чем причина?

В целом молодцы, с учетом замечаний справились с заданием.

Второе задание носит более практический характер. Вам предстоит произвести выбор сечения питающего провода, к которому подключены другие провода, нагрузка которых задана токами. При изучении проводников вы ознакомились с правилами выбора проводов по допустимому току. Примените эти знания. Провода для сравнения возьмите с медными и с алюминиевыми жилами. Выясните, для какого материала жил сечение больше, и что это значит с точки зрения надежности. Оболочка проводов выполнена из поливинилхлорида. Провод двухжильный, прокладка в трубах. (СЛАЙД). Справочные данные для выбора сечения прилагаются в таблице. Время выполнения 3 минуты.

Делаем взаимопроверку. (СЛАЙД).

Какие получились результаты? Молодцы, вы правильно справились с заданием.

Применение законов Кирхгофа также можно привести из повседневной жизни. В каждой квартире есть место, где соединяются несколько проводов. Например, ввод, где от вводного провода идет распределение электроэнергии по отдельным проводам в каждую комнату. И в каждой комнате есть распаечная коробка, иначе, клеммная коробка, от которой идет распределение для подключения розеток, светильников, и других бытовых приборов. Даже розетка, если вставить в нее, допустим, тройник , и подключить чайник, кофемолку, тостерницу, и все это включить сразу, то вот вами узел электрической цепи. Причем, если ток в проводе, питающем розетку , будет выше допустимого для него, то он может, в лучшем случае нагреться до отключения приборов, или сработает автоматический выключатель, а если он не правильно выбран, то проводка может оплавиться, что может привести к короткому замыканию.

А теперь давайте выясним, достигли ли мы тех целей, которые мы ставили в начале нашего занятия (СЛАЙД).

Цель нашего занятия: (СЛАЙД)

— выяснить, как можно использовать законы Кирхгофа на практике;

— как законы Кирхгофа связаны с другими фундаментальными законами;

— познакомиться с формулировками законов и составлением уравнений по законам Кирхгофа.

1 Где на практике применяются законы Кирхгофа?

2 С какими фундаментальными законами связаны законы Кирхгофа?

3Сформулируйте первый закон?

4 Сформулируйте второй закон?

Достигли мы цели?

Молодцы!

А теперь я хочу оценить вашу работу на уроке.

…….

Задание на дом представлено в опорном конспекте. Вам предстоит:

1. Прочитать материал по учебнику Лоторейчука Е.А. Теоретические основы электротехники страницы 41-43,

2. Доказать, что закон Ома для неразветвленной цепи является вытекающим из второго закона Кирхгофа.

Удачи вам.

Спасибо за работу на уроке.

Урок окончен. Благодарю за внимание. Досвидания.

вики: схемы: kirchoff_law [Weber’s Wiki]

Законы цепи Кирхгофа — невероятно полезный инструмент, который позволяет нам более легко вычислять ток и напряжение через некоторые элементы схемы, чем мы могли бы в противном случае.

Закон напряжения Кирхгофа (KVL)

Описание

Закон Кирхгофа по напряжению гласит, что сумма всех напряжений вокруг любого замкнутого контура в цепи должна быть 0.{n} V_k = 0 $$ где n — каждый резистор, источник напряжения, конденсатор и т. д., с которыми мы сталкиваемся в нашей петле (часто называемой «прогулкой»). Другими словами, сумма всех приростов напряжения в замкнутом контуре должна равняться сумме всех падений напряжения, или $ \ sum V_ {gain} = \ sum V_ {drop} $. Важно, чтобы ваши знаки были последовательными, иначе проблема не решится правильно. Обычно движение от минусовой к плюсовой сторонам компонента обозначается как положительное / усиление по напряжению , а от плюса к минусу — как отрицательное / падение напряжения .

Для очень простой схемы батарея / резистор это очень легко увидеть. Вы поднимаете батарею от отрицательного к положительному положению, так что это увеличение напряжения на $ V $. Затем, следуя циклу, мы уменьшаемся на $ R_sI $ вольт, если мы определим верхнюю часть резистора как положительную. Тогда наше уравнение выглядит следующим образом: $ V — R_sI = 0 $, или более часто записывается как $ V = R_sI $, что является общей формулой для напряжения на резисторе.

KVL также можно легко понять, посмотрев на простую схему с батареей и 2 резисторами, включенными параллельно.Из свойств цепей мы знаем, что падение напряжения на двух резисторах должно быть одинаковым. Мы можем доказать это с помощью KVL. Начиная с левого резистора, мы увеличиваем на $ R_1I_1 $ вольт, а затем уменьшаемся на $ R_2I_2 $ вольт (если мы определим верхнюю часть каждого резистора как положительную). Итак, окончательное уравнение $ R_1I_1 = R_2I_2 $, что мы знаем о параллельных схемах.

Примеры проблем

KVL обычно представляет собой инструмент, который вы используете вместе с другими свойствами схем, такими как комбинирование резисторов или KCL.Мы покажем пример того, как думать о решении более сложной проблемы.

Мы будем называть левую и правую петли Loop 1 и Loop 2 соответственно. Затем мы получаем $$ \ text {Цикл 1:} R_1I_1 + R_2I_2 = E_1 \ quad \ textrm {OR} \ quad 10I_1 + 4I_2 = 12 $$ $$ \ text {Цикл 2:} R_3 (I_1-I_2) -I_2R_2 = E_2 \ quad \ textrm {OR} \ quad 8 (I_1-I_2) -4I_2 = 12 $$

Мы упрощаем цикл 2 до $ 8I_1-12I_2 = 12 $ и умножаем первое уравнение на 3. Затем $$ 30I_1 + 12I_2 = 36 $$ $$ 8I_1-12I_2 = 12 $$ $$ \ text {______________} $$ $$ 38I_1 = 72 $$ Итак, $ I_1 = \ dfrac {72} {38} = 1.895A $, Путем простой подстановки получаем $ I_2 = .263A $

Это общее приложение того, как использовать KVL. При более сложных проблемах вам, скорее всего, придется использовать другие схемы помимо KVL.

Действующий закон Кирхгофа (KCL)

Описание

Текущий закон Кирхгофа — второе правило, широко используемое в электротехнике. Иногда его называют правилом соединения Кирхгофа или узловым правилом.

Закон Кирхгофа утверждает, что сумма токов, текущих в узел, равна сумме токов, вытекающих из узла.С алгебраической точки зрения это: $$ \ sum I_ {in} = \ sum I_ {out} $$

Термин узел обычно используется для описания любой ветви в цепи, где встречаются два или более элемента схемы. Важно отметить, что напряжение одинаково в любой точке одного и того же узла. Текущий закон Кирхгофа в основном является расширением сохранения электрического заряда для цепей. Поскольку заряд не может быть создан или уничтожен, узел не может спонтанно увеличивать или уменьшать ток, протекающий через него.

Применяя это правило, важно помнить, что перед током есть знак, указывающий его направление. На самом деле не имеет значения, идет ли положительный ток в узел или из него, важно то, что вы сохраняете свои знаки для тока, входящего и выходящего из узла, согласованными . Если вы хотите представить ток, входящий в узел, с положительным знаком, это нормально, если знак для всех других токов, входящих в узлы по всей цепи, положительный.Точно так же, если вы хотите представить все токи, выходящие из узла, как отрицательные, это даст правильный результат, если вы представите все другие токи, выходящие из узлов по всей цепи, с отрицательным знаком.

Примеры проблем

Первый пример, который мы сделаем, — это познакомимся с тем, как работает KCL. В следующей схеме мы извлекаем элементы схемы. Все, что имеет значение, это то, что какие-то токи входят и выходят из трех узлов в цепи.

Найдите $ i_a $ и $ i_d $:

Выглядит знакомо? Я сорвал это с учебника ECE 210. Если этот пример слишком простой, переходите к следующему. Я просто пытаюсь продемонстрировать основной принцип KCL и то, как его применять.
Первое, что вы должны сделать при использовании KCL, — это посмотреть, сколько там узлов. В этом примере есть три узла. На диаграмме помечены два узла, а третий — нет (потому что это действительно не обязательно для задачи).Но в целом вы должны найти все узлы. Обычно мы устанавливаем один узел в качестве опорного узла или земли, чтобы упростить вычисления.
Теперь, чтобы найти i _a, мы должны использовать KCL для узла 1. Посмотрев на схему, мы имеем i _a входит в узел 1, а i _b покидает узел 1.

Используя KCL, мы имеем:
$ \ sum i_ {in} = \ sum i_ {out} $
Итак:
i _a = i _b
i _a = 2 А

Чтобы найти i _d, мы смотрим на узел 3.Мы видим, что i _b входит в узел, а i _c и i _d покидает узел.
Итак, имеем: i _b = i _c + i _d
i _b — i _c = i _d
2-3 A = i _d
i _d = -1 A

В следующем примере показано, как можно найти напряжение в цепи, используя закон Кирхгофа по току.Этот метод известен как метод узлового напряжения или узловой анализ. По сути, мы собираемся использовать KCL для нескольких узлов, чтобы найти их неизвестные напряжения. При этом нам нужно будет установить ориентир или землю. Когда у нас есть M узлов, нам понадобится M-1 уравнений для решения их неизвестных напряжений.

Первое, что нужно сделать, это определить узлы в нашей цепи. В этом примере есть три узла, которые для нас удобно обозначены: $ v_0 $, $ v_1 $, $ v_2 $.

Следующим шагом является установка одного из наших узлов на землю.Неважно, какой узел вы установили на землю. Это приведет к тому, что наши напряжения будут разными, но относительные различия между $ v_0 $, $ v_1 $, $ v_2 $ не изменятся.

В этом примере я собираюсь установить $ v_0 $ в качестве нашей земли.

Теперь, когда у нас есть основания, мы можем начать применять KCL к $ v_1 $ и $ v_2 $.
Начнем с узла $ v_1 $. Глядя на узел $ v_1 $, у нас есть источник тока 6 А, обеспечивающий ток, идущий в узел, но как насчет чего-нибудь, что выходит? У нас есть два резистора, так что мы знаем?

Вспомните закон Ома:
$ V $ = $ I $$ R $
$ I = \ frac {V} {R} $

Используя это, мы можем представить токи, выходящие из узла, напряжением узла, откуда он исходит, напряжением узла, к которому он идет, и резистором, через который проходит ток.Итак, для узла $ v_1 $ у нас есть два тока, выходящие из узла. Мы можем представить ток, покидающий узел, в терминах напряжений в $ v_1 $ и $ v_2 $ и резистора, через который он проходит. Для узла $ v_1 $ имеем: $ i_ {out} = \ frac {v_1 — v_2} {3} + \ frac {v_1 — v_0} {8} $

Поскольку $ v_0 $ — это наша ссылка, напряжение на $ v_0 $ равно 0 В. Наше уравнение, представляющее токи, выходящие из узла $ v_1 $, принимает следующий вид:

$ i_ {out} = \ frac {v_1 — v_2} {3} + \ frac {v_1 — 0} {8}
$

Используя KCL на узле $ v_1 $, мы знаем, что сумма входящих токов равна сумме токов, выходящих из узла.Следовательно, наше узловое уравнение для $ v_1 $:

$ \ frac {v_1 — v_2} {3} + \ frac {v_1 — 0} {8} = 6 $

Умножив обе части на 24, мы можем избавиться от знаменателя:

$ 8v_1 — 8v_2 + 3v_1 = 144 $
$ 11v_1 — 8v_2 = 144 $

Для узла $ v_2 $ мы будем применять те же правила и использовать KCL. С учетом всего этого наше узловое уравнение становится:

$ \ frac {v_2 — v_1} {3} + \ frac {v_2 — 0} {2} +2 = 0 $

Когда мы избавляемся от знаменателей путем умножения на 6, наше узловое уравнение становится:

$ -2v_1 + 5v_2 + 12 = 0 $

Теперь, когда у нас есть два уравнения, мы можем решить два неизвестных напряжения для $ v_1 $ и $ v_2 $.
Наш окончательный ответ для узлов $ v_1 $ и $ v_2 $ оказывается:

$ v_1 = 16 В $
$ v_2 = 4 В $

Прочие ресурсы

Законов Кирхгофа — MyRank

Законы Кирхгофа

В 1845 году немецкий физик Густав Кирхгоф разработал пару или свод правил или законов, касающихся сохранения тока и энергии в электрических цепях.Эти два правила широко известны как Законы Кирхгофа с одним из законов Кирхгофа, касающихся тока, протекающего по замкнутой цепи, Закон Кирхгофа (KCL) , в то время как другой закон касается источников напряжения, присутствующих в замкнутой цепи. , Закон напряжения Кирхгофа, (KVL) .

Первый закон Кирхгофа — Действующий закон, (KCL)

Текущий закон Кирхгофа или KCL гласит, что «полный ток или заряд, входящий в соединение или узел, в точности равен заряду, выходящему из узла, поскольку ему некуда идти, кроме как уйти, поскольку заряд не теряется в пределах узел».Другими словами, алгебраическая сумма ВСЕХ токов, входящих и выходящих из узла, должна быть равна нулю, I _(выход) + I _(вход) = 0. Эта идея Кирхгофа широко известна как Сохранение заряда. .

Здесь 3 тока, входящие в узел, I ₁, I ₂ и I ₃, все имеют положительное значение, а 2 тока, выходящие из узла, I ₄ и I ₅ имеют отрицательное значение. . Тогда это означает, что мы также можем переписать уравнение как,

I ₁ + I ₂ + I ₃ — I ₄ — I ₅ = 0

Термин Узел в электрической цепи обычно относится к соединению или стыку двух или более токоведущих путей или элементов, таких как кабели и компоненты.Также для протекания тока в узел или из него должен существовать замкнутый контур. Мы можем использовать закон Кирхгофа при анализе параллельных цепей.

Второй закон Кирхгофа — Закон напряжения, (KVL)

Закон Кирхгофа о напряжении или KVL гласит, что «в любой сети с замкнутым контуром полное напряжение вокруг контура равно сумме всех падений напряжения в том же контуре» , которое также равно нулю. Другими словами, алгебраическая сумма всех напряжений в контуре должна быть равна нулю.Эта идея Кирхгофа известна как Сохранение энергии .

Запуск в любой точке цикла, продолжение в том же направлении , отмечая направление всех падений напряжения, положительных или отрицательных, и возвращаясь к той же начальной точке. Важно поддерживать одно и то же направление по часовой стрелке или против часовой стрелки, иначе итоговая сумма напряжений не будет равна нулю. Мы можем использовать закон напряжения Кирхгофа при анализе последовательных цепей.

При анализе цепей постоянного или переменного тока с использованием Законов Кирхгофа для цепей используется ряд определений и терминологии для описания частей анализируемой цепи, таких как: узел, пути, ветви, петли и сети. Эти термины часто используются в схемотехническом анализе, поэтому их важно понимать.

Закон Кирхгофа о цепях — Electronics-Lab.com

Введение

В этом руководстве мы представляем один из самых фундаментальных и важных наборов законов для электрических цепей.Эти законы получили название и были установлены немецким врачом Густавом Кирхгофом в 1845 году.

Как и многие другие физические законы, законы Кирхгофа (KCL) относительно легко понять и вытекают из наблюдения сохранения энергии , который, вероятно, является одним из старейших и наиболее фундаментальных принципов физики.

Тем не менее, KCL могут быть простыми и доступными для понимания, они остаются основным инструментом для анализа схем и до сих пор широко используются.

KCL состоит из двух различных законов относительно физических величин, определяющих энергию в электрической цепи: тока, и напряжения. Далее мы отдельно представляем в двух разделах, текущие законы Кирхгофа и законы напряжения .

Перед этими разделами стоит представить в первом разделе структуру, в которой используются законы KCL, и множество определений, связанных с этим принципом.

В третьем разделе показан пример того, как применить KCL к реальной схеме и решить проблему с неизвестными параметрами.

Наконец, в последнем разделе кратко представлены ограничения KCL для некоторых частных случаев.

Структура и определения

Основа для применения законов Кирхгофа — это электрических цепей , которые состоят из источника питания или генератора с обоими полюсами, соединенными с промежуточным звеном из компонентов в конфигурации с замкнутым контуром . Электрические цепи нарисованы в соответствии с моделью с сосредоточенными элементами , которая предполагает, что компоненты являются идеальными, и соответствующее представление показано на Рис. 1 ниже:

Рис.1: Модель электрической цепи с сосредоточенными элементами
Мы можем дать некоторые конкретные детали относительно топологии схем.Прямые линии представляют собой идеальные соединения / провода между различными элементами цепей, что означает, что они не проявляют резистивного или реактивного поведения, следовательно, отсутствуют явления потери мощности или фазового сдвига.
Источник обеспечивает схему энергией, которая состоит из сигналов напряжения и тока (постоянного или переменного тока). Компоненты пассивные , они состоят из комбинации резистора, конденсатора и катушки индуктивности. Они могут быть подключены параллельно, как в Рисунок 1 , или последовательно.Активные компоненты, такие как усилители, не рассматриваются в этом руководстве, поскольку с ними связан внешний источник питания. Группа компонентов, соединенных на обоих выводах проводами, называется ответвлением .
Два важных топологических определения важны для того, чтобы впоследствии полностью понять законы Кирхгофа: узлов и петли . Узлы представляют собой стыки между ветвями, и они выделены на рис. 1 синими кружками.Петли выделены красными круговыми стрелками на предыдущем рисунке и представляют собой замкнутый путь ветвей.
Действующий закон Кирхгофа
Текущий закон также известен как узловой или переходный закон и утверждает, что алгебраическая сумма токов, встречающихся в узле, равна нулю . Простой пример можно проиллюстрировать узлом, соединяющим три ветви:
рис. 2: Узловое соединение трех ветвей
Таким образом, закон гласит, что сумма токов, входящих в узел, равна току (токам) на выходе из соединения.В нашем примере это предложение математически переводится в I ₁ + I ₂ = I ₃ или I ₁ + I ₂ -I ₃ = 0 , текущий I ₃ отрицательный, потому что он выходит из узла.
В общем случае узловое соединение N ветвей, токи которых обозначены как I ₁, I ₂,…, I _N, удовлетворяет следующему Уравнению 1 :
уравнение 1: Текущий закон Кирхгофа
Знаковая функция sign равна +1 , если текущий I _k входит в узел, или -1 , если он существует.
Узловой закон прямо записан из наблюдения, что заряд в замкнутой системе инвариантен. Это предположение также известно как принцип сохранения заряда .
В физике принцип — это наблюдение, которое ни один опыт не подтвердил, но не продемонстрировал; это эквивалент постулатов в математике.
Закон Кирхгофа по напряжению
Закон напряжения также известен как правило петли , он очень похож на узловое правило, но применяется к петлям, а не к узлам. Этот второй закон гласит, что алгебраическая сумма напряжений в контуре цепи равна нулю. Простой пример можно проиллюстрировать с источником постоянного тока, питающим последовательный RC-фильтр:
рис. 3: Петля с тремя различными напряжениями
Знак напряжений определяется направлением стрелок, обычно источник считается положительным, так что стрелки по часовой стрелке являются положительными, а против часовой стрелки — отрицательными. Таким образом, закон Кирхгофа утверждает, что В _S = V _R + V _C или В _S -V _R -V _C = 0 .
Для контура с генерацией N и падением напряжений V ₁, V ₂,…, V _N, Уравнение 2 выполняется:
уравнение 2: закон напряжения Кирхгофа
Знаковая функция sgn равна +1 , когда генерируется напряжение (источник в нашем примере), или -1 , когда наблюдается падение (с пассивными компонентами в Рисунок 3 ).
Заявление KCL
В этом разделе мы показываем процесс решения типичных проблем, которые можно решить с помощью KCL.Рассмотрим три источника S ₁, S ₂ и S ₃, подключенных к резисторам R ₁, R ₂ и R ₃ в конфигурации, показанной на Рисунок 4 :
рис 4: Пример конфигурации схемы
Источники постоянного тока идеальны, что означает отсутствие внутреннего сопротивления. Возьмем S ₁ = 4 В, S ₂ = 3 В, S ₃ = 10 В и R ₁ = 3 Ом, R ₂ = 2 Ом, R ₃ = 1 Ом. .
Из действующего закона Кирхгофа мы можем записать следующие равенства для узлов 1 и 2:
Узел 1: I ₁ = I ₂ + I ₃
Узел 2: I ₂ + I ₃ = I ₁, что аналогично уравнению узла 1
Из закона напряжения Кирхгофа запишем равенства для контуров 1 и 2:
Петля 1: S ₁ = S ₂ + R ₂ × I ₂ + R ₁ × I ₁
Петля 2: S ₂ + R ₂ × I ₂ = S ₃ + R ₃ × I ₃
Мы можем по-разному записать эти уравнения, чтобы получить следующую систему из 3 уравнений с 3 неизвестными параметрами: I ₁, I ₂ и I ₃:
уравнение 3: Линейная система KCL уравнения
Эту систему можно решить с помощью метода исключения, который состоит из замены I ₁ на I ₂ + I ₃ во второй строке (L2) и исключения члена I ₃ путем сложения R ₃ × L2 + R ₁ × L3.
Мы непосредственно находим I ₂ = 4,2 A , затем мы можем найти I ₃, заменяя I ₂ в L3, что дает I ₃ = 1,4 A и, наконец, мы получаем I ₁ = I ₂ + I ₃ = 5,6 A .
Пределы KCL
В первом разделе мы видели структуру, в которой применяется KCL, но есть и другие, более тонкие условия, которые схема должна соблюдать. В этом разделе мы кратко выделим эти дополнительные условия для действия KCL.
Первое условие известно как квазистатическое приближение и состоит в том, что время распространения сигнала должно быть незначительным по сравнению с периодом сигнала, это дает условие на размеры схемы.
Например, рассмотрим сигнал переменного тока 200 кГц (T = 5 мкс), если приемник расположен в цепи на D = 10 см , время распространения будет Δt = D / c = 0,33 нс с c — скорость света. В этом случае Δt << T, квазистатическое приближение действительно и условие применения KCL соблюдается.
Однако, если приемник расположен вместо D = 1 км , время распространения становится Δt = 3,3 мкс и неравенство Δt << T не соблюдается, поэтому приближение недействительно и KCL не может применяться к цепи. .
В квазистатическом приближении считается, что любое изменение источника немедленно распространяется в любой точке цепи, что позволяет избежать запаздывающих эффектов, которые могут сделать недействительным KCL.
Это утверждение может быть продемонстрировано с помощью уравнения Максвелла-Ампера , в котором переменный член может быть исключен, когда квазистатическое приближение действительно, текущий закон Кирхгофа может быть продемонстрирован с помощью теоремы Грина-Остроградского .
Еще одно общее условие, придающее силу KCL, состоит в том, чтобы сказать, что изменениями магнитного потока в контурах цепи должны быть пренебрежимо малы. Согласно закону индукции изменения магнитного потока создают в цепи индуцированные токи и, следовательно, индуцированные напряжения.
Изменение магнитного потока делает недействительным правило петли, вводя новый термин напряжения, который объясняется не компонентами или топологией схемы, а внешним источником.
Заключение
KCL — это фундаментальные законы электроники, которые могут быть применены к электрическим схемам, состоящим из петель и узлов . Эти топологические определения наряду с другими представлены в первом разделе статьи, в котором описывается структура, в которой применяется KCL.
Законы Кирхгофа состоят из закона тока и напряжения, который отражает принцип сохранения энергии в цепи.
Текущий закон учитывает сохранение заряда , он утверждает, что алгебраическая сумма токов в узле равна нулю.Закон напряжения гласит, что алгебраическая сумма напряжений в контуре равна нулю.
В следующем разделе показано, что использование обоих этих законов может решить типичные электронные проблемы путем решения систем линейных уравнений.
Наконец, мы кратко представляем в последнем разделе, что некоторые тонкие условия относительно размеров цепи и существования внешнего магнитного потока должны быть соблюдены для того, чтобы KCL был действительным.
Законы Кирхгофа и спектроскопия | Астрономия 801: планеты, звезды, галактики и Вселенная
Дополнительная литература с www.Astronomynotes.com
Изучение излучения абсолютно черного тела — полезное упражнение. Однако я несколько раз подчеркивал, что излучение абсолютно черного тела испускается только «идеальным» или «идеальным» излучателем. На самом деле, немногие объекты излучают в точности спектр абсолютно черного тела. Например, рассмотрим два спектра, на которые вы смотрели на предыдущей странице: солнце и голубую отставшую звезду. Напомним, что излучение абсолютно черного тела непрерывно, без перерывов. Если вы посмотрите на два спектра звезд, вы увидите черные полосы на изображении спектра Солнца и области на графике, где интенсивность падает до нуля или почти равна нулю в спектре синего отставшего.Эти промежутки в спектре, где нет испускаемого света, называются линиями поглощения . Было обнаружено, что другие астрономические источники (а также источники света, которые вы можете проверить в лаборатории) создают спектры, которые показывают небольшую интенсивность на большинстве длин волн, но на нескольких точных длинах волн, где наблюдается большая интенсивность. Их называют эмиссионных линий.
На заре спектроскопии эксперименты показали, что существует три основных типа спектров. Различия в этих спектрах и описание того, как их создавать, были резюмированы в трех законах спектроскопии Кирхгофа:
Светящееся твердое вещество, жидкость или плотный газ излучает свет всех длин волн.
Горячий газ низкой плотности, видимый на более холодном фоне, излучает спектр ЯРКОЙ ЛИНИИ или ЛИНИИ ИЗЛУЧЕНИЯ.
Холодный газ низкой плотности перед более горячим источником непрерывного спектра создает спектр ТЕМНОЙ ЛИНИИ или ЛИНИИ ПОГЛОЩЕНИЯ.
Вы также можете резюмировать законы Кирхгофа в диаграмме, например, этой:
Рисунок 3.6: Три условия, которые приводят к трем законам Кирхгофа для создания непрерывного спектра поглощения и излучения.
Кредит: Астрономия и астрофизика штата Пенсильвания
Как и законы движения планет Кеплера, это эмпирические законы. То есть они были сформулированы на основе экспериментов. Чтобы понять происхождение линий поглощения и излучения, а также спектров, которые содержат эти линии, нам нужно сначала уделить время атомной физике. В частности, мы рассмотрим модель атома Бора.
Всякий раз, когда вы изучаете свет от астрономического объекта, помните, что вам нужно учитывать три вещи:
излучение света источником,
процессов, которые влияют на свет во время его движения от источника к наблюдателю, а
процесс обнаружения света наблюдателем.
Мы наблюдаем линии поглощения, когда свет от фонового источника проходит через холодный газ. Каким-то образом именно газ вызывает появление линий поглощения в том, что в противном случае казалось бы непрерывным спектром. Итак, что происходит внутри газа?
Облако газа состоит из атомов, которые являются мельчайшими компонентами элемента, сохраняющими все свойства этого элемента. Типичное облако газа в космосе, вероятно, будет содержать много водорода и гелия и следовые количества более тяжелых элементов, таких как кислород, азот, углерод и, возможно, железо.Атомы внутри газового облака состоят из ядра положительно заряженных протонов и нейтронов, которые не имеют заряда. Ядро окружают один или несколько отрицательно заряженных электронов. Вот созданное мной мультяшное изображение атома гелия:
Рисунок 3.7: Атом гелия с нейтронами, протонами и электронами, помеченными как
Кредит: Астрономия и астрофизика штата Пенсильвания
Частицы с меткой n — нейтроны, p — протоны и e — электроны.
Возвращаясь к атомной физике и спектроскопии, это электронов , которые являются основной причиной линий поглощения, которые мы видим в звездных спектрах.Бор предложил простую модель атомов, которая требовала, чтобы электроны занимали «орбиты» вокруг ядра. Ключевой частью его модели является понимание того, что электроны могут существовать на этих конкретных орбитах, а не между ними. С каждой орбитой связана определенная энергия — то есть, когда электрон находится на определенной орбите, он имеет определенное количество энергии. Таким образом, орбиты можно также обозначать как уровней энергии . Если электрон поглощает в точности разницу в энергии между уровнем, на котором он находится, и любым более высоким уровнем, он может перейти на более высокий уровень.Как только электрон окажется на более высоком уровне, он в конечном итоге упадет обратно на более низкий уровень (либо все сразу, либо сразу до уровня 1, либо серией шагов вниз до уровня 1), и каждый раз он упадет с одного уровня. к более низкому, он испускает фотон, который несет в точности количество энергии, равное разнице в энергии между начальным и конечным энергетическими уровнями электрона. Это показано ниже. На верхней панели электроны падают с более высоких уровней на более низкие уровни и излучают фотоны.На нижней панели электроны поглощают фотоны, заставляя их прыгать на более высокие уровни со своих более низких уровней.
Рис. 3.8: Уровни энергии электронов в модели Бора и их соответствие длинам волн линии поглощения или излучения в спектре объекта.
Кредит: Астрономия и астрофизика штата Пенсильвания
Напомним, что энергия, переносимая фотоном, определяется выражением E = hν. Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации». . Итак, если энергия электрона на уровне 2 задается E2, это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». а энергия, соответствующая уровню 1, задается E1. Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации»., то разница в энергии между этими уровнями может быть показана как ΔE = E2 — E1 Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». . Итак, если электрон находится в E2, это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». уровень энергии и падает до E1 Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации». уровень энергии, он будет излучать фотон с частотой, заданной как:
E = hν Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». ,
так, ν = E / h Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». ,
и в данном случае E = ΔE = E2 — E1 Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации».
дает нам ν = (E2 — E1) / h Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».
На верхней панели вверху изображен электрон, опускающийся с уровня 2 на уровень 1 и испускающий фотон с энергией, равной разнице энергий между этими двумя уровнями. Итак, астроном, изучающий свет этого газового облака, увидит в спектре этого облака эмиссионную линию желтого цвета, обозначенную цифрой «2 — 1» в спектре справа.
Давайте свяжем идею движения электронов между уровнями энергии с наблюдаемыми спектрами астрономических объектов.
Спектры поглощения
Непрерывный источник света излучает фотоны с разными энергиями. Когда эти фотоны проходят через облако (или облака) газа на переднем плане, они могут столкнуться с атомами этого газа, каждый из которых имеет набор электронов с определенными уровнями энергии. Те фотоны, которые имеют именно ту энергию, которая позволяет электрону в атоме газа подняться на более высокий уровень, могут быть поглощены.Все фотоны, у которых нет точного количества энергии для возбуждения электрона, проходят через облако, не поглощаясь. Таким образом, то, что мы видим после того, как свет от черного тела (то есть непрерывного источника) проходит через облако газа, — это то, что большинство фотонов в узком диапазоне частот (или цвета) не попадают в него, что приводит к разрывам, или линии поглощения, в противном случае непрерывный спектр источника света. Все линии поглощения точно соответствуют длинам волн или частотам, которые определяются разностью энергий между энергетическими уровнями электронов в атомах, составляющих облако.Итак, снова обращаясь к диаграмме уровней энергии выше, когда электрон переходит с уровня 1 на уровень 2, поглощая фотон, астроном будет наблюдать линию поглощения на частоте, которая соответствует этой 1-2 разнице уровней энергии.
Попробуй!
На веб-сайте интерактивного моделирования PhET есть моделирование, позволяющее исследовать модели атома водорода.
Перейти к моделированию атома водорода.
Щелкните кнопку воспроизведения в верхней части изображения моделирования, чтобы начать моделирование.(Примечание: ваш компьютер / браузер может потребовать от вас загрузить его, а не воспроизводить в браузере).
При моделировании используйте селектор в верхнем левом углу, чтобы выбрать «Прогноз».
Выберите «Bohr».
Включите питание электронной пушки (нажмите красную кнопку на рисунке) и наблюдайте за симуляцией.
Что происходит с фотонами, у которых нет правильной энергии? Что происходит с фотонами, которые имеют правильную энергию, когда они сталкиваются с электроном? Что происходит, когда электрон падает на более низкий энергетический уровень?
Спектры излучения
Если у вас есть газовое облако низкой плотности, которое нагревается каким-либо процессом, электроны в атомах в этом газовом облаке не будут находиться на самом низком уровне — они будут на более высоких уровнях.Таким образом, когда они спускаются вниз до уровня земли, они будут излучать фотоны с точными частотами, что приводит к появлению линий излучения. Неоновые огни, которые вы видите в витринах магазинов, содержат газ низкой плотности, и электроны возбуждаются, когда вы пропускаете ток через лампочку. По мере того, как электроны спускаются вниз до основного уровня (уровень 1), они излучают линии излучения в красной части спектра. Вот изображение лампы, содержащей неон, и спектр, который она создает, когда вы пропускаете свет через призму:
Рисунок 3.9: Свет от неоновой лампы
Рисунок 3.10: Спектр неоновой лампы
Несколько последствий
Наконец, давайте закончим обсуждение спектров несколькими следствиями из приведенной выше физики:
Уровни энергии электронов в атоме подобны отпечаткам пальцев — нет двух элементов с одинаковым набором уровней энергии, поэтому атомы двух элементов не образуют одинаковый рисунок линий поглощения или излучения. Это означает, что если мы наблюдаем линии поглощения, вызванные облаком газа, мы можем сказать, какие элементы составляют это облако, по длинам волн или частотам линий поглощения.Существуют таблицы, в которых перечислены все известные длины волн линий от конкретного элемента, измеренные в лаборатории.
Звезда создает линейчатый спектр поглощения, потому что непрерывный спектр, излучаемый плотным непрозрачным газом, составляющим большую часть звезды, проходит через более холодную и прозрачную атмосферу звезды.
Электроны в газовых облаках, которые создают линии поглощения, также должны в конечном итоге упасть обратно на уровень земли, поэтому они также должны излучать фотоны с точно такими же длинами волн, что и линии поглощения.Они делают это, но причина, по которой мы все еще наблюдаем линии поглощения, заключается в том, что повторно испускаемые фотоны могут излучаться в любом направлении, в то время как поглощение происходит только на нашем луче зрения.
Когда вы наблюдаете спектр поглощения астрономического объекта, любое облако газа между нами и объектом может поглощать свет. Итак, в типичной звезде вы видите линии поглощения от атмосферы объекта, вы можете видеть линии поглощения, вызванные промежуточными газовыми облаками между нами и этой звездой, и, наконец, атмосфера Земли также будет поглощать часть света звезды.
ошибок и их устранение при обмене безопасными ключами Кирхгофа-Лоу-Джонсона-шума
1.1 Безопасный обмен ключами KLJN
В сегодняшнюю эпоху сетевая безопасность стала одним из наиболее важных аспектов повседневной жизни. Будь то крупная, маленькая, частная или государственная организация, очень важно сосредоточиться на безопасности, особенно когда отправляемые, получаемые или хранимые данные содержат конфиденциальную, конфиденциальную информацию, такую как личная информация.
При защищенной связи на основе закрытого ключа две взаимодействующие стороны (Алиса и Боб) генерируют и совместно используют защищенный ключ, который обычно представлен случайной битовой последовательностью. Важно отметить, что безопасность связи не может быть лучше, чем безопасность обмена ключом, который он использует. Во время этого обмена ключами перехватчик (часто называемый Евой) постоянно отслеживает соответствующие данные. В сегодняшних безопасных коммуникациях на основе Интернета обычно используется программная генерация и распространение ключей.Однако в этом методе вся информация о секретном ключе является общедоступной [1], и доступ Евы к этой информации ограничен только ее вычислительной мощностью. Другими словами, этот метод обеспечивает только условный уровень безопасности ( в вычислительном отношении ) , который представляет безопасность без учета будущих требований [2] — [4]. Это означает, что с достаточно увеличенной вычислительной мощностью или эффективным будущим алгоритмом Ева сможет взломать ключ, и вся информация в сообщении станет доступной.
Таким образом, ученые и исследователи работают над изучением правильных законов физики, чтобы найти новые схемы обмена ключами, в которых информация, которую может измерить Ева, равна нулю. В частности, они изучали схемы обмена ключами, в которых объем информации, извлекаемой Евой, не зависит от ее вычислительной мощности. Когда меры безопасности определены с учетом максимальных возможностей Евы (ограниченных только законами физики и условиями работы протоколов), это обозначается как безусловная безопасность , термин, который часто заменяется на теоретическая безопасность информации [1].Теоретическая (безусловная) безопасность информации может быть совершенной , если Ева не может извлечь никакой информации, или несовершенной , если Ева может извлечь только небольшой, общепринятый объем информации. (Это разрешено для практических целей, потому что эта небольшая утечка информации может быть дополнительно уменьшена за счет усиления конфиденциальности, если точность обмена ключами между Алисой и Бобом достаточно высока.) Эти термины часто неправильно понимаются, и это частая ошибка в утверждениях. злоупотреблять безусловной безопасностью и тем самым подразумевать безупречную безопасность .
Важно подчеркнуть, что цель создания / распространения абсолютно безопасного ключа подобна приближающейся бесконечности. Совершенно безопасное распределение ключей конечной длины никогда не может быть достигнуто в реальной физической системе за конечный промежуток времени. Однако одна из целей физической информатики — найти схемы, которые могут произвольно приблизиться (но никогда не достичь) совершенной безопасности [2].
Самая ранняя и самая известная схема, основанная на законах физики, которая заявляет о безусловной безопасности, — это квантовое распределение ключей (QKD) [5].Теоретическая информационная безопасность этой схемы обычно основана на предположении, что действия Евы будут нарушать работу системы (в соответствии с теорией квантовых измерений и теоремой о запрете клонирования) и вызывать ошибки, которые обнаруживают подслушивание. Обратите внимание, что есть несколько многообещающих инициатив, не связанных с КРК, которые включают новые типы квантовых эффектов [6], [7].
На фундаментальной стороне продолжаются споры между экспертами о достижимых уровнях безопасности в QKD [8] — [12].С практической точки зрения с этой схемой связаны некоторые проблемы, такие как диапазон, цена и надежность. Более того, интересно отметить, что в последнее время все коммерческие устройства QKD и многие лабораторные устройства были взломаны с помощью квантового взлома [13] — [27]. Хотя большинство из этих практических недостатков кажутся недостатками конструкции, а не фундаментальными проблемами безопасности; они по-прежнему означают, что текущая практическая QKD еще имеет условную безопасность: условия таковы, что Ева недостаточно осведомлена или у нее нет надлежащего оборудования, чтобы использовать недостатки конструкции для атаки.Впечатляющий список статей [13] — [27] показывает, что на данный момент существует достаточно знающих Евы с достаточными ресурсами.
До 2005 года QKD была единственной принятой схемой, которая могла предложить обмен ключами с теоретической информационной безопасностью в идеальной (математической) ситуации. В 2005 году было введено безопасное распределение ключей Кирхгофа-Лоу-Джонсона (KLJN) [28], где вместо правильного выражения «совершенно безопасный» использовался термин «полностью безопасный». Позже (2006 г.) была построена и продемонстрирована система KLJN [29].KLJN также является схемой обмена ключами с теоретической информационной безопасностью [3], и она основана на законе петли Кирхгофа квазистатической электродинамики и теореме флуктуации и диссипации статистической физики. Его защита от пассивных атак в конечном итоге основана на втором законе термодинамики [28], что означает, что взломать обмен ключами так же сложно, как построить вечный двигатель (второго типа). В практических условиях он использует усиленный (генерируемый электроникой) шум Джонсона с высокой шумовой температурой, где квазистатические и термодинамические аспекты должны имитироваться как можно точнее, чтобы приблизиться к идеальной безопасности.
Сначала мы дадим краткое описание (основанное на [2] — [4], [28]) принципа работы системы KLJN. Основная система KLJN без схемы защиты от инвазивных атак и уязвимостей, представленных неидеальными элементами здания, показана на следующем рисунке.
Основной канал KLJN, см., Представляет собой проводную линию, к которой Алиса и Боб подключают случайно выбранные резисторы и, соответственно, где. представляет младший (0) бит и старший (1) бит соответственно [28].В начале каждого периода обмена битами BEP (также называемый периодом тактовой частоты KLJN) Алиса и Боб, которые обладают идентичными парами резисторов и случайным образом выбирают и подключают один из этих резисторов. Генераторы шума Гаусса напряжения представляют либо шумы Джонсона резисторов, либо внешние генераторы шума, дающие ограниченный по полосе белый шум с широко известной полосой пропускания и эффективной шумовой температурой [2], [3], [28], [29]. Напряжения шума Алисы и Боба равны и, соответственно, где и дают напряжение шума канала между проводной линией и землей и ток шума канала в проводе.
Алиса и Боб измеряют среднеквадратичные амплитуды напряжения и / или тока шума, то есть и / или в пределах BEP в линии. Таким образом, применяя формулу шума Джонсона и петлевой закон Кирхгофа, теоретический прогноз состоит в том, что среднеквадратичные шумовое напряжение и ток (т.е. интеграл соответствующих спектральных плотностей мощности [2], [28]) для заданной ширины полосы шума канала и температуры представлены следующим образом:
(1)
где представляет идеальное (бесконечное время) среднее значение по времени, — спектр плотности мощности шума напряжения канала, — спектр плотности мощности шума тока канала канала, — постоянная Больцмана, и.
В идеале, сравнивая результат точного измерения среднеквадратичного напряжения или тока канала с соответствующим теоретическим значением в формуле. 1 полное сопротивление контура будет общеизвестным. Алиса и Боб знают свои собственные значения резисторов, и поэтому они могут вывести это значение сопротивления из сопротивления контура, чтобы узнать сопротивление на другом конце. Следовательно, они могут отфильтровать фактическое значение бит на другой стороне провода.
Если Алиса и Боб используют одинаковые значения сопротивления, Ева также может распознать эту битовую ситуацию, потому что общее сопротивление является либо самым низким, либо самым высоким значением из трех возможных значений сопротивления.Таким образом, ситуации с резисторами (,) и (,) представляют собой небезопасный обмен битами, поскольку Ева также может узнать значения резисторов, их точное расположение и состояние битов. С другой стороны, случаи (,) и (,), которые дают идентичный среднеквадратичный шум в строке, представляют ситуацию безопасного обмена битами, потому что Ева не может найти резисторы, поэтому она не может решить, есть ли Алиса (и Bob) имеет бит 1 или 0. Эта безопасность обеспечивается Вторым законом термодинамики, который запрещает любую информацию о направлении, касающуюся резисторов с двух сторон в тепловом равновесии [2], [28].Другими словами, извлечь эти защищенные биты Евой так же сложно, как построить вечный двигатель (второго типа). В заключение, в среднем 50% битов могут быть сохранены, потому что они безопасны. Остальные 50% битов, представляющих небезопасные ситуации, отбрасываются протоколом.
Примечание: биты, которыми безопасно обмениваются, имеют противоположные значения у Алисы и Боба, поэтому они должны публично договориться, какой из них будет инвертировать обмененный бит, чтобы иметь одинаковые ключи на обоих концах.
Полностью вооруженная система KLJN защищена даже от атаки «человек посередине» [30]. Одним из важных потенциальных приложений [32] является интеграция системы KLJN на компьютерных микросхемах и обеспечение безусловной безопасности в компьютерах и высокозащищенных инструментах, где процессоры, жесткие диски, клавиатуры и т. Д. Будут защищать свою связь с помощью ключей, совместно используемых через KLJN. протокол. Другое возможное применение — в гораздо большем масштабе — создание сети систем KLJN с использованием уже существующих проводных линий [4], [33], [34], в частности, реализация и безоговорочно безопасная «умная сеть» [4] ( развитая сеть распределения электроэнергии).
1.2 Известные типы атак
Ниже, на основе [2], мы кратко рассмотрим все опубликованные типы атак. Из-за простоты системы KLJN доступно очень мало типов атак. Метод сравнения мгновенных значений напряжения и тока на двух концах и отбрасывание рискованных битов 01/10 [28], [30], [31] (не обсуждаемых здесь подробно) защищает от всех этих типов атак. Но даже без отбрасывания рискованных битов пассивные атаки Евы, использующие неидеальности, страдают от слабого отношения сигнал / шум из-за плохой статистики, см. Ниже.
Практически неважный, но теоретически допустимый тип атаки был продемонстрирован Хао [36], который указал, что неидеальная ситуация с разными температурами может разделить уровни шума 01 и 10 битных ситуаций, таким образом, они могут выдать некоторую информацию. Еве. В ответе Киша [37] было указано, что практические проблемы точности не ставят под сомнение концептуальную безопасность идеальных схем, и было подсчитано, что даже в практических ситуациях утечка информации из-за этой атаки незначительна.Позже это было показано в экспериментальной статье Mingesz et al. [29], что скромная 14-битная точность температур (генераторы шума) практически не позволяют Еве извлекать любую полезную информацию (с утечкой информации менее 10 ⁻¹⁰), используя атаку Хао.
Scheuer и Yariv [38] проанализировали случай ненулевого сопротивления провода, когда среднеквадратичные напряжения различны на двух концах в случае ситуаций 01 и 10 битов. Однако их расчет был неправильным, включая физические единицы некоторых основных результатов.Киш и Шойер [39] провели новые правильные расчеты и показали, что реальный эффект примерно в 1000 раз слабее, чем предсказывали Шойер и Ярив. Ранее Киш указывал [37] в своем ответе на [36], что при аналогичных условиях статистика Евы была очень плохой, а извлеченная информация была практически ничтожной даже без защиты от отбрасывания рискованных битов. Это утверждение было экспериментально подтверждено Mingesz et al. [29], которые показали, что при тактовом периоде, в 50 раз превышающем время корреляции шума,, и сопротивления проводов, утечка информации обмениваемых сырых битов на Еву была равна 0.19%, в то время как верность между Алисой и Бобом составляла 99,98%. Эти результаты показывают, что обмен ключами имеет отличную точность даже без исправления ошибок и что безопасность может быть достаточно хорошей даже без потери рискованных битов 01/10 (после сравнения тока / напряжения на двух концах) и без усиления конфиденциальности [29] .
Лю [41] использовал симулятор кабеля для оценки влияния задержек и отражений на безопасность. Он получил удивительные результаты: с экспериментальными параметрами [6] Ева успешно угадывала 70-80% битов ключа.В критическом исследовании моделирования Луи Киш и Хорват [31] указали, что выбранные волновые сопротивления смоделированного кабеля для достижения этих результатов были нефизичными: например, диаметр центрального провода в 1 миллиметр подразумевает коаксиальный кабель с внешним диаметром 28000 раз больше, чем размер известной Вселенной.
Наблюдение за переходными процессами после переключения резисторов было упомянуто как потенциальный источник утечки информации; однако до сих пор они ни разу не использовались. Во время экспериментальных исследований шум нарастал в начале периода тактовой частоты и снижался в конце, таким образом, переключение резисторов происходило, когда напряжение и токи в линии равнялись нулю.
Обратите внимание, что полностью свободный от переходных процессов протокол описан в недавней работе [48].
Согласно [40], одним из наиболее эффективных типов атак было бы использование емкостных токов через емкость кабеля, хотя он никогда не тестировался. Mingesz et al. [29] показали аппаратную защиту «убийцу емкости» от этой атаки. В конечном счете, метод отбрасывания рискованных битов после сравнения тока / напряжения на двух концах [28], [30], [31] и / или, в случае пренебрежимо малой вероятности ошибки, усиление конфиденциальности [35] являются инструментами для подход к совершенной безопасности.
Python rlc circuit
ПАРАЛЛЕЛЬНАЯ РЕЗОНАНСНАЯ ЦЕПЬ Базовым форматом последовательного резонансного контура является комбинация последовательного R-L-C последовательно с источником приложенного напряжения. Параллельный резонансный контур имеет базовую конфигурацию, показанную на рис. 20.21, комбинацию параллельных R-L-C параллельно с приложенным источником тока. Для последовательной цепи импеданс был минимальным на уровне
.
Circuit Solver не сравнивается с их исходной мощностью, но он оптимизирован для работы на мобильных устройствах, что делает его портативным и легко доступным для всех, кто нуждается в схемных решениях.Circuit Solver стремится проверить закон Ома, законы тока и напряжения Кирхгофа, создавая модели, которые являются одновременно стабильными и эффективными. Резонанс является важным понятием в колебательном движении. Резонансная частота — это характерная частота тела или системы, которая достигает максимальной степени колебаний. В этой статье мы обсудим формулу резонансной частоты с примерами. Давайте начнем интересную тему! Программное обеспечение для моделирования цепей для STEM работает в режиме онлайн, имитируйте и устраняйте неисправности в цепях в богатой среде моделирования, легко обучаемой.диэлектрики, граничные условия и схемы RLC. Некоторые другие темы включают волноводы, анизотропную кристаллическую оптику, линии передачи, волоконную оптику, отражение и преломление, а также специальную теорию относительности. … изучение основ утилит Linux и Python, взаимодействие со службами в базовом ядре Linux с использованием системы Python …
rlc_chart — это библиотека, которая отображает диаграммы импеданса в SVG с обычным сопротивлением по сравнению с сетками журнала регистрации частоты, но они также включают в себя сетки емкостей и индуктивностей.Их можно использовать для прямого считывания значений компонентов с графика импеданса. Это объясняется в разделе Введение в фазоры. Кривая тока резистора в RC-цепи последовательной зарядки. Вертикальная ось показывает ток через резистор в процентах от приложенного напряжения к RC-цепи. τ представляет собой постоянную времени RC. Заменяет существующее изображение PNG. Создано мной с использованием Python и matplotlib. См. Подробности в разговоре.
Напряжение и ток в цепях
Законы Кирхгофа: напряжение и ток в цепях
Содержание>
Законы Кирхгофа: напряжение и ток в цепях
Темы и файлы
Тема E&M
Напильник Capstone
Перечень оборудования
Введение
Цель этого упражнения — изучить два закона Кирхгофа для электрических цепей.Используйте датчик напряжения, датчик тока и программное обеспечение Capstone для измерения напряжения на и тока от до частей сложной цепи.
Фон
Закон Ома описывает взаимосвязь между током, напряжением и сопротивлением в простых цепях. Многие схемы более сложные и не могут быть решены с помощью закона Ома. Эти схемы имеют множество источников питания и ответвлений, что делает использование закона Ома непрактичным или невозможным.В 1857 году немецкий физик Густав Кирхгоф разработал методы решения сложных схем. Кирхгоф сделал два вывода, известных сегодня как законы Кирхгофа. Два закона Кирхгофа описывают уникальное соотношение между током, напряжением и сопротивлением в сложных электрических цепях.
Закон Кирхгофа по току: Ток, поступающий в любую точку соединения в цепи, равен току, выходящему из этого соединения. Другими словами: независимо от того, сколько путей в одну точку и из нее, весь ток, выходящий из этой точки, должен равняться току, прибывающему в эту точку.Этот закон иногда называют правилом перекрестка .
Закон Кирхгофа о напряжении: Алгебраическая сумма напряжений вокруг любого замкнутого контура равна нулю. Другими словами: падение напряжения в любом замкнутом контуре должно равняться приложенному напряжению. Этот закон иногда называют правилом петли .
Законы Кирхгофа могут быть связаны с сохранением энергии и заряда, если мы рассмотрим схему с одной нагрузкой и источником.Поскольку нагрузка потребляет всю мощность, поступающую от источника, энергия и заряд сохраняются. Поскольку напряжение и ток могут быть связаны с энергией и зарядом, тогда законы Кирхгофа повторяют законы, управляющие сохранением энергии и заряда. .

Сколько законов кирхгофа существует: Законы Кирхгофа — это… Что такое Законы Кирхгофа?

Законы Кирхгофа — это… Что такое Законы Кирхгофа?

Формулировка

Первый закон

Второй закон

Особенности составления уравнений для расчёта токов

О значении для электротехники

Закон излучения

Примечания

Литература

Законы Кирхгофа

Законы Кирхгофа простыми словами — Юридическая помощь

Закон кирхгофа для конденсаторов

Общие понятия и описание первого закона Кирхгофа

Закон Ома — первый кит электротехники

Токи и напряжения в сети

Для токов — узлы, для напряжений — контуры

Правило Кирхгофа для напряжений (2й закон)

Правило Кирхгофа для токов (1й закон)

Законы Кирхгофа простыми словами ⋆ diodov.net

Первый и второй закон Кирхгофа — доступное объяснение

Первый закон Кирхгофа

Законы Кирхгофа — формулы и примеры использования

Законы и уравнения Кирхгофа

Содержание:

Законы и уравнения Кирхгофа

Кирхгоф закон излучения — Справочник химика 21

Сценарий открытого урока по электротехнике «Законы Кирхгофа»

вики: схемы: kirchoff_law [Weber’s Wiki]

Закон напряжения Кирхгофа (KVL)

Описание

Примеры проблем

Действующий закон Кирхгофа (KCL)

Описание

Примеры проблем

Прочие ресурсы

Законов Кирхгофа — MyRank

Закон Кирхгофа о цепях — Electronics-Lab.com

Введение

Структура и определения

Действующий закон Кирхгофа

Закон Кирхгофа по напряжению

Заявление KCL

Пределы KCL

Заключение

Законы Кирхгофа и спектроскопия | Астрономия 801: планеты, звезды, галактики и Вселенная

Спектры поглощения

Попробуй!

Спектры излучения

Несколько последствий

ошибок и их устранение при обмене безопасными ключами Кирхгофа-Лоу-Джонсона-шума

1.1 Безопасный обмен ключами KLJN

1.2 Известные типы атак

Python rlc circuit

Напряжение и ток в цепях

Темы и файлы

Тема E&M

Напильник Capstone

Перечень оборудования

Введение

Фон

Добавить комментарий Отменить ответ