Поверхностный эффект в проводнике. Скин-эффект. Частотные свойства
Переменный ток сопровождается электромагнитными явлениями, которые приводят к вытеснению электрических зарядов с центра проводника на его периферию. Этот эффект называется — поверхностным эффектом, или скин-эффектом. В результате этого эффекта ток становится неоднородным. На периферии ток оказывается большим по величине, чем в центре. Это происходит из-за различия в плотности свободных носителей зарядов в перпендикулярном сечении проводника относительно направления тока.
Глубина проникновения тока определяется согласно выражению:
Используя приведённую выше формулу для медного проводника получаем, что при частоте тока в 50 Гц глубина проникновения составит приблизительно 9,2 мм. Фактически это означает, что имея проводник с круглым сечением с радиусом более 9,2 мм, ток в центре проводника будет отсутствовать, потому как там не будет свободных носителей зарядов.
Чем выше частота тока, тем меньше глубина проникновения. Увеличение частоты тока в два раза повлечет за собой уменьшение глубины проникновения в корень квадратный из двух. Если частота тока увеличится в 10 раз, то, соответственно, глубина проникновения уменьшится в корень из 10 раз.
График распределения тока.
На графике наглядно показано распределение плотности тока J в проводнике круглого сечения (цилиндрический). За пределами глубины проникновения плотность тока равна нулю или же ничтожно мала, потому как в этих местах проводника отсутствуют свободные электроны. Ток в этих местах отсутствует.
Если из центра такого проводника где отсутствует ток, извлечь проводящий материал, то мы получим полый проводник в виде трубки (трубчатый). Проводящие характеристики от этого не изменятся, потому как тока там и не было, сопротивление такого проводника не изменится, но могут поменяться такие характеристики как индуктивность и емкость проводника.
Сопротивление проводника в цепи переменного тока зависит не только от материала проводника, но также от частоты тока. При высоких частотах, за счет скин-эффекта, весь ток начинает протекать практически по границе проводника, там где он контактирует со внешней, не проводящей средой.
Практическое использование скин-эффекта.
Распределение плотности тока в проводнике в зависимости от частоты тока позволяет по одному проводу передавать электрические сигналы разных частот. Сигналы более высокой частоты проходят по внешнему радиусу (большему) проводника, а сигналы меньшей частоты по меньшему радиусу. Получается нечто вроде
Учитывая глубину проникновения тока для разных частот, если требуется проводник с радиусом большим, чем глубина проникновения, то разумно применять многожильный кабель. Скажем так, для 50 Гц частоты тока, предельный радиус примерно 9 мм, а это значит, что нет смысла эксплуатировать цельный проводник с радиусом больше 9 мм. Это не даст никакого увеличения проводимости, потому как ток в центре проводника будет отсутствовать, что является нерациональным использованием дорогостоящей меди. Вот поэтому при больших сечениях применяют многожильные провода и кабели.
При передачи высокочастотных сигналов, в целях экономии цветного металла, основной несущий провод изготавливают из дешевого стального сплава, который затем покрывают тонким слоем меди. Благодаря скин-эффекту ток протекает практически только по медной оболочке, а в стальном основании он отсутствует. Это позволяет значительно удешевить провода и кабели для высокочастотных средств связи.
Дата: 27.05.2016
© Valentin Grigoryev (Валентин Григорьев)
Скин эффект в проводнике — смерть для звука?
В погоне за максимальной достоверностью звука, аудиофилы начали яро пытаться подавить скин эффект в звуковых проводах. Но что на самом деле такое этот пресловутый скин эффект? Давайте выясним действительно ли это серьезное препятствие на пути качественного звука или же магия глянцевых журналов.
Что такое скин эффект?
Если вы не сильны в английском, то скин (skin) переводится как кожа или в данном случае скорее слой. В русскоязычной литературе, скин эффект называют поверхностным эффектом.
Говоря простым языком, скин эффект заключается в том, что протекающий по проводнику переменный ток, вытесняется к поверхности проводника с ростом частоты.
Чем выше частота сигнала F тем сильнее он вытесняется к поверхности и тем тоньше становится слой по которому он протекает. Этот слой называется скин слой. Красная область на рисунке — область по которой сигнал не течет.
Это приводит к тому, что скорость протекания сигнала на разной частоте различна. Происходит это потому, что для разных частот используется разная площадь поперечного сечения проводника, а разная площадь это разное сопротивление. Все это приводит к появлению фазовых искажений в сигнале.
Толщина скин слоя
Толщина скин слоя — это толщина слоя поверхности, углубившись на которую сигнал ослабевае
Поверхностный (скин-эффект) в проводнике
Звуковой сигнал изменяет свойства проводников, соединяющих компоненты электронной схемы. Причинами этого могут быть:
- частотные характеристики, вызванные взаимодействием параметров RCLD-кабеля, и неблагоприятные условия входного и выходного импеданса компонентов;
- конструкция кабеля и применяемые материалы.
Важно! Даже при оптимальных параметрах RCLD часто наблюдаются четкие различия в звуке.
Одной из причин, часто связанной с конструкцией кабеля, является поверхностный эффект.
Поверхностный эффект в проводе
Общее объяснение
При постоянном токе его плотность по всему поперечному сечению проводника одинакова. Но переменный ток регулярно меняет свое направление и силу, что генерирует изменяющееся магнитное поле. Изменение потока индуцирует вихревые токи в проводнике, направленные на противодействие току внутри провода. На поверхности их направления совпадают. В результате плотность тока экспоненциально уменьшается по направлению к центру. Ток смещения увеличивается с частотой переменного тока и диаметром проводника.
При высокочастотных сигналах центр проводника практически обесточивается. Сопротивление провода при этом значительно увеличивается за счет смещения тока. Однако это только упрощенная модель.
Распределение плотности тока в проводнике
Помимо скин эффекта, существует эффект близости, который создает дополнительную концентрацию плотности тока на стороне поперечного сечения линии, лежащей в области магнитного поля наибольшей силы. Она проявляется, например, на внутренних поверхностях при двухтактном возбуждении или на внешних сторонах в синхронной возбужденной двойной линии.
Глубина проникновения
Расстояние от поверхности проводника, на котором плотность тока упала до коэффициента 1 / e = 0,37, или -8,69 дБ, называется глубиной проникновения и рассчитывается по формуле:
d = √ (ρ / (π × μ × f)), где:
- d – глубина проникновения, мм;
- ρ – удельное сопротивление материала;
- μ – постоянная проницаемости = 4 × p × 10 -7 Генри / м;
- f – частота;
Отсюда можно составить эмпирическое правило для меди:
d = 66 × √ (ρ r / (μ r × f)), где:
- ρ r = ρ / ρ Cu = 1;
- μ r – для немагнитных материалов, таких как медь, равно 1.
Глубина скин слоя для э/м полей
Из формулы следует, что глубина проникновения для каждой частоты у сверхпроводников равна 0, то есть весь перенос заряда идет по поверхности, а для плохого проводника глубина проникновения очень велика. Глубина проникновения также пропорциональна потерям, возникающим в проводе.
Расчет увеличения сопротивления, возникающего во время скин эффекта, немного сложнее:
- Для круглой сплошной медной проволоки с диаметром 2 мм, что соответствует S = 3,15 мм², полученное сопротивление на частоте 100 кГц, по сравнению с таким же значением для частоты 32 кГц, возрастает в 1,5 раза;
- Для проводника с d = 0, 2 мм удвоение сопротивления происходит только на частоте 10 мГц.
Важно! Для исключения скин эффекта в звуковом диапазоне до 20 кГц проводник может иметь диаметр не более 1 мм. Если диапазон аудиосигнала величин до 50 кГц, диаметр проводника не может превышать 0,6 мм.
Приблизительная формула для определения частоты среза для данного диаметра проводника:
f c = 4 / (π × μ × s Cu × D 2) = 1 / (π 2 × 5,8 × D 2), где:
- f c – частота среза;
- D – диаметр проводника;
- s Cu= удельная проводимость меди = 5,8 × 10 7 (Ω × м) -1;
Несколько значений частоты среза для меди:
- 0,1 мм – 1,75 мГц;
- 0,3 мм – 194 кГц;
- 0,5 мм – 70 кГц;
- 0,8 мм – 27 кГц;
- 1 мм – 17 кГц;
- 2 мм – 4,4 кГц.
Фактический поверхностный эффект не является чистым увеличением сопротивления.
Часть э/м поля, которая не отражается на проводимости из-за неидеальных свойств провода, но проникает в него, можно назвать полем потерь. Компонента электрического поля ориентирована в осевом направлении вдоль длины проводника, а электромагнитная энергия распространяется радиально, начиная с поверхности. Это является причиной скин эффекта.
Таким образом, поле потерь напрямую зависит от проводимости, магнитной проницаемости и частоты сигнала и в конечном итоге преобразуется в тепло.
Способы подавления скин эффекта
Поверхностный эффект можно подавить или значительно уменьшить, используя вместо сплошной проволоки пучок тонких проводов, покрытых специальным изоляционным лаком. В высокочастотной технологии часто используются тонкостенные трубки, поверхность которых покрыта хорошо проводящим слоем, например, серебром.
Акустический кабель
Основные особенности подавления скин эффекта:
- Идеальные проводники для аудиодиапазона – не толще 0,3 мм;
- Структура кабеля должна быть такой, чтобы по всей длине образовывалось однородное магнитное поле между проводниками;
- Провод должен быть максимально чистым и однородным, с поверхностью, абсолютно свободной от оксида меди;
- Следует избегать рядом лежащих неэкранированных шнуров питания из-за генерируемых магнитных полей;
- В качестве диэлектрика лучше использовать материал с возможно меньшей диэлектрической постоянной.
Многожильные провода часто используются и для передачи токов низкой частоты. Сталь или углеродное волокно применяется для передачи мощности на большие расстояния. Широкие дорожки на печатной плате обеспечивают большую площадь поверхности и низкое сопротивление. С учетом этих простых предложений скин-эффекта можно избежать в большинстве случаев применения электроэнергии. Но правильное функционирование конструкций, работающих на сотнях мегагерц и даже гигагерцах, требует тщательного планирования и инженерных решений. Оптоволоконные кабели, в которых для передачи данных используется неметаллическая среда, обычно требуются, чтобы глубина поверхностного слоя стандартных проводников оставалась низкой.
Видео
Оцените статью:Скин-эффект — Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта
Физическая картина возникновения
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
- rotB=μj{\displaystyle \operatorname {rot} \mathbf {B} =\mu \mathbf {j} }
и выражения для j{\displaystyle \mathbf {j} } по закону Ома:
- j=γE{\displaystyle \mathbf {j} =\gamma \mathbf {E} }
Дифференцируя обе части полученного уравнения по времени, находим:
- rot∂B∂t=μγ∂E∂t{\displaystyle \operatorname {rot} {\frac {\partial \mathbf {B} }{\partial t}}=\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}
- −rotrotE=μγ∂E∂t{\displaystyle -\operatorname {rot} \operatorname {rot} \mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}.
Поскольку
- rotrotE=graddivE−∇2E{\displaystyle \operatorname {rot} \operatorname {rot} \mathbf {E} =\operatorname {grad} \operatorname {div} \mathbf {E} -\nabla ^{2}\mathbf {E} } и divE=0{\displaystyle \operatorname {div} \mathbf {E} =0}
окончательно получаем:
- ∇2E=μγ∂E∂t{\displaystyle \nabla ^{2}\mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}.
Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- jx=jx(y,t),jy=jz=0{\displaystyle j_{x}=j_{x}(y,t),\qquad j_{y}=j_{z}=0},
- Ex=Ex(y,t),Ey=Ez=0{\displaystyle E_{x}=E_{x}(y,t),\qquad E_{y}=E_{z}=0}.
Тогда
- ∂2Ex∂y2=μγ∂Ex∂t{\displaystyle {\frac {\partial ^{2}E_{x}}{\partial y^{2}}}=\mu \gamma {\frac {\partial E_{x}}{\partial t}}}.
В этом уравнении все величины гармонически зависят от t, и можно положить:
- Ex(y,t)=E0(y)eiωt{\displaystyle E_{x}(y,t)=E_{0}(y)e^{i\omega t}}.
Подставим это в наше уравнение и получим уравнение для E0(y){\displaystyle E_{0}(y)}:
- ∂2E0∂y2=iγμωE0{\displaystyle {\frac {\partial ^{2}E_{0}}{\partial y^{2}}}=i\gamma \mu \omega E_{0}}.
Общее решение этого уравнения таково:
- Ex=A1e−ky+A2eky{\displaystyle E_{x}=A_{1}e^{-ky}+A_{2}e^{ky}}.
Учитывая, что k=iγμω=α(1+i){\displaystyle k={\sqrt {i\gamma \mu \omega }}=\alpha (1+i)}, где α=γμω2{\displaystyle \alpha ={\sqrt {\frac {\gamma \mu \omega }{2}}}}, находим
- E0=A1e−αye−iαy+A2eαyeiαy{\displaystyle E_{0}=A_{1}e^{-\alpha y}e^{-i\alpha y}+A_{2}e^{\alpha y}e^{i\alpha y}}.
При удалении от поверхности проводника (y→∞{\displaystyle y\rightarrow \infty }) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, A2=0{\displaystyle A_{2}=0} и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачи имеет вид:
- Ex=A1e−αyei(ωt−αy){\displaystyle E_{x}=A_{1}e^{-\alpha y}e^{i(\omega t-\alpha y)}}.
Взяв действительную часть от этого выражения и перейдя с помощью соотношения j=γE{\displaystyle \mathbf {j} =\gamma \mathbf {E} } к плотности тока, получим
- jx(y,t)=A1e−αycos(ωt−αy){\displaystyle j_{x}(y,t)=A_{1}e^{-\alpha y}\cos {(\omega t-\alpha y)}}.
Принимая во внимание, что jx(0,0)=j0{\displaystyle j_{x}(0,0)=j_{0}} — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- jx(y,t)=j0e−αycos(ωt−αy){\displaystyle j_{x}(y,t)=j_{0}e^{-\alpha y}\cos {(\omega t-\alpha y)}}.
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине Δ{\displaystyle \Delta } становится меньше в е раз. Эта глубина называется толщиной скин-слоя и на основании полученного выше равна
- Δ=2γμω{\displaystyle \Delta ={\sqrt {\frac {2}{\gamma \mu \omega }}}}.
Очевидно, что при достаточно большой частоте ω{\displaystyle \omega } толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько Δ{\displaystyle \Delta }, так, уменьшение плотности тока в 100 раз происходит на глубине ≈4,6Δ{\displaystyle \approx 4,6\Delta }, если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | Δ{\displaystyle \Delta } | Примечания |
|---|---|---|
| 50 Гц | 9,34 мм | 50 Гц — частота электросети в большинстве стран Евразии и Африки |
| 60 Гц | 8,53 мм | 60 Гц — частота электросети в Северной, Центральной и частично Южной Америке |
| 10 кГц | 0,66 мм | |
| 100 кГц | 0,21 мм | |
| 500 кГц | 0,095 мм | |
| 1 МГц | 0,067 мм | |
| 10 МГц | 0,021 мм |
Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали (μ{\displaystyle \mu }=1000) Δ{\displaystyle \Delta }=0.74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- Δ=c2ε0ωμmρ{\displaystyle \Delta =c{\sqrt {2{\frac {\varepsilon _{0}}{\omega \mu _{m}}}\rho }}}.
Здесь ε0{\displaystyle \varepsilon _{0}} = 8,85419⋅10−12 Ф/м — электрическая постоянная, ρ{\displaystyle \rho } — удельное сопротивление, c — скорость света, μm{\displaystyle \mu _{m}} — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), ω=2π⋅f{\displaystyle \omega =2\pi \cdot f}. Все величины выражены в системе СИ.
- Δ=503ρμmf{\displaystyle \Delta =503{\sqrt {\frac {\rho }{\mu _{m}f}}}},
ρ{\displaystyle \rho } — удельное сопротивление, μm{\displaystyle \mu _{m}} — относительная магнитная проницаемость, f{\displaystyle f} — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется[1]: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется всё более явно с увеличением частоты переменного тока, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Скин-эффект значительно влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное влияние (до 10 %) на активное сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, вдобавок ещё и со свойствами полупроводника, и вносящего дополнительные потери на высоких частотах. Также применяется и покрытие золотом, у которого слой окислов отсутствует вовсе. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности из посеребрённого провода, серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует сжиженный водород или дистиллированная вода. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. При передаче больших мощностей на значительные расстояние применяются линии постоянного тока — HVDC, который не подвержен воздействию скин-эффекта.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы. Кроме того, на таких частотах особое внимание приходится уделять снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.
Примечания
- ↑ Сивухин Д. В. Общий курс физики. Том 4. Оптика. — 1980. — С. 454.
Литература
- А. Н. Матвеев. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
- A. A. Власов. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. — М.: Наука, 2005.
Высокочастотные токи. Скин-эффект
Свойства быстропеременных токов
Определение 1
Токами высокой частоты считают токи, которые имею частоту выше, чем $10000 Гц$. Для этих токов не выполняются условия квазистационарности. В процессе протекания такого тока по проводнику, в проводнике появляются вихревые токи, которые порождаются изменениями магнитного поля с высокой скоростью.
Изменения магнитного поля в проводнике происходят такие, что на его оси вихревой ток имеем направление встречное к основному току, а у поверхности проводника течение этого тока совпадает с направлением основного тока. Значит, ток высокой частоты имеет непостоянную плотность по поперечному сечению. Плотность тока в центре сечения проводника почти равна нулю. Она увеличивается при движении в направлении к наружной поверхности. При очень высокой частоте ток течет по тонкому наружному слою проводника.
Сейчас токи высокой частоты широко применяются. Высокочастотные плавильные печи применяют для быстрого прогрева металлических тел. С помощью высокочастотных токов проводят закаливание стальных деталей. Объект на короткое время размещают внутри катушки с током высокой частоты. Поверхностный слой детали разогревается вихревыми токами, ее внутренность при этом остается холодной. Деталь вынимают из катушки, внутренняя часть быстро отнимает тепло у поверхностного слоя, поверхность быстро охлаждается и закаляется. Глубину прогрева регулируют временем выдержки детали в катушке и частотой тока. После такой процедуры поверхность детали становится твердой и прочной, внутри металл сохраняет упругость и пластичность.
Скин —эффект
Постоянный ток по поперечному сечению проводника распределяется равномерно. У переменного тока из-за индукционного взаимодействия разных элементов тока проходит перераспределение плотности тока по поперечному сечению проводника. Явление, при котором ток преимущественно сосредотачивается в поверхностном слое проводника, называется скин-эффектом.
Пусть мы имеем цилиндрический проводник, по которому течет ток. Вокруг проводника с током образуется магнитное поле. Силовые линии этого поля — концентрические окружности, центр которых лежит на оси проводника. Если силу тока увеличить, то повысится индукция магнитного поля, но форма силовых линий не изменится. Соответственно, производная $\frac{\partial \overrightarrow{B}}{\partial t}$ направлена по касательной к линии индукции магнитного поля, линии производной также — окружности, которые совпадают с силовыми линиями. Мы знаем из закона электромагнитной индукции, что:
Вектор напряженности индукционного поля в областях расположенных ближе к оси проводника имеет направление противоположное вектору напряженности электрического поля, которое создает ток, в дальних областях направления этих векторов совпадают. В результате плотность тока уменьшается около оси и увеличивается ближе к поверхности проводника, то есть появляется скин-эффект.
В металлах в виду их высокой проводимости током смещения можно пренебречь в сравнении с током проводимости. Из-за чего проникновение магнитного поля в металл аналогично процессу диффузии в математическом отношении. За основу возьмем уравнение (1) и уравнение (2):
Используем закон Ома:
приравняем правые части выражений (2) и (3) и продифференцируем полученное выражение, в результате имеем:
Или учитывая формулу (1):
Используем известные соотношения:
окончательно получим:
Если ток течет по однородному бесконечному проводнику, который занимает полупространство y$>$0 вдоль оси X, причем поверхность проводника плоская, и можно записать:
В таком случае уравнение (7) преобразуется к виду:
Можно предположить, что:
Подставив выражение (11) в уравнение (10) получим:
Решением уравнения (12) является функция:
где $\alpha =\sqrt{\frac{\omega \sigma {\mu }_0\mu }{2}}$. Возьмем действительную часть выражения (13) и перейдем к плотности тока, используя закон Ома, получим:
Если считать, что амплитуда плотности тока $j_0=j_x\left(0,0\right)$, то выражение (14) примет вид:
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. На расстоянии $\triangle =\frac{1}{\alpha }\ \ от\ поверхности\ $она становится в e раз меньше. Почти весь ток находится в $\triangle $ слое, который называют толщиной скин — слоя. Толщина скин — слоя равна:
При высокой частоте тока толщина скин — слоя весьма мала.
Пример 1
Решение:
Толщина скин — слоя проводника рассчитывается по формуле:
\[\triangle =\sqrt{\frac{2}{\sigma \mu {\mu }_0\omega }}\left(1.1\right).\]Если дважды записать выражение (1.1) для разных частот тока, то получим:
\[\frac{{\triangle }_1}{{\triangle }_2}=\sqrt{\frac{{\omega }_2}{{\omega }_1}}\left(1.2\right).\]Проведем вычисления:
\[\frac{{\triangle }_1}{{\triangle }_2}=\sqrt{\frac{{10}^6}{{10}^4}}=10.\]Ответ: Толщина уменьшится в 10 раз.
Пример 2
Задание: Почему при высокой частоте тока можно убрать проводящий материал из цилиндрической области внутри проводника и оставить только проводящую оболочку?
Решение:
Как было показано в предыдущем примере, с увеличением частоты тока, глубина слоя в котором распространяется ток, становится очень небольшой. То есть ток течет лишь в малой части поперечного сечения проводника около его поверхности (скин — эффект). Следовательно, ничего не изменится, если убрать проводящий материал из цилиндрической области внутри проводника и оставить только цилиндрическую оболочку толщиной скин — слоя. Если проводник толстый, а частота его невелика, то ток течет по всему поперечному сечению и только немного ослабевает к оси провода. Так, при технической частоте в $50 Гц$ скин — эффект в обычных проводниках выражается очень слабо.
Скин-эффект — Большая советская энциклопедия
Скин-эффе́кт
(от англ. skin — кожа, оболочка)
поверхностный эффект, затухание электромагнитных волн по мере их проникновения в глубь проводящей среды, в результате которого, например, переменный ток по сечению проводника или переменный магнитный поток по сечению магнитопровода распределяются не равномерно, а преимущественно в поверхностном слое. С.-э. обусловлен тем, что при распространении электромагнитной волны в проводящей среде возникают Вихревые токи, в результате чего часть электромагнитной энергии преобразуется в теплоту. Это и приводит к уменьшению напряжённостей электрического и магнитного полей и плотности тока, т. е. к затуханию волны.
Чем выше частота ν электромагнитного поля и больше магнитная проницаемость μ проводника, тем сильнее (в соответствии с Максвелла уравнениями) вихревое электрическое поле, создаваемое переменным магнитным полем, а чем больше проводимость а проводника, тем больше плотность тока и рассеиваемая в единице объёма мощность (в соответствии с законами Ома и Джоуля — Ленца). Т. о., чем больше ν, μ и σ, тем сильнее затухание, т. е. резче проявляется С.-э.
В случае плоской синусоидальной волны, распространяющейся вдоль оси х в хорошо проводящей, однородной, линейной среде (токами смещения по сравнению с токами проводимости можно пренебречь), амплитуды напряжённостей электрического и магнитного полей затухают по экспоненциальному закону:
 ,
, 
где

— коэффициент затухания, μ0 —Магнитная постоянная. На глубине х = δ = 1/α амплитуда волны уменьшается в е раз. Это расстояние называется глубиной проникновения или толщиной скин-слоя. Например, при частоте 50 гц в меди (σ = 580 ксим/см; μ = 1) σ = 9,4 мм, в стали (α = 100 ксим/см, (μ = 1000) δ = 0,74 мм. При увеличении частоты до 0,5 Мгц δ уменьшится в 100 раз. В идеальный проводник (с бесконечно большой проводимостью) электромагнитная волна вовсе не проникает, она полностью от него отражается. Чем меньше расстояние, которое проходит волна, по сравнению с δ, тем слабее проявляется С.-э.
Для проводников при сильно выраженном С.-э., когда радиус кривизны сечения провода значительно больше δ и поле в проводнике представляет собой плоскую волну, вводят понятие поверхностного сопротивления проводника Zs (поверхностного импеданса). Его определяют как отношение комплексной амплитуды (См. Комплексная амплитуда) падения напряжения на единицу длины проводника к комплексной амплитуде тока, протекающего через поперечное сечение скин-слоя единичной длины. Комплексное сопротивление на единицу длины проводника:

где R0 — активное сопротивление проводника, определяющее мощность потерь в нём, X0 — индуктивное сопротивление, учитывающее индуктивность проводника, обусловленную магнитным потоком внутри проводника, lc — периметр поперечного сечения скин-слоя, ω = 2πν; при этом R0 = X0. При сильно выраженном С.-э. поверхностное сопротивление совпадает с волновым сопротивлением (См. Волновое сопротивление) проводника и, следовательно, равно отношению напряжённости электрического поля к напряжённости магнитного поля на поверхности проводника.
В тех случаях, когда длина свободного пробега l носителей тока становится больше толщины δ скин-слоя (например, в очень чистых металлах при низких температурах), при сравнительно высоких частотах С.-э. приобретает ряд особенностей, благодаря которым он получил название аномального. Поскольку поле на длине свободного пробега электрона неоднородно, ток в данной точке зависит от значения электрического поля не только в этой точке, но и в её окрестности, имеющей размеры порядка l Поэтому при решении уравнений Максвелла вместо закона Ома приходится использовать для вычисления тока кинетическое уравнение Больцмана. Электроны при аномальном С.-э. становятся неравноценными с точки зрения их вклада в электрический ток; при l >> δ основной вклад вносят те из них, которые движутся в скин-слое параллельно поверхности металла или под очень небольшими углами к ней и проводят, т. о., больше времени в области сильного поля (эффективные электроны). Затухание электромагнитной волны в поверхностном слое по-прежнему имеет место, но количественные характеристики у аномального С.-э. несколько иные. Поле в скин-слое затухает не экспоненциально (R0/X0=  ).
).
В инфракрасной области частот электрон за период изменения поля может не успеть пройти расстояние l. При этом поле на пути электрона за период можно считать однородным. Это приводит опять к закону Ома, и С.-э. снова становится нормальным. Т. о., на низких и очень высоких частотах С.-э. всегда нормальный. В радиодиапазоне в зависимости от соотношений между / и δ могут иметь место нормальный и аномальный С.-э. Всё сказанное справедливо, пока частота со меньше плазменной: ω < ω0 —(4πne2/m)1/2 (n — концентрация свободных электронов, е — заряд, m — масса электрона) (относительно более высоких частот см. ст. Металлооптика).
С.-э. часто нежелателен. В проводах переменный ток при сильном С.-э. протекает главным образом по поверхностному слою; при этом сечение провода не используется полностью, сопротивление провода и потери мощности в нём при данном токе возрастают. В ферромагнитных пластинах или лентах магнитопроводов трансформаторов, электрических машин и других устройств переменный магнитный поток при сильном С.-э. проходит главным образом по их поверхностному слою; вследствие этого ухудшается использование сечения магнитопровода, возрастают намагничивающий ток и потери в стали. «Вредное» влияние С.-э. ослабляют уменьшением толщины пластин или ленты, а при достаточно высоких частотах — применением магнитопроводов из магнитодиэлектриков (См. Магнитодиэлектрики).
С др. стороны, С.-э. находит применение в практике. На С.-э. основано действие электромагнитных экранов. Так для защиты внешнего пространства от помех, создаваемых полем силового трансформатора, работающего на частоте 50 гц, применяют экран из сравнительно толстой ферромагнитной стали; для экранирования катушки индуктивности, работающей на высоких частотах, экраны делают из тонкого слоя Al. На С.-э. основана высокочастотная поверхностная закалка стальных изделий (см. Индукционная нагревательная установка).
Лит.: Нетушил А. В., Поливанов К. М., Основы электротехники, т. 3, М., 1956; Поливанов К. М., Теоретические основы электротехники, ч. 3 — Теория электромагнитного поля, М., 1975; Нейман Л. Р., Поверхностный эффект в ферромагнитных телах, Л. — М., 1949. См. также лит. при ст. Металлы.
И. Б. Негневицкий.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- скин-эффект — [англ. skin кожа + эффект] – эл. явление, наблюдаемое при протекании по проводнику переменного тока высокой частоты и заключающееся в том, что ток проходит не по всему сечению сплошного проводника, а преимущественно по его поверхностному слою Большой словарь иностранных слов
- СКИН-ЭФФЕКТ — СКИН-ЭФФЕКТ (от англ. skin — кожа, оболочка) — (поверхностный эффект) — неоднородное распределение переменного тока и связанного с ним электромагнитного поля по сечению проводника. Большой энциклопедический словарь
- скин-эффект — сущ., кол-во синонимов: 1 эффект 29 Словарь синонимов русского языка
- скин-эффект — орф. скин-эффект, -а Орфографический словарь Лопатина
- СКИН-ЭФФЕКТ — (от англ. skin — кожа, оболочка) (поверхностный эффект), затухание эл.-магн. волн по мере их проникновения в глубь проводящей среды, в результате к-рого, напр., перем. ток по сечению проводника или перем. магн. Физический энциклопедический словарь

эффект — это… Что такое Скин-эффект?
Скин-эффект (поверхностный эффект) — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется неравномерно по сечению, а преимущественно в поверхностном слое.
Объяснение скин-эффекта
Физическая картина возникновения
 Физическая картина возникновения скин-эффекта.
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная направлена по касательной к линии индукции магнитного поля и, следовательно, линии также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
и выражения для по закону Ома:
Дифференцируя обе части полученного уравнения по времени, находим:
- .
Поскольку
- и
окончательно получаем:
- .
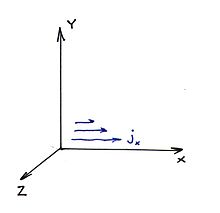 Скин-эффект в бесконечном проводнике с плоской границей.
Скин-эффект в бесконечном проводнике с плоской границей.Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- ,
- .
Тогда
- .
В этом уравнении все величины гармонически зависят от t, и можно положить:
- .
Подставим это в наше уравнение и получим уравнение для :
- .
Общее решение этого уравнения таково:
- .
Учитывая, что , где , находим
- .
При удалении от поверхности проводника () второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачии имеет вид:
- .
Взяв действительную часть от этого выражения и перейдя с помощью соотношения к плотности тока, получим
- .
Принимая во внимание, что — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- .
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает и на глубине становится меньше в е раз. Поэтому практически весь ток сосредоточен в слое толщиной . Она называется толщиной скин-слоя и на основании полученного выше равна
- .
Очевидно, что при достаточно большой частоте толщина скин-слоя может быть очень малой. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | |
|---|---|
| 60 Гц | 8,57 мм |
| 10 кГц | 0,66 мм |
| 100 кГц | 0,21 мм |
| 1 МГц | 66 мкм |
| 10 МГц | 21 мкм |
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- .
Здесь = 8,85419·10−12 Ф/м — абсолютная диэлектрическая проницаемость, — удельное сопротивление, c — скорость света, — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), . Все величины выражены в системе СИ.
- ,
— удельное сопротивление, — относительная магнитная проницаемость, — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако при очень низкой температуре ситуация резко меняется: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Борьба с эффектом
С увеличением частоты переменного тока скин-эффект проявляется всё более явно, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. Например, вместо обычных медных проводов могут применяться медные провода, покрытые тонким слоем серебра. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором благодаря скин-эффекту и протекает бо́льшая часть тока, оказывает сильное влияние на активное сопротивление проводника. Скин-эффект значительно влияет на характеристики колебательных контуров, такие как добротность. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Для борьбы со скин-эффектом применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Так, в ВЧ аппаратуре используют посеребрённые медные контуры, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, через которые пропускается жидкий водород для охлаждения. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. Все указанные методы борьбы со скин-эффектом малоэффективны для сверхвысокочастотного оборудования. В этом случае применяют колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы.



