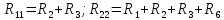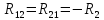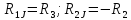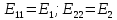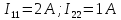Метод непосредственного применения законов Кирхгофа — Википедия
Материал из Википедии — свободной энциклопедии
Метод непосредственного применения правил Кирхгофа для расчета электрической цепи заключается в составлении системы из В уравнений с В неизвестными (B — количество ветвей в рассматриваемой цепи) по двум правилам Кирхгофа и последующем их решении.
Рассмотрим расчёт электрической цепи, не содержащей источников тока. Рассматриваемая цепь состоит из В ветвей и У узлов. Её расчёт сводится к нахождению токов в В ветвях. Для этого необходимо составить (У — 1) независимых уравнений по первому правилу Кирхгофа и К = (В — У + 1) независимых уравнений по второму правилу Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми (то есть содержащими хотя бы одну ветвь, не принадлежащую другим узлам/контурам).
Для решения составленной системы линейных алгебраических уравнений можно воспользоваться матричной формой
- AI=BE{\displaystyle AI=BE},
где
- A{\displaystyle A} и B{\displaystyle B} — квадратные матрицы коэффициентов при токах и ЭДС порядка B;
- I{\displaystyle I} и E{\displaystyle E} — матрицы-столбцы неизвестных токов и заданных ЭДС.
Решение системы:
- I=A−1BE=GE{\displaystyle I=A^{-1}BE=GE},
A−1{\displaystyle A^{-1}} =[a11a12⋯a1Ba21a22⋯a2B⋮⋮⋱⋮aB1aB2⋯aBB]−1={\displaystyle ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1B}\\a_{21}&a_{22}&\cdots &a_{2B}\\\vdots &\vdots &\ddots &\vdots \\a_{B1}&a_{B2}&\cdots &a_{BB}\end{bmatrix}}^{-1}=} =1Δ[Δ11Δ12⋯Δ1BΔ21Δ22⋯Δ2B⋮⋮⋱⋮ΔB1ΔB2⋯ΔBB]T={\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{12}&\cdots &\Delta _{1B}\\\Delta _{21}&\Delta _{22}&\cdots &\Delta _{2B}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{B1}&\Delta _{B2}&\cdots &\Delta _{BB}\end{bmatrix}}^{T}=} =1Δ[Δ11Δ21⋯ΔB1Δ12Δ22⋯ΔB2⋮⋮⋱⋮Δ1BΔ2B⋯ΔBB]{\displaystyle ={\frac {1}{\Delta }}{\begin{bmatrix}\Delta _{11}&\Delta _{21}&\cdots &\Delta _{B1}\\\Delta _{12}&\Delta _{22}&\cdots &\Delta _{B2}\\\vdots &\vdots &\ddots &\vdots \\\Delta _{1B}&\Delta _{2B}&\cdots &\Delta _{BB}\end{bmatrix}}}
— обратная матрица; Δ{\displaystyle \Delta } — определитель матрицы A; Δik{\displaystyle \Delta _{ik}} — алгебраические дополнения элементов aik{\displaystyle a_{ik}} (см. способы нахождения обратной матрицы).
- G=A−1B=[g11g12⋯g1Bg21g22⋯g2B⋮⋮⋱⋮gB1gB2⋯gBB]{\displaystyle G=A^{-1}B={\begin{bmatrix}g_{11}&g_{12}&\cdots &g_{1B}\\g_{21}&g_{22}&\cdots &g_{2B}\\\vdots &\vdots &\ddots &\vdots \\g_{B1}&g_{B2}&\cdots &g_{BB}\end{bmatrix}}}
— матрица собственных gii{\displaystyle g_{ii}} и взаимных gik{\displaystyle g_{ik}} проводимостей (см. метод наложения).
- {I1=g11E1+g12E2+⋯+g1BEB;I2=g21E1+g22E2+⋯+g2BEB;⋮IB=gB1E1+gB2E2+⋯+gBBEB;{\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+\cdots +g_{1B}E_{B};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+\cdots +g_{2B}E_{B};\\\vdots \\I_{B}=g_{B1}E_{1}+g_{B2}E_{2}+\cdots +g_{BB}E_{B};\end{matrix}}\right.}
— система уравнений, определяющих токи ветвей.
Зачастую при расчёте цепей подобным методом возникает необходимость составления большого количества уравнений и последующего расчёта матриц большого порядка. Поэтому на практике применяются и другие методы расчёта.
В качестве примера рассмотрим расчёт цепи, схема которой показана на рисунке — она содержит У = 2 узла и В = 3 ветви, то есть К = В − У + 1 = 3 − 2 + 1 = 2 независимых контура (на рисунке контуры отмечены пунктирной линией — можно выбрать любую пару из них — 1 и 2, или 2 и 3, или 1 и 3).
Произвольно выбираем положительные направления токов ветвей I1{\displaystyle I_{1}}, I2{\displaystyle I_{2}}, I3{\displaystyle I_{3}} (на рисунке направления уже отмечены). По первому закону Кирхгофа можно составить одно (У − 1 = 2 − 1 = 1) независимое уравнение, например для узла a
- −I1−I2+I3=0{\displaystyle -I_{1}-I_{2}+I_{3}=0},
и по второму закону Кирхгофа — два (К = 2) независимых уравнения, например, для контуров 1 и 2
- r1I1+r3I3=E1+E2{\displaystyle r_{1}I_{1}+r_{3}I_{3}=E_{1}+E_{2}};
- r2I2+r3I3=E2+E3{\displaystyle r_{2}I_{2}+r_{3}I_{3}=E_{2}+E_{3}}.
Представим систему из этих трёх уравнений в матричной форме:
- Y−1{ K{ [11−1r10r30r2r3][I1I2I3]=AI=[000101011][E1E2E3]=BE{\displaystyle {\begin{matrix}Y-1&\left\{~\right.\\K&\left\{{\begin{matrix}~\\~\end{matrix}}\right.\end{matrix}}{\begin{bmatrix}1&1&-1\\r_{1}&0&r_{3}\\0&r_{2}&r_{3}\end{bmatrix}}{\begin{bmatrix}I_{1}\\I_{2}\\I_{3}\end{bmatrix}}=AI={\begin{bmatrix}0&0&0\\1&0&1\\0&1&1\end{bmatrix}}{\begin{bmatrix}E_{1}\\E_{2}\\E_{3}\end{bmatrix}}=BE}
или
Теперь составим систему уравнений токов:
- {I1=g11E1+g12E2+g13E3;I2=g21E1+g22E2+g23E3;I3=g31E1+g32E2+g33E3,{\displaystyle \left\{{\begin{matrix}I_{1}=g_{11}E_{1}+g_{12}E_{2}+g_{13}E_{3};\\I_{2}=g_{21}E_{1}+g_{22}E_{2}+g_{23}E_{3};\\I_{3}=g_{31}E_{1}+g_{32}E_{2}+g_{33}E_{3},\end{matrix}}\right.}
где
- g11=(r2+r3)/r2{\displaystyle g_{11}=(r_{2}+r_{3})/r^{2}};
- g22=(r1+r3)/r2{\displaystyle g_{22}=(r_{1}+r_{3})/r^{2}};
- g33=(r1+r2)/r2{\displaystyle g_{33}=(r_{1}+r_{2})/r^{2}};
- g12=g21=−r3/r2{\displaystyle g_{12}=g_{21}=-r_{3}/r^{2}};
- g13=g31=r2/r2{\displaystyle g_{13}=g_{31}=r_{2}/r^{2}};
- g23=g32=r1/r2{\displaystyle g_{23}=g_{32}=r_{1}/r^{2}};
- r=r1r2+r1r3+r2r3{\displaystyle r={\sqrt {r_{1}r_{2}+r_{1}r_{3}+r_{2}r_{3}}}}.
При расчёте схем замещения с источниками тока возможны упрощения, поскольку токи ветвей с источниками тока известны, и рассчитывать их не нужно. Поэтому число независимых контуров (без источников тока), для которых необходимо составить уравнения по второму закону Кирхгофа, равно К = (В — ВJ{\displaystyle _{J}} — У + 1), где ВJ{\displaystyle _{J}} — число ветвей с источниками тока.
- Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
Алгоритм составления уравнений по законом Кирхгофа
Алгоритм составления уравнений по законом Кирхгофа:
Составляем уравнения по первому закону Кирхгофа
Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.
- Количество уравнений по 1 закону киргофа равно количеству узлов минус один.
- Произвольно задаемся направлением токов в каждой ветви электрической цепи.
- Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
- Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
- Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.
Составляем уравнения по второму закону Кирхгофа
Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.
- Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-ВI-У+1 независимых уравнений. Где В — число ветвей в схеме. ВI— число ветвей в схеме с источником тока. У — число узлов в схеме.
- Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
- Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров.
- Задаемся произвольным направление обхода независимых контуров.
- Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
- Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком «+». Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком «-«.
- Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет «плюс». Если не совпадает, то знак — «минус».
Расчет токов по правилам Кирхгофа
Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.
Правильность расчета проверяется составлением уравнения баланса мощностей.
p.s. Правила Кирхгофа необязательно использовать в виде систем уравнений. Они справедливы для любого узла и для любого замкнутого контура электрической цепи.
11. Расчёт сложных схем по уравнениям Кирхгофа.
Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системы линейных уравнений c l неизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)
Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.
Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:
Выбирают положительные направления токов в ветвях электрической цепи.
Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.
Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.
Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.
Решают систему из (l-m) линейных уравнений любым удобным способом.
Пример.
На
рисунке изображена схема сложной
электрической цепи, содержащей 4 узла
и 6 ветвей (k=4, l=6). Для расчета цепи
необходимо составить систему из 6
линейных уравнений. Предварительно
выберем направления токов в каждой из
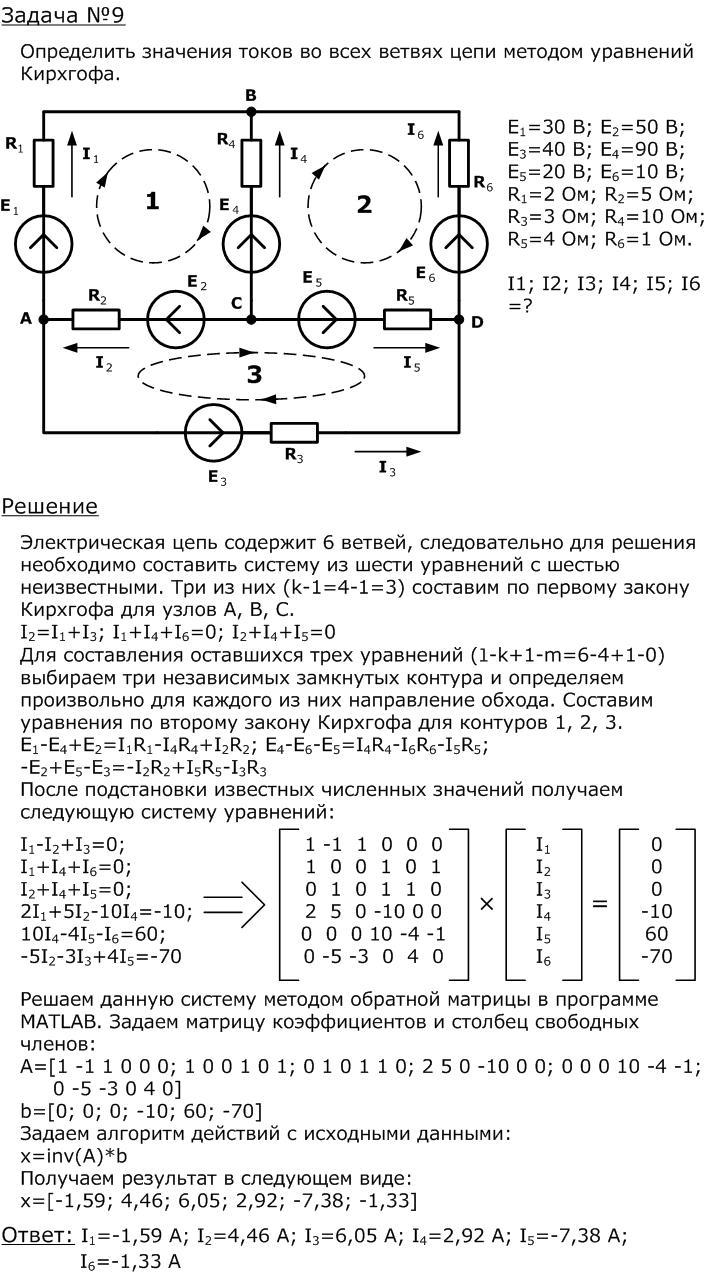
ветвей. По первому закону Кирхгофа 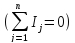
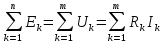 )
)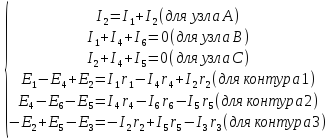
Подставляем известные значения
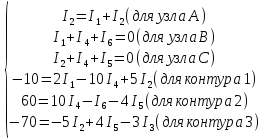
Решаем получившуюся систему.
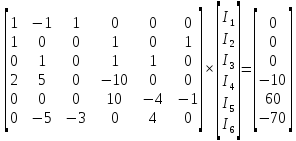
Получаем ответы в матричном виде.
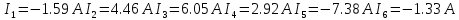
12. Метод контурных токов.
Теоретические сведения.
В данном методе расчета полагают, что в каждом контуре протекает свой контурный ток. Контурные токи и принимают за неизвестные, находят их, и уже затем через контурные токи определяют токи в ветвях. Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, количество неизвестных можно существенно сократить, включая источники в разные контура. В таких схемах применение этого метода наиболее рационально. Число неизвестных в данном методе равно количеству уравнений, которые необходимо было бы составить по второму закону Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.
Алгоритм расчета цепи методом контурных токов.
Определяем общее число ветвей p*
Определяем число ветвей с источниками тока pит.
Определяем число ветвей с неизвестными токами p*-pит
Определяем число контуров, необходимое и достаточное для определения всех неизвестных токов m= p*-(q-1).
Произвольно наносим на схему номера и направления неизвестных токов.
Обозначаем на схеме контура и выбираем направления их обхода. Необходимо, чтобы каждая ветвь входила хотя бы в один из обозначаемых контуров. При этом ветви с источниками тока обязательно включаем, но каждую в свой контур. Токи данных контуров считаем известными и равными токам источников – таким образом, число неизвестных сокращается.
Записываем выражения для токов в ветвях через контурные токи. Контурные токи в ветвях, не являющихся смежными, и будут истинными токами. Для ветвей, входящих в несколько контуров (смежных ветвей) истинный ток будет являться суммой либо разностью контурных токов данных контуров. При этом те контурные токи, которые совпадают по направлению с током в ветви, берем со знаком плюс, а те, направления которых противоположны – со знаком минус. Определяем собственные сопротивления контуров как сумму всех сопротивлений, входящих в контур (только для контуров без источников тока). Эти сопротивления обозначаются двойным повторяющимся индексом: и т.д.
Определяем сопротивления смежных ветвей и их знаки: плюс – если контурные токи сонаправлены в данной ветви, и минус, если их направления встречны. Эти сопротивления обозначаются двойным индексом, цифры которого указывают номера смежных контуров и т.д.
Аналогично определяем сопротивления ветвей, являющихся смежными с контурами, содержащими источники тока.
Определяем суммарную ЭДС контура (также обозначается двойным повторяющимся индексом — и т.д.). Это алгебраическая сумма ЭДС, входящих в данный контур, причем со знаком плюс берут те ЭДС, направления которых совпадают с выбранным направлением обхода, и наоборот, со знаком минус те, что направлены встречно.
Записываем систему уравнений по форме, приведенной ниже:
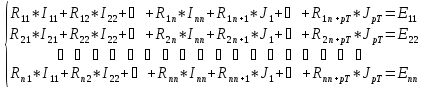
Решаем данную систему относительно контурных токов.
Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
Пример.
Найти токи в схеме рис. 35 с применением метода контурных токов.
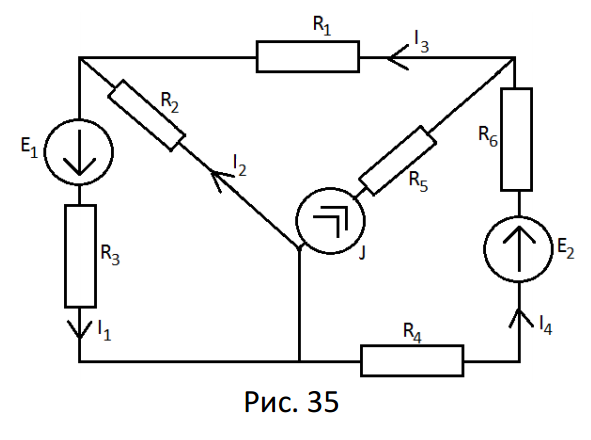
Дано: 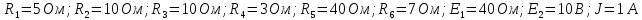
1.2.1.1. Топология цепи.
Определяем общее число ветвей: p*=5
Определяем число ветвей с источниками тока: pит=1.
Определяем число ветвей с неизвестными токами: p*- pит=4.Количество узлов – 3
Определяем необходимое и достаточное число контуров: 3
Произвольно наносим на схему номера и направления неизвестных токов (рис. 36)
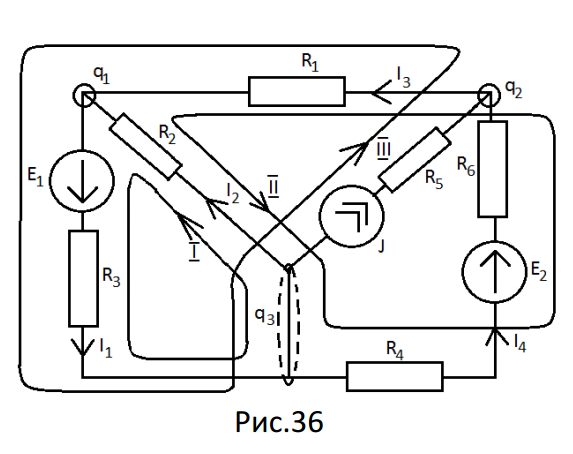
Определяем собственные сопротивления контуров (для контуров без источников тока):

Определяем сопротивления смежных ветвей и их знаки:

Аналогично определяем сопротивления ветвей, являющихся смежными с контуром, содержащим источник тока:

Определяем суммарную ЭДС контуров:

Записываем систему уравнений по форме:
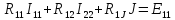
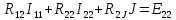
Если произвести подстановку сопротивлений, то видно, что данная система полностью совпала с системой, полученной в п. 7:
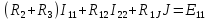
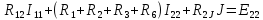
Решаем данную систему относительно контурных токов:

Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
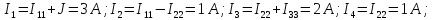
1.5. Методы расчета линейных электрических цепей Расчет цепей с использованием законов Кирхгофа
Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы через b, число ветвей, содержащих источники тока, через bИT, число узлов — у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется (b — bИT). Перед тем как составлять уравнения, необходимо произвольно выбрать: а) положительные направления токов в ветвях и обозначить их на схеме; б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.
Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т.е. у — 1. По второму закону Кирхгофа составляют число уравнений n , равное
n= b — bИT — (у — 1).
При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляются уравнения, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа, т.е. число уравнений по второму закону Кирхгофа равно числу независимых контуров.
Пример 1. Найти токи в ветвях схемы рис. 1.13, в которой Е1 = 80 В, Е2 = 64В, R1= 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4= 10 Ом.
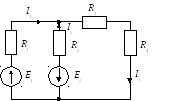
Рис. 1.13
Решение. Произвольно выбираем положительные направления тока в ветвях. В схеме рис. 1.13 b=3; bИТ=0; y=2.
Следовательно, по первому закону Кирхгофа можно составить только одно уравнение y-1=1:
 .
.
По второму закону Кирхгофа составим два уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.
Для контура R1E1R2E2
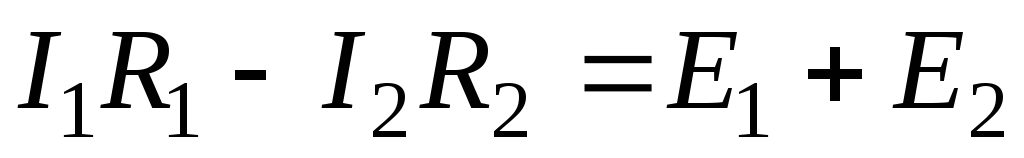 .
.
Знак плюс перед I1R1 взят потому, что направление тока совпадает с направлением обхода контура, а знак минус перед I2R2 потому, что направление I2 встречно обходу контура.
Для контура E2R2R3R4:
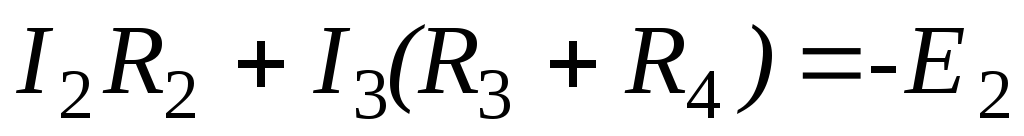 .
.
Совместное решение трех уравнений дает
I1 = 14 A, I2 = -15 A, I3 = -1 A.
В рассматриваемом примере отрицательными оказались токи I2 и I3, это следует понимать так, что в действительности токи I2 и I3 направлены в обратную сторону.
Метод контурных токов
При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
Таким образом, метод контурных токов можно определить как метод расчета, в котором в качестве неизвестных принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, составляемых для схемы по второму закону Кирхгофа. Преимуществом этого метода, по сравнению с методом на основе законов Кирхгофа, является меньшая вычислительная работа, так как в нем меньше уравнений.
Вывод основных расчетных уравнений проведем применительно к схеме рис. 1.14, содержащей два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток I11 , а в правой (также по часовой) — контурный ток I22. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что в смежной ветви (с сопротивлением Rs) течет сверху вниз ток I11 — I22. Направления обхода контуров примем также по часовой стрелке.
Для первого контура
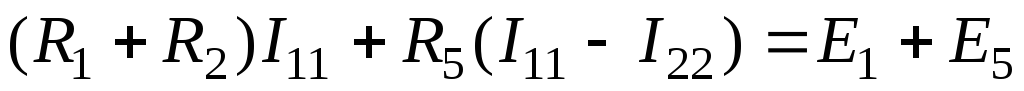
или
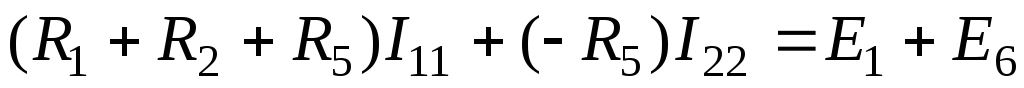 . (1.24)
. (1.24)
Для второго контура
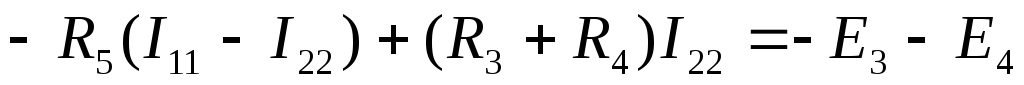
или
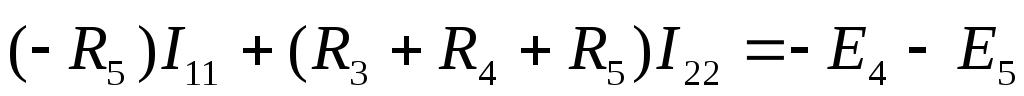 . (1.25)
. (1.25)
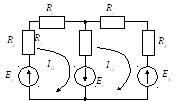
Рис. 1.14
В уравнении (1.24) множитель при токе I11, являющийся суммой сопротивлений первого контура, обозначим через R11, множитель при токе I22 (сопротивление смежной ветви, взятое со знаком минус), – через R12.
В уравнении (1.25) множитель при токе I22, являющийся суммой сопротивлений второго контура, обозначим через R22, множитель при токе I11(сопротивление смежной ветви, взятое со знаком минус), – через R21.
Перепишем эти уравнения следующим образом:
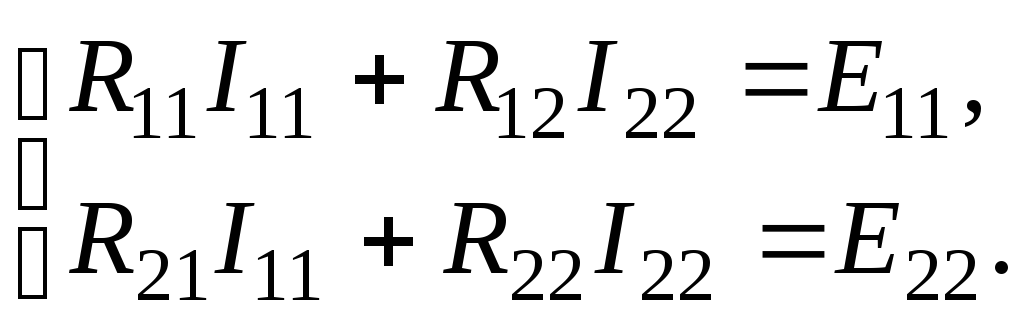
Здесь
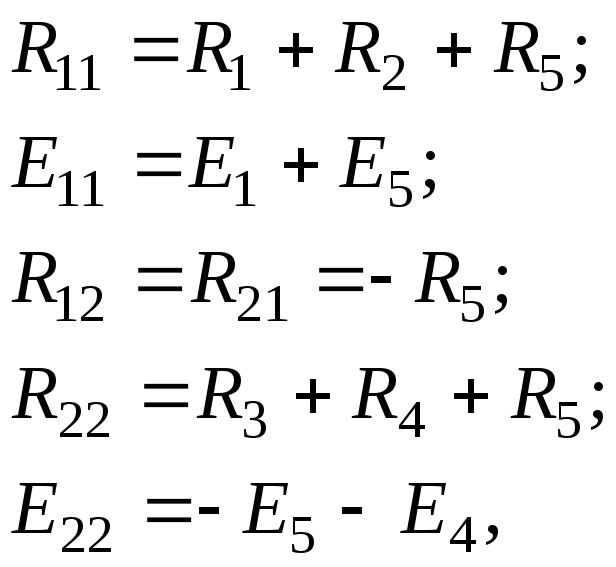
где R11 и R22 — полное или собственное сопротивление первого и второго контуров соответственно; E11 и Е22 — контурные ЭДС первого и второго контуров, равные алгебраической сумме ЭДС этих контуров; R12 = R21 -сопротивление смежной ветви между первым и вторым контуром, взятое со знаком минус, так как контурные токи по ветви протекают встречно.
Если в схеме больше контуров, например три, то система уравнений в общем виде выглядит следующим образом:
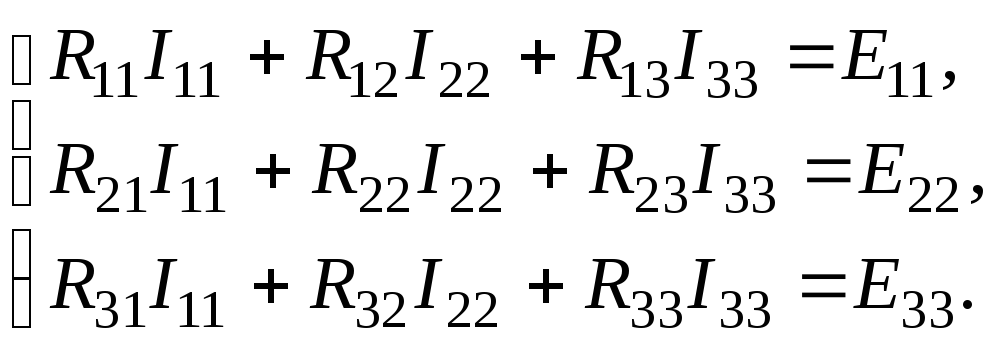 (1.26)
(1.26)
В результате решения системы уравнений (1.26) какой-либо один или несколько контурных токов могут оказаться отрицательными.
В ветвях, не являющихся смежными между соседними контурами, найденный контурный ток является истинным током ветви. В смежных ветвях через контурные токи определяются токи ветвей.
Если в электрической цепи имеется n независимых контуров, то число уравнений тоже равно n.
Общее решение системы n-уравнений относительно тока Ikk таково:
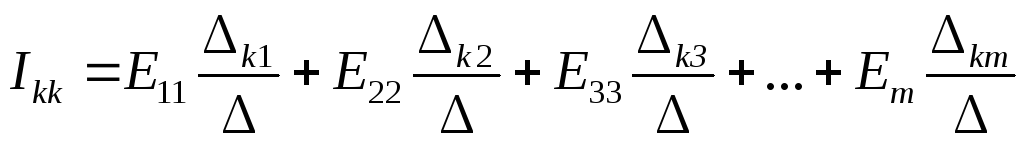 , (1.27)
, (1.27)
где — определитель системы.
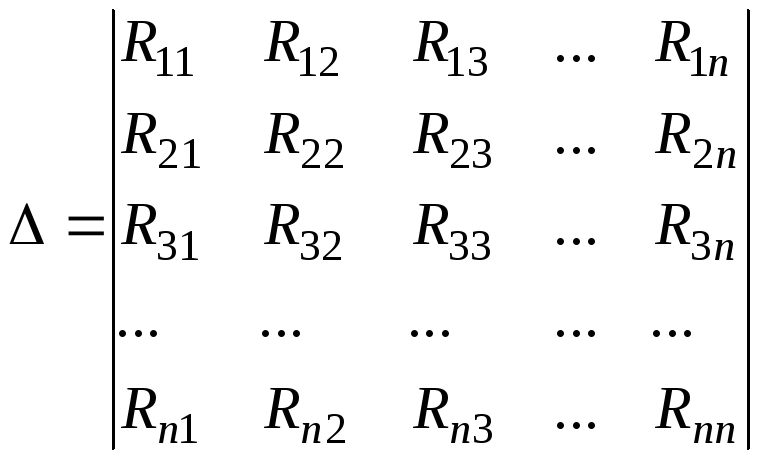 .
.
Алгебраическое дополнение ∆km, получено из определителя ∆ путем вычеркивания k-го столбца и m-й строки и умножения полученного определителя на (-1)k+ m.
Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока. Если для схемы рис. 1.15 принять, что контурный ток I11= J течет согласно направлению часовой стрелки по первой и второй ветвям, а контурный ток I22 = I3 замыкается также по часовой стрелке по второй и третьей ветвям, то, согласно методу контурных токов, получим только одно уравнение с неизвестным током I22:
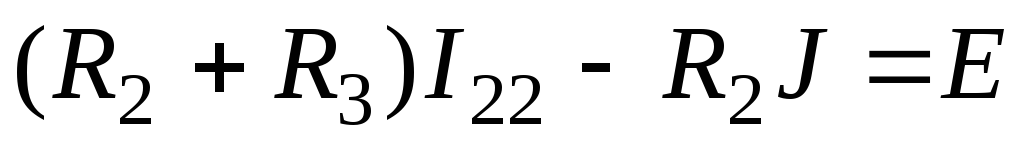 .
.
Отсюда 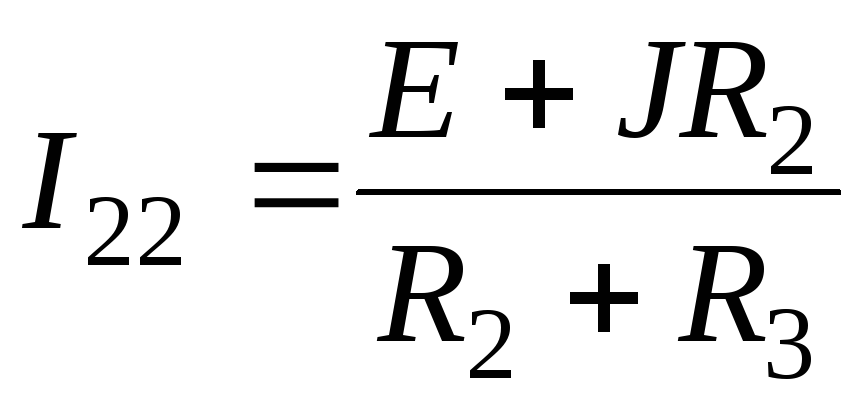 и ток второй ветвиI2=I11—I22=J—I22 .
и ток второй ветвиI2=I11—I22=J—I22 .
1
E3
Рис. 1.15
1.7.2 Метод законов Кирхгофа
Рассмотрим расчет сложной цепи методом законов Кирхгофа.
Для схемы, приведенной на рисунке 1.31, дано: Е1; Е3; R1; R2; R3.
Рисунок 1.31 — Расчетная схема
Найти
1. Все токи.
2. Проверить полученные результаты на баланс токов и баланс мощности.
3. Напряжения на всех элементах цепи.
4. Проверить напряжения на баланс напряжений.
Порядок расчета
Размечаем токи.
Как и ранее, токи размечаются стрелками непосредственно на проводах схемы. Стрелки токов направляются в произвольном направлении. Неизвестных токов будет столько, сколько имеется ветвей в сложной цепи. Индекс тока принимается равным индексу ветви.
2. Размечаем стрелки напряжений на элементах цепи. Стрелки расставляем не произвольно, а всегда против ранее размеченных стрелок токов. Произвольно стрелки напряжений размечать нельзя.
Составляем уравнения электрического состояния цепи.
Для решения нашей задачи требуется система из трех уравнений. По первому закону Кирхгофа число уравнений будет
. (1.56)
По второму закону Кирхгофа число уравнений будет
. (1.57)
Имеем:
; ;
; но , поэтому
; .
. (1.58)
Решаем систему уравнений.
При решении уравнений можно использовать вычислительную технику или производить данную операцию вручную. В данном случае применим метод определителей (метод Крамера).
Имеем:
; ;
(1.59)
; .
Тогда токи будут равны:
; ;. (1.60)
Проверяем полученный результат на баланс токов.
Проверка производится во всех независимых узлах сложной цепи по первому закону Кирхгофа.
.
Проверяем полученный результат на баланс мощности.
По закону сохранения энергии количество выработанной в цепи и потребленной энергии должны быть равны.
Выработано
, если .
Израсходовано
.
При правильном значении токов имеем:.
Непосредственное применение законов Кирхгофа к расчету сложной цепи приводит к весьма громоздким вычислениям, так как приходится решать систему с большим числом уравнений. Поэтому, этот метод на практике применяется крайне редко из за его неэкономичности.
1.7.3 Метод контурных токов
Метод контурных токов был предложен известным английским физиком и электротехником Джеймсом К. Максвеллом. По этому методу цепь разбивается на ряд контуров, соприкасающихся друг с другом. Число контуров подсчитывается по формуле (1.14).
Предполагается, на время расчета, что каждый контур обтекается только присущим ему током, который называется контурным током.
Контурный ток — нереальный ток, он является вспомогательным средством при решении цепей.
Контурных токов столько, сколько имеется в цепи независимых контуров. Контуров в цепи всегда меньше числа ветвей, так как, даже для простого контура требуется, по крайней мере, две ветви.
Указанное обстоятельство приводит к тому, что контурных токов в цепи всегда меньше числа реальных токов.
Таким образом, основное преимущество метода контурных токов перед методом законов Кирхгофа состоит в сокращении числа расчетных уравнений.
По известным контурным токам, действительные токи определяются простым алгебраическим сложением.
Рассмотрим порядок расчета цепи указанным методом.
Для цепи, изображенной на рисунке 1.32, дано: Е1; Е3; R1; R2; R3.
Рисунок 1.32 — Расчетная схема
Найти
1. Все токи.
2. Проверить полученные результаты на баланс токов и баланс мощности.
3. Напряжения на всех элементах цепи.
4. Проверить напряжения на баланс напряжений.
Порядок расчета
Размечаем контурные токи.
Направление токов выбирается произвольно, однако, где это возможно, желательно в смежных ветвях иметь их сумму.
Размечаем стрелки напряжений.
Стрелки напряжений расставляют по общему правилу, то есть всегда против ранее размеченных контурных токов. Стрелки напряжений снабжаются двумя индексами. Первый индекс — номер элемента, второй — номер контурного тока.
Составляем уравнения электрического состояния цепи.
Для этого обходим каждый контур в произвольном направлении и составляем уравнения по второму закону Кирхгофа
. (1.61)
Решаем уравнения электрического состояния цепи.
Решение, как и ранее, проводим с помощью определителей:
;
; (1.62)
.
Отсюда:
;
. (1.63)
Размечаем действительные токи в цепи.
Действительные токи можно направлять произвольно, однако, лучше учитывать при разметке направления и значения контурных токов, через которые они определяются. Стрелки действительных токов показаны на рисунке 1.32.
Определяем действительные токи.
Для этого имеем:
(1.64)
Проверяем значения токов на баланс токов.
Проверку производим в каждом узле цепи по первому закону Кирхгофа
. (1.65)
Проверяем значения токов на баланс мощности
. (1.66)
Метод контурных токов получил широкое распространение в инженерной практике, благодаря экономным затратам времени на расчет.
Первый и второй законы Кирхгофа и их практическое применение
Уравнения, или правила, Кирхгофа относят к основным законам электрических цепей.
Они вытекают из таких фундаментальных законов как, закон сохранения заряда и безвихревости электростатического поля, в своё время описанных уравнениями Максвелла. Уравнения Кирхгофа довольно часто используются благодаря своей универсальности, пригодности для решения многих задач в теории электротехники, в том числе и связанных с расчётами сложных электрических цепей, практичности. Применяя правила Кирхгофа к линейной электрической цепи можно получить систему линейных уравнений, из которых в свою очередь, можно найти значения токов на всех ветвях цепи и все межузловые напряжения.
В правилах Кирхгофа применяют такие понятия электрической цепи, как: узел, ветвь, контур. Участок электрической цепи с одним и тем же током называют ветвью, например отрезок 1-4, на рисунке 1, с протекающим по нему током i1 , есть ветвь. Точку, соединяющую три и более ветви называют узлом, например точки 1,2,3,4 на рисунке 1 есть узлы. Замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи называют контуром. Начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, и возвратившись в исходный узел, мы пройдём путь, который и называют замкнутым. Проходимые при таком обходе ветви и узлы принято называть принадлежащими данному контуру, при этом надо принимать во внимание, что ветвь и узел могут принадлежать одновременно нескольким контурам.
 Рисунок 1
Рисунок 1Первое правило Кирхгофа построено на основании утверждения о непрерывности электрического тока для любого узла электрической цепи или замкнутого контура.
Первое правило Кирхгофа трактует, что алгебраическая сумма токов ветвей , для любого узла или замкнутого сечения электрической цепи, равна нулю:

Выше сказанное говорит о том, что электрические заряды в узле (например, S2 на рисунок 1) или сечении (например, S14 на рисунке 1) любой электрической цепи накапливаться не могут. Иными словами, сколько тока втекает в узел, столько из него и вытекает.
Второе правило Кирхгофа основано на утверждении, что любая электрическая цепь является потенциальной, а работа по перемещению электрических зарядов в замкнутом контуре равна нулю:

где U – работа(электрическое напряжение), k – число источников выполняющих работу;
Рассмотрим цепь, изображённую на рисунке1, образованную двухполюсными элементами, где ветви в местах соединений образуют узлы 1,2,3,4 и где направления напряжений и токов в ветвях совпадают. Для составления уравнений Кирхгофа выберем произвольно узел S2 , замкнутое сечение S14 (”несколько узлов”) и замкнутый контур 1, направление обхода которого изображено на рисунке 1.
Если принять, что выходящие из сечений и узлов токи считать положительными, а входящие отрицательными, то тогда уравнения составленные по первому правилу Кирхгофа будут иметь вид:

Для составления уравнения по второму правилу Кирхгофа, напряжения совпадающие с направлением обхода контура считаем положительными, а не совпадающие отрицательными. При этом уравнение примет вид:

Рассмотрим второе правило Кирхгофа на более наглядном примере (рисунке 2, см. ниже) и с более понятной для практического применения трактовкой, утверждающей что: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
 Рисунок 2
Рисунок 2Применяя второе правило Кирхгофа составляем уравнение для замкнутого контура схемы(рисунок 2) :

При составлении полученного уравнения знаки учитывались как:
— ЭДС (E) положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
— падение напряжения (IR) на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Мы рассмотрели применение правил Кирхгофа на простых примерах цепей постоянного тока и напряжений. На самом деле электрические цепи бывают значительно сложнее и состоять из различных элементов (источников ЭДС и тока , нелинейных и т.п.). Например, для второго правила Кирхгофа физическое представление уравнения для переменного тока уже будет иметь вид:
Следует отметить, что для цепей синусоидального(переменного) тока правила Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Чтобы решать уравнения Кирхгофа для цепей синусоидального тока их составляют в комплексной форме, в которой учитываются ”мгновенные” изменения значений токов и напряжений.
Но какие сложные уравнения не приходилось бы составлять и решать, следует помнить, что физически второе правило(закон) Кирхгофа характеризует равновесие напряжений в любом контуре цепи.
Основы электротехники и электроники: Курс лекций, страница 3
При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.
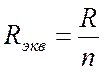
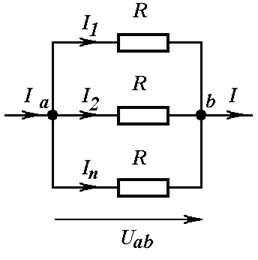
Рис. 3.3
Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:
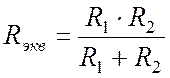
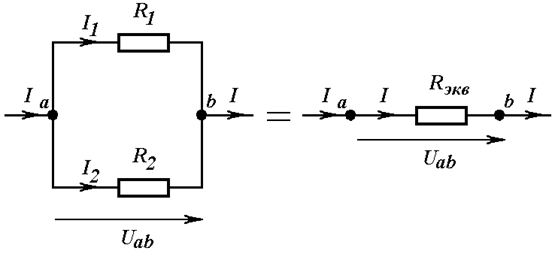
Рис. 3.4
4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.
Закон Ома
Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):
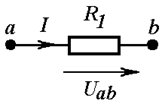
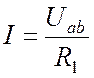
Рис. 4.1
Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.
В частности, ток в ветви, изображенной на Рис. 4.2, равен:
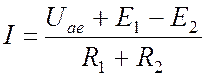 .
.
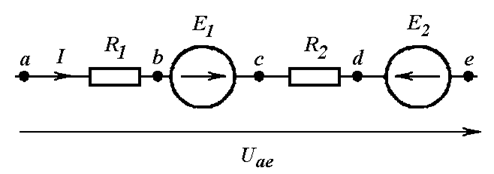
Рис. 4.2
Первый закон Кирхгофа
В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (Рис. 4.3).
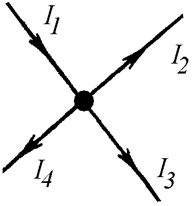
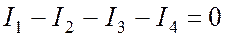
Рис. 4.3
По первому
закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема.
Но не все они будут независимыми. Если схема содержит 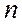 узлов,
независимыми будут
узлов,
независимыми будут 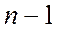 уравнений. Оставшееся
уравнение будет являться следствием всех предыдущих.
уравнений. Оставшееся
уравнение будет являться следствием всех предыдущих.
Второй закон Кирхгофа
В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.
При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.
Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:
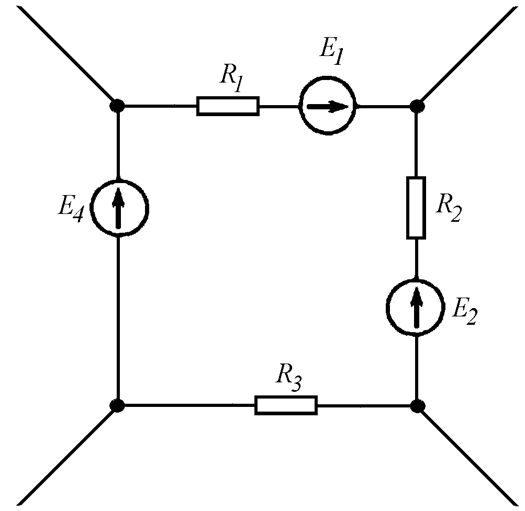
Рис. 4.4 а
- Задается направление токов в ветвях (Рис. 4.4 б).
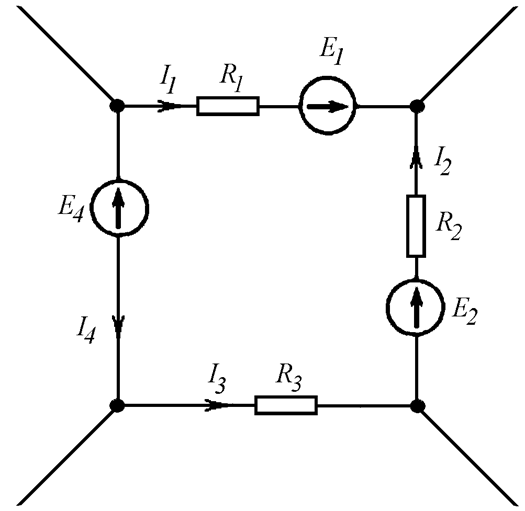
Рис. 4.4 б
- Выбирается направление обхода контура (Рис. 4.4 в).
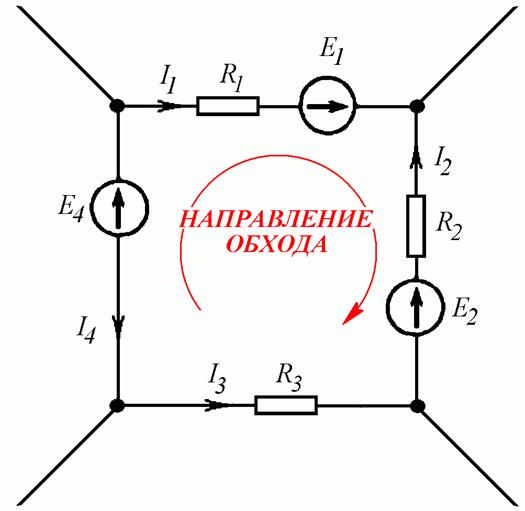
Рис. 4.4 в
- Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.
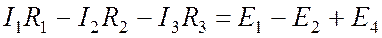
Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):
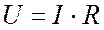
Применение второго закона Кирхгофа для незамкнутого участка цепи
Второй закон Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.
Пример 4.1:
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.
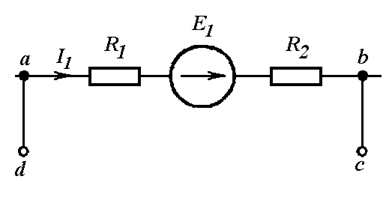
а)
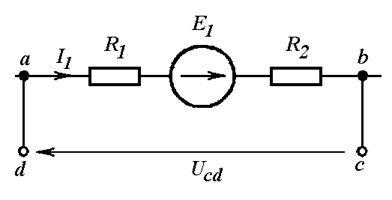
б)
Рис. 4.5
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:
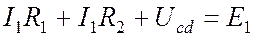
Применение законов Кирхгофа при наличии в цепи источника тока
Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.
При необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его заменяют напряжением на выводах источника тока.
Пример 4.2:
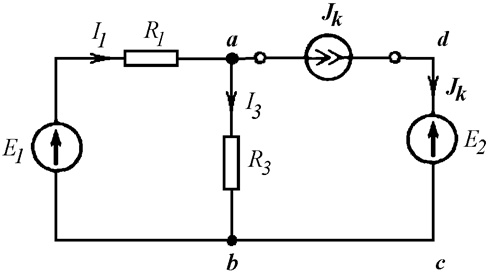
Написать уравнение по первому закону Кирхгофа для узла a и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
а)
б)
Рис. 4.6
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:
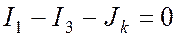
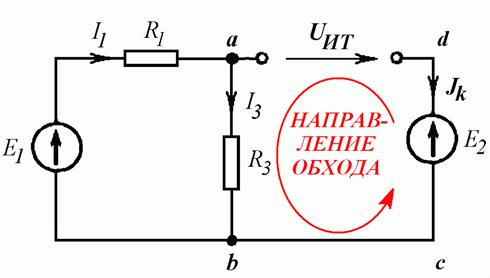
Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (Рис. 4.6 б), задаем направление обхода контура против часовой стрелки и получаем:
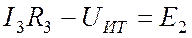
Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.
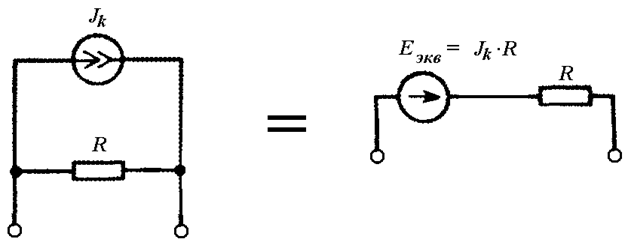
Рис. 4.7
Независимый контур цепи
В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.
Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.
Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).
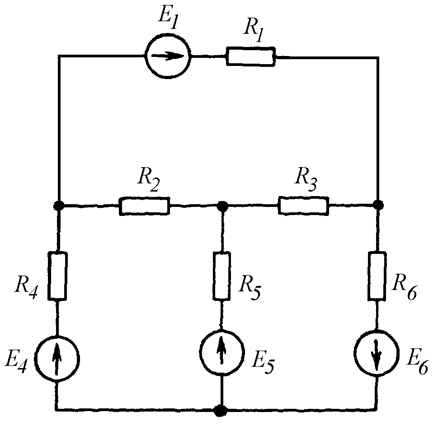
а)
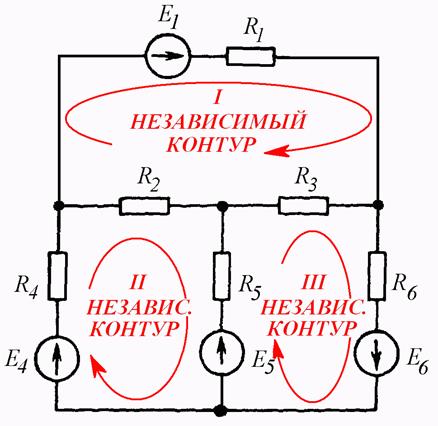
б)
Рис. 4.8
Если схема
содержит  ветвей и
ветвей и 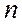 узлов,
число независимых контуров равно
узлов,
число независимых контуров равно
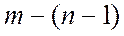 .
.
Схема на Рис. 4.8 б содержит три независимых контура.
5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.
Алгоритм составления системы уравнений по законам Кирхгофа