Система уравнений кирхгофа: Расчет электрической цепи по закону Кирхгофа

Содержание

Примеры решения задач на законы Кирхгофа

Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.

Задача 1

Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.

Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус.

Аналогично с источниками ЭДС.

На примере первого контура – ток I₁ и I₃ совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.

Уравнения для первого и второго контуров по второму закону будут:

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.

Задача 2

Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2

Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.

На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины

Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.

Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.

Читайте также — расчет простых цепей постоянного тока

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.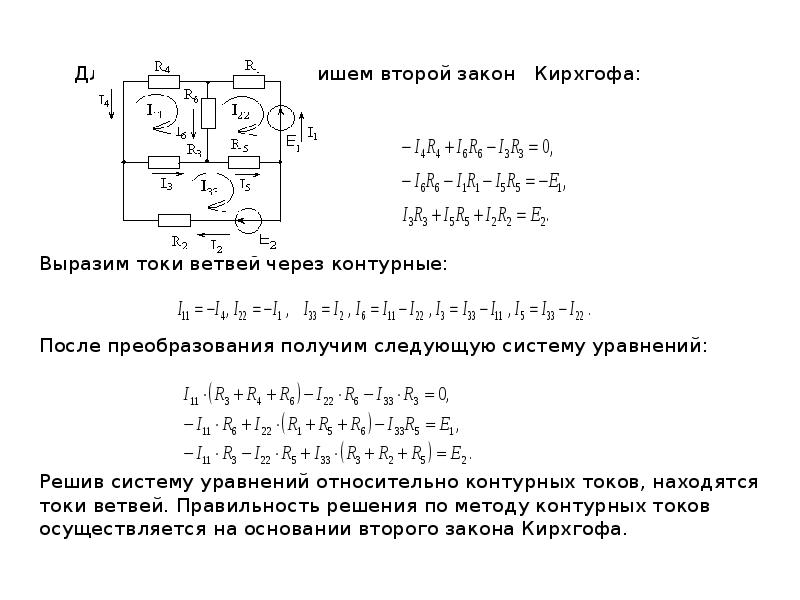

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить

замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

$$ \sum{i} = 0, $$

или в комплексной форме

$$ \sum{\underline{I}} = 0. $$

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

$$ \sum{\underline{Z} \cdot \underline{I}} = \sum{\underline{E}}. $$

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно $ N_\textrm{у}-1 $, где $ N_\textrm{у} $ – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно $ N_\textrm{в}-N_\textrm{у}+1 $, где $ N_\textrm{в} $ – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что

контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4.

Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока $ \underline{J}_{1} $, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0; $$

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0; $$

для узла «3 у.»:

$$ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0; $$

для узла «4 у.»:

$$ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0. $$

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1}; $$

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2}; $$

для контура «3 к.»:

$$ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3}; $$

где $ \underline{Z}_{C} = -\frac{1}{\omega C} $, $ \underline{Z}_{L} = \omega L $.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

$$ \begin{cases} \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0 \\ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0 \\ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0 \\ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0 \\ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1} \\ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2} \\ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3} \end{cases} $$

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

$$ \begin{bmatrix} 1 & -1 & -1 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 1 & 0 & -1 & 0 & 0 \\ \underline{Z}_{C1} & R_{2} & 0 & -\underline{Z}_{L1} & 0 & 0 & 0 \\ 0 & -R_{2} & R_{4} & 0 & \underline{Z}_{C2} & 0 & 0 \\ 0 & 0 & 0 & \underline{Z}_{L1} & 0 & R_{1}+\underline{Z}_{L2} & R_{3} \\ \end{bmatrix} \cdot \begin{bmatrix} \underline{I}_{1} \\ \underline{I}_{2} \\ \underline{I}_{3} \\ \underline{I}_{4} \\ \underline{I}_{5} \\ \underline{I}_{6} \\ \underline{I}_{7} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \underline{J}_{1} \\ \underline{E}_{1} \\ \underline{E}_{2} \\ \underline{E}_{3} \\ \end{bmatrix} $$

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1  -1 -1    0   0        0  0;
       -1   0  0   -1   0        1  0;
        0   1  0    1   1        0 -1;
        0   0  1    0  -1        0  0;
      Zc1  R2  0 -Zl1   0        0  0;
        0 -R2 R4    0 Zc2        0  0;
        0   0  0  Zl1   0 (R1+Zl2) R3];
>> b = [0;
        0;
        0;
       J1;
       E1;
       E2;
       E3];
>> I = A\b

В результате получим вектор-столбец $ \underline{\bold{I}} $ токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

1) Составить уравнения по законам Кирхгофа.

Некоммерческое акционерное общество

«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»

Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1

По дисциплине «Основы теории цепей»

На тему «Расчет линейных электрических цепей постоянного тока с зависимыми источниками»

Специальность «Информационные системы»

Выполнил Ануарбеков Шыңғыс Группа ИС-16-2

Принял доцент каф. ТОЭ Айтжанов Н.М.

_________ «____»____________2017г.

Алматы 2017

Содержание

Введение……………………………………………………………………………………………………3

Задание………………………………………………………………………………………………………4

Расчетная часть………………………………………………………………………………………….6

Уравнения по законам Кирхгофа………………………………………………………..6

Метод контурных токов……………………………………………………………………..7

Метод узловых потенциалов…………………………………………….. ……………….9

Сравнение результатов МКТ и МУП…………………………………………………10

Метод эквивалентного генератора……………………………………………………..11

Напряжение на зажимах источника тока……………………………………………13

Баланс мощностей…………………………………………………………………………….13

Заключение………………………………………………………………………………………………14

Список литературы…………………………………………………………………………………..15

Введение

Цель работы: умение составлять систему уравнений по законам Кир-хгофа; применение закона Ома; получение навыков расчётов электрических цепей постоянного тока с зависимыми источниками методами контурных токов, методом узловых потенциалов, эквивалентного генератора.

В цепи действуют независимые источники напряжения с ЭДС Е₁, Е₂, Е₃, источник тока J и зависимый источник напряжения Е_и, управляемый током. Номер схемы определяется по таблице 1.1, числовые значения параметров цепи приведены в таблицах 1.2 и 1.3.

Таблица 1.1

Год поступления	Первая буква фамилии
Четный	А БЯ	ГЭЕ	ЖЗЩ	КЛ	МН	ОПР	СТУ	ФЧЦ	ХШИ	ДЮВ
№ схемы	1. 1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	1.10
МЭГ	I₁	I₃	I₄	I₂	I₁	I₄	I₃	I₃	I₁	I₂

Таблица 1. 2

Год поступления	Последняя цифра номера студенческого билета
Четный	0	9	8	7	6	5	4	3	2	1
E₁, В	25	20	30	40	20	25	15	35	40	15
E₂, В	10	15	25	20	30	20	15	10	20	25
E₃, В	25	30	35	20	30	20	25	15	30	10
J, А	3	5	2	6	4	10	8	5	3	5
r, Ом	10	20	15	16	25	30	35	40	15	20

Таблица 1.3

Год поступления	Предпоследняя цифра номера студенческого билета
Четный	1	2	3	4	5	6	7	8	9	0
R₁, Ом	25	20	15	20	10	30	20	10	30	15
R₂, Ом	15	30	20	12	20	10	20	25	40	20
R₃, Ом	20	16	25	35	30	20	30	16	10	30
R₄, Ом	30	20	30	40	15	40	15	25	20	30
R, Ом	6	10	8	10	10	15	20	15	5	8

Рисунок 1.1

Задание:

1) Составить уравнения по законам Кирхгофа.

2) Рассчитать токи во всех ветвях методом контурных токов.

3) Рассчитать токи во всех ветвях методом узловых потенциалов. 4) Сравнить результаты, полученные в пунктах 2, 3 и свести их в

одну таблицу.

5) Рассчитать ток в одной ветви методом эквивалентного генератора (см. таблицу 1.1).

6) Определить напряжение на зажимах источника тока.

7) Проверить выполнение баланса мощности.

Расчетная часть

Первый закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю: . Со знаком «+» записываются токи, направленные к узлу, со знаком «-» записываются токи, направленные от узла (или наоборот). Число уравнений, составляемых по первому закону Кирхгофа, равно , где — число узлов в цепи. В цепи (рис 1.1) имеются 4 узла, исходя из этого У = 4-1 = 3 (количество уравнений по I закону Кирхгофа). Следовательно, достаточно записать уравнения для узлов 1, 2 и 3.

Второй закон Кирхгофа: в любом замкнутом контуре электрической цепи алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур равна алгебраической сумме ЭДС: . Напряжения записываются со знаком «+», если положительное направление тока совпадает с направлением обхода контура, со знаком «-», если направление тока противоположно направлению обхода контура; ЭДС , направления, которых совпадают с направлением обхода контура, записываются со знаком «+», а ЭДС , направленные против обхода контура – со знаком «-». Число уравнений, составляемых по второму закону Кирхгофа, равно: , где — число ветвей, — число источников тока. Исходя из этого, в цепи (рис 1.1) 6 ветвей, 1 источник тока и как было выше сказано – 4 узла. Следовательно, для второго закона Кирхгофа понадобится К = 6-1-3=2 уравнения. Выбираем два независимых контура, не имеющих источника тока, затем произвольно выбираем обход контура (рис 1.1). И для каждого контура (внешний контур и контур 1241) запишем уравнение по II закону Кирхгофа:

Общая система уравнений по законам Кирхгофа будет выглядеть следующим образом

2) Рассчитать токи во всех ветвях методом контурных токов.

Составим систему уравнений по методу контурных токов для цепи постоянного тока (рис 1.2):

Рисунок 1.2.

, где

= (

Решение:

= = =

= =

= = =

, тогда

=7,73 – 7,53 = 0,2А

= 7,53А

= 7,73А

= 10 – 7,53 = 2,47А

= 010– 7,73 = 2,27А

3) Рассчитать токи во всех ветвях методом узловых потенциалов.

Метод узловых потенциалов позволяет уменьшить число уравнений системы до числа . Суть метода узловых потенциалов заключается в определении потенциалов узлов электрической цепи, токи рассчитываются по закону Ома. При составлении уравнений по методу узловых потенциалов, потенциал одного из узлов принимают равным нулю, для определения потенциалов оставшихся узлов составляются уравнения.

Возьмем узел 3 за базовый и будем считать, что он равен нулю. Автоматически значение потенциала в узле 4 становится равным .

().

Составим систему уравнений по методу узловых потенциалов для цепи постоянного тока (рис 1.3), так как значения потенциалов в узлах 3 и 4 известны, то нам необходимо составить систему из 2 уравнений для узлов 1 и 2:

Рисунок 1.3

найдем, применив I закон Кирхгофа

Решение:

, тогда

=0,99*68,2694 = 67,586706В

= 0,115 А

= 7,47А

= 2,46А

= 2,25А

7,35А

Законы Кирхгофа и их применение

Для расчета разветвленной сложной электрической цепи существенное значение имеет число ветвей и узлов.
Ветвью электрической цепи и ее схемы называется участок, состоящий только из последовательно включенных источников ЭДС и приемников с одним и тем же током. Узлом цепи и схемы называется место или точка соединения трех и более ветвей (узлом иногда называют и точку соединения двух ветвей).
При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

На рис. 1.13 в качестве примера показана схема электрической цепи с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с резистивными элементами без источников ЭДС (ветвь 1 — у) и с сопротивлениями, практически равными нулю (ветвь 2 — р). Так как напряжение между выводами ветви 2 — р равно нулю (сопротивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один.
Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна пулю:

В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, направленные к узлу, с отрицательными знаками, а направленные от узла, — с положительными.
Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В дальнейшем будет показано, что в ряде случаев целесообразно писать в одной части равенства (1.19а) алгебраическую сумму токов в ветвях, а в другой части алгебраическую сумму токов, обусловленных источниками токов:

где I — ток одной из ветвей, присоединенной к рассматриваемому узлу, a J — ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в (1.196) с положительным знаком, если направлен к узлу, и с отрицательным, если направлен от узла.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю:

при этом положительные направления для напряжений на элементах и участках выбираются произвольно; в уравнении (1.20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.

Часто применяется другая формулировка второго закона Кирхгофа: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящими в этот контур, равна алгебраической сумме ЭДС:

В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике довольно часто встречаются задачи анализа. Кроме того, для овладения приемами синтеза цепей необходимо предварительно изучить методы их анализа, которые преимущественно и будут в дальнейшем рассматриваться.
Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны параметры всех элементов цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа и, наконец, составить уравнения для контуров на основании второго закона Кирхгофа.
Пусть электрическая цепь содержит В ветвей и У узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно У — 1 и В — У + 1 взаимно независимых уравнений, что в сумме дает необходимое и достаточное число уравнений для определения В токов (во всех ветвях).
На основании первого закона Кирхгофа для У узлов (рис. 1.13) можно написать У уравнений:

Так как любая ветвь связывает между собой только два узла, то ток каждой ветви должен обязательно войти в эти уравнения 2 раза, причем I₁₂=-I₂₁; I₁₃=-I₃₁ и т.д.
Следовательно, сумма левых частей всех У уравнений дает тождественно нуль. Иначе говоря, одно из У уравнений может быть получено как следствие остальных У — 1 уравнений или число взаимно независимых уравнений, составленных на основании первого закона Кирхгофа, равно У — 1, т. е. на единицу меньше числа узлов. Например, в случае цепи по рис. 1.14,о с четырьмя узлами

Добавим к этим У — 1 = 3 уравнениям уравнение

Суммируя четыре уравнения, получаем тождество 0 = 0; следовательно, из этих четырех уравнений любые три независимые, например первые три (1.21а).
Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности — сечению.

Законы Кирхгофа

Законы Кирхгофа: Первый и второй законы Кирхгофа.

Вытекает из закона сохранения заряда.
Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где i – число токов, сходящихся в данном узле.
Например, для узла электрической цепи ( рис. 1 ) уравнение по первому закону Кирхгофа можно записать в виде
I1 — I2 + I3 — I4 + I5 = 0

Рис. 1
В этом уравнении токи, направленные к узлу, приняты положительными.

Второй закон Кирхгофа.

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i — й ветви.
Рис. 2
Так, для замкнутого контура схемы ( рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
Замечание о знаках полученного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа.

Точечные тела (материальные точки) взаимодействуют с силами, равными по величине и противоположными по направлению и направленными вдоль прямой, соединяющей эти тела.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b, следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.
Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — ( y — 1 ) = b — y + 1.
Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
Составим систему уравнений Кирхгофа для электрической цепи ( рис. 3 ). Схема содержит четыре узла и шесть ветвей.
Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3, также три уравнения.
Произвольно выберем положительные направления токов во всех ветвях ( рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Рис. 3
Составляем необходимое число уравнений по первому и второму законам Кирхгофа
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.

Первый и второй законы Кирхгофа для электрических цепей

Понятия узла, ветви и контура электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа.
Преобразование электрической цепи треугольник-звезда с онлайн калькулятором.

Законы Кирхгофа, они же правила Кирхгофа (ибо фундаментальными законами не являются) – это ряд условий (в количестве двух штук) для составления системы линейных уравнений, описывающих соотношения между токами и напряжениями в разветвлённых электрических цепях.
Законы Кирхгофа довольно универсальны. Они справедливы для линейных и нелинейных цепей, постоянного и переменного токов и в совокупности с законом Ома позволяют определить параметры электрических цепей любой сложности.

Для формулирования своих правил Кирхгоф ввёл несколько понятий, таких как: узел, ветвь и контур, значение которых поясним на простом примере (Рис.1).

Рис.1 Пример схемы электрической цепи

Узлом называется точка соединения трёх и более ветвей (на принципиальных схемах обычно обозначается жирной точкой).
На Рис.1, приведённом в качестве примера электрической цепи – это точки А, В, С.

Ветвью называют участок электрической цепи с одним и тем же значением тока.
На Рис.1 – это 5 ветвей с токами I1…I5.

Контуром называется замкнутый путь, по которому протекает электрический ток, проходя через несколько участков цепи, включающих в себя узлы и ветви. На Рис.1 контуры изображены круглыми стрелками.

Теперь, определившись с терминами, можно переходить к формулированию законов Кирхгофа.

Первый закон или правило Кирхгофа вытекает из закона сохранения заряда и провозглашает, что алгебраическая сумма токов, сходящихся в каждом узле любой цепи, равна нулю.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Если следовать примеру, приведённому на Рис.1, то для узла А: I1+I4-I3=0.

Переходим ко второму закону Кирхгофа, который вытекает из третьего уравнения Максвелла и формулируется следующим образом:
Алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической (т. е. с учётом знака) сумме падений напряжений на всех элементах этого контура. Если в контуре нет источников ЭДС (генераторов напряжения), то суммарное падение напряжений равно нулю.
Направление обхода ветвей контура выбирается произвольно. Падение напряжения считают положительным, если направление тока ветви совпадает с ранее выбранным направлением обхода, в противном случае – отрицательным.
Припадаем к рисунку Рис.1, выбираем один из трёх контуров и констатируем:
U_R2 + U_R4 + U_R3 = Е2.

Законы законами, да и правила – вещь не самая бесполезная в радиолюбительском хозяйстве, только как воспользоваться всей этой полученной информацией на практике? Давайте с этим разберёмся и рассмотрим схему более приближённую к реальной жизни, чем та, которую мы приводили ранее в качестве примера, а конкретно – схему несбалансированного резистивного моста (Рис.2).

Рис.2 Пример применения правил
Кирхгофа

Для расчёта токов, протекающих в цепях, для начала воспользуемся первым правилом Кирхгофа:
I_общ = I1 + I4 = I2 + I5 ;
I1 = I2 + I3 ..

Согласно второму правилу и закону Ома:
I1*R1 + I2*R2 = E ;
I4*R4 + I5*R5 = E ;
I1*R1 + I3*R3 + I5*R5 = E .

Ну и хватит: пять уравнений, пять неизвестных – вполне достаточно, для того чтобы получить искомые значения всех токов.

Правда возникает резонный вопрос – КАК? Отвечу – матричным методом решения систем линейных алгебраических уравнений с ненулевым определителем. Согласен – геморрой! А поскольку мы ребята ленивые, но местами сообразительные, то и не станем искать сложных путей, а воспользуемся широко известным в узких кругах методом эквивалентного преобразования пассивных цепей – треугольник-звезда. Как это выглядит?

Рис.3 Преобразование треугольник-звезда

Преобразование треугольник ⇒ звезда:
R1_з=R1_т*R3_т /(R1_т+R2_т+R3_т) ;
R2_з=R1_т*R2_т /(R1_т+R2_т+R3_т) ;
R3_з=R2_т*R3_т /(R1_т+R2_т+R3_т) .

И обратное преобразование:
R1_т=R1_з+R2_з+ R1_з*R2_з /R3_з ;
R2_т=R2_з+R3_з+ R2_з*R3_з /R1_з ; R3_т=R1_з+R3_з+ R1_з*R3_з /R2_з .

Сопроводим рисунок простыми онлайн калькуляторами.

Калькулятор рсчёта элементов эквивалентного преобразования треугольник ⇒ звезда

Калькулятор рсчёта элементов эквивалентного преобразования звезда ⇒ треугольник

Вот теперь в схеме несбалансированного резистивного моста (Рис.2) можно выделить треугольник, состоящий из резисторов R2, R3 и R5, и заменить его на звезду (R1з…R3з, Рис.4 б).

Рис.4 Эквивалентное преобразование треугольник-звезда

Нужно нам это для того, чтобы, используя правила параллельного и последовательного соединения резисторов, свести всю нашу многозвенную цепь к одному элементу (Rэкв, Рис.4 г), после чего посредством простейшей манипуляции на калькуляторе или деревянных счётах вычислить величину: Iобщ = Е/Rэкв = 10В/2.239кОм = 4.47мА.
Теперь, перемещаясь к Рис.4 в) и воспользовавшись первым правилом Кирхгофа, констатируем:
I_R1з = I1 + I4 = Iобщ = 4.47мА.
Далее напрочь забываем о Густаве Робертовиче Кирхгофе вместе с его правилами и юзаем исключительно закон Ома в самом что ни на есть его чистом виде:
U_C = I_R1з * R1з = Iобщ * R1з = 4.47мА * 1кОм = 4.47В (Рис.4 в).
I1 * (R1 + R2з) = E — U_C (Рис.4 б),
отсюда:
I1 = (10В — 4.47В) / (1кОм + 600Ом) = 3.46мА.
Точно так же:
I4 = (E — U_C) / (R4 + R3з) = (10В — 4.47В) / (4кОм + 1.5кОм) = 1.01мА.
И последний финишный рывок мы совершим, вернувшись к первоначальной схеме (Рис.4 а):
U_А = Е — R1 * I1 = 10 В — 1кОм * 3.46мА = 6.54В.
U_В = Е — R4 * I4 = 10 В — 4кОм * 1.01мА = 5.96В.
I3 = (U_А — U_В) / R3 = (6.54В — 5.96В) / 3кОм = 0.19мА.
I2 = U_А / R2 = 6.54В / 2кОм = 3.27мА.
I5 = U_В / R5 = 5.96В / 5кОм = 1.19мА.

Всё, расчёт окончен! Ну а поскольку мы ребята не только сообразительные, но и пытливые умом и трезвым взглядом на вещи, то нам будет не влом проверить полученные результаты на симуляторе:

Вот теперь – точно всё! Отныне мы не только освоили оба правила Кирхгофа, но и основательно освежили в памяти основной закон электротехники – закон Ома.

Алгоритм составления уравнений по законом Кирхгофа

Алгоритм составления уравнений по законом Кирхгофа:

Составляем уравнения по первому закону Кирхгофа

Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.

Количество уравнений по 1 закону киргофа равно количеству узлов минус один.
Произвольно задаемся направлением токов в каждой ветви электрической цепи.
Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.

Составляем уравнения по второму закону Кирхгофа

Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.

Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-В_I-У+1 независимых уравнений. Где В — число ветвей в схеме. В_I— число ветвей в схеме с источником тока. У — число узлов в схеме.
Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров.
Задаемся произвольным направление обхода независимых контуров.
Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком «+». Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком «-«.
Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет «плюс». Если не совпадает, то знак — «минус».

Расчет токов по правилам Кирхгофа

Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.

Правильность расчета проверяется составлением уравнения баланса мощностей.

p.s. Правила Кирхгофа необязательно использовать в виде систем уравнений. Они справедливы для любого узла и для любого замкнутого контура электрической цепи.

правил Кирхгофа | Безграничная физика

Введение и значение

Законы цепи Кирхгофа — это два уравнения, которые касаются сохранения энергии и заряда в контексте электрических цепей.

Цели обучения

Опишите взаимосвязь между законами цепи Кирхгофа и энергией и зарядом в электрических цепях.

Основные выводы

Ключевые моменты

Кирхгоф использовал работу Георга Ома в качестве основы для создания закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) в 1845 году.Их можно вывести из уравнений Максвелла, появившихся 16-17 лет спустя.
Невозможно проанализировать некоторые схемы с обратной связью путем упрощения в виде суммы и / или ряда компонентов. В этих случаях можно использовать законы Кирхгофа.
Законы Кирхгофа — частные случаи сохранения энергии и заряда.

Ключевые термины

резистор : Электрический компонент, который передает ток прямо пропорционально напряжению на нем.
электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея.Она измеряется в вольтах (не в ньютонах, Н; ЭДС — это не сила).
конденсатор : Электронный компонент, состоящий из двух проводящих пластин, разделенных пустым пространством (иногда вместо этого между пластинами помещается диэлектрический материал), и способный хранить определенное количество заряда.

Введение в законы Кирхгофа

Законы цепи Кирхгофа — это два уравнения, впервые опубликованные Густавом Кирхгофом в 1845 году. По сути, они касаются сохранения энергии и заряда в контексте электрических цепей.

Хотя законы Кирхгофа можно вывести из уравнений Джеймса Клерка Максвелла, Максвелл не публиковал свою систему дифференциальных уравнений (которые составляют основу классической электродинамики, оптики и электрических цепей) до 1861 и 1862 годов. Кирхгоф, скорее, использовал Георга. Работа Ома как основа для текущего закона Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL) .

Законы Кирхгофа чрезвычайно важны для анализа замкнутых цепей.Рассмотрим, например, схему, показанную на рисунке ниже, состоящую из пяти резисторов, соединенных последовательно и параллельно. Упрощение этой схемы до комбинации последовательного и параллельного включения невозможно. Однако, используя правила Кирхгофа, можно проанализировать схему, чтобы определить параметры этой схемы, используя номиналы резисторов (R ₁, R ₂, R ₃, r ₁ и r ₂). . Также важно в этом примере то, что значения E ₁ и E ₂ представляют источники напряжения (например.г., батарейки).

Замкнутая цепь : Чтобы определить все переменные (т. Е. Падение тока и напряжения на различных резисторах) в этой цепи, необходимо применить правила Кирхгофа.

В заключение, законы Кирхгофа зависят от определенных условий. Закон напряжения является упрощением закона индукции Фарадея и основан на предположении, что в замкнутом контуре нет флуктуирующего магнитного поля. Таким образом, хотя этот закон может быть применен к схемам, содержащим резисторы и конденсаторы (а также другие элементы схемы), его можно использовать только как приближение к поведению схемы при изменении тока и, следовательно, магнитного поля.

Правило пересечения

Правило соединений Кирхгофа гласит, что в любом соединении цепи сумма токов, текущих в это соединение и из него, равна.

Цели обучения

Сформулируйте правило пересечения Кирхгофа и опишите его ограничения

Основные выводы

Ключевые моменты

Правило соединения Кирхгофа — это применение принципа сохранения электрического заряда: ток — это поток заряда за время, и если ток постоянный, то, что течет в точку в цепи, должно равняться тому, что вытекает из нее.{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex], где I _k — ток k, а n — общее количество проводов, входящих и выходящих из соединения. с учетом.
Закон перехода Кирхгофа ограничен в его применимости в регионах, в которых плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы током, нарушая закон.

Ключевые термины

электрический заряд : квантовое число, определяющее электромагнитные взаимодействия некоторых субатомных частиц; по соглашению, электрон имеет электрический заряд -1, а протон +1, а кварки имеют дробный заряд.
ток : временная скорость протекания электрического заряда.

Правило соединения Кирхгофа, также известное как текущий закон Кирхгофа (KCL), первый закон Кирхгофа, правило точки Кирхгофа и узловое правило Кирхгофа, является применением принципа сохранения электрического заряда.

Правило соединений Кирхгофа гласит, что в любом соединении (узле) в электрической цепи сумма токов, протекающих в этом соединении, равна сумме токов, вытекающих из этого соединения.Другими словами, при условии, что ток будет положительным или отрицательным в зависимости от того, течет ли он к стыку или от него, алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю. Визуальное представление можно увидеть на.

Закон соединения Кирхгофа : Закон соединения Кирхгофа, проиллюстрированный как токи, текущие в соединение и выходящие из него.

Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии.{\ text {n}} \ text {I} _ \ text {k} = 0 [/ latex]

, где n — общее количество ветвей, по которым ток идет к узлу или от него.

Этот закон основан на сохранении заряда (измеряемого в кулонах), который является произведением силы тока (в амперах) и времени (в секундах).

Ограничение

Применимость закона Кирхгофа ограничена. Это справедливо для всех случаев, когда полный электрический заряд (Q) постоянен в рассматриваемой области. На практике это всегда так, если закон применяется к определенной точке.Однако в определенной области плотность заряда может быть непостоянной. Поскольку заряд сохраняется, это возможно только при наличии потока заряда через границу области. Этот поток был бы током, что нарушало бы закон Кирхгофа.

Правило цикла

Правило петли Кирхгофа гласит, что сумма значений ЭДС в любом замкнутом контуре равна сумме падений потенциала в этом контуре.

Цели обучения

Сформулируйте правило петли Кирхгофа, учитывая его допущения.

Основные выводы

Ключевые моменты

Правило петли Кирхгофа — это правило, относящееся к схемам, основанное на принципе сохранения энергии.\ text {n} \ text {V} _ \ text {k} = 0 [/ latex].
Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур.

Ключевые термины

электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
резистор : Электрический компонент, который передает ток прямо пропорционально напряжению на нем.

Правило петли Кирхгофа (также известное как закон напряжения Кирхгофа (KVL), правило сетки Кирхгофа, второй закон Кирхгофа, или второе правило Кирхгофа ) является правилом, относящимся к схемам, и основано на принципе сохранения энергия.

Сохранение энергии — принцип, согласно которому энергия не создается и не разрушается — широко используется во многих исследованиях в области физики, включая электрические схемы. Применительно к схемотехнике подразумевается, что направленная сумма разностей электрических потенциалов (напряжений) вокруг любой замкнутой сети равна нулю.Другими словами, сумма значений электродвижущей силы (ЭДС) в любом замкнутом контуре равна сумме падений потенциала в этом контуре (которые могут исходить от резисторов).

Другое эквивалентное утверждение состоит в том, что алгебраическая сумма произведений сопротивлений проводников (и токов в них) в замкнутом контуре равна общей электродвижущей силе, доступной в этом контуре. Математически правило петли Кирхгофа можно представить как сумму напряжений в цепи, которая приравнивается к нулю:

Теория правил Кирхгофа петли и соединений : Мы оправдываем правила Кирхгофа, исходя из сохранения энергии.\ text {n} \ text {V} _ \ text {k} = 0 [/ latex].

Здесь V _k — напряжение на элементе k, а n — общее количество элементов в замкнутой цепи. Иллюстрация такой схемы показана на. В этом примере сумма v ₁, v ₂, v ₃ и v ₄ (и v ₅, если она включена) равна нуль.

Правило петли Кирхгофа : Правило петли Кирхгофа гласит, что сумма всех напряжений вокруг петли равна нулю: v1 + v2 + v3 — v4 = 0.

Учитывая, что напряжение является мерой энергии на единицу заряда, правило петли Кирхгофа основано на законе сохранения энергии, который гласит: общая энергия, полученная на единицу заряда, должна равняться количеству энергии, потерянной на единицу заряда .

Пример

иллюстрирует изменения потенциала в простой петле последовательной цепи. Второе правило Кирхгофа требует, чтобы ЭДС-Ir-IR ₁ -IR ₂ = 0. В перестановке это ЭДС = Ir + IR ₁ + IR ₂, что означает, что ЭДС равна сумме падений IR (напряжения) в контуре.ЭДС подает 18 В, которое уменьшается до нуля из-за сопротивления, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, всего 18 В.

Правило цикла : пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое снижается до нуля из-за сопротивлений, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки для всего 18 В.(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и понижается за счет сопротивлений. (Обратите внимание, что сценарий E означает ЭДС.)

Ограничение

Правило петли Кирхгофа является упрощением закона индукции Фарадея и выполняется при предположении, что нет флуктуирующего магнитного поля, связывающего замкнутый контур. В присутствии переменного магнитного поля могут индуцироваться электрические поля и возникать ЭДС, и в этом случае правило петли Кирхгофа нарушается.

Приложения

Правила Кирхгофа можно использовать для анализа любой схемы и модифицировать для схем с ЭДС, резисторами, конденсаторами и т. Д.

Цели обучения

Опишите условия, при которых полезно применять правила Кирхгофа.

Основные выводы

Ключевые моменты

Правила Кирхгофа применимы к любой цепи, независимо от ее состава и структуры.
Поскольку часто легко комбинировать элементы параллельно и последовательно, не всегда удобно применять правила Кирхгофа.
Для определения тока в цепи можно применить правила петли и соединения. Как только все токи связаны правилом соединения, можно использовать правило петли для получения нескольких уравнений, которые будут использоваться в качестве системы для нахождения каждого значения тока в терминах других токов. Их можно решить как систему.

Ключевые термины

электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.

Обзор

Правила Кирхгофа можно использовать для анализа любой схемы, изменяя их для схем с электродвижущими силами, резисторами, конденсаторами и т. Д. Однако с практической точки зрения правила полезны только для характеристики тех цепей, которые нельзя упростить, комбинируя элементы последовательно и параллельно.

Последовательные и параллельные комбинации, как правило, намного проще выполнить, чем применение любого из правил Кирхгофа, но правила Кирхгофа применимы более широко и должны использоваться для решения проблем, связанных со сложными схемами, которые нельзя упростить, комбинируя элементы схемы последовательно или параллельно.

Пример правил Кирхгофа

показывает очень сложную схему, но можно применить правила Кирхгофа для петель и соединений. Чтобы решить схему для токов I ₁, I ₂ и I ₃, необходимы оба правила.

Правила Кирхгофа: пример задачи : На этом изображении показана очень сложная схема, которую можно сократить и решить с помощью правил Кирхгофа.

Применяя правило Кирхгофа в точке a, находим:

[латекс] \ text {I} _1 = \ text {I} _2 + \ text {I} _3 [/ latex]

, потому что I ₁ течет в точку a, а I ₂ и I3 вытекает.То же самое можно найти в точке e. Теперь мы должны решить это уравнение для каждой из трех неизвестных переменных, что потребует трех разных уравнений.

Учитывая цикл abcdea, мы можем использовать правило цикла Кирхгофа:

[латекс] — \ text {I} _2 \ text {R} _2 + \ mathrm {\ text {emf}} _ 1- \ text {I} _2 \ text {r} _1- \ text {I} _1 \ text { R} _1 = — \ text {I} _2 (\ text {R} _2) + \ text {r} _1) + \ mathrm {\ text {emf}} _ 1- \ text {I} _1 \ text {R} _1 = 0 [/ латекс]

Подставляя значения сопротивления и ЭДС из рисунка на диаграмме и отменяя единицу измерения ампер, получаем:

[латекс] -3 \ text {I} _2 + 18-6 \ text {I} _1 = 0 [/ латекс]

Это вторая часть системы трех уравнений, которую мы можем использовать, чтобы найти все три текущих значения.Последний можно найти, применив правило цикла к циклу aefgha, которое дает:

[латекс] \ text {I} _1 \ text {R} _1 + \ text {I} _3 \ text {R} _3 + \ text {I} _3 \ text {r} _2- \ mathrm {\ text {emf}} _2 = \ text {I} _1 \ text {R} _1 + \ text {I} _3 (\ text {R} _3 + \ text {r} _2) — \ mathrm {\ text {emf}} _ 2 = 0 [/ латекс ]

Используя замену и упрощение, это становится:

[латекс] 6 \ text {I} _1 + 2 \ text {I} _3-45 = 0 [/ латекс]

В этом случае знаки поменялись местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении.

Теперь у нас есть три уравнения, которые можно использовать в системе. Второй будет использоваться для определения I ₂ и может быть изменен на:

[латекс] \ text {I} _2 = 6-2 \ text {I} _1 [/ латекс]

Третье уравнение может использоваться для определения I ₃ и может быть преобразовано в:

[латекс] \ text {I} _3 = 22,5-3 \ text {I} _1 [/ латекс]

Подставляя новые определения I ₂ и I ₃ (которые являются общими терминами I ₁) в первое уравнение (I ₁ = I ₂ + I ₃), получаем:

[латекс] \ text {I} _1 = (6-2 \ text {I} _1) + (22.5-3 \ text {I} _1) = 28,5-5 \ text {I} _1 [/ latex]

Упрощая, получаем, что I ₁ = 4,75 A. Подставляя это значение в два других уравнения, мы находим, что I ₂ = -3,50 A и I ₃ = 8,25 A.

Как схемы становятся уравнениями | Прядильные числа

«Решение схемы» означает решение системы одновременных уравнений для определения токов и напряжений. То, что вы получаете нужное количество уравнений при использовании одного из методов анализа цепей, может показаться удачей.Это не удача. Эти методы предназначены для надежного сбора информации, необходимой для решения схемы.

Автор Вилли Макаллистер.

Содержание

Куда мы направляемся

Сколько уравнений необходимо для решения схемы?
Каждый элемент содержит два неизвестных: $ i $ и $ v $. Итак, нам нужны два независимых уравнения для каждого элемента в схеме, $ 2E $, где $ E $ — количество элементов.

Откуда берутся эти уравнения?

Уравнения $ E $ происходят из законов $ i $ — $ v $ для каждого элемента схемы — закона Ома и т.п.
Дополнительные уравнения $ E $ получены из,
Текущий закон Кирхгофа — KCL вносит $ N — 1 $, где $ N $ — количество узлов.
Закон Кирхгофа о напряжении — KVL дает E — (N — 1) $.

В этой статье мы задаем несколько вопросов,

Сколько уравнений требуется для решения схемы?
Откуда они?

Ответы на эти вопросы заложены в различных методах анализа цепей,

Сколько независимых уравнений необходимо для решения схемы?

Этот ключевой вопрос определяет количество усилий, необходимых для выполнения анализа схемы.Как мы узнали на уроке алгебры при решении одновременных уравнений, количество независимых уравнений, необходимых для решения системы, равно количеству неизвестных переменных. Если у вас есть система с 10 долларами неизвестных, вам понадобится 10 долларов уравнений.

Сколько неизвестных в схеме?

Каждый двухконтактный элемент дает одно неизвестное напряжение и один неизвестный ток. Таким образом, элементы $ E $ вносят $ 2E $ неизвестных. Следовательно, схема с $ E $ элементами требует системы $ 2E $ независимых уравнений.

Проверка концепции: пример схемы

Мы проиллюстрируем эти вопросы на этом примере схемы. Если вы хотите проверить свое понимание терминологии схем, проверьте здесь.

Сколько элементов в цепи?

$ E = $ ______ элементов.

показать ответ
Эта схема содержит $ E = 5 $ элементов.
Сколько узлов в схеме?
$ N = $ ______ узлов.
показать ответ
Эта схема имеет $ N = 3 $ узлов.
Сколько петель в схеме?
______ петель.
показать ответ
6 $ петли. Циклы $ 3 $ $ \ goldD {\ text {I}} $, $ \ goldD {\ text {II}} $ и $ \ goldD {\ text {III}} $ называются сетками . Сетка — это петля, не содержащая других петель. Сетка также называется внутренней петлей .
Сколько из этих петель являются сетками?
______ ячеек.
показать ответ
Из 6 циклов в схеме 3 доллара из них — сетки (также известные как внутренние петли ).Сетки пронумерованы $ \ goldD {\ text {I}} $, $ \ goldD {\ text {II}} $ и $ \ goldD {\ text {III}} $.
Сколько уравнений нужно для решения этой схемы?
_______ уравнений.
показать ответ
Эта схема содержит $ E = 5 $ элементов. Мы должны придумать $ 2E = 10 $ независимых уравнений, чтобы решить эту схему.
Откуда берутся уравнения?
Уравнения возникают из двух источников: ограничений, накладываемых самими элементами схемы (законы $ i $ — $ v $ элементов) и связями между элементами (KCL и KVL).Система уравнений, которую вы пишете, фиксирует эти ограничения.
Половина уравнений исходит из законов элементов.
Другая половина поступает от KCL и KVL.
Половина уравнений исходит из законов элементов
Представьте себе неподключенные компоненты схемы, разбросанные по столешнице,
Каждый элемент имеет неизвестный ток и неизвестное напряжение,
Каждый элемент приводит к уравнению $ i $ — $ v $. Думайте о каждом элементе как о маленьком кусочке математики.
Эти отношения $ i $ — $ v $ представляют собой независимые от $ E $ уравнения. Это половина требуемой суммы.
А как насчет конденсаторов и катушек индуктивности?
Схема в этом примере не включает конденсаторы или катушки индуктивности. Если бы это было так, каждый внес бы одно уравнение $ i $ — $ v $,
$ i = \ text C \, \ dfrac {dv} {dt} \ quad $ или $ \ quad v = \ text L \, \ dfrac {di} {dt} $
Половина уравнений взята из законов Кирхгофа
Остальные уравнения $ E $ возникают из ограничений, созданных связями между элементами.Пример ограничения: «Эти два элемента включены последовательно, поэтому их токи должны быть одинаковыми». Мы разрабатываем уравнения связности $ E $ с использованием закона тока Кирхгофа (KCL) и закона напряжения Кирхгофа (KVL).
Допустим, в схеме есть $ E $ элементов и $ N $ узлов. В нашем примере $ E = 5 $ элементов и $ N = 3 $ узлов. Мы также знаем, что у него есть $ 6 $ петель, и $ 3 $ из этих петель являются сетками.
Покажи мне узлы
Покажи мне петли и сетки
В этой примерной схеме количество петель составляет 6 долларов.Циклы $ 3 $ $ \ goldD {\ text {I}} $, $ \ goldD {\ text {II}} $ и $ \ goldD {\ text {III}} $ называются сетками . Сетка — это петля, не содержащая других петель.
Наличие узлов по $ 3 и циклов по $ 6 — это много возможностей для получения дополнительных уравнений на $ E = 5 $, но мы должны быть осторожны. Сгенерированные нами уравнения должны быть на независимыми друг от друга на .
Что такое независимое уравнение?
Уравнение является линейно независимым , если оно не может быть получено с помощью линейных комбинаций других уравнений.Линейные комбинации — это когда вы объединяете уравнения с помощью сложения, вычитания или умножения на константу.
Мы сделаем пример с набором уравнений KCL. Одно из них , а не независимое, потому что может быть получено из других уравнений.
Сколько независимых уравнений получается из KCL?
Мы можем написать KCL уравнение для каждого узла в цепи. $ N $ узлов даст вам $ N $ уравнений. НО, набор $ N $ уравнений не является независимым , а не .Один из них избыточен. Всегда существует одно зависимое уравнение KCL, которое не вносит никакой новой информации, поэтому оно не требуется.
Давайте запишем все три уравнения KCL и покажем, что внутри скрывается линейная зависимость,
KCL для узла $ \ green a $: $ \ quad + i_1 -i_1 = 0 $
KCL для узла $ \ green b $: $ \ quad + i_1 — i_2 — i_3 + i _ {\ text S} = 0 $
KCL для узла $ \ green c $: $ \ quad -i_1 + i_2 + i_3 -i _ {\ text S} = 0 $
Узел $ a $ имеет тривиальное уравнение KCL.Один ток входит, а другой гаснет. Он подключает источник напряжения к резистору $ 20 \, \ Omega $ и отвечает за доставку $ i_1 $ в узел $ b $.
Уравнения ККЛ для узлов $ b $ и $ c $ оказываются линейно зависимыми. Мы продемонстрируем это, используя уравнение узла $ b $, чтобы вывести уравнение для узла $ c $. Если вы умножите узел $ b $ на $ -1 $, вы получите узел $ c $. (Это пример линейной комбинации — умножьте на константу.)
Это говорит нам, что уравнения $ b $ и $ c $ содержат точно такую же информацию.Это означает, что один из них избыточен. Нет необходимости носить с собой и то, и другое. Вы можете исключить одну из системы уравнений. Узел, который мы не учитываем, — это наш выбор. Обычно мы не учитываем наземный узел, потому что он самый сложный (имеет наибольшее количество соединений).
Имеется $ N = 3 $ узлов, но количество независимых уравнений составляет $ N-1 = 2 $.
Как правило, KCL вносит $ N-1 $ независимых уравнений.
Наш статус нахождения уравнения на данный момент:
Нам нужны уравнения $ 2E $.
Мы получаем $ E $ из уравнения $ i $ — $ v $ для каждого элемента.
Получаем от KCL $ N-1 $.
Остается найти $ 2E — E — (N-1) = E — (N-1) $ уравнений.
Достаем их от КВЛ.
Сколько независимых уравнений получается из KVL?
После написания $ N-1 $ уравнений с использованием KCL, нам не хватило $ 2E $ уравнений на $ E — (N-1) $. Для нашей примерной схемы нам нужно еще $ 5 — (3-1) = 3 $ уравнения. Откуда возьмутся эти дополнительные уравнения? Применяем КВЛ по петлям схемы.
Теория графов говорит нам о двух чудесных вещах,
KVL может составить нужное количество независимых уравнений, $ E — (N-1) $.
$ E — (N-1) $ совпадает с количеством ячеек.
Это означает, что мы знаем необходимое количество уравнений KVL путем подсчета сеток. Вам даже не нужно выполнять вычисление $ E — (N-1) $. Просто посчитайте меши.
В нашей примерной схеме есть $ 3 $ сетки. Мы сразу знаем, что нам нужно написать $ 3 $ уравнения КВЛ; Не больше, не меньше.
Ограничение: плоские и неплоские схемы
KVL выдает $ E — (N-1) $ уравнений для любых схем. Вы можете получить эти уравнения только с сетками , только если схема плоская .
Плоская цепь — это цепь, которую можно нарисовать плоской, без пересекающихся проводов. Если цепь не может быть плоской без пересечения проводов, это неплоская . Схема в нашем примере является планарной, как и большинство схем, которые вам нужно будет проанализировать вручную.
Слева: плоская схема, можно рисовать без перекрещивающихся проводов.
Справа: неплоская схема, можно нарисовать только перекрещенным проводом.
Метод токовой петли работает с неплоскими цепями.
Убедитесь, что уравнения KVL независимы
Мы хотим, чтобы уравнения КВЛ были независимыми. Это требует некоторой осторожности.
Простейшее руководство: Напишите уравнения КВЛ для сеток. Сетки гарантированно дают нужное количество уравнений, и они будут независимыми.
Если по какой-то причине вы хотите (или должны) включить другие уравнения, не связанные с петлей, есть еще одно руководство.Вы получите независимые уравнения, если каждый цикл включает один элемент, которого нет в любом другом цикле. Обычно этого бывает достаточно, чтобы получить нужные уравнения (есть интересное исключение, описанное ниже).
Выбор сеток и петель
В нашей примерной схеме есть доступные петли за 6 долларов. Из этого набора вариантов нам нужно составить $ 3 $ независимых уравнения КВЛ.
Самый простой способ — выбрать три сетки: $ \ goldD {\ text {I}} $, $ \ goldD {\ text {II}} $ и $ \ goldD {\ text {III}} $.Мы выигрываем! Сетки создают нужное количество уравнений, и они гарантированно независимы. Это основа метода Mesh Current.
Мы могли бы выбрать другой допустимый набор циклов из схемы примера, $ \ greenD {\ text {IV}} $, $ \ blueD {\ text V} $ и $ \ maroonC {\ text {VI}} $. Почему это может быть хороший набор?
Циклы $ 3 $ предоставляют $ 3 $ уравнения, как того требует $ E- (N-1) = 3 $.
Каждый элемент включен в цикл.
У этого набора петель есть интересная особенность.Проследите за циклами $ \ greenD {\ text {IV}} $ и $ \ blueD {\ text V} $ и обратите внимание, что вместе они содержат каждый элемент в цепи. Зачем вам нужно еще одно уравнение петли? Можно ли пропустить $ \ maroonC {\ text {VI}} $? Нет! Нам все еще нужно $ 3 $ уравнений. Еще раз внимательно посмотрите на циклы $ \ greenD {\ text {IV}} $ и $ \ blueD {\ text V} $. Они разделяют без элементов. На самом деле это две отдельные цепи, которые не соприкасаются. Задача уравнения цикла $ \ maroonC {\ text {VI}} $ — связать два других цикла вместе.
Проверка концепции
Некоторые варианты не соответствуют рекомендациям. Вы можете сказать почему?
$ \ goldD {\ text I} $, $ \ blueD {\ text V} $ и $ \ maroonC {\ text {VI}} \ quad $
почему?
В этом комплекте отсутствует резистор рядом с источником тока. Каждому элементу нужен шанс повлиять на результат.
$ \ greenD {\ text {IV}} $ и $ \ blueD {\ text {V}} $
почему?
Этот набор дает только 2 $ уравнений, и требуются 3 $. Это правда, даже если петли вместе проходят через каждый элемент. Вам по-прежнему необходимо иметь $ 3 $ уравнения, чтобы полностью описать / ограничить схему.Вот почему хороший набор, перечисленный выше, работает, $ \ greenD {\ text {IV}} $, $ \ blueD {\ text V} $ и $ \ maroonC {\ text {VI}} $.
$ \ goldD {\ text I} $, $ \ goldD {\ text {II}} $, $ \ goldD {\ text {III}} $ и $ \ maroonC {\ text {VI}} $
почему?
Вы можете получить ответ с помощью цикла по 4 доллара, но это больше, чем вам нужно. $ 4 $ превышает количество требуемых уравнений, $ E- (N-1) = 3 $. Это означает, что одно из уравнений линейно зависит от других и может быть опущено.
Не бойтесь использовать петли; просто будьте бдительны и внимательны к этому.
Когда я могу выбрать петли без сетки? В некоторых схемах мы хотим, чтобы использовала циклы, а другие, где заставили использовать циклы в дополнение к сеткам. Эти особые случаи описаны в методе токовой петли.
Сводка
Существуют три ограничения на токи и напряжения в цепи,
$ i $ — $ v $ законы элементов
Действующий закон Кирхгофа
Закон Кирхгофа о напряжении
Система уравнений, которую вы пишете, фиксирует эти ограничения.
Для схемы с элементами $ E $ и узлами $ N $
Для решения схемы необходимо $ 2E $ независимых уравнений.
Вы получаете
Уравнения $ E $ из закона $ i $ — $ v $ для каждого компонента (закон Ома и т.п.).
$ N-1 $ независимых узловых уравнений с использованием KCL.
$ E — (N-1) $ независимых петлевых уравнений с использованием KVL.
Подсчет сеток подскажет вам нужное количество независимых уравнений KVL для плоских цепей.
Если вы пишете уравнения KVL для контуров без сетки, цикл, по крайней мере, с одним элементом, отсутствующим в любом другом цикле, обязательно будет независимым.
Продолжайте выбирать циклы и записывать уравнения, пока не получите $ E — (N-1) $ уравнений.
Номер ссылки
Фельдманн, Питер и А. Рорер, Рональд. (1991). «Доказательство числа независимых уравнений Кирхгофа в электрической цепи». Схемы и системы, транзакции IEEE на. 38. 681 — 684. 10.1109 / 31.135739. Также попробуйте здесь.
В этой короткой статье представлено индуктивное доказательство, показывающее: для схемы с $ b $ ветвями и $ n $ узлами количество линейно независимых уравнений узла KCL равно $ n — 1 $, а количество независимых уравнений цикла KVL равно $ b. — n + 1 $. (Индуктивное доказательство начинается с очень простого и добавляет сложности.)
Закон Кирхгофа для сложных схем | ОРЕЛ
Закон
Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша схема более сложная? Возможно, вы разрабатываете электронику с параллельным и последовательным сопротивлением, и закон Ома начинает падать.Или что, если у вас нет источника постоянного тока? В таких ситуациях, когда нельзя использовать только V = IR, пора встать на плечи Ома и применить закон Кирхгофа. Здесь мы рассмотрим, что такое Закон Кирхгофа для цепей и как его использовать для анализа напряжения и тока сложных электрических цепей.
Что такое Окружной закон Кирхгофа?
Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться только на закон Ома, чтобы найти напряжение или ток.Здесь пригодится закон Кирхгофа, который позволяет рассчитывать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Существует два варианта закона Кирхгофа, в том числе:
Закон Кирхгофа: Для анализа полного тока сложной цепи
Закон Кирхгофа о напряжении : для анализа полного напряжения сложной цепи
Когда вы объединяете эти два закона, вы получаете Окружной закон Кирхгофа
Как и любой другой научный или математический закон, названный в честь их создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом.Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании. Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент периодической таблицы имеет свою уникальную длину волны. Открытие этого паттерна позволило дуэту открыть два новых элемента, цезий и рубидий.
Густав Кирхгоф (слева) и Роберт Бунзен (справа)
Кирхгоф позже применил свою теорию спектрального анализа к изучению состава Солнца, где он обнаружил множество темных линий в спектре длин волн Солнца.Это было вызвано тем, что газ Солнца поглощал световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.
Немного ближе к дому в мире электроники, Кирхгоф объявил свой свод законов для анализа тока и напряжения в электрических цепях в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа строится на основе, изложенной в законе Ома, и помогла проложить путь для анализа сложных схем, на который мы полагаемся сегодня.
Первый закон — Действующий закон Кирхгофа
Закон Кирхгофа по току гласит, что величина тока, входящего в узел, равна величине тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выходить наружу. Вы можете определить узел, в котором два или более пути соединены общей точкой. На схеме это будет точка соединения, соединяющая две пересекающиеся сетевые соединения.
Взгляните на изображение ниже, чтобы наглядно понять этот Закон.Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону Кирхгофа, взаимосвязь между токами, входящими в узел и выходящими из него, может быть представлена как I 1 + I 2 = I 3 + I 4 + I 5 .
Текущий закон Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)
Когда вы уравновешиваете это уравнение как алгебраическое выражение, вы заключаете, что текущий вход и выход из узла всегда будет равен 0, или I 1 + I 2 + (-I 3 + -I 4 + -I 5 ) = 0 Все должно уравновешиваться, и Кирхгоф назвал этот принцип Сохранением заряда .
Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже представлена схема с четырьмя узлами: A, C, E и F. Сначала ток течет от источника напряжения и отделяется в узле A, а затем протекает через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы протекать через резисторы R3, R4 и R5, где он встречается с узлом E и узлом F.
(Источник изображения)
Чтобы подтвердить закон Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:
Рассчитать полный ток цепи
Рассчитать ток, протекающий через каждый узел
Сравните входные и выходные токи в определенных узлах, чтобы подтвердить текущий закон Кирхгофа.
1. Рассчитайте общий ток
Здесь мы используем закон Ома, чтобы получить полный ток нашей цепи с I = V / R . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, подключенных параллельно, которое составляет:
Начиная с узла AC, мы получаем следующее сопротивление для параллельных резисторов R1 и R2:
И переходя к узлу CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:
Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы можем затем подключить к закону Ома I = V / R , чтобы получить общий ток в нашей цепи:
2.Расчет узловых токов
Теперь, когда мы знаем, что из нашей цепи выходит 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся помощью закона Ома в форме I = V / R , чтобы получить ток для каждой ветви узла.
Для начала нам нужны напряжения для узловых ветвей AC и CF:
Затем мы можем рассчитать ток для каждой ветви узла:
3. Подтвердите действующий закон Кирхгофа
После вычисления тока для каждой ветви узла у нас теперь есть две отдельные опорные точки, которые мы можем использовать для сравнения наших входных и выходных токов.Это позволит нам проанализировать нашу схему и подтвердить текущий закон Кирхгофа следующим образом:
Второй закон — Закон Кирхгофа о напряжении
Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром полное напряжение всегда будет равно сумме всех падений напряжения в контуре. Вы обнаружите, что падение напряжения происходит всякий раз, когда ток проходит через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Сохранением энергии .Опять же, то, что входит, должно выходить наружу.
Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение столкнется с пассивным компонентом, что вызовет заметное падение напряжения.
Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:
Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает.В приведенном ниже примере у нас есть две известные переменные: полное напряжение и падение напряжения на R1.
(Источник изображения)
Что нам нужно выяснить, так это падение напряжения на R2, и мы можем использовать закон напряжения Кирхгофа, чтобы выяснить это со следующей зависимостью:
Поскольку полное падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления нашей недостающей переменной. Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:
Давайте посмотрим на другой пример.В схеме ниже у нас есть три резистора, подключенных последовательно с батареей на 12 В.
Чтобы проверить закон напряжения Кирхгофа в этой цепи, нам нужно предпринять следующие шаги:
Рассчитайте общее сопротивление цепи
Вычислить полный ток цепи
Рассчитайте ток через каждого резистора
Рассчитайте падение напряжения на каждом резисторе
Сравните источник напряжения с общим падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении
1.Рассчитайте общее сопротивление
Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:
2. Рассчитайте общий ток
Теперь, когда мы знаем наше полное сопротивление, мы снова можем использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V / R, , который выглядит так:
3. Рассчитайте ток через каждый резистор
Поскольку все наши резисторы соединены последовательно, через них будет протекать одинаковый ток, который мы можем выразить как:
4.Рассчитайте падение напряжения на каждом резисторе
.
В наших окончательных расчетах мы снова будем использовать закон Ома, чтобы получить полное падение напряжения для каждого резистора в виде В = IR , которое выглядит следующим образом:
5. Подтвердите закон Кирхгофа о напряжении
Теперь у нас есть все необходимые данные, включая общее напряжение нашей цепи, а также каждое падение напряжения на каждом из наших резисторов. Собирая все это вместе, мы можем легко проверить закон напряжения Кирхгофа с помощью следующего соотношения:
Это также может быть выражено как:
Как видите, полное напряжение равно общему падению напряжения в нашей цепи.То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
Процесс использования закона Кирхгофа о схемах
Поняв, как работает закон Кирхгофа, в вашем наборе инструментов теперь есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:
Во-первых, начните с маркировки всех известных напряжений и сопротивлений на вашей цепи.
Затем назовите каждую ветвь в вашей цепи текущей меткой, например I1, I2, I3 и т. Д.Ветвь — это один или группа компонентов, соединенных между двумя узлами.
Затем найдите текущий закон Кирхгофа для каждого узла в вашей цепи.
Затем найдите закон напряжения Кирхгофа для каждого из независимых контуров в вашей цепи.
После того, как вы рассчитали законы Кирхгофа по току и напряжению, вы можете использовать свои уравнения, чтобы найти недостающие токи. Готовы попробовать это самостоятельно? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон тока Кирхгофа и закон напряжения с небольшой помощью Ома!
Свои ответы оставляйте в комментариях ниже!
Стоя на плечах Ома
Имея в руках Закон Кирхгофа о цепях, теперь у вас есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было раньше — закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем, основываясь на этих расчетах с законом Кирхгофа, увидите, соответствует ли ваша схема этим принципам тока и напряжения.
Готовы применить закон Кирхгофа в своем собственном проекте по разработке электроники? Попробуйте Autodesk EAGLE бесплатно сегодня!
электрического тока — есть ли простое доказательство того, что законы Кирхгофа всегда дают точно полный набор уравнений?
Этот ответ адаптирован из задачи 1.4 в Používáme lineární algebru, книге решенных задач линейной алгебры (свободно доступной в Интернете, но, к сожалению, только на чешском языке, AFAIK). Я покажу это при следующих предположениях:
Мы имеем дело с цепями постоянного или (низкочастотного) переменного тока, единственными элементами которых являются резисторы и идеальные источники напряжения,
Каждый край цепи имеет ненулевое (положительное) сопротивление,
Законы цепи Кирхгофа дают уникальное решение для тока и напряжения на каждом элементе схемы.
Сначала несколько комментариев. Уникальность легко понять по физическим причинам. Линейность законов Кирхгофа подразумевает, что может быть только более одного решения, если одна и та же схема с удаленными источниками (то есть их напряжение, установленное на ноль без изменения топологии схемы) может поддерживать нетривиальные токи. Предположение о положительном сопротивлении каждого края цепи делает это физически невозможным из-за сохранения энергии. По той же причине я считаю, что то же самое утверждение справедливо для цепей переменного тока с элементами, отличными от резисторов, до тех пор, пока импеданс каждого края имеет положительную действительную часть.Однако мне не сразу очевидно, как приведенный ниже аргумент обобщается на этот случай. Также легко увидеть, что отказ от предположения о положительном сопротивлении может привести как к двусмысленности в решении, так и к патологиям: см. Ответы Райана Хейзелтона и Альфреда Центавра. Наконец, тот же аргумент должен применяться к схемам с идеальными источниками тока из-за двойственности между двумя типами источников; предположение об идеальных источниках напряжения сделано только для простоты обозначений.
Теперь к делу. Я буду считать WLOG, что схема представлена связным графом; в противном случае просто рассматриваются все компоненты связности один за другим. Аргумент по существу следует методу узлового напряжения. На первом этапе мы понимаем, что второй закон Кирхгофа (напряжение) эквивалентен существованию потенциала на графике. Предположим, что схема имеет $ N $ вершин (узлов). Мы можем выбрать потенциал одного из них произвольно, скажем, $ u_1 = 0 $. Для данного решения законов Кирхгофа мы можем затем получить потенциал $ u_i $ $ i $ -й вершины, сложив падения напряжения на резисторах и напряжения, подаваемые источниками по любому пути, соединяющему $ i $ -ю вершину с $ u_1 $.Второй закон Кирхгофа гарантирует, что результат для $ u_i $ не зависит от выбора пути и, следовательно, хорошо определен.
На втором этапе мы имеем дело с системой уравнений для неизвестных потенциалов $ u_2, \ dotsc, u_N $, вытекающих из первого (текущего) закона Кирхгофа. Мы рассматриваем только вершины $ 2, \ dotsc, N $, что дает $ N-1 $ уравнений для $ N-1 $ неизвестных потенциалов. Уравнение для $ i $ -й вершины символически читается $$ \ sum_j \ frac1 {R_ {ij}} (u_i-u_j + U_ {ij}) = 0, $$ где сумма ведется по всем вершинам $ j $, соединенным с $ i $ ребром, $ R_ {ij} $ обозначает сопротивление на ребре $ ij $, а $ U_ {ij} $ — напряжение, передаваемое источниками в нем.T $ и $ \ vec U $ содержат исходные данные. Диагональные элементы матрицы $ M $ равны $$ M_ {ii} = \ sum_j \ frac1 {R_ {ij}}, $$ тогда как недиагональные элементы $$ M_ {ij} = \ begin {case} -1 / R_ {ij} \ text {если $ i $ и $ j $ связаны и $ j \ neq1 $,} \\ 0 \ text {иначе.} \ end {case} $$ Положительность всех сопротивлений означает, что $$ \ sum_ {j \ neq i} | M_ {ij} | \ leq | M_ {ii} | $$ для всех $ i = 2, \ dotsc, N $. Более того, существуют такие $ i $ (соединенные ребром с $ u_1 $), для которых выполняется строгое неравенство.Отсюда следует, что матрица $ M $ диагонально доминирующая и, следовательно, обратимая. Это гарантирует, что система уравнений для потенциалов $ u_2, \ dotsc, u_N $ имеет единственное решение.
Как только все потенциалы известны, токи через все края цепи легко восстанавливаются. Ток через край $ ij $ символически равен $$ I_ {ij} = \ frac1 {R_ {ij}} (u_i-u_j + U_ {ij}). $$ Это завершает аргумент и математически показывает, почему предположение о положительных сопротивлениях является достаточным условием для установления существования единственного решения.В более общем смысле, единственное решение существует, когда определенная выше матрица $ M_ {ij} $, которая зависит от топологии схемы и сопротивлений, но не от источников, является невырожденной. Если $ M_ {ij} $ является сингулярным, может быть более одного решения или не может быть решений вообще, как известно из линейной алгебры.
Что такое закон Кирхгофа и закон напряжения Кирхгофа?
Закон Кирхгофа: Немецкий физик Густав Кирхгоф разработал два закона, позволяющих легко анализировать взаимосвязь любого количества элементов схемы.Первый закон касается протекания тока и широко известен как закон Кирхгофа ( KCL), а второй закон касается падения напряжения в замкнутой сети и известен как закон напряжения Кирхгофа (KVL).
KCL утверждает, что сумма тока в переходе остается нулевой, и согласно KVL сумма электродвижущей силы и падения напряжения в замкнутой цепи остается нулевой.
При применении KCL входящий ток принимается как положительный, а исходящий — как отрицательный.Аналогично, при применении KVL повышение потенциала принимается как положительное, а падение потенциала — как отрицательное.
KVL и KCL помогают найти аналогичное электрическое сопротивление и импедансы сложной системы. Он также определяет ток, протекающий через каждую ветвь сети.
В комплекте:
Два закона описаны ниже
Действующий закон Кирхгофа
Текущий закон Кирхгофа гласит, что «алгебраическая сумма всех токов в любой узловой точке или стыке цепи равна нулю».
Σ I = 0
Учитывая приведенную выше цифру в соответствии с действующим законодательством Кирхгофа:
i ₁ + i ₂ — i ₃ — i ₄ — i ₅ + i ₆ = 0 ……… (1)
Направление входящих токов к узлу считается положительным, а исходящие токи — отрицательным. Также можно принять обратное, т. Е. Входящий ток как отрицательный, а исходящий как положительный. Это зависит от вашего выбора.
Уравнение (1) также можно записать как:
i ₁ + i ₂ + i ₆ = i ₃ + i ₄ + i ₅
Сумма входящих токов = Сумма исходящих токов
В соответствии с Законом Кирхгофа по току , алгебраическая сумма токов, входящих в узел, должна быть равна алгебраической сумме токов, покидающих узел в электрической сети.

Закон Кирхгофа о напряжении
Закон Кирхгофа о напряжении гласит, что алгебраическая сумма напряжений (или падений напряжения) на любом замкнутом пути сети, которая является поперечной в одном направлении, равна нулю.Другими словами, в замкнутой цепи алгебраическая сумма всех ЭДС и алгебраическая сумма всех падений напряжения (произведение тока (I) и сопротивления (R)) равна нулю.
Σ E + Σ V = 0
На приведенном выше рисунке показан замкнутый контур, также называемый сеткой. В соответствии с законом Кирхгофа о напряжении:
Здесь предполагаемый ток I вызывает положительное падение напряжения при переходе от положительного к отрицательному потенциалу, а отрицательное падение потенциала, когда ток течет от отрицательного к положительному потенциалу.
Учитывая другой рисунок, показанный ниже, и предполагая направление тока i
Следовательно,
Видно, что напряжение V ₁ отрицательно как в уравнении (2), так и в уравнении (3), тогда как V ₂ отрицательно в уравнении (2), но положительно в уравнении (3). Это происходит из-за изменения направления тока, принятого на обоих рисунках.
На рисунке A ток в обоих источниках V ₁ и V ₂ течет с отрицательной полярности на положительную, в то время как на рисунке B ток в источнике V ₁ отрицательный на положительный, но для V ₂ равен от положительной к отрицательной полярности.
Для зависимых источников в цепи также может применяться KVL. В случае расчета мощности любого источника, когда ток входит в источник, мощность поглощается источниками, в то время как источник подает мощность, если ток выходит из источника.
Важно знать некоторые термины, используемые в схеме при применении KCL и KVL, такие как узел, соединение, ветвь, петля, сетка. Они объясняются с помощью схемы, показанной ниже:
Узел
Узел — это точка в сети или цепи, где соединяются два или более элемента схемы.Например, на приведенной выше принципиальной схеме A и B — узловые точки.
Перекресток
Соединение — это точка в сети, в которой соединяются три или более элемента схемы. Это точка, где разделяется ток. В приведенной выше схеме B и D — это переходы.
Филиал
Часть сети, которая находится между двумя точками соединения, называется ветвью. В приведенной выше схеме DAB, BCD и BD являются ветвями схемы.
Петля
Замкнутый путь сети называется петлей.ABDA, BCDB — это петли на приведенной выше принципиальной схеме.
Сетка
Самая простая форма петли, которую нельзя разделить дальше, называется сеткой.
Закон
Ома / Закон Кирхгофа с использованием линейных дифференциальных уравнений первого порядка
В этой статье мы пытаемся понять закон Ома и закон Кирхгофа с помощью стандартных инженерных формул и объяснений, а также путем применения линейных дифференциальных уравнений первого порядка для решения примеров наборов задач.
Что такое электрическая цепь
Простейшая электрическая цепь обычно представляет собой последовательную цепь, имеющую источник энергии или вход электродвижущей силы, например, от батареи или генератора постоянного тока, и резистивную нагрузку, которая потребляет эту энергию, для Например, электрическая лампочка, как показано на схеме ниже:

Ссылаясь на схему, когда переключатель замкнут, ток I проходит через резистор, вызывая образование напряжения на резисторе.Это означает, что при измерении разности потенциалов в двух конечных точках резистора будут иметь разные значения. Это можно подтвердить с помощью вольтметра.

Из описанной выше ситуации стандартный закон Ома может быть выведен как:

Падение напряжения ER на резисторе пропорционально мгновенному току I и может быть выражено как:

ER = RI (Уравнение № 1)
В приведенном выше выражении R определяется как константа пропорциональности и называется сопротивлением резистора.
Здесь мы измеряем напряжение ER в вольтах, сопротивление R в омах и ток I в амперах.
Это объясняет закон Ома в его основной форме в простой электрической цепи.
В более сложных схемах есть еще два важных элемента в виде конденсаторов и катушек индуктивности.
Что такое индуктор
Катушка индуктивности может быть определена как элемент, который противодействует изменению тока, создавая инерционный эффект в потоке электричества, как это делает масса в механических системах.Эксперименты показали следующее для катушек индуктивности:
Падение напряжения EL на катушке индуктивности пропорционально мгновенной скорости изменения тока I. Это может быть выражено как:

EL = L dl / dt (Уравнение 2)
где L становится константой пропорциональности и называется индуктивностью индуктора и измеряется в Генри. Время t указано в секундах.
Что такое конденсатор
Конденсатор — это просто устройство, которое накапливает электрическую энергию.Эксперименты позволяют получить следующее объяснение:
Падение напряжения на конденсаторе пропорционально мгновенному электрическому заряду Q на конденсаторе, это может быть выражено как:

EC = 1 / C x Q ( Уравнение № 3)
, где C обозначается как емкость и измеряется в фарадах; заряд Q измеряется в кулонах.
Однако, поскольку I (C) = dQ / dt, мы можем записать приведенное выше уравнение как:
Значение тока I (t) может быть решено в данной схеме путем решения уравнение, полученное применением следующего физического закона:
Понимание закона Кирхгофа (KVL)
Густав Роберт Кирхгоф (1824-1887) был немецким физиком, его популярные законы можно понять, как изложено ниже:

Закон Кирхгофа по току (KCL) гласит:

В любой точке цепи сумма втекающих токов равна сумме выходящих токов.

Закон напряжения Кирхгофа (KVL) гласит, что:

Алгебраическая сумма всех мгновенных падений напряжения вокруг любого замкнутого контура равна нулю, или напряжение, приложенное к замкнутому контуру, равно сумме падения напряжения в остальной части контура.

Пример № 1: Ссылаясь на диаграмму RL ниже и комбинируя уравнение № 1,2 и напряжение Кирхгофа, мы можем получить следующее выражение:
Уравнение: 4
Давайте рассмотрим этот случай A с постоянной электродвижущей силой:
В описанном выше уравнении № 4, если E = E0 = constant, то мы можем управлять следующим уравнением:
Уравнение: 5
Здесь последний член приближается к нулю, поскольку t стремится к бесконечности, так что I (t) стремится к предельному значению E0 / R.После достаточно долгой задержки я доберусь до практически постоянного значения, не зависящего от значения c, что также подразумевает, что это не будет зависеть от начального условия, которое может быть вызвано нами.
Принимая во внимание начальное условие, I (0) = 0, получаем:
Уравнение: 5 *
Случай B (периодическая электродвижущая сила):

Учитывая E (t ) = Eo sin ωt, , тогда, принимая во внимание уравнение # 4, общее решение для случая B можно записать как:
(∝ = R / L)

Интегрирование по частям дает нам:

Это может быть дополнительно получен как:
ઠ = arc tan ωL / R
Здесь экспоненциальный член стремится к нулю, поскольку t стремится к бесконечности.Это означает, что по прошествии достаточно длительного периода времени ток I (t) достигает практически гармонических колебаний.

ЗАКОНЫ КИРХХОФФА
Щелкните или коснитесь примеров схем ниже, чтобы вызвать TINACloud, и выберите интерактивный режим постоянного тока, чтобы проанализировать их онлайн.
Получите недорогой доступ к TINACloud для редактирования примеров или создания собственных схем
Многие схемы слишком сложны, чтобы их можно было решить с помощью правил для последовательных или параллельных схем или методов преобразования в более простые схемы, описанные в предыдущих главах.Для этих схем нам нужны более общие методы решения. Самый общий метод дается законами Кирхгофа, которые позволяют вычислять все напряжения и токи цепей путем решения системы линейных уравнений.
Есть два закона Кирхгофа, закон напряжения и закон тока. Эти два закона можно использовать для определения всех напряжений и токов цепей.
Закон Кирхгофа по напряжению (KVL) гласит, что алгебраическая сумма возрастаний и падений напряжения в контуре должна быть равна нулю.
Петля в приведенном выше определении означает замкнутый путь в цепи; то есть путь, который покидает узел в одном направлении и возвращается к тому же узлу в другом направлении.
В наших примерах мы будем использовать для циклов направление по часовой стрелке; однако те же результаты будут получены при использовании направления против часовой стрелки.
Чтобы применить KVL без ошибок, мы должны определить так называемое опорное направление. Эталонное направление неизвестных напряжений указывает от знака + к знаку — предполагаемых напряжений.Представьте себе использование вольтметра. Положительный щуп вольтметра (обычно красный) следует разместить на опорной + клемме компонента. Если реальное напряжение положительное, оно находится в том же направлении, что и предполагалось, и и наше решение, и вольтметр покажут положительное значение.
При вычислении алгебраической суммы напряжений мы должны присвоить знак плюса тем напряжениям, где опорное направление совпадает с направлением контура, и отрицательные знаки в противоположном случае.
Другой способ сформулировать закон Кирхгофа для напряжения: приложенное напряжение последовательной цепи равно сумме падений напряжения на последовательных элементах.
Следующий короткий пример показывает использование закона напряжения Кирхгофа.
Найдите напряжение на резисторе R _2,, учитывая, что напряжение источника, В _S = 100 В, и что напряжение на резисторе R ₁ равно В ₁ = 40 В.
На приведенном ниже рисунке можно быть создан с помощью TINA Pro версии 6 и выше, в которой инструменты рисования доступны в редакторе схем.

Решение, использующее закон напряжения Кирхгофа: -V _S + V ₁ + V ₂ = 0 или V _S = V ₁ + V ₂
отсюда: V ₂ = В _S — В ₁ = 100-40 = 60 В
Обратите внимание, что обычно мы не знаем напряжения резисторов (если мы их не измеряем), и нам нужно использовать оба закона Кирхгофа для решения .
Текущий закон Кирхгофа (KCL) гласит, что алгебраическая сумма всех токов, входящих и выходящих из любого узла в цепи, равна нулю.
Далее мы даем знак + токам, выходящим из узла, и знак -, токам, входящим в узел.
Вот простой пример, демонстрирующий действующий закон Кирхгофа.

Найдите ток I ₂, если ток источника I _S = 12 A, а I ₁ = 8 A.
Используя закон Кирхгофа в узле, обведенном кружком: -I _S + I ₁ + I ₂ = 0, следовательно: I ₂ = I _S — I ₁ = 12-8 = 4 А, как вы можете проверить с помощью TINA (следующий рисунок).
В следующем примере мы будем использовать закон Кирхгофа и закон Ома для расчета тока и напряжения на резисторах.
На рисунке ниже вы заметите стрелку напряжения над резисторами. Это новый компонент, доступный в 6-й версии TINA и работающий как вольтметр. Если вы подключаете его к компоненту, стрелка определяет опорное направление (для сравнения с вольтметром, представьте, что красный датчик помещен в конец стрелки, а черный датчик — на наконечник).Когда вы запускаете анализ постоянного тока, фактическое напряжение на компоненте будет отображаться на стрелке.

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows
Чтобы начать использовать текущий закон Кирхгофа, мы видим, что токи через все компоненты одинаковы, поэтому давайте обозначим этот ток как I.
Согласно закону напряжения Кирхгофа: V _S = V ₁ + V ₂ + V ₃
Теперь используя закон Ома: V _S = I * R ₁ + I * R ₂ + I * R ₃
Отсюда ток цепи:
I = V _S / (R ₁ + R ₂ + R ₃) = 120 / (10 + 20 + 30) = 2 А
Наконец, напряжения резисторов:
В ₁ = I * R ₁ = 2 * 10 = 20 В; V ₂ = I * R ₂ = 2 * 20 = 40 В; V ₃ = I * R ₃ = 2 * 30 = 60 В
Те же результаты будут видны на стрелках напряжения при простом запуске интерактивного анализа постоянного тока TINA.

В этой следующей, более сложной схеме мы также используем как закон Кирхгофа, так и закон Ома, но мы обнаружили, что чаще всего решаем линейную систему уравнений.
Общее количество независимых применений законов Кирхгофа в цепи — это количество ветвей цепи, в то время как общее количество неизвестных (ток и напряжение каждой ветви) вдвое больше. Однако, также используя закон Ома для каждого резистора и простые уравнения, определяющие приложенные напряжения и токи, мы получаем систему уравнений, в которой количество неизвестных равно количеству уравнений.
Найдите токи ответвления I1, I2, I3 в цепи ниже.

Щелкните / коснитесь схемы выше, чтобы проанализировать в режиме онлайн, или щелкните эту ссылку, чтобы сохранить в Windows
Набор уравнений следующий:
Узловое уравнение для обведенного узла:
— I ₁ — I ₂ — I ₃ = 0
или умножение на -1
I ₁ + I ₂ + I ₃ = 0
Уравнения цикла (с использованием направления по часовой стрелке) для цикла L1, содержащий V ₁, R ₁ и R ₃
-V ₁ + I ₁ * R ₁ -I ₃ * R ₃ = 0
и для цикла L2, содержащий V ₂, R ₂ и R ₃
I ₃ * R ₃ — I ₂ * R ₂ + V ₂ = 0
Замена компонента значения:
I ₁ + I ₂ + I ₃ = 0-8 + 40 * I ₁-40 * I ₃ = 0 40 * I ₃ –20 * I ₂ +16 = 0
Express I ₁ с использованием узлового уравнения: I ₁ = -I ₂ — I ₃
затем подставьте его во второе уравнение:
-V ₁ — (I ₂ + I ₃) * R ₁ –I ₃ * R ₃ = 0 или –8- (I ₂ + I ₃) * 40 — I ₃ * 40 = 0
Экспресс I ₂ и подставляем его в третье уравнение, из которого уже можно рассчитать I ₃:
I ₂ = — (V ₁ + I ₃ * (R ₁ + R ₃)) / R ₁ или I ₂ = — (8 + I ₃ * 80) / 40
I ₃ * R ₃ + R ₂ * (V ₁ + I ₃ * (₁ + R ₃)) / R ₁ + V ₂ = 0 или I ₃ * 40 + 20 * (8 + I ₃ * 80) / 40 + 1 6 = 0
И: I ₃ = — (V ₂ + V ₁ * R ₂ / R ₁) / (₃ + (₁ + R ₃₎) * R ₂ / R ₁) или I ₃ = — (16 + 8 * 20/40) / (40 + 80 * 20/40)
Следовательно, I ₃ = — 0.25 А; I ₂ = — (8-0,25 * 80) / 40 = 0,3 A и I ₁ = — (0,3-0,25) = — 0,05 A
Или: I ₁ = -50 мА; I ₂ = 300 мА; I ₃ = -250 мА.
Теперь давайте решим те же уравнения с помощью интерпретатора TINA:
{Решение интерпретатора TINA}
Sys I1, I2, I3
I1 + I2 + I3 = 0
-V1 + I1 * R1-I3 * R3 = 0
I3 * R3-I2 * R2 + V2 = 0
конец;
I1 = [- 50 м]
I2 = [300 м]
I3 = [- 250 м]
Наконец, давайте проверим результаты с помощью TINA:

Затем давайте проанализируем следующую еще более сложную схему и определим ее токи ответвления и напряжения.
Щелкните / коснитесь схемы выше для анализа в режиме онлайн или щелкните эту ссылку, чтобы сохранить в Windows

Обозначим неизвестные напряжения и токи, добавив стрелки напряжения и тока к компонентам, а также покажем петли (L1, L2, L3) и узлы (N1, N2), в которых мы будем использовать уравнения Кирхгофа.
Вот система уравнений Кирхгофа для контуров (с использованием направления по часовой стрелке) и узлов.
-I _L + I _R1 — I _s = 0 (для N1)
— I _R1 + I _R2 + I _s3 = 0 (для N2)
-V _s1 — V _R3 + V _Is + V _L = 0 (для L1)
-V _Is + V _s2 + V _R2 + V _R1 = 0 (для L2)
-V _R2 — V _s2 + V _s3 = 0 (для L3)
Применение закона Ома:
V _L = I _L * R _L
V _R1 = I _R1 * R ₁
V _R2 = I _R2 * R ₂
V _R3 = — I _L * R ₃
Это 9 неизвестных и 9 уравнений.Самый простой способ решить эту проблему — использовать интерпретатор TINA
. Однако, если нас заставляют использовать ручные вычисления, отметим, что этот набор уравнений можно легко свести к системе из 5 неизвестных, подставив последние 4 уравнения в уравнения цикла L1, L2, L3. Кроме того, добавляя уравнения (L1) и (L2), мы можем исключить V _Is, сведя проблему к системе из 4 уравнений для 4 неизвестных (I _L, I _R1 I _R2, I _s3).Найдя эти токи, мы можем легко определить V _L, V _R1, V _R2, и V _R3, используя последние четыре уравнения (закон Ома).
Замена V _L, V _R1, V _R2, V _R3:
-I _L + I _R1 — I _s = 0 (для N1)
— I _R1 + I _R2 + I _s3 = 0 (для N2)
-V _s1 + I _L * R ₃ + V _Is + I _L * R _L = 0 (для L1)
-V _Is + V _s2 + I _R2 * R ₂ + I _R1 * R ₁ = 0 (для L2)
— I _R2 * R ₂ — V _s2 + V _s3 = 0 (для L3)
Складывая (L1) и (L2), получаем
-I _L + I _R1 — I _с = 0 (для N1)
— I _R1 + I _R2 + I _с3 = 0 (для N2)
-V _с1 + I _L * ₃ + I _L * R _L + V _s2 + I _R2 * R ₂ + I _R1 * R ₁ = 0 (L1) + (L2)
— I _R2 * R ₂ — V _s2 + V _s3 = 0 (для L3)
После подстановки значений компонентов легко найти решение этих уравнений.
-I _L + I _R1 — 2 = 0 (для N1)
-I _R1 + I _R2 + I _S3 = 0 (для N2)
-120 — + I _L * 90 + I _L * 20 + 60 + I _R2 * 40 + I _R1 * 30 = 0 (L ₁) + (L ₂)
-I _R2 * 40-60 + 270 = 0 (для L ₃)
от L ₃ I _R2 = 210/40 = 5,25 A (I)
от N ₂ I _S3 — I _R1 = — 5.25 (II)
от L ₁ + L ₂ 110 I _L + 30 I _R1 = -150 (III)
и для N ₁ I _R1 — I _L = 2 (IV)
Умножьте (IV) на –30 и прибавьте к (III) 140 I _L = -210, следовательно, I _L = — 1,5 A
Замените I _L на (IV) I _R1 = 2 + (-1,5) = 0,5 A
и I _R1 в (II) I _S3 = -5,25 + I _R1 = -4,75 A
И напряжения: V _R1 = I _R1 * R ₁ = 15 В; V _R2 = I _R2 * R ₂ = 210 В;
В _R3 = — I _L * R ₃ = 135 В; V _L = I _L * R _L = — 30 В; V _Is = V _S1 + V _R3 -V _L = 285 V
{Решение исходных уравнений интерпретатором TINA}
Sys IL, IR1, IR2, Is3, VIs, VL, VR1, VR3, VR2
-IL-Is + IR1 = 0
-IR1 + IR2 + Is3 = 0
-Vs1 + VR3 + Vis-VL = 0
-Vis + VR1 + VR2 + Vs2 = 0
-Vs3 + VR2 + Vs2 = 0
VR1 = IR1 * R1
VR2 = IR2 * R2
VR3 = -IL * R3
VL = IL * RL
конец;
IL = [- 1.5]
IR1 = [500 м]
IR2 = [5,25]
Is3 = [- 4,75]
VIs = [285]
VL = [- 30]
VR1 = [15]
VR2 = [210]
VR3 = [ 135]
Решение сокращенной системы уравнений с помощью интерпретатора:
{Решение сокращенной системы уравнений интерпретатором TINA}
Sys Il, Ir1, Ir2, Is3
-Il + Ir1 -2 = 0
-Ir1 + Ir2 + Is3 = 0
-120 + 110 * Il + 60 + 40 * Ir2 + 30 * Ir1 = 0
-40 * Ir2 + 210 = 0
конец;
Il = [- 1,5]
Ir1 = [500 м]
Ir2 = [5.25]
Is3 = [- 4,75]
Мы также можем ввести выражения для напряжений, и интерпретатор TINA вычислит их:
Il: = — 1,5;
Ir1: = 0,5;
Ir2: = 5,25;
Is3: = — 4,75;
Vl: = Il * RL;
Vr1: = Ir1 * R1
Vr2: = Ir2 * R2;
Vr3: = — Il * R3;
VI: = Vs1-Vl + Vr3;
Vl = [- 30]
Vr1 = [15]
Vr2 = [210]
Vr3 = [135]
VIs = [285]

Мы можем проверить результат с помощью TINA просто включив интерактивный режим TINA DC или используя Analysis / DC Analysis / Nodal Voltages
.

Примеры решения задач на законы Кирхгофа

Задача 1

Задача 2

Законы Кирхгофа для расчёта электрических цепей

Первый закон Кирхгофа

Второй закон Кирхгофа

Список использованной литературы

Рекомендуемые записи

1) Составить уравнения по законам Кирхгофа.

2) Рассчитать токи во всех ветвях методом контурных токов.

Законы Кирхгофа и их применение

Законы Кирхгофа

Законы Кирхгофа: Первый и второй законы Кирхгофа.

Второй закон Кирхгофа.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа.

Первый и второй законы Кирхгофа для электрических цепей

Алгоритм составления уравнений по законом Кирхгофа

Составляем уравнения по первому закону Кирхгофа

Составляем уравнения по второму закону Кирхгофа

Расчет токов по правилам Кирхгофа

правил Кирхгофа | Безграничная физика

Введение и значение

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Введение в законы Кирхгофа

Правило пересечения

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Ограничение

Правило цикла

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Пример

Ограничение

Приложения

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Обзор

Пример правил Кирхгофа

Как схемы становятся уравнениями | Прядильные числа

Содержание

Куда мы направляемся

Проверка концепции: пример схемы

Откуда берутся уравнения?

Половина уравнений исходит из законов элементов

Половина уравнений взята из законов Кирхгофа

Что такое независимое уравнение?

Сколько независимых уравнений получается из KCL?

Сколько независимых уравнений получается из KVL?

Убедитесь, что уравнения KVL независимы

Выбор сеток и петель

Проверка концепции

Сводка

Номер ссылки

Закон Кирхгофа для сложных схем | ОРЕЛ

Что такое Окружной закон Кирхгофа?

Первый закон — Действующий закон Кирхгофа

1. Рассчитайте общий ток

2.Расчет узловых токов

3. Подтвердите действующий закон Кирхгофа

Второй закон — Закон Кирхгофа о напряжении

1.Рассчитайте общее сопротивление

2. Рассчитайте общий ток

3. Рассчитайте ток через каждый резистор

4.Рассчитайте падение напряжения на каждом резисторе

5. Подтвердите закон Кирхгофа о напряжении

Процесс использования закона Кирхгофа о схемах

Стоя на плечах Ома

электрического тока — есть ли простое доказательство того, что законы Кирхгофа всегда дают точно полный набор уравнений?

Что такое закон Кирхгофа и закон напряжения Кирхгофа?

Действующий закон Кирхгофа