Переменный (синусоидальный) ток и основные характеризующие его величины.


Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):

 Рисунок 1
Рисунок 1

Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
- амплитуду тока обозначают lm;
- амплитуду напряжения Um.
Период Т— это время, за которое совершается одно полное колебание.
Частота f равна числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
f = 1/T
Угловая частота ω (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Обратите внимание! При обозначении величин на схемах или в расчетах важен регистр букв, то есть заглавные буквы (E,I,U…) или строчные (e, i ,u…). Так как строчными буквами принято обозначать мгновенное значение, а заглавными могут обозначаться действующее значение величины (подробнее о действующем значении в следующей статье).
Переменный синусоидальный ток

Колебания маятника также подчиняются закону синуса. Если записать проекцию траектории движения математического маятника на движущуюся бумажную ленту — получится синусоида.
Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по закону синуса.
Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи.
Переменный синусоидальный ток выражается формулой:
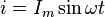 ,
где
,
где
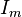
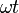 —
некоторый угол,
называемый фазой
синусоидального тока.
—
некоторый угол,
называемый фазой
синусоидального тока.
Фаза синусоидального
тока 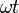 изменяется
пропорционально времени
изменяется
пропорционально времени  .
.
Множитель  ,
входящий в выражение фазы
,
входящий в выражение фазы 
Угловая
частота  синусоидального
тока зависит от частоты
синусоидального
тока зависит от частоты 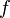 этого
тока и определяется формулой:
этого
тока и определяется формулой:
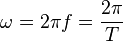 ,
где
,
где
 —
угловая частота
синусоидального тока;
—
угловая частота
синусоидального тока;
 —
частота синусоидального
тока;
—
частота синусоидального
тока; 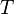 — период синусоидального
тока;
— период синусоидального
тока;
 —
центральный
угол окружности,
выраженный в радианах.
—
центральный
угол окружности,
выраженный в радианах.
Зависимость синусоидального тока от времени
Зависимость синусоидального тока от угла ωt
Периоду 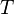
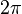 ,
половине периода
,
половине периода  угол
угол 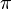 и
так далее…
и
так далее… Исходя
из формулы 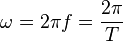 ,
можно определить размерность угловой
частоты:
,
можно определить размерность угловой
частоты:
 ,
где
,
где
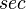
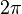 —
угол в радианах,
является безразмерной величиной.
—
угол в радианах,
является безразмерной величиной.
Фаза 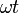 синусоидального
тока измеряется радианами.
синусоидального
тока измеряется радианами.
1
радиан = 57°17′, угол 90° =  радиан,
угол 180° =
радиан,
угол 180° = 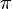 радиан,
угол 270° =
радиан,
угол 270° =
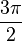 радиан,
угол 360° =
радиан,
угол 360° = 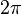 радиан,
где
радиан,
где  радиан;
радиан; 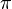 — число
«Пи», ° — угловой
градус и ′ — угловая
минута.
— число
«Пи», ° — угловой
градус и ′ — угловая
минута. Формула 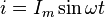
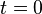 при
при 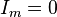 .
Если
.
Если  не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид:
не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид: 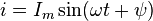 ,
где
,
где
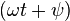
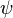 — угол,
называемый начальной
фазой переменного синусоидального
тока.
— угол,
называемый начальной
фазой переменного синусоидального
тока.
Начальная
фаза переменного тока 

Начальная
фаза переменного тока 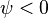
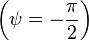
Если
в формуле 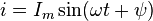 принять
принять 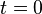 ,
то будем иметь
,
то будем иметь
 ,
,  и
и 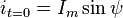 .
.
Начальная фаза — это фаза синусоидального тока в момент времени
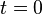 .
. Начальная
фаза переменного синусоидального тока
может быть положительной 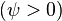 или
отрицательной
или
отрицательной 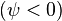 величиной.
При
величиной.
При  мгновенное
значение синусоидального тока в момент
времени
мгновенное
значение синусоидального тока в момент
времени 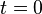 положительно,
при
положительно,
при 
Если
начальная фаза 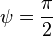 ,
то ток определяется по формуле
,
то ток определяется по формуле 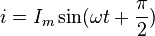 .
Мгновенное значение его в момент
времени
.
Мгновенное значение его в момент
времени  равно
равно
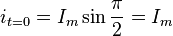 ,
то есть равно положительной амплитуде
тока.
,
то есть равно положительной амплитуде
тока.
Если
начальная фаза 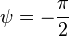
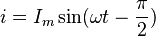 .
Мгновенное значение его в момент
времени
.
Мгновенное значение его в момент
времени 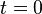 равно
равно 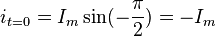 ,
то есть равно отрицательной амплитуде
тока.
,
то есть равно отрицательной амплитуде
тока.
9. Идеальные элементы электрической цепи синусоидального тока
11. Неразветвленная цепь синусоидального тока. Резонанс напряжений
Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Описание явления
Пусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f.
В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.
Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.
Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.
Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.
Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.
Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.
Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.
В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.
Переменный синусоидальный ток
Переменный ток — это ток, который периодически изменяется как по модулю, так и по направлению. Появляется переменный ток благодаря электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом контуре при изменении магнитного потока проходящего через него. Чтобы понять, как именно возникает ток, представим себе рамку (кусочек проволоки прямоугольной формы), которая находится под воздействием магнитного поля B.

Пока рамка находится в покое, тока в ней нет. Но как только мы начнём её поворачивать, электроны, которые находятся в рамке, начнут перемещаться вместе с ней, то есть двигаться в магнитном поле. Вследствие этого магнитное поле начинает действовать на электроны, заставляя их двигаться по рамке. Чем больше линий магнитного поля пронизывает рамку, тем сила действующая на электроны больше, следовательно, и электрический ток тоже. Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.
Ток, который получается при вращении рамки, изменяясь во времени, описывает синусоиду, то есть является синусоидальным. Переменный синусоидальный ток является частным случаем периодического переменного тока. Закон, описывающий изменение тока, имеет вид:


Амплитуда Im – это наибольшая абсолютная величина, которую принимает периодически изменяющийся ток.
Начальная фаза ψ — аргумент синусоидального тока (угол), отсчитываемый от точки перехода тока через нуль к положительному значению.
Время, за которое ток в проводнике дважды изменяет своё направление, называют периодом T. Период измеряется в секундах.
Циклической частотой f называется величина обратная периоду . Измеряется в Герцах, в домашней розетке циклическая частота тока равна 50 Гц, её также называют промышленной частотой. При такой частоте период тока равен  , это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.
, это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.
Угловая частота ω показывает с какой скоростью изменяется фаза тока и определяется как

Среднее значение Iср синусоидального тока за период Т определяют из геометрических представлений: площадь прямоугольника с основанием T/2 и высотой Iср приравнивают площади ограниченной кривой тока:

После упрощения получаем формулу:

Действующее значение синусоидального тока определяется из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как и данный ток i. То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
Для синусоидального тока действующее значение определяется по формуле:

или

Это основное что нужно знать о переменном синусоидальном токе.
Читайте также — Мгновенная мощность
Синусоидальный ток и его характеристики
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):
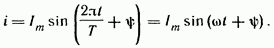
Максимальное
значение функции называют амплитудой.
Амплитуду тока обозначают  .
Период Т — это время, за которое
совершается одно полное колебание.
.
Период Т — это время, за которое
совершается одно полное колебание.
Частота
равна числу колебаний в 1 с (единица
частоты 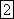 —
герц (Гц) или
—
герц (Гц) или 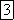
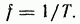
Угловая
частота (единица угловой частоты —
рад/с или 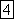 )
)
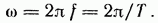
Аргумент
синуса, т. е.  называют
фазой. Фаза характеризует состояние
колебания (числовое значение) в данный
момент времени
называют
фазой. Фаза характеризует состояние
колебания (числовое значение) в данный
момент времени 
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ).
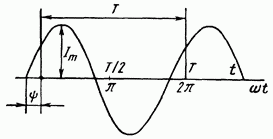
Рис. 3.1
Источник
синусоидальной ЭДС и источник
синусоидального тока обозначают на
электрических схемах так же, как и
источники постоянной ЭДС и тока, но
обозначают их  и
и 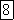
Синусоидальный ток
Синусоидальный ток представляет собой функцию времени. То есть в отличие от постоянного тока его значение меняется с течением времени. Основными характеристиками синусоидального тока являются. Амплитуда частота и начальная фаза.
Частота f это количество колебаний в единицу времени. За единицу времени в системе СИ принимается одна секунда. Таким образом, количество колебаний за секунду это и есть частота синусоидального тока. И измеряется она в Герцах. Названа в честь ученого Герца. Величина обратная частоте называется периодом колебания T=1/f. Период измеряется в секундах. Определение периода звучит так период это время полного колебания. Если представить себе маятник часов то период это время за которое он совершит движение из одного крайнего положения в другое и обратно.
Амплитуда синусоидального тока это максимальное значение тока, которое он достигает за период колебания. Опять же если рассматривать на примере маятника, то амплитуда это расстояние от положения равновесия до одного из крайних положений.
Начальная фаза синусоидального тока это то время, на которое отстает либо опережает синусоида начальный момент времени. Представим две синусоиды одна, из которых начинается условно в нуле а другая в 1. То можно сказать, что вторая синусоида отстаёт по фазе от первой. Если обе синусоиды начинаются в одной точке то можно сказать что они синфазные, то есть имеют одну фазу. При этом они обе могут отставать от начального момента времени на одну и ту же величину, то есть иметь одинаковую начальную фазу.
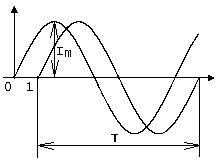
Рисунок 1 — Графическое представление синусоидального тока
Математически синусоидальный ток описывается уравнением:
i=Im*sin(wt+j)
где
i мгновенное значение тока это величина тока в определенный момент времени с учетом частоты и начальной фазы тока.
Im амплитуда тока.
j начальная фаза
w угловая частота выражается как
синусоидальное переменное напряжение ток | Электрознайка. Домашний Электромастер.
Действующее значение синусоидального
переменного напряжения – тока.
data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.
Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т.
Количество периодов переменного тока за 1 секунду, есть частота f.
Частота переменного тока f измеряется в герцах .
f = 1 / T.
Например.
Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен:
T = 1 / f = 1 / 50 = 0,02 сек.
Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.
Umax = Ua и Imax = Ia
За один период напряжение принимает эти значения два раза: + Ua и — Ua .
♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.
Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:
Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока
Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения
На все эти теоретические размышления можно посмотреть иначе!
♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.
Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.
♦На рисунке приняты обозначения:
Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.
Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.
P = Ua х Ia = Uд х Iд = U х I
♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.
Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.
data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
Представление синусоидальных величин с помощью векторов и комплексных чисел (Лекция N 3)
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем
| , | (1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
| , | (2) |
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц.
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е — мгновенное значение ЭДС ;
р— мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
— амплитуда тока;
— амплитуда напряжения;
— амплитуда ЭДС.
Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
| , | (3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2соответствуют уравнения:
.
Значения аргументов синусоидальных функций и называются фазами синусоид,
а значение фазы в начальный момент времени (t=0): и — начальной фазой
().
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2угол сдвига фаз:
.
Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
и .
Результирующий ток также будет синусоидален:
.
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.
На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической или
алгебраической — формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
.
Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
| , | (4) |
Комплексное число удобно представить в виде произведения двух комплексных чисел:
| , | (5) |
Параметр , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр — комплексом мгновенного значения.
Параметр является оператором поворота вектора на угол wt относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
| , | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
,
— то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:
.
Тогда мгновенное значение напряжения:
,
где .
При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)
| , | (7) |
а при (третий квадрант)
| (8) |
или
| (9) |
Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:
где ;
.
Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
.
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:
| . | (10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
.
Литература
1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
5. На рис. 5 , а . Определить .
Ответ: .
Часть 3. Переменный ток (краткая теория)
Получение, передача и распределение электрической энергии осуществляются в основном с помощью устройств и сооружений переменного тока. Для этого применяют генераторы, трансформаторы, линии передачи и распределительные сети переменного тока. Широко используют приемники электрической энергии, работающие на переменном токе.
Переменным током называют любой изменяющийся с течением времени электрический ток.
Переменным синусоидальным током называют изменяющийся по закону синуса (косинуса) с течением времени электрический ток.
В электротехнике чаще всего приходится иметь дело с переменным током, величина которого изменяется по периодическому синусоидальному закону. В некоторых случаях ток изменяется по периодическому несинусоидальному закону
В линейных электрических цепях переменный синусоидальныйток возникает под действием ЭДС такой же формы. Дляизучения электрических устройств и цепейпеременного тока необходимо прежде рассмотреть способы получения синусоидальной ЭДС и основные понятия, относящиеся к величинам, которые изменяются по синусоидальному закону.
3.1. Получение синусоидальной эдс
Переменным током (ЭДС) в электрических цепях называется такой ток (ЭДС), который изменяет свое значение и направление во времени.
В электротехнике в основном приходится иметь дело с током, величина которого изменяется по синусоидальному закону. Для получения ЭДС синусоидальной формы генератор переменного тока промышленного типа имеет определенные конструктивные особенности.
Рис. 3.1 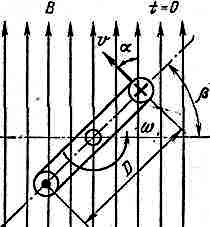
Синусоидально изменяющуюся величину ЭДС со временем можно получить, вращая с постоянной скоростью в однородном магнитном поле проводник в виде прямоугольной рамки. При движении проводника в магнитном поле в нем возбуждается ЭДС индукции
e=Bυlsina (3.1)
При вращении витка в магнитном поле с постоянной скоростью изменяется угол между направлением индукции магнитного поля и нормалью к плоскости рамки α = ωt, где ω — угловая скорость. Наибольшее значение ЭДС достигается при угле α = ωt = 90°:
ЕМ =Bυl. (3.2)
Синусоидальное изменение ЭДС достигается путем равномерного изменения угла, под которым виток пересекает линии магнитной индукции. Таким образом,
е = ЕМ sinα = ЕМ sin ωt (3.3)
Аналогично запишутся формулы переменного напряжения и тока: и = UМ sin ωt, i = IМ sin ωt
3.2. Характеристики синусоидальных величин
Синусоидально изменяющиеся ЭДС, напряжение и ток характеризуются следующими величинами: мгновенным значением, амплитудой, периодом, частотой, фазой (сдвигом фаз) (рис. 3.2). Мгновенное значение ЭДС, напряжения и силы тока – значение этих величин в любой момент времени. Мгновенные значения обозначаются строчными буквами е, и, i.
Амплитуда — это наибольшие значения, которые принимает ЭДС, напряжение и сила тока. Амплитудные значения обозначаются прописными буквами Еm , Um , Im .
Период Т — промежуток времени, в течение которого ЭДС, напряжение и ток совершают полное колебание и принимают прежнее по величине и знаку значение.
Рис.3.2 Графики изменения переменного тока и ЭДС.

Частота f (число периодов в
секунду) — величина, обратная периоду:f = 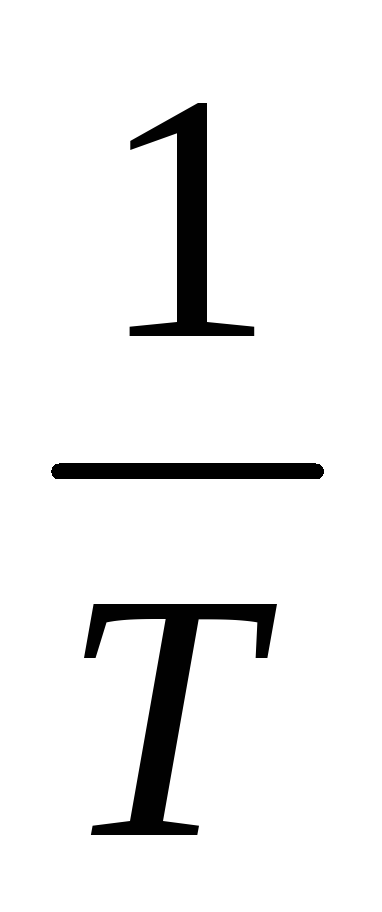 (3.4)
(3.4)
Единица частоты — герц (Гц). Стандартная промышленная частота 50 Гц. В США и Японии-60 Гц. В некоторых областях промышленности находят применение другие частоты.
Угловая частота ω есть величина, равная числу периодов
за 2п секунд.
Так как в течение периода α = 2π, то ω = 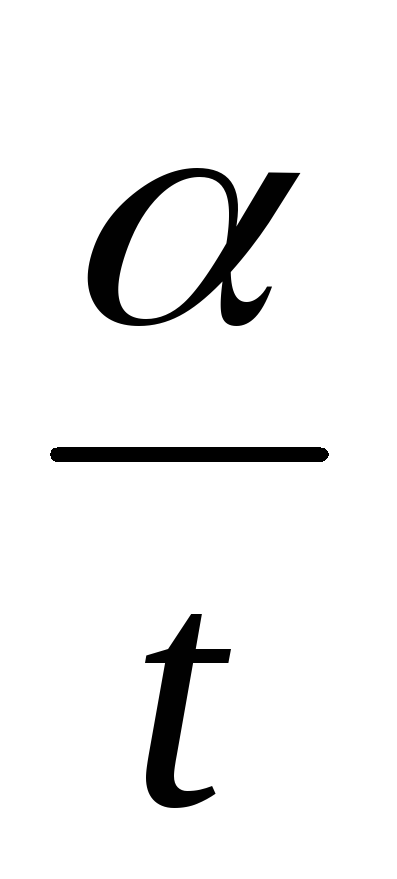 , т. е. ω =
, т. е. ω =  (3.5)
(3.5)
Размерность угловой частоты
— град/с или рад/с.ω = 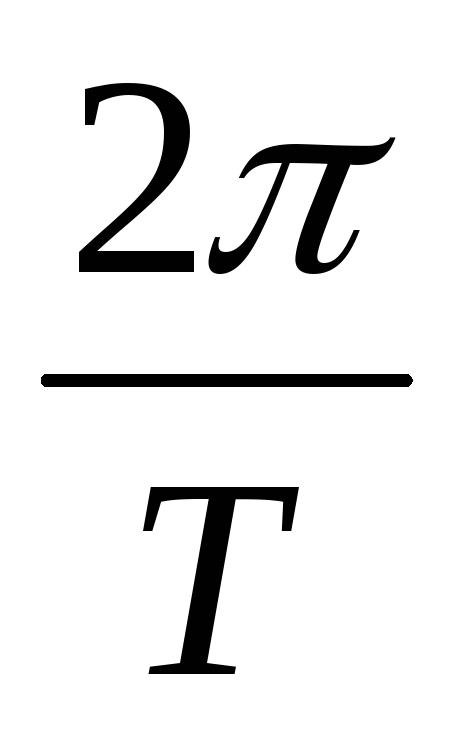 или ω = 2π f
или ω = 2π f
Фаза — угловое значение аргумента синусоидальной ЭДС, напряжения, тока, определяющее мгновенное значение этих величин. При α = ωt = 0 мгновенные значения е, и и i будут равны нулю. Если фаза имеет выражение (ωt + ψ), то при t = 0 фаза не равна нулю и мгновенное значение е будет равнo е = Еm sin(ωt + ψ),а фаза ψ называется начальной фазой.
Таким образом, в общем виде уравнение ЭДС может быть записано так:
е = Еm sin(ωt + ψ) (3.6)
где α = (ωt + ψ) — угол, называемый фазой. Аналогично запишутся выражения для переменного напряжения и тока.
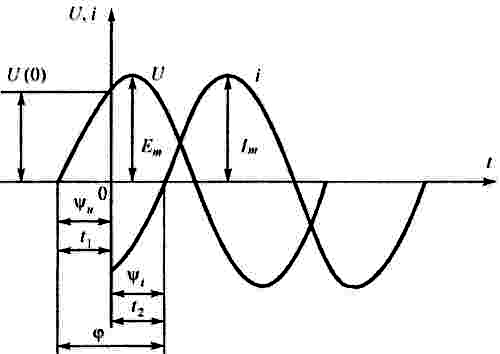
Две синусоидальные величины, имеющие разные начальные фазы, называются сдвинутыми по фазе (рис. 3.3). Угол сдвига фаз φ = ψu + ψi
Та величина, в которой начало периода, или положительная амплитуда достигается раньше, чем у другой, считается опережающей по фазе, а та, у которой те же значения достигаются позже — отстающей по фазе.
Изображенные на рис. 3.2 синусоидальные величины называют совпадающими по фазе. Если угол сдвига составляет π, то говорят, что они находятся в противофазе. Сдвиг по фазе можно установить и на графике. Для этого достаточно выбрать две ближайшие точки, соответствующие положительным амплитудам величин, и установить разность фазовых углов.
Действующая и средняя
величины переменного тока. Переменный
ток, как и постоянный, оказывает тепловое,
механическое, магнитное и химическое
действие. В формулы расчета теплового,
механического, магнитного и химического
действия переменного тока подставляют
действующее значение переменного тока.
Действующим значением переменного
тока называется постоянный ток,
который за время одного периода оказывает
такое тепловое (механическое и др.)
действие, как и данный переменный ток.
Действующее значение для данного
переменного тока есть величина постоянная
и равна амплитудному значению,
деленному на  ,
т. е.IД =
,
т. е.IД =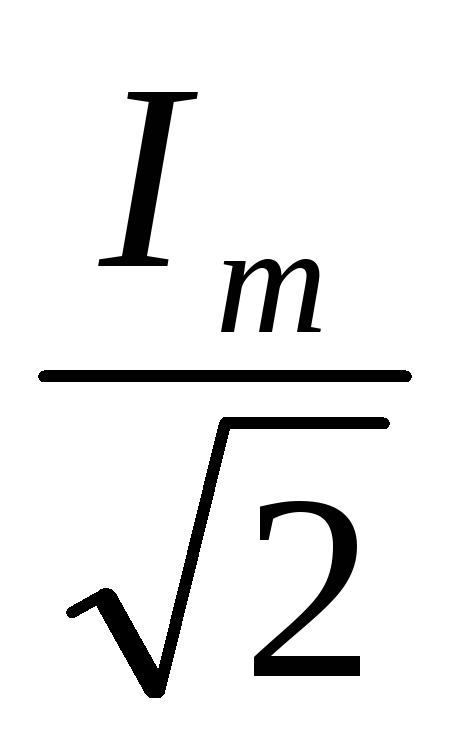
Для доказательства этого рассмотрим тепловое действие тока. Тепловое действие постоянного тока определяется по закону Джоуля -Ленца: Q = I2 RT (3.7)
где Т- время, равное одному периоду.Такое же количество теплоты в данном проводнике за это время выделится и при переменном токе i = 1тsinωt. Тогда формула (3.7) для переменного тока примет вид:Q = IД2RT, (3.8)
где IД — действующее значение переменного тока. Из формулы (3.8) можно записать
I Д2 R=Р (5.9)
где Р — средняя мощность
переменного тока за период. Мгновенная
мощность синусоидального тока равнаp = i2R =Iт2 sin2 ωt ·R =Iт2·R 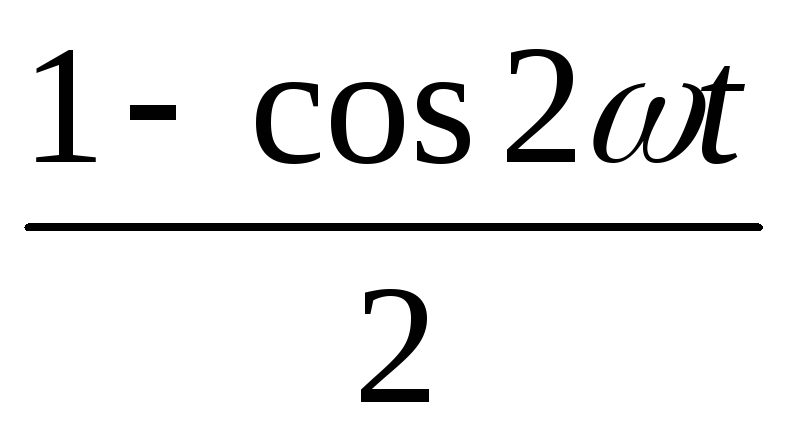 = Iт2·
= Iт2· −Iт2
−Iт2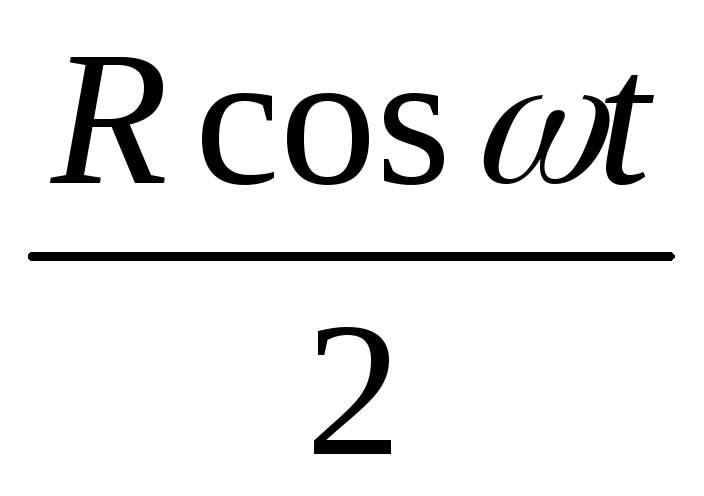 (3.10)
(3.10)
Как видно из формулы (3.10), мгновенная мощность переменного тока выражается двумя слагаемыми. Первое слагаемое является величиной постоянной и от времени не зависит, а второе − изменяется по синусоидальному закону и в сумме за период равно нулю. Следовательно, средняя мощность переменного тока за период может быть выражена формулой
р = Iт2·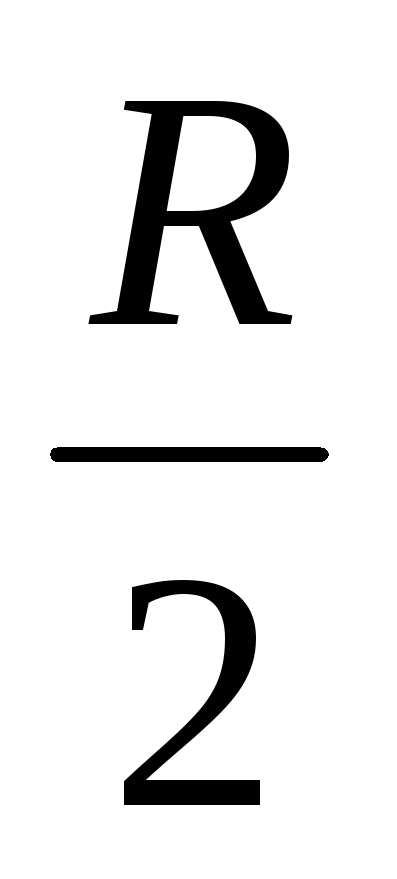 (3.11)
(3.11)
Из равенств (3.9) и (3.11) можно записать:
I Д2 R
= Iт2·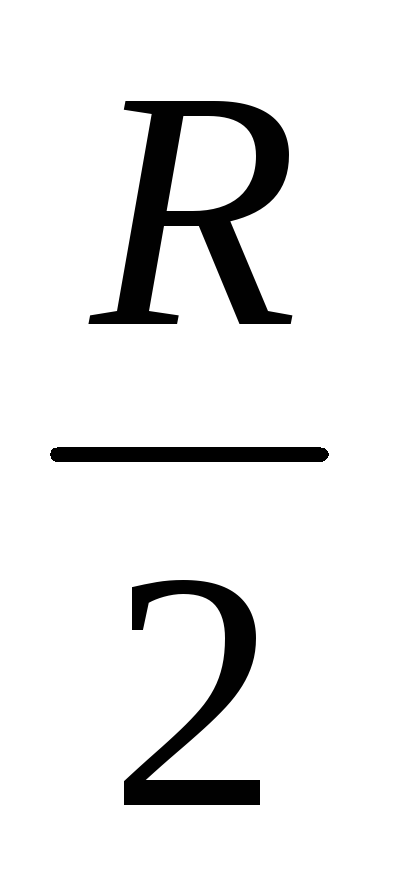 ,
т. е. IД =
,
т. е. IД =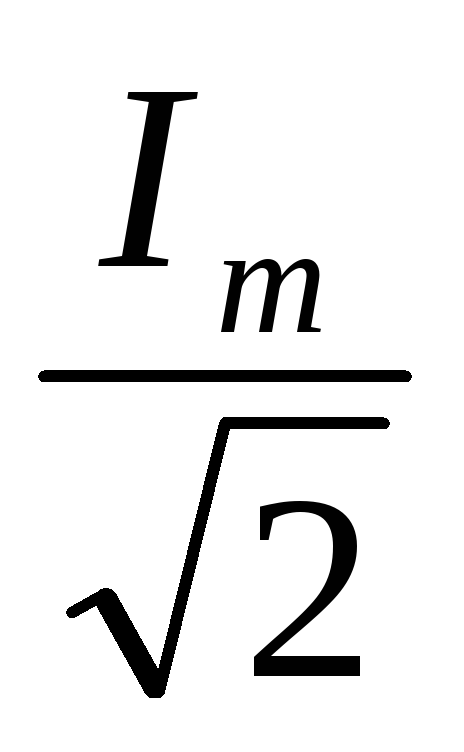 илиIД = 0,707 · Iт,
т. к.
илиIД = 0,707 · Iт,
т. к.  ≈1,41
≈1,41
Все определения и соотношения действующего значения переменного тока справедливы и для переменного напряжения, и для ЭДС.
Все амперметры и вольтметры при измерении переменного тока и напряжения показывают их действующие значения, так как принцип работы их основан на механическом или тепловом действии тока.Пусть при включении в сеть сопротивления R = 40 Ом амперметр показал ток 5,5 А. Действующее напряжение в сети U = R · I = 40 Ом • 5,5А = 220 В,
а амплитудное Um = 220В • 1,41 =310,2 В.
При изучении электрических машин, выпрямительных устройств пользуются средним значением ЭДС, силы тока и напряжения. Средним значением переменного тока, напряжения и ЭДС называется среднее арифметическое из всех мгновенных значений за полупериод.
Для
синусоидального тока IСР=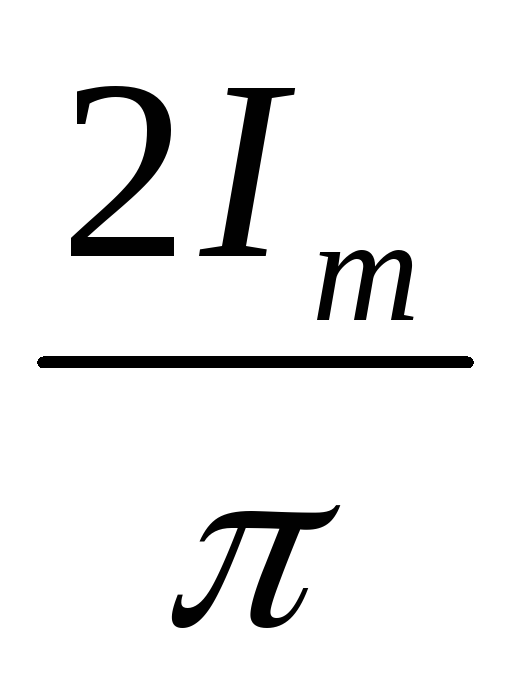 = 0,637 ·Iт
= 0,637 ·Iт
Изображение синусоидальных величин вращающимся вектором.
Прирасчете электрических цепей переменного тока пользуются простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.Пусть напряжение задано уравнением и = Um sin(ωt + ψ)
Проведем две перпендикулярные оси, затем из точки пересечения осей вектор длиной U в выбранном масштабе (рис/3.4). Направление вектора выбирается таким, чтобы с горизонтальной осью он составлял угол ψ, т. е. равный начальной фазе. Проекция этого вектора на ось ординат определяет мгновенные значения напряжения u(0) = Um sin ψt

Вращаем вектор U против часовой стрелки с угловой скоростью ω. Положение радиуса-вектора в любой момент времени определяется углом (ωt + ψ). Для произвольного значения времени t мгновенное значение напряжения определяется проекцией вектора U на вертикальную ось в этот момент времени. Например, для t = t1, u(t1) = Um sin(ωt1 + ψ), т. е. мы имеем уравнение такого вида, как и заданное. Это дает нам возможность изобразить напряжение вращающимся вектором, нанесенном на чертеж в начальном положении.Вращая вектор Um против часовой стрелки, построим в прямоугольной системе координат график изменения проекции его на вертикальную ось за один период. Соединив полученные точки, получим график синусоидальной функции, соответствующий заданному уравнению.Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты, называется векторной диаграммой.
Достоинством векторных диаграмм является простота и наглядность. Сложение и вычитание синусоидальных величин осуществляется по правилам сложения и вычитания векторов.



