Глава 12. Переменный ток . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать получение напряжения переменного тока с помощью генератора переменного тока.
• Дать определения цикла, герца, синусоиды, периода и частоты.
• Описать части генератора переменного тока.
• Дать определения пикового значения, полного размаха колебания и эффективного или среднеквадратичного значения.
• Объяснить соотношение между временем и частотой.
• Описать три основных вида несинусоидальных сигналов.
• Знать, что несинусоидальный сигнал имеет основную частоты и гармоники.
Переменный ток широко используется в настоящее время. В отличие от постоянного тока, который течет только в одном направлении, переменный ток периодически изменяет свое направление.
Переменный ток легче генерировать и передавать на большие расстояния. Генераторы переменного тока проще и более экономичны в работе. Напряжение переменного тока может быть увеличено или уменьшено с помощью трансформатора с очень малой потерей мощности. Кроме того, переменный ток легко преобразуется в постоянный.
Переменный ток можно использовать для передачи информации из одного пункта в другой по линиям передачи, а также преобразовать в электромагнитные волны и передавать и принимать с помощью антенных систем.
В этой главе описываются способы производства и важные электрические характеристики переменного тока.
12-1. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА
Генератор переменного тока преобразует механическую энергию в электрическую. Генератор переменного тока вырабатывает переменное напряжение, используя принципы электромагнитной индукции. Электромагнитная индукция — это процесс индуцирования напряжения в проводнике, движущемся в магнитном поле.
Электромагнитная индукция — это процесс индуцирования напряжения в проводнике, движущемся в магнитном поле.
Как описано в главе 9, правило левой руки для генераторов может быть использовано для определения направления тока в проводнике, который перемещается в магнитном поле: когда большой палец указывает направление движения проводника, а указательный (расположенный под прямым углом к большому) указывает направление магнитных силовых линий от севера к югу, то средний палец (расположенный под прямым углом к двум другим) укажет направление тока в проводнике. Максимальное напряжение индуцируется, когда проводник движется перпендикулярно силовым линиям. Если же проводник перемещается параллельно силовым линиям, напряжение не индуцируется.
На рис. 12-1 показана рамка, вращающаяся в магнитном поле.
В положении А рамка (т. е. ее горизонтальные проводники) перемещается параллельно силовым линиям, и напряжение при этом не индуцируется. Повернувшись в положение Б, рамка при движении пересекает максимальное число магнитных силовых линий и, следовательно, индуцируется максимальное напряжение. При перемещении рамки в положение В количество пересекаемых силовых линий уменьшается, и индуцированное напряжение уменьшается также. Поворот рамки из положения А
е. ее горизонтальные проводники) перемещается параллельно силовым линиям, и напряжение при этом не индуцируется. Повернувшись в положение Б, рамка при движении пересекает максимальное число магнитных силовых линий и, следовательно, индуцируется максимальное напряжение. При перемещении рамки в положение В количество пересекаемых силовых линий уменьшается, и индуцированное напряжение уменьшается также. Поворот рамки из положения А
Каждый раз, когда рамка генератора переменного тока делает полный оборот, говорят о завершении одного цикла. Величина выходного напряжения за время одного цикла возвращается к исходному значению.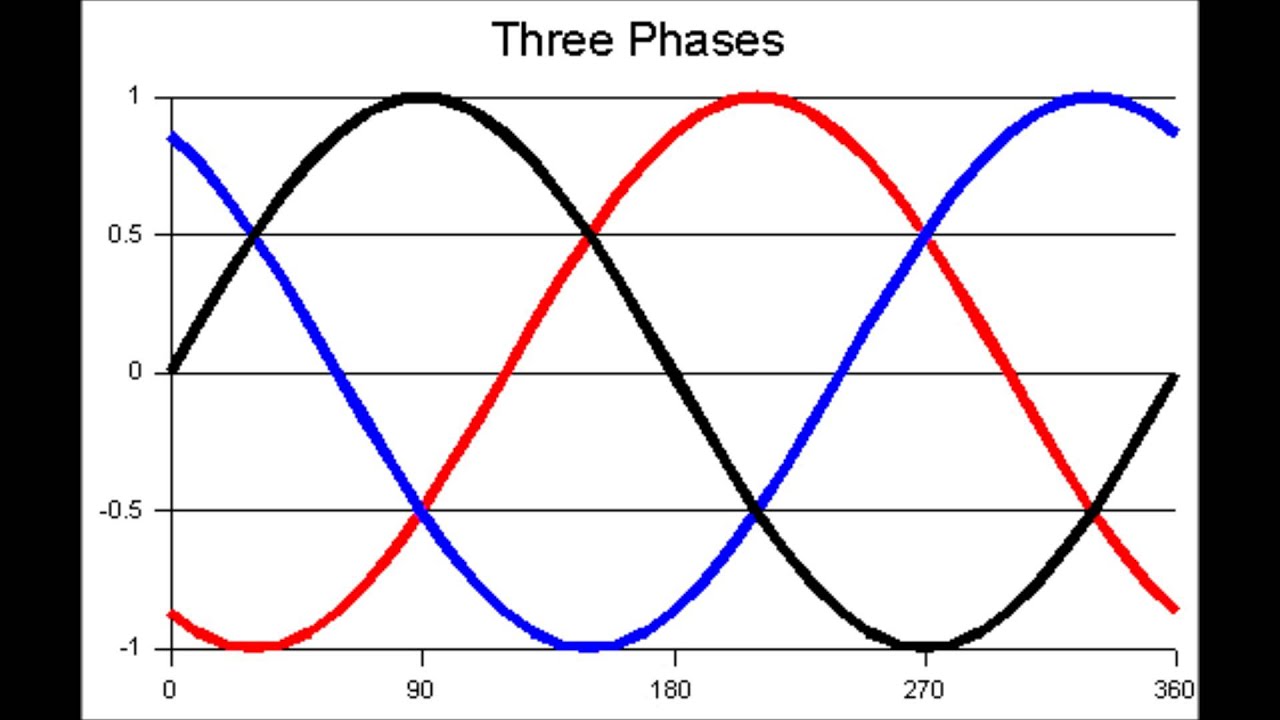 Время, в течение которого совершается полный цикл, называется
Время, в течение которого совершается полный цикл, называется
Аналогично, генератор вырабатывает в замкнутой цепи выходной ток, имеющий периодическую форму. Каждую половину периода происходит изменение полярности напряжения (рис. 12-2).
Рис. 12-2. Каждый цикл состоит из чередования положительных и отрицательных значений величин.
Напряжение имеет одну полярность в течение половины цикла (периода) и противоположную полярность в течение следующей половины цикла (периода). В первую половину периода вырабатывается напряжение положительной полярности, во вторую половину периода вырабатывается напряжение отрицательной полярности. Один цикл в секунду определяется как
Вращающаяся рамка называется якорем. Напряжение переменного тока, индуцируемое во вращающемся якоре, снимается с концов рамки с помощью скользящих контактов, расположенных с двух сторон якоря (рис. 12-3).
12-3).
Рис. 12-3. Напряжение снимается с якоря генератора переменного тока с помощью токосъемных колец.
Два металлических кольца, называемых токосъемными кольцами, подсоединены к двум концам рамки. Скользящие щетки, прилегающие к токосъемным кольцам, снимают переменное напряжение. На практике генератор переменного тока должен содержать много рамок для увеличения амплитуды индуцируемого напряжения.
Форма вырабатываемого генератором переменного тока напряжения называется синусоидой (рис. 12-4).
Рис. 12-4. Синусоида — основная форма переменного тока.
Синусоида является основной и наиболее широко используемой из всех форм переменного тока. Ее можно получить как механическим, так и электронным методом. И напряжение, и ток изменяются в виде синусоиды.
12-1. Вопросы
1.
2. Объясните, как работает генератор переменного тока.
3. Дайте определения следующих терминов:
а. Цикл
б. Период
в. Герц
г. Синусоида
4. Опишите главные части генератора переменного тока.
5. В чем разница между двумя половинами периода?
12-2. ВЕЛИЧИНА ПЕРЕМЕННОГО ТОКА
Каждая точка синусоиды характеризуется двумя параметрами. Один из них — угол, на который повернулся якорь. Второй указывает амплитуду индуцируемой величины.
Пиковое значение синусоиды — это наибольшее значение функции в течение периода (рис. 12-5).
Рис. 12-5. Пиковое значение синусоиды — это точка ее наибольшего значения. Пиковое значение может быть как положительным, так и отрицательным.
12-5. Пиковое значение синусоиды — это точка ее наибольшего значения. Пиковое значение может быть как положительным, так и отрицательным.
Существуют два пиковых значения — одно положительное, а другое отрицательное, они равны по абсолютной величине.
Значение полного размаха синусоиды означает вертикальное расстояние между двумя пиковыми значениями (рис. 12-6).
Рис. 12-6. Размах можно определить как сумму абсолютных величин пиковых значений разного знака.
Значение полного размаха можно определить сложением абсолютных значений пиковых величин.
Эффективное значение переменного тока — это такое значение постоянного тока, при котором на данном сопротивлении выделяется столько же тепла, что и при переменном токе. Эффективное значение можно определить, вычислив среднеквадратичное значение, поэтому эффективное значение часто называют 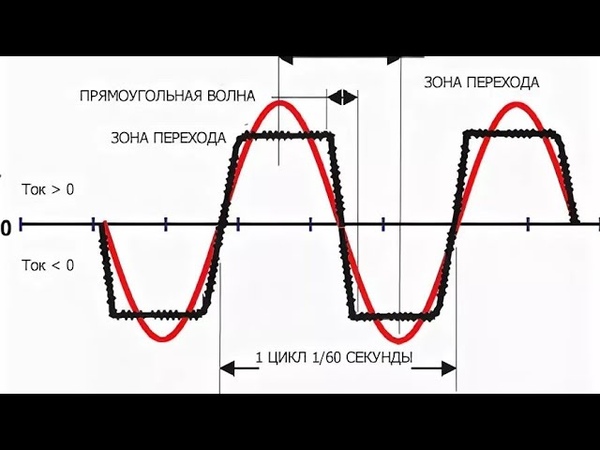 Вычисление среднеквадратичного значения показывает, что эффективное значение синусоиды равно 0,707 от пикового значения. Когда указывается значение переменного тока или напряжения без каких-либо уточнений, предполагается, что это эффективное значение. Большинство измерительных приборов проградуировано в эффективных значениях тока или напряжения.
Вычисление среднеквадратичного значения показывает, что эффективное значение синусоиды равно 0,707 от пикового значения. Когда указывается значение переменного тока или напряжения без каких-либо уточнений, предполагается, что это эффективное значение. Большинство измерительных приборов проградуировано в эффективных значениях тока или напряжения.
Еэфф = 0,707∙Емакс
где Еэфф — эффективное значение напряжения, Е
Iэфф = 0,707∙Iмакс
где Iэфф — эффективное значение тока, Iмакс — максимальное или амплитудное значение тока.
ПРИМЕР: Синусоида тока имеет максимальное (пиковое) значение 10 ампер. Чему равно эффективное значение?
Дано:
Iмакс = 10 А
Iэфф =?
Решение:
Iэфф =0,707∙Iмакс =(0,707)(10)
Iэфф =7,07 А
ПРИМЕР: Синусоида напряжения имеет эффективное значение 40 вольт. Чему равно максимальное (пиковое) значение синусоиды?
Чему равно максимальное (пиковое) значение синусоиды?
Дано:
Eэфф = 40 В
Eмакс =?
Решение:
Еэфф = 0,707∙Емакс
40 = 0,707∙Емакс
Eмакс = 56,58 В
Время, требуемое для завершения одного цикла синусоиды называется периодом. Период обычно измеряется в секундах. Для обозначения периода используется буква t.
Количество циклов, совершаемых за заданный промежуток времени называется частотой. Частота синусоиды переменного тока обычно выражается в количестве циклов за секунду. Единицей частоты является герц. Один герц равен одному циклу в секунду.
Период синусоиды обратно пропорционален ее частоте.
Чем выше частота, тем короче период. Соотношение между частотой и периодом синусоиды выражается следующими формулами:
f = 1/t;
t = 1/f
где f — частота, a t — период.
ПРИМЕР: Чему равна частота синусоиды с периодом 0,05 секунд?
Дано:
t = 0,05 сек
f =?
Решение:
f = 1/t = 1/0,05
f = 20 Гц
ПРИМЕР: Если синусоида имеет частоту 60 герц, то чему равен ее период?
Дано:
f = 60 Гц
t =?
Решение:
t = 1/f = 1/60
t = 0,0167 с или 16,7 мс.
12-2. Вопросы
1. Дайте определения следующих величин:
а. Пиковое (максимальное) значение;
б. Размах синусоиды;
в. Эффективное значение;
г. Среднеквадратичное значение.
2. Синусоида напряжения имеет пиковое значение 125 вольт. Чему равно эффективное значение?
3. Каково соотношение между временем и частотой?
4. Синусоида тока имеет эффективное значение 10 ампер. Чему равно ее пиковое значение?
5. Чему равен период синусоиды с частотой 400 герц?
12-3. НЕСИНУСОИДАЛЬНЫЕ КОЛЕБАНИЯ
В большинстве случаев форма переменного тока бывает синусоидальной. Однако в электронике используются не только синусоидальные колебания. Колебания, форма которых отличается от синусоиды, называются несинусоидальными периодическими колебаниями. Несинусоидальные колебания генерируются специальными электронными цепями.
Несинусоидальные колебания генерируются специальными электронными цепями.
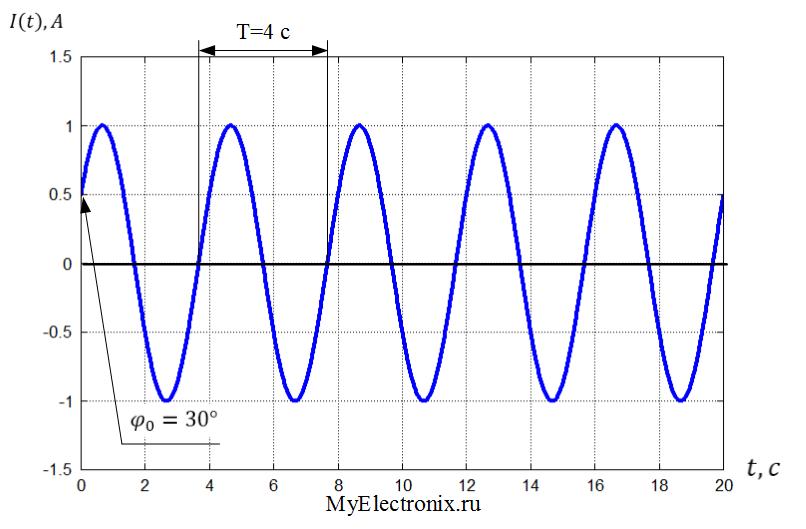
На рисунках 12-7, 12-8 и 12-9 изображены три основных вида несинусоидальных колебаний. Они могут представлять и ток, и напряжение. На рис. 12-7 изображены прямоугольные колебания, названные так потому, что положительные и отрицательные прямоугольные импульсы чередуются. Это указывает на то, что ток или напряжение мгновенно достигают максимального значения и остаются такими в течение половины периода. Когда полярность изменяется, ток или напряжение мгновенно достигают противоположного пикового значения и остаются неизменными до конца следующей половины периода. Ширина импульса равна половине периода. Ширина импульса — это отрезок времени, в течение которого напряжение имеет свое пиковое или максимальное значение. Прямоугольное колебание очень полезно как электронный сигнал, так как его характеристики могут быть легко изменены.
Рис. 12-7. Колебание прямоугольной формы.
На рис. 12-8 показан один период колебания треугольной формы. В течение первой половины периода сигнал возрастает по линейному закону от нуля до пикового значения, а затем опять уменьшается до нуля. В течение второй половины периода сигнал продолжает уменьшаться по линейному закону в отрицательном направлении до пикового значения, а после этого опять возрастает до нуля.
Треугольные колебания используются главным образом как электронные сигналы.
Рис. 12-8. Колебание треугольной формы
На рис. 12-9 показаны пилообразные колебания. Пилообразное колебание — это частный случай треугольного колебания. Сначала величина напряжения или тока возрастает по линейному закону, а после этого быстро падает до своего отрицательного пикового значения. Участок с положительным наклоном имеет относительно большую длительность и меньший по абсолютной величине угол наклона к оси времени, чем короткий участок. Пилообразные сигналы используются для переключения операций в электронных цепях. В телевизорах и осциллографах они используются для развертки электронного луча по экрану для создания изображения.
Пилообразные сигналы используются для переключения операций в электронных цепях. В телевизорах и осциллографах они используются для развертки электронного луча по экрану для создания изображения.
Импульсные колебания и другие несинусоидальные сигналы могут описываться двумя способами. Один метод рассматривает несинусоидальные сигналы как сумму скачкообразных изменений напряжения, следующих через некоторый интервал времени друг за другом. Второй метод рассматривает сигнал как алгебраическую сумму бесконечного числа синусоид, имеющих различные частоты и амплитуды. Этот метод полезен при расчете усилителей. Если усилитель не может пропустить все синусоидальные частоты, то он искажает сигнал.
Несинусоидальные сигналы состоят из колебаний основной частоты и гармоник. Основная частота соответствует скорости повторения сигнала. Гармоники являются синусоидами с более высокими частотами, которые кратны основной частоте. Четные гармоники имеют частоты, которые являются произведениями четных чисел и основной частоты.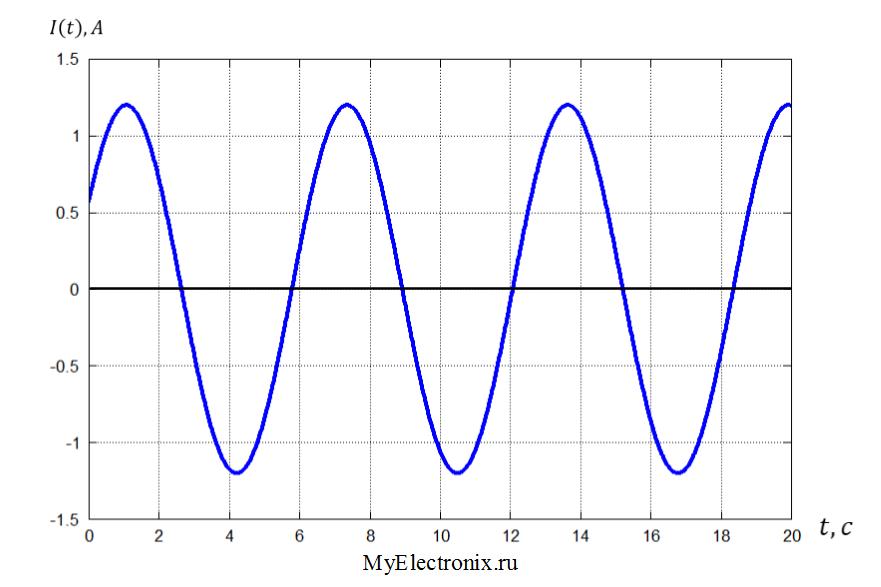 Нечетные гармоники имеют частоты, которые являются произведениями нечетных чисел и основной частоты.
Нечетные гармоники имеют частоты, которые являются произведениями нечетных чисел и основной частоты.
Прямоугольные колебания состоят из колебаний основной частоты и всех нечетных гармоник.
Треугольные колебания также состоят из колебаний основной частоты и всех нечетных гармоник, но, в отличие от прямоугольных колебаний, нечетные гармоники сдвинуты по фазе на 180 градусов относительно колебания основной частоты.
Пилообразные колебания содержат как четные, так и нечетные гармоники. Четные гармоники сдвинуты на 180 градусов по фазе относительно нечетных гармоник.
12-3. Вопросы
1. Что такое несинусоидальные колебания?
2. Нарисуйте два цикла (периода):
а. Прямоугольного колебания;
б. Треугольного колебания;
в. Пилообразного колебания.
3. Где применяются эти несинусоидальные колебания?
4. Опишите основную частоту и гармоники трех различных несинусоидальных колебаний.
Опишите основную частоту и гармоники трех различных несинусоидальных колебаний.
РЕЗЮМЕ
• Переменный ток — это наиболее широко используемый в технике тип тока.
• Переменный ток представляет собой ток, текущий сначала в одном направлении, а затем в противоположном.
• Один оборот якоря генератора переменного тока называется циклом.
• Герц — это один цикл в секунду.
• Форма переменного тока, вырабатываемого генератором, называется синусоидой.
• Пиковое значение синусоиды — это наибольшее значение функции за время периода.
• Размах синусоиды — это вертикальное расстояние между пиками противоположного знака.
• Эффективное значение переменного тока — это такое значение постоянного тока, при котором на данном сопротивлении выделяется столько же тепла, что и при переменном токе.
• Эффективное значение можно определить, вычислив среднеквадратичное значение величины.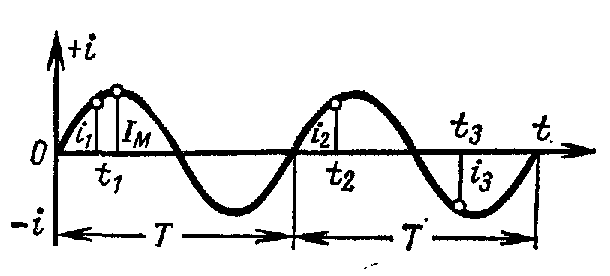
• Среднеквадратичное значение синусоиды равно 0,707 от пикового:
Еэфф = 0,707∙Емакс
Iэфф = 0,707∙Iмакс
• Время, необходимое для завершения одного цикла синусоиды, называется периодом (t).
• Количество циклов, совершаемых за заданный промежуток времени, называется частотой (f).
• Соотношение между частотой и периодом синусоиды выражается следующей формулой:
f = 1/t
• Прямоугольные колебания состоят из колебаний основной частоты и всех нечетных гармоник.
• Треугольные колебания состоят из колебаний основной частоты и всех нечетных гармоник, сдвинутых по фазе на 180 градусов относительно основной частоты.
• Пилообразные колебания содержат как четные, так и нечетные гармоники. Четные гармоники сдвинуты на 180 градусов по фазе относительно нечетных гармоник.
Четные гармоники сдвинуты на 180 градусов по фазе относительно нечетных гармоник.
Глава 12. САМОПРОВЕРКА
1. Что надо сделать для наблюдения электромагнитной индукции?
2. Объясните, как правило левой руки применяется к генераторам переменного тока?
3. Дайте определение полного размаха колебаний.
4. Как определяется эффективное значение переменного тока?
5. Нарисуйте примеры трех несинусоидальных колебаний, которые могут представлять и ток и напряжение.
6. Почему при изучении несинусоидальных колебаний важны гармоники?
Однофазные цени синусоидального тока: основные определения
Основные определения
Переменным называется электрический ток, величина и направление которого изменяются во времени.
Для периодического переменного тока его значения повторяются через одинаковые промежутки времени, т.е. . Здесь период — наименьший промежуток времени, через который значение переменного тока повторяется или промежуток времени, в течение которого ток совершает одно полное колебание.
Как известно, синусоида является простейшей периодической функцией. Несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид кратной частоты. Поэтому при изучении процессов в цепях переменного тока в первую очередь необходимо изучить особенности цепей синусоидального тока.
К синусоидальным функциям можно причислить и косинусоидальные функции, так как косинусоида может рассматриваться как сдвинутая синусоида. Колебания, выражаемые этими функциями, будем называть гармоническими. Рассмотрим основные понятия, характеризующие синусоидальную функцию, например синусоидальный ток.
Электрическая цепь синусоидального тока — электрическая цепь, в которой действуют ЭДС, напряжения и токи, изменяющиеся во времени по синусоидальному закону.
Синусоидальный ток — переменный ток, изменяющийся по синусоидальному закону. Синусоидальные или гармонические величины математически описываются функциями вида:
Здесь — максимальное значение тока или амплитуда, — фаза тока (аргумент синусоидальной функции), — начальная фаза тока (значение фазы в момент времени ), -частота (число колебаний в 1 секунду), — скорость изменения аргумента, называемая угловой частотой (число колебаний, совершаемых за секунд). Фазу и начальную фазу измеряют в градусах или в радианах, частоту — в герцах.
Значение функции в данный момент времени называется мгновенным значением и по соглашению обозначается строчной буквой, амплитуда обозначается прописной буквой с индексом .
При изображении синусоидальных функций на временных диаграммах удобно по горизонтальной оси откладывать не время , а величину в радианах (рис. 2.1). Начальная фаза определяется смещением начала периода синусоиды по горизонтали относительно начала координат.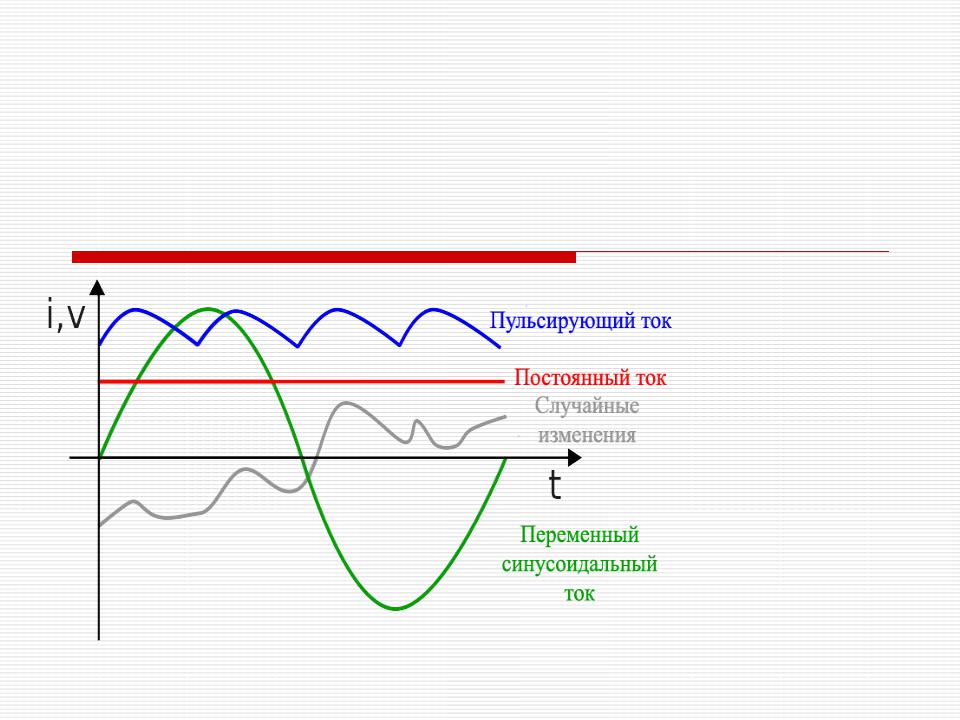 За начало периода считают момент времени, в который синусоида проходит через нулевое значение, после которого она положительна. При смещении начала периода влево начальная фаза , при смещении вправо — . На рис. 2.1 .
За начало периода считают момент времени, в который синусоида проходит через нулевое значение, после которого она положительна. При смещении начала периода влево начальная фаза , при смещении вправо — . На рис. 2.1 .
Действующее значение синусоидального тока. Действующим (эффективным) значением периодического переменного тока называется такой постоянный ток, при котором в сопротивлении выделяется за период то же количество энергии, что и при переменном токе.
Энергия, выделяющаяся в сопротивлении при переменном токе за бесконечно малый промежуток времени ,
а за время, равное периоду переменного тока,
Приравняв выражение (2.3) количеству тепла , выделяющемуся в том же сопротивлении при постоянном токе за то же время , получим:
Преобразовав выражение (2.4) получим действующее значение тока
Если ток то
С учетом того, что и действующее значение синусоидального тока
Таким образом, действующее значение синусоидального тока меньше его амплитуды в раз, т. е. .
е. .
Аналогично определяются действующие значения других синусоидальных величин, например, синусоидальной ЭДС и синусоидального напряжения . Понятие действующего значения очень широко используется в цепях переменного тока. Большинство измерительных приборов градуируются в действующих значениях. Технические данные электротехнических устройств указываются в действующих значениях.
В записи для действующих значений по соглашению используют прописные буквы без индекса, например, действующее значение тока или действующее значение напряжения .
Среднее значение синусоидального тока. Среднее значение периодической функции за период определяется по формуле
Отсюда видно, что среднее за период значение равно высоте прямоугольника с основанием , площадь которого равна площади, ограниченной функцией и осью абсцисс за один период.
В случае гармонического сигнала среднее значение за период равно нулю. Поэтому в электротехнике за средние значения синусоидального тока, напряжения и ЭДС принимают их среднеарифметические значения за положительный полупериод. Если ток , то среднее значение тока
Если ток , то среднее значение тока
Аналогично определяется среднее значение синусоидального напряжения и среднее значение синусоидальной ЭДС .
Сдвиг фаз. Сдвигом фаз (фазовым сдвигом) называют разность начальных фаз двух синусоидальных колебаний одинаковой частоты . Сдвиг фаз показывает, на какую часть периода или па какой промежуток времени одна синусоидальная величина достигает начала периода раньше другой величины.
Эта теория взята со страницы помощи с заданиями по электротехнике:
Помощь по электротехнике
Возможно эти страницы вам будут полезны:
Синусоидальный ток | Цепи переменного тока
Мгновенное значение синусоидального тока определяется выражением
где — максимальное значение или амплитуда тока. Аргумент синуса называется фазой. Угол ψ равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазой. Фаза с течением времени непрерывно растет. После ее увеличения на 2π весь цикл изменения тока повторяется. Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2π так, чтобы значение фазы находилось в пределах или в пределах, от 0 до 2π. В течение периода Т фаза увеличивается на 2π. Величина 2π/Т показывает скорость изменения фазы и обозначается буквой ω. Принимая во внимание, что f=1/Т, можно написать
Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2π так, чтобы значение фазы находилось в пределах или в пределах, от 0 до 2π. В течение периода Т фаза увеличивается на 2π. Величина 2π/Т показывает скорость изменения фазы и обозначается буквой ω. Принимая во внимание, что f=1/Т, можно написать
Это выражение, связывающее ω и f, послужило основанием называть ω угловой частотой. Измеряется w числом радианов, на которое увеличивается фаза в секунду. Так, например, при f=50 Гц имеем ω=314 рад/с. Введя в (3.1) обозначение ω для угловой частоты, получим
На рис. 3.3 построен график синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами:
По оси абсцисс отложены время t и пропорциональная времени величина ωt.
Начальная фаза отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t=0 (начало координат). При начало синусоиды тока сдвинуто влево, а при для тока — вправо от начала координат.
При начало синусоиды тока сдвинуто влево, а при для тока — вправо от начала координат.
Мгновенное значение синусоидального тока можно представить и в виде косинусоидальной функции времени
где
Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты относительно друг друга по фазе. Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 3.3, например, , т.е. ток опережает по фазе ток на угол , или, что то же самое, ток отстает по фазе от тока на угол .
Если у синусоидальных функций одной и той же частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе, если разность их фаз равна , то говорят, что они противоположны по фазе, и, наконец, если разность их фаз равна , то говорят, что они находятся в квадратуре.
Однофазные электрические цепи переменного тока в электротехнике (ТОЭ)
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной
10.1), то в каждой активной стороне этой рамки длиной
где а — угол, под которым активный проводник рамки пересекает магнитное поле (угол между ), или угол поворота рамки относительно нейтральной плоскости как углы со взаимно перпендикулярными сторонами.
Плоскость называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
как — величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
Синусоидальная ЭДС изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN». Как видно, синусоидальная ЭДС изменяется по величине и направлению.
Как видно, синусоидальная ЭДС изменяется по величине и направлению.
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е.
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как . Следовательно,
Тогда
Период — это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. = с.
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
где к — целое число.
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота — число периодов в единицу времени, т.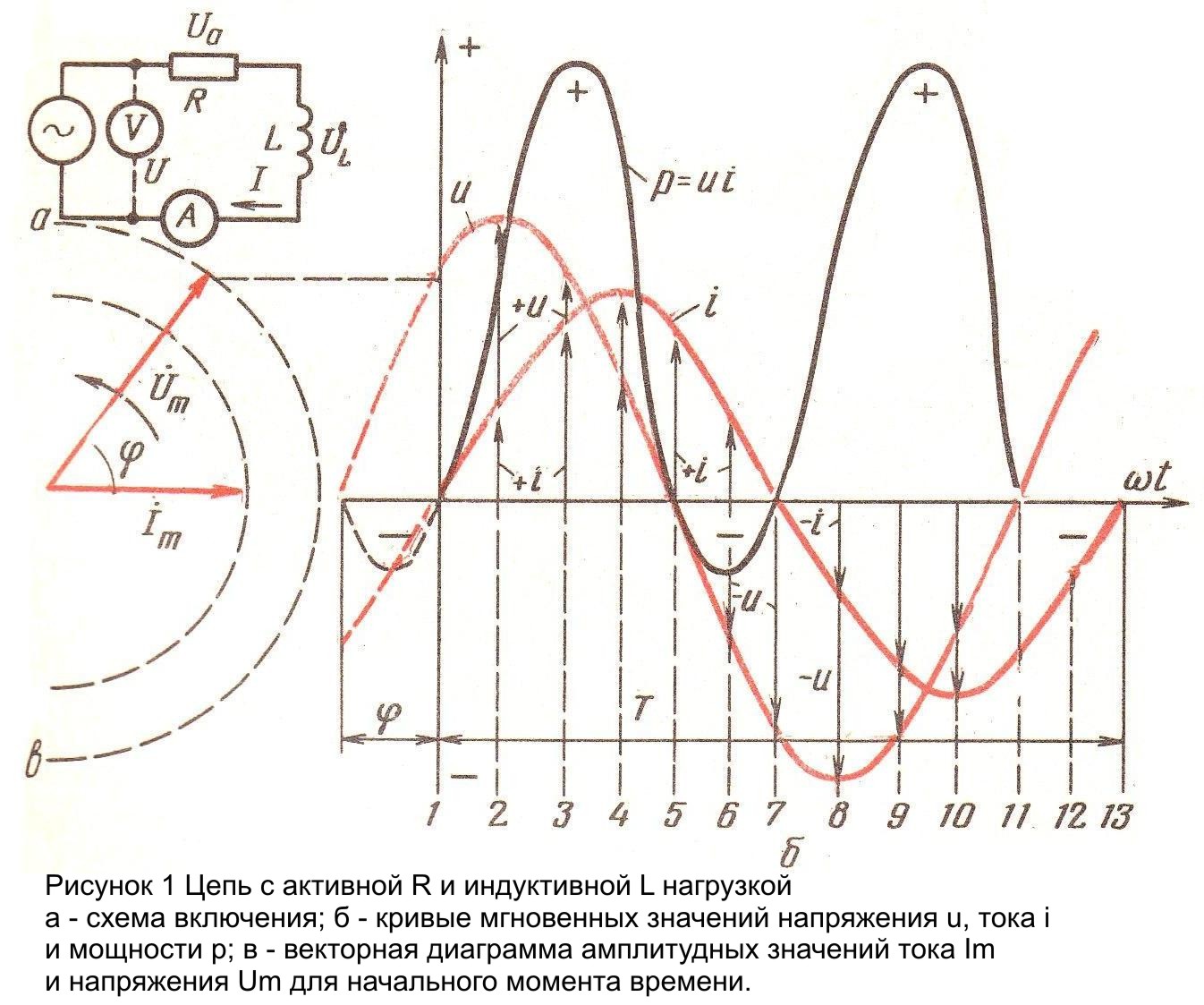 е. величина, обратная периоду.
е. величина, обратная периоду.
Обозначается частота буквой , и измеряется в герцах (Гц):
Стандартной частотой в электрических сетях России является частота = 50 Гц. Для установок электронагрева пользуются частотами Гц ( Гц = 1 МГц — мегагерц).
При частоте =50 Гц, т.е. 50 периодов в секунду, период
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой (омега):
Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:
Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки , мгновенные значения синусоидальных величин можно записать так:
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
где — углы, определяющие значения синусоидальных величин в начальный момент времени (t = 0), т.е.
Поэтому эти углы называют начальными фазами синусоид.
Начальные фазы этих ЭДС различны.
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой , угловой частотой со и начальной фазой . Для каждой синусоиды эти величины являются постоянными. В выражениях (10.4) начальные фазы синусоид равны нулю ( = 0).
Величина называется фазой синусоиды.
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:
При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. опережает по фазе или отстает по фазе (рис. 10.46). Угол сдвига фаз показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. опережает по фазе или отстает по фазе (рис. 10.46). Угол сдвига фаз показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз , которое можно выразить через период Т и частоту синусоиды следующим образом:
Среднее и действующее значения переменного токаКроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. .
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. = 0.
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
е.
Из выражения (2.1) значение переменного тока , откуда . Следовательно, среднее значение синусоидального тока с начальной фазой = 0 за полупериод определяется (рис. 10.6) выражением
где
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
Действующее значение переменного токаДействующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
Откуда действующее значение переменного тока
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т. е. , то действующее сечение такого синусоидального тока будет равно
е. , то действующее сечение такого синусоидального тока будет равно
Действующее значение синусоидального тока в =1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы и амплитуды .
Коэффициент формы определяется отношением действующего значения переменной величины к ее среднему значению:
Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
Коэффициент амплитуды определяется отношением амплитудного значения переменной величины к ее действующему значению:
Для синусоидальных величин коэффициент амплитуды равен
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений = 1,11 и = 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если = 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если
График прямоугольной формы имеет коэффициент амплитуды 1.
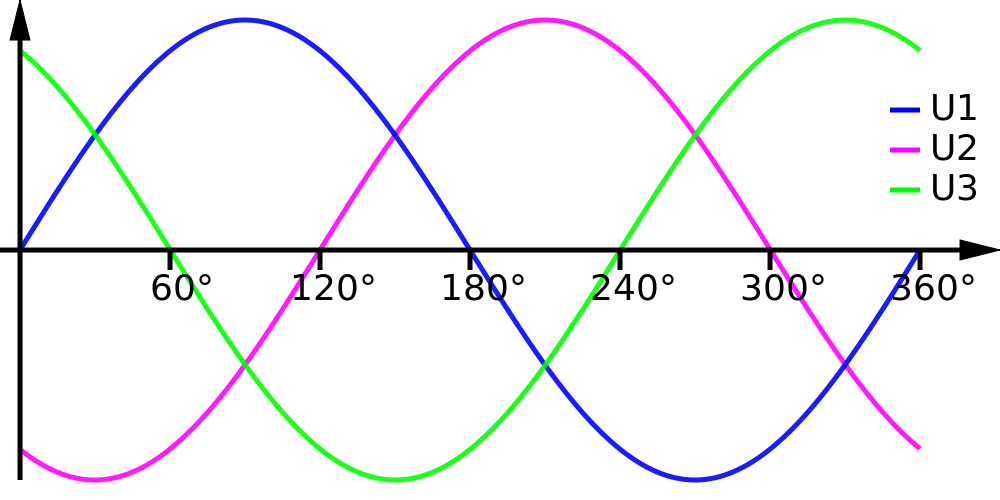
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте со этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t = 0), то они подвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс начальной фазе синусоиды. Таким образом, вектор учитывают все значения, характеризующие синусоидальную величину — амплитуду, угловую частоту и начальную фазу, пример, три синусоидальные ЭДС одинаковой частоты
можно изобразить векторами (рис. 10.7).
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты в начальный момент времени, называется векторной диаграммой.
На векторной диаграмме (рис. 10.7) на-ю видны величины синусоид (ампли-), их начальные фазы и углы сдвига между ними. Очевидно, наибольшую амплитуду имеет ЭДС , а наименьшую ЭДС ЭДС опережает по фазе угол 45°, а ЭДС отстает от ЭДС по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:
Очевидно, наибольшую амплитуду имеет ЭДС , а наименьшую ЭДС ЭДС опережает по фазе угол 45°, а ЭДС отстает от ЭДС по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:
При этом амплитуды ЭДС и углы сдвига фаз остаются неизменными (как и угловая частота), а меняются только начальные фазы синусоид, изображенных на векторной диаграмме (рис. 10.7). В расчетах, если специально не оговорено, начальные фазы не играют роли.
Сложение синусоидальных величинСложение и вычитание синусоидальных величин одинаковой частоты можно осуществлять аналитически и графически. В результате такого сложения (вычисления) получается синусоида с той же частотой, с определенной амплитудой и определенной начальной фазой.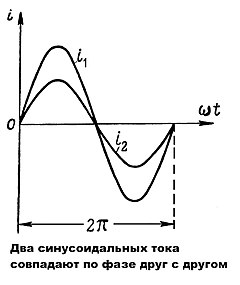
Аналитическое сложение предусматривает сложение мгновенных значений синусоидальных величин, выраженных аналитически, т. е.
где
Тогда
Математический анализ позволяет определить суммарную ЭДС е и ее аналитическое выражение.
Графическое сложение можно осуществлять по: 1) волновым (временном) диаграммам и 2) векторным диаграммам.
1. Графическое сложение по временным диаграммам (рис. 10.9) осуществляется следующим образом: ординаты суммарной синусоиды определяются сложением ординат слагаемых синусоид в различные моменты времени.
Как видно, в рассматриваемом примере амплитуда суммарной синусоиды не равна алгебраической сумме амплитуд слагаемых синусоид. Начальная фаза суммарной синусоиды также не является результатом арифметических действий, т.е. по временным диаграммам производятся только графические действия.
2. Графическое сложение по векторным диаграммам осуществляется в следующей последовательности. Прежде всего необходимо построить векторную диаграмму слагаемых синусоидальных величин (рис. 10.10а).
10.10а).
Определение вектора, изображающего суммарную синусоиду, осуществляется сложением векторов слагаемых синусоид по правилу многоугольника, т. е. из какой-либо точки О изображают вектор, соответствующий первой слагаемой синусоиде 10.106), из конца этого вектора изображают вектор, соответствующий второй слагаемой синусоиде, и т.д.
Вектор, соответствующий суммарной синусоиде, проводят из и О к концу последней слагаемой синусоиды.
Тот вектор (рис. 10.106), в масштабе изображения слагаемых синусоид, соответствует амплитуде суммарной синусоиды . Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
Вычитание синусоидальной величины равносильно умножение этой величины на отрицательную единицу (—1), что соответствует повороту вектора этой величины на 180″ (рис. 10. 10 в).
10 в).
Сложение и вычитание синусоидальных величин по векторный диаграммам рассматривается в примере 10.1.
Пример 10.1
Заданы мгновенные значения четырех токов:
Определить:
1)суммарный ток при условии
2)суммарный ток при условии
3)частоту f всех синусоид.
Решение
Для построения векторной диаграммы слагаемых токов задаются определенным масштабом токов (например, = 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
1. Для определения суммарного тока производится сложение векторов по правилу многоугольника (рис. 10.106). Суммарный ток в результате сложения будет равен . Амплитуда суммарного тока = 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром = 90°.
2. Построение многоугольника для заданного условия показано на рис. 10.10в. Из многоугольника определяется результирующий ток
3. Частота слагаемых и результирующих токов будет равна
Частота слагаемых и результирующих токов будет равна
В заключение можно сделать вывод, что самым удобным и, следовательно, распространенным методом сложения синусоидальных величин является метод графического сложения по векторным диаграммам. Этот метод и будет использован при расчете электрических цепей однофазного и трехфазного тока, изменяющегося по синусоидальному закону.
Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям (см. (10.9)), то вектор, отражающий в определенном масштабе амплитудное значение, в этом масштабе представляет действующее значение той же вены. Исходя из этого, в дальнейшем на векторных диаграммах будут изображаться векторы, в определенном масштабе представляющие не амплитудное, а действующее значение синусоидальной вены, которое чаще всего используется при расчетах цепей переменного тока.
Понятие о переменном токе, получение переменного тока
Переменным называется ток, величина и направление которого изменяются периодически во времени. В технике применяется переменный ток, изменяющийся по синусоиде.
В технике применяется переменный ток, изменяющийся по синусоиде.
Получение переменного тока основано на явлении электромагнитной индукции. На рис. 164 схематично изображено получение синусоидального переменного тока. Слева на схеме а показаны: полюсы магнита северный N и южный S, кружочками различные положения проводника в магнитном поле; при этом знаком плюс обозначается, что в данном положении ток идет от нас за плоскость чертежа, а точкой — что ток идет от плоскости чертежа на нас.
На схеме б (рис. 164) представлено изменение величины и направления тока во внешней цепи замкнутого проводника за один его полный поворот между полюсами магнитов. По горизонтальной оси графика отложено время, а по вертикальной оси — значение тока. Как видно из кривой графика, представляющей собой синусоиду, за один полный поворот, в зависимости от угла, под которым проводник пересекает магнитные силовые линии, значение тока изменяется по величине от нуля до максимального, а по знаку — от плюса до минуса.
Машина, служащая для получения переменного тока, называется генератором переменного тока, принцип действия которого можно уяснить из следующего.
Если выполнить проводник в виде витка, поместить его между полюсами (рис. 164,в) и вращать в направлении часовой стрелки, то в нем будет индуктироваться э.д.с., направленная при вращении его под северным полюсом — от нас и при вращении его под южным полюсом — на нас. Так как стороны витка попеременно перемещаются то под северным полюсом, то под южным и пересекают при этом магнитные силовые линии под различными углами, то э. д. с., индуктируемая в витке, будет изменяться по величине и направлению. Присоединив концы витка к двум контактным кольцам, изолированным между собой и от вала, и наложив на кольца неподвижные щетки, соединенные с внешней цепью, будем получать переменную э.д.с., и во внешней цепи потечет переменный ток.
Переменный ток характеризуется следующими величинами: периодом, частотой, амплитудой. Периодом называется время, в течение которого происходит полный цикл изменений тока по величине и направлению. Каждый последующий период тока является повторением предыдущего. Период обозначается буквой Т (рис. 164).
Периодом называется время, в течение которого происходит полный цикл изменений тока по величине и направлению. Каждый последующий период тока является повторением предыдущего. Период обозначается буквой Т (рис. 164).
Частотой называется число периодов в 1 сек. Частота — величина, обратная периоду, обозначается буквой f, т. е.
В России принята частота переменного тока 50 периодов в секунду. Это значит, что ток меняет свою величину и направление 50 раз в секунду. За единицу измерения частоты принят герц (гц).
Амплитудой называется наибольшее значение тока, которого он достигает в течение периода. Как видно из рис. 164 за один период переменный ток достигает амплитудного значения дважды.
Законы постоянного тока полностью применимы к цепям переменного тока только в тех случаях, когда эти цепи состоят из активных сопротивлений (лампы накаливания, реостаты и т. п.).
Однако во многих случаях цепь переменного тока, кроме активного сопротивления, содержит катушки самоиндукции, обмотки электродвигателей, дроссели, конденсаторы и другие приборы.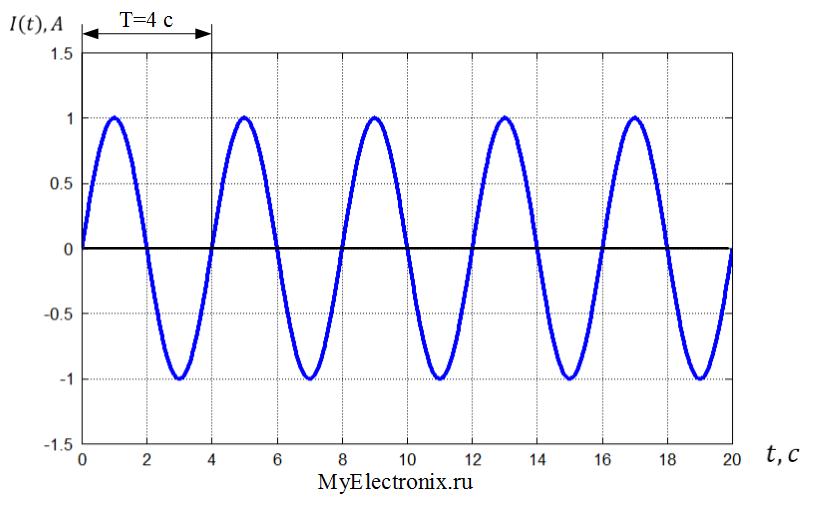 Наличие этих приборов вносит в цепь так называемое реактивное сопротивление, влияющее на ток в цепи
переменного тока. Вследствие чего, закон Ома в таком виде, как он применяется для цепи постоянного тока, для цепи переменного тока недействителен.
Наличие этих приборов вносит в цепь так называемое реактивное сопротивление, влияющее на ток в цепи
переменного тока. Вследствие чего, закон Ома в таком виде, как он применяется для цепи постоянного тока, для цепи переменного тока недействителен.
Схема цепи переменного тока, состоящая из активного (R), индуктивного (катушка самоиндукции) и емкостного (конденсатор) сопротивлений, соединенных последовательно, приведена на рис. 165.
Для того чтобы найти силу переменного тока в цепи, нужно подсчитать полное сопротивление цепи с учетом всех входящих в нее сопротивлений. При этом необходимо знать, что различные виды сопротивлений нельзя между собой складывать арифметически. Если включить в цепь переменного тока амперметр, то он покажет величину тока, в 1,4 раза меньшую амплитудного тока.
Это значение тока, показываемое измерительным прибором, называют действующим, или эффективным, значением переменноготока.
Для синусоидального переменного тока действующее эффективное значение напряжения U и электродвижущей силы Е будет также меньше амплитудных их значений в 1,4 раза.
Измерительные приборы, включенные в цепь переменного тока, всегда показывают действующие значения измеряемых величин.
В некоторых случаях требуется знать не действующее, а среднее значение переменного тока. Среднее значение переменного тока несколько меньше его действующего значения. Как показывают опыты и расчеты, оно равно его амплитудному значению, умноженному на 0,637.
Похожие статьи
Инверторы с чистым и модифицированным синусом для сети 220В и их работа с различными электроприборами
Содержание:1. Вступление. Описание рассматриваемых типов инверторов: трансформаторный, с вч преобразованием, с синусоидальной формой напряжения.
2. Виды электроприборов с активным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
3. Виды электроприборов с индуктивным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
4. Виды электроприборов с емкостным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
5. Виды электроприборов с выпрямителем на входе и особенности работы различных типов инверторов с данным видом нагрузки.
6. Сводная таблица отличий в работе различных типов инверторов с различными типами нагрузок. Заключение.
1. Вступление. Описание рассматриваемых типов инверторов: трансформаторный, модифицированный синус, чистый синус.
Инвертор- прибор преобразующий постоянное напряжение в переменное. Потребность в инверторах существует для решения задачи питания устройств для бытовой сети 220В 50Гц от источников постоянного напряжения, например аккумуляторов. С развитием электроники эта задача решалась все более сложными методами, дающими более качественные параметры выходной электроэнергии. Однако на практике применяются как современные, так и более архаичные приборы, поэтому рассмотрим основные типы инверторов в историческом порядке.
Первыми появились инверторы на основе трансформаторов работающих на частоте сети 50Гц. Блок-схема инвертора приведена на рис. №1.
Рис. №1. Блок-схема трансформаторного инвертора.
Источник энергии постоянного тока, в самом распространенном случае аккумулятор 12В, подключается к трансформатору через трехпозиционный коммутатор. Коммутатор представляет собой набор электронных ключей, обеспечивающий 3 состояния: к первичной обмотке трансформатора подключен источник питания положительной полярностью, к первичной обмотке трансформатора подключен источник питания отрицательной полярностью и состояние когда первичная обмотка закорочена. Последовательно переключая эти состояния, на первичной обмотке формируется переменное напряжение частотой 50Гц и амплитудой 12В. На вторичной обмотке трансформатора при этом формируется напряжение с той же частотой и формой, однако эффективное напряжение составляет 220В. Графики напряжения на трансформаторе приведены на рис. №2.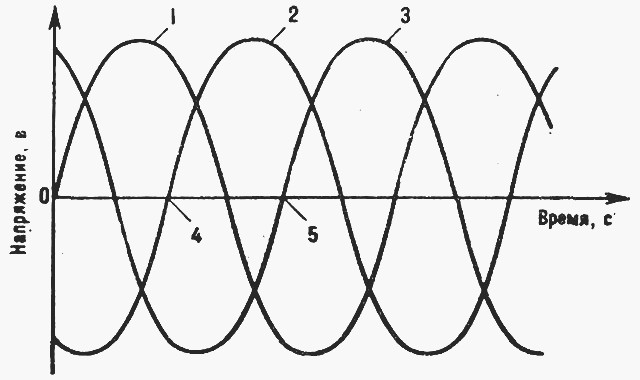 Выходное напряжение снимается с вторичной обмотки, поэтому имеет такие же параметры.
Выходное напряжение снимается с вторичной обмотки, поэтому имеет такие же параметры.
Рис. №2. Графики напряжения на трансформаторе
Данная форма напряжения называется «модифицированная синусоида» и широко применяется в инверторах для сети 50Гц, поэтому параметры, описывающие ее, рассмотрены более подробно. Вообще параметры, задающие форму модифицированной синусоиды, это амплитуда выходного напряжения и коэффициент заполнения, показывающий отношение длительности импульса к периоду сигнала. Эти параметры задаются при конструировании инверторов. Из соображений того, что инвертор должен заменять сеть 220В 50Гц, обычно выбирается амплитудное значение напряжения модифицированной синусоиды такое же, как и в сети, то есть 311В. При этом, чтобы обеспечить эффективное напряжение 220в, такое же как и в сети, коэффициент заполнения получается 0.5. Однако в инверторе этого типа амплитуда выходного напряжения получается зависящей прямо пропорционально от напряжения источника. Если в качестве источника энергии используется аккумулятор, а это самый распространенный случай, то его напряжение при разряде понижается, и амплитуда модифицированной синусоиды на выходе преобразователя также понижается, соответственно понижается и эффективное значение напряжение на выходе преобразователя. Для того чтобы улучшить качество энергии на выходе преобразователя в этих условиях часто применяют схемы управления, которые изменяют коэффициент заполнения выходного напряжения таким образом, чтобы поддерживать эффективное напряжение неизменным. Например, инвертор, рассчитанный на напряжение источника 12В, работает от разряженного аккумулятора с напряжением 10В. При этом амплитудное напряжение на выходе снижается пропорционально до 259В. Схема управления изменяет коэффициент заполнения выходного напряжения до 0.72, при этом эффективное напряжение остается равным 220В. Однако форма напряжения и его амплитуда меняется, что может быть недопустимо для некоторых нагрузок, что будет показано далее.
Для того чтобы улучшить качество энергии на выходе преобразователя в этих условиях часто применяют схемы управления, которые изменяют коэффициент заполнения выходного напряжения таким образом, чтобы поддерживать эффективное напряжение неизменным. Например, инвертор, рассчитанный на напряжение источника 12В, работает от разряженного аккумулятора с напряжением 10В. При этом амплитудное напряжение на выходе снижается пропорционально до 259В. Схема управления изменяет коэффициент заполнения выходного напряжения до 0.72, при этом эффективное напряжение остается равным 220В. Однако форма напряжения и его амплитуда меняется, что может быть недопустимо для некоторых нагрузок, что будет показано далее.
Так как основным элементом инвертора этого типа является трансформатор 50Гц, возможности по миниатюризации, уменьшении материалоемкости и повышении эффективности работы инвертора весьма ограничены. Поэтому на основе современной элементной базы были разработаны инверторы с вч преобразованием. Блок-схема такого инвертора приведена на рис. №3.
Блок-схема такого инвертора приведена на рис. №3.
Рис. №3. Блок-схема инвертора с вч преобразованием.
Источник энергии постоянного тока подключается на вход высокочастотного преобразователя постоянного напряжения (dcdc преобразователь). Данный блок преобразует входное напряжение в напряжение, соответствующее амплитуде сетевого напряжения, 311В. Это преобразование происходит с помощью трансформатора, работающего на повышенной (десятки и сотни килогерц) частоте, поэтому габариты и материалоемкость инвертора значительно уменьшились. Выходное напряжение преобразователя подается на коммутатор, аналогичный коммутатору в инверторе трансформаторного типа. График выходного напряжения коммутатора имеет такой же вид, как и напряжение на выходе коммутатора в трансформаторном инверторе, однако амплитуда напряжения достигает 311В. Выход коммутатора является выходом инвертора, и график выходного напряжения соответствует напряжению на вторичной обмотке трансформатора в трансформаторном инверторе (рис. 2). Соображения насчет формы выходного напряжения, изложенные выше, справедливы и для данного типа инвертора. Изменение же формы выходного напряжения в зависимости от величины входного напряжения может происходить либо нет, это зависит от топологии dcdc преобразователя. Если преобразователь стабилизированный, то при изменении входного напряжения выходное напряжение преобразователя не изменяется. При этом также форма и амплитуда выходного напряжения инвертора не изменяется. Однако существуют и более простые разновидности dcdc преобразователей, которые не являются стабилизированными, и выходное напряжение которых пропорционально входному. Для инверторов, собранных на основе таких преобразователей, справедливы заключения насчет изменения выходного напряжения для трансформаторных инверторов.
2). Соображения насчет формы выходного напряжения, изложенные выше, справедливы и для данного типа инвертора. Изменение же формы выходного напряжения в зависимости от величины входного напряжения может происходить либо нет, это зависит от топологии dcdc преобразователя. Если преобразователь стабилизированный, то при изменении входного напряжения выходное напряжение преобразователя не изменяется. При этом также форма и амплитуда выходного напряжения инвертора не изменяется. Однако существуют и более простые разновидности dcdc преобразователей, которые не являются стабилизированными, и выходное напряжение которых пропорционально входному. Для инверторов, собранных на основе таких преобразователей, справедливы заключения насчет изменения выходного напряжения для трансформаторных инверторов.
С развитием электроники появилась возможность создать инверторы с синусоидальной формой напряжения на основе вч преобразования электрической энергии. С помощью данных инверторов возможно получение выходного напряжения, удовлетворяющего стандартам на качество электроэнергии в энергетике, что невозможно для преобразователей ранее рассмотренных типов. Блок-схема инвертора приведена на рис. №4.
Блок-схема инвертора приведена на рис. №4.
Рис. №4. Блок-схема инвертора с синусоидальным выходным напряжением.
Источник энергии постоянного тока подключается на вход высокочастотного преобразователя постоянного напряжения, как и в инверторе с вч преобразованием, рассмотренном ранее. Выходное напряжение инвертора может быть различным в зависимости от конструкции, однако оно должно быть выше амплитудного напряжения сети, то есть выше 311В. Выходное напряжение преобразователя поступает на вч инвертор (dc/ac), представляющий собой управляемый понижающий импульсный преобразователь. Данный преобразователь может устанавливать на своем выходе напряжение по сигналу от схемы управления в диапазоне от нуля до напряжения питания, то есть до напряжения больше 311В. Вч инвертор обычно содержит два таких канала по мостовой схеме, таким образом, напряжение между их выходами может достигать от -311В до +311В, как и в сети 220В. Графики выходного напряжения по обоим выходным проводам и результирующее выходное напряжение инвертора представлены на рис.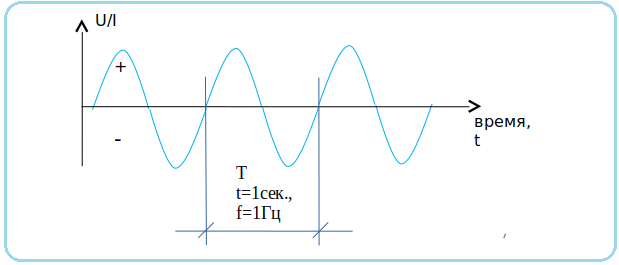 №5. Из графиков следует, что схема управления подает особый сигнал на каждый канал вч преобразователя, изменяющийся во времени таким образом, что выходное напряжение каждого канала вч преобразователя изменяется по синусоидальному закону с частотой 50Гц, и смещено по фазе на 180? между каналами. Напряжение же между выходами представляет собой синусоиду без постоянной составляющей амплитудой 311В. Изменение формы выходного напряжения в зависимости от величины входного напряжения не происходит вследствие того что либо dc/dc преобразователь либо вч инвертор исполняются стабилизированными, то есть выходное напряжение не зависит от входного.
№5. Из графиков следует, что схема управления подает особый сигнал на каждый канал вч преобразователя, изменяющийся во времени таким образом, что выходное напряжение каждого канала вч преобразователя изменяется по синусоидальному закону с частотой 50Гц, и смещено по фазе на 180? между каналами. Напряжение же между выходами представляет собой синусоиду без постоянной составляющей амплитудой 311В. Изменение формы выходного напряжения в зависимости от величины входного напряжения не происходит вследствие того что либо dc/dc преобразователь либо вч инвертор исполняются стабилизированными, то есть выходное напряжение не зависит от входного.
Рис. №5. Графики напряжения на выходах инвертора.
2. Виды электроприборов с активным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
Электрические приборы с активным характером сопротивления распространены повсеместно. К ним относятся различные виды нагревательных приборов, а также осветительные приборы на основе ламп накаливания. Также распространены комбинированные нагрузки, в которых кроме основного потребителя с активным характером сопротивления присутствуют другие потребители с различным характером сопротивления, однако мощность этих потребителей значительно ниже. Например, нагревательный элемент со схемой контроля температуры. Такие нагрузки также можно считать приближенными к активными, степень приближения определяется отношением мощностей основной активной нагрузки и дополнительной не активной. Вообще активная нагрузка является наиболее простым видом нагрузки для инвертора, потому что выходной ток инвертора в любой момент времени, то есть при любом мгновенном значении выходного напряжения, ограничен и определяется законом Ома. Поэтому допустима любая форма выходного напряжения инвертора, например модифицированная синусоида. Также весь выходной ток инвертора идет на создание выходной активной мощности, поэтому эффективность работы (величина коэффициента полезного действия) инверторов любого типа будет максимальна при данном типе нагрузки.
Также распространены комбинированные нагрузки, в которых кроме основного потребителя с активным характером сопротивления присутствуют другие потребители с различным характером сопротивления, однако мощность этих потребителей значительно ниже. Например, нагревательный элемент со схемой контроля температуры. Такие нагрузки также можно считать приближенными к активными, степень приближения определяется отношением мощностей основной активной нагрузки и дополнительной не активной. Вообще активная нагрузка является наиболее простым видом нагрузки для инвертора, потому что выходной ток инвертора в любой момент времени, то есть при любом мгновенном значении выходного напряжения, ограничен и определяется законом Ома. Поэтому допустима любая форма выходного напряжения инвертора, например модифицированная синусоида. Также весь выходной ток инвертора идет на создание выходной активной мощности, поэтому эффективность работы (величина коэффициента полезного действия) инверторов любого типа будет максимальна при данном типе нагрузки.
Для корректной работы активных нагрузок важно лишь среднеквадратичное значение напряжения, а все рассмотренные ранее типы инверторов способны выдавать такое же среднеквадратичное напряжение, как и сеть 220В. Однако потенциально важным моментом для работы с активной нагрузкой является способность инвертора выдавать постоянное среднеквадратичное напряжение при изменяющемся напряжении питания. Все рассмотренные ранее типы инверторов имеют такую возможность при соответствующих функциях системы управления, однако каждая конкретная модель инвертора может иметь или нет подобную функцию.
Также нагрузки с активным характером сопротивления могут быть линейными или нелинейными, то есть сопротивление нагрузки может быть постоянным или меняющимся во времени. Типичным примером нелинейной нагрузки является лампа накаливания, причем отличие в сопротивлении в горячем и холодном состоянии может достигать 10 раз. При работе инвертора с таким типом нагрузки может возникать кратковременное, но значительное увеличение тока нагрузки. В этом случае возможна потеря работоспособности инвертора из-за срабатывания защиты по максимальному выходному току. Однако работа схемы защиты не зависит от типа преобразователя, поэтому различия между работой различных моделей инверторов будут происходить из-за различия в системах защиты, а не из-за принципиального различия в типах инверторов.
В этом случае возможна потеря работоспособности инвертора из-за срабатывания защиты по максимальному выходному току. Однако работа схемы защиты не зависит от типа преобразователя, поэтому различия между работой различных моделей инверторов будут происходить из-за различия в системах защиты, а не из-за принципиального различия в типах инверторов.
Различие между типами инверторов с различной формой выходного напряжения можно оценить с помощью частотного анализа по гармоническому составу выходного напряжения. Инверторы с синусоидальной формой выходного напряжения содержат в спектре выходного напряжения только основную гармонику 50Гц. Инверторы же с выходным напряжением в виде модифицированной синусоиды содержат в спектре выходного напряжения также высшие нечетные гармоники значительной амплитуды. Так как форма выходного тока при активной нагрузке повторяет форму напряжения, то подобные заключения будут справедливы и про спектр выходного тока. Практически оценить различия в форме выходного тока можно по производимому им акустическому эффекту. Акустический эффект может иметь различную физическую природу, например сила Ампера, вынуждающая колебаться проводники с током, или магнитострикционный эффект в материалах, находящимся в магнитном поле, возбуждаемом током. Акустический эффект может возникать во всех участках последовательной выходной цепи, например в потребителе или соединительных проводах, или в самом инверторе. Человек способен на слух различать гармонический состав производимого акустического эффекта. Так, звук от инвертора с синусоидальной формой выходного напряжения ощущается как однотонный гудящий (низкочастотный) шум. А звук от инвертора с формой выходного напряжения в виде модифицированной синусоиды более тембрально окрашен, с выраженными обертонами, более походящий на стук.
Акустический эффект может иметь различную физическую природу, например сила Ампера, вынуждающая колебаться проводники с током, или магнитострикционный эффект в материалах, находящимся в магнитном поле, возбуждаемом током. Акустический эффект может возникать во всех участках последовательной выходной цепи, например в потребителе или соединительных проводах, или в самом инверторе. Человек способен на слух различать гармонический состав производимого акустического эффекта. Так, звук от инвертора с синусоидальной формой выходного напряжения ощущается как однотонный гудящий (низкочастотный) шум. А звук от инвертора с формой выходного напряжения в виде модифицированной синусоиды более тембрально окрашен, с выраженными обертонами, более походящий на стук.
3. Виды электроприборов с индуктивным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
Электрические приборы с индуктивным характером сопротивления часто встречаются в технике и в быту. К этим приборам относятся электровибрационные приборы, например бритвы и насосы, осветительные приборы с индуктивными балластами, электромеханические реле, электрические двигатели.
К этим приборам относятся электровибрационные приборы, например бритвы и насосы, осветительные приборы с индуктивными балластами, электромеханические реле, электрические двигатели.
Реальная индуктивная нагрузка представляет собой частично чистую индуктивность и частично активную нагрузку. Для описания индуктивной нагрузки возможно использовать последовательную модель, в которой нагрузка представляется в виде последовательно соединенных индуктивности и сопротивления. Для описания соотношения влияния этих элементов на выходной ток преобразователя используют параметр «коэффициент мощности (КМ)», который определяет отношение активной мощности к полной мощности. При индуктивной нагрузке КМ<1. Таким образом, полная мощность, потребляемая нагрузкой с индуктивным характером сопротивления, будет больше, чем активная мощность, обычно указываемая на электроприборе в качестве номинальной. Поэтому индуктивная нагрузка представляет собой более сложный вид нагрузки для инвертора, потому что выходной ток инвертора идет как на создание выходной активной мощности, так и на запасание энергии в индуктивности (реактивная мощность).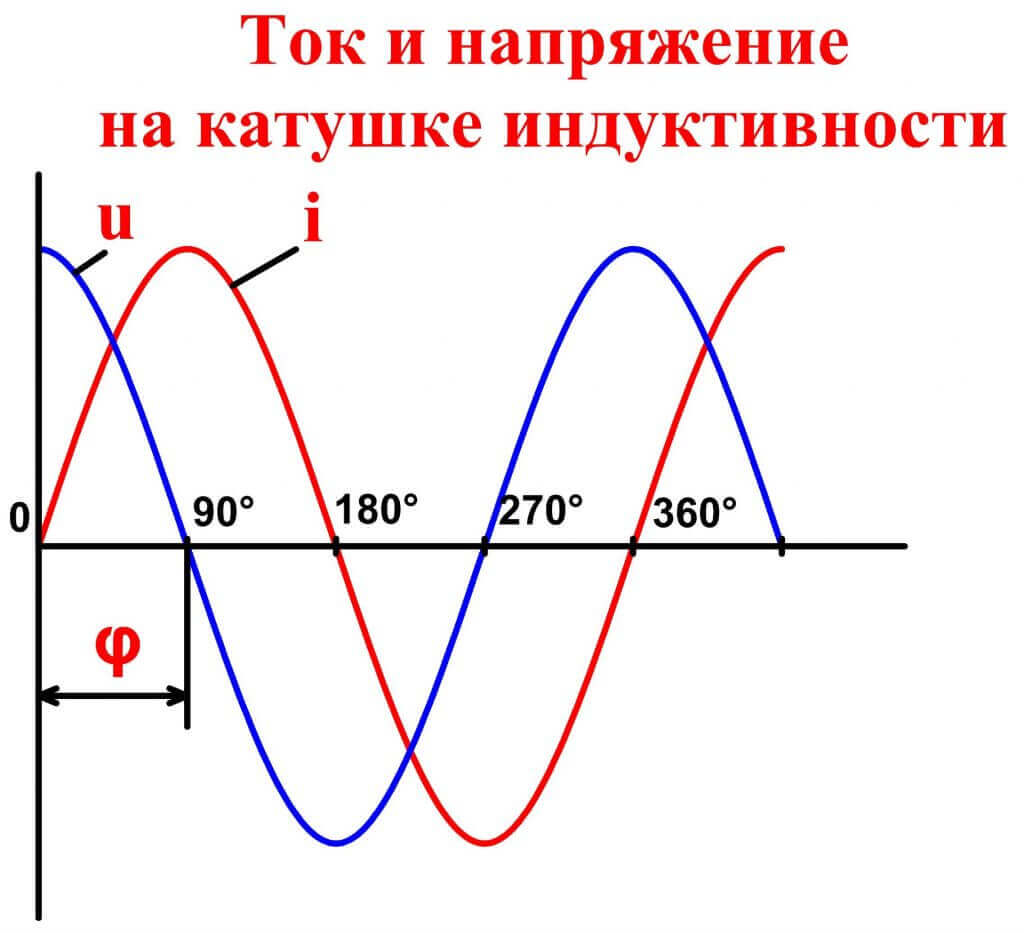 Потери энергии в инверторе при работе на нагрузку с индуктивным характером сопротивления будут больше чем при работе на нагрузку с активным характером сопротивления такой же номинальной (активной) мощности. Это очень важное свойство, поскольку часто при эксплуатации инверторов именно уровень потерь энергии, то есть тепловая мощность, нагревающая инвертор, является определяющей для обеспечения работоспособности. Однако для разных типов инверторов степень увеличения потерь при индуктивной нагрузке разная. Это связано с тем, что при различных топологиях построения инверторов путь выходного тока, нагревающего преобразователь, может быть различен и захватывать разное количество составных блоков преобразователя. Рассмотренные типы инверторов относительно данного вопроса разделяются на два вида: однокаскадные и двухкаскадные. Однокаскадным инвертором является трансформаторный инвертор. Выходной ток инвертора проходит через весь инвертор: через выходной трансформатор, в трансформированном виде через ключи инвертора и через источник входного напряжения.
Потери энергии в инверторе при работе на нагрузку с индуктивным характером сопротивления будут больше чем при работе на нагрузку с активным характером сопротивления такой же номинальной (активной) мощности. Это очень важное свойство, поскольку часто при эксплуатации инверторов именно уровень потерь энергии, то есть тепловая мощность, нагревающая инвертор, является определяющей для обеспечения работоспособности. Однако для разных типов инверторов степень увеличения потерь при индуктивной нагрузке разная. Это связано с тем, что при различных топологиях построения инверторов путь выходного тока, нагревающего преобразователь, может быть различен и захватывать разное количество составных блоков преобразователя. Рассмотренные типы инверторов относительно данного вопроса разделяются на два вида: однокаскадные и двухкаскадные. Однокаскадным инвертором является трансформаторный инвертор. Выходной ток инвертора проходит через весь инвертор: через выходной трансформатор, в трансформированном виде через ключи инвертора и через источник входного напряжения. При этом нагреваются все вышеназванные компоненты цепи и потери велики. Отличием двухкаскадных инверторов является наличие внутреннего звена постоянного тока. Инвертор с вч преобразованием, с формой выходного напряжения как модифицированной синусоидой так и с чистым синусом, является двухкаскадным инвертором. Он содержит емкостной накопитель энергии на выходе dcdc преобразователя, через который протекает часть реактивного выходного тока. Поэтому через входную часть преобразователя, то есть через dcdc преобразователь и источник входного напряжения, протекает значительно меньшая величина переменного тока, и соответственно эти блоки инвертора меньше нагреваются. Поэтому двухкаскадные типы инверторов могут иметь КПД выше, чем однокаскадные для данного типа нагрузок.
При этом нагреваются все вышеназванные компоненты цепи и потери велики. Отличием двухкаскадных инверторов является наличие внутреннего звена постоянного тока. Инвертор с вч преобразованием, с формой выходного напряжения как модифицированной синусоидой так и с чистым синусом, является двухкаскадным инвертором. Он содержит емкостной накопитель энергии на выходе dcdc преобразователя, через который протекает часть реактивного выходного тока. Поэтому через входную часть преобразователя, то есть через dcdc преобразователь и источник входного напряжения, протекает значительно меньшая величина переменного тока, и соответственно эти блоки инвертора меньше нагреваются. Поэтому двухкаскадные типы инверторов могут иметь КПД выше, чем однокаскадные для данного типа нагрузок.
При работе потребителей с индуктивным характером нагрузки от различных типов преобразователей проявляется различие эффективного тока нагрузки. Данный эффект существует потому что для индуктивной нагрузки кроме эффективного напряжения важно еще и среднее значение напряжения за период.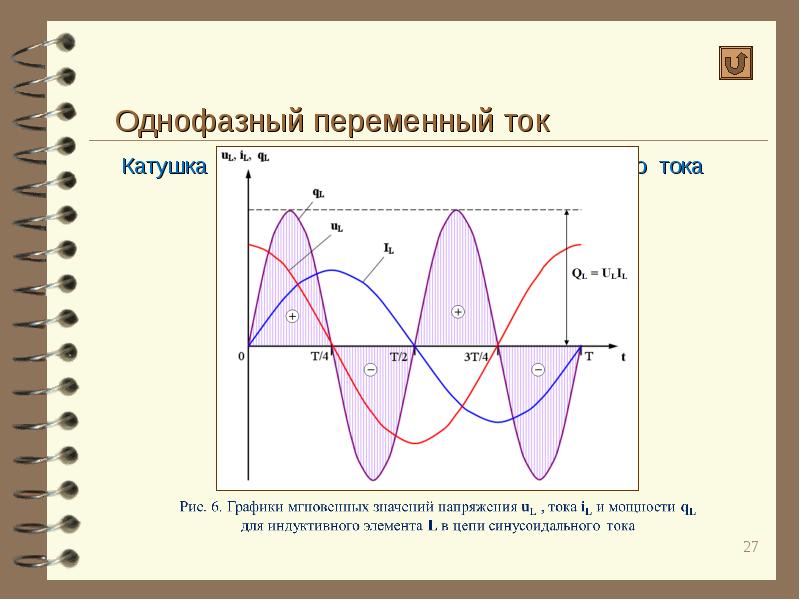 Этот вывод следует из закона электромагнитной индукции, согласно которому размах амплитуды переменного тока на индуктивности пропорционален приложенным вольт — секундам (В*С). А среднее напряжение для синусоиды с эффективным напряжением 220В и для модифицированной синусоиды с пиковым напряжением 311В и эффективным напряжением 220В весьма различно и составляет 198В и 156В соответственно. Для определения численного значения различия эффективного тока и активной мощности нагрузки произведено моделирование в среде micro-cap, результаты которого представлены на рис.№6. В качестве нагрузки при моделировании использовалась RL цепочка с КМ=0.7, т.е. ее активное сопротивление и модуль индуктивного сопротивления равны и составляют по 100Ом (величина индуктивности 318мГ).
Этот вывод следует из закона электромагнитной индукции, согласно которому размах амплитуды переменного тока на индуктивности пропорционален приложенным вольт — секундам (В*С). А среднее напряжение для синусоиды с эффективным напряжением 220В и для модифицированной синусоиды с пиковым напряжением 311В и эффективным напряжением 220В весьма различно и составляет 198В и 156В соответственно. Для определения численного значения различия эффективного тока и активной мощности нагрузки произведено моделирование в среде micro-cap, результаты которого представлены на рис.№6. В качестве нагрузки при моделировании использовалась RL цепочка с КМ=0.7, т.е. ее активное сопротивление и модуль индуктивного сопротивления равны и составляют по 100Ом (величина индуктивности 318мГ).
Ток в нагрузке. Красный график при источнике напряжения в виде чистой синусоиды, синий — при источнике напряжения в виде модифицированной синусоиды
Активная энергия, выделяющаяся в нагрузке. Красный график при источнике напряжения в виде чистой синусоиды, синий — при источнике напряжения в виде модифицированной синусоиды
Рис. №6. Графики тока и потребления активной энергии при индуктивной нагрузке.
№6. Графики тока и потребления активной энергии при индуктивной нагрузке.
Из графиков следует, что активная энергия более эффективно потребляется при синусоидальном источнике напряжения, причем разница составляет 16%. Такая же разница будет и в активной мощности. То есть, если подключить нагрузку, предназначенную для работы от сети 220В к инвертору с формой выходного напряжения в виде модифицированной синусоиды, то потребляемая активная мощность снизится на 16% . Эффективный ток при этом снизится на 9% . Для функционирования нагрузок данное понижение активной мощности будет иметь негативные последствия: электровибрационные приборы понизят механическую мощность, осветительные приборы будут светить тусклее.
4. Виды электроприборов с емкостным характером нагрузки и особенности работы различных типов инверторов с данным видом нагрузки.
Электрические приборы с емкостным характером сопротивления редко применяются как законченный блок, однако часто встречаются как часть других электроприборов, например емкостные компенсаторы реактивной мощности или фазосдвигающие емкостные цепи для электродвигателей. Так как остальные виды нагрузок рассматриваются в других разделах, имеет смысл рассмотреть отдельно работу инверторов различных типов на реальную емкость. Модель реальной емкости учитывает потери энергии в сопротивлении выводов применяемых конденсаторов и представляет собой последовательно включенные идеальный конденсатор и эмулирующий сопротивление выводов резистор.
Так как остальные виды нагрузок рассматриваются в других разделах, имеет смысл рассмотреть отдельно работу инверторов различных типов на реальную емкость. Модель реальной емкости учитывает потери энергии в сопротивлении выводов применяемых конденсаторов и представляет собой последовательно включенные идеальный конденсатор и эмулирующий сопротивление выводов резистор.
Сначала рассмотрим работу инвертора с формой выходного напряжения в виде чистой синусоиды на реальную емкость. Процессы, протекающие в этой цепи аналогичны процессам при работе такой же нагрузки от сети 220В. Как известно, конденсатор в цепи переменного тока представляет собой реактивную нагрузку, то есть полная мощность нагрузки большей частью состоит из циркулирующей от нагрузки к сети и обратно реактивной мощности и лишь небольшая часть полной мощности представляет собой активную мощность потерь. При этом полезный эффект нагрузки создает именно реактивная мощность, а активная мощность представляет собой паразитный эффект, нагревающий как саму нагрузку так и инвертор. Величина активной мощности, выделяющейся в инверторе, пропорциональна выходному сопротивлению инвертора.
Величина активной мощности, выделяющейся в инверторе, пропорциональна выходному сопротивлению инвертора.
Теперь же рассмотрим работу на такую же нагрузку инвертора с формой выходного напряжения в виде модифицированной синусоиды. Для получения наглядных результатов использовалось моделирование в среде micro-cap. Модель инвертора с формой выходного напряжения в виде модифицированной синусоиды представляет собой источник напряжения с формой модифицированной синусоиды и последовательно включенного сопротивления потерь Rг. Для сравнения использовалось моделирование схемы с той же самой нагрузкой, но работающей от источника переменного напряжения 220В 50Гц с таким же выходным сопротивлением. Схемы для моделирования представлены на рис. №7. Номиналы элементов типичны для обычных применений и составляют: Сн=10мкФ, Rн=Rг=1Ом.
Рис. №7. Схемы для моделирования в среде micro-cap
Результаты моделирования представлены на рис. №8. Из графиков тока нагрузки видно, что форма и амплитуда токов весьма различны.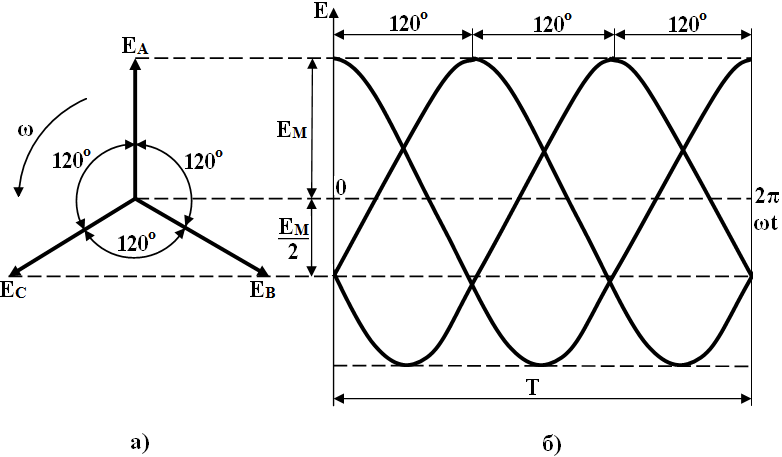 Ток нагрузки с синусоидальным источником напряжения имеет также синусоидальную форму и амплитуду 977мА, а ток нагрузки с источником напряжения в виде модифицированной синусоиды имеет вид экспоненциальных импульсов с амплитудой 152А и весьма короткой (десятки микросекунд) длительностью. Такие различия обусловлены тем, что в случае с источником напряжения в виде модифицированной синусоиды конденсатор заряжается от импульсного источника напряжения с высокой скоростью изменения напряжения, для которого конденсатор имеет низкое сопротивление. Поэтому напряжения на сопротивлениях потерь Rг и Rн в импульсе заряда велики и соответственно велики потери. Исходя из графика выделения энергии на сопротивлении потерь, общая мощность потерь составляет для синусоидального источника напряжения 0.95Вт, а для источника напряжения в виде модифицированной синусоиды 98Вт, то есть отличается в сто раз.
Ток нагрузки с синусоидальным источником напряжения имеет также синусоидальную форму и амплитуду 977мА, а ток нагрузки с источником напряжения в виде модифицированной синусоиды имеет вид экспоненциальных импульсов с амплитудой 152А и весьма короткой (десятки микросекунд) длительностью. Такие различия обусловлены тем, что в случае с источником напряжения в виде модифицированной синусоиды конденсатор заряжается от импульсного источника напряжения с высокой скоростью изменения напряжения, для которого конденсатор имеет низкое сопротивление. Поэтому напряжения на сопротивлениях потерь Rг и Rн в импульсе заряда велики и соответственно велики потери. Исходя из графика выделения энергии на сопротивлении потерь, общая мощность потерь составляет для синусоидального источника напряжения 0.95Вт, а для источника напряжения в виде модифицированной синусоиды 98Вт, то есть отличается в сто раз.
Ток в нагрузке. Красный график при источнике напряжения в виде чистой синусоиды, синий — при источнике напряжения в виде модифицированной синусоиды
Энергия, выделяющаяся в сопротивлении потерь. Красный график при источнике напряжения в виде чистой синусоиды, синий — при источнике напряжения в виде модифицированной синусоиды
Красный график при источнике напряжения в виде чистой синусоиды, синий — при источнике напряжения в виде модифицированной синусоиды
Рис. №8. Графики тока и энергии потерь для различных видов источников напряжения.
Можно показать, что мощность потерь при источнике напряжения в виде модифицированной синусоиды не зависит от сопротивления потерь, а только от величины конденсатора. Однако распределение потерь между инвертором и конденсатором пропорционально их внутренним сопротивлениям. Но в любом случае, такой высокий уровень пиковых токов и мощности потерь нежелателен как для инвертора, так и для нагрузки. Немногие типы конденсаторов для сети 220В способны работать с внутренними потерями в 100 раз большими, чем номинальные.
Также высокий уровень токов при источнике напряжения в виде модифицированной синусоиды создает повышенный акустический эффект при работе инвертора. Спектральный состав выходного тока инвертора с формой выходного напряжения в виде модифицированной синусоиды при работе на емкость весьма широкополосен, а амплитуда тока весьма велика, поэтому звуковой эффект производимый этим током весьма громкий и неприятный на слух.
5. Виды электроприборов с выпрямителем на входе и особенности работы различных типов инверторов с данным видом нагрузки.
Электрические приборы с выпрямителем на входе повсеместно встречаются в технике и в быту. К этим приборам относится бытовая электроника с трансформаторным или импульсным блоком питания. Эквивалентная схема подключения такой нагрузки представлена на рис №9. Источник питающего напряжения, в данном случае инвертор, представлен в виде генератора напряжения Vг с сопротивлением потерь Rг. Сам электрический прибор питается выпрямленным напряжением и представлен сопротивлением Rн. Блок питания электроприбора состоит из мостового выпрямителя и фильтрующего конденсатора Сн. Неидеальность конденсатора моделируется последовательным сопротивлением Rк. Сопротивление выпрямителя, входных проводников и трансформатора питания (в случае трансформаторного блока питания) моделируется последовательным сопротивлением Rп.
Рис. №9. Эквивалентная схема подключения электроприбора с выпрямителем на входе.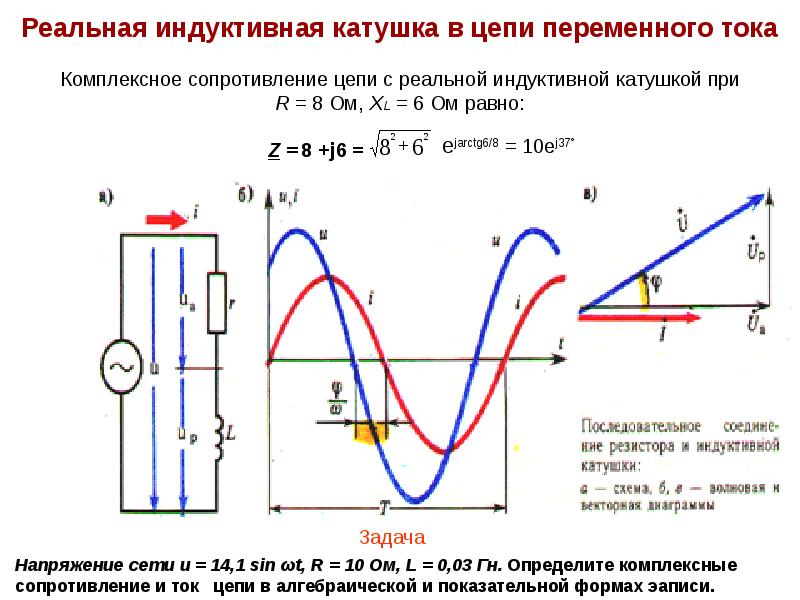
Работа такой нагрузки сильно отличается при использовании инверторов с различными видами выходного напряжения. Причина этого такая же, как и для емкостной нагрузки и заключается в том, что фильтрующий конденсатор Сн заряжается от входного источника напряжения. Если скорость изменения напряжения велика, как при работе от источника с формой напряжения в виде модифицированной синусоиды, то потери в элементах цепи увеличиваются многократно. Можно аналитически показать, что при работе от источника с формой напряжения в виде модифицированной синусоиды общие потери энергии будут зависеть лишь от амплитуды переменной составляющей напряжения на конденсаторе Сн и величины емкости этого конденсатора, и не зависеть от величины сопротивлений Rг, Rп и Rк. От величины этих сопротивлений будет зависеть только распределение потерь среди элементов схемы.
Для получения наглядных результатов снова использовалось моделирование в среде micro-cap. Для сравнения использовалось моделирование схемы с одной и той же нагрузкой, но работающей от инвертора с синусоидальной формой напряжения 220В 50Гц и от инвертора с формой напряжения в виде модифицированной синусоиды. Номиналы элементов схемы для моделирования составляют: Rн=500Ом, Сн=47мкФ, Rг=Rп=Rк=1Ом. Такие номиналы типичны для блока питания бытовой электроники мощностью 150Вт, например телевизора. Результаты моделирования представлены на рис. №10. Из графиков выходного тока инвертора видно, что форма и амплитуда токов весьма различны для инверторов с различными видами выходного напряжения. Ток инвертора с синусоидальным источником напряжения имеет плавную форму и амплитуду 3.1А, а ток нагрузки с источником напряжения в виде модифицированной синусоиды имеет вид экспоненциальных импульсов с амплитудой 20.2А и весьма короткой (сотни микросекунд) длительностью. Исходя из графика выделения энергии на сопротивлении потерь, общая мощность потерь составляет для синусоидального источника напряжения 3.5Вт, а для источника напряжения в виде модифицированной синусоиды 9.4Вт. Таким образом, общая мощность потерь при работе нагрузки от инвертора с формой напряжения в виде модифицированной синусоиды почти в 3 раза больше чем при работе той же нагрузки от инвертора с синусоидальной формой напряжения.
Номиналы элементов схемы для моделирования составляют: Rн=500Ом, Сн=47мкФ, Rг=Rп=Rк=1Ом. Такие номиналы типичны для блока питания бытовой электроники мощностью 150Вт, например телевизора. Результаты моделирования представлены на рис. №10. Из графиков выходного тока инвертора видно, что форма и амплитуда токов весьма различны для инверторов с различными видами выходного напряжения. Ток инвертора с синусоидальным источником напряжения имеет плавную форму и амплитуду 3.1А, а ток нагрузки с источником напряжения в виде модифицированной синусоиды имеет вид экспоненциальных импульсов с амплитудой 20.2А и весьма короткой (сотни микросекунд) длительностью. Исходя из графика выделения энергии на сопротивлении потерь, общая мощность потерь составляет для синусоидального источника напряжения 3.5Вт, а для источника напряжения в виде модифицированной синусоиды 9.4Вт. Таким образом, общая мощность потерь при работе нагрузки от инвертора с формой напряжения в виде модифицированной синусоиды почти в 3 раза больше чем при работе той же нагрузки от инвертора с синусоидальной формой напряжения.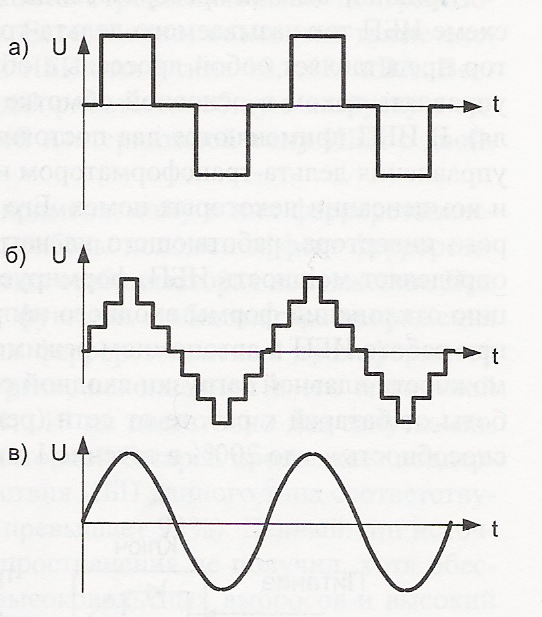 Так как сопротивления потерь включены последовательно, распределение мощности потерь на каждом конкретном элементе будет тоже сохраняться, поэтому например сам инвертор будет выделять мощности в 3 раза больше, конденсатор и трансформатор блока питания также будут греться в 3 раза больше. Элементы бытовых приборов могут не иметь трехкратного запаса по выходной мощности и выйти из строя в результате питания от инверторов с формой напряжения в виде модифицированной синусоиды.
Так как сопротивления потерь включены последовательно, распределение мощности потерь на каждом конкретном элементе будет тоже сохраняться, поэтому например сам инвертор будет выделять мощности в 3 раза больше, конденсатор и трансформатор блока питания также будут греться в 3 раза больше. Элементы бытовых приборов могут не иметь трехкратного запаса по выходной мощности и выйти из строя в результате питания от инверторов с формой напряжения в виде модифицированной синусоиды.
График тока в нагрузке. Зеленый график при источнике напряжения в виде чистой синусоиды, красный — при источнике напряжения в виде модифицированной синусоиды
Энергия, выделяющаяся в сопротивлении потерь. Зеленый график при источнике напряжения в виде чистой синусоиды, красный — при источнике напряжения в виде модифицированной синусоиды
Рис. №10. Графики выходного тока инвертора и энергии потерь для различных видов инверторов.
Как и для емкостной нагрузки, для нагрузки с выпрямителем на входе, высокий уровень токов при источнике напряжения в виде модифицированной синусоиды создает повышенный акустический эффект при работе инвертора.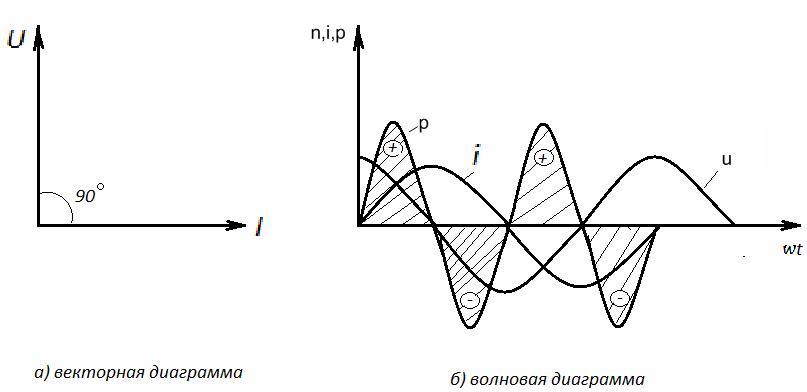 Спектральный состав выходного тока инвертора с формой выходного напряжения в виде модифицированной синусоиды при работе на нагрузку с выпрямителем на входе весьма широкополосен, а амплитуда тока весьма велика, поэтому звуковой эффект производимый этим током весьма громкий и неприятный на слух. При этом производить звуковой эффект может любой элемент схемы, через который протекает выходной ток инвертора, этот элемент может находиться в инверторе или в подключаемом электроприборе, или в соединительных проводах.
Спектральный состав выходного тока инвертора с формой выходного напряжения в виде модифицированной синусоиды при работе на нагрузку с выпрямителем на входе весьма широкополосен, а амплитуда тока весьма велика, поэтому звуковой эффект производимый этим током весьма громкий и неприятный на слух. При этом производить звуковой эффект может любой элемент схемы, через который протекает выходной ток инвертора, этот элемент может находиться в инверторе или в подключаемом электроприборе, или в соединительных проводах.
6. Сводная таблица отличий в работе различных типов инверторов с разными видами нагрузок. Заключение.
Для того чтобы систематизировать выявленные в предыдущих частях статьи отличия в работе различных типов инверторов с разными видами нагрузок была составлена табл. №1. Для сравнения акустического эффекта, тепловых потерь в нагрузке и эффективной мощности для одинаковых нагрузок в качестве отсчета была выбрана сеть переменного напряжения 220В 50Гц.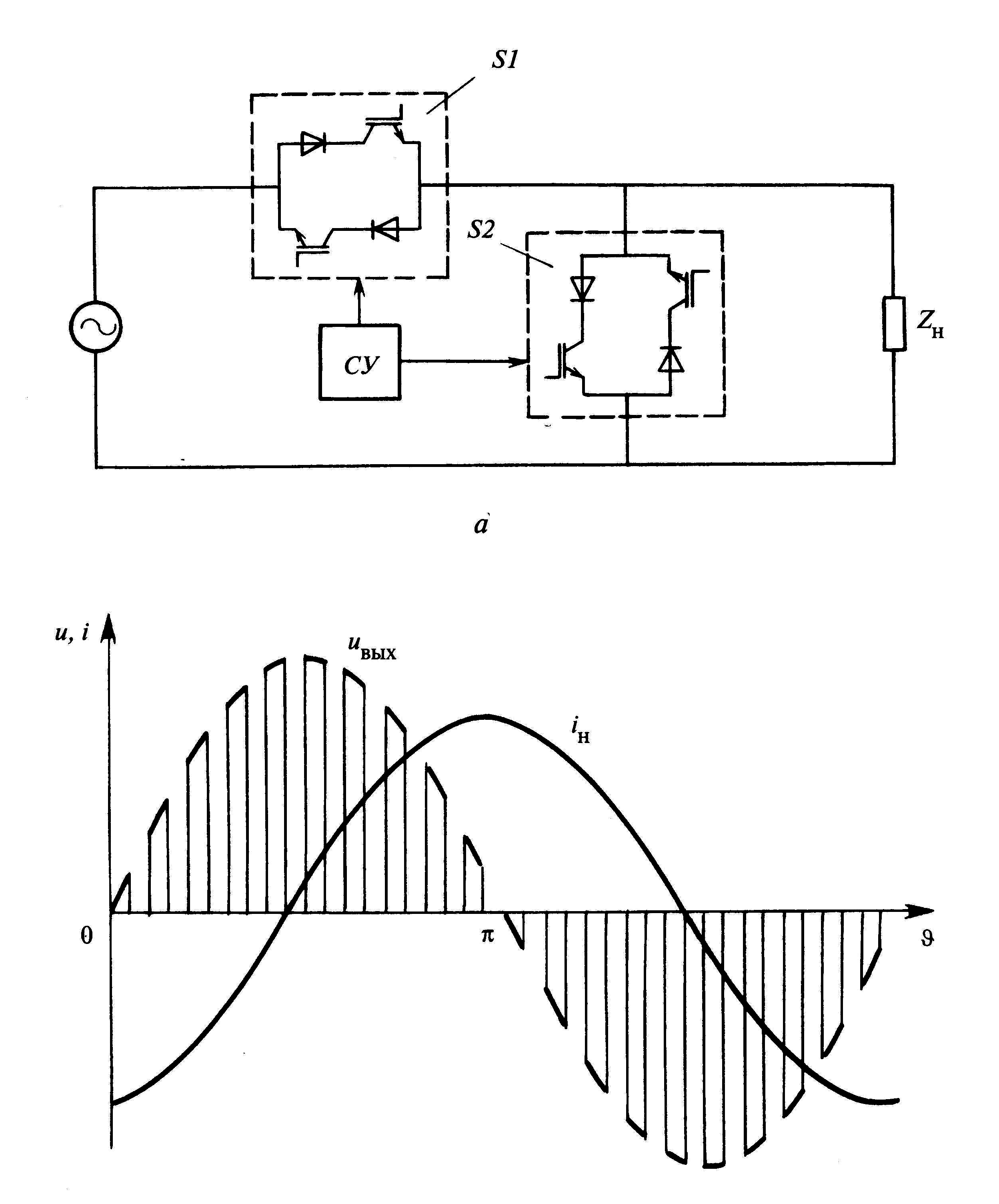 Для сравнения потерь в инверторе разных типов, но с одинаковым выходным сопротивлением, в качестве отсчета был выбран инвертор с синусоидальной формой выходного напряжения.
Для сравнения потерь в инверторе разных типов, но с одинаковым выходным сопротивлением, в качестве отсчета был выбран инвертор с синусоидальной формой выходного напряжения.
Табл. №1. Сводная таблица отличий в работе различных типов инверторов с разными видами нагрузок.
| . | . | Виды инверторов | ||
|---|---|---|---|---|
| Виды нагрузок | Параметры | Трансформаторный | ВЧ модиф. синус | Вч чистый синус |
| Активная | Эффективная мощность | Как при работе от сети 220В | Как при работе от сети 220В | Как при работе от сети 220В |
.
|
Акустический эффект | Больше, чем при работе от сети 220В | Больше, чем при работе от сети 220В | Как при работе от сети 220В |
| Индуктивная | Эффективная мощность | Меньше чем в сети 220В | Меньше чем в сети 220В | Как при работе от сети 220В |
| Емкостная | Потери в нагрузке | Больше, чем при работе от сети 220В | Больше, чем при работе от сети 220В | Как при работе от сети 220В |
| . | Потери в инверторе | Больше, чем с инвертором с синусоидальной формой напряжения | Больше, чем с инвертором с синусоидальной формой напряжения |
.
|
| . | Акустический эффект | Больше, чем при работе от сети 220В | Больше, чем при работе от сети 220В | Как при работе от сети 220В |
| С выпрямителем | Потери в нагрузке | Больше, чем при работе от сети 220В | Больше, чем при работе от сети 220В | Как при работе от сети 220В |
| . | Потери в инверторе | Больше, чем с инвертором с синусоидальной формой напряжения | Больше, чем с инвертором с синусоидальной формой напряжения | . |
| . | Акустический эффект | Больше, чем при работе от сети 220В | Больше, чем при работе от сети 220В | Как при работе от сети 220В |
Как следует из таблицы, применять для питания всевозможных типов нагрузки, не опасаясь негативных эффектов возможно только инверторы с выходным напряжением в виде чистой синусоиды. Инверторы с выходным напряжением в виде модифицированной синусоиды, возможно применять без опасений для питания активных нагрузок при невысоких требованиях к акустическому эффекту.
Инверторы с выходным напряжением в виде модифицированной синусоиды, возможно применять без опасений для питания активных нагрузок при невысоких требованиях к акустическому эффекту.
Синусоидальный ток
Переменным называется такой электрический ток, который изменяет со временем свою величину и направление. При этом изменения во времени повторяются, и время, через которое изменения начинают повторяться, называется периодом переменного тока Т
, а величина, обратная периоду, называется частотой f. Одной из простейших форм для расчета переменного тока является синусоидальный ток.
Синусоидальным называется такой ток, для которого мгновенные значения силы тока образуют синусоиду. Расчеты такого тока просты, так как производная по току является косинусоидой, которая не отличается от синусоиды по форме. При этом необходимо взять определенный отрезок Im, для которого длина равна максимальному значению синусоидальной величины. Данный вектор является вектором синусоидальной величины.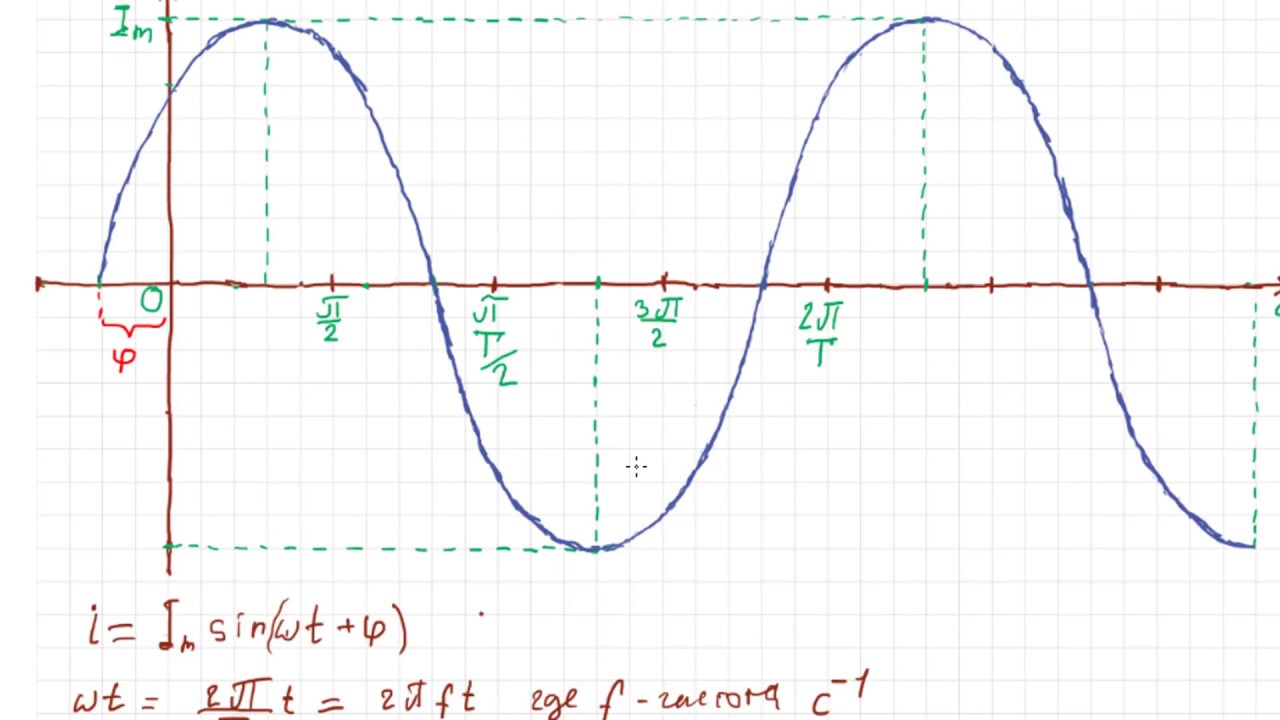 Исходное положение соответствует направлению вектора по горизонтальной оси (t = 0). Далее рассматривается равномерное вращение данного вектора в положительном направлении с периодом T = 2?. При этом мгновенное значение силы тока будет определяться как проекция вектора тока на горизонтальную ось.
Исходное положение соответствует направлению вектора по горизонтальной оси (t = 0). Далее рассматривается равномерное вращение данного вектора в положительном направлении с периодом T = 2?. При этом мгновенное значение силы тока будет определяться как проекция вектора тока на горизонтальную ось.
При повороте на угол ? = ?t проекция будет определяться формулой: Im sin?t. Т При повороте на угол ? = ?t проекция будет определяться формулой: Im sin?t. Таким образом, в каждый момент времени значение силы тока будет определяться уравнением:
i = Im sin?t,
где i — мгновенное значение силы тока, т. е. значение силы тока в каждый момент времени;
Im — максимальное значение силы тока.
В данном уравнении выражение, находящееся под знаком тригонометрической функции, называется фазой тока. Если вращение рассматриваемого вектора в момент времени равно нулю, вектор начинается не с горизонтального направления, а находится под некоторым углом ? к горизонтальной оси, данный угол называется начальной фазой.
Таким образом, уравнение переменного синусоидального тока примет общий вид:
i = Im sin(?t + ?).
Генераторы, вырабатывающие переменный синусоидальный ток, должны иметь э. д. с., определяемые соотношением:
e = Em sin(?t + ?),
где ? — начальная фаза э. д. с.
В случае, когда э. д. с. и ток в одной цепи проходят через нулевое или максимальное значения в различные моменты времени, говорят, что они сдвинуты по фазе друг относительно друга. Сдвиги фаз ? определяются как разность начальных фаз синусоидальных величин. Для данного случая ? = ? – ?, и векторы силы тока и напряжения расположены под углом ? друг относительно друга.
Измерение синусоидальной волны
- • Знайте измерения, связанные с синусоидальными волнами
- • а.
 Пиковое значение.
Пиковое значение. - • б. Амплитуда.
- • ок. Пиковое значение.
- • г. Периодическое время.
- • e. Средняя стоимость.
- • ф. Среднеквадратичное значение.
Рис 1.2.1 Характеристики синусоидальной волны
Форма волны — это график, показывающий изменение, обычно напряжения или тока, во времени.Горизонтальная ось показывает течение времени слева направо. Вертикальная ось показывает измеренную величину (это напряжение на рис. 1.2.1).
Шесть наиболее важных характеристик синусоиды:
ПИК ДО ПИК значения.
МГНОВЕННОЕ значение.
АМПЛИТУДА.
Пиковое значение.
ПЕРИОДИЧЕСКОЕ ВРЕМЯ.
СРЕДНЕЕ значение.
RMS значение.
Эти характеристики показаны на рис.2,1
Пиковое значение
Значение PEAK TO PEAK — это расстояние по вертикали между вершиной и основанием волны. Он будет измеряться в вольтах на осциллограмме напряжения и может быть обозначен как V PP или V PK − PK . В форме волны тока он будет обозначен как I PP или I PK-PK , поскольку I (не C) используется для представления тока.
В форме волны тока он будет обозначен как I PP или I PK-PK , поскольку I (не C) используется для представления тока.
Мгновенное значение
Это значение (напряжение или ток) волны в любой конкретный момент.часто выбирается, чтобы совпасть с каким-то другим событием. Например. Мгновенное значение синусоидальной волны на четвертой части цикла будет равно пиковому значению. См. Точку X на рис. 1.2.1.
Амплитуда
АМПЛИТУДА синусоидальной волны — это максимальное расстояние по вертикали, достигнутое в любом направлении от центральной линии волны. Поскольку синусоидальная волна симметрична относительно своей центральной линии, амплитуда волны составляет половину от максимального значения, как показано на рисунке 1.2.2.
Пиковое значение
Пиковое значение волны — это максимальное значение волны, превышающее опорное значение.Обычно используемое эталонное значение — ноль. В форме волны напряжения пиковое значение может быть обозначено как V PK или V MAX (I PK или I MAX в форме кривой тока).
Если измеряемая синусоида симметрична по обе стороны от нуля вольт (или от нуля ампер), это означает, что уровень постоянного или постоянного тока волны равен нулю вольт, тогда пиковое значение должно быть таким же, как амплитуда, то есть половина от максимального до максимального значения.
Рис. 1.2.2 Определение максимального значения V
PKОднако это не всегда так, если также присутствует постоянная составляющая, отличная от нуля вольт, синусоидальная волна будет симметричной относительно этого уровня, а не нуля.Нижняя осциллограмма на рис. 1.2.2 показывает, что пиковое значение теперь может быть даже больше, чем пиковое значение (однако, амплитуда волны остается той же самой, и это разница между пиковым значением и «центральной линией»). «формы волны).
Периодическое время и частота
ПЕРИОДИЧЕСКОЕ ВРЕМЯ (обозначенное символом T) — это время в секундах, миллисекундах и т. Д., Принятое для одного полного цикла волны.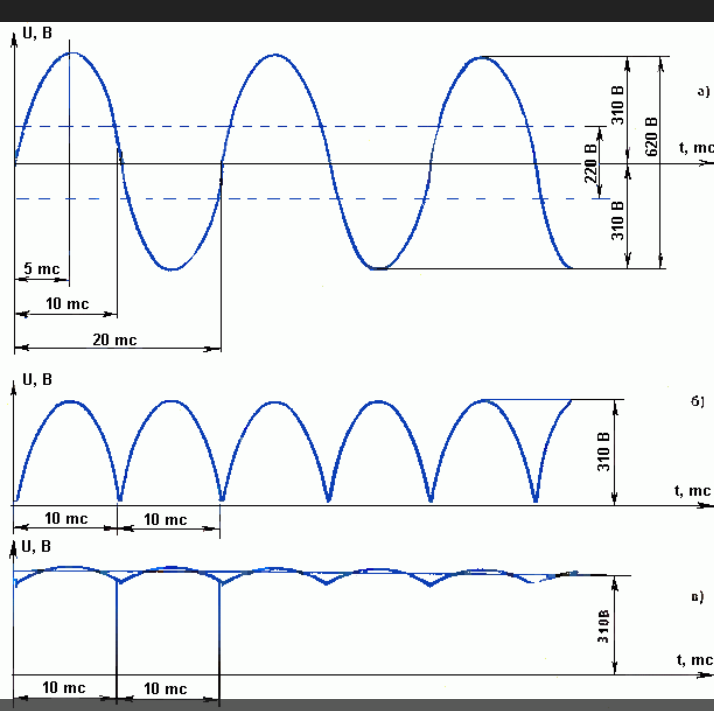 Его можно использовать для определения ЧАСТОТЫ волны ƒ по формуле T = 1 / ƒ
Его можно использовать для определения ЧАСТОТЫ волны ƒ по формуле T = 1 / ƒ
Таким образом, если периодичность волны составляет 20 мс (или 1/50 секунды), то должно быть 50 полных циклов волны за одну секунду.Частота 50 Гц. Обратите внимание, что при использовании этой формулы, если периодическое время указывается в секундах, частота будет в Гц.
Рис 1.2.3 Среднее значение синусоиды
Среднее значение
СРЕДНЕЕ значение. Обычно это означает среднее значение только половины периода волны. Если взять среднее значение полного цикла, оно, конечно, будет равно нулю, поскольку в синусоидальной волне, симметричной относительно нуля, есть равные отклонения выше и ниже нулевой линии.
Используя только половину цикла, как показано на рис. 1.2.3, среднее значение (напряжение или ток) всегда составляет 0,637 от пикового значения волны.
В AV = В PK x 0,637
или
I AV = I PK X 0,637
Среднее значение — это значение, которое обычно определяет напряжение или ток, показываемые на измерительном приборе. Однако есть некоторые измерители, которые будут считывать значение RMS, они называются «измерителями True RMS».
Однако есть некоторые измерители, которые будут считывать значение RMS, они называются «измерителями True RMS».
Среднеквадратичное значение.
RMS или ROOT MEAN SQUARED значение — это значение эквивалентного постоянного (неизменяемого) напряжения или тока, которые будут обеспечивать такую же энергию в цепи, как измеренная синусоидальная волна. То есть, если синусоидальная волна переменного тока имеет среднеквадратичное значение 240 вольт, она будет обеспечивать такую же энергию в цепи, что и источник постоянного тока на 240 вольт.
Можно показать, что среднеквадратичное значение синусоидальной волны составляет 0,707 пикового значения.
В RMS = В PK x 0.707 и I RMS = I PK x 0,707
Кроме того, пиковое значение синусоидальной волны равно 1,414 x среднеквадратичное значение.
Форм-фактор
Если V AV (0,637) умножить на 1,11, получится 0,707, что является среднеквадратичным значением. Это различие называется форм-фактором волны, и соотношение 1,11 справедливо только для идеальной синусоидальной волны. Если волна имеет другую форму, изменится либо среднеквадратичное значение, либо среднее значение (или оба), а также отношения между ними.Это важно при измерении переменного напряжения с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение просто путем умножения напряжения на 1,11. Следовательно, если измеряемая волна переменного тока не является идеальной синусоидальной волной, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить истинный измеритель RMS, который фактически вычисляет значение RMS несинусоидальных волн.
Это различие называется форм-фактором волны, и соотношение 1,11 справедливо только для идеальной синусоидальной волны. Если волна имеет другую форму, изменится либо среднеквадратичное значение, либо среднее значение (или оба), а также отношения между ними.Это важно при измерении переменного напряжения с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение просто путем умножения напряжения на 1,11. Следовательно, если измеряемая волна переменного тока не является идеальной синусоидальной волной, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить истинный измеритель RMS, который фактически вычисляет значение RMS несинусоидальных волн.
Электроснабжение
Чтобы продемонстрировать некоторые из этих характеристик при использовании, рассмотрим очень распространенную синусоидальную волну, напряжение сети или форму сигнала линии, которая во многих частях мира составляет номинальное напряжение 230 В.
Электрооборудование, подключаемое к сети, всегда имеет этикетку с информацией о том, к какому источнику питания может быть подключено оборудование. Эти метки довольно разные по внешнему виду, но часто есть изображение синусоидальной волны, показывающей, что переменный ток. необходимо использовать поставку. Указанное напряжение будет 230 В (или 120 В в США) или диапазон напряжений, включая эти значения. Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота источника питания составляет 50 Гц в Европе или 60 Гц в США.
Из этого небольшого количества информации можно определить другие значения:
а. Пиковое напряжение формы волны, как В PK = В RMS x 1,414
г. СРЕДНЕЕ значение сигнала, как V AV = V PK x 0,637
г. Значение PEAK TO PEAK формы волны. Это вдвое больше АМПЛИТУДЫ, которая (поскольку форма сигнала сети симметрична относительно нуля вольт) совпадает с величиной V PK .
Поскольку V PK уже известен из.следует, что V PP = V PK x 2
г. ПЕРИОДИЧЕСКОЕ ВРЕМЯ, равное T = 1 / ƒ
Синусоидальное напряжение— обзор
3.3 Амплитуда и фазовые отношения для элементов схемы
Начнем с резистора . Используя выражения для переменного напряжения и переменного тока и подставляя их в закон Ома, мы можем вывести отношения между пиковыми значениями и начальными фазами для резистора:
(3.8) v (t) = Vmcos (ωt + ϕV),
(3.9) i (t) = Imcos (ωt + ϕI),
(3.10) Vmcos (ωt + ϕV) = Ri (t) = RImcos ( ωt + ϕI).
Из последнего уравнения следует, что пиковые и начальные значения фаз тока и напряжения должны быть связаны следующим образом:
Следовательно, очевидно, что напряжение и ток через резистор имеют одинаковый начальный фазовый угол; другими словами, они совпадают по фазе . График переменного напряжения и тока на Рисунке 3.2 иллюстрирует этот факт.
Рисунок 3.2. Напряжение и ток переменного тока в случае резистора.
Теперь рассмотрим случай индуктора . Напомним, что соотношение между напряжением и током на клеммах в случае катушки индуктивности следующее:
Используя это уравнение, мы найдем желаемые соотношения. Сначала возьмем производную тока по времени:
(3.14) ddt (Imcos (ωt + ϕI)) = — ωImsin (ωt + ϕI).
Подставляя (3.1) и (3.14) в (3.13), находим:
(3.15) Vmcos (ωt + ϕV) = — LωImsin (ωt + ϕI).
Используя тригонометрическое тождество
(3.16) cos (α + π2) = — sinα,
, последнее уравнение можно переписать следующим образом:
(3.17) Vmcos (ωt + ϕV) = LωImcos (ωt + ϕI + π2).
Из этого уравнения мы находим, что:
Следовательно, переменное напряжение и ток не совпадают по фазе, и переменное напряжение на катушке индуктивности опережает переменный ток через катушку индуктивности на π / 2 Другой способ выразить пиковое значение и фазу отношения в катушке индуктивности
Последнее выражение предполагает, что ток отстает от напряжения на π / 2.Рисунок 3.3 дает графическое представление переменного напряжения и тока в случае катушки индуктивности.
Рисунок 3.3. Напряжение и ток переменного тока в случае индуктора.
Наконец, рассмотрим корпус конденсатора . Напомним, что соотношение между клеммами между током и напряжением в случае конденсатора:
Сначала возьмем производную напряжения по времени:
(3.23) ddt (Vmcos (ωt + ϕV)) = — ωVmsin (ωt + ϕV).
Подставив (3.23) и (3.5) в (3.22) находим:
(3.24) Imcos (ωt + ϕI) = — CωVmsin (ωt + ϕV).
Используя тригонометрическое тождество (3.16), преобразуем (3.24) следующим образом:
(3.25) Imcos (ωt + ϕI) = CωVmcos (ωt + ϕV + π2).
Из этого выражения мы находим, что пиковые значения и фазы связаны соотношением:
, которое также можно записать следующим образом:
Таким образом, в случае конденсаторов, мы видим, что переменное напряжение отстает от тока на π / 2 или, другими словами, переменный ток опережает переменное напряжение на π / 2.Рисунок 3.4 дает графическое представление переменного напряжения и тока в случае конденсатора.
Рисунок 3.4. Напряжение и ток переменного тока в случае конденсатора.
ПРИМЕР 3.1
Предположим, что у нас есть источник синусоидального напряжения с фиксированной амплитудой В м = 5 В и фиксированной частотой f = 1 МГц. Каким должен быть максимальный ток через (а) резистор 5 Ом, (б) индуктор 5 мкГн и (в) конденсатор 5 мкФ?
Решение: (a) Из (3.11) Im = Vm / R = 5V / 5Ω = 1 A, (b) из (3.20) Im = Vm / ωL = 5V / (2π × 106 Гц × 5 × 10−6H) = 1 / (2π) A = 159 мА, (c) из (3.26) Im = ωCVm = 2π × 106 Гц × 5 × 10–6F × 5V = 50π A = 157 A.
На основании предыдущего обсуждения мы можем сделать вывод, что напряжения переменного тока на резисторах, индукторах, а конденсаторы приводят к возникновению переменного тока, и наоборот. Этот факт следует из линейности соотношений выводов резисторов, конденсаторов и катушек индуктивности. Следовательно, если все источники напряжения и тока в цепи являются источниками переменного тока с одинаковой частотой, то напряжения и токи повсюду в цепи являются синусоидальными функциями с этой частотой.В следующих нескольких разделах мы представим метод анализа цепей, основанный на этом факте.
1.2: Синусоидальные формы сигналов — Engineering LibreTexts
Переменный или переменный ток назван так потому, что ток чередуется или переключается между двумя полярностями. Другими словами, ток (и, следовательно, напряжение) зависит от времени. Это принципиально отличается от постоянного тока, который имеет фиксированную полярность и, как правило, постоянный во времени. Например, лабораторный источник постоянного напряжения в идеале поддерживает заданное напряжение на своих выводах и не меняется с течением времени.Напротив, когда форма волны переменного тока колеблется вперед и назад во времени, ее форма может иметь широкие вариации, начиная от простых регулярных траекторий лабораторных стандартов, таких как синусоидальные волны, треугольные волны и прямоугольные волны, до гораздо более сложных и волнообразных форм создаваемых волн. музыкальными инструментами и человеческим голосом.
Синусоидальная волна — это простейшая волна, которую можно создать. Он представляет собой движение простого вектора, вращающегося с постоянной скоростью, например, вертикальное смещение секундной стрелки часов.Пример показан на рисунке \ (\ PageIndex {1} \). По горизонтальной оси отложено время. Он увеличивается по мере того, как мы движемся слева направо (т.е. если точка A находится справа от точки B, то A возникает позже, чем B). Вертикальная ось представлена здесь, как правило, в процентах от максимума, но обычно это измерение напряжения, тока, звукового давления и т.п.
Рисунок \ (\ PageIndex {1} \): синусоида.Обратите внимание на плавное изменение, которое начинается с нуля, поднимается до положительного пика через четверть пути, падает обратно до нуля на середине, продолжается до отрицательного пика через три четверти, а затем снова возрастает до того места, где оно началось.Затем этот процесс повторяется. Каждый повтор называется циклом. На рисунке \ (\ PageIndex {1} \) показан один полный цикл.
Синусоидальные волны демонстрируют четвертьволновую симметрию. То есть каждая четверть (по времени) волны идентична любой другой, если вы просто перевернете ее вокруг горизонтальной оси и / или повернете вертикально вокруг ее пика. Время, необходимое для завершения одного цикла, называется периодом и обозначается символом \ (T \) (для времени). Обратной величине периода является частота \ (f \).
\ [f = \ frac {1} {T} \ label {1.1} \]
Частота указывает, сколько циклов существует в одной секунде. Чтобы почтить память одного из исследователей 19 века в этой области, вместо того, чтобы называть единицу «циклов в секунду», мы используем Герц, названный в честь Генриха Герца и сокращенно Гц. На рисунке \ (\ PageIndex {2} \) показаны три синусоидальные волны с разными частотами; начальная волна (зеленый), волна с удвоенной частотой (синий) и третья с половиной частоты или с удвоенным периодом (красный).
Рисунок \ (\ PageIndex {2} \): Изменение частоты синусоидальной волны.Амплитуда (по вертикали) волны может быть выражена как пиковая величина, которая представляет собой изменение от центральной нулевой линии до наиболее положительного значения. Амплитуда также может быть выражена от пика до пика; расстояние от самого отрицательного до самого положительного. Для синусоидальной волны это всегда будет вдвое больше пикового значения, хотя это может быть не так для других волн, которые могут быть асимметричными. Серия из трех синусоид с разными амплитудами показана на рисунке \ (\ PageIndex {3} \). Рядом с исходным (зеленый) находятся версии с двойной амплитудой (синий) и половинной амплитуды (красный).
Рисунок \ (\ PageIndex {3} \): изменение амплитуды синусоидальной волны.Объединив эти параметры, рассмотрим форму волны напряжения, показанную на рисунке \ (\ PageIndex {4} \). Здесь мы видим два цикла формы волны переменного напряжения.
Рисунок \ (\ PageIndex {4} \): простой пример синусоидальной волны.Пиковое значение составляет 4 В, а значение полного размаха — 8 В (обычно сокращенно «8 В pp»). Период одного цикла составляет 0,2 секунды или \ (T = 200 \) миллисекунды. Далее, частота \ (f = 1/200 \) миллисекунд или 5 Гц (5 циклов за одну секунду).
Сигналыпеременного тока также могут быть объединены со смещением постоянного тока. Добавление положительного уровня постоянного тока сдвигает волну по вертикали, а отрицательный уровень постоянного тока смещает волну по вертикали. Это не изменяет частоту или переменную часть амплитуды (хотя абсолютные пики будут сдвинуты на величину постоянного тока). На рисунке \ (\ PageIndex {5} \) показано влияние различных смещений постоянного тока. Выше начальной волны (зеленый) находится идентичная в остальном волна с положительным смещением постоянного тока, равным 20% от исходного пикового значения (синий).Под оригиналом находится третья волна (красная), которая показывает отрицательное смещение постоянного тока, равное половине пикового значения оригинала.
Рисунок \ (\ PageIndex {5} \): Изменение смещения постоянного тока синусоидальной волны. {\ circ} \).{\ circ} \). Рисунок \ (\ PageIndex {6} \): Изменение фазы синусоидальной волны.Объединение вышеуказанных элементов позволяет нам разработать общий формат синусоидальной волны (показано напряжение):
\ [v (t) = V_ {DC} + V_ {P} \ sin (2 \ pi f t + \ theta) \ label {1.2} \]
где
- \ (v (t) \) — напряжение в некоторый момент времени \ (t \),
- \ (V_ {DC} \) — смещение постоянного тока, если оно есть,
- \ (V_ {P} \) — пиковое значение,
- \ (f \) — частота,
- \ (\ theta \) — фазовый сдвиг (+, если опережает и рисует влево, — если отстает и рисует вправо).
В качестве быстрого и практического примера сигнал, показанный на рисунке \ (\ PageIndex {4} \), имеет пиковую амплитуду 4 вольта, частоту 5 Гц и не имеет смещения постоянного тока или фазового сдвига. Таким образом, его выражение: \ (v (t) = 4 \ sin (2 \ pi 5 t) \)
Чтобы вычислить фазовый сдвиг, сначала определите разницу во времени между формой сигнала и эталоном, которую мы назовем \ (\ Delta t \). Эталоном может быть фиксированный момент времени (например, \ (t = 0 \)) или другой сигнал. Как правило, самый простой способ сделать это — измерить разницу в точках пересечения нуля при условии, что смещения постоянного тока нет.{\ circ} \ frac {\ Delta t} {T} \ label {1.3} \]
Помните, что если волна смещена влево, то она является опережающей и положительной, а смещение вправо — запаздывающим или запаздывающим во времени и, следовательно, отрицательным.
Пример \ (\ PageIndex {1} \)
Запишите выражение для формы сигнала, показанной на рисунке \ (\ PageIndex {7} \).
Рисунок \ (\ PageIndex {7} \): Форма волны для примера \ (\ PageIndex {1} \).Этот сигнал внешне может выглядеть так, как на рисунке \ (\ PageIndex {4} \), но не позволяйте этому вводить вас в заблуждение.Во-первых, разная шкала времени. Для этой формы сигнала один цикл завершается за 10 миллисекунд. Следовательно, частота
\ [\ begin {align} f & = \ frac {1} {T} \\ [4pt] & = \ frac {1} {10 мс} \\ [4pt] & = 100 Гц \ end {align} \ ]
Вторая проблема — смещение постоянного тока. Обратите внимание, что положительный пик возникает при 4 амперах, а отрицательный пик — при -2 ампера. Это указывает на максимальное значение 6 ампер. Без смещения положительный пик будет на уровне 3 ампер, следовательно, имеется смещение по постоянному току +1 ампер.Вертикальный центр формы волны смещен вверх от 0 до +1 ампер. Эта точка находится при t = 0, следовательно, сдвига фазы нет. Получающееся выражение:
\ [i (t) = 1 + 3 \ sin (2 \ pi 100 t) \ nonumber \]
Пример \ (\ PageIndex {2} \)
Запишите выражение для формы сигнала, показанной на рисунке \ (\ PageIndex {8} \).
Рисунок \ (\ PageIndex {8} \): Форма волны для примера \ (\ PageIndex {2} \).Во-первых, положительный пик составляет 2 вольта, а размах размаха — 4 вольта.Следовательно, смещения постоянного тока нет. Вертикальный центр волны не начинается в \ (t = 0 \), поэтому должен быть фазовый сдвиг. Значение при \ (t = 0 \) составляет 1,2 вольт. Волна достигает той же амплитуды за \ (t = 2 \) миллисекунды и начинает повторять другой цикл. Следовательно, период должен составлять 2 миллисекунды. Частота обратна этому значению, и, следовательно, \ (f = 500 \) Гц.
Форма сигнала смещена влево, что указывает на положительный или опережающий фазовый сдвиг. Если мы рассмотрим второй цикл, мы увидим, что он достигает нуля вольт при 1.{\ circ} \) представляет 72/360 или 0,2 цикла. Это соответствует временной задержке (сдвинутой вправо, потому что она отрицательна) 0,2 раза по 25 \ (\ mu \) с или 5 \ (\ mu \) s.
Первоначально часто лучше построить график через серию отдельных шагов, чем пытаться нарисовать все за один присест. Сначала нарисуйте синусоидальную волну с пиковой амплитудой 5 вольт и периодом 25 \ (\ mu \) с. Теперь опустите сигнал на 3 вольта так, чтобы положительный пик составлял всего 2 вольта, а отрицательный пик — при -8 вольт.Наконец, сдвиньте только что сдвинутый сигнал вправо на 5 \ (\ mu \) с. Результат показан на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \): Форма волны для примера \ (\ PageIndex {3} \).Лабораторные измерения
В лаборатории генератор функций используется для генерации синусов и других форм волн. Эти устройства позволят точно контролировать как амплитуду, так и частоту волны, а также при необходимости добавить смещение постоянного тока. Пример показан на рисунке \ (\ PageIndex {10} \).Соответствующий измерительный инструмент — это осциллограф, или, для краткости, просто осциллограф.
Рисунок \ (\ PageIndex {10} \): Лабораторный генератор сигналов.Осциллограф, пожалуй, самый полезный и универсальный измерительный прибор в лаборатории. Обычно они имеют два или четыре входных канала, хотя возможно и больше. Каждый входной канал имеет собственную настройку чувствительности, и все каналы имеют общую временную привязку. На дисплее отображаются формы сигналов так же, как на рисунках \ (\ PageIndex {1} \) — \ (\ PageIndex {9} \).Кроме того, они могут построить график зависимости одного напряжения от другого (режим X — Y). Современные осциллографы имеют дополнительные функции, такие как автоматическое измерение частоты, амплитуды, фазового сдвига и т. Д., Измерения с помощью курсора и возможность сохранять отображаемые изображения в виде графических файлов. Пример четырехканального цифрового осциллографа показан на рисунке \ (\ PageIndex {11} \).
Рисунок \ (\ PageIndex {11} \): цифровой осциллограф.Условные обозначения на схеме
Что касается схем, то символы для источников переменного напряжения и тока показаны на рисунке \ (\ PageIndex {12} \).Обозначения полярности и направления не являются абсолютными; в конце концов, это источники переменного тока, полярность и направление которых меняются назад и вперед. Вместо этого маркеры используются для установления временной привязки, особенно в схемах, использующих несколько источников.
Рисунок \ (\ PageIndex {12} \): условные обозначения для источника переменного напряжения (слева) и источника тока (справа).Следует помнить, что отрицание источника равносильно изменению его полярности. Это было верно для источников постоянного тока и остается верным для источников переменного тока.Это показано на рисунке \ (\ PageIndex {13} \). Иногда переключение или отрицание источника делает анализ немного более очевидным или более легким для визуализации.
Рисунок \ (\ PageIndex {13} \): Эквивалентность полярности / знака.Пример \ (\ PageIndex {4} \)
Предположим, что осциллограф отображает две волны, как показано на рисунке \ (\ PageIndex {14} \). Определите фазовый сдвиг меньшего пикового сигнала 20 В (синий) относительно сигнала большего пика 25 В (красный).
Рисунок \ (\ PageIndex {14} \): формы сигналов для примера \ (\ PageIndex {4} \).Во-первых, обратите внимание, что ни одна из волн не имеет смещения постоянного тока. Если бы у одного или обоих было смещение, волна (волны) должна была бы быть смещена по вертикали, чтобы их нормальные точки пересечения нуля были на одном уровне. При измерении любой волны период составляет 1 миллисекунду. Сдвиг по времени проще всего найти в любом из нулевых переходов (есть четыре места на выбор). Задержка составляет одно небольшое отклонение или 0,1 миллисекунды, при этом меньшая волна задерживается во времени или отстает от большей волны.{\ circ}) = — \ cos (2 \ pi ft) \). Взаимосвязь этих четырех волн проиллюстрирована на рисунке \ (\ PageIndex {15} \).
Рисунок \ (\ PageIndex {15} \): Временные отношения между синусами и косинусами.Также стоит отметить, что косинусоидальная волна представляет собой первую производную или наклон синусоидальной волны. Как вы, возможно, помните из других исследований, наклон или «крутизна» линии — это отношение вертикального изменения к горизонтальному изменению, иногда называемое «подъемом над разбегом». Для напряжения это будет изменение напряжения с течением времени или \ (\ Delta V / \ Delta t \).Для плавной, непрерывно изменяющейся кривой, такой как синусоида, наклон в данной точке правильно определяется как первая производная, или в данном случае \ (dv / dt \). Чтобы визуально убедиться в этом, обратите внимание, что самая крутая часть синусоидальной волны (зеленая) находится там, где она пересекает нулевую амплитуду. Когда он пересекает ноль при движении в положительном направлении (в точке \ (t = 0 \) или \ (t = 1 \) на рисунке \ (\ PageIndex {15} \)), косинус (синий) находится на своем положительном пике. Поскольку синус пересекает ноль при движении в отрицательном направлении (при \ (t = 0,5 \)), косинус находится на своем отрицательном пике.Кроме того, синусоидальная волна плоская с нулевым наклоном на положительных и отрицательных пиках (при t = 0,25 и соответственно при t = 0,75), и в это время амплитуда косинуса также равна нулю. . Также верно, что синусоида — это наклон отрицательной косинусоидальной волны, отрицательный косинус — это наклон отрицательного синуса, а отрицательный синус — это наклон косинуса. Двигаясь в обратном направлении, мы можем сказать, что антипроизводная (неопределенный интеграл) косинусоидальной волны является синусоидальной волной, интеграл синусоидальной волны является отрицательной косинусоидальной волной и т. Д.Эти отношения окажутся наиболее полезными, когда мы обратим наше внимание на реакцию конденсаторов и катушек индуктивности в цепях переменного тока.
— Среднеквадратичное измерение
Наряду с пиком и размахом, амплитуда может быть выражена как среднеквадратичное значение (среднеквадратичное значение). Фактически, если пик или размах не указан, предполагается, что измерение является среднеквадратичным. Среднеквадратичное значение — это специальный расчет, используемый для нахождения эквивалентной мощности постоянного тока (очень часто, например, с усилителями мощности звука). Другими словами, если мы хотим найти мощность в резисторе, расчет должен выполняться с использованием значений RMS для напряжения или тока, а не пиковых или размахов.Несоблюдение этого правила приведет к ошибочным полномочиям. Это верно независимо от формы волны; будь то синусоидальная волна, треугольная волна или сложные волны музыкальных сигналов. Если напряжение указано как среднеквадратичное, его можно рассматривать при расчетах мощности так же, как и напряжение постоянного тока эквивалентной величины. Например, среднеквадратичный синусоидальный сигнал 1 В будет производить такое же рассеивание мощности и нагрев в данном резисторе, что и 1 В постоянного тока. По этой причине среднеквадратичное значение иногда называют эффективным значением (т. Е. Эффективным значением постоянного тока).
Название среднеквадратичное описывает процесс определения действующего значения. Во-первых, вспомните, что мощность пропорциональна квадрату напряжения или тока. Таким образом, нашим первым шагом будет квадрат формы входного сигнала. Конечно, форма волны является функцией времени, и ее квадрат придаст некоторую новую форму. На этом этапе нам нужно найти среднее значение этой новой формы. Причина этого проста, но не всегда очевидна. Электрические и электронные компоненты имеют массу и поэтому не нагреваются или не охлаждаются мгновенно.У них есть тепловая постоянная времени. Следовательно, они реагируют на средний ввод с течением времени. Хотя мы могли бы вычислить каким-то образом «мгновенную пиковую мощность» в определенный момент времени, она не представляет собой эквивалентную мощность постоянного тока. Как только мы получили среднее значение этого квадрата сигнала, соответствующее значение постоянного тока будет просто квадратным корнем из среднего. 2 = \ frac {1} {2} — \ frac {1} {2} \ cos (2 \ pi 2 f t) \ nonumber \]
Это выражение описывает инвертированную косинусоидальную волну на удвоенной исходной частоте и половине исходной амплитуды, движущуюся на смещении постоянного тока, равном его пиковому значению.Другими словами, отрицательный пик косинуса равен нулю, а положительный пик равен 1. Следующий шаг — найти среднее или среднее значение этого промежуточного результата. Среднее значение равно смещению 0,5. Это можно представить как область над смещением, идеально заполняющую «провал» под смещением. Последний шаг — извлечь квадратный корень из среднего. Квадратный корень 0,5 равен единице над квадратным корнем из двух, или приблизительно 0,707. Следовательно, среднеквадратичное значение составляет 0,707 пикового значения.В качестве альтернативы вы можете разделить пик на квадратный корень из двух, или примерно 1,414. Этот процесс графически показан на рисунке \ (\ PageIndex {16} \).
Рисунок \ (\ PageIndex {16} \): Процесс определения среднеквадратичного коэффициента для синусов.В сумме для синусоидального сигнала среднеквадратичное значение всегда равно пиковому значению, умноженному на 0,707. Мы также можем сказать, что среднеквадратичное значение любой синусоидальной волны равно ее пику, деленному приблизительно на 1,414. Опять же, эти отношения не обязательно будут верны для несинусоидальных волн. Подробную информацию о других распространенных формах можно найти в Приложении C.Наконец, отношение пикового значения к среднеквадратичному значению называется амплитудным коэффициентом. Это фиксированное значение для синусоидальных волн (опять же, около 1,414), но для некоторых типов аудиосигналов оно может превышать 10: 1.
Длина волны
Еще один интересный момент — скорость распространения волны. Это сильно различается. В случае света в вакууме (или, в точном приближении, электрического тока в проводе) скорость составляет около 3E8 метров в секунду (то есть 300000 км / с) или около 186000 миль в секунду.
Учитывая скорость и период, мы можем представить, как далеко друг от друга находятся пики волны. Это расстояние называется длиной волны и обозначается греческой буквой лямбда \ (\ lambda \). Длина волны равна скорости, деленной на частоту, \ (\ lambda = v / f \). Таким образом, для громкоговорителя, производящего синусоидальную частоту 100 Гц, поскольку скорость звука в воздухе составляет 344 м / с, тогда \ (\ lambda = 344 м / с \, / \, 100 \) Гц или 3,44 метра (немного более 11 футов). Обратите внимание: чем выше частота, тем короче длина волны.Также обратите внимание, что чем выше скорость, тем больше длина волны. Расчеты длины волны особенно важны в области телекоммуникаций и акустики.
Термины сигналов переменного тока — Терминология синусоидальных сигналов
Цепи переменного тока — Терминология синусоидальной формы волны:
Амплитуда:
Амплитуда синусоидальной волны — это максимальное значение (V / I), достигаемое во время положительного или отрицательного чередования.
Пиковое значение:
Обозначает максимальное значение альтернативной величины, достигаемое в положительном или отрицательном направлении.
Обозначается как V m , I m
Мгновенное значение:
Значение напряжения или тока в конкретный момент (время) известно как мгновенное значение.
Обычно обозначается маленьким алфавитом (v для напряжения и i для тока).
Цикл:
Один полный набор положительных и отрицательных значений переменной величины называется циклом.
, т.е. в течение одного цикла волна от трассы 0 до + max до 0 до -max до 0.
Период:
Время, затраченное на один цикл, называется периодом времени или периодическим временем.(Т).
Его единица — время в секундах.
Частота:
Число циклов, совершаемых за одну секунду, называется частотой переменной величины.
Обозначается буквой f.
Единица измерения — Герцы или циклы в секунду
Пиковое значение:
Максимальное значение переменной величины (это может быть ток или напряжение) во время цикла называется ее пиковым значением.
Скалярная величина:
Величина, которая имеет только величину, но не имеет направления (например, сопротивление)
Векторное количество:
Величина, которая имеет как направление, так и величину (например, сопротивление).Сила)
Фаза:
Развитие количества переменного тока через различные стадии, так называемые фазы.
Синфазно:
Когда две переменные величины достигают своего максимума и минимума одновременно, эти величины называются синфазными.
Не в фазе:
Когда две переменные величины не достигают своих максимальных и минимальных значений одновременно, они находятся в противофазе. Это также известно как разность фаз.
Фазовый угол:
Это угловое смещение между двумя переменными величинами.
Среднее значение:
Среднее арифметическое всех значений переменной величины за один цикл называется средним значением.
Для синусоидального сигнала среднее значение составляет
I Avg = (2 / π) I м = 0,637I м
Среднеквадратичное значение (RMS):
Действующее значение переменного тока определяется как тот установившийся ток, который при прохождении через заданное сопротивление в течение заданного времени выделяет такое же количество тепла, как и при прохождении переменного тока. через одно и то же сопротивление в то же время.
Для синусоидального сигнала среднеквадратичное значение (СКЗ) составляет
В СКЗ = (1√2) * В м = 0,707 В м
I СКЗ = (1√2) * I м = 0,707I м
Пик-фактор:
Он определяется как отношение пикового или максимального значения к среднеквадратичному значению. значение формы волны.
Для синусоидального сигнала = В м / 0,707 В м = 1 / 0,707 = 1,414
Форм-фактор:
Определяется как отношение r.РС. значение к среднему значению.
Форм-фактор = среднеквадратичное значение / среднее значение
Для синусоидального сигнала = 0,707 / 0,637 = 1,11
Спасибо, что прочитали основную терминологию синусоидальной волны …
Подробнее:
Микроконтроллер Viva Вопросы и ответы
Мини-проект на основе Opamp
Интервью по силовой электронике Вопросы и ответы
Электрические объективные вопросы с ответами
Пожалуйста, оставьте свои комментарии ниже …
AC vs DC: в чем разница?
Одна из основных вещей, которую должен знать энтузиаст электроники, — это разница между переменным током и постоянным током.
Нет, мы не говорим о хард-рок-группе, мы говорим о переменном и постоянном токе в отношении электричества.
Возможно, некоторые из вас это уже знают. Даже если вы какое-то время увлекались электроникой и думаете, что поняли это, я настоятельно рекомендую прочитать весь этот пост, так как есть некоторые вещи, которые могут вас удивить.
Один из самых простых способов объяснить разницу между переменным током и постоянным током — рассмотреть каждый из них отдельно и вникнуть в некоторые детали каждого из них.
С этой целью мы сначала начнем с DC, потому что это немного проще объяснить, и большинство ваших творений будет использовать его.
Электрический ток (или напряжение, поскольку напряжение и ток пропорциональны) можно разделить на постоянный ток (DC) или переменный ток (AC).
Постоянный ток течет только в одном направлении, в то время как переменный ток периодически меняет направление.
В стране электричества другое слово для обозначения направления — полярность.
Но что мы на самом деле имеем в виду?
Если бы мы построили график зависимости напряжения идеальной батареи от времени, у нас была бы прямая линия, как вы, вероятно, уже знаете.С заданным источником постоянного тока эта линия может лежать либо на положительном конце оси Y, либо на отрицательном конце, но не на обоих сразу.
Чтобы понять, что я имею в виду, взгляните на простые картинки ниже.
Рисунок 1: положительное и отрицательное напряжение постоянного тока
Красные горизонтальные линии представляют напряжение постоянного тока. Слева мы видим положительное напряжение постоянного тока (оно также могло бы представлять ток, если бы мы обозначили ток по оси Y вместо напряжения).
Обратите внимание на то, как линия лежит выше оси x (которая представляет время) и как она никогда не опустится ниже оси x — если мы предположим установившееся напряжение — даже если мы перетащим ось x на бесконечность.
Однако часть ( b ) рисунка показывает напряжение, лежащее ниже оси x, что делает его отрицательным напряжением постоянного тока.
В обеих частях линия находится либо выше, либо ниже оси x, но на самом деле никогда не пересекает ось x, даже если мы наблюдаем за этой очень захватывающей «формой волны» бесконечное количество времени.
Переменный ток и постоянный ток: сюрприз постоянного токаДля большинства из нас совершенно очевидно, что плоская горизонтальная линия на графике представляет напряжение постоянного тока.
Станьте Создателем, которым вы были рождены. Попробуйте Arduino Academy БЕСПЛАТНО!
А как насчет рисунка ниже? Это переменный ток или постоянный ток?
Рисунок 2: Переменный ток и постоянный ток: это переменный или постоянный ток?
Если вы сказали DC, вы правы.
Хотя на этом графике нет плоской горизонтальной линии, он не становится отрицательным ни в одной точке (при условии, что он остается устойчивым и периодическим).
На рисунке 2 изображен так называемый пульсирующий постоянный ток.
Пульсирующий постоянный ток периодически изменяется от некоторого минимального напряжения (в данном случае нуля) до некоторого максимального напряжения, обратно до минимума, а затем повторяется.
Под периодичностью мы подразумеваем, что форма сигнала повторяется через регулярные предсказуемые интервалы. Я избавлю вас от математического определения периодичности.
Помните, пульсирующий постоянный ток , а не , изменяется с положительного на отрицательное напряжение и наоборот. Он остается либо положительным, либо отрицательным по всей оси x, независимо от амплитуды или формы волны.
Этот тип напряжения / тока возникает на выходе некоторых зарядных устройств аккумуляторов, а также на выходе двухполупериодного мостового выпрямителя, который является частью схемы, преобразующей переменный ток в постоянный.
Помните, пульсирующий или постоянный (как плоская линия) постоянный ток — это ток, который течет только в одном направлении.На рисунке 3 ниже показана эта концепция в простой схеме.
Рисунок 3: простая схема
Используя поток электронов (подробнее о потоке электронов и обычном потоке тока см. Пост), ток будет течь от отрицательной клеммы батареи через сопротивление к положительной клемме.
Это направление не изменится, если мы не изменим полярность источника. Если мы изменим полярность батареи, перевернув ее (отрицательный конец теперь вверху), ток будет течь в направлении, противоположном стрелке.
В любом случае, ток (и напряжение) постоянный, потому что он никогда не будет менять направление вперед и назад.
Переменный ток или переменный ток — это электрический ток сначала в одном направлении в течение определенного периода времени, а затем в обратном направлении в течение определенного периода времени.
Постоянный ток может изменяться только по величине, а переменный ток может изменяться как по величине, так и по полярности.
Большинство из нас знакомы с электропитанием переменного тока, подаваемым в наши дома.
Некоторые из нас могут быть знакомы с генератором переменного тока в нашем автомобиле, который вырабатывает энергию.Генератор вырабатывает переменный ток (отсюда и название), прежде чем он выпрямляется и используется для зарядки аккумулятора и питания аксессуаров автомобиля.
Мощность в розетке в вашем доме, а также мощность, создаваемая генератором переменного тока в вашем автомобиле (до выпрямления), поступает в виде синусоидальной волны.
Синус — это сокращение от синусоидального, которое, как мы можем видеть из графика математической / тригонометрической функции синуса, описывает форму волны.
На рисунке ниже изображена типичная синусоида, которую вы можете встретить в розетке в вашем доме.
Рис. 4. Типичная синусоида переменного тока
Электропитание переменного тока в вашем доме имеет синусоидальную природу, потому что оно генерируется вращающимися проводниками в магнитном поле. Если мы возьмем один цикл синусоидальной волны и сложим отрицательную половину влево, мы увидим, что получившаяся форма имеет несколько круговой характер.
Под циклом мы подразумеваем одно изменение от нуля до некоторого максимального положительного значения, обратно к нулю, где оно пересекает ось x, затем вниз до некоторого минимального отрицательного значения, затем снова обратно к нулю, где цикл заканчивается.
На рисунке 4 есть маленький «x», где заканчивается первый цикл и начинается второй цикл.
Поскольку мы вращаем что-то круговыми движениями (с помощью генератора) для выработки переменного тока, неудивительно, что синусоида имеет такую форму. И поскольку в круге 360 градусов, каждый цикл синусоидальной волны также проходит через 360 градусов.
Переменный ток против постоянного тока: более подробная информация о переменном токеМы знаем, что переменный ток получил свое название, потому что он чередуется с положительного на отрицательный, но что это на самом деле означает?
В течение одного полупериода электроны текут в одном направлении.Затем они переключаются и текут в противоположном направлении в течение другого полупериода.
Рисунок 5 из Introductory DC / AC Electronics иллюстрирует это.
Рисунок 5: как движется переменный ток
В части (b) рисунка мы видим типичную синусоидальную волну. Часть (C) показывает, как движутся электроны во время положительного изменения, а часть (d) показывает, как они движутся во время отрицательного изменения.
Итак, электроны в цепи переменного тока будут двигаться вперед и назад вокруг фиксированной точки.
Для пояснения рассмотрим простую схему на рисунке 3, только там вместо батареи есть источник переменного тока.
Теперь представьте, что вы очень маленькие и можете «сидеть» в центре резистора и видеть проходящие мимо электроны.
В одно мгновение они проходят мимо вас в одном направлении, в другое мгновение — в противоположном.
Фактически, если вы посчитаете количество электронов, которые проскальзывают мимо вас во время каждого изменения, вы увидите, что это не только одно и то же число в каждом направлении, но и если бы вы могли отличить каждого индивидуума от других, те же электроны будет продолжать проходить вас — сначала в одном направлении, затем в другом.
Все еще нужны разъяснения? Это фантастическое видео от Хуррама Танвира должно помочь.
На видео показаны основы работы генератора переменного тока.
Он также показывает, как электроны движутся вперед и назад вокруг фиксированной точки. Обратите внимание, что стрелка вольтметра движется вперед и назад (с 0 в качестве фиксированной точки), когда генератор вращается, создавая синусоидальную волну.
Один важный факт, связанный с переменным током, заключается в том, что он не обязательно должен быть синусоидальным.
На рисунке 6 изображены 3 других типа сигналов переменного тока вместе с синусоидальной волной.
Рисунок 6: другие типы сигналов переменного тока
Прямоугольная волна должна выглядеть знакомо; вы увидите похожие волны в цифровых схемах. Треугольные волны хороши для тестирования определенных типов устройств, например некоторых усилителей. Также часто возникают сложные волны. Они могут быть, а могут и не быть желательными, в зависимости от обстоятельств.
Например, синусоидальная волна с введенным в нее шумом может выглядеть как сложная волна на рисунке выше.Или радиосигнал AM может принимать аналогичную форму. Одно желательно, а другое — нет.
Независимо от формы, все они имеют одну общую черту: в течение некоторого времени они являются положительными, а затем отрицательными.
Я знаю, что это слово на букву «м» заставляет некоторых из вас прямо сейчас стонать, в то время как другие радуются, но я обещаю — все будет не так уж плохо.
Математическое описание типичной (непульсирующей) формы сигнала постоянного тока очень просто:
В (t) = В
Где t — время.
Другими словами, это плоская горизонтальная линия, а V — это напряжение, которое остается постоянным во времени (поэтому график представляет собой горизонтальную линию).
Описание типичной формы сигнала переменного тока зависит от формы, но для простоты мы будем предполагать синусоиду.
Математически синусоида переменного тока технически описывается приведенным ниже уравнением.
v (t) = V sin (ωt + φ)
Где ω = 2πf.
Это уравнение может быть более знакомо, если вы инженер или электронщик.
Омега в нижнем регистре (ω) — это частота в радианах, а не в герцах. Поскольку большинство любителей не слишком хорошо знакомы с радианами, уравнение можно изменить в более знакомую форму.
v (t) = V sin (2πft + φ)
Ниже приводится подробное описание того, что означает каждая часть этого уравнения.
t представляет время.
v (t) — это функция того, как напряжение изменяется или изменяется со временем.Другими словами, v (t) изменяется со временем. Текст справа от знака равенства описывает, как выглядит это изменение.
V — амплитуда синусоиды.
2 π — это константа, используемая для преобразования радианов, то есть угловой частоты (радиан в секунду) в герцы, единицы, с которыми вы, вероятно, более знакомы.
f — частота в герцах или циклах в секунду.В цепи 60 Гц один цикл занимает 1/60 секунды (это период волны , который описывает, как долго длится один цикл. В общем, период T = 1 / f, поэтому один цикл 60 Гц мощность длится около 17 мс). И наоборот, в цепи 60 Гц есть 60 циклов в одной секунде.
Φ — фаза волны. Это мера того, насколько волна смещена относительно времени и находится где-то между 0 и 360 градусами. Когда синусоида сдвигается на 360 градусов, кажется, что сдвига никогда не было.Волна такая же, потому что круг составляет 360 градусов. Другими словами, если бы я нарисовал круг с помощью циркуля, как только я повернул его на 360 градусов, круг замкнется и снова начнется с 0 градусов.
Вам может быть интересно, как это сочетается с напряжением 120 В, поступающим из розетки в вашем доме.
В США мощность переменного тока имеет пиковую амплитуду 170 В (120 В — среднеквадратичное значение) и частоту 60 Гц. Мы предполагаем отсутствие фазового сдвига.
С этой информацией мы можем записать
v (t) = 170 sin (2π60t)
, чтобы математически описать напряжение, исходящее от стены.
Не пытайтесь это сделать, но если бы вы увидели мощность переменного тока в своем доме на осциллографе, вы бы увидели синусоидальную волну 60 Гц с пиковой амплитудой 170 В.
Если мы изобразим это уравнение на графике Графический калькулятор или компьютер покажет то же самое — прицела не требуется.
Большинство моих гаджетов используют постоянный ток. Почему электроэнергетическая компания поставляет переменный ток?Если у вас есть опыт работы в электронике, вы, вероятно, знаете ответ. Если вы новичок, это может быть неочевидно.
Большинство вещей, которые подключаются к розеткам в вашем доме, преобразуют подающий переменный ток в постоянный ток. Сюда входит ваш телевизор, компьютер, DVD-плеер, Wi-Fi роутер и многое другое.
Есть несколько веских причин, по которым энергетическая компания поставляет питание переменного тока, а не постоянного тока.
- При питании от сети переменного тока вы можете легко повышать или понижать напряжение с помощью трансформатора. То же самое с DC сделать сложнее. Это позволяет сети использовать высокое напряжение и более низкий ток, что более эффективно. У проводов есть сопротивление, которое становится значительным, если они растянуты на много миль.Помните, Power = I 2 Чем больше ток, тем больше тепла теряется в сопротивлении всех этих проводов. Это потраченные зря деньги. Таким образом, вместо высокого тока они используют высокое напряжение (при сохранении низкого тока), которое позже можно легко уменьшить.
- Преобразовать переменный ток в постоянный намного проще, чем преобразовать постоянный ток в переменный.
- Генераторы, которые использует энергетическая компания, работают путем вращения проводников в магнитном поле. Как мы уже знаем, это естественным образом приводит к синусоидальному выходу переменного тока.Некоторые генераторы могут выдавать постоянный ток, но они более дорогие и более сложные. Кроме того, генераторы переменного тока обычно больше, что означает, что они могут генерировать больше энергии.
В качестве интересного примечания, битва между распределением мощности переменного и постоянного тока завершилась в 1890-х годах с переменным током в качестве победителя. Вот почему мы используем его сегодня.
Однако новая технология сделала сеть постоянного тока более осуществимой и эффективной. Есть несколько небольших областей по всему миру, которые тестируют эту идею. Достаточно сказать, что пройдет некоторое время, прежде чем вся сеть будет преобразована в постоянный ток, если это вообще произойдет.
Rockin ’Out с переменным током против постоянного тока
Мир переменного и даже постоянного тока — это гораздо больше, чем мы можем охватить в одном посте.
Например, мы не говорили о переходных процессах (DC) и не обсуждали такие вещи, связанные с переменным током, как RMS (среднеквадратичное значение), пиковое значение, размах колебаний или векторов во многих (или каких-либо) деталях.
Похоже, это место для будущей публикации в блоге!
А пока прокомментируйте и поделитесь темой, которую вы хотели бы осветить в следующем посте. Это может просто появиться?
Станьте Создателем, которым вы были рождены.Попробуйте Arduino Academy БЕСПЛАТНО!
Ссылки:
- Кук, Найджел П. Введение в электронику постоянного и переменного тока, 4-е изд. Prentice Hall, 1999. Печать.
- Александр, Чарльз К. и Мэтью, Садику Н.О. Основы электрических цепей, 2-е изд. Mc Graw Hill, 2004. Печать.
Принадлежности, преобразователь постоянного тока в переменный синусоидальный, 1500 Вт с установленным на заводе реле переключения и портом связи TCP / IP Ethernet, вход 24 В постоянного тока, выход 115 В переменного тока, ICT1500-24SWTC
]>СЕРИЯ SINE WAVE
Инвертор с чистой синусоидой на 1500 Вт постоянного тока в переменный s для приложений 115 или 230 В переменного тока
Высокая производительность и надежность со стандартным мониторингом и контролем TCP / IP со встроенным статическим переключателем
Серия ICT Sine Wave — это чистый синусоидальный инвертор мощностью 1500 Вт, который преобразует 48, 24 или 12 вольт постоянного тока в сверхчистый 115 или 230 вольт переменного тока на выходе с пиковым КПД 93%.Каждая модель серии Sine Wave включает TCP / IP Ethernet для удаленного мониторинга и управления и переключатель быстрой передачи статистики, позволяющий переключаться между инвертором и сетью переменного тока или мощностью генератора. Модели на 115 В переменного тока имеют две розетки NEMA 5-15 на передней панели, а также выходные разъемы переменного тока на задней панели. Модели на 230 В переменного тока имеют выходной разъем переменного тока только на задней панели.
Благодаря возможности подключения TCP / IP Ethernet, пользователь может контролировать состояние инвертора, переменного тока и батареи, получать уведомления об аварийных сигналах по электронной почте или включать и выключать питание выходов для перезагрузки подключенных нагрузок переменного тока.Доступ с тонкого клиента осуществляется через безопасное веб-соединение. SNMP также поддерживается для интеграции в систему управления сетью.
Серия Sine Wave разработана и произведена в Северной Америке компанией ICT для обеспечения высочайшего контроля качества и надежности.
Информация для заказа
| Деталь # | Рекомендуемое количество | Кол-во на полке Кол-во на заказ на поставку | Прейскурантная цена Ваша цена |
Если вы хотите разместить заказ по телефону, позвоните по номеру 1-888-WINNCOM (946-6266) (или +1 440 498 9510 для международных звонков)
Как генерируется форма волны — тригонометрия и генерация однофазного переменного тока для электриков
Если Фарадей и научил нас чему-либо, то это так: каждый раз, когда вы пропускаете проводник через магнитное поле, вы индуцируете напряжение.Если мы возьмем этот проводник, превратим его в петлю и непрерывно раскрутим через это магнитное поле, мы создадим генератор переменного тока.
Рисунок 50. Изображение генератора переменного токаЭто означает, что напряжение будет постоянно индуцироваться. Однако это не плоское линейное напряжение, как постоянный ток. Он создает колеблющееся напряжение, которое повышается и падает.
Ага, именно это я и имел в виду. Когда проводник вращается через поле, иногда он не перерезает никаких линий магнитного потока.Бывают моменты, когда он разрезает некоторые из линий магнитного потока, а будут времена, когда он разрезает максимальное количество линий потока, которое может. Это означает, что в какой-то момент во время генерации синусоидальной волны не будет генерироваться напряжение. Затем будет генерироваться некоторое напряжение, а затем будет генерироваться максимальное напряжение. Это создает эту прекрасную вещь. Синусоидальная волна.
Рисунок 51. Синусоидальная волнаЭтот волновой рисунок часто встречается в природе, включая океанские волны, звуковые волны и световые волны.Фактически, если вы возьмете дневное время суток и нанесете график с месяцами года, угадайте, что? Генерируется синусоида. Если вы хотите прочитать интересную статью о временах года и генерации синусоидальных волн, прочтите «Исчисление времен года». Разве природа не крутая? Но я отвлекся. Эта синусоида чрезвычайно важна для выработки электроэнергии. В будущих публикациях будет обсуждаться его важность и дан углубленный анализ формы волны.
В этом видео объясняется, как в генераторе переменного тока генерируется синусоида.
О, это весело, ладно. Поверьте мне. Если вы найдете этот материал интересным, его станет намного легче выучить и понять. (Отцовская лекция окончена). Если у вас есть базовое понимание этой концепции, то однофазная и трехфазная генерация должна быть несложной задачей.
Генерация синусоидальной волны.




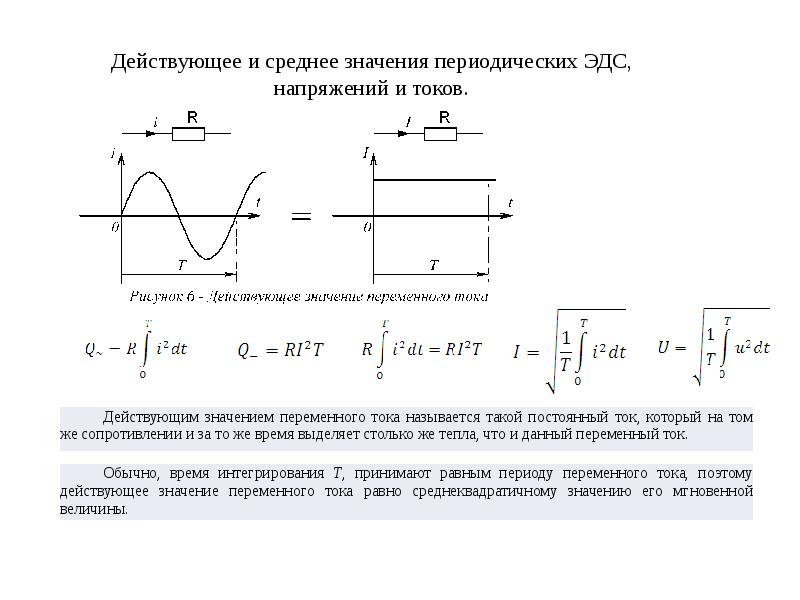 Пиковое значение.
Пиковое значение.