Мяч с массой 0,5 кг после удара, длящегося 0,02 с, приобретает скорость 10м/с. найти среднюю силу удара
На уроке не была, так что формулу не знаю, а решить надо)

Дополнен 8 лет назад

9 класс

Источник: Лицей номер 1580 (при МГТУ им. Баумана)

LaFleurNike Гуру (3656) Не за что. Тут главное представлять. Образно так, что векторный суммарный импульс некоторых точек равен векторному суммарному импульсу тех же точек при каких-либо изменениях(не учитывая диссипативных сил(сила трения)). Если векторы имеют в задаче разные направления, вводятся оси, как, впрочем, почти в любой задаче механики.

Остальные ответы

Dimasick Мастер (1358) хз, думал можно решить через F=ma, где а равно скорость в квадрате — начальная в квадрате и поделить на время, но получается большое число, поэтому незнаю…

Как определить силу удара?

С какой силой Земля притягивает яблоко, висящее на ветке? Вы скажите, с силой тяжести этого яблока. Но вот Ньютон этого не знал, когда сидел под яблоней. Несчастный первооткрыватель также не знал, с какой силой падающее яблоко приложится к его голове. На самом деле то, что Ньютон открыл свой великий закон притяжения после падения яблока, является лишь мифом, догадкой, легендой. Но не в этом суть. Иногда у нас возникают такие вопросы: «с какой силой боксёр бьёт грушу, человека?», «как её определить?», «от чего она зависит?», «как уцелеть в автомобильной аварии?» и, наконец, «как сильно яблоко ударило Ньютона?».

Яблоко, висящее на дереве, действительно притягивается к земле с силой своей тяжести. Эта сила постоянна во времени, то есть не меняется, и численно равна произведению массы яблока (например, 0,2 килограмма) на ускорение свободного падения (около 10 м/с*с).

То есть получим силу в 2 Ньютона. Именно такую силу нужно приложить, чтобы держать в руке наше яблоко.

Чтобы узнать ускорение свободного падения, можно бросить тело с высокой башни и вычислить из кинематических соображений быстроту, с которой тело набирало скорость, падая. Так и сделал в своё время Галилей. Формулу силы тяжести можно вывести и интуитивно: чем больше масса яблока и чем больше быстрота, с которой яблоко, падая, набирало скорость, тем больше его сила тяжести. Итак, с висящим яблоком разобрались. Теперь рассмотрим, с какой силой яблоко ударяется об голову Ньютона. Для наглядности перейдём к другой ситуации, а потом вернёмся к учёному.

Боксёр решил, что он натренировал свой кулак достаточно, и ударил с определённой силой по бетонной стене. В следующий миг, он усомнился в своих кулаках, испытав жгучую боль. Тогда боксёр надевает свои перчатки и снова бьёт в стену, причём с той же определённой силой. На этот раз боли он почти не почувствовал. Вы скажите, перчатки смягчили энергию удара, а может силу… Так что же именно? Перчатки не могут уменьшить энергию удара (вообще они её уменьшают, но не значительно). Они уменьшают лишь силу удара, а она по 3-ему закону нашего Ньютона как раз равна силе, с которой стена отталкивает назад кулак боксёра. Именно эта сила нам и нужна. А за счёт чего перчатки уменьшили силу удара? За счёт того, что они «размазали» или продлили удар во времени. Перчатки увеличили время контакта кулака со стеной. Без них время контакта было на несколько тысячных долей секунды меньше, чем с ними. Но этих миллисекунд хватает, чтобы время контакта в перчатках было больше времени контакта без них в несколько раз. Пусть в 5 раз. Тогда в 5 раз слабее ударит по стене боксёр и в 5 раз меньше боли при этом испытает. Естественно, я говорю о средней силе контакта, ведь на самом деле силу удара сначала увеличивается, потом уменьшается. Выведем интуитивно формулу для вычисления силы удара. Чем больше скорость, с которой двигался кулак до столкновения, чем больше его масса и чем меньше время контакта его со стеной, тем больше будет среднее значение силы, с которой кулак ударяется о стену. Только что мы с вами вывели 2-ой закон Ньютона в общем виде.  Эта  формула выглядит так:

в числителе стоит разница между скоростью кулака до удара и после него. В нашем примере кулак потом остановился, значит, скорость V₂ будет равна нулю. Из нашей формулы видно, что в бетонную стену бить больнее, чем в деревянную (ведь у деревянной стены время контакта больше, следовательно, знаменатель дроби больше и поэтому сила отдачи меньше), и что не следует бегать босиком по бетонному полу (ведь в этом случае нагрузка на коленный сустав в несколько раз выше, чем в случае, когда бегаешь по деревянному полу в обуви). Предостерегу: будете бегать босиком по бетону или кирпичу – износите свой коленный сустав и начнутся проблемы. Даже в тапках этого делать не следует. Лучше обувь с толстой подошвой. Это я заявляю вам из собственного жизненного опыта.

Возвращаясь к Ньютону и яблоку, оценим силу удара последнего. Падая с высота 3 метра, яблоко будет иметь скорость до удара порядка 8 метров в секунду. Пусть после удара оно отлетит в обратном направлении со скорость 2 метра в секунду (со знаком «–» раз в обратном направлении). И пусть время контакта – 0,004 секунды, то есть 4 миллисекунды. Это время можно измерять с помощью высокоскоростной камеры. Тогда по нашей формуле сила удара яблока составит 500 Ньютон, а это в 250 раз больше, чем сила притяжения яблока к Земле. Выглядит это неправдоподобно. Кажется, такая сила просто раздавит несчастного учёного. Но приняв тот факт, что сила эта действует на его голову лишь доли секунды, сказанное становится более реалистичным. Из всего этого можно сделать вывод: не сидите под яблонями.

Из вышесказанного следует: чем меньше время контакта в ударе, тем больше сила удара. Поэтому в автомобильных авариях везёт больше тем, кто сидит на задних сиденьях или у кого срабатывает подушка безопасности, ведь в этом случае они будут тормозить большее время и сила удара «размажется» во времени.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Репетитор-онлайн — подготовка к ЦТ

Пример 22. Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.

Решение. Мощность двигателей автомобилей определяется фор­мулой:

• для первого автомобиля

N1*=Fтяги1v1cosα,

• для второго автомобиля

N2*=Fтяги2v2cosα,

где F_тяги1 — величина силы тяги двигателя первого автомобиля; v₁ — модуль скорости первого автомобиля; F_тяги2 — величина силы тяги двигателя второго автомобиля; v₂ — модуль скорости второго автомобиля; α = 0° — угол между векторами силы тяги и скорости.

Силы, действующие на первый и второй автомобиль, направление движения и выбранная система координат показаны на рисунке.

Для определения величины силы тяги запишем второй закон Ньютона с учетом того, что автомобили движутся равноускоренно:

• для первого автомобиля

F→тяги1+m1g→+N→1=m1a→1,

или в проекциях на координатные оси —

Ox: Fтяги1=m1a1;Oy: N1−m1g=0,}

• для второго автомобиля

F→тяги2+m2g→+N→2=m2a→2,

или в проекциях на координатные оси —

Ox: Fтяги2=m2a2;Oy: N2−m2g=0,}

где m₁ — масса первого автомобиля; m₂ — масса второго автомобиля; g — модуль ускорения свободного падения; N₁ — модуль силы нормальной реакции, действующей на первый автомобиль со стороны дороги; N₂ — модуль силы нормальной реакции, действующей на второй автомобиль со стороны дороги; a₁ — модуль ускорения первого автомобиля; a₂ — модуль ускорения второго автомобиля.

Из записанных уравнений следует, что величины сил тяги первого и второго автомобиля определяются формулами:

• для первого автомобиля

F_тяги1 = m₁a₁,

• для второго автомобиля

F_тяги2 = m₂a₂.

Отношение модулей сил тяги (F_тяги1/F_тяги2) определяется отношением

Fтяги1Fтяги2=m1a1m2a2.

Движение автомобилей происходит равноускоренно без начальной скорости, поэтому их скорость с течением времени изменяется по законам:

• для первого автомобиля

v₁ = a₁t,

• для второго автомобиля

v₂ = a₂t,

где t — время.

Отношение модулей скоростей (v₁/v₂) определяется отношением величин ускорений (a₁/a₂):

v1v2=a1a2,

а отношение мощностей —

N1*N2*=Fтяги1v1cosαFтяги2v2cosα=Fтяги1Fтяги2v1v2.

Подставим в полученное отношение выражения для (F_тяги1/F_тяги2) и (v₁/v₂):

N1*N2*=m1a1m2a2a1a2=m1m2(a1a2)2.

Преобразование формулы с учетом равенства масс автомобилей (m₁ = m₂ = m) и замены (a₁/a₂ = v₁/v₂) дает искомое отношение мощностей:

N1*N2*=(v1v2)2=(2v2v2)2=22=4.

Таким образом, мощность первого автомобиля в 4 раза больше мощности второго автомобиля.

Движущая сила средняя — Справочник химика 21

    Движущая сила массопередачи, т. е. разность у—Ур) или Хр—х), постоянно меняется, поэтому для расчетов необходимо определить среднюю движущую силу процесса, которая зависит от типа массообменного процесса. [c.53]

    Заметим, что выражение (IX.8) аналогично вьфажению для средней движущей силы (средней разности температур) в процессах теплообмена оно справедливо не только при встречном движении контактирующих потоков, но и в случае прямотока. 

    Движущей силой массообмена является разность между рабочей и равновесной концентрацией (или наоборот) переходящего вещества в любой фазе. Как и для теплообмена (уравнения 35 и 36), средняя движущая сила (средняя разность концентраций) выражается как средняя логарифмическая разностей рабочей и равновесной концентраций в начале (Х — Хр и в конце (Х — Х , аппарата (в любой фазе) [c.268]

    Как было упомянуто ранее, размер ячейки илп длина волны (расстояние между центрами соседних ячеек) уменьшается с возрастанием величины возмущения. Так как последняя уменьшается со снижением движущей силы, средняя длина волны должна возрастать во времени. В табл. 6.3 показана эта зависимость для начальной концентрации кислоты в гликоле 10 вес. %. 

    С помощью общего решения [уравнение (3.61)] можно найти коэффициент массоотдачи (усредненный по длине х) через среднее логарифмическое движущей силы [среднее логарифмическое из (с,—Со) и (сг—Сзу)]  [c.235]

    Интеграл показывает, во сколько раз конечное изменение, достигнутое в фазе, больше среднего значения действовавшей в ходе этого конечного изменения движущей силы. [c.164]

    Здесь Дд , Д> — средние по высоте колонны движущие силы процесса, а индексы 1 и 2 относятся, соответственно, к месту ввода и вывода дисперсной фазы  [c.218]

    Как было показано в разделе П1. 1, вследствие упаковки элементов слоя в группы с различным коэффициентом пустот газ движется по слою с флуктуациями скорости. Такие флуктуации должны вызвать колебания в интенсивности массоотдачи по отдельным зернам. Действительно, наши опыты с определением убыли массы каждого отдельного зерна показали, что эта убыль рааглична с колебанием 4% вокруг среднего значения (в области Кеэ > 100). При обработке опытов коэффициент массоотдачи рассчитывали как усредненный по суммарной убыли массы на весь ряд. Проверкой корректности метода локального моделирования массообмена одним рядом возгоняемых шариков являются опыты с двумя рядами таких шариков, уложенными один на другой. Движущая сила переноса вещества, определяемая с учетом наличия нафталина в газе на входе в слой, для второго ряда меньше, чем для первого. Расчеты коэффициентов массоотдачи р в этих опытах показали, что в обоих рядах р практически одинаков. [c.149]

    Если целевым назначением аппарата является извлечение или насыщение по сплошной фазе, то высота колонны, необходимая для достижения заданной степени насыщения, уменьшается с уменьшением С. В отличие от извлечения из дисперсной фазы, в данном случае 2 0 при С— О, что формально следует из формулы (5.37). Физически это связано с тем, что при заданном расходе сплошной фазы уменьшению С соответствует увеличение Кд при этом возрастает не только средняя движущая сила процесса, но и поверхность контакта фаз и, следовательно, объемный коэффициент массопередачи. [c.224]

    Как подробно рассмотрено в гл. 3, в колонных аппаратах наблюдается продольное перемешивание по сплошной и дисперсной фазам. Это приводит к уменьшению средней движущей силы процесса и эффективности колонны. Таким образом, для расчета колонны необходимо знать распределение скоростей и механизм продольного перемешивания по сечению и высоте колонны. [c.231]

    В данном случае поправку на среднюю движущую силу можно найти так же, как для кожухотрубчатых теплообменников с одним ходом в межтрубном пространстве и четным числом ходов в трубах. С помощью рис. П.1, а получили вд = 0,77 тогда = [c.35]

    При решении задачи оптимального выбора теплообменника из нормализованного ряда число конкурентоспособных вариантов может быть увеличено, если снять или ослабить некоторые ограничения технологического характера. Например, можно допустить небольшое увеличение (в пределах 5—10 %) расхода охлаждающей воды без учета соответствующего увеличения затрат на нее. Это целесообразно в тех случаях, когда требуемая поверхность теплопередачи конкурентноспособного варианта несколько меньше, чем ее нормализованное значение. Так, в примере 1 требуемая поверхность для варианта IIк оказалась всего на 0,2 больше нормализованной, и он был отброшен как непригодный. Однако если допустить увеличение расхода охлаждающей воды всего на 5 %, средняя движущая сила увеличится на 0,3 град. (Л ср = 22,3 град.), коэффициент теплоотдачи к воде увеличится в (1,05)° раза [ а = 4440 Вт/(м -К)1, коэффициент теплопередачи увеличится т К = 1050 Вт/(м -К). При этом требуемая поверхность составит F = 77,8 м , и нормализованная поверхность (79,0 м ) станет достаточной с запасом А = 1,54 %. [c.41]

    Число общих единиц переноса зависит от средней движущей силы массопередачи, а последняя при прочих равных условиях определяется структурой потоков в каждой из фаз. Если движение фаз соответствует модели идеального вытеснения, то общие числа единиц переноса определяются интегральными выражениями  

Определение средней силы взаимодействия при ударе шаров равной массы

Постановка задачи. Определить среднюю силу взаимодействия шаров равной массы m₁=m₂=m при ударе. Угол начального отклонения правого шара равен . Длина подвесов l₁=l₂=l, время соударения .

Указания к решению. Импульсы сил, действующих на шары, равны

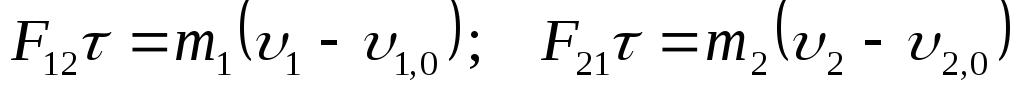(8.6)

Из (8.6) при m₁=m₂=m, ₁=_2,0=0, ₂=_1,0= получим

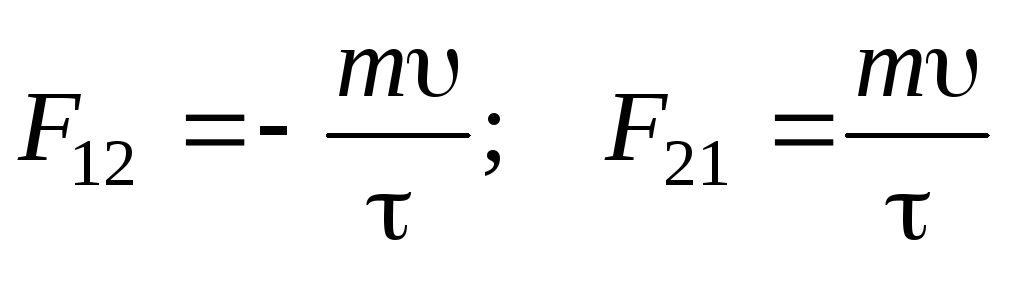(8.7)

Здесь F₁₂ и F₂₂ среднее за время удара значение сил взаимодействия между шарами.

Применим закон сохранения механической энергии при движении правого шара до удара (рис.8.1):

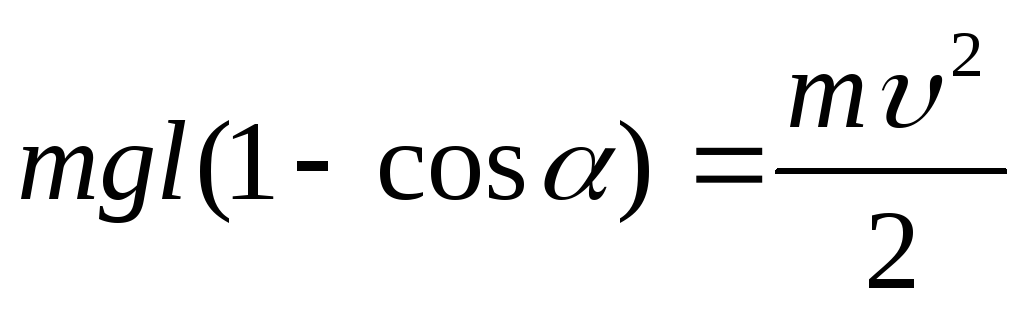(8.8)

Из (8.7) и (8.8) находим

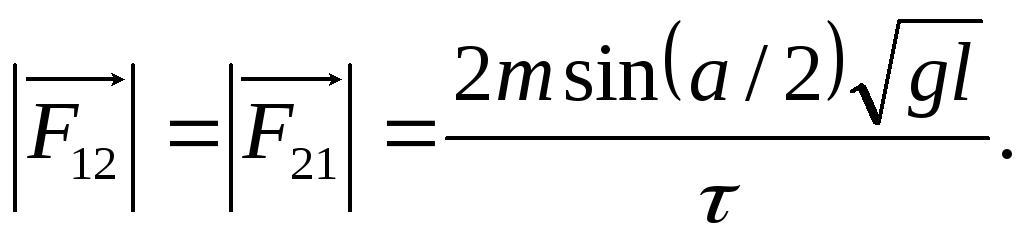(8.9)

Отметим, что реальный удар не является абсолютно упругим, поэтому часть механической энергии системыW перейдет в другие виды энергии (например, в теплоту). Доля механической энергии, перешедшей в другие виды энергии, может быть оценена по формуле

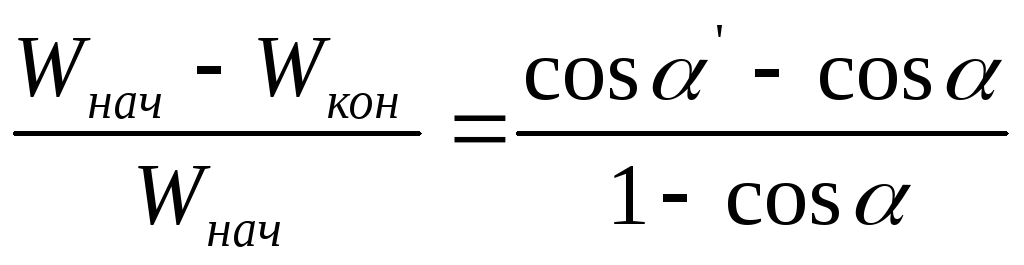(8.10)

Здесь ^’ – угол отклонения левого шара после удара.

Определение массы одного из шаров при их неупругом соударении

Постановка задачи. Два шара массами m₁ и m₂ подвешены на нитях так, что их центры находятся на одном уровне. Правый шар с известной массой m₁ (рис.8.2) отклоняют на угол ₁ и затем отпускают. При ударе шары соединяются замком и движутся вместе (осуществляется абсолютно неупругий удар). Шары при этом отклоняются на угол ₂. Определить массу левого шара.

Указание к решению. Применим закон сохранения механической энергии для определения скорости правого шара в момент соударения:

(8.11)

Здесь l – длина подвеса. Так как проекция внешних сил на ось 0_х равна нулю, можно воспользоваться законом сохранения импульса в проекции на ось 0_х. При неупругом ударе шаров получим

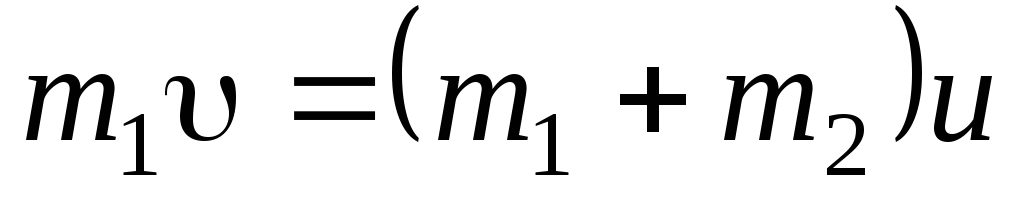(8.12)

Здесь U— скорость обоих шаров после неупругого удара.

Применим закон сохранения механической энергии при движении шаров после удара:

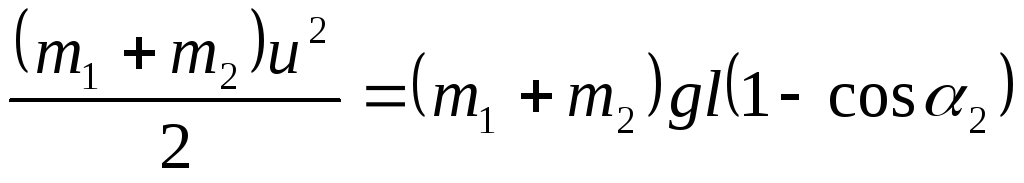(8.13)

Решая систему уравнений (8.11)-(8.13), получим соотношение для определения массы левого шара

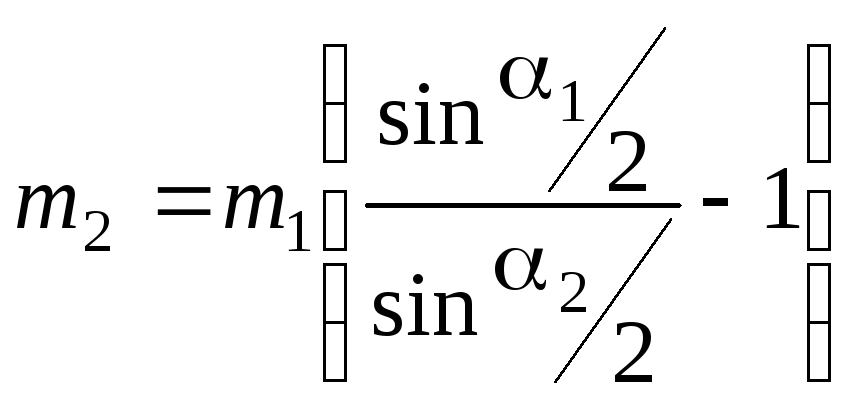(8.14)

Определение среднего момента относительно точки подвеса, создаваемого силой, возникающей при взаимодействии упругих шаров

Постановка задачи. Определить средний момент сил, возникающий при взаимодействии шаров равной массы m₁=m₂=m, равного радиуса R₁=R₂=R при упругом ударе. Угол начального отклонения правого шара равен , длины подвесов (до центров шаров) l₁=l₂=l время соударения .

Указания к решению. В момент соударения правый шар обладал моментом импульса относительно точки подвеса, равным L=I, где момент инерции I согласно теореме Гюйгенса- Штейнера равен

(2.15)

Используя (2.8), найдем

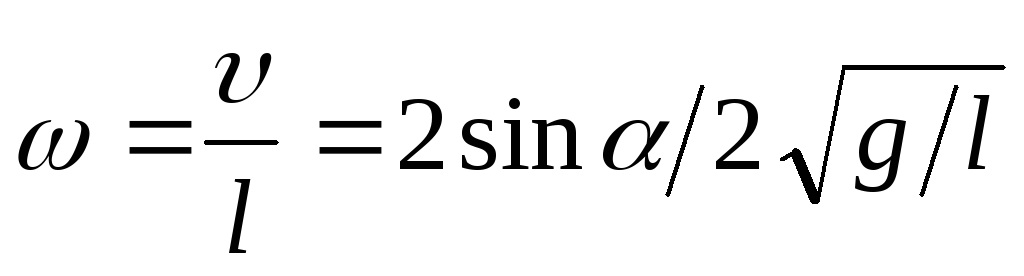(2.16)

Из основного закона динамики вращательного движения следует

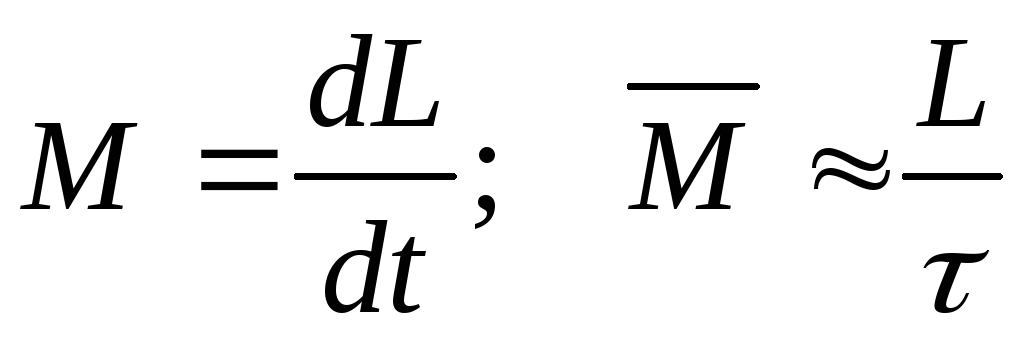(2.17)

Подставляя во второе соотношение (2.17) соотношения (2.15) и (2.16), получим среднее значение момента силы

8.3. Схема абсолютно упругого удара 8.4. Область существенного смятия при абсолютно упругом ударе двух шаров

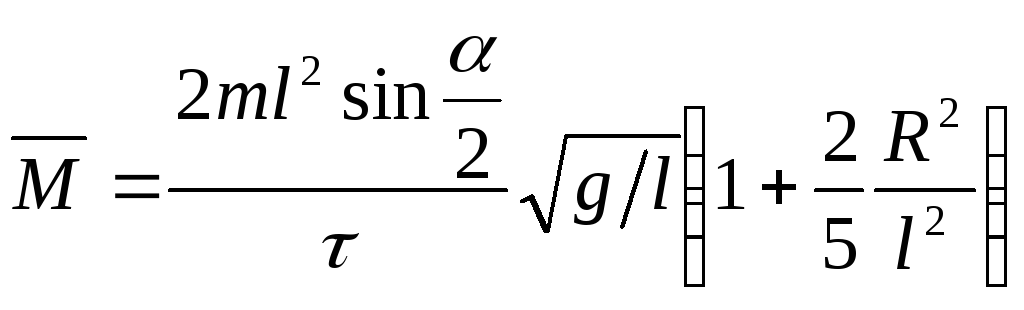
Определение средней силы взаимодействия соударяющихся шаров по радиусу площади их смятия в момент соударения

Постановка задачи. Определить среднюю длину взаимодействия шаров равной массы m₁=m₂=m, равного радиуса R_1`=R₂=R при упругом ударе. Угол начального отклонения правого шара равен , длины подвесов (до центра масс шаров) l₁=l₂=l, модули упругости материала шаров E₁=E₂=E, коэффициенты Пуассона ₁=₂=.

Указание к решению. В момент абсолютно упругого удара происходит смятие шаров за счет возникающих при ударе сил упругости (рис.8.3). Здесь R— радиус шаров, f-стрелка смятия, u=2f — сближение центров шаров в момент удара, 2а— диаметр площади смятия.

Из геометрических соображений (см. рис.8.3)

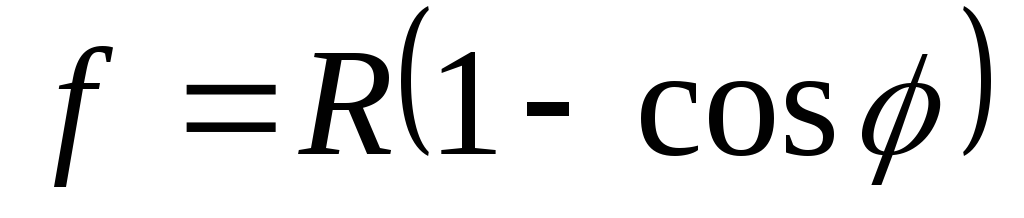(8.18)

Учитывая, что угол  мал, оставляем лишь правые два члена в разложении

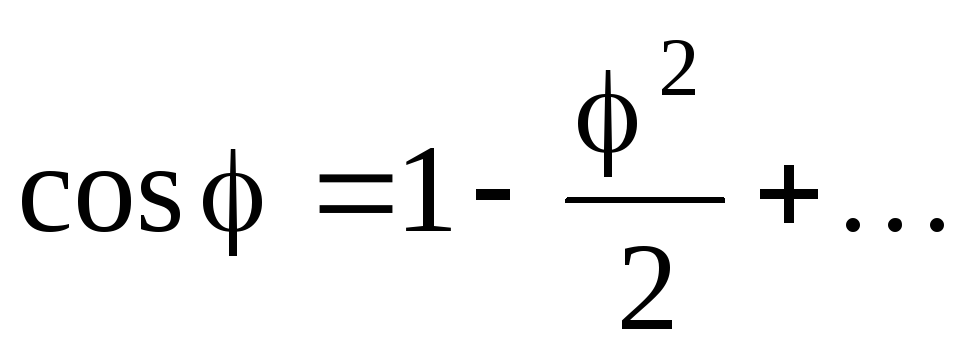
Из малости  следует также

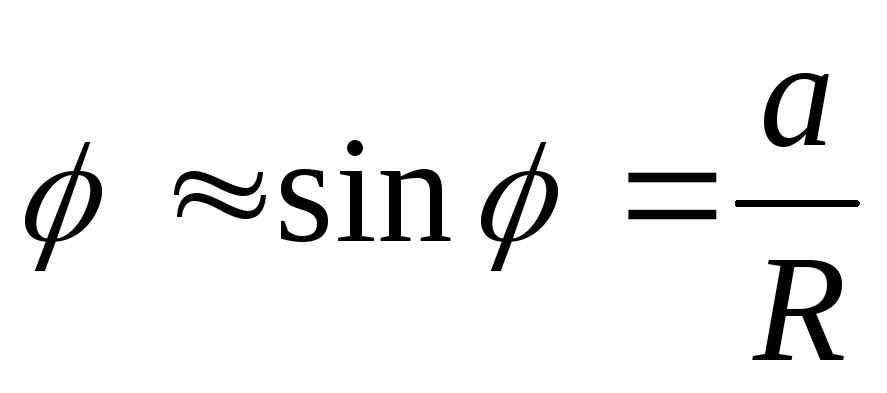
Отсюда из (8.18) получим

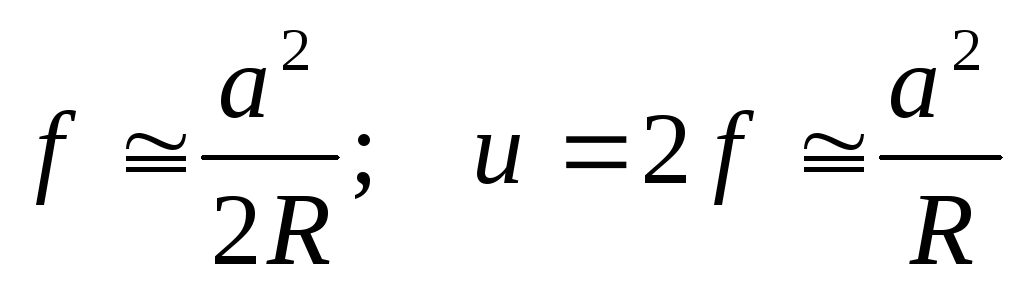(8.19)

Отметим, что соотношение (8.19) имеет смысл лишь при u<<R.

На площади смятия вследствие действия внешних сил возникает напряжение (сила, действующая на единицу площади)



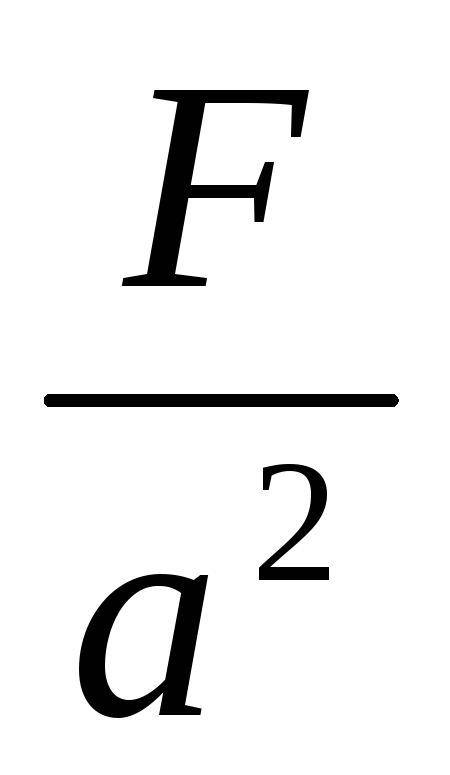
Отсюда, используя известный закон Гука = / Е, получим выражение для относительной деформации  (рис.8.4):



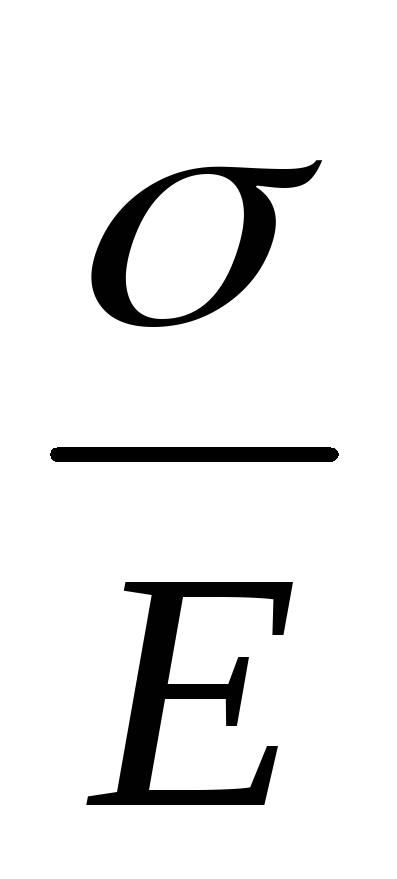
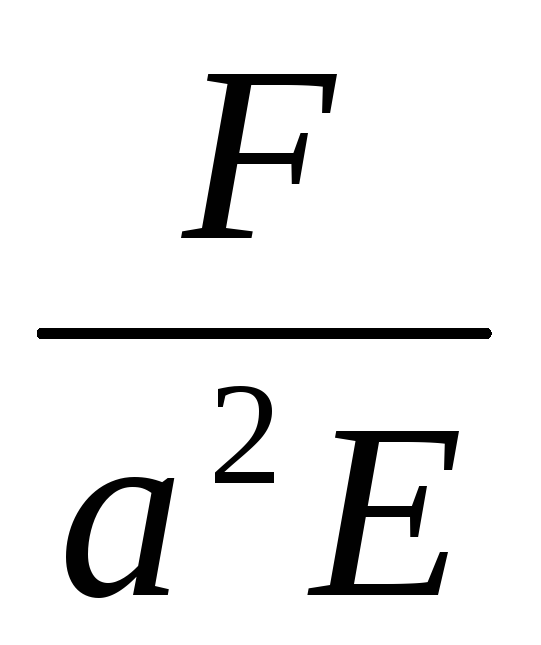
Точнее, с учетом трехмерного обжатия со стороны недеформированных частей шара



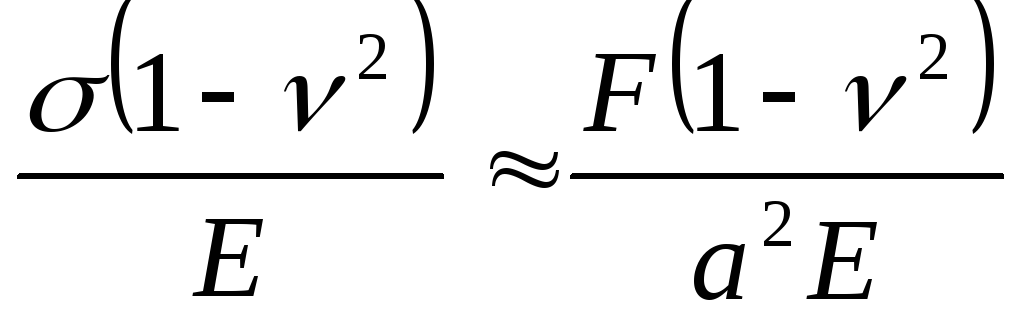
где - коэффициент Пуассона. Стрелки смятия

f a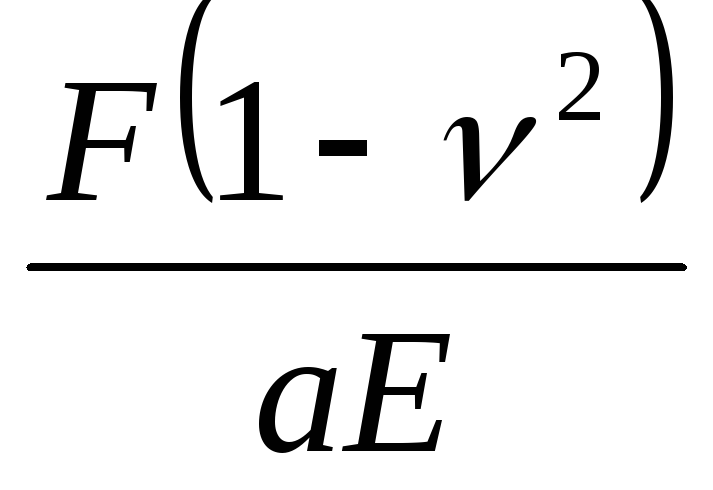. (8.20)

Используя выражение (8.19) и (8.20), определим размер радиуса смятия:

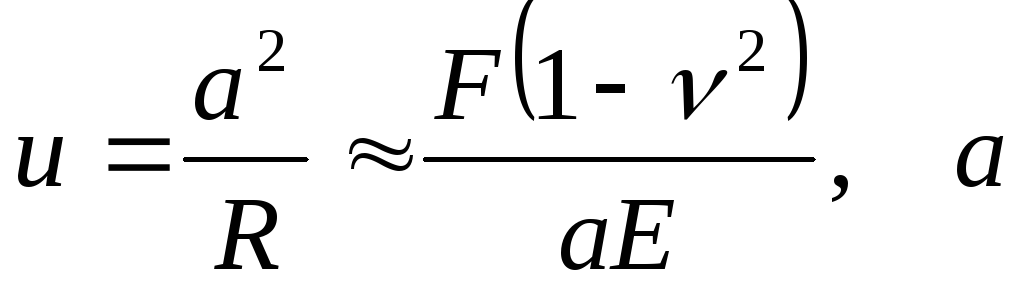
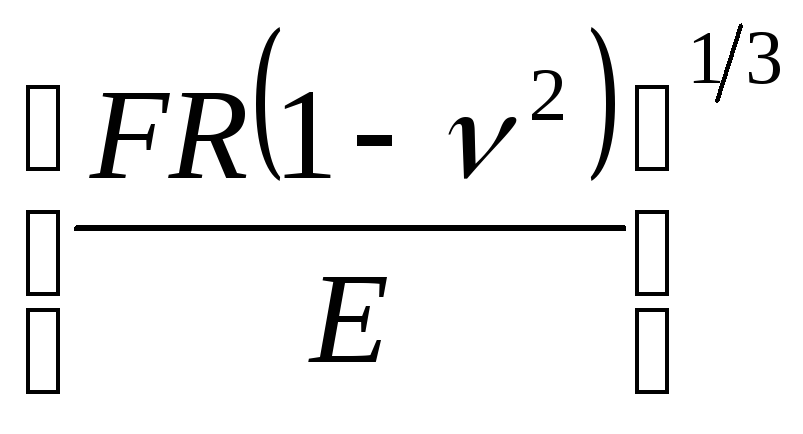. (8.21)

Заметим, что точное выражение имеет вид

.

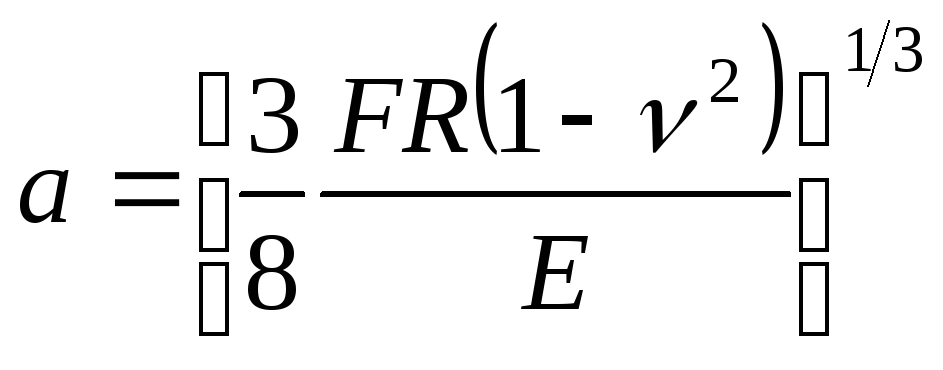Отсюда можно оценить среднюю силу взаимодействия при ударе

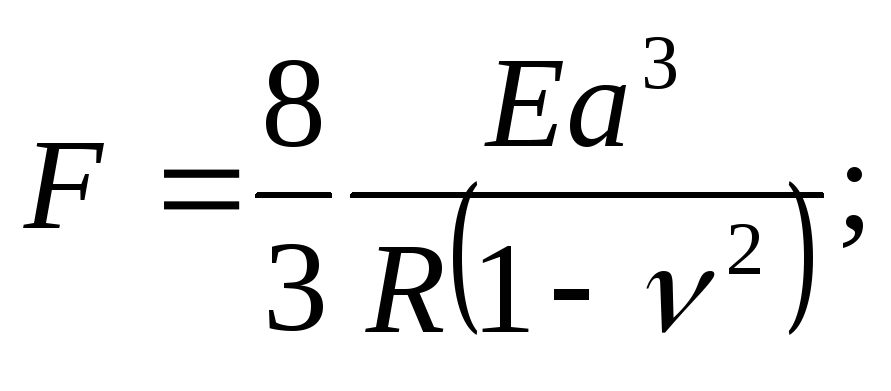Fa³ (8.22)

Указание: для получения отпечатка площади смятия между шарами следует вложить между ними папиросную бумагу с копировальной. Размеры отпечатка определяются с помощью специального микроскопа.

Проверка формулы Герца для соударяющихся упругих шаров

Постановка задачи. Применяя закон сохранения энергии в процессе соударения упругих шаров и учитывая нелинейный характер задачи (силы упругости растут с ростом радиуса смятия и с увеличением сближения шаров, Генрих Герц вывел соотношение (подробнее можно познакомиться с задачей Герца в книге[8]) между временем соударения и скоростью налетающего шара:   (1/)^1/5. Здесь — время соударения; — скорость налетающего шара.

Указания к решению. Скорость шара в момент начала соударения определяется из рис. 8.1. Задача решается с использованием закона сохранения энергии. Пусть в первый момент соприкосновения шаров механическая энергия 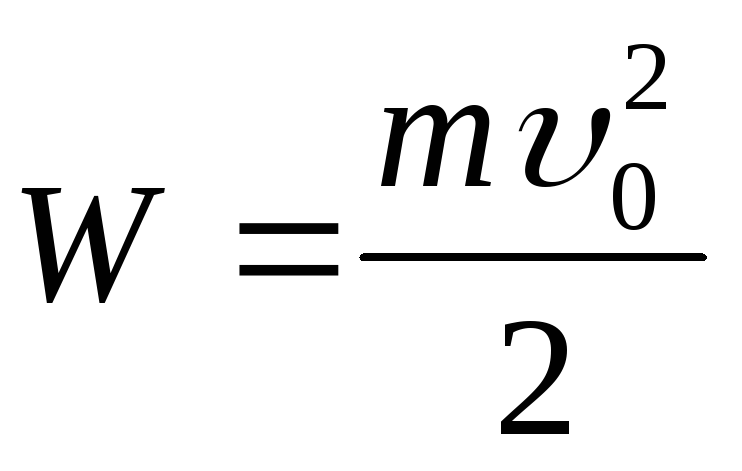. Тогда по мере взаимодействия и сближения шаров растет потенциальная энергия взаимодействия, а кинетическая энергия движущегося шара убывает. Из закона сохранения механической энергии имеем

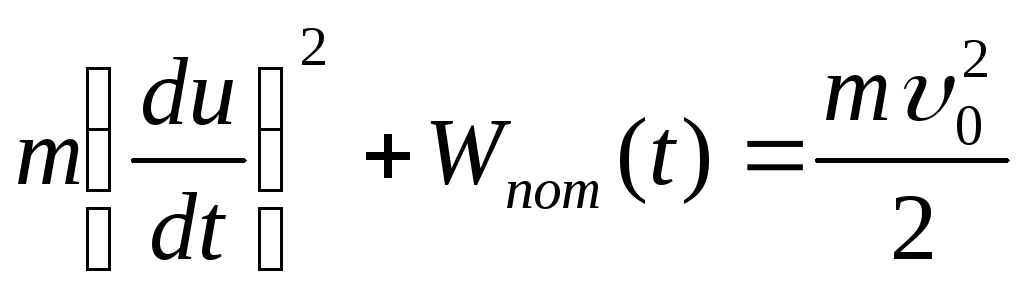(8.23)

Зависимость силы упругости от сближения шаров u получаем из (2.21)

F(-u3/2).

Из известного соотношения между потенциальной энергией и силой упругости

получим

W_потu^5/2; W_пот=ku^5/2. (8.24)

Здесь коэффициент пропорциональности k зависит от радиуса шаров и свойств материала. Из (8.23) и (8.24) получим уравнение

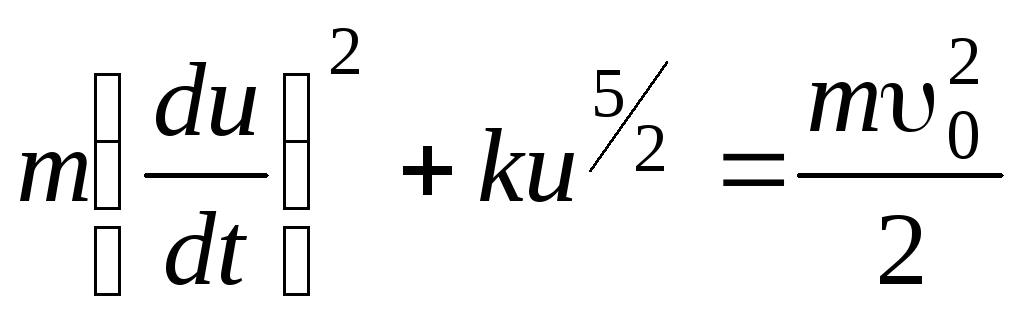(8.25)

Максимальное сближение шаров достигается при du/dt0. Решив уравнение (8.25), определим время , в течение которого длится соударение (при этом u меняется от 0 до u_mas и обратно). Хотя уравнение (8.25) легко решается разделением переменных, закон Герца запишем без вывода

.

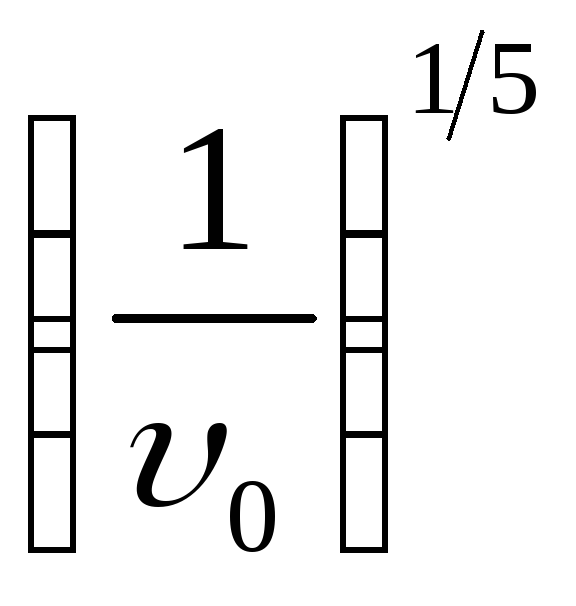Здесь, как и ранее, коэффициент пропорциональности зависит от масс и размеров шаров, свойств материала. Для проверки закона Герца следует построить график, где по оси абсцисс отложить ₀, а по оси ординат произведение ²₀.

Указание: при малых углах  возможна замена sin. Отметим, что  надо рассчитать в радианах.

Какая средняя сила удара рукой у человека?

Занимался восточными единоборставми скажу что максимальная сила удара боксера до 1000 кг/д, средняя в момент пиковой точки удара при этом может быть значительно ниже все зависет от уровня подготовки и тренированости, не трненированый человек, то удар его будет не более 100 гк/д

Всё зависит от массы тела и правильности выполнения удара!

У среднего ненатренированного мужчины она равна его весу

Что за бред вы несете? Какие 1000? Какие 560кг? Если вы далеки от этого, то лучше молчите, тайсон бил 800 кг, рекорд России армреслер 1100 кг, это бешшагные цифры, а вы говорите что это средний! В среднем не тренерованный человек окола 150 кг, боксеры в среднем 350!

У боксеров не столько сила удара, сколько выносливость играет роль, в Муай-Тай числа куда больше. Кстати 950-1000кг вполне реальные цифры, тот же упомянутый Тайсон не является показателем. У тяжеловесов довольно часто 840-870+ циферки бывают, причем даже на областных, а не чемпионов мира. У меня 197 рост, 92 вес, я правша но удар левый отрабатывал, так проще защиту пробить и бью 362 кг боковым с левой руки, ногой с хай-кика 441кг, но я и не профессиональный боец, скорее даже любитель — так что делайте выводы на сколько больше можно получить от профи.

посчитайте динамику удара по формуле F=M*A. А все эти высказывания про тонны…. Если человеку на голову статично на лицо по горизонтали положить груз массой 100 кг, он получит травму шеи, не говоря уже о тонне. А в ринге все бьют на максимальной мощности и никто пока шею не сломал. Все идет в сравнении, в сопоставлении с наукой.

Костя Дзю сила удара 500 кг

Хех может Тайсон весил больше??? Видноже как Тайсон дерется чего тут спорить то, он же огромный не никаких доказательств что, у когото 1100!!!кг удар. или 150,200 и тд вообще все акселерометры разные по величине и по весу может из-за этого только и удар получился сильным!? Так что нет доказательств и нет точных акселеметров и как там…

Сила удара зависит от массы + скорости + площади удара, вешу 65-66 кг. немного тренированный. При правильной технике прямым ударом удавалось выдавать 600-650 кг. Тут дело как говорится не в определенной характеристике, человек может весить 150кг но он например медленный и это смягчит удар, дело в совокупности характеристик которые и образуют силу удара.

У меня 310 кг тренированный 5 лет. 900 кг они бред несут это невозможно. акселерометры н правильно измеряют…

Ударніе показатели измерили показівают: человек низкой тренированности 342кг. Человек средней натренированности 401кг. Человек более чем 1 года 450 кг. Человек вісокого стиля (натренированности) — максимальная сила удара не привішает более чем 655 кг удара

Не тренированные люди ударяли только 90-10-200-332 кг. Все зависит от многих факторов например жесткая туловище, пресс, тяжелая рука

У моего друга 763 кг удар. Он занимался боксом, муай тай, карате рукопашный бой, борьба учился там в такой спец школе. и тренировал все тело начиная с шеи заканчивая до ног. все укреплял, набивал тренировал выносливость, силу удара. Шею межпальцы эспандером.

400 кг весом 75-90 кг

БРЕД! какие низкой тренированности 342кг. Человек средней натренированности 401кг. если ты 200 кг выбиваешь прямым, ты просто монстр !

У брюса ли было удар рукой 1700 килограмм

у обычного человека, 70-85 кг удар до 130-150, это еще у тех кто нет нет грушу бъют, а если пивососы, и на компе танчики режут то это до 90кг. а у тайсона на пике карьеры 1125кг кросс, на секундочку жим лежа он делал 180-200 кг. не равняйтесь с профи..

Я охреневаю.. самый неправильный ответ избран лучшим. Читайте ответ Дарика, вот он прав.

Здравствуйте. Мне проще сказать: прямой хорошо поставленный удар вот и все+масса помноженная на резкость:)

а у Чака Нориса удар 3тонны

У меня 2000000000кг я тебя убью нафиг

Тут же речь идет о идеально поставленом ударе.. а не вросто тыкнуть кулаком со всей силы

Мастер спорта по боксу в среднем 320 -380 кг .Какие тонны? Хватит пургу гнать .

лол, 16 лет, вес 73 кг, занимаюсь тайским боксом удар 305-315кг

Мне не понятно, что это за килограммы… Это какой-то бред. Реальные измерения проводятся в ньютонах… Что измеряют приборы, на соревнованиях когда в свободном стиле лупят всей площадью предплечья по мишени (мешок) и выбивают 1000+ кг. не известно. Объявляют в килограммах и все такие удар в тонну!!! В тонну зерна, кокаина, в тонну чего? К слову Тайсон бил боковые в 800 ньютонов, а мировой рекорд чуть больше 1000. Удар с ноги по мишени может быть выше, в виду большей площади ноги, и массы. Для среднестатистического неподготовленного человека хватит 150 ньютонов сконцентрированных в бороду, чтобы он упал (около 15 килограмм-силы или кгс, которые не является официальной измерительной величиной), и 300 ньютонов в голову (равносильно падению 20 кг при скорости 54 км/ч) чтобы он получил сотрясение или даже умер. Может все-таки речь идет об этой единице измерения? Боксер профессионал, вполне может влупить по измерительной мишени с силой в 0.5 кН и даже более, но производя тот же удар по более сложной поверхности тела, как например голова, сила этого же удара может оказаться другой. Так что любое измерение удара человека, весьма субъективны относительно «мишени» по которому этот человек бьет. Я думаю среднестатистическая сила удара неподготовленного мужчины массой 70 кг, составит от 90 до 250 ньютонов… Думайте сами…

Че вы тут несете? Я вешу 92кг. Не занимался бойцовскими видами спорта. Но на автомате кулаком вбил 985кг. До меня 895кг и ещё 756кг. Че за бред вы тут пишете? Какие 100кг? Какие 1000? Какие рекорды в 1100? Рекорды идут от 1500кг. До 1000 бьют спортсмены. Обычные люди бью 100-400. Быдло/гопота 300-750. За 1000 уже далеко не любители — а люди с разрядами. Мастера спорта от 1200-1300. Собрались тут мастера спорта по гуглу. Че вы там читаете, не понятно. И не надо путать удар в полную силу, технику и удары в экипировке. Тошно читать.

Десятки кг у обычного человека *допустим бьем по лицу* (качнешь головой будет больно) , сотня+ у спортсменов (отключишься или поплывешь) , сотни у оч сильных спортсменов заряженный фармой (может че то сломают тебе, может умрешь ) тонну люди уже не бьют это миф, удар белого медведя 1,5 тонны из вики брал (смерть, кем бы ты не был, хоть слон, хоть тиранозавр, хоть другой медведь ) .

Сила на подъём | Characters Force вики

Сила на подъём определяется как масса, которую персонаж может поднимать. Подталкивание, вытягивание и раздирание также считаются частью этой статистики. Она может или не может зависеть от силы на удар.

Ниже среднего: от 0 до 50 кг

Обычный человек: от 50 до 80 кг (Масса взрослого человека, или большие собаки)

Выше среднего человека: от 80 до 120 кг (Масса стиральной машины или сушильной машины)

Атлетический человек: от 120 до 227 кг (Масса взрослого Льва)

Пик человека: 227 до 454 кг (Олимпийские тяжелоатлеты)

Сверхчеловек:? (Любого уровня выше пиковой человеческой, которая по большей части неизвестны)

Класс 1: 454 до 1000 кг

Класс 5: от 1000 до 5000 кг (Способен поднимать небольшие Грузовики и т. д.)

Класс 10: 5000 до 10^4 кг (Масса взрослого слона)

Класс 25: 10^4 до 2.5х10^4 кг (Масса колокола Биг-Бена, грузовик, большой катер)

Класс 50: 2.5х10^4 до 5х10^4 кг (Масса полуприцепа грузовика)

Класс 100: 5х10^4 до 10^5 кг (Масса резервуара)

Класс К: 10 ^ 5 до 10 ^ 6 кг (Масса самого большого животного: синий кит, самый тяжелый из воздушных судов)

Класс М: 10^6 до 10^9 кг (Масса самого большого корабля, маленькие пирамиды)

Класс G: 10^9 до 10^12 кг (Масса мирового населения, крупнейших техногенных образований)

Класс T: 10^12 до 10^15 кг (Масса самой тяжелой горы)

Класс P: 10^15 до 10^18 кг (Масса мелких лун или астероидов)

Класс E: 10^18 до 10^21 кг (Масса атмосферы Земли)

Класс Z: 10^21 до 10^24 кг (Масса крупных спутников или малых планет)

Класс Y: 10^24 до 10^27 кг (Массы больших планет)

Предзвездный: 10^27 к 2 × 10^29 кг (Масса твердого объекта может доходить до гравитационного коллапса небольшой звезды)

Звездный: 2х10^29 к ? кг (Масса небольших звезд до Солнечной системы)

Мульти-звездный: (Массы нескольких звезд или солнечных систем)

Галактический: (Масса галактики)

Межгалактические: (Масса несколько галактик)

Вселенский: (Масса Вселенной или нескольких физических вселенных)

Бесконечный: (Счетно-бесконечная прочность по 3-мерных стандартов)

Неизмеримый: (За пределами трехмерных концепций массы: уровень поднятия гипермассы 4D и выше. Значение: уровень низкий 2-C до высокого 1-B.)

Не имеет значения: (За пределами всей размерности). Значение: уровень 1-A и выше.)