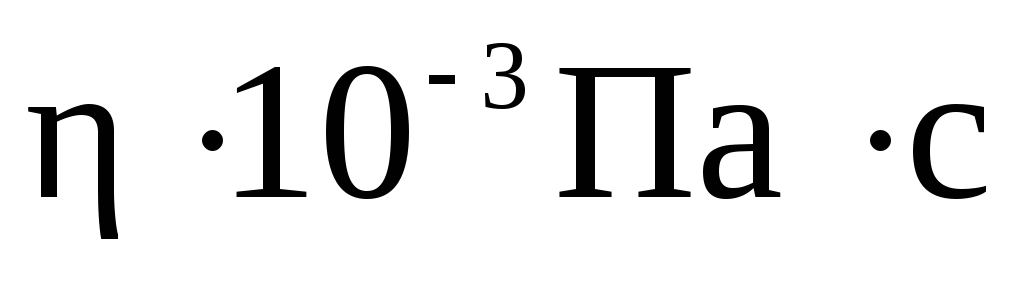Вязкое трение и сопротивление среды

Отличие вязкого трения от сухого заключается в том, что оно способно обращаться в ноль одновременно со скоростью. Даже при малой внешней силе может быть сообщена относительная скорость слоям вязкой среды.

Сила сопротивления при движении в вязкой среде

Замечание 1

Кроме сил трения при движении в жидких и газообразных средах возникают силы сопротивления среды, которые проявляются намного значительней, чем силы трения.

Поведение жидкости и газа по отношению к проявлениям сил трения не отличаются. Поэтому, приведенные ниже характеристики, относят к обоим состояниям.

Определение 1

Действие силы сопротивления, возникающей при движении тела в вязкой среде, обусловлено ее свойствами:

• отсутствие трения покоя, то есть передвижение плавающего многотонного корабля при помощи каната;
• зависимость силы сопротивления от формы движущегося тела, иначе говоря, от ее обтекаемости для уменьшения сил сопротивления;
• зависимость абсолютной величины силы сопротивления от скорости.

Сила вязкого трения

Определение 2

Существуют определенные закономерности, которым подчинены и силы трения и сопротивления среды с условным обозначением суммарной силы силой трения. Ее величина находится в зависимости от:

• формы и размеров тела;
• состояния его поверхности;
• скорости относительно среды и ее свойства, называемого вязкостью.

Для изображения зависимости силы трения от скорости тела по отношению к среде используют график рисунка 1.

Рисунок 1. График зависимости силы трения от скорости по отношению к среде

Если значение скорости мало, то сила сопротивления прямо пропорциональна относительно υ, а сила трения линейно увеличивается со скоростью:

Fтр=-k1υ (1).

Наличие минуса означает направление силы трения в противоположную сторону относительно направления скорости.

При большом значении скорости происходит переход линейного закона в квадратичный, то есть рост силы трения пропорционально квадрату скорости:

Fтр=-k2υ2 (2).

Если в воздухе уменьшается зависимость силы сопротивления от квадрата скорости, говорят о скоростях со значениями нескольких метров в секунду.

Величина коэф

Сила сопротивления Википедия

Четыре силы, действующие на самолёт

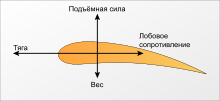
Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивление складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота). Чёрный объект не испытывает никакого сопротивления и движется по параболе, на голубой объект действует закон Стокса, на зелёный объект — закон вязкости Ньютона

Сопротивление при нулевой подъёмной силе[ | ]

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

X0=Cx0ρV

Силы сопротивления при движении твердых тел в жидкостях и газах

Мы уже упоминали о силе сопротивления воздуха. Именно из-за этой силы в некоторых случаях нельзя считать тело свободно падающим. Например, на падающий листок с дерева, действует сила сопротивления воздуха, которая сравнима с силой тяжести, поэтому, ускорение, с которым падает листок, значительно отличается от ускорения свободного падения.

Тот, кто хоть раз ездил на мотоцикле, с уверенностью может сказать, что сила сопротивления воздуха вполне ощутима. И чем больше скорость, тем больше эта сила.

То же самое можно сказать и воде: если плавно погружать тело в воду, то ее сопротивление значительно меньше, чем, если прыгнуть в нее. Заметим также, что какой-либо предмет может плыть по течению реки, не испытывая никакого сопротивления. Дело в том, что скорость этого предмета равна скорости течения реки. То есть, относительно реки его скорость равна нулю. Из этого можно заключить, что сила сопротивления среды равна нулю, если относительная скорость тела в этой среде тоже равна нулю.

Как вы знаете из бытового опыта, силы сопротивления различных сред будут зависеть не только от скорости, с которой двигается в них тело, но и от его формы и размеров. Именно, исходя из этого, люди делают лодки и корабли с острым носом, чтобы уменьшить сопротивление воды.

Вы можете провести простейший опыт: взять картонку и попробовать помахать ей из стороны в сторону сначала плашмя, а потом ребром. Очевидно, что во втором случае сила сопротивления будет в разы меньше.

Опытным путем было установлено, что для тел малых размеров, двигающихся с малыми скоростями, силу сопротивления среды можно считать прямо пропорциональной скорости тела относительно этой среды:

При больших скоростях или размерах тела, сила сопротивления становится пропорциональной квадрату относительной скорости:

.

Коэффициенты пропорциональности в этих зависимостях тоже определяются экспериментально для каждой среды.

Итак, мы выяснили, что, так или иначе, сила сопротивления среды возрастает по мере того, как возрастает скорость движения тела в этой среде. Например, чем быстрее тело падает, тем больше сопротивление воздуха. Возникает вопрос: а может ли сила сопротивления воздуха превысить силу тяжести? Такого, конечно, быть не может, и вот почему: в то время как сила сопротивления воздуха увеличивается, сила тяжести остается постоянной. Это значит, что при достаточно долгом падении в какой-то момент сила сопротивления воздуха станет равна силе тяжести. Поскольку сила тяжести будет направлена вниз, а сила сопротивления воздуха — вверх, равнодействующая сила станет равной нулю. А это значит, что тело начнет двигаться с постоянной скоростью, поскольку ускорение будет равно нулю. Эта скорость называется предельной скоростью.

Предельная скорость — это постоянная скорость, с которой начинает двигаться тело, как только сила сопротивления данной среды начинает уравновешивать силу, движущую тело в этой среде.

То же самое можно сказать о других газах и жидкостях: если сила, движущая тело в данной среде станет равной по модулю силе сопротивления, то тело начнет двигаться с постоянной скоростью.

Пожалуй, самый очевидный пример использования силы сопротивления воздуха — это парашют. Парашют имеет довольно большую площадь, поэтому, предельная скорость достигается сравнительно быстро.

Рассмотрим еще один интересный пример. В аэродинамике есть такое понятие, как подъемная сила — это сила, возникающая в результате несимметричности обтекания крыла потоком воздуха. С помощью этой силы самолет, набирая определенную скорость, взлетает. В аэродинамике, сила сопротивления воздуха называется лобовым сопротивлением. Таким образом, при разбеге самолета, тяге противостоит лобовое сопротивление, а подъемной силе, разумеется, противостоит вес самолета.

Как видно из формулы, подъемная сила зависит от скорости набегающего потока воздуха. Скорость же, в свою очередь, будет зависеть от лобового сопротивления (чем больше это сопротивление, тем больше времени потребуется самолету для разбега, прежде чем самолет взлетит).

Примеры решения задач.

Задача 1. Мотоциклист едет со скоростью 72 км/ч, и на мотоцикл действует сила трения равная 2 кН. Сила сопротивления воздуха подчиняется квадратичной зависимости с коэффициентом пропорциональности равным 0,6 кг/м. Определите силу тяги мотоцикла.

Задача 2. Определите предельную скорость капель дождя, если масса капли равна 500 мг. Сила сопротивления воздуха в данном случае прямо пропорциональна скорости, а коэффициент пропорциональности равен 0,02 кг/с.

От чего зависит сопротивление

☰

Сила тока в проводнике прямо пропорциональна напряжению на нем. Это значит, что с увеличением напряжения увеличивается и сила тока. Однако при одинаковом напряжении, но использовании разных проводников сила тока различна. Можно сказать по-другому. Если увеличивать напряжение, то хотя сила тока и будет увеличиваться, но везде по-разному, в зависимости от свойств проводника.

Зависимость силы тока от напряжения для данного конкретного проводника представляет собой сопротивление этого проводника. Оно обозначается R и находится по формуле R = U/I. То есть сопротивление определяется как отношение напряжения к силе тока. Чем больше сила тока в проводнике при данном напряжении, тем меньше его сопротивление. Чем больше напряжение при данной силе тока, тем больше сопротивление проводника.

Формулу можно переписать по отношению к силе тока: I = U/R (закон Ома). В таком случае нагляднее, что чем больше сопротивление, тем меньше сила тока.

Можно сказать, что сопротивление как бы мешает напряжению создавать большую силу тока.

Само сопротивление является характеристикой проводника. Оно не зависит от поданного на него напряжения. Если будет подано большое напряжение, то изменится сила тока, но не изменится отношение U/I, т. е. не изменится сопротивление.

От чего же зависит сопротивление проводника? Оно зависти от

• длины проводника,
• площади его поперечного сечения,
• вещества, из которого изготовлен проводник,
• температуры.

Чтобы связать вещество и его сопротивление, вводится такое понятие как удельное сопротивление вещества. Оно показывает, какое будет сопротивление в данном веществе, если проводник из него будет иметь длину 1 м и площадь поперечного сечения 1 м². Проводники такой длины и толщины, изготовленные из разных веществ, будут иметь разные сопротивления. Это связано с тем, что у каждого металла (чаще всего именно они являются проводниками) своя кристаллическая решетка, свое количество свободных электронов.

Чем меньше удельное сопротивление вещества, тем лучшим проводником электрического тока оно является. Маленьким удельным сопротивлением обладают, например, серебро, медь, алюминий; куда большее у железа, вольфрама; очень большое у различных сплавов.

Чем длиннее проводник, тем большее сопротивление он имеет. Это становится понятно, если принять во внимание, что движению электронов в металлах мешают ионы, составляющие кристаллическую решетку. Чем их больше, т. е. чем длиннее проводник, тем больше у электрона шанс замедлить свой путь.

Однако увеличение площади поперечного сечения делает как бы дорогу шире. Электронам легче течь и не сталкиваться с узлами кристаллической решетки. Поэтому чем толще проводник, тем его сопротивление меньше.

Таким образом, сопротивление прямо пропорционально зависит от удельного сопротивления (ρ) и длины (l) проводника и обратно пропорционально зависит от площади (S) его поперечного сечения. Получаем формулу сопротивления:

R = ρl/S

В этой формуле на первый взгляд не отражается зависимость сопротивления проводника от его температуры. Однако удельное сопротивление вещества меряется при определенной температуре (обычно 20 °C). Поэтому температура учитывается. Для вычислений удельные сопротивления берут из специальных таблиц.

Для металлических проводников чем больше температура, тем сопротивление больше. Это связано с тем, что при повышении температуры ионы решетки начинают сильнее колебаться и больше мешать движению электронов. Однако в электролитах (растворах, где заряд несут ионы, а не электроны) с повышением температуры сопротивление уменьшается. Здесь это связано с тем, что чем выше температура, тем больше происходит диссоциация на ионы, и они быстрее двигаются в растворе.

2.6.4.Сила вязкого трения и сопротивления среды.

Сила вязкого трениявозникает между слоями одного и того же сплошного тела (жидкости или газа). Сила вязкого трения за­висят от относительной скорости смещения отдельных слоев газа или жидкости друг относительно друга. Например, вязкое трение возникает при течении жидкости или газа по трубам со скоростью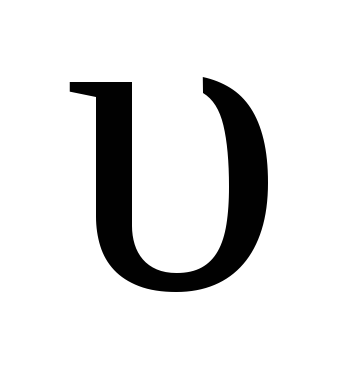(рис. 2.3).

Скорость слоев жидкости уменьшается при приближении их к стенкам трубы. Отношение разности скоростей в двух близких слоях, расположенных на расстоянии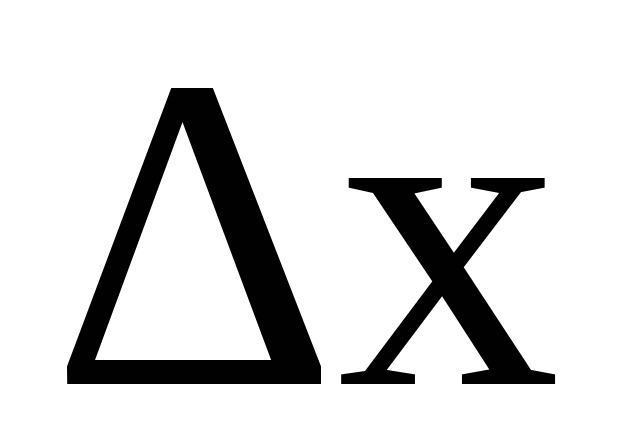, называется средним градиентом скорости.

В соответствии с уравнением Ньютона модуль средней силы вязкого трения

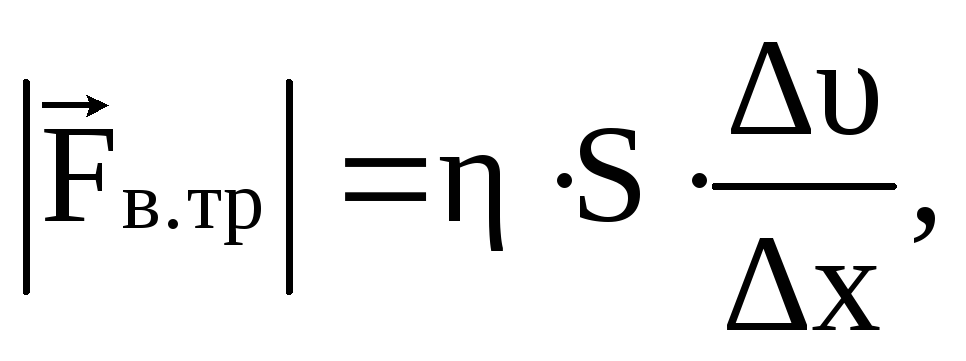(2.54)

где 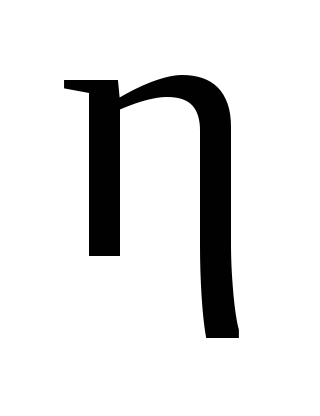–коэффициент вязкости,S– площадь взаимодействующих слоев среды, расположенных на расстоянии ∆xдруг от друга.

Коэффициент вязкости зависит от агрегатного состояния и температуры вещества.

Коэффициент вязкости

Вещество	Вода	Водяной пар	Машинное масло	Воздух
t0C	20	100	30	20
	1,0	0,013	200	0,018

Сила сопротивления 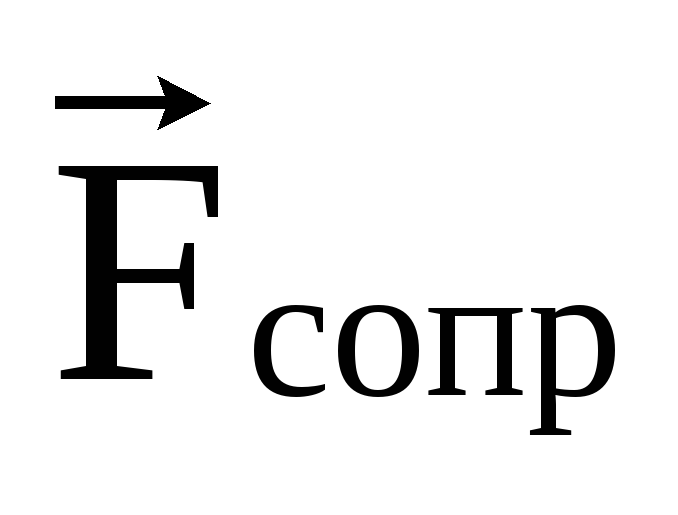возникает при движении твердых тел в жидкости или газе. Модуль силы сопротивления пропорционален плотности среды, площади поперечного сечения движущегося телаSи квадрату его скорости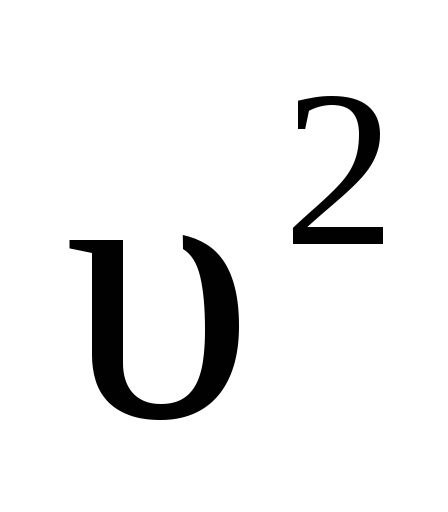

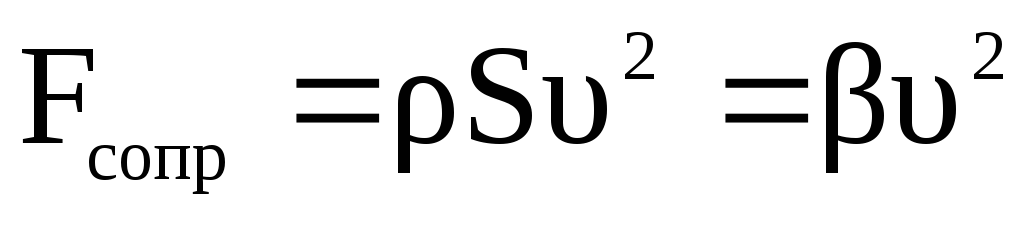, (2.55)

где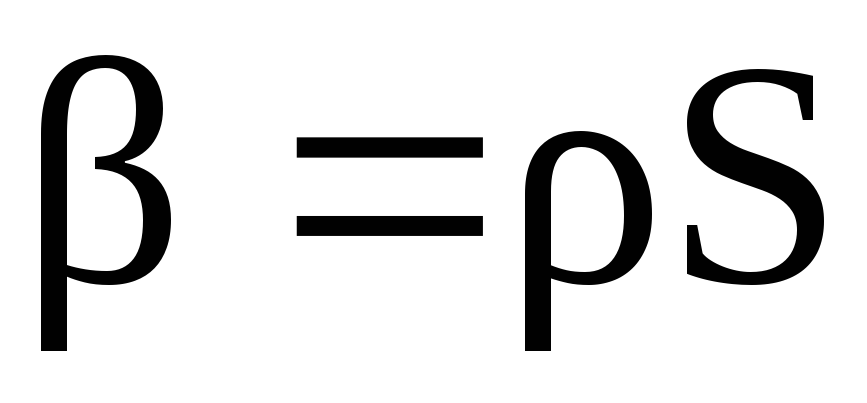[кг/м] – коэффициент сопротивления среды.

Тело, движущееся в среде испытывает действие силы вязкого трения (F_тр) и силы сопротивления (F_сопр). При небольших скоростях сила сопротивления меньше силы вязкого трения, а при больших – значительно превосходит ее (рис. 2.4).

При некотором значении скорости 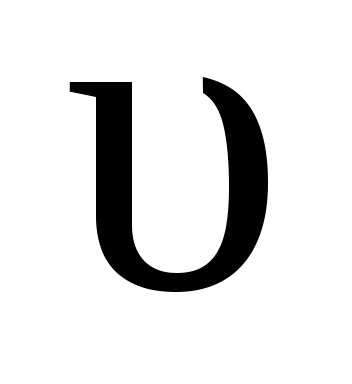силыF_триF_сопрстановятся равными по модулю.

Сила сопротивления среды зависит от формы движущегося тела. Форму тела, при которой сила сопротивления мала, называют обтекаемой. Ракетам, самолетам, автомобилям и другим машинам, движущимся с большими скоростями в воздухе или в воде, придают обтекаемую, каплеобразную форму

2.6.5.Сила упругости. Закон Гука.

П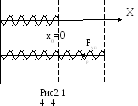ри действии на тело внешних сил, возникает упругая и неупругая деформация.

П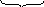

x

x₀=0

ри упругой деформации тело после прекращения действия внешних сил полностью восстанавливает свою форму и размеры. При неупругой деформации форма и размеры тела не восстанавливаются.

Упругая деформация пружины.

При растяжении пружины (рис 2.14) на величину относительно её равновесного состояния (х₀= 0) возникает упругая сила, которая возвращает пружину в прежнее положение после прекращения действия внешней силы. Модуль упругой силы, возникающей при линейном растяжении или сжатии пружины определяется законом Гука.

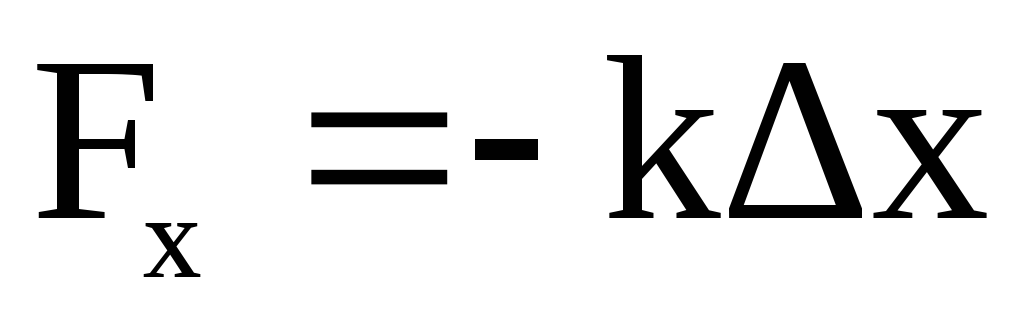, (2.56)

где 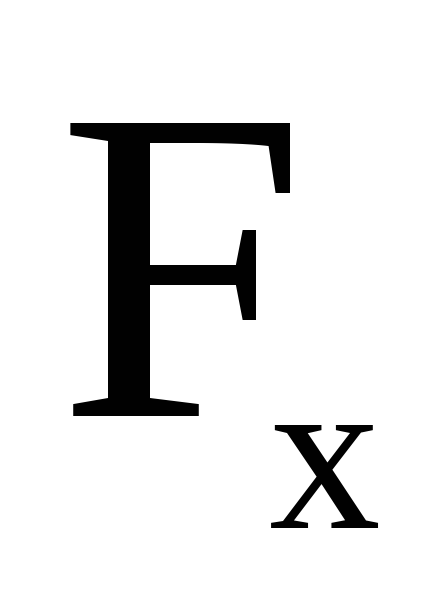– проекция силы упругости на осьx, знак минус учитывает противоположные направления силыи перемещения пружины.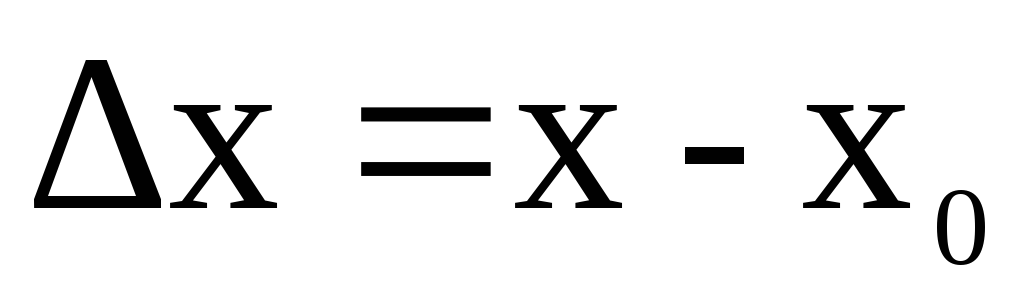

Деформация стержня

Стержень длинной l₀ и сечениемSпри действии сил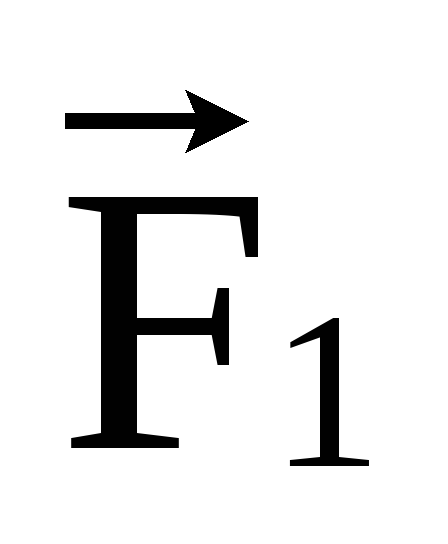иперпендикулярно его торцам в противоположных направлениях деформируется (растягивается или сжимается) (рис 2.15). Деформация стержня определяется относительной величиной

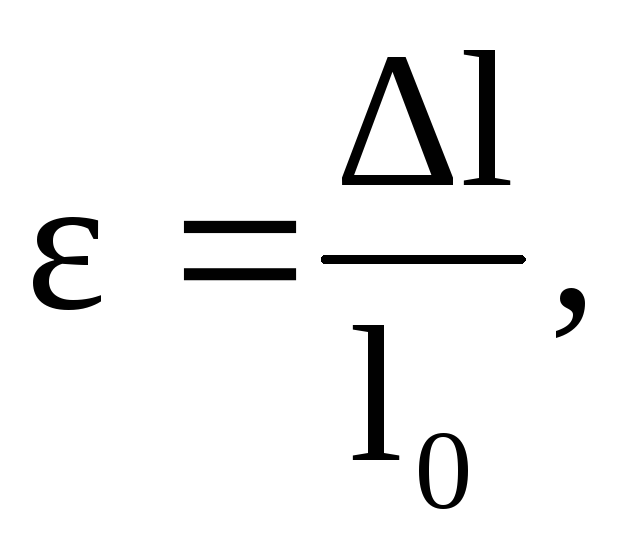(2.57)

где ∆l =l — l₀ , l—длинна стержня после деформации.

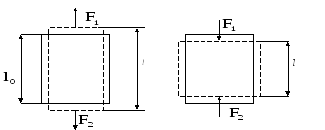
Рис. 2.15

Опыт показывает, что

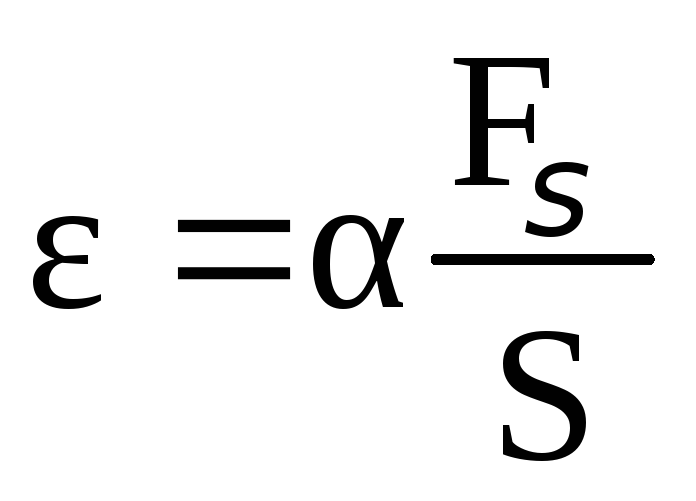, (2.58)

где α – коэффициент упругости стержня,

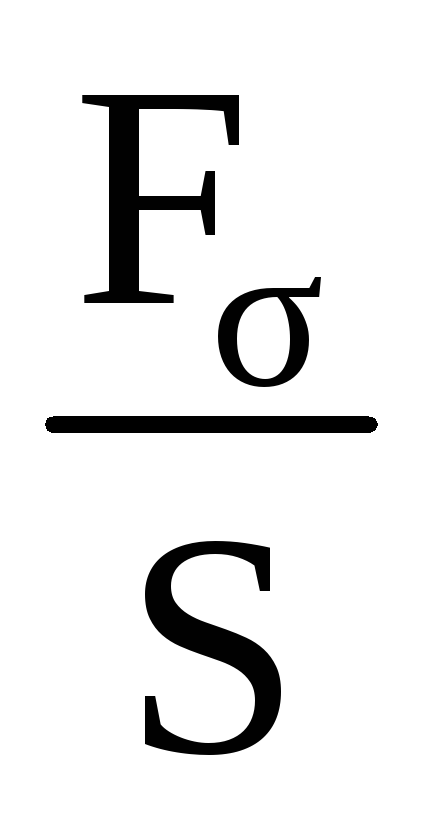=σ – нормальное напряжение, измеряемое в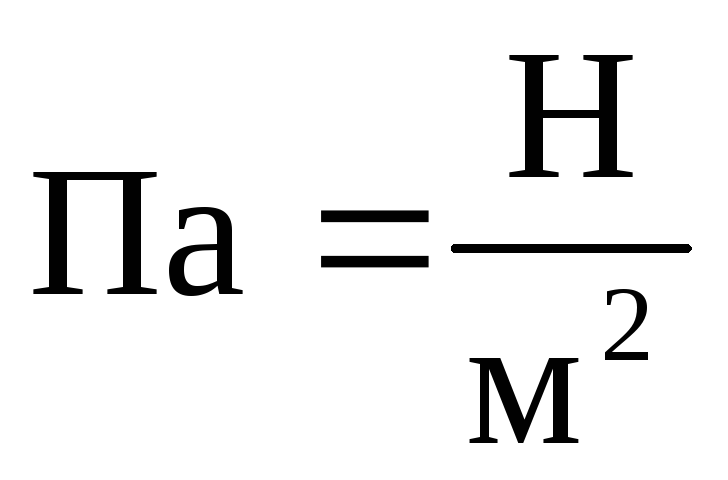(паскаль).

Наряду с коэффициентом упругости aдля характеристики упругих свойств тел при нормальных напряжениях используютмодуль ЮнгаЕ = 1/a, который, как и напряжение, измеряется в паскалях.

Относительное удлинение (сжатие) и модуль Юнга в соответствии с равенствами (2.13 и 2.14) определяется из соотношений:

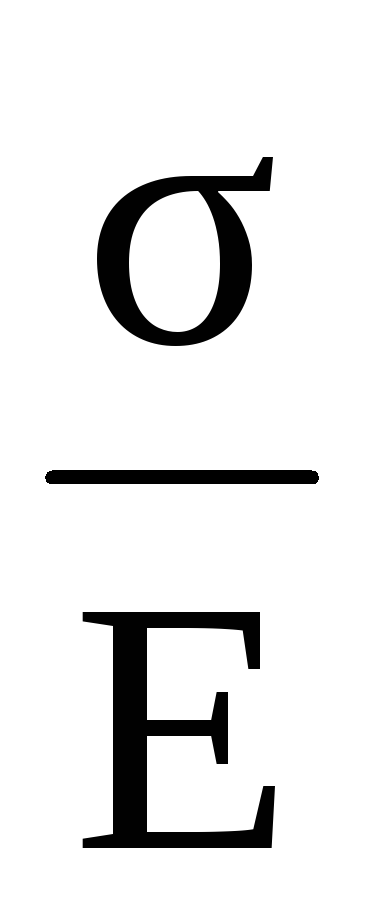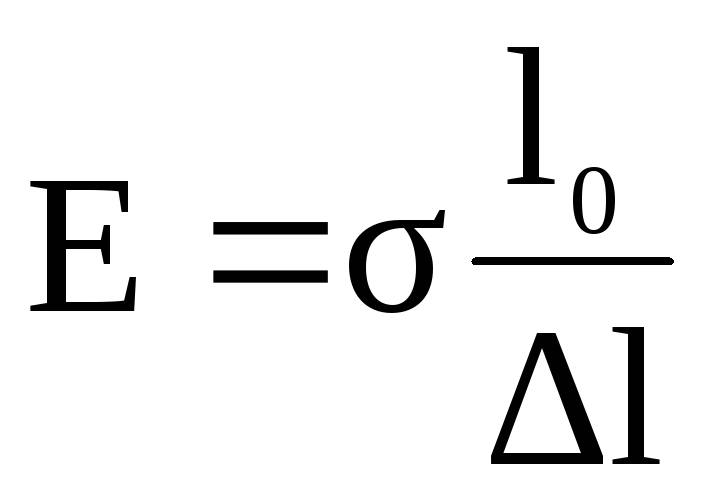,. (2.59)

Модуль Юнга равен такому нормальному напряжению, при котором деформация стержня Dlравна его первоначальной длинеl₀. В действительности при таких напряжениях происходит разрушение стержня.

Решая уравнение (2.58) относительно F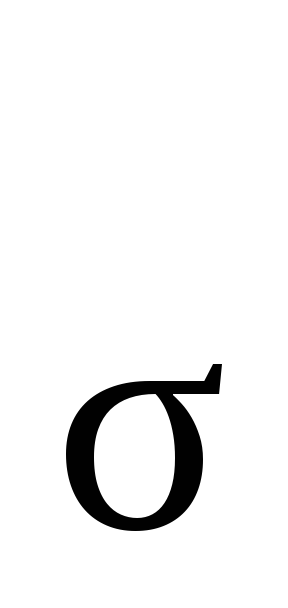, и подставляя вместоe=Dl/l₀,a= 1/Е, получим формулу для определения силы деформирующей стержень с сечениемSна величину

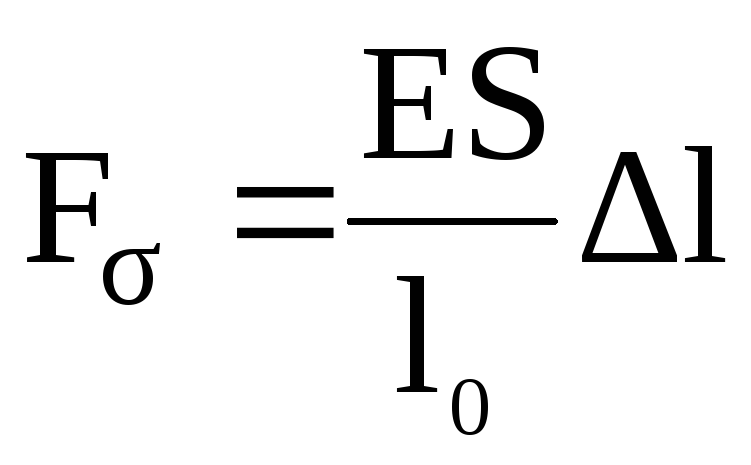, (2.60)

где 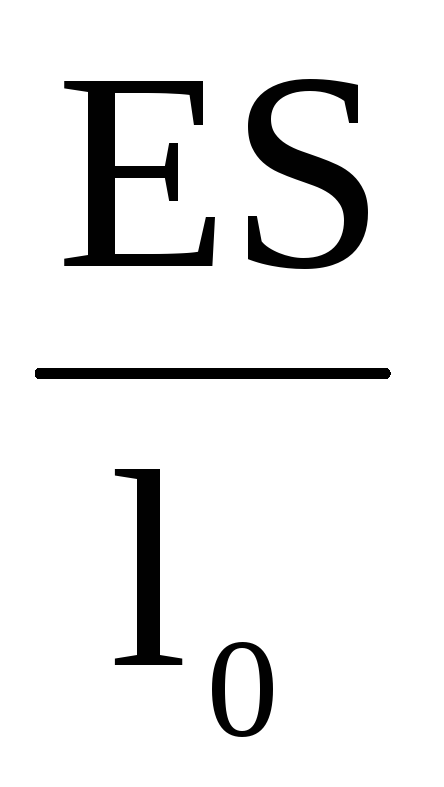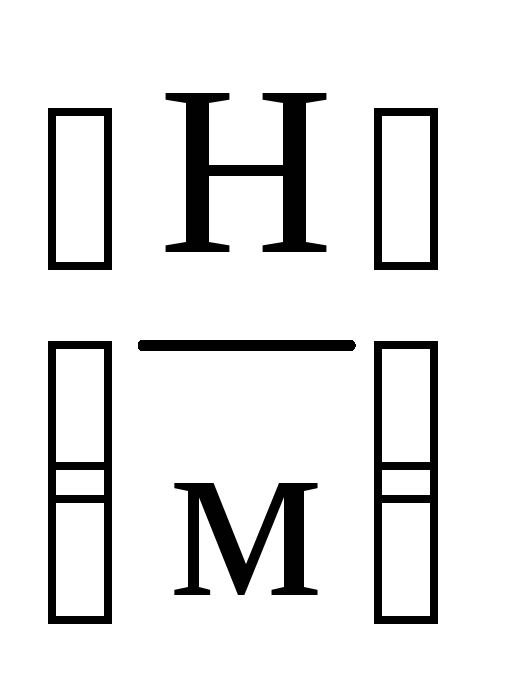– постоянный для стержня коэффициент, который в соответствии с законом Гука соответствует коэффициенту упругости стержня при его сжатии и растяжении.

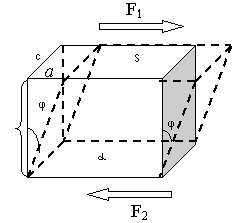
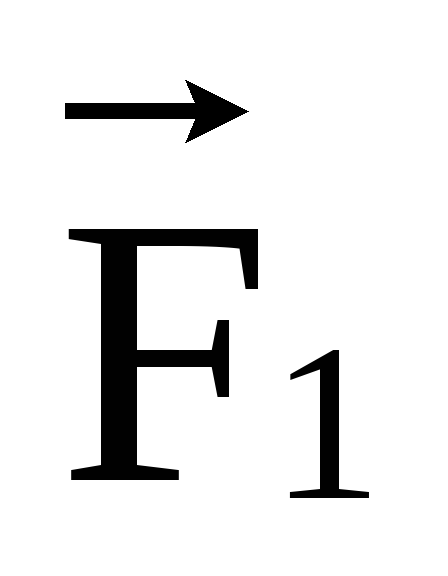
При действии на стержень касательного (тангенциального) напряжения

силы F₁ иF₂приложены параллельно противоположным граням площадьюSпрямоугольного стержня вызываютдеформацию сдвига (рис 2.16).

b

Рис. 2.16

Если действие сил равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникает тангенциальное напряжение 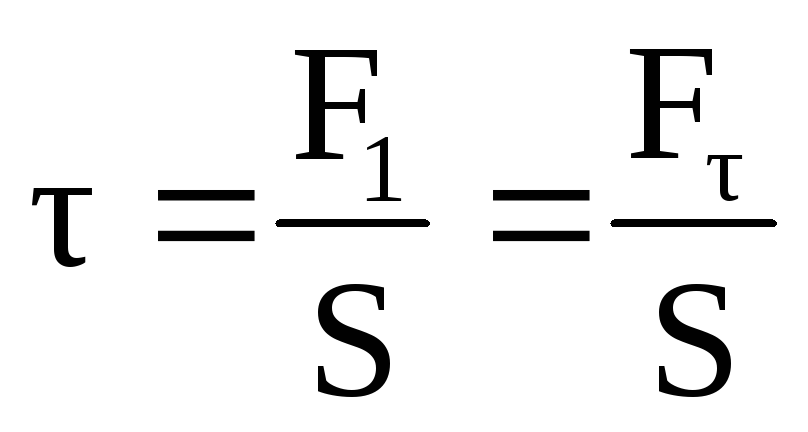. Под действием напряжений тело деформируется так, что одна грань сместиться относительно другой на некоторое расстояниеа. Если тело мысленно разбить на элементарные, параллельные рассматриваем граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.

При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, отклонится на некоторый угол φ. тангенс которого называется относительным сдвигом

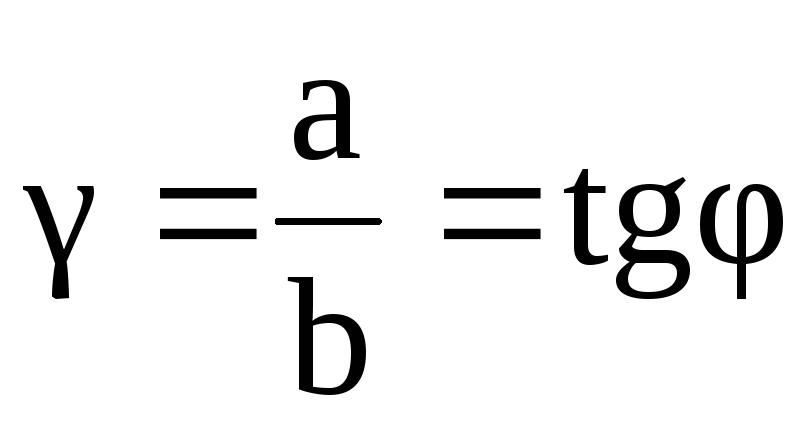, (2.61)

где b– высота грани. При упругих деформациях угол φ очень мал, поэтому можно считать, чтои.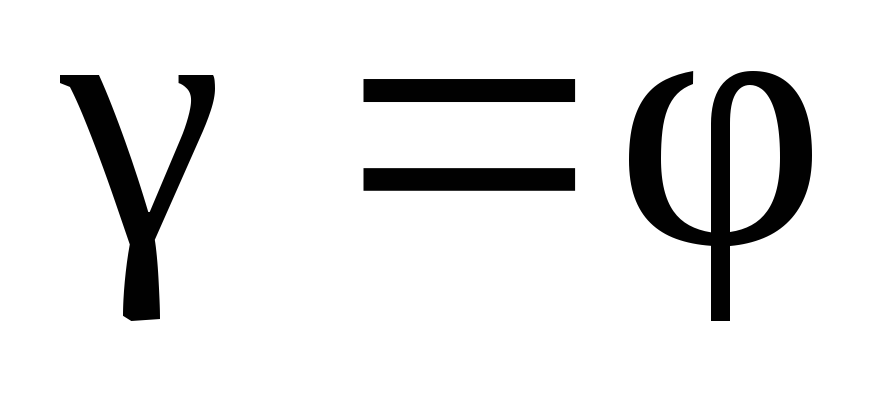

Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению

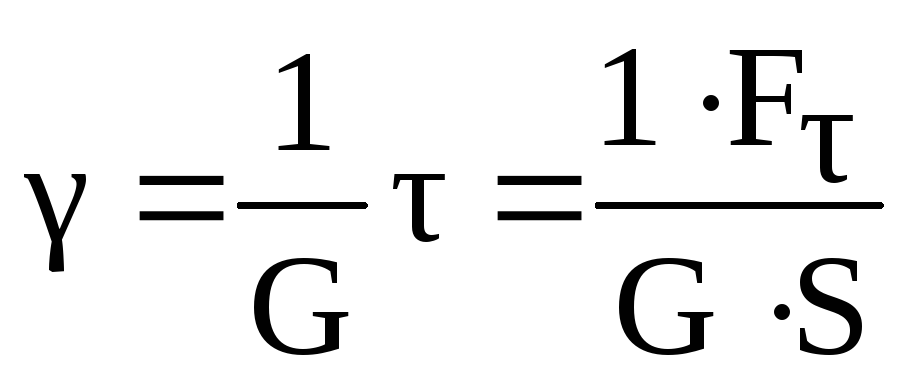, (2.62)

где G– модуль сдвига.

Модуль сдвига зависит только от свойств материала и равен тангенциальному напряжению при угле φ = 45˚. Модуль сдвига так же, как и модуль Юнга измеряется в паскалях (Па). Сдвиг стержня на уголвызывает сила

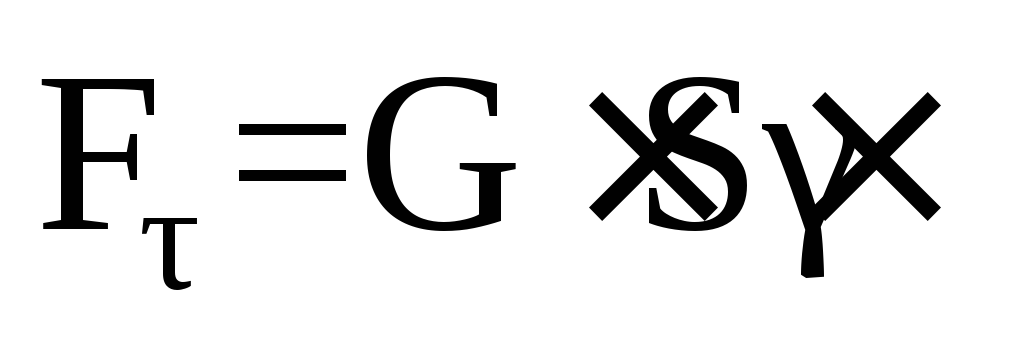=GSφ, (2.63)

где G·S– коэффициент упругости стержня при деформации сдвига.

Сила сопротивления Википедия

Четыре силы, действующие на самолёт

Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивление складывается из двух типов сил: сил касательного (тангенциального) трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности. Сила сопротивления является диссипативной силой и всегда направлена против вектора скорости тела в среде. Наряду с подъёмной силой является составляющей полной аэродинамической силы.

Сила лобового сопротивления обычно представляется в виде суммы двух составляющих: сопротивления при нулевой подъёмной силе и индуктивного сопротивления. Каждая составляющая характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Лобовое сопротивление может способствовать как обледенению летательных аппаратов (при низких температурах воздуха), так и вызывать нагревание лобовых поверхностей ЛА при сверхзвуковых скоростях ударной ионизацией.

Траектории трёх объектов (угол запуска — 70°, Distance — расстояние, Height — высота). Чёрный объект не испытывает никакого сопротивления и движется по параболе, на голубой объект действует закон Стокса, на зелёный объект — закон вязкости Ньютона

Сопротивление при нулевой подъёмной силе

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

X0=Cx0ρV22S{\displaystyle X_{0}=C_{x0}{\frac {\rho V^{2}}{2}}S}

Cx0{\displaystyle C_{x0}} — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

• в простейшем случае (шар) — площадь поперечного сечения;
• для крыльев и оперения — площадь крыла/оперения в плане;
• для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
• для подводных объектов обтекаемой формы — площадь смачиваемой поверхности;
• для продолговатых тел вращения, ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V^2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости (P=X0⋅V=Cx0ρV32S{\displaystyle P=X_{0}\cdot V=C_{x0}{\dfrac {\rho V^{3}}{2}}S}).

Индуктивное сопротивление в аэродинамике

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления. На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы (так, в случае отрицательной работы подъёмной силы направление вектора индуктивного сопротивления противоположно вектору силы, обусловленной тангенсальным трением), но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху. При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ{\displaystyle \lambda }, плотности среды ρ и квадрату скорости V:

Xi=CxiρV22S=Cy2πλρV22S=1πλY2ρV22S{\displaystyle X_{i}=C_{xi}{\frac {\rho V^{2}}{2}}S={\frac {C_{y}^{2}}{\pi \lambda }}{\frac {\rho V^{2}}{2}}S={\frac {1}{\pi \lambda }}{\frac {Y^{2}}{{\frac {\rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

X=X0+Xi{\displaystyle X=X_{0}+X_{i}}

Так как сопротивление при нулевой подъёмной силе X0{\displaystyle X_{0}} пропорционально квадрату скорости, а индуктивное Xi{\displaystyle X_{i}} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости X0{\displaystyle X_{0}} растёт, а Xi{\displaystyle X_{i}} — падает, и график зависимости суммарного сопротивления X{\displaystyle X} от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых X0{\displaystyle X_{0}} и Xi{\displaystyle X_{i}}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

См. также

Сопротивление воздуха

Литература

• Юрьев Б. Н. Экспериментальная аэродинамика. Часть II Индуктивное сопротивление, НКОП СССР, 1938, 275 с.

Ссылки

Сила сопротивления разгону

Сила сопротивления разгону воз­никает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.

Сила сопротивления разгону, Н:

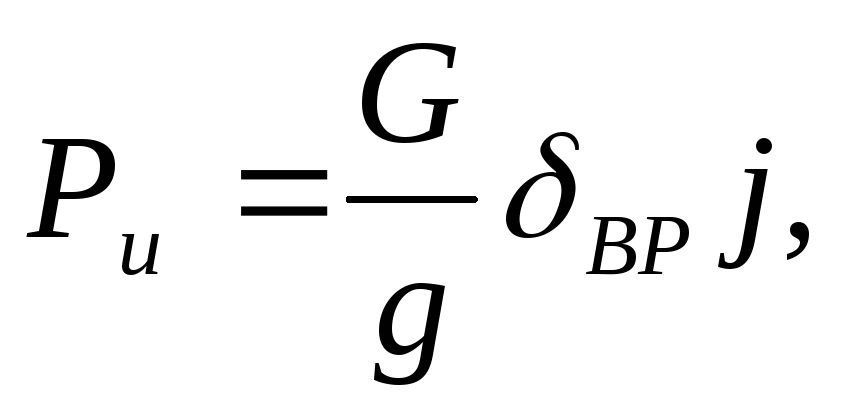
где G — вес автомобиля, Н; g — ус­корение силы тяжести, м/с²; δ_вр — коэффициент учета вращающихся масс автомобиля; j — ускорение ав­томобиля, м/с².

Мощность, кВт, затрачиваемая на разгон:

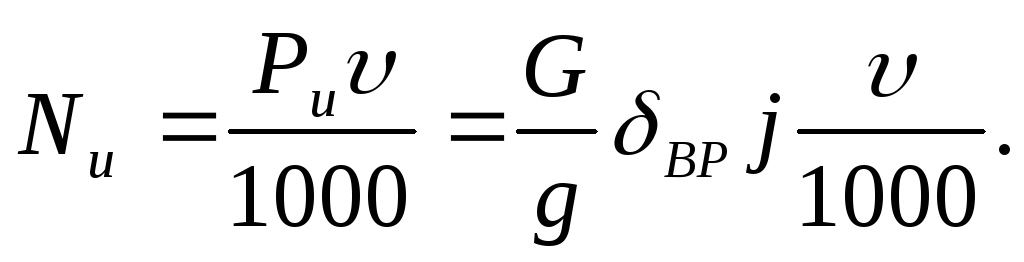
Зависимости силы сопротивления разгону Р_и и мощности N_И, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 3.20.

Коэффициент учета вращающихся масс

Этот коэффициент учитывает дополнительное сопротивление разгону автомобиля, вызванное раскручиванием вращающихся ча­стей двигателя, трансмиссии и колес.

Коэффициент учета вращающихся масс показывает, во сколь­ко раз мощность, затрачиваемая на разгон автомобиля, больше мощности, не

обходимой для установившегося движения:

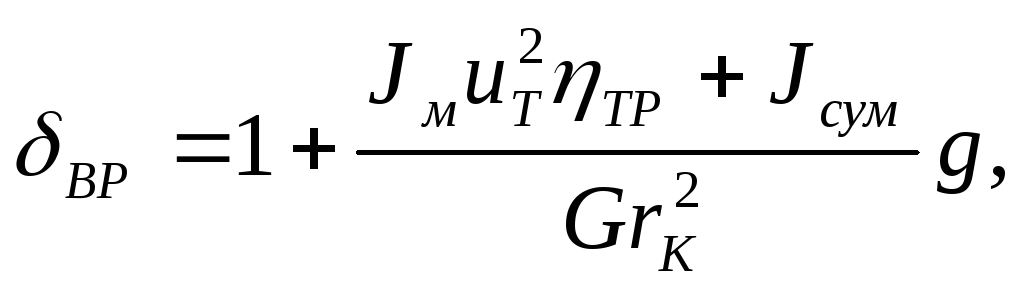
где J_м — момент инерции маховика; u_T, η_тр — передаточное число и КПД трансмиссии; J_сум — суммарный момент инерции всех ко­лес автомобиля.

Коэффициент учета вращающихся масс для автомобиля с пол­ной нагрузкой можно приближенно рассчитать по формуле

47

где u_к, u_д — передаточные числа основной и дополнительной ко­робок передач.

Условие равномерного движения при отсутствии буксования ведущих колес записывается в вид

3.12. Уравнение движения автомобиля

Для вывода уравнения движения рассмотрим разгон автомоби­ля на подъеме (рис. 3.21).

Спроецируем все силы, действующие на автомобиль, на по­верхность дороги:

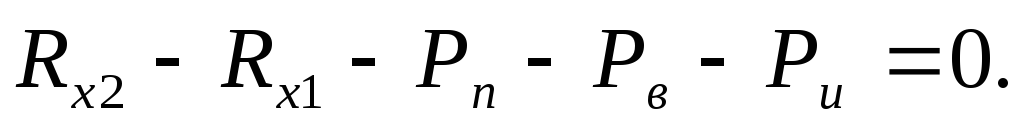(3.19)

Подставим в формулу (3.19) касательные реакции дороги R_x1, и R_x2,

объединим члены с коэффициентом сопротивления каче­нию ƒ и члены с ускорением j и, принимая во внимание соотно­шения ƒ(R_z2+R_z1 ) = Р_K, и j_k1 + j_k2 = j_k , а также коэффициент уче­та вращающихся масс, получим уравнение движения автомобиля в общем виде:

Или

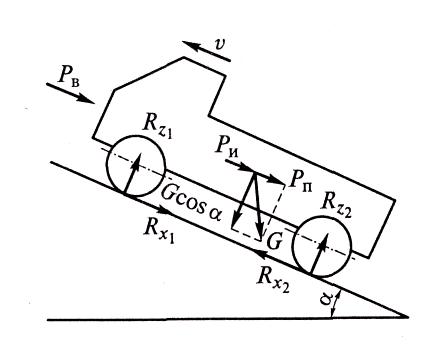
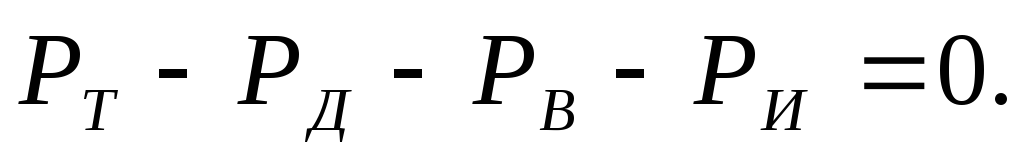(3.20)

Уравнение движения автомобиля выражает связь между дви­жущими силами и силами сопротивления

Рис. 3.21. Схема сил, действую­щих на автомобиль на подъеме

движению. Оно позволяет определить режим движения автомобиля в любой момент.

Так, например, при установившемся (равномерном) движе­нии

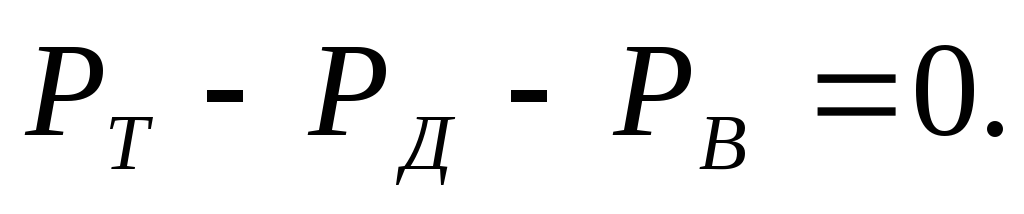
Из уравнения (3.20) следует, что безостановочное движение автомобиля возможно только при условии

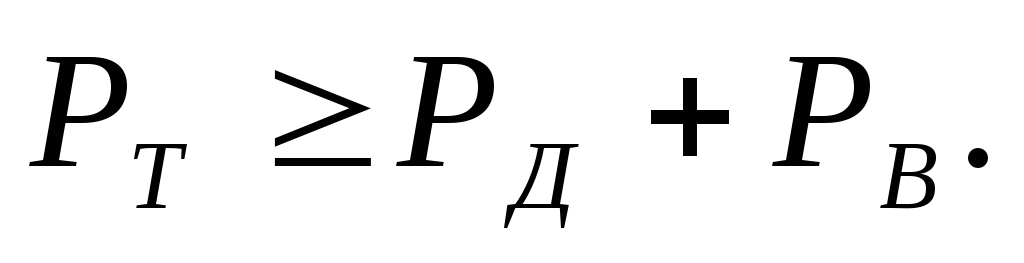
р

^гв-

Данное неравенство связыва­ет конструктивные параметры ав­томобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Одна­ко оно не гарантирует отсутствия буксования ведущих колес. Безо­становочное движение автомоби­ля без буксования ведущих колес возможно лишь при соблюдении условия

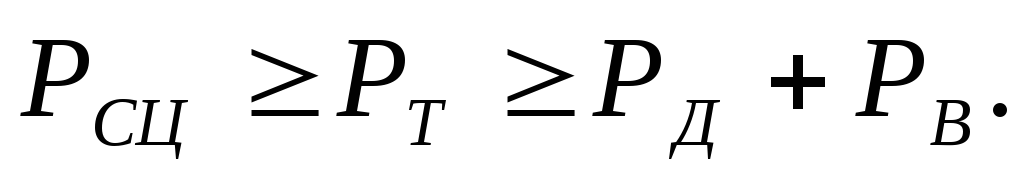
Условия равномерного движения при отсутствии буксования ведущих колёс записывается в виде

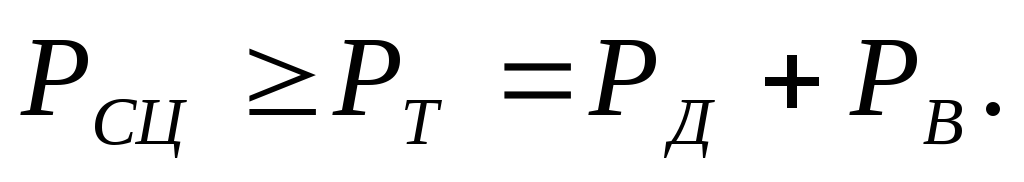
3.13. Силовой баланс автомобиля

Представим уравнение движения автомобиля в следующем виде: 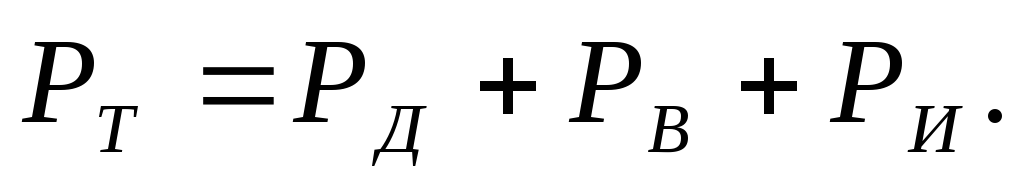(3.21)

В такой форме оно называется уравнением силового баланса автомобиля и выражает соотношение между тяговой силой на ве­дущих колесах и силами сопротивления движению.

На основании уравнения (3.21) строится график силового ба­ланса, позволяющий оценивать тягово-скоростные свойства ав­томобиля.

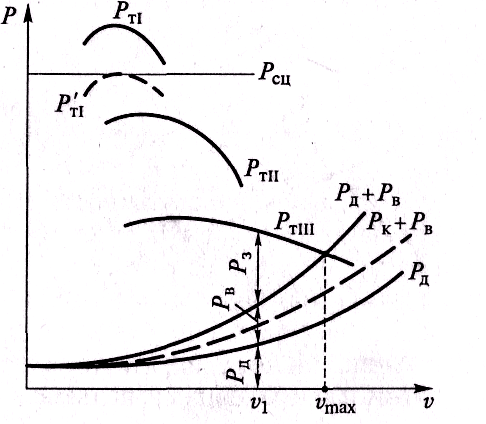При построении графика силового баланса (рис. 3.22) сначала строят тяговую характеристику автомобиля. Затем наносят зави­симость силы сопротивления дороги от скорости. Если коэффи­циент сопротивления дороги — постоянная величина, то указан­ная зависимость представляет собой прямую линию, параллель­ную оси абсцисс, а при непостоянном коэффициенте сопротив­ления дороги — кривую параболической формы. После этого от кривой, характеризующей силу сопротивления дороги, отклады­вают вверх значения силы сопротивления воздуха при различных скоростях движения. Полученная зависимость