Урок 4. магнитные свойства вещества. электроизмерительные приборы — Физика — 11 класс
Физика, 11 класс
Урок 4. Магнитные свойства вещества. Электроизмерительные приборы
Перечень вопросов, рассматриваемых на уроке:
1. Магнитные свойства вещества.
2. Свойства диа-, пара- и ферромагнетиков.
3. Принцип действия электроизмерительных приборов.
Глоссарий по теме:
Магнитная проницаемость – это физическая скалярная величина, показывающая, во сколько раз индукция магнитного поля в данном веществе отличается от индукции магнитного поля в вакууме.
Диамагнетики – вещества, у которых магнитная проницаемость чуть меньше единицы. К таким веществам относятся золото, серебро, углерод, висмут.
Парамагнетики – вещества, у которых магнитная проницаемость чуть больше единицы. Это алюминий, вольфрам, щелочные металлы, магний, платина.
Ферромагнетики – вещества у которых магнитная проницаемость много больше единицы.
Точка Кюри – температура, при которой ферромагнетики теряют ферромагнитные свойства.
Ферриты – ферромагнитные материалы, не проводящие электрического тока.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 27-30.
2.Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 113.
3. ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения.
Все вещества в окружающей нас природе в какой — то мере обладают магнитными свойствами. Ещё с глубокой древности была известна способность некоторых минералов притягивать железные предметы. Среди многих приборов навигации, необходимых для прокладывания курса кораблей или самолётов, обязательно должен быть и магнитный компас. Во многих измерительных приборах основными деталями служат постоянные магниты. Что же происходит с веществом, помещённом в магнитное поле? Вспомним, как магнитные свойства катушки, по которой течёт ток, усиливаются, если в катушку вставлен железный сердечник. Железный сердечник намного увеличивает магнитное поле в катушке с током. Мы знаем, что вокруг катушки с электрическим током возникает магнитное поле, а железный сердечник, создаёт своё магнитное поле и, согласно принципу суперпозиции полей, векторы этих двух полей складываются. Таким образом, мы наблюдаем усиление магнитного поля. Магнитную индукцию, создаваемую электрическим током, обозначим через (В
Во многих измерительных приборах основными деталями служат постоянные магниты. Что же происходит с веществом, помещённом в магнитное поле? Вспомним, как магнитные свойства катушки, по которой течёт ток, усиливаются, если в катушку вставлен железный сердечник. Железный сердечник намного увеличивает магнитное поле в катушке с током. Мы знаем, что вокруг катушки с электрическим током возникает магнитное поле, а железный сердечник, создаёт своё магнитное поле и, согласно принципу суперпозиции полей, векторы этих двух полей складываются. Таким образом, мы наблюдаем усиление магнитного поля. Магнитную индукцию, создаваемую электрическим током, обозначим через (В
Магнитной проницаемостью вещества называется физическая скалярная величина показывающая, во сколько раз индукция магнитного поля в данном веществе отличается от индукции магнитного поля в вакууме.
Французский физик Андре Мари Ампер сравнивал магнитные поля, создаваемые полосовым магнитом и проводниками с током. В итоге, Ампер выдвинул гипотезу, что внутри молекул и атомов циркулируют элементарные электрические токи. Круговые электрические токи – это токи, обусловленные орбитальными движениями электронов вокруг ядра.
Английский физик Майкл Фарадей исследовал влияние вещества на магнитное поле. В итоге, он определил, что все вещества изменяют магнитное поле, если их поместить во внешнее магнитное поле. Получается если вещество поместить во внешнее магнитное поле, оно становится источником своего магнитного поля. Это явление называют намагничиванием. Таким образом, Майкл Фарадей обнаружил, что вещества делятся на три группы — диа-, пара-, и ферромагнетики.
Таким образом, Майкл Фарадей обнаружил, что вещества делятся на три группы — диа-, пара-, и ферромагнетики.
Диамагнетики – это вещества, у которых магнитная проницаемость чуть меньше единицы. К таким веществам относятся золото, серебро, углерод, висмут. Магнитная проницаемость висмута равна 0,9998. Значит, магнитное поле ослабляется, когда в него помещают это вещество В˂В
Парамагнетики – вещества, у которых магнитная проницаемость чуть больше единицы. Это алюминий, вольфрам, щелочные металлы, магний, платина. Эти вещества намагничиваются очень слабо, намагничиваются вдоль намагничивающего поля. Вектор магнитной индукции поля, создаваемого веществом, направлен в ту же сторону, что и вектор магнитной индукции поля, создаваемого током.
Ферромагнетики – это вещества, у которых магнитная проницаемость во много раз больше единицы. Это такие вещества как железо, кобальт, никель и сплавы металлов. Для железа магнитная проницаемость равна одна тысяча (1000).
Это такие вещества как железо, кобальт, никель и сплавы металлов. Для железа магнитная проницаемость равна одна тысяча (1000).
Магнитные поля создаются ферромагнетиками не только вследствие обращения электронов вокруг ядер, но и вследствие их собственного вращения. Собственный вращательный момент (момент импульса) электрона называется спином. Согласно простейшим представлениям, электроны вращаясь вокруг собственной оси обладая зарядом, имеют, магнитное поле наряду с полем, появляющимся за счёт их орбитального движения вокруг ядер. В ферромагнетиках существуют области с параллельными ориентациями спинов, называемыми
Ферромагнитные свойства у веществ существуют только в определённой области температуры.
Большое применение получили ферромагнитные материалы, не проводящие электрического тока – ферриты. Это химические соединения оксидов железа с оксидами других веществ. К их числу относится и магнитный железняк.
Стальной или железный сердечник в катушке усиливает создаваемое ею магнитное поле, не увеличивая силу тока в катушке. Это экономит электроэнергию. Сердечники трансформаторов, генераторов, электродвигателей и т. д. изготовляют из ферромегнетиков. При выключении внешнего магнитного поля ферромагнетик остаётся намагниченным, таким образом создаёт магнитное поле в окружающем пространстве. Это объясняется тем, что домены не возвращаются в прежнее положение и их ориентация частично сохраняется. Благодаря этому существуют постоянные магниты. Постоянные магниты широко применяются в электроизмерительных приборах, громкоговорителях и телефонах, звукозаписывающих аппаратах, магнитных компасах и т.д. Электроизмерительный прибор является необходимым устройством в связи, промышленности, на транспорте, в медицине и в научных исследованиях.
д. изготовляют из ферромегнетиков. При выключении внешнего магнитного поля ферромагнетик остаётся намагниченным, таким образом создаёт магнитное поле в окружающем пространстве. Это объясняется тем, что домены не возвращаются в прежнее положение и их ориентация частично сохраняется. Благодаря этому существуют постоянные магниты. Постоянные магниты широко применяются в электроизмерительных приборах, громкоговорителях и телефонах, звукозаписывающих аппаратах, магнитных компасах и т.д. Электроизмерительный прибор является необходимым устройством в связи, промышленности, на транспорте, в медицине и в научных исследованиях.
Примеры и разбор решения заданий:
1. Для каких целей применяют ферромагнитные материалы? Выберите один правильный ответ.
Варианты ответов:
1) для усиления силы тока;
2) для ослабления магнитного поля;
3) для усиления магнитного поля;
4) для ослабления силы тока.
Пояснение: ферромагнетики и ферромагнитные материалы это вещества, которые создают наиболее сильные магнитные поля.
Правильный ответ: 3) для усиления магнитного поля.
2. По графику определите магнитную проницаемость стали при индукции В0 намагничивающего поля 1) 0,4 мТл, 2) 1,2 мТл.
Дано:
1) B0 = 0.4 мТл
2) B0 = 1,2 мТл
µ1 -? µ2 -?
Решение:
По определению магнитная проницаемость µ показывает, во сколько раз индукция магнитного поля В в веществе превышает индукцию намагничивающего поля В
- При В0 = 0,4 мТл по графику находим что В = 0,8 Тл, следовательно:
2) При В0 = 1.2 мТл, по графику В = 1,2 Тл
Следовательно:
Ответ: µ1 = 2000; µ2 = 1000
Магнитная проницаемость | |
Физическая величина, показывающая, во сколько раз индукция магнитного поля в одной среде больше или меньше индукции магнитного поля в вакууме, называется магнитной проницаемостью µ. | |
Вещество, создающее собственное магнитное поле, называетсянамагниченным. Намагниченность возникает при помещении вещества во внешнее магнитное поле. Гипотеза Ампера: магнитные свойства тела определяются микроскопическими электрическими токами (орбитальное движение электронов в атомах, наличие у электрона собственного магнитного момента, имеющего квантовую природу) внутри вещества. Если направления этих токов неупорядочены, порождаемые ими магнитные поля компенсируют друг друга, т.е. тело не намагничено. Во внешнем магнитном поле происходит упорядочение этих токов, вследствие чего в веществе и возникает «собственное» магнитное поле (намагниченность). | |
Магнитные свойства вещества
| |
Для пара- и диамагнетиков намагниченность I прямо пропорциональна индукции B0 магнитного поля в вакууме. | |
3. Ферромагнетики— µ >>1. µстали = 8.103 (железо, никель, кобальт и их сплавы). Сплав железа с никелем: µ =2,5.105. Свойства ферромагнетиков
| |
Для характеристики явления намагничивания вещества вводится величина Iназываемая намагниченностью вещества. Намагниченность в СИ определяется формулой Для ферромагнитных тел намагниченность Iявляется сложной нелинейной функцией B0. | |
Магнитным гистерезисом (От греческого «hysteresis» — отставание следствия от его причины) ферромагнетика называется отставание изменения величины намагниченности ферромагнитного вещества от изменения внешнего магнитного поля, в котором находится вещество. Важнейшей причиной магнитного гистерезиса является характерная для ферромагнетика зависимость его магнитных характеристик (µ, I) не только от состояния вещества в данный момент, но и от значений величин µ и I в предыдущие моменты времени. Таким образом, существует зависимость магнитных свойств от предшествующей намагниченности вещества. Петлей гистерезиса называется кривая зависимости изменения величины намагниченности ферромагнитного тела, помещенного во внешнее магнитное поле, от изменения индукции этого поля от + Во/µ0 до — Во/µ0 и обратно. | |
Коэрцитивная сила и форма петли гистерезиса характеризуют свойство ферромагнетика сохранять остаточное намагничивание и определяют использование ферромагнетиков для различных целей. Ферромагнетики с широкой петлей гистерезиса называются жесткими магнитными материалами (углеродистые, вольфрамовые, хромовые, алюминиево-никелевые и другие стали). Они обладают большой коэрцитивной силой и используются для создания постоянных магнитов различной формы (полосовых,подковообразных, магнитных стрелок). К мягким магнитным материалам,обладающим малой коэрцитивной силой и узкой петлей гистерезиса, относятся железо, сплавы железа с никелем. |
|
При температурах меньших точки Кюри любое ферромагнитное тело состоит из доменов — малых областей с линейными размерами порядка 10-2 -10-3 см, внутри которых существует наибольшая величина намагниченности, равная намагниченности насыщения. Домены называются иначе областями самопроизвольной намагниченности. В отсутствие внешнего магнитного поля векторы магнитных моментов отдельных доменов ориентированы внутри ферромагнетика совершенно беспорядочно, так что суммарный магнитный момент всего тела равен нулю (рис. Применение ферромагнетиков в технике. Роторы генераторов и электродвигателей; сердечники трансформаторов, электромагнитных реле; в электронно-вычислительных машинах (ЭВМ), телефонах, магнитофонах, на магнитных лентах. | |
|
Урок |
|||
|
1/1 |
Что изучает физика. Физические термины. Наблюдения и опыты. | § 1 — 3, Л № 5, 12 | |
| 2/2 | Физические величины. Измерение физических величин. Погрешность и точность измерений | § 4, 5, упр.1 | |
| 3/3 | Определение цены деления измерительного прибора | § 4, 5 | |
| 4/4 | Физика и техника | § 6, | |
| Первоначальные сведения о строении вещества | |||
| 5/1 | Строение вещества. Молекулы Молекулы |
§ 7, 8 | |
| 6/2 | Определение размеров малых тел | § 7, 8 | |
| 7/3 | Движение молекул. Диффузия в газах, жидкостях и твердых телах | § 9, | |
| 8/4 | Взаимодействие молекул | ||
|
9/5 |
Три состояния вещества | § 11, 12 | |
| 10/6 | Повторение. Контрольная работа №1 «Первоначальные сведения о строении вещества» | § 12 | |
Магнитные свойства вещества
Просмотр содержимого документа
«Магнитные свойства вещества»
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
10 класс
§ 84 (стр. 274-249)
274-249)
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Вещество, создающее собственное магнитное поле, называется намагниченным.
Намагниченность возникает при помещении вещества во внешнее магнитное поле.
Магнитная индукция в веществе В выражается через магнитную индукцию внешнего поля В о (в той же точке пространства) по формуле:
В = μ В о ,
где μ — коэффициент, характеризующий магнитные свойства среды ( магнитная проницаемость среды ) .
ГИПОТЕЗА АМПЕРА:
магнитные свойства тела определяются микроскопическими электрическими токами (орбитальное движение электронов в атомах, наличие у электрона собственного магнитного момента, имеющего квантовую природу) внутри вещества.
Если направления этих токов неупорядочены, порождаемые ими магнитные поля компенсируют друг друга, т.е. тело не намагничено. Во внешнем магнитном поле происходит упорядочение этих токов, вследствие чего в веществе и возникает «собственное» магнитное поле (намагниченность).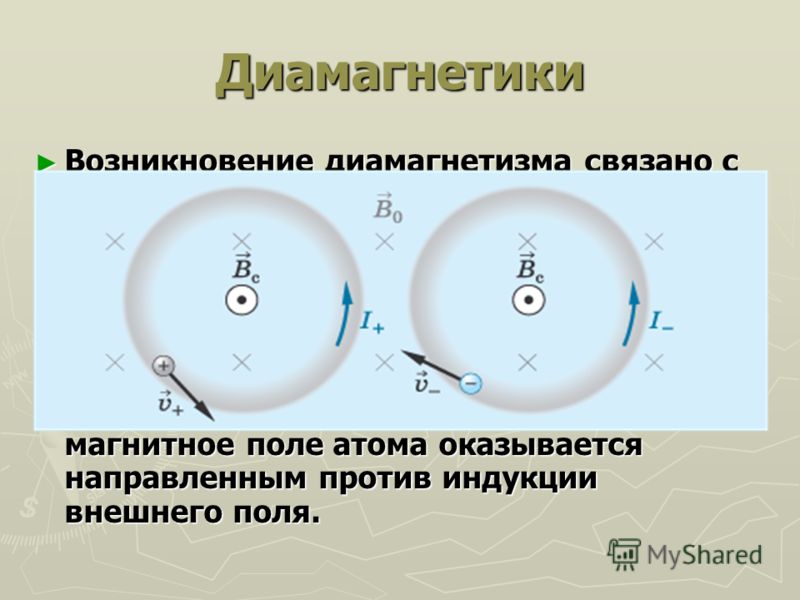
Классификация веществ по их магнитным свойствам
μ 1
Слабомагнитные
вещества
ДИАМАГНЕТИКИ
μ 1
ПАРАМАГНЕТИКИ
μ 1
Сильномагнитные
вещества
ФЕРРОМАГНЕТИКИ
(железо, никель, кобальт,
некоторые сплавы)
Домашнее задание:
§ 84 (стр. 247-249), опорный конспект «Магнитные свойства вещества».
Физика
Основы электродинамики
Урок 1. Магнитное поле и его свойства. Магнитная индукция
Магнитное поле и его свойства. Магнитная индукция
Урок 2. Магнитное поле постоянного электрического тока. Модуль вектора магнитной индукции
Урок 3. Действие магнитного поля на движущийся электрический заряд. Применение закона Ампера
Урок 4. Сила Лоренца. Магнитные свойства вещества
Урок 5. Явление электромагнитной индукции. Магнитный поток
Урок 6. Закон электромагнитной индукции. Вихревое поле
Закон электромагнитной индукции. Вихревое поле
Урок 7. Направление индукционного тока. Правило Ленца
Урок 8. Индуктивность. Самоиндукция
Урок 9. Энергия магнитного поля тока. Электромагнитное поле
Колебания и волны
Урок 10. Свободные и вынужденные колебания. Математический маятник
Математический маятник
Урок 11. Гармонические колебания. Фаза колебаний
Урок 12. Превращение энергии при гармонических колебаниях. Вынужденные колебания. Резонанс
Урок 13. Свободные и вынужденные электромагнитные колебания
Урок 14. Колебательный контур. Превращение энергии при электромагнитных колебаниях
Урок 15. Переменный электрический ток. Активное сопротивление
Переменный электрический ток. Активное сопротивление
Урок 16. Конденсатор и катушка индуктивности в цепи переменного тока
Урок 17. Резонанс в электрической цепи. Автоколебания
Урок 18. Генерирование электрической энергии. Трансформаторы
Урок 19. Производство и использование электрической энергии. Передача электрической энергии
Урок 20.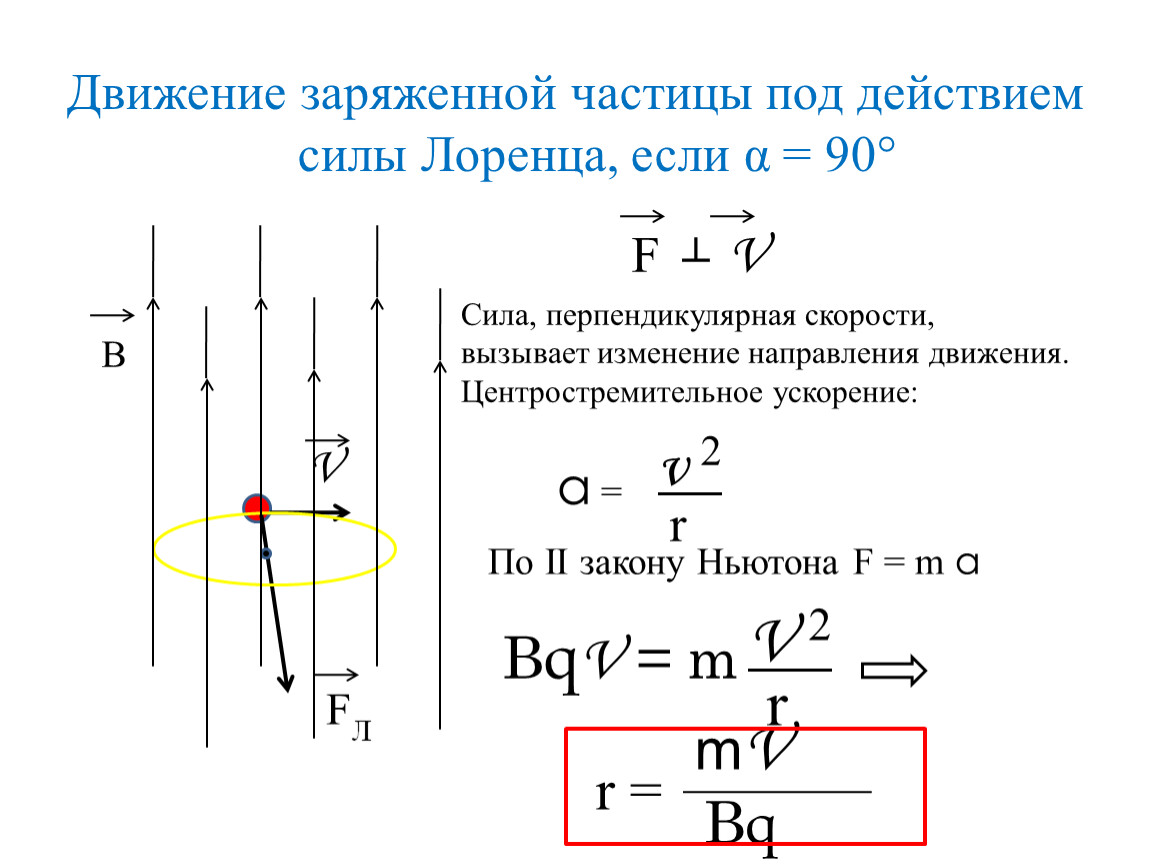 Волновые явления. Распространение механических волн. Длина и скорость волны
Волновые явления. Распространение механических волн. Длина и скорость волны
Урок 21. Распространение волн в упругих средах. Звуковые волны
Урок 22. Электромагнитная волна. Плотность потока излучения
Урок 23. Принцип радиосвязи. Простейший радиоприёмник
Урок 24. Модуляция и детектирование. Свойства электромагнитных волн
Урок 25. Распространение радиоволн. Радиолокация. Понятие о телевидении. Развитие средств связи
Распространение радиоволн. Радиолокация. Понятие о телевидении. Развитие средств связи
Оптика
Урок 26. Развитие взглядов на природу света. Скорость света
Урок 27. Закон отражения света
Урок 28. Закон преломления света
Урок 29. Полное отражение
Урок 30. Линза. Построение изображений в линзе. Формула тонкой линзы
Линза. Построение изображений в линзе. Формула тонкой линзы
Урок 31. Дисперсия света. Интерференция света
Урок 32. Дифракция света. Дифракционная решётка
Урок 33. Поперечность световых волн. Поляризация света
Урок 34. Постулаты теории относительности
Урок 35. Следствия из специальной теории относительности. Релятивистская динамика
Следствия из специальной теории относительности. Релятивистская динамика
Урок 36. Спектры и спектральные аппараты. Виды спектров
Урок 37. Спектральный анализ. Инфракрасное и ультрафиолетовое излучения
Урок 38. Рентгеновские лучи. Гамма-излучение. Шкала электромагнитных волн
Квантовая физика
Урок 39. Фотоэффект. Уравнение Эйнштейна
Фотоэффект. Уравнение Эйнштейна
Урок 40. Фотоны. Применение фотоэффекта
Урок 41. Химические действия света. Фотография
Урок 42. Строение атома. Опыты Резерфорда
Урок 43. Квантовые постулаты Бора. Модель атома водорода по Бору
Урок 44. Лазеры
Урок 45. Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц
Урок 46. Открытие радиоактивности. Альфа-, бета- и гамма-излучение
Урок 47. Радиоактивные превращения. Закон радиоактивного распада. Период полураспада
Урок 48. Изотопы. Открытие нейтрона
Урок 49. Строение атомного ядра. Ядерные силы
Урок 50. Энергия связи атомных ядер. Дефект масс. Ядерные реакции
Энергия связи атомных ядер. Дефект масс. Ядерные реакции
Урок 51. Деление ядер урана. Цепные реакции. Ядерный реактор
Урок 52. Применение ядерной энергии. Биологическое действие радиоактивных излучений
Урок 53. Физика элементарных частиц. Открытие позитрона. Античастицы
Астрономия
Урок 54. Видимые движения небесных тел. Законы движения планет
Видимые движения небесных тел. Законы движения планет
Урок 55. Система Земля-Луна. Физическая природа планет и малых тел Солнечной системы
Урок 56. Общие сведения о Солнце. Внутреннее строение Солнца и звёзд главной последовательности
Урок 57. Основные характеристики звёзд. Эволюция звёзд
Урок 58. Млечный Путь – наша Галактика. Галактики
Урок 59. Строение и эволюция Вселенной
Строение и эволюция Вселенной
Значение физики для объяснения мира и развития производительных сил общества
Урок 60. Единая физическая картина мира
Урок «Магнитные свойства вещества» 11 класс | Методическая разработка по физике (11 класс) по теме:
І. Тема: «Магнитные свойства вещества», 11 класс
УМК линии Г.Я.Мякишева
1.Цель урока: организация работы по усвоению учениками понятий о магнитных свойствах вещества, научных фактов по данному вопросу.
2. Задачи урока:
1) образовательные: а) познакомить учащихся с разными веществами по их магнитным свойствам и их применением; б) дать представление о магнитной проницаемости, о доменах; в) рассмотреть соответственные опыты; г) активизировать познавательную активность учащихся;
2) развивающие: а) продолжить развитие интеллектуальных умений анализировать, сопоставлять, сравнивать, выделять главное, б) формировать умения работы в группах в медиацентре гимназии; в) продолжить развитие умения принимать самостоятельные решения, доказывать свою точку зрения и принимать чужую; г) формировать умения работы с различными источниками учебной информации; д) продолжить формирование информационной компетентности;
3) воспитательные: а) создание учениками личного опыта в приобретении знаний и продукта своей деятельности; б) воспитание ученика субъектом, конструктором своего образования, полноправным источником и организатором своих знаний; в) обеспечение индивидуального личностного роста потенциала ученика.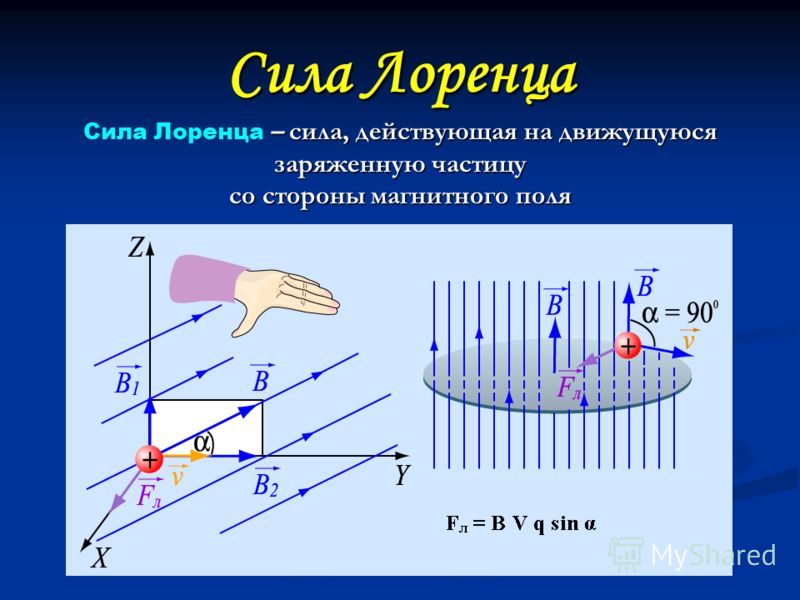
3.Тип урока: урок формирования новых знаний.
4.Вид урока: мультимедийный урок, состоящий из двух стандартных уроков по 45 минут.
5.Методы обучения, методические приемы, педагогические технологии: а) технология модерации, интеграции предметов и информационная технология; педагогика сотрудничества; б) эвристическое обучение с использованием дебатов; в) прием выхода за рамки своего учебного предмета, чтобы попросить помощи учеников как сотрудников в использовании компьютерной технологии; г) частично поисковые, исследовательские методы обучения; д) форма работы: групповая.
6.Оборудование: а) компьютерный класс в медиацентре гимназии; б) источники информации: Интернет, специальная литература по теме; в) дидактические средства обучения: базовые листы опроса для повторения материала, перечень тем для презентаций с планами, листы защиты презентации.
II. Актуализация:
Опорные знания, которые необходимо активизировать в сознании учащихся: магнитное поле как особая форма материи, правило определения направления вектора магнитной индукции, особенности линий магнитной индукции, сила Ампера, сила Лоренца, правило левой руки для двух сил, гипотеза Ампера, температура Кюри.
Проверка знаний: использование базовых листов опроса учащихся.
Способы формирования мотивации в обучении, интереса к предмету: сообщение о веществах с разными магнитными свойствами, показ их практической значимости.
Контроль за ходом работы: беседы с «консультантами» групп при необходимости теоретических консультаций по теме.
Приемы самоконтроля и взаимоконтроля: отчет «сборщика информации» о ходе работы два раза за весь период урока.
Форма получения обратной связи: создание по конкретной теме презентации от группы, которую представляет «системный администратор». Защита продукта работы любым представителем группы, то есть «оратором», кого ученики выбирают сами.
III. Формирование новых понятий, способов действия:
Новые понятия, подлежащие изучению: 1) магнитная проницаемость, формула расчета; 2) смысл опыта Штерна – Герлаха; 3) график зависимости намагничивания от магнитной индукции; 4) домены в магнетизме; 5) виды и применение разных магнитных материалов Приемы формирования способов деятельности:
работа в группах в медиацентре гимназии; самостоятельное добывание знаний при работе с различными источниками учебной информации; установление межпредметных связей с информатикой; установление партнерских отношений между учителем и учениками.
IV. Применение (формирование умений и навыков):
1) формирование умения анализировать, сопоставлять, сравнивать, выделять главное, приводить примеры применения разных магнетиков;
2) способы получения обратной связи: а) защита продукта работы, то есть презентации на уроке; оформление опорных конспектов в тетрадях в соответствии с планом презентации каждой группы. «Сборщикам информации» оформить электронные варианты опорных конспектов.
б) дидактические средства обучения: базовые листы опроса для повторения материала; темы для создания презентаций с указанием плана, листы защиты презентации.
в) использование дебатов для формирования умения доказывать свою точку зрения и принимать чужую.
V. Домашнее задание:
а) традиционное задание: оформить опорные конспекты в тетрадях в соответствии с планом презентации каждой группы. «Сборщикам информации» оформить электронные варианты опорных конспектов для ксерокопирования для всего класса.
б) творческое задание №1(конкретным ученикам): приготовить презентации по теме «Диамагнетики» по установленному плану.
творческое задание №2 (по желанию): создать кроссворд по теме «Магнитные свойства вещества».
МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
где F — сила в ньютонах, I — ток в амперах, l — длина в метрах. Единицей измерения магнитной индукции является тесла (Тл)
(см. также
).
Гальванометр — чувствительный прибор для измерения слабых токов. В гальванометре используется вращающий момент, возникающий при взаимодействии подковообразного постоянного магнита с небольшой токонесущей катушкой (слабым электромагнитом), подвешенной в зазоре между полюсами магнита. Вращающий момент, а следовательно, и отклонение катушки пропорциональны току и полной магнитной индукции в воздушном зазоре, так что шкала прибора при небольших отклонениях катушки почти линейна. Намагничивающая сила и напряженность магнитного поля. Далее следует ввести еще одну величину, характеризующую магнитное действие электрического тока. Предположим, что ток проходит по проводу длинной катушки, внутри которой расположен намагничиваемый материал. Намагничивающей силой называется произведение электрического тока в катушке на число ее витков (эта сила измеряется в амперах, так как число витков — величина безразмерная). Напряженность магнитного поля Н равна намагничивающей силе, приходящейся на единицу длины катушки. Таким образом, величина Н измеряется в амперах на метр; ею определяется намагниченность, приобретаемая материалом внутри катушки. В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н:
Намагничивающей силой называется произведение электрического тока в катушке на число ее витков (эта сила измеряется в амперах, так как число витков — величина безразмерная). Напряженность магнитного поля Н равна намагничивающей силе, приходящейся на единицу длины катушки. Таким образом, величина Н измеряется в амперах на метр; ею определяется намагниченность, приобретаемая материалом внутри катушки. В вакууме магнитная индукция B пропорциональна напряженности магнитного поля Н:
где m0 — т.н. магнитная постоянная, имеющая универсальное значение 4pЧ10-7 Гн/м. Во многих материалах величина B приблизительно пропорциональна Н. Однако в ферромагнитных материалах соотношение между B и Н несколько сложнее (о чем будет сказано ниже). На рис. 1 изображен простой электромагнит, предназначенный для захвата грузов. Источником энергии служит аккумуляторная батарея постоянного тока. На рисунке показаны также силовые линии поля электромагнита, которые можно выявить обычным методом железных опилок.

Рис. 1. ЭЛЕКТРОМАГНИТ создает магнитное поле благодаря электрическому току в обмотке.
Крупные электромагниты с железными сердечниками и очень большим числом ампер-витков, работающие в непрерывном режиме, обладают большой намагничивающей силой. Они создают магнитную индукцию до 6 Тл в промежутке между полюсами; эта индукция ограничивается лишь механическими напряжениями, нагреванием катушек и магнитным насыщением сердечника. Ряд гигантских электромагнитов (без сердечника) с водяным охлаждением, а также установок для создания импульсных магнитных полей был сконструирован П.Л.Капицей (1894-1984) в Кембридже и в Институте физических проблем АН СССР и Ф.Биттером (1902-1967) в Массачусетском технологическом институте. На таких магнитах удавалось достичь индукции до 50 Тл. Сравнительно небольшой электромагнит, создающий поля до 6,2 Тл, потребляющий электрическую мощность 15 кВт и охлаждаемый жидким водородом, был разработан в Лосаламосской национальной лаборатории. Подобные поля получают при криогенных температурах.

Магнитная проницаемость и ее роль в магнетизме. Магнитная проницаемость m — это величина, характеризующая магнитные свойства материала. Ферромагнитные металлы Fe, Ni, Co и их сплавы обладают очень высокими максимальными проницаемостями — от 5000 (для Fe) до 800 000 (для супермаллоя). В таких материалах при сравнительно малых напряженностях поля H возникают большие индукции B, но связь между этими величинами, вообще говоря, нелинейна из-за явлений насыщения и гистерезиса, о которых говорится ниже. Ферромагнитные материалы сильно притягиваются магнитами. Они теряют свои магнитные свойства при температурах выше точки Кюри (770° С для Fe, 358° С для Ni, 1120° С для Co) и ведут себя как парамагнетики, для которых индукция B вплоть до очень высоких значений напряженности H пропорциональна ей — в точности так же, как это имеет место в вакууме. Многие элементы и соединения являются парамагнитными при всех температурах. Парамагнитные вещества характеризуются тем, что намагничиваются во внешнем магнитном поле; если же это поле выключить, парамагнетики возвращаются в ненамагниченное состояние.
 Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля. На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1-2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1-3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)-(4) соответствует коэрцитивной силе, препятствующей размагничиванию.
Намагниченность в ферромагнетиках сохраняется и после выключения внешнего поля. На рис. 2 представлена типичная петля гистерезиса для магнитно-твердого (с большими потерями) ферромагнитного материала. Она характеризует неоднозначную зависимость намагниченности магнитоупорядоченного материала от напряженности намагничивающего поля. С увеличением напряженности магнитного поля от исходной (нулевой) точки (1) намагничивание идет по штриховой линии 1-2, причем величина m существенно изменяется по мере того, как возрастает намагниченность образца. В точке 2 достигается насыщение, т.е. при дальнейшем увеличении напряженности намагниченность больше не увеличивается. Если теперь постепенно уменьшать величину H до нуля, то кривая B(H) уже не следует по прежнему пути, а проходит через точку 3, обнаруживая как бы «память» материала о «прошлой истории», откуда и название «гистерезис». Очевидно, что при этом сохраняется некоторая остаточная намагниченность (отрезок 1-3). После изменения направления намагничивающего поля на обратное кривая В (Н) проходит точку 4, причем отрезок (1)-(4) соответствует коэрцитивной силе, препятствующей размагничиванию. Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант — участок 4-5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.
Дальнейший рост значений (-H) приводит кривую гистерезиса в третий квадрант — участок 4-5. Следующее за этим уменьшение величины (-H) до нуля и затем возрастание положительных значений H приведет к замыканию петли гистерезиса через точки 6, 7 и 2.Рис. 2. ТИПИЧНАЯ ПЕТЛЯ ГИСТЕРЕЗИСА для магнитно-твердого ферромагнитного материала. В точке 2 достигается магнитное насыщение. Отрезок 1-3 определяет остаточную магнитную индукцию, а отрезок 1-4 — коэрцитивную силу, характеризующую способность образца противостоять размагничиванию.
Магнитно-твердые материалы характеризуются широкой петлей гистерезиса, охватывающей значительную площадь на диаграмме и потому соответствующей большим значениям остаточной намагниченности (магнитной индукции) и коэрцитивной силы. Узкая петля гистерезиса (рис. 3) характерна для магнитно-мягких материалов — таких, как мягкая сталь и специальные сплавы с большой магнитной проницаемостью. Такие сплавы и были созданы с целью снижения обусловленных гистерезисом энергетических потерь.
 Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.
Большинство подобных специальных сплавов, как и ферриты, обладают высоким электрическим сопротивлением, благодаря чему уменьшаются не только магнитные потери, но и электрические, обусловленные вихревыми токами.Рис. 3. ТИПИЧНАЯ ПЕТЛЯ ГИСТЕРЕЗИСА для магнитно-мягкого материала (например, железа). Поскольку площадь петли пропорциональна потерям энергии, такие материалы слабо сопротивляются размагничиванию и характеризуются малыми потерями энергии.
Магнитные материалы с высокой проницаемостью изготовляются путем отжига, осуществляемого выдерживанием при температуре около 1000° С, с последующим отпуском (постепенным охлаждением) до комнатной температуры. При этом очень существенны предварительная механическая и термическая обработка, а также отсутствие в образце примесей. Для сердечников трансформаторов в начале 20 в. были разработаны кремнистые стали, величина m которых возрастала с увеличением содержания кремния. Между 1915 и 1920 появились пермаллои (сплавы Ni с Fe) с характерной для них узкой и почти прямоугольной петлей гистерезиса.
 Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой — сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).
Особенно высокими значениями магнитной проницаемости m при малых значениях H отличаются сплавы гиперник (50% Ni, 50% Fe) и му-металл (75% Ni, 18% Fe, 5% Cu, 2% Cr), тогда как в перминваре (45% Ni, 30% Fe, 25% Co) величина m практически постоянна в широких пределах изменения напряженности поля. Среди современных магнитных материалов следует упомянуть супермаллой — сплав с наивысшей магнитной проницаемостью (в его состав входит 79% Ni, 15% Fe и 5% Mo).Теории магнетизма. Впервые догадка о том, что магнитные явления в конечном счете сводятся к электрическим, возникла у Ампера в 1825, когда он высказал идею замкнутых внутренних микротоков, циркулирующих в каждом атоме магнита. Однако без какого-либо опытного подтверждения наличия в веществе таких токов (электрон был открыт Дж.Томсоном лишь в 1897, а описание структуры атома было дано Резерфордом и Бором в 1913) эта теория «увяла». В 1852 В.Вебер высказал предположение, что каждый атом магнитного вещества представляет собой крошечный магнит, или магнитный диполь, так что полная намагниченность вещества достигается, когда все отдельные атомные магниты оказываются выстроенными в определенном порядке (рис.
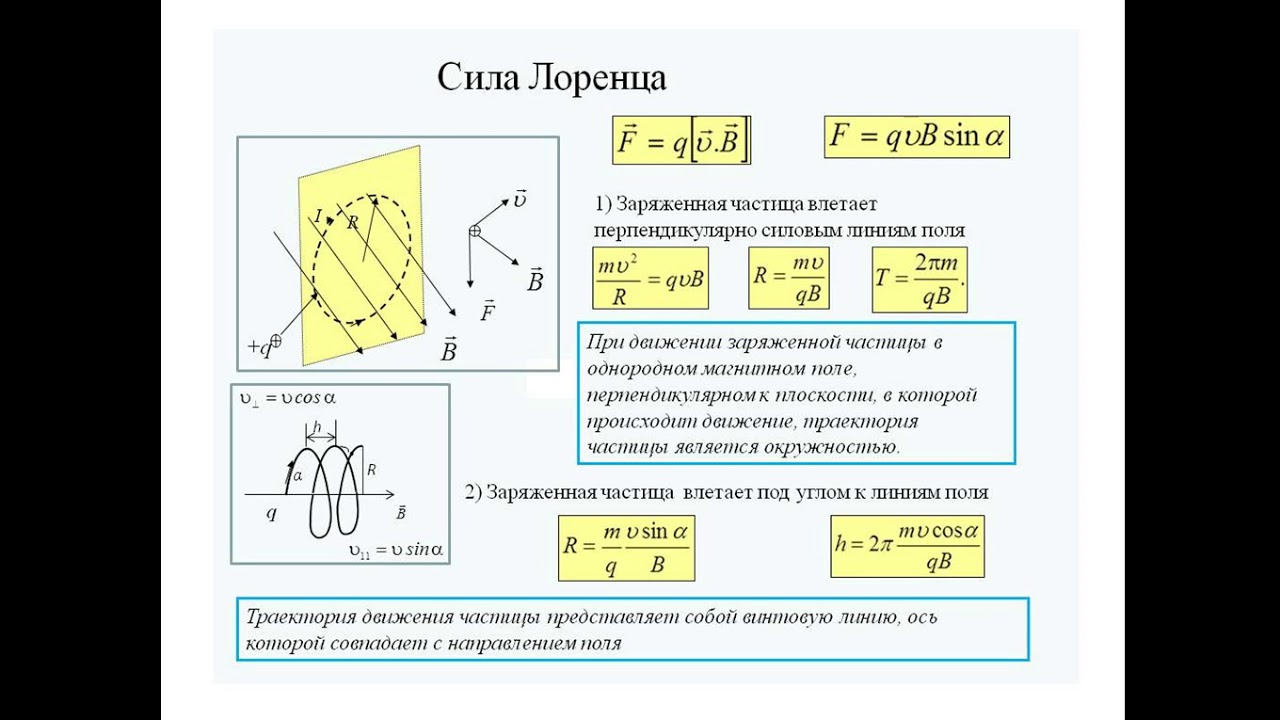 4,б). Вебер полагал, что сохранять свое упорядочение вопреки возмущающему влиянию тепловых колебаний этим элементарным магнитам помогает молекулярное или атомное «трение». Его теория смогла объяснить намагничивание тел при соприкосновении с магнитом, а также их размагничивание при ударе или нагреве; наконец, объяснялось и «размножение» магнитов при разрезании намагниченной иглы или магнитного стержня на части. И все же эта теория не объясняла ни происхождения самих элементарных магнитов, ни явлений насыщения и гистерезиса. Теория Вебера была усовершенствована в 1890 Дж.Эвингом, заменившим его гипотезу атомного трения идеей межатомных ограничивающих сил, помогающих поддерживать упорядочение элементарных диполей, которые составляют постоянный магнит.
4,б). Вебер полагал, что сохранять свое упорядочение вопреки возмущающему влиянию тепловых колебаний этим элементарным магнитам помогает молекулярное или атомное «трение». Его теория смогла объяснить намагничивание тел при соприкосновении с магнитом, а также их размагничивание при ударе или нагреве; наконец, объяснялось и «размножение» магнитов при разрезании намагниченной иглы или магнитного стержня на части. И все же эта теория не объясняла ни происхождения самих элементарных магнитов, ни явлений насыщения и гистерезиса. Теория Вебера была усовершенствована в 1890 Дж.Эвингом, заменившим его гипотезу атомного трения идеей межатомных ограничивающих сил, помогающих поддерживать упорядочение элементарных диполей, которые составляют постоянный магнит.Рис. 4. РАННЯЯ ТЕОРИЯ МАГНЕТИЗМА: предполагалось, что вещество намагничивается, когда его отдельные атомы (каждый из которых является маленьким магнитом), в отсутствие поля расположенные хаотически (а), под действием внешнего поля располагаются в определенном порядке (б).
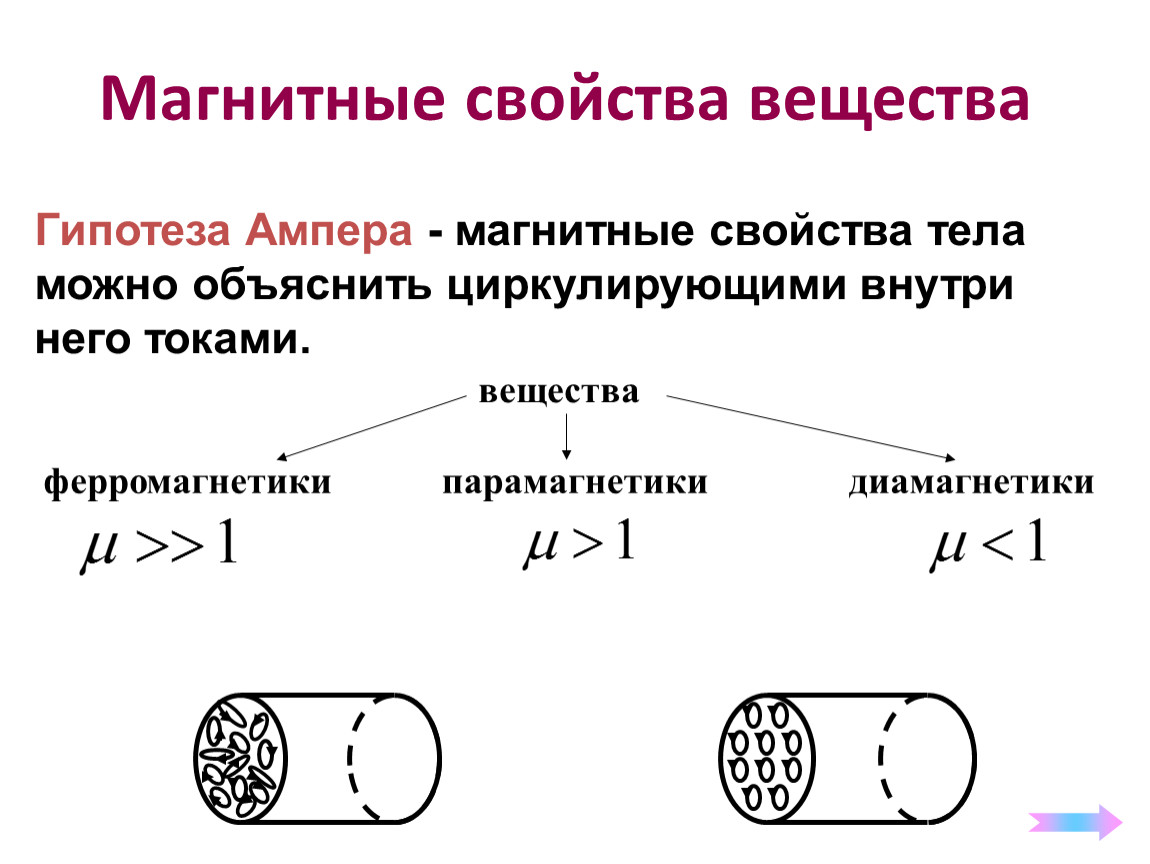
Подход к проблеме, предложенный когда-то Ампером, получил вторую жизнь в 1905, когда П.Ланжевен объяснил поведение парамагнитных материалов, приписав каждому атому внутренний нескомпенсированный электронный ток. Согласно Ланжевену, именно эти токи образуют крошечные магниты, хаотически ориентированные, когда внешнее поле отсутствует, но приобретающие упорядоченную ориентацию после его приложения. При этом приближение к полной упорядоченности соответствует насыщению намагниченности. Кроме того, Ланжевен ввел понятие магнитного момента, равного для отдельного атомного магнита произведению «магнитного заряда» полюса на расстояние между полюсами. Таким образом, слабый магнетизм парамагнитных материалов обусловлен суммарным магнитным моментом, создаваемым нескомпенсированными электронными токами. В 1907 П. Вейс ввел понятие «домена», ставшее важным вкладом в современную теорию магнетизма. Вейс представлял домены в виде небольших «колоний» атомов, в пределах которых магнитные моменты всех атомов в силу каких-то причин вынуждены сохранять одинаковую ориентацию, так что каждый домен намагничен до насыщения.
 Отдельный домен может иметь линейные размеры порядка 0,01 мм и соответственно объем порядка 10-6 мм3. Домены разделены так называемыми блоховскими стенками, толщина которых не превышает 1000 атомных размеров. «Стенка» и два противоположно ориентированных домена схематически изображены на рис. 5. Такие стенки представляют собой «переходные слои», в которых происходит изменение направления намагниченности доменов.
Отдельный домен может иметь линейные размеры порядка 0,01 мм и соответственно объем порядка 10-6 мм3. Домены разделены так называемыми блоховскими стенками, толщина которых не превышает 1000 атомных размеров. «Стенка» и два противоположно ориентированных домена схематически изображены на рис. 5. Такие стенки представляют собой «переходные слои», в которых происходит изменение направления намагниченности доменов.Рис. 5. ДОМЕН в теории магнетизма — это малая намагниченная область материала, в которой моменты атомов параллельны друг другу. Домены отделены друг от друга переходным слоем, называемым блоховской стенкой. Показаны два домена с противоположной ориентацией и блоховская стенка с промежуточной ориентацией.
В общем случае на кривой первоначального намагничивания можно выделить три участка (рис. 6). На начальном участке стенка под действием внешнего поля движется сквозь толщу вещества, пока не встретит дефект кристаллической решетки, который ее останавливает.
 Увеличив напряженность поля, можно заставить стенку двигаться дальше, через средний участок между штриховыми линиями. Если после этого напряженность поля вновь уменьшить до нуля, то стенки уже не вернутся в исходное положение, так что образец останется частично намагниченным. Этим объясняется гистерезис магнита. На конечном участке кривой процесс завершается насыщением намагниченности образца за счет упорядочения намагниченности внутри последних неупорядоченных доменов. Такой процесс почти полностью обратим. Магнитную твердость проявляют те материалы, у которых атомная решетка содержит много дефектов, препятствующих движению междоменных стенок. Этого можно достичь механической и термической обработкой, например путем сжатия и последующего спекания порошкообразного материала. В сплавах алнико и их аналогах тот же результат достигается путем сплавления металлов в сложную структуру.
Увеличив напряженность поля, можно заставить стенку двигаться дальше, через средний участок между штриховыми линиями. Если после этого напряженность поля вновь уменьшить до нуля, то стенки уже не вернутся в исходное положение, так что образец останется частично намагниченным. Этим объясняется гистерезис магнита. На конечном участке кривой процесс завершается насыщением намагниченности образца за счет упорядочения намагниченности внутри последних неупорядоченных доменов. Такой процесс почти полностью обратим. Магнитную твердость проявляют те материалы, у которых атомная решетка содержит много дефектов, препятствующих движению междоменных стенок. Этого можно достичь механической и термической обработкой, например путем сжатия и последующего спекания порошкообразного материала. В сплавах алнико и их аналогах тот же результат достигается путем сплавления металлов в сложную структуру.Рис. 6. КРИВАЯ НАМАГНИЧИВАНИЯ и доминирующие процессы на разных ее участках.
Кроме парамагнитных и ферромагнитных материалов, существуют материалы с так называемыми антиферромагнитными и ферримагнитными свойствами.
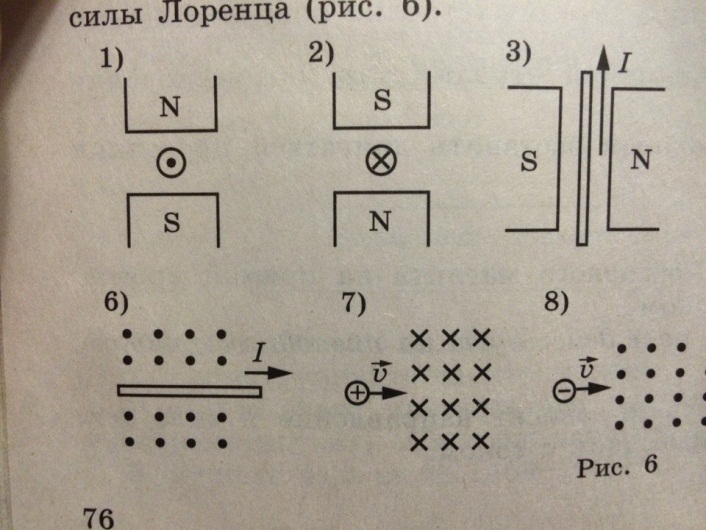 Различие между этими видами магнетизма поясняется на рис. 7. Исходя из представления о доменах, парамагнетизм можно рассматривать как явление, обусловленное наличием в материале небольших групп магнитных диполей, в которых отдельные диполи очень слабо взаимодействуют друг с другом (или вообще не взаимодействуют) и потому в отсутствие внешнего поля принимают лишь случайные ориентации (рис. 7,а). В ферромагнитных же материалах в пределах каждого домена существует сильное взаимодействие между отдельными диполями, приводящее к их упорядоченному параллельному выстраиванию (рис. 7,б). В антиферромагнитных материалах, напротив, взаимодействие между отдельными диполями приводит к их антипараллельному упорядоченному выстраиванию, так что полный магнитный момент каждого домена равен нулю (рис. 7,в). Наконец, в ферримагнитных материалах (например, ферритах) имеется как параллельное, так и антипараллельное упорядочение (рис. 7,г), итогом чего оказывается слабый магнетизм.
Различие между этими видами магнетизма поясняется на рис. 7. Исходя из представления о доменах, парамагнетизм можно рассматривать как явление, обусловленное наличием в материале небольших групп магнитных диполей, в которых отдельные диполи очень слабо взаимодействуют друг с другом (или вообще не взаимодействуют) и потому в отсутствие внешнего поля принимают лишь случайные ориентации (рис. 7,а). В ферромагнитных же материалах в пределах каждого домена существует сильное взаимодействие между отдельными диполями, приводящее к их упорядоченному параллельному выстраиванию (рис. 7,б). В антиферромагнитных материалах, напротив, взаимодействие между отдельными диполями приводит к их антипараллельному упорядоченному выстраиванию, так что полный магнитный момент каждого домена равен нулю (рис. 7,в). Наконец, в ферримагнитных материалах (например, ферритах) имеется как параллельное, так и антипараллельное упорядочение (рис. 7,г), итогом чего оказывается слабый магнетизм.Рис. 7. ТИПЫ УПОРЯДОЧЕНИЯ магнитных моментов атомов в парамагнитных (а), ферромагнитных (б), антиферромагнитных (в) и ферримагнитных (г) веществах.
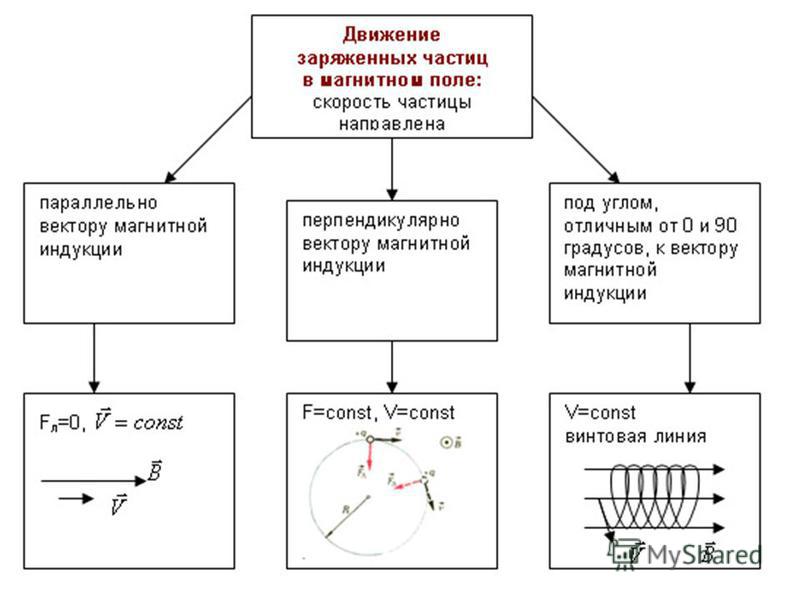
Имеются два убедительных экспериментальных подтверждения существования доменов. Первое из них — так называемый эффект Баркгаузена, второе — метод порошковых фигур. В 1919 Г.Баркгаузен установил, что при наложении внешнего поля на образец из ферромагнитного материала его намагниченность изменяется небольшими дискретными порциями. С точки зрения доменной теории это не что иное, как скачкообразное продвижение междоменной стенки, встречающей на своем пути отдельные задерживающие ее дефекты. Данный эффект обычно обнаруживается с помощью катушки, в которую помещается ферромагнитный стерженек или проволока. Если поочередно подносить к образцу и удалять от него сильный магнит, образец будет намагничиваться и перемагничиваться. Скачкообразные изменения намагниченности образца изменяют магнитный поток через катушку, и в ней возбуждается индукционный ток. Напряжение, возникающее при этом в катушке, усиливается и подается на вход пары акустических наушников. Щелчки, воспринимаемые через наушники, свидетельствует о скачкообразном изменении намагниченности.
 Для выявления доменной структуры магнита методом порошковых фигур на хорошо отполированную поверхность намагниченного материала наносят каплю коллоидной суспензии ферромагнитного порошка (обычно Fe3O4). Частицы порошка оседают в основном в местах максимальной неоднородности магнитного поля — на границах доменов. Такую структуру можно изучать под микроскопом. Был предложен также метод, основанный на прохождении поляризованного света сквозь прозрачный ферромагнитный материал. Первоначальная теория магнетизма Вейса в своих основных чертах сохранила свое значение до настоящего времени, получив, однако, обновленную интерпретацию на основе представления о нескомпенсированных электронных спинах как факторе, определяющем атомный магнетизм. Гипотеза о существовании собственного момента у электрона была выдвинута в 1926 С.Гаудсмитом и Дж.Уленбеком, и в настоящее время в качестве «элементарных магнитов» рассматриваются именно электроны как носители спина. Для пояснения этой концепции рассмотрим (рис.
Для выявления доменной структуры магнита методом порошковых фигур на хорошо отполированную поверхность намагниченного материала наносят каплю коллоидной суспензии ферромагнитного порошка (обычно Fe3O4). Частицы порошка оседают в основном в местах максимальной неоднородности магнитного поля — на границах доменов. Такую структуру можно изучать под микроскопом. Был предложен также метод, основанный на прохождении поляризованного света сквозь прозрачный ферромагнитный материал. Первоначальная теория магнетизма Вейса в своих основных чертах сохранила свое значение до настоящего времени, получив, однако, обновленную интерпретацию на основе представления о нескомпенсированных электронных спинах как факторе, определяющем атомный магнетизм. Гипотеза о существовании собственного момента у электрона была выдвинута в 1926 С.Гаудсмитом и Дж.Уленбеком, и в настоящее время в качестве «элементарных магнитов» рассматриваются именно электроны как носители спина. Для пояснения этой концепции рассмотрим (рис.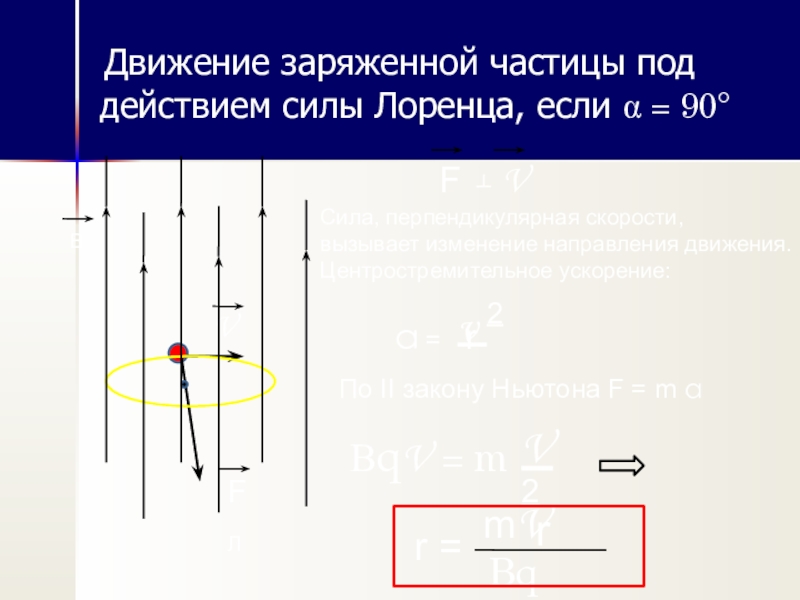 8) свободный атом железа — типичного ферромагнитного материала. Две его оболочки (K и L), ближайшие к ядру, заполнены электронами, причем на первой из них размещены два, а на второй — восемь электронов. В K-оболочке спин одного из электронов положителен, а другого — отрицателен. В L-оболочке (точнее, в двух ее подоболочках) у четырех из восьми электронов положительные, а у других четырех — отрицательные спины. В обоих случаях спины электронов в пределах одной оболочки полностью компенсируются, так что полный магнитный момент равен нулю. В M-оболочке ситуация иная, поскольку из шести электронов, находящихся в третьей подоболочке, пять электронов имеют спины, направленные в одну сторону, и лишь шестой — в другую. В результате остаются четыре нескомпенсированных спина, чем и обусловлены магнитные свойства атома железа. (Во внешней N-оболочке всего два валентных электрона, которые не дают вклада в магнетизм атома железа.) Сходным образом объясняется магнетизм и других ферромагнетиков, например никеля и кобальта. Поскольку соседние атомы в образце железа сильно взаимодействуют друг с другом, причем их электроны частично коллективизируются, такое объяснение следует рассматривать лишь как наглядную, но весьма упрощенную схему реальной ситуации.
8) свободный атом железа — типичного ферромагнитного материала. Две его оболочки (K и L), ближайшие к ядру, заполнены электронами, причем на первой из них размещены два, а на второй — восемь электронов. В K-оболочке спин одного из электронов положителен, а другого — отрицателен. В L-оболочке (точнее, в двух ее подоболочках) у четырех из восьми электронов положительные, а у других четырех — отрицательные спины. В обоих случаях спины электронов в пределах одной оболочки полностью компенсируются, так что полный магнитный момент равен нулю. В M-оболочке ситуация иная, поскольку из шести электронов, находящихся в третьей подоболочке, пять электронов имеют спины, направленные в одну сторону, и лишь шестой — в другую. В результате остаются четыре нескомпенсированных спина, чем и обусловлены магнитные свойства атома железа. (Во внешней N-оболочке всего два валентных электрона, которые не дают вклада в магнетизм атома железа.) Сходным образом объясняется магнетизм и других ферромагнетиков, например никеля и кобальта. Поскольку соседние атомы в образце железа сильно взаимодействуют друг с другом, причем их электроны частично коллективизируются, такое объяснение следует рассматривать лишь как наглядную, но весьма упрощенную схему реальной ситуации.Рис. 8. НЕСКОМПЕНСИРОВАННЫЕ ЭЛЕКТРОННЫЕ СПИНЫ как причина магнетизма. Изображены оболочки и подоболочки свободного атома железа, имеющего четыре нескомпенсированных электронных спина в 3d-подоболочке М-оболочки, которыми и обусловлены магнитные свойства железа.
Теорию атомного магнетизма, основанную на учете спина электрона, подкрепляют два интересных гиромагнитных эксперимента, один из которых был проведен А. Эйнштейном и В.де Гаазом, а другой — С.Барнеттом. В первом из этих экспериментов цилиндрик из ферромагнитного материала подвешивался так, как показано на рис. 9. Если по проводу обмотки пропустить ток, то цилиндрик поворачивается вокруг своей оси. При изменении направления тока (а следовательно, и магнитного поля) он поворачивается в обратном направлении. В обоих случаях вращение цилиндрика обусловлено упорядочением электронных спинов. В эксперименте Барнетта, наоборот, так же подвешенный цилиндрик, резко приведенный в состояние вращения, в отсутствие магнитного поля намагничивается. Этот эффект объясняется тем, что при вращении магнетика создается гироскопический момент, стремящийся повернуть спиновые моменты по направлению собственной оси вращения.
Рис. 9. ЭКСПЕРИМЕНТ ЭЙНШТЕЙНА — ДЕ ГААЗА. При пропускании тока по обмотке, охватывающей ферромагнитный цилиндрик, последний поворачивается в направлении стрелки. Если изменить направление тока, то цилиндрик поворачивается в другую сторону.
За более полным объяснением природы и происхождения короткодействующих сил, упорядочивающих соседние атомные магнитики и противодействующих разупорядочивающему влиянию теплового движения, следует обратиться к квантовой механике. Квантово-механическое объяснение природы этих сил было предложено в 1928 В.Гейзенбергом, который постулировал существование обменных взаимодействий между соседними атомами. Позднее Г.Бете и Дж.Слэтер показали, что обменные силы существенно возрастают с уменьшением расстояния между атомами, но по достижении некоторого минимального межатомного расстояния падают до нуля.
МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
Одно из первых обширных и систематических исследований магнитных свойств вещества было предпринято П.Кюри. Он установил, что по своим магнитным свойствам все вещества можно разделить на три класса. К первому относятся вещества с резко выраженными магнитными свойствами, подобными свойствам железа. Такие вещества называются ферромагнитными; их магнитное поле заметно на значительных расстояниях (см. выше). Во второй класс попадают вещества, называемые парамагнитными; магнитные свойства их в общем аналогичны свойствам ферромагнитных материалов, но гораздо слабее. Например, сила притяжения к полюсам мощного электромагнита может вырвать из ваших рук железный молоток, а чтобы обнаружить притяжение парамагнитного вещества к тому же магниту, нужны, как правило, очень чувствительные аналитические весы. К последнему, третьему классу относятся так называемые диамагнитные вещества. Они отталкиваются электромагнитом, т.е. сила, действующая на диамагнетики, направлена противоположно той, что действует на ферро- и парамагнетики.
Измерение магнитных свойств. При изучении магнитных свойств наиболее важное значение имеют измерения двух типов. Первый из них -измерения силы, действующей на образец вблизи магнита; так определяется намагниченность образца. Ко второму относятся измерения «резонансных» частот, связанных с намагничением вещества. Атомы представляют собой крошечные «гироскопы» и в магнитном поле прецессируют (как обычный волчок под влиянием вращающего момента, создаваемого силой тяжести) с частотой, которая может быть измерена. Кроме того, на свободные заряженные частицы, движущиеся под прямым углом к линиям магнитной индукции, действует сила, как и на электронный ток в проводнике. Она заставляет частицу двигаться по круговой орбите, радиус которой дается выражением R = mv/eB, где m — масса частицы, v — ее скорость, e — ее заряд, а B — магнитная индукция поля. Частота такого кругового движения равна
где f измеряется в герцах, e — в кулонах, m — в килограммах, B — в теслах. Эта частота характеризует движение заряженных частиц в веществе, находящемся в магнитном поле. Оба типа движений (прецессию и движение по круговым орбитам) можно возбудить переменными полями с резонансными частотами, равными «естественным» частотам, характерным для данного материала. В первом случае резонанс называется магнитным, а во втором — циклотронным (ввиду сходства с циклическим движением субатомной частицы в циклотроне). Говоря о магнитных свойствах атомов, необходимо особо остановиться на их моменте импульса. Магнитное поле действует на вращающийся атомный диполь, стремясь повернуть его и установить параллельно полю. Вместо этого атом начинает прецессировать вокруг направления поля (рис. 10) с частотой, зависящей от дипольного момента и напряженности приложенного поля.
Рис. 10. ПРЕЦЕССИЯ АТОМА. Атом с магнитным моментом p прецессирует в магнитном поле с индукцией B.
Прецессия атомов не поддается непосредственному наблюдению, поскольку все атомы образца прецессируют в разной фазе. Если же приложить небольшое переменное поле, направленное перпендикулярно постоянному упорядочивающему полю, то между прецессирующими атомами устанавливается определенное фазовое соотношение и их суммарный магнитный момент начинает прецессировать с частотой, равной частоте прецессии отдельных магнитных моментов. Важное значение имеет угловая скорость прецессии. Как правило, это величина порядка 1010 Гц/Тл для намагниченности, связанной с электронами, и порядка 107 Гц/Тл для намагниченности, связанной с положительными зарядами в ядрах атомов. Принципиальная схема установки для наблюдения ядерного магнитного резонанса (ЯМР) представлена на рис. 11. В однородное постоянное поле между полюсами вводится изучаемое вещество. Если затем с помощью небольшой катушки, охватывающей пробирку, возбудить радиочастотное поле, то можно добиться резонанса на определенной частоте, равной частоте прецессии всех ядерных «гироскопов» образца. Измерения сходны с настройкой радиоприемника на частоту определенной станции.
Рис. 11. ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС. Исследуемое вещество в стеклянной пробирке помещается в постоянное магнитное поле. В катушке, намотанной на пробирку, возбуждается резонанс на частоте, равной частоте гироскопической прецессии атома в магнитном поле.
Методы магнитного резонанса позволяют исследовать не только магнитные свойства конкретных атомов и ядер, но и свойства их окружения. Дело в том, что магнитные поля в твердых телах и молекулах неоднородны, поскольку искажены атомными зарядами, и детали хода экспериментальной резонансной кривой определяются локальным полем в области расположения прецессирующего ядра. Это и дает возможность изучать особенности структуры конкретного образца резонансными методами.
Расчет магнитных свойств. Магнитная индукция поля Земли составляет 0,5*10 -4 Тл, тогда как поле между полюсами сильного электромагнита — порядка 2 Тл и более. Магнитное поле, создаваемое какой-либо конфигурацией токов, можно вычислить, пользуясь формулой Био — Савара — Лапласа для магнитной индукции поля, создаваемого элементом тока. Расчет поля, создаваемого контурами разной формы и цилиндрическими катушками, во многих случаях весьма сложен. Ниже приводятся формулы для ряда простых случаев. Магнитная индукция (в теслах) поля, создаваемого длинным прямым проводом с током I (ампер), на расстоянии r (метров) от провода равна
Индукция в центре кругового витка радиуса R с током I равна (в тех же единицах):
Плотно намотанная катушка провода без железного сердечника называется соленоидом. Магнитная индукция, создаваемая длинным соленоидом c числом витков N в точке, достаточно удаленной от его концов, равна
Здесь величина NI/L есть число ампер (ампер-витков) на единицу длины соленоида. Во всех случаях магнитное поле тока направлено перпендикулярно этому току, а сила, действующая на ток в магнитном поле, перпендикулярна и току, и магнитному полю. Поле намагниченного железного стержня сходно с внешним полем длинного соленоида с числом ампер-витков на единицу длины, соответствующим току в атомах на поверхности намагниченного стержня, поскольку токи внутри стержня взаимно компенсируются (рис. 12). По имени Ампера такой поверхностный ток называется амперовским. Напряженность магнитного поля Ha, создаваемая амперовским током, равна магнитному моменту единицы объема стержня M.
Рис. 12. АТОМНЫЕ ТОКИ внутри намагниченного стержня полностью компенсируют друг друга, так что остается лишь амперовский ток на его поверхности.
Если в соленоид вставлен железный стержень, то кроме того, что ток соленоида создает магнитное поле H, упорядочение атомных диполей в намагниченном материале стержня создает намагниченность M. В этом случае полный магнитный поток определяется суммой реального и амперовского токов, так что B = m0(H + Ha), или B = m0(H + M). Отношение M/H называется магнитной восприимчивостью и обозначается греческой буквой c; c — безразмерная величина, характеризующая способность материала намагничиваться в магнитном поле.
Величина B/H, характеризующая магнитные свойства
материала, называется магнитной проницаемостью и обозначается через ma, причем ma = m0m, где ma — абсолютная, а m — относительная проницаемости, m = 1 + c. В ферромагнитных веществах величина c может иметь очень большие значения -до 10 4-10 6. Величина c у парамагнитных материалов немного больше нуля, а у диамагнитных — немного меньше. Лишь в вакууме и в очень слабых полях величины c и m постоянны и не зависят от внешнего поля. Зависимость индукции B от H обычно нелинейна, а ее графики, т.н. кривые намагничивания, для разных материалов и даже при разных температурах могут существенно различаться (примеры таких кривых приведены на рис. 2 и 3). Магнитные свойства вещества весьма сложны, и для их глубокого понимания необходим тщательный анализ строения атомов, их взаимодействий в молекулах, их столкновений в газах и их взаимного влияния в твердых телах и жидкостях; магнитные свойства жидкостей пока наименее изучены.
ЛИТЕРАТУРА
Карцев В.П. Магнит за три тысячелетия. М., 1972 Ахиезер А.И. Общая физика. Электрические и магнитные явления. Киев, 1981 Мишин Д.Д. Магнитные материалы. М., 1981 Каганов М.И., Цукерник В.М. Природа магнетизма. М., 1982 Белов К.П., Бочкарев Н.Г. Магнетизм на Земле и в космосе. М., 1983 Вонсовский С.В. Магнетизм. М., 1984 Мнеян М.Г. Новые профессии магнита. М., 1985
Энциклопедия Кольера. — Открытое общество. 2000.
- СВЕТ
- МЕХАНИКА
Полезное
Смотреть что такое «МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА» в других словарях:
СВЕРХСИЛЬНЫЕ МАГНИТНЫЕ ПОЛЯ — поля с напряжённостью Н?0,5=1,0 МЭ (граница условна). Нижнее значение С. м. п. соответствует макс. значению стационарного поля =500 кЭ, к рое может быть доступно средствам совр. техники, верхнее полю 1 МЭ, даже кратковрем. воздействие к рого… … Физическая энциклопедия
ФИЗИКА ТВЕРДОГО ТЕЛА — раздел физики, изучающий структуру и свойства твердых тел. Научные данные о микроструктуре твердых веществ и о физических и химических свойствах составляющих их атомов необходимы для разработки новых материалов и технических устройств. Физика… … Энциклопедия Кольера
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ — раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера
ФИЗИКА — (от древнегреч. physis природа). Древние называли физикой любое исследование окружающего мира и явлений природы. Такое понимание термина физика сохранилось до конца 17 в. Позднее появился ряд специальных дисциплин: химия, исследующая свойства… … Энциклопедия Кольера
МОМЕНТЫ АТОМОВ И ЯДЕР — Термин момент применительно к атомам и атомным ядрам может означать следующее: 1) спиновый момент, или спин, 2) магнитный дипольный момент, 3) электрический квадрупольный момент, 4) прочие электрические и магнитные моменты. Различные типы… … Энциклопедия Кольера
СЕГНЕТОЭЛЕКТРИЧЕСТВО — электрический аналог ферромагнетизма. Подобно тому как в ферромагнитных веществах при помещении их в магнитное поле проявляется остаточная магнитная поляризация (момент), в сегнетоэлектрических диэлектриках, помещенных в электрическое поле,… … Энциклопедия Кольера
МАГНИТНЫЙ РЕЗОНАНС — резонансное (избирательное) поглощение радиочастотного излучения некоторыми атомными частицами, помещенными в постоянное магнитное поле. Большинство элементарных частиц, подобно волчкам, вращаются вокруг собственной оси. Если частица обладает… … Энциклопедия Кольера
МАГНИТНАЯ ГИДРОДИНАМИКА — (сокращенно МГД), раздел науки, занимающийся взаимодействием электропроводящих потоков с электрическим и магнитным полями. Когда в поперечном магнитном поле движется текучая среда, проводящая электричество, в ней наводятся токи. Эти токи вызывают … Энциклопедия Кольера
МЕТАЛЛОВЕДЕНИЕ ФИЗИЧЕСКОЕ — применение физических принципов и экспериментальных методов для изучения и целенаправленного улучшения характеристик металлов и сплавов. Среди экспериментальных методов, применяемых к металлам и сплавам, ведущим является микроскопия.… … Энциклопедия Кольера
магнитотвёрдые материалы — (магнитожёсткие материалы), намагничиваются до насыщения и перемагничиваются в сравнительно сильных магнитных полях напряжённостью в тысячи и десятки тысяч А/м. Характеризуются высокими значениями коэрцитивной силы, остаточной магнитной индукции … Энциклопедический словарь
Магнитные свойства материи — определение, диаметр и парамагнетизм
Магнитные силы опосредуют подмножество физического явления, известного как магнетизм. Магнетизм материи — это сила, проявляемая магнитами, когда они притягиваются или отталкиваются друг от друга. Магнитные моменты и электрические токи основных частиц создают магнитное поле, которое действует на другие магнитные моменты и моменты тока. Магнитное состояние материала на основе давления, температуры и приложенного магнитного поля.Когда эти переменные меняются, вещество может проявлять несколько форм магнетизма. Магнитные свойства материи можно найти в различных материалах Земли, которые действуют как изоляторы и проводники разной степени и формы.
Майкл Фарадей — первый статистик, который классифицирует вещества по их магнитным свойствам в 19 веке. Сила магнитного поля всегда уменьшается с расстоянием, хотя требуемое математическое соотношение между силой и расстоянием меняется.
Магнитные диполи были признаны, хотя некоторые теории предсказывают существование магнитных монополей.
[Изображение будет загружено в ближайшее время]
Все знают эти четыре основных факта о поведении магнитов:
У магнита есть две конечные точки, называемые полюсами, одна называется северным полюсом или также называется полюсом, направленным на север, и другой называется южным полюсом или также называется полюсом поиска на юг.
Северный полюс первого магнита притягивает южный полюс второго магнита, в то время как северный полюс первого магнита отталкивает полюс второго магнита.
Магнит создает магнитное поле и представляет собой нематериальную сферу магнетизма по всей его поверхности.
Северный полюс магнита примерно направлен к северному полюсу Земли и наоборот. Это потому, что сама Земля состоит из магнитных материалов и ведет себя как гигантский магнит.
Источник магнетизма
Магнетизм происходит от двух источников:
Электрический ток.
Спиновые магнитные моменты элементарных частиц.
Магнитные свойства вещества в основном обусловлены магнитными моментами атомов, вращающихся вокруг электронов. Магнитные моменты ядер атомов очень малы, чем «магнитные» моменты электронов, поэтому они пренебрежимо малы в условиях намагничивания материалов.
Кроме того, это часто происходит даже тогда, когда электронная конфигурация такова, что есть неспаренные электроны, а также незаполненные подоболочки. В этом случае различные электроны в твердом состоянии будут давать магнитные моменты этой точки в разных случайных направлениях, так что материал не будет магнитным.Следовательно, магнитное поведение материала зависит от его структуры, в частности, от его электронной конфигурации, а также от температуры. В зависимости от того, существует ли притяжение или отталкивание между северным и южным полюсами магнита, материя классифицируется как парамагнитная или диамагнитная соответственно.
Магнитные свойства вещества
Существует несколько свойств магнетизма материи, включая намагниченность, диамагнетизм и парамагнетизм соответственно.
Намагничивание
В этом разделе мы узнаем о намагничивании и концепции магнитной напряженности.
В электромагнетизме намагниченность, также называемая магнитной поляризацией, представляет собой векторное поле, которое способствует измерению плотности индуцированного или постоянного магнитного дипольного момента в данном магнитном материале. Намагниченность — это магнетизм материи, открытый Уильямом Гилбертом. Изменения в этой ветви описываются направлением и могут быть осевыми или диаметральными.Как мы знаем, намагниченность возникает в результате магнетизма, который возникает в результате движения электронов в атомах или спина электронов в атоме или ядрах.
Теория намагничивания помогает нам классифицировать материалы на основе их магнитных свойств. Чистая намагниченность — это результат реакции материала на внешнее магнитное поле. Намагниченность материала образца M называется чистым магнитным моментом для этого материала на единицу объема. Математическая формула поля намагничивания или M-поля:
M = \ [\ frac {m_ {net}} {V} \]
[Изображение будет загружено в ближайшее время]
В магнитном поле парамагнитные материалы имеют слабый индуцированный магнетизм, который исчезает, когда магнитное поле устраняется, и ферромагнетики и ферримагнетики обладают сильной намагниченностью.Его можно намагнитить, чтобы сохранить свой магнетизм в отсутствие внешнего поля, что приведет к созданию постоянного магнита.
Диамагнетизм
Майкл Фарадей открыл диамагнетизм в сентябре 1845 года. Это слабая форма магнетизма, которая возникает в присутствии внешнего магнитного поля. Это создает очень маленький магнитный момент в направлении, противоположном направлению приложенного поля. Диамагнетизм — это магнетизм вещества, в котором материалы противостоят магнитным полем, приложенное магнитное поле создает в них индуцированное магнитное поле, которое обычно имеет противоположное направление, вызывая силу отталкивания.Кроме того, парамагнитные и ферромагнитные материалы притягиваются магнитным полем.
При размещении внутри сильные диамагнитные и электромагнитные материалы притягиваются к областям, где магнитное поле слабое. В ферромагнетиках и парамагнетиках слабая диамагнитная сила контролируется силой притяжения магнитных диполей в материале.
[Изображение будет загружено в ближайшее время]
Диамагнетизм был впервые обнаружен Майклом Фарадеем в 1845 году.Кроме того, когда Антон Бругманс заметил в 1778 году, что висмуту противодействуют магнитные поля. В химии используется простое эмпирическое правило, чтобы определить, является ли частица, атом или железо парамагнитными или диамагнитными материалами. В диамагнитном материале все электроны в атоме спарены, и вещество состоит из этого атома. Парамагнитный материал имеет неспаренный электрон.
Парамагнетизм
Парамагнетизм имеет неспаренный электрон в материале, поэтому большинство атомов не полностью заполнены атомными орбиталями.Отсюда этот атом называется парамагнетизмом. Парамагнетизм — это форма магнетизма, при которой несколько материалов слабо притягиваются сильным магнитным полем. Кроме того, парамагнетизм создает магнитное поле в направлении приложенного магнитного поля. Парамагнетизм был открыт британским ученым Майклом Фарадеем в 1845 году. Материалы, образующие парамагнетизм, называются парамагнетиками. Следовательно, истинные парамагнетики имеют магнитную восприимчивость, соответствующую законам Кюри-Вейсса, и проявляют парамагнетизм в широком диапазоне температур.
Этот тип намагничивания зависит от закона Кюри. Согласно закону Кюри, у парамагнитных материалов магнитная восприимчивость χ обратно пропорциональна их температуре. Он представлен как;
M = χH = C / T x H
Где,
M = намагниченность,
χ = магнитная восприимчивость,
C = зависящая от материала константа Кюри,
T = абсолютная (по Кельвину) температура,
H = дополнительное магнитное поле.
[Изображение будет загружено в ближайшее время]
Вот несколько примеров парамагнитных материалов, алюминия, кислорода, титана и оксида железа (FeO).Кроме того, в химии используется простое практическое правило, чтобы определить, является ли частица, атом или молекула парамагнитными или диамагнитными. Это правило зависит от парного или неспаренного электрона.
Добро пожаловать в экспериментальную лабораторию Donald A. Glaser Physics 111 B
Профессор Дональд А. Глейзер на протяжении всей своей карьеры был мастером экспериментальной науки. Он родился в Кливленде, получил образование в Технологическом институте Кейса, получил докторскую степень в Калифорнийском технологическом институте и преподавал в Мичиганском университете, прежде чем занять должность в Калифорнийском университете в Беркли в 1959 году.В начале своей карьеры доктор Глейзер экспериментировал со способами сделать работу субатомных частиц видимой. За последующее изобретение пузырьковой камеры он был удостоен Нобелевской премии по физике 1960 года. Затем он начал исследовать новую область молекулярной биологии, совершенствуя методы работы с бактериальными фагами, бактериями и клетками млекопитающих. Разрабатывая оборудование для автоматизации своих экспериментов и их масштабирования, он мог проводить тысячи экспериментов одновременно, генерируя достаточно данных, чтобы продвинуть науку вперед.Осознавая последствия для медицины, доктор Глейзер и двое его друзей создали в 1971 году новаторскую биотехнологическую компанию Cetus Corporation, тем самым положив начало индустрии генной инженерии.
Позже в своей карьере доктор Глейзер продолжил свои экспериментальные исследования, разработав математические модели для понимания фундаментальных процессов человеческого зрения. На протяжении всей своей жизни он сочетал научную работу с не менее страстным интересом к классической музыке, везде играл на альте в ансамблях камерной музыки.Жадно любопытный, новаторский и преданный развитию научных знаний, доктор Глейзер был очень востребованным консультантом и советником до своей смерти в 2013 году.
Экспериментальная лабораторияPhysics 111 — это интенсивный лабораторный курс из трех частей для студентов 3-го и 4-го курсов физики в Калифорнийском университете в Беркли. Он следует за приборной лабораторией Physics 111A , которая знакомит студентов с электроникой, методами измерения, обработкой сигналов, компьютеризированным сбором данных и управлением.С помощью этих инструментов учащиеся секции «Экспериментальная лаборатория» курса «Физика 111» проводят четыре эксперимента, на выполнение каждого из которых уходит около 2 недель. Студенты выбирают эти эксперименты из 19 или около того экспериментов, постоянно установленных в 111-Lab. Они представляют широкий спектр тем и методов, используемых в экспериментальной физике. Многие эксперименты повторяют исследования, получившие Нобелевскую премию, и все они предназначены для развития навыков, необходимых для исследования.
Что делать в первую очередь Перед тем, как прийти в лабораторию по физике 111-Lab
- Чтобы уменьшить накладные расходы и риск получения несогласованных данных, вы должны убедиться, что у вас есть блоки последовательных дней для завершения некоторых экспериментов (см. Список доступных экспериментов для этого требования Подписки оборудования).
- Все студенты входят в bCourses, заполняют карточку подписи и отправляют ее через Интернет, прежде чем вы придете в лабораторию. Вы должны выполнить это, прежде чем начинать что-либо в лаборатории.
- Все ученики приходят на ознакомительную встречу в 251 LeConte Hall в первый учебный день в 14:10.
- Каждый студент должен иметь свою фотографию в Калифорнийском университете на сайте bCourses Беркли. Если НЕТ, вы должны сдать ФОТОГРАФИЮ НА ПАСПОРТ (не свой паспорт, а настоящую фотографию паспортного типа) в первый день Лаборатории в целях безопасности.
- Все студенты экспериментальной лаборатории по физике 111B должны выполнить упражнение по анализу ошибок , назначенное в течение первой недели (см. Сроки выполнения).
- Приготовьтесь к одному обязательному устному докладу с профессором. Это может быть первый, второй или третий эксперимент.
- При доступе к компьютерам 111B-Lab, если вы НЕ можете войти в систему, сделайте следующее:
Перейдите в Calnet Active Directory и синхронизируйте свое имя CalNet.
Внимание: в 111-Lab НИКОГДА нельзя есть и пить, кроме как на скамейках с СИНЕЙ полосой вокруг в комнатах 282 и 286 LeConte .
В начало
В начало
В начало
Об этом сайте
Этот сайт дополняет сайт «Инструменты» Physics 111A Instrumentation Course, предоставляя лабораторные руководства для каждого эксперимента в Physics 111B Experimentation Laboratory . Каждая ссылка в меню «Эксперименты в экспериментальной лаборатории» вверху ведет на страницы, содержащие руководство по эксперименту, которое включает вопросы перед лабораторией, вопросы промежуточной лаборатории, справочные материалы, теорию и инструкции.
В начало
Для студентов, обучающихся на данном курсеВы можете просматривать и распечатывать любые страницы на сайте экспериментальной лаборатории, не имея учетной записи или входа в систему.
Если вы видите ошибки в описаниях лабораторных работ или в местах, которые нуждаются в улучшении, поговорите со своими инструкторами или Winthrop Williams . Они могут быстро редактировать страницы, внося незначительные изменения, чтобы следующий учащийся получил улучшенную версию. Если вы видите необходимость внесения значительных изменений, распечатайте страницу и напишите свои предложения, чтобы передать их инструктору.Вы также можете написать комментарии в оценочном опросе внизу описания, и мы внесем изменения по мере необходимости, если они предложат некоторые полезные улучшения. Мы действительно ценим вклад студентов в улучшение лабораторных работ.
В начало
Для других посетителейЭтот сайт открыт для всех, но не для редактирования и комментирования. Авторские права принадлежат Регентам Калифорнийского университета. Однако мы с радостью предоставляем контент другим школам для некоммерческого использования в образовательных целях.Некоторые ссылки на защищенные авторским правом ссылки и программное обеспечение недоступны никому без аутентификации в качестве студента или сотрудника Physics 111.
В начало
В начало
БлагодарностиЭтот сайт был разработан Доном Орландо и Сегре Студентами. Стажер Segrè, Натан Белмор, потратил большую часть июля 2014 года на преобразование лабораторных отчетов из Wiki в Drupal, разработку нового веб-сайта и преобразование всех кодов.Уинтроп Уильямс в настоящее время администрирует веб-страницы. Преподавательский состав и Уинтроп Уильямс занимаются редактированием и обслуживанием.
Персонал лаборатории:
В начало
Домашняя страница физического факультета
Электромагнитная сила — Energy Education
Электромагнитная сила , также называемая силой Лоренца , объясняет, как взаимодействуют движущиеся и неподвижные заряженные частицы. Это называется электромагнитной силой, потому что она включает ранее отличавшиеся друг от друга электрическую силу и магнитную силу; магнитные силы и электрические силы на самом деле являются одной и той же фундаментальной силой. [1] Электромагнитная сила — одна из четырех основных сил.
Электрическая сила действует между всеми заряженными частицами, независимо от того, движутся они или нет. [1] Магнитная сила действует между движущимися заряженными частицами. Это означает, что каждая заряженная частица излучает электрическое поле, независимо от того, движется она или нет. Движущиеся заряженные частицы (например, находящиеся в электрическом токе) излучают магнитные поля. Эйнштейн разработал свою теорию относительности, исходя из того, что если наблюдатель движется вместе с заряженными частицами, магнитные поля трансформируются в электрические и наоборот! Одним из частных случаев электромагнитной силы, когда все заряды являются точечными (или могут быть разбиты на точечные заряды), является закон Кулона.
Поскольку вычисление силы каждого отдельного заряда на каждый другой отдельный заряд смехотворно сложно, физики разработали инструменты для упрощения этих расчетов. Эти упрощенные вычисления превращаются в макроскопические повседневные явления, перечисленные ниже:
- повседневных сил нравится
- большая часть химии
- удерживая атомы вместе
- химические связи между атомами с образованием молекул, как при горении
- сохранение твердой формы определенной формы
- Липкие предметы, такие как клейкая лента или смола, прилипающие к поверхностям
- Магниты для наклеивания картин на холодильник
- Сила, ощущаемая электронами в проволочной петле, когда они находятся рядом с изменяющимся магнитным полем.Электромагнитная сила очень тесно связана с электродвижущей силой, которая заставляет электрический ток течь.
Современная физика объединила электромагнитные и слабые силы в электрослабую. Полное понимание электромагнитной силы и всех последствий электромагнетизма требует многих лет изучения. Некоторые хорошие места, где можно найти дополнительную информацию об электромагнетизме, включают гиперфизику.
Ниже представлены серии Scishow по фундаментальным силам, часть 4a (электричество) и 4b (магнетизм):
А вот и часть 2.
Другие видеоролики посвящены сильному ядерному взаимодействию, слабому ядерному взаимодействию и гравитации. Посетите их канал на YouTube, чтобы увидеть больше подобных видео! (замечательный ресурс для любознательных).
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
- ↑ 1.0 1.1 Р. Д. Найт, «Закон силы Лоренца» в журнале Physics for Scientists and Engineers: A Strategic Approach, 3-е изд.Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 35, раздел 5, стр. 1096-1097.
Страница не найдена — Vijaya College
404 Страница не найдена
Вернуться на главную Виджая колледж% PDF-1.5 % 1 0 объект > / Метаданные 2 0 R / PageLayout / OneColumn / Pages 3 0 R / StructTreeRoot 5 0 R / Тип / Каталог >> эндобдж 2 0 obj > поток 2013-08-15T13: 48: 26-07: 002013-08-15T13: 48: 19-07: 002013-08-15T13: 48: 26-07: 00Acrobat PDFMaker 10.1 для Worduuid: 0e0a0fa3-55e0-4c9f-a67b- 59b8cbbe3f23uuid: 4d456159-bc0e-4613-8a67-f3e0f0271ad0
Сдвиговые волны, индуцированные силой Лоренца для приложений магнитно-резонансной эластографии
Предлагаемый Метод заключается в создании плотности силы Лоренца в гелях, имитирующих ткань (фантомах), которые, в свою очередь, вызывают сдвиговые волны, которые регистрируются с помощью клинической системы МРТ и обрабатываются для получения информации об эластичности. Выражение плотности силы Лоренца [Nm -3 ] дается как
$$ {\ varvec {f}} = {\ varvec {j}} \ times {\ varvec {B}} $$
(1)
, где \ ({\ varvec {j}} \) — плотность тока [А · м −2 ] и \ ({\ varvec {B}} \) магнитное поле [Тл] 35 .Здесь сильное однородное магнитное поле МР-сканера и приложенные извне токи использовались для создания силы Лоренца.
Экспериментальная установка
Во всех экспериментах, описанных в настоящей рукописи, фантомы агара были залиты в 3D-печатную форму и пересечены электрическим током \ ({\ varvec {j}} \) и магнитным полем \ ({\ varvec {B}} \) (рис. 1а). Подробная информация о различных используемых фантомах представлена в абзацах ниже и в таблице 1. Солевые ванны (20% масс.) Были спроектированы с двух сторон держателя фантома для обеспечения электрического контакта между фантомом и внешними электродами.Это позволило избежать механических контактов между электродами и фантомом, что позволило изолировать плотность силы Лоренца как источник движения (т.е. избежать артефактов движения). Электрический ток подводился с помощью электродов (медных проводов), погруженных в физиологический раствор. Провода помещали параллельно направлению статического магнитного поля от конца отверстия к держателю фантома и удерживали прикрепленными сверху держателя фантома к солевым ваннам. Особое внимание было уделено тому, чтобы избежать механических контактов между проводами и остальной частью установки, чтобы исключить другие артефакты движения.Фантом помещали в 32-канальную головную катушку только для приема в канале МРТ-сканера 3 Т (Achieva TX, Philips Healthcare, Best, Нидерланды). Катушка была расположена в изоцентре отверстия, чтобы минимизировать вихревые токи и облегчить воспроизводимость экспериментов. Фантом был ориентирован вдоль магнитного поля (ось z, красная стрелка на рис. 1a), и ток в основном протекал вдоль оси y (зеленая стрелка на рис. 1a) между двумя электродами, так что магнитное поле и ток были перпендикулярны.Индуцированная сила Лоренца колебалась вдоль оси x (черная стрелка на рис. 1а) с частотой тока. Затем создавалось поле движения с компонентами в плоскости, параллельными и перпендикулярными силе Лоренца, то есть вдоль осей x и z . Электрический ток создавался генератором сигналов (Agilent, 33250A, 80 МГц), усиливался (Brüel & Kjr, усилитель мощности, тип 2706) и проходил через шунтирующее сопротивление 2 Ом последовательно с фантомом и генератором.В экспериментах последовательно использовались две синусоидальные формы волны 60 Гц и 90 Гц.
Рисунок 1( a ) Экспериментальная установка. \ ({\ varvec {B}} \) — статическое магнитное поле вдоль оси z, создаваемое системой МРТ. \ ({\ varvec {j}} \) — плотность гармонического тока, приложенного к фантому с помощью внешних электродов, погруженных в солевые ванны и с основным направлением колебаний вдоль оси y. \ ({\ varvec {f}} \) — сила Лоренца, создаваемая внутри фантома из комбинации B и j , и с основным направлением колебаний вдоль оси x.Для наглядности основные направления \ ({\ varvec {j}} \) и \ ({\ varvec {f}} \) представлены и увеличены в поперечном сечении пунктиром. В первом эксперименте использовались электрические токи с частотами 60 Гц и 90 Гц и размахом амплитуды 137,5 мА. Фантом A был однородным и легированным NaCl для обеспечения электропроводности. См. Таблицу 1 для содержимого фантома и Рис. 5 для деталей второго эксперимента. ( b ) Диаграмма импульсной последовательности MRE. МЭГ противоположной полярности обозначены красными и синими пунктирными линиями.θ представляет собой фазовый сдвиг между срабатыванием и MEG. MEG в разных направлениях (выбор среза, фазовое кодирование и считывание) последовательно активируются в отдельных сборах.
Таблица 1 Свойства фантома.МРТ-снимки
Для срабатывания и обнаружения движения подача тока к фантому была синхронизирована с градиентами кодирования движения (MEG) двумерной градиентной эхо-последовательности, адаптированной к экспериментам по эластографии 36 (рис. 1b). Генератор тока запускался MR-сканером в начале последовательности импульсов MRE, так же, как и с другими стандартными механическими преобразователями.{\ tau} \ gamma {\ varvec {G}} \ left (t \ right) \ bullet {\ varvec {u}} \ left ({{\ varvec {r}}} _ {0}, t \ right) dt $$
(2)
, где γ [рад с −1 T −1 ] — гиромагнитное отношение образца, τ [с] период срабатывания, а G [T m −1 ] движение кодирование амплитуды градиента. Генерируемое движение кодировалось в трех ортогональных направлениях (передне-заднее, право-левое, стопа-головка). Параметры последовательности эластографии были: время повторения TR = 50 и 56 мс (скорректировано, чтобы соответствовать кратному периоду колебаний поперечной волны), время эхо-сигнала TE = 15 и 20 мс, пространственное разрешение = 1.25 мм × 1,25 мм, толщина среза = 5 мм, фазы эластографии = 4, амплитуда градиентов кодирования движения = 31 мТл / м (самое высокое значение, доступное для обеспечения максимального обнаружения в самых удаленных от источника движения областях), и кодирование движения по один цикл.
Для измерений поля смещения были последовательно получены два фазовых изображения с помощью МЭГ противоположных полярностей. Затем второе фазовое изображение было вычтено из первого с использованием экспоненциальной формы комплексного МР-сигнала для устранения потенциальных статических фазовых сдвигов, тем самым создавая однофазное разностное изображение, свободное от нежелательного постоянного фона.Во время получения (всего TR) обоих фазовых изображений генератор непрерывно подавал один и тот же колебательный электрический ток. Индуцированный фазовый сдвиг из-за подачи тока в фантом был тогда таким же на этих изображениях и, следовательно, был нейтрализован в операции разности фаз. Кроме того, приемные катушки были синтезированы с ларморовской частотой протона водорода и, следовательно, показали низкую чувствительность к токам низкой частоты, используемым в нашем исследовании. Чтобы вычислить карты смещения из изображений разности фаз, коэффициент кодирования | ξ | в [рад м −1 ] было вычислено с использованием \ (\ left | \ xi \ right | = \ left | \ frac {\ gamma {G} _ {0} \ left (\ mathit {sin} \ left (\ pi f \ tau \ right) -2sin \ left (\ frac {1} {2} \ pi f \ tau \ right) \ right)} {\ pi f} \ right | \), что аппроксимирует градиенты, обнуляющие первый момент, и где γ [рад с −1 T −1 ] — гиромагнитное отношение образца, τ [с] и G 0 [T m −1 ] — период и амплитуда МЭГ соответственно, а f [Гц] — частота возбуждения 37 .{2} {\ varvec {u}} = \ nabla \ bullet G \ nabla {\ varvec {u}} + \ nabla \ left (\ lambda + G \ right) \ nabla \ bullet {\ varvec {u}} $ $
(3)
, где ρ — плотность материала [кг м −3 ], ω угловая скорость движения [рад с −1 ], u поле движения [м], λ [Н · м -2 ] первый коэффициент Ламе 38 и G [Н · м -2 ] комплексный модуль сдвига.В агаровых и легированных агаром фантомах реальная часть комплексного модуля сдвига (накопительный модуль) значительно преобладает над мнимой частью (модуль потерь) 39,40 . LFE, который игнорирует модуль потерь, был затем выбран для извлечения первой информации об эластичности из смещений, вызванных силой Лоренца в агаровых фантомах, учитывая его доступность и широкое использование в сообществе MRE. Реконструкции LFE могут позволить проверить рабочую гипотезу, чтобы показать возможность применения метода MRE с силой Лоренца на клиническом сканере.Кроме того, известно, что LFE более устойчив к шуму, чем другие прямые методы, включающие оценку производных второго или более высокого порядка 11,13 .
LFE заключается в применении пар фильтров к выбранной гармонике данных смещения в пространстве k . Эти фильтры называются логнормальными квадратурными фильтрами и обычно сосредоточены на частотах, разделенных одной октавой 41 . Отношение смещений, обрабатываемых каждым фильтром одной пары, равно локальному волновому числу.{2} {\ varvec {u}} = \ boldsymbol {} \ mu \ Delta {\ varvec {u}} \), которое является упрощенной версией уравнения Навье в предположении несжимаемости ткани, локальной однородности и отсутствия затухание поперечной волны. Карты модуля сдвига, рассчитанные на основе перемещений вдоль направления срабатывания (ось x ), представлены в этом исследовании.
Перед инверсией фазовые изображения автоматически разворачивали с помощью программного обеспечения, встроенного в сканер (Resoundant Inc., Рочестер, Миннесота). Затем изображения модуля сдвига были отфильтрованы для удаления выбросов с использованием сглаженной функции Matlab 42,43 .Для отображения смещения (рис. 3) использовалась отдельная процедура разворачивания фаз 44,45,46 .
Эксперимент 1
Для демонстрации предложенного метода были разработаны два экспериментальных условия, оба из которых заключались в генерации поперечных волн в гелях, имитирующих ткань. Первый предназначен для демонстрации возможности генерации поперечных волн с помощью силы Лоренца при благоприятных условиях (т.е.электропроводный, мягкий и однородный фантом, названный фантомом A в таблице 1), а также для наблюдения за ними с помощью сканера МРТ.Были использованы два синусоидальных электрических тока амплитудой 137,5 мА с частотами 60 Гц и 90 Гц соответственно. Такая интенсивность в 69 раз превышает значения, указанные в протоколах электростимуляции (ES), проводимых на людях ( i ES = 2 мА от пика до пика) 47 . Результаты показаны на рис. 3.
Эксперимент 2
Целью второго эксперимента было показать, что индуцированные силой Лоренца поперечные волны можно использовать для различения областей с разными механическими свойствами внутри одной и той же гетерогенной структуры с использованием фантомов с разными механическими свойствами ( обозначенные B, C, D и E в таблице 1), и менее проводящая среда, соответствующая физиологическим условиям.Для создания гетерогенной структуры фантом B был залит поверх фантома C в одном держателе фантома (рис. 1a и 5A), а фантом D был залит поверх фантома E в другом держателе фантома (рис. 1a и 5A). Были использованы синусоидальные токи 62,22 мА от пика до пика на частотах 60 Гц и 90 Гц, что соответствует \ (33 \ times {i} _ {ES} \).
Моделирование
Физическая модель конечных элементов, соответствующая первому эксперименту с фантомом A, была разработана с помощью Comsol 5.5 (COMSOL LiveLink с Matlab, Inc., Пало-Альто, Калифорния), чтобы оценить картины смещения, полученные из свертки точечных источников, и сравнить с экспериментальными данными. Моделирование состояло из двух этапов: во-первых, вычислялось распределение плотности силы Лоренца внутри фантома, а во-вторых, вычислялось волновое поле, возникающее из этого члена источника плотности силы Лоренца. Для вычисления распределения плотности силы Лоренца с помощью модуля электрического тока решалась следующая краевая задача:
$$ \ left \ {\ begin {array} {ll} \ nabla \ cdot \ left (\ sigma \ nabla u \ справа) = 0 \ quad in \; \; фантом \\ I = {\ int} _ {in} \ sigma \ frac {\ partial u} {\ partial {\ varvec {n}}} dS = — {\ int} _ {out} \ sigma \ frac {\ частичный u} {\ partial {\ varvec {n}}} dS \ quad electric \; контакты \; (in \; and \; out) \\ \ nabla u \ times n = 0 \ quad на \; электрические \; контакты \\ \ sigma \ frac {\ partial u} {\ partial {\ varvec {n}}} = 0 \ quad на \; фантом \; стены \ люфт электрический \; контакты \; в \; а также\; из \ end {array} \ right.$$
, где u — электрический потенциал [В], σ электропроводность [См -1 ], I электрический ток [A], S площади поверхности [м 2 ] электрического контакта, а n — единичный вектор, перпендикулярный внешней границе. Внешний электрический ток I моделировался перпендикулярно фантому в месте электрического контакта (рис. 1а). Сила и частота тока были такими же, как в первом эксперименте (60 Гц и 90 Гц, размах амплитуды 137.5 мА). Фантомная проводимость была однородной и составляла 1 См / м, поскольку она не влияла ни на распределение плотности тока внутри фантома, ни на его интенсивность, которые регулируются граничными условиями в этой модели. Из распределения электрического потенциала и плотность тока была вычислена с использованием закона Ома: \ ({\ varvec {J}} = — \ sigma \ nabla u \) . . Распределение плотности силы Лоренца в фантоме (рис. 2) было затем вычислено с использованием уравнения. (1):
$$ {\ varvec {f}} = \ left (\ genfrac {} {} {0pt} {} {{j} _ {x}} {\ begin {array} {c} {j } _ {y} \\ {j} _ {z} \ end {array}} \ right) \ times \ left (\ genfrac {} {} {0pt} {} {{B} _ {x}} {\ begin {array} {c} {B} _ {y} \\ {B} _ {z} \ end {array}} \ right) = \ left (\ genfrac {} {} {0pt} {} {{j } _ {x}} {\ begin {array} {c} {j} _ {y} \\ {j} _ {z} \ end {array}} \ right) \ times \ left (\ genfrac {} { } {0pt} {} {0} {\ begin {array} {c} 0 \\ {B} _ {z} \ end {array}} \ right) $$
где \ (\ left | {\ varvec {B}} \ right | = \ left | {{\ varvec {B}}} _ {{\ varvec {z}}} \ right | = 3 Тл \) — магнитное поле, создаваемое МР-сканером. {\ prime}} s \; стены \ end {array} \ right.$$
, где u — поле смещения [м], ρ — плотность материала [кг · м -3 ], ω — пульсация [рад с −1 ], G — комплексный модуль сдвига [Н · м −2 ], K — объемный модуль [Н · м −2 ], и f — плотность силы Лоренца [Н · м −3 ] ]. Модуль объемной упругости был установлен равным 2,2 ГПа (вода). Хотя приближение отсутствия затухания поперечной волны остается приемлемым для агаровых фантомов при вычислении решения обратной задачи, такое приближение имеет большие последствия для расчетного решения прямой задачи.Таким образом, было обнаружено, что определение модуля потерь необходимо для учета небольшого демпфирования фантома.
Для фиксации модуля потерь G «использовалась заявленная тенденция взаимосвязи между модулями накопления и модулями потерь в агаровых фантомах. Как упоминалось выше, было показано, что модуль накопления доминирует над модулем потерь в агаровых фантомах и фантомах, допированных агаром. В частности, между этими двумя параметрами можно наблюдать разницу примерно на порядок величины 39,40 .Модули накопления на обеих частотах затем были зафиксированы из распределений модулей сдвига на фиг. 4, а модули потерь были зафиксированы из вышеупомянутого соотношения G ’- G ”. Однако, учитывая неопределенность точных механических свойств фантома (изменчивость карт на рис. 4 для G ’и приближенного G ”), прямая задача решалась несколько раз с использованием различных наборов комплексных модулей сдвига. В первом моделировании значения G ’на обеих частотах были установлены равными средним значениям распределений модуля сдвига на фиг.4: G ‘ 60 Гц = 1546 Па и G ‘ 90 Гц = 1768 Па. Модули потерь G «были установлены на 1/10 модуля накопления: G ” 60 Гц = 155 Па и G ” 90 Гц = 177 Па. Результаты показаны на рис. 3. Во втором и третьем моделировании использовались те же значения G ‘и Значения G «варьировались и последовательно устанавливались на 1/5 и 1/20 от значений G ‘.В четвертом и пятом моделировании значения G ‘были изменены в сторону более низких значений в распределении модуля сдвига на рис. 4, а G «были установлены на 1/10 от G ‘ в каждом случае. Результаты представлены показаны на рис. 3. Все комбинации параметров G ‘и G «собраны в таблице 2. Эта итерационная структура предназначена для демонстрации того, что, несмотря на неопределенности в отношении точных механических характеристик фантома, различные возможные модули накопления и потерь оказывают влияние модели распространения поперечных волн и их длины волн, но не ставят под сомнение происхождение плотности силы Лоренца в создаваемых полях движения, что и должно было подчеркнуть моделирование.
Рис. 3Первый эксперимент: Реальная и мнимая части экспериментальных и смоделированных полей комплексного смещения в фантоме A вдоль направлений x, y и z в MR-срезе. Происхождение упругих волн отчетливо проявляется в центре карт смещения. Изображения были получены (эксперимент) и извлечены (моделирование) в серой сагиттальной плоскости, расположенной в центре фантома, как показано на рис. 1 (метка «плоскость изображения»). Были использованы два электрических тока с частотой 60 Гц и 90 Гц и силой 137.Размах 5 мА как в эксперименте, так и при моделировании. Комплексные модули сдвига, использованные для получения отображаемых карт смоделированных смещений, были следующими: G 60 Гц = 1546 + j155 Па и G 90 Гц = 1768 + j177 Па. Профили линий реальной и мнимой частей смещений вдоль направлений распространения ( пунктирная белая линия) нанесены для каждой комбинации модулей накопления и потерь, описанных в таблице 2. Из этих профилей линий появляются дифракционные картины, характерные для срабатывания объемной силы, независимо от комплексных модулей сдвига.
Рисунок 4Первый эксперимент: карты накопительного модуля сдвига однородного фантома A от смещений по оси x с гармоническими срабатываниями 60 Гц и 90 Гц и с интенсивностью 137,5 мА от пика до пика. Предполагается, что локальные максимумы связаны с ограничениями LFE, возникающими из-за наличия силы Лоренца и отражений волн от границ. Изображения были получены в отображаемой плоскости, показанной на рис. 1а. Средние значения по всему полю обзора равны \ (\ mu {} _ {60Hz} \) = 1546 ± 383 Па и \ (\ mu {} _ {90Hz} = 1768 \ pm 440 \) Па.
Таблица 2 Комплексные модули сдвига G = G ’+ j G ” в [Па], использованные в моделировании.Что касается геометрии, то боковые границы (стенки держателя фантома) были зафиксированы, а верхняя граница оставлена свободной, чтобы имитировать конфигурацию, показанную на рис. 1. Оба расчета (электрический потенциал и поле смещения) были выполнены в частотной области. Затем были извлечены сложные смещения в отображаемой плоскости, и Фурье преобразовали во временную область, согласованную с экспериментальными данными смещения, а Фурье преобразовали обратно в частотную область для отображения реальной и мнимой частей на рис.3. Адаптация сетки была выполнена для обеспечения возможности уточнения там, где градиенты решений были высокими. В окончательных результатах зависимости от сетки не наблюдалось.
Выявление фотонной силы Лоренца как микроскопического источника топологических фотонных состояний
Заряженные частицы, такие как электроны, движущиеся в магнитном поле, сталкиваются с силой Лоренца, которая управляет образованием электронных топологических краевых состояний в квантовых системах с эффектом Холла. Здесь мы показываем, что фотоны, переносящиеся в магнитооптических материалах и структурах, также сталкиваются с физическим эффектом, называемым фотонной силой Лоренца, через косвенное взаимодействие с магнитооптической средой, поддерживаемой эффективным магнитным полем.Этот эффект может вызвать полупериодное спиральное движение света на поверхности однородной металлической магнитооптической среды и неоднородных магнитооптических фотонных кристаллов, и он определяет интригующие односторонние транспортные свойства устойчивости и невосприимчивости к дефектам, нарушениям и препятствия. Таким образом, фотонная сила Лоренца служит фундаментальным микроскопическим источником макроскопических фотонных топологических состояний, во многом так же, как классическая сила Лоренца делает с электронными топологическими состояниями.
1 Введение
Сила Лоренца [1], рассматриваемая как одна из важнейших основ классической электродинамики, происходит от магнитного поля B → действующего на частицу заряда q (например, электрон), движущуюся со скоростью v →. Эта сила приводит к дрейфующим или локализованным циклотронным движениям зарядов и лежит в основе широкого спектра интригующих макроскопических и микроскопических электромагнитных явлений, таких как эффект Холла, квантовые эффекты Холла и многие инструменты, включая электронные микроскопы, циклотронные ускорители и космические аппараты. детекторы лучей.Электронная сила Лоренца (ELF) используется, чтобы нарисовать исчерпывающую полуклассическую физическую картину квантового эффекта Холла (рис. 1A). Электроны внутри квантовой системы эффекта Холла быстро подвергаются локализованным циклотронным движениям вокруг магнитного потока из-за эффекта СНЧ. Приближаясь к границе, электроны отскакивают от жесткого края и, таким образом, перескакивают вперед по краю. Электроны с краями не подвержены влиянию примесей, обладают иммунитетом к обратному рассеянию и образуют топологически защищенный односторонний краевой ток.Эта полуклассическая картина хорошо раскрывает микроскопическое происхождение электронного топологического состояния и качественно объясняет многие уникальные транспортные поведения систем с квантовыми эффектами Холла [2].
Рисунок 1:
Физические изображения топологических электронных состояний и топологических фотонных состояний.
(A) Квантовые эффекты Холла в системе электронного газа. Иллюстрация циклотронного движения электронов. v → представляет скорость электронов, а F → E соответствует СНЧ. (B) Топологические фотонные состояния в магнитооптической системе.Красные и синие стрелки указывают направления потока энергии и PLF соответственно. Зеленые волнистые стрелки представляют собой исчезающие электромагнитные волны.
Недавно, вдохновленные аналогией между электронами и фотонами [3], [4], было проведено множество исследований топологических фотонных состояний в различных системах [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. Выдающимся средством создания топологических фотонных состояний является магнитооптическая система, погруженная в магнитное поле [16], [17].Большинство предыдущих работ в основном полагаются на численные расчеты дисперсионных диаграмм (т.е. зонной структуры) для предсказания топологических фотонных состояний, а для понимания этих состояний заимствованы понятия топологической физики и математики (например, число Черна, фаза и кривизна Берри и т. Д.) [18], [19], [20], [21], [22], [23], [24], [25], [26]. Однако немногие из них касаются фундаментальных вопросов о том, что заставляет фотоны, первоначально излучаемые точечным источником, теперь изотропно распространяться только в одну сторону по краю, и почему эти односторонние переносящие фотоны невосприимчивы к обратному рассеянию, сильному дефекту и беспорядку.Таким образом, микроскопическое происхождение и физическая картина топологических фотонных состояний в настоящее время остаются неясными даже после того, как было проведено так много теоретических, численных и экспериментальных исследований [27], [28], [29], [30], [31], [32], [33].
Здесь мы сообщаем, что существует физический эффект, который мы называем фотонной силой Лоренца (PLF), который вызывает циклотронное движение электромагнитных волн и фотонов в магнитооптических системах, во многом то же самое, что ELF для электронов. Этот PLF может хорошо объяснить микроскопическое происхождение топологических фотонных состояний и помочь составить исчерпывающую физическую картину их транспортного поведения в различных магнитооптических устройствах.Как показано на рисунке 1B, энергия, излучаемая источником на краю, делится на две части. С одной стороны, одна часть излучает в магнитооптическую среду с ослабленной амплитудой из-за металличности магнитооптического материала. Более того, такая электромагнитная волна отклоняется вправо или влево из-за эффекта PLF, что приводит к однонаправленному вихревому движению электромагнитных волн в тонком слое у края. Во время вихревого движения энергия уходит в воздух, и большая часть ее отбрасывается обратно в магнитооптическую среду за счет эффекта PLF.С другой стороны, другая часть просачивается в воздух, потому что нет жесткой границы, ограничивающей излучение энергии. Другими словами, когда потоки энергии распространяются вправо или влево, они всегда сопровождаются утечкой небольшой энергии в воздух.
2 Транспортное поведение электромагнитных волн
Транспортное поведение электромагнитных волн и фотонов можно предсказать, решив уравнения Максвелла в терминах электромагнитного поля и потока энергии (вектора Пойнтинга).Мы выводим выражение потока энергии в бесконечной стационарной однородной магнитооптической среде (ионный гранат иттрия с диэлектрической проницаемостью), и подробный процесс вывода приведен в дополнительном материале. Для простоты рассматривается только поперечный электрический (TE) режим (с ненулевым значением E z , H x и H y ).
Сначала рассмотрим случай отсутствия внешнего магнитного поля (т.е.е. мк = 1). Согласно k → × E → = ωμH → для плоской волны, переносящейся в k → (kx, ky, 0), получаем Hx = Ezωky и Hy = −Ezωkx. Основываясь на определении вектора Пойнтинга S → = E → × H → *, получаем
(1) S → = Ez2ω [(kxx → + kyy →)].
Тогда, согласно [34], импульс фотонного волнового пакета можно упростить до P → = D → × B → в бесконечно однородной магнитооптической среде, так что
(2) P → = ϵEz2ω [ (kxx → + kyy →)].
Далее, согласно F → = dP → dt, получаем
(3) F → = 2iωe2iωt⋅ϵEz2ω [(kxx → + kyy →)].
Уравнения (1–3) показывают, что S →, P → и F → параллельны волновому вектору k →, что означает, что поведение света при переносе согласуется с поведением в однородных немагнитных диэлектрических средах.
Однако, когда магнитооптическая среда погружается в статическое магнитное поле, индуцируется сильная гиромагнитная анизотропия, которая создает тензор проницаемости. Основываясь на уравнениях Максвелла для TE-моды, получаем
(4) S → = Ez2ωμr2μr2 − μk2 [(kxx → + kyy →) + iμkμr (kyx → −kxy →)].
(5) P → = Ez2ωϵμr [(kxx → + kyy →) + iμkμr (kyx → −kxy →)].
(6) F → = 2iωe2iωt⋅Ez2ωϵμr [(kxx → + kyy →) + iμkμr (kyx → −kxy →)].
Очевидно, что все эти уравнения (4–6) состоят из двух частей, которые являются чисто действительными и мнимыми, соответственно, т.е. S → = S → r + iS → i, P → = P → r + iP → i, и F → = F → r + iF → i. Одновременно, поскольку (kxx → + kyy →) ⋅ (kyx → −kxy →) = 0, чисто действительная и мнимая части перпендикулярны друг другу, т.е. S → r⊥S → i, P → r⊥P → i, и F → r⊥F → i. Кроме того, S → r (S → i) пропорционально P → r (P → i) и F → r (F → i), а при удалении магнитного поля [т.е. H = 0 ( μ = μ r = 1, μ k = 0)], уравнения (4–6) возвращаются к уравнениям (1–3), соответственно.Следовательно, вполне разумно, что мы можем использовать поведение переноса потоков энергии S →, чтобы напрямую и наглядно охарактеризовать транспортные свойства P → и F →. Обратите внимание, однако, что сила F →, определенная в уравнениях (3) и (6) для фотона и электромагнитной волны, не имеет обычного физического смысла механической силы для массивных частиц, таких как электроны, потому что все поведение переноса фотонов и Электромагнитные волны могут быть хорошо описаны пространственно-временной эволюцией электромагнитных полей, связанных с фотонами и электромагнетизмом.Следовательно, очень редко можно говорить о механической силе, налагаемой чем-либо на фотоны; вместо этого очень популярно и хорошо установлено говорить о механической силе, налагаемой на массивные частицы фотонами и электромагнитными волнами. PLF, принятый и обсуждаемый в этой статье, представляет собой просто полезный и удобный концептуальный инструмент, разработанный для наглядного описания поведения переноса фотонов TPS и электромагнитных волн в магнитно-оптических структурах и устройствах, и, по сути, это не настоящая механическая сила.
Пусть Q = Ez2ωμr2μr2 − μk2 и B (H) = μkμr; тогда уравнение (4) можно переписать как
(7) S → = Q [(kxx → + kyy →) + iB (H) (kyx → −kxy →)].
Это уравнение состоит из двух частей [S → r = Q (kxx → + kyy →) и S → i = QB (H) (kyx → −kxy →)], и
(8) S → r⊥S → я.
Мы предполагаем, что действительная часть S → r соответствует обычному вектору Пойнтинга, представляющему направление переноса потоков энергии и количество света, в то время как мнимая часть S → i описывает PLF, вызывая поведение переноса света, напоминающее циклотронные движения электронов. .Это явление возникает из-за антисимметричного тензора проницаемости, индуцированного магнитным полем.
Мы определяем B ( H ) как функцию магнитного поля, чтобы проиллюстрировать рациональность сравнения между B ( H ) в PLF и B z в ELF. На рисунке 2 на частотах f 1 = 4,480 и f 2 = 9,464 ГГц, интенсивности B ( H ) демонстрируют почти идеальную линейность как магнитное поле. увеличивается, что означает B ( H ) ≈ βH , где β — постоянная величина.В этом случае уравнение (7) выражается как
Рисунок 2:
Отношения B ( H ) — H на разных частотах.
Связь B ( H ) с H при: (A) f 1 = 4,480 ГГц, (B) f 2 = 9,464 ГГц. Черные пунктирные линии — это контрольные линии.
(9) S → ≈Q [(kxx → + kyy →) + iβH (kyx → −kxy →)].
Это означает, что PLF почти пропорционален количеству H , которое аналогично тому, что есть в всем известном ELF.Кроме того, мы выбираем H = 1600 G и находим, что B ( H ) равно +1 и –1 при f 1 и f 2 , соответственно. Эти два случая при f, , , 1, , , и , f, , , 2, , , , могут быть аналогичны положительному и отрицательному заряду в электрических системах соответственно. Тогда уравнение (7) упрощается до S → = Q [(kxx → + kyy →) ± i (kyx → −kxy →)], что указывает на то, что значения S → r и S → i равны, и, таким образом, Соответственно происходит совершенное циклическое движение.Следует отметить, что мы сосредотачиваемся только на узком частотном диапазоне для достижения линейности ради упрощения формулы, чтобы провести лучшую аналогию с электронной системой. На самом деле линейность здесь не является обязательным требованием.
Кроме того, для ELF нас интересует заряд (т.е. электрон), движущийся в двумерной плоскости x — y со скоростью v → = (vx, vy, 0) под действием магнитного поля B → = (0, 0, Bz) по направлению z .Тогда уравнение магнитной силы:
(10) F → E = qv → × B → = q | x → y → z → vxvy000Bz | = qBz (vyx → −vxy →),
, где F → E — ELF и он перпендикулярен v → = vxx → + vyy → всегда из-за (vxx → + vyy →) ⋅ (vyx → −vxy →) = 0, поэтому
(11) v → ⊥F → E.
Интересно, что существует удивительное сходство между уравнениями (8) и (11), которые оба описывают циклотронные движения фотонов и электронов в магнитном поле соответственно. Для краткости физический эффект, названный PLF и записанный как F → i, пропорционален величине S → i и единодушно вызывает циклотронное движение фотонов.Этот эффект аналогичен классической силе Лоренца F → E, а потоки энергии, характеризующиеся S → r, пропорциональны k → и аналогичны скорости v → электронов.
Более того, многие классические концепции ELF могут одинаково хорошо применяться и к PLF. Здесь мы определяем закон левой руки, чтобы интуитивно судить о направлении PLF относительно направления переноса потоков энергии. Согните левую руку и дайте магнитному полю пройти через ладонь. Если четыре пальца указывают S → r, большой палец, перпендикулярный четырем пальцам, представляет S → i.Кроме того, положительный B ( H ) соответствует большому пальцу, указывающему на S → i, а отрицательный B ( H ) соответствует противоположному направлению. Тем не менее, очень важное различие между PLF и ELF состоит в том, что S → i является «виртуальным». Таким образом, фотон не действует напрямую с магнитным полем, а скорее действует с эффективным магнитным полем, созданным магнитооптическими материалами. Поскольку фотоны имеют импульс, пропорциональный | k → |, они сталкиваются с PLF F → P (F → i) ∝S → i и изменяют траекторию своего прохождения.Их движения рассматриваются как суперпозиция быстрого кругового движения и медленного дрейфующего движения, которое очень похоже на движение электронов под действием СНЧ.
3 Модельная проверка фотонной силы Лоренца
Чтобы подтвердить вышеупомянутые экзотические транспортные свойства, в которых доминирует PLF, мы рассматриваем электромагнитную волну, излучаемую точечным источником, колеблющимся с частотой f 1 = 4,480 ГГц [ниже резонансной частоты f 0 = 6,509 ГГц и, следовательно, B ( H ) = + 1] в бесконечной однородной магнитооптической среде.Мы строим синтетическую картину, накладывая диаграмму линий тока (явно отражающую направление потока энергии) на картину поля E z . Рисунок 3A показывает, что когда H = 0, получается S → i = 0 и F → P = 0, поэтому электромагнитные волны излучаются равномерно во всех направлениях, а S → r параллельны каждой k → точке волнового фронта повсюду. Наоборот, рисунок 3B показывает, что когда H = 1600 G , согласно закону левой руки, S → r подчиняется правой части PLF, которая пропорциональна S → i (перпендикулярна S → r повсюду), расходясь наружу.PLF вызывает отклонение электромагнитной волны вправо и в конечном итоге формирует вихревое электромагнитное поле по часовой стрелке, которое излучается наружу (рис. 3B). Эта физическая картина дополнительно подтверждается распределениями H x и H y на рисунках 3B1 и B2. Приведенные выше физические картины никогда не возникают в обычных однородных немагнитных средах.
Рисунок 3:
Численное моделирование приводит к бесконечной однородной магнитооптической среде.
(A) E z -поле для H = 0, (B) E z -поле для H = 1600 G ; пурпурная пунктирная стрелка представляет направление вихря электромагнитных волн. (B1, B2) H x — и H y -поле, соответствующее (B). Во всех этих случаях точечный источник, обозначенный красными сияющими звездами, излучает f 1 = 4.480 ГГц. Красные и синие стрелки обозначают S → r и S → i соответственно.
Перейдем к рассмотрению случая границы раздела между воздухом и магнитооптической средой. На рисунках 4A1 и A2 показано, что когда H = 0, большая часть энергии излучается в нижнюю диэлектрическую среду, а распределение поля E z симметрично относительно нормали к границе раздела. Однако, когда H = 1600 G , S → i перпендикулярно S → r всюду в магнитооптической среде, что подчиняется закону левой руки.Следовательно, электромагнитная волна отклоняется влево из-за PLF, что приводит к асимметричному распределению поля E z -поля. Из-за вторичного излучения (или отражения) энергетических вихрей от нижней магнитооптической среды, его смесь с прямым сферическим излучением от источника вызовет асимметричную картину поля E z и присутствие обоих S → r и S → i в верхней воздушной зоне около границы раздела (рис. 4B1).Хотя S → r и S → i больше не перпендикулярны друг другу, PLF все еще существует, чтобы воздействовать на фотоны в окрестности границы раздела и вызывать его отклонение вправо, и этот эффект можно рассматривать как остаточный выступание сильной ФНЧ в магнитооптической среде. В некоторой степени поток энергии все еще формирует циклотронное движение электромагнитной волны, окружающей источник по часовой стрелке. В дальней зоне, намного выше границы раздела в воздухе, сохраняется только прямое сферическое поле излучения, а S → i исчезает, что приводит к диаграмме направленности, почти идентичной случаю диэлектрической среды.
Рисунок 4:
Результаты численного моделирования в полубесконечных системах.
(A1) H = 0, (A2) | E | при разных y i ( i = 1, 2, 3, 4, 5) в (A1), (B1) H = 1600 G , (B2) | E | различных y i ( i = 1, 2, 3, 4, 5) в (B1). Во всех этих случаях источник излучает на частоте f 1 = 4,480 ГГц. Красные и синие стрелки обозначают S → r и S → i соответственно.
Далее рассмотрим случай одиночного магнитооптического стержня. Как показано на рисунках 5A1 и A2, стержень имеет диаметр 11,6 см, что больше длины волны возбуждения (7 см), поэтому происходит сильное рассеяние Ми. Рисунок 5A1 показывает, что когда H = 0, излучение электромагнитной волны демонстрирует регулярный дипольный отклик и S → i = 0 везде, так что в этом немагнитном случае PLF не существует. Когда H = 1600 G (рис. 5A2), диаграмма направленности резко отличается, и внутри стержня преимущественно возбуждается четкая мода квадрупольного резонанса.Четыре полюса вместе со всем полем E z вращаются против часовой стрелки с течением времени, что приводит к вихревому распределению поля и четырехлопастному ветряному движению электромагнитной волны. Эти своеобразные характеристики переноса поля полностью отличаются от хорошо известной радиальной квадрупольной диаграммы направленности в немагнитной среде, которая хорошо объясняется с помощью PLF.
Рисунок 5:
Результаты численного моделирования.
(A1, A2) Одиночный магнитооптический стержень в воздухе при f 1 = 4,480 ГГц. (B1, B2) Одиночный магнитооптический стержень в воздухе на f 2 = 9,464 ГГц. Пурпурные стрелки обозначают направление переноса электромагнитных волн.
Чтобы увидеть, что происходит, когда f > f 0 , мы выбираем f 2 = 9,464 ГГц [ B ( H ) = — 1], где магнитооптическая среда показывает металлический поведение.Результаты для стержня диаметром 19,35 см, намного превышающего длину волны возбуждения (3 см), показаны на рисунках 5B1 и B2. Когда H = 0, поле E z имеет гексапольную форму и излучает равномерно (рис. 5B1). Напротив, когда H = 1600 G , на рис. 5B2 показана октапольная ветряная мельница энергетического вихря по часовой стрелке, вращающаяся вдоль края стержня с выступающими светлыми хвостами. В отличие от случая f 1 [где B ( H ) = + 1], теперь более сильный поток энергии локализован вдоль края стержня, и, что более интересно, направление его вращения инвертируется с против часовой стрелки на по часовой стрелке, поскольку B ( H ) изменяется с положительного на отрицательный.
Присутствие и действие PLF в различных магнитооптических структурах указывает на плодотворные границы электромагнетизма, которые еще не раскрыты. Важно отметить, что эта фундаментальная концепция PLF может прекрасно раскрыть микроскопическое происхождение и построить исчерпывающую картину топологических фотонных состояний. Далее мы рассмотрим границу раздела между воздухом и магнитооптической средой на частоте f > f 0 [ B ( H ) <0].Как показано на рисунке 6A, из-за сильных металлических свойств потоки энергии могут проникать только на определенную глубину с ослаблением. Согласно закону левой руки, PLF указывает в противоположном направлении большого пальца, вызывает световой вихрь против часовой стрелки и заставляет поток энергии отклоняться влево. Таким образом, при совместном действии PLF и металлических свойств создается одностороннее краевое состояние при условии B ( H ) = — 1 (Рисунок 6B). Диаграмма потока энергии на рисунке 6B хорошо согласуется со схематической диаграммой на рисунке 6A.
Рисунок 6:
Топологические фотонные состояния в полубесконечной системе при f 2 .
(A) Принципиальная схема. (B) Результаты моделирования поля E z с S → r и S → i.
4 Формирование топологических фотонных состояний
Далее мы используем физическую концепцию PLF для построения основных физических изображений топологических фотонных состояний и понимания их уникального поведения при пропускании в гораздо более сложных магнитооптических фотонных кристаллах (MOPC) [16] , [17].Поскольку структуры MOPC обладают гораздо лучшей эффективной металличностью, обеспечиваемой фотонной запрещенной зоной, топологические фотонные состояния демонстрируют гораздо меньшую транспортную диссипацию и потери по сравнению с металлическими магнитооптическими системами на рисунке 6. На рисунке 7A1 точечный источник, колеблющийся при f 3 = 7,765 ГГц ( f 3 > f 0 = 3 ГГц) расположен близко к краю сотового MOPC. Энергия сильно локализована на краю и распространяется вправо.Поскольку f 3 находится вне светового конуса, топологическое фотонное состояние не связано с воздушными модами, и электромагнитная энергия хорошо ограничивается краем зигзага для однонаправленного распространения. В этой открытой системе и в воздушно-магнитооптической системе на рис. 6 оба топологических фотонных состояния возникают в результате комбинированного действия эффективной металличности и PLF. Однако физическая картина на рисунках 7A1 – A3 отличается от рисунков 6, и мы можем обратиться к рисунку 5B2, чтобы лучше понять это различие.На рисунке 5B2 показан одиночный магнитооптический стержень с вихрем энергии ветряной мельницы по часовой стрелке, а на рисунке 7A2 показано коллективное поведение микроскопических вихрей на рисунке 5B2, образующих макроскопический односторонний перенос. Существует два транспортных канала: основной и вторичный. Большая часть потока энергии переносится вправо по краю зигзага, образуя основной канал, в то время как меньшая часть энергии, излучаемой назад, полностью отбрасывается назад и распространяется вперед через петлю против часовой стрелки вдоль внутренних краев всего шестиугольника (см. Рисунок 7A1), образуя вторичный канал.
Рисунок 7:
Топологические фотонные состояния в различных MOPC.
(A1) открытый сотовый MOPC, (B1) квадратный волновод MOPC и (C1) квадратный волновод MOPC с препятствием. Диаграммы включают | E | распределения (A1, B1, C1), схематические диаграммы (A2, B2, C2) и распределения потока энергии (A3, B3, C3). Черные стрелки обозначают направление переноса, синие стрелки указывают направление и интенсивность энергетического вихря вокруг магнитооптического стержня, а темно-синие слои представляют собой идеальный электрический проводник.Индекс 1–4 в (C1) означает четыре критических магнитооптических стержня (стержни 1–4), обсуждаемых в основном тексте.
Квадратные волноводы MOPC также могут достигать топологических фотонных состояний в запрещенной зоне [16]. Однако эти топологические фотонные состояния находятся внутри светового конуса и вызывают утечку света в воздух, поэтому волновод, состоящий из квадратного MOPC и металлической оболочки, формирует канал без потерь для топологических фотонных состояний. Рабочая частота f 4 = 4.3 ГГц ( f 4 < f 0 = 6,509 ГГц). Согласно закону левой руки, как показано на рис. 7B1 – B3, поток энергии вращается против часовой стрелки, образуя ветряную мельницу вокруг магнитооптических стержней, как показано на рис. 5B. Физика топологических фотонных состояний в одностороннем волноводе может быть описана физической картиной, изображенной на рисунке 7B2, где топологическое фотонное состояние возникает из общих эффектов связи вихря энергии против часовой стрелки вокруг каждого стержня и транспортных мод в волновод.Большая часть энергии распространяется вправо по основному каналу, то есть по волноводу. Энергия, излучаемая назад, постепенно отклоняется, перемещаясь вперед и образуя вторичный канал под действием PLF и запрещенной зоны. Строгое моделирование (рис. 7B1 и B3) полностью подтверждает этот физический анализ на основе PLF. Кроме того, энергия, излучаемая в воздух, отражается обратно металлической оболочкой и попадает в основной или дополнительный канал для распространения вправо. Таким образом, физическая картина, очерченная PLF, хорошо объясняет наличие топологических фотонных состояний в квадратном MOPC.
Наконец, мы рассмотрим наиболее интригующую особенность топологических фотонных состояний, то есть их устойчивость и невосприимчивость к обратному рассеянию, вызванному препятствием. Мы вставляем препятствие в волновод (рисунок 7B1) и показываем результат моделирования (рисунок 7C1). Физическое изображение изображено (рис. 7C2) на основе PLF. Критическим шагом для надежного перемещения вокруг препятствия является прохождение электромагнитной волны через левый острый угол 90 °, подъем через острый конец препятствия и прохождение через правый острый угол 90 °.Согласно рисункам 7C2 и C3, перенос энергии по-прежнему следует по основному и вторичному каналам, обозначенным толстыми и тонкими красными стрелками соответственно (рисунок 7C2). В основном канале входящая волна сначала проходит по прямому волноводу в виде топологического фотонного состояния (рис. 7B1 – B3). Когда он попадает в левый острый угол, поток энергии сильно рассеивается на самом дальнем магнитооптическом стержне в углу (стержень 1). Благодаря PLF большая часть потока энергии рассеивается вниз, буксируется вправо, ударяется о поверхность препятствия и одновременно рассеивается влево, вверх и вниз.Затем левый (или нисходящий) поток энергии снова буксируется вниз (или вправо) PLF. Электромагнитная волна повторяет такое нисходящее спиральное движение за полупериод против часовой стрелки многократно и образует основной канал переноса энергии. Такой спирально пропускаемый основной поток энергии в конечном итоге попадает в левый магнитооптический стержень, ближайший к нижнему концу металлического среза препятствия (стержень 2). Затем он продолжает свое полупериодное спиральное движение (теперь вправо) под действием PLF и ударяется о соседний правый стержень МО (стержень 3).Затем он поднимается вверх, следуя полупериодному спиральному движению также под действием PLF, и проходит через правый острый угол 90 ° и стержень 4. Наконец, он перемещается вправо по волноводу в виде топологического фотонного состояния. На рис. 7C1 – C3 основной канал по существу следует траектории, образованной металлическим препятствием и его левым и правым ближайшими соседними рядами магнитооптических стержней.
Вторичный канал потока энергии начинается с вторичного рассеяния вверх электромагнитной волны, когда основной поток энергии проходит вокруг стержня 1 и ударяется о левую поверхность препятствия.Из-за эффекта PLF этот вторичный поток энергии начинает свой длинный путь спирального движения за полупериод по траектории, по существу такой же, как и в основном канале. На рис. 7C2 и 4C3 другой источник, вносящий вклад в основной поток энергии, исходит от вторичной волны рассеяния вниз, когда входящая электромагнитная волна ударяется о стержень прямо перед стержнем 1. Этот поток вторичной энергии вливается в основной канал, становится его частью и увеличивает его общую интенсивность. Проще говоря, устойчивый перенос топологического фотонного состояния через металлическое препятствие происходит из полупериодного спирального движения электромагнитной волны под действием PLF.Физические картины циклического движения, изображенные на Рисунке 7, полностью перекликаются с изображениями, показанными на Рисунке 1, как для электронов, так и для фотонов под действием ELF и PLF, соответственно.
5 Выводы
Таким образом, мы обнаружили, что фотоны, переносящиеся в магнитооптических материалах и структурах, будут сталкиваться с PLF через косвенное взаимодействие фотонов с эффективным магнитным полем, поддерживаемым магнитооптической средой, аналогично ситуации для электронов. в системах конденсированного состояния с квантовым эффектом Холла.Этот эффект может вызвать полупериодное спиральное движение света на поверхности однородной металлической магнитооптической среды и неоднородных MOPC, а также управлять интригующими односторонними транспортными свойствами устойчивости и невосприимчивости к обратному рассеянию, вызванному дефектами, нарушениями и препятствиями. Если углубиться в уравнения Максвелла для магнитооптических материалов с внешним магнитным полем, поток энергии электромагнитной волны можно разделить на чисто реальную и чисто мнимую части S → r и S → i, которые всегда перпендикулярны друг другу. (S → r⊥S → i) независимо от направления распространения электромагнитной волны.Мнимая часть потока электромагнитной энергии играет важную физическую роль в переносе топологических фотонных состояний в магнитооптической среде. Этот момент никогда не отмечался в классической электродинамике, электромагнетизме и оптике и противоречит общепринятому мнению, согласно которому мнимой частью потока электромагнитной энергии можно пренебречь. PLF — это косвенное взаимодействие с фотонами через эффективное магнитное поле, поддерживаемое магнитооптической средой, в отличие от случая классической силы Лоренца, возникающей из магнитного поля, действующего непосредственно на заряженные частицы, такие как электроны.Кроме того, мы определяем закон левой руки, чтобы интуитивно судить о направлении PLF против направления переноса света.
Мы более глубоко исследуем физические явления в бесконечных, полубесконечных одностержневых системах, соответственно, и строим хорошо проясненные микроскопические физические изображения топологических фотонных состояний в различных структурах MOPC на основе действия PLF. Эти изображения могут хорошо объяснить все соответствующие специфические макроскопические транспортные свойства света в топологических системах фотонных состояний и дополнительно подтвердить, что PLF является микроскопическим источником этих специфических поведений.В некотором смысле микроскопическая картина может хорошо соответствовать полуклассической физической картине для электронных топологических состояний в системе квантового эффекта Холла и критической роли силы Лоренца в формировании этих топологических фотонных состояний. С другой стороны, фундаментальное сходство и различие между электронами и фотонами указывает на то, что существует более тесная связь между источником заряда (электронами) и излучением (фотонами), чем предыдущее общее понимание, выраженное в стандартных учебниках классической электромагнетизма и электродинамики.Выявление физического эффекта PLF может дать полезные подсказки для глубокого изучения вытекающих из этого нетривиальных физических значений в топологических фотонных системах, а в более широком аспекте науки поможет раскрыть обширную новую физику, такую как PLF, в старой научной дисциплине электродинамики, электромагнетизма и т. Д. оптика.
Источник финансирования: Национальный фонд естественных наук Китая
Идентификатор награды / номер гранта: 11434017
Идентификатор награды / номер гранта: 11504114
Источник финансирования: Группа инновационных исследований и предпринимательства провинции Гуандун
Идентификатор премии / номер гранта: 2016ZT06C594
Заявление о финансировании: Авторы благодарны за финансовую поддержку Национальному фонду естественных наук Китая (11434017, 11504114), Программе науки и технологий Гуанчжоу (201
- 0105), Гуандун Программа инновационных и предпринимательских исследований (2016ZT06C594), Программа внедрения ведущих инновационных и предпринимательских талантов в Дунгуане, Национальная программа ключевых исследований и разработок Китая (2018YFA 0306200) и Фонды фундаментальных исследований для центральных университетов (2019ZD50).
Ссылки
[1] Дарригол О. Электродинамика от Ампера до Эйнштейна. Оксфорд, Англия: Oxford University Press, 2000. Искать в Google Scholar
[2] Shen SQ. Топологические изоляторы, 2-е изд. Гонконг, Китай: Университет Гонконга, 2017. Поиск в Google Scholar
[3] Haldane FDM, Raghu S. Возможная реализация направленных оптических волноводов в фотонных кристаллах с нарушенной симметрией относительно обращения времени. Phys Rev Lett 2008; 100: 013904. Искать в Google Scholar
[4] Raghu S, Haldane FDM.Аналоги краевых состояний квантового эффекта Холла в фотонных кристаллах. Phys Rev A 2008; 78: 033834. Искать в Google Scholar
[5] Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Наблюдение за однонаправленным обратным рассеянием иммунных топологических электромагнитных состояний. Природа 2009; 461: 772–5. Искать в Google Scholar
[6] Рехтсман М.К., Цойнер Дж. М., Плотник Ю. и др. Фотонные топологические изоляторы Флоке. Природа 2013; 496: 196–200. Искать в Google Scholar
[7] Chen WJ, Jiang SJ, Chen XD, et al.Экспериментальная реализация фотонного топологического изолятора в одноосном метакристаллическом волноводе. Нац Коммуна 2014; 5: 5782. Искать в Google Scholar
[8] Гао В., Лоуренс М., Ян Б. и др. Топологическая фотонная фаза в хиральных гиперболических метаматериалах. Phys Rev Lett 2015; 114: 037402. Искать в Google Scholar
[9] He C, Sun XC, Liu XP и др. Фотонный топологический изолятор с нарушенной симметрией относительно обращения времени. Proc Natl Acad Sci USA 2016; 113: 4924–28. Искать в Google Scholar
[10] Mittal S, Ganeshan S, Fan J, Vaezi A, Hafezi M.Измерение топологических инвариантов в двумерной фотонной системе. Нат Фотон 2016; 10: 180–3. Искать в Google Scholar
[11] Слобожанюк А., Мусави Ш., Ни Х, Смирнова Д., Кившар Ю.С., Ханикаев А.Б. Трехмерный полностью диэлектрический фотонный топологический изолятор. Нат Фотон 2017; 11: 130–6. Искать в Google Scholar
[12] Fang C, Lu L, Liu J, Fu L. Топологические полуметаллы с геликоидными поверхностными состояниями. Nat Phys 2016; 12: 936–41. Искать в Google Scholar
[13] Gao F, Xue H, Yang Z, et al.Топологически защищенное преломление устойчивых состояний излома в долинных фотонных кристаллах. Nat Phys 2018; 14: 140–4. Искать в Google Scholar
[14] Донг Дж. У., Чен XD, Чжу Х, Ван И, Чжан Х. Фотонные кристаллы долины для управления спином и топологией. Nat Mater 2017; 16: 289–302. Искать в Google Scholar
[15] Kang Y, Ni X, Cheng X, Khanikaev AB, Genack AZ. Связанные краевые состояния псевдоспин-долина в фотонном топологическом изоляторе. Нац Коммуна 2018; 9: 3029. Искать в Google Scholar
[16] Wang Z, Chong YD, Joannopoulos JD, Soljačić M.Безотражательные односторонние краевые моды в гиромагнитном фотонном кристалле. Phys Rev Lett 2008; 100: 013905. Искать в Google Scholar
[17] Poo Y, Wu RX, Lin Z, Yang Y, Chan CT. Экспериментальная реализация самонаводящихся однонаправленных электромагнитных краевых состояний. Phys Rev Lett 2011; 106: 093903. Искать в Google Scholar
[18] Лу Л., Фу Л., Джоаннопулос Дж. Д., Солячич М. Точки Вейля и узлы линий в гироидных фотонных кристаллах. Нат Фотон 2013; 7: 294–9. Искать в Google Scholar
[19] Skirlo SA, Lu L, Soljačić M.Многомодовые односторонние волноводы с большими числами Черна. Phys Rev Lett 2014; 113: 113904. Искать в Google Scholar
[20] Skirlo SA, Lu L, Igarashi Y, Yan Q, Joannopoulos JD, Soljačić M. Экспериментальное наблюдение больших чисел Черна в фотонных кристаллах. Phys Rev Lett 2015; 115: 253901. Искать в Google Scholar
[21] Лу Л, Ван З, Йе Д и др. Экспериментальное наблюдение точек Вейля. Наука 2015; 349: 622–4. Искать в Google Scholar
[22] Но Дж, Хуанг С., Лейкам Д., Чонг Ю.Д., Чен К.П., Речтсман М.С.Экспериментальное наблюдение оптических точек Вейля и поверхностных состояний, подобных дуге Ферми. Nat Phys 2017; 13: 611–7. Искать в Google Scholar
[23] Chen WJ, Xiao M, Chan CT. Фотонные кристаллы, обладающие множественными точками Вейля, и экспериментальное наблюдение устойчивых поверхностных состояний. Нац Коммуна 2016; 7: 13038. Искать в Google Scholar
[24] Xiao M, Lin Q, Fan S. Гиперболическая точка Вейля в взаимно хиральных метаматериалах. Phys Rev Lett 2016; 117: 057401. Искать в Google Scholar
[25] Гао В., Ян Б., Тремейн Б. и др.Экспериментальное наблюдение вырождения фотонных узловых линий в метакристаллах. Nat Commun 2018; 9: 950. Искать в Google Scholar
[26] Ян Б., Го К., Тремейн Б. и др. Идеальные точки Вейля и геликоидные поверхностные состояния в искусственных фотонно-кристаллических структурах. Наука 2018; 359: 1013–6. Искать в Google Scholar
[27] Ao X, Lin Z, Chan CT. Односторонняя краевая мода в магнитооптическом сотовом фотонном кристалле. Phys Rev B 2009; 80: 033105. Поиск в Google Scholar
[28] Лю С., Лу В., Линь З, Чуй СТ.Магнитно-управляемые однонаправленные электромагнитные волноводные устройства на основе метаматериалов. Appl Phys Lett 2010; 97: 2011 13. Искать в Google Scholar
[29] Liu S, Lu W, Lin Z, Chui ST. Формовочное отражение от метаматериалов на основе магнитных поверхностных плазмонов. Phys Rev B 2011; 84: 045425. Искать в Google Scholar
[30] Lian J, Fu JX, Gan L, Li ZY. Прочные и устойчивые к беспорядкам односторонние волноводы с магнитной перестройкой в гиромагнитном фотонном кристалле. Phys Rev B 2012; 85: 125108.Искать в Google Scholar
[31] Лю Дж, Шен Л, Дэн Х, Ли Х, Чжэн Х. Влияние формы границы фотонного кристалла на существование односторонней краевой моды. Appl Opt 2013; 52: 5216–20. Искать в Google Scholar
[32] Li Z, Wu RX, Li QB, et al. Наблюдение широкополосного однонаправленного пропускания путем объединения односторонних краевых состояний гиромагнитных фотонных кристаллов. Opt Express 2015; 23: 9658–63. Искать в Google Scholar
[33] Li FF, Wang HX, Xiong Z, et al. Топологический захват света на дислокации.Nat Commun 2018; 9: 2462. Искать в Google Scholar
[34] Онода М., Мураками С., Нагаоса Н. Геометрические аспекты в динамике оптических волновых пакетов.




 .
.  ).
). Зависимость I от величины Во/µ0 называется кривой намагниченности (рис.2). Кривая указывает на явление магнитного насыщения: начиная с некоторого значения Во/µ0= В0н/µ0, намагниченность практически остается постоянной, равной Iн(намагниченность насыщения).
Зависимость I от величины Во/µ0 называется кривой намагниченности (рис.2). Кривая указывает на явление магнитного насыщения: начиная с некоторого значения Во/µ0= В0н/µ0, намагниченность практически остается постоянной, равной Iн(намагниченность насыщения).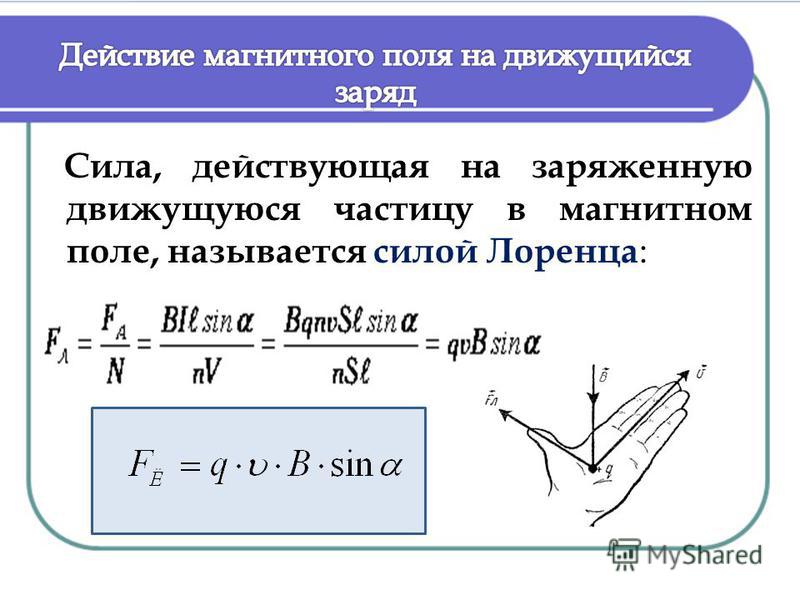 Значение + Во/µ0 соответствует намагниченности насыщения Iн. Для того чтобы полностью размагнитить ферромагнитное тело, необходимо изменить направление внешнего поля. При некотором значении магнитной индукции — В0к , которой соответствует величина В0к/µ0, называемая коэрцитивной(задерживающей) силoй, намагниченность I тела станет равной нулю.
Значение + Во/µ0 соответствует намагниченности насыщения Iн. Для того чтобы полностью размагнитить ферромагнитное тело, необходимо изменить направление внешнего поля. При некотором значении магнитной индукции — В0к , которой соответствует величина В0к/µ0, называемая коэрцитивной(задерживающей) силoй, намагниченность I тела станет равной нулю. Эти материалы используются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в переменных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса.
Эти материалы используются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в переменных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса. ). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках, а целых областей самопроизвольной намагниченности — доменов. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагниченности достигает максимального значения — наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов доменов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов.
). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках, а целых областей самопроизвольной намагниченности — доменов. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагниченности достигает максимального значения — наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов доменов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов.