Закон Ампера — Студопедия
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.
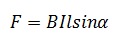
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
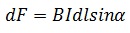
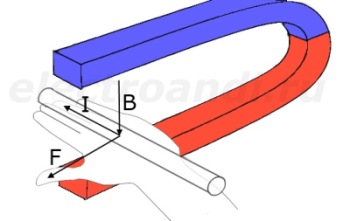
Направление силы Ампера определяется по правилу левой руки.
Правило левой руки: если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90
МП движущего заряда. Действие МП на движущийся заряд. Сила Ампера, Лоренца.
Любой проводник с током создает в окружающем пространстве магнитное поле. При этом электрический же ток является упорядоченным движением электрических зарядов. Значит можно считать, что любой движущийся в вакууме или среде заряд порождает вокруг себя магнитное поле. В результате обобщения многочисленных опытных данных был установлен закон, который определяет поле В точечного заряда Q, движущегося с постоянной нерелятивистской скоростью v. Этот закон задается формулой
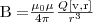
где r — радиус-вектор, который проведен от заряда Q к точке наблюдения М (рис. 1). Согласно (1), вектор В направлен перпендикулярно плоскости, в которой находятся векторы v и r: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.
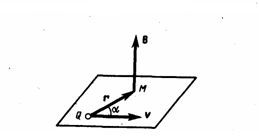
Рис.1
Модуль вектора магнитной индукции (1) находится по формуле
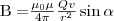
где α — угол между векторами v и r. Сопоставляя закон Био-Савара-Лапласа и (1), мы видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: Idl = Qv
Действие МП на движущийся заряд.
Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и задается выражением: F = Q где В — индукция магнитного поля, в котором заряд движется.
Чтобы определить направление силы Лоренца используем правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q На рис. 1 продемонстрирована взаимная ориентация векторов v, В (поле имеет направление на нас, на рисунке показано точками) и F для положительного заряда. Если заряд отрицательный, то сила действует в противоположном направлении.
Модуль силы Лоренца, как уже известно, равен F = QvB sin a; где α — угол между v и В.
МП не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.
Зная действие силы Лоренца на заряд можно найти модуль и направление вектора В, и формула для силы Лоренца может быть применена для нахождения вектора магнитной индукции В.
Поскольку сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, то данная сила может менять только направление этой скорости, не изменяя при этом ее модуля. Значит, сила Лоренца работы не совершает.
В случае, если на движущийся электрический заряд вместе с магнитным полем с индукцией В действует еще и электрическое поле с напряженностью Е, то суммарная результирующая сила F, которая приложена приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F = QE + Q[v,B]
Сила Ампера, Лоренца.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F = B.I.l. sin α — закон Ампера.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца: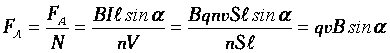
Явление электромагнитной индукции. Закон Фарадея. ЭДС индукции в движущихся проводниках. Самоиндукция.
Фарадей предположил, что если вокруг проводника с током существует магнитное поле, то естественно ожидать, что должно происходить и обратное явление – возникновение электрического тока под действием магнитного поля. И вот в 1831 г. Фарадей публикует статью, где сообщает об открытии нового явления – явления электромагнитной индукции.
Опыты Фарадея были чрезвычайно просты. Он присоединял гальванометр G к концам катушки L и приближал к ней магнит. Стрелка гальванометра отклонялась, фиксируя появление тока в цепи. Ток протекал, пока магнит двигался. При отдалении магнита от катушки гальванометр отмечал появление тока противоположного направления. Аналогичный результат отмечался, если магнит заменяли катушкой с током или замкнутым контуром с током.
Движущиеся магнит или проводник с током создают через катушку L переменное магнитное поле. В случае их неподвижности создаваемое ими поле постоянно. Если вблизи замкнутого контура поместить проводник с переменным током, то в замкнутом контуре также возникнет ток. На основе анализа опытных данных Фарадей установил, что ток в проводящих контурах появляется при изменении магнитного потока через площадь, ограниченную этим контуром.
Этот ток был назван индукционным. Открытие Фарадея было названо явлением электромагнитной индукции и легло в дальнейшем в основу работы электрических двигателей, генераторов, трансформаторов и подобных им приборов.
Итак, если магнитный поток через поверхность, ограниченную некоторым контуром, изменяется, то в контуре возникает электрический ток. Известно, что электрический ток в проводнике может возникнуть только под действием сторонних сил, т.е. при наличии э.д.с.. В случае индукционного тока э.д.с., соответствующая сторонним силам, называется электродвижущей силой электромагнитной индукции εi.
Э.д.с. электромагнитной индукции в контуре пропорциональна скорости изменения магнитного потока Фm сквозь поверхность, ограниченную этим контуром:
 |
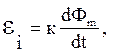где к – коэффициент пропорциональности. Данная э.д.с. не зависит от того, чем вызвано изменение магнитного потока – либо перемещением контура в постоянном магнитном поле, либо изменением самого поля.
Итак, направление индукционного тока определяется правилом Ленца: При всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
Обобщением закона Фарадея и правила Ленца является закон Фарадея — Ленца: Электродвижущая сила электромагнитной индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:
 |
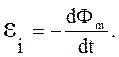Это выражение представляет собой основной закон электромагнитной индукции.
При скорости изменения магнитного потока 1Вб/с в контуре индуцируется э.д.с. в 1 В.
Пусть контур, в котором индуцируется э.д.с., состоит не из одного, а из N витков, например, представляет собой соленоид. Соленоид – это цилиндрическая катушка с током, состоящая из большого числа витков. Так как витки в соленоиде соединяются последовательно, εi в данном случае будет равна сумме э.д.с., индуцируемых в каждом из витков по отдельности
 |
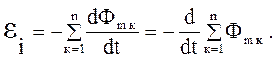Величину Ψ = ΣΦm называют потокосцеплением или полным магнитным потоком. Если поток, пронизывающий каждый из витков, одинаков (т.е. Ψ = NΦm), то в этом случае
 |
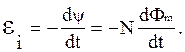Немецкий физик Г. Гельмгольц доказал, что закон Фарадея-Ленца является следствием закона сохранения энергии. Пусть замкнутый проводящий контур находится в неоднородном магнитном поле. Если в контуре течет ток I, то под действием сил Ампера незакрепленный контур придет в движение. Элементарная работа dA, совершаемая при перемещении контура за время dt, будет составлять
dA = IdФm,
где dФm – изменение магнитного потока сквозь площадь контура за время dt. Работа тока за время dt по преодолению электрического сопротивления R цепи равна I2Rdt. Полная работа источника тока за это время равна εIdt. По закону сохранения энергии работа источника тока затрачивается на две названные работы, т.е.
εIdt = IdФm + I2Rdt.
Разделив обе части равенства на Idt, получим
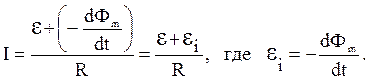
Следовательно, при изменении магнитного потока, сцепленного с контуром, в последнем возникает электродвижущая сила индукции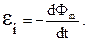 
Электромагнитные колебания. Колебательной контур.
Электромагнитные колебания — это колебания таких величин, индуктивность, как сопротивление, ЭДС, заряд, сила тока.
Колебательный контур — это электрическая цепь, которая состоит из последовательно соединенных конденсатора, катушки и резистора. Изменение электрического заряда на обкладке кон- денсатора с течением времени описывается дифференциальным уравнением:
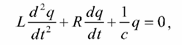
Электромагнитные волны и их свойства.
В колебательном контуре происходит процесс перехода электрической энергии конденсатора в энергию магнитного поля катушки и наоборот. Если в определенные моменты времени компенсировать потери энергии в контуре на сопротивление за счет внешнего источника, то получим незатухающие электрические колебания, которые через антенну могут быть излучены в окружающее пространство.
Процесс распространения электромагнитных колебаний, периодических изменений напряженностей электрического и магнитных полей, в окружающем пространстве называется электромагнитной волной.
Электромагнитные волны охватывают большой спектр длин волн от 105 до 10 м и по частотам от 104 до 1024 Гц. По названию электромагнитные волны разделяются на радиоволны, инфракрасное, видимое и ультрафиолетовое излучения, рентгеновские лучи и -излучение. В зависимости от длины волны или частоты свойства электромагнитных волн меняются, что является убедительным доказательством диалектико-материалистического закона перехода количества в новое качество.
Электромагнитное поле материальное и обладает энергией, количеством движения, массой, перемещается в пространстве: в вакууме со скоростью С, а в среде со скоростью: V= , где = 8,85 ;
Объемная плотность энергии электромагнитного поля . Практическое использование электромагнитных явлений весьма широкое. Это — системы и средства связи, радиовещания, телевидения, электронно-вычислительная техника, системы управления различного назначения, измерительные и медицинские приборы, бытовая электро- и радиоаппаратура и другие, т.е. то, без чего невозможно представить себе современное общество.
Как действует на здоровье людей мощное электромагнитное излучение, точных научных данных почти нет, есть только неподтвержденные гипотезы и, в общем-то, небезосновательные опасение, что все неестественное действует губительно. Доказано, что ультрафиолетовое, рентгеновское и -излучение большой интенсивности во многих случаях наносят реальный вред всему живому.
Геометрическая оптика. Законы ГО.
Геометрическая (лучевая) оптика использует идеализированное представление о световом луче – бесконечно тонком пучке света, распространяющемся прямолинейно в однородной изотропной среде, а также представления о точечном источнике излучения, равномерно светящем во все стороны. λ – длина световой волны, – характерный размер
предмета, находящегося на пути волны. Геометрическая оптика является предельным случаем волновой оптики и ее принципы выполняются при соблюдении условия:
h/D << 1 т. е. геометрическая оптика, строго говоря, применима лишь к бесконечно коротким волнам.
В основе геометрической оптики лежит так же принцип независимости световых лучей: лучи при перемещении не возмущают друг друга. Поэтому перемещения лучей не мешают каждому из них распространяться независимо друг от друга.
Для многих практических задач оптики можно не учитывать волновые свойства света и считать распространение света прямолинейным. При этом картина сводится к рассмотрению геометрии хода световых лучей.
Основные законы геометрической оптики.
Перечислим основные законы оптики, следующие из опытных данных:
1) Прямолинейное распространение.
2) Закон независимости световых лучей, то есть два луча, пересекаясь, никак не мешают друг другу. Этот закон лучше согласуется с волновой теорией, так как частицы в принципе могли бы сталкиваться друг с другом.
3) Закон отражения. луч падающий, луч отраженный и перпендикуляр к поверхности раздела, восстановленный в точке падения луча, лежат в одной плоскости, называемой плоскостью падения; угол падения равен углу
Отражения.
4) Закон преломления света.
Закон преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела, восстановленный из точки падения луча, лежат в одной плоскости – плоскости падения. Отношение синуса угла падения к синусу угла отражения равно отношению скоростей света в обеих средах.
Sin i1/ sin i2 = n2/n1 = n21
где – относительный показатель преломления второй среды относительно первой среды. n21
Если вещество 1 – пустота, вакуум, то n12 → n2 – абсолютный показатель преломления вещества 2. Можно легко показать, что n12 = n2 /n1 , в этом равенстве слева относительный показатель преломления двух веществ (например, 1 – воздух, 2 – стекло), а справа – отношение их абсолютных показателей преломления.
5) Закон обратимости света (его можно вывести из закона 4). Если направить свет в обратном направлении, он пройдёт по тому же пути.
Из закона 4) следует, что если n2 > n1 , то Sin i1 > Sin i2 . Пусть теперь у нас n2 < n1 , то есть свет из стекла, например, выходит в воздух, и мы постепенно увеличиваем угол i1.
Тогда можно понять, что при достижении некоторого значения этого угла (i1)пр окажется, что угол i2 окажется равным π /2 (луч 5). Тогда Sin i2 = 1 и n1 Sin (i1)пр = n2 . Итак Sin
(i1)пр = n2 / n1 .
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.
В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда, — скорость заряда, — индукция магнитного поля, — угол между векторами и .
2. Сила Лоренца перпендикулярна обоим векторам и . Иными словами, вектор перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов , и для положительного заряда показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен . Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике, — их концентрация (число в единице объёма). Тогда:
где — объём проводника, — площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле . Ток течёт по рамке в направлении ; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом между векторами и .
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и , приложенные к сторонам и , действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и , приложеные соответственно к сторонам и . Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси вращения рамки.
Пусть длина стороны равна . Тогда
Пусть длина стороны равна . Плечо силы , как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и . Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы и направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор к вектору (убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы и сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении ; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Лекция по физике на тему «Сила Ампера и Лоренца «
Тема: Действие магнитного поля на проводнике с током на движущийся заряд. Сила Ампера. Действие магнитного поля на ток движущегося заряда. Сила Лоренца.
Магнитное поле действует на все участки проводника с током. Зная силу, действующую на каждый малый участок проводника, можно вычислить силу, действующую на весь замкнутый проводник в целом. Закон, определяющий силу, действующую на весь замкнутый проводник в целом. Закон, определяющий силу, действующую на отдельный участок проводника, был установлен в 1820 г. А. Ампером. Ампер сумел установить выражение для силы, действующей на отдельный элемент тока. Сила достигает максимального значения Fm когда магнитная индукция перпендикулярна проводнику.
Модулем вектора магнитной индукции назовем отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка:
B=Fm/Iδl
Магнитное поле полностью характеризуется, вектором магнитной индукции В. В каждой точке магнитного поля могут быть определены направление вектора магнитной индукции и его модуль с помощью измерения силы, действующей на участок проводника с током. Максимальная сила Ампер согласно равна:
Fm=IΔlB
F=В|I|Δlsin
Это выражение называют законом Ампера.
Сила Ампера равна произведению вектора магнитной индукции на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника. Правила левой руки – если руку расположить так, чтобы перпендикулярная у проводнику составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлению тока, то отогнутый на 900 большой палец покажет направление силы, действующей на отрезок проводника.
Единица магнитной индукции получила название тесла (Тл) в честь югославского ученого-электротехника Н. Тесла.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца, основателя электронной теории строения вещества. Эту силу можно найти с помощью закона Ампера. Fm=v Δq B
Если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда, то отогнутый на 900 большой палец покажет направление действующей на заряд силы Лоренца Fл.
F=Fэл.+FЛ
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. Согласно второму закону Ньютона:
mυ2/r=|q|υB Отсюда : r=mv/gВ
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
F = q n S Δl υB sin α. |
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна
FЛ = q υ B sin α. |
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью 
и вектором магнитной индукции 
. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов , и 
для положительно заряженной частицы показано на рис. 1.18.1.
Сила Лоренца направлена перпендикулярно векторам и
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору 
то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
|
Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле |
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
|
Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам 
и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила 
и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле 
. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
|
Рисунок 1.18.4. Селектор скоростей и масс-спектрометр |
Если скорость частицы имеет составляющую 
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ+ вектора 
а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
|
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле |
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
|
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током |
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что северный магнитный полюс Земли сейчас находится вблизи северного географического полюса и постепенно перемещается. Природа земного магнетизма до сих пор не изучена.
|
Рисунок 1.18.7. Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния |
 |
Модель. Движение заряда в магнитном поле |
 |
Модель. Масс-спектрометр |
 |
Модель. Селектор скоростей |