Сила Лоренца — это… Что такое Сила Лоренца?
Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Уравнение (единицы СИ)
Заряженная частица
Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- , где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.
Частные случаи
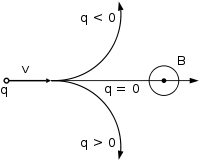Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :
Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :
Применение силы Лоренца
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеВ электроприборах
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
Другие применения
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
См. также
Ответы@Mail.Ru: правило Лоренца
Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>fond2019.ru</a> Выплатили 28 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие фонды, на работу бы ходить не пришлось:)
Как найти направление силы Лоренца?
Направление силы Лоренца можно определить по правилу левой рука: «если левую руку расположить так, чтобы составляющая вектора магнитной индукции B, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного) , то отогнутый на 90° большой палец покажет направление действующей на заряд силы Лоренца.
po pravilu shtopora (buravchika)
да, силовые лини магнитного поля должны входить в ладонь, 4 вытянутых пальца указывают направление движения ПОЛОЖИТЕЛЬНО заряженной частицы, а большой палец указывает напрвление силы
F=g[v*B] Правило векторного произведения знаете? Тройка некомпланарных векторов abc называется правой, если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой руки. У вас вектор v, B и F должны образовывать такую правую тройку.
1.4. Сила Лоренца. Правило левой руки для определения направления силы Лоренца
…В 1936 г. Лоренц вывел следующее правило: инстинкты вызываются не рефлексами, а внутренними побуждениями.. .
http://mirslovarei.com/content_psy/LORENC-KONRAD-3058.html
____
…Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца.. .
http://www.edu.delfa.net/CONSP/mag25.html
____
…Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.
Сила Лоренца определяется соотношением:
Fл = q·V·B·sina
где q — величина движущегося заряда;
V — модуль его скорости;
B — модуль вектора индукции магнитного поля;
a — угол между вектором скорости заряда и вектором магнитной индукции.
См. ссылку — здесь символы искажаются: http://www.nvtc.ee/e-oppe/Baksejeva/magn/_4.html
Нет ПРАВИЛА ЛОРЕНЦА, есть знаменитое ПРАВИЛО ЛЕВОЙ РУКИ:
Сила Лоренца перпендикулярна векторам В и v, и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного) , то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.
Сила Лоренца зависит от модулей скорости частицы и индукции магнитного поля. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Частица равномерно движется по окружности радиуса r.
___
Ещё формулировка:
ЛЕВОЙ РУКИ ПРАВИЛО — правило, определяющее направление силы, которая действует на находящийся в магнитном поле проводник с током (или движущуюся заряженную частицу) . Оно гласит: если левую руку расположить так, чтобы вытянутые пальцы показывали направление тока (скорости частицы) , а силовые линии магнитного поля (линии магнитной индукции) входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник (положительную частицу; в случае отрицательной частицы направление силы противоположно) .
http:// barsic. spbu. ru/www/lab1108/ref/l.htm (убрать пробелы)
Правило левой руки: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник.
http://physics.ru/courses/op25part2/content/chapter1/section/paragraph26/theory.html
Силой Лоренца называют силу, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:F = q(E+vB),
где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.
Сила Лоренца очень похожа по своему принципу на силу Ампера, разница заключается в том, что последняя действует на весь проводник, который в целом электрически нейтральный, а сила Лоренца описывает влияние электромагнитного поля лишь на единичный движущийся заряд.
Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц.
В природе сила Лоренца позволяет защищать Землю от воздействия космической радиации. Под её воздействием падающие на
Сила Лоренца — Вікіпедія
Си́ла Ло́ренца — сила, що діє на рухомий електричний заряд, який перебуває в електромагнітному полі.
- F=qE+q[v×B]{\displaystyle \mathbf {F} =q\mathbf {E} +{q}[\mathbf {v} \times \mathbf {B} ]}.
Тут F{\displaystyle \mathbf {F} } — сила, q{\displaystyle q} — величина заряду, E{\displaystyle \mathbf {E} } — напруженість електричного поля, v{\displaystyle \mathbf {v} } — швидкість руху заряду, B{\displaystyle \mathbf {B} } — вектор магнітної індукції[1]. Іноді силою Лоренца називають лише другу складову цього виразу — силу, яка діє на заряд, що рухається, з боку магнітного поля (F=q[v×B]{\displaystyle \mathbf {F} ={q}[\mathbf {v} \times \mathbf {B} ]}).
Електричне поле діє на заряд із силою, направленою вздовж силових ліній поля. Магнітне поле діє лише на рухомі заряди. Сила дії магнітного поля перпендикулярна до силових ліній поля й до швидкості руху заряду.
Названа на честь Гендрика Лоренца, який розробив це поняття 1895 року.
Виведення із використанням закону Кулона та спеціальної теорії відносності[ред. | ред. код]
Попередні перетворення[ред. | ред. код]
Попередні перетворення
Перетворення Лоренца для радіус-вектора:
r′=r+Γu(u⋅r)c2−γut{\displaystyle \ \mathbf {r} ‘=\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}-\gamma \mathbf {u} t},
γ=11−u2c2{\displaystyle \ \gamma ={\frac {1}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}}
Γ=γ−1u2c2=γ21+γ{\displaystyle \ \Gamma ={\frac {\gamma -1}{\frac {u^{2}}{c^{2}}}}={\frac {\gamma ^{2}}{1+\gamma }}}
u{\displaystyle \ \mathbf {u} } — відносна швидкість між двома інерціальними системами відліку.
При t=0{\displaystyle \ t=0} вираз перетворюється у наступний:
r′=r+Γu(u⋅r)c2(.1){\displaystyle \ \mathbf {r} ‘=\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}\qquad (.1)}.
Якщо піднести ліву і праву частину до квадрату, можна буде отримати:
r′2=r2+γ2c2(u⋅r)2(.2){\displaystyle \mathbf {r} ‘^{2}=\mathbf {r} ^{2}+{\frac {\gamma ^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )^{2}\qquad (.2)}.
Виведення.
r′2=r2+2Γ(u⋅r)2c2+Γ2u2(u⋅r)2c4=r2+(u⋅r)2u2[2(γ−1)+(γ−1)2]=r2+(u⋅r)2c2[(γ−1)c2u2(γ+1)]={\displaystyle \mathbf {r} ‘^{2}=\mathbf {r} ^{2}+2\Gamma {\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}+\Gamma ^{2}u^{2}{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{4}}}=\mathbf {r} ^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{u^{2}}}\left[2(\gamma -1)+(\gamma -1)^{2}\right]=\mathbf {r} ^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}\left[{\frac {(\gamma -1)c^{2}}{u^{2}}}(\gamma +1)\right]=}
=|Γ=γ−1u2c2=γ21+γ|=|r|2+(u⋅r)2c2γ2{\displaystyle =\left|\Gamma ={\frac {\gamma -1}{\frac {u^{2}}{c^{2}}}}={\frac {\gamma ^{2}}{1+\gamma }}\right|=|\mathbf {r} |^{2}+{\frac {(\mathbf {u} \cdot \mathbf {r} )^{2}}{c^{2}}}\gamma ^{2}}.
Якщо скалярно домножити (.1){\displaystyle \ (.1)} на u{\displaystyle \ \mathbf {u} }, то можна буде отримати:
(u⋅r′)=(u⋅r)+Γ|u|2c2(u⋅r)=(u⋅r)(1+γ−1)=γ(u⋅r)(.3){\displaystyle \ (\mathbf {u} \cdot \mathbf {r} ‘)=(\mathbf {u} \cdot \mathbf {r} )+\Gamma {\frac {|\mathbf {u} |^{2}}{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )=(\mathbf {u} \cdot \mathbf {r} )(1+\gamma -1)=\gamma (\mathbf {u} \cdot \mathbf {r} )\qquad (.3)}.
Накінець,
(v′⋅r′)=(r⋅v)γ(1−(v⋅u)c2)−γ(r⋅u)(.4){\displaystyle \ (\mathbf {v} ‘\cdot \mathbf {r} ‘)={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}-\gamma (\mathbf {r} \cdot \mathbf {u} )\qquad (.4)}.
Виведення.
(r′⋅v′)=([r+Γuc2(u⋅r)]⋅v+Γuc2(u⋅v)−γuγ(1−(u⋅v)c2))=(r⋅v)γ(1−(u⋅v)c2)+Γc2(u⋅r)(u⋅v)(2+Γ2u2c2)−γ(u⋅r)(1+Γu2c2)γ(1−(u⋅v)c2)={\displaystyle \ (\mathbf {r} ‘\cdot \mathbf {v} ‘)=\left(\left[\mathbf {r} +{\frac {\Gamma \mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )\right]\cdot {\frac {\mathbf {v} +{\frac {\Gamma \mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {v} )-\gamma \mathbf {u} }{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\right)={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}+{\frac {{\frac {\Gamma }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )(\mathbf {u} \cdot \mathbf {v} )\left(2+{\frac {\Gamma ^{2}u^{2}}{c^{2}}}\right)-\gamma (\mathbf {u} \cdot \mathbf {r} )\left(1+{\frac {\Gamma u^{2}}{c^{2}}}\right)}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}=}
=|2+Γ2u2c2=γ+1=γ2Γ,1+Γu2c2=γ|=(r⋅v)γ(1−(u⋅v)c2)−γ2(r⋅u)(1−(u⋅v)c2)γ(1−(u⋅v)c2)=(r⋅v)γ(1−(u⋅v)c2)−γ(r⋅u){\displaystyle \ =\left|2+{\frac {\Gamma ^{2}u^{2}}{c^{2}}}=\gamma +1={\frac {\gamma ^{2}}{\Gamma }},\quad 1+{\frac {\Gamma u^{2}}{c^{2}}}=\gamma \right|={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}-{\frac {\gamma ^{2}(\mathbf {r} \cdot \mathbf {u} )\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}={\frac {(\mathbf {r} \cdot \mathbf {v} )}{\gamma \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}-\gamma (\mathbf {r} \cdot \mathbf {u} )}.
Вираз для перетворення 3-вектора сили при переході до нової ІСВ:
Fγ(1−(v⋅u)c2)=F′+γu(F′⋅v′)c2+Γu(u⋅F′)c2(.5){\displaystyle \ {\frac {\mathbf {F} }{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}=\mathbf {F} ‘+\gamma {\frac {\mathbf {u} (\mathbf {F} ‘\cdot \mathbf {v} ‘)}{c^{2}}}+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {F} ‘)}{c^{2}}}\qquad (.5)}.
Власне, сила Лоренца[ред. | ред. код]
Базовим виразом для аналізу взаємодії заряда Q{\displaystyle \ Q} із деяким пробним зарядом q{\displaystyle \ q} є закон Кулона: для статичних зарядів у вакуумі відносно інерціальної системи відліку, що перебуває у спокої, можна записати, що сила їхньої взаємодії дорівнює
- F=qQ|r|3r{\displaystyle \ \mathbf {F} ={\frac {qQ}{|\mathbf {r} |^{3}}}\mathbf {r} }.
Для того, щоб визначити, як буде виглядати ця сила в інерціальній системі відліку, що рухається, можна розглянути наступний «віртуальний» експеримент.
Нехай у вакуумі знаходяться два заряди, скріплені пружинкою. Заряди розглядаються відносно інерціальної системи відліку, у якій вони перебувають у спокої протягом досить великого проміжку часу. Пружинка забезпечує статичність зарядів, а розтяг пружинки чисельно характеризує силу взаємодії зарядів. Якщо прибрати пружинку й розглянути деяке мале відхилення від статичного стану, наприклад, одного заряду, то можна проаналізувати час, за який другий заряд «відчує» зміну стану першого, тим самим експериментально визначивши швидкість розповсюдження взаємодії між зарядами. Проте в рамках експерименту (заряди скріплені пружинкою) про швидкість розповсюдження взаємодії нічого не можна сказати, оскільки система є статичною. Таким чином, закон Кулона, який описує взаємодію статичних зарядів, не несе, без додаткових припущень, жодної інформації про швидкість розповсюдження взаємодії між зарядами. А отже, релятивістський та класичний опис взаємодії зарядів у статичному випадку збігаються.
Для подальшого аналізу взаємодії цих зарядів можна розглянути їх відносно інерційної системи відліку, що довільно рухається. У такому разі, система вже не буде статичною, а це означає, що можна оцінити швидкість розповсюдження взаємодії. Якщо припустити, що виконується аксіома абсолютності одночасності, то швидкість розповсюдження взаємодії нескінченна, а це, загалом, означає, що до закона Кулона застосовуються перетворення Галілея, що залишають його інваріантним відносно вибору інерціальної системи відліку. А якщо припустити, що аксіома абсолютності одночасності не виконується, то швидкість розповсюдження взаємодії скінченна, і це означає, що до закону Кулона застосовуються перетворення Лоренца, які не залишають вираз для сили Кулона інваріантним відносно вибору інерційної системи відліку.
Саме останньому випадку і присвячені наступні викладки.
Можна записати вираз для сили Кулона точкового заряду Q{\displaystyle \ Q} відносно системи відліку K’, що рухається у вакуумі зі швидкістю u{\displaystyle \ \mathbf {u} } відносно системи S{\displaystyle \ S}, у якій заряд Q{\displaystyle \ Q} перебуває у спокої, а заряд q{\displaystyle \ q} рухається із швидкістю v{\displaystyle \ \mathbf {v} } відносно нього. Перед цим треба ввести постулат про інваріантність заряду, Q′=Q{\displaystyle \ Q’=Q}. Тоді
F′=qQ|r′|3r′(.6){\displaystyle \ \mathbf {F} ‘={\frac {qQ}{|\mathbf {r} ‘|^{3}}}\mathbf {r} ‘\qquad (.6)}.
Якщо підставити (.6){\displaystyle \ (.6)} у (.5){\displaystyle \ (.5)}, то, з урахуванням попередніх перетворень (.1)−(.4){\displaystyle \ (.1)-(.4)}, можна буде отримати вираз для сили F′{\displaystyle \ \mathbf {F} ‘}, що діє на заряд q{\displaystyle \ q} у системі S{\displaystyle \ S} відносно системи відліку S′{\displaystyle S’}:
F=qQγ(r2+γ2(r⋅u)2c2)32[r+1c2[v×[u×r]]](.7){\displaystyle \ \mathbf {F} ={\frac {qQ\gamma }{\left(\mathbf {r} ^{2}+\gamma ^{2}{\frac {(\mathbf {r} \cdot \mathbf {u} )^{2}}{c^{2}}}\right)^{\frac {3}{2}}}}\left[\mathbf {r} +{\frac {1}{c^{2}}}[\mathbf {v} \times [\mathbf {u} \times \mathbf {r} ]]\right]\qquad (.7)}.
Виведення.
Fγ(1−(v⋅u)c2)=Qq|r′|3[r′+γu(r′⋅v′)c2+Γu(u⋅r′)c2]=Qq|r′|3[r+Γu(u⋅r)c2+γuc2((u⋅r)γ(1−(u⋅v)c2)−γ(u⋅r))+Γγu(u⋅r)c2]={\displaystyle \ {\frac {\mathbf {F} }{\gamma (1-{\frac {(\mathbf {v} \cdot \mathbf {u} )}{c^{2}}})}}={\frac {Qq}{|\mathbf {r} ‘|^{3}}}\left[\mathbf {r} ‘+\gamma \mathbf {u} {\frac {(\mathbf {r} ‘\cdot \mathbf {v} ‘)}{c^{2}}}+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} ‘)}{c^{2}}}\right]={\frac {Qq}{|\mathbf {r} ‘|^{3}}}\left[\mathbf {r} +\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}+\gamma {\frac {\mathbf {u} }{c^{2}}}\left({\frac {(\mathbf {u} \cdot \mathbf {r} )}{\gamma (1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}})}}-\gamma (\mathbf {u} \cdot \mathbf {r} )\right)+\Gamma \gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}\right]=}
Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+Γu(u⋅r)c2(1+γ)−uc2γ2(u⋅r)+γuc2(v⋅r)]=|Γ(1+γ)=γ2|={\displaystyle \ {\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+\Gamma \mathbf {u} {\frac {(\mathbf {u} \cdot \mathbf {r} )}{c^{2}}}(1+\gamma )-{\frac {\mathbf {u} }{c^{2}}}\gamma ^{2}(\mathbf {u} \cdot \mathbf {r} )+\gamma {\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]=|\Gamma (1+\gamma )=\gamma ^{2}|=}
=Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+γ2uc2(u⋅r)−uc2γ2(u⋅r)+γuc2(v⋅r)]=Qq|r′|3(1−(u⋅v)c2)[r(1−(u⋅v)c2)+uc2(v⋅r)]={\displaystyle \ ={\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+\gamma ^{2}{\frac {\mathbf {u} }{c^{2}}}(\mathbf {u} \cdot \mathbf {r} )-{\frac {\mathbf {u} }{c^{2}}}\gamma ^{2}(\mathbf {u} \cdot \mathbf {r} )+\gamma {\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]={\frac {Qq}{|\mathbf {r} ‘|^{3}\left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)}}\left[\mathbf {r} \left(1-{\frac {(\mathbf {u} \cdot \mathbf {v} )}{c^{2}}}\right)+{\frac {\mathbf {u} }{c^{2}}}(\mathbf {v} \cdot \mathbf {r} )\right]=}
=|u(v⋅r)=[v×[u×r]]+r(u⋅r)|=Qq|r′|3(1−(u⋅v)c