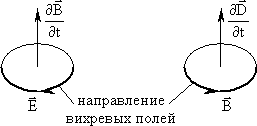Сила Лоренца (эл. И магн. Часть). Закон Ампера. Действие магнитного поля на движущийся заряд. Сила Лоренца
Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
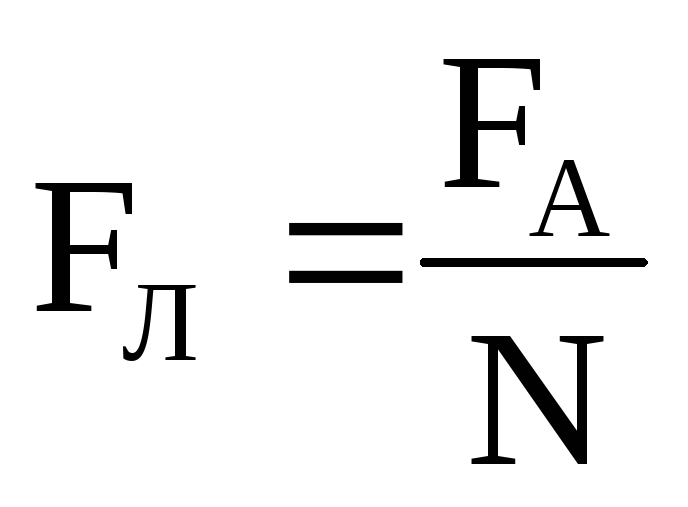
Сила
Ампера равна  ,
сила тока равна
,
сила тока равна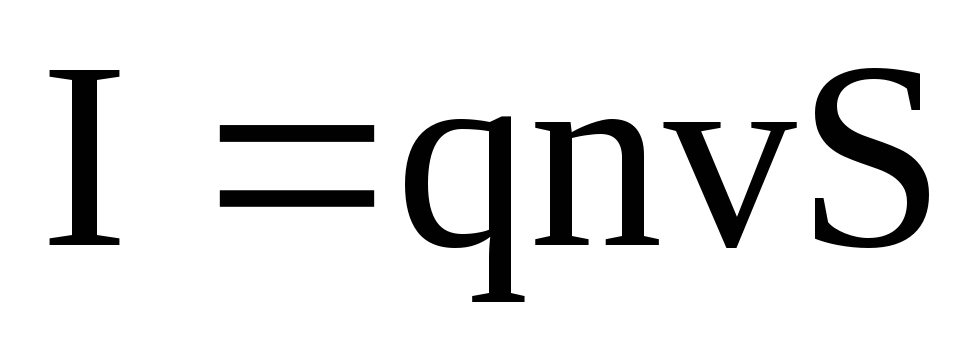
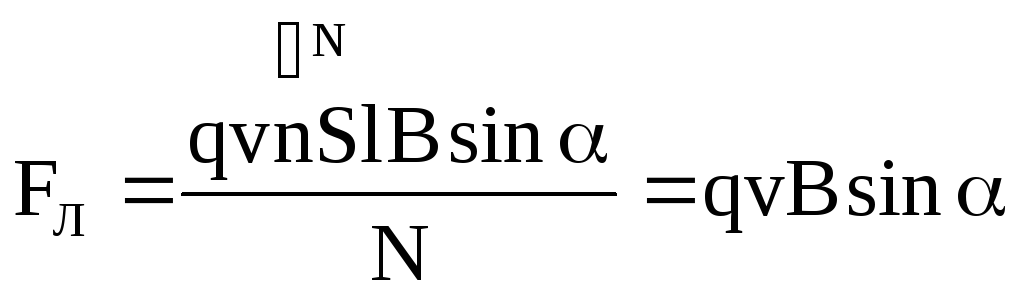
где  — угол между векторами скорости и
магнитной индукции.
— угол между векторами скорости и
магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Закон Ампера
Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsin, где — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по
Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
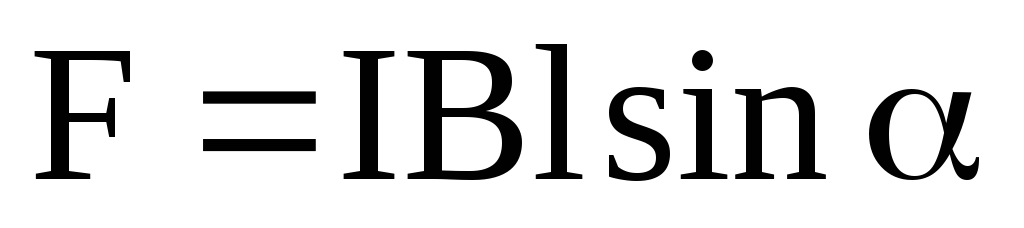
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
2. Чистые полупроводники
Чистые полупроводники – это полупроводники, обладающие собственной проводимостью, возникающей в результате разрыва ковалентных связей в чистом полупроводнике.
Рассмотрим кристалл кремния.
У атома кремния на внешней оболочке имеется 4 валентных электрона. В твердом состоянии это вещество имеет кристаллическую решетку, в которой каждый атом имеет четыре ближайших соседа. Связь между соседними атомами ковалентная, т.е. два соседних атома объединяют два своих валентных электрона.
При низких температурах электроны связаны с атомами, а при повышении температуры отдельные электроны могут получить избыточную энергию для отрыва от атома. Появляются свободные электроны, а в оболочке атома полупроводник остается свободное место, которое принято называть «дыркой». Атом приобретает положительный заряд, который приписывают «дырке».
Нагревание полупроводника ведет к образованию подвижных носителей зарядов электронов и «дырок».


В полупроводнике электронно-дырочная проводимость.
Электрическим током в полупроводнике называется направленное движение электронов в положительному полюсу, а дырок к отрицательному полюсу (собственная проводимость).
3. Примесные полупроводник.
Примесные полупроводники, это полупроводники у которых электропроводимость обусловлена (возникает) внесением в их кристаллическую решетку примесей.
В зависимости от вида примесных центров возникает материал с электронной проводимостью (
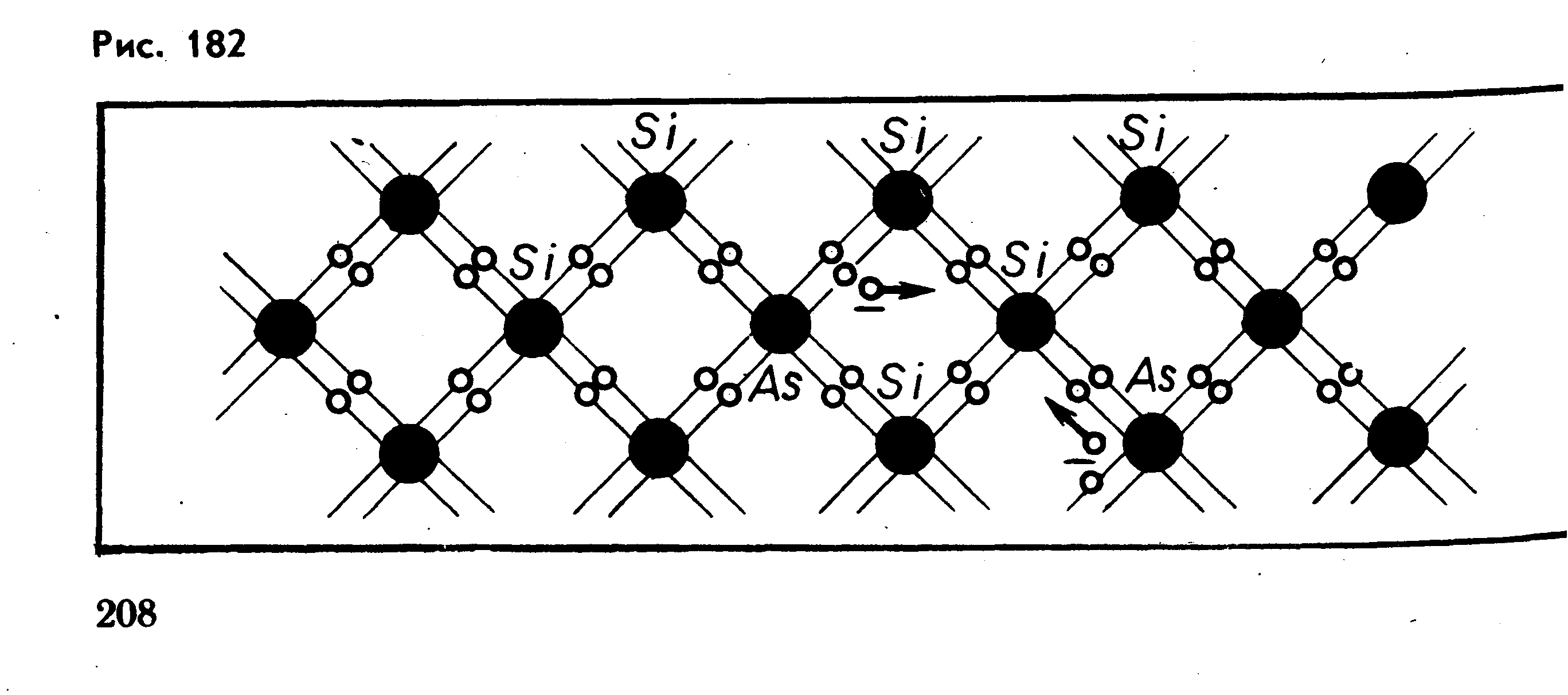
Полупроводники (n — типа) имеют донорую примесь.
Донорная примесь – это примесь, отдающая свой лишний электрон, неучаствующий в создании ковалентной связи.
Например:
Введение примесных доноров – атомов с 5 внешними электронами (например, фосфора) в кристаллы кремния с 4 валентными электронами. При каждом атоме фосфора один электрон становится свободным, он лишний в ковалентной связи.
Полупроводники (р — типа) имеют акцепторную примесь.
Акцепторная примесь – это примесь, у которой не достает электронов до полной ковалентной связи с соседними атомами.
Например:
Введение примесных акцепторов – атомов с3внешними электронами в кристаллы кремния с4 внешними электронами, например индия, приводит к появлению дырок – место электрона остается не занятым. Эта дырка имеет такие же свойства, как и положительный носитель заряда.
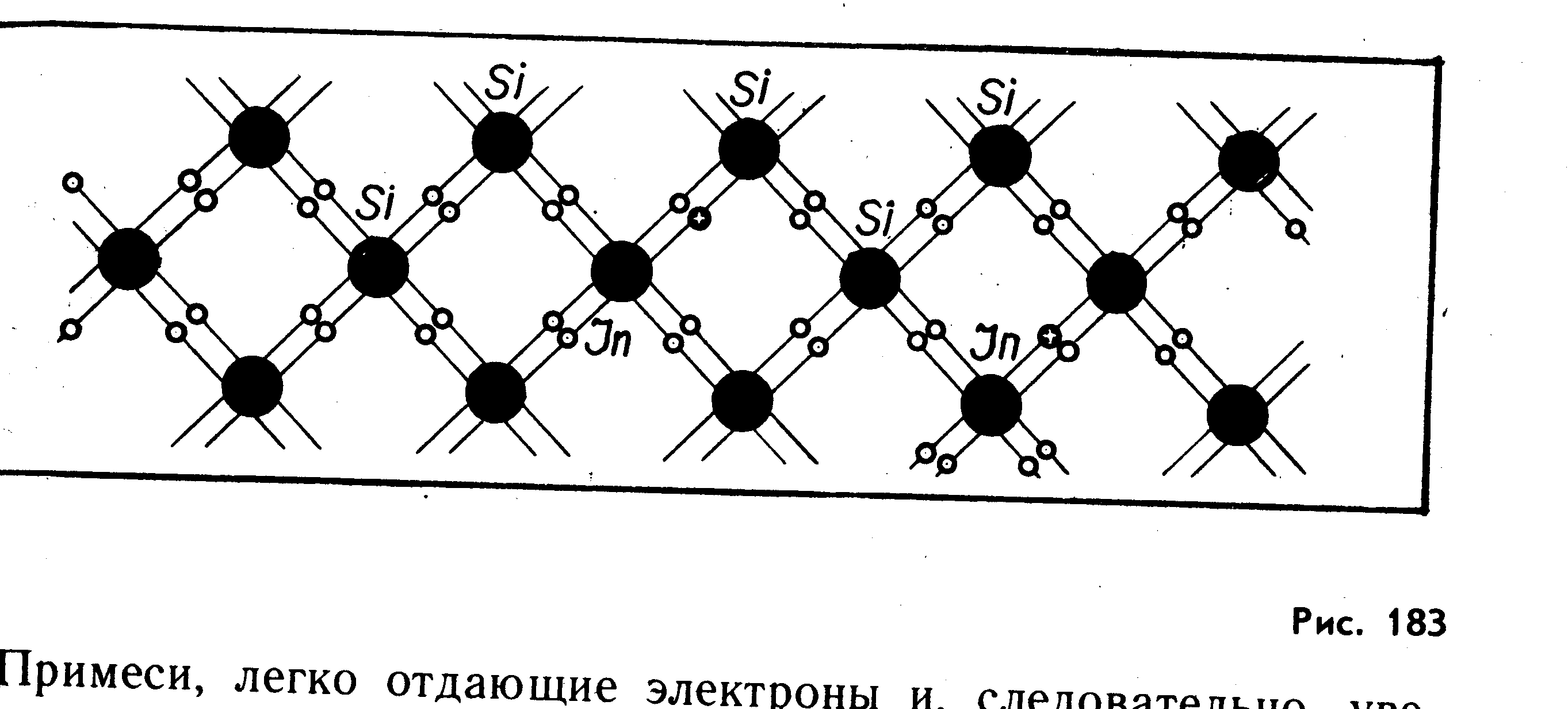
Полупроводники с акцепторными примесями обладают дырочной проводимостью и называются полупроводниками р – типа.
Изменяя концентрацию примесей, можно значительно изменить число носителей зарядов того или иного знака. Благодаря этому можно создать полупроводники с преимущественной концентрацией либо отрицательно либо отрицательно заряженных носителей зарядов.
Р – n переход.
Электронно – дырочный переход представляет собой контакт между полупроводниками р и n типа.




Для самопроверки заполни таблицу:
вещество | определение | проводимость | условие | применение |
металл | ||||
электролит | ||||
газ | ||||
вакуум | ||||
Полупроводник: | ||||
чистый | ||||
донорный | ||||
акцепторный | ||||
43. Сила Ампера. Сила Лоренца
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B.I.ℓ.sin α — закон Ампера.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:
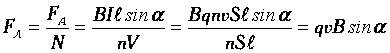
Если
вектор vчастицы
перпендикуляренвектору В,то
частица описывает траекторию в виде
окружности: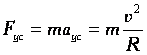
Роль
центростремительной силы играет сила
Лоренца: 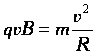
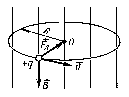
При
этом радиус окружности: 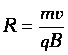 ,
,
Если вектор скорости и частицы не перпендикулярен В, то частица описывает траекторию в виде винтовой линии (спирали).
44.
Теорема о циркуляции вектора магнитной
индукции. Применение теоремы о циркуляции
вектора магнитной индукции для расчета
поля прямого тока. Циркуляция вектора
магнитной индукции через замкнутый
контур=произведению магнитной постоянной
на алгебраическую сумму токов, охватываемых
контуром.
∫BdL=μ0I;
I=ΣIi 
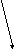
I2
I1>0 I2<0
Теорема говорит о том, что магнитное поле не является потенциальным, а является вихревым.
Применение в тетради
45. Закон электромагнитной индукции. Правило Ленца
Фарадей
экспериментально установил, что при
изменении магнитного потока в проводящем
контуре возникает ЭДС индукции εинд,
равная скорости изменения магнитного
потока через поверхность, ограниченную
контуром, взятой со знаком минус: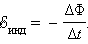
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Правило
Ленца отражает тот экспериментальный
факт, что εинди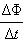 всегда
имеют противоположные знаки (знак
«минус» в формуле Фарадея). Правило
Ленца имеет глубокий физический смысл
– оно выражает закон сохранения энергии.
всегда
имеют противоположные знаки (знак
«минус» в формуле Фарадея). Правило
Ленца имеет глубокий физический смысл
– оно выражает закон сохранения энергии.
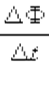
εi=-N, гдеN- кол-во витков
Способ возникновения ЭДС:
1.рамка неподвижна, но изменяется магнитный поток за счёт движения ккатушки или за счет изменения силы тока в ней.
2.рамка перемещается в поле непожвижной катушки.
46. Явление самоиндукции.
Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется явлением самоиндукции.
Магнитный поток, обусловленный собственным током контура (сцепленный с контуром), пропорционален магнитной индукции, которая, в свою очередь, по закону Био-Савара-Лапласа, пропорциональна току.
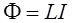 ,
где L –коэффициент самоиндукции или
индуктивность, «геометрическая»
характеристика проводника, так как
зависит от его формы и размеров, а также
от магнитных свойств среды.
,
где L –коэффициент самоиндукции или
индуктивность, «геометрическая»
характеристика проводника, так как
зависит от его формы и размеров, а также
от магнитных свойств среды.
47. Уравнения Максвелла в интегральной форме. Свойства уравнений Максвелла.
Закон
Гаусса 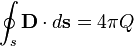
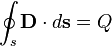 Поток
электрической индукции через замкнутую
поверхность s пропорционален величине
свободного заряда, находящегося в объёме
v, который окружает поверхность s.
Поток
электрической индукции через замкнутую
поверхность s пропорционален величине
свободного заряда, находящегося в объёме
v, который окружает поверхность s.
Закон
Гаусса для магнитного поля 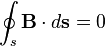
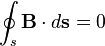 Поток магнитной индукции через
замкнутую поверхность равен нулю
(магнитные заряды не существуют).
Поток магнитной индукции через
замкнутую поверхность равен нулю
(магнитные заряды не существуют).
Закон
индукции Фарадея 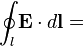
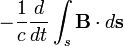
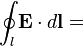
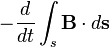 Изменение потока
магнитной индукции, проходящего через
незамкнутую поверхность
Изменение потока
магнитной индукции, проходящего через
незамкнутую поверхность ,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре
,
взятое с обратным знаком, пропорционально
циркуляции электрического поля на
замкнутом контуре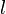 ,
который является границей поверхности
,
который является границей поверхности .
.
Теорема
о циркуляции магнитного поля 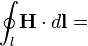
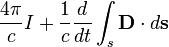
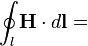
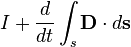
Полный
электрический ток свободных зарядов и
изменение потока электрической индукции
через незамкнутую поверхность  ,
пропорциональны циркуляции магнитного
поля на замкнутом контуре
,
пропорциональны циркуляции магнитного
поля на замкнутом контуре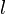 ,
который является границей поверхности
,
который является границей поверхности .
.
Свойства уравнений Максвелла.
А. Уравнения Максвелла линейны. Они содержат только первые производные полейEиBпо времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции.
Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:
∫pdv=const
В. Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.
Г. О симметрииуравнений Максвелла.
Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и j=0 ,уравнения Максвелла приобретают симметричный вид, т.е.Eтак связано с(dB/dt) , какBсdE/dt.
| Различие только в знаках перед производными(dB/dt) и(dD/dt) показывает, что линии вихревого электрического поля, индуцированного уменьшением поляB, образуют с вектором(dB/dt) левовинтовую систему, в то время как линии магнитного поля, индуцируемого изменениемD, образуют с вектором (dD/dt) правовинтовую систему. |
Д. Об электромагнитных волнах.
Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещения(dD/dt) играет в этом явлении первостепенную роль.
20.Сила Ампера. Сила Лоренца
Сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции: F ~ IΔl sin α.
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции.
F = I·L·B·sina
I — сила тока в проводнике;
B — модуль вектора индукции магнитного поля;
L — длина проводника, находящегося в магнитном поле;
a — угол между вектором магнитного поля инаправлением тока в проводнике.
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, F = IBΔl sin α
может быть выражена через силы, действующие на отдельные носители заряда.
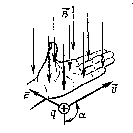
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: I = q n υ S. Выражение для силы Ампера можно записать в виде: F = q n S Δl υB sin α. Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна FЛ = q υ B sin α. Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика.
21.Классификация веществ по магнетическим свойствам
По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп:
диамагнетики,
парамагнетики,
ферромагнетики,
антиферромагнетики
ферримагнетики.
Перечисленным видам магнетиков соответствуют пять различных видов магнитного состояния вещества: диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм.
К диамагнетикам относят вещества, у которых магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля.
К парамагнетикам относят вещества с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля.
К ферромагнетикам относят вещества с большой положительной магнитной восприимчивостью (до 106), которая сильно зависит от напряженности магнитного поля и температуры.
Антиферромагнетиками являются вещества, в которых ниже некоторой температуры спонтанно возникает антипараллельная ориентация элементарных магнитных моментов одинаковых атомов или ионов кристаллической решетки. При нагревании антиферромагнетик испытывает фазовый переход в парамагнитное состояние.
К ферримагнетикам относят вещества, магнитные свойства которых обусловлены нескомпенсированным антиферромагнетизмом. Подобно ферромагнетикам они обладают высокой магнитной восприимчивостью, которая существенно зависит от напряженности магнитного поля и температуры. Наряду с этим ферримагнетики характеризуются и рядом существенных отличий от ферромагнитных материалов.
Свойствами ферримагнетиков обладают некоторые упорядоченные металлические сплавы, но, главным образом,- различные оксидные соединения, среди которых наибольший практический интерес представляют ферриты.
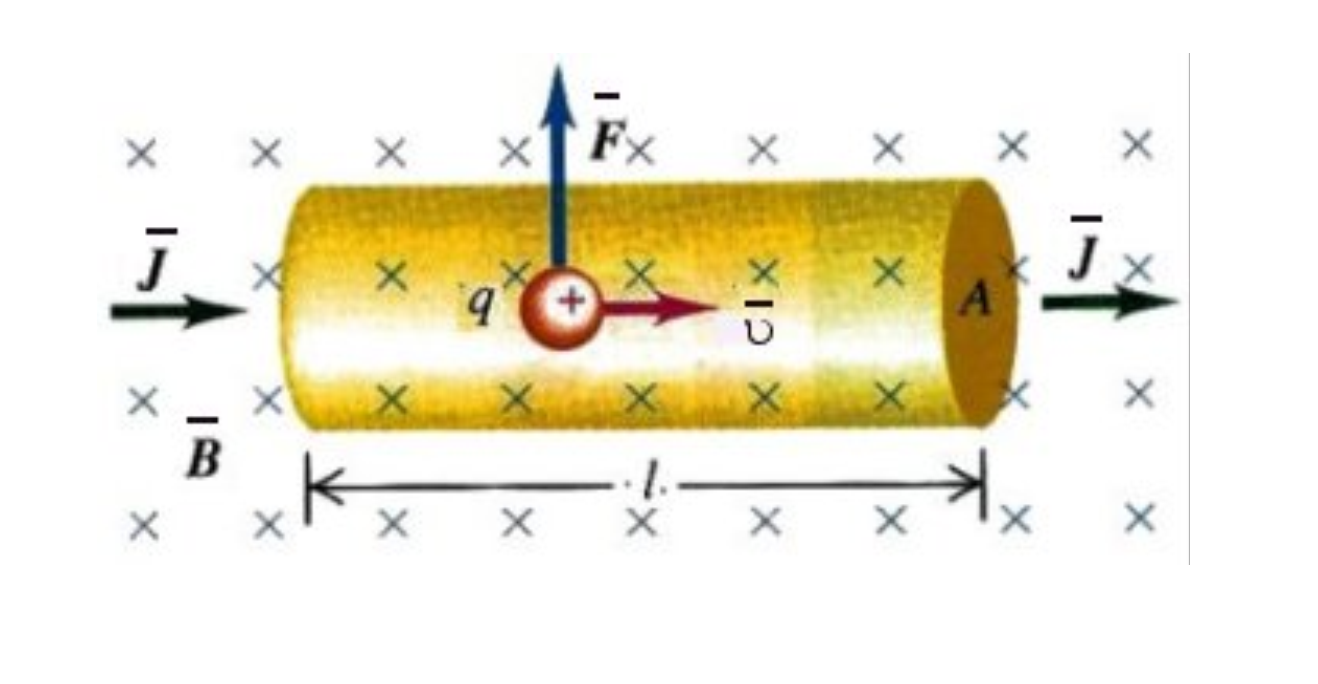
8.2. Сила Лоренца и ее магнитная составляющая. Магнитное поле
В разделе
“Электростатика” изучались свойства
поля электрических сил
,
действующих на покоящийся пробный зарядq.
В качестве характеристики поля был
введен вектор 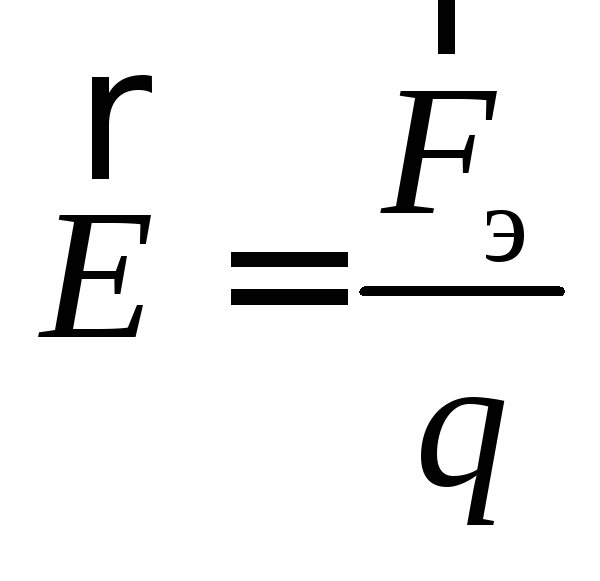 ,
не зависящий от величины пробного зарядаq.
Однако, как показывает опыт, сила
,
не зависящий от величины пробного зарядаq.
Однако, как показывает опыт, сила 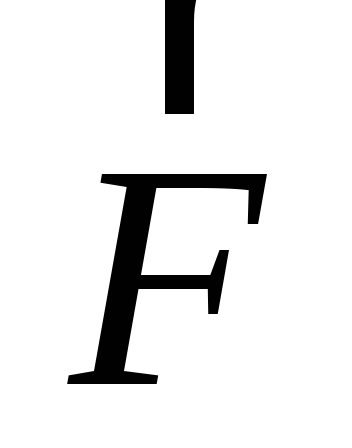 ,
действующая на движущийся заряд, может
отличаться от электрической силы
,
действующая на движущийся заряд, может
отличаться от электрической силы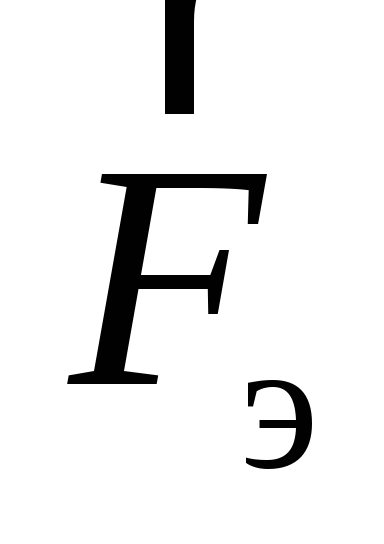 .
Это отличие связано с существованием
так называемой магнитной силы
.
Это отличие связано с существованием
так называемой магнитной силы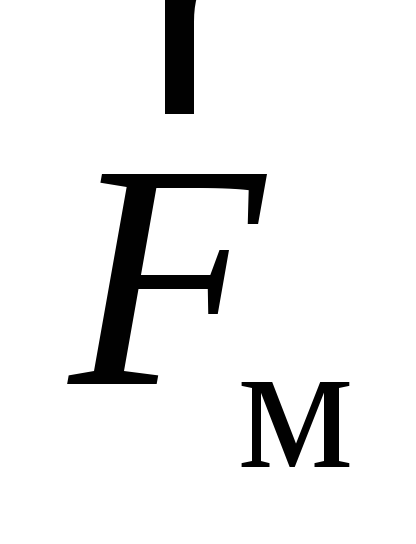 .
.
Обобщением опытных данных являются следующие три основные свойства магнитной силы, действующей на движущуюся заряженную частицу.
1. Величина магнитной силы пропорциональна заряду движущейся частицы и величине ее скорости.
2. Направление магнитной силы всегда перпендикулярно направлению движения заряженной частицы.
3. В любой точке пространства существует такое направление, двигаясь в котором частица не испытывает действия магнитной силы. Другими словами существует такая ориентация вектора скорости, при котором магнитная сила равна нулю.
Перечисленные свойства магнитной силы можно описать количественно, для чего удобно ввести понятие магнитного поля.
Характеризуя это
поле вектором индукции магнитного поля  ,
запишем выражение для магнитной силы:
,
запишем выражение для магнитной силы:
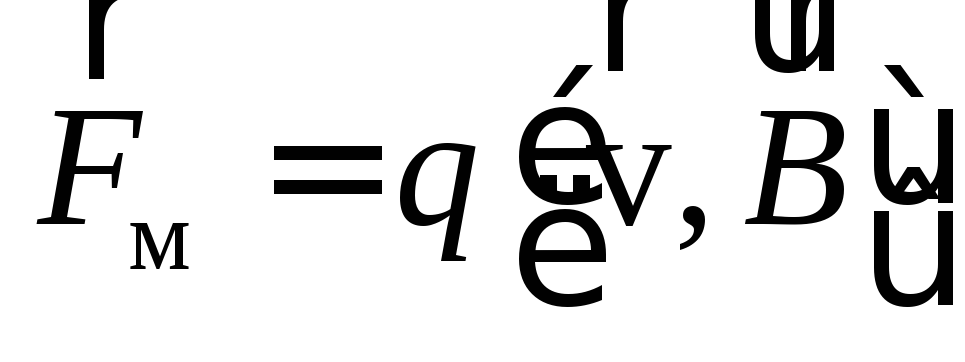 (3)
(3)
В итоге полная сила, действующая со стороны электромагнитного поля на движущуюся относительно избранной системы отсчета заряженную частицу описывается формулой
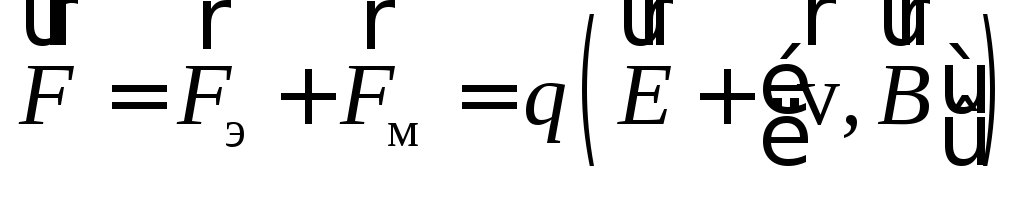 (4)
(4)
Эту силу называют силой Лоренца.
По действию силы
на заряженную частицу можно в принципе
определить векторы электрического  и
магнитного
и
магнитного  полей.
Следовательно, выражение для силы
Лоренца (4) можно рассматривать как
определение электрического и магнитного
полей (векторов
полей.
Следовательно, выражение для силы
Лоренца (4) можно рассматривать как
определение электрического и магнитного
полей (векторов  и
и  ).
).
В самом деле,
измерив ускорение  движущейся
заряженной частицы массойm,
определим полную электромагнитную силу
по второму закону Ньютона(электрическая
движущейся
заряженной частицы массойm,
определим полную электромагнитную силу
по второму закону Ньютона(электрическая  и
магнитная
и
магнитная составляющие
электромагнитной силы
составляющие
электромагнитной силы относятся
к одной и той же системе отсчета. Более
того, эта система отсчета должна быть
инерциальной, иначе пришлось бы учитывать
силы инерции):
относятся
к одной и той же системе отсчета. Более
того, эта система отсчета должна быть
инерциальной, иначе пришлось бы учитывать
силы инерции):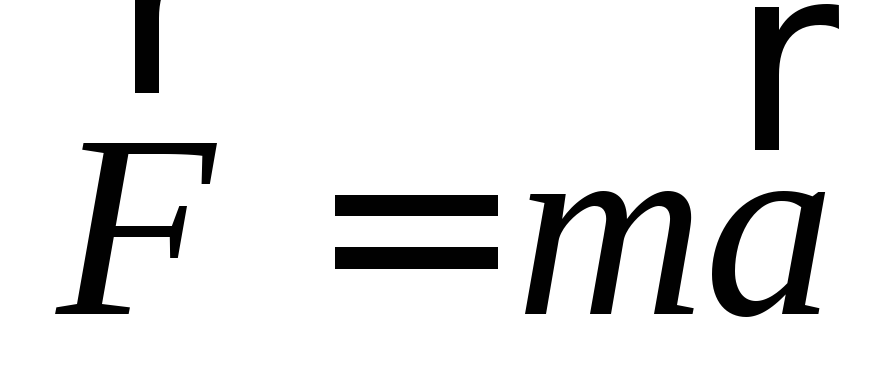 .
Далее, остановив частицу и измерив силу
.
Далее, остановив частицу и измерив силу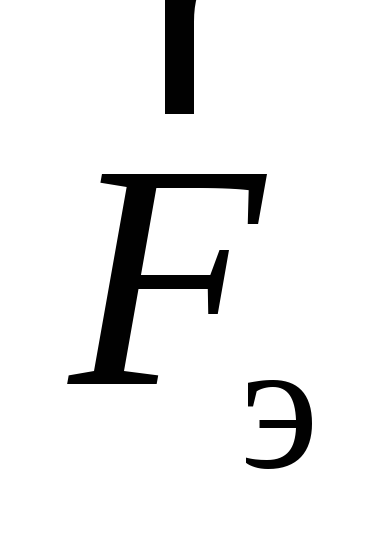 ,
действующую на неподвижный зарядq в той же самой точке пространства,
например с помощью динамометра, определим
как напряженность электрического поля
,
действующую на неподвижный зарядq в той же самой точке пространства,
например с помощью динамометра, определим
как напряженность электрического поля
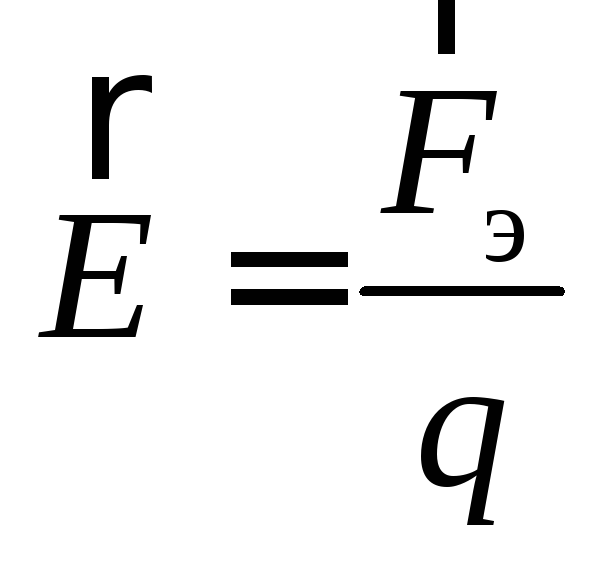 ,
так и вектор магнитной силы
,
так и вектор магнитной силы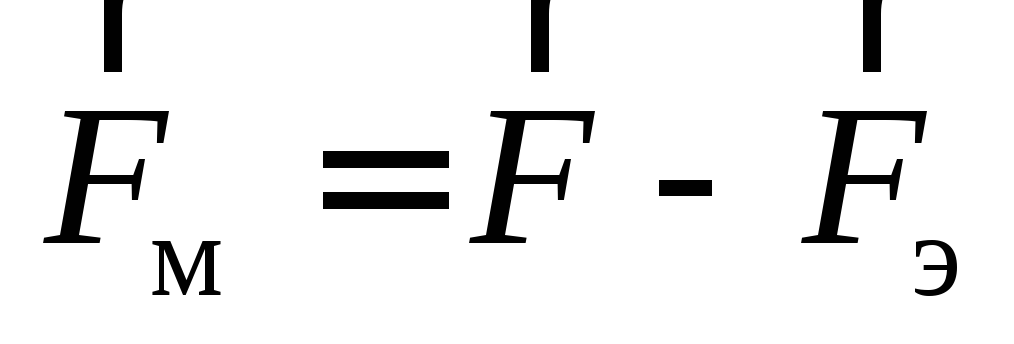 . Затем, испытывая все возможные
направления движения, найдем такое,
двигаясь вдоль которого частица не
подвергается действию магнитной силы,
— это и есть направление вектора индукции
магнитного поля
. Затем, испытывая все возможные
направления движения, найдем такое,
двигаясь вдоль которого частица не
подвергается действию магнитной силы,
— это и есть направление вектора индукции
магнитного поля  в
данной точке пространства. При этом не
должно смущать то обстоятельство, что
процедура испытания различных направлений
движения может потребовать много
времени. Дело в том, что рассматриваемый
эксперимент скорее мысленный, чем
лабораторный, хотя в принципе его можно
осуществить и в лаборатории.
в
данной точке пространства. При этом не
должно смущать то обстоятельство, что
процедура испытания различных направлений
движения может потребовать много
времени. Дело в том, что рассматриваемый
эксперимент скорее мысленный, чем
лабораторный, хотя в принципе его можно
осуществить и в лаборатории.
Теперь пусть
частица движется со скоростью  ,
перпендикулярной к направлению вектора
,
перпендикулярной к направлению вектора  .
Умножим векторно слева на
.
Умножим векторно слева на  выражение
(1), записанное для такого случая:
выражение
(1), записанное для такого случая:
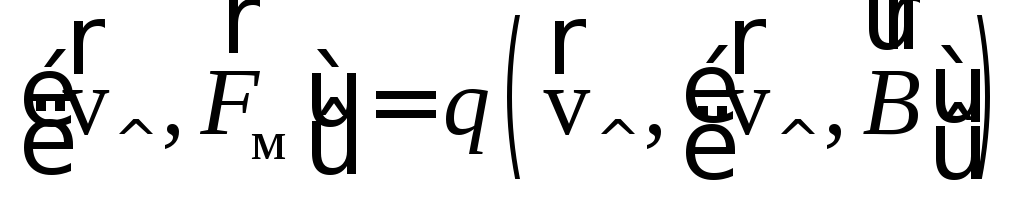
Учитывая здесь
известное тождество векторной алгебры 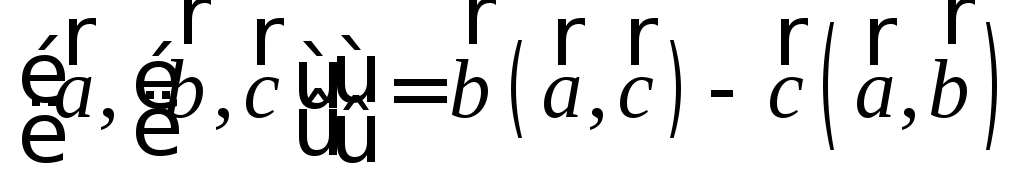 ,
а также соотношения
,
а также соотношения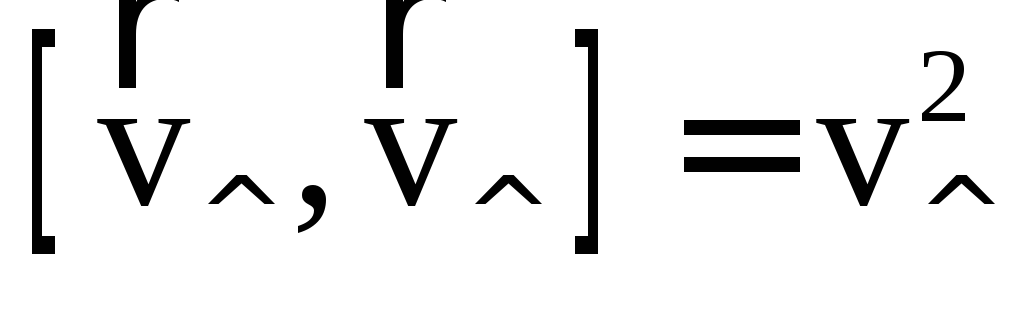 и
и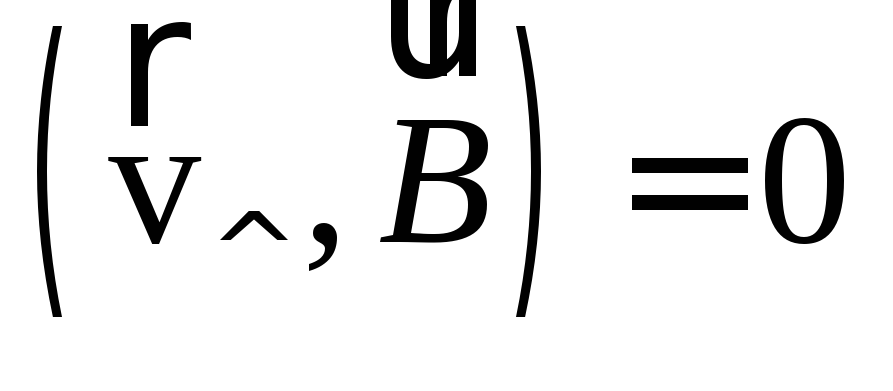 ,
найдем окончательно
,
найдем окончательно
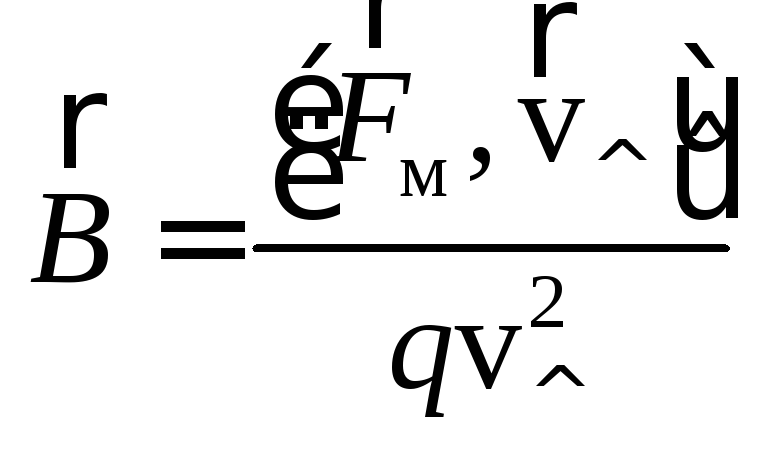 (5)
(5)
Отметим, что
выражение для электромагнитной силы
(4) остается справедливым для переменных
полей и произвольных значений скорости
заряда  .
.
Аналогично
электрическому полю векторов  поле
магнитной индукции
поле
магнитной индукции  может
быть геометрически наглядно представлено
с помощью линий поля, проведенных так,
что касательная к этим линиям в каждой
точке совпадает с направлением вектора
индукции
может
быть геометрически наглядно представлено
с помощью линий поля, проведенных так,
что касательная к этим линиям в каждой
точке совпадает с направлением вектора
индукции 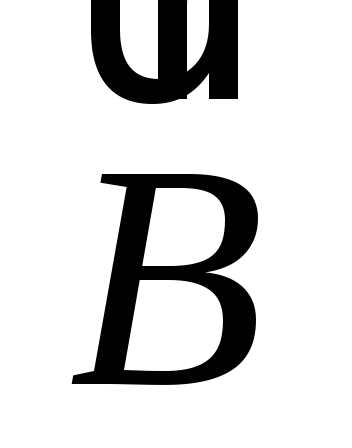 ,
а густота линий пропорциональная модулю
вектора
,
а густота линий пропорциональная модулю
вектора 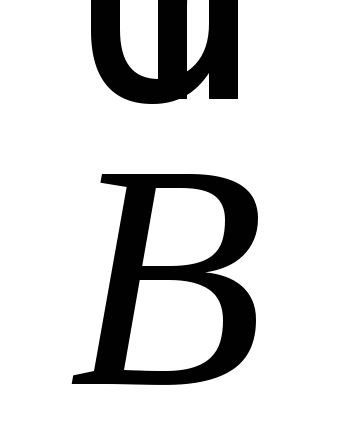 в
данном месте. Однако магнитное поле в
отличие от электростатического устроено
так, что изобразить его с помощью линий
поля не всегда возможно.
в
данном месте. Однако магнитное поле в
отличие от электростатического устроено
так, что изобразить его с помощью линий
поля не всегда возможно.
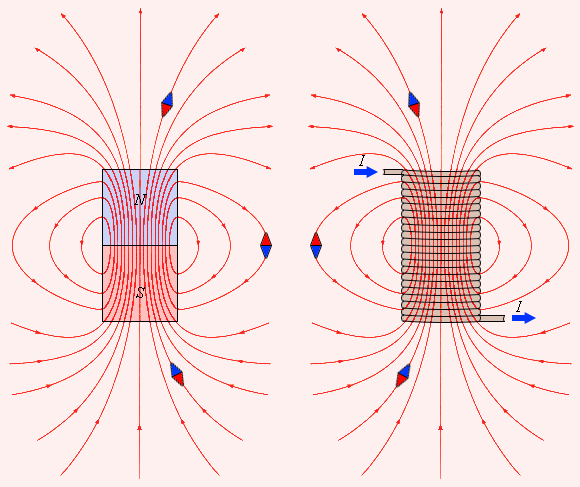
ИЛЛЮСТРАЦИИ. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
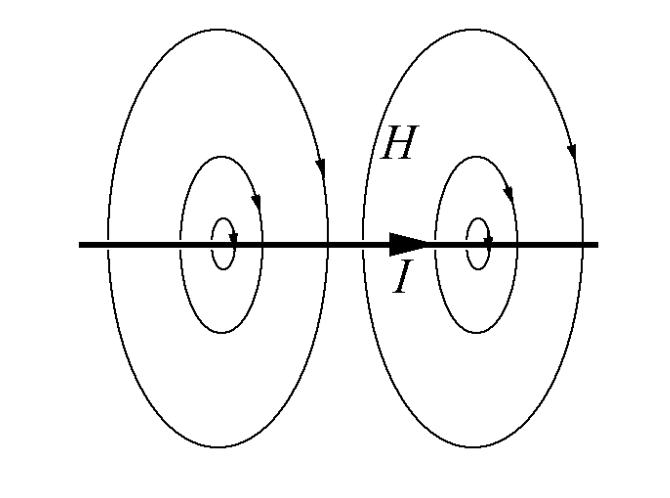
1. Линейный ток
2. Виток с током.
Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис.
|
Рисунок Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции |
Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током.
Вообще мы увидим,
что линии  в простых случаях замкнуты (если не
уходят на ).Это
означает, что магнитное поле не имеет
источников – магнитных зарядов.
Поля, в которых возможны замкнутые
силовые линии (таково поле
в простых случаях замкнуты (если не
уходят на ).Это
означает, что магнитное поле не имеет
источников – магнитных зарядов.
Поля, в которых возможны замкнутые
силовые линии (таково поле  ),
кратко называют соленоидальными
или вихревыми,
в противоположность потенциальным
полям, типа электростатического.
),
кратко называют соленоидальными
или вихревыми,
в противоположность потенциальным
полям, типа электростатического.
Однако не следует
думать, что силовые линии магнитного
поля всегда замкнуты. Это распространенное
заблуждение, проникшее даже в учебники.
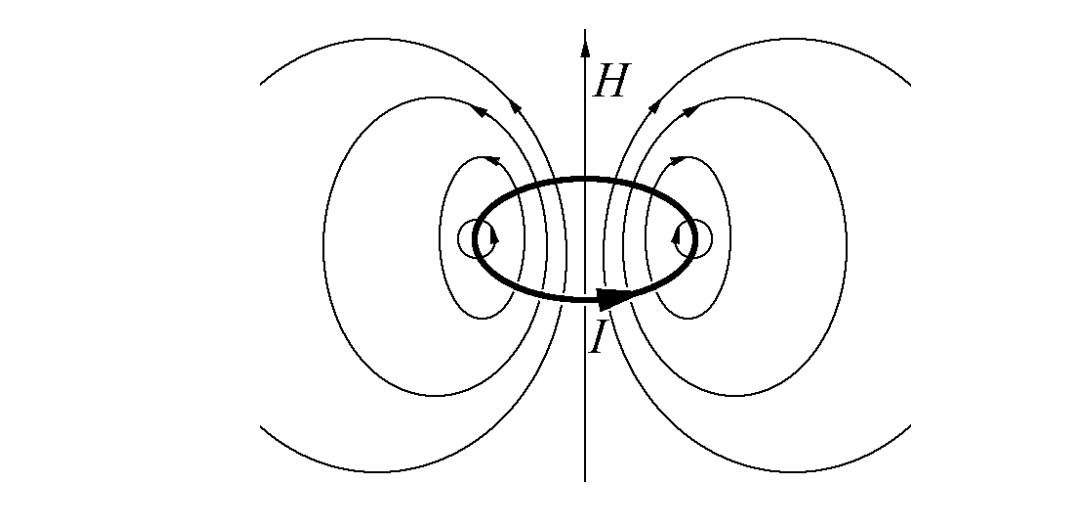
Замкнуты линии  ,
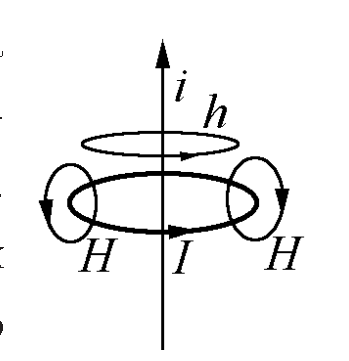
например, у кольцевого витка с током I (рис.). Но если пропустить через виток
провод с малым током i,
добавится малое поле h,
перпендикулярное начальному Н.
Силовая линия суммарного поля станет
спиралью, бесконечно навивающейся на
кольцо, и замкнуться может только
случайно. При «общем» соотношении токов
и при произвольной их геометрии
практически все линии будут незамкнуты,
причем вполне заметно. Рис.
,
например, у кольцевого витка с током I (рис.). Но если пропустить через виток
провод с малым током i,
добавится малое поле h,
перпендикулярное начальному Н.
Силовая линия суммарного поля станет
спиралью, бесконечно навивающейся на
кольцо, и замкнуться может только
случайно. При «общем» соотношении токов
и при произвольной их геометрии
практически все линии будут незамкнуты,
причем вполне заметно. Рис. 
Урок на тему «Сила Ампера и Сила Лоренца»
Разработка открытого урока по физике
Тема: «Действие магнитного поля на проводник с током. Закон Ампера. Действие магнитного поля на движущийся заряд. Сила Лоренца. Магнитосфера Земли и её взаимодействие с солнечным ветром. Пара-, диа- и ферромагнитные вещества.»
Цель урока:Познакомить с силой Ампера и Лоренца, усвоить особенности действия магнитного поля на движущийся заряд и проводник с током , научиться использовать правило «левой руки» для определения направления действия силы Лоренца в незнакомой ситуации.
Задачи урока:
Образовательные:
Обосновать связь между силой тока в проводниках и силой их взаимодействия. Продолжить работу по формированию умений работать с рисунками и заданиями учебника.
Проконтролировать уровень усвоения основных положений, характеризующих силу Ампера. Сформировать умения применять правило «левой руки».
Воспитательные:
Показать, что взаимосвязь силы Ампера и силы Лоренца является примером проявления одного из признаков метода диалектического познания явлений.
Развития мышления:
Формировать элементы творческого поиска, умение доказывать и отстаивать свою точку зрения, давать свою оценку изучаемым явлениям.
Тип урока: урок сообщения новых знаний
Оборудование: проектор, тесты, карточки с заданием, презентация.
Ход урока:
Организационный момент. Приветсвие класса. Постановка целей и задач урока./3-4мин/
Критерии оценок
ДисциплинаОпрос домашнего задания /10 мин /
(проводится в виде тестирования, по окончанию взаимопроверка и оценивание)
Вариант 1.
Вставьте пропущенные слова или выберите один правильный ответ.
1. Как располагаются железные опилки в магнитном поле прямого тока?
а. Беспорядочно.
б. По прямым линиям вдоль проводника.
в.По замкнутым кривым, охватывающим проводник.
2. Когда к магнитной стрелке поднесли ……….. полюс постоянного магнита, то южный полюс стрелки оттолкнулся.
3. Разноименные магнитные полюсы …………, а одноименные — …………… .
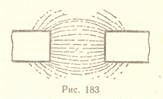
4. Одноименными или разноименными полюсами образована картина магнитных линий (рис. 183)?
а. Одноименными.б. Разноименными.
5. Магнитная индукция величина …
6. Направление вектора магнитной индукции устанавливают с помощью правила
7. Магнитных зарядов в природе …
Вариант 2.
Вставьте пропущенные слова или выберите один правильный ответ.
1. Северный магнитный полюс расположен у … географического полюса, а южный — у …
2. Магнитная индукция измеряется в …
3. Какие вещества из указанных ниже совсем не притягиваются магнитом?
А. Стекло. Б. Сталь. В. Никель. Г. Чугун.
4.Магнитная индукция обозначается буквой …
5. Направление магнитных линий зависит от направления …… в проводнике, взаимосвязь этих направлений можно определить по ………….. …………………
6. За направление магнитных линий принято направление, которое указывает …… конец магнитной стрелки.
7. Магнитная стрелка остается неподвижной возле проводника с током.Это означает, что в проводнике …
Ключ
2
3
4
5
6
7
Вар 1
в.По замкнутым кривым, охваты-вающим проводник.
притягиваются
Притягиваются, отталкиваются
б) разноименными
буравчика
нет
Вар2
Южного
северного
Теслах(Тл)
стекло
В
Движущимися электрическими зарядами
северный
Тока нет
«5» — 7 правильных ответов
«4» — 5-6 правильных ответов
«3» — 3-4 правильных ответа
Изложение нового материала
Что такое магнитное поле?
/материя определяющая магнитное взаимодействие движущихся заряженных частиц или проводников с током/
Какими свойствами обладает магнитное поле ?/действует на проводник с током и движущуюся заряженную частицу/
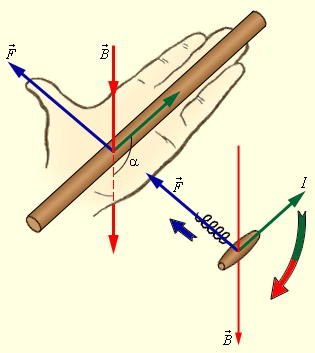
Направление силы Ампера и силы Лоренца определяется по правилу левой руки: если расположить левую руку так, чтобы линии индукции 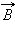 входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (на заряженную частицу).
входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (на заряженную частицу).
Работа магнитного поля , совершаемая при перемещении проводника с током определяется по формуле:
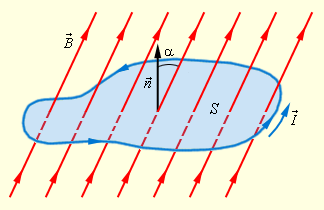
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением: Φ = B · S · cos α
Единица измерения магнитного потока в систем СИ — 1 Вебер (1 Вб). 1 Вб = 1 Тл · 1 м2
Работа в группах (составление кластера) /15 мин/
Магнитные свойства веществ.
Закрепление. Решение задач./15 мин/
/у доски/
задача 1
Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45 градусов к вектору магнитной индукции. Магнитная индукция составляет 0,5 Тл.
Задача 2
Какова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного поля действует сила 32 Н. Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.
1 вариант
На «4»
1. Какова индукция магнитного поля в котором на проводник с длиной 5 см действует сила 50 мН? Сила тока в проводнике 25 А. проводник расположен перпендикулярно индукции магнитного поля.
2. В однородном магнитном поле с индукцией 0,8 Тл на проводник с током в 30 А, длина которого 10 см, действует сила 1,5 Н. Найти угол между векторам магнитной индукции и силой тока.
3.Электрон движется в вакууме со скоростью 3*106 м/с в однородном магнитном поле с магнитной индукцией 0,1 Тл. Чему равна сила, действующая на электрон, если угол между направлением скорости электронаи линиями индукци равен 900.
4. В направлении, перпендикулярном линиям индукции, влетает в магнитное поле электрон со скоростью 10 Мм/с. Найти индукцию поля, если электрон описал в поле окружность радиусом 1 см. /е=- 1,6*10-19 Кл, me=9,1*10-31кг/.
На «5»
Сформулировать и решить задачу
I
Fa
. . . . .
. . . . v
. . . . .B
FЛ
2 вариант
На «4»
1. В однородное магнитное поле с индукцией 0,085 Тл влетает электрон со скоростью 4,6*107 м/с, направленной перпендикулярно линиям индукции поля. Определите радиус окружности и период, по которой движется электрон.
2. Протон в однородном магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость движения протона /р=1,6*10-19 Кл, mp=1,6*10-27 кг/
3. На прямой проводник длиной 0,5 м расположенный перпендикулярно силовым линиям поля с индукцией 0,02 Тл, действует сила 0,15 Н.найти силу тока , протекающего по проводнику.
4. Какова сила тока в проводнике, находящемся в однородном магнитном поле с индукцией 2 Тл, если длина активной части проводника 20 см, сила ,действующая на проводник, 0,75 Н, а угол между направлением линий индукции и током 490?
На «5»
Сформулировать и решить задачу
FA
I
X X v X
X X X
X X X B
3.
Fa
4. Вектор В направлен вверх, сила Faнаправлена вправо. Куда направлен ток?
Рефлексия /7 мин/
Итоги урока. Домашнее задание. Оценивание./3 мин/
Сила Лоренца — FizikatTYT
Сила Лоренца — сочетание электрического и магнитного взаимодействия, которое возникает, когда положительно или отрицательно заряженная частица движется в электромагнитном поле. Она перпендикулярна направлениям векторов магнитной индукции и скорости заряда. Под её действием частица изменяет траекторию своего движения и скорость.
Этот вид сил впервые описал Джеймс Максвелл в 1865 году, а в 1892 году голландский физик Хендрик Лоренц записал для неё математическое выражение. Хотя первый вывод формулы исследователи приписывают Оливеру Хевисайду.
Вариация этой базовой силы действует на проводник с током, когда его помещают между полюсами магнита. Если в проводнике существует ток, то он будет отклоняться во внешнем магнитном поле, так как сила Лоренца будет действовать на все движущиеся в нём электроны. В какую сторону отклонится провод с током наглядно продемонстрирует правило левой руки.
Это явление и возникающую силу используют в экспериментальной физике для:
- увеличения скорости элементарных частиц и ионов в различных циклотронах и других ускорителях;
- определения удельного заряда и массы положительных ионов, относительной атомной массы изотопов химических элементов в масс-спектрографии;
- в магнетронах и скоростных фильтрах.
В быту такое воздействие на заряженную частицу нашло применение в телевизорах с электронно-лучевой трубкой, электродвигателях, колонках, генераторах.
Какова природа силы?
Эта сила принадлежит спектру сил электромагнитного взаимодействия. Магнитное поле создают заряженные частицы, такие как протон или электрон, во время своего движения. Движущийся заряд поместим во внешнее поле, например, между полюсами магнита. Поле точечного заряда и внешнее поле будут взаимодействовать определённым образом: притягиваться или отталкиваться. Это зависит от знака заряда и от взаимного расположения линий магнитной индукции полей.
Формула для вычисления модуля силы Лоренца демонстрирует её зависимость от скорости частицы v, абсолютного значения её заряда q, от модуля индукции внешнего магнитного поля B и угла α, показывающего взаимное расположение векторов скорости и магнитной индукции.
На рисунке представлены все величины, фигурирующие в формуле:
Из уравнения видно, что если v (скорость) стремится к нулю, то на точечный заряд не будет действовать и сила Лоренца. Кроме того, если заряд перемещается в направлении, параллельном направлению вектора магнитной индукции, то есть sin (0) = 0, снова будем наблюдать отсутствие внешней силы (Fл=0). А при движении, перпендикулярном линиям внешнего магнитного поля, сила Лоренца становится центростремительной и искривляет траекторию объекта (наблюдается движение по окружности). Протон представлен на рисунке а), рисунок б) описывает электрон.
Правило левой руки
Для положительно заряженной частицы необходимо расположить ладонь левой руки, чтобы четыре вытянутых пальца направить параллельно её движению, а линии магнитной индукции входили в ладонь перпендикулярно, то отогнутый на 90° большой палец покажет направление силы Лоренца. А для отрицательного заряда силу Лоренца направляем в противоположную сторону.