Сила Лоренца — Википедия
Материал из Википедии — свободной энциклопедии
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:
F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца[3].
Уравнение (единицы СИ)
Заряженная частица
Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:
F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}
где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
- F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}
где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
- dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}
где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
| СГС | СИ |
|---|---|
|
|
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:
| СГС | СИ |
|---|---|
|
|
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:
| СГС | СИ |
|---|---|
|
|
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеСм. также
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
I = qnvS ( 2 )Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:
F = | I |B Δl sin αПодставляя в эту формулу выражение ( 2 ) для силы тока, получаем:
F = | q | nvS Δl B sin α = v | q | NB sin α, где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.Другие заметки по физике
Сила Лоренца — Википедия
Материал из Википедии — свободной энциклопедии
Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще
F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца[3].
Уравнение (единицы СИ)
Заряженная частица
![{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}](/800/600/https/upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Lorentz_force_particle.svg/200px-Lorentz_force_particle.svg.png)
Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:
F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}
где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:
- F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}
где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Для непрерывного распределения заряда, сила Лоренца принимает вид:
- dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}
где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}
где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.
Частные случаи
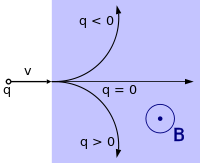 Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
| СГС | СИ |
|---|---|
|
|
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:
| СГС | СИ |
|---|---|
|
|
Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:
| СГС | СИ |
|---|---|
|
|
Использование
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне
Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеСм. также
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
Лоренца сила — это… Что такое Лоренца сила?
ЛОРЕНЦА СИЛА — сила, действующая на заряж. ч цу, движущуюся в эл. магн. поле. Ф ла для Л. с. F впервые получена X. А. Лоренцем, обобщившим эксперим. данные, имеет вид: F = eE+e/c(vB), (*) где е заряд ч цы, Е напряжённость электрич. поля, В магнитная индукция, v … Физическая энциклопедия
ЛОРЕНЦА СИЛА — ЛОРЕНЦА СИЛА, сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х.А. Лоренцем в конце 19 в. формулой f= qE+q(vxB) (в СИ), где q, v заряд и скорость частицы соответственно; E напряженность… … Современная энциклопедия
ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в кон. 19 в. формулой: (в СГС системе единиц), где ?, ? заряд и скорость частицы, Е напряженность электрического поля, В… … Большой Энциклопедический словарь
Лоренца сила — ЛОРЕНЦА СИЛА, сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х.А. Лоренцем в конце 19 в. формулой f= qE+q(vxB) (в СИ), где q, v заряд и скорость частицы соответственно; E напряженность… … Иллюстрированный энциклопедический словарь
Лоренца сила — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в конце XIX в. формулой: (в СГС системе единиц), где e, v заряд и скорость частицы, E напряжённость электрического поля, B … Энциклопедический словарь
Лоренца сила — сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Формула для Л. с. F была впервые получена Х. А. Лоренцом как результат обобщения опыта и имеет вид: F = eE + υB]. Здесь е заряд частицы, Е… … Большая советская энциклопедия
ЛОРЕНЦА СИЛА — сила, действующая со стороны заданного электромагнитного поля на движущуюся заряженную частицу. Выражение для Л. с. Fбыло впервые дано Г. Лоренцем (см. [1]): где Е напряженность электрич. поля, В магнитная индукция, V скорость заряженной частицы… … Математическая энциклопедия
ЛОРЕНЦА СИЛА — сила, действующая со стороны электромагнитного поля на движущуюся заряж. частицу. Л. с. F равна F = QE + О [v, В], где О заряд частицы, Е напряжённость электрич. поля, В магнитная индукция, a v скорость частицы относительно той инерциальной… … Большой энциклопедический политехнический словарь
ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в эл. магн. поле; выражается установленной X. А. Лоренцем и кон. 19 в. ф лой: f= е(Е+1/C[vB]) (в СГС системе единиц), где е, v заряд и скорость частицы, Е напряжённость электрич. поля, В… … Естествознание. Энциклопедический словарь
СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… … Большая политехническая энциклопедия
Сила Лоренца — это… Что такое Сила Лоренца?
Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Уравнение (единицы СИ)
Заряженная частица
Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- , где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.
Частные случаи
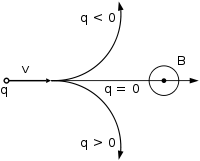 Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :
Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :
Применение силы Лоренца
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеВ электроприборах
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
Другие применения
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
См. также
Сила Лоренца — это… Что такое Сила Лоренца?
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Уравнение (единицы СИ)
Заряженная частица
Сила ЛоренцаСила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единичный 3-объём)Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- , где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.
Частные случаи
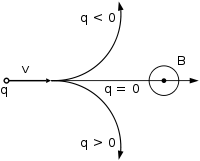 Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :
Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :
Применение силы Лоренца
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеВ электроприборах
Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
Другие применения
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
См. также
Обсуждение:Сила Лоренца — Википедия
User:Shevello заменил везде обозначение скорости c u на v (с аппеляцией к английской velocity). Это в общем логично, если бы это была отдельная статья. На самом деле обозначение u было введено здесь для согласование с главной и избранной статьей по электродинамике Уравнения Максвелла, в которой обозначение v конфликтовало бы с обозначением объема (volume) в многочисленных интегралах. Поскольку скорость в электродинамике менее важный параметр, я предлагаю все-таки вернуться здесь к менее нагруженной букве u. —Astrohist 09:26, 16 октября 2010 (UTC)
- Простите, что не учёл здесь этот момент. Я всё-таки считаю, что мы не должны ровняться только на статью про уравнения Максвелла. Есть в Вики и много других статей по электричеству. Поэтому я считаю, что нужно оставить v. Но не настаиваю. Shevello 19:33, 18 октября 2010 (UTC)
- Вообще, для однообразия статей одной тематики, я думаю, это было бы логично. — Артём Коржиманов 19:51, 19 октября 2010 (UTC)
Читал статью. Обьясните для чего в некоторых формулах стоят «Квадратные скобки», а не круглые ? (Например в формуле: «Силы действующей со стороны магнитного поля» в СИ, Первый раздел.). — spiker01 17:53, 26 мая 2011 (UTC)
В том определении силы Лоренца, которая дана в статье, ее работа не всегда равна нулю. 84.237.43.242 08:30, 7 марта 2013 (UTC)guest
- О нулевой работе сказано только в разделе «Частные случаи» для случая постоянного магнитного поля. — Артём Коржиманов 14:07, 7 марта 2013 (UTC)
Работа массы равна нулю при движении по замкнутой орбите только в потенциальных полях. Какие потенциальные поля в круговых ускорителях? Это дело править надо. И срочно.—Михаил Певунов 22:02, 1 февраля 2016 (UTC)
О разделе «Непрерывное распределение заряда»[править код]
А если B создано потоком непрерывного заряда в проводнике (например в соленоиде), то какой вид приобрела бы формула и насколько мал d в сравнении с радиусом например электрона или длиной проводника? С уважением. (андроид) 91.205.25.30 15:24, 9 марта 2013 (UTC)
Уравнения Максвелла и физическая интерпретация[править код]
Думаю, тут было бы правильным описать в этой статье положение сил Лоренца в системе уравнений Максвелла, какой физический смысл (механизм появления этих сил) предполагался изначально, стал предполагаться в рамках модели Максвелла и в рамках ОТО. —Nashev 14:20, 28 марта 2013 (UTC)
- Сила Лоренца не входит в систему уравнений Максвелла, а дополняет их. Поэтому вопрос непонятен. — Артём Коржиманов 19:23, 28 марта 2013 (UTC)
- Ну вот как-то подробнее сказать, почему не входит — а заодно, рассказать, как Максвелл без неё обошёлся, когда делал свои уравнения, и кто и как потом обнаружил, что надо вот дополнять… —Nashev 16:27, 25 апреля 2013 (UTC)
Длина волны, кванты, фотоны..?[править код]
Если фотоны — это калибровочные бозоны электромагнитного взаимодействия, то при воздействии магнитного или электрического поля на заряд нужно привлекать понятие фотона. А у фотона есть длина волны (или частота). Отсюда вопрос — какой длины волны фотоны случаются при статическом действии силы Лоренца или при столь же статическом действии силы Кулона? И вообще, где место силам Лоренца и Ампера в квантовой электродинамике? Что там вместо них? —Nashev 16:23, 25 апреля 2013 (UTC)
Это утверждение в начале статьи ошибочно.
Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется.
Для всех сил Природы, третий закон Ньютона выполняется всегда.
При движении заряда, например в БАКе, движение заряда по окружности обеспечивается равенством силы Лоренца q[V×H], как центростремительной, и центробежной силы заряда mV2/R.
q[V×H] = mV2/R
Отсюда ясно, зачем у БАКа такой громадный радиус.
Если масса заряда (протона) в правой части релятивистки растет, то и напряженность магнитного поля Н надо соответственно наращивать. Уменьшить центробежную силу можно только увеличением радиуса. Возможности увеличения напряженности магнитного поля ограничены.
Отсюда выводы.
1. Третий закон для силы Лоренца безусловно выполняется. 2. Но, а если масса релятивистски не растет, тогда что?
Тогда возникает довольно интересная тема.—Михаил Певунов 21:31, 27 декабря 2014 (UTC)
Эйнштейн первый обратил внимание, что сила Лоренца непондеромоторна — источник энергии для силы отсутствует. Источник заблуждения — невнимание к принципу относительности. Т.е. не так все просто. А.Пономарев 176.62.180.101 12:21, 17 февраля 2017 (UTC)176.62.180.101 12:23, 17 февраля 2017 (UTC)
Третий Закон Ньютона для силы Ампера.[править код]
Ампер, Бир и Савар установили следующие закономерности взаимодействия магнитных полей токов на проводники.
F→12=[I2×h2]{\displaystyle {\vec {F}}_{12}=[I_{2}\times H_{1}]}
F→21=[I1×h3]{\displaystyle {\vec {F}}_{21}=[I_{1}\times H_{2}]}
Эти уравнения со всей очевидностью показывают третий закон действия и взаимодействия сил в законе Ампера и в формуле Лоренца.
Еще Лаплас показал, что закон Ампера справедлив и для потока зарядов в проводнике и для одиночного заряда в магнитном поле.
Источник Википедия. Закон Био — Савара — Лапласа
https://ru.wikipedia.org/wiki/1820_%D0%B3%D0%BE%D0%B4
Данный текст необходим в статье, чтобы не вводить читателей в заблуждение
—Михаил Певунов 13:01, 29 января 2016 (UTC)



