сила кулоновского взаимодействия двух точечных зарядов 1)прямо пропорциональна расстоянию
Аэростат летит равномерно и прямолинейно параллельно горизонтальной дороге, на которой находится неподвижный автомобиль. Выберите правильное утвержден … ие. 1) Система отсчёта, связанная с аэростатом, является инерциальной, а система отсчёта, связанная с автомобилем, инерциальной не является. 2) Система отсчёта, связанная с автомобилем, является инерциальной, а система отсчёта, связанная с аэростатом, инерциальной не является. 3) Система отсчёта, связанная с любым из этих тел, является инерциальной. 4) Система отсчёта, связанная с любым из этих тел, не является инерциальной.
Определите количество вещества содержащееся в 22 кг CO2?
На нагрівач, в якому знаходиться 2л води і який мас опір 10 Ом, подасться напруга 12 в. Нагрівач нагрів воду до 80º С. Температура більше не піднімаєт
… ься. За який час після вимкнення живлення нагрівача, температура води знизиться на 2 С? Питома теплоємність води — 4200 Дж/кг °C, густина води — 1000 кг/м3.
Фобос, один з двох супутників Марса, обертається навколо планети на відстані 377 км від її поверхні з періодом 7 год 39,2 хв. Визнач швидкість руху су … путни- ка навколо планети. Радіус Марса дорівнює з 390 км. Уважати орбіту супутника Зауваження. Під час розв’язування задачі зроби малюнок і познач на ньому ра- діус орбіти супутника. коловою.
якої висоти має целіндр радіусом основи 2,5 см щоб його об’єм = об’єму бруска
определить скорость самолёта который 6 МИН ПРОЛЕТЕЛ РАССТОЯНИЕ 45 КМ
В однородном магнитном поле с индукцией 8,5·10 -3 Тл влетает электрон со скоростью 4,6 ·10 6 м/с, направленной перпендикулярно линиям индукции. Рассчи … тайте силу, действующую на элетрон в магнитном поле.
Из точки A в точку B движутся Петя (начальная координата мальчика 0,5 км) и волк навстречу друг другу. Через какое время они встретятся, если скорость
… Пети в 3 раза меньше скорости волка? Расстояние между A и B составляет 15 км.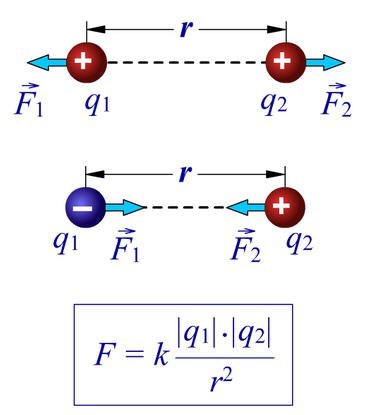 Скорость Пети рассчитай по графику.
Ответ (округли до сотых): ___ч.
Скорость Пети рассчитай по графику.
Ответ (округли до сотых): ___ч.
Силы взаимодействия кулоновские — Справочник химика 21
Наконец, применение гель-хроматографии возможно и в том случае, когда все вещества анализируемой смеси обладают одинаковой молекулярной массой. Тогда в основе разделения лежит различие во взаимодействии анализируемых вешеств с фазой геля. Обычно рассматривают два вида взаимодействия кулоновское между заряженными молекулами разделяемой смеси и ионогенными группами в скелете геля и взаимодействие, связанное с дисперсионными силами взаимодействия между растворенными вещест-. вами и фазой набухшего геля. Этот вариант гель-хроматографии широко применяется для разделения смеси веществ низкой молекулярной массы.Здесь qdq Dт — кулоновская сила взаимодействия заряда, расположенного на сфере, и элемента заряда йд, удаленного на расстояние г от центра сферы.

В работе [107] определялось сечение захвата для случая, когда меньшая из частиц радиусом Я 2 несет свободный заряд Q . Обе частицы проводящие. При расчетах не учитывалось молекулярное взаимодействие частиц и силы их гидродинамического взаимодействия. Сумма этих сил ранее определялась формулой (5.18). Электрические силы взаимодействия считались кулоновскими и определялись взаимодействием заряда Са с индуцированным зарядом на частице Я . Для сечения захвата было получено выражение
Например, энергия кулоновского взаимодействия обратно пропорциональна расстоянию между зарядами 17 = йвг/г. Если эту энергию разделить на расстояние между зарядами, то получим силу взаимодействия, отражаемую законом Кулона Г = 111 г = йй/г . [c. 237]
237]
В реакциях (а) и (б) преобладают электростатические кулоновские силы взаимодействия, в реакции (в) — ковалентный характер молекулярного возмущения.
Капли, попадая в электрическое поле, поляризуются, и их форма приближается к эллипсоидальной (рис. 1.1). Соударение и слияние капель происходит за счет кулоновского взаимодействия противоположных по знаку поляризационных зарядов частиц, оказавшихся вблизи друг от друга. Из электростатики известно, что заряд поляризации qn = Еа . Следовательно, сила взаимодействия, определяющая сближение и слияние капель [c.8]
У ионных кристаллов (рис. 1.9, 6 решетка построена из чередующихся ионов с противоположными зарядами, связь между которыми осуществляется за счет сил электростатического взаимодействия — кулоновских сил. Хотя энергия связи в решетке этого типа такая же, что и у атомного [составляет (8 — 12) X X 10 кДж/моль], прочность тел с этой структурой значительно ниже, так как в них связь рассеянная , ненаправленная.
Проведенное рассмотрение показывает, что в более сложно организованной системе характер взаимодействия может существенно отличаться от простого кулоновского взаимодействия — в выражение для силы взаимодействия не входит заряд частиц, вместо него электрические свойства участников взаимодействия характеризуются дипольным моментом. Изменяется показатель степени в выражении для зависимости взаимодействия от расстояния. Однако природа взаимодействий остается прежней— это кулоновские взаимодействия между электрическими зарядами.
Нет оснований полагать, что между ионами в каком-либо растворе кулоновские силы отсутствуют. Но поскольку для воздуха D Ai Ij а для воды D 80, то при перенесении молекулы электролита из воздуха в воду сила взаимодействия между ионами, ее составляющими, падает в 80 раз.
Допустим в качестве первого приближения, что потенциал парного взаимодействия ионов есть сумма потенциалов — отталкивания, связанного с короткодействующими валентными силами, и- кулоновского [c.316]
Проведенное термодинамическое рассмотрение не дает представления о механизме процесса. Для этого мы можем привлечь известное уже нам понятие полярности, как меры интенсивности молекулярного силового поля. Молекула спирта, находящаяся на поверхности, втягивается в глубину объемной фазы слабее, чем молекула воды (поскольку взаимодействие вода — вода сильнее, чем вода — спирт) и, попав в поверхностный слой, окажется уже вытесненной из динамической решетки молекул воды в объемной фазе это приведет к обогащению поверхностного слоя спиртом. Наоборот, ионы, например Na+ или С1″, будут втягиваться в объемную фазу сильнее, чем молекулы НгО, поскольку силы взаимодействия Na+—НгО больше, чем НгО — НгО.
Цепочка. Объясняется это тем, что в органической кислоте с ростом длины цепочки кулоновские силы взаимодействия между Н+-ионами и отрицательно заряженным концом молекулы увеличиваются. Н. А. Измайлов показал, что при переходе от растворителя к растворителю константы диссоциации кислот изменяются иногда в миллионы, а соотношения в силе кислот — в тысячи раз.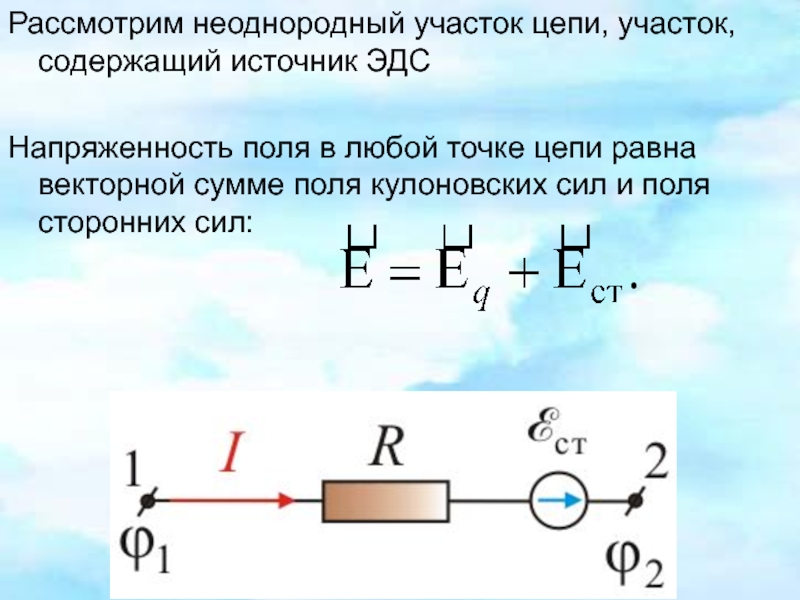
Когда электролиты, полностью диссоциированные в воде, растворяются в растворителях с низкой диэлектрической постоянной, кулоновское притяжение оказывается достаточным для образования ионных ассоциатов при предельно низких концентрациях ионов. Сила взаимодействия между ионами обратно пропорциональна диэлектрической постоянной среды (разд. 6.1). Таким образом, все электролиты являются слабыми электролитами в растворителях с низкой диэлектрической постоянной. К растворителям, играющим важную роль при изучении неводных растворов электролитов, принадлежат спирты, жидкий аммиак, диоксан, ацетон и другие кетоны, безводная муравьиная кислота и уксусная кислота, пиридин, некоторые амины и нитросоединения.
Наряду с получением общего рещения задачи определения сил взаимодействия двух проводящих частиц больщое значение имеет исследование асимптотического поведения сил на больщих и малых расстояниях между их поверхностями. Взаимодействие частиц на больших расстояниях в приближениях диполь-дипольного, диполь-кулоновского и кулоновского взаимодействий изучено достаточно полно [91]. Поэтому в этой области основным является вопрос о точности указанных приближений. Для случая малых расстояний между частицами силы электростатического взаимодействия изучены меньше. В следующих разделах будут рассмотрены два указанных предельных случая. [c.296]
Поэтому в этой области основным является вопрос о точности указанных приближений. Для случая малых расстояний между частицами силы электростатического взаимодействия изучены меньше. В следующих разделах будут рассмотрены два указанных предельных случая. [c.296]
Расчитанная прочность в отличие от найденной из экспериментальных данных называется теоретической. Теоретическая прочность зависит от природы сил взаимодействия между частицами (ионная, ковалентная, металлическая связь и др.) и от структуры материала. Точный расчет значений теоретической прочности является весьма сложной задачей. Поэтому более или менее строгий расчет был проделан к настоящему времени только для каменной соли, чей монокристалл представляет собой кубическую решетку из ионов Ыа и С1 , между которыми действуют кулоновские силы притяжения. [c.11]
Интересно отметить, что качественно этот результат соответствует результатам, представленным в работе Русанова, где расчетным путем показано, что в средней части поры плотность адсорбата обратно пропорциональна кубу радиуса поры (для сил Ван-дер-Ваальса). В нашем случае возможно более существенны кулоновские силы взаимодействия. [c.214]
В нашем случае возможно более существенны кулоновские силы взаимодействия. [c.214]
Как обычно, силу взаимодействия V мы описываем безразмерной константой связи и, которая получается сравнением энергии V[a) кулоновского отталкивания мономеров, находящихся в соседних узлах решетки, и тепловой энергии Т [c.339]
Величина л определяется так же, как и р. иа основании учета кулоновских сил взаимодействия диполей воды друг с другом, а также диполей воды с иоиом данного заряда и радиуса. Величины у и 1т по отдсльдюсти ие определимы, гго их разность можно вычислить. При проведет и расчета авторы пренебрегают различием в размерах образовавшегося и исходного тетраэдров. При замене в тетраэдре одной молекулы воды на ион наблюдгется переориентация четырех моле- [c.61]
Если исходить из предположения, что адсорбция ионов на ртути определяется исключительно электростатическими силами, то все анионы должны изменять ход лишь восходящей ветви электрокапиллярной кривой, где поверхность ртути заряжена положительно. Напротив, влияние катионов должно локализоваться только иа кисходя1цей ветви, где они электростатически притягиваются к отрицательно заряженной поверхности ртути. В действительности, как это было найдено еще Гуи, многие анионы изменяют ход элек-трокапиллярпой кривой справа от точки максимума, а некоторые катионы влияют не только на нисходящую, но и на восходящую ветвь кривой. Такое поведение ионов нельзя объяснить действием только кулоновских сил. Оно связано с силами взаимодействия, отличными от простых электростатических сил. Такими силами, специфическими для данного рода частиц, могут быть, например, силы Ваи-дер-Ваальса или химические (валентные). Благодаря этим силам ионы в состоянии удерживаться на одноименно заряженной поверхности ртути и влиять на электрокапиллярные свойства границы металл — раствор. Точно так же нельзя на основе одних только электростатических представлений объяснить влияние неиоинзированных органических веществ на ход электрокапиллярных кривых. Дело в том, что большинство органических веигеств обладает меньшей диэлектрической постоянной, чем вода, и поэтому должны были бы изгоняться ею из двойного слоя уже при не- [c.
Напротив, влияние катионов должно локализоваться только иа кисходя1цей ветви, где они электростатически притягиваются к отрицательно заряженной поверхности ртути. В действительности, как это было найдено еще Гуи, многие анионы изменяют ход элек-трокапиллярпой кривой справа от точки максимума, а некоторые катионы влияют не только на нисходящую, но и на восходящую ветвь кривой. Такое поведение ионов нельзя объяснить действием только кулоновских сил. Оно связано с силами взаимодействия, отличными от простых электростатических сил. Такими силами, специфическими для данного рода частиц, могут быть, например, силы Ваи-дер-Ваальса или химические (валентные). Благодаря этим силам ионы в состоянии удерживаться на одноименно заряженной поверхности ртути и влиять на электрокапиллярные свойства границы металл — раствор. Точно так же нельзя на основе одних только электростатических представлений объяснить влияние неиоинзированных органических веществ на ход электрокапиллярных кривых. Дело в том, что большинство органических веигеств обладает меньшей диэлектрической постоянной, чем вода, и поэтому должны были бы изгоняться ею из двойного слоя уже при не- [c.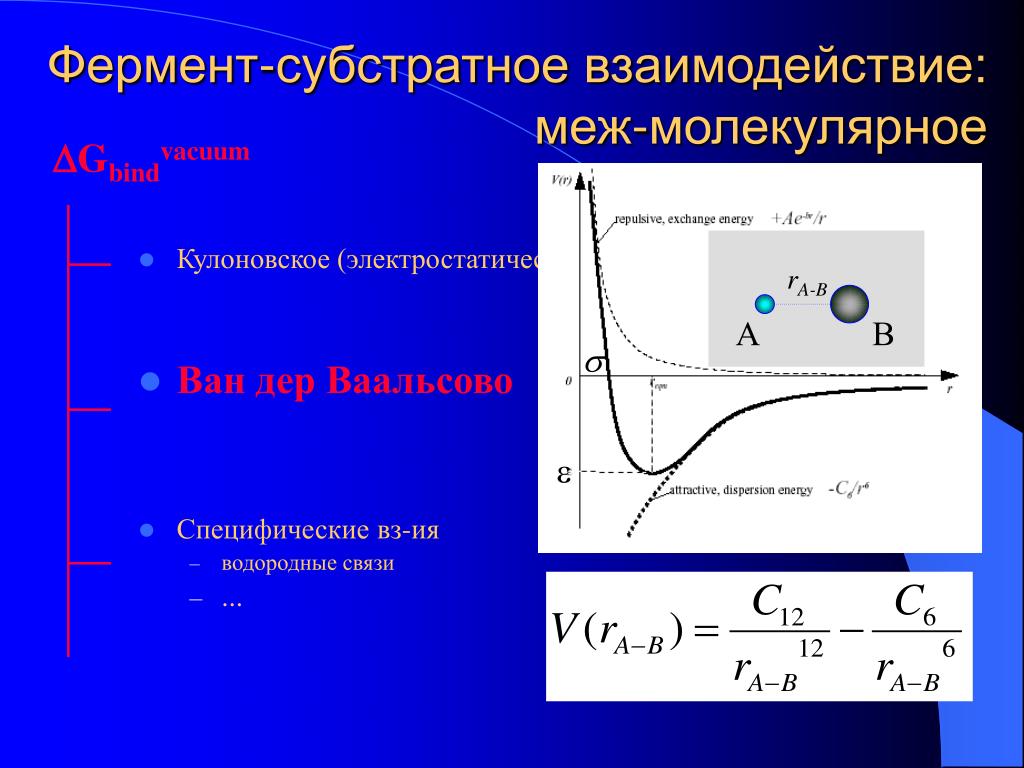 239]
239]
Подобные отклонения можно объяснить двояко. Отказавшись от постулата 3, приходим к представлению о хемосорбции на однородной поверхности, сопровождающейся взаимодействием сорбированных частиц. Если это взаимодействие заключается во взаимном отталкивании, теплота адсорбции должна уменьшаться с увеличением степени заполнения в согласии с опытными данными. Выбрав некоторую зависимость коэффициента адсорбции Ь [связанного с теплотой адсорбции соотношением (1.6) ] от степени заполнения поверхности и подставив ее в уравнение (1.5), можем аппроксимировать таким образом любую экспериментальную изотерму адсорбции. Отталкивание хемосорбированных молекул может являться следствием квантово-механического обменного взаимодействия [9]. Силы кулоновского или диполь-динольного взаимодействия играют малую роль, так как они долнщы сказываться лишь при значительной плотности сорбированных молекул, между тем отклонения от изотермы Лангмюра (или изотермы Генри) часто становятся заметными уже при очень малых степенях заполнения поверхности. Весьма правдоподобно объяснение природы сил взаимодействия сорбированных частиц через посредство электронного газа кристаллической решетки катализатора (см. постулат 3, а также работы [9, 10]) сила такого взаимодействия незначительно уменьшается [c.17]
Весьма правдоподобно объяснение природы сил взаимодействия сорбированных частиц через посредство электронного газа кристаллической решетки катализатора (см. постулат 3, а также работы [9, 10]) сила такого взаимодействия незначительно уменьшается [c.17]
Натансон [594]j рассматривал также наличие кулоновских и поляризационных сил взаимодействия между частицами и цилиндром и вывел уравнения для эффективности захвата, подобные уравнениям Кремера и Джонстона. Они были рассмотрены в обзоре Пяча [643] я здесь приводиться не будут. [c.325]
Например, энергия кулоновского взаимодействия обратио пропорцио-пальиа расстоянию между зарядами И=д1д. г. Если же эту энергию разделить иа расстояние между заряда И, получим силу взаимодействия, отражаемую законом Кулона Р=и г д . 1г. [c.22]
В промышленно выпускаемых приборах обычно используют консоли из нитрида кремния с пирамидальными остриями (основа 4 х 4 мкм, высота 4мкм). Номинальный радиус кривизны вершины острия обычно составляет от 20 до 50 нм. В идеальном случае на вершине острия размещается один атом (рис. 10.5-8). В методе АСМ острие всегда находится в контакте с поверхностью (это называют контактным режимом). Вследствие этого всегда существуют межатомные силы отталкивания в области контакта из-за перекрывания электронных оболочек атомов острия и субстрата. Кроме этих близкодействующих сил возникают также дальнодействующие силы (например, кулоновские силы между зарядами, диполь-дипольные взаимодействия, поляризационные силы, вандерваальсовы дисперсионные силы, капиллярные силы, обусловленные наличием пленок адсорбата между острием и субстратом), которые могут быть силами притяжения или отталкивания (рис. 10.5-8). Хотя оба типа сил вносят вклад в обш ую силу, действующую на кантилевер, только изменяющаяся сила межатомного отталкивания позволяет получить изображение поверхности с [c.375]
Номинальный радиус кривизны вершины острия обычно составляет от 20 до 50 нм. В идеальном случае на вершине острия размещается один атом (рис. 10.5-8). В методе АСМ острие всегда находится в контакте с поверхностью (это называют контактным режимом). Вследствие этого всегда существуют межатомные силы отталкивания в области контакта из-за перекрывания электронных оболочек атомов острия и субстрата. Кроме этих близкодействующих сил возникают также дальнодействующие силы (например, кулоновские силы между зарядами, диполь-дипольные взаимодействия, поляризационные силы, вандерваальсовы дисперсионные силы, капиллярные силы, обусловленные наличием пленок адсорбата между острием и субстратом), которые могут быть силами притяжения или отталкивания (рис. 10.5-8). Хотя оба типа сил вносят вклад в обш ую силу, действующую на кантилевер, только изменяющаяся сила межатомного отталкивания позволяет получить изображение поверхности с [c.375]
В химии основное внимание уделяется взаимодействиям между атомами, ионами и молекулами, приводящим к образованию (или разрыву) химических связей.
 Вместе с тем уже более ста лет изучаются слабые и очень слабые взаимодействия систем с замкнутой оболочкой, между которыми в обычных лабораторных условиях не осуществляются реакции в химическом смысле этого слова. Существование жидкого (а в случае молекулярных кристаллов) и твердого состояния обусловлено наличием сил притяжения между молекулами. Равновесное расстояние между молекулами, образующими ассоциаты в жидкой и твердой фазах, определяется компенсацией сил притяжения и отталкивания. Экспериментально установлено, что силы отталкивания очень быстро ослабевают с увеличением межмолекулярного расстояния (приблизительно обратно пропорционально его двенадцатой степени), тогда как возрастание сил притяжения при уменьшении межмолекулярного расстояния происходит не так быстро (грубо говоря, обратно пропорционально шестой степени расстояния). Это обстоятельство имеет важное значение в то время как силы отталкивания на расстояниях порядка длины химической связи оказываются почти неощутимыми, силы притяжения не могут считаться пренебрежимо малыми вплоть до расстояний 0,4 нм, и поэтому о них говорят как о дально-действующих силах.
Вместе с тем уже более ста лет изучаются слабые и очень слабые взаимодействия систем с замкнутой оболочкой, между которыми в обычных лабораторных условиях не осуществляются реакции в химическом смысле этого слова. Существование жидкого (а в случае молекулярных кристаллов) и твердого состояния обусловлено наличием сил притяжения между молекулами. Равновесное расстояние между молекулами, образующими ассоциаты в жидкой и твердой фазах, определяется компенсацией сил притяжения и отталкивания. Экспериментально установлено, что силы отталкивания очень быстро ослабевают с увеличением межмолекулярного расстояния (приблизительно обратно пропорционально его двенадцатой степени), тогда как возрастание сил притяжения при уменьшении межмолекулярного расстояния происходит не так быстро (грубо говоря, обратно пропорционально шестой степени расстояния). Это обстоятельство имеет важное значение в то время как силы отталкивания на расстояниях порядка длины химической связи оказываются почти неощутимыми, силы притяжения не могут считаться пренебрежимо малыми вплоть до расстояний 0,4 нм, и поэтому о них говорят как о дально-действующих силах. Среди таких сил важная роль принадлежит дисперсионным силам в разд. 17.2 рассматривается их квантовомеханическое обоснование в рамках простой модели. В данной главе будут выведены выражения, основанные на теории возмущений и пригодные для описания межмолекулярного взаимодействия. Но прежде чем перейти к их выводу, скажем несколько слов о происхождении кулоновских, индукционных и дисперсионных сил. Для кулоновского взаимодействия обе влияющие друг на друга системы могут формально рассматриваться как состоящие из ряда мультиполей. Во втором случае происходит взаимодействие между постоянным и индуцированным мультиполями двух систем. В третьем случае мы имеем дело с взаимодействием между системами, не имеющими постоянных диполей однако и в этих системах в результате флук- [c.482]
Среди таких сил важная роль принадлежит дисперсионным силам в разд. 17.2 рассматривается их квантовомеханическое обоснование в рамках простой модели. В данной главе будут выведены выражения, основанные на теории возмущений и пригодные для описания межмолекулярного взаимодействия. Но прежде чем перейти к их выводу, скажем несколько слов о происхождении кулоновских, индукционных и дисперсионных сил. Для кулоновского взаимодействия обе влияющие друг на друга системы могут формально рассматриваться как состоящие из ряда мультиполей. Во втором случае происходит взаимодействие между постоянным и индуцированным мультиполями двух систем. В третьем случае мы имеем дело с взаимодействием между системами, не имеющими постоянных диполей однако и в этих системах в результате флук- [c.482] Исследование адсорбции ароматических аминов (анилин, о-то-луидин, 2,3- и 2,6-диметиланилин, пиридин, хинолин) в 0,1 н. НС1, выполненное Бломгреном я Бокрисом [73], также показало, что адсорбция этих соединений, которые в кислом электролите находятся в виде катионов [КНз]+, при потенциалах, соответствующих положительной ветви электрокапиллярной кривой, определяется в основном я-электронным взаимодействием.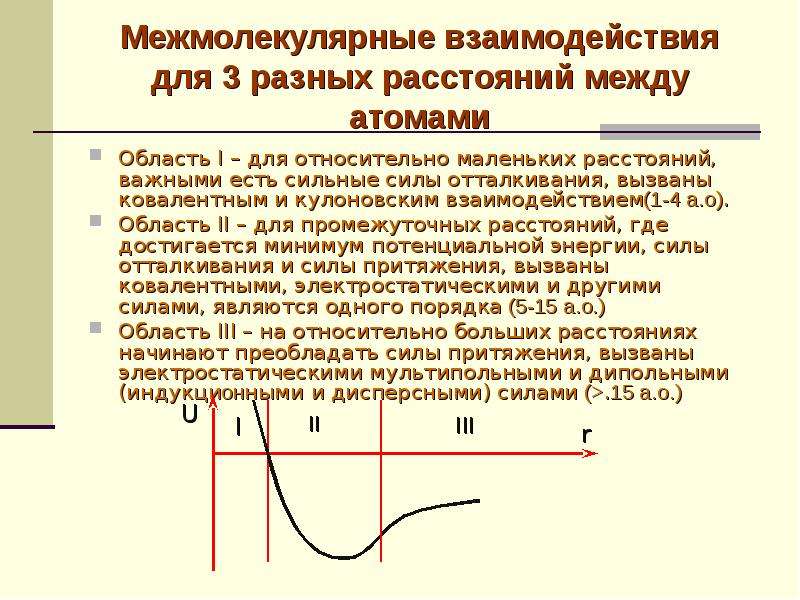 Оно облегчается при плоском расположении частиц по поверхности электрода. При потенциалах, соответствующих отрицательной ветви электрокапиллярной кривой, адсорбция определяется кулоновскими силами взаимодействия. Из этого видно, что теория электростатического взаимодействия между поверхностью ртути и адсорбируемым веществом не в состоянии объяснить все экспериментальные данные. [c.135]
Оно облегчается при плоском расположении частиц по поверхности электрода. При потенциалах, соответствующих отрицательной ветви электрокапиллярной кривой, адсорбция определяется кулоновскими силами взаимодействия. Из этого видно, что теория электростатического взаимодействия между поверхностью ртути и адсорбируемым веществом не в состоянии объяснить все экспериментальные данные. [c.135]
Закон кулона
Закон Кулона и квантовая электродинамика
С точки зрения квантовой электродинамики взаимодействие заряженных тел происходит посредством обмена виртуальными фотонами. Существование таких ненаблюдаемых частиц и нулевой массы, но не нулевыго заряда косвенно подтверждается принципом неопределенности. Согласно этому принципу, виртуальный фотон может существовать между мгновениями испускания такой частицы и ее поглощения. Чем меньше расстояние между телами, тем меньше времени затрачивает фотон на прохождение пути, следовательно, тем больше энергия испускаемых фотонов. При небольшой дистанции между наблюдаемыми зарядами принцип неопределенности допускает обмен и коротковолновыми и длинноволновыми частицами, а при больших расстояниях коротковолновые фотоны в обмене не участвуют.
При небольшой дистанции между наблюдаемыми зарядами принцип неопределенности допускает обмен и коротковолновыми и длинноволновыми частицами, а при больших расстояниях коротковолновые фотоны в обмене не участвуют.
Задача 2
Два одинаковых заряженных шарика подвешены в среде с диэлектрической проницаемостью на нитях одинаковой длины , закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны .
Рис. 15. Рисунок к условию задачи 2
Порассуждаем: на каждый из шариков будут действовать три силы – сила тяжести ; сила электростатического взаимодействия и сила натяжения нити (см. рис. 16).
Рис. 16. Силы, действующие на шарики
По условию шарики одинаковые, то есть их заряды равны как по модулю, так и по знаку, а значит, сила электростатического взаимодействия в данном случае будет силой отталкивания (на рис. 16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:
16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:
Так как в условии сказано, что шарики подвешены в среде с диэлектрической проницаемостью , а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:
Решение
Распишем первый закон Ньютона в проекциях на оси координат. Ось направим горизонтально, а ось вертикально (см. рис. 17).
Рис. 17. Выбор направления осей координат
Рис. 18. Силы в проекциях на оси координат
Так как на шарики действуют одинаковые силы тяжести и силы электростатического взаимодействия, нити тоже одинаковые – они отклонятся на одинаковые углы (см. рис. 19).
Рис. 19. Углы, на которые отклоняются шарики, одинаковые
В сумме эти углы дают нам , это означает, что:
Тогда из прямоугольного треугольника можно найти углом :
Добавим к двум уравнениям, которые мы записали, выражение для модуля силы электростатического взаимодействия:
Расстояние найдем геометрически – найдем прилежащий к углу катет и умножим его на 2:
Мы получили систему из 4-х уравнений:
Математическое решение можно пронаблюдать в свертке.
Ответ:
Решение системы уравнений
Выразим из второго уравнения силу натяжения нити и подставим в первое:
Отсюда выразим силу электростатического взаимодействия:
Приравняем выражение для силы электростатического взаимодействия, которое мы сейчас выразили с третьим уравнением:
Подставим сюда выражение для
Выразим искомый заряд
Так как угол , то , тогда:
На этом наш урок закончен
Спасибо за внимание
Список литературы
1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт physics.ru ()
2. Интернет-сайт «Класс!ная физика» (Источник)
Домашнее задание
1. Запишите формулу закона Кулона.
2. Как взаимодействуют разноименно заряженные тела?
3. Решите задачу: два заряда, 10 нКл и -2 нКл, закреплены на расстоянии 10 см друг от друга. Определите силу, с которой они взаимодействуют.
2. История открытия
Догадки о том, что взаимодействие между електризованимы телами подчиняется тому же закону оберененои пропорциональности квадрату расстояния, и тяжести, неоднократно высказывались исследователями в середине 18 в. В начале 1770-х ее экспериментально открыл Генри Кавендиш, однако своих результатов не опубликовал, и о них стало известно только в конце 19 в. после изучения и публикации его архивов. Шарль Кулон опубликовал закон 1785 году в двух мемуарах, представленных на рассмотрение Французской академии наук . 1835 Карл Гаусс опубликовал выведенную на основе закона Кулона, теорему Гаусса. В виде теоремы Гаусса закон Кулона входит в основных уравнений электродинамики.
Применение на практике
Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.
В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.
Напоследок рекомендуем просмотреть видео, на котором предоставлено подробное объяснение Закона Кулона:
Полезное по теме:
- Закон Джоуля-Ленца
- Зависимость сопротивления проводника от температуры
- Правила буравчика
- Закон Ома простыми словами
Определение электрического поля (Е)
Электрическое поле (напряженность поля) E в данной точке определяется как значение, равное отношению силы F, действующей на положительный испытательный заряд q, к значению нагрузки:
Движение заряженных частиц в поле происходит под действием силы F = Q*E.
Аддитивность полей
Поле E является аддитивным вектором, что означает, что результирующее электрическое поле представляет собой векторную сумму полей E 1 , E 2 , E 3 …, полученных из отдельных зарядов:
Линии напряженности электрических полей
Концепция силовых линий поля была также введена Майклом Фарадеем (1791-1867). Линии напряженности поля представляют собой воображаемые кривые в пространстве, находящиеся в каждой точке, касающейся вектора E в этой точке. Это также означает, что в каждой точке линии поля имеется касательный вектор силы, действующий в этом поле для испытательной нагрузки (небольшой положительный заряд). Как показано на рисунке ниже, силовая линия — это траектория положительного испытательного заряда (маленький красный шарик), движущегося в поле E , причем сила F является результирующей (векторной суммой) двух сил: силы, отталкивающей испытательный заряд от положительного заряда F Q, и силы притяжения испытательная нагрузка на отрицательный заряд F q. Такая картина силовых линий верна только тогда, когда пренебрегают силами инерции (центробежными), возникающими из-за ненулевой массы груза. Линии напряженности поля никогда не пересекаются друг с другом. Представляя силовые линии, принимается соглашение о вытягивании, согласно которому плотность силовых линий пропорциональна напряженности поля в этом месте. Силовые линии в окрестности системы двух точечных нагрузок, положительной и отрицательной, одинакового абсолютного значения показаны на рисунке:
Закон Кулона- основной закон электростатики.
Установите значения величин, приведенных в таблице. Запишите значения сил для каждого случая.
q1 в опытах 1,2?Значение заряда q1 увеличилось в __________________________________
Как изменилось значение силы в опытах 1,2? Во сколько раз?
Значение силы _________________________ в _______________________
Какая зависимость между силой и зарядом q1: прямая, обратная?
Между силой и зарядом q1 _____________________зависимость.
Как изменилось значение заряда q2 в опытах 2,3? Во сколько раз?
Значение заряда q2 _____________________в _______________________
Как изменилось значение силы в опытах 2,3? Во сколько раз?
Значение силы _________________________ в _______________________
Какая зависимость между силой и зарядом q2: прямая, обратная?
Между силой и зарядом q2 _____________________зависимость.
Задание 2. Наблюдение за изменением зависимости силы взаимодействия между зарядами от расстояния между ними.
Расположите заряды q1 и q2 на одной горизонтальной прямой, на расстоянии 150 см.
Установите заряд q3=0.
Установите значения величин, приведенных в таблице. Запишите значения сил для каждого случая.
Расстояние между зарядами _____________________в _______________________
Как изменился квадрат расстояния между зарядами?Во сколько раз?
Квадрат расстояния между зарядами _____________________в _______________
Как изменилось значение силы? Во сколько раз?
Значение силы _________________________ в _______________________
Какая зависимость между силой и квадратом расстояния между зарядами: прямая, обратная?
Между силой и квадратом расстояния_____________________зависимость.
Встаньте, потянитесь, поставьте руки на пояс, наклоны головы вправо-влево (3раза), наклоны туловища вправо-влево (3 раза). Посмотрите вверх-вниз, вправо-влево (3 раза), зажмурьтесь, откройте глаза и сядьте за парту.
Прочитайте результаты ваших наблюдений. Как сила взаимодействия между зарядами зависит от величины этих зарядов и от расстояния между ними?
Запишите закон Кулона в тетрадь (слайд 9 анимированный; при наведении курсора на физическую величину в формуле, она выделяется).
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
F=k
k=
k — коэффициент пропорциональности.
Физический смысл k: F=k, если r=1 м, q1=q2 =1Кл (слайд 10)
Кулоновские силы направлены вдоль прямой, соединяющей заряды, поэтому их называют центральными.
Границы применения закона Кулона:
Закон справедлив для точечных зарядов.
Заряженные тела должны быть неподвижными. (слайд 11)
Закрепление (8 мин).
Прочитайте закон Кулона и формулу (по буквам и по названиям физических величин) – 2 человека.
Ответьте на вопросы в парах:
Как вы понимаете выражение «Сила прямо пропорциональна произведению модулей зарядов»?
Как вы понимаете выражение «Сила обратно пропорциональна квадрату расстояния между зарядами»?
На каком рисунке заряды являются точечными? Почему?
4. В каком случае выполняется закон Кулона? Почему?
Как изменится сила кулоновского взаимодействия, если…
А) величина одного из зарядов увеличится в 2 раза;
Б) величина одного из зарядов увеличится в 3 раза, а второго уменьшится в 9 раз;
В) расстояние между зарядами увеличится в 6 раз;
Г) величина одного из зарядов увеличится в 4 раза, а расстояние между ними уменьшится в 2 раза;
Выполните задания в тетради.
Разноуровневые задания:
1. Являются ли заряды точечными? Покажите направление сил кулоновского взаимодействия.2. Продолжите предложение. С увеличением расстояния между зарядами сила кулоновского взаимодействия…. С увеличением величины одного из зарядов сила кулоновского взаимодействия… .
1. Покажите направление сил кулоновского взаимодействия.
2. Продолжите предложение. С уменьшением расстояния между зарядами сила кулоновского взаимодействия…. С уменьшением величины одного из зарядов сила кулоновского взаимодействия… .
2 уровень
2 уровень
В
А)
Б)
каком случае выполняется закон Кулона. Покажите для этого случая направление силы кулоновского взаимодействия.Как изменится сила кулоновского взаимодействия, если величина заряда увеличится в 10 раз? Ответ обоснуйте.
1. В каком случае заряды изображенные на рисунке являются точечными? Покажите для этого случая направление силы кулоновского взаимодействия.
2. Как изменится сила кулоновского взаимодействия, если расстояние между зарядами уменьшится в 10 раз? Ответ обоснуйте.
3 уровень
3 уровень
1. На рисунке изображены точечные заряды и силы кулоновского взаимодействия. Как будет выглядеть рисунок, если величину одного из зарядов уменьшить в 2 раза?
2. Как изменится сила кулоновского взаимодействия, если величина одного из зарядов увеличится в 5 раз, а расстояние между зарядами уменьшится в 5 раз?
1. На рисунке изображены точечные заряды и силы кулоновского взаимодействия. Как будет выглядеть рисунок, если расстояние между зарядами уменьшить в 2 раза?
2. Как изменилось расстояние между зарядами, если сила кулоновского взаимодействия увеличилась в 64 раза?
VII. Итог урока (3мин).
Отметьте знаком «плюс» то, что вы хорошо поняли на уроке и знаком «минус» то, что поняли плохо или вообще не поняли. (слайд 12)
VIII. Домашнее задание (1мин).§8.2, упр.16 (1-5) (слайд 13)
Разноуровневые задания:
1. Являются ли заряды точечными? Покажите направление сил кулоновского взаимодействия.2. Продолжите предложение. С увеличением расстояния между зарядами сила кулоновского взаимодействия…. С увеличением величины одного из зарядов сила кулоновского взаимодействия… .
1. Покажите направление сил кулоновского взаимодействия.
2. Продолжите предложение. С уменьшением расстояния между зарядами сила кулоновского взаимодействия…. С уменьшением величины одного из зарядов сила кулоновского взаимодействия… .
2 уровень
2 уровень
В
А)
Б)
каком случае выполняется закон Кулона. Покажите для этого случая направление силы кулоновского взаимодействия.Как изменится сила кулоновского взаимодействия, если величина заряда увеличится в 10 раз? Ответ обоснуйте.
1. В каком случае заряды изображенные на рисунке являются точечными? Покажите для этого случая направление силы кулоновского взаимодействия.
2. Как изменится сила кулоновского взаимодействия, если расстояние между зарядами уменьшится в 10 раз? Ответ обоснуйте.
3 уровень
3 уровень
1. На рисунке изображены точечные заряды и силы кулоновского взаимодействия. Как будет выглядеть рисунок, если величину одного из зарядов уменьшить в 2 раза?
2. Как изменится сила кулоновского взаимодействия, если величина одного из зарядов увеличится в 5 раз, а расстояние между зарядами уменьшится в 5 раз?
1. На рисунке изображены точечные заряды и силы кулоновского взаимодействия. Как будет выглядеть рисунок, если расстояние между зарядами уменьшить в 2 раза?
2. Как изменилось расстояние между зарядами, если сила кулоновского взаимодействия увеличилась в 64 раза?
Сила электростатического взаимодействия двух точечных зарядов
\(F\) — сила, действующая на заряд 2 со стороны заряда 1 \((Н)\)
\(r\) — расстояние от заряда 1 до заряда 2 \((м)\)
\(q_1\) — электрический заряд \((Кл)\)
\(q_2\) — электрический заряд \((Кл)\)
\(k = \frac{1}{4 \pi \varepsilon_0}\) — коэффициент пропорциональности в электричестве \(\approx 8.{-12}\) \(\frac{Ф}{м}\)
\(\pi\) — число Пи \(\approx 3.14\)
Богданов К.Ю. — учебник по физике для 10 класса
§ 34. ЗАКОН КУЛОНА.
Согласно закону Кулона сила взаимодействия между двумя неподвижными заряженными точечными телами пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними.
Электрическая сила взаимодействия между заряженными телами зависит от величины их зарядов, размеров тел, расстояния между ними, а также от того, в каких частях тел находятся эти заряды. Если размеры заряженных тел значительно меньше расстояния между ними, то такие тела называют точечными. Сила взаимодействия между точечными заряженными телами зависит только от величины их зарядов и расстояния между ними.
Закон, описывающий взаимодействие двух точечных заряженных тел, был установлен французским физиком Ш. Кулоном, когда он измерял силу отталкивания между небольшими одноимённо заряженными металлическими шариками (см. рис. 34а). Установка Кулона состояла из тонкой упругой серебряной нити (1) и подвешенной на ней лёгкой стеклянной палочки (2), на одном конце которой был укреплён заряженный металлический шарик (3), а на другом противовес (4). Сила отталкивания между неподвижным шариком (5) и шариком 3 приводила к закручиванию нити на некоторый угол, a, по которому можно было определить величину этой силы. Сближая и отдаляя между собой одинаково заряженные шарики 3 и 5, Кулон установил, что сила отталкивания между ними обратно пропорциональна квадрату расстояния между ними.
Чтобы установить, как сила взаимодействия между шариками зависит от величины их зарядов, Кулон поступал следующим образом. Сначала он измерял силу, действующую между одинаково заряженными шариками 3 и 5, а потом касался одного из заряженных шариков (3) другим, незаряженным шариком такого же размера (6). Кулон справедливо полагал, что при соприкосновении одинаковых металлических шариков электрический заряд поровну распределится между ними, и поэтому на шарике 3 останется только половина его первоначального заряда. При этом, как показали опыты, сила отталкивания между шариками 3 и 5 уменьшалась в два раза, по сравнению с первоначальной. Изменяя подобным образом заряды шариков, Кулон установил, что они взаимодействуют с силой, пропорциональной произведению их зарядов.
В результате многочисленных опытов Кулон сформулировал закон, определяющий модуль силы F12, действующей между двумя неподвижными точечными телами с зарядами q1 и q2, расположенными на расстоянии r друг от друга:
где k – коэффициент пропорциональности, значение которого зависит от используемой системы единиц, и который часто по причинам, связанным с историей введения систем единиц, заменяют на (4pe0)-1 (см. 34.1). e0 называют электрической постоянной. Вектор силы F12 направлен вдоль прямой, соединяющей тела, так, что разноимённо заряженные тела притягиваются, а одноимённо заряженные отталкиваются (рис. 34б). Этот закон (см. 34.1) называют законом Кулона, а соответствующие электрические силы – кулоновскими.
Закон Кулона, а именно зависимость силы взаимодействия от второй степени расстояния между заряженными телами, до сих пор подвергается экспериментальной проверке. В настоящее время показано, что показатель степени в законе Кулона может отличаться от двойки не более, чем на 6.10-16.
В системе СИ единицей электрического заряда служит кулон (Кл). Заряд в 1 Кл равен заряду, проходящему за 1 с через поперечное сечение проводника при силе тока, равной 1 амперу (А). В системе СИ
k = 9.109 Н.м2/Кл2 , а e0 = 8,8.10-12 Кл2 /( Н.м2) (34.2)
Элементарный электрический заряд, e, в СИ равен:
e = 1,6.10-19 Кл . (34.3)
По своему виду закон Кулона очень похож на закон всемирного тяготения (11.1), если заменить в последнем массы на заряды. Однако, несмотря на внешнее сходство, гравитационные силы и кулоновские отличаются друг от друга тем, что
1. гравитационные силы всегда притягивают тела, а кулоновские могут как притягивать, так и отталкивать тела,
2. кулоновские силы гораздо сильнее гравитационных, например, кулоновская сила, отталкивающая два электрона друг от друга, в 1042 раз больше силы их гравитационного притяжения.
Вопросы для повторения:
· Что такое точечное заряженное тело?
· Опишите опыты, с помощью которых Кулон установил закон, названный его именем?
Рис. 34. (а) — схема экспериментальной установки Кулона для определения сил отталкивания между одноимёнными зарядами; (б) – к определению величины и направления действия кулоновских сил при использовании формулы (34.1).
Сила взаимодействия между двумя неподвижными точечными зарядами. Закон Кулона
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?
Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался
крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.
Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается,
и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы).
С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.
В те времена еще не было приборов для точного определения величины заряда, но
Кулон сумел приготовить небольшие шарики с известным соотношением зарядов.
Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком,
то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.
Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.
Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила,
с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила;
если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние
между телами остается постоянным.
Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату
расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.
Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна произведению их зарядов Q 1 и Q 2 и обратно пропорциональна квадрату расстояния между ними:
Здесь k -коэффициент пропорциональности.
Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами,
гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона.
Показатель степени 2 установлен в настоящее время с точностью 10 -16 , т.е. он равен
2 ± 2×10 -16 .
Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения,
чтобы постоянная к в формуле равнялась единице.
И действительно, такая система единиц еще недавно широко использовалась в физике.
Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.
Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).
Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.
В системе СИ постоянная k имеет величину k = 8,988×10 9 Нм 2 /Кл 2 .
Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т.п.),
по порядку величины составляют микрокулон и меньше (1 мкКл = 10 -6 Кл).
Заряд электрона (отрицательный) приблизительно равен 1,602×10 -19 Кл.
Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е , его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)×10 -19 Кл, или е ≈ 1,602×10 -19 Кл.
Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических зарядов (заряду 1 мкКл соответствуют примерно 10 13 электронов) и считаем заряд непрерывным.
Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды.
Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны.
Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.
Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой,
равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.
Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:
где F 12 — вектор силы, действующей на заряд Q 1 со стороны заряда Q 2,
— расстояние между зарядами,
— единичный вектор, направленный от Q 2 к Q 1.
Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров.
В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем
более что распределение заряда может быть и неоднородным.
Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер.
Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда.
Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд,
будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов.
Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ε 0 , так называемую
электрическую постоянную, которая связана с k соотношением k = 1/(4πε 0) .
С учетом этого закон Кулона можно переписать в следующем виде:
где с наивысшей на сегодня точностью
или округленно
Запись большинства других уравнений электромагнитной теории упрощается при использовании ε 0 , поскольку 4π в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:
Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой .
Продолжение следует. Коротко о следующей публикации:
Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.
Замечания и предложения принимаются и приветствуются!
Заряды и электричество — это термины, обязательные для тех случаев, когда наблюдается взаимодействие заряженных тел. Силы отталкивания и притяжения словно исходят от заряженных тел и распространяются одновременно во всех направлениях, постепенно затухая на расстоянии. Эту силу в свое время открыл известный французский естествоиспытатель Шарль Кулон, и правило, которому подчиняются заряженные тела, с тех пор называется Закон Кулона.
Шарль Кулон
Французский ученый родился во Франции, где получил блестящее образование. Он активно применял полученные знания в инженерных науках и внес значительный вклад теорию механизмов. Кулон является автором работ, в которых изучалась работа ветряных мельниц, статистика различных сооружений, кручение нитей под влиянием внешних сил. Одна из этих работ помогла открыть закон Кулона-Амонтона, объясняющий процессы трения.
Но основной вклад Шарль Кулон внес в изучение статического электричества. Опыты, которые проводил этот французский ученый, подвели его к пониманию одного из наиболее фундаментальных законов физики. Именно ему мы обязаны знанием природы взаимодействия заряженных тел.
Предыстория
Силы притяжения и отталкивания, с которыми электрические заряды действуют друг на друга, направлены вдоль прямой, соединяющей заряженные тела. С увеличением расстояния эта сила ослабевает. Спустя столетие после того, как Исаак Ньютон открыл свой всемирный закон тяготения, французский ученый Ш. Кулон исследовал экспериментальным путем принцип взаимодействия между заряженными телами и доказал, что природа такой силы аналогична силам тяготения. Более того, как оказалось, взаимодействующие тела в электирическом поле ведут себя так же, как и любые тела, обладающие массой, в гравитационном поле.
Прибор Кулона
Схема прибора, при помощи которого Шарль Кулон делал свои измерения, приведена на рисунке:
Как можно видеть, по существу эта конструкция не отличается от того прибора, которым в свое время Кавендиш измерял величину гравитационной постоянной. Изолирующий стержень, подвешенный на тонкой нити, заканчивается металлическим шариком, которому сообщен определенный электрический заряд. К шарику приближают другой металлический шарик, а затем, по мере сближения, измеряют силу взаимодействия по степени закручивания нити.
Эксперимент Кулона
Кулон предположил, что к силе, с которой закручивается нить, можно применить уже известный тогда Закон Гука. Ученый сравнил изменение силы при различной дистанции одного шарика от другого и установил, что сила взаимодействия изменяет свое значение обратно пропорционально квадрату дистанции между шариками. Кулон сумел изменять значения заряженного шарика от q до q/2, q/4, q/8 и так далее. При каждом изменении заряда сила взаимодействия пропорционально меняла свое значение. Так, постепенно, было сформулировано правило, которое впоследствии было названо «Закон Кулона».
Определение
Экспериментальным путем французский ученый доказал, что силы, с которыми взаимодействуют два заряженных тела, пропорциональны произведению их зарядов и обратно пропорциональны квадрату расстояния между зарядами. Это утверждение и представляет собой закон Кулона. В математическом виде он может быть выражен так:
В этом выражении:
- q- количество заряда;
- d — расстояние между заряженными телами;
- k- электрическая постоянная.
Значение электрической постоянной во многом зависит от выбора единицы измерения. В современной системе величина электрического заряда измеряется в кулонах, а электрическая постоянная, соответственно, в ньютон×м 2 / кулон 2 .
Последние измерения показали, что данный коэффициент должен учитывать диэлектрическую проницаемость среды, в которой проводится опыт. Сейчас величину показывают в виде соотношения k=k 1 /e, где к 1 является уже знакомой нам электрической константой, а не является показателем диэлектрической проницаемости. В условиях вакуума эта величина равна единице.
Выводы из закона Кулона
Ученый экспериментировал с различной величиной зарядов, проверяя взаимодействие между телами с различной величиной заряда. Разумеется, измерить электрический заряд в каких-либо единицах он не мог — не хватало ни знаний, ни соответствующих приборов. Шарль Кулон смог разделять снаряд, прикасаясь к заряженному шарику незаряженным. Так он получал дробные значения исходного заряда. Ряд опытов показал, что электрический заряд сохраняется, происходит обмен без увеличения или уменьшения количества заряда. Этот фундаментальный принцип лег в основу закона сохранения электрического заряда. В настоящее время доказано, что этот закон соблюдается и в микромире элементарных частиц и в макромире звезд и галактик.
Условия, необходимые для выполнения закона Кулона
Для того чтобы закон выполнятся с большей точностью, необходимо выполнение следующих условий:
- Заряды должны быть точечными. Другими словами, дистанция между наблюдаемыми заряженными телами должна быть намного больше их размеров. Если заряженные тела имеют сферическую форму, то можно считать, что весь заряд находится в точке, которая является центром сферы.
- Измеряемые тела должна быть неподвижными. Иначе на движущийся заряд будут влиять многочисленные сторонние факторы, например, сила Лоренца, которая придает заряженному телу дополнительное ускорение. А также магнитное поле движущегося заряженного тела.
- Наблюдаемые тела должны находиться в вакууме, чтобы избежать воздействия потоков воздушных масс на результаты наблюдений.
Закон Кулона и квантовая электродинамика
С точки зрения квантовой электродинамики взаимодействие заряженных тел происходит посредством обмена виртуальными фотонами. Существование таких ненаблюдаемых частиц и нулевой массы, но не нулевыго заряда косвенно подтверждается принципом неопределенности. Согласно этому принципу, виртуальный фотон может существовать между мгновениями испускания такой частицы и ее поглощения. Чем меньше расстояние между телами, тем меньше времени затрачивает фотон на прохождение пути, следовательно, тем больше энергия испускаемых фотонов. При небольшой дистанции между наблюдаемыми зарядами принцип неопределенности допускает обмен и коротковолновыми и длинноволновыми частицами, а при больших расстояниях коротковолновые фотоны в обмене не участвуют.
Есть ли пределы применения закона Кулона
Закон Кулона полностью объясняет поведение двух точечных зарядов в вакууме. Но когда речь идет о реальных телах, следует принимать во внимание объемные размеры заряженных тел и характеристики среды, в которой ведется наблюдение. Например, некоторые исследователи наблюдали, что тело, несущее в себе небольшой заряд и принудительно внесенное в электрическое поле другого объекта с большим зарядом, начинает притягиваться к этому заряду. В этом случае утверждение, что одноименно заряженные тела отталкиваются, дает сбой, и следует искать другое объяснение наблюдаемому явлению. Скорее всего, здесь не идет речь о нарушении закона Кулона или принципа сохранения электрического заряда — возможно, что мы наблюдаем неизученные до конца явления, объяснить которые наука сможет немного позже.
В электростатике одним из основополагающих является закон Кулона. Он применяется в физике для определения силы взаимодействия двух неподвижных точечных зарядов или расстояния между ними. Это фундаментальный закон природы, который не зависит ни от каких других законов. Тогда форма реального тела не влияет на величину сил. В этой статье мы расскажем простым языком закон Кулона и его применение на практике.
История открытия
Ш.О. Кулон в 1785 г. впервые экспериментально доказал взаимодействия описанные законом. В своих опытах он использовал специальные крутильные весы. Однако еще в 1773 г. было доказано Кавендишем, на примере сферического конденсатора, что внутри сферы отсутствует электрическое поле. Это говорило о том, что электростатические силы изменяются в зависимости от расстояния между телами. Если быть точнее — квадрату расстояния. Тогда его исследования не были опубликованы. Исторически сложилось так, что это открытие было названо в честь Кулона, аналогичное название носит и величина, в которой измеряется заряд.
Формулировка
Определение закона Кулона гласит: В вакууме F взаимодействия двух заряженных тел прямо пропорционально произведению их модулей и обратно пропорционально квадрату расстояния между ними.
Звучит кратко, но может быть не всем понятно. Простыми словами: Чем больший заряд имеют тела и чем ближе они находятся друг к другу, тем больше сила.
И наоборот: Если увеличить расстояние межу зарядами — сила станет меньше.
Формула правила Кулона выглядит так:
Обозначение букв: q — величина заряда, r — расстояние межу ними, k — коэффициент, зависит от выбранной системы единиц.
Величина заряда q может быть условно-положительной или условно-отрицательной. Это деление весьма условно. При соприкосновении тел она может передаваться от одного к другому. Отсюда следует, что одно и то же тело может иметь разный по величине и знаку заряд. Точечным называется такой заряд или тело, размеры которого много меньше, чем расстояние возможного взаимодействия.
Стоит учитывать что среда, в которой расположены заряды, влияет на F взаимодействия. Так как в воздухе и в вакууме она почти равна, открытие Кулона применимо только для этих сред, это одно из условий применения этого вида формулы. Как уже было сказано, в системе СИ единица измерения заряда — Кулон, сокращено Кл. Она характеризует количество электричества в единицу времени. Является производной от основных единиц СИ.
1 Кл = 1 А*1 с
Стоит отметить, что размерность 1 Кл избыточна. Из-за того что носители отталкиваются друг от друга их сложно удержать в небольшом теле, хотя сам по себе ток в 1А небольшой, если он протекает в проводнике. Например в той же лампе накаливания на 100 Вт течет ток в 0,5 А, а в электрообогревателе и больше 10 А. Такая сила (1 Кл) примерно равна действующей на тело массой 1 т со стороны земного шара.
Вы могли заметить, что формула практически такая же, как и в гравитационном взаимодействии, только если в ньютоновской механике фигурируют массы, то в электростатике — заряды.
Формула Кулона для диэлектрической среды
Коэффициент с учетом величин системы СИ определяется в Н 2 *м 2 /Кл 2 . Он равен:
Во многих учебниках этот коэффициент можно встретить в виде дроби:
Здесь Е 0 = 8,85*10-12 Кл2/Н*м2 — это электрическая постоянная. Для диэлектрика добавляется E — диэлектрическая проницаемость среды, тогда закон Кулона может применяться для расчетов сил взаимодействия зарядов для вакуума и среды.
С учетом влияния диэлектрика имеет вид:
Отсюда мы видим, что введение диэлектрика между телами снижает силу F.
Как направлены силы
Заряды взаимодействуют друг с другом в зависимости от их полярности — одинаковые отталкиваются, а разноименные (противоположные) притягиваются.
Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r 12 и как радиус-вектор от первого ко второму заряду и наоборот. Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:
Сила, приложенная к первому заряду со стороны второго обозначается как F 12. Тогда в векторной форме закон Кулона выглядит следующим образом:
Для определения силы приложенной ко второму заряду используются обозначения F 21 и R 21 .
Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.
Применение на практике
Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.
В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.
Полезное
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд — это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные — притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда .
В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
q 1 + q 2 + q 3 + … +q n = const. |
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы — нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e .
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером . Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела — дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными . Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков — частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр ( или электроскоп) — прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Шарлем Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора — крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка 10 -9 Н.
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Силы взаимодействия подчиняются третьему закону Ньютона:
Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой .
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон — это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения .
Коэффициент k в системе СИ обычно записывают в виде:
Где — электрическая постоянная .
В системе СИ элементарный заряд e равен:
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции:
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов .
Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна
где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.
В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции 1 . Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.
Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.
Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна
где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
Рассмотрим теперь решение данных в первой части книги задач.
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой
Заряды отталкиваются (ответ 2 ).
Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2 ).
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17.1.3 — ответ 4 ).
Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3 ).
При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4 ).
При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2 ).
Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3 ).
Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2 ).
Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9 ). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4 ).
В системе двух заряженных шариков, связанных нитью (задача 17.1.10 ), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.
Этой величине и будет равна сила натяжения нитей (ответ 4 ). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).
Для нахождения силы, действующей на заряд — в задаче 17.2.2 , используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4 ).
(ответ 3 ).
Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4 . В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3 ).
В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
где . Поэтому и результирующая сила равна этому выражению (ответ 2 )
В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы
где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
Из этих формул следует, что наибольшей сила будет в точке — ответ 1 .
Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины
которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1 ).
Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3 .
Поделитесь статьей с друзьями:
Похожие статьи
Кулоновская сила | физика | Britannica
Кулоновская сила , также называемая электростатическая сила или Кулоновское взаимодействие , притяжение или отталкивание частиц или объектов из-за их электрического заряда. Одна из основных физических сил, электрическая сила, названа в честь французского физика Шарля-Огюстена де Кулона, который в 1785 году опубликовал результаты экспериментального исследования правильного количественного описания этой силы.
Два одинаковых электрических заряда, как положительные, так и отрицательные, отталкиваются друг от друга по прямой линии между их центрами.Два разных заряда, положительный и отрицательный, притягиваются друг к другу по прямой линии, соединяющей их центры. Электрическая сила действует между зарядами на расстояниях не менее 10 — 1 6 метров, или приблизительно одной десятой диаметра атомных ядер. Из-за своего положительного заряда протоны внутри ядер отталкиваются друг от друга, но ядра удерживаются вместе из-за другой базовой физической силы, сильного взаимодействия или ядерной силы, которая сильнее, чем электрическая сила.Массивные, но электрически нейтральные астрономические тела, такие как планеты и звезды, связаны в солнечных системах и галактиках еще одной базовой физической силой — гравитацией, которая, хотя и намного слабее, чем электрическая сила, всегда притягивает и является доминирующей силой на больших расстояниях. . На расстояниях между этими крайностями, включая расстояния повседневной жизни, единственная значимая физическая сила — это электрическая сила во многих ее разновидностях, а также связанная с ней магнитная сила.
Подробнее по этой теме
электричество: электростатика
… равновесие устанавливается быстро, потому что электрическая сила чрезвычайно велика.Математические методы электростатики позволяют …
Величина электрической силы F прямо пропорциональна количеству одного электрического заряда, q 1 , умноженному на другой, q 2 , и обратно пропорциональна квадрату расстояния r между их центрами. Выраженное в форме уравнения, это соотношение, называемое законом Кулона, может быть записано путем включения коэффициента пропорциональности k как F = kq 1 q 2 / r 2 .В системе единиц сантиметр – грамм – секунда коэффициент пропорциональности k в вакууме принимается равным 1, а единичный электрический заряд определяется законом Кулона. Если электрическая сила в одну единицу (один дин) возникает между двумя равными электрическими зарядами на расстоянии одного сантиметра друг от друга в вакууме, величина каждого заряда равна одной электростатической единице, эсу или статкулону. В системе метр – килограмм – секунда и системе СИ единица силы (ньютон), единица заряда (кулон) и единица расстояния (метр) определяются независимо от закона Кулона, поэтому коэффициент пропорциональности k должен принимать значение, соответствующее этим определениям, а именно: k в вакууме равно 8.98 × 10 9 ньютон на квадратный метр на квадратный кулон. Такой выбор значения для k позволяет включать практические электрические единицы, такие как ампер и вольт, в общие метрические механические единицы, такие как метр и килограмм, в одной и той же системе.
Учебник по физике: закон Кулона
Взаимодействие между заряженными объектами — это неконтактная сила, действующая на некотором расстоянии друг от друга. Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных.Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два отталкивающих одинаково заряженных шара или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критических переменных, которые влияют на прочность. взаимодействия. В этом разделе Урока 3 мы исследуем важность этих трех переменных.
Электрическая сила, как и все силы, обычно выражается в единицах Ньютон.Сила электрического взаимодействия является векторной величиной, которая имеет как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации. Зная тип заряда на двух объектах, можно определить направление силы, действующей на любой из них, с небольшими рассуждениями. На диаграмме ниже объекты A и B имеют одинаковый заряд, заставляющий их отталкиваться друг от друга.Таким образом, сила на объект A направлена влево (от B), а сила на объект B направлена вправо (от A). С другой стороны, объекты C и D имеют противоположный заряд, заставляя их притягиваться друг к другу. Таким образом, сила, действующая на объект C, направлена вправо (к объекту D), а сила, действующая на объект D, направлена влево (к объекту C). Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а любит отталкиваться), используя небольшие рассуждения.
Электрическая сила также имеет величину или силу. Как и большинство типов сил, существует множество факторов, которые влияют на величину электрической силы. Два одинаково заряженных шара будут отталкивать друг друга, и сила их силы отталкивания может быть изменена путем изменения трех переменных. Во-первых, количество заряда на одном из воздушных шаров влияет на силу отталкивающей силы. Чем больше заряжен воздушный шар, тем больше сила отталкивания.Во-вторых, количество заряда на втором воздушном шаре влияет на силу отталкивающей силы. Аккуратно натрите два шарика шерстью животных, и они немного оттолкнутся. Сильно потрите два шара, чтобы передать им больший заряд, и они сильно оттолкнутся. Наконец, расстояние между двумя воздушными шарами будет иметь значительное и заметное влияние на силу отталкивания. Электрическая сила наиболее сильна, когда воздушные шары находятся максимально близко друг к другу. Уменьшение разделительного расстояния увеличивает силу.Величина силы и расстояние между двумя воздушными шарами составляет , обратно пропорционально .
Уравнение закона КулонаКоличественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и обратно пропорциональна квадрату разделительного расстояния между двумя объектами.В форме уравнения закон Кулона может быть записан как
, где Q 1 представляет количество заряда на объекте 1 (в кулонах), Q 2 представляет количество заряда на объекте 2 (в кулонах), а d представляет собой расстояние между два объекта (в метрах). Символ k — это константа пропорциональности, известная как постоянная закона Кулона. Значение этой постоянной зависит от среды, в которую погружены заряженные объекты.В случае воздуха это значение составляет приблизительно 9,0 x 10 9 Н • м 2 / C 2 . Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы на k таковы, что при подстановке в уравнение единицы на зарядке (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.
Уравнение закона Кулона обеспечивает точное описание силы между двумя объектами, когда объекты действуют как точечных зарядов .Заряженная проводящая сфера взаимодействует с другими заряженными объектами так, как будто весь ее заряд находится в ее центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно рассматривать как центр сферы. Сфера действует как точечный заряд, избыточный заряд которого находится в центре. Поскольку закон Кулона применяется к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда для обоих объектов (а не расстояние между их ближайшими поверхностями).
Символы Q 1 и Q 2 в уравнении закона Кулона представляют собой количества заряда на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются в виде значений «+» или «-». Знак заряда просто показывает, есть ли в объекте избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект).Может возникнуть соблазн использовать знаки «+» и «-» при вычислении силы. Хотя такая практика не рекомендуется, в этом нет никакого вреда. При использовании знаков «+» и «-» в расчете силы результат будет таков, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, если Q 1 и Q 2 имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, если Q 1 и Q 2 имеют противоположный заряд — один — «+», а другой — «-». Это согласуется с концепцией, что противоположно заряженные объекты обладают притягивающим взаимодействием, а одноименные заряженные объекты — отталкивающим. В конце концов, если вы мыслите концептуально (а не просто математически), вы сможете определить природу силы — притягивающую или отталкивающую — без использования знаков «+» и «-» в уравнении.
Расчеты по закону Кулона В курсах физики закон Кулона часто используется как разновидность алгебраического рецепта для решения словесных задач физики. Здесь показаны три таких примера.
| Пример A Предположим, что два точечных заряда, каждый с зарядом +1,00 Кулона, разделены расстоянием 1.00 метр. Определите величину электрической силы отталкивания между ними. |
Это не самая сложная математическая задача, которую можно было выбрать. Он определенно был выбран не из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использоваться, чтобы проиллюстрировать ее полезность для решения любой проблемы закона Кулона.
Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме.Здесь мы знаем заряды двух объектов (Q 1 и Q 2 ) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о силе. Так что F elect — неизвестное количество. Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = 1.00 С | Найти: F избранный = ??? |
Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
F elect = k • Q 1 • Q 2 / d 2F elect = (9,0 x 10 9 Н • м 2 / C 2 ) • (1,00 C) • (1,00 C) / (1,00 м) 2
F избранный = 9,0 x 10 9 N
Сила отталкивания двух +1.00 кулоновских зарядов, находящихся на расстоянии 1 метра друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сопоставимая с массой более 2000 лайнеров.
Эта задача была выбрана в первую очередь из-за ее концептуального послания. Объекты просто не получают зарядов порядка 1,00 кулонов. Фактически, более вероятные значения Q составляют порядка 10 -9 или, возможно, 10 -6 кулонов. По этой причине греческий префикс часто используется перед кулоном в качестве единицы заряда. Заряд часто выражается в единицах микрокулонов (мкКл) и нанокулонов (нКл). Если проблема указывает заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в уравнение закона Кулона.Следующие эквиваленты единиц измерения помогут в таком преобразовании.
1 кулон = 10 6 микрокулон1 кулон = 10 9 нано-кулон
Стратегия решения проблем, использованная в примере A, включала три этапа:
- Определите и перечислите известную информацию в переменной форме.
- Перечислите неизвестную (или желаемую) информацию в переменной форме.
- Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию.(В некоторых случаях и для некоторых студентов может быть проще сначала выполнить алгебру, используя переменные, а затем выполнить замену в качестве последнего шага.)
Эта же стратегия решения проблем продемонстрирована в Пример B ниже.
| Пример B Два шара заряжаются одинаковым количеством и типом заряда: -6,25 нКл. Их разделяют на расстоянии 61.7 см. Определите величину электрической силы отталкивания между ними. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указано расстояние разделения (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестная величина — электрическая сила (F). Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = -6,25 нКл = -6,25 x 10 -9 С | Найти: F избранный = ??? |
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации.Эта подстановка и алгебра показаны ниже.
F elect = k • Q 1 • Q 2 / d 2F elect = (9,0 x 10 9 Н • м 2 / C 2 ) • (6,25 x 10 -9 C) • (6,25 x 10 -9 C) / (0,617 м) 2
F избранный = 9,23 x 10 -7 N
Обратите внимание, что знак «-» был удален из значений Q 1 и Q 2 до подстановки в уравнение закона Кулона.Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q 1 и Q 2 одинаково заряжены, и отрицательному значению силы, если Q 1 и Q 2 имеют противоположный заряд. Полученные знаки «+» и «-» на F обозначают, является ли сила притягивающей (значение «-» F) или отталкивающей (значение «+» F).
| Пример C Два шара с зарядом +3.37 мкКл и -8,21 мкКл притягивают друг друга с силой 0,0626 Ньютона. Определите расстояние между двумя воздушными шарами. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в микрокулонах (мкКл), будет выполнено преобразование в кулоны. В задаче также указывается электрическая сила (F). Неизвестная величина — это расстояние разделения (d). Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = +3,37 мкКл = +3,37 x 10 -6 ° С | Найти: d = ??? |
Как упоминалось выше, использование знаков «+» и «-» необязательно.Однако, если они используются, то они должны использоваться последовательно для значений Q и F. Их использование в уравнении проиллюстрировано в этой задаче.
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации. В этом случае сначала выполняется алгебра, а в последнюю — подстановка. Эта алгебра и подстановка показаны ниже.
F elect = k • Q 1 • Q 2 / d 2d 2 • F elect = k • Q 1 • Q 2
d 2 = k • Q 1 • Q 2 / F elect
d = SQRT (k • Q 1 • Q 2 ) / F elect
d = КОРЕНЬ [(9.0 x 10 9 Н • м 2 / C 2 ) • (-8,21 x 10 -6 C) • (+3,37 x 10 -6 C) / (-0,0626 Н)]
d = Sqrt [+3,98 м 2 ]
d = +1,99 м
Сравнение электрических и гравитационных силЭлектрическая сила и гравитационная сила — это две бесконтактные силы, обсуждаемые в учебном пособии по физике.Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирного тяготения.
Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделительным расстоянием. И оба уравнения показывают, что сила пропорциональна произведению количества, вызывающего силу, — заряда в случае электрической силы и массы в случае силы тяжести. Однако между этими двумя силами есть поразительные различия.Во-первых, сравнение констант пропорциональности — k и G — показывает, что постоянная закона Кулона (k) значительно больше, чем универсальная гравитационная постоянная Ньютона (G). Впоследствии единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы только притягивают; электрические силы могут быть как притягивающими, так и отталкивающими.
Обратное квадратичное соотношение между силой и расстоянием, вплетенное в уравнение, является общим для обеих бесконтактных сил.Эта взаимосвязь подчеркивает важность разделительного расстояния, когда речь идет об электрической силе между заряженными объектами. Этому и посвящен следующий раздел Урока 3.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения по закону Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащемуся исследовать влияние заряда и разделительного расстояния на величину электрической силы между двумя заряженными объектами.
Используйте свое понимание, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.
1. Q в уравнении закона Кулона обозначает _____.
а. масса заряженного объекта
г. # избыточных электронов на объекте
г. ток заряженного объекта
г. расстояние между заряженными объектами
e.заряд заряженного объекта
2. Символ d в уравнении закона Кулона обозначает расстояние от ___.
а. От A до B
г. От A до D
г.От B до C
г. От B до D
e. C по D
ф. От A до G
г. От B до F
ч. C по E
3.Определите электрическую силу притяжения между двумя воздушными шарами с отдельными зарядами +3,5 x 10 -8 C и -2,9 x 10 -8 C при разделении на расстояние 0,65 м.
4. Определите электрическую силу притяжения между двумя воздушными шарами, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд на воздушных шарах составляет 6,0 x 10 -7 C, и они разделены расстоянием 0.50 м.
5. Джоанна натерла шар шерстью, чтобы получить заряд -1,0 x 10 -6 C. Затем она достает пластиковую трубку для гольфа с зарядом +4,0 x 10 -6 C, локализованным в заданном месте. позиция. Она удерживает место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над воздушным шаром. Определите электрическую силу притяжения между трубкой для гольфа и воздушным шаром.
6. Баллон с зарядом 4,0 мкКл удерживают на расстоянии 0,70 м от второго баллона с таким же зарядом. Рассчитайте величину силы отталкивания.
7. На каком расстоянии разделения должны быть расположены два заряда размером 1,00 микрокулонов, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) 1.00-кг масса?
16.2: Кулоновская сила — Physics LibreTexts
Кулон был первым, кто дал подробное количественное описание силы между заряженными объектами. В настоящее время мы используем (производную) единицу СИ «кулон» (Кл) для обозначения заряда. «Заряд» объекта соответствует чистому избытку (или недостатку) электронов на объекте. Электрон имеет заряд \ (- е = -1.{19} \) электроны.
Путем тщательного изучения силы между двумя заряженными сферами Кулон обнаружил 1 , что:
- Сила притягивает, если объекты имеют противоположные заряды, и отталкивающая, если объекты имеют одинаковый заряд. {2}} \ hat r_ {21} \]
, где \ (\ hat r_ {21} \) — единичный вектор от \ (Q_2 \) до \ (Q_1 \), а \ (r \) — расстояние между двумя зарядами, как показано на рисунке \ (\ PageIndex {1} \).{-2} \) — более фундаментальная константа, как мы увидим в следующих главах.
Рисунок \ (\ PageIndex {1} \): Векторы, участвующие в применении закона Кулона.Если два заряда имеют позиции \ (\ vec r_1 \) и \ (\ vec r_2 \), соответственно, тогда вектор \ (\ hat r_ {21} \) задается следующим образом: \ [\ begin {align} \ hat r_ {21} = \ frac {\ vec r_2 — \ vec r_1} {|| \ vec r_2 — \ vec r_1 ||} \ end {align} \] Закон Кулона математически идентичен силе тяготения в Универсальной теории Ньютона гравитации. Вместо количества массы, определяющей силу гравитационной силы, именно количество заряда определяет силу электрической силы.Единственное существенное отличие состоит в том, что гравитация всегда притягивает, тогда как кулоновская сила может быть отталкивающей.
Упражнение \ (\ PageIndex {1} \)
Кулоновская сила консервативна.
- Верно.
- Ложь.
- Ответ
Произведение \ (Q_1Q_2 \) в числителе кулоновской силы положительно, если два заряда имеют одинаковый знак (как положительные, так и отрицательные), и отрицательное, если заряды имеют противоположные знаки.Снова обращаясь к рисунку \ (\ PageIndex {1} \), если два заряда положительны, сила на \ (Q_1 \) будет указывать в том же направлении, что и \ (\ hat r_ {21} \) (поскольку все скаляров положительны по закону Кулона) и поэтому отталкиваемы. Если вместо этого два заряда имеют противоположные знаки, произведение \ (Q_1Q_2 \) будет отрицательным, а вектор силы на \ (Q_1 \) будет указывать в противоположном направлении от \ (\ hat r_ {21} \) и сила притягательна.
Пример \ (\ PageIndex {1} \)
Вычислите величину электрической силы между электроном и протоном в атоме водорода и сравните ее с гравитационной силой между ними.{-47} \ text {N} \ end {align} \]
Обсуждение:
Как мы видим, электрическая сила между электроном и протоном на \ (39 \) порядков больше силы тяжести! Это показывает, что гравитационная сила чрезвычайно мала в масштабе частиц и практически не влияет на физику элементарных частиц. Действительно, лучшая современная теория физики элементарных частиц и наиболее точно проверенная теория в физике, «Стандартная модель», не обязательно должна включать гравитацию, чтобы обеспечить поразительно точное описание частиц.Тем не менее, одна из больших задач теоретической физики — разработать теорию, объединяющую гравитационную силу с другими силами.
Пример \ (\ PageIndex {2} \)
Три заряда, \ (Q_1 = 1 \ text {nC} \), \ (Q_2 = -2 \ text {nC} \) и \ (q = -1 \ text {nC} \), фиксируются на три угла равностороннего треугольника со сторонами длиной \ (a = 1 \ text {cm} \) с системой координат, показанной на рисунке \ (\ PageIndex {2} \). Каков вектор электрической силы заряда \ (q \)? (Обратите внимание, что \ (1 \ text {nC} = 1 \ times 10 ^ {- 9} \ text {C} \)).
Рисунок \ (\ PageIndex {2} \): Три заряда, расположенные в равностороннем треугольнике со стороной \ (a \).Решение :
Чистая электрическая сила, действующая на заряд \ (q \), будет векторной суммой сил от зарядов \ (Q_1 \) и \ (Q_2 \). Таким образом, нам нужно определить векторы силы на \ (q \) от каждого заряда, используя закон Кулона, а затем сложить эти два вектора, чтобы получить чистую силу на \ (q \). Векторы силы, действующие на \ (q \) от каждого заряда, показаны на рисунке \ (\ PageIndex {3} \).{-5} \ text {N} \).
Обсуждение:
В этом примере мы определили результирующую силу, действующую на заряд, используя принцип суперпозиции; а именно, что мы можем рассматривать силы, действующие на \ (q \) со стороны \ (Q_1 \) и \ (Q_2 \) независимо, без необходимости учитывать тот факт, что \ (Q_1 \) и \ (Q_2 \) действуют на друг с другом.
Кулоновская сила — обзор
4.1.4 Работа силы электростатического поля и потенциал электростатического поля
Кулоновские силы являются центральными и, следовательно, консервативными; поле этих сил является потенциальным (см. раздел 1.4.4, рисунок 1.29 и ур. (1.4.24)). Действительно, по определению элементарная работа dA силы F при перемещении dl определяется как: dA = F dl = qE dl = qE dl cos α , где E = Q /4 πε 0 r 2 и dl cos α = dr. Тогда dA = qQdr /4 πε 0 r 2 и A 12 = ( qQ /4 πε 0 ) ∫r1r2dr / r2.Следовательно,
A12 = qQ4πɛ0 (1r1-1r2),
т.е. работа фактически зависит не от пройденного расстояния, а от r 1 и r 2 , радиус-векторов исходных и заключительные моменты. Если заряд, начавший с начальной точки, возвращается к нему, то работа электростатических сил равна нулю: A = q ∫ L E l dl = 0, где E l = E cos α — проекция вектора E на вектор смещения d l .Тогда ∮LEldl = 0: циркуляция напряженности электростатического поля по замкнутой траектории равна нулю. Это определение потенциального характера силового поля.
Из уравнения ∮LEldl = 0 следует, что силовые линии электростатического поля не могут быть замкнуты (в противном случае при положительном обходе интеграл был бы по существу положительным). Они начинаются с положительных зарядов и заканчиваются отрицательными зарядами (или уходят в бесконечность).
Работу сил электростатического поля можно представить как уменьшение потенциальной энергии, A = U 1 — U 2 = — Δ U .Из сравнения этого уравнения с приведенным выше, потенциальная энергия заряда q в поле другого заряда Q может быть записана как U = ( qQ / 4π ε 0 r ) + C. Если принять, что при r = ∞ потенциальная энергия U (∞) равна нулю, тогда C = 0 и в итоге потенциальная энергия равна
(4.1.21) U = qQ4πɛ0r.
Электростатический потенциал φ — это величина, численно равная потенциальной энергии единичного положительного точечного заряда, помещенного в данную точку поля.Тогда
(4.1.22) φ = Uq.
Следовательно, потенциал точечного заряда равен
(4.1.23) φ = Q4πɛ0r.
Так как U = qφ , то
(4.1.24) A12 = U1-U2 = q (φ1-φ2) = — qΔφ.
Если принять φ (∞) = 0, то A 1∞ = qφ 1 ; следовательно, φ 1 = A 1 ∞ / q . Это означает, что потенциал численно равен работе силы, совершаемой при перемещении единичного положительного точечного заряда из данной точки на бесконечность.
Потенциал поля — это скалярная характеристика мощности электростатического поля. Потенциал поля, созданного системой неподвижных зарядов, подчиняется принципу суперпозиции, то есть каждый заряд создает поле независимо от присутствия других зарядов в пространстве . Поскольку потенциал — это скалярная величина, потенциал в любой точке поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых каждым зарядом в отдельности:
(4.1.25) φ (r) = Σi = 1Nφi (r),
, где N — общее количество зарядов.
С точки зрения распределения потенциала электростатическое поле может быть графически охарактеризовано поверхностями с равным потенциалом, то есть эквипотенциальными поверхностями с φ = константа (рисунок 4.13). Силовые линии всегда перпендикулярны им.
Рисунок 4.13. Силовые линии и эквипотенциальные поверхности.
Поскольку напряженность электрического поля E ( r ) и потенциал φ ( r ) являются функциями радиуса-вектора точки r, между ними должна быть взаимосвязь.Давайте найдем это. Элементарная работа полевой силы может быть определена как dA = F dl = qE dl или dA = — dU = — q dφ . Сравнивая их, можно прийти к E l = — dφ / dl .
Если поле создается сферически симметричным зарядом, E и φ оба зависят от r ; поэтому
(4.1.26) Er (r) = — dφ (r) dr.
В случае линейной зависимости
(4.1.27) Ex (x) = — dφ (x) dx.
В общем случае r ( x , y , z ), E ( r ) и φ ( r ) связаны между собой посредством
(4.1.28 ) E (r) = — (dφdxi + dφdyj + dφdzk) = — grad φ (r),
т.е. напряженность электростатического поля равна градиенту потенциала электрического поля, взятому с противоположным знаком. Видно, что вектор напряженности поля всегда перпендикулярен эквипотенциальным поверхностям (рис. 4.13).
Из ур. (4.1.26) — (4.1.28), что функция φ ( r ) не может быть разрывной функцией. Фактически, если функция терпит разрыв (например, в точке x 0 ), то согласно ур. (4.1.27),
E (x0) = limΔx → 0ΔφΔx → ∞,
, так как в этой точке Δ x → 0, но Δ φ стремится к конечной разности; это означает, что E ( x 0 ) равно бесконечности. Этого не может быть.
Установленная связь между напряженностью электростатического поля и потенциалом позволяет найти зависимость φ ( r ), зная функцию E ( r ) для всех рассмотренных выше примеров. Фактически, это следует из ур. (4.1.26) и (4.1.27) следует, что
φ (r) = — ∫E (r) dr + C
и
φ (x) = — ∫E (x) dx + C.
Подставив сюда уже известные функции E ( r ) и E ( x ), мы можем вычислить функции φ ( r ) и φ ( x ).Константа C отражает тот факт, что функция φ , а также потенциальная энергия, как известно, находятся в пределах константы; его можно найти из граничных условий. Выбор C может обеспечить непрерывность функции φ . Таким образом, потенциал рассматриваемых проблем может быть получен. Соответствующие графики изображены на рисунках 4.6, 4.7, 4.9–4.11.
Для расчета разности потенциалов Δ φ интегрирование следует проводить в определенных пределах.Так, например, разность потенциалов в плоском конденсаторе составляет
Δφ = -∫0dE (x) dx = -E∫0ddx = -Ed,
, где d — расстояние между пластинами.
Обратная задача (зная φ , вычислить E ) также может быть получена. Этот метод будет использоваться, например, при вычислении электрического дипольного поля (поскольку вычисление потенциала проще, чем вычисление напряженности поля, поскольку первое является скалярным значением, а второе имеет векторное качество).
Кулоновская сила — обзор
3.1 Эффекты, индуцированные неоднородным электрическим полем
В однородном электрическом поле кулоновские силы генерируются с обеих сторон нейтральной частицы. Дипольный момент, индуцированный в частице, может быть представлен двумя равными и противоположными зарядами (δ + и δ — ) на границе частицы, что приводит к нулевой результирующей силе на частицу. Однако, когда электрическое поле неоднородно, неравные поля, действующие с каждой стороны, создают силу, называемую диэлектрофоретической силой (DEP), направленную вдоль градиента электрического поля, которая толкает нейтральное тело в область более сильного (положительный DEP) или более слабого электрическое поле (отрицательный DEP).Диэлектрофоретическое движение нейтрального тела, подвешенного в среде, показано на рисунке 16, на котором сигнал переменного тока, приложенный между пластиной и острием электрода, используется для создания неоднородного электрического поля.
Рис. 16. Направление нейтральной частицы в неоднородных электрических полях в зависимости от реакции диэлектрофореза: (а) положительный DEP и (b) отрицательный DEP.
До и Чо (2005). С разрешения.В случае идеального диэлектрического шара, подвешенного в среде (здесь жидкость) и подверженного неоднородному электрическому полю E , диэлектрофоретическая сила F → DEP может быть записана как:
(8) F → DEP = 2πε0εmr3Re [ fCM] ∇E2
, где r — радиус сферической частицы, ε 0 — диэлектрическая проницаемость вакуума (8.854 × 10 −12 Кл / В м), ε м — относительная диэлектрическая проницаемость среды, а f CM — эффективная поляризуемость. Эффективная поляризуемость — это комплексная переменная, известная как фактор Клаузиуса-Моссотти. Это зависит от электрических свойств частицы и окружающей среды, а также от частоты f приложенного переменного тока. В случае сферической частицы с диэлектрической проницаемостью ε p и электропроводностью σ p , подвешенной в среде с диэлектрической проницаемостью ε м и проводимостью σ м , эффективная поляризуемость равна определяется по формуле:
(9) fCM = εp ∗ −εm ∗ εp ∗ + 2εm ∗
, где ε ∗ — комплексная диэлектрическая проницаемость, выражаемая как: ε ∗ = ε0ε + iσω; с i : мнимым вектором (i = −1) и ω : угловой частотой A.Поле C. ( ω = 2π f ). Коэффициент поляризуемости определяет, является ли сила DEP на частице положительной (притягивающей) или отрицательной (отталкивающей), рис. 16. Теоретически его значение может находиться в диапазоне от -0,5 до +1,0 (Pethig and Markx, 1997; Khoshmanesh et al., 2011) . Из этого уравнения видно, что для низких частот эффективная поляризуемость в основном зависит от электропроводности, тогда как на высоких частотах влияние диэлектрической проницаемости становится доминирующим.Это означает, что частицы могут испытывать положительную или отрицательную силу DEP в одной и той же системе в зависимости от частоты приложенного сигнала переменного тока.
Для высоких частот или при незначительной электропроводности жидкости диэлектрофорезная сила увеличивается с увеличением разницы между диэлектрической проницаемостью частицы и жидкости. Когда диэлектрическая проницаемость частицы больше средней ( ε p > ε m ), частица мигрирует в направлении области сильного поля (положительная DEP).Действительно, асимметричные силы поля ускоряют движение частицы больше, чем жидкость, концентрируя ее в самом высоком поле (Ballantyne and Holtham, 2010). Напротив, частицы с диэлектрической проницаемостью ниже средней ( ε m > ε p ) выталкиваются в область наименьшей напряженности поля. Диэлектрическая проницаемость (также называемая диэлектрической постоянной или поляризуемостью) некоторых жидкостей, минералов, керамики и пластиков представлена Лином и Бенгиги (1983) и Баллантайном и Холтхэмом (2010).
В то время как действительная часть фактора Клаузиуса-Моссотти Re [ f CM ] определяет диэлектрофоретическую силу, мнимая часть Im [ f CM ] определяет диэлектрофоретическую силу бегущей волны (TW-DEP). Эта сила существует только тогда, когда электрическое поле имеет градиент фазы. Соответствующая диэлектрофоретическая сила бегущей волны определяется выражением (Khoshmanesh et al., 2011):
(10) F → TW-DEP = −4πε0εmr3Im [fCM] E2λTW
, где λ TW — длина бегущей волны. электрическое поле величиной, равной повторяющемуся расстоянию между электродами одной фазы.
ROCO Глава 4: Электростатический потенциал
Электростатический потенциал
Электростатика — это часть физики, которая описывает взаимодействия между стационарными зарядами. Вы наверное знакомы с законом Кулона, центральным законом электростатики. Этот Закон гласит, что две заряженные частицы действуют друг на друга равно:
F = q 1 q 2 / r 12 2
Электростатическая сила F пропорциональна произведение зарядов двух частиц, q 1 и q 2 , и обратно пропорционально квадрату расстояния, разделяющего частицы, r 12 .
Еще одна важная характеристика заряженной системы — его потенциальная энергия, ПЭ. Потенциальная энергия создается электростатическим взаимодействия между заряженными частицами и равно:
PE = q 1 q 2 / r 12
Обратите внимание, что эта формула выглядит почти так же, как Закон Кулона. Единственная разница в том, что потенциальная энергия обратно пропорционально расстоянию между зарядами, а кулоновская сила обратно пропорциональна квадрату расстояния.
Самым полезным количеством для наших целей является электростатический разряд . потенциал. Эта величина относится к PE следующим образом: электростатический потенциал, создаваемый системой зарядов в определенной точке пространство, ( x, y, z ), равно изменению потенциальной энергии это происходит, когда в этот момент вводится +1 ион.
Это определение можно прояснить с помощью следующие картинки.Представьте себе молекулу, состоящую из электрона. облако плотности и несколько положительно заряженных ядер. Мы могли бы представлять молекула из мультфильма:
Теперь предположим, что мы хотим узнать электростатический потенциал. эта молекула создает в точке ( x, y, z ). Мы можем получить потенциал, введя заряд +1 в ( x, y, z ) и вычислив изменение энергии. Новое изображение выглядит так:
Изменение энергии — это просто потенциальная энергия создается взаимодействием между зарядом +1 и зарядами в молекула.Мы можем вычислить эту энергию, вычислив (+1) (q молекула ) / r для каждого заряда в молекуле, q молекулы , и добавление поднять все эти энергии. Эта энергия является электростатической энергией молекулы. потенциал.
Электростатический потенциал является одновременно молекулярным свойством. и пространственное свойство. Это зависит от того, какие сборы существуют в молекулы и как они там распределяются. Это также зависит от какую точку (x, y, z) мы выбираем для исследования.Если мы выберем точка, в которой заряд +1 притягивается молекулой, потенциал будет отрицательным в этот момент. С другой стороны, если мы выберем точка, в которой отталкивается заряд +1, потенциал будет положительным.
Молекулы содержат много заряженных частиц, ядер и электронов, и суммарное воздействие этих частиц на +1 «зонд» может быть определен только компьютером. Однако, поскольку мы знаем, что потенциальная энергия и расстояние обратно связаны, вероятно что заряд (ы) молекулы, ближайший к +1 частице, имеет самый большой эффект.
Например, на следующей диаграмме показан ионный соединение, состоящее из трех ионов. Вполне вероятно, что потенциал в непосредственной близости от каждого иона во многом определяется этим ion, а более удаленные ионы имеют относительно небольшой эффект. На с другой стороны, потенциал в любой области, близкой к двум или большее количество ионов должно быть определено тщательным расчетом.
В синих регионах потенциал большой и положительный, и большой и отрицательный в розовой области.
Такое поведение наблюдается практически во всех система. Положительные частицы, такие как атомные ядра или многоатомные катионы, окружены регионами с положительным потенциалом. Точно так же отрицательный частицы, как и многоатомные анионы, окружены областями отрицательный потенциал. На нескольких страницах я покажу вам, как использовать электростатический потенциалы, чтобы сделать качественные утверждения об атомных зарядах. Когда я это сделаю, я буду предполагать, что потенциал в данной области контролируется «локальным» атомом, поэтому положительный потенциал будет указывать на положительно заряженный «локальный» атом и отрицательный потенциал укажет на отрицательно заряженный «местный» атом.
Определение кулоновской силы в физике.
Примеры кулоновской силы в следующих темах:
Нервная проводимость и электрокардиограммы
- Диффузия K + и Cl-, таким образом, создает слои положительного и отрицательного заряда снаружи и внутри мембраны, а сила Кулона , сила предотвращает диффузию ионов через всю их целостность.
- Результат — два слоя заряда прямо на мембране, при этом диффузия уравновешивается силой Кулона силы .
- Таким образом, мембрана временно становится проницаемой для Na +, который затем устремляется внутрь под действием как диффузии, так и кулоновской силы .
- Это пример активного транспорта, при котором энергия клетки используется для перемещения ионов через мембраны против градиентов диффузии и кулоновской силы .
- Диффузия перемещает ионы K + и Cl- в показанном направлении до тех пор, пока кулоновская сила не остановит дальнейший перенос.
Сферическое распределение заряда
- Математическая формула для электростатической силы называется законом Кулона в честь французского физика Шарля Кулона (1736–1806), который провел эксперименты и первым предложил формулу для ее расчета.
- Современные эксперименты подтвердили закон Кулона с большой точностью.
- Закон Кулона выполняется даже внутри атомов, правильно описывая силу между положительно заряженным ядром и каждым из отрицательно заряженных электронов.
- Электрическое поле — это векторное поле, которое связывает с каждой точкой пространства кулоновскую силу , которая испытывает испытательный единичный заряд.
- Опишите форму Кулон силы от сферического распределения заряда
Величина магнитной силы
- Магнитные поля действуют сил на движущиеся заряды, и поэтому они воздействуют на другие магниты сил , все из которых имеют движущиеся заряды.
- Магнитная сила так же важна, как электростатическая или кулоновская сила .
- Тем не менее, магнитная сила более сложна как по количеству факторов, влияющих на нее, так и по ее направлению, чем относительно простая кулоновская сила .
- Магнитные поля действуют на движущиеся заряды сил .
- Эта сила — одна из самых основных известных.
Суперпозиция сил
- Принцип суперпозиции (свойство суперпозиции) утверждает, что для всех линейных сил общая сила является векторной суммой отдельных сил .
- Для закона Кулона стимулы составляют сил и .
- Следовательно, принцип предполагает, что общая сила является векторной суммой отдельных сил .
- Скалярная форма закона Кулона связывает величину и знак электростатической силы F, действующей одновременно на два точечных заряда q1 и q2:
- Принцип линейной суперпозиции позволяет расширить закон Кулона , чтобы включить любое количество точечных зарядов, чтобы получить силу на любой точечный заряд путем векторного сложения этих отдельных сил , действующих в одиночку на эту точку плата.
Сила рассеивания
- Эти межмолекулярные силы также иногда называют «индуцированным дипольным диполем» или «мгновенным диполем» сил .
- Лондонская дисперсия сил является частью ван-дер-Ваальсовых сил , или слабого межмолекулярного притяжения. 2} $ r +.
- Закон Кулона с использованием векторов можно записать как:
- Общая сила на поле заряда q возникает из-за приложения силы , описанной в векторной записи закона Кулона , от каждого заряда источника.
- Закон Кулона применялся к более чем одному заряду точечного источника, обеспечивая сил на полевой заряд.
- Объясните, когда можно использовать векторные обозначения закона Кулона
Ядерный синтез
- Происхождение энергии, выделяющейся при слиянии легких элементов, происходит из-за взаимодействия двух противостоящих сил : ядерной силы , которая сближает протоны и нейтроны, и кулоновской силы , которая заставляет протоны отталкиваться. друг с другом.
- Эта сила , называемая сильной ядерной силой , преодолевает электрическое отталкивание на очень близком расстоянии.
- Влияние ядерной силы не наблюдается вне ядра, следовательно, сила сильно зависит от расстояния; Это ближний усилие .
- Ядерная сила , сильнее, чем Кулоновская сила , , для атомных ядер, меньших, чем железо, поэтому создание этих ядер из более легких ядер путем синтеза высвобождает дополнительную энергию от чистого притяжения этих частиц.
- На расстояниях между ядрами ядерная сила притяжения сильнее, чем отталкивающая электростатическая сила .
Свойства электрических зарядов
- Его единица СИ известна как Кулон (C), что представляет 6,242 × 1018e, где e — заряд протона.
- Электрический заряд — это свойство, которое создает сил , которые могут притягивать или отталкивать материю.
- Это известно как закон Кулона .
- Формула для гравитационной силы имеет точно такую же форму, что и закон Кулона , но связывает произведение двух масс (а не зарядов) и использует другую константу.
- Сумма сил (F1 и F2) дает общую силу , которая рассчитывается по закону Кулона и пропорциональна произведению зарядов q1 и q2 и обратно пропорциональна квадрату расстояния ( r21) между ними.
Напряжение и деформация
- Точечный заряд создает электрическое поле, которое можно рассчитать с помощью закона Кулона .
- Эффект ощущается как сила , и когда заряженные частицы не движутся, эта сила известна как электростатическая сила .
- Электростатическая сила , как и сила тяжести, сила , действующая на расстоянии.
- Если испытательный заряд был отрицательным, сила , ощущаемая на этом заряде, составляла бы
- Вышеупомянутое математическое описание электрического поля точечного заряда известно как закон Кулона .
Электрическое поле точечного заряда
- Точечный заряд создает электрическое поле, которое можно рассчитать с помощью закона Кулона .
- Эффект ощущается как сила , и когда заряженные частицы не движутся, эта сила известна как электростатическая сила .
- Электростатическая сила , как и сила тяжести, сила , действующая на расстоянии.
- Если испытательный заряд был отрицательным, сила , ощущаемая на этом заряде, составляла бы:
- Вышеприведенное математическое описание электрического поля точечного заряда известно как закон Кулона .



