Сила Кориолиса — Википедия
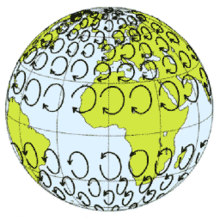
При вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Переместить тело вдоль радиуса так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б») можно, увеличив скорость тела, то есть придав ему ускорение. Если система отсчёта вращается вместе с диском, то видно, что тело «не хочет» оставаться на радиусе, а «пытается» уйти влево — с точки зрения наблюдателя во вращающейся системе отсчёта это результат действия силы Кориолиса. Траектории шарика при движении без трения по поверхности вращающейся тарелки в разных системах отсчёта (вверху — в инерциальной по прямой, внизу — в неинерциальной, вращающейся вместе с тарелкой).
Траектории шарика при движении без трения по поверхности вращающейся тарелки в разных системах отсчёта (вверху — в инерциальной по прямой, внизу — в неинерциальной, вращающейся вместе с тарелкой).Си́ла Кориоли́са — одна из сил инерции, использующаяся при рассмотрении движения материальной точки относительно вращающейся системы отсчёта. Добавление силы Кориолиса к действующим на материальную точку физическим силам позволяет учесть влияние вращения системы отсчёта на такое движение
Названа по имени французского учёного Гаспа́ра-Гюста́ва де Кориоли́са, впервые описавшего её в статье, опубликованной в 1835 году[2][3]. Иногда высказываются мнения, что первым математическое выражение для силы получил Пьер-Симон Лаплас в 1775 году[4], а эффект отклонения движущихся объектов во вращающихся системах отсчёта был описан Джованни Баттиста Риччоли и Франческо Мария Гримальди в 1651 году[5].
Часто под термином «эффект Кориолиса» подразумевается наиболее важный случай проявления силы Кориолиса — который возникает в связи с суточным вращением Земли.
Так как угловая скорость вращения Земли мала (1 оборот в день), эта сила, как правило, мала по сравнению с другими силами.
Эффекты обычно становятся заметными только для движений, происходящих на больших расстояниях при длительных периодах времени, таких как крупномасштабное движение воздуха атмосферы (вихреобразные циклоны) или воды в океане (Гольфстрим). Такие движения, как правило, происходят вдоль поверхности Земли, поэтому для них часто важна только горизонтальная составляющая силы Кориолиса. Она заставляет движущиеся вдоль поверхности Земли объекты отклоняться вправо (по отношению к направлению движения) в северном полушарии и влево в южном. Эффект горизонтального отклонения сильнее близ полюсов, так как эффективная скорость вращения вокруг локальной вертикальной оси значительнее там и уменьшается до нуля у экватора
Если в какой-либо инерциальной системе отсчёта материальная точка (МТ) равномерно движется вдоль радиуса, равномерно вращающегося вокруг перпендикулярной к нему оси, и её скорость направлена в сторону от центра вращения, то при этом вместе с увеличением расстояния от центра вращения возрастает и компонента скорости тела, направленная перпендикулярно радиусу. Значит, в данном случае компонента ускорения точки, перпендикулярная радиусу, отлична от нуля. Эта компонента ускорения МТ в инерциальной системе отсчёта и представляет собой
При рассмотрении того же самого движения в неинерциальной системе отсчёта, вращающейся вместе с радиусом, наблюдаемая картина будет другой. Действительно, в этой системе отсчёта скорость МТ не изменяется и, соответственно, компонента её ускорения , перпендикулярная радиусу, равна нулю. Значит, движение выглядит так, как будто во вращающейся системе отсчёта на МТ действует дополнительная сила, направленная противоположно ускорению Кориолиса и компенсирующая его. Эта дополнительная «сила», вводимая для удобства описания движения, но в действительности отсутствующая, и есть сила Кориолиса. Понятно, что данная «сила» позволяет учесть влияние вращения подвижной системы отсчёта на относительное движение МТ, но при этом никакому реальному взаимодействию МТ с другими телами не соответствует.
Более строго — ускорение Кориолиса есть удвоенное векторное произведение вектора угловой скорости вращения системы координат на вектор скорости движения МТ относительно вращающейся системы координат[6]. Соответственно, сила Кориолиса равна произведению массы МТ на её ускорение Кориолиса, взятому со знаком минус[1].
Пусть имеются две системы отсчёта, одна из которых (S){\displaystyle (S)} инерциальная, а другая (S′){\displaystyle \left(S\,’\right)} движется относительно первой произвольным образом и в общем случае является неинерциальной. Будем также рассматривать движение произвольной материальной точки массы m{\displaystyle m}. Её ускорение по отношению к первой системе отсчёта обозначим a→a{\displaystyle {\vec {a}}_{a}}, а по отношению ко второй — a→r{\displaystyle {\vec {a}}_{r}}.
Связь между ускорениями a→a{\displaystyle {\vec {a}}_{a}} и a→r{\displaystyle {\vec {a}}_{r}} следует из теоремы Кориолиса (см. ниже):
- a→a=a→r+a→e+a→K,{\displaystyle {\vec {a}}_{a}={\vec {a}}_{r}+{\vec {a}}_{e}+{\vec {a}}_{K},}
где a→e{\displaystyle {\vec {a}}_{e}} — перено́сное ускорение, а a→K{\displaystyle {\vec {a}}_{K}} — ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы S′{\displaystyle S\,’} относительно системы S{\displaystyle S}, в которой в данный момент находится рассматриваемая материальная точка
После умножения на массу точки и учёта второго закона Ньютона ma→a=F→{\displaystyle m{\vec {a}}_{a}={\vec {F}}}, данное соотношение можно представить в виде
- ma→r=F→+(−ma→e)+(−ma→K).{\displaystyle m{\vec {a}}_{r}={\vec {F}}+(-m{\vec {a}}_{e})+(-m{\vec {a}}_{K}).}
Величину (−ma→e){\displaystyle (-m{\vec {a}}_{e})} называют переносной силой инерции, а величину (−ma→K){\displaystyle (-m{\vec {a}}_{K})} — силой Кориолиса (кориолисовой силой). Обозначив их F→e{\displaystyle {\vec {F}}_{e}} и F→K{\displaystyle {\vec {F}}_{K}} соответственно, можно записать
- ma→r=F→+F→e+F→K.{\displaystyle m{\vec {a}}_{r}={\vec {F}}+{\vec {F}}_{e}+{\vec {F}}_{K}.}
Полученное выражение выражает основной закон динамики для неинерциальных систем отсчёта.
Из кинематики известно, что
- a→K=2[ω→×v→r],{\displaystyle {\vec {a}}_{K}=2\left[{\vec {\omega }}\times {\vec {v}}_{r}\right],}
где ω→{\displaystyle {\vec {\omega }}} — угловая скорость вращения неинерциальной системы отсчёта S′{\displaystyle S\,’}, v→r{\displaystyle {\vec {v}}_{r}} — скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется
- F→K=−2m[ω→×v→r].{\displaystyle {\vec {F}}_{K}=-2\,m\,\left[{\vec {\omega }}\times {\vec {v}}_{r}\right].}
Замечания
- Следует иметь в виду, что, согласно принятой в русскоязычной литературе терминологии, кориолисово ускорение материальной точки — это часть её ускорения в инерциальной системе отсчёта S{\displaystyle S}[6][8]. Этим оно отличается, например, от центробежного ускорения, возникающего в неинерциальной системе отсчёта S′{\displaystyle S\,’}.
- В иноязычной литературе встречается альтернативное определение кориолисового ускорения с противоположным знаком: a→K≡−2[ω→×v→r]{\displaystyle {\vec {a}}_{K}\equiv -2\left[{\vec {\omega }}\times {\vec {v}}_{r}\right]}. В таком случае кориолисово ускорение и кориолисова сила оказываются связаны соотношением: a→K=FKm{\displaystyle {\vec {a}}_{K}={\frac {F_{K}}{m}}}
Пусть точка совершает сложное движение: движется относительно неинерциальной системы отсчёта S′{\displaystyle S\,’} со скоростью v→r{\displaystyle {\vec {v}}_{r}} ; система S′{\displaystyle S\,’} при этом сама движется относительно инерциальной системы координат S{\displaystyle S} , причём линейная скорость движущегося в трёхмерном пространстве произвольным образом мгновенного центра скоростей O{\displaystyle O} равна v→0{\displaystyle {\vec {v}}_{0}}, а угловая скорость вращения системы S′{\displaystyle S\,’} относительно мгновенного центра скоростей равна ω→{\displaystyle {\vec {\omega }}}. Мгновенный центр скоростей находится с помощью теоремы вращения Эйлера.
Тогда абсолютная скорость рассматриваемой точки (то есть её линейная скорость в инерциальной системе координат) будет такой:
- v→=v→0+[ω→×R→]+v→r{\displaystyle {\vec {v}}={\vec {v}}_{0}+\left[{\vec {\omega }}\times {\vec {R}}\right]+{\vec {v}}_{r}} , причём ddtR→=[ω→×R→]+v→r{\displaystyle {\frac {d}{dt}}{\vec {R}}=\left[{\vec {\omega }}\times {\vec {R}}\right]+{\vec {v}}_{r}} ,
где R→{\displaystyle {\vec {R}}} — радиус-вектор точки относительно мгновенного центра скоростей O{\displaystyle O} . Первые два слагаемых в правой части равенства представляют собой переносную скорость точки, а последнее — её относительную скорость.
Продифференцируем это равенство по времени:
- ddtv→=ddtv→0+ddt[ω→×R→]+ddtv→r.{\displaystyle {\frac {d}{dt}}{\vec {v}}={\frac {d}{dt}}{\vec {v}}_{0}+{\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]+{\frac {d}{dt}}{\vec {v}}_{r}.}
Найдём значение каждого слагаемого в инерциальной системе координат:
- ddtv→0=a→0,{\displaystyle {\frac {d}{dt}}{\vec {v}}_{0}={\vec {a}}_{0},}
- ddt[ω→×R→]=[ε→×R→]+[ω→×ddtR→]=[ε→×R→]+[ω→×[ω→×R→]]+[ω→×v→r],{\displaystyle {\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\frac {d}{dt}}{\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+{\biggl [}{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]{\biggr ]}+\left[{\vec {\omega }}\times {\vec {v}}_{r}\right],}
- ddtv→r=[ω→×v→r]+dr v→rdt,{\displaystyle {\frac {d}{dt}}{\vec {v}}_{r}=\left[{\vec {\omega }}\times {\vec {v}}_{r}\right]+{\frac {{\stackrel {~}{d_{r}}}{\vec {v}}_{r}}{dt}},}
где a→r=dr v→rdt{\displaystyle {\vec {a}}_{r}={\frac {{\stackrel {~}{d_{r}}}{\vec {v}}_{r}}{dt}}} — линейное ускорение точки относительно системы S′{\displaystyle S\,’} , ε→=dω→dt{\displaystyle {\vec {\varepsilon }}={\frac {d{\vec {\omega }}}{dt}}} — угловое ускорение системы S′{\displaystyle S\,’} .
Таким образом, имеем:
- ddtv→=a→=a→0+[ε→×R→]+[ω→×[ω→×R→]]+a→r+2[ω→×v→r].{\displaystyle {\frac {d}{dt}}{\vec {v}}={\vec {a}}={\vec {a}}_{0}+\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+{\biggl [}{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]{\biggr ]}+{\vec {a}}_{r}+2\left[{\vec {\omega }}\times {\vec {v}}_{r}\right].}
Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного 2[ω→×v→r]{\displaystyle 2\left[{\vec {\omega }}\times {\vec {v}}_{r}\right]} .
Используя обозначения a→e=a→0+[ε→×R→]+[ω→×[ω→×R→]]{\displaystyle {\vec {a}}_{e}={\vec {a}}_{0}+\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+{\biggl [}{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]{\biggl ]}} и a→K=2[ω→×v→r]{\displaystyle {\vec {a}}_{K}=2\left[{\vec {\omega }}\times {\vec {v}}_{r}\right]}, получим запись теоремы Кориолиса в более сжатом виде:
- a→a=a→e+a→r+a→K.{\displaystyle {\vec {a}}_{a}={\vec {a}}_{e}+{\vec {a}}_{r}+{\vec {a}}_{K}.}
Сам Кориолис выражал в 1835 г. свои результаты в иной форме, вводя в рассмотрение переносную и кориолисову силы инерции; общепринятая же ныне чисто кинематическая формулировка теоремы Кориолиса предложена в 1862 г. Анри Эме Резалем[13].
Заметим, что в частном случае вращательного движения инерциальной системы отсчёта относительно начала координат для того, чтобы точка относительно неинерциальной системы отсчёта двигалась прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к ней силу, которая будет противодействующей суммы силы Кориолиса −2m[ω→×v→r]{\displaystyle -2m\left[{\vec {\omega }}\times {\vec {v}}_{r}\right]} , переносной вращательной силы −m[ε→×R→]{\displaystyle -m\left[{\vec {\varepsilon }}\times {\vec {R}}\right]} и переносной силы инерции поступательного движения системы отсчёта −ma→0{\displaystyle -m{\vec {a}}_{0}} . Составляющая же ускорения [ω→×[ω→×R→]]{\displaystyle \left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]} не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение [ω→×[ω→×R→]]+a→r=0{\displaystyle \left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]+{\vec {a}}_{r}=0}, которое если умножить векторно на R→{\displaystyle {\vec {R}}}, то с учётом [R→×[ω→×[ω→×R→]]]=0{\displaystyle \left[{\vec {R}}\times \left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]\right]=0} получим относительно v→r{\displaystyle {\vec {v}}_{r}} дифференциальное уравнение [R→×dr v→rdt]≡0{\displaystyle \left[{\vec {R}}\times {\frac {{\stackrel {~}{d_{r}}}{\vec {v}}_{r}}{dt}}\right]\equiv 0}, имеющее при любых R→{\displaystyle {\vec {R}}} и v→r{\displaystyle {\vec {v}}_{r}} общим решением [R→×v→r]=Const→{\displaystyle \left[{\vec {R}}\times {\vec {v}}_{r}\right]={\vec {Const}}}, которое и является уравнением такой прямой — [R→×v→r]=0→{\displaystyle \left[{\vec {R}}\times {\vec {v}}_{r}\right]={\vec {0}}} .
Правило Жуковского[править | править код]
Н. Е. Жуковский предложил удобный способ нахождения кориолисова ускорения:
Ускорение Кориолиса a→K{\displaystyle {\vec {a}}_{K}} можно получить, спроецировав вектор относительной скорости точки v→{\displaystyle {\vec {v}}} на плоскость, перпендикулярную вектору переносной угловой скорости ω→{\displaystyle {\vec {\omega }}}, увеличив полученную проекцию в 2ω{\displaystyle \ 2\omega } раз и повернув её на 90 градусов в направлении переносного вращения.
Физический смысл[править | править код]
Пусть точка движется со скоростью v→{\displaystyle {\vec {v}}} вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).
Тогда данное движение приведёт к изменению расстояния до центра вращения R{\displaystyle \ R} и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой — её переносной скорости.
Как мы знаем, эта скорость движения равна
- v→e=[ω→×R→].{\displaystyle {\vec {v}}_{e}=\left[{\vec {\omega }}\times {\vec {R}}\right].}
Данное изменение будет равно:
- dv→e=[ω→×dR→].{\displaystyle d{\vec {v}}_{e}=\left[{\vec {\omega }}\times d{\vec {R}}\right].}
Проведя дифференцирование по времени, получим
- a→=[ω→×v→].{\displaystyle {\vec {a}}=\left[{\vec {\omega }}\times {\vec {v}}\right].}
(Направление данного ускорения перпендикулярно ω→{\displaystyle {\vec {\omega }}} и v→{\displaystyle {\vec {v}}}).
С другой стороны, вектор v→{\displaystyle {\vec {v}}} для точки, остающейся неподвижной относительно инерциального пространства, повернётся относительно неинерциального на угол ωdt{\displaystyle \omega dt}. Или приращение скорости будет
- dvr=vsinωdt=v
|
При движении тела относительно вращающейся системы отсчета, кроме центростремительной и центробежной сил, появляется еще одна
сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик).
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 4.10). Рис. 4.10 Запустим в направлении от О к А шарик со скоростью . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила , перпендикулярная направлению движения шарика. Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета. Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска), шарик движется с постоянной по направлению скоростью. Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции:
Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу. Таким образом, всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании явлений, связанных с движением тел относительно земной поверхности. Например, при свободном падении тел на них действует кориолисова сила, обусловливающая отклонение к востоку от линии отвеса. Эта сила максимальна на экваторе и обращается в нуль на полюсах. Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции. Например, при выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в восточном направлении. Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 4.11).Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей. Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты предположим, что маятник расположен на полюсе (рис. 4.12). На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки. Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так: плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот.Таким образом, вращение плоскости качаний маятника Фуко дает непосредственное доказательство вращения Земли вокруг своей оси. Если тело удаляется от оси вращения, то сила направлена противоположно вращению и замедляет его.Если тело приближается к оси вращения, то направлена в сторону вращения. С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета (4.5.6) примет вид:
|
7
Вопрос 7. Неинерциальные системы отсчета. Силы инерции, понятие о принципе эквивалентности.
Системы отсчета, движущиеся с ускорением относительно инерциальной системы отсчета, называются неинерциальными.
Сила инерции — это сила, используемая для описания движения при переходе в неинерциальных системах отсчета (то есть при движении с ускорением). Эта сила равна по величине силе, вызывающей ускорение, но направлена в сторону, противоположную ускорению. Именно поэтому в ускоряющемся транспорте сила инерции тянет пассажиров назад, а в тормозящем транспорте — наоборот, вперед.
Сила
инерции — векторная
величина, численно равная произведению
массы m
материальной точки на модуль её ускорения  и направленная противоположно ускорению.
и направленная противоположно ускорению.

Существует 2 главные разновидности сил инерции: кориолисова сила и переносная сила инерции. Переносная сила инерции состоит из 3 слагаемых
-m —
поступательная сила инерции
—
поступательная сила инерции
m 2r
2r — центробежная
сила инерции
— центробежная
сила инерции
-m[ r]-
вращательная сила инерции
r]-
вращательная сила инерции
В динамике относительным движением называется движение по отношению к неинерциальной системе отсчёта, для которой законы механики Ньютона несправедливы. Чтобы уравнения относительного движения материальной точки сохранили тот же вид, что и в инерциальной системе отсчёта, надо к действующей на точку силе взаимодействия с другими телами F присоединить переносную силу инерции Fпер = –maпер и Кориолиса силу инерции Fkop = –makop, где m — масса точки. Тогда
maoтн = F + Fпер + Fkop
maoтн = F–makop–maпер
maoтн = F+2m[Vотн ]-mV0+m
]-mV0+m 2r
2r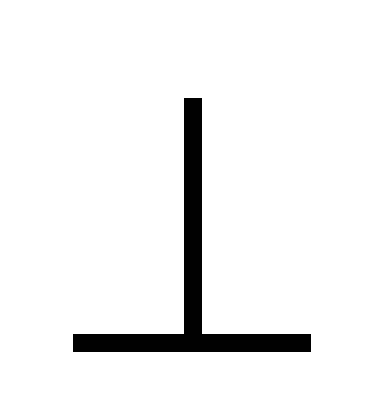 —m[
—m[ r]
r]
Fkop = –makop=2m[Vотн ]-кориолисова
сила
]-кориолисова
сила
Fпер = –maпер=
-m m
m 2r
2r —m[
—m[ r]
— переносная
сила инерции.
r]
— переносная
сила инерции.
Примеры. Математический маятник, расположенный на движущейся с ускорением тележке. Маятник Любимова.
Центробежная сила инерции – сила, с которой движущаяся материальная точка действует на тела (связи), стесняющие свободу её движения и вынуждающие её двигаться криволинейно. ( или Сила, с которой связь действует на материальную точку, равномерно движущуюся по окружности, в системе отсчета, связанной с этой точкой.)
Fц.б.=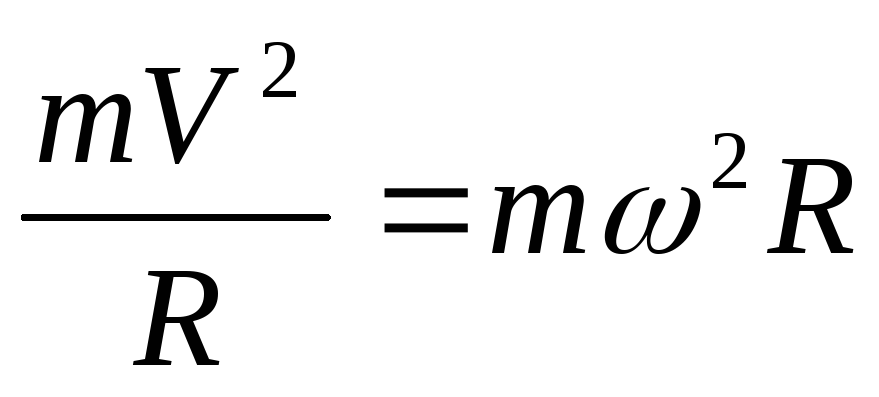 ,
R-
радиус кривизны траектории.
,
R-
радиус кривизны траектории.
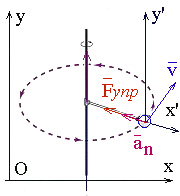 Рис.
К понятию центробежной силы инерции.
Рис.
К понятию центробежной силы инерции.
Центробежная сила направлена от центра кривизны траектории по её главной нормали (при движении по окружности по радиусу от центра окружности).
Центробежная сила — это тоже сила инерции — она направлена против центростремительной силы, вызывающей круговое движение.
Центробежная сила и центростремительная сила равны по величине, направлены противоположно.
Сила Кориолиса — одна из сил инерции, вводимая для учёта влияния вращения подвижной системы отсчёта на относительное движение тела.
При движении тела относительно вращающейся системы отсчета появляется сила инерции, называемая силой Кориолиса или кориолисовой силой инерции. Проявление силы Кориолиса можно рассмотреть на диске, вращающемся вокруг вертикальной оси (рис.1).
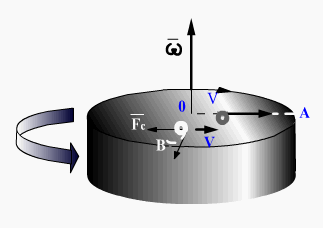
На
диске нанесена радиальная прямая ОА и
находится движущийся со скоростью V в
направлении от О к А шарик.
Если диск не вращается, шарик будет
катиться вдоль прочерченной прямой.
Если же диск привести в равномерное
вращение с угловой скоростью 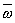 ,
то шарик будет катиться по кривой ОВ,
причем его скорость V относительно
диска будет изменять свое направление.
Следовательно, по отношению к вращающейся
системе отсчета шарик ведет себя так,
как если бы на него (перпендикулярно к
его скорости) действовала какая-то сила,
которая, однако, не вызвана взаимодействием
шарика с каким-либо телом. Это — сила
инерции, названная силой Кориолиса.
Величина этой силы пропорциональна
массе тела m, относительной скорости
движения тела V и угловой скорости
вращения системы w: Fк=2mVw.
,
то шарик будет катиться по кривой ОВ,
причем его скорость V относительно
диска будет изменять свое направление.
Следовательно, по отношению к вращающейся
системе отсчета шарик ведет себя так,
как если бы на него (перпендикулярно к
его скорости) действовала какая-то сила,
которая, однако, не вызвана взаимодействием
шарика с каким-либо телом. Это — сила
инерции, названная силой Кориолиса.
Величина этой силы пропорциональна
массе тела m, относительной скорости
движения тела V и угловой скорости
вращения системы w: Fк=2mVw.
Сила
Кориолиса Fc лежит в плоскости
диска: она перпендикулярна векторам V и 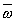 и
направлена в сторону, определяемую
векторным произведением [V
и
направлена в сторону, определяемую
векторным произведением [V 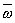 ]:
]: 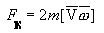 .
.
Сила Кориолиса как сила инерции направлена противоположно кориолисову ускорению aк:
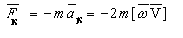 Если
векторы V и
Если
векторы V и  параллельны,
то сила Кориолиса обращается в нуль.
параллельны,
то сила Кориолиса обращается в нуль.
Проявление действия силы Кориолиса:
— размытие правых берегов рек, текущих на юг в северном полушарии;
— движение маятника Фуко;
— наличие дополнительного бокового давления на рельсы, а, следовательно, их неравномерный износ, возникающих при движении поездов.
Сила Кориолиса проявляется, например, в работе маятника Фуко. Кроме того, поскольку Земля вращается, то сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в северном полушарии более крутые — их подмывает вода под действием этой силы. В южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за возникновение циклонов и антициклонов.
Принцип эквивалентности Эйнштейна.
Поле силы инерции эквивалентно однородному полю силы тяжести. Это утверждение представляет собой принцип эквивалентности Эйнштейна.
Принципом эквивалентности и формулируется так: сила тяжести по своему физическому действию не отличается от равной ей по величине силе инерции.
Из принципа Эйнштейна вытекает эквивалентность инертной и гравитационной масс в ограниченной области пространства. В ограниченной, поскольку поле гравитационных сил в общем случае не является однородным (сила взаимодействия уменьшается по мере удаления тел друг от друга).
Сила Кориолиса в гидроаэромеханике — Википедия
 Гаспар-Гюстав де Кориолис
Гаспар-Гюстав де КориолисСила Кориоли́са в гидроаэромеханике — одна из сил инерции, действующая на упорядоченный или флуктуационный поток жидкости или газа во вращающейся неинерциальной системе отсчёта[источник не указан 30 дней].
Задача геофизической и астрофизической гидродинамики состоит в физическом описании турбулентного течения жидкости (или газа) на вращающихся объектах. В геофизике естественно использовать систему координат, жестко связанную с вращающейся Землей. Такая система координат является неинерциальной. Для описания относительного движения в такой системе координат можно использовать систему уравнений гидромеханики Навье — Стокса[1], если в них ввести две дополнительные силы инерции — центробежную силу и силу Кориолиса[2]. Сила Кориолиса в гидромеханике, в отличие от механики твердого тела, имеет свои особенности и важные приложения.[источник не указан 30 дней]
В системе координат, вращающейся с угловой скоростью ω,{\displaystyle \mathbf {\omega } ,} материальная точка, двигающаяся с относительной скоростью v,{\displaystyle \mathbf {v} ,} участвует в сложном движении и, согласно теореме Кориолиса, приобретает добавочное поворотное, или кориолисово ускорение, равное векторному произведению 2ω×v{\displaystyle 2\mathbf {\omega } \times \mathbf {v} }. При этом считается, что псевдовектор ω{\displaystyle \mathbf {\omega } } направлен по оси вращения согласно правилу правого винта.
Если v{\displaystyle \mathbf {v} } — вектор относительной скорости потока жидкости или газа, обладающего плотностью ρ,{\displaystyle \rho ,} то во вращающейся системе координат вектор силы Кориолиса, приходящийся на единицу объёма, равен
- Fc=−2ω×ρv.(1){\displaystyle \mathbf {F_{c}} ={-}2\mathbf {\omega } \times \rho \mathbf {v} .\qquad (1)}
В гидроаэромеханике скорость потока и характеристики состояния вещества, в том числе плотность, подвержены флуктуациям разной природы — тепловое движение молекул, звуковые колебания, турбулентность. Влияние гидродинамических флуктуаций на динамику потока исследуется методами статистической гидромеханики. В статистической гидромеханике уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса[3]. Если, следуя методу О. Рейнольдса, представить ρ=ρ¯+ρ′, v=v¯+v′,{\displaystyle \rho ={\overline {\rho }}+\rho ‘,\ \mathbf {v={\overline {v}}+v’} ,} где черта сверху — знак осреднения, а штрих — отклонения от среднего, то вектор осреднённой плотности импульса [3] приобретёт вид:
- ρv¯=ρ¯ v¯+S,(2){\displaystyle {\overline {\rho \mathbf {v} }}={\overline {\rho }}~{\overline {\mathbf {v} }}+\mathbf {S} ,\qquad (2)}
где S=ρ′v′¯{\displaystyle \mathbf {S} ={\overline {\rho ‘\mathbf {v} ‘}}} — вектор плотности флуктуационного потока массы (или «плотность турбулентного импульса» [3]). Осредняя (1) и учитывая (2), получаем, что плотность осреднённой силы Кориолиса будет состоять из двух частей:
- Fc¯=−2ω×(ρ¯ v¯+S).(3){\displaystyle {\overline {\mathbf {F_{c}} }}={-}2\mathbf {\omega } \times ({\overline {\rho }}~{\overline {\mathbf {v} }}+\mathbf {S} ).\qquad (3)}
Таком образом, в турбулентной среде возникла вторая часть силы Кориолиса, называемая[кем?]«плотность турбулентной силы Кориолиса». Она приводит к появлению в гидродинамических явлениях дополнительных эффектов, отсутствующих в механике твердого тела.
Сила Кориолиса в физике атмосферы и океана[править | править код]
 Циклон над Исландией 4 сентября 2003
Циклон над Исландией 4 сентября 2003Наиболее важную роль сила Кориолиса играет в глобальных геофизических процессах. Равновесие горизонтальной компоненты силы барического градиента и силы Кориолиса приводит к установлению потока, скорость которого направлена вдоль изобар (геострофический ветер). За исключением экваториальной зоны за пределами планетарного пограничного слоя движение атмосферы близко к геострофическому. Дополнительный учёт центробежной силы и силы трения дает более точный результат. Совместное действие этих сил приводит к формированию в атмосфере циклонов, в которых ветер вращается против часовой стрелки в Северном полушарии, оставляя область низкого давления слева от себя. В антициклоне, в центре которого находится область повышенного давления, вращение происходит в противоположном направлении[4]. В Южном полушарии направление вращения изменяется на противоположное.
Циклоны и антициклоны — это крупномасштабные вихри, участвующие в общей циркуляции атмосферы. В тропосфере в целом, под действием силы барического градиента и силы Кориолиса формируется общая циркуляция атмосферы. В каждом полушарии образуются по три циркуляционных ячейки: от экватора до широты 30° — ячейка Хэдли, примерно между 30° и 65° — ячейка Феррела, и в полярной области — Полярная ячейка. Атмосферная тепловая машина приводит эти шесть «колес» циркуляции во вращение. Сила Кориолиса, отклоняя ветер, циркулирующий в вертикальной плоскости, приводит к появлению пассатов — восточных ветров в нижней части атмосферы в тропическом поясе. Отклоняющее действие силы Кориолиса в ячейке Феррела приводит к преобладанию западных ветров умеренного пояса. В верхней части тропосферы направление ветров противоположное.
Сила Кориолиса таким же образом участвует в формировании общей циркуляции океана.
В пограничных слоях атмосферы и океана, в том числе в переходном слое между атмосферой и океаном, наряду с силой Кориолиса и силой барического градиента, существенную роль играет также и сила внутренного трения. Действие трения в пограничном слое (слое Экмана) приводит к отклонению ветра от геострофического в область пониженного давления. В результате, в нижней части циклона воздух направляется к его центру. Происходит «всасывание» воздуха, поднимающегося в центре циклона вверх, что, из-за конденсации водяного пара приводит к выделению теплоты парообразования, образованию осадков и поддержанию энергии его вращения. В антициклонах движение ветра противоположное, что приводит к опусканию воздуха в его центре и рассеиванию облаков. По мере удаления от подстилающей поверхности роль силы трения падает, что приводит к повороту вектора скорости потока в сторону направления геострофического ветра. Поворот ветра с высотой в пограничном слое атмосферы на угол ~ 20-40° называется «спираль Экмана». Этот эффект наглядно проявляется в отклонении направления дрейфа льда от вектора скорости геострофического ветра, впервые обнаруженного Ф. Нансеном во время полярной экспедиции 1893—1896 гг. на судне «Фрам». Теорию явления представил В.Экман в 1905 году.
В инерциальной системе отсчета инерционным является равномерное и прямолинейное движение. А на вращающейся планете на каждую материальную точку (а также, на поток), свободно двигающуюся по искривленной траектории, действуют две силы инерции — центробежная сила и сила Кориолиса. Эти силы могут уравновешивать друг друга. Пусть v{\displaystyle \ v} — относительная линейная скорость точки, направленная в горизонтальной плоскости по часовой стрелке в Северном, и против часовой стрелки — в Южном полушарии (как в антициклоне). Тогда, равновесие сил инерции наступает, если
- v2R=fv{\displaystyle {\frac {v^{2}}{R}}=fv},
где R=v/f{\displaystyle \ R=v/f} — радиус кривизны траектории частицы, f=2ωsinφ{\displaystyle \ f=2\omega \sin \varphi } — параметр Кориолиса, φ{\displaystyle \varphi } — географическая широта. В отсутствии других сил, равновесие силы Кориолиса и центробежной силы приведет к вращению частицы (потока) по дуге, называемой «круг инерции», имеющей радиус R{\displaystyle \ R}. Материальная точка совершает полный оборот по кругу инерции за период, равный 2π/f{\displaystyle \ 2\pi /f} — половине маятниковых суток.
В средних широтах параметр Кориолиса имеет порядок 10−4 с−1. Геострофическая скорость в тропосфере составляет около 10 м/с, чему соответствует круг инерции с радиусом около 100 км. Средней скорости течения в океане 10 см/с соответствует круг инерции, имеющий радиус порядка 1 км. Циркуляция потока по кругу инерции образует антициклонический вихрь для возникновения которого не требуется каких-либо иных причин, кроме инерции[5].
Если для жидкости (или газа) сила Кориолиса является основной силой, возвращающей частицу в состояние равновесия, то её действие приводит к появлению планетарных инерционных волн (называемых также «инерционными колебаниями»). Период таких колебаний равен 2π/f{\displaystyle \ 2\pi /f}, а колебательный процесс развивается в направлении, поперечном к вектору скорости распространения волн. Математическое описание инерционных волн можно, в частности, получить в рамках теории мелкой воды[6]. В средних широтах период инерционных колебаний порядка 17 часов.
Изменение параметра Кориолиса с широтой создает условия для возникновения в атмосфере, или в океане, волн Россби. Эти волны приводят к меандрированию струйных течений, в результате чего и формируются основные синоптические процессы.
Работа «турбулентной силы Кориолиса»[править | править код]
В гидромеханике величина механической работы, производимой силой в единице объёма за единицу времени (то есть мощность), есть скалярное произведение вектора силы на вектор скорости потока. (Считается, что понятие работы было введено в механику Кориолисом). Поскольку в механике материальной точки сила Кориолиса всегда направлена под прямым углом к её скорости, работа этой силы тождественно равна нулю. Поэтому сила Кориолиса не может изменить кинетическую энергию в целом, однако она может отвечать за перераспределение этой энергии между её компонентами. В статистической гидромеханике существует два уравнения кинетической энергии — уравнение кинетической энергии упорядоченного движения и уравнение баланса энергии турбулентности[3]. При этом возникает понятие работы турбулентной силы Кориолиса, определяющей обмен кинетической энергией между упорядоченным и турбулентным движением, происходящим под действием этой силы[7]. За единицу времени в единице объёма турбулентная сила Кориолиса производит работу, равную
- Nc=(Fc¯v¯)=−2(ω×Sv¯){\displaystyle \ N_{c}=(\mathbf {{\overline {F_{c}}}{\overline {v}}} )=-2\mathbf {(\omega \times S{\overline {v}})} }.
Положительному значению Nc{\displaystyle \ N_{c}} соответствует переход кинетической энергии упорядоченного движения в энергию турбулентности[3] .
Сила Кориолиса играет ключевую роль в геофизической гидродинамике, однако, вклад в энергетику гидродинамических процессов вносит только работа относительно малой, но важной, турбулентной силы Кориолиса. Анализ аэрологических данных[8] указывает на то, что этот эффект даёт основной вклад в энергию упорядоченного движения, приводящий к суперротации атмосферы.
Аналогичные физические механизмы, основанные на действии силы Кориолиса, формируют циркуляцию атмосферы на других планетах, (возможно) циркуляцию в жидком ядре планет, а также в звёздах, в аккреционных дисках, в газовых компонентах вращающихся галактик.[9],[10],[11][источник не указан 1915 дней]
Если жидкость (или газ) неоднородна (в частности, если она неравномерно нагрета), то в ней возникает флуктуационный поток вещества S≠0{\displaystyle \ \mathbf {S\neq 0} }. Этот поток зависит как от градиента плотности, так и от энергии турбулентных флуктуаций. Во вращающейся жидкости этот поток порождает турбулентную силу Кориолиса, работа которой приводит к обратимому обмену кинетической энергии между упорядоченной и турбулентной компонентами. Но поскольку турбулентный поток вещества зависит от энергии турбулентности, то возникает обратная связь. При благоприятных условиях такая обратная связь приводит к возникновению так называемой гиротурбулентной неустойчивости[12]. В процессе гиротурбулентных колебаний происходит периодическая перекачка энергии между упорядоченной и неупорядоченной формами движения. Поскольку эти колебания возникают в результате действия турбулентной силы Кориолиса, то их следует рассматривать как особый вид инерционных колебаний.
Турбулентная сила Кориолиса — величина сравнительно малая. Но, несмотря на это, гиротурбулентная неустойчивость отвечает за сравнительно медленные, но очень мощные геофизические и астрофизические природные процессы типа цикла индекса.
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — М.: Наука, 1988. — C. 736
- ↑ Хайкин С. Э. Физические основы механики. — М.: Наука, 1971. — С. 752
- ↑ 1 2 3 4 5 Монин А. С., Яглом А. М. Статистическая гидромеханика. Ч. 1. — М.: Наука, 1965. — 639 с.
- ↑ Матвеев Л. Т. Курс общей метеорологии. Физика атмосферы. — Л.: Гидрометеоиздат, 1984. — С. 751
- ↑ Халтинер Дж. Мартин Ф. Динамическая и физическая метеорология. М.: Иностранная литература.— 1960.— 436 с.
- ↑ Гилл А. Динамика атмосферы и океана. В 2-х частях. — М.: Мир, 1986.
- ↑ Krigel A. M. The theory of the index cycle in the general circulation of the atmosphere // Geophys. Astrophys. Fluid Dynamics.— 1980.— 16.— p. 1-18.
- ↑ Кригель А. М. Анализ механизмов трансформации энергии турбулентности в упорядоченную циркуляцию атмосферы // Вестник Ленинградского Государственного Университета. Сер. 7. — 1989. — Вып. 2 (№ 14). — С. 91—94.
- ↑ Кригель А. М. Теория стационарной дисковой аккреции на звезды и ядра галактик // Астрофизика . — 1989. — 31. — Вып.1. — с.137-143.
- ↑ Кригель А. М. Влияние турбулентности на радиальное движение в газовых дисках галактик // Кинематика и физика небесных тел. — 1990. — 6. — №1. — с.73-78.
- ↑ Кригель А. М. Численное моделирование гиротурбулентных колебаний светимости рентгеновских звёзд // Астрономический журн. — 1990. — 67. — Вып 6. — с.1174-1180.
- ↑ Кригель А. М. Неустойчивость струйного течения в турбулентной вращающейся неоднородной жидкости // Журнал технической физики. — 1985. — 55. — Вып. 2. — С. 442—444.
Физические основы механики
В предыдущем параграфе было рассмотрено тело, неподвижное во вращающейся системе отсчета. Если во вращающейся системе отсчета тело движется, то, помимо центробежной силы, на него будет действовать ещё одна сила инерции, называемая силой Кориолиса или кориолисовой силой инерции.
Пусть шарик массой движется без трения вдоль радиуса диска (рис. 8.5) с постоянной скоростью , направленной в некую точку на краю диска.
Рис. 8.5. Отклонение шарика, движущегося во вращающейся системе отсчета
Если диск не вращается, то шарик движется по радиусу и попадает в точку . Если же диск привести во вращение с угловой скоростью , то к моменту достижения шариком края диска на месте точки окажется другая точка . Если шарик оставляет след, то он прочертит свою траекторию относительно диска — кривую линию . При этом на шарик не действуют никакие видимые силы, и относительно инерциальной системы он по-прежнему движется с постоянной скоростью . Скорость же шарика относительно диска изменяла свое направление. Значит, в системе отсчета, связанной с вращающимся диском, на шарик действовала сила инерции, не параллельная скорости . Стало быть, она не была направлена по радиусу, откуда следует, что эта сила отлична от рассмотренной выше центробежной силы инерции. Ее и называют силой Кориолиса.
Рис. 8.6 Движение шарика по гладкой поверхности вращающегося диска. Сверху — с точки зрения внешнего наблюдателя. Снизу — с точки зрения наблюдателя, неподвижного относительно диска
Дополнительная информация
http://kvant.mirror1.mccme.ru/1975/04/sila_koriolisa.html — журнал «Квант» — сила Кориолиса (Я. Смородинский).
Найдем выражение для силы Кориолиса в частном случае (рис. 8.7), когда частица массой движется относительно вращающейся системы отсчета К’ равномерно по окружности, лежащей в плоскости, перпендикулярной к оси вращения , с центром на оси вращения.
Рис. 8.7. К выводу выражения для силы Кориолиса
Скорость частицы относительно вращающейся системы К’ обозначим через . В неподвижной (инерциальной) системе отсчета К частица также движется по окружности, но ее линейная скорость равна
где — угловая скорость вращающейся системы, — радиус окружности. Для того, чтобы частица двигалась относительно неподвижной системы отсчета K по окружности со скоростью , на нее должна действовать направленная к центру окружности сила (например, натяжение нити), причем величина этой силы равна
Относительно вращающейся системы отсчета K’ в этом случае частица движется с ускорением
Из полученного выше уравнения второго закона Ньютона для частицы получаем:
Слева стоит произведение массы на ускорение частицы во вращающейся системе отсчета. Значит, справа должны стоять силы, на нее действующие. Первое слагаемое понятно: это сила натяжения нити, которая одинакова как для инерциальной, так и для неинерциальной систем. С третьим слагаемым мы тоже уже имели дело: это направленная по радиусу (от центра) центробежная сила инерции. Второе слагаемое и есть сила Кориолиса. В данном случае она также направлена от центра, но зависит от скорости частицы. Модуль кориолисовой силы в этом примере равен . Ее направление совпадает с движением штопора, ручка которого поворачивается от вектора скорости к вектору угловой скорости .
Можно показать, что в общем случае сила Кориолиса определяется как
Сила Кориолиса ортогональна вектору скорости. В случае радиального движения, показанного на рис. 8.5, она отклоняла шарик направо, вынуждая его двигаться по траектории .
Возникновение силы Кориолиса при движении тела относительно вращающейся системы отсчета демонстрируется в опыте на рис. 8.6.
Дополнительная информация
http://www.plib.ru/library/book/17005.html — Стрелков С.П. Механика Изд. Наука 1971г. — стр.165–166 (§ 48): опыт Хайкина по демонстрации силы Кориолиса.
Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Приведем некоторые примеры.
Рис. 8.8. Сила Кориолиса на поверхности Земного шара
В северном полушарии наблюдается более сильное подмывание правых берегов рек, правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, а циклоны вращаются по часовой стрелке. В южном же полушарии все происходит наоборот.
При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу — в южном (рис. 8.9).
Рис. 8.9. На Земле движущиеся тела отклоняются направо в северном полушарии, и налево в южном
При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к земле, если выстрел произведен на запад, и поднимать его кверху, если выстрел произведен в восточном направлении.
Видео 8.9. Сила Кориолиса: попробуй, попади! Стрельба на вращающейся платформе.
Пример. Поезд массой = 150 тонн идет в меридиональном направлении на север со скоростью = 72 км/ч. Найдем, чему равна кориолисова сила, прижимающая его в боковом направлении к рельсам, и определим, каков эффект действия центробежной силы. Поезд находится на широте Москвы = 56°.
Угол между вектором угловой скорости суточного вращения Земли и касательной к меридиану равен широте места (рис. 8.10).
Рис. 8.10. Кориолисова сила направлена от нас перпендикулярно плоскости рисунка
Поэтому кориолисова сила равна
Подставляя числовые данные, находим
Эта сила соответствует весу массы
и составляет от веса поезда.
Расстояние поезда от оси вращения Земли равно , так что центробежная сила будет
Направлена она по перпендикуляру к оси вращения. Следовательно, ее составляющая
направленная вдоль радиуса Земли, уменьшает вес поезда:
Подставляя числовые данные, получаем
Это соответствует весу массы
и составляет 1,1·10–3 от веса поезда.
Другая составляющая центробежной силы
направлена по касательной к меридиану и тормозит поезд. Она равна
что соответствует весу массы
и составляет 1,6·10–3 от веса поезда.
Таким образом, влияние центробежной силы проявляется в десятых долях процента, а проявления кориолисовой силы — на порядок меньше (что связано, разумеется, с небольшой скоростью поезда).
Французский физик Фуко экспериментально доказал вращение Земли вокруг своей оси с помощью 67-метрового маятника, подвешенного к вершине купола парижского Пантеона. Подобный маятник до недавнего времени можно было увидеть в Петербурге в Исаакиевском соборе.
Рис. 8.11. Маятник Фуко
Колебания маятника Фуко зависят от того, как они были возбуждены. Если маятник отклонить на максимальный угол, а затем отпустить его без начальной скорости, то маятник будет колебаться, как изображено на рис. 10. Скорость движения маятника в положении максимального отклонения будет равна нулю.
Рис. 8.12. Колебания маятника Фуко при отклонении на максимальный угол и отпускании без начальной скорости
Несколько иной характер траектории получится, если маятник приводится в движение коротким толчком из положения равновесия. Этому случаю соответствует рис. 8.11. и 8.13. Скорость маятника в положении максимального отклонения соответствует скорости вращения Земли на широте наблюдения.
Рис. 8.13. Колебания маятника Фуко при сообщении ему скорости при отклонении на максимальный угол
Видео 8.10. Настольный маятник Фуко
Дополнительная информация
http://www.plib.ru/library/book/17005.html — Стрелков С.П. Механика Изд. Наука 1971 г. — стр.172–174: движение маятника Фуко.
http://mehanika.3dn.ru/load/24-1-0-3278 — Тарг С.М. Краткий курс теоретической механики, Изд. Высшая школа, 1986 г. — стр. 155–164, §§ 64-67, — преобразования скорости и ускорения материальной точки при переходе из одной системы отсчета в другую, теорема Кориолиса.
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 353–356 (§ 67): выведены формулы для расчета отклонения падающих тел от направления отвеса.
http://kvant.mirror1.mccme.ru/1995/05/komu_nuzhna_vysokaya_bashnya.html — журнал «Квант» — из истории физики — падение тел с Пизанской башни и других высоких построек (А. Стасенко).
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 360–366 (§ 69): проясняются физические причины приливов и отливов в морях и океанах на Земле.
Эффект Кориолиса • Джеймс Трефил, энциклопедия «Двести законов мироздания»
получил вопросы по почте.Sun Dec 20 23:17:47 2009
From: a_b
To: fatyalink
Answer to:
>
цитата……Представьте, что кто-то, находясь на…
Вопрос первый. Отчего у Вас такая путаница с системами отсчета?
Вопрос второй. Известны ли Вам другие описания эффекта Кориолиса, кроме этой статьи? В них также не акцентируется, что эффект возникает при _движении_ во вращающейся системе отсчета, а на покоящиеся в ней эта фиктивная сила не действует?
Первое.
Это не у меня путаница, это чехарда от придуманной относительности.
Вместо того чтобы прямо заявить, что неподвижная система отсчета какая-либо звезда, нам просто пудрят мозги, короче, чем больше путаница, тем легче скрыть собственное непонимание. Прием известный, а дяденьки Лорентц, Эйнштейн и прочие применяли его гениально.
Физический эффект присутствует, но он не может быть объяснен с позиции механики. Никакое физическое движение нельзя разрешить или запретить математической абстракцией – выбором места наблюдения.
Он действительно зависит от вращения земли. Но не напрямую. И фиктивными выдуманными воздействиями объяснен быть не может.
Такое объяснение и будет фикцией.
Цитата из «ФИЗИЧЕСКИЙ ЭНЦИКЛОПЕДИЧЕСКИЙ СЛОВАРЬ»
— М.: Советская энциклопедия, 1983 г. стр. 311.
«Кориолисова сила — одна из сил инерции; вводится для учета влияния вращения подвижной системы отсчета на относительной движение материальной точки; названная по имени французского ученого Г. Кориолиса.
К.с. равна произведению массы точки на ее Кориолиса ускорение и направлена противоположно этому ускорению. Эффект, учитываемый К.с. состоит в том, что во вращающей системе отсчета материальная точка движущаяся непараллельно оси этого вращения, отклоняется по направлению, перпендикулярному к ее относительной скорости, или оказывает давление на тело, препятствующее этому отклонению. На Земле этот эффект, обусловленный ее суточным вращением, заключается в том, что свободно падающие тела отклоняются от вертикали к востоку, а тела движущиеся вдоль земной поверхности, отклоняются в Северном полушарии — вправо, а в Южном — влево от направления их движения.
Вследствие медленного вращения Земли эти отклонения весьма малы и заметно сказываются или при больших скоростях движения (например., у ракет, самолетов, и у артиллерийских снарядов с большими дальностями полета), или когда движение длится очень долго, например, подмыв соответствующих берегов рек (правые берега рек в Северном полушарии имеют более крутые берега. т.н. закон Бэра), возникновение некоторых воздушных и морских течений и др…»
Более или менее толково изложена сама суть явления.
С несколькими но, если смотреть на южный полюс отклонения всегда на восток.
И что это за разновидность сил инерции? их что немеряно?
И это не инерция!!! Она вообще ни причем. Смещение бы было в другую сторону. Хотя и силы инерции тоже фиктивные и классическое их объяснение – фикция, непонимание происходящего. На безрыбье и рак рыба. Посчитали, что и так сойдет. Чтоб не забросить формулировку ньютона в мусор. Насчет прямолинейного и равномерного движения. Начисто забывают, что инерция это свойство тела, на которое явно никакие силы не действуют. А значит это внутренняя его энергия. Аккумулированная и расходуемая при сопротивлении среды. Силы есть, но они внутренние, а не внешние.
Проявление эффекта только при Непараллельности направления движения оси вращения. О какой непараллельности идет речь? Поверхность земли определяет непараллельность. Но это не факт, что при параллельности этого не будет, поскольку для проверки тоннель рыть надо, что накладно. С другой стороны несоосность не должна влиять на качественную сторону, только на количественную.
С этим эффектом пытаются связать значительные отклонения от вертикали при определении ускорения свободного падения методом бросания. Отклонение происходит по ходу вращения земли. Причем для разных материалов разные. Не знаю, учитывается ли это в метрологии (в гравиметрии не учитывается). Растет длина пути.
Как правило его вообще не учитывают. http://arlenasong.ru/_14/index.php?k=5.html
http://www.inauka.ru/blogs/article91056.html
http://www.kscnet.ru/ivs/publication/tutorials/geophys_studi
сам эффект отклонения обнаружен шахтным методом наблюдений.
Кроме того, для намагниченных тел присутствует отклонение в сторону полюсов в зависимости от полушария, мало того имеется и элемент вращения. Это магнитное наклонение и магнитное склонение.
На самом деле все это якобы силами Кариолиса не вызывается.
Кстати, этого отклонения нет вообще на магнитном экваторе, не географическом. Нет зависимости от вращения.
При свободном падении сильно заметного движения вдоль поверхности земли нет, а эффект проявляется и не зависит от самого вращения земли, то есть от той самой вращающейся системы отсчета.
Якобы Проявление эффекта с подмывом правых берегов в северном полушарии. Множество народа пытается опровергнуть это заблуждение и совершенно правильно. Земля крутится неравномерно, то быстрее то медленнее. скорость вращения на разных широтах разная.Попробуйте походить со стаканом воды в руке, да посмотрите где уровень будет больше. В стороне противоположной направлению движения. И именно за счет подвижности текучести. Показано только для северного полушария, а для южного такого многообразия подходящих примеров нет. Так и суши такой как на севере нет и речек так же текущих.
так что отнесение данного эффекта только на счет Кариолиса
проблематично.http://gatchina3000.ru/brockhaus-and-efron-enc
Напрямую это явление связано с маятником Фуко, плоскость качания которого на экваторе тоже не изменяется. Еще хохма… маятник Фуко запускается ОДИН РАЗ! и колебания не затухают. Есть еще одно! маятник Фуко реагирует на солнечные затмения уж очень непредсказуемо, как магнитная стрелка на полюсе. Работа реального (не математического) маятника Фуко зависит от высоты подвеса.
Чем выше, тем больше скорость. В общем, это второе и главное.
Третье.
Некоторые заморочки со вращением (медного диска) и магнитным полем земли обнаружил Фарадей и прекрасно описал в своих трудах. Читаешь и поражаешься, а куда все смотрят?
Тут мужик со светом (сайт я дал) поработал, так еще выясняются и некоторые совпадения с солнечной активностью.
С уважением, АВФ
Кориолисова сила — это… Что такое Кориолисова сила?
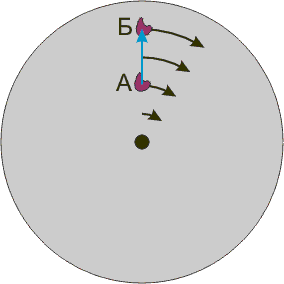 При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса.
При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса. 
Движение шарика по поверхности вращающейся тарелки.
Си́ла Кориоли́са (по имени французского учёного Гюстава Гаспара Кориолиса, впервые его описавшего) — одна из сил инерции, существующая в неинерциальной (вращающейся) системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Ускорение Кориолиса было получено Кориолисом в 1833 г., Гауссом в 1803 г. и Эйлером в 1765 г.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. FK = − ma. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Математическое определение
Сила Кориолиса равна:
где m — точечная масса, 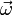 — вектор угловой скорости,
— вектор угловой скорости, 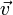 — вектор скорости движения точечной массы.
— вектор скорости движения точечной массы.
Кориолисово ускорение — это векторная величина, равная ![\vec{a}_k=2 \left[ \vec \omega \times \vec v \right],](/800/600/https/dic.academic.ru/pictures/wiki/files/55/7b078ba4ad487c59c24ab9381f405b3f.png) где
где 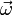 — угловая скорость неинерциальной системы отсчёта относительно инерциальной,
— угловая скорость неинерциальной системы отсчёта относительно инерциальной, 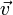 — скорость объекта в неинерциальной системе отсчёта.
— скорость объекта в неинерциальной системе отсчёта.
Получение
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью 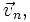 а сама система движется поступательно с линейной скоростью
а сама система движется поступательно с линейной скоростью 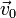 в инерциальной системе координат и одновременно вращается с угловой скоростью
в инерциальной системе координат и одновременно вращается с угловой скоростью 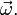
Тогда линейная скорость тела в инерциальной системе координат равна:
![\vec v= \vec {v}_0 + \left[ \vec \omega \times \vec R \right] + \vec {v}_n,](/800/600/https/dic.academic.ru/pictures/wiki/files/100/d3ee4158828c2b1125e1761fd6670ab5.png)
где 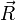 — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:
![\frac{d}{dt}\vec v= \frac{d}{dt}\vec {v}_0 + \frac{d}{dt}\left[ \vec \omega \times \vec R \right] +\frac{d}{dt} \vec {v}_n.](/800/600/https/dic.academic.ru/pictures/wiki/files/51/3af4b9a812a8b372387d54168f2dba94.png)
Найдём значение каждого слагаемого в инерциальной системе координат:
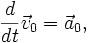
![\frac{d}{dt} \vec {v}_n = \vec {a}_n + \left[ \vec\omega \times \vec {v}_n \right],](/800/600/https/dic.academic.ru/pictures/wiki/files/53/564bf2b000132c2b979c4abe8bbcd2c5.png)
![\frac{d}{dt} \left[ \vec\omega \times \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \frac{d}{dt} \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \vec {v}_n \right] + \left[ \vec\omega \times \left[ \vec\omega \times \vec R \right] \right],](/800/600/https/dic.academic.ru/pictures/wiki/files/101/e5ef1554861e7cb48ef0e7a990349ddd.png) где
где 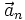 — линейное ускорение относительно системы,
— линейное ускорение относительно системы, 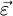 — угловое ускорение.
— угловое ускорение.
Таким образом, получаем:
![\frac{d}{dt}\vec v = \vec a=\vec {a}_0 + \vec {a}_n + \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec \omega \times \left[ \vec \omega \times \vec R \right] \right] + 2\left[ \vec \omega \times \vec {v}_n \right].](/800/600/https/dic.academic.ru/pictures/wiki/files/99/cee134148f3010b2696e9e0f94b9b9d3.png) Последнее слагаемое и будет кориолисовым ускорением.
Последнее слагаемое и будет кориолисовым ускорением.
Физический смысл
Пусть тело движется со скоростью 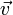 вдоль прямой к центру вращения инерциальной системы отсчёта.
вдоль прямой к центру вращения инерциальной системы отсчёта.
Тогда данное движение приведёт к изменению расстояния до центра вращения R и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой.
Как мы знаем, эта скорость движения равна ![\vec {v}_e = \left[ \vec \omega \times \vec R \right].](/800/600/https/dic.academic.ru/pictures/wiki/files/97/aa9de6f46034488f4bbca755d76bc9f5.png)
Данное изменение будет равно:
![d \vec {v}_e= \left[ \vec\omega \times d \vec R \right].](/800/600/https/dic.academic.ru/pictures/wiki/files/48/0baa1c9caf22087ed731e63f30de4be5.png)
Проведя дифференцирование по времени, получим ![\vec a = \left[ \vec\omega \times \vec v \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png) (направление данного ускорения перпендикулярно
(направление данного ускорения перпендикулярно 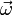 и
и 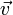 ).
).
C другой стороны, вектор 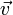 , оставшись неподвижным относительно инерциального пространства, повернётся относительно неинерциального на угол ωdt. Или приращение скорости будет
, оставшись неподвижным относительно инерциального пространства, повернётся относительно неинерциального на угол ωdt. Или приращение скорости будет
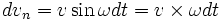 при
при 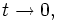 соответственно второе ускорение будет:
соответственно второе ускорение будет:
![\vec a= \left[ \vec\omega \times \vec v \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png)
Общее ускорение будет ![\vec {a}_k=2 \left[ \vec\omega \times \vec v \right].](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2852b6463402e829d89a249960f33f2c.png) Как видно, система отсчёта не претерпела изменения угловой скорости
Как видно, система отсчёта не претерпела изменения угловой скорости 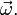 Линейная скорость относительно неё не меняется и остаётся
Линейная скорость относительно неё не меняется и остаётся 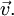 Тем не менее, ускорение не равно нулю.
Тем не менее, ускорение не равно нулю.
Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется ![\vec a = \left[ \vec\omega \times \vec v \right],](/800/600/https/dic.academic.ru/pictures/wiki/files/51/3537afd827222e73c0737864244d6b7b.png) а также прибавляется ускорение в результате изменения центростремительного ускорения точки.
а также прибавляется ускорение в результате изменения центростремительного ускорения точки.
Сила Кориолиса в природе
Самый простой пример использования силы Кориолиса — это эффект ускорения кручения танцоров. Чтобы ускорить свое вращение, человек может начать крутиться с широко разведёнными в стороны руками, а затем — уже в процессе — резко прижать руки к туловищу, что вызовет увеличение круговой скорости (согласно закону сохранения момента импульса). Эффект силы Кориолиса проявится в том, что для такого движения руками придётся прикладывать усилия не только по направлению к телу, но и в направлении по вращению. При этом возникает ощущение, что руки отталкиваются от чего-то, при этом ещё больше ускоряясь.
Сила Кориолиса также проявляется, например, в работе маятника Фуко. Кроме того, поскольку Земля вращается, то сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов.
Вопреки расхожему мнению, маловероятно, что сила Кориолиса полностью определяет направление закручивания воды в водопроводе — например, при сливе в раковине. Хотя в разных полушариях она действительно стремится закручивать водяную воронку в разных направлениях, при сливе возникают и побочные потоки, зависящие от формы раковины и конфигурации канализационной системы. По абсолютной величине создаваемые этими потоками силы превосходят силу Кориолиса, поэтому направление вращения воронки как в Северном, так и в Южном полушарии может быть как по часовой стрелке, так и против неё.
См. также
Wikimedia Foundation. 2010.