Формула электрического тока. По какой формуле можно рассчитать силу тока. Закон Ома.
Электрический ток, это именно та сила, которая течет во всей электротехники заставляя ее работать. Но сводить все к простому течению электротока по электрическим цепям в схемах неразумно, должна быть какая-то мера, определенная величина этой силы тока. Ведь если в электрической схеме пойдет слишком большой ток по проводникам, которые на него не рассчитаны, то просто эта схема выгорит. Из школьных уроков мы помним, что существуют так называемые формулы, которые и позволяют вычислять конкретные неизвестные величины имея при этом известные.
Вот самая базовая, наиболее используемая формула тока, по которой и вычисляется эта самая сила тока. В ней всего лишь три электрических величины (базовые электрические величины) — ток, напряжение и сопротивление.
Итак, сила тока на схемах обычно обозначается большой английской буквой «I». Единицей измерения тока является «Ампер». Формула тока звучит следующим образом — электрический ток равен отношению напряжения (разности потенциалов) к сопротивлению. То есть, чтобы найти силу тока нам нужно просто напряжение разделить на сопротивление. Единицей измерения электрического напряжения является «Вольт», а сопротивления «Ом». Следовательно, известные вольты делим на известные омы и получаем ранее неизвестные амперы.
То есть, чтобы найти силу тока нам нужно просто напряжение разделить на сопротивление. Единицей измерения электрического напряжения является «Вольт», а сопротивления «Ом». Следовательно, известные вольты делим на известные омы и получаем ранее неизвестные амперы.
Эта же формула еще называется законом Ома. Она помогает найти из двух известных величин третью, которая неизвестна. Чтобы найти напряжение, то нужно силу тока перемножить на сопротивление, а для нахождения сопротивления нужно будет напряжение разделить на силу тока. Все достаточно просто. Данная формула тока подходит и для постоянного тока и для переменного, но именно с активным сопротивлением. То есть, по ней можно рассчитать те электрические цепи (участки цепей в схемах), которые содержать сопротивления в виде обычных нагревателей, резисторов, лампочек (не имеющих индуктивную и емкостную составляющую). Индуктивностью обладают все катушки, а емкостью обладают все конденсаторы (они уже имеют реактивное сопротивление и рассчитываются по другой формуле).
Если говорить о формуле тока, которая ближе к научной сфере, то она уже будет иметь вид немного другой. Электрический ток изначально выражается как отношение количества электрических зарядов ко времени их прохождения через проводник.
Электрический ток это упорядоченное движение электрических зарядов (в твердых телах это электроны, а в жидких и газообразных телах это ионы). Так вот ток, это непосредственное движение этих зарядов и, естественно, что он определяется их количеством и временем течения. Электрические заряды измеряются в «Кулонах», ну а время в «секундах». Следовательно, чтобы узнать силу электрического тока нужно количество зарядов разделить на время их прохождения. То есть, кулоны делим на секунды и получаем амперы.
Повторюсь, что на практике при измерении и вычислении силы тока пользуются именно формулой закона Ома, поскольку приходится использовать при расчетах напряжение и сопротивление. Именно они повсеместно будут встречаться в электрических схемах той или иной электротехники. Никаких кулонов (количества зарядов) вы при своей работе электриком не увидите!
Никаких кулонов (количества зарядов) вы при своей работе электриком не увидите!
Ну, и поскольку выше я затронул тему реактивного сопротивления, то пожалуй приведу формулу для нахождения силы тока именно для цепей, содержащих индуктивное и емкостное сопротивление.
По данной формуле можно найти силу тока, которая будет течь в электрической цепи с переменным, синусоидальным напряжением и содержащая реактивное сопротивление в виде катушки (индуктивности) или конденсатора (емкости). Думаю вы заметили, что в приведенной формуле изменился лишь тип сопротивления. Сама же основа — это все та же формула закона Ома, что была приведена в самом начале. Просто тут для нахождения индуктивного и емкостного сопротивления уже используются такие величины как частота, емкость и индуктивность, ну и еще «ПИ», которое равно 3,14.
P.S. Формулу электрического тока вы просто обязаны знать наизусть (если вы конечно электрик или электронщик). Формула закона Ома будет вам полезна очень много раз. Как только нужно найти силу тока, напряжение или сопротивление (зная любые две величины из трех) вы быстро и без проблем сразу подставляете числа в эту формулу и вычислите неизвестные электрические величины.
Как только нужно найти силу тока, напряжение или сопротивление (зная любые две величины из трех) вы быстро и без проблем сразу подставляете числа в эту формулу и вычислите неизвестные электрические величины.
09-б. Сила электрического тока
§ 09-б. Сила электрического тока
В § 8-и мы рассмотрели опыт с лампочкй и двумя спиралями. Мы отметили, что под изменением силы тока будем понимать изменение потока электронов внутри проводника. Это относилось к твёрдым металлическим проводникам. Напомним: в газообразных и жидких проводниках, например, в расплавленных или растворённых веществах электроток создаётся как электронами, так и ионами (см. § 8-й).
Важно: все движущиеся заряженные частицы являются носителями (переносчиками) электрического заряда. Следовательно, под силой тока более верно понимать не общее количество самых разнообразных заряженных частиц (электронов и/или ионов), переносящих разные заряды за выбранное время наблюдения, а общий заряд, переносимый через проводник за единицу времени. В виде формулы это выглядит так:
В виде формулы это выглядит так:
Формула для вычисления силы электрического тока через заряд и время его протекания.
| I = | q | I – сила электрического тока в проводнике, А | |||
| t |
Итак, сила тока – физическая величина, показывающая заряд, проходящий через проводник за единицу времени.
Для измерения силы тока используют прибор амперметр (см. рисунок). Его всегда включают последовательно с тем участком цепи, в котором нужно измерить силу тока. Единица силы тока –

За 1 ампер принимают силу такого тока, который при прохождении по двум параллельным прямым проводникам бесконечной длины и малого диаметра, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает на каждый 1 м длины силу взаимодействия 0,0000002 H.
Познакомимся теперь с законами распределения сил токов в цепях с различными соединениями проводников. Проведём опыты.
На схемах а-б-в лампа и реостат соединены последовательно. Сначала амперметр включён между реостатом и лампой (схема а), и сила тока обозначена символом Iобщ. Затем амперметр помещён слева от реостата (схема б), и сила тока обозначена символом I1. После амперметр помещён слева от лампы (схема в), и сила тока обозначена символом I2.
Многократные измерения в этом и во всех других аналогичных опытах показывают, что во всех участках цепи с последовательным соединением проводников силы токов равны друг другу (то есть одинаковы):
Сила тока между последовательно соединёнными потребителями равна силам токов в проводах, подводящих энергию к потребителям.
| Iобщ = I1 = I2 = … |
На схемах г-д-е две лампы соединены параллельно. Сначала амперметр расположен в неразветвлённой части цепи (схема г), и сила тока обозначена символом Iобщ. Затем амперметр помещён слева от первой лампы (схема д), и сила тока обозначена I1. После амперметр помещён слева от второй лампы (схема е), и сила тока обозначена I2.
Многократные измерения показывают, что
Сила тока в проводах, подводящих энергию источника к параллельному соединению, равна сумме сил токов, идущих в каждом из потребителей.
| Iобщ = I1 + I2 + … |

Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsbox зачет по физике 8класс помогите.Пожалуйста!!!
1. Что такое электрический ток? Направление
1.Электри́ческий ток — направленное (упорядоченное) движение частиц или квазичастиц — носителей электрического заряда.2.Сила тока ( I )- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шелток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
3.Ампер это единица силы тока.
4.Амперметр
5.Шкалу амперметров градуируют в микроамперах, миллиамперах, амперах или килоамперах в соответствии с пределами измерения прибора. В электрическую цепь амперметр включается последовательно с тем участком электрической цепи, силу тока в котором измеряют.
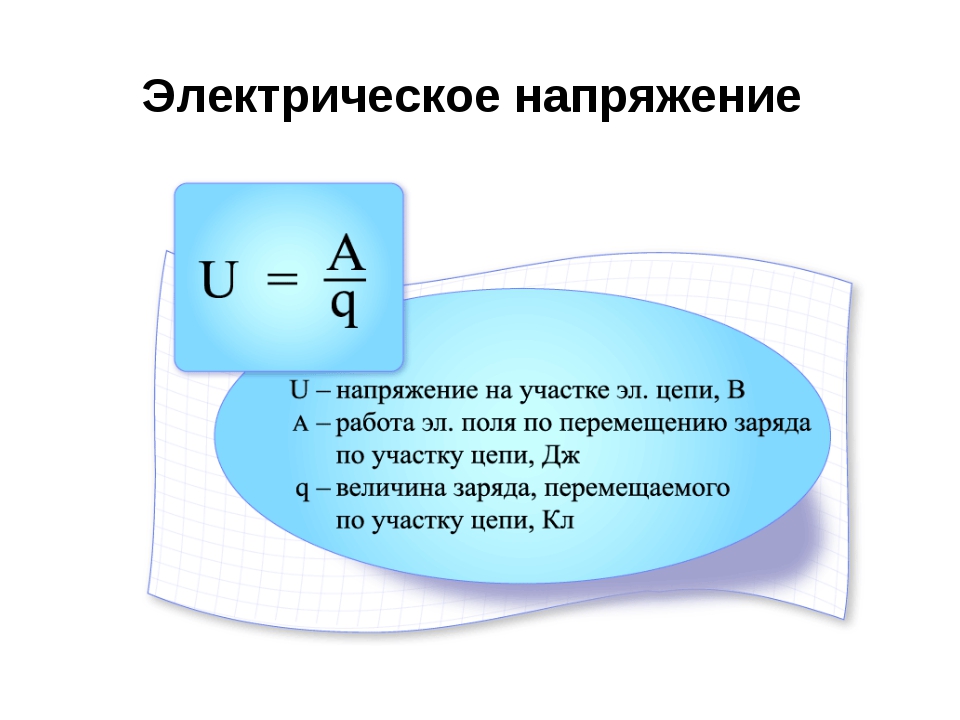
6.Напряжение показывает, какую работу совершает электрическое поле при перемещении еденичного электрического заряда из одной точки в другую ( обзначается U )
8. Параллельно измеряемому участку / элементу цепи.
Параллельно измеряемому участку / элементу цепи.
9.Электрическое сопротивление, Закон Ома, формула.Электрическое сопротивлениеопределяет силу тока, текущего по цепи при заданном напряжении. Под Электрическим сопротивлением R понимаютотношение напряжения на концах проводника к силе тока, текущего по проводнику.
10.причина электрическогосопротивления заключается в том, что электроны при своем движении испытывают соударения с ионами металла. Эти соударения производят такой же результат, как и действие некоторой постоянной силы трения, стремящейся тормозить движение электронов.
11.Закон Ома для участка цепигласит: ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этойцепи увеличится во столько же раз.
12.Удельное сопротивление проводника — скалярная физическая величина, численно равная сопротивлениюоднородного цилиндрическогопроводника, изготовленного из данного вещества и имеющего длину 1 м и площадь поперечного сечения 1 м2, или сопротивлениюкуба с ребром 1 м.
13.-
14.Реоста́т (потенциометр, переменное сопротивление, переменный резистор, от греч. ρηος — поток и греч. στατος — стоящий) — электрический аппарат, служащий для регулировки и получения требуемой величины сопротивления. Как правило, состоит из проводящего элемента с устройством регулирования электрического сопротивления
15.При последовательном соединении проводников сила тока во всехпроводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
16.-
17.При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
18.-
19. Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Формула:
A= U*I*t
1 Джоуль = 1 Вольт * 1 Ампер * 1 секунда
______
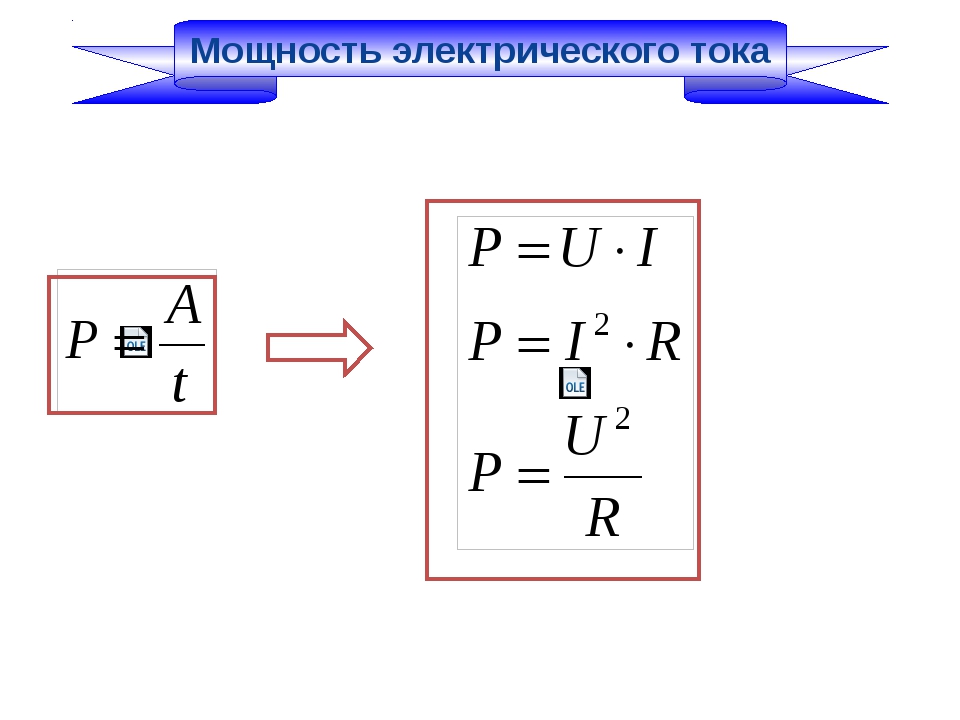
Мощность электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока.
Формула:
P=UI
1 Ватт = 1 Вольт * 1 Ампер
20.
21.Зависимость тепловой энергии от силы тока в проводнике определяется по закону Джоуля-Ленца. При прохождении электрического тока по проводнику количество тепла, выделяемого током в проводнике, прямо пропорционально силе тока, взятой во второй степени, величине сопротивления проводника и времени действия тока.
22.Ла́мпа нака́ливания — искусственный источник света, в котором свет испускает тело накала, нагреваемое электрическим током до высокой температуры. В качестве тела накала чаще всего используется спираль из тугоплавкого металла (чаще всего — вольфрама), либо угольная нить.
23.Коро́ткое замыка́ние (КЗ) — электрическое соединение двух точек электрической цепи с различными значениями потенциала, не предусмотренное конструкцией устройства и нарушающее его нормальную работу.
24.Предохранитель — коммутационный электрический аппарат, предназначенный для отключения защищаемой цепи размыканием или разрушением специально предусмотренных для этого токоведущих частей под действием тока, превышающего определённое значение.
Электрический ток, сила и плотность тока
В электродинамике — разделе учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел, важнейшим понятием является понятие электрического тока.
Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Ε свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля, т.е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела, то возникает так называемый конвекционный ток.
В проводнике под действием приложенного электрического поля Ε свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля, т.е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела, то возникает так называемый конвекционный ток.
Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно, а с другой – наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.
Количественной мерой электрического тока служит сила тока I — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:
Ток, сила и направление которого не изменяются со временем, называется постоянным. Для постоянного тока
Для постоянного тока
где Q — электрический заряд, проходящий за время t через поперечное сечение проводника.
Единица силы тока – ампер (А). Более детально ток можно охарактеризовать с помощью вектора плотности тока j.
Плотностью тока называется физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока:
Направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м2).
Выразим силу и плотность тока через скорость v упорядоченного движения зарядов в проводнике. Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то за время dt через поперечное сечение S проводника переносится заряд
Сила тока
,а плотность тока
.
Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т. е.
,где dS = n dS (n — единичный вектор нормали к площадке dS, составляющей с вектором j угол ).
|
Электрический ток и условный ток
Современное электричество — это движущиеся заряженные частицы. Если вы позволите заряду, который накапливается в статическом электричестве, течь, вы получите ток.
Ток — это скорость потока заряда; — это количество заряда, протекающего через проводник в секунду.
Уравнение для расчета тока:
Где:I = ток (амперы, A)
Q = заряд, протекающий через точку в контуре (кулоны, C)
t = время, необходимое для прохождения заряда (секунды, с)
Таким образом, ток в 1 ампер равен 1 кулону заряда, проходящего через точку каждую секунду.
Точно так же кулон — это то же самое, что и ампер-секунда!
( Примечание: , если вы построите график зависимости тока от времени, площадь под графиком будет равна перемещенному заряду.)
Ну, сначала вам нужно иметь проводник, чтобы он протекал через него, а затем вам нужно притягивать или отталкивать заряженные частицы, чтобы заставить их двигаться. Величина вашего притяжения или отталкивания измеряется в вольтах и называется напряжением или разностью потенциалов (стр.d. для краткости).
Эти заряженные частицы заставляют их двигаться, поэтому напряжение является мерой количества энергии, выделяемой на один кулон заряда.
1 вольт = 1 джоуль на кулон.
Уравнение для расчета напряжения:
Где:
Вт = количество энергии (джоуль, Дж)
В = напряжение (вольт, В)
Q = заряд (кулон, Кл)
Когда заряженные частицы обтекают контур, они не расходуются; это энергия, которую переносят заряженные частицы, которая уменьшается при движении по цепи.
(Бегуны, бегущие по беговой дорожке длиной 400 м, бегают полностью, но при беге теряют энергию).
Таким образом, ток не расходуется — если у вас есть 12 ампер, выходящих из батареи, в цепи будет 12 ампер и 12 ампер возвращаются в батарею.
Напряжение изменяется при перемещении заряда по цепи. Потенциальная энергия, отданная заряду, в контуре превращается в тепловую энергию. Электрон может покинуть батарею с напряжением 6 В, но вернется к батарее с напряжением 0 В.Это дает изменение потенциала на 6 В, отсюда и слова «разность потенциалов».
Существует два основных типа схем, о которых вам нужно знать, и у каждого из них есть два правила, упрощающих вычисления:
Последовательные цепи:
В последовательной цепи …
- ток одинаковый по всей цепи.
- напряжение делится между компонентами в цепи.
Параллельные цепи:
В параллельной цепи …
- ток делится, чтобы пройти по каждой петле.
- напряжение одинаково на каждом контуре.
Первоначально ученые полагали, что в цепях текут положительно заряженные частицы, и поэтому цепи всегда помечены током, протекающим от положительного к отрицательному выводу ячейки в цепи.Мы называем этот ток обычным током. На самом деле электроны текут в противоположном направлении!
Нажмите на кнопки ниже, чтобы увидеть это в действии:
Обычный ток — это поток положительных частиц. Все ссылки на ток в диаграммах и в вопросах на уровне A относятся к обычному току, если в вопросе специально не указано иное.
Для измерения тока используется амперметр . Он включен последовательно в цепь для измерения количества заряда, протекающего через него за секунду. (Вы можете сравнить это с турникетом, подсчитывающим людей на стадионе.)
Для измерения напряжения используем вольтметр. Он размещается параллельно для сравнения потенциала в двух разных точках по обе стороны от компонента. Затем он может измерить разность потенциалов или напряжение на компоненте.
Quantity of Electricity Chemistry Tutorial
Quantity of Electricity Chemistry Tutorial Больше бесплатных руководств Стать членом Члены Вход & тире; в Связаться с намиХотите игры по химии, упражнения, тесты и многое другое?
Вам необходимо стать членом AUS-e-TUTE!
Ключевые понятия
- Гальванический элемент (гальванический элемент) производит поток электронов.
Этот поток электронов называется электрическим током.
Ток обозначен символом I и измеряется в единицах ампер (амперы, А). - Количество заряда, проходящего через точку в электрической цепи, зависит от электрического тока и времени, в течение которого ток может течь.
Количество заряда обозначается символом Q и измеряется в кулонах (C).
- Количество заряда (или электричества), содержащегося в токе, протекающем в течение определенного времени, можно вычислить:
Q = I × т
Q = количество заряда (электричества) в кулонах (Кл)
I = ток в амперах (амперы, A)
t = время (секунды) - Это уравнение можно преобразовать для вычисления электрического тока с учетом количества заряда (электричества) и времени:
I = Q ÷ t
- Это уравнение можно переформулировать, чтобы вычислить время, затраченное на количество заряда (электричества) и электрический ток:
t = Q ÷ I
- Это уравнение можно использовать для определения количества заряда, электрического тока или продолжительности времени, необходимого для проведения эксперимента по электролизу, например:
(i) для гальваники
Промышленный пример: электролитическое рафинирование меди(ii) электролиз расплавов солей для извлечения металла
Промышленный пример: извлечение алюминия из бокситов
Промышленный пример: извлечение натрия из расплавленного хлорида содуима(iii) электролиз водных растворов для извлечения элемента:
Пример из промышленности: электролитическое извлечение меди
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Рабочий пример: расчет количества заряда
Вопрос: Рассчитайте количество заряда (электричества) Q, полученное при прохождении тока силой 25 ампер в течение 1 минуты.
Решение:
(на основе подхода StoPGoPS к решению проблем.)
- Что вас просят сделать?
Рассчитать количество заряда
Q =? C - Какие данные (информацию) вы указали в вопросе?
Извлеките данные из вопроса:
I = ток = 25 А
t = время = 1 минута
Преобразуйте время в минутах во время в секундах, умножив на 60
t = 1мин× 60 сек /мин= 60 секунд - Какая связь между тем, что вы знаете, и тем, что вам нужно выяснить?
Напишите уравнение: Q = I × t
- Подставьте значения в уравнение и решите относительно Q:
Q = 25 × 60
= 1500 С - Правдоподобен ли ваш ответ?
Работа в обратном направлении: используйте рассчитанное вами значение Q и ток, указанный в вопросе, для расчета времени, затем сравните его со временем, указанным в вопросе:
Q = 1500 С
I = 25 Аt = Q ÷ I = 1500 ÷ 25 = 60 секунд
60 секунд = 1 минутаПоскольку рассчитанное здесь время совпадает с указанным в вопросе, мы достаточно уверены, что наш ответ для Q правильный.
- Укажите свое решение задачи «рассчитать количество заряда»:
Q = 1500 C
Рабочий пример: расчет тока
Вопрос: Рассчитайте ток, необходимый для обеспечения 30 000 кулонов заряда (электричества) за 5 минут.
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Что вас просят сделать?
Рассчитать текущий
I =? А - Какие данные (информацию) вы указали в вопросе?
Извлеките данные из вопроса:
Q = 30 000 ° C
t = 5 минут
Преобразуйте время в минутах во время в секундах, умножив на 60
t = 5мин× 60 сек /мин= 300 секунд - Какая связь между тем, что вы знаете, и тем, что вам нужно выяснить?
Напишите уравнение: I = Q ÷ t
- Подставьте значения и решите для I:
I = Q ÷ t
= 30 000 ÷ 300
= 100 ампер - Правдоподобен ли ваш ответ?
Работа в обратном направлении: используйте значение тока, вычисленное выше, и количество заряда (электричества), указанное в вопросе, чтобы рассчитать затраченное время, и сравните его со временем, указанным в вопросе:
I = 100 А
Q = 30 000 ° Ct = Q ÷ I = 30,000 ÷ 100 = 300 секунд
Преобразуйте время в секундах во время в минутах, разделив на 60
t = 300сек÷ 60сек/ мин = 5 минутПоскольку время, вычисленное здесь, такое же, как и время, указанное в вопросе, мы уверены, что наше рассчитанное значение для тока верное.
- Изложите свое решение задачи «рассчитать ток»:
I = 100 А
Рабочий пример: расчет времени
Вопрос: Рассчитайте время в минутах, необходимое для получения заряда (электричества) 12 000 C с использованием тока 10 ампер.
Решение:
(На основе подхода StoPGoPS к решению проблем.)
- Что вас просят сделать?
Рассчитать время в минутах
т =? минут - Какие данные (информацию) вы указали в вопросе?
Извлеките данные из вопроса:
Q = 12 000 ° C
I = 10 А - Какая связь между тем, что вы знаете, и тем, что вам нужно выяснить?
Напишите уравнение: t = Q ÷ I
- Подставьте значения и решите для t:
т = Q ÷ I
= 12 000 ÷ 10
= 1200 секундПреобразуйте время в секундах во время в минутах, разделив на 60
t = 1,200сек÷ 60сек/ мин
= 20 минут - Правдоподобен ли ваш ответ?
Работа в обратном направлении: используйте рассчитанное вами значение времени и силы тока, указанные в вопросе, чтобы рассчитать количество заряда, и сравните это значение со значением, указанным в вопросе:
t = 20 минут = 20 × 60 = 1200 секунд
I = 10 А
Q = I × t = 10 × 1200 = 12000 ° CПоскольку вычисленное здесь значение Q совпадает со значением, указанным в вопросе, мы уверены, что наше вычисленное значение для времени является правильным.
- Укажите свое решение задачи «рассчитать время в минутах»:
t = 20 минут
Предупреждение!
Некоторое содержимое на этой странице не может быть отображено.
Пожалуйста, включите JavaScript и всплывающие окна для просмотра всего содержимого страницы.
© AUS-e-TUTEwww.ausetute.com.au
Заряд и ток — Заряд, ток и напряжение — CCEA — GCSE Physics (Single Science) Revision — CCEA
Электрический ток — это поток заряженных частиц.
В металлических проводниках заряженными частицами являются свободные электроны.
Электроны могут свободно перемещаться от одного иона к другому, и чистый поток этих электронов в одном направлении представляет собой электрический ток.
Источник энергии, такой как элемент или батарея, необходим для того, чтобы свободные электроны двигались в одном направлении.
Заряд
Электроны — это отрицательно заряженные частицы, которые передают электрическую энергию от ячейки через проводящие провода в виде электрического тока.
Заряд измеряется в кулонах , C.
Заряд электрона равен 1,6 x 10 -19 C.
Другими словами, требуется 6,250,000,000,000,000,000 электронов, чтобы составить 1 кулон заряда.
Кулон заряда — это просто очень большая группа электронов.
Связь между током I и количеством заряда Q
Электрический ток — это поток заряженных частиц.
Величина электрического тока — это скорость протекания заряда.
Ток I = \ (\ frac {\ text {количество заряда Q}} {\ text {время t}} \)
I = \ (\ frac {\ text {Q}} {\ text {t }} \)
Его часто вспоминают как:
Количество заряда Q = ток I x время t
Q = It
Где:
Q = количество заряда в кулонах, C
I = ток в амперы, А
t = время в секундах, с
| I = \ [\ frac {\ text {Q}} {\ text {t}} \] | I = Q ÷ t |
| Q = It | Q = I xt |
| t = \ [\ frac {\ text {Q}} {\ text {I}} \] | t = Q ÷ I |
Один ампер — это ток, который протекает, когда один кулон заряда проходит через точку в цепи за одну секунду.
Текущий — Физический факультет
Электрический ток
Электрический ток определяется как скорость, с которой течет заряд. Большой ток, такой как тот, который используется для запуска двигателя грузовика, перемещает большое количество заряда за короткое время, тогда как небольшой ток, такой как тот, который используется для работы портативного калькулятора, перемещает небольшое количество заряда через длительный период времени. В форме уравнения электрический ток определяется как
, где — количество заряда, проходящего через заданную область во времени.(Как и в предыдущих главах, начальное время часто принимается равным нулю, и в этом случае.) (См. (Рисунок)). Единицей измерения тока в системе СИ является ампер (А), названный в честь французского физика Андре-Мари Ампера (1775 г.). –1836). Поскольку мы видим, что ампер равен одному кулону в секунду:
Не только предохранители и автоматические выключатели рассчитаны на токи (или амперы), но и многие электрические приборы.
Скорость потока заряда текущая. Ампер — это расход одного кулона через область за одну секунду.
Расчет токов: ток в аккумуляторной батарее грузовика и портативный калькулятор
(a) Какой ток возникает, когда аккумулятор грузового автомобиля приводит в движение заряд 720 C за 4,00 с при запуске двигателя? (b) Сколько времени требуется 1,00 C заряда, чтобы пройти через портативный калькулятор, если протекает ток 0,300 мА?
Стратегия
Мы можем использовать определение тока в уравнении, чтобы найти ток в части (а), поскольку даны заряд и время.В части (b) мы изменяем определение тока и используем заданные значения заряда и тока, чтобы найти необходимое время.
Решение для (а)
Ввод заданных значений заряда и времени в определение тока дает
Обсуждение для (а)
Это большое значение тока иллюстрирует тот факт, что большой заряд перемещается за небольшой промежуток времени. Токи в этих «стартерных двигателях» довольно велики, потому что при приведении чего-либо в движение необходимо преодолевать большие силы трения.
Решение для (b)
Решение зависимости времени и ввод известных значений заряда и тока дает
Обсуждение для (б)
На этот раз чуть меньше часа. Малый ток, используемый портативным калькулятором, требует гораздо больше времени для перемещения меньшего заряда, чем большой ток стартера грузовика. Так почему же мы можем использовать наши калькуляторы всего через несколько секунд после их включения? Это потому, что калькуляторы потребляют очень мало энергии.Такие небольшие требования к току и энергии позволяют портативным калькуляторам работать от солнечных элементов или много часов использовать от небольших батарей. Помните, что у калькуляторов нет движущихся частей, как у двигателя грузовика с цилиндрами и поршнями, поэтому технология требует меньших токов.
(рисунок) показывает простую схему и стандартное схематическое изображение батареи, проводящего пути и нагрузки (резистора). Схемы очень полезны для визуализации основных характеристик схемы.Одна схема может отображать самые разные ситуации. Схема на (Рисунок) (b), например, может представлять что угодно, от аккумулятора грузовика, подключенного к фаре, освещающей улицу перед грузовиком, до небольшой батареи, подключенной к фонарику, освещающему замочную скважину в двери. Такие схемы полезны, потому что анализ одинаков для самых разных ситуаций. Нам нужно понять несколько схем, чтобы применить концепции и анализ к большему количеству ситуаций.
(а) Простая электрическая схема.Замкнутый путь прохождения тока обеспечивается проводящими проводами, соединяющими нагрузку с выводами батареи. (b) На этой схеме батарея представлена двумя параллельными красными линиями, проводящие провода показаны прямыми линиями, а зигзаг представляет собой нагрузку. На схеме представлено большое количество подобных схем.
Обратите внимание, что направление тока на (Рисунок) — от положительного к отрицательному. Направление обычного тока — это направление, по которому протекает положительный заряд .В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, например, ток переносится электронами, то есть движутся отрицательные заряды. В ионных растворах, таких как соленая вода, движутся как положительные, так и отрицательные заряды. То же самое и с нервными клетками. Генератор Ван де Граафа, используемый для ядерных исследований, может производить ток чисто положительных зарядов, таких как протоны. (Рисунок) иллюстрирует движение заряженных частиц, составляющих ток. Тот факт, что обычный ток считается направленным в направлении протекания положительного заряда, можно проследить до американского политика и ученого Бенджамина Франклина 1700-х годов.Он назвал тип заряда, связанный с электронами, отрицательным задолго до того, как стало известно, что они переносят ток во многих ситуациях. Франклин, по сути, совершенно не подозревал о мелкомасштабной структуре электричества.
Важно понимать, что в проводниках существует электрическое поле, ответственное за производство тока, как показано на (Рисунок). В отличие от статического электричества, когда проводник в равновесии не может иметь в себе электрического поля, проводники, несущие ток, имеют электрическое поле и не находятся в статическом равновесии.Электрическое поле необходимо для подачи энергии для перемещения зарядов.
Выполнение подключений: расследование на вынос — электрический ток, иллюстрация
Найдите соломинку и горошины, которые могут свободно перемещаться в соломе. Положите соломинку на стол и засыпьте ее горошком. Когда вы вставляете одну горошину с одного конца, другая горошина должна выскочить с другого. Эта демонстрация является аналогией с электрическим током. Определите, что сравнивается с электронами и с запасом энергии.Какие еще можно найти аналогии с электрическим током?
Обратите внимание, что поток гороха основан на том, что горох физически сталкивается друг с другом; электроны текут из-за взаимно отталкивающих электростатических сил.
Ток — это скорость, с которой заряд движется по площади, например по поперечному сечению провода. Обычный ток — это движение в направлении электрического поля. (а) Положительные заряды движутся в направлении электрического поля и в том же направлении, что и обычный ток.(б) Отрицательные заряды движутся в направлении, противоположном электрическому полю. Обычный ток идет в направлении, противоположном движению отрицательного заряда. Поток электронов иногда называют электронным потоком.Расчет количества электронов, проходящих через калькулятор
Если ток 0,300 мА через калькулятор, упомянутый в примере (Рисунок), переносится электронами, сколько электронов проходит через него в секунду?
Стратегия
Ток, вычисленный в предыдущем примере, был определен для потока положительного заряда.Для электронов величина такая же, но знак противоположный. Поскольку каждый электрон имеет заряд, мы можем преобразовать ток в кулонах в секунду в электроны в секунду.
Раствор
Исходя из определения тока, имеем
Делим это на заряд на электрон, так что
Обсуждение
Даже при малых токах движется так много заряженных частиц, что отдельные заряды не замечаются, так же как отдельные молекулы воды не замечаются в потоке воды.Еще более удивительно то, что они не всегда идут вперед, как солдаты на параде. Скорее они похожи на толпу людей, движущихся в разных направлениях, но имеющих общую тенденцию двигаться вперед. В металлической проволоке много столкновений с атомами и, конечно же, с другими электронами.
Скорость дрейфа
Известно, что электрические сигналы передаются очень быстро. Телефонные разговоры по проводам проходят на большие расстояния без заметных задержек. Свет загорается при нажатии переключателя.Большинство электрических сигналов, переносимых токами, передаются со скоростью порядка значительной доли скорости света. Интересно, что отдельные заряды, составляющие текущий , движутся в среднем намного медленнее , обычно дрейфуя со скоростью порядка. Как согласовать эти две скорости и что это говорит нам о стандартных проводниках?
Высокая скорость электрических сигналов является результатом того факта, что сила между зарядами быстро действует на расстоянии.Таким образом, когда свободный заряд вводится в провод, как на (Рисунок), входящий заряд толкает другие заряды впереди себя, которые, в свою очередь, проталкивают заряды дальше по линии. Плотность заряда в системе не может быть легко увеличена, поэтому сигнал передается быстро. Возникающая в результате электрическая ударная волна движется по системе почти со скоростью света. Если быть точным, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.
Когда заряженные частицы вдавливаются в этот объем проводника, такое же количество быстро вынуждено покинуть его.Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только один заряд входит, другой почти сразу уходит, быстро передавая сигнал вперед.
У хороших проводников много бесплатных зарядов. В металлах свободными зарядами являются свободные электроны. (Рисунок) показывает, как свободные электроны движутся по обычному проводнику. Расстояние, на которое может перемещаться отдельный электрон между столкновениями с атомами или другими электронами, довольно мало.Таким образом, пути электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа — это средняя скорость свободных зарядов. Скорость дрейфа довольно мала, так как свободных зарядов очень много. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем вычислить скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.
Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью, и она направлена в направлении, противоположном электрическому полю для электронов. Столкновения обычно передают энергию проводнику, требуя постоянного подвода энергии для поддержания постоянного тока.Проведение электричества и тепла
Хорошие электрические проводники также часто являются хорошими проводниками тепла.Это связано с тем, что большое количество свободных электронов может переносить электрический ток и тепловую энергию.
Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле действительно перемещает электроны на расстояние, но эта работа не увеличивает кинетическую энергию (и, следовательно, скорость) электронов. Работа передается атомам проводника, возможно повышение температуры. Таким образом, для поддержания протекания тока требуется постоянная подача энергии.Исключение, конечно же, составляют сверхпроводники по причинам, которые мы рассмотрим в следующей главе. Сверхпроводники могут иметь постоянный ток без постоянной подачи энергии — большая экономия энергии. Напротив, может быть полезен источник энергии, например, в лампочке накаливания. Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить светилась.
Установление соединений: домашнее исследование — наблюдения за нитью
Найдите лампочку с нитью накала.Внимательно посмотрите на нить и опишите ее структуру. К каким точкам подключена нить?
Мы можем получить выражение для связи между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на (Рисунок). Количество бесплатных зарядов на единицу объема обозначено символом и зависит от материала. Заштрихованный сегмент имеет объем, так что количество бесплатных зарядок в нем составляет . Таким образом, заряд в этом сегменте равен, где — сумма заряда на каждом носителе.(Напомним, что для электронов это.) Ток — это заряд, перемещаемый за единицу времени; таким образом, если все первоначальные заряды уходят из этого сегмента во времени, ток равен
Обратите внимание, что это величина скорости дрейфа, поскольку заряды перемещаются на среднее расстояние за время. Переставляя термины дает
где — ток через провод поперечного сечения из материала со свободной плотностью заряда. Каждый из носителей тока имеет заряд и движется с большой скоростью дрейфа.
Все заряды в заштрихованном объеме этой проволоки перемещаются со временем, имея скорость дрейфа величины. См. Текст для дальнейшего обсуждения.Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона намного больше его дрейфовой скорости. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые это делают, могут двигаться несколько быстрее или медленнее, чем скорость дрейфа. Итак, что мы подразумеваем под свободными электронами? Атомы в металлическом проводнике упакованы в виде решетчатой структуры.Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают притяжения ядер в такой степени, как внутренние электроны. Это свободные электроны. Они не связаны ни с одним атомом, а вместо этого могут свободно перемещаться между атомами в «море» электронов. Эти свободные электроны реагируют ускорением при приложении электрического поля. Конечно, при движении они сталкиваются с атомами в решетке и другими электронами, генерируя тепловую энергию, и проводник нагревается.В изоляторе организация атомов и структура не допускают наличие таких свободных электронов.
Основные электротехнические формулы и уравнения
Основные формулы напряжения, тока, мощности и сопротивления в цепях переменного и постоянного тока
Ниже приведены электротехнические формулы и уравнения для основных величин, т. Е. тока , напряжения , мощности , сопротивление и полное сопротивление в цепях постоянного и переменного тока (однофазные и трехфазные).
Формулы электрического токаФормулы электрического тока в цепи постоянного тока
Формулы электрического тока в однофазной цепи переменного тока
- I = P / (В x Cosθ)
- I = (В / Z)
Формулы электрического тока в трехфазной цепи переменного тока
Формулы напряжения или электрического потенциалаФормула электрического потенциала или напряжения в цепях постоянного тока
- В = I x R
- В = P / I
- В = √ (P x R)
Формулы напряжения или электрического потенциала в однофазных цепях переменного тока
- В = P / (I x Cosθ)
- В = I x Z
Напряжение Формулы для трехфазных цепей переменного тока
Формулы для электроэнергииФормулы мощности в цепях постоянного тока
- P = V x I
- P = I 9 0168 2 x R
- P = V 2 / R
Формулы мощности в однофазных цепях переменного тока
- P = V x I Cosθ
- P = I 2 x R Cosθ
- P = (V 2 / R) Cosθ
Формулы мощности в трехфазных цепях переменного тока
- P = √3 x V L x I L Cosθ
- P = 3 x V P x I P Cosθ
Формулы электрического сопротивления и импеданса в цепях постоянного тока
Формулы электрического сопротивления и импеданса в цепях переменного тока
В цепях переменного тока, емкостная или индуктивная нагрузка Сопротивление = Импеданс i.например, R = Z
- Z 2 = R 2 + X 2 … В случае сопротивления и реактивного сопротивления
- Z = √ (R 2 + X L 2 )… В случае индуктивной нагрузки
- Z = √ (R 2 + X C 2 )… В случае емкостной нагрузки
- Z = √ (R 2 + (X L — X C) ) 2 … Для индуктивных и емкостных нагрузок
Импеданс — это сопротивление цепей переменного тока i.е. резистивная, захватывающая и индуктивная цепи (уже упоминалось выше). Где «Z» — импеданс в омах, «R» — сопротивление в омах, а «X» — реактивные сопротивления в омах.
Полезно знать:
- I = ток в амперах (A)
- V = напряжение в вольтах (В)
- P = мощность в ваттах (Вт)
- R = сопротивление в Ом (Ом)
- Z = импеданс = сопротивление цепей переменного тока в Ом
- Cosθ = коэффициент мощности = разность фаз между напряжением и током в цепях переменного тока
- В PH = фазное напряжение
- В L = линейное напряжение
Также,
X L = Индуктивное реактивное сопротивление
X L = 2π f L… Где L = Индуктивность в Генри
А;
X C = Емкостное реактивное сопротивление
X C = 1 / 2π f C… Где C = емкость в фарадах.
Также ω = 2π f
[/ box]
В следующей таблице показаны уравнения и формулы тока, напряжения, мощности и сопротивления для цепей постоянного и переменного тока 1-Φ и 3-Φ.
| Количество | Постоянный ток | Однофазный переменный ток | Трехфазный переменный ток |
| Ток (I) | ) | ||
| Напряжение (В) |
|
|
|
| Мощность (P) |
|
| |
| Сопротивление (R) |
| ||
Электропроводность:
G = 1 / R
Это обратная величина (т.е.е. обратная) сопротивления. Единица проводимости — Симен или Мхо и представлена символом «G» или «℧».
Емкость:
C = Q / V
Где «C» — емкость в фарадах, «Q» — заряд в кулонах, а «V» — напряжение в вольтах. Единица измерения емкости — фарад «Ф» или микрофарад «мкФ».
Индуктивность:
В L = -L (di / dt)
Где «L» — индуктивность в Генри, «V L » — мгновенное напряжение на катушке индуктивности в вольтах, а « di / dt »- скорость изменения тока в Амперах в секунду.Единицей измерения индуктивности «L» является «H» Генри. Он также известен как закон Ома для индуктивности.
Заряд:
Q = C x V
Где Q — заряд в кулонах, C — емкость в фарадах, а V — напряжение в вольтах.
Частота:
f = 1 / T
Период времени
T = 1/ f
Где « f » — частота в герцах (Гц) «T» — это периоды времени в секундах.
Связанные сообщения:
Q = It E = QV расчеты Закон Ома V = ИК исследующие факторы, влияющие на сопротивление Характеристики графика ВАХ диод омический проводник лампа накаливания igcse / gcse 9-1 Physics revision notes
Электричество 3: Закон Ома, экспериментальные исследования сопротивления
а также I-V графики и расчеты с использованием I = V / R, Q = It и E = QV
Редакция Доктора Брауна по физике Банкноты
Подходит для курсов GCSE / IGCSE Physics / Science или их эквивалент
Что такое закон Ома? Как вы делаете расчеты по закону Ома / с?
Какие факторы влияют на стойкость схема?
Как построить и использовать схему для исследовать закон Ома?
Как рассчитать количество электричества? заряд движется по цепи?
Подиндекс этой страницы
1.Закон Ома, простая схема исследования и расчеты V = IR
2. Движение и единица заряда, кулон, расчеты с использованием Q = It
3. Возможная разница и передача электроэнергии, E = QV расчеты
4а. Электрическое сопротивление — задействованные факторы
4б. Изучение сопротивление провода при постоянной температуре, различной длины и ширины
4с.Изучение вольт-амперные характеристики провода — объяснение графика
4д. Расследование ВАХ металлической лампы накаливания — график
4e. Изучение вольт-амперные характеристики диода — объяснение графика
См. Также ПРИЛОЖЕНИЕ 1 для обзора всей электроэнергии уравнения вам могут понадобиться
1а.Ома Закон (и упоминание других единиц, рассматриваемых в других разделах)
Закон Ома гласит, что ток через провод между двумя точками прямо пропорционален напряжению на две точки в цепи.
Он включает в себя самое фундаментальное уравнение что нужно знать для расчета электричества.
Математически это можно выразить как: я = V / R
перестановок: В = ИК а также R = V / I
I = ток в амперах, амперах, А ; мера скорости потока электрического заряда.
В = разность потенциалов, п.о., вольт, V ; мера потенциальной энергии, передаваемой электрическому заряду течет.
Разность потенциалов в цепи это энергия, передаваемая на один кулон электрического заряда , что течет между двумя точками в электрической цепи.
Кулон ( C ) — это единица электрического заряда (см. Q = это примечания к уравнению).
Передаваемая энергия рассчитывается от п.о. и количество электрического заряда ( Q ) перемещен p.d. в V (см. E = QV примечания к уравнениям).
R = сопротивление провода, Ом, Ом ; мера сопротивления проводника препятствовать поток заряда.
Чем больше сопротивление резистор, тем больше он сопротивляется и замедляет ток электричества.
Закон Ома означает, что R в этом уравнении является константой, не зависящей от величины протекающего электрического тока.
Закон правильно применяется к так называемому омическому сопротивлению . проводники , где протекающий ток прямо пропорционален приложенная разность потенциалов, но некоторые резисторы не подчиняются этому закону, например нагретая нить лампочка.
1b.Просто эксперимент по измерению сопротивления отдельного компонента
Если вы настроили схему 31 (правая диаграмма), вы можете измерить сопротивление постоянного резистора [R].
Изменяя напряжение источника питания с помощью переменной резистора, вы легко можете получить множество пар показаний p.d. (V) и текущее (А).
Затем используйте уравнение закона Ома (R = V / I), чтобы вычислить значение фиксированное сопротивление.
Затем вы можете усреднить значения R, рассчитанные для более надежный результат.
Более подробная информация приведена ниже, чтобы получить полную ВАХ графики, а также как получить сопротивление графическим методом.
Это основная установка для исследования ВАХ любого компонента Р.
1c. Примеры расчеты с использованием Ома Закон V = IR
Q1 Когда стр.d. от 4,5 В приложен к сопротивлению, течет ток 0,5 А.
Какое значение имеет резистор?
R = V / I = 4,5 / 0,5 = 9,0 Ом
Q2 Сопротивление имеет значение 50 Ом.
Какой п.о. должен быть применен к нему чтобы через него протекал ток 5,0 А?
V = ИК = 5 x 50 = 250 V
3 квартал А п.d. 240 В подается на резистор нагревательного элемента сопротивлением 30 Ом.
Сколько тока проходит через обогреватель?
I = V / R = 240/30 = 8.0 А
4 квартал Три батареи на 1,5 В были подключены последовательно к трем лампочкам.
Если амперметр измеряет ток 0,50 А, какое сопротивление у каждой лампочки?
I = V / R, поэтому R = V / I = (3 x 1.5) / 0,50 = 9,0 Ом
Так как общее сопротивление = сумма сопротивления, сопротивление каждой лампочки = 9,0 / 3 = 3.0 Ом
Q5
ВЕРХ СТРАНИЦЫ и субиндекс
2. Движение заряда
2а. Расчет заряда, проходящего через точку в цепи Q = It
Ток (I в амперах) — это скорость протекания электрического заряжать вокруг цепи.
Чем больше поток заряда в данный момент времени, тем больше электрический ток.
Скорость протекания электрического заряда равна измеряется в кулонах в секунду.
Вы можете рассчитать заряд, проходящий через точку в цепи в в заданное время по формуле
Q = Оно
, где Q = электрический заряд в кулонах ( C ) — блок электрического заряда
I = ток в амперах ( A ) и t = время ( с )
перестановок из Q = It, I = Q / т и t = Q / I
Ток в 1 А равен скорость потока заряда 1 Кл / с.
2b. Примеры расчетных вопросов с участием уравнение Q = It
Q1 Если ток 3,0 А проходит через прибор в течение 1 часа 30 минут, сколько электрического заряда передается в процессе?
Q = It, Q = 3,0 x 1,5 x 60 x 60 = 16 200 C = 1,62 х 10 4 С
Q2 Если Заряд 9000 C проходит через точку в электрической цепи в 12.0 минут, какой текущий поток?
I = Q / t = 9000 / (12 x 60) = 9000/720 = 12,5 А
Q3 Сколько времени займет электрическая цепь в минутах и секундах ток 20.0 А передать 5000 С заряда?
t = Q / I = 5000/20 = 250 секунд = 4 минут и 10 секунд
Q4 Портативный компьютер зарядное устройство пропускает ток 1.20 А на 30 минут с выходом p.d. 15.0 В.
(a) Рассчитайте, сколько заряда перенесена в компьютерную батарею.
Q = It = 1,2 х 30 х 60 = 2160 С
(б) Какое сопротивление зарядное устройство?
В = ИК, R = V / I = 15 / 1,2 знак равно 12,5 Ом
(c) Когда аккумулятор ноутбука полностью заряжено в нем хранит 3000 с.
Сколько времени потребуется, чтобы полностью заряжать разряженный аккумулятор?
Q = It, t = Q / I = 3000 / 1,2 = 2500 с (41 мин 40 с)
Q5
ВЕРХ СТРАНИЦЫ и субиндекс
3. Возможная разница и передача энергии
3а.Введение в электрическую энергию передача
Передача энергии на единицу заряда = разность потенциалов (п.о.) и расчеты на основе E = QV
В предыдущем разделе мы рассмотрели, как рассчитать количество заряда, движущегося в цепи, но ничего не сказал об энергии переведен.
Напоминания :
Электрические цепи, используемые термины, условные обозначения цепей, параллельные объяснение цепей и последовательных цепей
Разность потенциалов (стр.d. в вольт, В ) — энергия, передаваемая на единицу заряда в виде электрического заряд перемещается из одной точки в другую в электрической цепи.
Измеряется вольтметром, который всегда подключается параллельно через компонент схемы.
Передает электрический ток энергия
Подумайте обо всех электрических бытовые приборы, которыми вы пользуетесь — все они нуждаются в подаче энергии для работы!
Блок питания работает на заряжается и передает ему энергию.
Работа должна производиться на зарядке для увеличения его потенциальной энергии.
Электрический заряд измеряется в кулоны (C)
Заряд и его движение уже было рассмотрено в раздел 2 (Q = It).
Заряды передают энергию компонентов по мере их прохождения, выполняя работу против сопротивления компонент.
Если работа сделана, то энергия переведен.
Если электрический заряд испытывает разность потенциалов, этот заряд будет течь, передавая энергию.
Энергия подается из энергоаккумулятора источник питания — аккумулятор, электросеть и т. Д.
При прохождении заряда по любому р.d. Падение высвобождает энергию (с более высокого уровня потенциальной энергии на более низкий).
например в тонкой проволоке сопротивление , выделяется тепло.
Разница потенциалов между двумя баллов равняется проделанной работе на единицу заряда.
разность потенциалов (В) = проделанная работа ( энергия передано в Дж) заряд (К)
т.е. 1 вольт соответствует 1 джоуля за кулон или V = J / C
Чем больше падение в р.д., тем больше энергия передается, потому что заряд начинается с большим потенциалом энергия.
Следовательно, блок питания с большим источником шт. (В) может подавать на больше энергии в схему на единицу электрического заряда ( кулон, В).
Чем больше p.d., тем больше энергии такое же количество электрический заряд может нести.
3b.Еще одно уравнение для расчета электрического передача энергии
В количество переносимой энергии можно рассчитать по формуле:
переданная энергия = заряд x потенциал разница.
E = QV (поэтому Q = E / V и V = E / Q )
E = передаваемая энергия в джоулях ( Дж )
Q = количество электрический заряд в кулонах ( C )
В = разность потенциалов ( В )
отмечая, что: V = E / Q = энергия, передаваемая на единицу заряда (Дж / К)
Попутно и несколько напоминаний:
Чем больше энергии передается в данном время, тем больше мощность устройства или электроприбора.
г. V говорит вам, сколько энергия на каждую единицу передачи электрического заряда, 900 · 10
так, V = E / Q , (шт. J / C), см. Расчеты E = QV ниже).
Текущий I говорит вам, сколько заряд проходит заданную точку в цепи за единицу времени (кулонов в секунду, К / с ).
Это означает, что оба p.d. В и текущий I влияет на скорость передачи энергии устройству из накопителя электроэнергии в другие накопители энергии.
И некоторые математические связи на основании раздела 2. Q = It, а здесь, в разделе 3, E = QV
Из Q = It и E = QV, подставляя дает E = ItV,
так (i) E = IVt (I в A, t в с, В в вольтах)
Перестановка E = IVt дает IV = Е / т
Это соединяется с уравнения для мощности
(ii) Мощность = энергия переведено / время получено = E / t (Дж / с), и
( iii ) Мощность = ток x напряжение = P (Вт) = I (A) x V (В), Р = IV
Из (ii) и (iii) E / t = IV, поэтому E = IVt , что является уравнением (i) !!!
3c.Расчет q использование на основе E = QV (иногда с участием других уравнений электричества)
Q1 Электродвигатель Модель автомобиля питается от аккумулятора 1,5 В.
Если 120 C заряда проходит через цепь двигателя в движущемся вагоне,
(а) сколько энергии передается?
E = QV = 120 x 1,5 = 180 Дж
(b) Опишите вероятный накопитель энергии меняется, когда машина работает.
Химическая потенциальная энергия запас батареи уменьшается и превращается в электрическую энергию.
Накопитель кинетической энергии автомобиль увеличивается из-за потери тепла от трения и звуковой энергии переданы в накопитель тепловой энергии окрестностей.
Q2 Какое количество заряд необходим для передачи 500 Дж энергии, если п.о.цепи 24,0 В?
E = QV, Q = E / V = 500/24 = 20,8 С (3 SF)
Q3 Какой потенциал разность требуется в цепи для передачи 2000 Дж энергии с заряд 50 кулонов?
E = QV, V = E / Q = 2000/50 = 40 В
4 квартал А 12.Батарея 0 В пропускает через лампу ток 2,0 А в течение 5 минут.
(а) Рассчитайте, сколько заряда прошло через лампу.
Q = It = 2 x 5 x 60 = 600 С
(b) Рассчитайте, сколько электроэнергии был перенесен лампой.
Два пути:
(i) E = QV = 600 x 12 = 7200 Дж, самый простой, но вы можете рассчитать его, не зная Q, из:
(ii) E = IVt = 2 x 12 x 5 x 60 = 7200 Дж
5 квартал Устройство имеет мощность 1.5 кВт и работает от сети 230 В.
Если прибор используется в течение 15 минут, сколько заряда прошло по цепи?
1,5 кВт ≡ 1500 Вт ≡ 1500 Дж / с
Общая переданная энергия = мощность x время = 1500 x 15 x 60 = 1 350 000 Дж
E = QV, поэтому Q = E / V = 1350 000/230 = 5870 С (3 SF)
Ответ можно рассчитать по другой маршрут
P = IV, I = P / V = 1500/230 = 6.522 A
Q = It = 6,522 x 15 x 60 = 5870 С (3 SF)
Q6
3d. Еще немного о разности потенциалов — действие двух последовательно соединенных резисторов
На схеме 41 показаны два подключенных резистора. последовательно.
Справа показано, что происходит с p.d. по часовой стрелке по цепи (направление условного тока).
Повышается потенциальный запас аккумулятора разность потенциалов заряда до 12 В.
По мере прохождения заряда через 1-й резистор R 1 , он теряет энергию и п.д. падает на 8 В до п.п. из 4 В.
По мере прохождения заряда через 2-ю резистор R 1 , он снова теряет энергию и п.о. падает на 4 В до p.d. из 0 В.
Пока есть полная цепь, процесс повторяется.
Поскольку E = QV, выделяется вдвое больше энергии резистором R 1 (p.d. 8 В), чем R 2 (p.d. 4 В) для тот же ток.
ВЕРХ СТРАНИЦЫ и субиндекс
4. Электрическое сопротивление — эксперименты по исследовать ВАХ различных сопротивлений и достоверность, или в противном случае Закона Ома
4а. Что влияет на сопротивление провода? Сопротивление постоянный?
и s графики вольт-амперных характеристик (ВАХ) объяснил
Сопротивление цепи зависит от несколько факторов:
(i) толщина сопротивления провод — для однокомпонентного резистора
(ii) длина сопротивления провод — для однокомпонентного резистора
(iii) если более одного сопротивления, они подключены последовательно или параллельно?
(iv) температура компонента действует как сопротивление
Раздел 4.описывает и объясняет несколько примеров графиков ВАХ — которые можно исследовать с помощью схемы 31 (справа)
На принципиальной схеме 31 справа показано как можно исследовать изменение тока через сопротивление (или любой компонент) при изменении разности потенциалов.
Графики разности потенциалов тока используются, чтобы показать, как ток через компонент изменяется в зависимости от разности потенциалов на нем.
Сопротивление некоторых резисторов / компонентов действительно меняется. как действующий и п.д. изменения например диодная или лампа накаливания.
Узнайте, как и почему в разделах 4d. и 4e.
ВЕРХ СТРАНИЦЫ и субиндекс
4b. Исследование электрического сопротивления провода — изменение длины или ширины
Схема 30 показывает, как исследовать сопротивление провода
Относительно тонкая проволока закреплена на каждый конец на линейке с разметкой в миллиметрах с помощью зажимов типа «крокодил».
Вам понадобится амперметр для измерения ток в амперах и вольтметр для измерения p.d. через провод в вольт.
Провод соединен в серии с аккумуляторным блоком питания, переключателем и амперметром для измерения силы тока течет по проводу в амперах.
Вольтметр , для измерения p.d, есть подключен параллельно через резистивный провод.
Обратите внимание, что амперметр всегда подключается к последовательно с компонентом , но вольтметр всегда подключается параллельно по любому исследуемому компоненту.
Один конец провода, подключенный через вольтметр закреплен (слева), но на другом конце есть зажим типа «крокодил», который действует как подвижный точки контакта для размещения на различном расстоянии вдоль провода сопротивления от слева направо.
Замкните выключатель, чтобы замкнуть цепь и начинаем снимать показания.
Лучше всего открыть переключатель между показания, чтобы свести к минимуму риск нагрева провода.
Вы изменяете расстояние d (мм) от слева (0 мм) в точку дальше вправо и возьмите серию пар из п.d и текущие показания, например каждые 50 мм (можно работать в см, получается нет разницы!).
Используя закон Ома, вы вычисляете сопротивление в омах из уравнения R = V / I
Ты затем можно построить график зависимости сопротивления (Ом) от длины провода d (мм) — показано справа.
Вы должны обнаружить, что график является линейным с его начало координат x, y в точке 0,0.
Это означает, что сопротивление пропорционально длине провода .
Если не закрепить провод точно на 0 мм, график по-прежнему должен быть линейным, но начало линии не будет быть 0,0.
Если повторить эксперимент с провода разного диаметра, вы должны обнаружить, что градиент становится ниже, толще проволока.
Для провода той же длины сопротивление меньше толще проволока — хорошая аналогия — легкость, с которой вода течет через труба тонкого или большего диаметра.
ВЕРХ СТРАНИЦЫ и субиндекс
4c. Изучение ток — напряжение характеристики проволоки
Это эксперимент по закону Ома
Схема 31 показывает, как исследовать, как I изменяется в зависимости от V для сопротивления
.Расследование сводится к поиску из …
… как ток течет через резистор меняются в зависимости от разности потенциалов на нем?
Постоянный резистор представляет собой ‘компонент’ в цепи и должен иметь постоянную температуру на протяжении всего эксперимента (см. ниже температура эффекты).
В этом случае простой проволочный резистор соединены последовательно с блоком питания и амперметром.
г. измеряется по фиксированному сопротивление с вольтметром,
Тем не мение, также подключенный последовательно, добавлен переменный резистор, так что вы можете удобно изменить разность потенциалов и тем самым изменить ток протекает через компонент.
Это позволяет собрать целую серию пар показаний I и V, с помощью которых можно построить подходящие графики — в этом случай V против I, но часто делается как I против V.
Используя переменный резистор, вы постепенно увеличивайте разность потенциалов на компоненте, принимая соответствие текущему чтению, например увеличиваясь на 0,5 В. за раз. Повторите каждый читать дважды и использовать среднее значение.
После этого можно поменять местами клеммы аккумулятора и повторить все показания.
Если вы построите p.d. по сравнению с текущим, график линейный , если он подчиняется закону Ома — тогда он называется ‘ омический кондуктор ‘.
Это я изобразил графиком вверху справа, а градиент равен сопротивлению в Ом .
Это соответствует закону Ома . уравнение V = IR , поэтому градиент равен R .
Если график остается линейным, сопротивление остается постоянным.
Этот график не представляет показания сняты после перестановки полюсов аккумулятора.
Однако показывает, как получить значение сопротивления графическим методом.
Это линейный график и фраза линейный компонент может использоваться.
Для таких компонентов, как провод, который не нагревается, вы должны получить линейный график p.d. (V) против I (A) с градиент R (Ω). (правый график).
Вы должны убедиться, что провод не сильно нагревается — если начинает нагреваться, сразу отключите резистор («выключите») и дайте ему остыть.
Если вы построите график зависимости I от V, градиент будет 1 / R (обратная величина сопротивление), линейный график .
Этот график показывает, что вы получаете построение всех данных, включая показания I-V, снятые после реверсирования клеммы аккумулятора.
График (1) является построенный на поперечной оси. Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Обратите внимание, что вы получите только линейный график, если температура проволоки остается постоянной .
Когда ток (А) пропорционален к p.d (V) он описывается как омический провод (подчиняется закону Ома!).
С помощью схемы 31 вы можете проверить любой резистор или любой другой тип компонента схемы, и результаты обсуждается ниже, начиная с резюме факторов, влияющих на сопротивление.
Так, сопротивление омического проводника, например цепь компонент не меняется независимо от того, проходит ли ток — постоянный градиент 1 / R для графика 1.
Это ожидаемые линейные графики для фиксированный резистор с использованием схемы 31 выше.
Думая против часовой стрелки на диаграмме, разные линии графика могут отображать убывающее сопротивление е.грамм. (i) резистивный провод становится короче при том же диаметре, или (ii) увеличение диаметра при фиксированной длине провода.
При постоянной температуре ток, протекающий через омический проводник прямо пропорционален разности потенциалов на это — уравнение V = IR или I = V / R .
Однако это только правда, так как линейный график, если температура не изменение.
Комментарии к переменным в этом частный эксперимент с законом Ома
Ток всегда определяется комбинация п.о. (В) и сопротивление R (Ом).
Независимая переменная что мы изменяем или контролируем в эксперименте — в этом случае вы можете считать его р.д. управляется переменным резистором.
Одно из соглашений состоит в том, чтобы построить график независимая переменная на оси абсцисс, а зависимая переменная на оси ось y.
Этот означает, что сопротивление R, является обратной величиной градиента — немного больше неудобно рассчитать сопротивление, чем на графике V в зависимости от I, где градиент — это сопротивление. Закон Ома: I = В / р.
Зависимая переменная — это то, что мы тестируем или измеряем в эксперименте, это ток I (A), который зависит от настройки переменного резистора, который, в свою очередь, контролирует разность потенциалов на резисторе.
Управляющие переменные — это то, что мы сохраняем то же самое во время эксперимента, чтобы убедиться, что это честный тест например в этом случае провод и температура сохраняются постоянная, НЕ должна изменяться — не меняйте провод и не допускайте нагреть.
ВЕРХ СТРАНИЦЫ и субиндекс
4г.
Исследование вольт-амперных характеристик металла
лампа накаливания
Когда электрический заряд проходит через высокое сопротивление, как тонкая металлическая нить лампы накаливания, она передает часть электроэнергия к накопителю тепловой энергии нити накала. Электрический заряд делает работают против сопротивления .
Схема 45 показывает, как можно исследовать характеристики разности токов и потенциалов нить лампочка.
Вольтметр подключен параллельно термистор, п.д. В измеряется в вольтах ( В ).
Переменный резистор позволяет варьировать п.д. и текущий поток.
Амперметр, подключенный последовательно, дает текущее значение I в амперах ( A ).
В прохождение тока нагревает нить накала и поднимается в температура вызывает повышение сопротивления . Итак, нить Лампа представляет собой неомический провод .
Этот «эффект нагрева» влияет на все резисторы.
По мере увеличения тока выделяется больше тепловой энергии, и нить накаливания становится все горячее и горячее, поэтому дальнейшее повышение температуры еще больше увеличивает сопротивление.
Уменьшает скорость увеличения тока с увеличение разности потенциалов .
Следовательно, градиент I-V кривая графика уменьшается, и все больше с увеличением температура — график 2. Это нелинейный график .
Если градиент меняется, тогда сопротивление меняется.
График (2) является построенный на поперечной оси.Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Фраза нелинейная компонент может быть использован.
Когда ток (А) равен НЕ пропорциональная p.d (V) лампа накаливания описывается как неомический провод (не подчиняется закону Ома!).
У вас такой же график в форме треугольника. для термистор.
Теория — со ссылкой на схему металлической конструкции
Металлическая кристаллическая решетка состоит из неподвижных ионов и свободно движущихся электроны между ними. С повышением температуры ионы металлов колеблются сильнее. сильно, в котором электроны сталкиваются, и это препятствует прохождению электронов, уменьшая поток плата. По мере увеличения тока вибрации увеличиваются, вызывая больше электрической энергии, которая будет преобразована в тепло — увеличивая температура И сопротивление металлической нити, тем самым еще больше понижая ток.
Итак, увеличиваем i n по температуре увеличивает сопротивление лампы накаливания (или большинства других резисторы) и снижает ток, протекающий для заданного p.d.
Если резистор становится слишком горячим, ток почти не будет течь.
Есть одно важное исключение к этому «правилу» см. примечания к термистор, где сопротивление фактически падает с повышение температуры.
Лампа накаливания — лишь одна из многих примеры были энергия передается с пользой , НО есть всегда теряется тепловая энергия в накопитель тепловой энергии устройства и Окрестности .
Нить накала часто изготавливается из металлический вольфрам, плавящийся при> 3400 o C и ярко светящийся при 2500 o C, но он все равно испаряется очень медленно. Инертный газ например, добавляется аргон или азот, чтобы уменьшить это испарение — любое испаренные атомы вольфрама попадают в инертный (и, следовательно, неокисляющий) Ar или N 2 молекул и, надо надеяться, снова конденсируются на нити.
См. Сохранение энергии, передача-преобразование энергии, эффективность — расчеты
ВЕРХ СТРАНИЦЫ и субиндекс
4e. Исследование вольт-амперных характеристик диода
Модель ток через диод протекает только в одном направлении — см. график 3.
Сопротивление в обратном направлении очень высока — следовательно, это фактически «односторонняя» система.
Цепь 43 показывает, как можно исследовать вольт-амперная характеристика диода.
Вольтметр подключен параллельно термистор, п.д. В измеряется в вольтах ( В ).
Переменный резистор позволяет варьировать п.д. и текущий поток.
Амперметр, подключенный последовательно, дает текущее значение I в амперах ( A ).
Диод имеет очень высокое сопротивление в обратное направление .
Также есть порог р.о. (например, 1,4 В) до того, как ток вообще потечет — внимательно посмотрите на график — есть короткий горизонтальный участок, прежде чем ток поднимется с нуля и со временем становится линейным.
Таким образом, вы получаете верхнюю правую часть графика 3 по сравнению с графиками 1 и 2 выше.
Это потому, что когда вы делаете экспериментируйте, используя схему, описанную выше, по изменению подключений, вы не обнаружите никаких текущих потоков при изменении p.d.
Его нелинейный График .
Если градиент меняется, то сопротивление меняется.
Когда ток (А) равен НЕ пропорциональный p.d (V), диод описывается как неомический провод (не подчиняется закону Ома!).
Фраза нелинейный компонент может быть использовано.
График (3) является построенный на поперечной оси. Верхняя правая половина — это ваш первый набор результатов, затем вы переверните клеммы на источнике питания и повторите эксперимент дает нижнюю левую часть графика.
Так как ток течет только в одну сторону через диод его можно использовать для преобразования переменного тока в постоянный Текущий.
ВЕРХ СТРАНИЦЫ и субиндекс
Практическая работа по помощь в развитии ваших навыков и понимания, возможно, включала следующее:
использование ламп накаливания и резисторов для исследования разности потенциалов — Текущий характеристики,
ПРИЛОЖЕНИЕ 1: Важные определения, описания, формулы и ед.
|
ВЕРХ СТРАНИЦЫ и субиндекс
Что дальше?
Электричество и ревизия магнетизма индекс нот
1.Полезность электроэнергии, безопасность, передача энергии, расчеты стоимости и мощности, P = IV = I 2 R, E = Pt, E = IVt
2. Электрические схемы и как их рисовать, условные обозначения схем, параллельность схемы, объяснение последовательных схем
3. Закон Ома, экспериментальные исследования сопротивление, I-V графики, расчеты V = IR, Q = It, E = QV
4. Схемы устройств и как они используются? (е.грамм. Термистор и LDR), соответствующие графы GCSE пересмотра физики
5. Подробнее о последовательных и параллельных цепях. электрические схемы, измерения и расчеты gcse физика
6. Электроснабжение «Национальной сети», экология вопросы, использование трансформаторов gcse примечания к редакции физики
7. Сравнение способов производства электроэнергии gcse Заметки о пересмотре физики (энергия 6)
8.Статическое электричество и электрические поля, использование и опасность статического электричества gcse примечания к редакции физики
9. Магнетизм — магнитные материалы — временные (индуцированные) и постоянные магниты — использует gcse физика
10. Электромагнетизм, соленоидные катушки, применение электромагнитов gcse примечания к редакции физики
11. Моторное воздействие электрического тока, электродвигатель, громкоговоритель, правило левой руки Флеминга, F = BIL
12.Эффект генератора, приложения напр. генераторы производство электричества и микрофон gcse физика
ВСЕ мои GCSE Примечания к редакции физики
ИЛИ воспользуйтесь [GOGGLE ПОИСК]
Версия IGCSE заметки по закону Ома исследования сопротивления V = IR Q = It вычисления KS4 физика Научные заметки на Исследование сопротивления по закону Ома V = IR Q = It расчеты GCSE руководство по физике примечания к закону Ома исследования сопротивления V = IR Q = It расчеты для школ, колледжей, академий, научных курсов, репетиторов, изображений рисунки-диаграммы для исследования сопротивления по закону Ома V = IR Q = Он вычисляет научные исправления примечания на Исследование сопротивления по закону Ома V = IR Q = It расчеты для пересмотра модулей физики примечания по темам физики, чтобы помочь в понимании Исследование сопротивления по закону Ома V = IR Q = It расчеты университетские курсы физики карьера в науке и физике вакансии в машиностроении технический лаборант стажировка инженер стажировка по физике США 8 класс 9 класс 10 AQA Заметки о пересмотре GCSE 9-1 по физике по закону Ома исследования сопротивления V = IR Q = It вычисления GCSE примечания к закону Ома исследования сопротивления V = IR Q = It расчеты Edexcel GCSE 9-1 физика наука примечания к редакции Исследование сопротивления по закону Ома V = IR Q = It расчеты для OCR GCSE 9-1 21 век научные заметки по физике об исследованиях сопротивления по закону Ома V = IR Q = Расчет OCR GCSE 9-1 Шлюз физики примечания к пересмотру исследований сопротивления по закону Ома V = IR Q = It вычисления WJEC gcse science CCEA / CEA gcse science
ВЕРХ СТРАНИЦЫ и субиндекс
.



 Чистый заряд в движении тогда q = neAv d т.
а ток I = q / t = neAv d .
Чистый заряд в движении тогда q = neAv d т.
а ток I = q / t = neAv d . 2а ниже)
2а ниже)

 Сумма токов, входящих в любой переход
равна сумме токов, выходящих из этого перехода. Этот
это просто заявление о сохранении заряда.
Сумма токов, входящих в любой переход
равна сумме токов, выходящих из этого перехода. Этот
это просто заявление о сохранении заряда.