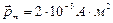Закон Ампера (сила, действующая на проводник с током в магнитном поле)
 ,
,  ,
,
где  – сила тока в проводнике,
– сила тока в проводнике, 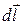 – элемент проводника,
– элемент проводника,  – магнитная индукция поля,
– магнитная индукция поля,  – угол между векторами
– угол между векторами 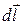 и
и 
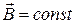 ) сила Ампера, действующая на прямолинейный проводник длиной
) сила Ампера, действующая на прямолинейный проводник длиной  ,
, .
.
Максимальная сила при 
 .
.
Связь магнитной индукции 
 магнитного поля
магнитного поля ,
,
где μ – магнитная проницаемость изотропной среды; μ0 – магнитная постоянная.
Закон Био-Савара-Лапласа
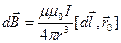 или
или  ,
,
где 
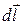 с током I;
с током I; 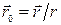 – единичный вектор радиус-вектора
– единичный вектор радиус-вектора 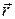 , направленный от элемента проводника к точке, в которой определяется магнитная индукция; α – угол между направлением элемента провода
, направленный от элемента проводника к точке, в которой определяется магнитная индукция; α – угол между направлением элемента провода 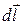 и радиус-вектором
и радиус-вектором 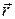
Магнитная индукция в центре кругового тока
 ,
,
где R – радиус кругового витка.
Магнитная индукция на оси кругового тока
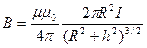 ,
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока


где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током (рис. 1.1),
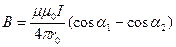 .
.
 Обозначения ясны из рисунка. Направление вектора магнитной индукции обозначено точкой – это значит, что В направлен перпендикулярно плоскости чертежа к нам.
Обозначения ясны из рисунка. Направление вектора магнитной индукции обозначено точкой – это значит, что В направлен перпендикулярно плоскости чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция, –cos
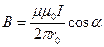
Магнитная индукция поля соленоида
В = μμ0nI,
где n – отношение числа витков соленоида к его длине.
Магнитный момент плоского контура с током

где 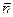 – единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
– единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
 или М = pmBsinα,
или М = pmBsinα,
где α – угол между векторами 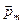 и
и 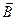 .
.
Сила Лоренца
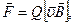 или
или 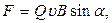
где  – скорость заряженной частицы;
– скорость заряженной частицы;  – угол между векторами
– угол между векторами  и
и 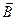 .
.
Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение

Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
Ф = BScosα или Ф = BnS,
где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции:
б) в случае неоднородного поля и произвольной поверхности
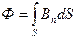
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток)
Ψ = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
А = IΔФ.
ЭДС индукции
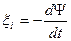 .
.
Разность потенциалов на концах провода, движущегося со скоростью u в магнитном поле,
U = Blusinα,
где l – длина провода; α – угол между векторами  и
и 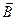 .
.
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур,
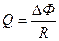
 ,
,где R – сопротивление контура.
Индуктивность контура
 .
.
ЭДС самоиндукции
 .
.
Индуктивность соленоида
L = μμ0n2V,
где n – отношение числа витков соленоида к его длине; V – объем соленоида.
Период электромагнитных колебаний в контуре, состоящем из емкости

Если мало сопротивление R, то период колебаний определяется формулой Томсона

где L – индуктивность; C – электроемкость.
Если R не равно нулю, то колебания будут затухающими, и напряжение на емкости будет меняться по закону
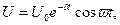
здесь δ = R/2L – коэффициент затухания; χ = δT
Если δ = 0, то колебания будут незатухающими

Закон Ома для переменного тока
Iэф = Uэф/Z
где Iэф и Uэф – эффективные значения тока и напряжения связанные с их амплитудными значениями I0 и U0

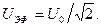
Полное сопротивление цепи переменного тока

При этом сдвиг фаз между напряжением и током определяется по формуле

Мощность переменного тока
P = IЭФUЭФcosφ
Связь между длиной и частотой электромагнитной волны

где λ — длина волны; ν — частота колебаний; c – скорость света в вакууме.
План решения задач
1. При расчете силы Ампера, действующей на проводник с током в магнитном поле, решение следует начать с рисунка, на котором нужно отразить форму проводника и направление вектора магнитной индукции поля, в котором находится проводник.
2. Необходимо иметь в виду, что формула силы Ампера справедлива только для прямого проводника с током длиной , который находится в однородном магнитном поле с индукцией . В случае неоднородного МП, а также для проводника криволинейной формы, проводник следует разделить на элементы тока и показать на рисунке векторы сил , действующих на элементы тока. Для этого необходимо выбрать два элемента тока, расположенных симметрично. Направление векторов определяем по правилу векторного произведения или по правилу левой руки: располагаем руку так, чтобы линии магнитной индукции входили в ладонь, четыре пальца направляем вдоль тока , тогда отогнутый большой палец покажет направление силы Сила, действующая на весь проводник, определяется как сумма векторов элементарных сил по всей длине проводника :
.
3. Свободный замкнутый контур с током (рамка или виток) устанавливается в магнитном поле так, чтобы его магнитный момент был сонаправлен с вектором магнитной индукции . При этом механический (вращающий) момент , а силы Ампера , действующие на элементы тока контура, растягивают его. Такое положение ( контура с током в однородном магнитном поле является состоянием устойчивого равновесия контура.
Задача 32. По трем параллельным прямым проводникам, находящимся на одинаковом расстоянии друг от друга (рис. 63 а) текут одинаковые токи В двух проводниках направления токов совпадают. Вычислите для каждого проводника силу, действующую на единицу длины проводника.
Дано Решение
Сначала рассмотрим взаимодействие двух проводников – первого и второго (рис. 63 б). На второй проводник с током действует магнитное поле с индукцией , созданное током в первом проводе (соответственно, и на первый проводник действует магнитное поле , созданное вторым проводом). Выберем на втором проводнике элемент тока , проведем линию магнитной индукции (это окружность радиусом ) и по касательной к ней направим вектор . Сила Ампера, действующая на выбранный элемент тока второго проводника со стороны МП первого тока
(1)
Модуль этой силы
, (2)
где угол между векторами и (линия магнитного поля расположена в плоскости, перпендикулярной проводу). Согласно формуле (2), сила, действующая со стороны первого провода на единицу длины второго провода:
(3)
В формуле (3) индукция МП, созданная прямым длинным проводом с током в точках на расстоянии от провода, определяется следующим выражением:
(4)
Направление силы определяем по правилу левой руки, располагая ладонь в плоскости рисунка: элемент тока притягивается к первому проводнику. По третьему закону Ньютона, на элемент тока первого проводника будет действовать сила , т. е. равная по модулю (см. формулу (3)) и противоположно направленная (см. рис. 63 б). Таким образом, параллельные токи одинакового направления притягиваются друг к другу. Изменим мысленно на рис. 63 б направление второго тока на противоположное (как ток ) и правило левой руки покажет, что сила, действующая на элемент тока , направлена вправо, т. е. параллельные токи противоположных направлений взаимно отталкиваются.
На каждый из проводников действуют магнитные поля двух других токов. Величину каждой силы парного взаимодействия -того и -того проводов запишем, подставляя индукцию магнитного поля, определяемую формулой (4) (в данной задаче ), в формулу (3):
. (5)
В соответствии с полученным выражением (5), величина силы парного взаимодействия на единицу длины одинакова для каждого проводника.
Результирующую силу, действующую на каждый проводник, находим с помощью принципа суперпозиции сил:
(6)
Покажем эти силы магнитного взаимодействия токов на рис. 63 в, учитывая, во-первых, взаимное направление токов, и во-вторых, равенство модулей всех сил парного взаимодействия . На рисунке заменим элементарную силу силой, действующей на весь i-тый провод со стороны -того тока, так как эти силы сонаправлены: .
Согласно формулам (6), сложим по два вектора сил, действующих на каждый проводник, геометрически: по правилу параллелограмма (треугольника) (см. рис. 63 в). Так как треугольники, имеющие сторонами векторы сил , равносторонние, то модули этих сил
(7)
Модуль силы найдем по теореме косинусов:
(8)
Силы, действующие на единицу длины провода, с учетом формулы (5), представятся выражениями, соответствующими формулам (7) и (8):
; (9)
(10)
Вычисляем силы: а) на единицу длины первого и второго провода:
.
б) на единицу длины третьего провода:
.
Задача 33. Квадратная проволочная рамка со стороной расположена в одной плоскости с длинным прямым поводом (рис. 64 а). Расстояние от провода до ближайшей стороны рамки . Ток в проводе , в рамке . Определите силы , действующие на каждую сторону рамки, и силу, действующую на всю рамку.
Дано Решение
Индукция магнитного поля, создаваемого длинным прямым проводом с током в точке, находящейся на расстоянии от провода, определяется следующей формулой:
. (1)
Величина уменьшается по мере увеличения расстояния , следовательно, это магнитное поле неоднородное. Направление вектора определяем по такому вращению буравчика, чтобы винт перемещался бы вдоль тока . В области, где находится рамка, вектор направлен перпендикулярно плоскости рамки «от нас» (рис. 64 б).
Найдем силу , действующую на сторону , суммируя бесконечно малые силы , действующие на элементы тока :
; (2)
(3)
По правилу левой руки определяем, что все векторы , перпендикулярные вектору магнитной индукции , лежат в плоскости рамки, а в этой плоскости они перпендикулярны стороне . Силы являются сонаправленными, причем, сторона притягивается к проводу, так как ток в ней одинакового направления с током в проводе (см. рис. 64 б). Модуль силы :
(4)
Здесь величина (в соответствии с формулой (1), в которой для стороны ) одинакова во всех точках МП, где находится сторона рамки . Тогда действующая на нее сила
(5)
Аналогичный расчет будет и для силы , действующей на сторону рамки , так как вдоль этой стороны величина также одинакова, но меньше, чем для стороны , так как расстояние от провода больше: . Соответственно и модуль силы :
(6)
Вектор также перпендикулярен стороне рамки ( ), но он направлен от провода с током : токи в проводе и в стороне противоположных направлений, поэтому они отталкиваются (см. рис. 64 б).
Силы , действующие на стороны и рамки с током, также перпендикулярны элементам тока и вектору магнитной индукции , в соответствии с векторным произведением в формуле (2), и направления их определяем также по правилу левой руки (см. рис. 64 б). Стороны рамки и расположены одинаково по отношению к проводу с током , магнитное поле которого действует на ток в рамке. Следовательно, модули этих сил одинаковы: .
Рассчитаем, например, силу , суммируя элементарные силы по длине стороны :
. (7)
Здесь величина не одинакова вдоль стороны , но уменьшается по мере удаления элемента тока от провода, согласно формуле (1). В подинтегральном выражении (7) заменим (см. рис. 64 б), чтобы перейти к одной переменной – расстоянию элемента тока от провода; пределы по этой переменной: , – соответствуют начальному и конечному элементам тока на стороне . Продолжим расчет силы
(8)
Вычислим модули сил, действующих на стороны рамки, по формулам (5), (6) и (8):
.
.
.
Найдем результирующую силу, действующую на рамку в целом, складывая векторы сил, действующих на стороны рамки:
(9)
Здесь , так как и вектор (см. рис. 64 б). Так как сила , то модуль результирующей силы
Направление вектора результирующей силы совпадает с направлением большего из векторов сил – с вектором .
Таким образом, в неоднородном магнитном поле на данную рамку с током действует сила в направлении градиента индукции МП: , который направлен в область более сильного МП. Силы растягивают рамку с током, что соответствует данному случаю , где – магнитный момент рамки с током.
Задача 34.На оси контура с током, магнитный момент которого , находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси первого контура. Расстояние межу контурами , причем, размеры контуров малы по сравнению с расстоянием Определите механический момент , действующий на второй контур.
Магнитный момент контура с током – это вектор , направленный по нормали к плоскости контура так, что направление вектора связано с направлением тока в контуре правилом буравчика (правого винта). Первый контур с током создает магнитное поле с индукцией . Величина в точках на оси кругового контура рассчитана в решении задачи 27:
, (1)
где – расстояние от точек контура до точки в МП, в которой определяется величина . Так как по условию задачи расстояние велико по сравнению с радиусом контура, то величина .
На второй контур с током в магнитном поле с индукцией действует механический (вращающий) момент , величина которого определяется следующей формулой:
. (2)
Так как размеры второго контура тоже малы, то величина несущественно изменяется вдоль плоскости второго контура. Поэтому примем ее равной , определяемой формулой (1), в которой . Согласно векторному произведению в формуле (2), вектор перпендикулярен плоскости, в которой лежат векторы и , т. е. он перпендикулярен плоскости рисунка (см. рис. 65). Этот механический момент будет стремиться повернуть второй контур до положения, в котором вектор (при этом величина обратится в нуль).
Модуль вращающего момента, согласно формуле (2),
, (3)
где – угол между векторами магнитного момента контура и индукцией магнитного поля . По условию задачи вектор , а последний создает магнитное поле , следовательно, вектор (см. рис. 65) и .
Подставляя величину магнитной индукции по формуле (1) в выражение (3), получаем следующую расчетную формулу:
. (4)
Вычисляем по формуле (4) механический момент, действующий на второй контур с током в магнитном поле, созданном первым контуром с током:
.
Задача 35.Два прямолинейных длинных параллельных проводника находятся на расстоянии друг от друга. По проводникам в одном направлении текут токи и . Какую работу (на единицу длины проводника) нужно совершить, чтобы раздвинуть эти проводники до расстояния ?
Дано Решение
Параллельные токи одинакового направления притягиваются друг к другу, т. е. второй проводник с током притягивается к первому силой Ампера . Чтобы его отодвинуть от первого проводника, нужно приложить внешнюю силу , незначительно превышающую силу притяжения проводников: . Работа этой внешней силы
(1)
Найдем силу Ампера – силу магнитного взаимодействия проводников с током, как силу, с которой магнитное поле первого проводника действует на ток во втором проводнике:
(2)
В уравнении (2) суммируются элементарные силы , действующие на элементы тока , расположенные по всей длине второго проводника с током. Направление сил определяем по правилу левой руки, размещая ладонь в плоскости рисунка (рис. 66), так как вектор магнитной индукции перпендикулярен плоскости рисунка (он направлен «к нам»). Силы , действующие на элементы тока , сонаправлены, поэтому можем складывать их модули:
(3)
Здесь , так как вектор ; – магнитная индукция поля, созданного прямым током , она определяется формулой
, (4)
где – расстояние от проводника с током до точки, в которой определяется индукция магнитного поля.
Подставим величину в подинтегральное выражение (3) и выполним интегрирование, отметив, что расстояние всех элементов тока второго проводника от первого одинаково, так как проводники параллельные:
(5)
Сила Ампера, действующая на единицу длины проводника, в соответствии с формулой (5), представится следующим выражением:
(6)
Согласно полученной формуле, эта сила уменьшается с увеличением расстояния между проводниками, т. е. имеем дело с работой переменной силы, которая определяется, как сумма элементарных работ, интегралом (1). Работу на единицу длины проводника найдем, подставляя силу по формуле (6) в подинтегральное выражение (1):
(7)
Вычислим работу, которую совершает внешняя сила при удалении от первого проводника с током второго проводника с током на единицу его длины, принимая, что магнитная проницаемость воздуха :
.
Задача 36.Тонкий проводник в виде полукольца радиусом находится в однородном магнитном поле с индукцией . Плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода расположены вдоль линий . По проводнику протекает ток . Определите силу , действующую на проводник.
Выделим на полукольце элемент тока и определим направление действующей на него силы Ампера
(1)
Для этого используем правило левой руки, располагая ладонь в плоскости рисунка (рис. 67). Так как элементы тока кольцевого проводника имеют различную ориентацию, то векторы , перпендикулярные элементам тока , образуют «веер векторов» в плоскости полукольца. Для сложения таких векторов каждый элементарный вектор силы разложим на составляющие по осям :
(2)
Силу, действующую на весь проводник длины , находим, суммируя по всей длине полукольца векторы сил, действующих на элементы тока:
(3)
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» — правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. — М: Дрофа, 2009. – С.109 — 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом  За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом

Отношение  зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:

Единицей измерения магнитной индукции является 1 тесла (Тл).
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:

где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 900 большой палец покажет направление силы Ампера.
Сила Ампера — сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:

 – заряд частицы;
– заряд частицы;
 – скорость частицы;
– скорость частицы;
B – модуль магнитной индукции;
 – угол между векторами скорости частицы и магнитной индукции.
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 900 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.




Согласно 2-му закону Ньютона

Отсюда

Время, за которое частица делает полный оборот (период обращения), равно:

Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?

Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
 — точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
— точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т. е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10—¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:

Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.
Найти: F
Решение:
Запишем формулу силы Ампера:

Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:

Отсюда следует:

Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти: 
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
 .
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,

Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:

Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Закон Ампераустанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
F = BIlsin(a) (a — угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.
Таким образом, модуль вектора магнитной индукции есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.
Если проводник имеет произвольную формулу и поле неоднородно, тоЗакон Ампера принимает вид:
dF = I*B*dl∙sin(a)
Закон Ампера в векторной форме:
dF = I [dl B]
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.
Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
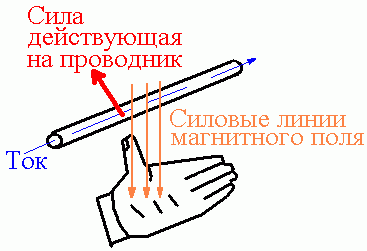
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B∙I∙ℓ∙ sin α — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.


Французский физик Доминик Франсуа Араго (1786-1853) на заседании Парижской академии наук рассказал об опытах Эрстеда и повторил их. Араго предложил естественное, как всем казалось, объяснение магнитного действия электрического тока: проводник в результате протекания по нему электрического тока превращается в магнит. На демонстрации присутствовал другой академик, математик Андре Мари Ампер. Он предположил, что суть вновь открытого явления – в движении заряда, и решил сам провести необходимые измерения. Ампер был уверен, что замкнутые токи эквивалентны магнитам. 24 сентября 1820 г. он подключил к вольтову столбу две проволочные спирали, которые превратились в магниты.
Т.о. катушка с током создает такое же поле, что и полосовой магнит. Ампер создал прообраз электромагнита, обнаружив, что стальной брусок, помещенный внутрь спирали с током, намагничивается, многократно усиливая магнитное поле. Ампер предположил, что магнит представляет собой некоторую систему внутренних замкнутых токов и показал (и на основе опытов, и помощью расчетов), что малый круговой ток (виток) эквивалентен маленькому магнитику, расположенному в центре витка перпендикулярно его плоскости, т.о. всякий контур с током можно заменить магнитом бесконечно малой толщины.
Гипотеза Ампера, что внутри любого магнита существуют замкнутые токи, наз. гипотезой о молекулярных токах и легла в основу теории взаимодействия токов – электродинамики.
На проводник с током, находящийся в магнитном поле, действует сила, которая определяется только свойствами поля в том месте, где расположен проводник, и не зависит от того, какая система токов или постоянных магнитов создала поле. Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы.
Закон Ампера: сила, действующая на элемент длины проводника с током I, помещенного в магнитное поле  ,
,
где  сила,
сила, 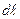 — вектор элемента длины проводника
— вектор элемента длины проводника , проведенный в направлении тока.
, проведенный в направлении тока.
Модуль магнитной силы:  , где
, где 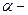 угол между
угол между 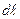 и
и  .
.
Следовательно, когда проводник расположен вдоль линий поля  , магнитная сила отсутствует.
, магнитная сила отсутствует.
Направление вектора 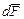 может быть найдено по общим правилам векторного произведения. В простейшем случае, когда проводник с током и поле взаимно перпендикулярны
может быть найдено по общим правилам векторного произведения. В простейшем случае, когда проводник с током и поле взаимно перпендикулярны  , для определения направления магнитной силы можно воспользоваться правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор
, для определения направления магнитной силы можно воспользоваться правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 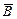 , а четыре вытянутых пальцев расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
, а четыре вытянутых пальцев расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
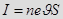 , где
, где  число свободных электронов в единице объема проводника (концентрация частиц),
число свободных электронов в единице объема проводника (концентрация частиц),  — заряд электрона,
— заряд электрона,  — скорость упорядоченного движения электронов,
— скорость упорядоченного движения электронов,  — площадь поперечного сечения проводника.
— площадь поперечного сечения проводника.
В отличие от кулоновских сил, которые являются центростремительными, сила Ампера не является центральной. Она направлена перпендикулярно к линиям магнитной индукции.
Закон Ампера может быть использован для определения модуля вектора магнитной индукции. Модуль вектора индукции в данной точке однородного магнитного поля равен наибольшей силе, которая действует на помещенный в окрестности данной точки проводник единичной длины, по которому протекает ток в единицу силы тока:  . Значение
. Значение 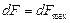 достигается при условии, что проводник расположен перпендикулярно к линиям индукции.
достигается при условии, что проводник расположен перпендикулярно к линиям индукции.
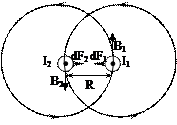
Закон Ампера применяется для определения силы взаимодействия двух токов.
Между двумя параллельно расположенными бесконечно длинными проводниками, по которым протекают постоянные токи, возникает сила взаимодействия. Проводники с одинаково направленными токами притягиваются, с противоположно направленными токами – отталкиваются.
Сила взаимодействия, приходящаяся на единицу длины каждого из параллельных проводников, пропорциональна величинам токов 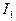 и
и 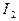 и обратно пропорциональна расстоянию между R между ними.
и обратно пропорциональна расстоянию между R между ними.  Такое взаимодействие проводников с параллельными токами объясняется правилом левой руки. Модуль силы, действующий на два бесконечных прямолинейных тока
Такое взаимодействие проводников с параллельными токами объясняется правилом левой руки. Модуль силы, действующий на два бесконечных прямолинейных тока 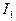 и
и 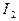 , расстояние между которыми равно R:
, расстояние между которыми равно R:
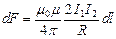 , т.е.
, т.е. .
.
В неоднородном магнитном поле на контур с током действует сила 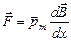 , где
, где 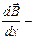 изменение
изменение 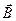 , рассчитанное на единицу длины вдоль направления, совпадающего с направлением
, рассчитанное на единицу длины вдоль направления, совпадающего с направлением 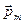 .
.
Сила  втягивает магнитный диполь в область больших значений магнитной индукции.
втягивает магнитный диполь в область больших значений магнитной индукции.
Задача 3. Определить степень неоднородности магнитного поля  , если максимальная сила, действующая на точечный магнитный диполь
, если максимальная сила, действующая на точечный магнитный диполь 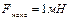 . Магнитный момент точечного диполя
. Магнитный момент точечного диполя 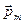 =2 мА?м2.
=2 мА?м2.
Дано: Решение:

 ,
,