Силы в электрическом поле. Силы, действующие на точечный заряд, диполь и непрерывно распределенный заряд. Силы, действующие на диэлектрик и проводник. Энергетический метод определения сил.

На точечный заряд в электрическом поле действует сила:

.

На непрерывно распределенный заряд:

,

объемная плотность сил:

.

Объемные силы, действующие на диэлектрик – это сумма сил, действующих на диполи внутри диэлектрика.

— особенно для жидкостей и газов.

Под действием элементарных сил на малые объемы эти элементы сдвигаются в направление роста

. На поверхности раздела сила всегда направлена в сторону диэлектрика с меньшим.

Силы в магнитном поле: , объемная плотность сил. У диамагнетиков, поэтому сила направлена в сторону уменьшения магнитного поля.

Работа, которая совершается током, не является результатом превращения кинетической энергии электронов в другие виды энергии. Носитель энергии – не электроны, а поля. В частном случае джоулева тепла кинетическая энергия электрона не является промежуточной формой энергии.

Пусть — объемная плотность тепловой мощности, выделяемой в проводнике. Покажем, что:. Джоулево тепло, выделяемое в объеме,

.

, . Получаем:

. Получаем 3 интеграла:

.

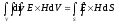Окончательно получаем:

.

Здесь 1-я скобка – энергия поля (электрическое + магнитное), а производное – изменение этой энергии в объеме .

, здесь — вектор Умова-Пойнтинга, или же плотность потока.

Изменение энергии в объеме равно работе энергии тока проводимости и потоку энергии через , которая ограничивает

. Работа, производимая в замкнутом объеме, совершается за счет потока энергии через поверхность, ограничивающую объем.

Для плоской волны, у которой иколеблются в фазе, в любой момент времени, откуда можно получить вектор Умова-Пойнтинга. Рассмотрим в качестве примера отрезок проводника, по которому течет ток

:

. Из закона полного тока можно получить поле на расстоянии от центра:. Тогда поток через поверхность цилиндра – это поток Умова-Пойнтинга.. Это поток энергии, которая втекает в объемчерез поверхность

. Т.е. энергия электромагнитного поля втекает в боковую поверхность проводника и выделяется в виде тепла Джоуля-Ленца. Если в пределах проводника действуют сторонние силы, то в замкнутой цепи постоянного тока энергия от участков, где действуют сторонние силы, передается другим участкам цепи не вдоль проводников, а через окружающее пространство в виде потоков энергии.

Как видно из рисунка, поток вектора Умова-Пойнтинга направлен вне провода.

20. Закон электромагнитной индукции Фарадея. Дифференциальная формулировка закона электромагнитом индукции Фарадея.

Электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью электромагнитного поля. Эта фундаментальная задача была решена в 1831 г. английским физиком М.Фарадеем, открывшим явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и ЭДС электромагнитной индукции

определяются только скоростью изменения магнитного потока. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС:

.

Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.

Действие магнитного поля на движущийся электрический заряд

Если бы Андре Мари Ампер (рис. 1) знал о действии электрического тока, то продвинулся бы гораздо дальше в своих открытиях.

Рис. 1. Андри Мари Ампер (Источник)

Как и многие ученые того периода, Ампер придерживался «модели эфира»: электрический ток – эфир, некая жидкость, которая протекает по проводникам. Именно отсюда и сам термин «электрический ток» – то, что течет. Только в самом конце XIX века – начале ХХ модели эфиров стали отходить, а на смену им стали появляться новые модели, адекватнее отражающие наблюдаемые явления. В частности, были открыты катодные лучи, была выявлена радиоактивность, проведены исследования Фарадея по электролизу – все это наводило на мысль о существовании заряженных частиц, которые как-то движутся.

Ученый Хендрик Лоренц (рис. 2) предложил так называемую «электронную модель» металлов.

Рис. 2. Хендрик Лоренц (Источник)

При образовании кристаллической решетки металлов от каждого атома металла отрывается по одному внешнему электрону, таким образом, в узлах кристаллической решетки находятся положительные ионы, а в объеме этой решетки почти свободно могут двигаться электроны (рис. 3).

Рис. 3. Кристаллическая решетка

Модель, предложенная Лоренцом, была хороша хотя бы тем, что достаточно легко объясняла возникновение электрического тока в металлах. При обычных условиях эти электроны находятся в беспорядочном движении вокруг кристаллической решетки. И только при подаче разности потенциалов на конце проводника, когда внутри проводника появляется электрическое поле, кроме этой хаотической составляющей появляется другая – упорядоченная составляющая, или направленное движение. Именно это движение, согласно модели Лоренца, представляет собой электрический ток.

Вы знаете, что стороны магнитного поля (B) на проводник с током (I) действует сила Ампера (F), перпендикулярная направлению тока и направлению линий магнитного поля (рис. 4).

Рис. 4. Направление силы Ампера

«Если электрический ток представляет собой направленное движение зарядов, то не будет ли со стороны магнитного поля действовать такая же сила на сами заряды?» – примерно так рассуждал Лоренц. В выражение для силы Ампера вместо силы тока подставим определение силы тока – отношение перенесенного заряда в проводнике ко времени, за которое было осуществлено данное перенесение:

Также заметим, что отношение элемента длины проводника к интервалу времени – скорость движения заряда:

Тогда выражение принимает вид:

Модуль силы равен произведению величины магнитной индукции поля на количество переносимого через проводник заряда на скорость частиц, которые переносят заряд и на синус угла между направлением движения заряда и направлением вектора магнитной индукции.

Учтем, что носителями электрического тока в проводнике являются электроны, величина зарядов которых одинакова. Поэтому можно записать, что совокупный заряд, переносимый через поперечное сечение проводника, – произведение заряда электрона q на количество электронов N, переносимых через поперечное сечение проводника.

Тогда:

Вывод приведенной формулы был сугубо формальным, однако даже такой вывод позволял предположить, что не только на проводник с током, но и на отдельный заряд в магнитном поле будет действовать сила со стороны этого поля. Предположим, что число зарядов равно единице и этот заряд движется не внутри кристаллической решетки, а в свободном пространстве. Возникает вопрос: что произойдет с этим зарядом, если он войдет в область, где существует однородное магнитное поле? Согласно нашей гипотезе, на частицу, движущуюся в однородном магнитном поле, должна действовать сила, которая перпендикулярна скорости этой частицы (поскольку именно так будет направлен электрический ток, связанный с движением этих частиц) и перпендикулярна линиям магнитного поля (рис. 5).

Рис. 5. Направление действия силы на движущийся заряд

Величина этой силы будет определяться так:

Открытие катодных лучей, а также радиоактивности позволили проверить экспериментально гипотезу Лоренца. Воспользуемся электронно-лучевой трубкой.

В вакуумной трубке размещены две пластины: анод и катод. На катод подается отрицательный потенциал, на анод – положительный. Для того чтобы в трубке возникли свободные электроны, катод нагревается нитью накала. Свободные электроны металлического катода вблизи его поверхности могут покидать эту поверхность, обладая высокой кинетической энергией за счет нагревания – явление термоэлектронной эмиссии. Свободные электроны, покинувшие поверхность катода, попадают в зону действия электрического поля между анодом и катодом. Линии напряженности этого поля направлены от анода к катоду (изображены белыми стрелками). Электроны, будучи отрицательно заряженными частицами, движутся от катода к аноду – против линии напряженности поля (направление движения изображено красными стрелками). Так, в трубке возникает электрический ток, направленный от анода к катоду (рис. 6).

Рис. 6. Электронно-лучевая трубка

Если использовать экран, покрытый специальным материалом, который светится при попадании на него заряженных частиц, можно пронаблюдать место попадания электронов по световому пятну. Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).

Рис. 7. Работа электронно-лучевой трубки

Воспользуемся осциллографом. Для удобства будем следить не за световым пятном, а за светящейся линией (рис. 8).

Рис. 8. Светящаяся линия на экране осциллографа

Когда одним из полюсов подводят к горизонтальной линии, находящейся на осциллографе, она отклоняется от своего первоначального значения в направлении, перпендикулярном направлению скорости и направлению линий магнитного поля, поскольку магнитное поле направлено от северного полюса к южному. Это на качественном уровне подтверждает гипотезу (рис. 9).

  

Рис. 9. Отклонения электронов в электронно-лучевой трубке

Попытаемся получить не только качественные, но и количественные результаты. Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.

Рис. 10. При уменьшении яркости искажение линии уменьшается

Сила, действующая на заряды со стороны магнитного поля, пропорциональна индукции – если поднести несколько магнитов к осциллографу, то искажение будет гораздо сильнее.

Рис. 11. При усилении магнитного поля искажение линии увеличивается

Величина силы действующей со стороны магнитного поля на движущийся заряд зависит от взаимного направления вектора магнитной индукции и вектора скорости движения частиц. При поднесении магнитов к осциллографу южным полюсом линия будет искажаться в противоположном направлении.

Рис. 12. При поднесении магнитов южным полюсом линия искажается в противоположном направлении

Обобщим выводы из проделанных экспериментов. На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «левой руки».

Таким образом, полученное ранее выражение для силы описывает взаимодействие магнитного поля с движущимся в этом поле электрическим зарядом. Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.

Сделаем еще несколько замечаний.

1. Вектор силы Лоренца перпендикулярен вектору скорости:

2. Если сила перпендикулярна вектору скорости, то она называется центростремительной. Под ее действием тело движется по окружности. Следовательно, сила Лоренца – центростремительная сила.

3. Под действием силы Лоренца заряд движется по дуге окружности, следовательно, он обладает центростремительным ускорением. Центростремительное ускорение может быть рассчитано как квадрат скорости движения, деленный на радиус окружности, который описывает тело:

 

4. Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:

Силы, действующие на проводники в электрическом поле

В конечном итоге, все силы, которые возникают в электростатическом поле, являются силами, которые действуют на заряды, несмотря на то, что в формулы для силы величины зарядов входят не всегда. Поэтому напомним необходимую в данном случае формулу. Сила, которая действует на точечный заряд, равна:

Как мы уже неоднократно говорили, весь заряд, который находится на проводнике, распределяется по его поверхности. Поэтому элемент заряда проводника выражается как:

где $\sigma$ — поверхностная плотность распределения заряда, $dS$ — элемент поверхности на которой этот заряд находится.

На заряд $dq$ действует только половина напряженности поля, которое имеется у поверхности проводника, так как вторая половина создается самим зарядом элемента поверхности и не может на него действовать.

Мы видим, что на поверхности проводника сила всегда действует в направлении внешней нормали и как бы стремится увеличить его объем или еще говорят, что эта сила стремится удалить электричество с поверхности проводника. Формула (3) записана для проводника, который находится в вакууме.

В том случае, если проводник находится в жидком или газообразном диэлектрике, то на элемент поверхности проводника (dS) действует сила, которая равна:

\[d\overrightarrow{F}=\frac{\sigma^2}{2{\varepsilon \varepsilon}_0}dS\cdot \overrightarrow{n}=\frac{{\varepsilon \varepsilon}_0E^2}{2}dS\cdot \overrightarrow{n}\left(4\right).\]

Результирующая сила

Результирующая сила, которая действует на проводник в целом, может быть вычислена в соответствии с формулой:

\[\overrightarrow{F}=\frac{1}{2}\int\limits_S{\frac{\sigma^2}{\varepsilon {\varepsilon }_0}\overrightarrow{n}dS=\frac{1}{2}\int\limits_S{\frac{\sigma^2}{\varepsilon {\varepsilon }_0}d\overrightarrow{S}}\ \left(5\right),}\]

где $S$ — поверхность проводника. Так, используя (5) легко вычислить силу, которая действует на обкладку плоского конденсатора площадью $S$. Так как поле однородно, выражение $\frac{\sigma^2}{\varepsilon {\varepsilon }_0}$ — постоянно. Она будет равна:

\[\overrightarrow{F}=\frac{1}{2}\frac{\sigma^2}{\varepsilon {\varepsilon }_0}S\overrightarrow{n}=\frac{\varepsilon {\varepsilon }_0E^2}{2}S\overrightarrow{n}\left(6\right).\]

Для вычисления сил притяжения, которые действуют на обкладки плоского конденсатора, необходимо учитывать, что если пространство между пластинами конденсатора заполнено твердым диэлектриком, то силы действуют такие же, как если бы между ними был вакуум, то есть:

\[\overrightarrow{F}=\frac{1}{2}\frac{\sigma^2}{{\varepsilon }_0}S\overrightarrow{n}\left(7\right).\]

Формула (6) справедлива при $\varepsilon \ne 1$ для жидких и газообразных диэлектриков.

Сила $\overrightarrow{F}$ в плоском конденсаторе направлена внутрь.

Пример 2

Задание: Пластины плоского конденсатора заряжены до 100 нКл. Площадь пластин S=0,01 м2. Найдите силу притяжения пластин, если в качестве диэлектрика используют керосин при 200С, который имеет при данной температуре диэлектрическую проницаемость равную $\varepsilon =2.$

Решение:

Так как между пластинами в качестве диэлектрика используется жидкость — керосин, то для расчета силы взаимодействия пластин необходимо использовать формулу:

\[F=\frac{q^2}{2\varepsilon {\varepsilon }_0S}\ \left(2.1\right).\]

Переведем вне системные единицы в систему СИ:

\[q=100\ нКл={10}^{-7}Кл.\]

Проведем расчет:

\[F=\frac{{\left({10}^{-7}\right)}^2}{2\cdot 2\cdot 8,85\cdot {10}^{-12}\cdot 0,01}=\frac{{10}^{-14}}{35,4\cdot {10}^{-14}}=0,028\ \left(Н\right).\]

Ответ: $F=0,028\ Н.$

7. Сила, действующая на заряд, движущийся в

электромагнитном поле

Рассмотрим заряд , двигающийся со скоростью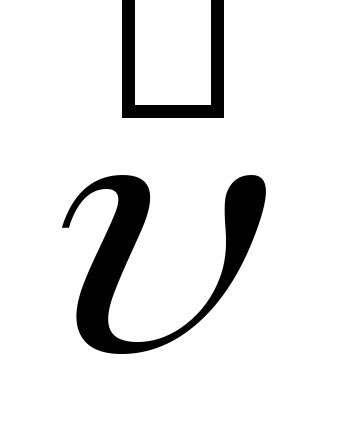в электромагнитном поле с напряженностьюи магнитной индукцией.

Сила, действующая на элемент тока

магнитная сила, действующая на движущийся в магнитном поле заряд.

Электрическая сила, действующая на заряд, определяется напряженностью электрического поля

Сила, действующая на заряд, движущийся в электромагнитном поле

— сила Лоренца.

Пример:

Рассмотрим 2 одинаковых по величине заряда , двигающихся параллельно друг другу с одинаковыми скоростями. Найдем силу взаимодействия зарядов

Магнитная индукция, создаваемая 2 зарядом в месте нахождения заряда 1, т.е. на перпендикуляре, проведенном к траектории движения заряда 2 из точки, в которой он в данной момент находится:

Найденное магнитное поле является полем движущегося заряда, оно и действует на заряд, летящий параллельно первому, с магнитной силой:

.

Опред.

—магнитное поле движущегося заряда.

Полученное соотношение 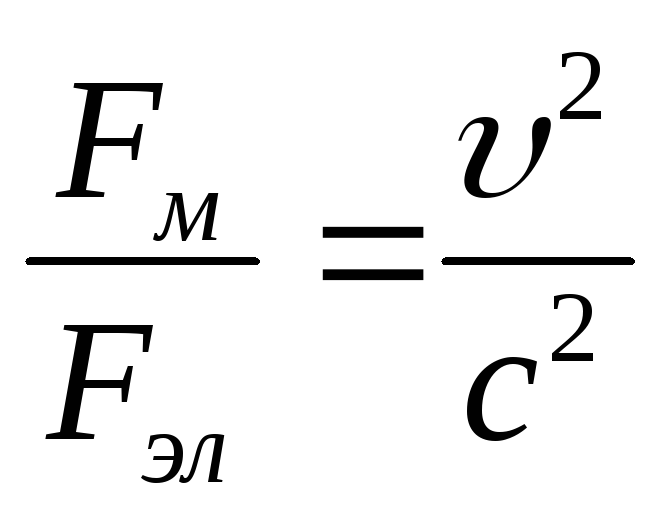справедливо и при релятивистских скоростях.

Если перейти в систему отсчета зарядов, то в ней магнитных сил не будет, и заряды будут взаимодействовать с электрической силой .

Вопр.Что же получается: в зависимости от того, из какой системы смотреть, изменяется сила? Ну а заряды как на это посмотрят? Они-то какую силу чувствуют? Может быть, мы сделали что-то не так?

Отв.Действительно, мы совершенно безосновательно считали, что электрическое поле

движущегося заряда . В нерелятивистском приближении полная сила, действующая на заряд в любой системе, должна быть одна и та же, но в системе, связанной с зарядом, она чисто электрическая, а в лабораторной системе она разделяется на электрическую и магнитную, следовательно, электрическое и магнитное поля переходят друг в друга, а так как заряды могут двигаться с высокими скоростями, то полная теория электромагнетизма должна быть релятивистской.

Электрические и магнитные поля при переходе из одной инерциальной системы в

другую преобразуются в соответствии с преобразованиями Лоренца (именно для этого Лоренц и написал свои преобразования, являющиеся краеугольным камнем Теории относительности).

Пусть движется относительносо скоростью, тогда при переходе в системукомпоненты электромагнитного поля преобразуются следующим образом:

;

;

;.

Здесь .

Или разложив , где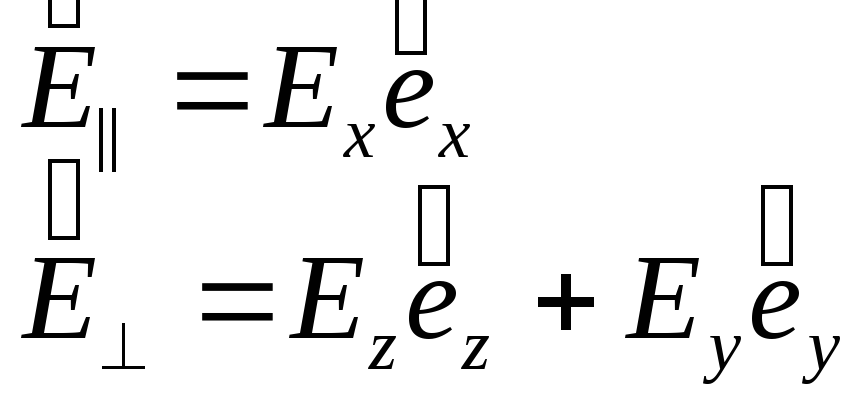, имеем:

;

;

В нашем случае:

;, то есть, в самом деле;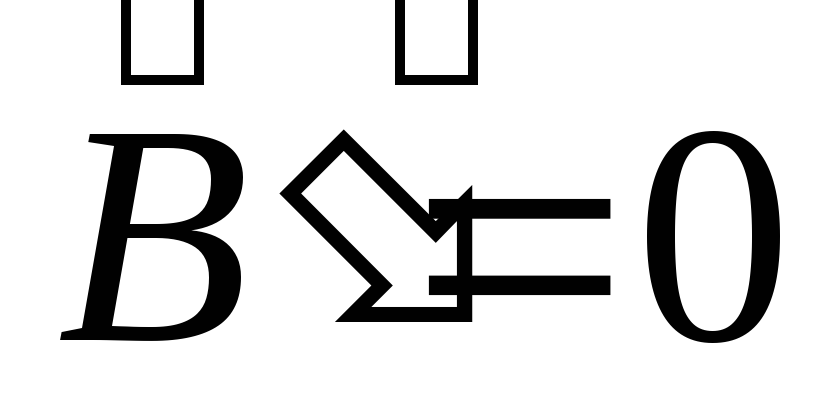

Т.о. в собственной системе заряды “чувствуют” меньшее электрическое поле, которое определяет собой такую же силу взаимодействия, как суммарная сила в лабораторной системе. Эта сила включает в себя нашу «лабораторную» электрическую силу и противодействующую ей «лабораторную» магнитную силу.

Выводы:

• справедливо и при релятивистских скоростях.

• Разделение силы на электрическую и магнитную условно и зависит от выбора системы отсчета.

8. Элементы векторного анализа. II часть

Продолжаем изучать свойства векторных полей. На очереди понятия:

циркуляция С и ротор.

1) Циркуляция

Пусть в любой точке пространства существует поле с напряженностью сила, действующая на единичный объект, равна.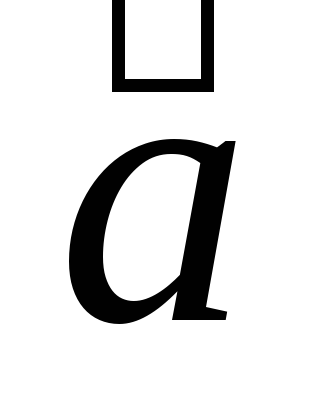

— работа поля по перемещению единичного объекта на.

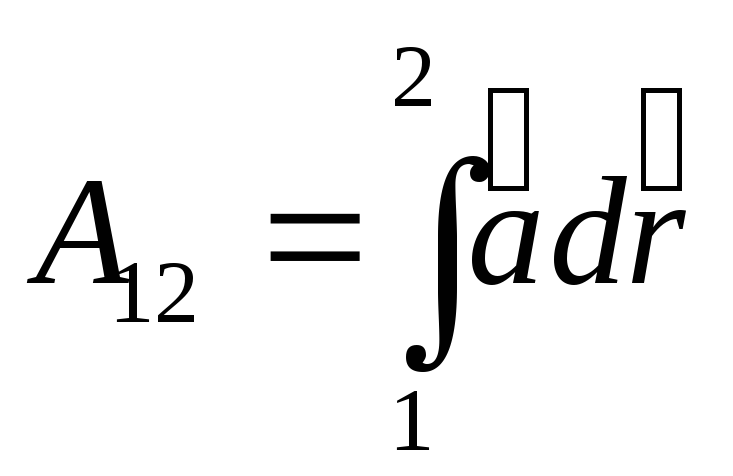
Если , то есть контур замкнутый, то — циркуляцияпо.

Физический смысл циркуляции: циркуляция — это работа сил поля по перемещению единичного объекта по замкнутому контуру.

Свойства циркуляции:

1. — алгебраическая скалярная величина.

2. зависит от направления обхода

3. Для консервативного поля сил .

Условие консервативности:

Именно потому, что электростатические поля консервативны, мы до сих пор не

использовали понятие циркуляции для нахождения распределения таких полей. Полезно иметь в виду, что условия равенства нулю являются, как правило, отрицающими или запрещающими, а не созидающими, т.к. по ним можно сказать только, чего нет и не может быть ( мы вернемся к этому вопросу, когда будем обсуждать смысл уравнений Максвелла).

Пример:

Векторное поле

Т.к. , то— неконсервативное поле.

4. Аддитивность

Циркуляция скорости — кинематическая характеристика течений жидкости или газа, которая служит мерой завихренности течения.

Если циркуляция скорости по любому замкнутому контуру, проведенному внутри

жидкости, равна нулю, то течение – безвихревое или потенциальное.

(Потенциальные скорости – однозначные функции координат).

Если , то существует вихри, которые, обтекая тело, приводят к существованию

силы, таково происхождение подъемной силы, в часности, крыла самолета, перпендикулярной к скорости :, где— плотность жидкости или газа.

Если, то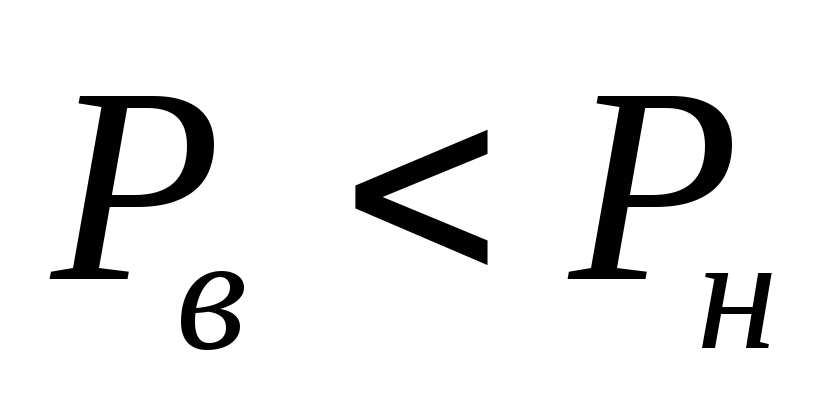— давление

2) Ротор== вихрь

Определение ротора:

Вихревое движение – это движение непрерывной среды, при котором перемещение её малых элементов состоит не только из поступательного движения, но и вращения около некоторой мгновенной оси.

Пример: смерчи, водовороты.

Если — поле скоростей частиц, то вихревая линия (линия, касательная к ротору) есть мгновенная ось вращения этих частиц.

Т.о. ротор определяет собой направление мгновенной оси вращения частицы, находящейся в данной точке.

Вихревые линии не могут начинаться и кончаться внутри однородной среды:

они или замкнуты или кончаются на границе раздела сред (поверхности Земли, жидкости, чашки, реки, ванны).

—такой вектор от данного, компоненты которого определяются циркуляцией данного вектора по трем ортогональным контурам.

— одно из обозначений.

Найдемдля декартовых координат из определения. В этом случае:

— что и требовалось доказать.

Аналогично:

Потенциальные (консервативные) поля являются безвихревыми,

т.к. для них все компоненты ротора равны 0 (.

Свойства :

1. — векторная функция векторного аргумента.

2. Аддитивность

3. 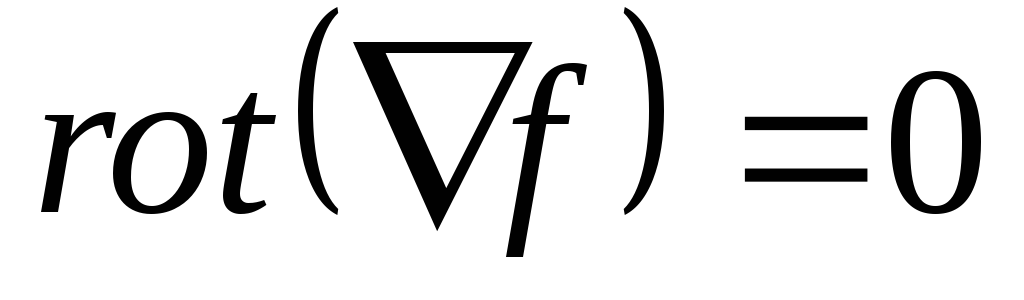нет завихрений в потенциальном поле.

Вопр.А как же смерчи на Земле?

Отв.Смерчи – следствие трения, также как воронки в ванне – следствие вязкости ,

в сверхтекучей жидкости турбулентности нет.

4. ,у вихрей нет источников.

5.

3) Теорема Стокса

Циркуляция по произвольному замкнутому контуруравна потокучерез произвольную поверхность, ограниченную данным контуром:

.

16.Сила, действующая на движущийся заряд в магнитном поле

5.3. Движение зарядов в магнитном и электрическом полях.

Экспериментально обнаружен факт, что магнитное поле действует на движущиеся в нем частицы, имеющие электрические заряд (см. п.5.1). В соответствии с (5.1), магнитная индукция численно равна максимальной силе, действующей со стороны магнитного поля на заряженную частицу, движущуюся в поле с единичной скоростью, отнесенной к величине заряда частицы. Если заряженная частица влетает в магнитное поле со скоростью (рис.5.18), то действующая со стороны поля сила оказывается перпендикулярной и скорости частицы, и магнитной индукции. Направление вектора таково, что выполняется соотношение

(5.29)

Таким образом, при и при . Оба этих случая изображены на рис. 5.18. Поскольку сила, действующая на частицу, перпендикулярна ее скорости, то ускорение, сообщаемое этой силой, тоже перпендикулярно скорости частицы, т.е. оно является нормальным ускорением. Следовательно, прямолинейная траектория полета частицы будет искривляться при ее попадании в магнитное поле.

Так как 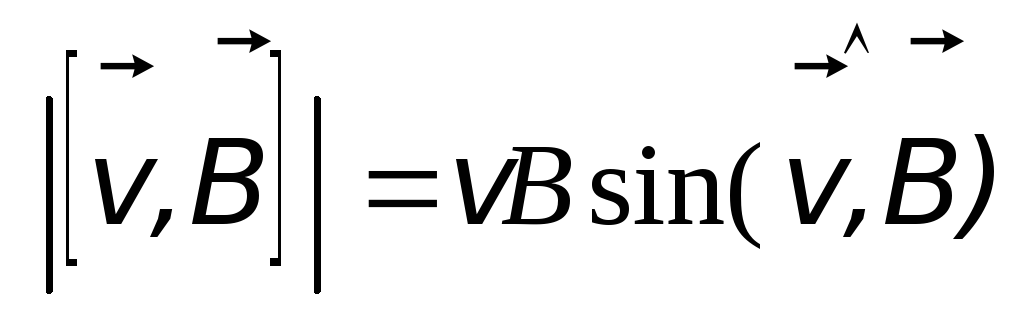, то при , т.е. магнитное поле не действует на электрически заряженную частицу, влетающую в поле вдоль линий магнитной индукции.

Если же частица влетает в поле перпендикулярно линиям магнитной индукции, то из (5.29) следует, что . Тогда можно записать второй закон Ньютона:

, или ,

где m – масса частицы, а R – радиус кривизны траектории. Получаем, что в однородном поле (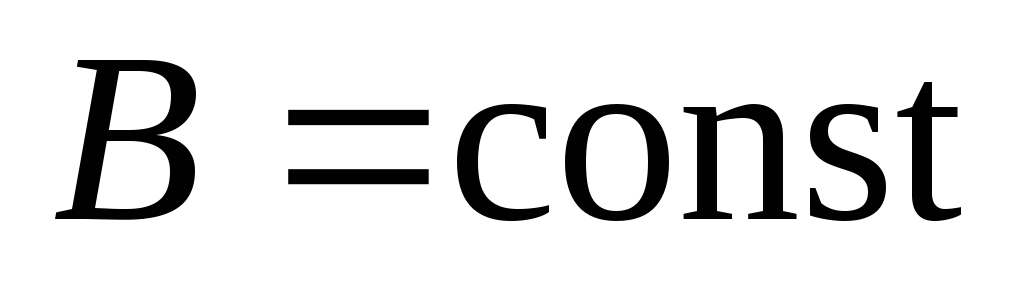) частица будет двигаться по окружности радиуса

. (5.30)

Период обращения частицы по этой окружности не зависит от скорости частицы. Действительно,

.

Следует отметить, что при любом попадании частицы в магнитное поле, частица не будет менять свою кинетическую энергию. Т.к. , то сила перпендикулярна перемещению частицы в любой точке траектории, а, следовательно, сила со стороны магнитного поля не совершает работы по перемещению свободно двигающейся частицы.

Направление силы , согласно (5.29), можно определить по правилу “левой руки”: если расположить ладонь левой руки так, чтобы четыре пальца показывали направление скорости частицы, а линии магнитной индукции входили в раскрытую ладонь, то отогнутый под прямым углом большой палец покажет направление силы, действующей на положительно заряженную частицу. Если заряд частицы отрицателен, то направление силы будет противоположным.

Если же заряженная частица попадает в область совместного действия электрического и магнитного полей, то, в соответствии с (1.5) и (5.29), на нее действует сила

. (5.31)

Сила, определяемая соотношением (5.31), называется силой Лоренца (в честь голландского физика Х.-А. Лоренца, получившего в 1902 г. Нобелевскую премию за описание поведения заряженных частиц в электромагнитном поле). Первое слагаемое (5.31) определяет электрическую компоненту силы Лоренца, а второе – магнитную.

Рассмотрим некоторые примеры практического использования воздействия магнитного и электрического полей на заряженные частицы. На рис. 5.19 показана схема работы селектора частиц, т.е. устройства, разделяющего пучок частиц по их скоростям или энергиям. В таком устройстве существует область, в которой созданы однородные электрическое и магнитное поля. Векторы напряженности и индукции этих полей взаимно перпендикулярны. На рисунке вектор магнитной индукции направлен “на нас”, а вектор напряженности электрического поля вправо. Пусть в селектор влетает пучок одинаковых положительно заряженных частиц, имеющих разные скорости. Тогда, если частицы движутся так, что и , то электрическая и магнитная компоненты силы Лоренца направлены в противоположные стороны. При определенном значении модуля скорости эти компоненты равны:

, т.е. .

Это означает, что все частицы пучка, модули скоростей которых равны , пролетят селектор, в соответствии с первым законом Ньютона, не отклоняясь от своего первоначального направления. Частицы пучка, модули скоростей которых больше, чем , отклонятся влево. Для них , т.е. магнитная компонента силы Лоренца превосходит электрическую. Остальные частицы отклонятся вправо, т.к. для них . Таким образом, на выходе из селектора будет получен моноэнергетический пучок частиц, т.е. пучок частиц, обладающих одинаковой кинетической энергией.

Если пучок образован частицами разных масс, то дальнейшее воздействие магнитного поля на него способно разделить частицы по массе. На этом основано действие масс-спектрометра (рис.5.20). Пусть пучок частиц, прошедших селектор, попадает в однородное магнитное поле, индукция которого перпендикулярна скорости частиц. Тогда частицы пучка, масса которых равна , будут, согласно (5.30), в дальнейшем двигаться по окружности радиусом 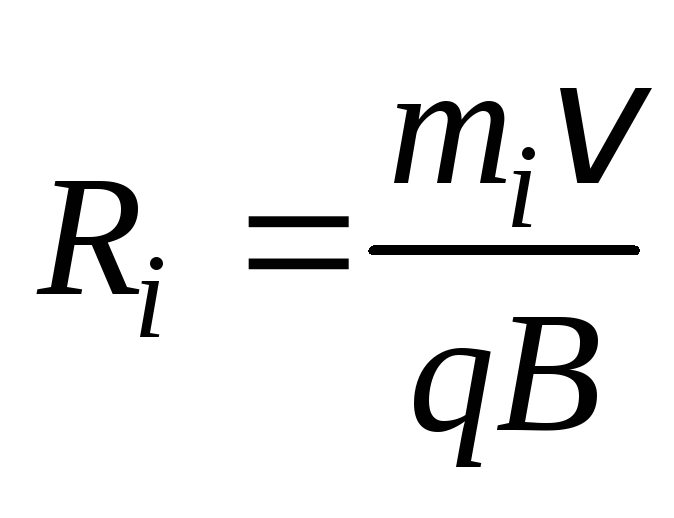. Соответственно, чем больше удельный заряд частицы (отношение ее заряда к массе), тем меньше радиус траектории ее движения. Экспериментально выяснено, что в природе нет различных элементарных частиц с одинаковым удельным зарядом. Таким образом, масс-спектрометр позволяет установить состав исследуемого пучка частиц.

Воздействие магнитного поля на пучки движущихся частиц приводит иногда к неожиданным экспериментальным результатам. В 1879 г. американский физик Э.Г. Холл обнаружил эффект, названный впоследствии его именем. Эффект Холла заключается в возникновении в проводнике с током, помещен-ном в магнитное поле, разности потенциалов в направлении, перпендикулярном плотности тока и магнитной индукции.

Р ассмотрим фрагмент плоского металлического проводника толщиной b, в котором электрическим полем с напряженностью создан электрический ток плотностью (рис. 5.21, а). В отсутствие магнитного поля свободные электроны металла упорядоченно движутся со скоростью , направленной противоположно вектору . Если проводник поместить в магнитное поле так, что , то на электроны будет действовать магнитная компонента силы Лоренца , направление которой показано на рисунке. Ее действие приведет к поперечному смещению электронов, в результате чего между верхней и нижней поверхностями проводника появится электрическое поле разделенных зарядов. Если проводник достаточно тонкий, то напряженность этого поля можно считать постоянной. Процесс смещения электронов прекратится, когда скомпенсируются силы, действующие на них со стороны магнитного и электрического полей: . В проводнике установится суммарное электрическое поле с напряженностью (рис.5.21, б). Изменение направления суммарного электрического поля в проводнике приведет к изменению положения эквипотенциальных плоскостей, т.к. они должны быть перпендикулярны . Раньше такая плоскость проходила через точки M и N проводника (рис.5.21, в). Теперь она пройдет через точки и N. Поэтому между точками M и N возникнет разность потенциалов. Для однородного электрического поля будет справедливо (см.(1.19)) соотношение . Поскольку , где п – концентрация свободных электронов в металле, то

.

Полученное выражение называется “холловской разностью потенциалов”, ее экспериментальное измерение при заданных размерах проводника и силе тока в нем позволяет определить магнитную индукцию поля, в которое помещен холловский датчик. Это – один из основных методов измерения магнитной индукции постоянных магнитных полей.

Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца.

Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику. Этот вывод подтверждается, в частности, еще и тем, что пучок свободно летящих заряженных частиц отклоняется магнитным полем.

Сила Ампера, действующая на элемент тока в магнитном поле с индукцией :

,

где α – угол между направлением тока в проводнике и вектором.

Пусть– скорость упорядоченного движения зарядов в проводнике;q – заряд носителя тока (в металлах q = — e). Для элемента тока можем написать:

dNq,

где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl. Тогда, сила, действующая в магнитном поле на один заряд, будет:

или в векторном виде.

Эту силу называют силой Лоренца (Lorentz H., 1853-1928).

Свойства силы Лоренца:

1. сила Лоренца действует только на движущуюся заряженную частицу;

2. и одновременно ;

3. поскольку , то сила Лоренцане совершает работу, а следовательно, не может изменить энергию частицы.

Полная сила, действующая на заряженную частицу в электромагнитном поле (которую также называют силой Лоренца) есть: .

4.3. Движение заряженной частицы в однородном постоянном магнитном поле.

В данном случае и сила Лоренца имеет только магнитную составляющую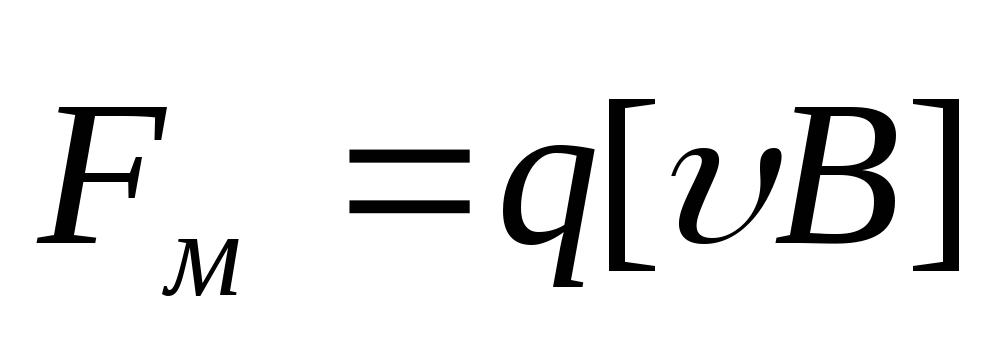. Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является:.

Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля (рис. 4.6.).

Рисунок 4.6. Движение заряженной частицы в магнитном поле ().

В системе координат, показанной на рисунке ,, и уравнение движения принимает вид:

,

откуда следует, что вектор полного ускорения частицы лежит в плоскости, перпендикулярной вектору. Легко убедиться также в том, что вектор ускоренияперпендикулярен вектору скорости частицыи составляет вместе с векторомправую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно,

.

Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:

.

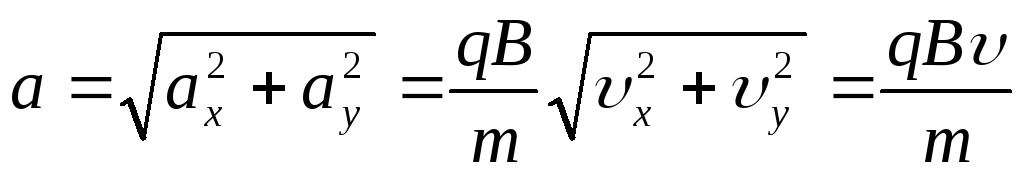Траекторией движения является окружность, радиусR которой находим из условия: , то есть, откуда:.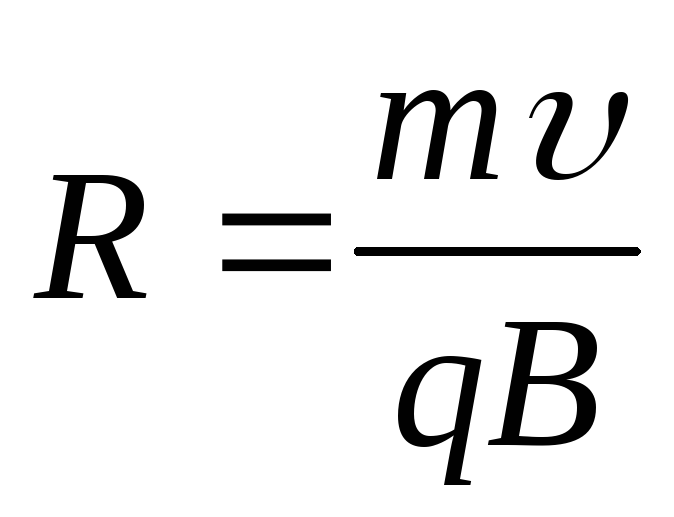

Период обращения частицы

Отметим, что период обращения и соответственно угловая скорость движения частицы не зависят от линейной скорости .

Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля.

Рисунок 4.7. Общий случай движения заряженной частицы в однородном магнитном поле.

Разложим вектор скорости на две составляющие:— параллельную векторуи— перпендикулярную. Поскольку составляющая силы Лоренца в направленииравна нулю, она не может повлиять на величину. Что касается составляющей, то этот случай был рассмотрен выше. Таким образом, движение частицы можно представить как наложениедвух движений: одного – равномерного перемещения вдоль направления силовых линий поля со скоростью , второго –равномерного вращения в плоскости, перпендикулярной . В итоге траекторией движения будетвинтовая линия.

Шаг винтовой линии определяется по формул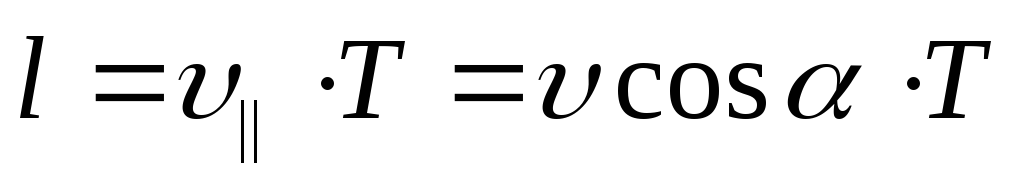е: , где .Радиус витка находим по формуле:

Направление, в котором закручивается винтовая линия, зависит от знака заряда частицы. Если заряд частицы положительный, то винтовая линия закручивается против часовой стрелки, если смотреть вдоль направления , и наоборот –по часовой стрелке, если заряд частицы отрицательный.

Действие электрического поля на электрические заряды — Мегаобучалка

Электризация тел

Электризация – явление накопления телом электрического заряда. В электризации всегда участвуют не менее двух тел. Для протекания явления между телами необходим тесный контакт. Иногда такой контакт достигается за счёт трения между телами, что приводит к ошибочному мнению о необходимости трения или совершения работы по электризации тел. Явление электризации объясняется через движение свободных зарядов (электронов).

Существует несколько способов электризации.

1. Электризация трением. При этом используются два ранее незаряженные тела, изготовленные из разных веществ. В процессе электризации заряд накапливают оба тела, одно – положительный, другое – отрицательный и равный по модулю заряду первого тела (закон сохранения заряда). С точки зрения молекулярно-кинетической теории, при электризации трением вещество с более сильным взаимодействием захватывает электроны у второго вещества и накапливает отрицательный заряд.

2. Электризация соприкосновением. При этом могут участвовать несколько тел, вещества которых способны проводить электрические заряды. До соприкосновения одно или несколько тел обладали электрическими зарядами. После соприкосновения заряды перераспределяются пропорционально электроёмкости тел.

3. Электризация электростатической индукцией (смотрите раздел «Проводники в электрическом поле»).

Взаимодействие зарядов. Два вида заряда

Электрический заряд – основная скалярная физическая величина, определяющая интенсивность электромагнитных взаимодействий. Говорят, что тело обладает электрическим зарядом, если при его взаимодействии с другими телами обнаруживаются силы электрической или магнитной природы. Единица электрического заряда вводится через единицу силы тока.

[q] = Кл = А∙с.

 

1 Кл – это заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.

Рассмотрим свойства электрического заряда, полученные экспериментально.

1. Существуют два вида электрических зарядов. Положительным называют заряд стеклянной палочки, полученный ею при электризации трением о шёлк. Положительный заряд – это недостаток у тела электронов. Отрицательным называют заряд эбонитовой палочки, полученный ею при электризации трением о шерсть (мех). Отрицательный заряд – это избыток у тела электронов.

2. Одноимённые заряды отталкиваются, разноимённые притягиваются. Силы взаимодействия точечных зарядов направлены вдоль прямой, их соединяющей. Величина взаимодействия описана в законе Кулона.

3. Существует предел делимости электрического заряда. Элементарным называют минимальный (неделимый) электрический заряд тела. Элементарная частица, обладающая положительным элементарным зарядом, – протон, отрицательным – электрон. Значение элементарного заряда является фундаментальной физической постоянной: e = 1,6∙10^–19 Кл.

Электрический заряд дискретен: |q| = Ne.

Электрический заряд обладает свойством сохранения.

Для обнаружения зарядов используется электроскоп.

 

Закон сохранения электрического заряда

Одним из основных свойств электрического заряда является его способность к сохранению. Закон сохранения электрического заряда: в электрически изолированной системе алгебраическая сумма электрических зарядов всех тел, входящих в эту систему, остается постоянной.

Электрически изолированная система – система, через границу которой нет переноса заряда ни в одном направлении.

Закон Кулона

Закон взаимодействия электрических зарядов был установлен экспериментально французским физиком Ш. Кулоном во второй половине XVIII века. Закон формулируется следующим образом: модуль силы взаимодействия двух неподвижных точечных зарядов прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

Для вакуума и воздуха закон Кулона записывают так:

где k – коэффициент пропорциональности, зависящий от выбора системы единиц. В СИ

где – электрическая постоянная.

Для бесконечной однородной и изотропной диэлектрической среды закон Кулона имеет вид:

где ε – диэлектрическая проницаемость среды, в которой находятся заряды.

Закон Кулона справедлив для точечных зарядов – заряженных тел, размеры которых много меньше других размеров рассматриваемой системы. Если заряженное тело в условиях данной задачи нельзя считать точечным зарядом, то его рассматривают как совокупность точечных зарядов. Сила, с которой такое тело будет действовать на другое тело, определяется согласно принципу суперпозиции сил.

 

Действие электрического поля на электрические заряды

Для описания взаимодействия электрических зарядов в начале XIX века английский физик М. Фарадей предложил использовать понятие электрического поля.

Электрическое поле – материальная среда, являющаяся посредником действия одного заряда на другой и передающая это действие с конечной скоростью.

 

Идея Фарадея: любой электрический заряд создаёт во всём окружающем его пространстве материальный объект – электрическое поле, которое действует на другие электрические заряды с некоторой силой, называемой электрической силой, и убывает по мере удаления от заряда, его создающего.

Заряд наделяет окружающее пространство особыми физическими свойствами, главное из которых – действие с электрической силой на любой заряд, помещённый в это пространство.

Поле, создаваемое неподвижными электрическими зарядами, не изменяется со временем и называется электростатическим.

Электрические поля принято представлять графически с помощью силовых линий – линий, касательные к которым в любой точке совпадают с направлением вектора напряжённости в этой точке. Графическое преставление электрических полей даётся с соблюдением следующих правил:

1) силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных;

2) силовые линии не пересекаются;

3) плотность линий пропорциональна модулю вектора напряжённости в данном месте поля.

На рисунках приведено несколько примеров графического изображения полей.