Модуль силы Ампера вычисляется по формуле

где
α – угол между векторами  и
и  .
.
II. 11. Взаимодействие параллельных токов в магнитном поле.
Два параллельных тока одинакового направления притягиваются друг к другу с силой
 (2.10)
(2.10)
На рисунке 2.15 приведен пример взаимодействия параллельных токов одинакового направления.

Рис. 2.15
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (2.10).
II. 12. Сила Лоренца.
Сила,
действующая со стороны магнитного поля
на электрический заряд Q, движущийся в
этом поле со скоростью  ,
называется силой Лоренца и выражается
формулой
,
называется силой Лоренца и выражается
формулой
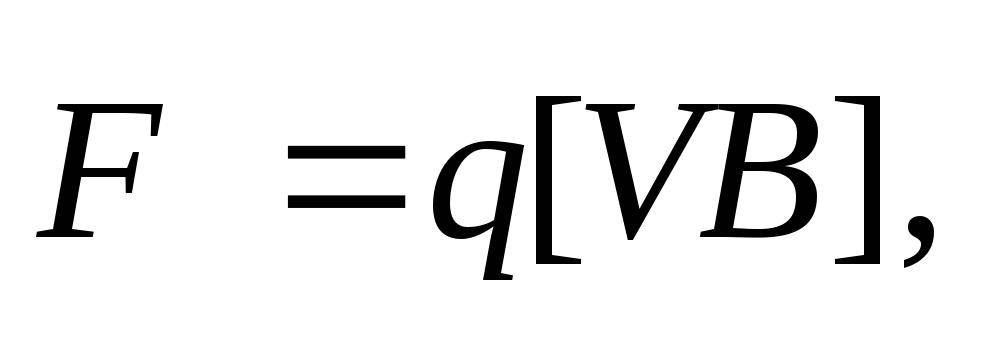
где  – индукция магнитного поля, в котором
заряд движется.
– индукция магнитного поля, в котором
заряд движется.
Направление
силы Лоренца определяется с помощью
правила левой руки: если ладонь левой
руки расположить так, чтобы в нее входил
вектор  ,
а четыре вытянутых пальца направить
вдоль вектора скорости положительного
заряда, то отогнутый под углом 900 большой палец покажет направление силы,
действующей на положительный заряд. На
рис. 2.16 показана взаимная ориентация
векторов
,
а четыре вытянутых пальца направить
вдоль вектора скорости положительного
заряда, то отогнутый под углом 900 большой палец покажет направление силы,
действующей на положительный заряд. На
рис. 2.16 показана взаимная ориентация
векторов 
 и
и  для положительного заряда. На отрицательный
заряд сила действует в противоположном
направлении. Модуль силы Лоренца равен
для положительного заряда. На отрицательный
заряд сила действует в противоположном
направлении. Модуль силы Лоренца равен 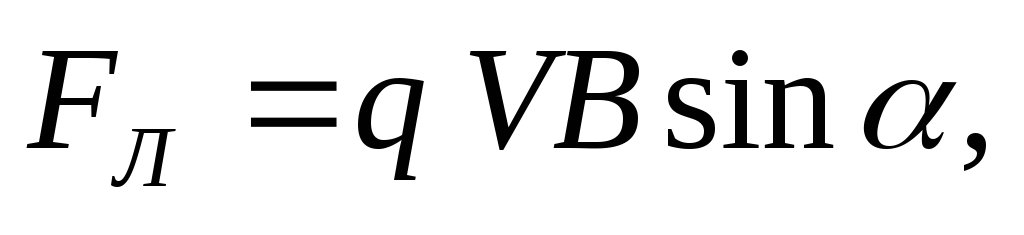
где
α – угол между 
 .
. 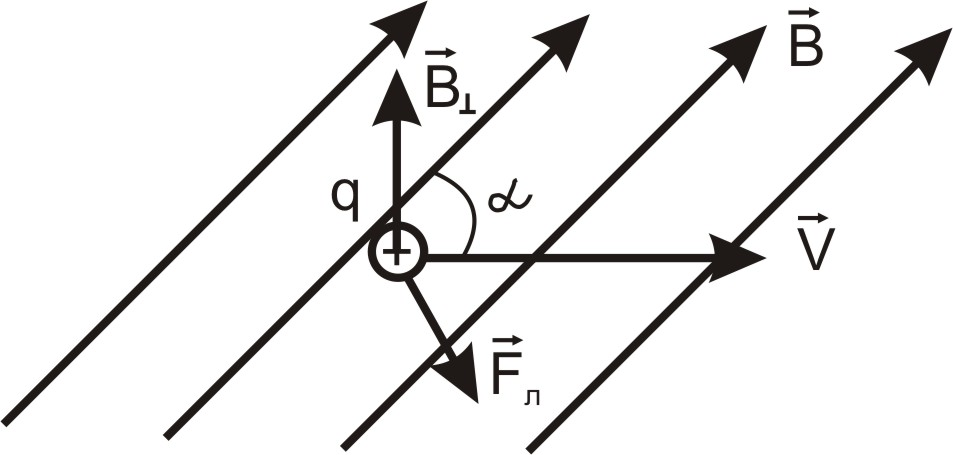
Рис. 2.16
II. 13. Движение заряженных частиц в магнитном поле под действием силы Лоренца?
а) Если заряженная частица массой m влетает параллельно силовым линиям, то на нее магнитное поле не действует, сила Лоренца Fл=0. Траектория ее движения есть прямая линия (рис. 2.17).

Рис. 2.17
 ,
перпендикулярной вектору
,
перпендикулярной вектору  ,
то сила Лоренца (рис. 2.18)
,
то сила Лоренца (рис. 2.18) 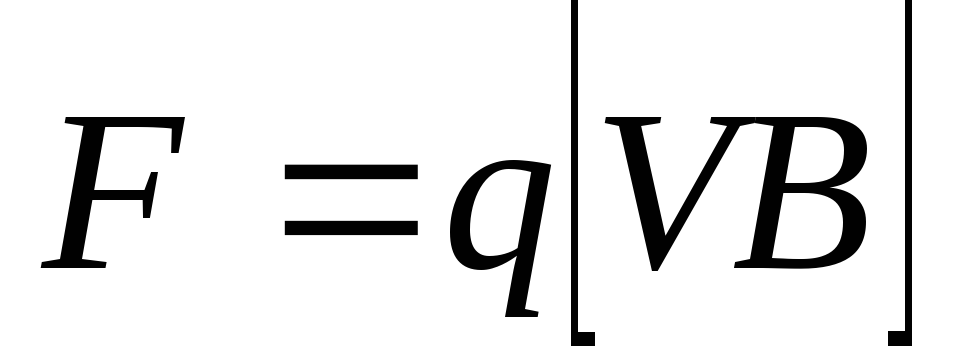 постоянна по модулю и нормальна к
траектории частицы. Согласно 2-му закону
Ньютона, эта сила создает центростремительное
ускорение. Отсюда следует, что частица
будет двигаться по
окружности,
радиус r которой определяется из условия
qVB
= mV2/r,
откуда
постоянна по модулю и нормальна к
траектории частицы. Согласно 2-му закону
Ньютона, эта сила создает центростремительное
ускорение. Отсюда следует, что частица
будет двигаться по
окружности,
радиус r которой определяется из условия
qVB
= mV2/r,
откуда 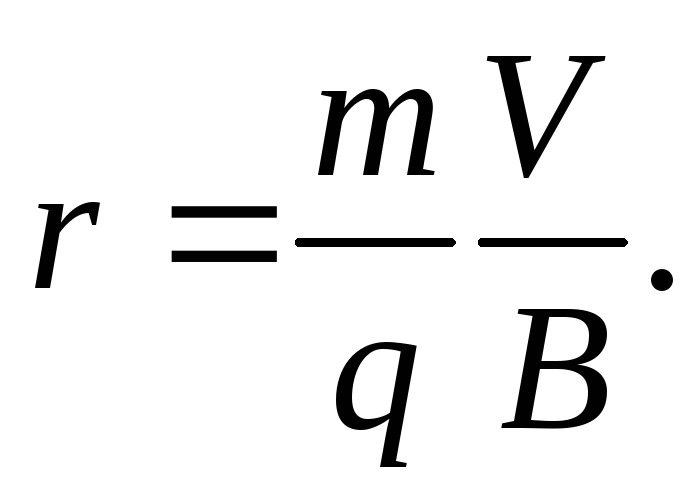
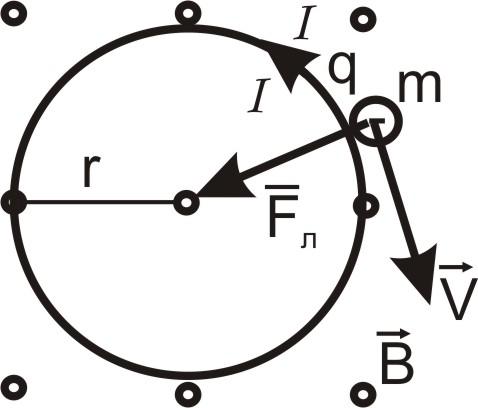
Рис. 2.18
Период вращения частицы, т. е. время Т, за которое она совершит один полный оборот,

Или с учетом r
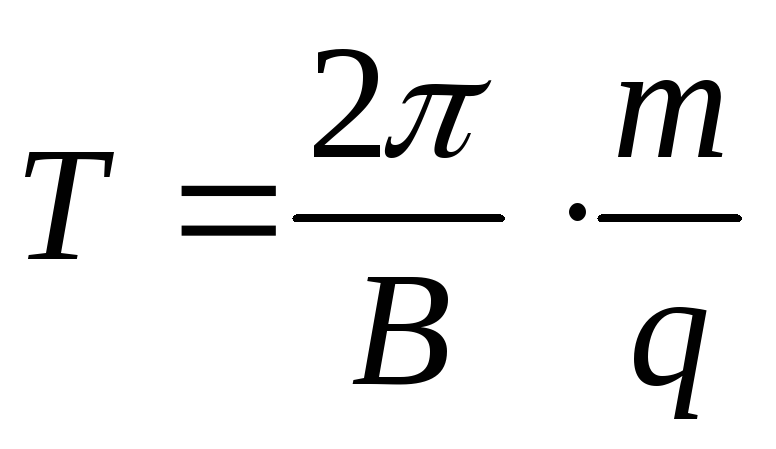
в)
Если скорость 
 (рис. 2.19), то ее движение можно представить
в виде суперпозиции:
(рис. 2.19), то ее движение можно представить
в виде суперпозиции:1) равномерного прямолинейного движения вдоль поля со скоростью
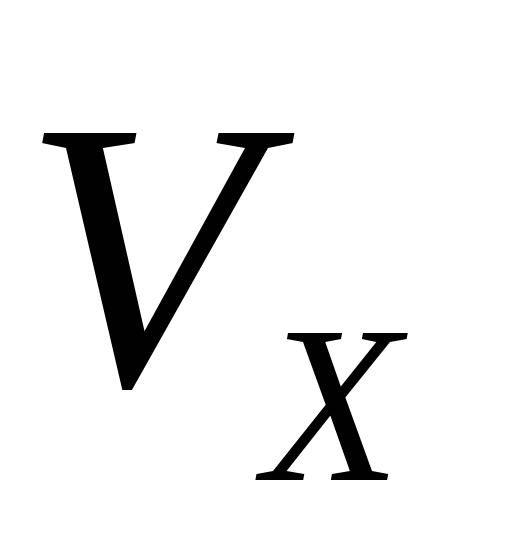 =
=  соs α;
соs α;
2)
равномерного движения со скоростью 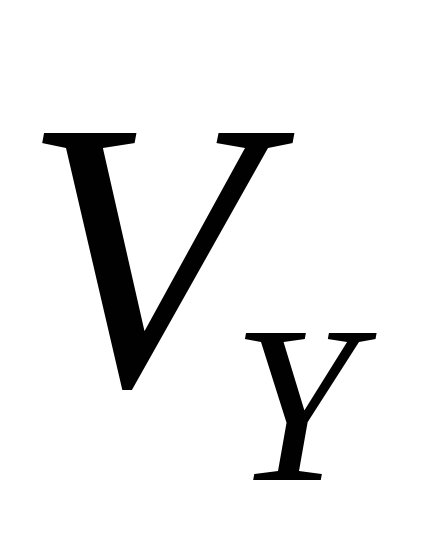
 sin α по окружности в плоскости, перпендикулярной
полю. Радиус окружности определяется
формулой
sin α по окружности в плоскости, перпендикулярной
полю. Радиус окружности определяется
формулой 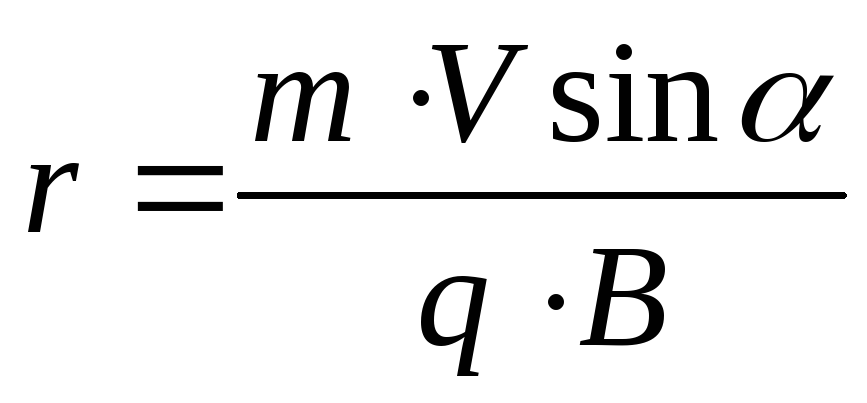
В результате сложения обоих движений возникает движение по спирали, ось которого параллельна магнитному полю.

Рис. 2.19
Шаг винтовой линии
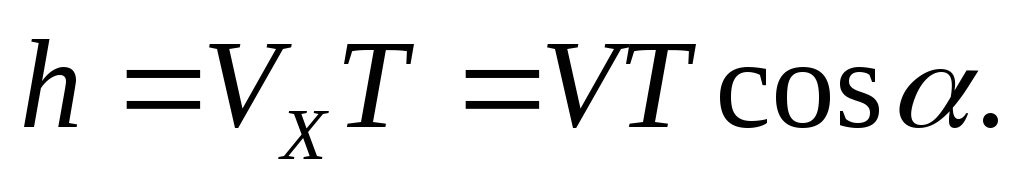
Подставив сюда Т, получим выражение,

Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если
скорость  заряженной частицы составляет угол α
с направлением вектора
заряженной частицы составляет угол α
с направлением вектора 
Сила Ампера
И — 4
Между полюсами электромагнита создается магнитное поле с индукцией В=0,1Тл. По проводу длиной L=7см, размещенному под углом
α=300 к направлению магнитного поля, течет ток I=70A. Найти силу F, действующую на провод со стороны магнитного поля.
Решение:
На элемент длины dL проводника с током I в магнитном поле с индукцией B действует сила Ампера:
dF=[IdL×B].
Направление этой силы определяется по правилу векторного произведения: вектор dF направлен перпендикулярно плоскости векторов IdL и B так, чтобы из конца вектора δF поворот от вектора (IdL) к вектору B был виден против часовой стрелки.
Модуль силы Ампера вычисляется по формуле:
dF= IdL×B×sin a,
где α – угол между направлением тока и вектором В.
Модуль силы Ампера, действующей на весь проводник:
L | |
F = IBò | sin a dL = IBLsin a = 70× 0,1× 0,7 × 0,5 = 2,45 (H) . |
0 |
|
| И -5 |
По П– образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка АВ длиной ℓ, массой m и сопротивлением R. Система находится в однородном магнитном поле с индукцией В, направленном вертикально. В момент времени t = 0 на перемычку начали действовать постоянной горизонтальной силой F, и перемычка начала перемещаться вправо. Найти зависимость скорости перемычки от времени. Индуктивность контура и сопротивление П- образного проводника пренебрежимо малы.

| B |
|
|
|
|
| A |
|
| При перемещении перемычки | ||||
|
|
|
|
|
|
| на расстояние dx = v×dt площадь | |||||||
|
|
|
| R |
|
|
|
| контура возрастает на dS = | ℓ×dx , | ||||
| F |
|
|
| F |
| что вызывает изменение магнитного | |||||||
|
|
|
|
|
|
| ℓ | потока |
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
| dФ = B×dS . |
| |
|
| В |
| dx |
|
|
|
|
|
|
| В | контуре возникает | ЭДС |
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
| индукции |
| ||
|
|
|
|
|
|
|
| e = | dΦ | = B × | dx | = B v . |
| |
|
|
|
|
|
|
| dt | dt |
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||
По цепи пойдет ток
I = εRi = BRv ,
который согласно правилу Ленца, своим магнитным полем должен мешать изменению магнитного потока, поэтому на перемычку будет действовать сила Ампера, направленная против внешней приложенной силы F
FA = IBℓ = | e i | B = | B2 2v . | |
R | ||||
|
| R |
Применив II закон Ньютона для описания движения перемычки, получим:
ma = F – FA | или m dv | = F — | B2 2v . |
| dt |
| R |
Разделив переменные, проинтегрируем полученное уравнение:
v |
| dv |
| t | dt |
ò |
|
|
| = ò | m , |
F — | B2 2 | v | |||
0 | R | 0 |
| ||
|
|
|
|
|
— R |
|
| B2 2 |
|
| v | t |
| |
|
|
|
| ||||||
ln | F — | v |
| = | , | ||||
2 2 | R | m | |||||||
B |
|
|
| 0 |
| ||||
|
|
|
|
|
|
|
| ||
откуда зависимость скорости перемычки от времени имеет вид:
v = | RF | (1- exp(- | B2 2 | t)) . |
2 2 | mR | |||
| B |
| ||
Сила Лоренца
И — 5
Электрон, ускоренный разностью потенциалов U = 1кВ, влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля В = 1,19 мТл. Найти радиус R окружности, по которой движется электрон, период обращения Т и момент импульса L электрона. (Действием силы тяжести можно пренебречь).
Решение:
На движущуюся заряженную частицу со стороны магнитного поля действует сила Лоренца:
FЛ= q[v×B],
где q – заряд частицы, v – её скорость, B – индукция магнитного поля. Направление силы Лоренца определяется по правилу векторного
произведения: вектор силы Fл, действующей на положительно заряженную движущуюся частицу, направлен перпендикулярно плоскости векторов v и B так, чтобы из конца вектора силы Fл поворот от вектора скорости v к вектору магнитной индукции B был виден против часовой стрелки.
Примеч.: для отрицательно заряженной частицы – направление силы Fл противоположно направлению силы Fл, действующей на положительно заряженную движущуюся частицу.
Модуль силы Лоренца:
FЛ= q×v×B×sin a,
где α — угол, образованный вектором скорости движущейся частицы и вектором магнитной индукции. Поскольку начальная скорость
электрона перпендикулярна вектору магнитной индукции, то sinα=1 и
траектория электрона лежит на плоскости. По второму закону Ньютона сила Лоренца сообщает электрону нормальное ускорение
mv2/R = q×v×B.
где q — заряд, v — скорость и m — масса электрона; В – магнитная индукция; R – радиус кривизны траектории.
Отсюда выразим радиус кривизны траектории R:
R = mv/qB.
Период обращения электрона по окружности
T = 2pR/v = 2pm/qB.
Электрон приобретает кинетическую энергию за счет работы, совершаемой ускоряющим электрическим полем:
mv2/2 = qUуск., откуда импульс электрона mv = (2mqUуск.)1/2. Момент импульса электрона
L = mvR =(mv)2/qB = (2mqUуск.)/qB.
Подставляя числовые данные, получим:
R=mv/qB =(2mUуск./q)1/2/B =(2×9,1×10-31×103/1,6×10-19)1/2/1,19×10-3@9 см, T = 2pm/qB = 2×3,14×9,1×10-31/1,6×10-19×1,19×10-3 = 3×10-8 с,
L= 2mUуск./B = 2×9,1×10-31×103/1,19×10-3 = 1,53×10-24 Дж×с.
Сила Ампера
Самые простые задачи на определение силы, индукции поля, длины проводника или угла, под которым этот проводник расположен. Направление силы определяем по правилу ЛЕВОЙ руки: если расположить руку так, чтобы магнитные линии втыкались в ладонь, а четыре пальца направить по току, то отведенный большой палец укажет направление действия силы.
Задача 1. Прямолинейный проводник длиной  м находится в однородном магнитном поле с индукцией
м находится в однородном магнитном поле с индукцией  Тл. Сила тока в проводнике
Тл. Сила тока в проводнике  А. Проводник перпендикулярен магнитной индукции (рис.). Найти модуль и направление силы, действующей на проводник.
А. Проводник перпендикулярен магнитной индукции (рис.). Найти модуль и направление силы, действующей на проводник.

К задаче 1
Со стороны поля на проводник с током действует сила Ампера:
![Rendered by QuickLaTeX.com \[F_A=BlI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89edeeeb273e54270368fa10b93183a8_l3.png)
У нас проводник перпендикулярен линиям индукции, поэтому 
![Rendered by QuickLaTeX.com \[F_A= BlI=0,25\cdot2\cdot0,5=0,25\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d500489f007f529597584f6a5f72b778_l3.png)
Определяем направление. Левую руку расположим так, чтобы линии индукции втыкались в ладонь, то есть ладошкой вниз. Четыре вытянутых пальца направим вдоль тока – то есть влево. Тогда большой палец укажет направление действия силы – за плоскость рисунка, от нас.
Ответ:  Н, от нас за плоскость рисунка.
Н, от нас за плоскость рисунка.
Задача 2. Прямолинейный проводник длиной  м находится в однородном магнитном поле (рис.). На проводник со стороны поля действует сила
м находится в однородном магнитном поле (рис.). На проводник со стороны поля действует сила  Н. Сила тока в проводнике
Н. Сила тока в проводнике  А. Найти модуль и направление индукции магнитного поля, если она перпендикулярна проводнику.
А. Найти модуль и направление индукции магнитного поля, если она перпендикулярна проводнику.

К задаче 2
Со стороны поля на проводник с током действует сила Ампера:
![Rendered by QuickLaTeX.com \[F_A=BLI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a7140e51cd84b1b61114a6b8a60354a6_l3.png)
У нас проводник перпендикулярен линиям индукции, поэтому 
![Rendered by QuickLaTeX.com \[B=\frac{F_A}{lI}=\frac{2}{5\cdot1}=0,4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-44c3589249eca5fc1bd3ff3fd162896e_l3.png)
Для определения направления левую руку расположим пальцами вниз – они указывают направление тока, большим пальцем вправо – он указывает направление действия силы. Тогда ладонь окажется развернутой к нам – в раскрытую ладонь должны втыкаться линии магнитной индукции, следовательно, они направлены от нас за плоскость чертежа.
Ответ:  Тл, от нас за плоскость чертежа.
Тл, от нас за плоскость чертежа.
Задача 3. На прямой проводник длиной  м, расположенный под углом
м, расположенный под углом  к силовым линиям поля с индукцией
к силовым линиям поля с индукцией  Тл, действует сила
Тл, действует сила  Н. Найти силу тока в проводнике.
Н. Найти силу тока в проводнике.
Со стороны поля на проводник с током действует сила Ампера:
![Rendered by QuickLaTeX.com \[F_A=BlI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89edeeeb273e54270368fa10b93183a8_l3.png)
![Rendered by QuickLaTeX.com \[I=\frac{F_A}{lB\sin\alpha}=\frac{0,15}{0,5\cdot2\cdot 10^{-2}\cdot0,5}=30\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-94a3cfdd384bcb293d28ed3589fa4753_l3.png)
Ответ: 30 А.
Задача 4. Прямой провод длиной  см находится в однородном магнитном поле с индукцией
см находится в однородном магнитном поле с индукцией  Тл. Сила тока в проводнике
Тл. Сила тока в проводнике  А. Найти угол
А. Найти угол  между направлением магнитной индукции и направлением тока, если на провод действует сила
между направлением магнитной индукции и направлением тока, если на провод действует сила  Н.
Н.
Со стороны поля на проводник с током действует сила Ампера:
![Rendered by QuickLaTeX.com \[F_A=BlI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89edeeeb273e54270368fa10b93183a8_l3.png)
![Rendered by QuickLaTeX.com \[\sin\alpha =\frac{F_A}{BLI}=\frac{0,01}{0,01\cdot0,1\cdot 20}=0,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b1d6b6d12d6108586b5097e4ae5c0f20_l3.png)
Синус, равный  , имеет угол в
, имеет угол в  .
.
Ответ:  .
.
Задача 5. Проводник находится в равновесии в горизонтальном магнитном поле с индукцией  мТл. Сила тока в проводнике
мТл. Сила тока в проводнике  А. Угол между направлением тока и вектором магнитной индукции
А. Угол между направлением тока и вектором магнитной индукции  . Определить длину проводника, если его масса
. Определить длину проводника, если его масса  кг.
кг.
Так как поле горизонтально, а проводник в нем «висит», то очевидно, что сила Ампера уравновесила силу тяжести:
![Rendered by QuickLaTeX.com \[mg=F_A\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b03c09b94b284f8955bf5d74e18dbe45_l3.png)
![Rendered by QuickLaTeX.com \[mg= BlI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-80e4a7f06e106b42b64ba724360ed06d_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[l=\frac{ mg }{ BI\sin\alpha }=\frac{0,0237\cdot10}{48\cdot10^{-3}\cdot23\cdot\frac{\sqrt{3}}{2}}=0,258\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b6bbf0970226317ff4ee1627cece0b34_l3.png)
Ответ: 25,8 см.
Задача 6. Проводник длиной  м расположен перпендикулярно силовым линиям горизонтального магнитного поля с индукцией
м расположен перпендикулярно силовым линиям горизонтального магнитного поля с индукцией  мТл. Какой должна быть сила тока в проводнике, чтобы он находился в равновесии в магнитном поле? Масса проводника
мТл. Какой должна быть сила тока в проводнике, чтобы он находился в равновесии в магнитном поле? Масса проводника  кг.
кг.
Аналогично предыдущей задаче,
![Rendered by QuickLaTeX.com \[mg=F_A\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b03c09b94b284f8955bf5d74e18dbe45_l3.png)
![Rendered by QuickLaTeX.com \[mg= BlI\sin\alpha\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-80e4a7f06e106b42b64ba724360ed06d_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[I=\frac{ mg }{ Bl\sin\alpha }=\frac{8\cdot10^{-2}}{8\cdot10^{-3}\cdot1\cdot1}=10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-870767a2524dc8924aee2abad89c6a37_l3.png)
Ответ: 10 А.
Работа сил ампера при перемещении проводника в магнитном поле. Формула. Вывод
Как и любая другая сила, сила Ампера имеет возможность совершить работу. По определению механической работы:
(1)Рис. 1. Работа силы Ампера
Пусть в нашей системе проводник длиной
, находящийся в однородном магнитном поле индукции , по которому течёт ток , движется под действием силы Ампера и перемещается на расстояние (рис. 1). Тогда, при условии, что сила Ампера равна , получим: (2)Пометим
— площадь, «заметаемая» при движении проводника. Т.е. площадь, которую «прошёл» проводник во время движения. Тогда, в общем случае: (3)Соотношение (3) указывает на работу сил Ампера. Однако, если использовать определение изменения потока магнитного поля:
Ф (4)получим:
Ф (5)Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…



