Магнетизм — Вікіпедія

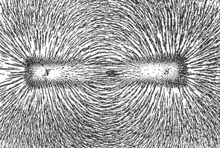Силові лінії магнітного поля навколо магніта, сформовані залізними ошурками на папері

Магнети́зм — форма взаємодії «рухомих» електричних зарядів, яка здійснюється на відстані за допомогою магнітного поля. Поряд з електрикою, магнетизм — один із проявів електромагнітної взаємодії.

Магнетизм — це клас фізичних явищ, зумовлених магнітними полями. Електричні струми і магнітні моменти елементарних частинок породжують магнітне поле, яке діє на інші струми та магнітні моменти. Найбільш знайомі ефекти відбуваються у феромагнітних матеріалах, які дуже притягуються магнітними полями і можуть намагнічуватися, перетворюючись на постійні магніти, та самі створювати магнітні поля. Лише деякі речовини є феромагнітними; найбільш поширеними є залізо, кобальт і нікель та їх сплави, такі як сталь. Приставка «феро» стосується заліза, тому що постійний магнетизм вперше спостерігався в залізняку, формі природної залізної руди, званої магнетитом, Fe3O4.

Хоча феромагнетизм охоплює більшість виявів магнетизму, що зустрічаються в повсякденному житті, на всі інші матеріали в деякій мірі, впливає магнітне поле, а також деякі інші види магнетизму. Парамагнітні речовини, такі як алюміній і кисень, слабко притягуються до прикладеного магнітного поля; діамагнітні речовини, такі як мідь і вуглець, слабко відштовхуються; у той час як антиферомагнітні матеріали, такі як хром і спінове скло, мають більш складний зв’язок з магнітним полем. Сила магнетизму на парамагнітні, діамагнітні і антиферомагнітні матеріали зазвичай занадто слабка, щоб її можна було відчути, тож її можна виявити лише лабораторними приладами, тому в повсякденному житті ці речовини часто називають немагнітними.

Магнітний стан (або магнітна фаза) матеріалу залежить від температури та інших змінних умов, таких як тиск і прикладене магнітне поле. Матеріал може проявляти більше ніж одну форму магнетизму у разі зміни умов.Можливе як намагнічування так і розмагнічування магніту. Пропускання змінного струму або удар по нагрітому магніту в напрямку схід-захід, це способи розмагнічування магніту.

Магнетизм було вперше виявлено в стародавньому світі, коли люди помітили, що магніти — природно намагнічені шматочки мінерального магнетиту, можуть притягати залізо. Слово «магніт» походить від грецького терміну «μαγνῆτις λίθος magnētis lithos», «магнезійний камінь, підніжний камінь». У стародавній Греції Аристотель приписав перше з того, що можна було б назвати науковою дискусією про магнетизм, філософу Фалесу Мілетському, який жив з 625 р до н.е. до 545 р до н.е. Древній індійський медичний допис «Сушрута самхита» описує використання магнетиту для видалення стріл, застряглих в тіло людини.

У стародавньому Китаї найперше літературне посилання на магнетизм, міститься в книзі 4-го століття до нашої ери, названої на честь її автора, «Мудрець Долини Привидів». Найперша згадка про притягнення голки — в роботі 1-го століття «Луньхен» ( «Збалансовані запити»): «Магніт притягує голку». Китайський учений 11-го століття Шень Куо був першою людиною, яка змалювала в «Есе басейну снів», магнітний стрілковий компас і те що він підвищив точність навігації, використовуючи астрономічне Поняття справжньої півночі. До 12-го століття китайці, як було відомо, використовували компас-магніт для навігації. Вони виліпили напрямну ложку з каменю таким чином, що ручка ложки завжди вказувала на південь.

Олександр Некк, до 1187 року, був першим в Європі, хто описав компас і його використання для навігації. У 1269 році Пітер Перегрінусе де Марікура написав Epistola de magnete, перший збережений трактат, що змальовує властивості магнітів. 1282 року поведінку магнітів і сухих компасів обговорював Халіль аль-Ашраф, єменський фізик, астроном і географ.

У 1600 році Вільям Гілберт оприлюднив власні книги («Про магніт і магнітні тіла», «Великий магніт Землі»). У цих роботах він змальовує багато своїх дослідів з власною моделлю землі, званою Террелл. Завдяки ним, він прийшов до висновку, що Земля сама по собі є магнітною, і саме тому компас вказує на північ (раніше деякі вважали, що саме полярна зірка (Polaris) або великий магнітний острів на північному полюсі притягував стрілку компасу).

Розуміння взаємозв’язку між електрикою і магнетизмом, почалося 1819 року з роботи професора Копенгагенського університету Ганса Крістіана Ерстеда, який виявив під час випадкового посмикування стрілки компаса біля проводу, що електричний струм може створити магнітне поле. Цей знаменний дослід відомий як Експеримент Ерстеда. Кілька інших дослідів пішли від Андре-Марі Ампера, який 1820 року виявив, що магнітне поле, котре циркулює замкненим шляхом, було пов’язано зі струмом, який протікає по периметру кола; Карл Фрідріх Гаусс; Жан-Батіст Біо і Фелікс Савар, обидва з яких 1820 року вигадали закон Біо-Савара, що дає рівняння для магнітного поля від провідника зі струмом; Майкл Фарадей, який в 1831 році виявив, що мінливий в часі магнітний потік крізь петлю дроту, викликав напругу, а інші знаходили подальші зв’язки між магнетизмом та електрикою. Джеймс Клерк Максвелл узагальнив і розширив це розуміння рівнянь Максвелла та об’єднав електрику, магнетизм і оптику в галузь електромагнетизму. 1905 року, Ейнштейн використовував ці закони, пояснюючи власну гіпотезу спеціальної теорії відносності та наполягав, щоби вони застосовувалися у всіх інерційних системах відліку.

Електромагнетизм продовжував розвиватися в 21 столітті, і був включеним до більш основоположних теорій: калібрувальних, квантової електродинаміки, електрослабкої теорії і, нарешті, стандартної моделі.

Визначення. Загальна інформація[ред. | ред. код]

Магнетизм — сукупність явищ і властивостей, пов´язаних з впливом магнітного поля, що може бути зумовлений протіканням макроскопічних електричних струмів (соленоїд, електромагніт), або атомних (магнітний момент). Магнетизм проявляється, зокрема, у взаємному притягуванні і відштовхуванні між магнітами, електричними струмами, між струмами і магнітами, мікрочастинками (електронами, протонами тощо).

Магнітні властивості речовини визначаються неспареними (нескомпенсованими) спінами електронів; у випадку відсутності їх прояву говоримо про діамагнетики, у протилежному разі — про парамагнетики — коли взаємодія між спінами слабка, та феромагнетики — коли взаємодія сильна і спричиняє паралельне орієнтування спінів у певній області (так званих магнітних доменах), антиферомагнетиках, коли вплив сприяє паралельному розташуванню спінів (на відміну від феромагентиків, антиферомагнетики у зовнішньому магнітному полі не виявляють сильного намагнічування і їхні властивості подібні до парамагнетиків), і феримагнетиків, коли спіни електронів сусідніх атомів орієнтуються різним чином, проте створені ними магнітні моменти не компенсуються повністю.

Магнетизмом називають також підрозділ фізики, який вивчає взаємодію електрично заряджених частинок (тіл) або частинок (тіл) з магнітним моментом, яка здійснюється через магнітне поле.

Магнетизм як спеціальність охоплює теоретичне та експериментальне вивчення природи впорядкованих (феромагнетизм, антиферомагнетизм, феримагнетизм) та невпорядкованих (діамагнетизм, парамагнетизм, спінове скло) магнетних станів у діелектричних, напівпровідникових та металевих матеріалах.

Основні рівняння і закони[ред. | ред. код]

Сучасна теорія магнетизму базується на таких основних рівняннях і законах:

Областю досліджень є експериментальні та теоретичні дослідження у таких напрямках:

• атомний механізм магнетизму, магнітні властивості окремих атомів, перехідні d- та f-елементи;
• діамагнетизм атомів та молекул;
• магнетні властивості електронів провідності в металах: діамагнетизм Ландау та парамагнетизм Паулі;
• парамагнетизм твердих тіл;
• магнетовпорядковані стани, їх структура та властивості: феромагнетизм, антиферомагнетизм, феримагнетизм;
• магнетні фазові переходи в магнетних речовинах;
• магнетооптичні та магнетоелектричні явища;
• невпорядковані магнетики: аморфні магнетики та спінове скло;
• елементарні збудження в магнетних матеріалах;
• магнетні домени та стінки, процеси перемагнічування;
• резонансні явища, ЕПР, ЯМР, ФМР, АФМР, ЯГР;
• магнетні властивості надпровідників;
• магнетні властивості низьковимірних систем;
• магнетні властивості мезоскопічних систем;
• фізичні основи створення нових магнетних матеріалів;
• магнетні властивості мезоскопічних систем.

Магнетизм макротіл — властивості тіл, які виявляються при взаємодії їх з магнітним полем. Зумовлений спільним магнетизмом частинок, які складають тіла і макрострумів у них. Усі речовини за їх магнітними властивостями поділяються на діа-, пара-, феромагнітні. Залежно від характеру взаємодії частинок-носіїв магнітного моменту, у речовин може спостерігатися феромагнетизм, феримагнетизм, антиферомагнетизм, парамагнетизм, діамагнетизм та інші види магнетизму

Магнетизм мікрочастинок[ред. | ред. код]

Магнетизм мікрочастинок — властивість мікрочастинок, яку вони проявляють в електромагнітній взаємодії. Для окремих елементарних частинок це прояв їх спінового магнітного моменту. Магнетизм атомів і молекул обумовлюється спіновим магнетизмом електронів, їх орбітальними магнітними моментами та власними і орбітальними моментами нуклонів у ядрах. Причому магнітні моменти ядер не є простою сумою магнітних моментів нуклонів, що пояснюється впливом ядерних сил між нуклонами. Загальний магнітний момент атома складається із суми магнітних моментів його електронів і ядра. Магнітний момент парамагнітних атомів не дорівнює нулю, діамагнітні атоми мають нульовий магнітний момент.

Сила Ампера і закон Ампера

Закон Ампера

Що таке сила Ампера

Правило лівої руки

Застосування сили Ампера

Сила Ампера, відео

Важко уявити наше сучасне життя без електрики, адже зникни вона, це б миттєво привело до глобальних катастрофічних наслідків. Так що в будь-якому випадку з електрикою ми відтепер не розлучні. А ось для того, щоб мати з нею справу потрібно знати певні фізичні закони, одним з яких, безумовно, є закон Ампера. А знаменита магнітна сила Ампера – головна складова цього закону.

Закон Ампера

Отже, давайте сформулюємо закон Ампера: в паралельних провідниках, де електричні струми течуть в одному напряму, з’являється сила тяжіння. А в провідниках, де струми течуть в протилежних напрямках, навпаки виникає сила відштовхування. Якщо ж говорити простою життєвою мовою, то закон Ампера можна сформулювати гранично просто «протилежності притягуються», і адже в реальному житті (а не тільки фізиці) ми спостерігаємо подібне явище, чи не так?

Але повернімося до фізики, в ній також під законом Ампера розуміють закон, що визначає силу дії магнітного поля на ту частину провідника, по якій протікає струм.

Що таке сила Ампера

Власне сила ампера і є тією силою дії магнітного поля на провідник, по якому йде струм. Сила Ампера визначається за формулою як результат множення щільності струму, що йде по провіднику на індукцію магнітного поля, в якому знаходиться провідник. Як результат формула сили Ампера буде виглядати так

са = ст*ДчП*ми

Де, са – сила Ампера, ст – сила струму, ДчП – довжина частини провідника, ми – магнітна індукція.

Правило лівої руки

Правило лівої руки призначене для того, щоб допомогти запам’ятати, куди направлена сила Ампера. Воно звучить наступним чином: якщо рука займає таке положення, що лінії самої магнітної індукції зовнішнього поля заходять в долоню, а пальці з мізинця по вказівний вказують напрямок в сторону руху струму в провіднику, то відірваний під кутом в 90 градусів великий палець долоні і буде вказувати, куди направлена сила Ампера, що діє на елемент провідника.

Приблизно так виглядає правило лівої руки на цій схемі.

Застосування сили Ампера

Застосування сили Ампера в сучасному світі дуже широке, можна навіть без перебільшення сказати, що ми буквально оточені силою Ампера. Наприклад, коли ви їдете в трамваї, тролейбусі, електромобілі, його в рух приводить саме вона, сила Ампера. Аналогічно ліфти, електричні ворота, двері, будь-які електроприлади, все це працює саме завдяки силі Ампера.

Сила Ампера, відео

І на завершення невеликий відео урок про силу Ампера.

Закон Ампера — Gpedia, Your Encyclopedia

Взаємодія двох елементарних струмів: а — паралельних, б — антипаралельних (всі відрізки (вектори) лежать в одній площині)

Закон Ампера — закон взаємодії постійних струмів. Установлений Андре-Марі Ампером в 1820 році. Із закону Ампера виходить, що паралельні провідники з постійними струмами, що течуть в одному напрямі, притягуються, а в протилежному — відштовхуються. Законом Ампера називається також закон, що визначає силу, з якою магнітне поле діє на малий відрізок провідника із струмом.

Сила Ампера — це сила, з якою магнітне поле діє на провідник зі струмом .

F=BILsin⁡α{\displaystyle F=BIL\sin \alpha \!}

Сила Ампера залежить від сили струму I{\displaystyle I}, елемента (частини) довжини провідника dl{\displaystyle dl}, кута між напрямом струму і напрямом ліній магнітного поля α{\displaystyle \alpha } та магнітної індукції B{\displaystyle B}, і задається формулою

dF=BIdlsin⁡α{\displaystyle dF=BIdl\sin \alpha \!}

У векторній формі сила Ампера записується

dF=I[dl,B]{\displaystyle d\mathbf {F} =I[\mathbf {dl} ,\mathbf {B} ]}.

dF=BIdlsin⁡α{\displaystyle dF=BIdl\sin \alpha \!}

Джерела

Закон Ампера — Максвелла — Википедия

Закон Ампера — Максвелла (синоним: обобщенная теорема Ампера о циркуляции) — закон электромагнетизма, исторически завершивший создание замкнутой и непротиворечивой классической электродинамики.

Открыт Максвеллом, обобщившим теорему Ампера о циркуляции магнитного поля на общий случай, включающий переменные несоленоидальные (незамкнутые) токи и меняющиеся во времени поля.

Формулировка этого закона составляет четвёртое уравнение Максвелла:

∮∂S⁡B⋅dl=∫S(j+∂E∂t)⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}{\Big (}\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}{\Big )}\cdot \mathbf {dS} }

Единицы и обозначения

Здесь уравнение записано в интегральной форме в наиболее простом и фундаментальном виде: для вакуума, в рационализированной системе единиц с кулоновской константой 1/(4π){\displaystyle 1/(4\pi )} и скоростью света равной единице. S — любая поверхность, интеграл в правой части — сумма обычного тока (первый член) и тока смещения (второй член), введенного в уравнение Максвеллом. ∂S{\displaystyle \partial S} — край этой поверхности, представляющий собой замкнутую кривую, по которой взят контурный интеграл в левой части — циркуляция магнитного поля (вектора магнитной индукции) В; j — плотность тока, Е — напряженность электрического поля, ∂/∂t{\displaystyle \partial /\partial t} — производная по времени.

• Запись для вакуума и среды в разных системах единиц — см. ниже.

Это же уравнение в дифференциальной форме:

∇×B=j+∂E∂t{\displaystyle \nabla \times \mathbf {B} =\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}}

(здесь в левой части ротор магнитного поля, ∇{\displaystyle \nabla } — оператор набла, ×{\displaystyle \times } — векторное произведение).

Запись в системе СГС

В обычной гауссовой системе единиц (с кулоновской константой 1, в отличие от единиц, примененных в статье выше) эти уравнения выглядят так:

Для вакуума:

∮∂S⁡B⋅dl=4πc∫Sj⋅dS+1c∫S∂E∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} ={\frac {4\pi }{c}}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c}}\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} }

или

∇×B=4πcj+1c∂E∂t.{\displaystyle \nabla \times \mathbf {B} ={\frac {4\pi }{c}}\mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}.}

Для диэлектрической среды:

∮∂S⁡H⋅dl=4πc∫Sj⋅dS+1c∫S∂D∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {H} \cdot \mathbf {dl} ={\frac {4\pi }{c}}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c}}\int \limits _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {dS} }

или

∇×H=4πcj+1c∂D∂t.{\displaystyle \nabla \times \mathbf {H} ={\frac {4\pi }{c}}\mathbf {j} +{\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}.}

Запись в системе СИ

Для вакуума:

∮∂S⁡B⋅dl=μ0∫Sj⋅dS+1c2∫S∂E∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\mu _{0}\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +{\frac {1}{c^{2}}}\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} }

или

∇×B=μ0j+1c2∂E∂t.{\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {j} +{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}.}

Для диэлектрической среды:

∮∂S⁡H⋅dl=∫Sj⋅dS+∫S∂D∂t⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {H} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +\int \limits _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot \mathbf {dS} }

или

∇×H=j+∂D∂t.{\displaystyle \nabla \times \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}.}

Обобщение теоремы Ампера о циркуляции потребовало^[1] ввести в формулу Ампера дополнительный член с током смещения.

Теорема Ампера о циркуляции магнитного поля, сводящаяся к формуле

∮∂S⁡B⋅dl=∫Sj⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} }

Единицы и обозначения

Здесь снова записываем уравнение в том же виде, как в начале статьи, то есть для вакуума, в рационализированной системе единиц с кулоновской константой 1/(4π){\displaystyle 1/(4\pi )} и скоростью света равной единице.

S — любая поверхность, интеграл в правой части — электрический ток через эту поверхность. ∂S{\displaystyle \partial S} — граница этой поверхности — замкнутая кривая, по которой взят контурный интеграл в левой части — циркуляция магнитного поля (вектора магнитной индукции) В; j — плотность тока.

верная в рамках магнитостатики (и никак не меняющаяся при добавлении электростатики) достаточно хорошо обоснована эмпирически для статических (а также и для медленно меняющихся со временем) полей. Теоретически она прямо связана с законом Био-Савара (аналогом закона Кулона в магнитостатике) и может быть доказана как теорема исходя из него (так же как и обратно закон Био — Савара может быть получен из основных уравнений магнитостатики — формулы Ампера и закона Гаусса для магнитного поля).

Поэтому при поиске варианта этой формулы для общего случая меняющихся полей и токов, то есть аналогичного закона в электродинамике, можно исходить из хорошо обоснованного постулата, что теорема Ампера верна для постоянных токов и постоянных во времени полей (из чего исторически и исходил Максвелл).

Однако при переходе к общему случаю переменных токов (и меняющихся во времени полей), обнаруживается, что мы не можем пользоваться этой формулой, по крайней мере, не можем пользоваться ею в неизменном виде (а это означает, что формула должна быть как-то исправлена, хотя, по-видимому, общую её структуру хотелось бы сохранить, раз уж она хорошо работает в магнитостатическом случае).

Возникающую проблему (состоящую в том, что формула Ампера становится внутренне противоречивой при попытке использовать её вне магнитостатики) мы опишем несколько по-разному в двух параграфах ниже, так же как и несколько по-разному обоснуем в каждом из них необходимую поправку.

Элементарное обоснование на частном примере[править | править код]

Рассмотрим конкретно представленную на схеме электрическую цепь, содержащую конденсатор^[2].

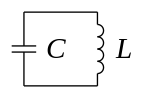
Например, это может быть простой колебательный контур, как на рисунке (конденсатор обозначен на нём как C, а L — катушка индуктивности). (Нас на самом деле будет интересовать только часть цепи вблизи конденсатора, а остальная часть схемы не важна, то есть вместо L может быть просто провод^[3], а может содержать и какое угодно устройство, способное (автоматически или вручную) изменять ток, текущий в конденсатор, например, это может быть электрическая батарея с выключателем. Будем считать для простоты, что зазор между пластинами конденсатора не содержит способной поляризоваться среды, то есть это вакуум (или, скажем, воздух, поляризуемостью которого можно с хорошей точностью пренебречь).

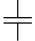
Иными словами, мы здесь можем ограничиться рассмотрением только вот этой части цепи:

Теперь можно приступить к анализу работы формулы Ампера в этом нашем конкретном примере.

1. Непротиворечивость исходной теоремы в нашем примере для случая постоянного тока:

В случае наложенного условия постоянности тока в цепи, оказывается, что ток через конденсатор просто не может течь. Действительно, если ток, втекающий на пластины конденсатора не меняется со временем, то заряд на пластинах растет до бесконечности, что, очевидно, физически бессмысленно, и такой вариант можно смело исключить из рассмотрения^[4]. Таким образом, теорема Ампера в этом случае очевидно работает, так как нет никаких токов и магнитных полей, т.е. левая и правая часть уравнения

∮∂S⁡B⋅dl=∫Sj⋅dS{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} }

просто нулевые^[5].

Однако всё коренным образом меняется, когда мы рассматриваем переменные токи (которые, конечно же, возможны в реальности). Эта формула начинает давать противоречивые результаты, если попытаться её использовать.

2. Противоречие исходной формулы в случае переменного тока:

Действительно, выберем конкретную поверхность интегрирования S=S1{\displaystyle S=S_{1}} такой, чтобы она проходила между пластинами конденсатора (то есть на рисунке — почти горизонтальной, чтобы проходить между горизонтальными пластинами, не касаясь их; будем — просто для определенности и удобства — считать, что она почти горизонтальна и за краями пластин конденсатора; можно выбрать её и строго горизонтальной) и выходящей за его края, то есть большей площади, чем пластины. Тогда край этой поверхности ∂S1{\displaystyle \partial S_{1}}, представляющий собой контур для вычисления интеграла (циркуляции B) в левой части, будет некоторой кривой вокруг конденсатора (а если мы выбрали S1{\displaystyle S_{1}} строго горизонтальной, то этот контур будет также лежать в горизонтальной плоскости).

Поверхность S1{\displaystyle S_{1}} нигде не пересекается проводником, через неё нигде не течет ток (j в зазоре конденсатора везде равно нулю, там нет зарядов, способных переносить ток). Значит, правая часть уравнения равна нулю, и, в предположении что само уравнение верно — нулю равна и левая — то есть циркуляция магнитного поля по краю S1{\displaystyle S_{1}}:

∮∂S1⁡B⋅dl=∫S1j⋅dS1=0.{\displaystyle \oint \limits _{\partial S_{1}}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{1}}\mathbf {j} \cdot \mathbf {dS_{1}} =0.}

Обозначим C этот край поверхности S1{\displaystyle S_{1}} (контур интегрирования в левой части уравнения): C=∂S1{\displaystyle C=\partial S_{1}}.

Однако S1{\displaystyle S_{1}} — не единственная поверхность, имеющая такой край. На контур C можно «натянуть» и другую, не совпадающую с S, поверхность, и даже бесконечно много различных поверхностей (так что край у всех будет совпадать).

Конкретно выберем («натянем» на C) другую поверхность S2{\displaystyle S_{2}} так, чтобы её край совпадал с C, а сама она проходила не через зазор конденсатора, а чуть выше, пересекая провод, подводящий к конденсатору ток (такую поверхность можно получить из S1{\displaystyle S_{1}} несколько выгнув её вверх).

Очевидно, что интеграл в правой части, представляющий собой электрический ток через поверхность S2{\displaystyle S_{2}} не равен нулю:

∮∂S2⁡B⋅dl=∫S2j⋅dS2≠0.{\displaystyle \oint \limits _{\partial S_{2}}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} \neq 0.}

Получилось противоречие, т.к. в левой части, вследствие

∂S1=∂S2=C{\displaystyle \partial S_{1}=\partial S_{2}=C}

стоит один и тот же контурный интеграл по контуру C, а правые части дают разный результат:

∮C⁡B⋅dl=∫S1j⋅dS1=0,{\displaystyle \oint \limits _{C}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{1}}\mathbf {j} \cdot \mathbf {dS_{1}} =0,}

∮C⁡B⋅dl=∫S2j⋅dS2≠0.{\displaystyle \oint \limits _{C}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} \neq 0.}

Следовательно, формула Ампера в своем первоначальном виде в случае переменных токов^[6].

3. Нахождение поправки, устраняющей противоречие:

Уже чисто качественно довольно очевидно, что в зазоре конденсатора (там, где проходит поверхность S1{\displaystyle S_{1}} и где j = 0), есть, наверное, единственное, что могло бы заменить собой j, чтобы интеграл по S1{\displaystyle S_{1}} дал тот же результат, что по S2{\displaystyle S_{2}}, и этим самым устранилось противоречие. Это меняющееся электрическое поле.

Более того, сразу видно, что быстрота изменения напряженности электрического поля ∂E/∂t{\displaystyle \partial E/\partial t} в конденсаторе пропорциональна току, подходящему к этому конденсатору (а этот ток — и есть интеграл по второй поверхности:

I=∫S2j⋅dS2.{\displaystyle I=\int \limits _{S_{2}}\mathbf {j} \cdot \mathbf {dS_{2}} .}

Значит, есть шанс, что проинтегрировав ∂E/∂t{\displaystyle \partial E/\partial t} по поверхности S1{\displaystyle S_{1}} мы получим результат, совпадающий с I (может быть, домножив на какой-то коэффициент).

Теперь осталось выяснить, каким должен быть этот коэффициент и убедиться, что все детали вычислений совпадают.

Для этого выразим теперь поле в конденсаторе количественно: E=σ{\displaystyle E=\sigma } (в выбранных нами здесь единицах измерения^[7]).

Если законно пренебречь краевыми эффектами (считая площадь пластин конденсатора очень большой, а расстояние между ними маленьким)^[8], можем пользоваться формулой для напряженности поля, выписанной выше, по всей площади конденсатора (за исключением самых краев, областями вблизи которых мы пренебрегаем), а направление вектора E всюду (за тем же исключением) перпендикулярно пластинам (на рисунке — вертикально). Плотность заряда σ{\displaystyle \sigma } (в том же приближении) не зависит от положения (постоянна на подавляющей части пластины).

Исходя из всего этого поток

ΦS1,∂E/∂t=∫S1∂E∂t⋅dS1=∫S1∂E∂tdS1=∫S1∂σ∂tdS1=∂Q∂t=I,{\displaystyle \Phi _{S_{1},\partial \mathbf {E} /\partial t}=\int \limits _{S_{1}}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS_{1}} =\int \limits _{S_{1}}{\frac {\partial E}{\partial t}}dS_{1}=\int \limits _{S_{1}}{\frac {\partial \sigma }{\partial t}}dS_{1}={\frac {\partial Q}{\partial t}}=I,}

То есть он точно равен I, а значит коэффициент не нужен (он равен единице)^[9].

Итак, имеем для поправочного члена (который мы обосновали для интегрирования по S1{\displaystyle S_{1}}, но который, видимо, должен оставаться таким и для произвольной поверхности интегрирования)

I+=∫S∂E∂t⋅dS{\displaystyle I_{+}=\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} },

а сама формула Ампера после добавки этого поправочного члена приобретает вид:

∮∂S⁡B⋅dl=I+I+{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =I+I_{+}}

или

∮∂S⁡B⋅dl=∫Sj⋅dS+∫S∂E∂t⋅dS.{\displaystyle \oint \limits _{\partial S}\mathbf {B} \cdot \mathbf {dl} =\int \limits _{S}\mathbf {j} \cdot \mathbf {dS} +\int \limits _{S}{\frac {\partial \mathbf {E} }{\partial t}}\cdot \mathbf {dS} .}

(В нашем примере когда мы интегрируем по S1{\displaystyle S_{1}} — «работает» член I+{\displaystyle I_{+}} — на этой поверхности I=0{\displaystyle I=0}, а когда по S2{\displaystyle S_{2}} — «работает» член I{\displaystyle I} — на этой поверхности I+{\displaystyle I_{+}} превращается в ноль^[10]).

Таким образом, мы нашли поправочный член Максвелла к формуле Ампера и показали, что он устраняет противоречивость формулы в нашем простом примере. На самом деле он устраняет противоречивость формулы не только в этом частном случае, а всегда. Доказательство последнего утверждения содержится в следующем параграфе, оно чуть более формальное.

Стандартное общее обоснование[править | править код]

Здесь мы покажем, что поправка к формуле Ампера необходима и что она может иметь вид, предложенный Максвеллом, а также по возможности проследим, как она может быть точно построена из достаточно естественных и конструктивных соображений.

1. Начнем с утверждения о сохранении заряда.^[11]

Сохранение заряда выражается уравнением непрерывности:

∇⋅j+∂ρ∂t=0,{\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0,}

где j{\displaystyle \mathbf {j} } — плотность тока, ρ{\displaystyle \rho } — плотность заряда, ∇⋅j{\displaystyle \nabla \cdot \mathbf {j} } — дивергенция плотности токаj{\displaystyle \mathbf {j} }.

2. Проанализируем непротиворечивость формулы Ампера в магнитостатическом случае вот в каком смысле:

В её левой части стоит циркуляция по некоторому контуру, который является краем поверхности интегрирования в правой части. При этом утверждается, что формула верна всегда, то есть для любых поверхностей. Однако две разные поверхности (и вообще сколь угодно много разных поверхностей) могут иметь совпадающий край; иными словами, мы можем натянуть на один и тот же контур две разные поверхности (а если надо, то и больше).

Очевидно, что для двух разных поверхностей, натянутых на один и тот же контур, левая часть уравнения будет одинаковой. В правой же части будет ток (поток j) через две разные поверхности, и если он не окажется одинаковым, то формула Ампера внутренне противоречива уже в магнитостатике. Покажем, что это не так.

В принципе достаточно было бы заметить, что линии тока замкнуты либо уходят на бесконечность. (Это утверждение представляется интуитивно очевидным, если заметить, что токи в магнитостатике по определению постоянны, а заряд сохраняется — и следовательно источников и стоков у плотности тока нет , а значит у линий тока нет начал или концов, и значит все они либо замкнуты, либо уходят на бесконечность). Тогда в любую замкнутую поверхность (или в пару разных поверхностей, натянутых на один и тот же контур, которая и образует вместе одну замкнутую поверхность) входит столько же линий тока, сколько из неё выходит.

Таким образом, в магнитостатике поле j соленоидально.

Сейчас полезно показать это и исходя из уравнения непрерывности.

В магнитостатике ∂ρ∂t=0,{\displaystyle {\frac {\partial \rho }{\partial t}}=0,} поскольку изменение плотности заряда привело бы к изменению порождаемого ею электрического поля, т.е. нарушило бы условие постоянства полей.

Подставив это в уравнение непрерывности, сразу получаем, что для магнитостатики оно имеет вид:

∇⋅j=0{\displaystyle \nabla \cdot \mathbf {j} =0}

Это и есть условие соленоидальности поля j (так как проинтегрировав дивергенцию j по любому объёму, получим^[12] поток через его поверхность, и он будет равен нулю, так как дивергенция везде ноль.^[13]

3. Теперь заметим, что в случае перехода к общему (электродинамическому) случаю соленоидальность поля j сразу же теряется.

Действительно, теперь, вообще говоря, ∂ρ∂t≠0,{\displaystyle {\frac {\partial \rho }{\partial t}}\neq 0,} а следовательно и ∇⋅j≠0.{\displaystyle \nabla \cdot \mathbf {j} \neq 0.}

Таким образом мы получаем результат, что первоначальная аналитическое выражение закономерности, выведенной Ампером, содержит в правой части формулы только обозначение силы тока, и может принята, но с условием внутренней противоречивости (по причинам, разобранным выше, а именно, если ∇⋅j≠0{\displaystyle \nabla \cdot \mathbf {j} \neq 0}, то найдётся объём, интеграл по которому от такой дивергенции не равен нулю, и следовательно имеется не нулевой ток из этой поверхности^[14], а значит можно найти две поверхности, натянутые на один и тот же контур, через которые течёт ток разных величин, а значит, если первоначальная формула Ампера верна. В этом случае, мы получим два разных взаимоисключающих значения циркуляции по одному и тому же контуру, то есть противоречие. Достаточно условное.

4. Теперь осталось найти исправление, которое устранило бы это противоречие.

Исходя из того, что мы хотим оставить общую структуру формулы Ампера, наиболее естественным путём её исправления было бы попытаться восстановить представление поля как соленоид (в правой части), но поскольку поле j в общем случае представленное в виде соленоида теряет наглядность модели, то естественно — было бы представить, какой более полной модели оно потребует для восстановления соленоидальности (после чего формула станет внутренне непротиворечивой, вероятно, в общем случае).

Заметим также, что эта поправка должна исчезать в случае постоянных во времени полей и постоянных токов.

Поскольку, при доказательстве гипотезы о «соленоидальности» поля j в магнитостатике, при несоленоидальных моделях, в электростатике приходится принимать уравнение непрерывности. Тогда, путём естественной логики может быть выведена мысль попытаться использовать именно его для введения поправок. Ведь в магнитостатическом случае одновременно приобретают нулевое значение оба выражения — и ∇⋅j{\displaystyle \nabla \cdot \mathbf {j} }, и ∂ρ/∂t{\displaystyle \partial \rho /\partial t}. А для компенсации ненулевого потока, описываемого первой частью в общем случае, естественно было бы использовать вторую, так как их сумма всегда будет равна нулю.

Поищем, как использовать ρ{\displaystyle \rho }.

Из электростатики известно^[15], что^[16]

∇⋅E=ρ.{\displaystyle \nabla \cdot \mathbf {E} =\rho .}

Постулируя, что это уравнение верно и в электродинамике, сопоставим его с уравнением непрерывности

∇⋅j+∂ρ∂t=0.{\displaystyle \nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0.}

Очевидно, что продифференцировав первое уравнение по времени, мы сразу получим в его правой части интересующий нас член ∂ρ/∂t{\displaystyle \partial \rho /\partial t}:

∇⋅∂E∂t=∂ρ∂t.{\displaystyle \nabla \cdot {\frac {\partial \mathbf {E} }{\partial t}}={\frac {\partial \rho }{\partial t}}.}

Подставив его в уравнение непрерывности, сразу имеем:

∇⋅j+∇⋅∂E∂t=0{\displaystyle \nabla \cdot \mathbf {j} +\nabla \cdot {\frac {\partial \mathbf {E} }{\partial t}}=0}

и

∇⋅(j+∂E∂t)=0.{\displaystyle \nabla \cdot {\Big (}\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}{\Big )}=0.}

То есть, поле (j+∂E∂t){\displaystyle {\Big (}\mathbf {j} +{\frac {\partial \mathbf {E} }{\partial t}}{\Big )}} — соленоидально.

И значит, если добавить в формуле Ампера к j следующее дополнение ∂E∂t{\displaystyle {\frac {\partial \mathbf {E} }{\partial t}}}, то эта формула утрачивает, как нам кажется, внутреннюю противоречивость (по крайней мере, при рассмотрении нами якобы имеющихся противоречий в исходной формуле Ампера) и приобретает свойства и форму, очень близкие к свойствам и форме исходной формулы Ампера, для случая магнитостатических сил. А при переходе к магнитостатике, поправка пропадает, то есть, выполняется

Сила Ампера Википедия

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила оказывается линейно зависимой как от тока, так и от магнитной индукции B{\displaystyle B}. Выражение для силы dF→{\displaystyle d{\vec {F}}}, с которой магнитное поле действует на элемент объёма dV{\displaystyle dV} проводника с током плотности j→{\displaystyle {\vec {j}}}, находящегося в магнитном поле с индукцией B→{\displaystyle {\vec {B}}}, в Международной системе единиц (СИ) имеет вид:

dF→=j→×B→dV.{\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV.}

Если ток течёт по тонкому проводнику, то j→dV=Idl→{\displaystyle {\vec {j}}dV=Id{\vec {l}}}, где dl→{\displaystyle d{\vec {l}}} — «элемент длины» проводника — вектор, по модулю равный dl{\displaystyle dl} и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы dF→{\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

dF=IBdlsin⁡α,{\displaystyle dF=IBdl\sin \alpha ,}

где α{\displaystyle \alpha } — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Сила F{\displaystyle F} максимальна, когда проводник с током расположен перпендикулярно линиям магнитной индукции (α=90∘,sin⁡α=1{\displaystyle \alpha =90^{\circ },\sin \alpha =1}):

F=BLI{\displaystyle F=BLI}, где L{\displaystyle L} — длина проводника.

Два параллельных проводника

Два бесконечных параллельных проводника в вакууме

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r{\displaystyle r} друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}. Требуется найти силу, действующую на единицу длины проводника.

В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током I1{\displaystyle I_{1}} в точке на расстоянии r{\displaystyle r} создаёт магнитное поле с индукцией

B1(r)=μ04π2I1r,{\displaystyle B_{1}(r)={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}}{r}},}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

dF→1−2=I2dl→×B→1(r).{\displaystyle d{\vec {F}}_{1-2}=I_{2}d{\vec {l}}\times {\vec {B}}_{1}(r).}

По правилу буравчика, dF→1−2{\displaystyle d{\vec {F}}_{1-2}} направлена в сторону первого проводника (аналогично и для dF→2−1{\displaystyle d{\vec {F}}_{2-1}}, а значит, проводники притягиваются).

Модуль данной силы (r{\displaystyle r} — расстояние между проводниками):

dF1−2=μ04π2I1I2rdl.{\displaystyle dF_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}dl.}

Интегрируем по участку проводника длины L{\displaystyle L} (пределы интегрирования по l{\displaystyle l} от 0 до L{\displaystyle L}):

F1−2=μ04π2I1I2r⋅L.{\displaystyle F_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}\cdot L.}

Если L{\displaystyle L} — единичная длина, то это выражение задаёт искомую силу взаимодействия.

Полученная формула используется в СИ для установления численного значения магнитной постоянной μ0{\displaystyle \mu _{0}}. Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10⁻⁷ньютона»^[1].

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м точно.

Проявления

• Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
• Раздвигание токопроводов рельсотронов при выстреле.

Применение

Любые узлы в электротехнике, где под действием электромагнитного поля происходит движение каких-либо элементов, используют закон Ампера. Принцип работы электромеханических машин (движение части обмотки ротора относительно части обмотки статора) в основан на использовании закона Ампера, и самый широко распространённый и используемый чуть ли не во всех технических конструкциях агрегат — это электродвигатель, либо, что конструктивно почти то же самое — генератор. Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др).

Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеют движущиеся узлы, основаны на эксплуатации закона Ампера.

Также, он находит применение во многих других видах электротехники, например, в динамическое головке (динамике): в динамике (громкоговорителе) для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит, на него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.

Также:

История

В 1820 году Ханс Кристиан Эрстед открыл, что провод, по которому идёт ток, создает магнитное поле и заставляет отклоняться стрелку компаса. Он заметил, что магнитное поле перпендикулярно току, а не параллельно ему, как можно было бы ожидать. Ампер, вдохновлённый демонстрацией опыта Эрстеда, обнаружил, что два параллельных проводника, по которым течёт ток, притягиваются или отталкиваются в зависимости от того, в одну ли или разные стороны по ним идёт ток. Таким образом ток не только производит магнитное поле, но магнитное поле действует на ток. Уже через неделю после объявления Эрстедом о своём опыте, Ампер предложил объяснение: проводник действует на магнит, потому что в магните течёт ток по множеству маленьких замкнутых траекторий^[2][3].

Сила Ампера и третий закон Ньютона

Пусть есть два тонких проводника с токами I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}} , заданные кривыми C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}}. Сами кривые могут быть заданы радиус-векторами r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}}. Найдем силу, действующую непосредственно на токовый элемент одного провода со стороны токового элемента другого провода. По закону Био — Савара — Лапласа токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, создает в точке r2{\displaystyle \mathbf {r} _{2}} элементарное магнитное поле dB1(r2)=μ04πI1[dr1,r2−r1]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0} \over 4\pi }{\frac {I_{1}[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. По закону Ампера сила, действующая со стороны поля dB1(r2){\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})} на токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, равна

d2F12=I2dr2×dB1(r2)=μ0I1I24π[dr2,[dr1,r2−r1]]|r2−r1|3.{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}=I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}.}

Токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, создает в точке r1{\displaystyle \mathbf {r} _{1}} элементарное магнитное поле

dB2(r1)=μ04πI2[dr2,r1−r2]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0} \over 4\pi }{\frac {I_{2}[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Сила Ампера, действующая со стороны поля dB2(r1){\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})} на токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, равна

d2F21=I1dr1×dB2(r1)=μ0I1I24π[dr1,[dr2,r1−r2]]|r2−r1|3.{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}=I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}.}

В общем случае для произвольных r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}} силы d2F12{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}} и d2F21{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}} даже не коллинеарны, а значит, не подчиняются третьему закону Ньютона: d2F12+d2F21≠0{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}+\mathrm {d} ^{2}\mathbf {F} _{21}\neq 0}. Однако ничего страшного в этом нет. Физиками доказано, что постоянный ток может течь только по замкнутому контуру. Поэтому третий закон Ньютона должен действовать только для сил, с которыми взаимодействуют два замкнутых проводника с током. Убедимся, что для двух таких проводников третий закон Ньютона выполняется.

Пусть кривые C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} являются замкнутыми. Тогда ток I1{\displaystyle I_{1}} создает в точке r2{\displaystyle \mathbf {r} _{2}} магнитное поле

B1(r2)=μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3,{\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}},}

где интегрирование по C1{\displaystyle C_{1}} производится в направлении течения тока I1{\displaystyle I_{1}}. Сила Ампера, действующая со стороны поля B1(r2){\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})} на контур C2{\displaystyle C_{2}} с током I2{\displaystyle I_{2}}, равна

F12=∮C2⁡(I2dr2×B1(r2))=∮C2⁡(I2dr2×μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3)=μ0I1I24π∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3,{\displaystyle \mathbf {F} _{12}=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathbf {B} _{1}(\mathbf {r} _{2}))=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times {\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}})={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}},}

где интегрирование по C2{\displaystyle C_{2}} производится в направлении течения тока I2{\displaystyle I_{2}}. Что характерно, порядок интегрирования значения не имеет.

Аналогично сила Ампера, действующая со стороны поля B2(r1){\displaystyle \mathbf {B} _{2}(\mathbf {r} _{1})}, создаваемого током I2{\displaystyle I_{2}}, на контур C1{\displaystyle C_{1}} с током I1{\displaystyle I_{1}}, равна

F21=∮C1⁡(I1dr1×B2(r1))=μ0I1I24π∮C1⁡∮C2⁡[dr1,[dr2,r1−r2]]|r2−r1|3=∮C1⁡∮C2⁡d2F21.{\displaystyle \mathbf {F} _{21}=\oint \limits _{\mathbb {C} _{1}}(I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathbf {B} _{2}(\mathbf {r} _{1}))={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}\mathrm {d} ^{2}\mathbf {F} _{21}.}

Равенство F12+F21=0{\displaystyle \mathbf {F} _{12}+\mathbf {F} _{21}=0} эквивалентно равенству ∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡[dr1,[dr2,r2−r1]]|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Чтобы доказать это последнее равенство, заметим, что выражение для силы Ампера очень похоже на выражение для циркуляции магнитного поля по замкнутому контуру, в котором внешнее скалярное произведение заменили векторным произведением. Тогда понятно, в каком направлении нужно двигаться.

Пользуясь тождеством Лагранжа, двойное векторное произведение в левой части доказываемого равенства можно записать так:

[dr2,[dr1,r2−r1]]=dr1(dr2,r2−r1)−(r2−r1)(dr2,dr1).{\displaystyle [\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]=\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})-(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1}).}

Тогда левая часть доказываемого равенства примет вид:

∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3−∮C1⁡∮C2⁡(r2−r1)(dr2,dr1)|r2−r1|3.{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}-\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}.}

Рассмотрим отдельно интеграл ∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, который можно переписать в следующем виде:

∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3=∮C1⁡dr1∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3.{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\mathrm {d} \mathbf {r} _{1}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}.}

Сделав замену переменной во внутреннем интеграле на r=r2−r1{\displaystyle \mathbf {r} =\mathbf {r} _{2}-\mathbf {r} _{1}}, где вектор r{\displaystyle \mathbf {r} } изменяется по замкнутому контуру C2′{\displaystyle C_{2}’}, обнаружим, что внутренний интеграл является циркуляцией градиентного поля по замкнутому контуру. А значит, он равен нулю:

∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3=∮C2′⁡(r,dr)|r|3=−∮C2′⁡(grad(1|r|),dr)=0.{\displaystyle \oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{2}’}{\frac {(\mathbf {r} ,\mathrm {d} \mathbf {r} )}{|\mathbf {r} |^{3}}}=-\oint \limits _{\mathbb {C} _{2}’}(\mathrm {grad} ({\frac {1}{|\mathbf {r} |}}),\mathrm {d} \mathbf {r} )=0.}

Значит, и весь двойной криволинейный интеграл равен нулю. В таком случае для силы F12{\displaystyle \mathbf {F} _{12}} можно записать:

F12=μ0I1I24π∮C1⁡∮C2⁡(r1−r2)(dr2,dr1)|r2−r1|3.{\displaystyle \mathbf {F} _{12}={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{1}-\mathbf {r} _{2})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}.}

Выражение для силы F21{\displaystyle \mathbf {F} _{21}} можно получить из выражения для силы F12{\displaystyle \mathbf {F} _{12}}, просто исходя из соображений симметрии. Для этого произведем замену индексов: 2 меняем на 1, а 1 — на 2. В таком случае для силы F21{\displaystyle \mathbf {F} _{21}} можно записать:

F21=μ0I1I24π∮C1⁡∮C2⁡(r2−r1)(d