Сигнал называется дискретным: Дискретным называют сигнал: а) принимающий конечное число определённых значений б) непрерывно

Содержание

Аналоговые, дискретные и цифровые сигналы

Содержание

Обнаружили ошибку? Выделите ее мышью и нажмите

Вводные понятия

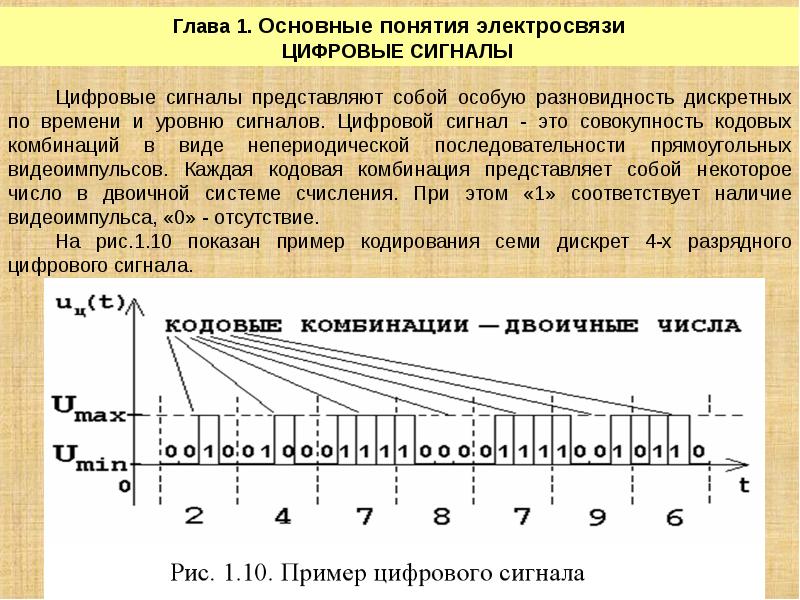
Рисунок 1. Аналоговый, дискретный и цифровой сигналы

Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени , — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым .

Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

(1)

Вектор отсчетов цифрового сигнала может быть помещен в память вычислительного устройства с возможность многократной перезаписи и копирования без потери точности, в то время как перезапись и копирование аналоговых сигналов неизбежно сопровождается потерей части информации. Кроме того, обработка цифровых сигналов позволяет добиться потенциально-возможных характеристик устройств, ввиду возможности выполнения вычислительных операций без потерь, или с пренебрежимо малыми потерями качества.

Указанные преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов.

Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где — целое число, взятых через равноотстоящие промежутки времени .

Рисунок 2. Структурная схема аналого-цифрового преобразователя

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

Рисунок 3. Временны́е осциллограммы АЦП

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются короткие выборки сигнала длительности , взятые через интервал дискретизации .

Оценка дискретного сигнала может быть представлена в виде

(2)

где — прямоугольный импульс длительности единичной амплитуды, который мы уже рассматривали в предыдущих разделах.

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени с некоторой погрешностью, ввиду изменения сигнала на интервале .

Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

(3)

где — смещенная на дельта-функция Дирака, которую мы подробно рассматривали в одном из предыдущих разделов.

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

(4)

где индекс указывает временной интервал следования дельта-функций.

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

(5)

Заметим, что (5) уже не является приближенной оценкой, а представляет собой истинную модель дискретного сигнала.

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Рисунок 4. Модель дискретного сигнала
на основе решетчатой функции

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

(6)

где — конечный интервал интегрирования дискретного сигнала в окрестности .

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Размерность дискретного сигнала

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт . Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

Преобразование Фурье решетчатой функции

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

(7)

где , рад/с — частота дискретизации,

(8)

Тогда (7) с учетом (8):

(9)

Заметим, что знак аргумента комплексной экспоненты выражения (9) можно изменить, потому что суммирование ведется от минус бесконечности до бесконечности с положительными и отрицательными .

Тогда:

(10)

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

(11)

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

(12)

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

(13)

Сравнивая (13) с (10) можно заключить, что:

(14)

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Рисунок 5. Решетчатая функция:
а — временно́е представление; б — спектральная плотность

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).

Спектральная плотность дискретного сигнала

\label{discrete_introduction:ft_discrete} Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

(15)

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

(16)

Преобразуем (16), используя фильтрующее свойство дельта-функции:

(17)

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Рисунок 6. Спектральная плотность дискретного сигнала

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

(18)

Таким образом, из (18) можно заключить, что при дискретизации сигнала, его спектральная плотность переходит в спектр, а размерность спектра дискретного сигнала совпадает с размерностью исходного аналогового сигнала .

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию мы можем назвать спектром, а не спектральной плотностью.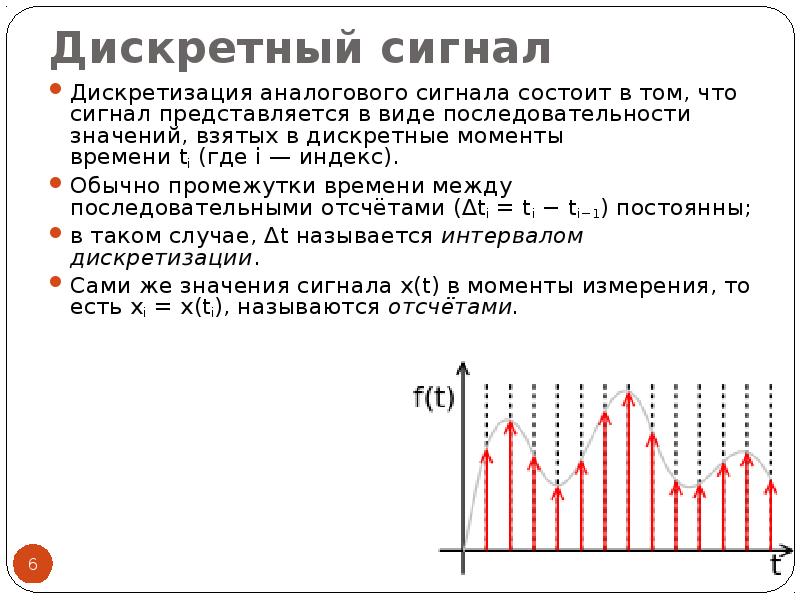

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друга на величину равную частоте дискретизации.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Facebook

Twitter

Мой мир

Вконтакте

Одноклассники

Список литературы

[1] Гоноровский И. С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы. Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Bracewell R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 07.02.2021 (14:06:14)

Страница создана Latex to HTML translator ver. 5.20.11.14

Виды дискретных сигналов. Аналоговый, дискретный, цифровой сигналы

Сигналы могут быть: аналоговые (непрерывные) и дискретные.

Дискретный сигнал — информационный сигнал. Сигнал называется дискретным, если он может принимать лишь конечное число значений.

См. также

Дискретный сигнал — сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

Литература

Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К. : Вища школа, 1987. — 375 с.

Wikimedia Foundation . 2010 .

Дискретное преобразование Фурье над конечным полем
Дискриминируемые группы населения в Японии

Смотреть что такое «Дискретный сигнал» в других словарях:

Дискретный сигнал — сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи. По английски: Discrete signal Синонимы:… … Финансовый словарь

дискретный сигнал

дискретный сигнал — Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени. [Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика

Дискретный сигнал — 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник …

дискретный сигнал — diskretusis signalas statusas T sritis automatika atitikmenys: angl. sampled signal vok. abgetastetes Signal, n rus. дискретный сигнал, m pranc. signal échantillonné, m; signal discret, m … Automatikos terminų žodynas

дискретный сигнал — Сигнал, описываемый дискретной функцией времени … Политехнический терминологический толковый словарь

дискретный сигнал времени — diskretinamojo laiko signalas statusas T sritis radioelektronika atitikmenys: angl. discrete time signal vok. diskretes Zeitsignal, n rus. дискретный сигнал времени, m pranc. signal discret de temps, m … Radioelektronikos terminų žodynas

Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Дискретный — (от лат. discretus раздельный, прерывистый). Это прилагательное может употребляться в разных контекстах: В дискретной математике дискретным называется счётное множество, эта концепция также важна в комбинаторике и теории вероятностей. В общей… … Википедия

дискретный — 4.2.6 дискретный: Относящийся к данным, которые состоят из отдельных элементов, таких как символы, или к физическим величинам, имеющим конечное число различных распознаваемых значений, а также к процессам и функциональным блокам, использующим эти … Словарь-справочник терминов нормативно-технической документации

Сигналы могут быть: аналоговые (непрерывные) и дискретные.

См. также

Литература

Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К. : Вища школа, 1987. — 375 с.

Wikimedia Foundation . 2010 .

Дискретное преобразование Фурье над конечным полем
Дискриминируемые группы населения в Японии

Смотреть что такое «Дискретный сигнал» в других словарях:

дискретный сигнал

Дискретный сигнал — 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник …

Каждый день люди сталкиваются с использованием электронных приборов. Без них невозможна современная жизнь. Ведь речь идет о телевизоре, радио, компьютере, телефоне, мультиварке и прочем. Раньше, еще несколько лет назад, никто не задумывался о том, какой сигнал используется в каждом работоспособном приборе. Сейчас же слова «аналоговый», «цифровой», «дискретный» уже давно на слуху. Некоторые виды сигналов из перечисленных являются качественными и надежными.

Цифровая передача стала использоваться намного позже, чем аналоговая. Это связано с тем, что такой сигнал намного проще обслуживать, да и техника на тот момент не была настолько усовершенствована.

С понятием «дискретность» сталкивается каждый человек постоянно. Если переводить это слово с латинского языка, то означать оно будет «прерывистость». Углубляясь далеко в науку, можно сказать, что дискретный сигнал представляет собой метод передачи информации, который подразумевает изменение во времени среды-переносчика. Последняя принимает любое значение из всех возможных. Сейчас дискретность уходит на второй план, после того, как было принято решение производить системы на чипе. Они являются целостными, а все компоненты тесно взаимодействуют друг с другом. В дискретности же все с точностью наоборот — каждая деталь завершена и связана с другими за счет специальных линий связи.

Сигнал

Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.

В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.

Описываемый код задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.

В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.

Виды сигналов

Существует несколько имеющихся сигналов. Рассмотрим, какие бывают виды.

По физической среде носителя данных разделяют электрический сигнал, оптический, акустический и электромагнитный. Имеется еще несколько видов, однако они малоизвестны.
По способу задания сигналы делятся на регулярные и нерегулярные. Первые представляют собой детерминированные методы передачи данных, которые задаются аналитической функцией. Случайные же формулируются за счет теории вероятности, а также они принимают любые значения в различные промежутки времени.
В зависимости от функций, которые описывают все параметры сигнала, методы передачи данных могут быть аналоговыми, дискретными, цифровыми (способ, который является квантованным по уровню). Они используются для обеспечения работы многих электрических приборов.

Теперь читателю известны все виды передачи сигналов. Разобраться в них не составит труда любому человеку, главное — немного подумать и вспомнить школьный курс физики.

Для чего обрабатывается сигнал?

Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.

Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.

В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.

Создание и формирование

Зачастую для формирования сигналов необходим аналого-цифровой (АЦП) и Чаще всего они оба используются лишь в ситуации с применением DSP-технологий. В остальных случаях подойдет только использование ЦАП.

При создании физических аналоговых кодов с дальнейшим применением цифровых методов полагаются на полученную информацию, которая передается со специальных приборов.

Динамический диапазон

Вычисляется разностью большего и меньшего уровня громкости, которые выражены в децибелах. Он полностью зависит от произведения и особенностей исполнения. Речь идет как о музыкальных треках, так и об обычных диалогах между людьми. Если брать, например, диктора, который читает новости, то его динамический диапазон колеблется в районе 25-30 дБ. А во время чтения какого-либо произведения он может вырастать до 50 дБ.

Аналоговый сигнал

Аналоговый сигнал является непрерывным во времени способом передачи данных. Недостатком его можно назвать присутствие шума, который иногда приводит к полной потере информации. Очень часто возникают такие ситуации, что невозможно определить, где в коде важные данные, а где обычные искажения.

Именно из-за этого цифровая обработка сигналов приобрела большую популярность и постепенно вытесняет аналоговую.

Цифровой сигнал

Цифровой сигнал является особым он описывается за счет дискретных функций. Его амплитуда может принять определенное значение из уже заданных. Если аналоговый сигнал способен поступать с огромным количеством шумов, то цифровой отфильтровывает большую часть полученных помех.

Помимо этого, такой вид передачи данных переносит информацию без лишней смысловой нагрузки. Через один физический канал может быть отправлено сразу несколько кодов.

Виды цифрового сигнала не существуют, так как он выделяется как отдельный и самостоятельный метод передачи данных. Он представляет собой двоичный поток. В наше время такой сигнал считается самым популярным. Это связано с простотой использования.

Применение цифрового сигнала

Чем же отличается цифровой электрический сигнал от других? Тем, что он способен совершать в ретрансляторе полную регенерацию. Когда в оборудование связи поступает сигнал, имеющий малейшие помехи, он сразу же меняет свою форму на цифровую. Это позволяет, например, телевышке снова сформировать сигнал, но уже без шумового эффекта.

В том случае, если код поступает уже с большими искажениями, то, к сожалению, восстановлению он не подлежит. Если брать в сравнении аналоговую связь, то в аналогичной ситуации ретранслятор может извлечь часть данных, затрачивая много энергии.

Обсуждая сотовую связь разных форматов, при сильном искажении на цифровой линии разговаривать практически невозможно, так как не слышны слова или целые фразы. Аналоговая связь в таком случае более действенна, ведь можно продолжать вести диалог.

Именно из-за подобных неполадок цифровой сигнал ретрансляторы формируют очень часто для того, чтобы сократить разрыв линии связи.

Дискретный сигнал

Сейчас каждый человек пользуется мобильным телефоном или какой-то «звонилкой» на своем компьютере. Одна из задач приборов или программного обеспечения — это передача сигнала, в данном случае голосового потока. Для переноса непрерывной волны необходим канал, который имел бы пропускную способность высшего уровня. Именно поэтому было предпринято решение использовать дискретный сигнал. Он создает не саму волну, а ее цифровой вид. Почему же? Потому что передача идет от техники (например, телефона или компьютера). В чем плюсы такого вида переноса информации? С его помощью уменьшается общее количество передаваемых данных, а также легче организуется пакетная отправка.

Понятие «дискретизация» уже давно стабильно используется в работе вычислительной техники.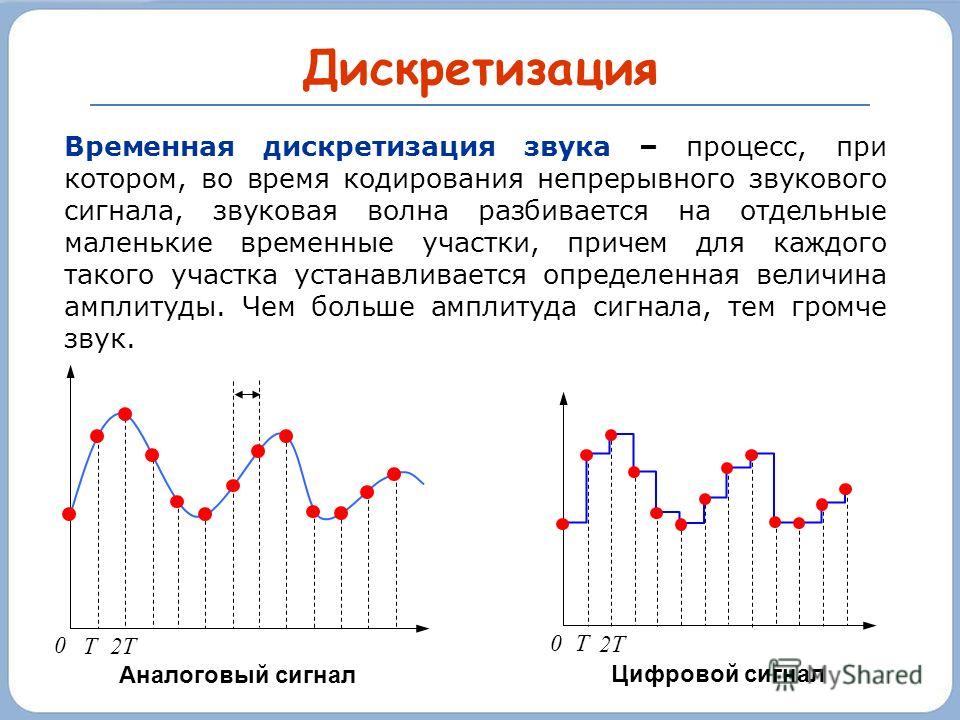 Благодаря такому сигналу передается не непрерывная информация, которая полностью закодирована специальными символами и буквами, а данные, собранные в особенные блоки. Они являются отдельными и законченными частицами. Такой метод кодировки уже давно отодвинулся на второй план, однако не исчез полностью. С помощью него можно легко передавать небольшие куски информации.

Сравнение цифрового и аналогового сигналов

Покупая технику, вряд ли кто-то думает о том, какие виды сигналов использованы в том или другом приборе, а об их среде и природе уж тем более. Но иногда все же приходится разбираться с понятиями.

Уже давно стало ясно, что аналоговые технологии теряют спрос, ведь их использование нерационально. Взамен приходит цифровая связь. Нужно понимать, о чем идет речь и от чего отказывается человечество.

Если говорить коротко, то аналоговый сигнал — способ передачи информации, который подразумевает описание данных непрерывными функциями времени. По сути, говоря конкретно, амплитуда колебаний может быть равна любому значению, находящемуся в определенных границах.

Цифровая обработка сигналов описывается дискретными функциями времени. Иначе говоря, амплитуда колебаний этого метода равна строго заданным значениям.

Переходя от теории к практике, надо сказать о том, что аналоговому сигналу характерны помехи. С цифровым же таких проблем нет, потому что он успешно их «сглаживает». За счет новых технологий такой метод передачи данных способен своими силами без вмешательства ученого восстановить всю исходную информацию.

Говоря о телевидении, можно уже с уверенностью сказать: аналоговая передача давно изжила себя. Большинство потребителей переходят на цифровой сигнал. Минус последнего заключается в том, что если аналоговую передачу способен принимать любой прибор, то более современный способ — только специальная техника. Хоть и спрос на устаревший метод уже давно упал, все же такие виды сигналов до сих пор не способны полностью уйти из повседневной жизни.

Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами.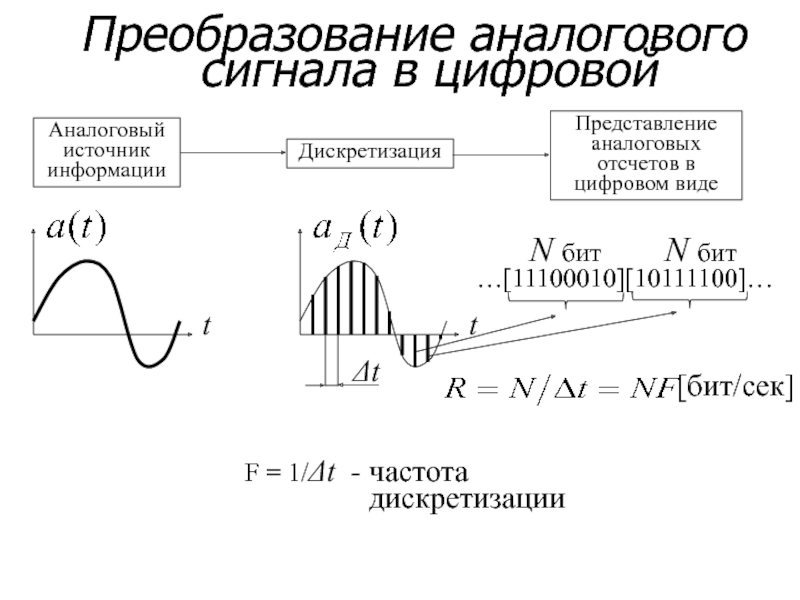

Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
Рис. 1 В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT , следующими строго через интервал T . Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n . При n = 0 значение равно значению сигнала в момент времени t = 0. При n > 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT .

Рис. 2 Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов. Все средства связи, которые на сегодняшний день используются в мире, основаны на передаче электрического тока из одной точки в другую. Как работа в сети Internet, так и разговор с другом по телефону обеспечиваются за счет постоянного протекания тока по оборудованию телекоммуникационной инфраструктуры. По каналам связи могут передаваться различные типы сигналов. В этой книге рассматриваются два основных типа сигналов: аналоговые и цифровые. Некоторые виды физической передающей среды, как, например, волоконно-оптический кабель, используются для передачи данных в сети провайдера в виде световых сигналов. Принципы цифровой передачи для такой среды такие же, однако для ее организации используются лазеры и светодиоды. Аналоговые и цифровые сигналы коренным образом отличаются друг от друга.

Условно можно сказать, что они находятся на разных концах одного и того же спектра. Из-за таких существенных различий между двумя типами сигналов для организации «моста» между ними приходится использовать промежуточные устройства, наподобие цифро-аналоговых преобразователей (они рассматриваются ниже в текущей главе). Основное различие между аналоговыми и цифровыми сигналами заключается в самой структуре сигнального потока. Аналоговые сигналы представляют собой непрерывный поток, характеризующийся изменениями частоты и амплитуды. Это означает, что форма аналогового сигнала обычно похожа на синусоиду (т.е. гармоническую волну), представленную на рис. 1.2. Зачастую на иллюстрациях, изображающих гармоническую волну, весь сигнал характеризуется одним и тем же соотношением частоты и амплитуды, однако при графическом представлении сложной волны видно, что такое соотношение изменяется в зависимости от частоты.
Цифровым сигналам соответствуют дискретные электрические значения, которые передаются индивидуально по некоторой физической передающей среде.

В отличие от аналоговых сигналов, в которых количество возможных значений амплитуды почти бесконечно, для цифровых сигналов она может принимать одно из двух (или четырех) различных значений — как положительных, так и отрицательных. Цифровые сигналы передаются в виде единиц и нулей, которые обычно называют двоичными. Более подробно потоки цифровых сигналов рассматриваются в главе 3, «Аналого-цифровое преобразование». Как и в любой другой технологии, для описания аналоговых сигналов используются базовые концепции и собственная терминология. Непрерывные аналоговые сигналы имеют три основные характеристики: амплитуду; длину волны; частоту.

ВВЕДЕНИЕ В ЦИФРОВУЮ ОБРАБОТКУ СИГНАЛОВ

Цифровая обработка сигналов (ЦОС или DSP — digital signal processing) является одной из новейших и самых мощных технологий, которая активно внедряется в широкий круг областей науки и техники, таких как коммуникации, метеорология, радиолокация и гидролокация, медицинская визуализация изображений, цифровое аудио- и телевизионное вещание, разведка нефтяных и газовых месторождений и др. Можно сказать, что происходит повсеместное и глубокое проникновение технологий цифровой обработки сигналов во все сферы деятельности человечества. Сегодня технология ЦОС относится к числу базовых знаний, которые необходимы ученым и инженерам всех отраслей без исключения.

Сигналы

Что такое сигнал? В наиболее общей формулировке это зависимость одной величины от другой. Т.е., с математической точки зрения сигнал является функцией. Чаще всего рассматриваются зависимости от времени. Физическая природа сигнала может быть различной. Очень часто это электрическое напряжение, реже – ток.

Формы представления сигнала :

1. временная;

2. спектральная (в частотной области).

Стоимость цифровой обработки данных меньше аналоговой и продолжает снижаться, а производительность вычислительных операций непрерывно возрастает. Немаловажным является и то, что системы ЦОС отличаются высокой гибкостью. Их можно дополнять новыми программами и перепрограммировать на выполнение различных операций без изменения оборудования. Поэтому интерес к научным и к прикладным вопросам цифровой обработки сигналов возрастает во всех отраслях науки и техники.

ПРЕДИСЛОВИЕ К ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ

Дискретные сигналы

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и др.) преобразуется в последовательность чисел , которая затем подвергается математическим преобразованиям в ВУ.

Аналоговые, дискретные и цифровые сигналы

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты t, называются аналоговыми .

Какой сигнал называется цифровым? Рассмотрим некоторый аналоговый сигнал (рис. 1.1 а). Он задан непрерывно на всем рассматриваемом временном интервале. Считается, что аналоговый сигнал абсолютно точен, если не учитывать погрешности при измерении.

Рис. 1.1 а) Аналоговый сигнал

Рис. 1.1 б) Дискретизированный сигнал

Рис. 1. 1 в) Квантованный сигнал

Для того, чтобы получить цифровой сигнал, нужно провести две операции – дискретизацию и квантование . Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией, а результат такого преобразования — дискретным сигналом .Т. обр., дискретизация заключается в составлении выборки из аналогового сигнала (рис. 1.1 б), каждый элемент которой, называемый отсчетом , будет отстоять по времени от соседних отсчетов на некотором интервале Т , называемом интервалом дискретизации или (поскольку интервал дискретизации чаще неизменен) – периодом дискретизации . Величина, обратная периоду дискретизации называется частотой дискретизации и определяется как:

(1.1)

При обработке сигнала в вычислительном устройстве его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием . Возникающие при этом ошибки округления называются ошибками или шумами квантования . Т. обр., квантование – это приведение уровней дискретизированного сигнала к некоторой сетке (рис. 1.1 в), чаще обычным округлением в сторону большего. Дискретный во времени и квантованный по уровню сигнал и будет являться цифровым.

Условия, при которых возможно полное восстановление аналогового сигнала по его цифровому эквиваленту с сохранением всей исходно содержавшейся в сигнале информации, выражаются теоремами Найквиста, Котельникова, Шеннона, сущность которых практически одинакова. Для дискретизации аналогового сигнала с полным сохранением информации в его цифровом эквиваленте максимальные частоты в аналоговом сигнале должны быть не менее, чем вдвое меньше, чем частота дискретизации, то есть f max £ (1/2)f d , т.е. на одном периоде максимальной частоты должно быть минимум два отсчета. Если это условие нарушается, в цифровом сигнале возникает эффект маскирования (подмены) действительных частот более низкими частотами. При этом в цифровом сигнале вместо фактической регистрируется «кажущаяся» частота, а, следовательно, восстановление фактической частоты в аналоговом сигнале становится невозможным. Восстановленный сигнал будет выглядеть так, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от частоты (1/2)f d в нижнюю часть спектра и наложились на частоты, уже присутствующие в этой части спектра. Этот эффект называется наложением спектров или алиасингом (aliasing). Наглядным примером алиасинга может служить иллюзия, довольно часто встречающаяся в кино – колесо автомобиля начинает вращаться против его движения, если между последовательными кадрами (аналог частоты дискретизации) колесо совершает более чем пол-оборота.

Преобразование сигнала в цифровую форму выполняется аналого-цифровыми преобразователями (АЦП). Как правило, они используют двоичную систему счисления с определенным числом разрядов в равномерной шкале. Увеличение числа разрядов повышает точность измерений и расширяет динамический диапазон измеряемых сигналов. Потерянная из-за недостатка разрядов АЦП информация невосстановима, и существуют лишь оценки возникающей погрешности «округления» отсчетов, например, через мощность шума, порождаемого ошибкой в последнем разряде АЦП. Для этого используется понятие отношения «сигнал/шум» — отношение мощности сигнала к мощности шума (в децибелах). Наиболее часто применяются 8-, 10-, 12-, 16-, 20- и 24-х разрядные АЦП. Каждый дополнительный разряд улучшает отношение сигнал/шум на 6 децибел. Однако увеличение количества разрядов снижает скорость дискретизации и увеличивает стоимость аппаратуры. Важным аспектом является также динамический диапазон, определяемый максимальным и минимальным значением сигнала.

Обработка цифровых сигналов выполняется либо специальными процессорами, либо на универсальных ЭВМ и компьютерах по специальным программам. Наиболее просты для рассмотрения линейные системы. Линейными называются системы, для которых имеет место принцип суперпозиции (отклик на сумму входных сигналов равен сумме откликов на каждый сигнал в отдельности) и однородность (изменение амплитуды входного сигнала вызывает пропорциональное изменение выходного сигнала).

Если входной сигнал x(t-t 0) порождает однозначный выходной сигнал y(t-t 0) при любом сдвиге t 0 , то систему называют инвариантной во времени . Ее свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал — единичный импульс (импульсная функция).

Единичный импульс (единичный отсчет) u 0 (n ) (рис. 1.2):

Рис. 1.2. Единичный импульс

В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы. Отклик на единичный импульс (импульс с единичной амплитудой) называют импульсной характеристикой системы h(n). Знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, произвольный сигнал {x(n)} можно представить в виде линейной комбинации единичных отсчетов.

Аналоговый, дискретный, цифровой сигналы. Информационные сигналы. Аналоговые сигналы. Дискретные сигналы

Сигнал информационный — физический процесс, имеющий для человека или технического устройства информационное значение. Он может быть непрерывным (аналоговым) или дискретным

Термин “ «сигнал» очень часто отождествляют с понятиями “данные” (data) и “информация” (information). Действительно, эти понятия взаимосвязаны и не существуют одно без другого, но относятся к разным категориям.

Сигнал — это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко — полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.

Передается информация в виде сигналов. Сигнал есть физический процесс, несущий в себе информацию. Сигнал может быть звуковым, световым, в виде почтового отправления и др

Сигнал является материальным носителем информации, которая передается от источника к потребителю. Он может быть дискретным и непрерывным (аналоговым)

Аналоговый сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений.

Аналоговые сигналы описываются непрерывными функциями времени, поэтому аналоговый сигнал иногда называют непрерывным сигналом. Аналоговым сигналам противопоставляются дискретные (квантованные, цифровые).

Примеры непрерывных пространств и соответствующих физических величин: (прямая: электрическое напряжение; окружность: положение ротора, колеса, шестерни, стрелки аналоговых часов, или фаза несущего сигнала; отрезок: положение поршня, рычага управления, жидкостного термометра или электрический сигнал, ограниченный по амплитуде различные многомерные пространства: цвет, квадратурно-модулированный сигнал.)

Свойства аналоговых сигналов в значительной мере являются противоположностью свойств квантованных или цифровых сигналов.

Отсутствие чётко отличимых друг от друга дискретных уровней сигнала приводит к невозможности применить для его описания понятие информации в том виде, как она понимается в цифровых технологиях. Содержащееся в одном отсчёте «количество информации» будет ограничено лишь динамическим диапазоном средства измерения.

Отсутствие избыточности. Из непрерывности пространства значений следует, что любая помеха, внесенная в сигнал, неотличима от самого сигнала и, следовательно, исходная амплитуда не может быть восстановлена. В действительности фильтрация возможна, например, частотными методами, если известна какая-либо дополнительная информация о свойствах этого сигнала (в частности, полоса частот).

Применение:

Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, аналоговый электрический сигнал, снимаемый с термопары, несет информацию об изменении температуры, сигнал с микрофона — о быстрых изменениях давления в звуковой волне, и т.п.

Дискретный сигнал слагается из счетного множества (т.е. такого множества, элементы которого можно пересчитать) элементов (говорят – информационных элементов). Например, дискретным является сигнал “кирпич”. Он состоит из следующих двух элементов (это синтаксическая характеристика данного сигнала): красного круга и белого прямоугольника внутри круга, расположенного горизонтально по центру. Именно в виде дискретного сигнала представлена та информация, которую сейчас осваивает читатель. Можно выделить следующие ее элементы: разделы (например, “Информация”), подразделы (например, “Свойства”), абзацы, предложения, отдельные фразы, слова и отдельные знаки (буквы, цифры, знаки препинания и т.д.). Этот пример показывает, что в зависимости от прагматики сигнала можно выделять разные информационные элементы. В самом деле, для лица, изучающего информатику по данному тексту, важны более крупные информационные элементы, такие как разделы, подразделы, отдельные абзацы. Они позволяют ему легче ориентироваться в структуре материала, лучше его усваивать и готовиться к экзамену. Для того, кто готовил данный методический материал, помимо указанных информационных элементов, важны также и более мелкие, например, отдельные предложения, с помощью которых излагается та или иная мысль и которые реализуют тот или иной способ доступности материала. Набор самых “мелких” элементов дискретного сигнала называется алфавитом, а сам дискретный сигнал называют также сообщением .

Дискретизация – это преобразование непрерывного сигнала в дискретный (цифровой).

Разница между дискретным и непрерывным представлением информации хорошо видна на примере часов. В электронных часах с цифровым циферблатом информация представляется дискретно – цифрами, каждая из которых четко отличается друг от друга. В механических часах со стрелочным циферблатом информация представляется непрерывно – положениями двух стрелок, причем два разных положения стрелки не всегда четко отличимы (особенно если на циферблате нет минутных делений).

Непрерывный сигнал – отражается некоторой физической величиной, изменяющейся в заданном интервале времени, например, тембром или силой звука. В виде непрерывного сигнала представлена настоящая информация для тех студентов – потребителей, которые посещают лекции по информатике и через звуковые волны (иначе говоря, голос лектора), носящие непрерывный характер, воспринимают материал.

Как мы увидим в дальнейшем, дискретный сигнал лучше поддается преобразованиям, поэтому имеет преимущества перед непрерывным. В то же время, в технических системах и в реальных процессах преобладает непрерывный сигнал. Это вынуждает разрабатывать способы преобразования непрерывного сигнала в дискретный.\

Для преобразования непрерывного сигнала в дискретный используется процедура, которая называется квантованием .

Цифровой сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.

Дискретный цифровой сигнал сложнее передавать на большие расстояния, чем аналоговый сигнал, поэтому его предварительно модулируют на стороне передатчика, и демодулируют на стороне приёмника информации. Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.

Замечание. Следует иметь в виду, что реальный цифровой сигнал по своей физической природе является аналоговым. Из-за шумов и изменения параметров линий передачи он имеет флуктуации по амплитуде, фазе/частоте (джиттер), поляризации. Но этот аналоговый сигнал (импульсный и дискретный) наделяется свойствами числа. В результате для его обработки становится возможным использование численных методов (компьютерная обработка).

Любая система цифровой обработки сигналов независимо от ее сложности содержит цифровое вычислительное устройство — универсальную цифровую вычислительную машину, микропроцессор или специально разработанное для решения конкретной задачи вычислительное устройство. Сигнал, поступающий на вход вычислительного устройства, должен быть преобразован к виду, пригодному для обработки на ЭЦВМ. Он должен иметь вид последовательности чисел, представленных в коде машины.

В некоторых случаях задача представления входного сигнала в цифровой форме решается сравнительно просто. Например, если нужно передать словесный текст, то каждому символу (букве) этого текста нужно поставить в соответствие некоторое число и, таким образом, представить передаваемый сигнал в виде числовой последовательности. Легкость решения задачи в этом случае объясняется тем, что словесный текст по своей природе дискретен.

Однако большинство сигналов, с которыми приходится иметь дело в радиотехнике, являются непрерывными. Это связано с тем, что сигнал является отображением некоторого физического процесса, а почти все физические процессы непрерывны по своей природе.

Рассмотрим процесс дискретизации непрерывного сигнала на конкретном примере. Допустим, на борту некоторого космического аппарата производится измерение температуры воздуха; результаты измерения должны передаваться на Землю в центр обработки данных. Температура

Рис. 1.1. Виды сигналов: а — непрерывный (континуальный) сигнал; 6 — дискретный сигнал; в — АИМ-колебание; г — цифровой сигнал

воздуха измеряется непрерывно; показания датчика температуры также являются непрерывной функцией времени (рис. 1.1, а). Но температура изменяется медленно, достаточно передавать ее значения один раз в минуту. Кроме того, нет необходимости измерять ее с точностью выше чем 0,1 градуса. Таким образом, вместо непрерывной функции можно с интервалом в 1 мин передавать последовательность числовых значений (рис. 1.1, г), а в промежутках между этими значениями можно передавать сведения о давлении, влажности воздуха и другую научную информацию.

Рассмотренный пример показывает, что процесс дискретизации непрерывных сигналов состоит из двух этапов: дискретизации по времени и дискретизации по уровню (квантования). Сигнал, дискретизированный только по времени, называют дискретным; он еще не пригоден для обработки в цифровом устройстве. Дискретный сигнал представляет собой последовательность, элементы которой в точности равны соответствующим значениям исходного непрерывного сигнала (рис. 1.1, б). Примером дискретного сигнала может быть последовательность импульсов с изменяющейся амплитудой — амплитудно-импульсно-модулированное колебание (рис. 1.1, в). Аналитически такой дискретный сигнал описывается выражением

где исходный непрерывный сигнал; единичный импульс АИМ-колебания.

Если уменьшать длительность импульса сохраняя его площадь неизменной, то в пределе функция стремится к -функции. Тогда выражение для дискретного сигнала можно представить в виде

Для преобразования аналогового сигнала в цифровой после дискретизации по времени должна следовать дискретизация по уровню (квантование). Необходимость квантования вызвана тем, что любое вычислительное устройство может оперировать только числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. Так в рассмотренном примере производится округление значений температуры до трех значащих цифр (рис. 1.1, г). В других случаях число разрядов передаваемых значений сигнала может быть иным. Сигнал, дискретизированный и по времени, и по уровню, называется цифровым.

Правильный выбор интервалов дискретизации по времени и по уровню очень важен при разработке цифровых систем обработки сигналов. Чем меньше интервал дискретизации, тем точнее дискретизированный сигнал соответствует исходному непрерывному. Однако при уменьшении интервала дискретизации по времени возрастает число отсчетов, и для сохранения общего времени обработки сигнала неизменным приходится увеличивать скорость обработки, что не всегда возможно. При уменьшении интервала квантования требуется больше разрядов для описания сигнала, вследствие чего цифровой фильтр становится более сложным и громоздким.

Мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная . Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации , а изменение какой-либо характеристики носителя мы будем называть сигналом .
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый ) и дискретный .
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Сигнал называется дискретным , если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).

Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.

Вернемся к примерам, рассмотренным в начале сообщения — мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да — приведите примеры.

Дискретные сигналы естественно возникают в тех случаях, когда источник сообщений выдает информацию в фиксированные моменты времени. Примером могут служить сведения о температуре воздуха, передаваемые радиовещательными станциями несколько раз в сутки. Свойство дискретного сигнала проявляется здесь предельно ярко: в паузах между сообщениями никаких сведений о температуре нет. Фактически же температура воздуха изменяется во времени плавно, так что результаты измерения возникают за счет дискретизации непрерывного сигнала — операции, которая фиксирует отсчетные значения.

Дискретные сигналы приобрели особое значение в последние десятилетия под влиянием совершенствования техники связи и развития способов обработки информации быстродействующими вычислительными устройствами. Большие успехи достигнуты в разработке и использовании специализированных устройств для обработки дискретных сигналов, так называемых цифровых фильтров.

Настоящая глава посвящена рассмотрению принципов математического описания дискретных сигналов, а также теоретических основ построения линейных устройств для их обработки.

15.1. Модели дискретных сигналов

Различие между дискретными и аналоговыми (непрерывными) сигналами подчеркивалось в гл. 1 при классификации радиотехнических сигналов. Напомним основное свойство дискретного сигнала: его значения определены не во все моменты времени, а лишь в счетном множестве точек. Если аналоговый сигнал имеет математическую модель вида непрерывной или кусочно-непрерывной функции, то отвечающий ему дискретный сигнал представляет собой последовательность отсчетных значений сигнала в точках соответственно.

Дискретизирующая последовательность.

На практике, как правило, отсчеты дискретных сигналов берут во времени через равный промежуток А, называемый интервалом (шагом) дискретизации:

Операцию дискретизации, т. е. переход от аналогового сигнала к дискретному сигналу , можно описать, введя в рассмотрение обобщенную функцию

называемую дискретизирующей последовательностью.

Очевидно, дискретный сигнал представляет собой функционал (см. гл. 1), определенный на множестве всевозможных аналоговых сигналов и равный скалярному произведению функции

Формула (15.3) указывает путь практической реализации устройства для дискретизации аналогового сигнала. Работа дискретизатора основана на операции стробирования (см. гл. 12) — перемножения обрабатываемого сигнала и «гребенчатой» функции Поскольку длительность отдельных импульсов, из которых складывается дискретизирующая последовательность, равна нулю, на выходе идеального дискретизатора в равноотстоящие моменты времени возникают отсчетные значения обрабатываемого аналогового сигнала.

Рис. 15.1. Структурная схема импульсного модулятора

Модулированные импульсные последовательности.

Дискретные сигналы начали использовать еще в 40-х годах при создании радиотехнических систем с импульсной модуляцией. Этот вид модуляции отличается тем, что в качестве «несущего колебания» вместо гармонического сигнала служит периодическая последовательность коротких импульсов.

Импульсный модулятор (рис. 15.1) представляет собой устройство с двумя входами, на один из которых подается исходный аналоговый сигнал На другой вход поступают короткие синхронизирующие импульсы с интервалом повторения . Модулятор построен таким образом, что в момент подачн каждого синхронизирующего импульса происходит измерение мгновенного значения сигнала х(t). На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, пропорциональную соответствующему отсчетному значению аналогового сигнала.

Сигнал на выходе импульсного модулятора будем называть модулированной импульсной последовательностью (МИП). Естественно, что дискретный сигнал является математической моделью МИП.

Отметим, что с принципиальной точки зрения характер импульсов, из которых складывается МИП, безразличен. В частности, эти импульсы могут иметь одинаковую длительность, в то время как их амплитуда пропорциональна отсчетным значениям дискретизируемого сигнала. Такой вид преобразования непрерывного сигнала получил название амплитудно-импульсной модуляции (АИМ). Возможен другой способ — широтно-импульсная модуляция (ШИМ). Здесь амплитуды импульсов на выходе модулятора постоянны, а их длительность (ширина) пропорциональна мгновенным значениям аналогового колебания.

Выбор того или иного способа импульсной модуляции диктуется рядом технических соображений, удобством схемной реализации, а также характерными особенностями передаваемых сигналов. Например, нецелесообразно использовать АИМ в случае, если полезный сигнал изменяется в очень широких пределах, т. е., как часто говорят, имеет широкий динамический диапазон. Для неискаженной передачи такого сигнала требуется передатчик со строго линейной амплитудной характеристикой. Создание такого передатчика — самостоятельная, технически сложная проблема. Системы ШИМ не предъявляют требований к линейности амплитудных характеристик передающего устройства. Однако их схемная реализация может оказаться несколько сложнее по сравнению с системами АИМ.

Математическую модель идеальной МИП можно получить следующим образом. Рассмотрим формулу динамического представления сигнала (см. гл. 1):

Поскольку МИП определена лишь в точках интегрирование в формуле (15.4) следует заменить суммированием по индексу к. Роль дифференциала будет играть интервал (шаг) дискретизации . Тогда математическая модель модулированной импульсной последовательности, образованной бесконечно короткими импульсами, окажется заданной выражением

где — выборочные значения аналогового сигнала.

Спектральная плотность модулированной импульсной последовательности.

Исследуем спектр сигнала, возникающего на выходе идеального импульсного модулятора и описываемого выражением (15.5).

Заметим, что сигнал вида МИП с точностью до коэффициента пропорциональности А равен произведению функции и дискретизирующей последовательности

Известно, что спектр произведения двух сигналов пропорционален свертке их спектральных плотностей (см. гл. 2). Поэтому бели известны законы соответствия сигналов и спектров:

то спектральная плотность МИП-сигнала

Чтобы найти спектральную плотность дискретизирующей последовательности, разложим периодическую функцию в комплексный ряд Фурье:

Коэффициенты этого ряда

Обратившись к формуле (2.44), получаем

т. е. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта-импульсов в частотной области. Данная спектральная плотность является периодической функцией с периодом

Наконец, подставив формулу (15.8) в (15.7) и изменив порядок следования операций интегрирования и суммирования, находим

Итак, спектр сигнала, полученного в результате идеальной дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа «копий» спектра исходного аналогового сигнала. Копии располагаются на оси частот через одинаковые интервалы равные значению угловой частоты первой гармоники дискретизирующей импульсной последовательности (рис. 15.2, а, б).

Рис. 15.2. Спектральная плотность модулированной импульсной последовательности при различных значениях верхней граничной частоты: а — верхняя граничная частота велика; б — верхняя граничная частота мала (цветом обозначена спектральная плотность исходного сигнала, подвергнутого дискретизации)

Восстановление непрерывного сигнала по модулированной импульсной последовательности.

В дальнейшем будем полагать, что вещественный сигнал имеет низкочастотный спектр, симметричный относительно точки и ограниченный верхней граничной частотой Из рис. 15.2, б следует, что если , то отдельные копии спектра не накладываются друг на друга.

Поэтому аналоговый сигнал с таким спектром, подвергнутый импульсной дискретизации, может быть совершенно точно восстановлен с помощью идеального ФНЧ, на вход которого подана импульсная последовательность вида (15.5). При этом наибольший допустимый интервал дискретизации , что согласуется с теоремой Котельникова.

Действительно, пусть фильтр, восстанавливающий непрерывный сигнал, имеет частотный коэффициент передачи

Импульсная характеристика этого фильтра описывается выражением

Принимая во внимание, что МИП-сигнал вида (15.5) есть взвешенная сумма дельта-импульсов, находим отклик на выходе восстанавливающего фильтра

Данный сигнал с точностью до масштабного коэффициента повторяет исходное колебание с ограниченным спектром.

Идеальный ФНЧ физически нереализуем и может служить лишь теоретической моделью для объяснения принципа восстановления сообщения по его дискретным импульсным отсчетам. Реальный фильтр нижних частот имеет АЧХ, которая либо охватывает несколько лепестков спектральной диаграммы МИП, либо, концентрируясь вблизи нулевой частоты, оказывается значительно уже центрального лепестка спектра. Для примера на рис. 15.3, б-е приведены кривые, характеризующие сигнал на выходе RC-цепи, используемой в качестве восстанавливающего фильтра (рис. 15.3, а).

Рис. 15.3. Восстановление непрерывного сигнала по его импульсным отсчетам с помощью RC-цепи: а — схема фильтра; б — дискретный входной сигнал; в, г — АЧХ фильтра и сигнал на его выходе в случае ; д, е — то же, для случая

Из приведенных графиков видно, что реальный восстанавливающий фильтр неизбежно искажает входное колебание.

Заметим, что для восстановления сигнала можно использовать как центральный, так и любой боковой лепесток спектральной диаграммы.

Определение спектра аналогового сигнала по совокупности отсчетов.

Располагая МИП-представлением, можно не только восстановить аналоговый сигнал, но и найти его спектральную плотность. Для этого следует прежде всего непосредственно связать спектральную плотность МИП с отсчетными значениями:

(15.13)

Данная формула исчерпывающе решает поставленную задачу при указанном выше ограничении.

Сигнал

Виды сигналов

Существует несколько имеющихся сигналов. Рассмотрим, какие бывают виды.

По физической среде носителя данных разделяют электрический сигнал, оптический, акустический и электромагнитный. Имеется еще несколько видов, однако они малоизвестны.
По способу задания сигналы делятся на регулярные и нерегулярные. Первые представляют собой детерминированные методы передачи данных, которые задаются аналитической функцией. Случайные же формулируются за счет теории вероятности, а также они принимают любые значения в различные промежутки времени.
В зависимости от функций, которые описывают все параметры сигнала, методы передачи данных могут быть аналоговыми, дискретными, цифровыми (способ, который является квантованным по уровню). Они используются для обеспечения работы многих электрических приборов.

Для чего обрабатывается сигнал?

Создание и формирование

Динамический диапазон

Аналоговый сигнал

Цифровой сигнал

Применение цифрового сигнала

Дискретный сигнал

Сравнение цифрового и аналогового сигналов

INFOблог: Непрерывные и дискретные сигналы

В предыдущем посте мы рассматривали различные определения понятия «информация» и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация — знания, данные, сведения, характеристики, отражения и т.д. — категория нематериальная. Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации, а изменение какой-либо характеристики носителя мы будем называть сигналом.
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый) и дискретный.
В учебнике даны следующие определения.

Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

2 Цифровые и дискретные сигналы

Системы цифровой обработки сигналов непосредственно оперируют с последовательностями цифровых кодов (чисел), которые называют цифровыми сигналами. Цифровой сигнал в радиоэлектронных системах образовывается в результате аналого–цифрового преобразования непрерывных (континуальных) сигналов. Аналого-цифровое преобразование (АЦП) включает три этапа: дискретизацию сигнала по времени (пространству), квантование по уровню и цифровое кодирование.

На первом этапе образуется дискретный сигнал x[D], который является функцией дискретной переменной D, принимающей только фиксированные значения. Если эти значения являются равноотстоящими D=nT_¶, (T_¶=const), то выбрав соответствующий масштаб, их можно приравнять натуральным числам. В этом случае дискретный сигнал определяют функцией номера отсчета (выборки) x[n]. Говорят, что T_¶=1/f_¶ это период дискретизации, f_¶ — частота дискретизации, а n— номер отсчета.

Второй этап АЦП дает дискретный квантованный сигнал x_кв[nT_¶], отличающийся конечным множеством принимаемых им значений. На третьем этапе получается цифровой сигнал x_ц[nT_¶] в виде последовательности цифровых кодов с заданным числом разрядов.

Вычислительные средства в соответствии с заданным алгоритмов цифровой обработки F преобразуют сигнал x_ц[nT_¶] в выходной цифровой сигнал y_ц[nT_¶] = F{x_ц[nT_¶]}. В цифровых системах с аналоговым выходом цифровая форма выходного сигнала y_ц[nT_¶] преобразуется в аналоговую y(t) с помощью цифро-аналогового преобразования.

1.1. Дискретизация сигналов и теорема отсчетов

Наиболее удобным с точки зрения организации обработки и естественным способом дискретизации является представление сигналов в виде выборок их значений (отсчетов) в отдельных, регулярно расположенных точках T_¶= . Практически операция дискретизации осуществляется путем измерения значений сигнала с помощью датчика, действие которого можно описать как свертку с некоторым ядром :

(1)

1.2. Представление дискретных сигналов с помощью функциональных рядов

В системах обработки сигналы задаются на определенном интервале изменения переменной. Для дискретного сигнала – это счетное множество точек, например [0, N-1] или [0, ¥]. В первом случае говорят, что дискретные сигналы определены на конечном интервале [0, N-1], включающем в себя N точек.

Дискретное представление можно рассматривать как аппроксимации аналоговых сигналов с помощью рядов. При этом происходит замена непрерывных значений коэффициентами ряда. Дискретные сигналы представляются в виде линейной комбинации базисных функций. Процесс представления заключается в проектировании сигнала на заданный базис. Коэффициенты представления находятся как скалярные произведения сигнала на соответствующие базисные функции:

(12)

Размерность базиса (количество коэффициентов ) ограничивают, основываясь на требуемой точности аппроксимации сигналов , конечной суммой

(13)

Оптимальные базисы дискретного представления сигналов.

Естественно считать оптимальным такой способ дискретизации, при котором размерность базиса минимальна при заданной точности восстановления сигнала.

Пусть — сигнал, удовлетворяющий следующим условиям:

, (14)

где – оператор стробирования, выделяющий из сигнала участок протяженностью ; – идеальный полосовой фильтр, пропускающий только частоты спектра в интервале ; – ошибки такого усечения по протяжённости и по спектру.

Тогда наилучшим является представление сигнала по функциям, являющимися решением уравнения

, (15)

и называемым сфероидальными волновыми функциями (СВФ), причём

, (16)

если – наименьшее целое число, превышающее [3]. При – сфероидальные волновые функции приближаются к отсчётным функциям , и разложение по ним переходит в разложение по теореме отсчётов. При конечном представление (13) по СВФ сигналов, заданных (14), лучше их разложения по отсчётным функциям при том же .

При статистическом описании сигналов оптимальный – мерный базис для представления отдельных реализаций сигналов обычно определяют как базис, при котором норма ошибки, усреднённая по ансамблю реализаций, минимальна. В этом случае получается результат, известный как теорема Карунена – Лоэва [3]. Минимальное значение нормы ошибки при представлении сигналов на интервале протяженностью достигается при использовании в качестве базиса собственных функций, составляющих наибольших собственных значений оператора l_k, ядром которого является корреляционная функция сигналов :

. (17)

Минимальное значение нормы ошибки при этом равно

. (18)

Такое представление называется разложением Карунена – Лоэва. Коэффициенты разложения Карунена – Лоэва являются некоррелированными (ввиду ортогональности ) случайными величинами).

Для стационарных процессов, когда корреляционная функция зависит только от разности аргументов , при (становится достаточно большим по сравнения с протяжённостью ) собственные функции приближаются к комплексным дискретным экспоненциальным функциям с частотами .

В случае бесконечного интервала определения дискретные сигналы представляются с помощью дискретного преобразования Лапласа (ДПЛ)

Здесь изображение X(s) есть периодическая функция непрерывной комплексной переменной s=a + jw.. Для удобства ДПЛ часто используют в несколько модифицированном виде, носящим название Z преобразование и получающее путем введения новой переменной z=exp(s).

Z— преобразование дискретной последовательности имеет вид

интегрирование осуществляется в области сходимости функции.

В частотно временной области сигнал x[n] может быть описан с помощью дискретного во времени преобразования Фурье

, .

Дискретное во времени преобразование Фурье связано с преобразованием Фурье непрерывного сигнала соотношением

В случае конечного интервала определения, для периодического дискретного сигнала, повторяющегося с периодом NT_¶, x[n] = x[n+lN], удобно использовать базис ортогональных дискретно экспоненциальных функций (ДЭФ). Такое представление называется дискретным преобразованием Фурье (ДПФ) и имеет вид

Здесь сигнал x[n] и его спектр X(k) являются дискретными функциями, определенными на конечном интервале N.

Для анализа нестационарных, всплесковых, сигналов часто используют представление с помощью вейвлетных функций в виде коротких, солитоноподобных колебаний Понятие частоты классического спектрального анализа при этом заменяется масштабом a, а чтобы перекрыть всю временную ось вводится сдвиг функции во времени b.

1.3. Цифровые сигналы

Операция квантования непрерывной величины состоит в том, что континуум ее возможных значений заменяется счетным числом значений. Существующие устройства квантования обычно осуществляют равномерное квантование сигналов, при котором границы интервалов квантования размещаются равномерно в заданном диапазоне значений сигнала, а представители уровней квантования располагаются посередине между этими границами. В случае равномерной процедуры количество порогов квантования оценивается величиной

где и — максимальная и минимальная амплитуды дискретизируемого сигнала. Пороги квантования разбивают интервал на (r + 1) интервалов – уровней квантования.

Отсчет непрерывного процесса в АЦП преобразуется в двоичный код из m разрядов, каждый из которых представлен нулем или единицей. Число разрядов определяется числом уровней квантования

При когерентной обработке, когда требуется осуществлять цифровую фильтрацию сигналов, когерентную компенсацию помех, число уровней квантования нужно увеличивать, чтобы уменьшить по возможности искажения (из-за квантования) сигналов и помех. На практике часто выбирают , где — дисперсия собственного шума приемника. При этом, число порогов квантования равно , где — динамический диапазон аналоговой части приемника. Отсюда получаем требуемое число разрядов кода и соответственно число разрядов АЦП:

Системы счисления в системах цифровой обработки сигналов. Цифровая система обработки является конечной машиной, работающая с конечным множеством чисел. Невозможно использовать это множество для выполнения арифметических операций в поле вещественных чисел (R, +, ´), поскольку R — бесконечное множество, большинство элементов которого непредставимо в вычислительной машине.

На практике в процессе обработки осуществляют аппроксимацию арифметики в поле (R,+,´). Часто для такой аппроксимации используется множество F так называемых чисел с плавающей точкой (или машинных чисел). Множество F является частью множества вещественных чисел со следующими свойствами.

1. F – конечное подмножество множества рациональных чисел Q .

2. Элементы F распределены неравномерно на вещественной прямой. Интервал между двумя “соседними” машинными числами очень мал вблизи нуля, а при удалении от него постепенно увеличивается. Интервал между максимально возможным машинным числом и соседним с ним очень велик.

3. Система (F, +, ´) не будет полем (главным образом из-за того, что нет замкнутости относительно обеих указанных бинарных операций.

Практичный выход из возникающих трудностей состоит в представлении вещественного числа x ближайшим к нему машинным числом ; тем самым вводя ошибку округления . Из-за отсутствия замкнутости ошибки округления возникают также в результате арифметических операций над элементами F. Например, если и — два соседних элемента F , то число уже не принадлежит F. Его следует заменить на — элемент в F, ближайший к z. В этом примере совпадает либо с , либо с .

Представление целых чисел в системе счисления по смешанным основаниям.

Рассмотрим упорядоченный набор из n целых чисел

компоненты которого r₁, r₂,…,r_n называются основаниями. Пусть N есть произведение оснований, т.е. . Известно, что каждое целое число s, такое, что можно представить в виде

где d₀, d₁,…,d_n_-1 являются цифрами стандартного представления для смешанного основания и удовлетворяют неравенствам i = 0,1,…, n-1. Упорядоченный набор цифр d₀, d₁,…,d_n_-1 для данного s записывается в виде кода . Например, если r = [2, 3, 5], то N = 30, Следовательно, число 29 можно записать в виде 29 = 1+2(2)+4(2×3) и представление числа по смешанному основанию r имеет вид (29)_r =(1, 2, 4).

Стандартной системой счисления со смешанным основанием r называется множество всевозможных наборов цифр типа для целых чисел sÎ[0, N). В частном случае r₁ = r₂ = … = r_n приходим к известному представлению числа в позиционной системе с фиксированным основанием.

Контрольные вопросы и задачи

В лекции «2.16 Архитектура русского барокко» также много полезной информации.

1. Определить условие наложения спектров для q₁, q₂ двух сигналов и , если они дискретизируются с интервалом T_¶_{= Dt.}

2. Показать, что если в предыдущей задаче положить , где m – целое число, то возникает эффект комплексно-сопряженного наложения.

3. Пояснить, в чем различие между преобразованием Фурье непрерывного сигнала, дискретного во времени преобразованием Фурье и дискретным преобразованием Фурье.

4. Определить код представления числа 25 в системе счисления по смешанному основанию N=60.

Как аналоговый сигнал преобразуется в цифровой

Телевизионный сигнал — совокупность электрических сигналов, содержащая информацию о телевизионном изображении и звуке. Телевизионный сигнал может передаваться по радио или по кабелю. Термин употребляется в большинстве случаев применительно к аналоговому телевидению, потому что цифровое оперирует таким понятием, как поток данных.

В электронике сигналы делят на: аналоговые, дискретные и цифровые. Начнем с того, что все, что мы чувствуем, видим, слышим в большинстве своем является аналоговым сигналом, а то, что видит процессор компьютера – это цифровой сигнал. Звучит не совсем понятно, поэтому давайте разбираться с этими определениями и с тем как один вид сигналов преобразовывается в другой.

Типы сигналов

В электрическом представлении аналоговый сигнал, судя по его названию, является аналогом реальной величины. Например, вы чувствуете температуру окружающей среды постоянно, на протяжении всей жизни. Нет никаких перерывов. При этом вы чувствуете не только два уровня «горячо» и «холодно», а бесконечное число ощущений, которые описывают эту величину.

Для человека «холодно» может быть по разному, это и осенняя прохлада и зимний мороз, и легкие заморозки, но не всегда «холодно» это отрицательная температура, как и «тепло» — не всегда положительная температура.

Отсюда следует, что у аналогового сигнала две особенности:

1. Непрерывность во времени.

2. Число величин сигнала стремится к бесконечности, т.е. аналоговый сигнал нельзя точно поделить на части или проградуировать, разбив шкалу на конкретные участки. Способы измерения – основаны на единице измерений, и их точность зависит лишь от цены деления шкалы, чем она меньше, тем точнее измерение.

Дискретные сигналы – это сигналы, которые представляют собой последовательность отчетов или измерений какой-либо величины. Измерения таких сигналов не непрерывны, а периодичны.

Попытаюсь объяснить. Если вы установили термометр где-нибудь он измеряет аналоговую величину – это следует из вышеописанного. Но вы, фактически следя за его показаниями, получаете дискретную информацию. Дискретный – значит отдельный.

Например, вы проснулись и узнали, сколько градусов на термометре, в следующий раз вы на него посмотрели на градусник в полдень, и третий раз вечером. Вы не знаете, с какой скоростью изменялась температура, равномерно, или резким скачком, вы знаете только данные в тот момент времени, который наблюдали.

Цифровые сигналы – это набор уровней, типа 1 и 0, высокий и низкий, есть или нет. Глубина отражения информации в цифровом виде ограничена разрядностью цифрового устройства (набора логики, микроконтроллера, процессора etc.) Получается что для хранения булевых данных он подходит идеально. Пример, можно привести следующий, для хранений данных типа «День» и «Ночь», достаточно 1 бита информации.

Бит – это минимальная величина представления информации в цифровом виде, в нём может храниться только два типа значений 1 (логическая единица, высокий уровень), или 0 (логический ноль, низкий уровень).

В электронике бит информации представляется в виде низкого уровня напряжения (близкое к 0) и высокого уровня напряжения (зависит от конкретного устройства, часто совпадает с напряжением питания данного цифрового узла, типовые значения – 1.7, 3.3. 5В, 15В).

Все промежуточные значения между принятыми низким и высоким уровнем являются переходной областью и могут не обладать конкретным значением, в зависимости от схемотехники, как устройства в целом, так и внутренней схемы микроконтроллера (или любого другого цифрового устройства) могут иметь разный переходный уровень, например для 5-тивольтовой логики за ноль могут приниматься значения напряжения от 0 до 0.8В, а за единицу от 2В до 5В, при этом промежуток между 0.8 и 2В – это неопределенная зона, фактически с ее помощью отделяется ноль от единицы.

Чем более точные и ёмкие значения нужно хранить, тем больше нужно бит, приведем таблицу-пример с отображением в цифровом виде четырёх значений времени суток:

Ночь – Утро – День – Вечер

Для этого нам нужно уже 2 бита:

Аналогово-цифровое преобразование

В общем случае аналогово-цифровым преобразованием называется процесс перевода физической величины в цифровое значение. Цифровым значением является набор единиц и нолей воспринятых обрабатывающим устройством.

Такое преобразование нужно для взаимодействия цифровой техники с окружающей средой.

Так как аналоговый электрический сигнал повторяет своей формой входной сигнал, он не может быть записан в цифровом виде «так как есть» поскольку он имеет бесконечное число значений. Примером можно привести процесс записи звука. Он в первичном виде выглядит так:

Он представляет собой сумму волн с различными частотами. Которые, при разложении по частотам (подробнее об этом смотрите преобразования Фурье), так или иначе, можно приблизить к похожей картинке:

Теперь попробуйте это представить в виде набора типа «111100101010100», довольно сложно, не так ли?

Другим примером необходимости преобразования аналоговой величины в цифровую, является её измерение: электронные термометры, вольтметры, амперметры и прочие измерительные приборы взаимодействую с аналоговыми величинами.

Как происходит преобразование?

Сначала посмотрите на схему типового преобразования аналогового сигнала в цифровой и обратно. Позже мы к ней вернемся.

Фактически это сложный процесс, который состоит из двух основных этапов:

1. Дискретизация сигнала.

2. Квантование по уровню.

Дискретизация сигнала это определения промежутков времени, на которых измеряется сигнал. Чем короче эти промежутки – тем точнее измерение. Периодом дискретизации (Т) называется отрезок времени от начала считывания данных до его конца. Частота дискретизации (f) – это обратная величина:

fд=1/Т

После считывания сигнала происходит его обработка и сохранение в память.

Получается, что за время, которое считываются и обрабатываются показания сигнала, он может измениться, таким образом, происходит искажение измеряемой величины. Есть такая теорема Котельникова и из нее вытекает такое правило:

Частота дискретизации должны быть как минимум в 2 раза больше чем частота дискретизируемого сигнала.

Это скриншот из википедии, с выдержкой из теоремы.

Для определения численного значение необходимо квантование по уровню. Квант – это определенный промежуток измеряемых значений, усреднено приведенный к определенному числу.

X1…X2=Xy

Т.е. сигналы величиной от X1 до X2, условно приравнивается к определенному значению Xy. Это напоминает цену деления стрелочного измерительного прибора. Когда вы снимаете показания, зачастую вы их равняете по ближайшей отметке на шкале прибора.

Так и с квантованием по уровню, чем больше квантов, тем более точные измерения и тем больше знаков после запятой (сотых, тысячных и так далее значений) они могут содержать.

Точнее сказать число знаков после запятой скорее определяется разрядностью АЦП.

На картинке изображен процесс квантования сигнала с помощью одного бита информации, как я описывал выше, когда при превышении определенного предела принимается значение высокого уровня.

Справа показано квантование сигнала, и запись в виде двух бит данных. Как видите, этот фрагмент сигнала разбит уже на четыре значения. Получается, что в результате плавный аналоговый сигнал превратился в цифровой «ступенчатый» сигнал.

Количество уровней квантования определяется по формуле:

де n — количество разрядов, N — уровень квантования.

Вот пример сигнала разбитого на большее число квантов:

Отсюда очень хорошо видно, что чем чаще снимаются значения сигнала (больше частота дискретизации), тем точнее он измеряется.

На этой картинке изображено преобразование аналогового сигнала в цифровой вид, а слева от оси ординат (вертикальной оси) запись в цифровом 8-битном виде.

Аналогово-цифровые преобразователи

АЦП или Аналогово-цифровой преобразователь может выполняться в виде отдельного устройства или быть встроенным в микроконтроллер.

Ранее в микроконтроллеры, например семейства MCS-51, не содержали в своем составе АЦП, использовалась для этого внешняя микросхема и возникала необходимость писать подпрограмму обработки значений внешней ИМС.

Сейчас они есть в большинстве современных микроконтроллеров, например AVR AtMEGA328, который является основой большинства популярных плат Ардуино, он встроен в сам МК. На языке Arduino чтение аналоговых данных осуществляется просто – командой AnalogRead(). Хотя в микропроцессоре, который установлен в той же не менее популярной Raspberry PI его нет, так что не все так однозначно.

Фактически существует большое число вариантов аналогово-цифровых преобразователей, у каждого из которых есть свои недостатки и преимущества. Описывать которые в пределах этой статьи не имеет особого смысла, так как это большой объём материала. Рассмотрим лишь общую структуру некоторых из них.

Самым старым запатентованным вариантом АЦП, является патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Это 5-ти битный АЦП прямого преобразования. Из названия патента приходят мысли о том, что использование этого прибора было связано с передачей данных через телеграф.

Если говорить о современных АЦП прямого преобразования имеют следующую схему:

Отсюда видно, что вход представляет собой цепочку из компараторов, которые на выходе своем выдают сигнал при пересечении какого-то порогового сигнала. Это и есть разрядность и квантование. Кто хоть немного силен в схемотехнике, увидел этот очевидный факт.

Кто не силен, то входная цепь работает таким образом:

Аналоговый сигнал поступает на вход «+», на все сразу. На выходы с обозначением «-» поступает опорное напряжение, которое раскладывается с помощью цепочки резисторов (резистивного делителя) на ряд опорных напряжений. К примеру, ряд для этой цепи выглядит наподобие такого соотношения:

Urefi=(1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16)*Uref

В скобках через запятую указано, какую часть от общего опорного напряжения Uref подают на вход каждого входного напряжения.

Т.е. каждый из элементов имеет два входа, когда напряжение на входе со знаком «+»превышает напряжение на входе со знаком «-», то на его выходе появляется логическая единица. Когда на положительном (неинвертирующем) входе напряжение меньше, чем на отрицательно (инвертирующем), то на выходе – ноль.

Напряжение делиться таким образом, чтобы входное напряжение разбить на нужное количество разрядов. При достижении напряжения на входе на выходе соответствующего элемента появляется сигнал, схема обработки выводит «правильный» сигнал в цифровом виде.

Такой компаратор хорош скоростью обработки данных, все элементы входной цепи срабатывают параллельно, основная задержка этого вида АЦП формируется из задержки 1 компаратора (все же одновременно параллельно срабатывают) и задержки шифратор.8 компараторов, а это целых 256 штук. Для десятиразрядного (в ардуино 10-разрядный АЦП, кстати, но другого типа) нужно 1024 компаратора. Судите сами о целесообразности такого варианта обработки, и где он может понадобиться.

Есть и другие виды АЦП:

Заключение

Преобразование аналогового сигнала в цифровой нужно для считывания параметров с аналоговых датчиков. Есть отдельный вид цифровых датчиков, они представляют собой либо интегральные микросхемы, например DS18b20 – на его выходе уже цифровой сигнал и его можно обрабатывать любыми микроконтроллерами или микропроцессорами без необходимости применения АЦП, или аналоговый датчик на плате на которой уже размещен свой преобразователь. У каждого типа датчиков есть свои плюсы и минусы, такие как помехоустойчивость и погрешность измерений.

Знание принципов преобразование обязательно для всех кто работает с микроконтроллерами, ведь не в каждой даже современной системе встроены такие преобразователи, приходится использовать внешние микросхемы. Для примера можно привести такую плату, разработанную специально под GPIO-разъём Raspberry PI, с прецизионным АЦП на ADS1256.

Ранее ЭлектроВести писали, что власти Вены запустили тестирование технологии умных камер, которые будут распознавать приближение пешеходов и подавать сигнал на светофор.

По материалам: electrik.info.

Page

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ

2. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ С ПОМОЩЬЮ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ

3. МОДЕЛИРОВАНИЕ И АНАЛИЗ ЦИФРОВЫХ СИСТЕМ В ПАКЕТЕ SIMULINK СИСТЕМЫ MATLAB

4. ПРЕОБРАЗОВАНИЕ ФОРМ ЛИНЕЙНЫХ МОДЕЛЕЙ ЦИФРОВЫХ СИСТЕМ

Контрольные вопросы

Лабораторная работа № 13

Моделирование и исследование

цифровых систем управления

Цель работы: проанализировать линейные стационарные системы управления с дискретным временем.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Любая система автоматического регулирования и управления представляет собой совокупность элементов, предназначенных для преобразования сигналов, поступающих на ее вход, чтобы обеспечить выполнение цели управления [4]. Если на вход всех элементов системы поступают сигналы, которые могут быть описаны непрерывными функциями времени, система называется непрерывной. Система, содержащая, по крайней мере, один элемент, выходным сигналом которого является дискретный сигнал, называется дискретной.

Дискретный сигнал – это такой сигнал, который определяется последовательностью значений а₀, а₁, а₂, ¼, а_n_,_¼_.Сигналы могут быть дискретными по уровню, по времени, а также одновременно по уровню и по времени.

В зависимости от способов получения дискретных сигналов может быть введена следующая классификация дискретных систем [4, 18]:

1) импульсная система – это система, в которой используются сигналы, дискретные по времени;

2) релейная система – это система, в которой используются сигналы, дискретные по уровню;

3) цифровая система – это система, в которой используются сигналы, дискретные как по времени, так и по уровню.

На рис. 13.1 показана идеализированная амплитудно-импульсная модуляция непрерывного сигнала на основе идеальных импульсов, ширина которых бесконечна малая, а высота равна значениям непрерывного сигнала в дискретные моменты времени. Если f(t) есть непрерывный сигнал, то выделение дискретных значений f(kT) называется квантованием сигнала f(t) по времени с постоянным шагом квантования или периодом дискретизации Т. В то же время f(kT) называют решетчатой функцией. Другим видом импульсной модуляции является широтно-импульсная модуляция, при которой амплитуда импульсов постоянная, а их ширина пропорциональна в некоторых пределах значениям f(kT). Еще возможна фазоимпульсная модуляция сигнала, которая осуществляется за счет смещения импульсов в пределах шага квантования Т. Величина смещения пропорциональна значениям f(kT).

Рис. 13.1. Идеальное квантование непрерывного сигнала по времени

Квантование (дискретизация) непрерывного сигнала по уровню с шагом h показано на рис. 13.2. Оно может быть получено, если преобразовать непрерывный сигнал с помощью многоступенчатого релейного устройства. Дискретный по уровню сигнал, представленный на рис. 13.2, может быть описан в соответствии с выражением [4]:

При квантовании по уровню в произвольные моменты времени выделяются значения непрерывного сигнала при достижении им фиксированных дискретных уровней [18]. Как отмечалось, квантование по уровню характерно для релейных систем автоматического управления, которые представляют собой достаточно большой класс динамических систем, в состав которых входят нелинейные звенья с разрывной характеристикой. Основными достоинствами релейных систем автоматического управления является их простота, связанная с ней высокая надежность, а также экономичность в расходе энергии питания. В то же время к ним не могут быть применены методы анализа и синтеза гладких систем.

Рис. 13.2. Квантование непрерывного сигнала по уровню

Характер квантования по уровню и по времени непрерывного сигнала показан на рис. 13.3. В этом случае непрерывный сигнал f(t) заменяется фиксированными дискретными (по уровню) значениями, ближайшими к значениям непрерывной функции f(t) в дискретные моменты времени 0, Т, 2Т, ¼ . Квантование по уровню и по времени осуществляется в цифровых системах управления при преобразовании непрерывных сигналов в цифровую форму или в коды. Если цифровое устройство оперирует с числовым представлением со значительным количеством разрядов (что характерно для современных компьютеров), то квантованием по уровню можно пренебречь. Тогда цифровую систему можно рассматривать как импульсную систему с амплитудно-импульсной модуляцией.

Рис. 13.3. Квантование сигнала по уровню и по времени

Цифровая система управления включает объект управления (обычно непрерывный объект или процесс), чувствительные элементы (или датчики), аналого-цифровой преобразователь (АЦП), цифровое вычислительное устройство (микропроцессор или компьютер) и цифроаналоговый преобразователь (ЦАП). Функциональная схема цифровой системы управления показана на рис. 13.4.

Discrete Time Signal — обзор

Дискретный сигнал времени на выходе Synthesis FilterBank (SFB) определяется как [6]

(11.1) s [l] = ∑m = 0M − 1∑ndm, ngm , n [l],

, где dm, n — ( вещественных -значных) символов амплитудно-импульсной модуляции (PAM) (полусимволы смещенной квадратурной амплитудной модуляции (OQAM)), и

gm, n [l] = g [l − nM2] ej2πMm (l − Lg − 12) ejφm, n

, где g — это действительный симметричный импульсный отклик прототипа (здесь предполагается единичная энергия) длины Lg, M — четное число поднесущих и φm, n = π2 (m + n) −mnπ [6].Фильтр g обычно имеет длину Lg = KM с коэффициентом перекрытия K . Двойной индекс (⋅) m, n обозначает (m, n) -ю частоту-время (F-T) точку. Таким образом, m — это индекс поднесущей, а n — временной индекс символа FBMC / OQAM. Выходной сигнал модулятора передается по каналу длиной Lh, который, как обычно при блочной передаче, считается неизменным по длительности символа MultiCarrier (MC) [7]. На входе приемника добавляется шум v , который предполагается белым гауссовским с нулевым средним и дисперсией σv2.Выходной сигнал канала с шумом определяется выражением

(11.2) r [l] = ∑k = 0Lh − 1s [k − l] h [k] + v [l],

, где

h = [h [0 ] h [1] ⋯ h [Lh-1]] T

— импульсная характеристика канала (CIR).

Импульс g разработан так, что соответствующие функции поднесущей gm, n ортогональны в поле действительного , то есть

(11.3) Re {∑lgm, n [l] gp, q⁎ [l ]} = δm, pδn, q,

где δi, j — символ Кронекера. Это означает, что даже при отсутствии канальных искажений и шума и с идеальной временной и частотной синхронизацией на выходе Analysis FilterBank (AFB) будут некоторые межнесущие (и / или межсимвольные) помехи, которые являются чисто реальными или мнимыми ( в зависимости от четности точки FT) и называется внутренней помехой [8].Предполагая, для простоты представления, что обработка AFB включает в себя умножение на e − jφm, n, помехи всегда можно рассматривать как мнимые, и, следовательно, мы можем записать ответ FBMC / OQAM TransMUltipleXer (TMUX) из FT точка (m, n) в (p, q) как

(11.4) Γp, mq, n = ∑lgm, n [l] gp, q⁎ [l] = j 〈g〉 m, np, q

для (p, q) ≠ (m, n), где (используя обозначения из [9]) 〈g〉 m, np, q вещественнозначно. Кроме того, Γp, pq, q = 1. Пример (даже для p ) приведен в таблице 11.1, где использован фильтр-прототип PHYDYAS [10] с K = 4. Обратите внимание, что это TMUX с почти идеальной реконструкцией (NPR), как можно видеть в ячейках, заштрихованных серым, которые будут содержать нули для системы идеальной реконструкции (PR). Более важно отметить тот факт, что (как показано в табличном примере) нет никаких помех от несмежных поднесущих в одно и то же время символа (интерференция между несущими (ICI)). Помехи от предшествующих и последующих моментов времени и от соседних поднесущих, т.е.е., из точек F-T (m ± 2, n ± 1), в общем случае очень мало [4]. Для PHYDYAS TMUX он равен нулю.

Таблица 11.1. Отклик FBMC / OQAM TMUX, использующего фильтр-прототип PHYDYAS [10] с K = 4. Показан случай четного индекса поднесущей p

Изучение систем FBMC / OQAM может быть значительно упрощено с помощью приближений, основанных на пропускная способность и время когерентности канала, а также хорошая частотно-временная локализация, которыми обладает фильтр-прототип g .Таким образом, для каналов длиной Lh, относительно небольшой по сравнению с размером ( M ) FilterBank (FB), можно показать, что выходной сигнал AFB в точке FT (p, q) может быть аппроксимирован [9]

(11.5) yp, q = Hp, qdp, q + j∑m = 0M − 1∑n︸ (m, n) ≠ (p, q) Hm, ndm, n 〈g〉 m, np, q︸Ip , q + ηp, q,

где Hm, n — частотная характеристика канала (CFR) в точке (m, n), а ηp, q — шум на выходе AFB, который также является гауссовым с нулевым средним и дисперсией ση2. = σv2, но коррелирован как по времени, так и по частоте из-за фильтрации AFB [4].Даже в рамках этой модели с плоским подканалом оценка канала должна учитывать интерференционный член Ip, q, который, как правило, является комплексным, а не чисто мнимым из-за комплексных коэффициентов усиления CFR [8,9]. Следующим шагом на пути к простоте мультиплексирования с ортогональным частотным разделением и циклическим префиксом (CP-OFDM) является использование того факта, что помехи от точек FT за пределами окрестности Ωp, q из (p, q) пренебрежимо малы при допущении, что CFR (почти) постоянный в этой частотно-временной области.Последнее, конечно, подразумевает даже более короткий разброс задержки канала, чем требуется для проверки (11.5), что затем может быть записано как

(11.6) yp, q≈Hp, qxp, q + ηp, q,

, а именно , в режиме CP-OFDM, где

(11.7) xp, q = dp, q + j∑ (m, n) ∈Ω¯p, qdm, n 〈g〉 m, np, q︸up, q = dp, q + jup, q,

с Ω¯p, q = Ωp, q ∖ {(p, q)}, виртуальных переданных символов в (p, q), состоящих из самого переданного символа плюс — помехи, исходящие из его частотно-временной (TF) окрестности,

(11.8) вверх, q = ∑ (m, n) ∈Ω¯p, qdm, n 〈g〉 m, np, q.

Ω¯p, q обычно рассматривается как T-F-окрестность первого порядка точки (p, q), состоящая из ее ближайших соседних точек F-T (показаны заштрихованными в примере таблицы 11.1). Можно показать, что соответствующие веса интерференции j 〈g〉 m, np, q удовлетворяют следующим симметриям [4]:

(11.9) j (−1) pδ − jβj (−1) pδ − j (−1) pγdp , qj (−1) pγj (−1) pδjβj (−1) pδ

, где горизонтальное направление соответствует времени, а вертикальное — частоте. Таким образом, помеха от (p − 1, q) равна −jβdp − 1, q и т. Д.Величины β, γ, δ могут быть априори вычислены из g (подробные выражения см. В [4]), они положительны и меньше единицы. Обычно γ> β> δ. В примере таблицы 11.1 β = 0,2393, γ = 0,5644 и δ = 0,2058. Вышеупомянутые симметрии играют центральную роль в разработке обучающих входных данных и связанных методов оценки канала, как это будет показано в дальнейшем.

250+ TOP MCQ по сигналам дискретного времени и ответам

5. x (n) * δ (n-k) =?
A. x (n)
B. x (k)
C.x (k) * δ (n-k)
D. x (k) * δ (k)
Ответ: C
Уточнение: Данный сигнал определяется только тогда, когда n = k по определению дельта-функции. Итак, x (n) * δ (n-k) = x (k) * δ (n-k).

6. Действительный сигнал x (n) называется антисимметричным, если ___________
A. x (n) = x (-n)
B. x (n) = — x (-n)
C. x (n) = — x (n)
D. Ни один из упомянутых
Ответ: B
Уточнение: Согласно определению антисимметричного сигнала, сигнал x (n) должен быть симметричным относительно начала координат. Итак, чтобы сигнал x (n) был симметричным, он должен удовлетворять условию x (n) = — x (-n).

7. Нечетная часть сигнала x (t) равна?
A. x (t) + x (-t)
B. x (t) -x (-t)
C. (1/2) * (x (t) + x (-t))
D. (1/2) * (x (t) -x (-t))
Ответ: D
Уточнение: Пусть x (t) = x _e (t) + x _o (t)
=> x (-t) = x _e (-t) -x _o (-t)
Вычитая два приведенных выше уравнения, мы получаем
x _o (t) = (1/2) * (x ( текст)).

8. Операция масштабирования времени также известна как ___________
A. Понижающая дискретизация
B. Повышающая дискретизация
C.Выборка
D. Ни один из упомянутых
Ответ: A
Уточнение: если сигнал x (n) был первоначально получен путем дискретизации сигнала x _a (t), то x (n) = x _a (nT) . Теперь y (n) = x (2n) (скажем) = x _a (2nT). Следовательно, операция масштабирования по времени эквивалентна изменению частоты дискретизации с 1 / T на 1 / 2T, то есть уменьшению частоты в 2 раза. Таким образом, масштабирование по времени также называется понижающей дискретизацией.

9. Каково условие, при котором сигнал x (n) = Br ⁿ, где r = e ^αT, должен называться убывающим экспоненциальным сигналом?
А.0B. 0C. r> 1
D. rОтвет: B
Уточнение: когда значение «r» находится между 0 и 1, тогда значение x (n) продолжает экспоненциально уменьшаться с увеличением значения «n». Итак, сигнал называется затухающим экспоненциальным сигналом.

10. Функция, заданная уравнением x (n) = 1, для n = 0; x (n) = 0, для n 0 является _____________
A. Шаговая функция
B. Линейная функция
C. Треугольная функция
D. Импульсная функция
Ответ: D
Уточнение: Согласно определению импульсной функции, он определен только при n = 0 и не определен где-либо еще в соответствии с заданным сигналом.

Что такое непрерывный и дискретный сигнал времени? — Цвета-NewYork.com

Что такое непрерывный и дискретный сигнал времени?

Независимые переменные для сигнала могут быть непрерывными или дискретными. Сигнал считается непрерывным временным сигналом, если он определен по континууму независимой переменной. Сигнал считается дискретным по времени, если независимая переменная имеет только дискретные значения.

В чем разница между дискретным и цифровым сигналом?

Цифровой сигнал — сигнал непрерывный во времени, но дискретный по амплитуде.Дискретность по амплитуде означает, что сигнал не может иметь несколько значений амплитуды. Это может быть 1 или 0. Дискретный сигнал — сигнал дискретный по времени, но непрерывный по амплитуде.

Какое определение означает непрерывный сигнал?

Непрерывный сигнал — это непрерывная функция времени, определенная на вещественной прямой R, обозначенной символом. s (t), t — время. Сигнал может быть комплексным. Непрерывный сигнал называется аналоговым. сигнал.

Что такое пример дискретного сигнала?

Напротив, дискретный сигнал имеет счетную область, как и натуральные числа.Другими примерами непрерывных сигналов являются синусоидальная волна, косинусная волна, треугольная волна и т. Д. Сигнал определяется в области, которая может быть или не быть конечной, и существует функциональное отображение области на значение сигнала.

Возраст непрерывен или дискретен?

Возраст измеряется в единицах, которые, если достаточно точны, могут быть любым числом. Следовательно, набор, из которого они происходят, бесконечен. Например, кому-то может быть 22,32698457 или 22,32698459 лет. Мы могли бы быть бесконечно точными и использовать бесконечное количество десятичных знаков, таким образом делая возраст непрерывным.

Как узнать, являются ли ваши данные дискретными или непрерывными?

Дискретные данные — это числовой тип данных, который включает целые конкретные числа с конкретными и фиксированными значениями данных, определяемыми путем подсчета. Непрерывные данные включают комплексные числа и переменные значения данных, которые измеряются в течение определенного интервала времени.

Пол — дискретная или непрерывная переменная?

Я намеренно дал понять, что переменная либо дискретная, либо непрерывная…. Справочная таблица переменных: несколько примеров.

Переменная	Тип переменной	Переменная шкала
Пол	Дискретный	Категориальный
Пол как двоичное кодирование 1/0	Дискретный	Категориальный
Верно / Неверно	Дискретный	Категориальный
Телефон	Дискретный	Номинал

Деньги непрерывны или дискретны?

Непрерывное распределение должно иметь бесконечное количество значений от 0 до $.00 и 0,01 доллара. У денег нет этого свойства — всегда есть неделимая единица наименьшей валюты. Таким образом, деньги — это дискретная величина.

Является ли группа крови непрерывной или дискретной?

Группа крови не является дискретной случайной величиной, потому что она категориальна. Непрерывные случайные переменные имеют числовые значения, которые могут быть любым числом в интервале. Например, (точный) вес человека — это непрерывная случайная величина. Длина стопы также является непрерывной случайной величиной.

Стоимость — это дискретная или непрерывная переменная?

Стоимость технически является непрерывной переменной. Учтите, что что-то может стоить 0,01 доллара — бесконечность.

В чем разница между дискретной и непрерывной переменной?

Дискретная переменная — это переменная, значение которой получается путем подсчета. Непрерывная переменная — это переменная, значение которой получается путем измерения. Дискретная случайная величина X имеет счетное число возможных значений.

Почему деньги непрерывны?

Однако деньги непрерывны, потому что они могут иметь много и любую ценность и иметь любую сумму, в значительной степени.Например, платите, тогда как она может иметь бесконечное значение.

Является ли занятость дискретной переменной?

Доход — непрерывная переменная. Размер домохозяйства и количество компьютеров — дискретные переменные. (*) Род занятий главы семьи и тип подключения к Интернету являются качественными переменными.

Почтовый индекс непрерывный или дискретный?

непрерывный дискретный атрибут Имеет только конечный или счетно бесконечный набор значений. Примеры из текста: почтовые индексы, счетчики или набор слов в коллекции документов, двоичные данные.

Да или нет дискретная переменная?

Дискретные данные можно подразделить на три категории: двоичные, номинальные и порядковые. Двоичные данные: двоичные данные принимают только два возможных значения. Например, лампа горит или лампа выключена, ответ — истина или ложь, 0 или 1, да или нет и т. Д. Эти пять ответов упорядочены, так что это будет пример порядковых данных.

Процент — это дискретная переменная?

С технической точки зрения процентные данные являются дискретными, поскольку базовые данные, на основании которых рассчитываются проценты, являются дискретными.На практике процентные данные часто рассматриваются как непрерывные, потому что процентные данные могут принимать любое значение в континууме от нуля до 100%.

Скорость автомобиля непрерывна или дискретна?

Да, скорость — это обычная непрерывная переменная, а значение выбирается случайным образом. Мы знаем, что это непрерывно, потому что всегда есть другое возможное значение между любыми двумя значениями скорости.

Население дискретно или непрерывно?

Подсчет населения обычно называют дискретными или количественными данными.Почему плотность населения является непрерывным типом данных, когда она обычно измеряется для агрегированных областей, таких как переписные участки или районы / кварталы (т. Е. Ее нельзя измерить в любой точке поверхности, такой как градиент или температура).

Какой набор данных дискретный?

Определение: набор данных называется дискретным, если значения, принадлежащие набору, являются различными и отдельными (несвязанные значения). Примеры: рост лошади (может быть любым значением в пределах диапазона роста лошади).Время на выполнение задачи (может быть измерено до долей секунды).

Могут ли данные быть как дискретными, так и непрерывными?

Дискретные данные — это информация, которая может принимать только определенные значения. Рост, вес, температура и длина — все это примеры непрерывных данных. …

Почему непрерывные данные лучше дискретных?

Но когда вы можете это получить, непрерывные данные — лучший вариант… .Некоторые заключительные преимущества непрерывных данных над дискретными.

Непрерывные данные	Дискретные данные
Выводы можно сделать с помощью нескольких точек данных — достоверный анализ можно выполнить с небольшими образцами.	Чтобы сделать эквивалентный вывод, необходимо больше точек данных (большая выборка).

Являются ли дискретные данные количественными или качественными?

Количественные разновидности: непрерывные данные и дискретные данные Существует два типа количественных данных, которые также называются числовыми данными: непрерывные и дискретные. Как правило, подсчеты являются дискретными, а измерения — непрерывными. Дискретные данные — это счет, который невозможно уточнить.

Могут ли качественные данные быть дискретными?

Качественные данные содержат категориальные переменные, а количественные данные содержат числовые переменные.Категориальные переменные бывают номинальными или порядковыми, тогда как числовые переменные могут быть дискретными или непрерывными.

В чем разница между качественными дискретными и непрерывными данными?

Качественные данные — это не числа. Они могут включать любимые блюда; религии; национальности; и т. д. Дискретные данные — это числа, которые могут принимать определенные, разделенные значения. Непрерывные данные — это числа, которые могут принимать всевозможные десятичные или дробные значения.

Температура тела дискретная или постоянная?

Температура является непрерывной переменной, так как имеет дробное значение.Например: сегодняшняя температура составляет 30,5 градусов Цельсия, здесь 30,5 не является дискретной переменной и, следовательно, является непрерывной переменной.

Дискретный и аналоговый ввод / вывод для ПЛК

Так что вы думаете, этот стакан наполовину полон или наполовину пуст? Для меня это может быть немного сложно ответить и может варьироваться в зависимости от дня, который у меня есть, но если мы спрашиваем об уровне, почему бы не позволить ПЛК ответить? На самом деле, почему бы ПЛК не сообщать нам уровень, температуру воды, скорость потока, с которой она была заполнена, доступную емкость стакана и давление, оказываемое на дно? Хорошо, обычно вы не будете использовать ПЛК для такого небольшого приложения, но в более крупном масштабе, например, резервуар, ПЛК может ответить на все эти вопросы.Но как заставить ПЛК «видеть» этот резервуар, не говоря уже о том, насколько он полон? Что ж, я рад, что ты спросил, или я спросил, или что-то в этом роде. Нам нужно устройство, которое может позволить ПЛК получать информацию из своего окружения и обрабатывать ее. Нам также нужно устройство, которое позволит ПЛК влиять на свое окружение по мере необходимости. Нам нужен ввод-вывод, а под вводом-выводом я подразумеваю вводы и выводы. В этом обсуждении мы сосредоточимся на двух основных типах ввода-вывода: аналоговом и дискретном.

Дискретный ввод / вывод

Давайте сначала возьмем самое простое, дискретное.Дискретные сигналы — это сигналы, которые либо включены, либо выключены, истинны или ложны. Подумайте о выключателе в вашем доме. Выключатель либо включает свет, либо выключает его, если это не люминесцентная лампа — тогда он, вероятно, все еще мигает. Поскольку дискретные сигналы существуют в одном из этих двух состояний, они представлены прямоугольной волной, как показано ниже. В мире ПЛК существует множество применений дискретного ввода-вывода. Некоторые из устройств, которые подают сигналы включения / выключения, — это кнопки, фотоэлементы, концевые выключатели, поплавковые выключатели и бесконтактные выключатели.В дни стартапа я много работал с определенной службой доставки посылок. Они используют множество датчиков включения / выключения и контроля, чтобы отслеживать посылки и доставлять их в нужное место назначения или на грузовик. Фотоэлементы, которые представляют собой устройства, которые излучают инфракрасный световой луч и могут определять, когда этот луч был прерван, широко используются для обнаружения и отслеживания пакетов в процессе их сортировки. Применение вашей системы управления определит типы дискретных устройств, которые вы выберете. Существует множество дискретных оконечных устройств и модулей, которые можно использовать в системе ПЛК для отправки и приема сигналов включения / выключения.Эти устройства могут быть переменного или постоянного тока и доступны в различных диапазонах напряжения. 0–24 В постоянного тока и 0–230 В переменного тока — это два доступных диапазона напряжения, где 0 — это сигнал ВЫКЛ, а 24 В постоянного тока или 230 В переменного тока — сигнал ВКЛ. Обычно существует порог обнаружения, при котором модуль 0-24 В постоянного тока обнаруживает все, что выше 22 В постоянного тока, как сигнал ВКЛ, и все, что ниже 2 В постоянного тока, как ВЫКЛ. Теперь давайте посмотрим на аналог.

Аналоговый ввод / вывод

Аналоговые сигналы — это сигналы, которые могут изменяться или изменяться. Мы живем в аналоговом мире, и наши чувства — аналоговые приемники.«Почувствуй, как жарко!», «Ты можешь говорить?» и «Посмотрите на все цвета!» это утверждения, которые показывают, как вариации аналоговых сигналов, таких как температура, звук и свет, могут влиять на наши чувства. Вернемся к примеру с выключателем света; Давайте теперь установим в нашем доме небольшую декоративную подсветку. Вместо штатного выключателя мы будем использовать диммер. Переключатель диммера будет изменять сопротивление в линии, заставляя свет тускнеть или становиться ярче по нашему выбору. Новые диммерные переключатели усовершенствованы, чтобы быть более эффективными, но в этом примере мы придерживаемся старой школы.Напряжение, подаваемое на светильник, не будет постоянным уровнем, а будет изменяться между верхним и нижним пределами. Обычно это синусоида.

Использование датчиков

Положение, уровень, температура, давление, расход и скорость — это лишь некоторые из измерений, которые аналоговые устройства могут предоставить системе управления. Вы, вероятно, спрашиваете себя: «Как давление, являющееся физической величиной, становится электрическим сигналом?» Это отличный вопрос! Преобразование выполняется с помощью преобразователей.Преобразователь принимает физическую величину, например давление, и преобразует ее в электрический сигнал. Многие преобразователи используют физическую величину для управления сопротивлением в электрической цепи. Например, RTD (датчик температуры сопротивления) будет изменять значение сопротивления в зависимости от нагрева. По мере увеличения тепла увеличивается и сопротивление в цепи, изменяя подаваемое напряжение или ток. То же самое верно и для датчиков давления, в которых используются тензодатчики. При приложении давления к тензодатчику сопротивление в цепи увеличивается, а уровень напряжения или тока изменяется.Некоторые детекторы потока будут использовать поток жидкости для толкания ребра, соединенного с поворотным потенциометром. Более быстрый поток означает большее изменение сопротивления. Одним из самых крутых датчиков, с которыми я столкнулся в дни работы в морской нефтяной промышленности, был детектор песка. Этот преобразователь был акустическим и крепился к трубам, по которым нефть выводилась со дна моря. Он действительно будет слышать трение песка о внутреннюю часть трубы. Уровень звука был преобразован в аналоговый сигнал, используемый для предупреждения персонала, если при бурении извлекается слишком много песка, что может привести к обрушению скважины.Электрические сигналы, которые выдают преобразователи, могут быть основаны на напряжении или токе. От 4 до 20 мА, от 0 до 20 мА, от 0 до 10 В постоянного тока и от -10 до +10 В постоянного тока — вот лишь некоторые из доступных диапазонов, производимых датчиками. ПЛК подает напряжение или ток, а датчик возвращает значение в заданном диапазоне. Это значение будет пропорционально имеющемуся давлению, расходу и т. Д. Теперь мы подошли к двум важным частям этого обсуждения: масштабированию и разрешению.

Масштабирование

Масштабирование — это когда мы берем необработанное возвращаемое значение напряжения или тока и преобразуем его в значимое измерение.Допустим, у меня есть расходомер 4–20 мА, который возвращает сигнал 8 мА на ПЛК. Это будет означать, что в это время течет 8 мА жидкости, верно? Конечно, нет. Нам нужно взять исходное значение и масштабировать его до чего-то значимого, скажем, галлонов в минуту. Мы знаем от производителя, что расходомер откалиброван для считывания расхода от 0 до 200 галлонов в минуту. Следовательно, мы можем масштабировать исходное значение 4-20 мА до 0-200 галлонов в минуту в нашей системе. Обычно это можно сделать с помощью программного обеспечения для программирования, как показано ниже, и после масштабирования нашего значения 8 мА мы видим, что в настоящее время поток составляет 50 галлонов в минуту.

Разрешение

Теперь посмотрим на разрешение. Разрешение и точность идут рука об руку; Чем больше у вас разрешение, тем точнее будут ваши измерения. Аналоговые модули имеют разрешение, которое они обеспечивают. Доступны 12-битные, 13-битные и 16-битные разрешения. Итак, что значит иметь модуль 4-20 мА с 12-битным разрешением? 12-битное двоичное слово может иметь 4096 различных комбинаций. Таким образом, наш модуль с 12-битным разрешением может иметь 4096 (4095 со знаком) различных измерений в диапазоне 4-20 мА.Другими словами, диапазон 4-20 можно разбить на 4096 различных частей. Чем больше штук, тем точнее. Насколько точно? Что ж, наш общий диапазон составляет 16 мА (20 минус 4), и если мы разделим наш общий диапазон на 4096 частей, мы увидим, что наш модуль может обнаруживать каждое изменение на 0,003

мА.

Шум

И последнее: при использовании аналоговых сигналов важно помнить, что они очень чувствительны к шуму. Шум может вызвать неправильные показания и неустойчивое поведение системы управления. Взгляните на схему ниже.Моя система откроет предохранительный клапан на резервуаре, когда необработанный сигнал давления изнутри резервуара достигнет 5,9 В постоянного тока. С ответным сигналом слева это не проблема. Удачи с наведенным справа шумом! Если вам нужна дополнительная информация об автоматизации или процессе автоматизации, загрузите нашу электронную книгу «Автоматизация 101: отраслевое руководство по проектированию систем управления».

сигналов дискретного времени Вопросы и ответы

Этот набор вопросов и ответов с множественным выбором для цифровой обработки сигналов (MCQ) посвящен «сигналам дискретного времени».

1. Если x (n) — сигнал с дискретным временем, то значение x (n) при нецелочисленном значении «n» равно?
a) Ноль
b) Положительное
c) Отрицательное
d) Не определено
Посмотреть ответ

Ответ: d
Объяснение: Для сигнала дискретного времени значение x (n) существует только при целых значениях n. Итак, для нецелого значения «n» значение x (n) не существует.

2. Функция дискретного времени, определяемая как u (n) = n для n≥0; u (n) = 0 для n <0, является _____________
a) Сигнал единичной выборки
b) Сигнал единичного шага
c) Модульное линейное изменение сигнал
d) Ни один из упомянутых
Посмотреть ответ

Ответ: c
Объяснение: Когда мы строим график для данной функции, мы получаем прямую линию, проходящую через начало координат с единичным положительным наклоном.Итак, функция называется единичным линейным сигналом.

3. Фазовая функция дискретного сигнала времени x (n) = a ⁿ, где a = r.e ^jθ равно?
a) tan (nθ)
b) nθ
c) tan ^-1 (nθ)
d) ни один из упомянутых
Просмотреть ответ

Ответ: b
Объяснение: дано x (n) = a ⁿ = (re ^jθ) ⁿ = r ⁿ .e ^jnθ
=> x (n) = r ⁿ. (cosnθ + jsinnθ)
Фазовая функция — tan ^-1 (cosnθ / sinnθ) = tan ^-1 (tan nθ) = nθ.2 \) известен как __________
a) Энергетический сигнал
b) Энергетический сигнал
c) Сигнал выполненной работы
d) Ни один из упомянутых
Просмотр ответа

Ответ: a
Объяснение: Мы использовали квадраты величин x (n), так что наше определение применимо как к комплексным, так и к действительным сигналам. Если энергия сигнала конечна, т. Е. 0

5. x (n) * δ (n-k) =?
a) x (n)
b) x (k)
c) x (k) * δ (nk)
d) x (k) * δ (k)
Просмотреть ответ

Ответ: c
Пояснение: данный сигнал определяется только тогда, когда n = k по определению дельта-функции.Итак, x (n) * δ (n-k) = x (k) * δ (n-k).

6. Действительный сигнал x (n) называется антисимметричным, если ___________
a) x (n) = x (-n)
b) x (n) = — x (-n)
c) x (n) = — x (n)
d) ни один из упомянутых
Посмотреть ответ

Ответ: b
Пояснение: Согласно определению антисимметричного сигнала, сигнал x (n) должен быть симметричным относительно начала координат. Итак, чтобы сигнал x (n) был симметричным, он должен удовлетворять условию x (n) = — x (-n).

7. Нечетная часть сигнала x (t) равна?
a) x (t) + x (-t)
b) x (t) -x (-t)
c) (1/2) * (x (t) + x (-t))
d) (1/2) * (x (t) -x (-t))
Посмотреть ответ

Ответ: d
Пояснение: Пусть x (t) = x _e (t) + x _o (t)
=> x (-t) = x _e (-t) -x _o (-t)
Вычитая два приведенных выше уравнения, мы получаем
x _o (t) = (1/2) * (х (т) -х (-т)).

8. Операция масштабирования времени также известна как ___________
a) Понижающая дискретизация
b) Повышающая дискретизация
c) Выборка
d) Ни один из упомянутых
View Answer

Ответ: a
Объяснение: Если сигнал x ( n) был первоначально получен путем дискретизации сигнала x _a (t), затем x (n) = x _a (нТл). Теперь y (n) = x (2n) (скажем) = x _a (2nT). Следовательно, операция масштабирования по времени эквивалентна изменению частоты дискретизации с 1 / T на 1 / 2T, то есть уменьшению частоты в 2 раза.Таким образом, масштабирование по времени также называется понижающей дискретизацией.

9. Каково условие, при котором сигнал x (n) = Br ⁿ, где r = e ^αT, должен называться убывающим экспоненциальным сигналом?
a) 0 b) 0 c) r> 1
d) r <0
Просмотреть ответ

Ответ: b
Пояснение: Когда значение ‘r’ находится между 0 и 1, то значение x (n) продолжает экспоненциально уменьшаться с увеличением значения ‘n’. Итак, сигнал называется затухающим экспоненциальным сигналом.

10. Функция, заданная уравнением x (n) = 1, для n = 0; x (n) = 0, для n 0 является _____________
a) Шаговая функция
b) Функция линейного изменения
c) Треугольная функция
d) Импульсная функция
Просмотр ответа

Ответ: d
Пояснение: Согласно определению импульсная функция, она определена только при n = 0 и не определена где-либо еще в соответствии с заданным сигналом.

Sanfoundry Global Education & Learning Series — Цифровая обработка сигналов.

Чтобы практиковаться во всех областях цифровой обработки сигналов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .

Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Дискретно-временная серия Фурье

Введение

А действительный, Н -периодический, дискретный сигнал x [n] может быть представлен линейная комбинация сложных экспоненциальных сигналов

как

В эти выражения, , и дискретное время фундаментального частота — это .Это дискретного времени Представление ряда Фурье дает представление о частотном содержании сигналов с дискретным временем и очень удобен для расчетов с линейные, инвариантные во времени системы, поскольку комплексные экспоненты являются собственными функциями систем LTI.

комплексные коэффициенты могут быть вычислены из выражения

называются спектральными коэффициентами сигнала x [n]. График vs k называется спектром звездных величин x [n] , и график зависимости от k называется фазовым спектром x [n] . Эти графики, особенно спектр звездных величин, дают картину частотный состав сигнала. Обратите внимание, что спектральные коэффициенты повторить как k варьируется. Особенно, для любого значения к ,

Первый апплет — входящие сигналы

Первый апплет — вход в Spectra

Это апплет иллюстрирует представление ряда Фурье в дискретном времени для N = 5 .Окна дисплея показывают

два повторы амплитудного и фазового спектров,

в отдельные частотные компоненты (часто называемые фазорами , )

в сумма этих векторных составляющих,

два периоды сигнала x [n] .

Вы может ввести амплитуду и фазовый спектр с помощью мыши, а затем наблюдать частотные составляющие фазора и генерация сигнала из этих частотные составляющие.Или вы можете войти сигнал x [n] с помощью мыши и наблюдать соответствующие частотные спектры и генерацию сигнала от частотных составляющих вектора.

Упражнения

(1) Повторение спектрального коэффициенты, как показано выше, подразумевают, что . Какие еще закономерности или симметрии вы наблюдаете в спектр звездных величин? Можете ли вы математически обосновать свой ответ?

(2) Повторение спектрального коэффициенты означает, что .Какие еще закономерности или симметрии вы наблюдаете в фазовый спектр? Можете ли вы математически обосновать свой ответ?

(3) Используя (1) и (2) , объясните, почему и для каждого (реального) сигнал x [n] .

(4) Предположим, что x [n] равно даже , то есть x [ — n] = x [n] . Что вы можете сделать по поводу спектральных коэффициентов? Ты можешь математически обосновать свой ответ? (Для удобства ввода сигнала это удобно выразить свойство четности как x [n] = x [5 — n] .)

(5) Предположим, что x [n] имеет ровно один ненулевое значение за период. Что вы наблюдаете в спектре звездных величин? Имеет ли значение, где встречается ненулевое значение? Вы можете обосновать свой ответ математически?

(6) Если x [n] имеет ровно одно ненулевое значение за период, что вы наблюдаете насчет фазового спектра? Имеет ли значение, где встречается ненулевое значение?

Второй апплет

Для в этом апплете вы можете ввести значение N от 4 до 32, а затем введите либо сигнал, либо частотный спектр.Только показаны один период сигнала и одно повторение спектров.

Упражнения

(1) Если период N является четным целым числом и x [n + N / 2] = — x [n] , какой образец вы выберете? наблюдать в спектре звездных величин? Можете ли вы математически обосновать свой ответ?

(2) Если N — четное целое число и x [n + N / 2] = x [n] , какую закономерность вы наблюдаете в спектре звездных величин? Можете ли вы математически обосновать свой ответ?

(3) Если N = 20 , какие частоты соответствуют спектральным коэффициентам для k = 0, 9 и 19? Какие из этих частот вы бы назвали высокими, а какие? вы звоните низко?

(4) Если N = 20 , каков сигнал, у которого все спектральные коэффициенты равны нулю? кроме ? Какой сигнал если ?

(5) Если N делится на 4, каковы спектральные коэффициенты соответствующие синусоидальным волнам с периодами N , Н / 2 , Н / 4?

возврат на страницу демонстраций

Top 40 Обработка сигналов дискретного времени Viva Questions

1.Определите дискретный сигнал времени и цифровой сигнал.

Ответ:
Дискретный сигнал времени:
• Это сигнал, дискретный по времени и дискретный по амплитуде, и его значение может быть получено только в моменты времени выборки.
• Это цифровое представление сигнала непрерывного времени, которое может быть получено из сигнала непрерывного времени методом Эйлера.

Цифровой сигнал:
• Это сигнал с дискретной амплитудой и непрерывным во времени, а амплитуда цифрового сигнала равна 1 или 0, т.е.e ВЫКЛ или ВКЛ.
• Это форма сигнала дискретного времени, который может быть получен путем дискретизации, квантования и кодирования сигнала дискретного времени.
2. Перечислите различные методы представления дискретного сигнала времени.
Ответ:

a) Графическое представление
б) Табличное представление
c) Представление последовательности
г) Функциональное представление
3.Определите выборку и наложение.
Ответ:
Преобразование сигнала непрерывного времени в сигнал дискретного времени называется дискретизацией.

Наложение помех — это эффект, при котором разные сигналы становятся неразличимыми.
4. Теорема государственной выборки и ее приложения.
Ответ:
• Теорема выборки может быть определена как преобразование аналогового сигнала в дискретную форму, если частота дискретизации равна удвоенной частоте входного аналогового сигнала.
• В нем говорится, что «непрерывная форма изменяющегося во времени сигнала может быть представлена в дискретной форме сигнала с помощью выборок, а дискретизированный (дискретный) сигнал может быть восстановлен в исходную форму, когда частота сигнала дискретизации Fs имеет большую значение частоты, равное или равное частоте входного сигнала Fm.
• Fs ≥ 2Fm

Для поддержания качества звука в музыкальных записях.
• Процесс отбора проб применим при преобразовании аналоговой формы в дискретную.
• Системы распознавания речи и системы распознавания образов.
• Системы модуляции и демодуляции
• В системах обработки данных датчиков
• Возможен отбор образцов радиолокационной и радионавигационной систем.
5. Напишите краткую заметку о ДПФ.
Ответ:

• Дискретное преобразование Фурье вычисляет значения z-преобразования для равномерно расположенных точек вокруг единичной окружности для заданной последовательности.
• Если представляемая последовательность имеет конечную продолжительность i.е., имеет только конечное число ненулевых значений, используется преобразование DFT.
• Пусть x (n) — последовательность конечной продолжительности. N-точечное ДПФ последовательности x (n) задается следующим образом: где k = 0,1,… ..N-1
6. Перечислите свойства ДПФ.
Ответ:
• Периодичность
• Линейность
• Круговая симметрия последовательности
• Обратное время последовательности
• Комплексно-сопряженное свойство
• Круговая свертка
• Переменное имущество
• Круговая корреляция
7.Как вы классифицируете сигналы дискретного времени?
Ответ:
Причинные и не причинные, периодические и непериодические, четные и нечетные, энергетические и энергетические сигналы.
8.Когда вы можете сказать, что сигнал дискретного времени является периодическим?
Ответ:
Если некоторый набор выборок повторяется через определенный интервал времени, то он называется периодическим.
9. Установите связь ДПФ с Z-преобразованием.
Ответ:
10. Определите БПФ (быстрое преобразование Фурье).
Ответ:
БПФ — это компьютерный алгоритм, используемый в цифровой обработке сигналов (DSP) для изменения, фильтрации и декодирования цифрового звука, видео и изображений.БПФ обычно меняют временную область на частотную.

Аналоговые, дискретные и цифровые сигналы

Виды дискретных сигналов. Аналоговый, дискретный, цифровой сигналы

См. также

Литература

Смотреть что такое «Дискретный сигнал» в других словарях:

См. также

Литература

Смотреть что такое «Дискретный сигнал» в других словарях:

Сигнал

Виды сигналов

Для чего обрабатывается сигнал?

Создание и формирование

Динамический диапазон

Аналоговый сигнал

Цифровой сигнал

Применение цифрового сигнала

Дискретный сигнал

Сравнение цифрового и аналогового сигналов

Аналоговый, дискретный, цифровой сигналы. Информационные сигналы. Аналоговые сигналы. Дискретные сигналы

15.1. Модели дискретных сигналов

Дискретизирующая последовательность.

Модулированные импульсные последовательности.

Спектральная плотность модулированной импульсной последовательности.

Восстановление непрерывного сигнала по модулированной импульсной последовательности.

Определение спектра аналогового сигнала по совокупности отсчетов.

Сигнал

Виды сигналов

Для чего обрабатывается сигнал?

Создание и формирование

Динамический диапазон

Аналоговый сигнал

Цифровой сигнал

Применение цифрового сигнала

Дискретный сигнал

Сравнение цифрового и аналогового сигналов

INFOблог: Непрерывные и дискретные сигналы

2 Цифровые и дискретные сигналы

1.1. Дискретизация сигналов и теорема отсчетов

Рекомендуемые файлы

1.2. Представление дискретных сигналов с помощью функциональных рядов

1.3. Цифровые сигналы

Контрольные вопросы и задачи

Как аналоговый сигнал преобразуется в цифровой

Page

Discrete Time Signal — обзор

250+ TOP MCQ по сигналам дискретного времени и ответам

Что такое непрерывный и дискретный сигнал времени? — Цвета-NewYork.com

Что такое непрерывный и дискретный сигнал времени?

В чем разница между дискретным и цифровым сигналом?

Какое определение означает непрерывный сигнал?

Что такое пример дискретного сигнала?

Возраст непрерывен или дискретен?

Как узнать, являются ли ваши данные дискретными или непрерывными?

Пол — дискретная или непрерывная переменная?

Деньги непрерывны или дискретны?

Является ли группа крови непрерывной или дискретной?

Стоимость — это дискретная или непрерывная переменная?

В чем разница между дискретной и непрерывной переменной?

Почему деньги непрерывны?

Является ли занятость дискретной переменной?

Почтовый индекс непрерывный или дискретный?

Да или нет дискретная переменная?

Процент — это дискретная переменная?

Скорость автомобиля непрерывна или дискретна?

Население дискретно или непрерывно?

Какой набор данных дискретный?

Могут ли данные быть как дискретными, так и непрерывными?

Почему непрерывные данные лучше дискретных?

Являются ли дискретные данные количественными или качественными?

Могут ли качественные данные быть дискретными?

В чем разница между качественными дискретными и непрерывными данными?

Температура тела дискретная или постоянная?

Дискретный и аналоговый ввод / вывод для ПЛК

Дискретный ввод / вывод

Аналоговый ввод / вывод

Использование датчиков

Масштабирование

Разрешение

Шум