Закон Джоуля-Ленца: история возникновения :: SYL.ru
Довольно трудно представить жизнь современного человека без электричества. Оно стало одним из главных и самых ценных атрибутов современного существования. Фактически любой человек, который когда-либо работал с электричеством, знает, что при прохождении по проводам тока у них есть свойство нагреваться. Отчего же это зависит?
Что такое ток
Ток – это упорядоченное движение заряженных частиц, которые называются электронами. И если ток протекает по проводнику, то в нём начинают происходить разные физические процессы, а именно сталкиваются электроны с молекулами.
Молекулы бывают нейтральные или те, которые потеряли свою отрицательно заряженную частицу. В результате столкновений или электроны могут становиться нейтральными молекулами, или при этом выбивается из другой такой же молекулы электрон, образовавший положительно заряженный ион. Во время этих столкновений расходуется кинетическая энергия заряженных частиц. Именно эта энергия и становится теплом.
На тепловой нагрев проводника может влиять и сопротивление. Например, можно взять определённое тело и тащить его по земле. Земля в этом случае — сопротивление. Что же с ним будет? Правильно, между телом и поверхностью будет происходить сила трения, которая, в свою очередь, нагревает тело. Ток в этом случае ведёт себя точно так же.

Зависимость
И, внимая все вышеупомянутое, учёным удалось определить эту зависимость между силой тока, сопротивлением и количеством тепла. Эта зависимость носит название закон Джоуля-Ленца, формула которого известна всем физикам. В 1832—1833 годах русским физиком Эмилием Ленцем было обнаружено, что при тепловом воздействии на металлические проводники их проводимость капитально изменялась. Это фактически усложняло работу учёного и мешало рассчитывать электрические цепи.
Тогда же молодому учёному пришла в голову мысль о том, что, возможно, существует какая-то зависимость между силой тока и температурой проводника. Но как быть? В то время отсутствовали точные электрические приборы, позволяющие измерить силу тока, сопротивление, не было даже источника стабильного ЭДС. Ленца это не остановило, он решил провести опыт.
Опыты русского физика
Суть этого опыта была настолько проста, как и все гениальное, что его может повторить даже школьник. Учёный сконструировал специальный прибор, который служил для измерения количества тепла, выделяемого проводником. Этим прибором оказался обычный сосуд, вовнутрь которого Ленц заливал раствор разбавленного спирта и ставил проводник – платиновую проволоку, на которую подавался электрический ток.
После того как прибор был создан, учёный начал проводить опыты. Он измерял точное количество времени, необходимое для того, чтобы спирт в сосуде был нагрет до 10 оС. На это было потрачено много не только месяцев, но и лет. И в 1843 году, спустя 10 лет, был опубликован закон, суть которого заключалась в том, что нагревание проводника током пропорционально квадрату служащего для нагревания тока.
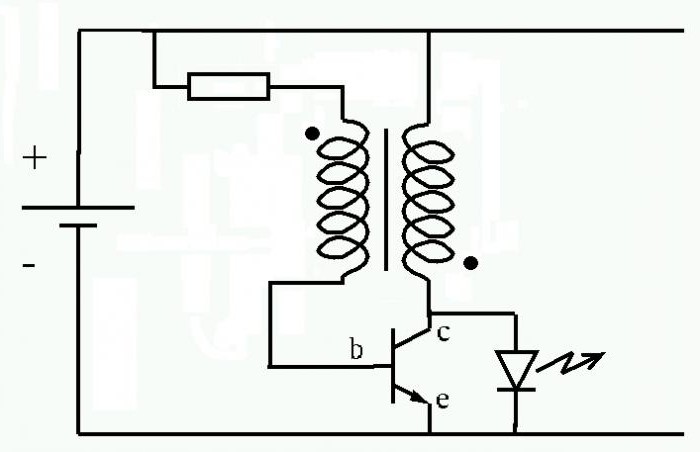
Джоуль и Ленц
Но не тут-то было! Оказывается, несколько лет назад английский физик Джеймс Прескотт Джоуль проводил аналогичные опыты, и уже опубликовал свои наблюдения. Как быть? Ленц не сдался и внимательно изучил работу Джоуля и пришёл к выводу, что, пусть они и проводили одинаковые эксперименты, опыты Ленца были гораздо точнее. В связи с чем научное сообщество добавило к работе Джоуля поправки Ленца и этот закон стал называться как закон Джоуля-Ленца. Математическая формулировка закона выглядит таким образом:
Q = I*U*t, где:
- I – сила тока, А;
- U – напряжение, В;
- t – время, которое ток затрачивает на прохождение проводника, с.
Сам же закон звучит так: количество тепловой энергии, выделяемой в проводнике, через который течёт электрический ток, равно произведению силы тока, напряжения и времени прохождения тока через проводник.

Закон Ома
Однако будет ли всегда верным это утверждение? Можно попробовать вывести его, используя закон Ома. Судя по нему U = I*R, где R — сопротивление, Ом.
Учитывая закон Ома, можно подставить значение в формулу Q = I*U*t = I2*R*t. Из этого можно сделать вывод, что количество теплоты напрямую зависит и от сопротивления проводника. Также для закона Джоуля-Ленца будет справедливо и это утверждение: I = Q = I*U*t.
Все три формулы будут верны, однако Q = I2*R*t будет верной для любых ситуаций. Две другие тоже являются правильными, однако при определённых обстоятельствах.
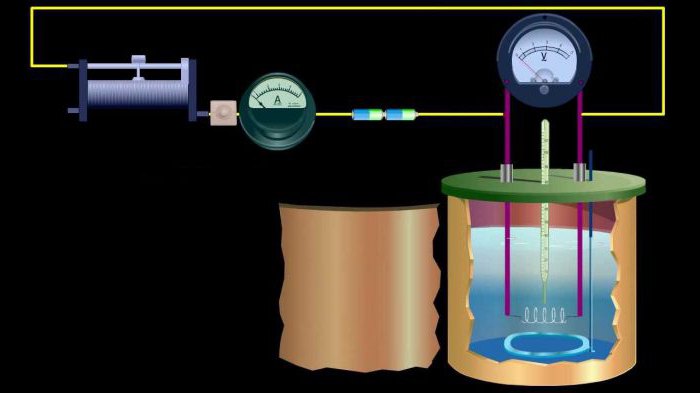
Проводники
Теперь о проводниках. Изначально в своих опытах Джоуль и Ленц использовали платиновые проволоки, как и было упомянуто выше. Во всех похожих экспериментах учёные того времени использовали в основном металлические проводники, так как они были довольно недорогими и стабильными. Не удивительно, ведь до сих пор металлические проводники – основной тип проводников, в связи с чем изначально считалось, что закон Джоуля-Ленца был применим только к ним. Однако чуть позже было обнаружено, что этот закон применим не только к металлическим проводникам. Он верен для любых из них. Сами проводники по классификации можно разделить на:
- Металлические (медь, железо, серебро и т.д.). Главную роль в них играют отрицательно заряженные частицы (электроны), которые протекают по проводнику.
- Жидкие. В них же за движение зарядов отвечают ионы – это атомы, в которых или слишком много, или слишком мало электронов.
- Газообразные. В отличие от своих коллег, в таких проводниках ток определяется движением как ионов, так и электронов.
И несмотря на различия, в любом случае при увеличении силы тока или сопротивления увеличится и количество тепла.

Применение закона другими физиками
Открытие закона Джоуля-Ленца сулило огромные перспективы. Ведь, по сути, этот закон позволил создавать своего рода разные электронагревательные приборы и элементы. Например, чуть позже после открытия закона учёные заметили, что при нагревании определённых элементов они начинают светиться. Они захотели поэкспериментировать с ними, используя разные проводники, и в 1874 году русский инженер Александр Николаевич Лодыгин изобрёл современную лампу накаливания, нить которой была сделана из вольфрама.
Применяется закон Джоуля-Ленца и в электротехнике – например, при создании плавких предохранителей. Плавкий предохранитель – это некий элемент электрический цепи, конструкция которого сделана так, что при протекании по нему тока выше допустимого значения (например, при коротком замыкании) он перегревается, плавится и размыкает силовую цепь. Даже обычный электрический чайник или микроволновая печь, которая есть фактически у каждого, работает согласно этому закону.

Заключение
Довольно трудно определить вклад этих учёных в современную электронику и электротехнику, но одно можно сказать точно – появление закона Джоуля-Ленца перевернуло представление людей об электричестве и дало более конкретные знания о том, что такое электрическое поле в проводнике с током.
Без сомнения, открытый этими великими учеными-физиками закон стал определяющей ступенью во всей науке, именно благодаря этому открытию впоследствии были совершены другие более или менее грандиозные достижения других ученых. Вся наука представляет собой тесное переплетение открытий, каких-то разрешенных и неразрешенных задач. Рассмотренный в этой статье закон определенным образом повлиял на многие исследования и оставил неизгладимый и вполне отчетливый след в науке.
Закон Джоуля — Ленца
В проводах линии передачи электрической энергии, обмоток якорей и полюсов электрических машин, электробытовых приборов и других потребителей происходит преобразование электрической энергии в тепловую.
Т ок I, протекая
по проводнику с сопротивлением R, нагревает
этот
проводник. За время t в
этом проводнике выделяется тепло,
количество которого определяется
количеством электрической энергии,
затраченной в этом проводнике, т. е.
ок I, протекая
по проводнику с сопротивлением R, нагревает
этот
проводник. За время t в
этом проводнике выделяется тепло,
количество которого определяется
количеством электрической энергии,
затраченной в этом проводнике, т. е.
где Q — количество тепла, выделенного в проводнике, Вт с.
Приведенная зависимость является математическим выражением закона Джоуля — Ленца.
Таким образом, закон Джоуля — Ленца
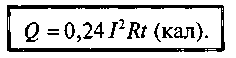 Количество
тепла Q измеряется
иногда внесистемной единицей
— калорией (количество тепла, необходимое
для нагревания I
г воды на 1 °С). Причем 1 кал = 4,187 Дж,
следовательно, Вт-с
= 1 Дж = 0,24 кал. Для
определения количества тепла Q в
калориях пользуются выражением:
Количество
тепла Q измеряется
иногда внесистемной единицей
— калорией (количество тепла, необходимое
для нагревания I
г воды на 1 °С). Причем 1 кал = 4,187 Дж,
следовательно, Вт-с
= 1 Дж = 0,24 кал. Для
определения количества тепла Q в
калориях пользуются выражением:
Коэффициент 0,24 называют электротермическим эквивалентом, который устанавливает зависимость между электрической и тепловой энергией.
Например, количество тепла, выделенное в проводнике с сопротивлением R = 24 Ом, по которому проходит ток I= 5 А в течение 2 часов (t=2 часа=2-3600 = 7200 с) составляет:
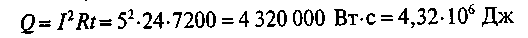
и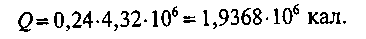 ли
ли
Преобразование электрической энергии в тепловую широко используется в разнообразных электронагревательных приборах. Однако преобразование электрической энергии в тепловую вызывает и непроизводительные расходы энергии в электрических машинах, трансформаторах и других элементах электрической цепи и снижает их КПД.
Понятие о противо — эдс. Понятие о режимах электрической цепи и ее элементов: номинальный, рабочий, холостого хода, короткого замыкания.
Если мы возьмем проводящий контур, или катушку (соленоид) и пропустим по нему ток I, то в контуре (соленоиде) возникнет магнитное поле. В свою очередь это поле «породит» магнитный поток, проходящий через этот контур (соленоид), причём этот поток будет увеличиваться от нуля до некоторой величины (очевидно, т.к. мгновенно он возникнуть не может). Раз поток изменяется (увеличивается), то в контуре возникнет ЭДС индукции. Притом так, чтобы препятствовать пропускаемому току, по
Из этих размышлений следуют две вещи.
Первое: ток, протекающий в контуре, создает магнитный поток, проходящий через этот контур.
Второе: возникающая ЭДС имеет полярность, противоположная порождающему её току. Такую ЭДС называют противо-ЭДС, или ЭДС самоиндукции.
Правило Ленца — правило для определения направления индукционного тока: индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток.
В обобщенной формулировке правило Ленца гласит, что возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которое вызвало этот ток.
Режимы работы электрических цепей
В электрической цепи различают активные и пассивные элементы (участки). Активными считаются элементы, в которых (Преобразование энергии сопровождается возникновением ЭДС ^(аккумуляторы, генераторы). Пассивными считаются элементы, :й которых ЭДС не возникает.
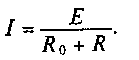 Параметры,
характеризующие работу электрической
цепи (рис.2.5)
при различных режимах, определяются
следующими выражениями.
Ток в замкнутой цепи
Параметры,
характеризующие работу электрической
цепи (рис.2.5)
при различных режимах, определяются
следующими выражениями.
Ток в замкнутой цепи
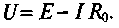 Напряжение
на клеммах источника
Напряжение
на клеммах источника
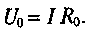
Падение напряжения на сопротивлении источника
П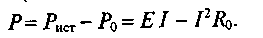 олезная
мощность (мощность потребителя)
олезная
мощность (мощность потребителя)
Исследуем изменение этих величин при изменении сопротивления R от бесконечности (режим холостого хода) до нуля (режим короткого замыкания).
1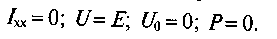 . В
режиме холостого хода (ключ К разомкнут) R = °°,
. В
режиме холостого хода (ключ К разомкнут) R = °°,
В режиме короткого замыкания R = 0,
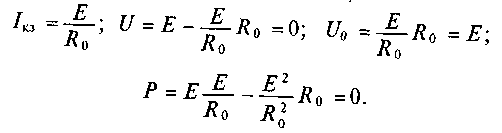
Таким образом, полезная мощность Р при холостом ходе и коротком замыкании равна нулю. Следовательно, при каком-то значении сопротивления R полезная мощность Р имеет максимальную величину.
Д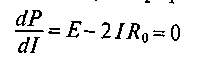 ля
определения этого значения определим
первую производную
полезной мощности по току и приравняем
ее к нулю, т. е.
ля
определения этого значения определим
первую производную
полезной мощности по току и приравняем
ее к нулю, т. е.
и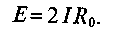 ли
ли
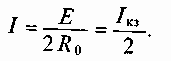
Следовательно, максимальная мощность будет при токе
М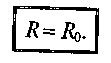 аксимальная
полезная мощность выделяется при
аксимальная
полезная мощность выделяется при
Полезная мощность максимальна, когда сопротивление потребителя R станет равным внутреннему сопротивлению источника R0. Это и есть условие максимальной отдачи мощности источником.
П ри
максимальной отдаче мощности ток
в цепи равен
ри
максимальной отдаче мощности ток
в цепи равен
а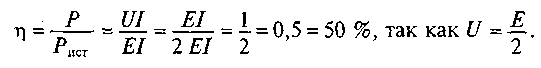 коэффициент полезного действия
коэффициент полезного действия
К 100 % КПД цепи приближается в режиме, близком к холостому ходу.
Максимальной отдачи мощности добиваются в маломощной аппаратуре: звуковоспроизводящей, радио, магнитофонах и др. В мощных энергетических установках добиваются максимального КПД.

Зависимость напряжений и полезной мощности от нагрузки (тока I) показана на рис. 2.7.
Режим короткого замыкания в электрических установках нежелателен, так как он приводит к большому току (больше номинального), т. е. резкому увеличению выделения тепла и выходу из строя аппаратуры. Нормальным (рабочим) называется режим работы цепи, при котором ,ток, напряжение и мощность не превышают номинальных значений — значений, на которые источник (приемники энергии рассчитаны заводом-изготовителем.
Закон Джоуля-Ленца Википедия
Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
Определения[ | ]
В словесной формулировке звучит следующим образом[2]:
Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.
Математически может быть выражен в следующей форме:
- w=j→⋅E→=σE2,{\displaystyle w={\vec {j}}\cdot {\vec {E}}=\sigma E^{2},}
где w{\displaystyle w} — мощность выделения тепла в единице объёма, j→{\displaystyle {\vec {j}}} — плотность электрического тока, E→{\displaystyle {\vec {E}}} — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.
В интегральной форме этот закон имеет вид
- dQ=I2Rdt,{\displaystyle dQ=I^{2}Rdt,}
- Q=∫t1t2
ДЖОУЛЯ-ЛЕНЦА ЗАКОН — это… Что такое ДЖОУЛЯ-ЛЕНЦА ЗАКОН?
- ДЖОУЛЯ-ЛЕНЦА ЗАКОН
(по имени англ. физика Дж. П. Джоуля и рус. физика Э. X. Ленца) — закон, характеризующий тепловое действие электрич. тока. Согласно Д. — Л. э., кол-во теплоты О. выделяющейся в проводнике при прохождении по нему пост. электрич. тока, зависит от силы тока I, сопротивления проводника R и времени прохождения тока t:О = I*Rt.
Большой энциклопедический политехнический словарь. 2004.
- ДЖОУЛЬ
- ДЖОУЛЯ-ТОМСОНА ЭФФЕКТ
Смотреть что такое «ДЖОУЛЯ-ЛЕНЦА ЗАКОН» в других словарях:
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяющееся в проводнике с сопротивлением Л за время t при прохождении через него тока I: Q=aI2Rt. Коэфф. пропорциональности а зависит от выбора ед. измерений: если I измеряется в амперах, R в омах, t в секундах, то… … Физическая энциклопедия
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — ДЖОУЛЯ ЛЕНЦА ЗАКОН, определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. Джоулем и Э.… … Энциклопедический словарь
Джоуля — Ленца закон — определяет количество тепла Q, выделяющегося в проводнике при прохождении через него электрического тока: Q пропорционально сопротивлению R проводника, квадрату силы тока I в цепи и времени прохождения тока t, Q = aI2Rt. Здесь а… … Большая советская энциклопедия
Джоуля-Ленца закон — определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. Х. Ленцем в… … Энциклопедический словарь
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяемой в проводнике при прохождении через него электрич. тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. X. Ленцем в нач. 40 х гг.… … Естествознание. Энциклопедический словарь
Закон Джоуля — Ленца — Закон Джоуля Ленца физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймса Джоуля и Эмилия Ленца. В словесной формулировке звучит следующим образом[1] Мощность тепла … Википедия
ЗАКОН ДЖОУЛЯ-ЛЕНЦА — закон, определяющий тепловое действие электрического тока; согласно этому закону количество теплоты Q, выделяющееся в проводнике при прохождении по нему постоянного электрического тока, равно произведению квадрата силы тока I, сопротивления… … Большая политехническая энциклопедия
Закон Джоуля-Ленца — (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) закон, дающий количественную оценку теплового действия электрического тока. При протекании тока по… … Википедия
Закон Джоуля — Ленца — (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) закон, дающий количественную оценку теплового действия электрического тока. При протекании тока по… … Википедия
закон Джоуля-Ленца — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Joule Lenz s lawJoule s law … Справочник технического переводчика
определение, практическое значение 🚩 закон джоуля ленца формулировка 🚩 Естественные науки
Закон Джоуля-Ленца определяет количество теплоты, выделяющейся в проводнике, обладающим сопротивлением за время t, при прохождении через него электрического тока.
Q = a*I*2R*t, где
Q — колическтво выделяемой теплоты (в Джоулях)
a — коэффициент пропорциональности
I — сила тока ( в Амперах)
R — Сопротивление проводника (в Омах)
t — Время прохождения (в секундах)
Закон Джоуля-Ленца объясняет, что электрический ток — это заряд, который перемещается под действием электрического поля. При этом поле совершает работу, а ток обладает мощностью и выделяется энергия. Когда эта энергия проходит по неподвижному металлическому проводнику, то она становится тепловой, так как направлена на нагревание проводника.
В дифференциальной форме закон Джоуля-Ленца выражается как объемная плотность тепловой мощности тока в проводнике будет равна произведению удельной электрической проводимости на квадрат напряженности электрического поля.
Лампы накаливания были придуманы в 1873 году русским инженером Лодыгиным. В лампах накаливания, как и в электронагревательных приборах, применяется закон Джоуля-Ленца. В них используют нагревательный элемент, который является проводником с высоким сопротивлением. За счет этого элемента можно добиться локализованного выделения тепла на участке. Выделение тепла будет появляться при повышении сопротивления, увеличении длины проводника, выбором определенного сплава.
Одной из областей применения закона Джоуля-Ленца является снижение потерь энергии.
Тепловое действие силы тока ведет к потерям энергии. При передаче электроэнергии, передаваемая мощность линейно зависит от напряжения и силы тока, а сила нагрева зависит от силы тока квадратично, поэтому если повышать напряжение, при этом понижая силу тока перед подачей электроэнергии, то это будет более выгодно. Но повышение напряжения ведет к снижению электробезопасности. Для повышения уровня электробезопасности повышают сопротивление нагрузки соответственно повышению напряжения в сети.
Также закон Джоуля-Ленца влияет на выбор проводов для цепей. При неправильном подборе проводов возможен сильный нагрев проводника, а так же его возгорание. Это происходит когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии. При правильном подборе проводов для электрических цепей стоит следовать нормативным документам.
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — это… Что такое ДЖОУЛЯ — ЛЕНЦА ЗАКОН?
- ДЖОУЛЯ — ЛЕНЦА ЗАКОН
- ДЖОУЛЯ — ЛЕНЦА ЗАКОН ДЖО́УЛЯ — ЛЕ́НЦА ЗАКО́Н, определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. Джоулем и Э. Х. Ленцем (см. ЛЕНЦ Эмилий Христианович) в нач. 40-х гг. 19 в.
Энциклопедический словарь. 2009.
- ДЖОУЛЬ (единица измерения энергии)
- ДЖОУЛЯ — ТОМСОНА ЭФФЕКТ
Смотреть что такое «ДЖОУЛЯ — ЛЕНЦА ЗАКОН» в других словарях:
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяющееся в проводнике с сопротивлением Л за время t при прохождении через него тока I: Q=aI2Rt. Коэфф. пропорциональности а зависит от выбора ед. измерений: если I измеряется в амперах, R в омах, t в секундах, то… … Физическая энциклопедия
ДЖОУЛЯ-ЛЕНЦА ЗАКОН — (по имени англ. физика Дж. П. Джоуля и рус. физика Э. X. Ленца) закон, характеризующий тепловое действие электрич. тока. Согласно Д. Л. э., кол во теплоты О. выделяющейся в проводнике при прохождении по нему пост. электрич. тока, зависит от силы… … Большой энциклопедический политехнический словарь
Джоуля — Ленца закон — определяет количество тепла Q, выделяющегося в проводнике при прохождении через него электрического тока: Q пропорционально сопротивлению R проводника, квадрату силы тока I в цепи и времени прохождения тока t, Q = aI2Rt. Здесь а… … Большая советская энциклопедия
Джоуля-Ленца закон — определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. Х. Ленцем в… … Энциклопедический словарь
ДЖОУЛЯ — ЛЕНЦА ЗАКОН — определяет кол во теплоты Q, выделяемой в проводнике при прохождении через него электрич. тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. П. Джоулем и Э. X. Ленцем в нач. 40 х гг.… … Естествознание. Энциклопедический словарь
Закон Джоуля — Ленца — Закон Джоуля Ленца физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймса Джоуля и Эмилия Ленца. В словесной формулировке звучит следующим образом[1] Мощность тепла … Википедия
ЗАКОН ДЖОУЛЯ-ЛЕНЦА — закон, определяющий тепловое действие электрического тока; согласно этому закону количество теплоты Q, выделяющееся в проводнике при прохождении по нему постоянного электрического тока, равно произведению квадрата силы тока I, сопротивления… … Большая политехническая энциклопедия
ДЖОУЛЯ — ЛЕНЦА ЗАКОН определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока: Q прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Открыт Дж. Джоулем и Э. Х.… … Большой Энциклопедический словарь
Закон Джоуля-Ленца
Закон Джоуля — Ленца — (по имени английского физика Джеймса Джоуля и русского физика Эмилия Ленца, одновременно, но независимо друг от друга открывших его в 1840г) закон, дающий количественную оценку теплового действия электрического тока. При протекании тока по… … Википедия
Классическая теория электропроводности и ее затруднения. Объяснение законов Ома, Джоуля-Ленца, Видемана-Франца на основе классической электронной теории.
В металлах содержится большое количество электронов. Совокупность всех электронов образует «электронный газ». К «электронному газу» полностью применимы законы идеального газа.
Носителями тока в металлах являются свободные электроны, т. е. Электроны, слабо связанные с ионами кристаллической решетки металлов. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде и разработанной в последствии нидерландским физиком Х. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории. Поэтому: электрический ток в металлах – направленное движение электронов, а не ионов (опыт Рикке: при длительном пропускании тока не наблюдалось взаимного проникновения вещества).
Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. Итак:
Электроны в металлах совершают хаотичное (тепловое) движение со скоростью
 ,
любой электрон имеет энергию:
,
любой электрон имеет энергию:
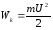 ;
;
Эта
энергия равна 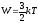 ,T
– температура электронного газа.
,T
– температура электронного газа.
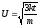 —
скорость хаотичного движения электрона.
—
скорость хаотичного движения электрона.
В
обычных условиях — порядок скорости
приблизительно 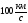
 .
. 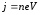 ;
;
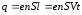 ;
;
 ;
;
 – концентрация
электронов (
– концентрация
электронов (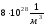
 – плотность тока
(
– плотность тока
(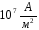 ).
).
 .
.
Казалось
бы, что полученные результаты противоречат
факту практически мгновенной передачи
электрических сигналов на большие
расстояния. Дело в том, что замыкание
цепи влечет за собой распространение
электрического поля со скоростью света.
И через время 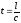 (
(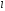 -длина
цепи) вдоль цепи установится стационарное
электрическое поле, и в ней начнется
упорядоченное движение электронов.
Поэтому электрический ток в цепи
возникает практически одновременно с
её замыканием.
-длина
цепи) вдоль цепи установится стационарное
электрическое поле, и в ней начнется
упорядоченное движение электронов.
Поэтому электрический ток в цепи
возникает практически одновременно с
её замыканием.
Объяснение закона Ома с точки зрения классической электронной теории.
Пусть
в металлическом проводнике существует
электрическое поле с напряженностью 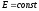 .
Тогда движение электронов в проводнике
носит характер свободных пробегов от
столкновения к столкновению с ионами.
Сила, которая действует со стороны
источника, – вызывает ускорение электрона
на пути
.
Тогда движение электронов в проводнике
носит характер свободных пробегов от
столкновения к столкновению с ионами.
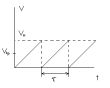
Сила, которая действует со стороны
источника, – вызывает ускорение электрона
на пути за время
за время .
.
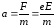 ;
;
;
где  -максимальная
скорость электрона на участке свободного
пробега.
-максимальная
скорость электрона на участке свободного
пробега.
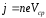 ;
;
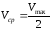 ;
;
 ;
;
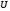 —
тепловая скорость электронов, а
—
тепловая скорость электронов, а 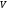 —
средняя скорость упорядоченного движения
электронов.
—
средняя скорость упорядоченного движения
электронов.
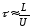 ;
;
Плотность тока в металлическом проводнике:
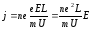 ;
;
Коэффициент
пропорциональности между  и
и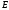 — ни что иное как проводимость,
следовательно:
— ни что иное как проводимость,
следовательно:
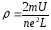 ;
;
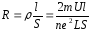 ;
;
Объяснение закона Джоуля-Ленца с точки зрения классической электронной теории
Температура определяется энергией ионов металла. Электроны при столкновении с ионами отдают энергию, следовательно, температура повышается. К концу свободного пробега электрон под действием поля приобретает дополнительную энергию:
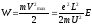
Один электрон в одну секунду может отдать энергию:
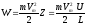 ;
;
где Z-число столкновений.
В объеме за время t выделяется теплота:
 ;
;
приводим к виду:
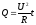 ,
где
,
где 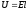 .
.
Следовательно, закон Джоуля-Ленца был доказан классической теорией.
Закон Видемана-Франца
Металл обладает как электропроводностью, а так как электроны – газ, то и теплопроводностью. Электроны, перемещаясь в металле переносят не только электрический заряд, но и присущую им электрическую энергию.
-теплопроводность электронного газа.
 – плотность
электронного газа
– плотность
электронного газа
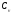 – удельная
теплопроводность при V=const
– удельная
теплопроводность при V=const
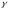 —
электропроводность.
—
электропроводность.
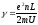 ;
;
 ;
;
— закон, полученный из опыта.
Недостатки теории:
Из опыта

 ,
из теории
,
из теории 

 ;
;Квантовая теория сообщает, что электронный газ вообще не имеет теплоемкости.
Потенциальность электростатического поля. Скалярный потенциал. Неоднозначность скалярного потенциала и его нормировка. Потенциал точечного заряда, системы точечных зарядов и непрерывного распределения зарядов.
Потенциал электростатического поля.Способы описания электростатического поля:
Векторный (
 )
– силовая характеристика,
)
– силовая характеристика,Скалярный (φ) – энергетическая характеристика.
φ (x,y,z) — потенциал электростатического поля, скалярная характеристика электростатического поля полностью (!) описывающая электростатическое поле
φ
(x,y,z) <=> 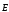 (x,y,z) (т.е зная φ можно восстановить
(x,y,z) (т.е зная φ можно восстановить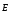 и наоборот). В СИ единица измерения φ =
[В]
и наоборот). В СИ единица измерения φ =
[В]
Определение Разностью потенциалов в двух точках (1) и (2) φ-φ2 — называется отношение A12 (работы по перемещению пробного единичного положительного заряда из (1) в (2), которую совершает поле) к заряду qпр.

Расчетная формула
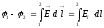
интеграл может быть взят по любому пути соединяющему (1) и (2)
если (1) и (2) лежат на силовой линии, то в качестве линии, соединяющей (1) и (2) нужно взять силовую.
Понятие потенциала можно ввести для любого потенциального векторного поля. (потенциал гравит. силы, потенциал скорости и т.д.)
Потенциал Часто в качестве точки (2) выбирают точку, потенциал которой по определению = 0.
φ2 = 0
В
теории – такая точка бесконечно
удаленная: 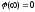 .
.
Замечание Это можно сделать лишь тогда, если заряды располагаются в ограниченной области пространства и их нет на бесконечности.
На
практике 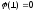 — потенциал земли = 0.
— потенциал земли = 0.
Потенциал электростатического поля в т. B(x,y,z) назыв.
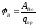 потенциал
какой-то точки, когда в
= 0.
потенциал
какой-то точки, когда в
= 0.
Расчетная
формула: 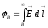
Потенциал поля точечного заряда
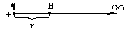
Рис. 18
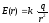
Путь из точки B в ∞ может быть любым, т.к. поле потенциально. Наиболее удобно выбрать L вдоль радиуса вектора, проведенного из точечного заряда
=> dl = dr;
El = Er =
E(r); =>  =>
=>
 формула имеет
смысл для r ≠ 0, т.к. r →∞ .
формула имеет
смысл для r ≠ 0, т.к. r →∞ .
Т.к. поле точечного заряда фундаментально => для нахождения потенциала поля системы зарядов нужно применить принцип суперпозиций:
потенциал поля системы точечных зарядов равен сумме потенциалов, издаваемых в рассматриваемой точке каждым из зарядов.
а) потенциал поля системы точечных зарядов:
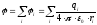
б) потенциал поля непрерывного распределения зарядов:
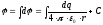
где dq = ρ∙dV — при объемном распределении заряда,
dq = σ∙dS — при поверхностном
dq = λ∙dl — при линейном.
Применение формулы поля точечного заряда и принципа суперпозиций составляет основу метода непосредственного интегрирования и позволяет рассчитать потенциал поля новой системы зарядов. Графически потенциал изображается в виде эквипотенциальных поверхностей и линий на которой он принимает постоянное значение = const.
Примеры расчета потенциала
Равномерно заряженная бесконечная нить. (Рис. 19)
Дано: ;
;
_____________
(r1)-(r2) -?
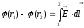
Т.к.
поле нити имеет осевую симметрию и 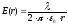 =>
в качестве линииL, соединяющей 1 и 2 берем отрезок силовой
линии, соединяющей точки 1 и 2. =>
=>
в качестве линииL, соединяющей 1 и 2 берем отрезок силовой
линии, соединяющей точки 1 и 2. => 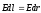 =>
=>
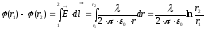




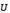 ,
любой электрон имеет энергию:
,
любой электрон имеет энергию: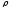
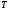 ,
из теории
,
из теории 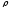
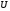
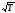 ;
;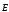 )
– силовая характеристика,
)
– силовая характеристика,