1.5.3 Вынужденные колебания. Резонанс. Резонансная кривая
Видеоурок: Резонанс — Физика в опытах и экспериментах
Лекция: Вынужденные колебания. Резонанс. Резонансная кривая
 Вынужденные колебания
Вынужденные колебанияВсе мы замечали, что однажды раскаченные качели, возвращаются в состояние равновесия. Все это происходит из-за того, что во время колебаний часть энергии идет на преодоление сил тяжести, трения и других. Для поддержания необходимой амплитуды следует пополнять расходуемую энергию.
Колебания, которые совершаются под действием периодических внешних и внутренних сил рассматриваемой системы, называются вынужденными.
К вынужденным колебаниям можно отнести дрожь стекла по причине проезжающего рядом тяжелого транспорта, колебания ушных перепонок под действием воздуха и звуков.
В тот момент, когда внешние и внутренние силы приводят системы к одинаковым частотам колебаний, происходит резонанс.
 Резонанс и резонансная кривая
Резонанс и резонансная криваяПример из истории:
В 1750 году во Франции полководец вел свое войско на сражение. Во время своего движения все воины шли в одну ногу. Оказавшись на мосту, они своей внешней силой привели его колебания к резонансной частоте, в результате чего мост обрушился. Таким образом, сражение было проиграно, даже не начавшись. Таких случаев в истории существует огромное множество.
По причине резонанса в начале эры развития авиационного транспорта произошло огромное количество аварий, во время которых самолеты из-за высоких частот разрушались на части прямо в воздухе.

В то время, когда частота внутренних и внешних сил колебаний совпадают, амплитуда начинает стремиться к бесконечности.
2.4. Резонансная кривая последовательного контура
Когда частота питающего генератора не равна собственной частоте контура, контур называют расстроенным.
Разность
между частотой генератора и собственной
частотой контура принято называть абсолютной расстройкой и обозначать  :
:
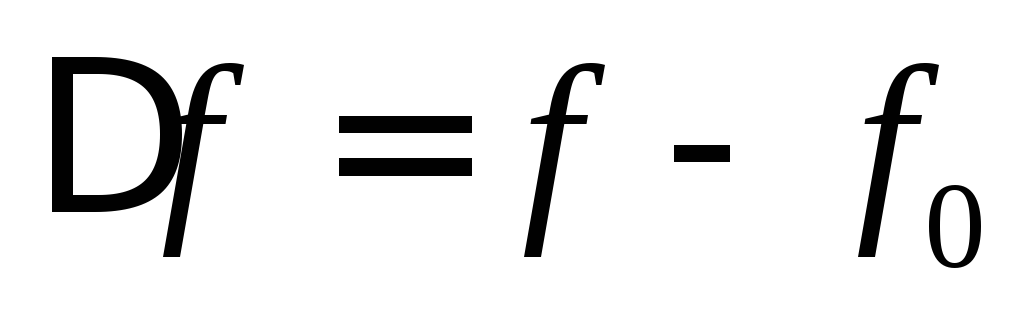 .
.
Абсолютная расстройка выражается в единицах частоты. При резонансе частота генератора и собственная частота контура равны и абсолютная расстройка равна нулю.
Есличастота генератора
 контура, расстройка
считается положительной (
контура, расстройка
считается положительной ( ).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
(
).
При частоте генератора меньше собственной
частоты контура расстройка отрицательна
( ).
). Отношение
абсолютной расстройки к собственной
частоте контура  называютотносительной расстройкой.
называютотносительной расстройкой.
При резонансе относительная расстройка равна нулю:
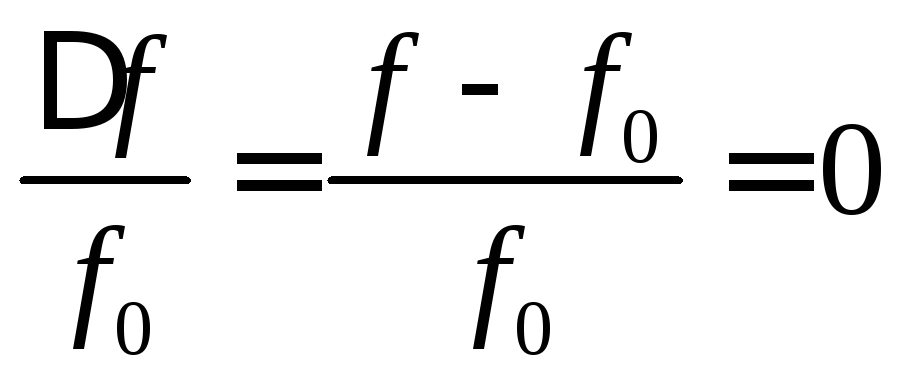 .
.
Ток в контуре тем меньше, чем больше расстройка контура.
Иногда
оказывается более удобной резонансная
кривая, построенная в относительном
масштабе. Для получения такой кривой
вдоль вертикальной оси откладывается
отношение тока в контурепри
данной расстройке к току при резонансе  ,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
,
а вдоль горизонтальной оси –
абсолютная или относительная расстройка
(на рис.9 – абсолютная
расстройка).Выведем
уравнение резонансной кривой.
Ток в
контуре при любой частоте 
 .
.
Ток при резонансе
 .
.
Отсюда получаем:
 .
.
Числитель
и знаменатель полученной дроби сначала
разделим на  ,
где
,
где
 ,
и преобразуем выражение
,
и преобразуем выражение  .
.
Получаем следующее выражение:
 .
.
Учитывая,
что 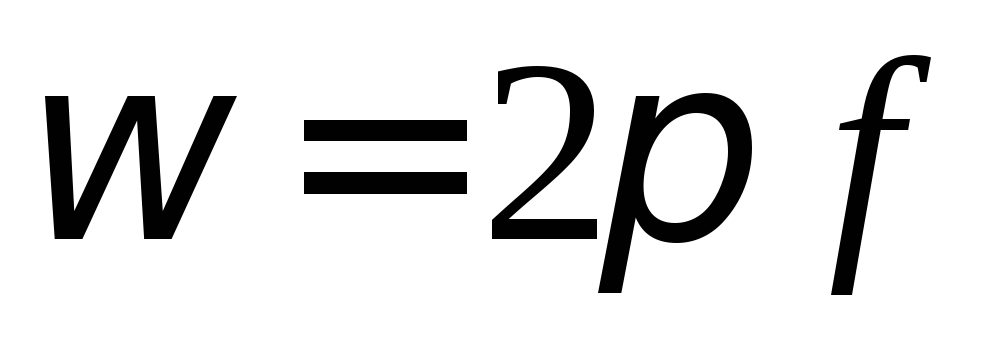 ,
получим
,
получим

Преобразуем
выражение  :
:
 .
.
Считая
приближенно, что 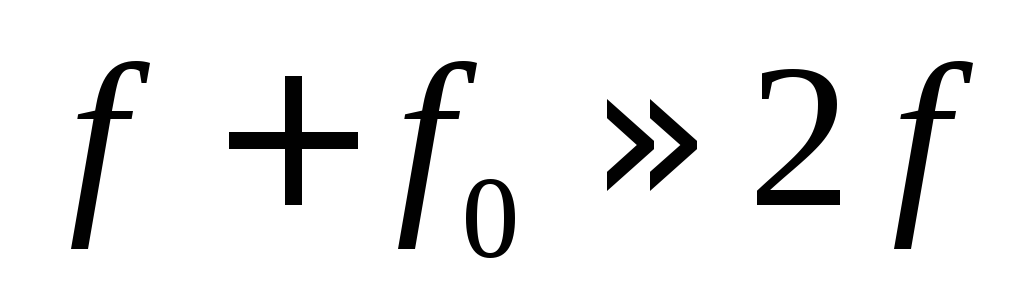 и обозначив
и обозначив (абсолютная
расстройка), получим
(абсолютная
расстройка), получим
 .
.
 .
.
Относительная расстройка
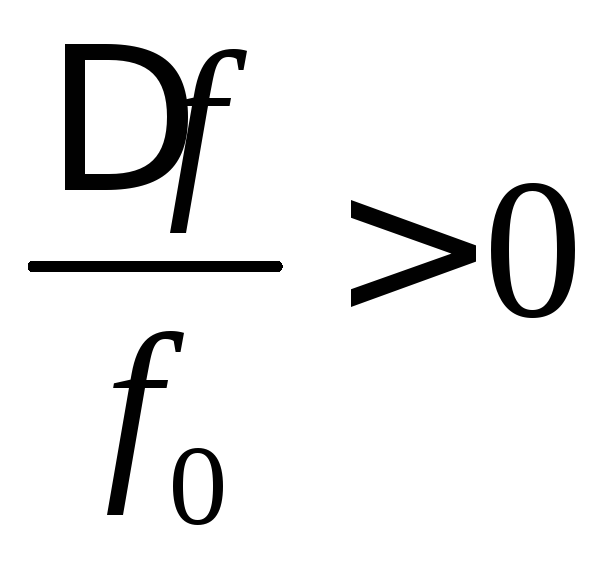 если
если 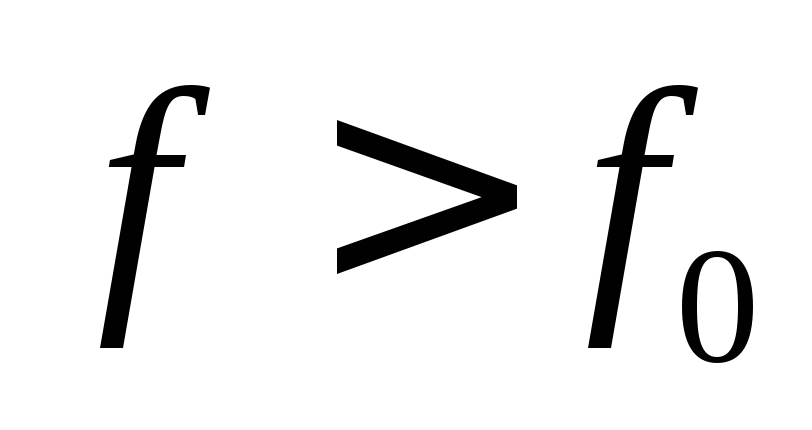 ,
,
 ,если
,если  .
.
Введем обозначения:

 .
.Тогда для уравнения резонансной кривой в относительном масштабе получим выражение

Уравнению такого вида соответствует кривая, изображенная на рис.9.

Рис.9. Резонансная кривая последовательного контура
Построение резонансных кривых в относительном масштабе дает возможность легко и удобно сравнивать между собою различные по качеству контуры, а также производить расчеты элементов радиотехнических схем
2.5. Полоса пропускания последовательного контура
Сопротивление последовательного контура вблизи резонанса резко изменяется в зависимости от частоты генератора; в соответствии с этим резко изменяется и ток в контуре. Контур по-разному ведет себя при различных значениях частоты питающего тока. Эти свойства могут быть оценены формой резонансной кривой или добротностью контура. Однако во многих случаях для такой оценки оказывается более удобным пользоваться понятием полосы пропускания контура, так как сигнал каждого передатчика представляет собой спектр частот и занимает некоторую полосу частот. Для неискаженной передачи и приема сигналов необходимо, чтобы все частоты, входящие в состав сигнала, в одинаковой степени излучались передающим устройством, а будучи приняты приемной антенной, в одинаковой степени усиливались приемником. Необходимо, чтобы колебательные контуры пропускали полосу частот, соответствующую спектру сигнала. Поэтому вопрос о полосе частот, пропускаемых контуром, имеет важное значение в радиотехнических устройствах.
Полосой
пропускания контура называют полосу частот, в пределах
которой ток в контуре уменьшается не
более чем в 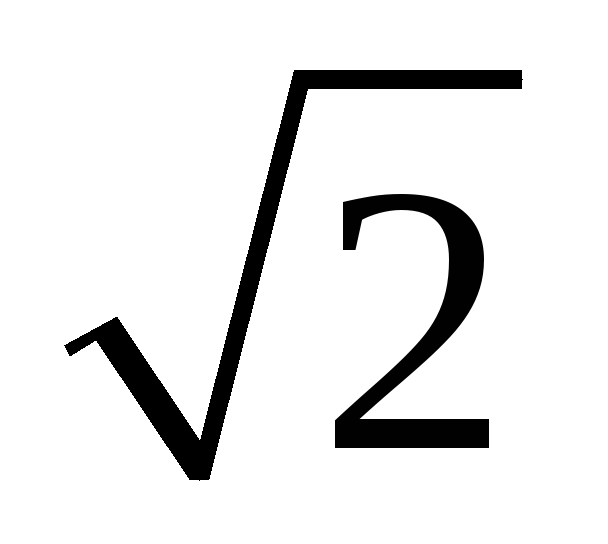 раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна
раз по сравнению с током при резонансе.
Иначе, полосой пропускания контура
называют полосу частот, в пределах
которой контурный ток составляет 0,7 или
больше от тока при резонансе. На
рис.10 изображена резонансная
кривая последовательного контура.
Полоса пропускания этого контура равна 
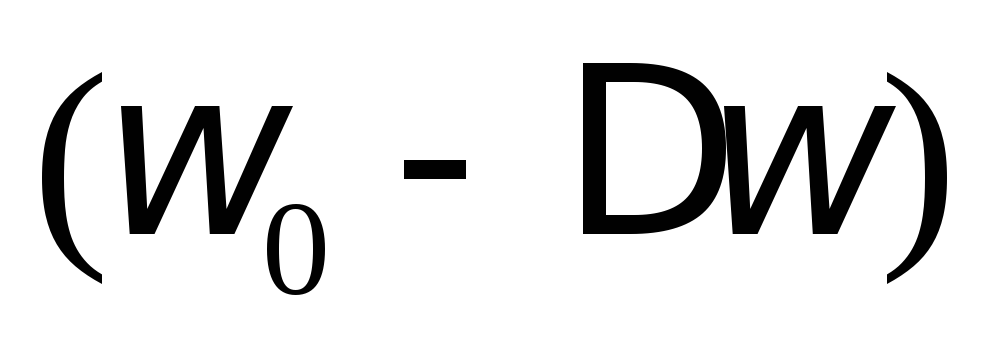 до
до  контур пропускает, а частоты ниже
контур пропускает, а частоты ниже и выше
и выше не пропускает.
не пропускает.Ширина полосы пропускания прямо пропорциональна резонансной частоте и обратно пропорциональна добротности контура, или прямо пропорциональна затуханию при неизменной резонансной частоте.
Полоса пропускания контура зависит от его добротности: чем ниже добротность, тем «тупее» резонансная кривая и тем шире полоса пропускания контура.

Рис.10. Полоса пропускания последовательного контура
Зависимость модуля
тока от частоты, выражаемая обычно в
виде отношения  ,
носит названиерезонансной
характеристики последовательного
контура:
,
носит названиерезонансной
характеристики последовательного
контура:
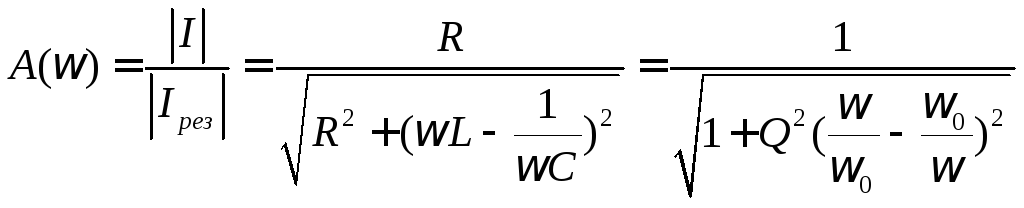 .
.
На границах полосы
пропускания контура  ,
откуда следует простая формула для
практического определения добротности:
,
откуда следует простая формула для
практического определения добротности:  .
.
2.10. Добротность и резонансная кривая поглощения осциллятора
Как видно из формулы (21), добротность определяется собственной частотой 0 и активной составляющей импеданса (сопротивлением среды). Получим еще одно выражение для добротности осциллятора, непосредственно связанное с зависимостью поглощения энергии осциллятором от частоты вынуждающей силы.
Предварительно определим энергию, передаваемую вынуждающей силой осциллятору, за единицу времени. За период осциллятор получает энергию, определяемую выражением (17*) (см § 2.8). За единицу времени энергия, передаваемая осциллятору (мощность P, передаваемая осциллятору), равна:
P =  =
=  =
= 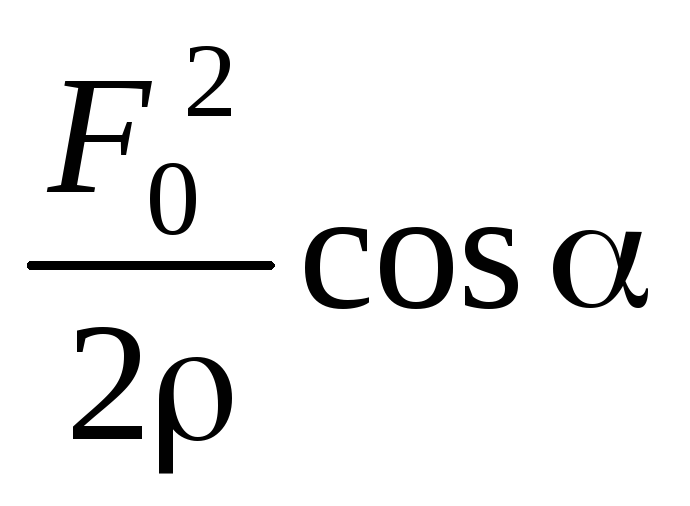 =
=  , (23)
, (23)
т.к.
=  и cos
=
и cos
=  =
= 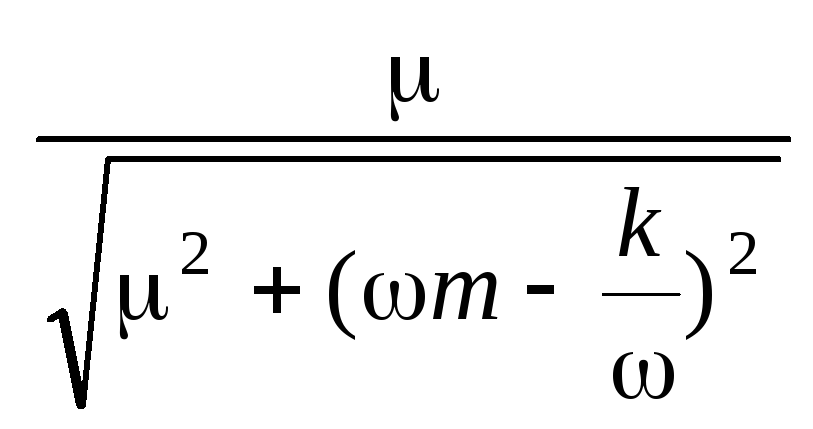 (см. рис. 14).
Импеданс минимален при условии
(см. рис. 14).
Импеданс минимален при условии  (т.е. при
(т.е. при =0).При этом
условии
=
и
осциллятору
передается максимальная мощность. При
= 0 наблюдается
резонансное поглощение энергии. Резонансная
мощность поглощения имеет вид:
=0).При этом
условии
=
и
осциллятору
передается максимальная мощность. При
= 0 наблюдается
резонансное поглощение энергии. Резонансная
мощность поглощения имеет вид:
 Pр =
Pр = 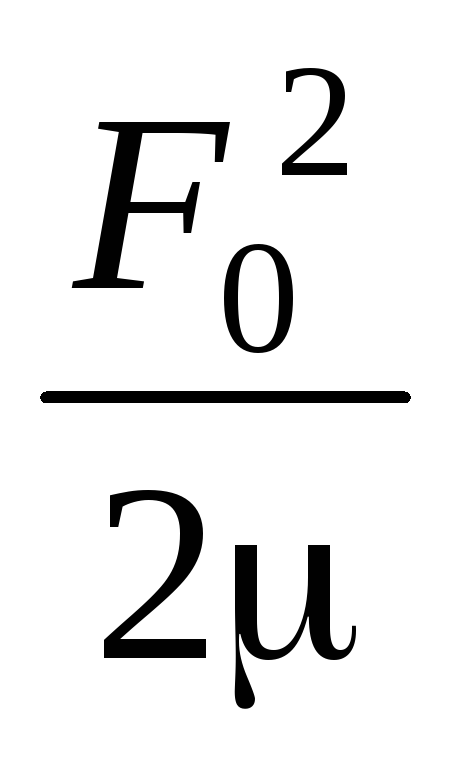 .
(24)
.
(24)
Напомним, при условии = 0 наблюдаем резонанс скорости (см § 2.7, рис. 19). Таким образом, при максимальной скорости осциллятора (при резонансе скорости) наблюдается максимальное поглощение энергии (резонанс мощности поглощения), передаваемое осциллятору внешней вынуждающей силой. На рисунке 22 приведена кривая зависимости мощности поглощения от частоты вынуждающей силы (23). На рисунке частоты 1 и 2 соответствуют мощности поглощения, которая равна половине резонансной мощности.
Покажем, что
добротность осциллятора можно выразить
отношением: Q =  .
Попутно заметим, разность частот (2 1)
определяет остроту
резонансной кривой (или, как говорят, остроту
резонансного максимума).
.
Попутно заметим, разность частот (2 1)
определяет остроту
резонансной кривой (или, как говорят, остроту
резонансного максимума).
Частоты 1 и 2 находим из условия  =
=  =
= 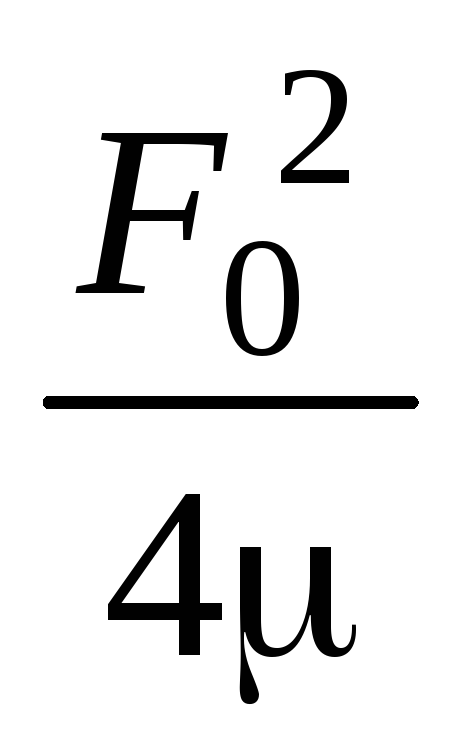 .
Отсюда следует, что при частотах 1 и 2 имеем равенство:
2 = 22.
Из равенства
.
Отсюда следует, что при частотах 1 и 2 имеем равенство:
2 = 22.
Из равенства 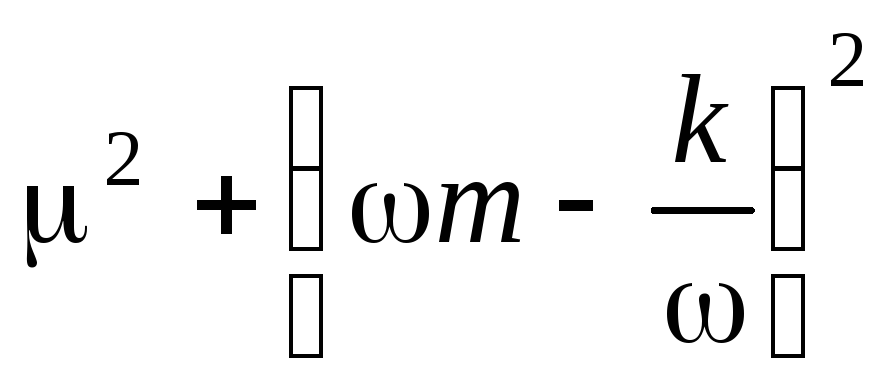 =
22 получим:
=
22 получим:
 =
.
=
.
При 2 >1:  =
+
и
=
+
и 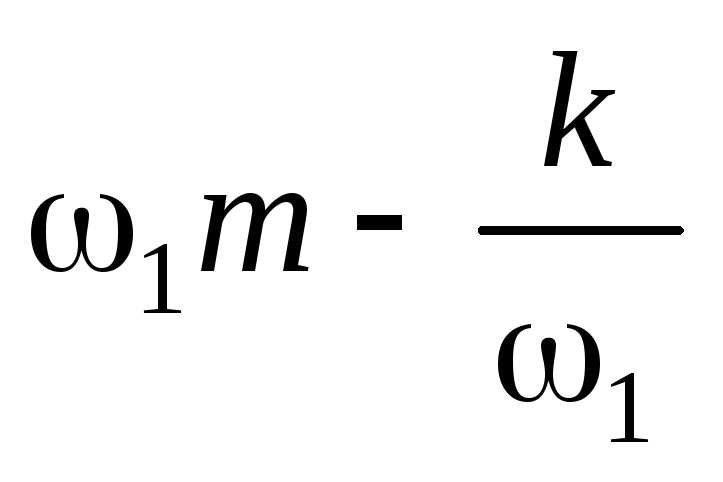 =
.
=
.
Исключив из этих уравнений жесткость k, получим:
2 1 = .
Подставим полученное значение разности частот в формулу добротности (21):
Q = =
= =
= .
(25)
.
(25)
Разность частот (2 1) называют частотной шириной поглощения
Итак, по остроте резонансной кривой поглощения можно судить о добротности колебательной системы: чем острее резонанс, т.е. чем меньше частотная ширина поглощения (2 1), тем добротнее осциллятор. Например, добротность кварцевого резонатора, используемого в прецизионных генераторах радиочастотного диапазона, достигает значений ~106. У таких резонаторов при 0 = 1МГц ширина частоты поглощения ~ 1Гц.
При частотах вынуждающей силы 1 и 2 осциллятор поглощает в единицу времени энергию, равную половине резонансной мощности поглощения при 0. Определим значения амплитуды скорости на частотах 1 и 2 и сравним их с резонансной амплитудой скоростью Vp..
Амплитуда скорости
определяется выражением: V = =
X (см. уравнение14).
Резонансная скорость (15): Vр. =
=
X (см. уравнение14).
Резонансная скорость (15): Vр. =  =
=  .
Так как
.
Так как 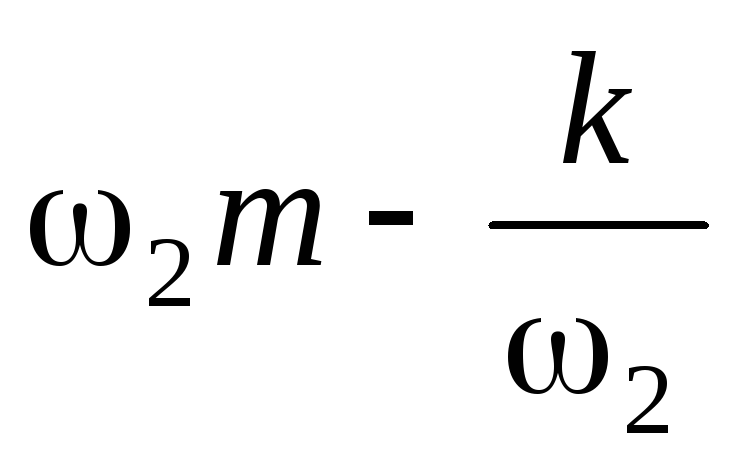 =
+
и
=
+
и 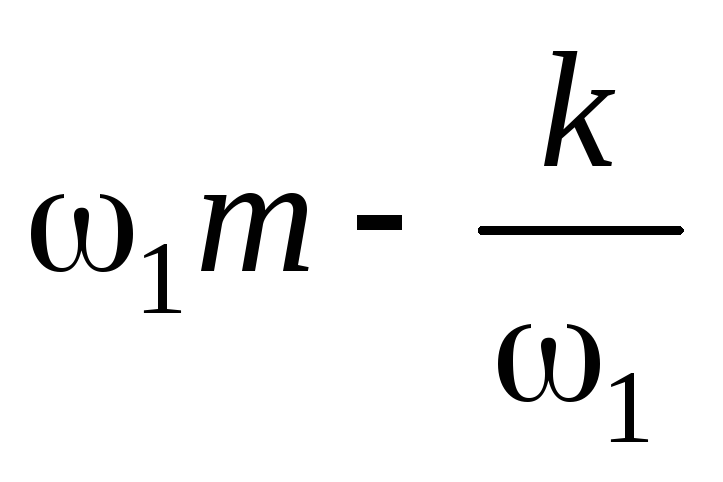 =
то при частотах 1 и 2 импеданс имеет вид:
=
=
то при частотах 1 и 2 импеданс имеет вид:
=  =
=
 .
.
Отсюда следует, что при частотах 1 и 2 амплитудное значение скорости:
V = =
=  =
=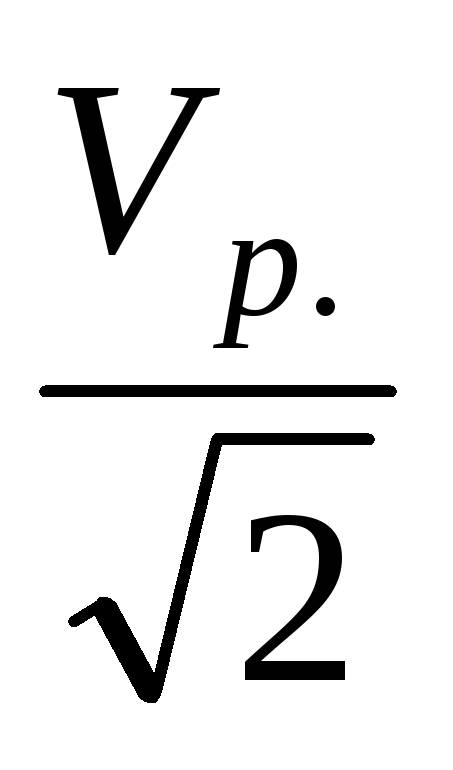 .
(26)
.
(26)
В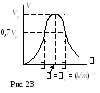 еличина
еличина ≈
0,707. Интервал(2 1)
на уровне 0,7
называют еще частотной
шириной пропускания колебательной
системы по скорости (рис. 23).
Именно в интервале этих частот вынуждающей
силы колебательная система отвечает
на внешнее воздействие заметной
скоростью. Если частота вынуждающей
силы F окажется вдали от интервала (2 1),
то колебательная
система практически не реагирует на
такое внешнее воздействие.
≈
0,707. Интервал(2 1)
на уровне 0,7
называют еще частотной
шириной пропускания колебательной
системы по скорости (рис. 23).
Именно в интервале этих частот вынуждающей
силы колебательная система отвечает
на внешнее воздействие заметной
скоростью. Если частота вынуждающей
силы F окажется вдали от интервала (2 1),
то колебательная
система практически не реагирует на
такое внешнее воздействие.
Словарь — основные понятия теории колебаний (к главе 2)
Понятие | Содержание понятия |
Состояние физической системы | это некоторая физическая ситуация, реализованная в физической системе. Состояние системы определяется физическими величинами, характеризующими систему. Состояние известно, если известны все эти физические величины. Изменение состояния выражается в изменении динамических переменных системы со временем. |
Классификация физических величин в контексте понятия состояния физической системы | 1. Параметры физической системы. Параметры характеризуют собственные свойства системы и считаются неизменными при изменении состояния системы. Примером параметров являются масса m, заряд q, разного рода коэффициенты (например, коэффициент трения ). 2. Динамические переменные физической системы определяют состояние системы. Изменение состояния и выражается в изменении этих динамических переменных. Примерами динамических переменных являются координаты (x,y,z), скорость v, ускорение a, сила F , импульс p, энергия E, напряженность электрического поля E, индукция магнитного поля B и т.п. |
Периодические колебания динамической переменной системы | Колебание динамической переменной s(t), при котором значение переменной повторяется через равные промежутки времени T , т.е. если s(t) = s(t+nT) для любого значения t, где n = 1, 2, 3 …) |
Гармонические колебания | Колебания, совершаемые по закону синуса (косинуса): s(t) = A cos [(t)], где (t) – фаза колебания динамической переменной s(t). |
Осциллятор | Колебательная система (как материальный объект), у которой динамические переменные изменяются по некоторому периодическому закону. |
Гармонический осциллятор | Колебательная система (как материальный объект), у которой динамические переменные изменяются по синусоидальному закону. |
Свободные колебания без трения | Колебания осциллятора, совершаемые только под действием возвращающей силы, возникающей в самом осцилляторе при выведении его из состояния равновесия. |
Квазиупругая возвращающая сила | Силы вида F = kx вне зависимости от природы силы |
Период свободных колебаний T | Минимальный промежуток времени, через который значение колеблющейся динамической переменной повторяется вновь |
Частота свободных колебаний | Число колебаний в единицу времени |
Амплитуда свободных колебаний | Максимальное значение колеблющейся динамической переменной |
Уравнение гармонического колебания динамической переменной | Уравнение колебания динамической переменной осциллятора (например, уравнение x(t) = A cos(t + )), описывающего функциональную зависимость переменной от времени |
Динамическое уравнение колебания | Дифференциальное уравнение, раскрывающее причинно-следственные связи в колебательной системе, которые определяют вид колебания, т.е. уравнение колебания |
Динамическое уравнение свободных колебаний без трения | Уравнение
вида |
Решение динамического уравнения свободных колебаний без трения | x = A cos (0t + ) |
Собственная частота колебательной системы (осциллятора) | Частота,
определяемая собственными свойствами
колебательной системы. Например:
собственная частота математического
маятника |
Динамическое уравнение затухающих колебаний | Уравнение
вида |
Решение динамического уравнения затухающих колебаний | x(t) = Aet cos (/t + ) |
Амплитуда затухающих колебаний | Амплитуда затухающих колебаний Aet уменьшается со временем, где A – начальная амплитуда, — коэффициент затухания |
Частота / и период T затухающих колебаний | / = |
Смысл коэффициента затухания | Коэффициент
затухания
равен обратной величине того промежутка
времени ,
за которое амплитуда затухающих
колебаний уменьшается в e
2,7 раз:
= |
Время затухания (время релаксации) | Промежуток времени, через которое амплитуда затухающих колебаний уменьшается в e 2,7 раз |
Логарифмический декремент затухания | = T |
Число колебаний Ne за время затухания | Число колебаний, по завершении которых амплитуда затухающих колебаний уменьшается в e 2,7 раз |
Добротность осциллятора Q | Добротность Q является характеристикой быстроты уменьшения энергии осциллятора при затухающих колебаниях. Добротность может быть выражена в разных формах: Q = |
Динамическое уравнение вынужденных колебаний |
|
Гармоническая вынуждающая сила | Вынуждающая сила вида F = F0 cost. |
Уравнение установившегося вынужденного колебания | x(t) = Хcos (t ) |
Амплитуда смещения вынужденного колебания | Х = |
Резонанс смещения | Xр. = |
Импеданс колебательной системы (осциллятора) | Импеданс
пружинного маятника
= |
Резонанс скорости смещения | Vр. = |
Мощность поглощения колебательной системой | P = |
Резонанс мощности поглощения | Pр = |
Частотная ширина поглощения мощности по уровню Pp/2 | 2 1 = |
Частотная ширина осциллятора по
скорости по уровню Vр/ | 2 1 = |
1Число динамических переменных, характеризующих физическую систему, ничем не ограничено. Однако для задания состояния системы достаточно знать только некоторый минимальный набор динамических переменных. Например, состояние механической системы в данный момент времени известно, если известны координаты и скорости объектов механической системы. Эти динамические переменные называютсяпеременными состояния. Другие динамические переменные могут быть (если это необходимо) рассчитаны по уравнениям связи. Например, если скоростьv задана, то автоматически известна и кинетическая энергиюmv2/2, известен импульсp = mv(параметр – массаm– считаются заданным). Аналогично, состояние электромагнитной системы известно, если известны напряженность электрического поляE и индукция магнитного поляB. Заряды и материальные константы среды как параметры считаются заданными. Состояние термодинамической системы характеризуется температуройT, внутренней энергией U, давлениемp, энтропиейS, множеством различных термодинамических потенциалов. Однако состояние термодинамической системы можно задать двумя переменными, например, температурой и энтропией системы. Остальные переменные могут быть рассчитаны.
§5. Резонансные кривые.
Чтобы определить
резонансную частоту  для
амплитуды падения напряжения на емкости,
нужно найти максимум функции:
для
амплитуды падения напряжения на емкости,
нужно найти максимум функции:
 (21)
(21)
Продифференцировав
выражение (21) по  и приравняв 0, получим уравнение:
и приравняв 0, получим уравнение:
 (22)
(22)
Решая уравнение (22), можно получить, что максимум амплитуды падения напряжения на емкости достигается при
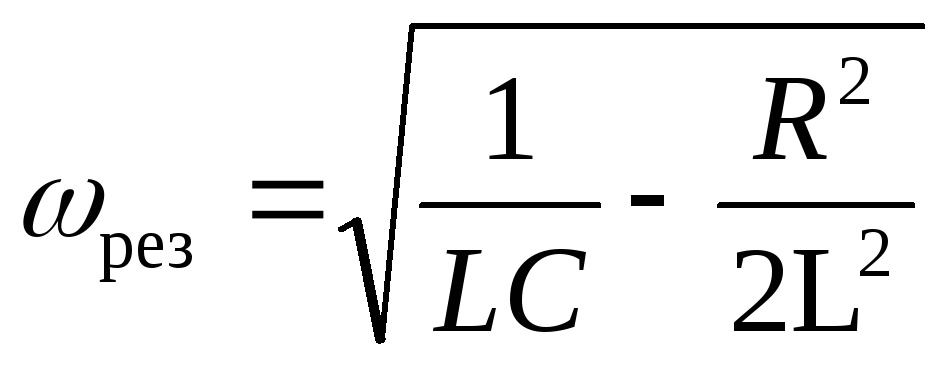 (23)
(23)
Таким образом,
резонансная частота для 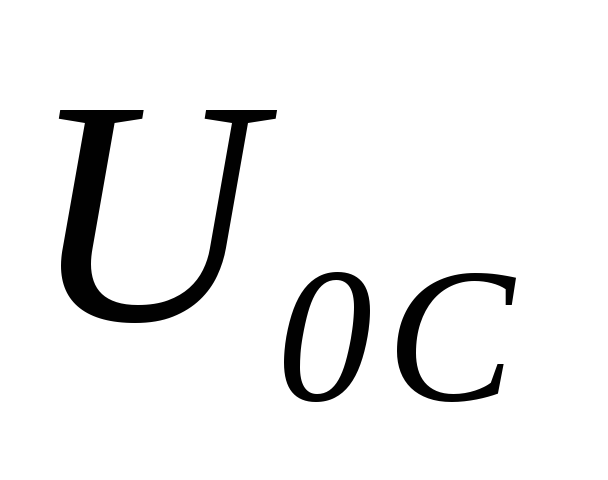 несколько меньше чем собственная частота
колебаний в контуре. Если ввести
обозначения
несколько меньше чем собственная частота
колебаний в контуре. Если ввести
обозначения и
и ,
то выражение (23) перепишется так:
,
то выражение (23) перепишется так:

Резонансные кривые
для 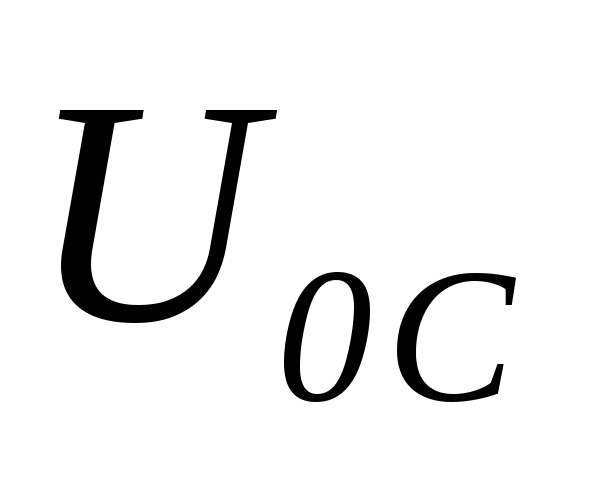 изображены на (рис.7) при различных
изображены на (рис.7) при различных .
В соответствии с (20), (21), чем меньше
коэффициент затухания
.
В соответствии с (20), (21), чем меньше
коэффициент затухания ,
тем выше и правее лежит максимум данной
кривой. По поводу этих резонансных
кривых (рис.7) можно сделать следующие
замечания. При стремлении частоты
,
тем выше и правее лежит максимум данной
кривой. По поводу этих резонансных
кривых (рис.7) можно сделать следующие
замечания. При стремлении частоты к нулю кривые стремятся к одному значению
к нулю кривые стремятся к одному значению ,
то есть к напряжению, возникающему на
конденсаторе при подключении его к
источнику постоянного напряжения
величиной
,
то есть к напряжению, возникающему на
конденсаторе при подключении его к
источнику постоянного напряжения
величиной .
При стремлении
.
При стремлении к бесконечности все кривые асимптотически
стремятся к нулю. Чем меньше
к бесконечности все кривые асимптотически
стремятся к нулю. Чем меньше ,
тем сильнее изменяется с частотой
амплитуда
,
тем сильнее изменяется с частотой
амплитуда вблизи резонанса, тем “острее” максимум
резонансной кривой. Остроту резонансных
кривых характеризует также добротность
вблизи резонанса, тем “острее” максимум
резонансной кривой. Остроту резонансных
кривых характеризует также добротность ,
чем больше добротность контура, тем уже
и выше максимум на кривой зависимости
амплитуды вынужденного колебания от
частоты
,
чем больше добротность контура, тем уже
и выше максимум на кривой зависимости
амплитуды вынужденного колебания от
частоты внешнего воздействия. Резонанс напряжений
широко используется в радиотехнике,
когда нужно усилить колебание напряжения
какой-либо определенной частоты, что
позволяет выделить из многих сигналов
различных радиостанций только одно
колебание определенной частоты
(настроиться на определенную станцию).
внешнего воздействия. Резонанс напряжений
широко используется в радиотехнике,
когда нужно усилить колебание напряжения
какой-либо определенной частоты, что
позволяет выделить из многих сигналов
различных радиостанций только одно
колебание определенной частоты
(настроиться на определенную станцию).
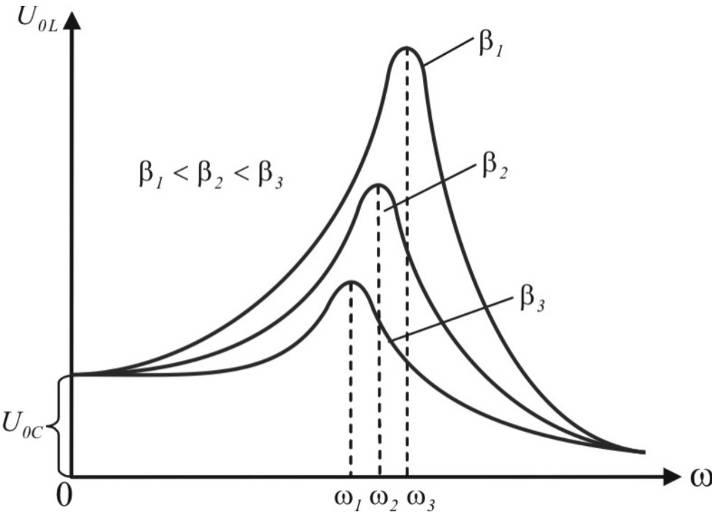
рис.7
Изучение резонанса напряжений.
Приборы и принадлежности:
1. Генератор сигналов звуковой частоты представляет собой источник переменного напряжения звуковой частоты в пределах от 17,7 до 200000 Гц (рис.8).

рис.8
На передней панели звукового генератора находится:
1.1. Тумблер подключения прибора к сети “вкл.” – “откл.”.
1.2. Вольтметр на выходе генератора является индикатором напряжения (Регулятор амплитуды напряжения грубой и тонкой настройки).
1.3. Ручка переключения предела частот (множитель частоты) на четыре положения: 17,7–200 Гц; 177–2000 Гц; 1770–200000 Гц.
1.4. Лимб со шкалой (главный регулятор частоты), поворачивая который избирается нужная частота.
1.5. Клеммы – выход звукового генератора, к которым подключается нагрузка (в данном случае колебательный контур).
2. Ламповый милливольтметр (предназначен для замеров напряжения в колебательном контуре) (рис.9).
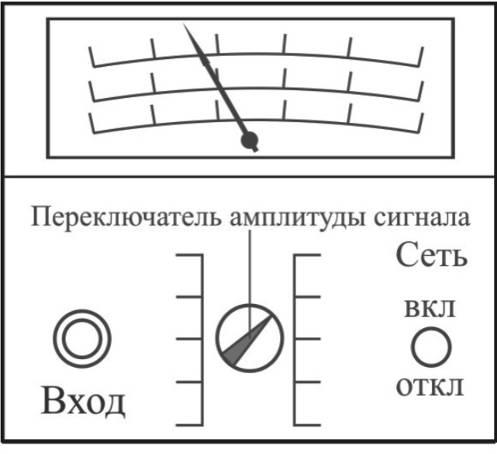
рис.9
На передней панели лампового милливольтметра находится:
2.1. Ручка переключения пределов амплитуды сигнала (замеряемой величины напряжения).
2.2. Клеммы — вход вольтметра.
2.3 Тумблер подключения прибора к сети “вкл.” – “откл.”.
В случае больших или наоборот малых значении напряжения, измеряемого ламповым вольтметром, необходимо изменить предел измерения напряжений ручкой переключения амплитуды сигнала (пределов).
После подключения приборов к сети нужно дать им прогреться 2–3 мин., после чего приступить к работе.
22. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
При вынужденных колебаниях сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Амплитуда установившихся вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F0, обратно пропорциональна массе m системы и уменьшается с увеличением коэффициента затухания β. При постоянных F0, m и β амплитуда зависит только от соотношения циклических частот вынуждающей силы β и свободных незатухающих колебаний системы.
Если нет диссипации т.е β=0, то амплитуда колебаний
 растет с увеличением циклической частоты
ω вынуждающей силы Fвн и при становится
бесконечно большой (след. рисунок)
растет с увеличением циклической частоты
ω вынуждающей силы Fвн и при становится
бесконечно большой (след. рисунок)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы называется резонансом:

1 – колебательная система без трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 – реальные резонансные кривые для колебательных систем с различным трением: β2<β3<β4.
23 Волны. Монохроматические волны.
Волна — это явление распространения в пространстве с течением времени возмущения (чередование максимумов и минимумов) физической величины, например, плотности вещества, напряжённости электрического поля, температуры и т.д.
Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны способны удаляться на значительные расстояния от места своего возникновения.
В зависимости от физической среды, в которой распространяются волны, их свойства различны и поэтому различают:
электромагнитные волны (радиоволны, свет, рентгеновские лучи) ;
упругие волны (звук, сейсмические волны) ;
волны в плазме;
гравитационные волны;
объёмные волны (распространяющиеся в толще среды) ;
волны на поверхности жидкости.
По отношению к направлению колебаний частиц среды, в которой распространяется волна, выделяют:
продольные волны (волны сжатия, P-волны) волна распространяется параллельно колебаниям частиц среды (звук) ;
поперечные волны (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред) ;
волны смешанного типа.
По виду фронта волны (поверхности равных фаз):
плоская волна — плоскости фаз перпендикулярны направлению распространения волны;
сферическая волна — поверхностью фаз является сфера;
цилиндрическая волна — поверхность фаз напоминает цилиндр.
Волновая поверхность — геометрическое место точек, колеблющихся в одинаковой фаз.
Волновой фронт — это поверхность, до которой дошли колебания к данному моменту времени. Волновой фронт является частным случаем волновой поверхности.
Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.
24. Поляризация волн. Три вектора, определяющих электромагнитную волну. Световой вектор. Виды поляризации.
Поляризация волн — характеристика волн, определяющая пространственную направленность векторных волновых полей.
Различают продольно и поперечно поляризованные волны в зависимости от ориентации вектора поля относительно волнового вектора.
Вектора, определяющие электромагнитную волну:
E – напряженность
Н – магнитность
k – волновой вектор(определяет направление распространения поверхности волновой поверхности)

Световой вектор— вектор плотности светового потока, которыйя определяет величину и направление переноса световой энергии.
Резонансные кривые для амплитуды силы тока в контуре, для амплитуды скорости материальной точки в механической системе
Запишем
формулу (5.68) для амплитуды силы тока  в наиболее удобном виде
в наиболее удобном виде
 ,
,
и
исследуем эту зависимость для различных
значений  .
.
1. ω=0
: 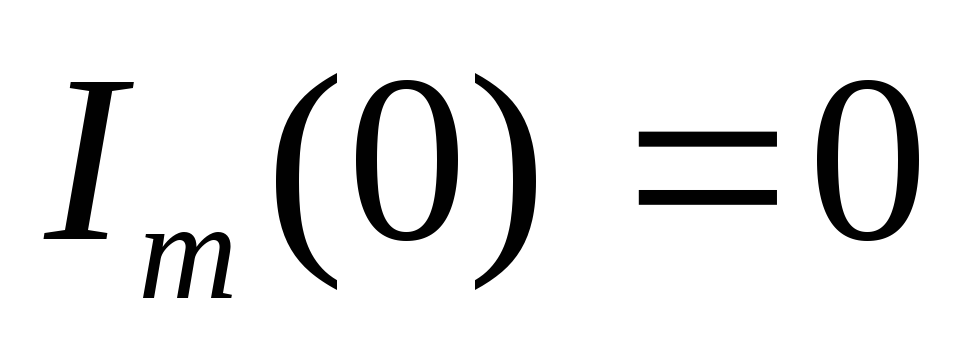 ,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
,
т.е. постоянный электрический ток через
цепь, содержащую конденсатор, не
протекает.
2. 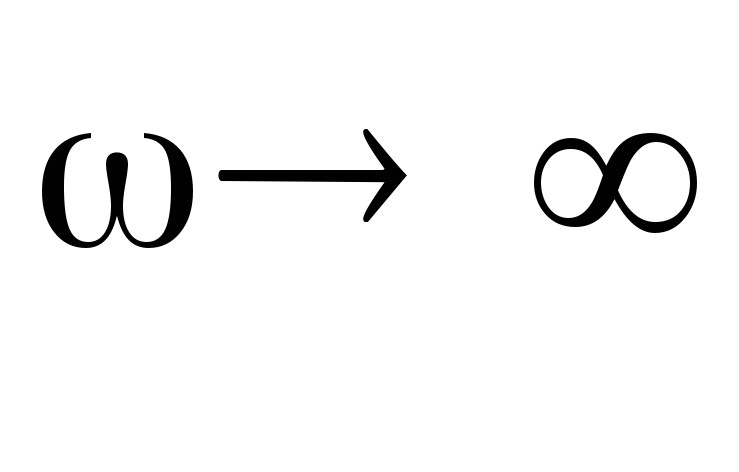 :
: 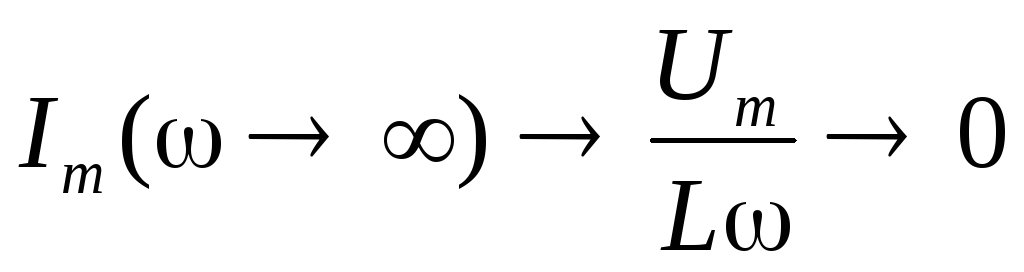 .
.
3.
Максимум функции наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум
наблюдается тогда, когда подкоренное
выражение в знаменателе будет минимальным,
т.е. первое слагаемое в подкоренном
выражении должно быть равным нулю.
Поэтому максимум  соответствует
частоте
соответствует
частоте 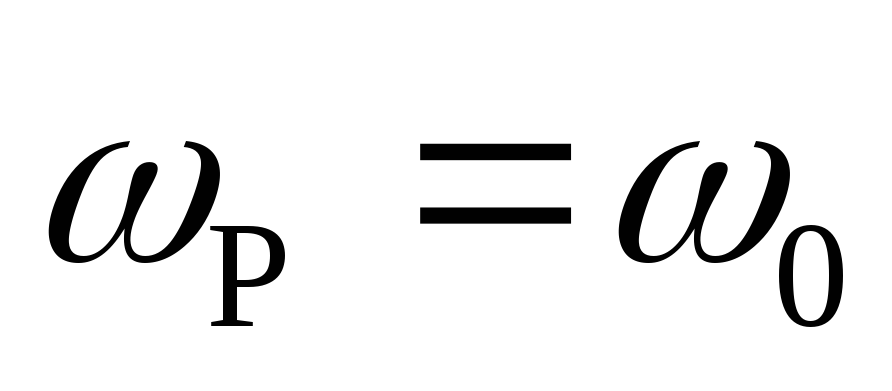 ,
а само максимальное значение будет
равно
,
а само максимальное значение будет
равно
 .
(5.74)
.
(5.74)
На
рис. 5.18 приведены резонансные кривые  в случае идеального колебательного
контура (
в случае идеального колебательного
контура ( )
и для двух разных значений сопротивления
)
и для двух разных значений сопротивления 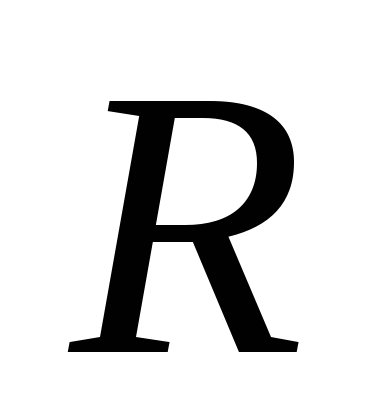 в нем (
в нем ( ,
т.е.
,
т.е. )
при постоянном значении
)
при постоянном значении  .
Как видно, максимум функции с увеличением
.
Как видно, максимум функции с увеличением  уменьшается, а его смещение по оси частот
уменьшается, а его смещение по оси частот не происходит.
не происходит.
Используя
табл. аналогий 5.1, можно записать формулы,
описывающие резонансные кривые для
амплитуды колебаний скорости  тела (м.т.) в механической системе:
тела (м.т.) в механической системе:
 ,
(5.75)
,
(5.75)
 :
:  .
(5.76)
.
(5.76)
График  для трех значений коэффициента
сопротивления (
для трех значений коэффициента
сопротивления ( )
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых
)
среды приведены на рис. 5. 18,б. Эти графики
аналогичны графикам резонансных кривых  .
.
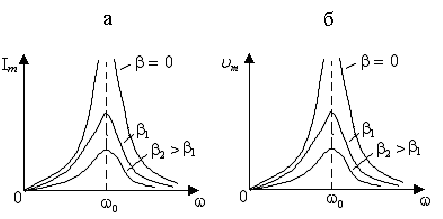
Рис. 5.18
Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении колебательного контура. Фазовые резонансные кривые
Перепишем
формулы (5.64) для I и  в
удобном виде
в
удобном виде
 ,
,  ,
,
и добавим к ним формулы для UL и UR:
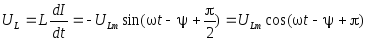 ,
, .(5.77)
.(5.77)
Найдем
в соответствии с полученными формулами
разность фаз колебаний между силой тока  и напряжениями на конденсаторе
и напряжениями на конденсаторе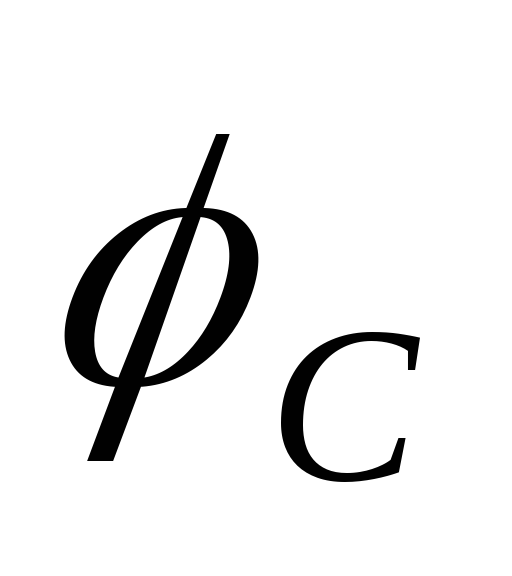 ,
индуктивности
,
индуктивности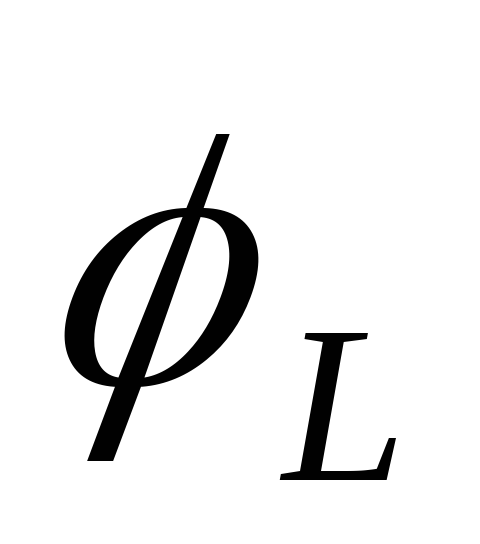 и активного сопротивления
и активного сопротивления :
:
 ,
(5.78)
,
(5.78)
 ,
(5.79)
,
(5.79)
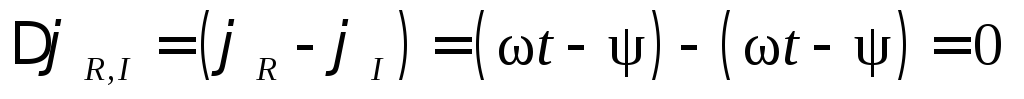 .
(5.80)
.
(5.80)

Рис. 5.19
Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π/2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π/2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.На
ней указаны амплитуды векторов напряжений
на отдельных участках электрической
цепи. При этом фаза колебания силы тока
в контуре принимается равной нулю, т.е.
амплитуда вектора силы тока располагается
вдоль оси  .
.
На
такой диаграмме вектор амплитуды
внешнего напряжения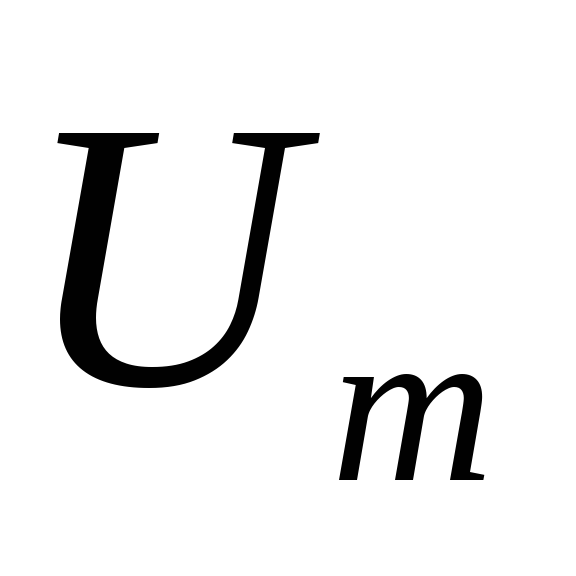 ,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (
,
подаваемого в колебательный контур,
можно представить как сумму векторов
амплитуд напряжений (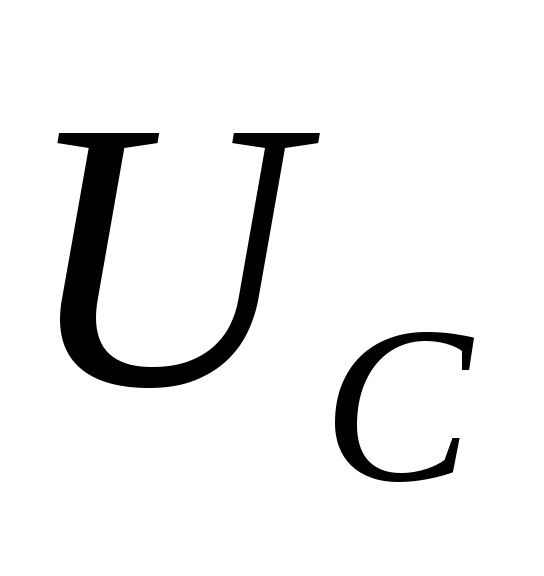 ,
, ,
,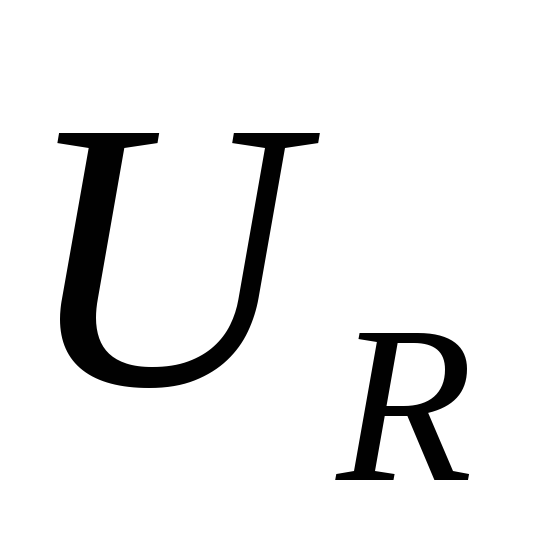 )
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот
)
на разных его участках. Это позволяет
записать следующую формулу для модуля
вектора амплитуды внешнего напряжения
(например, для частот ,
рис. 5.20,а):
,
рис. 5.20,а):
 ,
(5.81)
,
(5.81)
из
которой с учетом формул (5.19) и (5.20) ( )
можно получить выражение (5.65) для
зависимости амплитуды колебания заряда
от частоты внешнего напряжения
)
можно получить выражение (5.65) для
зависимости амплитуды колебания заряда
от частоты внешнего напряжения


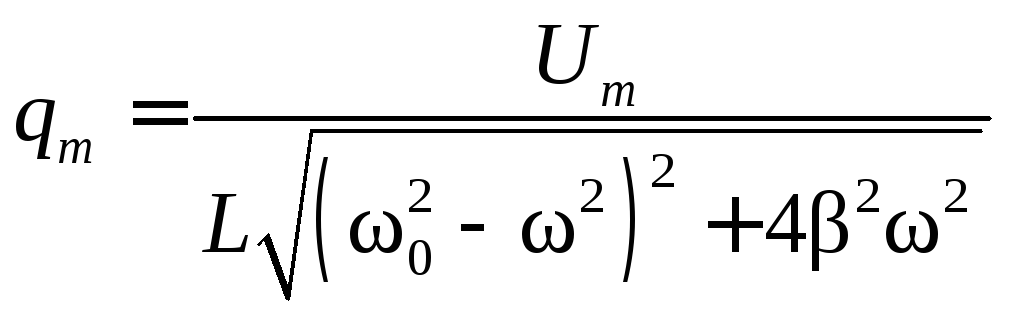 .
.

Рис. 5.20
Под фазовыми
резонансными кривыми понимают, например, зависимости разности
фаз
между внешним напряжением  и напряжением
и напряжением  на конденсаторе, разности фаз
на конденсаторе, разности фаз  между внешним напряжением
между внешним напряжением  и силой токаI в контуре от частоты
и силой токаI в контуре от частоты  внешнего напряжения. Наиболее интересными
из них являются зависимости
внешнего напряжения. Наиболее интересными
из них являются зависимости  ,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз
,
так как они позволяют выяснить
эффективность поступления энергии в
контур (колебательную систему). В
соответствии с формулами (5.64) и (5.66) для
разности фаз  и
и  можно
записать
можно
записать
 ,
,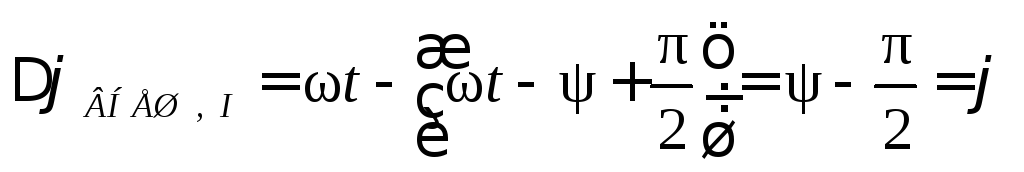 .
(5.82)
.
(5.82)
Отметим,
что разность фаз  для цепей переменного тока обозначают
буквой
для цепей переменного тока обозначают
буквой  :
:  .
.
На
рис. 5.21 приведены фазовые резонансные
кривые  и
и ,
построенные по формулам (5.66) и (5.82) при
значениях параметра
,
построенные по формулам (5.66) и (5.82) при
значениях параметра  :
:  .
.

Рис. 5.21
Из
них следует, что внешнее напряжение
опережает по фазе напряжение на
конденсаторе на угол  .
На векторной диаграмме это означает,
что вектор амплитуды
.
На векторной диаграмме это означает,
что вектор амплитуды  располагается выше вектора амплитуды
располагается выше вектора амплитуды (рис. 5.20 а,б,в). Причем угол
(рис. 5.20 а,б,в). Причем угол изменяется от нулевого значения для
частоты
изменяется от нулевого значения для
частоты  , равной нулю
(
, равной нулю
( ),
до значения равного
),
до значения равного  при частоте внешнего напряжения
стремящегося к бесконечности (
при частоте внешнего напряжения
стремящегося к бесконечности ( ,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения
,
рис. 5.21,а). При резонансе амплитуды
векторов внешнего напряжения  и напряжения на конденсаторе
и напряжения на конденсаторе взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной
взаимно перпендикулярны (см. рис. 5.20,б),
что приводит к разности фаз между ними,
равной (
(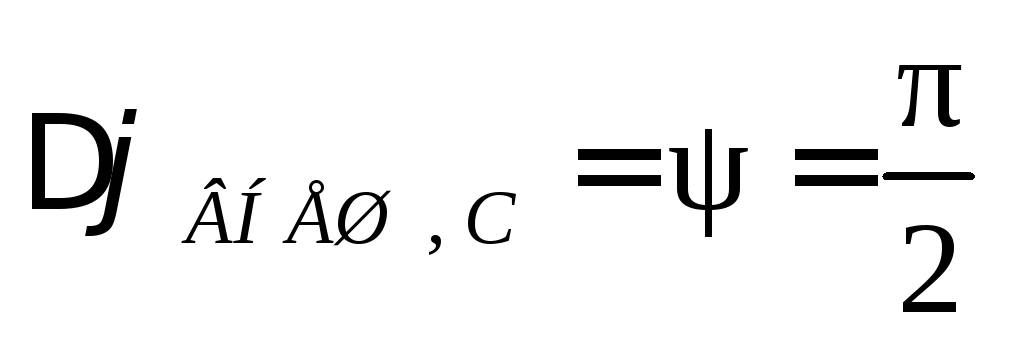 ,
Рис. 5.21,а).
,
Рис. 5.21,а).
Из
другой фазовой резонансной кривой
следует, что фаза внешнего напряжения
для частот  отстает от
фазы тока в контуре на угол
отстает от
фазы тока в контуре на угол  (рис.5.21,б). Для частот
(рис.5.21,б). Для частот 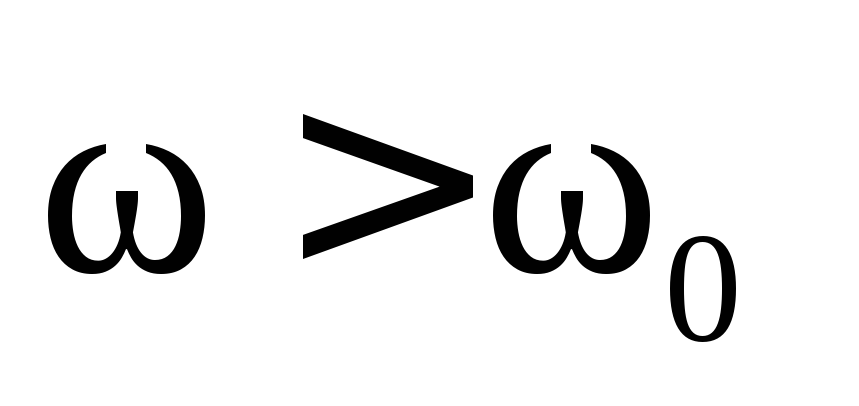 фаза внешнего
напряжения опережает на угол
фаза внешнего
напряжения опережает на угол  фазу колебаний силы тока в контуре и
при увеличении частоты
фазу колебаний силы тока в контуре и
при увеличении частоты  стремится к значению, равному
стремится к значению, равному  . При резонансе
(
. При резонансе
(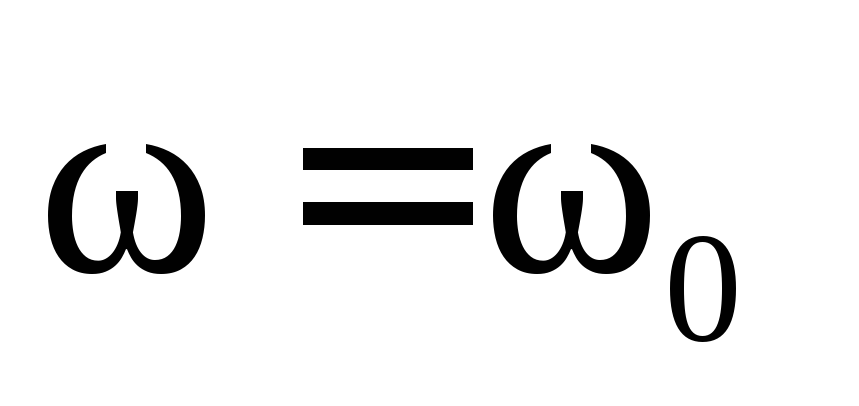 ,.
,. )
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.
)
фаза колебаний силы тока и внешнего
напряжения совпадают, т.е.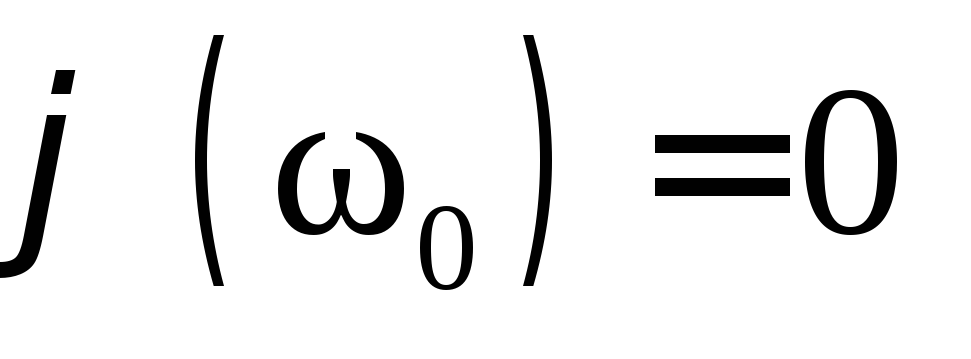 и вектора амплитуд
и вектора амплитуд  и
и направлены одинаково, вдоль оси
направлены одинаково, вдоль оси (рис.
5.21,б).
(рис.
5.21,б).
При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q >>1) и формулы (5.64) и (5.66) запишем
 :
: 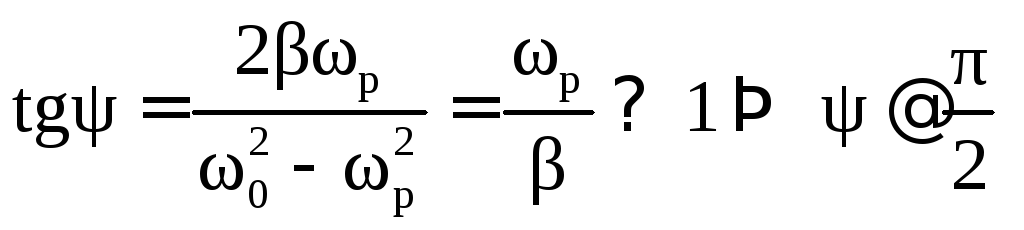 ;
;
 ,
, 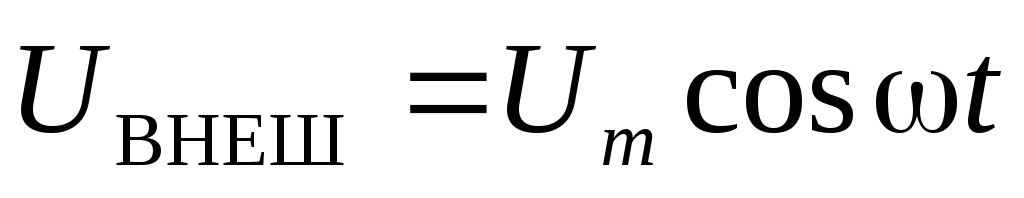 .
.
Такое
поступление энергии в контур при
резонансе приводит к большим амплитудам
колебаний, их числовые значения
определяются диссипацией (рассеянием)
энергии системы, т. е. коэффициентом
затухания 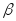 (формула (5.70)).
(формула (5.70)).
При
частотах  ,
больших или меньших
,
больших или меньших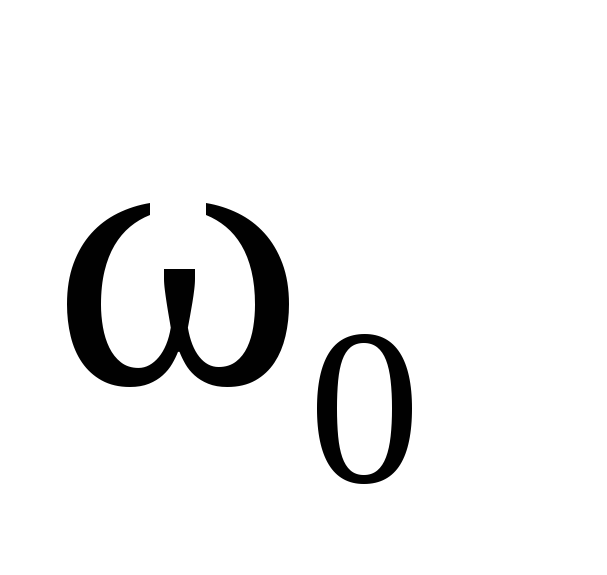 (
(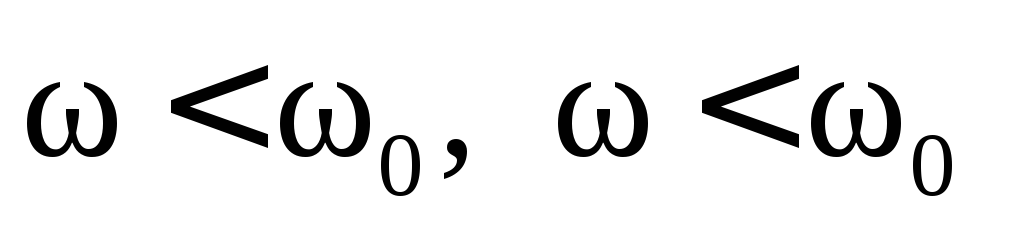 )
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии (
)
амплитуда вынужденных колебаний даже
в отсутствии диссипации энергии ( )
будет уменьшаться, она определяется
расстройкой резонанса (
)
будет уменьшаться, она определяется
расстройкой резонанса ( ),
т.е. разностью частот
),
т.е. разностью частот  и
и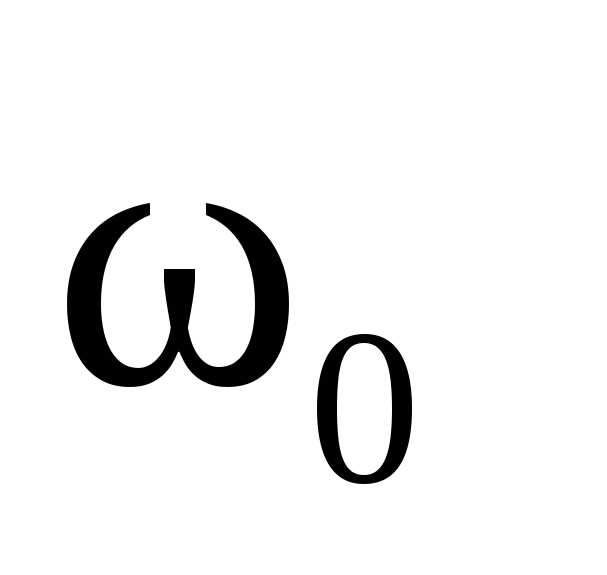 .
.
Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.
7.5. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с
Любой
резонансный контур, в том числе и
последовательный принято характеризовать
добротностью Q и характеристическим
сопротивлением 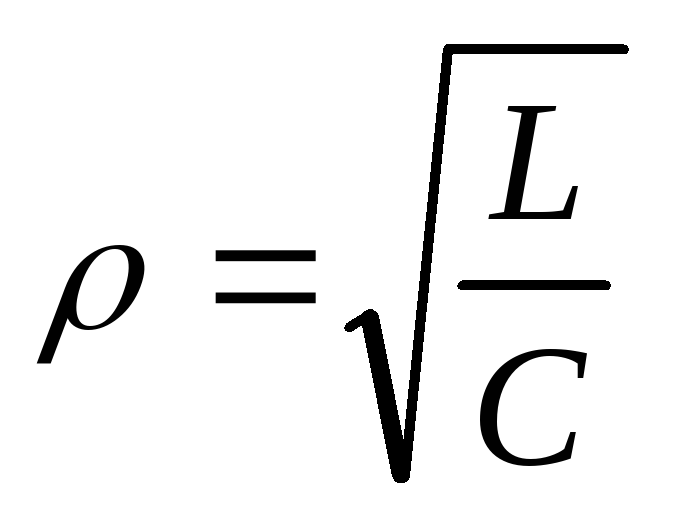 .
.
Напомним, что в данном случае будем рассматривать определение добротности контура при изменении частоты источника питания.
При
резонансе 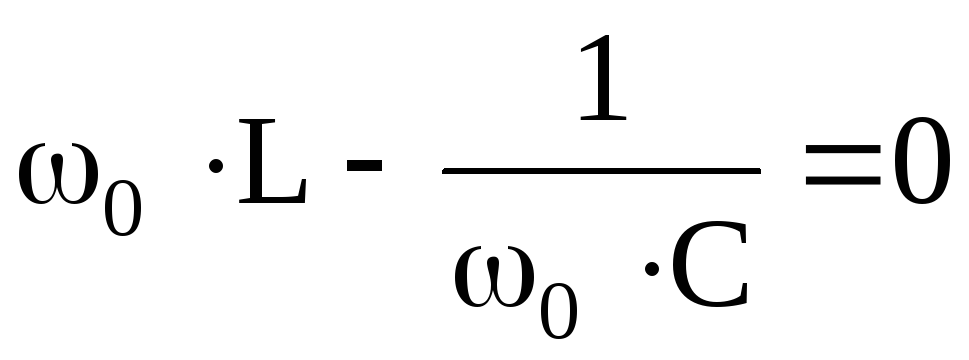 .
.
Добротность контура определяет кратность превышения напряжения на зажимах индуктивного или емкостного элемента сопротивления при резонансе над напряжением всей цепи U = UR.
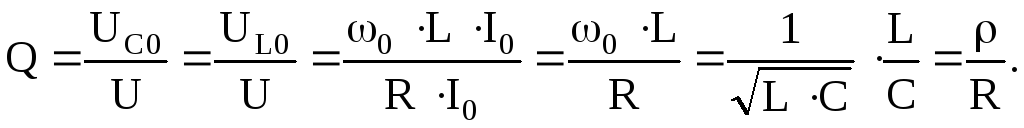
В электротехнических и радиотехнических установках добротности могут быть любого порядка, вплоть до десятков тысяч. При больших добротностях (50–500) UL0 >> UR, UR = UВХ = U, т. е. напряжение на индуктивности (или на емкости) во много раз больше приложенного напряжения.
Выясним влияние добротности на резонансные кривые при последовательном соединении
R, L, С. Ток в цепи равен
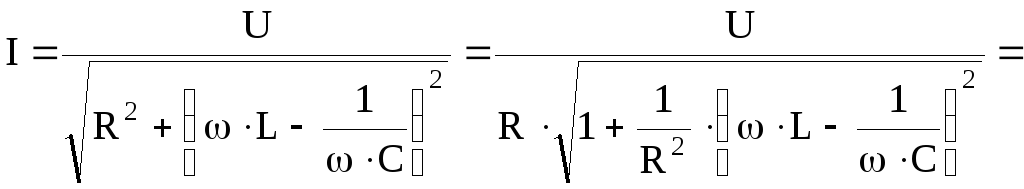

Относительное
значение тока: 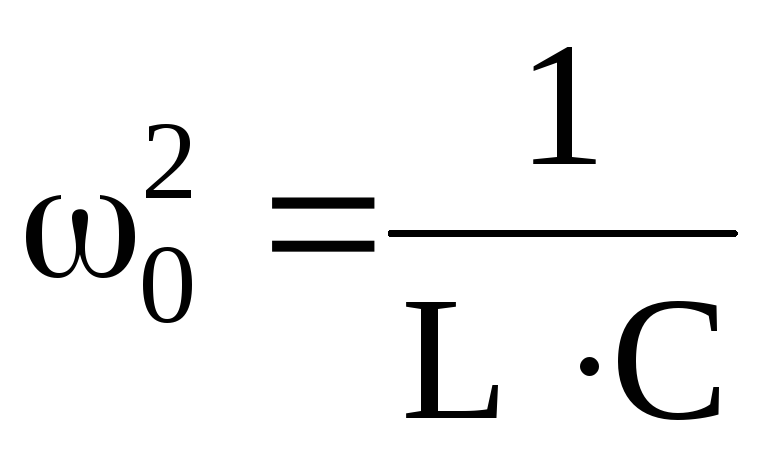 ,
т.е.
,
т.е. .
.
Пои
выводе этой формулы учитывалось, что 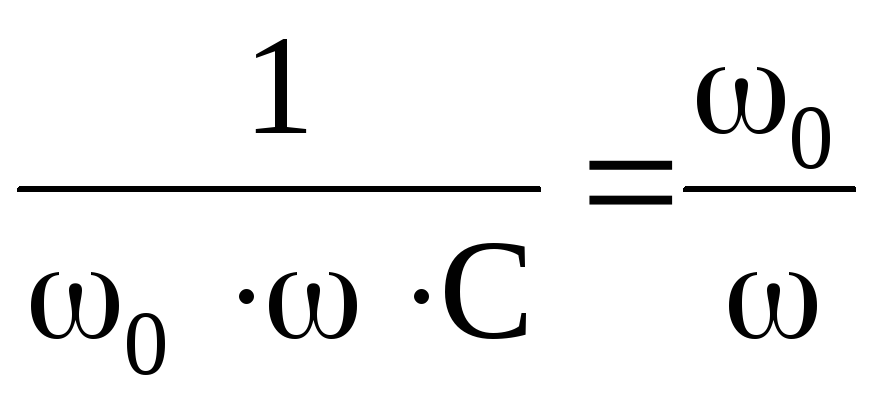 .
.
Иногда
вводят понятие относительной частоты  .
.
Тогда
предыдущая формула запишется так 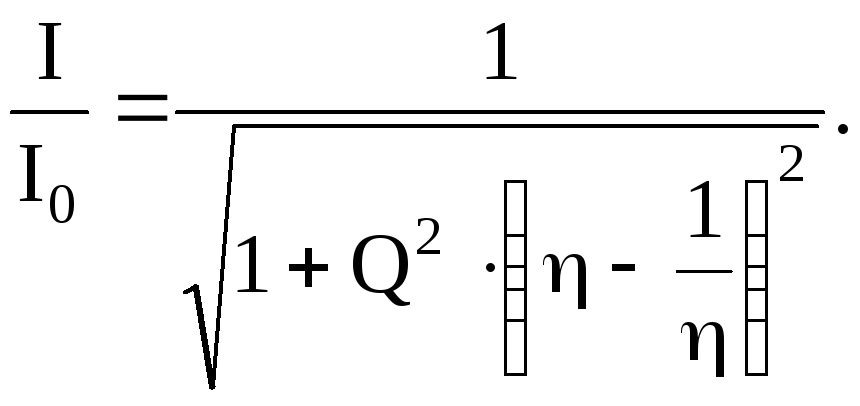

Построим
резонансные кривые в относительных (по
току) единицах (рис. 7.8) для трех
добротностей. Рассматривая три резонансные
кривые, видим, что чем больше добротность,
тем острее получается резонансная
кривая. Полоса пропускания контура
определяется разностью частот, которые
получатся при пересечении резонансной
кривой горизонтальной линией на уровне  .
.
Из рис. 7.8 видно, что чем меньше добротность, тем шире полоса пропускания. В радиоприемниках колебательные контуры имеют большие добротности (500–1000), поэтому эти контуры обладают достаточно узкими полосами пропускания, что способствует избирательному радиоприему только одной станции.
7.6. Определение добротности по резонансной кривой
На практике резонансные частотные характеристики реальных контуров можно получать, изменяя частоту генератора в определенных пределах и снимая показания вольтаметра, подключенного параллельно резистору (см. рис. 7.9 а). Строят экспериментальную резонансную кривую и по этой кривой определяют полосу пропускания. Выведем соответствующую формулу для расчета добротности по резонансной кривой, снятой экспериментально.

Из рис. 7.9 б следует:
 .
.
В
этом равенстве знаменатели равны,
поэтому 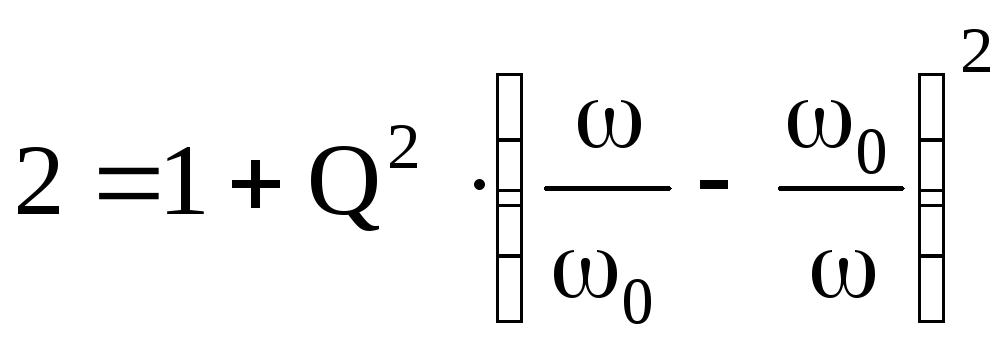
Отсюда  .
.
Запишем
дважды: при  и
и такие выражения
такие выражения ;
;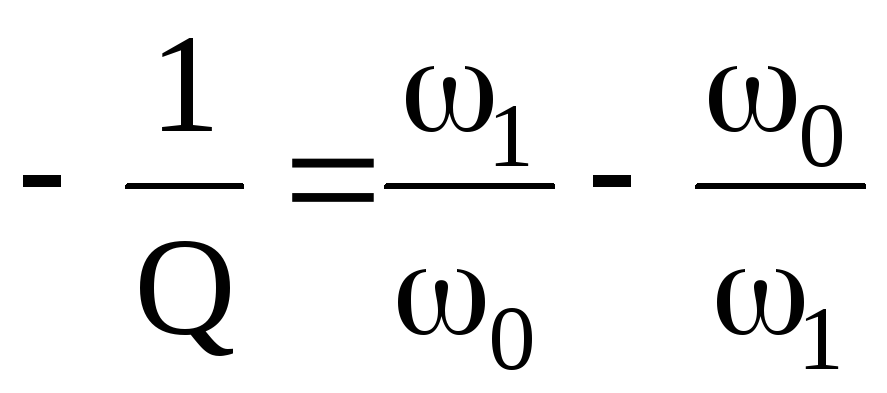 .
.
После
сложения последних выражений получим 
или 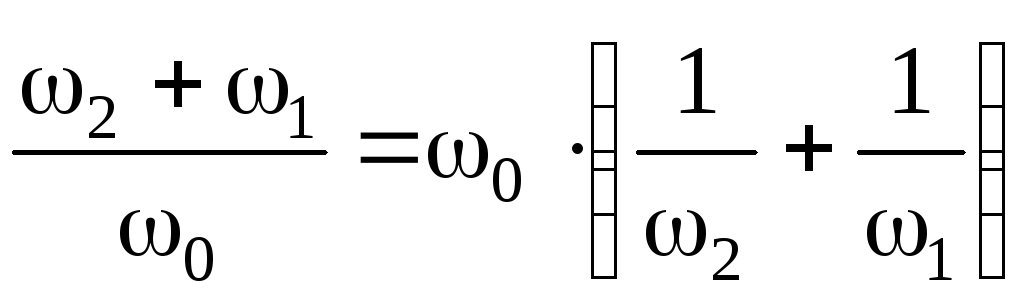
Отсюда 
И
далее  .
.
Очень
важно: добротность обратно пропорциональна  .
.
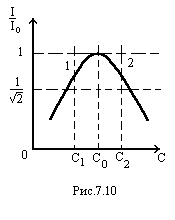
Для последовательного контура R, L, С построена резонансная кривая тока при изменении
емкости С (рис. 7.10).
Пользуясь этой кривой, определим добротность контура. Выражение для тока

Выполним ряд преобразований последней формулы
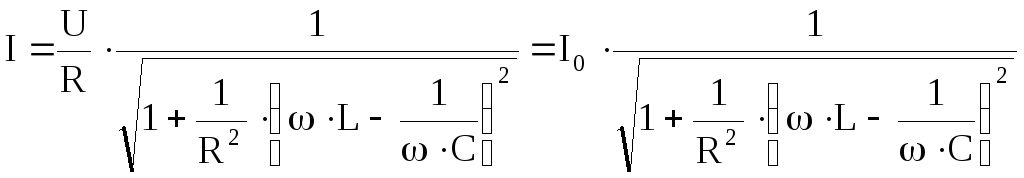 ;
;
 .
.
Проведем
горизонтальную прямую на уровне 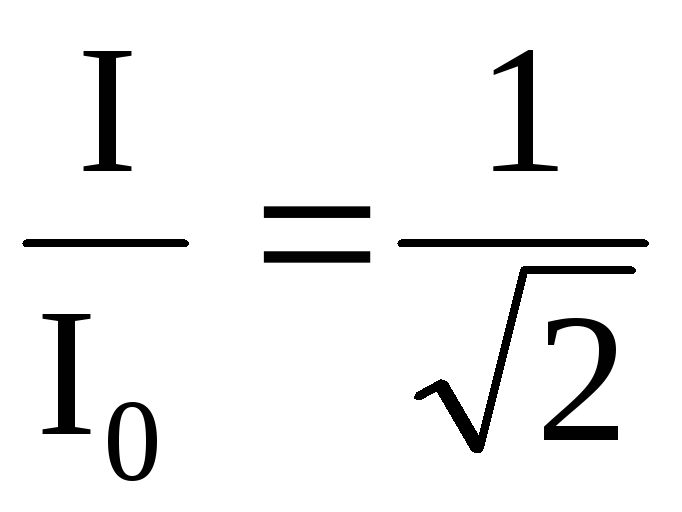 .
.
Отметим значения емкости C1 и С2.
Далее сделаем ряд очевидных выкладок. Выразим добротность Q через значения
емкости С1 и С2. Запишем
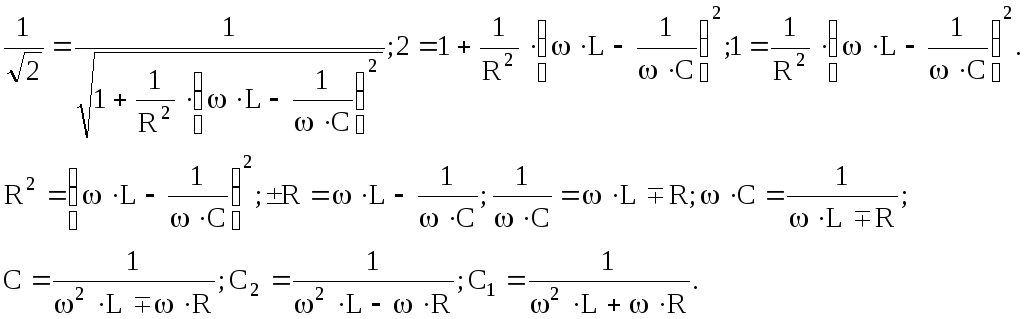
Найдем сумму и разность емкостей

Запишем
отношение  .
.
Напомним, что добротность контура определяется превышением напряжения на индуктивном (или емкостном) сопротивлении при резонансе над напряжением всей цепи (или напряжением на активном сопротивлении), т. е.

Таким
образом, 
Кроме этого результата, представляется возможным получить значения параметров катушки индуктивности (L и R)
 .
.
Откуда  ;
; .
.
Откуда 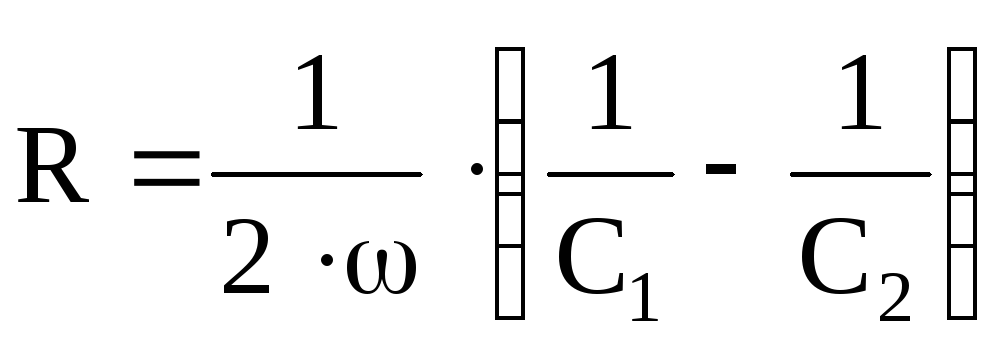 .
.
Величина емкости С0, при которой наступает резонанс, определится так:
 ;
;  ;
; ;
; .
.
Откуда  .
.

Резонанс напряжений может наблюдаться в схеме, показанной на рис. 7.11.
Входное сопротивление такой схемы

При резонансе реактивная составляющая входного сопротивления должна быть равна нулю, т. е.





 +
+ 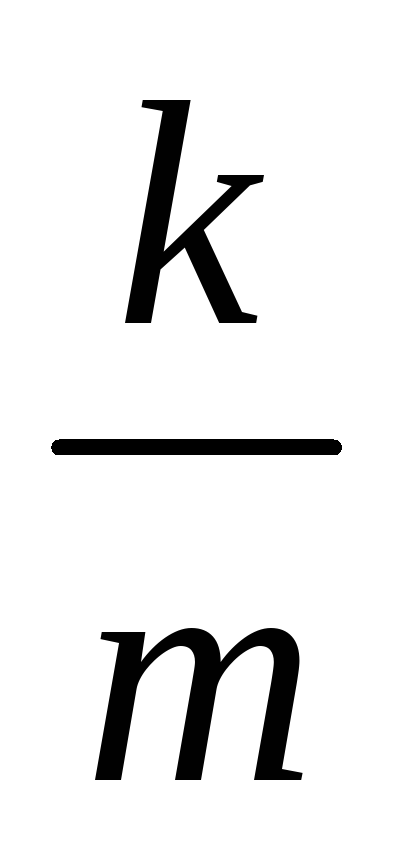 x = 0 (или в компактной форме записи:
x = 0 (или в компактной форме записи: 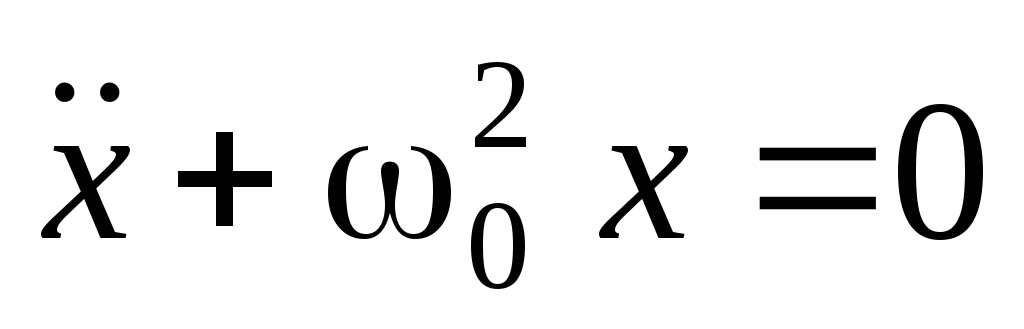 ).
). ;
собственная частота пружинного
маятника
;
собственная частота пружинного
маятника =
=  ;
собственная частота колебательного
контура
;
собственная частота колебательного
контура  =
= 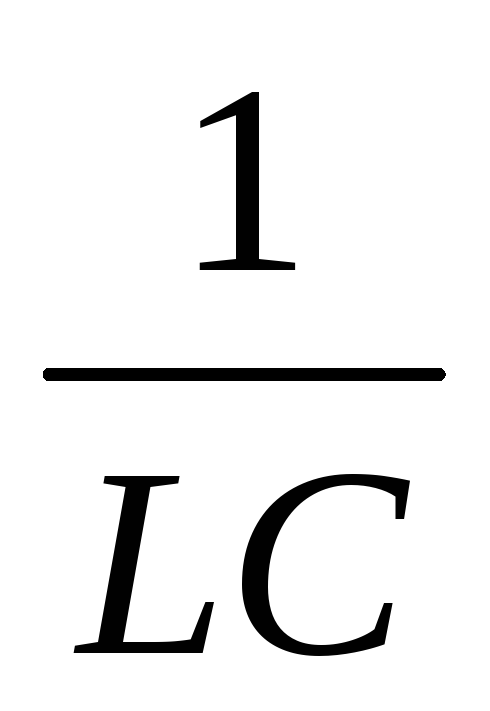 .
.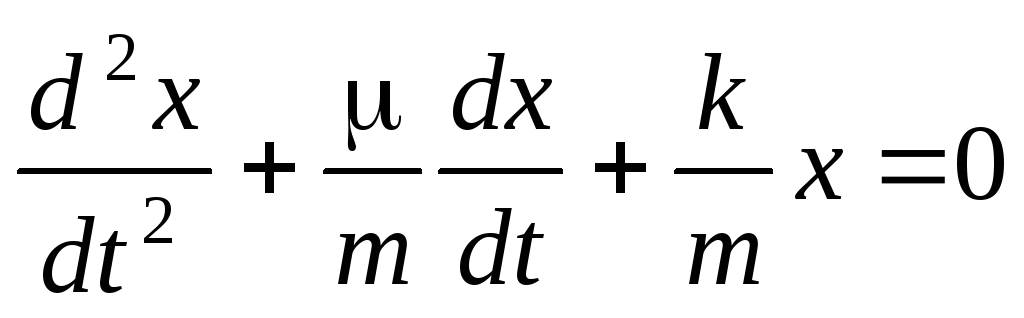 (или в компактной форме записи
(или в компактной форме записи
 , T =
, T =  .
.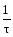
 =
Ne; Q =
=
Ne; Q = 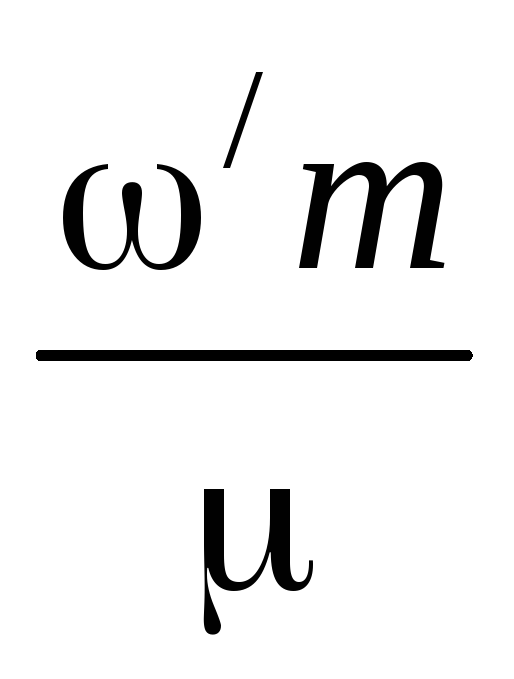
 ;Q =
;Q = =
= .
. (или в компактной
форме записи:
(или в компактной
форме записи:  )
) =
= 
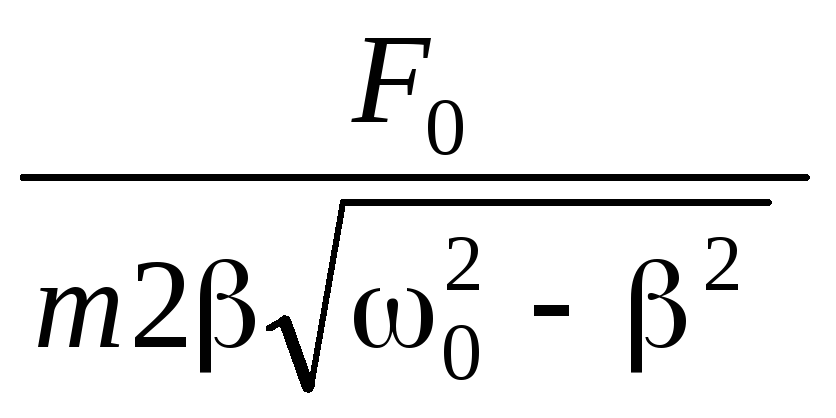 =
=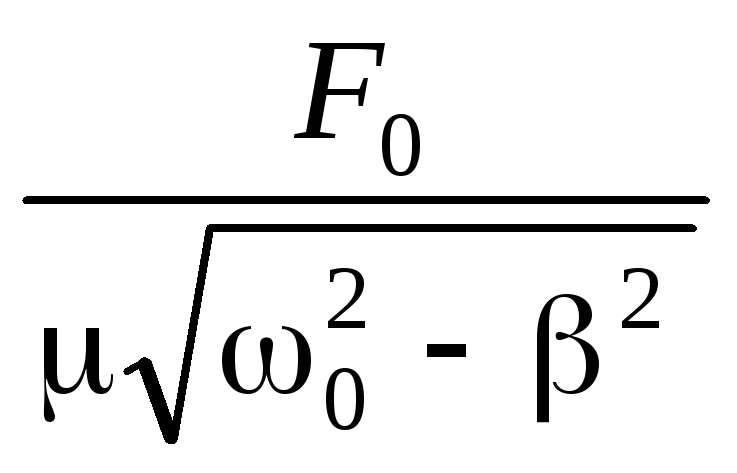 =
=
 ,
импеданс колебательного контура Z =
,
импеданс колебательного контура Z = 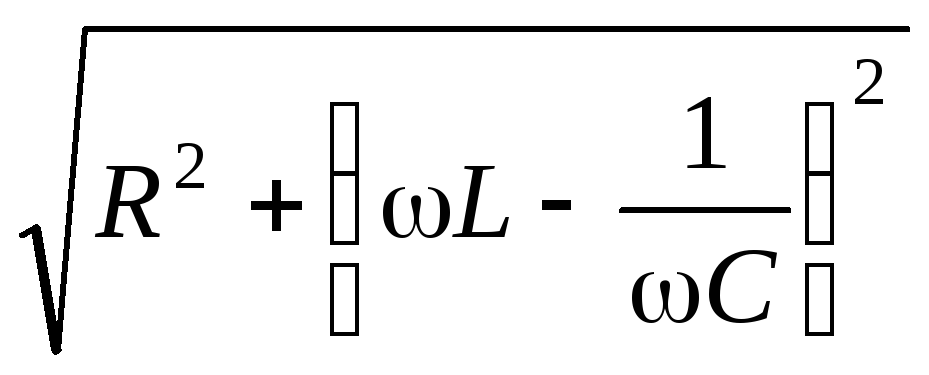 .
. =
= 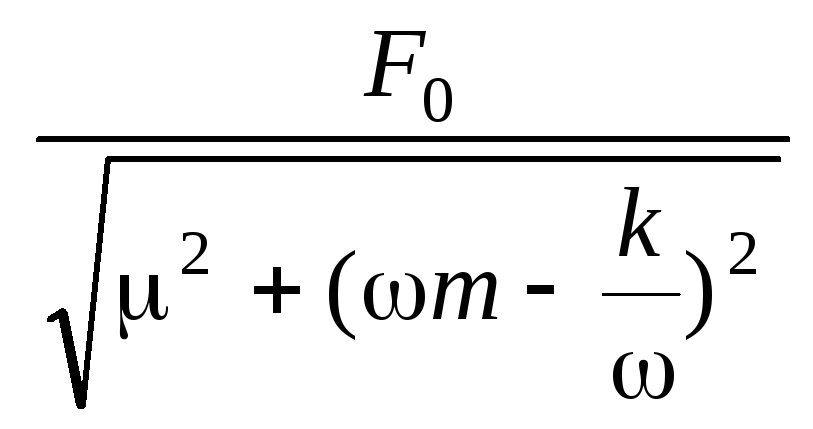 =
=  .
. =
= 
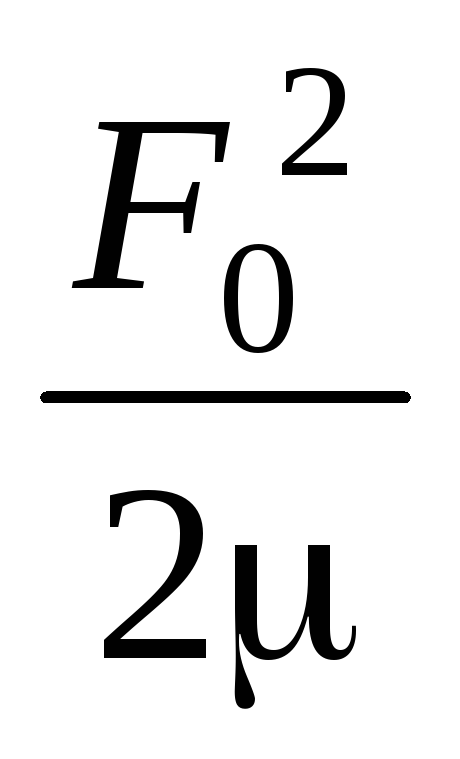
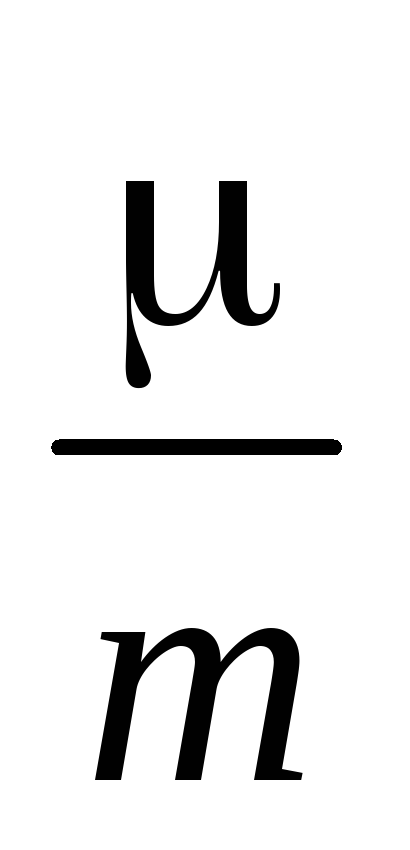 .
.
 .
.