Резонанс в электрической цепи — Класс!ная физика

Резонанс в электрической цепи

«Физика — 11 класс»

В механике резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы.
Резонанс возможен и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.

При механике резонанс выражен при малом трении.
В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R.
Наличие активного сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника (проводник нагревается).
Поэтому резонанс в электрическом колебательном контуре выражен отчетливо при малом активном сопротивлении R.

Если активное сопротивление мало, то собственная циклическая частота колебаний в контуре:

Сила тока при вынужденных колебаниях достигает максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура:

Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.

Амплитуда силы тока при резонансе.

При резонансе в колебательном контуре создаются условия для поступления энергии от внешнего источника в контур.
Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением.
В механике аналогично: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).

После включения внешнего переменного напряжения амплитуда колебаний силы тока нарастает постепенно, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:

тогда:

I_mR = U_m

Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением

При R → 0 резонансное значение силы тока неограниченно возрастает: (I_m)_рез → ∞.
Наоборот, с увеличением R максимальное значение силы тока уменьшается.

Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R₁ < R₂ < R₃):

Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности.
Эти напряжения при малом активном сопротивлении во много раз превышают внешнее напряжение.

Использование резонанса в радиосвязи

Явление электрического резонанса используется в радиосвязи.
На явлении резонанса основана вся радиосвязь.
Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте.

С антенной индуктивно связан колебательный контур.

Из-за электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот.
Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте.
Настройка контура на нужную частоту ω₀ осуществляется путем изменения емкости конденсатора.
В этом обычно состоит настройка радиоприемника на определенную радиостанцию.

Необходимость учета возможности резонанса в электрической цепи

Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии.
Чрезмерно большие токи могут перегреть провода.
Большие напряжения приводят к пробою изоляции.

Итак,
при вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Резонанс в электрической цепи

Начнём с основных определений.

Определение 1

Резонанс — это явление, при котором частота колебаний какой-либо системы увеличивается колебаниями внешней силы.

Вынужденные колебания, источником которых является внешняя сила, увеличивают даже те колебания, амплитуда которых имеет довольно небольшие значения. Максимальный резонанс с наибольшей амплитудой возможен именно при совпадении частот внешнего воздействия и рассматриваемой системы.

Примером резонанса является раскачивание моста ротой солдат. Частота шага солдат, являющаяся по отношению к мосту примером вынужденных колебаний, при этом синхронизирована и может совпасть с собственной частотой колебаний моста. В результате мост может разрушиться.

Электрический резонанс в физике считается одним из распространенных в мире физических явлений, без которого было бы невозможным, например, телевидение и диагностика с помощью медицинских аппаратов.

Одними из наиболее полезных видов резонанса в электрической цепи являются:

• резонанс токов;
• резонанс напряжений.

Возникновение резонанса в электрической цепи

Замечание 1

Возникновению резонанса в электрической цепи способствует резкое увеличение амплитуды стационарных собственных колебаний системы при условии совпадения частоты внешней стороны воздействия и соответствующей колебательной резонансной частоты системы.

Схема $RLC$ представляет электрическую цепь с соединенными последовательным или параллельным образом элементами (резистора, индуктора, конденсатора). Название $RLC$ состоит из простых символов электрических элементов: сопротивления, емкости, индуктивности.

Векторная диаграмма последовательной $RLC$-цепи представлена в одной из трех вариаций:

• емкостной;
• активной;
• индуктивной.

В последней вариации резонанс напряжений возникает при условии нулевого сдвига фаз, и совпадении значений индуктивного и емкостного сопротивлений.

Резонанс напряжений

При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.

Резонанс напряжений обычно достигается тремя способами:

• подбором индуктивности катушки;
• подбором емкости конденсатора;
• подбором угловой частоты $w_0$.

При этом все значения емкости, частоты и индуктивности определяются с использованием формул:

$L_0 = \frac{1}{w^2C}$

$C_0 = \frac{1}{w^2L}$

Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:

$\frac{U}{r}$

Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.

Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:

$Q = \frac{U_c0}{U}$

Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.

Резонанс токов через реактивные элементы

Резонанс токов появляется в электроцепях цепях переменного тока при условии параллельного соединения ветвей с разнохарактерными реактивными сопротивлениями. В резонансном режиме токов реактивная индуктивная проводимость цепи будет равнозначной ее собственной реактивной емкостной проводимости, т.е. $BL = BC$.

Колебания контура, частота которых имеет определённое значение, в данном случае совпадают по частоте с источником напряжения.

Простейшей электроцепью, в которой мы наблюдаем резонанс токов, считается цепь с параллельным соединением конденсатора с катушкой индуктивности.

Поскольку сопротивления реактивности равнозначны по модулю, амплитуды токов $I_c$ и $I_u$ будут одинаковыми и смогут достигать максимальной амплитуды. На основании первого закона Кирхгофа $IR$ равен току источника. Ток источника, иными словами, протекает только через резистор. При рассмотрении отдельного параллельного контура $LC$, на резонансной частоте его сопротивление оказывается бесконечно большим: $ZL = ZC$. При установлении гармонического режима с резонансной частотой, в контуре наблюдается обеспечение источником установившейся определенной амплитуды колебаний, а мощность источника тока при этом расходуется исключительно на пополнение потерь в активном сопротивлении.

Таким образом, у последовательной $RLC$ цепи импеданс оказывается минимальным на резонансной частоте и равным активному сопротивлению контура. В то же время, у параллельной $RLC$ цепи импеданс максимальный на резонансной частоте и считается равным сопротивлению утечки, фактически также активному сопротивлению контура. С целью обеспечения условий для резонанса силы тока или напряжения, требуется проверка электрической цепи для предопределения ее комплексного сопротивления или проводимости. Помимо этого, её мнимая часть должна приравниваться к нулю.

Применение явления резонанса

Хороший пример использования резонансного явления представляет электрический резонансный трансформатор, разработанный Николой Тесла ещё в 1891 году. Ученый проводил эксперименты на разных конфигурациях, состоящих в сочетании из двух, а зачастую и трех резонансных электроцепей.

Замечание 2

Термин «катушки Теслы» применяют к высоковольтным резонансным трансформаторам. Устройства используют при получении высокого напряжения, частоты переменного тока. Обычный трансформатор необходим для эффективной передачи энергии с первичной на вторичную обмотку, резонансный используется для временного хранения электроэнергии.

Устройство отвечает за управление воздушным сердечником настроенного резонансно трансформатора с целью получения высоких напряжений при малых значениях силы токов. Каждая обмотка обладает емкостью и функционирует в качестве резонансного контура. Для произведения наибольшего выходного напряжения первичный и вторичный контуры настраивают в резонанс друг с другом.

Резонанс в электрических цепях

Резонанс в электрических цепях

Реактивное сопротивление или проводимость двухполюсника, в состав которого входят конденсаторы и катушки индуктивности, в зависимости от частоты приложенного напряжения могут принимать как положительные, так и отрицательные значения. При определенных условиях реактивное сопротивление (проводимость) может оказаться равным нулю, а эквивалентное сопротивление (проводимость) всей цепи становится активным. В этом случае ток и напряжение на входе цепи совпадают по фазе. Такое явление называют резонансом, а соотношение 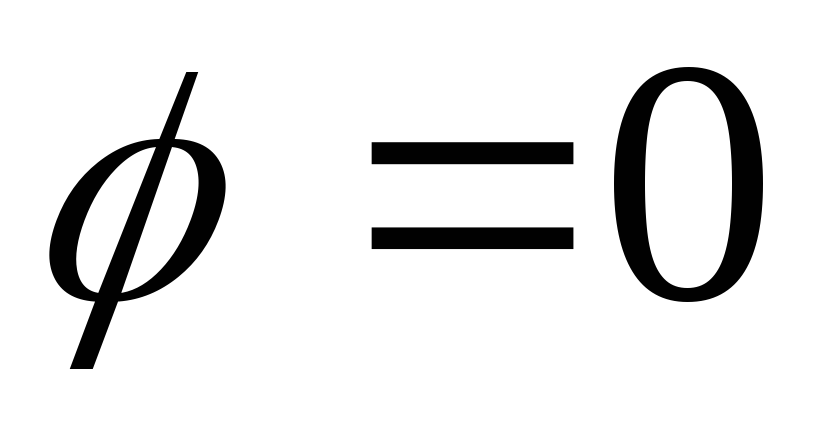−условием резонанса.

Эквивалентные параметры двухполюсника связаны соотношениям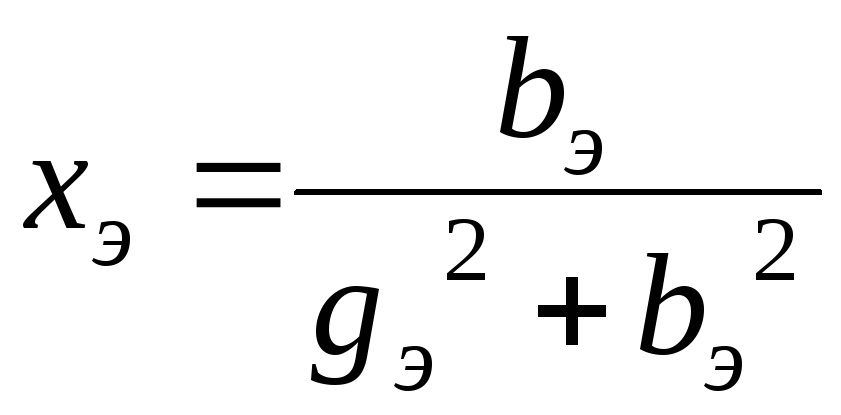и

и ,

поэтому условие 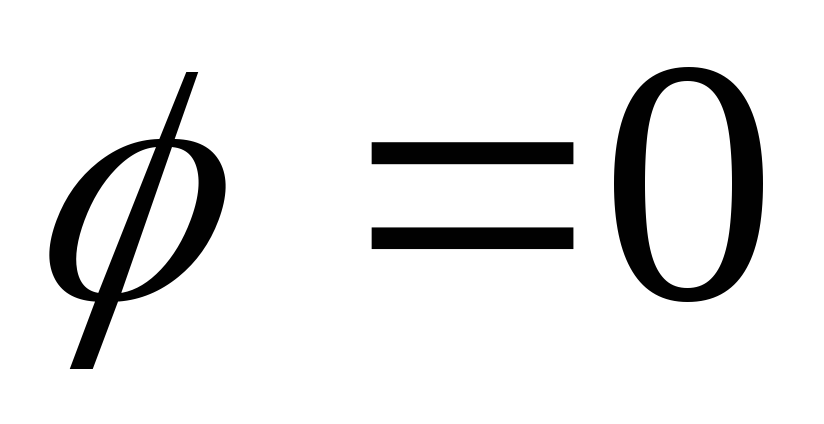эквивалентно выполнению равенств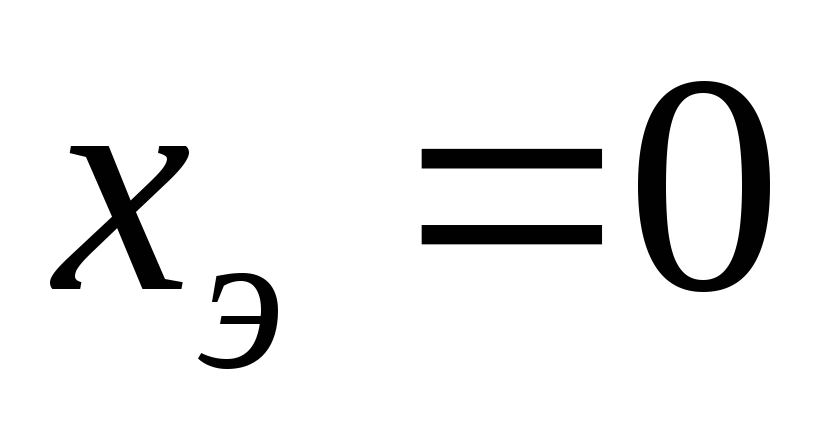или.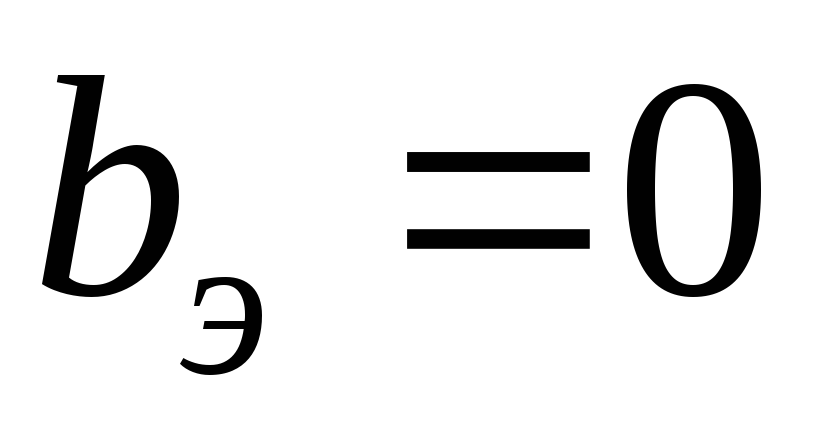

Из условий 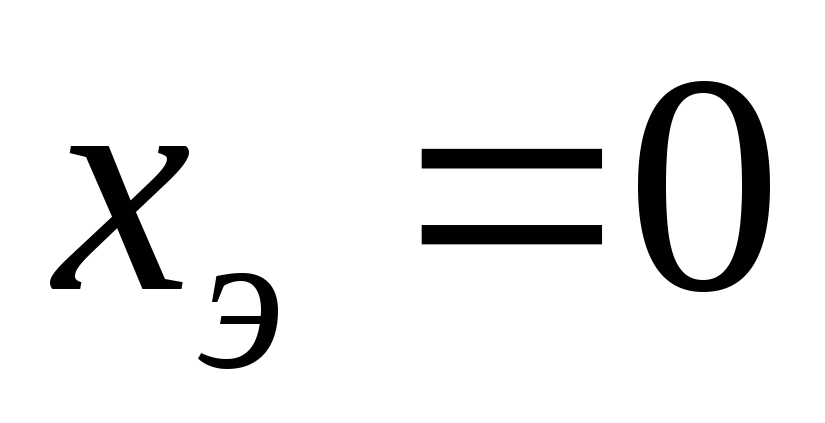,могут быть определены значения параметров элементов электрической цепи, при которых наблюдается явление резонанса, а также значения частотырезонанса.

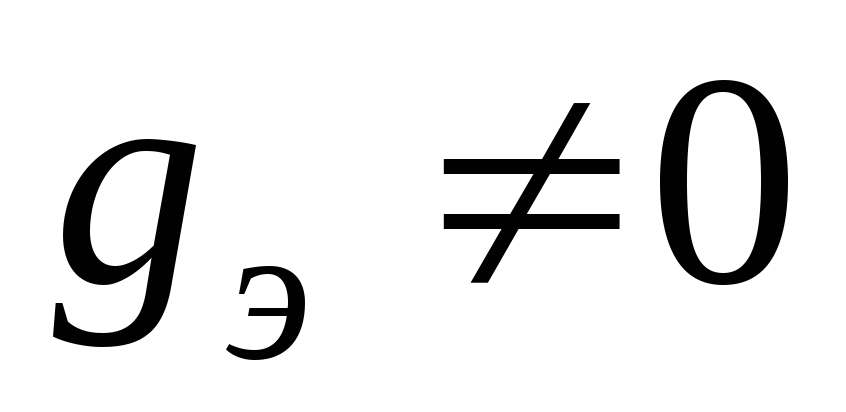Если для двухполюсника и, то для определения значений резонансных частот может быть использовано любое из услови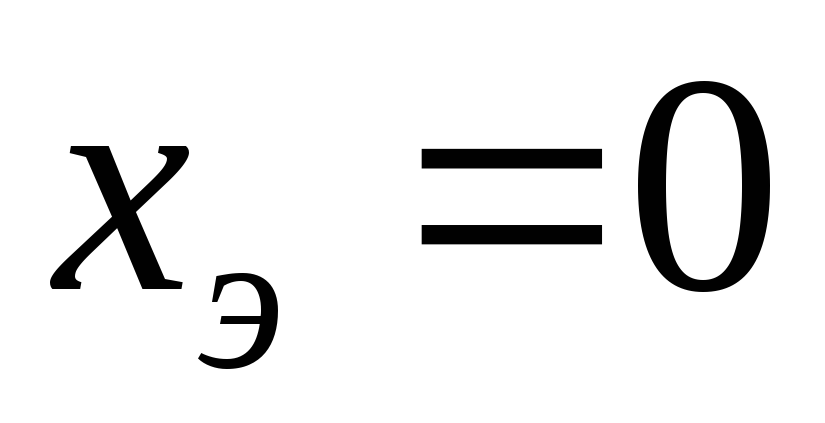йили.

В случае, когда активное эквивалентное сопротивление или активная эквивалентная проводимость двухполюсника равны нулю, для определения значений резонансных частот следует использовать оба условия и, так как при этом. Равенства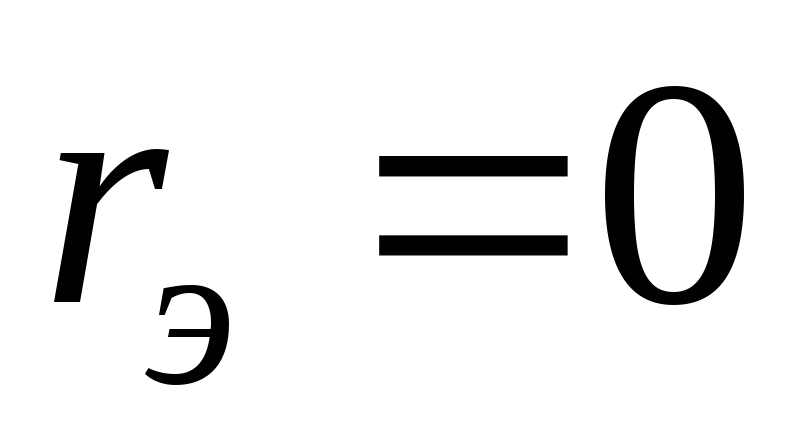ивыполняются, в частности, для цепей, содержащих только катушки индуктивности и конденсаторы.

Для описания частотных свойств электрических цепей широко используются частотные характеристики. Под частотными характеристиками понимают зависимости от частоты входных параметров цепи: r , x , z , g , b , y , а также величин, определяемых этими параметрами 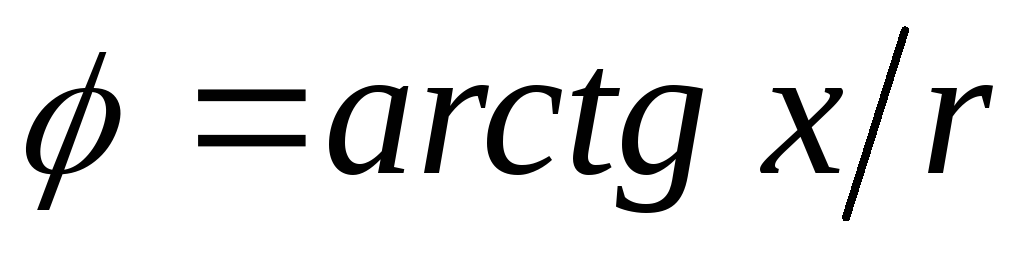,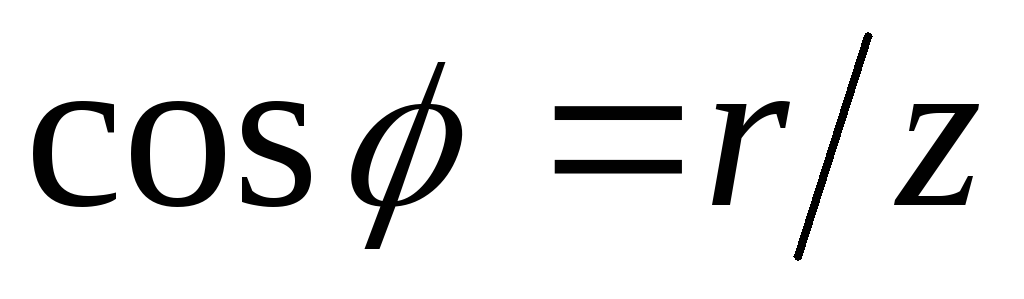и т.д. Рассмотрим далее частотные свойства простейших цепей, в которых возможен резонанс.

Резонанс в цепи при последовательном соединении элементов

Рассмотрим цепь, изображенную на рис. 10.1а

Комплексное сопротивление цепи равно

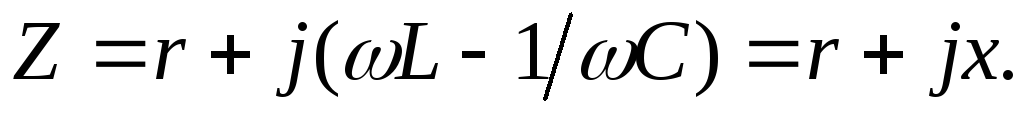
Угол сдвига между входным током и напряжением обращается в нуль при равенстве нулю реактивного сопротивления цепи, то есть при выполнении условия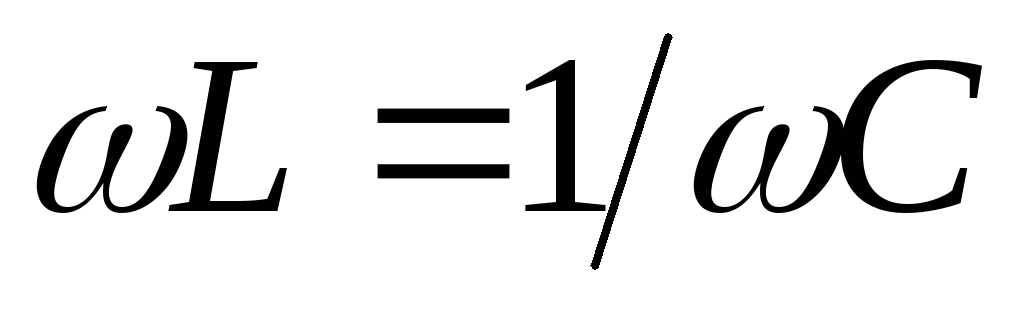. Таким образом, состояние резонанса в цепи наступает при частоте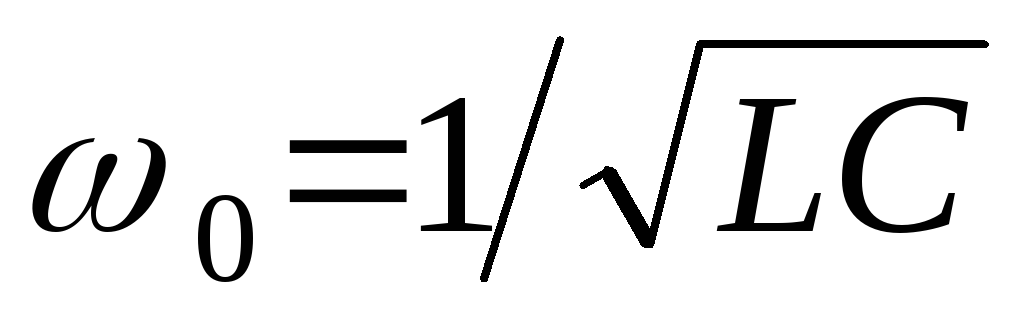. Эта угловая частота называетсярезонансной. Векторная диаграмма для токов и напряжений в последовательном rLC контуре, построенная при , изображена на рис. 10.1б. Как видно из векторной диаграммы, вектораиравны по величине и противоположны по направлению, таким образом, напряжение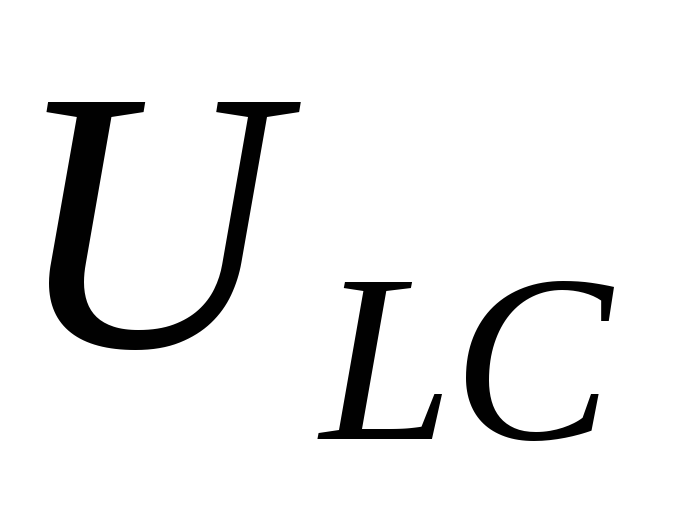при резонансной частоте равно нулю. Индуктивное и равное ему емкостное сопротивление цепи при резонансной частоте

,

обозначаемое символом , носит названиеволнового сопротивления колебательного контура и измеряется в омах.

Отношение волнового сопротивления к активному сопротивлению в последовательном колебательном контуре называется добротностью, а величина, обратная добротности − затуханием:

, .

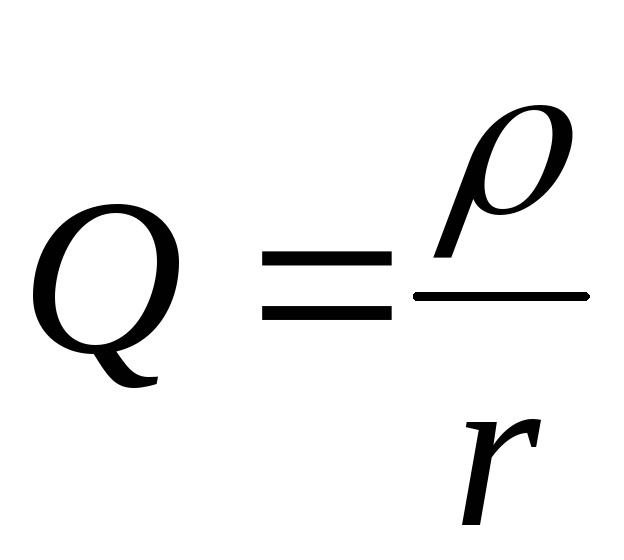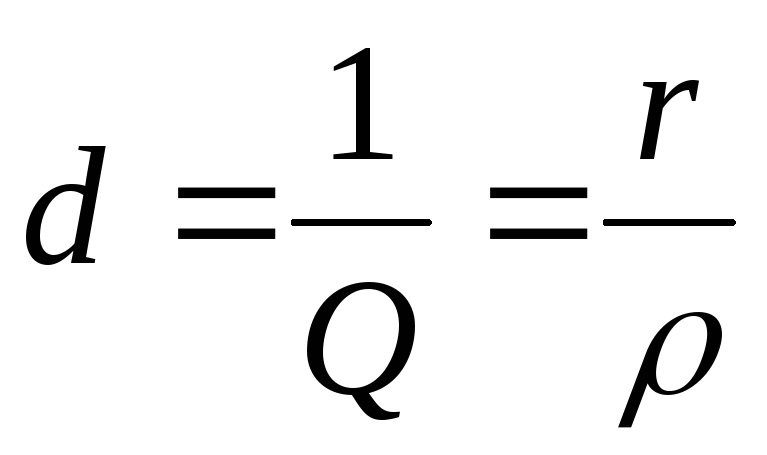Как следует из приведенных соотношений, добротность и затухание являются безразмерными величинами. Поскольку во всех элементах цепи, изображенной на рис. 10.1а протекает один и тот же ток, добротность показывает, во сколько раз напряжение на реактивных элементах при резонансе превышает входное напряжение. В реальных колебательных контурах эта величина может достигать значительного уровня. Поэтому резонанс в цепи с последовательным соединением элементов r ,L ,C иногда называютрезонансом напряжений.

При резонансной частоте полное сопротивление z

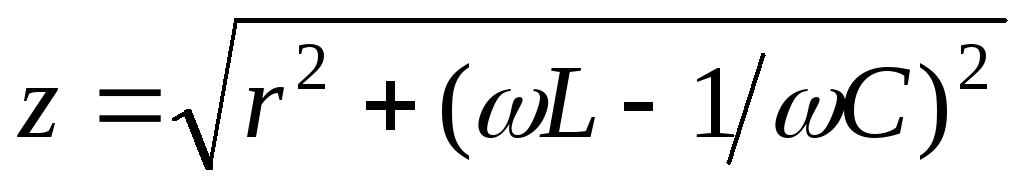
равно сопротивлению резистора r , ток и входное напряжение совпадают по фазе.

Таким образом, вся мощность, поставляемая в цепь источником, равна активной мощности, потребляемой единственным резистивным элементом, а реактивная мощность цепи равна нулю. Это означает, что в резонансе взаимный обмен энергии происходит только между конденсатором и катушкой индуктивности. Уменьшение энергии электрического поля при разряде конденсатора сопровождается увеличением энергии магнитного поля катушки и наоборот. Обмен энергией между источником и реактивными элементами отсутствует.

Рассмотрим частотные свойства цепи с последовательно соединенными элементами r ,L ,C . Будем считать, что на входе цепи действует синусоидальное напряжение с постоянной амплитудой и угловой частотой 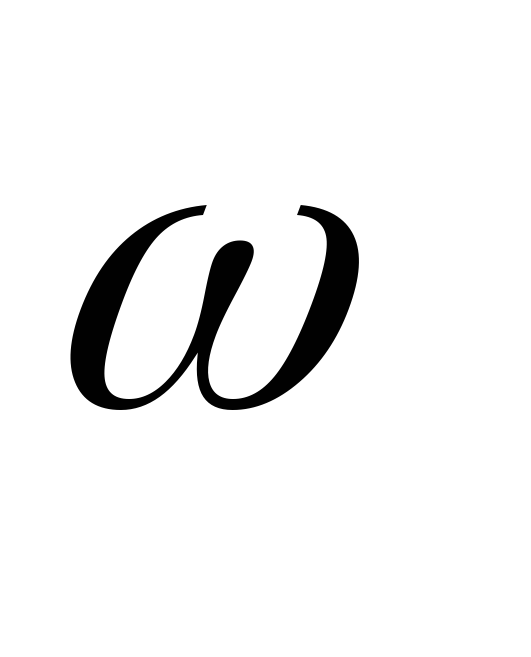, меняющейся в пределах от 0 до ∞ . Изменение частоты приводит к изменению параметров цепиx , z , . На рисунке 10.2 приведены соответствующие частотные характеристики

,

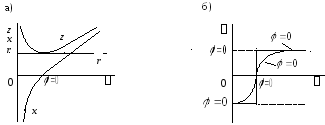Рис. 10.2

Активное сопротивление рассматриваемой цепи не зависит от частоты, а реактивное при определенных значениях частоты ( ) становится равным либо нулю либо бесконечности. Эти характерные значения называют соответственно нулями и полюсами частотной характеристики. Важным свойством функции

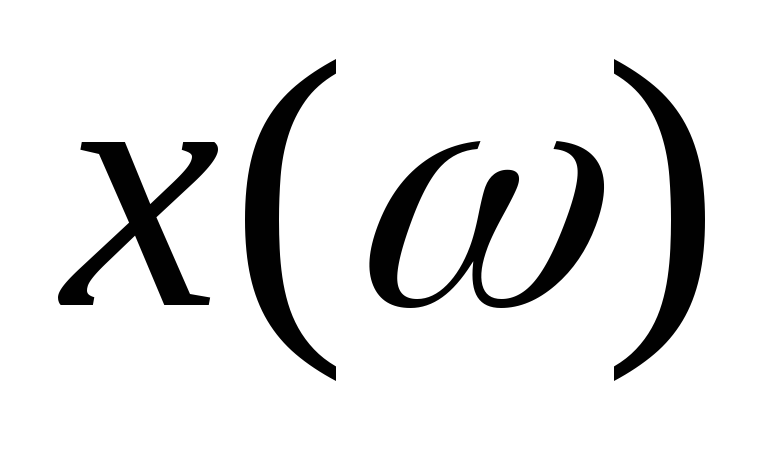
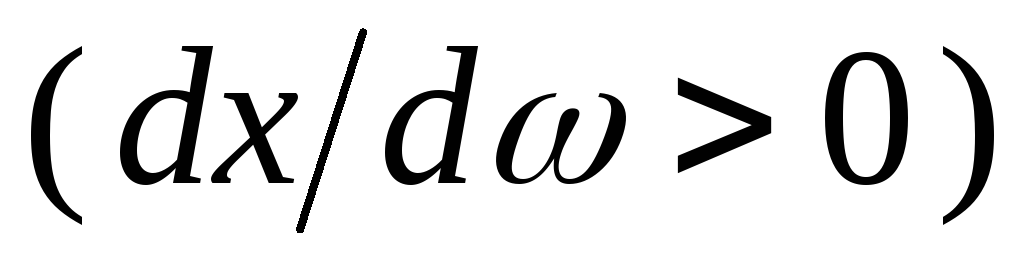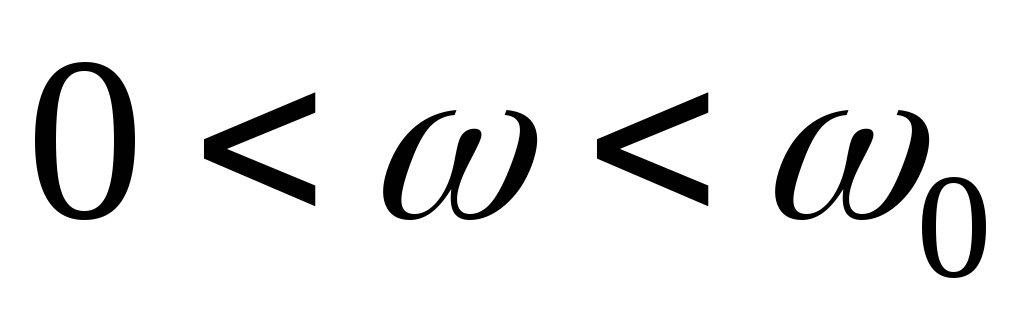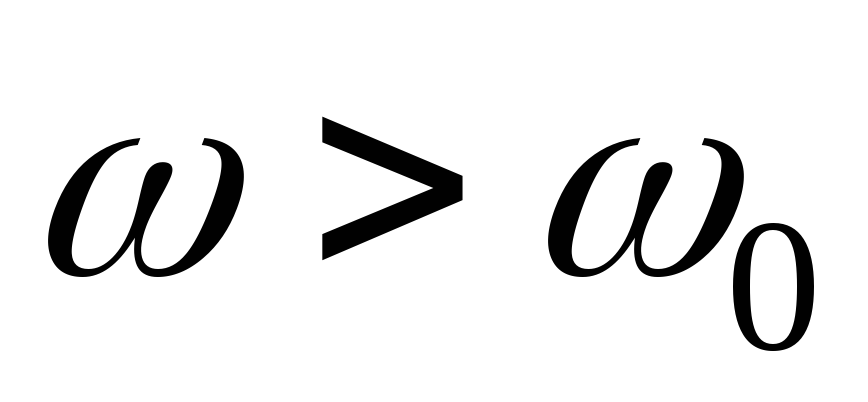является то, что она монотонно возрастает при увеличении частоты. В интервале частотреактивное сопротивление возрастает от − ∞ до 0 и имеетемкостнойхарактер, приреактивное сопротивление возрастает от 0 до ∞ и имеетиндуктивныйхарактер.

Рассмотрим зависимость тока в rLC контуре от частоты приложенного напряжения:

.

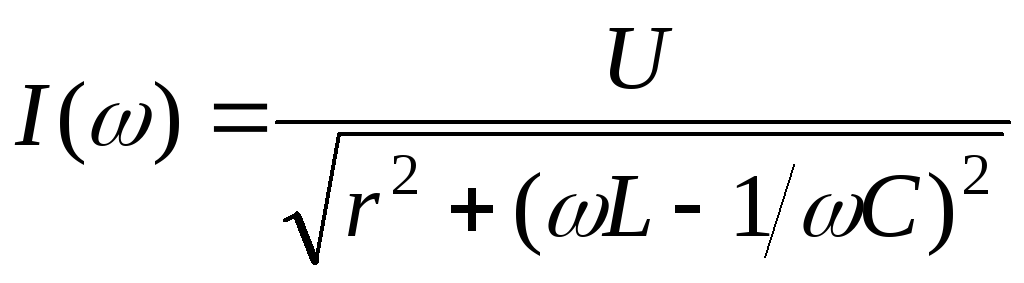
Анализ этого выражения показывает, что при 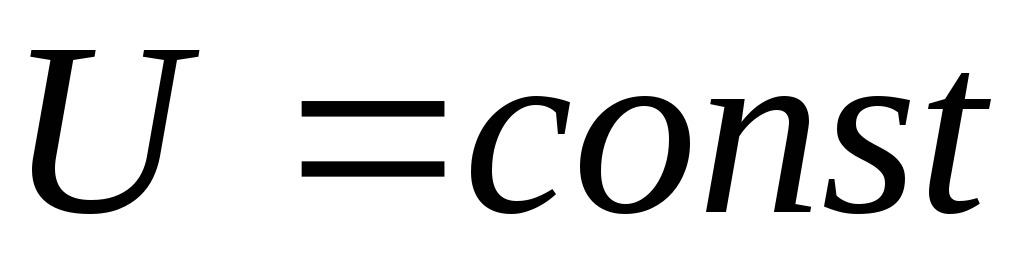максимального значения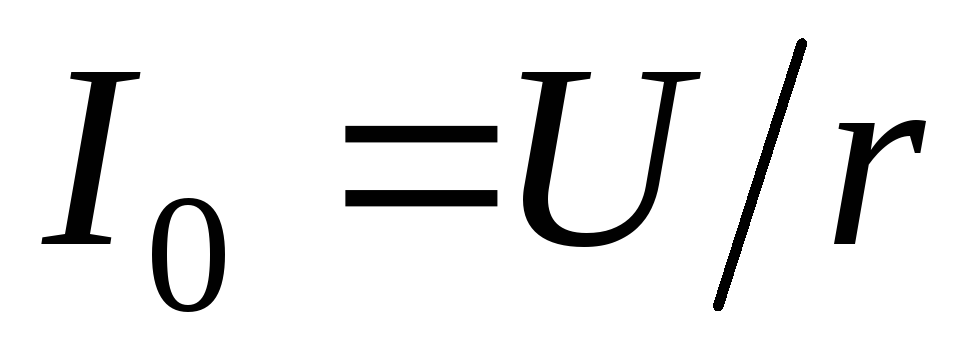ток достигает в точке, соответствующей резонансной частоте.

Важной характеристикой rLC контура является ширина резонансной кривой или полоса пропускания, которую определяют как разность верхнейи нижней

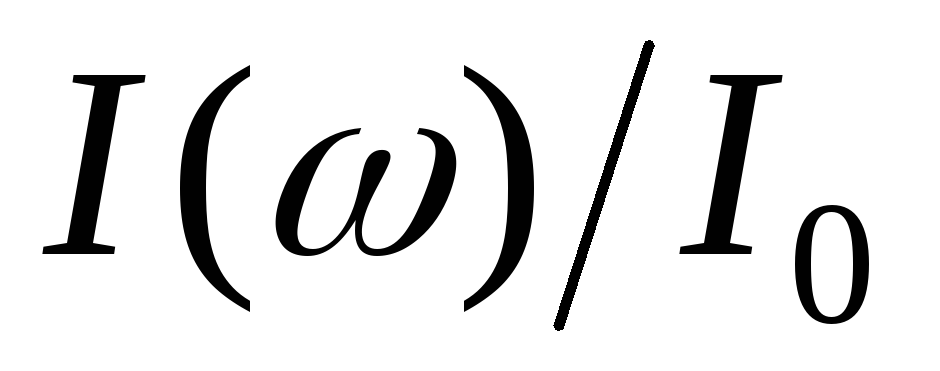частот, для которых отношениесоставляет:

.

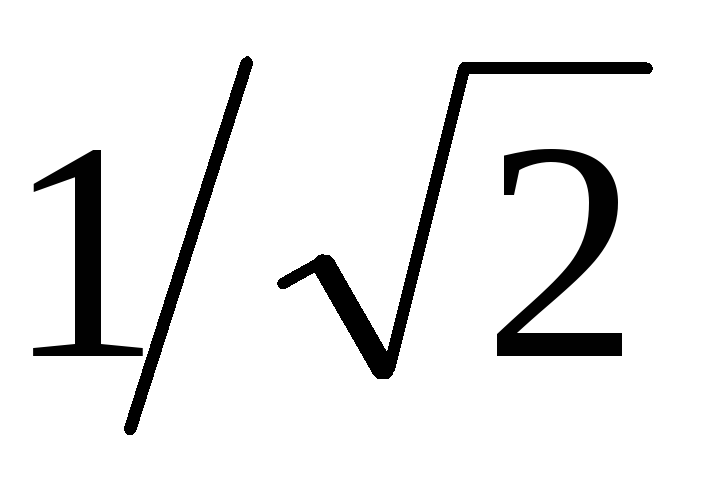Частоты 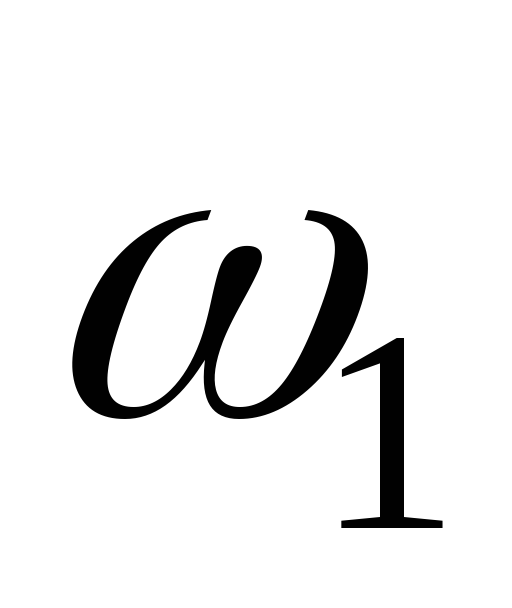и, ограничивающие полосу пропускания, могут быть определены из соотношения

,

откуда следует, что на границах полосы пропускания реактивные сопротивления по абсолютной величине равны активному

.

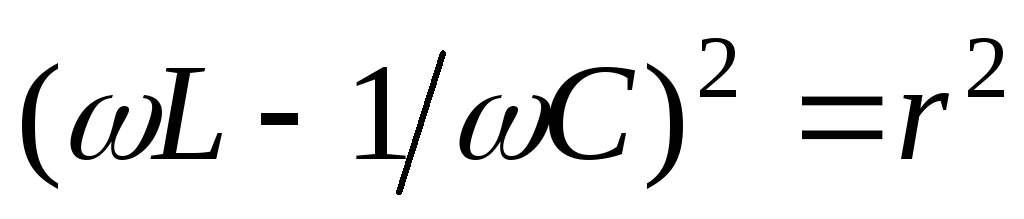Последнее соотношение эквивалентно равнству

,

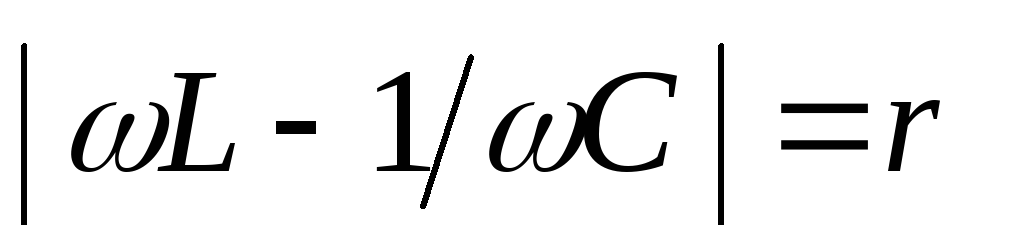Откуда ,.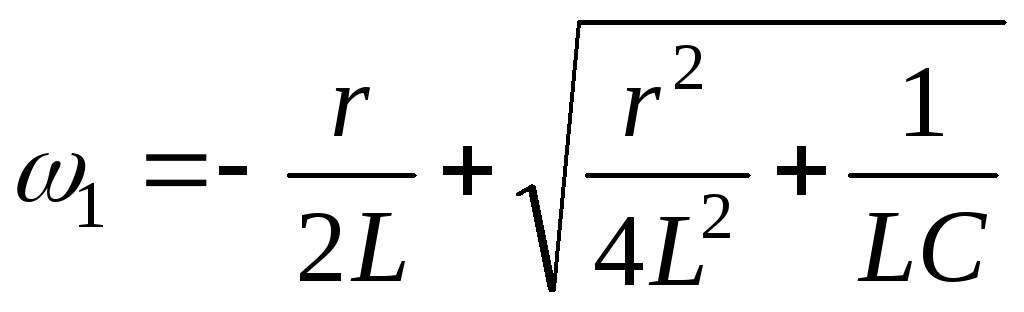

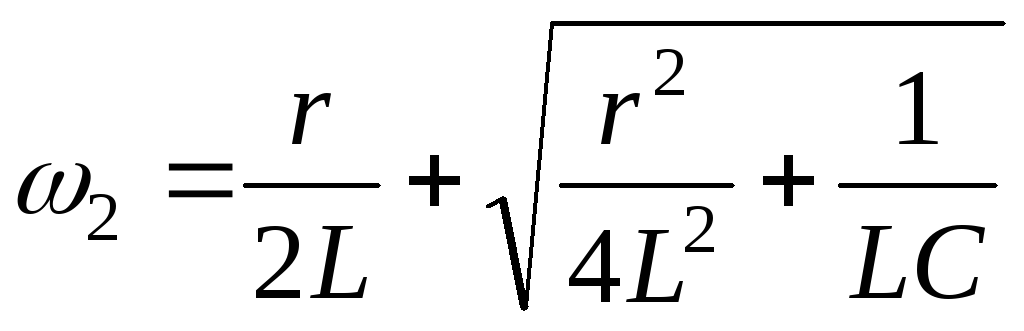Разность частот 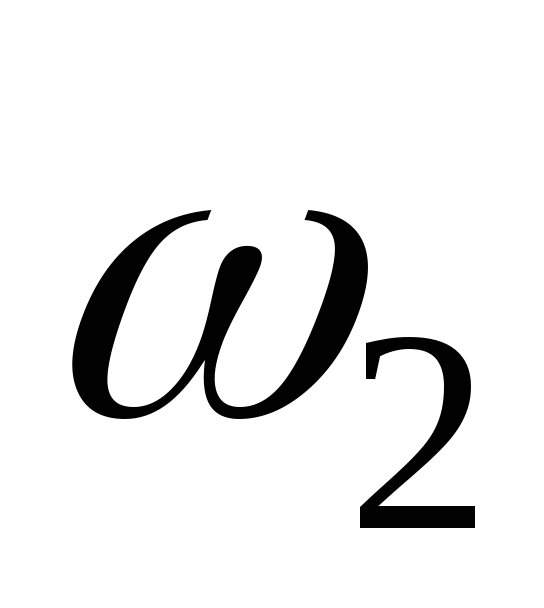и( полоса пропускания ) определяется выражением

Если построить зависимость 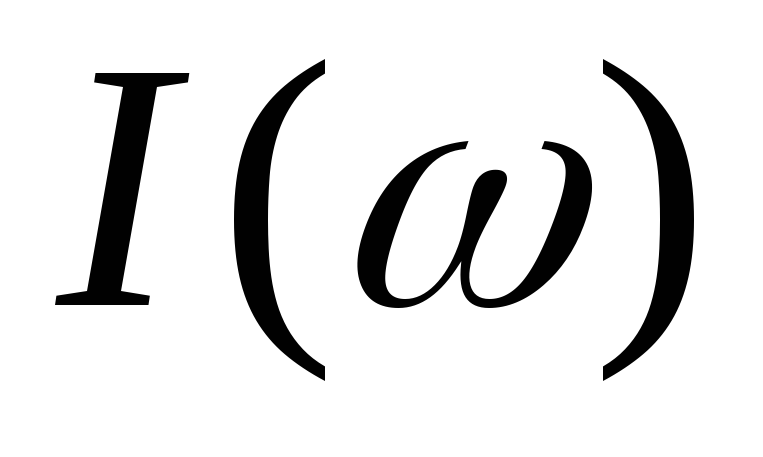в системе относительных координат,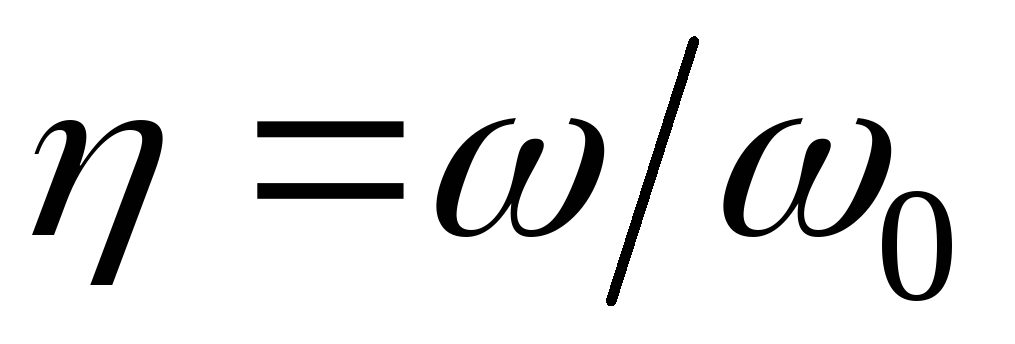(рис.10.3), то ширина полосы пропускания оказывается равной затуханию контура.

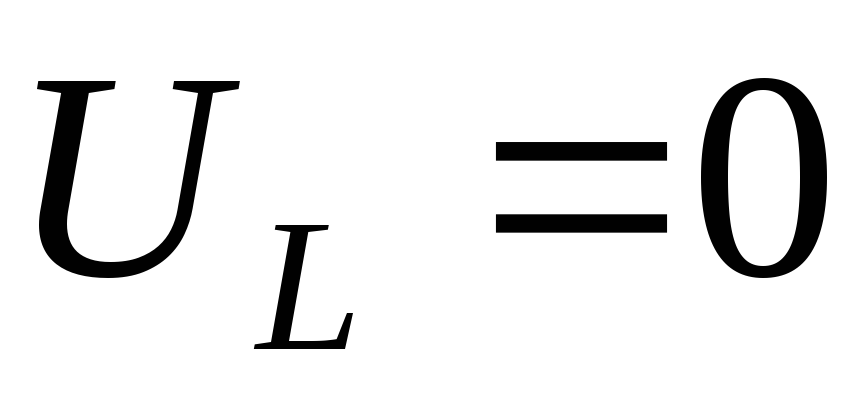В выражении напряжения на катушке индуктивности оба сомножителя зависят от частоты. Принапряжение. С увеличением частоты напряжение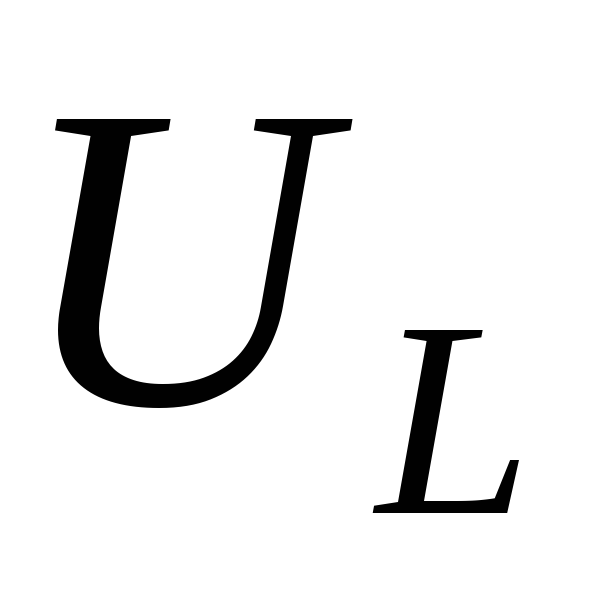возрастает и стремится к входному при. Можно показать, что при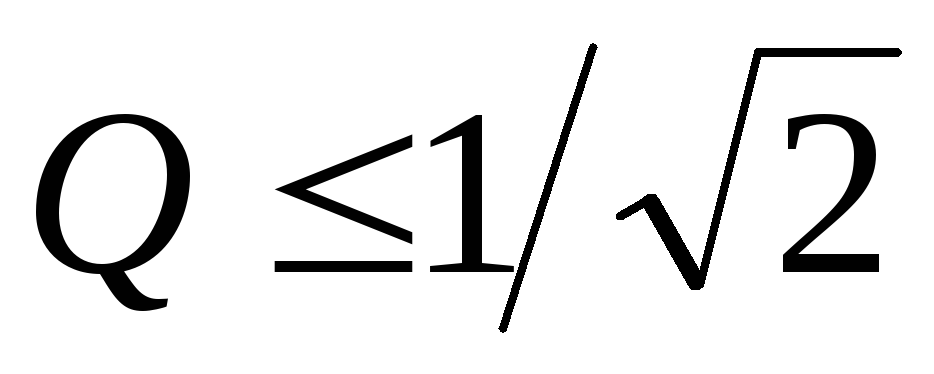эта зависимость монотонна, а приимеет максимум ( рис. 10.4 ).

Напряжение на конденсаторе 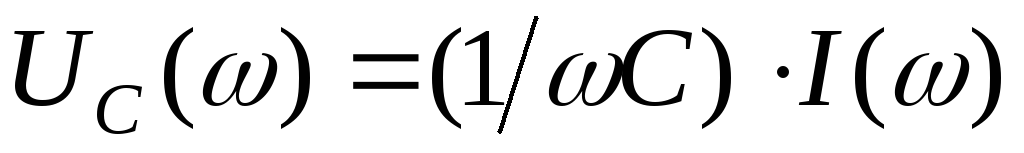. Приток в контуре отсутствует и все входное напряжение оказывается приложенным к конденсатору. При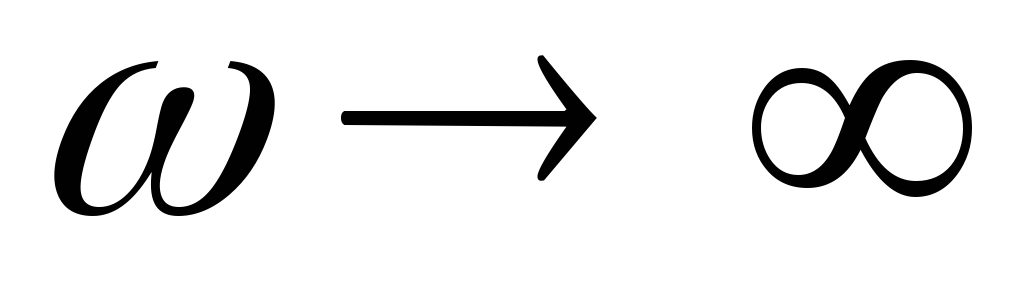напряжение на конденсаторе стремится к нулю. Для цепи, добротность которой превышает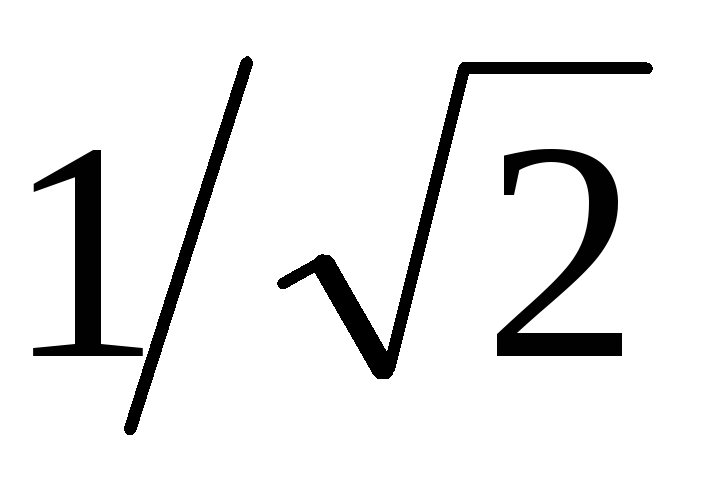, зависимость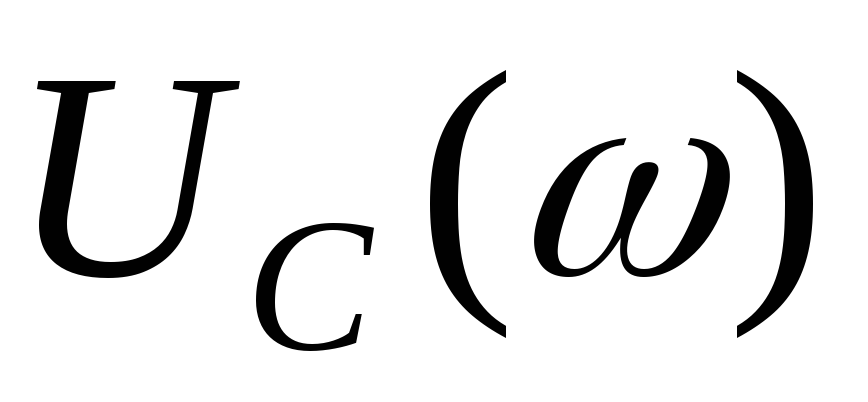имеет максимум; если, напряжение на конденсаторе монотонно уменьшается с ростом частоты.

ТОЭ Лекции — №27 Явление резонанса в электрических цепях

Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер: Z = R; сдвиг фаз отсутствует (φ=0).

В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным характерами сопротивлений, резонанс называется резонансом напряжений. Рассмотрим простейшую цепь, которую часто называют последовательным контуром. Для нее резонанс наступает при x = xL – xC = 0 или xL = xC, откуда:

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 27.1, а).

Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений:

Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.

Из условия выше следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 27.2). Емкость С0, при которой наступает резонанс, можно определить из формулы: С0=1/(ω2L).

Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C. Векторная диаграмма ее резонансного режима приведена на рис. 27.1, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 27.3, а).

Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.

Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:

Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:

или

Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B1 и B2. Заменяя схему на рис. 27.3, а эквивалентной (рис. 27.3, б), параметры которой вычисляем по формулам, и используя условие резонанса (B = B1 – B2 = 0), снова приходим к конечному выражению.

Схеме на рис. 27.3, б соответствует векторная диаграмма, приведенная на рис. 27.4

Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.

Понятие о резонансе в электрических цепях

низких частот может быть приближенно заменен прямой, имеющей наклон 6 дБ/окт, а в области высоких частот — прямой, параллельной оси частот.

Амплитудно частотные характеристики пассивных линейных цепей с одним реактивным элементом имеют вид монотонно изменяющихся кривых, поэтому ам плитуда отклика этих цепей монотонно изменяется при увеличении или уменьше нии частоты внешнего воздействия. Более сложный характер имеют процессы в электрических цепях, содержащих реактивные элементы различных типов. Ампли туда отклика этих цепей может резко изменяться, когда частота внешнего воздейст вия достигает некоторых определенных значений. Явление резкого возрастания ам плитуды отклика цепи при приближении частоты внешнего воздействия к опреде ленному значению называется резонансом.

Такое определение резонанса заимствовано из механики и оказывается не удобным для применения в теории цепей в связи с тем, что в общем случае различ ные величины, характеризующие процессы в электрической цепи, достигают мак симальных значений при различных, хотя, возможно, и очень близких значениях частоты. Возникает вопрос о том, какую именно из этих частот считать резонансной, или, другими словами, закон изменения какой величины следует наблюдать для решения вопроса о том, находится ли цепь в режиме резонанса. В отличие от приня тых в механике амплитудных критериев резонанса в теории цепей, как правило, применяют фазовый критерий резонанса, при этом под резонансом понимают та­ кой режим работы электрической цепи, содержащей емкости и индуктивности, при котором ее комплексное входное сопротивление имеет чисто резистивный харак­ тер, и, следовательно, сдвиг фаз между током и напряжением на входе равен нулю.

Частота, соответствующая фазовому критерию резонанса, может совпадать с частотой, соответствующей одному из амплитудных критериев резонанса. В частно сти, амплитуда тока последовательного колебательного контура принимает макси мальное значение на частоте, когда ток и напряжение на входе контура совпадают по фазе, причем эта частота будет несколько выше частоты, на которой амплитуда напряжения на емкости достигает максимального значения и несколько ниже час тоты, соответствующей максимуму амплитуды напряжения на индуктивности.

Для устранения неоднозначности при определении резонанса в дальнейшем бу­ дем использовать только фазовый критерий резонанса, и под резонансной частотой цепи будем понимать только значение частоты, соответствующее этому крите­ рию, т. е. частоту f0 = ⁄2 , при которой входное сопротивление цепи имеет чисто резистивный характер.

Электрические цепи, в которых имеют место явления резонанса, называют ре­ зонансными или колебательными.

Простейшей электрической цепью, в которой наблюдается явление резонанса, является одиночный колебательный контур, представляющий собой замкнутую

Резонанс в электрической цепи: причины резонанса

В том случае, когда электрическая цепь содержит элементы с емкостными, а также с индуктивными свойствами может возникнуть режим резонанса. Кроме того, резонанс в электрической цепи появляется в случае совпадения по фазе тока и напряжения. Реактивное сопротивление и проводимость на входе имеют нулевое значение. Полностью отсутствует сдвиг фаз, и цепь становится активной.

Причины резонанса

Резонанс напряжений появляется в случае последовательного соединения участков, содержащих сопротивления индуктивного и емкостного характера, а также резисторы. Такая простая цепь очень часто носит название последовательного или параллельного контура.

В резонансном контуре вовсе не обязательно присутствие резистивного сопротивления. Тем не менее, его необходимо учитывать при определении сопротивления проводников. Таким образом, резонансный режим полностью зависит от параметров и свойств электрической цепи. На него никак не влияют внешние источники электрической энергии.

Для того, чтобы определить условия, при которых возникает режим резонанса, необходимо проверить электрическую цепь с целью определения ее проводимости или комплексного сопротивления. Кроме того, её мнимая часть должна быть выделена и приравнена к нулю.

Характеристики резонанса

Все параметры, входящие в цепь, и присутствующие в полученном уравнении, так или иначе, влияют на показатели, характеризующие резонансные явления. В зависимости от параметров, входящих в состав уравнения, решение может иметь несколько различных вариантов. При этом, все решения будут соответствовать собственному варианту и в дальнейшем обретать физический смысл.

В различных видах электро цепей, явление резонанса рассматривается, как правило, при анализе в случае нескольких вариантов. В этих же случаях может проводиться синтез цепи, в котором заранее заданы резонансные параметры.

Электрические цепи которые имеют большое количество связей и реактивных элементов, представляют собой серьезную проблему при проведении анализа. Их никогда не используют при синтезе с заранее заданными свойствами, поскольку далеко не всегда возможно получение желаемого результата. Поэтому, в практической деятельности производится исследование двухполюсных приборов самых простых конструкций и на основании полученных данных проводится создание более сложных цепей с заранее заданными параметрами.

Таким образом, резонанс электрической цепи представляет собой достаточно сложное явление, благодаря использованию в ней определенных элементов. Учет этого явления позволяет наиболее полно определить параметры и прочие характеристики.

Резонансы токов и напряжений

Резонанс напряжений: формулировка, условие наступления, применение

Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.

Описание явления

Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.

Рис. 1. Резонанс в электрической цепи

Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.

Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.

Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.

Формула

Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: X_общ = X_L — X_c , где X_L = ωL — индуктивное реактивное сопротивление, выражение X_c = 1/ωC — это ёмкостное реактивное сопротивление.

На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости R_L (график б) и как при этом возрастает ток (график в).

Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления

Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).

Рис. 3. Последовательный колебательный контурРис. 4. Параллельный колебательный контур

В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:

Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:

K = U_вых / U_вх = U_C0 / U = Q

Формулировка

На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.

Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].

В случае, если X_L = X_c – справедливо равенство: ωL = 1/ωC , отсюда получаем:

Если ω = ω₀ – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):

где R – общее активное сопротивление.

Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.

Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.

Поскольку X_L и X_c зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.

Условия наступления

Резонансные явления наступают только при наличии следующих условий:

1. Наличие минимального активного сопротивления на участке электрической цепи.
2. Равенство реактивных сопротивлений, возникших на цепочке LC.
3. Совпадение входной частоты источника питания с резонансной частотой колебательного контура.

При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.

Примеры применения на практике

Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.

В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.

Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.

Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.

Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Катушки индуктивности

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.

Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.