формула индуктивности катушки и резонансной частоты

Любая колебательная система характеризуется собственной частотой. Если на систему периодически воздействовать извне, и частота воздействия будет совпадать с внутренней периодичностью возмущения силового поля материи, то можно наблюдать резкое увеличение амплитуды колебаний. Данное явление является резонансом. Для ремонта и конструирования радиотехнических устройств необходимо уметь производить расчет резонансных частот колебательных контуров.

Что такое колебательный контур

Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.

Параллельный контур колебаний

При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.

Как работает контур колебаний

Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.

Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.

Процессы в системе

Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.

Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.

Осциллограмма

При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.

Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.

Зависимость предельной частоты от добротности

Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.

Формула индуктивности

Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:

• Количество и расположение витков обмотки;
• Наличие или отсутствие сердечника;
• Материал сердечника.

Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.

Приборы индуктивности различных типов

Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.

Формула резонансной частоты

Формула резонансной частоты колебательного контура не зависит от его типа, а также от метода подключения – последовательного или параллельного. Выглядит она следующим образом:

f0=1/(2∙π∙√L∙C),

где f0 – частота резонанса

Как видно из формулы, для получения заданной частоты резонанса, существует бесконечное количество пар емкостей и индуктивностей. На деле, от выбранного соотношения параметров зависит также и добротность.

Как правильно рассчитать частоту контура колебаний

Для последовательного колебательного контура добротность растет с увеличением значения индуктивности. Таким образом, при расчетах элементов, следует учитывать величину добротности. Также, необходимо иметь в виду, что емкости конденсаторов выбираются из стандартного ряда значений, и на этом основании изготавливается катушка индуктивности.

Явление резонанса позволяет использовать колебательные контуры в качестве частотно зависимых цепей и в элементах фильтров. Радиоприемные устройства наиболее широко используют избирательные свойства колебательных систем. Если вместо емкости использовать кварцевый резонатор, то можно получить электрическую цепь с катушкой индуктивности, обладающей очень высокой добротностью. Такие схемы широко используются в задающих генераторах, где требуется высокая точность для определения периода изменения направления частиц.

§ 3. РЕЗОНАНС

tgϕ =

2βω

;

(4.7)

ω02 − ω2

ϕ = arctg

2βω

.

(4.8)

ω2 − ω2

0

По теореме Пифагора:

f 02 = (ω2 −ω2 )2 A 2

+ 4β2 A 2

ω2 .

0

Амплитуда вынужденных колебаний равна:

A(ω ) =

f 0

.

(4.9)

(ω02 −ω2)2 + 4β2 ω2

Амплитуда вынужденных колебаний зависит от частоты вынуждающей

силы.

Проанализируем, как амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота ωрез – резонансной. Для определения ωрез исследуем функцию A(ω) (формула (4.9)) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω). Возьмем от него производную по ω и приравняем к нулю:

— 2(w20 — w2) × 2w + 8 b2 w = 0,

откуда резонансная частота:

ωрез = ω02 − 2β2			.	(4.10)

При 2β2 > ω20 резонанс отсутствует ( ωрез – мнимое число).

Амплитуда при резонансе

Амплитуда при резонансе получается при подстановке найденного выражения ωрез (4.10) в формулу для A(ω) (4.9):

Aрез =		f 0		.	(4.11)
	2β
		ω02	− β2

Из (4.11) следует, что при уменьшении коэффициента затухания β резонансная амплитуда возрастет. Если β→0, то Арез→∞. При этом резонансная

частота (4.10) стремится к частоте незатухающих собственных колебаний ω0.

При β<<ω0:

	Aрез ≈	f 0	.	(4.12)
		2β ω0

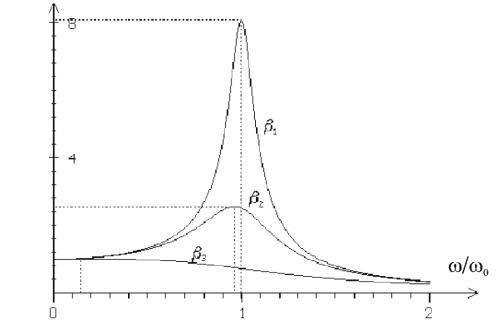
Резонансные кривы е

Графики зависимости A(ω) при различных β носят название резонансных кривых. Они представлены на рис. 4.4.

А(ω)/A(0)

Рис. 4.4

На рис 4.4β1<β2<β3. В случае, если 2β32 > ω02 – резонанса нет.

Резонанс необходимо учитывать в технике. Жилые дома, промышленные корпуса, железные дорог и, мосты, туннели и т. д. являютс я колебательными системами, в которых при определенных условиях могут возникать вынужденные колебания . Иногда амплитуда вынужденных колебаний становится столь большой , что это может вызвать разрушения. В ряде случаев резонанс может давать пол ожительный эффект, например, при погружении свай и труб на строительстве м орских и озерных сооружений.

Исключительно важ ную роль играет резонанс в радиотехникеи электронике, где резонан сные свойства колебательного контура и других резонансных электрических систем используются для вы деления сигналов нужной частоты. Например, настройка на нужную ст анцию радио- и телевизионных приемников производится путем изменения со бственных частот колебательных контуров в этих устройствах.

ИТОГИ ЛЕКЦИИ № 4

1. Вынужденные колебания возникают в том сл учае, когда на колеблющуюся систему действует внешняя периодически изменяющаяся сила.

2. Частота установившихся вынужденных колебаний равна частоте вынуждающей силы. Дифференциальное уравнение, описывающее вынужденные колебания, имеет вид (4.2):

	∙∙		∙
	ξ	(t) + 2bξ(t) + ω02 x(t) = f 0			× cos wt .
	3. Амплитуда установившихся вынужденных колебаний зависит от
амплитуды вынуждающей силы f0 и ее частоты ω (4.9):
		A(ω) =		f 0				.
				(ω02 −ω2)2 + 4β2 ω2

4. Резонансом называют резкое возрастание амплитуды вынужденных колебаний, происходящее при приближении частоты вынужденных колебаний к резонансной частоте колебаний системы. Амплитуда при резонансе дается формулой (4.11):

	Aрез =		f 0		.
		2β	ω02 − β2

5. Резонансная частота ωрез зависит от частоты собственных колебаний ω0 и коэффициента затухания β (4.10):

ωрез = 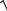ω20 − 2β2 .

При 2β2> ω20 резонанса нет.

ВОЛНЫ

ЛЕКЦИЯ № 5

Волны в упругой среде

Упругие волны. Основные определения для волнового процесса. Уравнение плоской волны. Фазовая скорость.

Уравнение сферической волны. Волновое уравнение

§ 1. УПРУГАЯ ВОЛНА

Среда называется упругой, если между ее частицами существуют силы взаимодействия, препятствующие какой-либо деформации этой среды. Существует объемная упругость и упругость формы. Например, давление газов на стенки сосуда обеспечивает способность газов сопротивляться изменению их объема. В то же время, газы беспрепятственно изменяют свою форму. Следовательно, газы обладают объемной упругостью, но не обладают упругостью формы. Такими же свойствами обладают жидкости. Твердые тела обладают как объемной упругостью, так и упругостью формы.

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться в среде от частицы к частице, создавая упругие волны. Колебания твердых тел при взрывах и землетрясениях, звуковые волны – все это примеры упругих волн.

Частицы среды при волновом процессе не переносятся волной, а лишь колеблются около своих положений равновесия. Причем, вследствие инерции колебания частиц сдвинуты по фазе. Распространение колебаний в среде связано с передачей энергии от одной колеблющейся частицы к другой. Таким образом, волны переносят энергию от одной колеблющейся частицы к другой.

Итак, упругая волна – это процесс распространения механических колебаний вупругой среде. Характерное свойство волны – перенос энергии без переноса вещества.

Для описания волны надо ввести функцию, в общем случае – векторную, задающую смещение от положения равновесия каждой частицы упругой среды

для любого момента времени. Обозначим эту функцию греческой буквой ξ

(кси). Аргументами ее, в соответствии с вышесказанным, будут три пространственные переменные – x, y, z, задающие положение частицы (или радиус-вектор r ) и время t, т. е.

ξ = ξ(x, y, z, t) = ξ(r, t) .

Скорость движения частиц упругой среды – это частная производная от смещения по времени, т. е.

		=	∂ξ(r, t) .
	vr
			∂t

Параметрический осциллятор — Википедия

Параметрический осциллятор — осциллятор, параметры которого могут изменяться в определённой области.

Параметрический осциллятор принадлежит к классу незамкнутых колебательных систем, в которых внешнее воздействие сводится к изменению во времени её параметров. Изменения параметров, например, собственной частоты колебаний ω или коэффициента затухания β, приводит к изменению динамики всей системы.

Всем известный пример параметрического осциллятора — это ребенок на качелях, где периодически изменяющаяся высота центра массы означает периодическое изменение момента инерции, что приводит к увеличению амплитуды колебаний качелей [3, с. 157]. Другим примером механического параметрического осциллятора служит физический маятник, точка подвеса которого совершает заданное периодическое движение в вертикальном направлении, или математический маятник, длина нити которого может периодически изменяться.

Широко используемым на практике примером параметрического осциллятора может служить используемый во многих областях параметрический генератор. Периодическое изменение ёмкости диода с помощью специальной схемы, называемой «насосом», приводит к классическим колебаниям варакторного параметрического генератора. Параметрические генераторы были разработаны в качестве малошумящих усилителей, которые особенно эффективны в радио- и микроволновом диапазоне частот. Поскольку в них периодически изменяются не активные (омические), а реактивные сопротивления, тепловые шумы в таких генераторах минимальны. В СВЧ-электронике волновод / ИАГ на основе параметрического осциллятора действует таким же образом. Для того, чтобы в системе возбудить параметрические колебания, конструкторы периодически изменяют параметр системы. Ещё одним классом приборов, часто использующих метод параметрических колебаний, являются преобразователи частоты, в частности, преобразователи от аудио к радиочастотам. Например, оптический параметрический генератор преобразует входную волну лазера в две выходные волны более низкой частоты (ωs, ωi). С параметрическим осциллятором тесно связано понятие параметрического резонанса.

Параметрический резонанс — это увеличение амплитуды колебаний в результате параметрического возбуждения. Параметрическое возбуждение отличается от классического резонанса, поскольку создаётся в результате временного изменения параметров системы и связано с её стабильностью и устойчивостью.

Параметрами одномерного осциллятора, движущегося с трением, являются его масса m{\displaystyle m}, коэффициент упругости k{\displaystyle k} и коэффициент затухания β{\displaystyle \beta }. Если эти коэффициенты зависят от времени, и m=m(t),k=k(t),β=β(t){\displaystyle m=m(t),k=k(t),\beta =\beta (t)}, то уравнение движения имеет вид

ddt(mx˙)+βx˙+kx=0,{\displaystyle {\frac {d}{dt}}(m{\dot {x}})+\beta {\dot {x}}+kx=0,}

(1){\displaystyle (1)}

Сделаем замену переменной времени t{\displaystyle t} →τ{\displaystyle \tau }, где dτ=dt/m(t){\displaystyle d\tau =dt/m(t)}, что приводит уравнение (1) к виду

d2xdτ2+βdxdτ+kmx=0,{\displaystyle {\frac {d^{2}x}{d\tau ^{2}}}+\beta {\frac {dx}{d\tau }}+kmx=0,}

(2){\displaystyle (2)}

Сделаем еще одну замену x(τ){\displaystyle x(\tau )} → q(τ){\displaystyle q(\tau )}:

q(τ)=expB(τ)⁡x(τ),B(τ)=12∫0τβ(ξ)dξ,{\displaystyle q(\tau )=\exp ^{B(\tau )}x(\tau ),B(\tau )={\frac {1}{2}}\int _{0}^{\tau }\beta (\xi )d\xi ,}

(3){\displaystyle (3)}

Это позволит избавиться от члена, связанного с затуханием:

d2qdτ2+δ2(τ)q=0,δ2(τ)=km−β˙2−β24,{\displaystyle {\frac {d^{2}q}{d\tau ^{2}}}+\delta ^{2}(\tau )q=0,\delta ^{2}(\tau )=km-{\frac {\dot {\beta }}{2}}-{\frac {\beta ^{2}}{4}},}

(4){\displaystyle (4)}

Поэтому фактически, без всякого ограничения общности, вместо уравнения (1) достаточно рассмотреть уравнение движения вида

d2xdt2+ω2(t)x=0,{\displaystyle {\frac {d^{2}x}{dt^{2}}}+\omega ^{2}(t)x=0,}

(5){\displaystyle (5)}

которое получилось бы из уравнения (1) при m=const{\displaystyle m=const}.

Интересно, что в отличие от случая постоянной частоты ω2(t)=ω02{\displaystyle \omega ^{2}(t)=\omega _{0}^{2}}, аналитическое решение уравнения (5) в общем виде неизвестно. В частном случае периодической зависимости ω(t){\displaystyle \omega (t)} уравнение (5) является уравнением Хилла, а в случае гармонической зависимости ω(t){\displaystyle \omega (t)} — частным случаем уравнения Матье. Наиболее хорошо уравнение (5) изучено в случае, когда частота колебаний гармонически изменяется относительно некоторого постоянного значения.

---

1. Рассмотрим случай, когда ω2(t)=ω02[1+hcos⁡(ω0+ε)t]{\displaystyle \omega ^{2}(t)=\omega _{0}^{2}[1+h\cos(\omega _{0}+\varepsilon )t]}, то есть уравнение (5) имеет вид

d2xdt2+ω02[1+hcos⁡(ω0+ε)t]x=0,{\displaystyle {\frac {d^{2}x}{dt^{2}}}+\omega _{0}^{2}[1+h\cos(\omega _{0}+\varepsilon )t]x=0,}

(6){\displaystyle (6)}

Где ω0{\displaystyle \omega _{0}} — частота собственных гармонических колебаний, амплитуда гармонических вариаций частоты h≪1{\displaystyle h\ll 1}, постоянная ε≪ω0{\displaystyle \varepsilon \ll \omega _{0}} — небольшая вариация частоты. Надлежащим изменением начала отсчета времени постоянную h можно выбрать положительной, поэтому, не ограничивая общности, будем считать, что h>0{\displaystyle h>0}. Вместо решения уравнения (6) поставим более скромный вопрос: при каких значения параметра ε{\displaystyle \varepsilon }, происходит резкое возрастание амплитуды колебаний, то есть решение x(t){\displaystyle x(t)} неограниченно возрастает? Можно показать [1], что это происходит в том случае, когда

−524<εh3ω0<124,{\displaystyle -{\frac {5}{24}}<{\frac {\varepsilon }{h^{2}\omega _{0}}}<{\frac {1}{24}},}

(7){\displaystyle (7)}

2. Рассмотрим случай, когда ω2(t)=ω02[1+hcos⁡(2ω0+ε)t]{\displaystyle \omega ^{2}(t)=\omega _{0}^{2}[1+h\cos(2\omega _{0}+\varepsilon )t]} , то есть уравнение (5) имеет вид

d2xdt2+ω02[1+hcos⁡(2ω0+ε)t]x=0,{\displaystyle {\frac {d^{2}x}{dt^{2}}}+\omega _{0}^{2}[1+h\cos(2\omega _{0}+\varepsilon )t]x=0,}

(8){\displaystyle (8)}

Иными словами, гармоническое изменение свободных колебаний происходит с частотой y=2ω0+ε{\displaystyle y=2\omega _{0}+\varepsilon }. В этом случае параметрический резонанс, с точностью до членов h3{\displaystyle h^{2}}, происходит в случае, когда

−132h−12<εhω0<−132h+12,{\displaystyle -{\frac {1}{32}}h-{\frac {1}{2}}<{\frac {\varepsilon }{h\omega _{0}}}<-{\frac {1}{32}}h+{\frac {1}{2}},}

(9){\displaystyle (9)}

В частности, укажем условия параметрического резонанса для малых колебаний математического маятника с колеблющейся в вертикальном положении точкой подвеса, для которого уравнения колебаний имеют вид

ϕ¨+ω02[1+4alcos⁡(2ω0+ε)t]ϕ=0,{\displaystyle {\ddot {\phi }}+\omega _{0}^{2}[1+{\frac {4a}{l}}\cos(2\omega _{0}+\varepsilon )t]\phi =0,}

(10){\displaystyle (10)}

где ω02=gl{\displaystyle \omega _{0}^{2}={\frac {g}{l}}}, и h=4al{\displaystyle h={\frac {4a}{l}}}. В случае, когда a≪l{\displaystyle a\ll l} и ограничиваясь первым порядком разложения по h{\displaystyle h}, получим, что

−2agl32<ε<2agl32,{\displaystyle -{\frac {2a{\sqrt {g}}}{l^{\frac {3}{2}}}}<\varepsilon <{\frac {2a{\sqrt {g}}}{l^{\frac {3}{2}}}},}

(11){\displaystyle (11)}

Тот факт, что параметрический резонанс происходит в окрестности частоты свободных колебаний ω=ω0{\displaystyle \omega =\omega _{0}} и её удвоенного значения ω=2ω0{\displaystyle \omega =2\omega _{0}}, — не случаен. Можно показать (см. напр. [2]), что в случае уравнения

d2xdt2+ω02[1+hcos⁡(ωt)]x=0,{\displaystyle {\frac {d^{2}x}{dt^{2}}}+\omega _{0}^{2}[1+h\cos(\omega t)]x=0,}

(12){\displaystyle (12)}

Параметрический резонанс имеет место, когда

ω=2ω0n,n=1,2,…,{\displaystyle \omega ={\frac {2\omega _{0}}{n}},n=1,2,…,}

(13){\displaystyle (13)}

Главный резонанс происходит при удвоенной частоте собственных колебаний гармонического маятника ω0{\displaystyle \omega _{0}}, а ширина резонанса равна hω0{\displaystyle h\omega _{0}}. Важно также, что при наличии трения (см. ур-е (2)), в уравнении

d2xdt2+3γdxdt+ω02[1+hcos⁡(ωt)]x=0,{\displaystyle {\frac {d^{2}x}{dt^{2}}}+3\gamma {\frac {dx}{dt}}+\omega _{0}^{2}[1+h\cos(\omega t)]x=0,}

(14){\displaystyle (14)}

Имеет место явление параметрического резонанса не при любых h≪1{\displaystyle h\ll 1}, а лишь при тех h>4γω02−γ2{\displaystyle h>{\frac {4\gamma }{\omega _{0}^{2}-\gamma ^{2}}}}. Т.о., при наличии трения

4γω02−γ<h≪1,{\displaystyle {\frac {4\gamma }{\omega _{0}^{2}-\gamma }}<h\ll 1,},

(15){\displaystyle (15)}

что позволяет надлежащим выбором параметров γ{\displaystyle \gamma },ω0{\displaystyle \omega _{0}}, и h{\displaystyle h}, в зависимости от практической необходимости, усилить или ослабить явление параметрического резонанса.

1. Пример параметрической неустойчивости [1]

1. Броуновский параметрический осциллятор [2]

[1] Л. Д. Ландау, Е. М. Лифшиц. Курс теоретической физики I. Механика. Москва. Наука. 1973 с. 103—109

[2] А. М. Федорченко. Теоретическая механика. 1975. Киев. Высшая школа. 516 с.

[3] К. Магнус. Колебания: Введение в исследование колебательных систем. 1982. Москва. Мир. 304 с.

Резонансная частота — это… Что такое Резонансная частота?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.

Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.

В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Электроника

В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Примечания

См. также

Ссылки

Richardson LF (1922), Weather prediction by numerical process, Cambridge.

Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.

Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.

Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.

Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.

Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.

Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.

Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.

Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука

Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М.: Наука — 232 с.

Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука

Wikimedia Foundation. 2010.
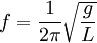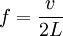
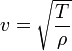
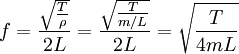