Резонанс — урок. Физика, 9 класс.

если вам случалось путешествовать на поезде, то наверняка вы обратили внимание на заметное, сильное  раскачивание железнодорожного вагона при случайном совпадении его собственной частоты колебаний на рессорах с частотой ударов колёс на стыках рельсов.

 

 

Ещё один очень яркий пример проявления явления резонанса — это несколько случаев обрушения мостов, когда по ним строевым шагом проходила рота солдат.

Чеканный шаг солдатских сапог совпал с собственной частотой колебаний моста. Мост стал колебаться с такой амплитудой, на которую его прочность не была рассчитана и… развалился. Тогда и родилась новая воинская команда «…не в ногу». Она звучит, когда пешая или конная рота солдат проходит по мосту.

Однако самый яркий пример разрушительного действия резонанса — это рухнувший \(7\) ноября \(1940\) года почти двухкилометровый Такомский подвесной мост в США (штат Вашингтон).

 

 

Данный случай и видео волнообразного раскачивания конструкции даже рекомендованы к просмотру на факультетах физики некоторых университетов — как самый хрестоматийный пример такого явления резонанса.

Разрушение подвесного моста под действием ветра — это иллюстрация того, как относительно постоянная сила вызывает резонанс. При этом происходит следующее:

 

1. порыв ветра отклоняет часть конструкции в сторону движения ветра — внешняя сила способствует возникновению колебаний;

2. при обратном движении конструкции сопротивления воздуха недостаточно, чтобы погасить колебание или значительно снизить его амплитуду;

3. вследствие упругости системы начинается новое движение по ветру, которое он (ветер) и усиливает, продолжая дуть в одном направлении.

Это пример поведения комплексного объекта, где резонанс развивается на фоне высокой добротности и значительной упругости под действием постоянного воздействия силы в одном направлении. К сожалению, Такомский мост — это не единственный пример обрушения конструкций. Случаи, аналогичные описанному, наблюдались и наблюдаются по всему миру, в том числе и в России.

Звуковой резонанс — урок. Физика, 9 класс.

Рассмотрим явление резонанса звуковых колебаний.

 

Обрати внимание!

При резонансе амплитуда установившихся вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с собственной частотой колебательной системы.

Пример:

допустим, вы шагаете по тонкой доске, перекинутой через речку. Когда частота ваших шагов совпадёт с частотой или периодом всей системы (доска-человек), то доска начинает сильно колебаться (гнуться вниз и вверх). Если вы продолжите двигаться такими же шагами, то резонанс вызовет сильную амплитуду колебания доски, которая выходит за пределы допустимого значения системы, и это в конечном счёте приведёт к неминуемой поломке мостика.

Резонанс может быть вызван и действием звуковых волн.

 

Возьмём два камертона с одинаковыми собственными частотами и поставим их рядом, обратив отверстия ящиков, на которых они укреплены, навстречу друг другу (рис. \(1\)).

Ударяя резиновым молоточком по левому камертону, приведём его в колебание, а затем приглушим пальцами. Мы услышим звук, издаваемый правым камертоном, который отзывается на колебания левого камертона.

Звуковые волны, образованные левым камертоном, дойдя до правого камертона, возбуждают в нём вынужденные колебания. Поскольку собственные частоты колебаний камертонов одинаковы, то имеет место резонанс: правый камертон колеблется с наибольшей возможной амплитудой и издаёт звук.

 

Рис. \(1\)

 

Если изменить период колебания правого камертона, надев на его ножку небольшую муфточку, то он перестанет отзываться на колебания левого камертона.

При наличии на правом камертоне муфты его собственная частота колебаний меняется, и амплитуда колебаний уменьшается настолько, что звука мы не услышим.

 

Обрати внимание!

Ящики, на которых установлены камертоны (резонаторы), способствуют усилению звука и наиболее полной передаче энергии от одного камертона к другому.

Усиление звука происходит за счёт колебаний самого резонатора и, особенно, столба воздуха в нём. Размеры резонатора подбирают таким образом, чтобы собственная частота воздушного столба в нём совпадала с частотой колебаний камертона. При этом столб воздуха колеблется в резонанс с камертоном, то есть амплитуда его колебаний и, соответственно, громкость звука достигают наибольших значений.

Камертон, снабжённый резонатором, издаёт более громкий, но менее длительный звук (по закону сохранения энергии).

 

Обрати внимание!

В музыкальных инструментах роль резонаторов выполняют части их корпусов.

В гитаре, скрипке и других подобных им струнных инструментах резонаторами служат деки, которые усиливают издаваемые струнами звуки и придают звучанию инструмента характерную для него окраску — тембр (рис. \(2\)).

 

Рис. \(2\)

 

Тембр звука музыкального инструмента зависит не только от формы и размера резонатора, но и от того, из какого дерева он изготовлен, и даже от состава лака, покрывающего его. Тембр определяется также материалом, из которого сделана струна, и тем, гладкая она или витая.

 

Резонаторы имеются и в голосовом аппарате человека.

Источники звука в голосовом аппарате — голосовые связки (рис. \(3\)). Они приходят в колебание благодаря продуванию воздуха из лёгких и возбуждают звук, основной тон которого зависит от их натяжения. Этот звук богат обертонами.

 

 

Гортань усиливает те из обертонов, частота колебаний которых близка к её собственной частоте. Дальше звуковые волны попадают в полость рта.

Полости глотки, рта, носа являются как бы продолжением гортани и называются верхними (головными) резонаторами. Те резонаторы, которые находятся ниже гортани, в грудной клетке — трахея, бронхи — нижние резонаторы (грудные).

Для произнесения каждой гласной необходимо особое положение губ, языка и определённая форма резонаторной полости во рту.

Резонанс — Википедия

Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы^[1]. Для линейных колебательных систем значения частот резонанса совпадает с частотами собственных колебаний, а их число соответствует числу степеней свободы^[1].

Под действием резонанса, колебательная система оказывается особенно отзывчивой на действие внешней силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованию маятников и музыкальных струн.

[2]^[3]

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния можно найти по формуле:

f=12πgL{\displaystyle f={1 \over 2\pi }{\sqrt {g \over L}}},

где g — это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна и включает эллиптический интеграл.) Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (

высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут приводить как к разрушению, так и к усилению устойчивости механических систем.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую и наоборот. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, её частота зависит от скорости v, с которой волна распространяется по струне:

f=v2L{\displaystyle f={v \over 2L}}

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

v=Tρ{\displaystyle v={\sqrt {T \over \rho }}}

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

f=Tρ2L=Tm/L2L=T4mL{\displaystyle f={{\sqrt {T \over \rho }} \over 2L}={{\sqrt {T \over m/L}} \over 2L}={\sqrt {T \over 4mL}}},

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты

f, например, 2f, 3f, 4f^[4], и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

Электроника

В электрических цепях резонансом называется такой режим пассивной цепи, содержащий катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или ее входная реактивная проводимость равны нулю. При резонансе ток на входе цепи, если он отличен от нуля, совпадает по фазе с напряжением.

В электрических цепях резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.

Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.

Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно (тогда возникает резонанс напряжений), так и параллельно (резонанс токов). При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.

Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения

ωL=1ωC⇒ω=1LC{\displaystyle \omega L={\frac {1}{\omega C}}\Rightarrow \omega ={\frac {1}{\sqrt {LC}}}},

где ω=2πf{\displaystyle \omega =2\pi f} ; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с

полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.

В электронных устройствах также применяются различные электромеханические резонансные системы.

СВЧ

В СВЧ электронике широко используются объёмные резонаторы, чаще всего цилиндрической или тороидальной геометрии с размерами порядка длины волны, в которых возможны добротные колебания электромагнитного поля на отдельных частотах, определяемых граничными условиями. Наивысшей добротностью обладают сверхпроводящие резонаторы, стенки которых изготовлены из сверхпроводника и диэлектрические резонаторы с модами шепчущей галереи.

Оптика

В оптическом диапазоне самым распространенным типом резонатора является резонатор Фабри-Перо, образованный парой зеркал, между которыми в резонансе устанавливается стоячая волна. Применяются также кольцевые резонаторы с бегущей волной и оптические микрорезонаторы с модами шепчущей галереи.

Акустика

Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, корпус у барабанов.

Для акустических систем и громкоговорителей резонанс отдельных элементов (корпуса, диффузора) является нежелательным явлением, так как ухудшает равномерность амплитудно-частотной характеристики устройства и верность звуковоспроизведения. Исключением являются акустические системы с фазоинвертором, в которых намеренно создаётся резонанс для улучшения воспроизведения низких частот.

Астрофизика

Орбитальный резонанс в небесной механике — это ситуация, при которой два (или более) небесных тела имеют периоды обращения, которые относятся как небольшие натуральные числа. В результате эти небесные тела оказывают регулярное гравитационное влияние друг на друга, которое может стабилизировать их орбиты.

См. также

Видео-урок: резонанс

Примечания

Литература

• Richardson LF (1922), Weather prediction by numerical process, Cambridge.
• Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457—472.
• Бломберген Н. Нелинейная оптика, М.: Мир, 1965. — 424 с.
• Захаров В. Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431—453.
• Арнольд В. И. Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны / Ред. А. В. Гапонов-Грехов. — М.: Наука, 1979. С. 116—131.
• Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275—309.
• Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
• Филлипс O.М. Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. — М.: Мир, 1984. — С. 297—314.
• Журавлёв В. Ф., Климов Д. М. Прикладные методы в теории колебаний. — М.: Наука, 1988.
• Сухоруков А. П.. Нелинейные волновые взаимодействия в оптике и радиофизике. — Москва: Наука, 1988. — 230 с. — ISBN 5-02-013842-8. Архивировано 13 апреля 2014 года.
• Брюно А. Д. Ограниченная задача трёх тел. — М.: Наука, 1990.
• Широносов В. Г. Резонанс в физике, химии и биологии. — Ижевск: Издательский дом «Удмуртский университет», 2000. — 92 с.
• Резонанс // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1978. — Т. 4. — С. 585—586. — 976 с.

Ссылки

РЕЗОНАНС — это… Что такое РЕЗОНАНС?

РЕЗОНАНС — (франц. resonance, от лат. resono звучу в ответ, откликаюсь), относительно большой селективный (избирательный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте её собств. колебаний. При Р.… …   Физическая энциклопедия

РЕЗОНАНС — (фр., от лат. resonare раздаваться). В акустике: условия полного распространения звука. Доска, служащая для усиления звучности струн в музыкальных инструментах. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910.… …   Словарь иностранных слов русского языка

Резонанс — Резонанс: а резонансные кривые линейных осцилляторов при различной добротности Q(Q3>Q2>Q1), x интенсивность колебаний; б зависимость фазы от частоты при резонансе. РЕЗОНАНС (французское resonance, от латинского resono откликаюсь), резкое… …   Иллюстрированный энциклопедический словарь

РЕЗОНАНС — РЕЗОНАНС, резонанса, мн. нет, муж. (от лат. resonans дающий отзвук). 1. Ответное звучание одного из двух тел, настроенных в унисон (физ.). 2. Способность увеличивать силу и длительность звука, свойственная помещениям, внутренняя поверхность… …   Толковый словарь Ушакова

резонанс — отзвук, резонон, мезомерия, отклик, адрон, частица, отголосок Словарь русских синонимов. резонанс см. отклик Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2 …   Словарь синонимов

РЕЗОНАНС — РЕЗОНАНС, резкое увеличение амплитуды колебаний механической или акустической системы, в случае вынужденных колебаний, вызванных внешним источником. Это явление возникает, когда ЧАСТОТА приложенной силы равна собственной частоте колебаний системы …   Научно-технический энциклопедический словарь

РЕЗОНАНС — (франц. resonance от лат. resono откликаюсь), резкое возрастание амплитуды установившихся вынужденных колебаний при приближении частоты внешнего гармонического воздействия к частоте одного из собственных колебаний системы …   Большой Энциклопедический словарь

РЕЗОНАНС — РЕЗОНАНС, а, муж. 1. Возбуждение колебаний одного тела колебаниями другого той же частоты, а также ответное звучание одного из двух тел, настроенных в унисон (спец.). 2. Способность усиливать звук, свойственная резонаторам или помещениям, стены к …   Толковый словарь Ожегова

РЕЗОНАНС — муж., франц. зык, гул, рай, отзвук, отгул, гул, отдача, наголосок; звучность голоса, по местности, по размерам комнаты; звучность, звонкость музыкального орудия, по устройству его. | В рояле, фортепиано, гуслях: дек, палуба, ·стар. полочка, доска …   Толковый словарь Даля

РЕЗОНАНС — 1. В общем механическом смысле отклик тела, способного колебаться с определенным периодом (т. наз. собственным периодом колебаний), на дошедшие до него колебания того же периода. Явления Р. выражаются обычно в значительном увеличении амплитуды… …   Морской словарь

Резонанс Фано — Википедия

Резонанс Фано — тип резонанса с асимметричным профилем, возникающего в результате интерференции двух волновых процессов. Природа интерферирующих процессов может быть самой различной, поэтому такой резонанс носит универсальный характер и появляется в различных физических системах.

В 1935 году Бойтлер наблюдал в спектрах поглощения благородных газов линии с ярко выраженной асимметрией профиля^[1]. В том же году Уго Фано, молодой ученик Энрико Ферми, предложил^[2] первое объяснение этого эффекта на основе квантовомеханического принципа суперпозиции. Это предположение было развито Фано в знаменитой работе 1961 года^[3], являющейся одной из наиболее цитируемых статей второй половины XX века.

Рис. 1. Зависимость сечения от энергии, построенная согласно формуле Фано (с нормировкой на 1+q2{\displaystyle 1+q^{2}}), при различных значениях параметра асимметрии.

Согласно Фано, фотоионизация атома может происходить по двум различным каналам: а) прямая ионизация, то есть возбуждение электрона в непрерывный континуум состояний, находящийся выше порога ионизации; б) автоионизация, то есть возбуждение атома на некоторый квазидискретный уровень, который затем спонтанно распадается с испусканием электрона (например, по механизму Оже). Таким образом, переход между одними и теми же начальным и конечным состояниями может осуществляться двумя различными путями, которые могут интерферировать между собой. Рассмотрев такую квантовую суперпозицию, Фано получил формулу для резонансного профиля сечения процесса:

σ=(ϵ+q)2ϵ2+1{\displaystyle \sigma ={\frac {(\epsilon +q)^{2}}{\epsilon ^{2}+1}}},

где q{\displaystyle q} — феноменологический параметр асимметрии формы линии, ϵ=2(E−EF)/Γ{\displaystyle \epsilon =2(E-E_{F})/\Gamma } — нормированная энергия, EF{\displaystyle E_{F}} — резонансная энергия автоионизационного (дискретного) уровня, Γ{\displaystyle \Gamma } — его ширина. Параметр q{\displaystyle q} в работе Фано символизировал отношение вероятностей перехода в дискретное состояние и в непрерывный континуум. При q→∞{\displaystyle q\rightarrow \infty } форма линии определяется исключительно переходом в дискретное состояние и описывается стандартным симметричным лоренцевым профилем (резонанс Брейта — Вигнера, см. рис. 1, синяя кривая). При q{\displaystyle q} порядка единицы оба варианта перехода имеют сравнимую вероятность, а профиль линии становится асимметричным. В случае q=0{\displaystyle q=0} наблюдается симметричный провал (антирезонанс, рис. 1, чёрная кривая). Таким образом, резонанс Фано характеризуется асимметричным профилем, содержащем один максимум (σ=1+q2{\displaystyle \sigma =1+q^{2}} при ϵ=1/q{\displaystyle \epsilon =1/q}) и один минимум (σ=0{\displaystyle \sigma =0} при ϵ=−q{\displaystyle \epsilon =-q}), в промежутке между которыми находится резонансная энергия EF{\displaystyle E_{F}} (или ϵ=0{\displaystyle \epsilon =0}).

Формула Фано была успешно использована для объяснения различных экспериментальных данных в терминах квантовомеханического взаимодействия между дискретным и непрерывным состояниями. Её применение ограничено описанием изолированных одиночных резонансов (суперпозиция не более двух путей), а также достаточно малой шириной, которой должен обладать дискретный уровень. Дальнейшее развитие этого подхода, в особенности его обогащение методами теории резонансов Фешбаха (Feshbach resonance, см. также Feshbach–Fano partitioning), позволило получить строгое выражение для параметра асимметрии. Подход, развитый Фано, оказался плодотворным для различных областей физики, в частности атомной и ядерной физики, физики конденсированного состояния и так далее, поскольку позволял выразить всю сложность физических процессов, скрывающихся за асимметрией профиля, посредством нескольких ключевых параметров^[4].

Универсальность метода Фано может быть проиллюстрирована следующим примером. Возможно, первым, кто наблюдал линии асимметричной формы, был Роберт Вуд, обнаруживший в 1902 году в спектре отражательной дифракционной решётки очень быстрые вариации интенсивности (аномалии Вуда), которые не могли быть объяснены стандартной теорией решёток^[5]. Первое объяснение этому явлению дал лорд Рэлей в 1907 году^[6]. Его динамическая теория позволила получить правильные значения длин волн, на которых возникают аномалии, но форма линий оставалась необъяснённой (на рэлеевских длинах волн возникали сингулярности). В конце 1930-х — начале 1940-х годов Фано попытался преодолеть эти сложности, предположив, что аномалии связаны с резонансным возбуждением вблизи решётки вытекающих (leaking) поверхностных волн^[7][8][9]. Получающийся в итоге асимметричный профиль хорошо описывается формулой Фано и может быть представлен как результат интерференции поверхностной волны (аналог дискретного состояния) и падающего излучения (аналог континуума). Подобные асимметричные профили могут возникать в различных физических системах и объясняются интерференцией волн, природа которых может быть совершенно различной.

Рассмотрим простую механическую систему, в которой возможно возникновение асимметричного резонанса^[10]. Возьмем два связанных гармонических осциллятора, один из которых подвергается воздействию со стороны внешней периодической силы. Такая система описывается следующей парой дифференциальных уравнений для смещения каждого осциллятора:

x¨+g1x˙+ω12x+hy=fexp⁡(iωt){\displaystyle {\ddot {x}}+g_{1}{\dot {x}}+\omega _{1}^{2}x+hy=f\exp {(i\omega t)}}, y¨+g2y˙+ω22y+hx=0{\displaystyle {\ddot {y}}+g_{2}{\dot {y}}+\omega _{2}^{2}y+hx=0},

где ω1{\displaystyle \omega _{1}} и ω2{\displaystyle \omega _{2}} — собственные частоты осцилляторов, h{\displaystyle h} — параметр связи осцилляторов, g1{\displaystyle g_{1}} и g2{\displaystyle g_{2}} — их константы затухания, f{\displaystyle f} — амплитуда внешней силы, ω{\displaystyle \omega } — её частота. Поиск решения в виде вынужденных колебаний x=c1exp⁡(iωt){\displaystyle x=c_{1}\exp {(i\omega t)}} и y=c2exp⁡(iωt){\displaystyle y=c_{2}\exp {(i\omega t)}}, приводит к следующим выражениям для амплитуд колебаний:

c1=fω2−ω22−iωg2(ω12−ω2+iωg1)(ω2−ω22−iωg2)+h3{\displaystyle c_{1}=f{\frac {\omega ^{2}-\omega _{2}^{2}-i\omega g_{2}}{(\omega _{1}^{2}-\omega ^{2}+i\omega g_{1})(\omega ^{2}-\omega _{2}^{2}-i\omega g_{2})+h^{2}}}}, c2=c1hω2−ω22−iωg2{\displaystyle c_{2}=c_{1}{\frac {h}{\omega ^{2}-\omega _{2}^{2}-i\omega g_{2}}}}.

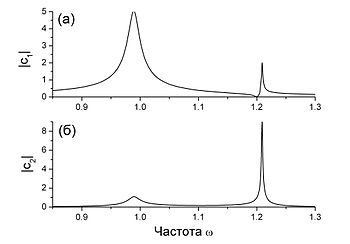
Пример резонанса, рассчитанного по этим формулам, показан на рис. 2. Видно, что в такой системе имеется два резонанса, расположенных вблизи собственных частот ω1{\displaystyle \omega _{1}} и ω2{\displaystyle \omega _{2}}. Первый резонанс в спектре возбуждаемого осциллятора описывается обычной симметричной огибающей лоренцевского типа (резонанс Брейта — Вигнера), тогда как второй резонанс характеризуется асимметричным профилем [см. рис. 2(а)]. На собственной частоте второго, связанного осциллятора ω2{\displaystyle \omega _{2}} амплитуда возбуждаемого осциллятора обращается в ноль. Это является результатом деструктивной интерференции колебаний, приходящих от внешней силы и от связанного осциллятора. Стоит отметить, что резонансные профили последнего симметричны [см. рис. 2(б)]. Таким образом, рассмотренная простая механическая аналогия демонстрирует свойственную резонансу Фано асимметрию, возникающую вследствие процессов деструктивной интерференции.

Системы со сложной геометрией[править | править код]

Одним из основных методов моделирования асимметричных резонансов является выбор такой геометрии модели, что в ней возможны как минимум два возможных пути распространения волн. Простейшей моделью такого типа является так называемая модель Фано — Андерсона^[11], которая описывает взаимодействие линейной цепочки элементов (аналог континуума) и одиночного состояния Фано. Гамильтониан такой системы может быть записан в виде

H=C∑(ϕnϕn−1∗+ϕn−1ϕn∗)+EF|ψ|2+VF(ψ∗ϕ0+ϕ0∗ψ){\displaystyle H=C\sum (\phi _{n}\phi _{n-1}^{*}+\phi _{n-1}\phi _{n}^{*})+E_{F}|\psi |^{2}+V_{F}(\psi ^{*}\phi _{0}+\phi _{0}^{*}\psi )},

где ψ{\displaystyle \psi } и ϕn{\displaystyle \phi _{n}} — амплитуды поля состояния Фано и n{\displaystyle n}-го элемента цепочки соответственно, C{\displaystyle C} — параметр взаимодействия соседних элементов цепочки, EF{\displaystyle E_{F}} — энергия состояния Фано, VF{\displaystyle V_{F}}$ — коэффициент взаимодействия состояния Фано и одного из элементов цепочки ϕ0{\displaystyle \phi _{0}}. Звездочка означает комплексное сопряжение. Волна имеет два возможных пути распространения вдоль цепочки — напрямую или с посещением состояния Фано. Решение уравнения Шредингера для указанного модельного гамильтониана позволяет получить выражение для коэффициента пропускания такой системы:

T=αk2αk2+1{\displaystyle T={\frac {\alpha _{k}^{2}}{\alpha _{k}^{2}+1}}},

где αk=ck(EF−ωk)/VF2{\displaystyle \alpha _{k}=c_{k}(E_{F}-\omega _{k})/V_{F}^{2}}, ck=2Csin⁡k{\displaystyle c_{k}=2C\sin k}, ωk=2Ccos⁡k{\displaystyle \omega _{k}=2C\cos k} — частота плоской волны (моды), которая может распространяться в системе. Полученное выражение для коэффициента пропускания соответствует формуле Фано при q=0{\displaystyle q=0} и при EF=ωk{\displaystyle E_{F}=\omega _{k}} демонстрирует полное подавление распространения (антирезонанс). Наличие минимума, вызванного деструктивной интерференцией волн, является характерным признаком резонанса Фано.

Модель Фано — Андерсона была подвергнута обобщению в ряде работ с целью получения ненулевых значений параметра асимметрии q{\displaystyle q}. Этого можно добиться введением в цепочку дефектов или увеличением числа связанных состояний Фано^[12]. В последнем случае также наблюдается не один, а несколько резонансов. Другим способом усложнения модели является введение в неё нелинейных поправок. В этом случае появляется зависимость коэффициента пропускания от интенсивности падающей плоской волны и, как следствие, сдвиг положения резонанса при изменении интенсивности и возможность бистабильного поведения коэффициента пропускания в определённом диапазоне изменения параметров^[11]. В нескольких работах рассматривалось распространение солитонов в нелинейных цепочках и их рассеяние на дефектах Фано^[13][14][15]. В качестве примера реализации модели типа Фано — Андерсона может рассматриваться набор канальных волноводов, некоторые из которых («дефекты») обладают квадратичной нелинейностью. Тогда фундаментальная мода такой системы может рассматриваться как континуум, в то время как вторая гармоника, возникающая при выполнении условий фазового синхронизма, — как дискретное состояние. В результате пропускание системы демонстрирует резонансный отклик типа фановского^[16].

Системы со сложной динамикой[править | править код]

В другом типе моделей резонанса Фано используется не сложная геометрия системы, обеспечивающая существование нескольких взаимодействующих состояний, а сложное её поведение, динамическим образом порождающее несколько интерферирующих каналов распространения волн. Такая возможность возникает за счёт нелинейности взаимодействия, приводящей к возникновению периодически изменяющихся со временем потенциалов рассеяния волн. Примером является рассеяние волн на дискретных бризерах (breather) — пространственно локализованных и периодически зависящих от времени состояниях решётки, являющихся результатом баланса между нелинейностью и дискретностью модели. Рассеяние волн дискретными бризерами может быть рассмотрено при помощи дискретного нелинейного уравнения Шредингера, решение которого можно представить в виде суммы статической и динамической частей. Рассеяние волны на таком двухкомпонентном потенциале демонстрирует характерное зануление коэффициента пропускания на определённой (резонансной) частоте^[17][18]. Варианты резонансного рассеяния по бризерному механизму были предложены для плазмонов в системе джозефсоновских контактов^[19] и для атомных волн материи в случае бозе-эйнштейновского конденсата, находящегося в оптической решётке^[20]. Аналогичный результат может быть получен на основе решения непрерывного нелинейного уравнения Шредингера, например, для рассеяния на оптическом солитоне, возникающем в нелинейной волноводной структуре^[21].

Рассеяние света, в том числе фотонными и плазмонными структурами[править | править код]

Резонанс Фано может наблюдаться в фотонных структурах типа микрорезонаторов, связанных с волноводом. В качестве волноводно-резонаторных систем на основе фотонного кристалла, позволяющих получать асимметричный резонанс, могут выступать, например, волноводы с частично отражающими элементами (дефектами)^[22] или даже резкие изгибы фотонно-кристаллического волновода, характеризуемые специфическими локализованными состояниями^[23]. Интерференция волн, одна из которых напрямую распространяется по волноводу, а вторая взаимодействует с резонатором (в том числе нелинейным), может быть использована для создания оптических фильтров^[24], получения и усиления таких нелинейных эффектов как оптическое переключение и бистабильность^[25][26]. Даже рассеяние излучения от одиночного фотонно-кристаллического резонатора позволяет наблюдать резонанс типа фановского и управлять величиной параметра асимметрии^[27]. В системе из двух связанных фотонно-кристаллических резонаторов возможно осуществление взаимодействия двух резонансов, что приводит к таким эффектам, как захват и хранение излучения чисто оптическими средствами^[28] или прозрачность, индуцированная связанными резонаторами (coupled-resonators induced transparency — оптический аналог эффекта электромагнитно-индуцированной прозрачности, EIT)^[29]. В спектрах пропускания и отражения фотонных кристаллов без дефектов также наблюдались асимметричные резонансы, возникающие за счёт взаимодействия направляемых мод структуры и мод свободного пространства^[30]. В случае нелинейности среды этот эффект можно использовать для получения компактных бистабильных устройств^[31].

Асимметричные резонансы возникают в результате общего решения (теория Ми) задачи о рассеянии на малых (рэлеевских) частицах со слабым затуханием (пример — плазмонные наночастицы). В качестве резонанса Фано выступает квадрупольный резонанс, который по интенсивности рассеяния может превосходить дипольный (обратная иерархия резонансов). Аналогом дискретных уровней Фано в этой задаче выступают локализованные поверхностные плазмоны (поляритоны)^[32][33]. В литературе сообщалось о других примерах резонанса Фано в плазмонных наноструктурах, таких как металлический диск внутри кольца^[34] или димерная наночастица^[35]. Новый тип нелинейного резонанса Фано наблюдался в гибридных молекулах, состоящих из металлической и полупроводниковой наночастиц: в системе возникает взаимодействие между плазмонами (непрерывный спектр) и экситонами (дискретный спектр) посредством резонансного переноса энергии по механизму Фёрстера^[36]. Плазмоны играют решающую роль в объяснении аномалий Вуда в спектрах рассеяния металлических решёток (см. выше). Тем же механизмом обусловлено усиление пропускания или отражения при взаимодействии света с двумерным набором отверстий в тонкой металлической пленке^[37][38][39]. Подробности теоретического и экспериментального изучения резонанса Фано в плазмонных материалах и метаматериалах и его возможные применения можно найти в обзоре^[40].

Эксперименты по взаимодействию света с квантовыми точками показали возможность нелинейного резонанса Фано в спектрах поглощения таких структур, то есть изменение параметра асимметрии при изменении мощности лазерного излучения^[41]. Более того, параметр асимметрии способен принимать комплексные значения, что может быть использовано для изучения степени декогеренции при распространении волн, возникающей вследствие процессов поглощения или дефазировки^[42]. Асимметричные резонансы, форма которых удовлетворяет формуле Фано, наблюдались также в рамановских спектрах сильно легированных полупроводников^{[43][44][45][46]} и высокотемпературных сверхпроводников^[47][48][49].

Перенос заряда в квантовых точках[править | править код]

Резонанс Фано наблюдался при измерении зависимостей проводимости квантовой точки, соединённой с двумя контактами (схема на основе полупроводниковой гетероструктуры), от приложенного напряжения затвора. В данном случае он является следствием интерференции различных каналов, по которым могут проходить электроны через квантовую точку в условиях сильной связи точки и контактов; при слабой связи существенным оказывается только один канал (режим кулоновской блокады)^[50]. Дополнительный канал может быть по желанию добавлен искусственным образом, что превращает систему в своеобразный интерферометр, который позволяет управлять асимметрией резонансов при изменении напряжения затвора^[51]. В системе с аналогичной геометрией возможно управление резонансами при помощи внешнего магнитного поля, причем форма линий повторяется с периодом, величина которого может быть получена из теории эффекта Ааронова — Бома (такую систему можно назвать интерферометром Ааронова — Бома)^[52]. Экспериментальные результаты в этой области неплохо объясняются в рамках модельных расчетов^[53]. Среди других результатов стоит отметить возможность получения отдельных резонансов Фано для электронов с различным направлением спина, что может быть использовано для создания так называемых спиновых фильтров^[54]. Резонансы Фано были обнаружены также в особенностях электронного транспорта через углеродные нанотрубки различных типов^{[55][56][57][58]}.

Столкновения частиц[править | править код]

В процессах столкновения и рассеяния двух частиц возможно наблюдение резонансов Фано, возникающих вследствие интерференции несвязанных состояний частиц (континуум) и квазисвязанных состояний. Описание этих процессов производится в рамках концепции резонансов Фешбаха, представление о которых появилось в контексте теории составного ядра^[59][60]. В случае трехчастичных столкновений возможно образование слабо связанных тримерных состояний в условиях, когда двухчастичные взаимодействия слишком слабы, чтобы образовывать связанные состояния (димеры). Это явление носит название эффекта Ефимова (Efimov effect)^[61][62][63]. При определённых интенсивностях двухчастичных взаимодействий наблюдается резонансное усиление и подавление трехчастичных столкновений с характерным асимметричным профилем, который может быть объяснен в терминах резонанса Фано^[64].

1. ↑ Beutler H. Uber absorptionsserien von argon, krypton und xenon zu termen zwischen den beiden ionisierungsgrenzen 2P32/0{\displaystyle 2P_{3}^{2/0}} und 2P12/0{\displaystyle 2P_{1}^{2/0}} // Z. Phys. A. — 1935. — Vol. 93. — P. 177—196.
2. ↑ Fano U. Sullo spettro di assorbimento dei gas nobili presso il limite dello spettro d’arco // Nuovo Cimento. — 1935. — Vol. 12. — P. 154—161.
3. ↑ Fano U. Effects of configuration interaction on intensities and phase shifts // Phys. Rev. — 1961. — Vol. 124. — P. 1866—1878.
4. ↑ Miroshnichenko A. E., Flach S., Kivshar Yu. S. Fano resonances in nanoscale structures // Rev. Mod. Phys. — 2010. — Vol. 82. — P. 2257—2298.
5. ↑ Wood R. On the remarkable case of uneven distribution of light in a diffraction grating spectrum // Proc. Phys. Soc. London. — 1902. — Vol. 18. — P. 269—275.
6. ↑ Rayleigh. On the dynamical theory of gratings // Proc. R. Soc. London A. — 1907. — Vol. 79. — P. 399—416.
7. ↑ Fano U. Some theoretical considerations on anomalous diffraction gratings // Phys. Rev. — 1936. — Vol. 50. — P. 573.
8. ↑ Fano U. On the Anomalous Diffraction Gratings. II // Phys. Rev. — 1937. — Vol. 51. — P. 288.
9. ↑ Fano U. The theory of anomalous diffraction gratings and of quasistationary waves on metallic surfaces (Sommerfeld’s waves) // J. Opt. Soc. Am. — 1941. — Vol. 31. — P. 213—222.
10. ↑ Joe Y. S., Satanin A. M., Kim C. S. Classical analogy of Fano resonances // Phys. Scr. — 2006. — Vol. 74. — P. 259—266.
11. ↑ ^{1 2} Miroshnichenko A. E., Mingaleev S.F., Flach S., Kivshar Yu. S. Nonlinear Fano resonance and bistable wave transmission // Phys. Rev. E. — 2005. — Vol. 71. — P. 036626.
12. ↑ Miroshnichenko A. E., Kivshar Yu. S. Engineering Fano resonances in discrete arrays // Phys. Rev. E. — 2005. — Vol. 72. — P. 056611.
13. ↑ Miroshnichenko A. E., Flach S., Malomed B. Resonant scattering of solitons // Chaos. — 2003. — Vol. 13. — P. 874—879.
14. ↑ Burioni R., Cassi D., Sodano P., Trombettoni A., Vezzani A. Propagation of discrete solitons in inhomogeneous networks // Chaos. — 2005. — Vol. 15. — P. 043501.
15. ↑ Wulf U., Skalozub V. V. Pulse propagation in resonant tunneling // Phys. Rev. B. — 2005. — Vol. 72. — P. 165331.
16. ↑ Miroshnichenko A. E., Kivshar Yu. S., Vicencio R. A., Molina M. I. Fano resonance in quadratic waveguide arrays // Opt. Lett. — 2005. — Vol. 30. — P. 872—874.
17. ↑ Flach S., Miroshnichenko A. E., Fistul M. V. Wave scattering by discrete breathers // Chaos. — 2003. — Vol. 13. — P. 596—609.
18. ↑ Flach S., Miroshnichenko A. E., Fleurov V., Fistul M. V. Fano resonances with discrete breathers // Phys. Rev. Lett. — 2003. — Vol. 90. — P. 084101.
19. ↑ Miroshnichenko A. E., Schuster M., Flach S., Fistul M. V., Ustinov A. V. Resonant plasmon scattering by discrete breathers in Josephson-junction ladders // Phys. Rev. B. — 2005. — Vol. 71. — P. 174306.
20. ↑ Vicencio R. A., Brand J., Flach S. Fano blockade by a Bose-Einstein condensate in an optical lattice // Phys. Rev. Lett. — 2007. — Vol. 98. — P. 184102.
21. ↑ Flach S., Fleurov V., Gorbach A. V., Miroshnichenko A. E. Resonant light scattering by optical solitons // Phys. Rev. Lett. — 2005. — Vol. 95. — P. 023901.
22. ↑ Fan S. Sharp asymmetric line shapes in side-coupled waveguide-cavity systems // Appl. Phys. Lett. — 2002. — Vol. 80. — P. 908—910.
23. ↑ Miroshnichenko A. E., Kivshar Yu. S. Sharp bends in photonic crystal waveguides as nonlinear Fano resonators // Opt. Express. — 2005. — Vol. 13. — P. 3969—3976.
24. ↑ Fan S., Villeneuve P. R., Joannopoulos J. D., Haus H. A. Channel drop tunneling through localized states // Phys. Rev. Lett. — 1998. — Vol. 80. — P. 960—963.
25. ↑ Mingaleev S. F., Miroshnichenko A. E., Kivshar Yu. S. Low-threshold bistability of slow light in photonic-crystal waveguides // Opt. Express. — 2007. — Vol. 15. — P. 12380—12385.
26. ↑ Yang X., Husko C., Wong C. W., Yu M., Kwong D.-L. Observation of femtojoule optical bistability involving Fano resonances in high-Q/Vm silicon photonic crystal nanocavities // Appl. Phys. Lett. — 2007. — Vol. 91. — P. 051113.
27. ↑ Galli M., Portalupi S. L., Belotti M., Andreani L. C., O’Faolain L., Krauss T. F. Light scattering and Fano resonances in high-Q photonic crystal nanocavities // Appl. Phys. Lett. — 2009. — Vol. 94. — P. 071101.
28. ↑ Yanik M. F., Fan S. Stopping light all optically // Phys. Rev. Lett. — 2004. — Vol. 92. — P. 083901.
29. ↑ Smith D. D., Chang H., Fuller K. A., Rosenberger A. T., Boyd R. W. Coupled-resonator-induced transparency // Phys. Rev. A. — 2004. — Vol. 69. — P. 063804.
30. ↑ Fan S., Joannopoulos J. D. Analysis of guided resonances in photonic crystal slabs // Phys. Rev. B. — 2002. — Vol. 65. — P. 235112.
31. ↑ Lousse V., Vigneron J. P. Use of Fano resonances for bistable optical transfer through photonic crystal films // Phys. Rev. B. — 2004. — Vol. 69. — P. 155106.
32. ↑ Tribelsky M. I., Luk’yanchuk B. S. Anomalous light scattering by small particles // Phys. Rev. Lett. — 2006. — Vol. 97. — P. 263902.
33. ↑ Tribelsky M. I., Flach S., Miroshnichenko A. E., Gorbach A. V., Kivshar Yu. S. Light scattering by a finite obstacle and Fano resonances // Phys. Rev. Lett. — 2008. — Vol. 100. — P. 043903.
34. ↑ Hao F., Sonnefraud Y., van Dorpe P., Maier S. A., Halas N. J., Nordlander P. Symmetry breaking in plasmonic nanocavities: Subradiant LSPR sensing and a tunable Fano resonance // Nano Lett. — 2008. — Vol. 8. — P. 3983—3988.
35. ↑ Bachelier G., Russier-Antoine I., Benichou E., Jonin C., Fatti N. D., Vallee F., Brevet P.-F. Fano profiles induced by near-field coupling in heterogeneous dimers of gold and silver nanoparticles // Phys. Rev. Lett. — 2008. — Vol. 101. — P. 197401.
36. ↑ Zhang W., Govorov A. O., Bryant G. W. Semiconductor-metal nanoparticle molecules: Hybrid excitons and the nonlinear Fano effect // Phys. Rev. Lett. — 2006. — Vol. 97. — P. 146804.
37. ↑ Ebbesen T., Lezec H., Ghaemi H., Thio T., Wolf P. Semiconductor-metal nanoparticle molecules: Hybrid excitons and the nonlinear Fano effect // Nature. — 1998. — Vol. 391. — P. 667—669.
38. ↑ Ghaemi H., Thio T., Grupp D. E., Ebbesen T., Lezec H. Surface plasmons enhance optical transmission through subwavelength holes // Phys. Rev. B. — 1998. — Vol. 58. — P. 6779—6782.
39. ↑ de Abajo F. J. G. Colloquium: Light scattering by particle and hole arrays // Rev. Mod. Phys. — 2007. — Vol. 79. — P. 1267—1290.
40. ↑ Luk’yanchuk B., Zheludev N. I., Maier S. A., Halas N. J., Nordlander P., Giessen H., Chong C. T. The Fano resonance in plasmonic nanostructures and metamaterials // Nature Materials. — 2010. — Vol. 9. — P. 707—715.
41. ↑ Kroner M., Govorov A. O., Remi S., Biedermann B., Seidl S., Badolato A., Petroff P. M., Zhang W., Barbour R., Gerardot B. D., Warburton R. J., Karrai K. The nonlinear Fano effect // Nature. — 2008. — Vol. 451. — P. 311—314.
42. ↑ Barnthaler A., Rotter S., Libisch F., Burgdorfer J., Gehler S., Kuhl U., Stockmann H.-J. Probing decoherence through Fano resonances // Phys. Rev. Lett. — 2010. — Vol. 105. — P. 056801.
43. ↑ Hopfield J. J., Dean P. J., Thomas D. G. Interference between Intermediate States in the Optical Properties of Nitrogen-Doped Gallium Phosphide // Phys. Rev. — 1967. — Vol. 158. — P. 748—755.
44. ↑ Cerdeira F., Fjeldly T. A., Cardona M. Effect of Free Carriers on Zone-Center Vibrational Modes in Heavily Doped p-type Si. II. Optical Modes // Phys. Rev. B. — 1973. — Vol. 8. — P. 4734—4735.
45. ↑ Chandrasekhar M., Renucci J. B., Cardona M. Effects of interband excitations on Raman phonons in heavily doped n-Si // Phys. Rev. B. — 1978. — Vol. 17. — P. 1623—1633.
46. ↑ Magidson V., Beserman R. Fano-type interference in the Raman spectrum of photoexcited Si // Phys. Rev. B. — 2002. — Vol. 66. — P. 195206.
47. ↑ Friedl B., Thomsen C., Cardona M. Determination of the superconducting gap in RBa2{\displaystyle _{2}}Cu3{\displaystyle _{3}}O7−δ{\displaystyle _{7-\delta }} // Phys. Rev. Lett. — 1990. — Vol. 65. — P. 915—918.
48. ↑ Limonov M. F., Rykov A. I., Tajima S., Yamanaka A. Raman Scattering Study on Fully Oxygenated YBa2{\displaystyle _{2}}Cu3{\displaystyle _{3}}O

резонанс — это… Что такое резонанс?

РЕЗОНАНС — (франц. resonance, от лат. resono звучу в ответ, откликаюсь), относительно большой селективный (избирательный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте её собств. колебаний. При Р.… …   Физическая энциклопедия

РЕЗОНАНС — (фр., от лат. resonare раздаваться). В акустике: условия полного распространения звука. Доска, служащая для усиления звучности струн в музыкальных инструментах. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910.… …   Словарь иностранных слов русского языка

Резонанс — Резонанс: а резонансные кривые линейных осцилляторов при различной добротности Q(Q3>Q2>Q1), x интенсивность колебаний; б зависимость фазы от частоты при резонансе. РЕЗОНАНС (французское resonance, от латинского resono откликаюсь), резкое… …   Иллюстрированный энциклопедический словарь

РЕЗОНАНС — РЕЗОНАНС, резонанса, мн. нет, муж. (от лат. resonans дающий отзвук). 1. Ответное звучание одного из двух тел, настроенных в унисон (физ.). 2. Способность увеличивать силу и длительность звука, свойственная помещениям, внутренняя поверхность… …   Толковый словарь Ушакова

резонанс — отзвук, резонон, мезомерия, отклик, адрон, частица, отголосок Словарь русских синонимов. резонанс см. отклик Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2 …   Словарь синонимов

РЕЗОНАНС — РЕЗОНАНС, резкое увеличение амплитуды колебаний механической или акустической системы, в случае вынужденных колебаний, вызванных внешним источником. Это явление возникает, когда ЧАСТОТА приложенной силы равна собственной частоте колебаний системы …   Научно-технический энциклопедический словарь

РЕЗОНАНС — (франц. resonance от лат. resono откликаюсь), резкое возрастание амплитуды установившихся вынужденных колебаний при приближении частоты внешнего гармонического воздействия к частоте одного из собственных колебаний системы …   Большой Энциклопедический словарь

РЕЗОНАНС — РЕЗОНАНС, а, муж. 1. Возбуждение колебаний одного тела колебаниями другого той же частоты, а также ответное звучание одного из двух тел, настроенных в унисон (спец.). 2. Способность усиливать звук, свойственная резонаторам или помещениям, стены к …   Толковый словарь Ожегова

РЕЗОНАНС — муж., франц. зык, гул, рай, отзвук, отгул, гул, отдача, наголосок; звучность голоса, по местности, по размерам комнаты; звучность, звонкость музыкального орудия, по устройству его. | В рояле, фортепиано, гуслях: дек, палуба, ·стар. полочка, доска …   Толковый словарь Даля

РЕЗОНАНС — (от лат. resonare – повторять) колебания одного из колеблющихся тел, «настроенных» на определенное число колебаний (все тела более или менее способны производить их), которые взаимодействуют с колебаниями, производимыми др. телом, колеблющимся с… …   Философская энциклопедия

РЕЗОНАНС — 1. В общем механическом смысле отклик тела, способного колебаться с определенным периодом (т. наз. собственным периодом колебаний), на дошедшие до него колебания того же периода. Явления Р. выражаются обычно в значительном увеличении амплитуды… …   Морской словарь

Ответы@Mail.Ru: Что такое резонанс?

Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам) , определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

usilenie iz-za nalogenija voln

По-простому: резонанс-это явление совпадения частоты колебаний одного тела с частотой колебаний другого.

МАГНИТНЫЙ РЕЗОНАНС, резонансное (избирательное) поглощение радиочастотного излучения некоторыми атомными частицами, помещенными в постоянное магнитное поле. Большинство элементарных частиц, подобно волчкам, вращаются вокруг собственной оси. Если частица обладает электрическим зарядом, то при ее вращении возникает магнитное поле, т. е. она ведет себя подобно крошечному магниту. При взаимодействии этого магнитика с внешним магнитным полем происходят явления, позволяющие получить информацию о ядрах, атомах или молекулах, в состав которых входит данная элементарная частица. Метод магнитного резонанса представляет собой универсальный инструмент исследований, применяемый в столь различных областях науки, как биология, химия, геология и физика. Различают магнитные резонансы двух основных видов: электронный парамагнитный резонанс и ядерный магнитный резонанс. См. также МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА; ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ. Электронный парамагнитный резонанс (ЭПР) . ЭПР был открыт в 1944 русским физиком Е. К. Завойским. Электроны в веществах ведут себя как микроскопические магниты. В разных веществах они переориентируются по-разному, если поместить вещество в постоянное внешнее магнитное поле и воздействовать на него радиочастотным полем. Возврат электронов к исходной ориентации сопровождается радиочастотным сигналом, который несет информацию о свойствах электронов и их окружении. Такой метод, представляющий собой один из видов спектроскопии, применяется при исследовании кристаллической структуры элементов, химии живых клеток, химических связей в веществах и т. д. См. также СПЕКТР; СПЕКТРОСКОПИЯ. Ядерный магнитный резонанс (ЯМР) . ЯМР был открыт в 1946 американскими физиками Э. Перселлом и Ф. Блохом. Работая независимо друг от друга, они нашли способ резонансной «настройки» в магнитных полях собственных вращений ядер некоторых атомов, например водорода и одного из изотопов углерода. Когда образец, содержащий такие ядра, помещают в сильное магнитное поле, их ядерные моменты «выстраиваются» подобно железным опилкам вблизи постоянного магнита. Эту общую ориентацию можно нарушить радиочастотным сигналом. По выключении сигнала ядерные моменты возвращаются в исходное состояние, причем быстрота такого восстановления зависит от их энергетического состояния, типа окружающих ядер и ряда других факторов. Переход сопровождается испусканием радиочастотного сигнала. Сигнал подается на компьютер, который обрабатывает его. Таким путем (метод компьютерной ЯМР-томографии) можно получить изображения. (При изменении внешнего магнитного поля малыми ступенями достигается эффект трехмерного изображения. ) Метод ЯМР обеспечивает высокую контрастность разных мягких тканей на изображении, что крайне важно для выявления больных клеток на фоне здоровых. ЯМР-томография считается более безопасной, нежели рентгеновская, поскольку не вызывает ни разрушения, ни раздражения тканей (см. также РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ) . ЯМР позволяет также изучать живые клетки, не нарушая их жизнедеятельности. Поэтому следует ожидать, что применение ЯМР в клинической медицине будет расширяться. См. также ХИРУРГИЯ.

Резонанс — это резкое возрастание амплитуды установившихся вынужденных колебаний при приближении частоты внеш. гармонич. воздействия к частоте одного из собственных колебаний системы.

Резкое увеличение амплитуды. Очень коротко и понятно.

увеличение амплитуды

червяк Копатыча

О­л­ь­г­а, сп­ас­и­бо, что п­осо­в­ето­вал­а <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&amp;st.cmd=logExternal&amp;st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&amp;https://mail.ru &amp;st.name=externalLinkRedirect&amp;st» target=»_blank»>fond2019.ru</a> Вы­платил­и 28 тыс­я­ч за 20 м­ину­т ка­к ты и н­а­п­ис­а­л­а. Ж­ал­ь что р­ан­ь­ше не з­н­а­ла п­р­о т­а­ки­е фон­ды, н­а р­а­бо­ту бы хо­д­и­т­ь не п­р­и­ш­л­о­сь:)