Резистор. Нелинейные резисторы | Для дома, для семьи
Здравствуйте, уважаемые читатели сайта sesaga.ru. Продолжаем тему о резисторах. Во второй части статьи мы рассмотрели резисторы переменного сопротивления, а в этой заключительной части познакомимся с нелинейными резисторами.
Нелинейные резисторы относятся к классу саморегулирующихся резисторов, изменяющих свое сопротивление под воздействием внешних электрических или неэлектрических факторов. Благодаря своим специфическим качествам нелинейные резисторы применяются в схемах автоматики, схемах защиты от перенапряжений, в устройствах контроля и регулирования различных величин, в качестве датчиков в измерительных приборах и т.д.
Нелинейными называются резисторы, для которых не выполняется линейная зависимость между током и приложенным к ним напряжением. Наиболее широкое применение в электронике и электротехнике нашли варисторы, терморезисторы, фоторезисторы и тензорезисторы.

1. Тензорезисторы.
Тензорезистор – это резистор, деформация которого вызывает изменение его электрического сопротивления. Тензорезисторы широко применяются в качестве чувствительных элементов тензометрических датчиков, используемых для измерения деформаций, внутренних усилий, перемещений, биений, крутящих моментов, давления и др.
В основе принципа работы тензорезистора лежит явление тензоэффекта, заключающееся в изменении электрического сопротивления проводника при его растяжении или сжатии, изгибе, кручении и сдвига. Однако чаще всего рассматривают линейную деформацию растяжения или сжатия. На рисунке показан тензодатчик, применяемый в конвейерных весах для измерения веса материала.

Тензорезистор представляет собой проводник, выполненный в виде плоской петлеобразной обмотки прямоугольной формы (решетки), к концам которой припаяны (приварены) выводы из медного провода, предназначенные для включения тензорезистора в электрическую цепь. Решетка с помощью специального клея закрепляется на тонкой прямоугольной полоске из бумаги, клеевой или лаковой пленки, служащей для решетки подложкой. С помощью подложки тензорезистор крепится к поверхности тензодатчика или исследуемого объекта.
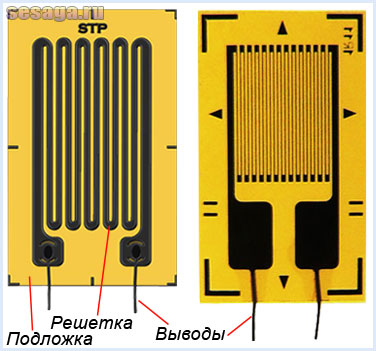
Проводники для тензорезисторов изготавливают из специальной константановой микропроволоки толщиной 0,025…0,035 мм, тонкой фольги из медноникелевого сплава толщиной 0,01…0,02 мм или же напыляются методом фототравления для получения плёнки металла.

Принцип работы тензорезистора достаточно прост. Для проведения измерений тензорезистор приклеивают к исследуемому объекту, благодаря чему деформация устройства практически точно воспринимается решеткой тензорезистора. В процессе измерения исследуемый объект деформируется, соответственно, и решетка тензорезистора испытывает деформацию растяжения или сжатия, отчего меняется ее поперечное сечение, а значит, и сопротивление.
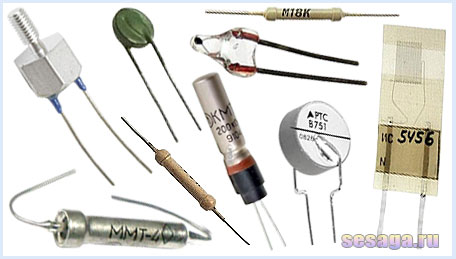
Отечественной промышленностью выпускаются проволочные, фольговые и полупроводниковые тензорезисторы. На рисунке показан внешний вид фольговых тензорезисторов типа ТКФ, 2ФКП.
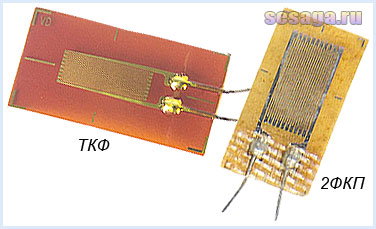
На следующем рисунке показан фольговый тензорезистор для измерения трех компонент деформации.

Основными параметрами тензорезисторов являются:
1. Коэффициент тензочувствительности (чувствительность тензорезистора) — характеризует интенсивность изменения сопротивления проводника в зависимости от воздействующей деформации.
2. Номинальное сопротивление, R (Ом) – значение активного сопротивления чувствительного элемента (решетки) тензорезистора. Тензорезисторы выпускаются с номинальным сопротивлением 10…1000 Ом и наиболее распространенными являются величиной 120, 200, 350, 400, 1000 Ом.
3. Предельная деформация, Ɛmax (%) – наибольшее значение деформации в мкм/м (или в %), в отношении которой завод-изготовитель гарантирует надежную работу тензорезистора.
4. Ползучесть, % (ч) – проявляется в виде изменения выходного сигнала при заданном и неизменном значении деформации. Причиной ползучести является упругое несовершенство подложки и клея. Обычно ползучесть тензорезисторов не превышает 0,5 — 1% за первый час после приклеивания и соответственно 1 – 1,5% за 6 часов.
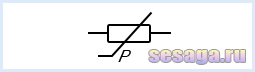
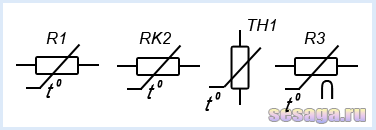
На принципиальных схемах тензорезисторы обозначают основным символом резистора и знаком нелинейного саморегулирования с буквой «Р», обозначающей механическое усилие – давление.
Измерение деформации с помощью тензорезистивных преобразователей является одним из самых сложных в технике электрических измерений из-за малого диапазона изменения сопротивления тензорезистора при воздействии деформации. Изменение сопротивления 100-омного датчика составляет около 0,0002 Ом на деформацию в 1 мкм/м, поэтому для преобразования таких малых изменений питающее напряжение к тензорезистору подводят через мостовую схему, где тензорезистор может быть включен в одно из плеч моста, либо в два плеча, либо мостовая цепь составляется целиком из тензорезисторов.
В зависимости от количества тензорезисторов, включаемых в измерительный мост, возможны три модификации мостовой схемы: «четверть моста», «полумост» и «полный мост».
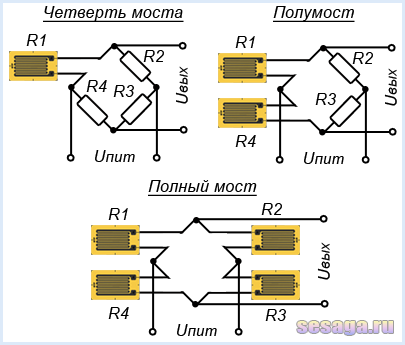
Тензорезисторы обычно выносятся за пределы измерительного устройства и располагаются на исследуемом объекте, тогда как резисторы, дополняющие мост, как правило, расположены в измерительном устройстве.
2. Терморезисторы.
Терморезистором называют полупроводниковый резистор, сопротивление которого изменяется под действием температуры. Резистивный элемент таких резисторов выполнен из полупроводниковых материалов на основе окислов металлов.
Терморезисторы используются для температурной компенсации различных электрических цепей, стабилизации токов и напряжений, в качестве датчиков контроля температуры, в автоматике для регулирования и измерения температуры, в измерителях мощности и т.д.
Основными параметрами терморезисторов является номинальное сопротивление, изменяющееся при определенной температуре, и температурный коэффициент сопротивления (ТКС), показывающий на какую величину изменяется сопротивление резистора при изменении температуры на 1°С. Также учитывают тепловую инерцию, которая характеризуется постоянной времени, т.е. промежутком времени, в течение которого сопротивление резистора изменится на 63°С при перенесении его из воздушной среды с температурой 0°С в воздушную среду с температурой 100°С.
В зависимости изменения сопротивления от температуры терморезисторы изготавливают с отрицательным и положительным

Нагрев терморезистора осуществляют прямым или косвенным способом.
При прямом нагреве сопротивление резистора изменяется под действием окружающего воздуха или непосредственно проходящим через резистор током. Терморезисторы с прямым нагревом используются для измерения температуры, температурной компенсации положительного ТКС различных электрических цепей, стабилизации токов и напряжений, в качестве предохранителей в схемах защиты от перегрузок по току и напряжению, в качестве переключателей в пусковых устройствах.
Отечественная промышленность выпускает термисторы серии КМТ, ММТ, СТ1-2, СТ1-17, СТ3-6, СТ4-2, ПТ1, ПТ3, ТР1 — ТР4, ТП и т.д., а также позисторы серии СТ5-1, СТ6-1А, СТ10-1, СТ11-1Г, СТ14-3, СТ15-2-220В и т.д.
При косвенном нагреве изменение сопротивления происходит под действием тепла, выделяемого специальным нагревателем. В резисторах косвенного нагрева резистивный и нагревательный элементы размещены в одном корпусе, но гальванически разделены друг от друга. Нагревательным элементом задается температура резистивного элемента и, тем самым, изменяется сопротивление терморезистора. Терморезисторы косвенного нагрева используются в качестве переменного резистора, управляемого напряжением, приложенным к нагревательному элементу терморезистора.

Отечественной промышленностью выпускаются резисторы косвенного нагрева серии ТКП-20, ТКПМ-20, ТКП-50, ТКПМ-50, ТКП-300А, ТКПМ-300А, СТ1-21, СТ1-30, СТ1-31, СТ3-21, СТ3-27, СТ3-31, СТ3-33 и т.д.
На принципиальных схемах терморезисторы изображают в виде нелинейного резистора со знаком температуры «t°». Условное изображение терморезистора косвенного нагрева обозначается с дополнительным символом подогревателя в виде перевернутой латинской буквой «U».
3. Варисторы.
Варистором называют полупроводниковый резистор, обладающий свойством уменьшения сопротивления полупроводника при увеличении приложенного напряжения.

Варисторы обладают высоким омическим сопротивлением, составляющим сотни мегаом, и включаются в электрическую цепь параллельно питающему напряжению и нагрузке. Они работают в диапазоне напряжений от 4 до 1500 В постоянного или переменного тока и рассчитаны на определенное рабочее напряжение.

Варисторы применяются для защиты электрооборудования от импульсных напряжений и используются в маломощных стабилизаторах, системах автоматической регулировки усиления, в схемах защиты от перегрузок и т.п. Принцип действия варистора заключается в его способности мгновенно понижать свое сопротивление при увеличении или скачках питающего напряжения, а затем также мгновенно его восстанавливать при возвращении напряжения на первоначальный уровень.
Работает варистор следующим образом: в обычном режиме (при отсутствии скачков напряжения) он находится под действием питающего напряжения защищаемого оборудования и проходящий ток через варистор очень мал (менее 1 мА) и варистор никак не влияет на работу защищаемого оборудования.
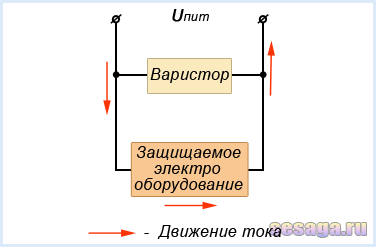
При скачке питающего напряжения варистор резко уменьшает свое сопротивление до нескольких ом и шунтирует нагрузку, пропуская весь пиковый ток через себя. При этом поглощаемая варистором энергия скачков напряжения рассеивается в виде теплового излучения, и в этот момент через варистор могут кратковременно протекать токи в десятки или тысячи ампер.
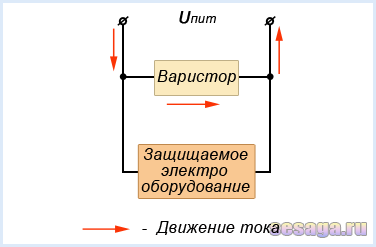
Так как варистор обладает большим быстродействием (не более 25 нс), то после прекращения скачков напряжения он быстро восстанавливает свое сопротивление до номинального значения и питающее напряжение опять поступает на оборудование.
При длительном воздействии повышенным напряжением варистор может перегреться и выйти из строя из-за превышения максимально допустимого тока. Геометрические размеры и мощность варистора играют значительную роль, так как общая площадь его поверхности имеет пропорциональное влияние на эффективность рассеивания энергии бросков напряжения и удержание пиковых токов нагрузки без угрозы быть поврежденным. Поэтому на корпусе зарубежных и некоторых отечественных варисторов помимо рабочего напряжения указывают его диаметр в миллиметрах:

Но все же полную информацию о варисторе необходимо смотреть на сайте производителя или в сопроводительной документации, так как производители маркируют их с небольшим отличием.
Основные параметры варисторов:
1. Номинальное рабочее напряжение, Un – классификационное напряжение, при котором через варистор протекает ток 1мА.
2. Максимально допустимое переменное Um~ и постоянное Um= напряжение – величина, при которой варистор включается в работу.
3. Напряжение ограничения — максимальное напряжение между выводами варистора, воздействующее на защищаемое электрооборудование в момент шунтирования его варистором.
4. Допустимая поглощаемая энергия, W (Дж) при воздействии одиночного импульса. От этой величины зависит, как долго может действовать перегрузка с максимальной мощностью без опасности повредить варистор.
5. Емкость, Со, измеренная в закрытом состоянии. При работе ее значение зависит от приложенного напряжения. Когда варистор пропускает пиковый ток, величина емкости падает до нуля.
Расчет рабочего режима варистора сводится к оптимальному выбору значения его классификационного напряжения и допустимой энергии рассеивания. Для ориентировочных расчетов рекомендуется, чтобы рабочее переменное напряжение не превышало Uвх ≤ 0,6Un, а рабочее постоянное напряжение не превышало Uвх ≤ 0,85Un.
Для сети с напряжением 220В 50Гц используют варисторы с классификационным напряжением не ниже 380…430В. Для варистора с классификационным напряжением 430 В при импульсе тока 100 А напряжение будет ограничено на уровне около 600 В.
Для повышения рассеиваемой мощности варисторы включают последовательно или параллельно. При последовательном включении через варисторы протекает одинаковый ток, а общее напряжение разделяется пропорционально их сопротивлениям. В этих же соотношениях разделяется поглощаемая энергия.
При параллельном включении используется последовательно-параллельная схема включения варисторов: варисторы последовательно собираются в столбы, а столбы соединяются параллельно. Затем подбором варисторов добиваются совпадения ВАХ столбов варисторов.
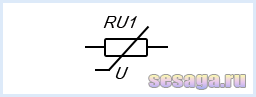
На принципиальных схемах варистор обозначается в виде нелинейного резистора с латинской буквой «U» у излома знака саморегулирования.
Из советских и российских наибольшее применение нашли варисторы серии СН1 (устарели и не выпускаются), СН2 и ВР-1, а из зарубежных, варисторы серии FNR, CNR, TWR, JVR, WMR, HEL, MYG и т.д.
Отечественные варисторы изготавливаются в виде дисков толщиной до 10 мм (в зависимости от классификационного напряжения) и маркируются буквенным и цифровым кодом. Варисторы СН2-1 и ВР-1 имеют проволочные однонаправленные выводы диаметром 0,8 мм (варисторы СН2-1 варианта «в» имеют выводы диаметром 0,6 мм). Варисторы СН2-2 вариант «А» имеют штуцерные выводы с резьбой М5, вариант «Б» имеет массивные выводы, переходящие в шпильки с резьбой М5, вариант «Г» имеет массивные дисковые выводы с резьбой М5, а варианты «В» и «Д» имеют контактные поверхности, покрытые серебром.
Маркировка отечественных варисторов:
1. Две первые буквы СН и ВР указывают, что это варистор.
2. Цифра сразу после букв обозначает материал, из которого сделан варистор: СН2 – оксидноцинковые, ВР-1 — оксидноцинковые.
3. Вторая цифра, написанная через дефис, обозначает тип варистора (1 – дисковые варисторы, 2 – силовые варисторы). У варисторов ВР вторая цифра является типоразмером (габариты).
4. Буква сразу после второй цифры указывает на вариант варистора (а–д – проволочные выводы; А–Д – силовые выводы).
5. Третье число является номинальным напряжением (в вольтах).
6. Четвертое число обозначает допускаемое отклонение от номинального напряжения (в процентах).
Примеры маркировки:
СН2-1а 430В ±10% — оксидноцинковый варистор, дисковый, с проволочными выводами, номинальным напряжением 430 В с допускаемым отклонением ±10%.
ВР-1-1 22В ±10% — оксидноцинковый варистор, дисковый, с проволочными выводами, номинальным напряжением 22 В с допускаемым отклонением ±10%.
Примеры маркировки зарубежных варисторов:
FNR 14 K471:
FNR – серия или название производителя;
14 — диаметр варистора 14 мм;
K – допускаемое отклонение от номинального напряжения ±10%;
471 – рабочее напряжение 470 В – смотри цифровая маркировка резисторов.
CNR 07D 390K:
CNR — серия или название производителя;
07— диаметр варистора 7мм;
D – дисковый;
390 — рабочее напряжение 39 В;
K – допускаемое отклонение от номинального напряжения ±10%.
271 KD 14:
271 — рабочее напряжение 270 В;
K — допускаемое отклонение от номинального напряжения ±10%;
D – дисковый;
14 — диаметр варистора 14 мм.
4. Фоторезисторы.
Фоторезистором называют полупроводниковый фотоэлектрический прибор, электрическое сопротивление которого зависит от освещенности. Фоторезисторы работают в цепях постоянного и переменного тока, и нашли широкое применение в радио и электротехнике. Их применяют в системах фотоэлектрической автоматике и телемеханике, в промышленной и бытовой электронике и вычислительной технике.

Принцип действия фоторезистора основан на эффекте фотопроводимости полупроводника при его освещении. В результате поглощения полупроводником лучистой энергии образуется дополнительное количество подвижных носителей заряда, вследствие чего улучшается электропроводность полупроводника и, как следствие, уменьшается сопротивление, т.е. возникает дополнительная проводимость, называемая фотопроводностью полупроводника.
Если поверхность полупроводника освещать непрерывно, то его сопротивление снижается, и через фоторезистор начинает течь световой ток. После прекращения освещения восстанавливается прежняя величина проводимости и через неосвещенный фоторезистор течет малый ток, называемый темновым. Разность между световым и темновым током называют фототоком.
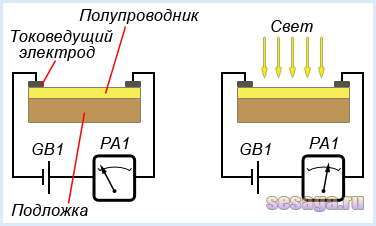
Более удобно пользоваться понятием темновое сопротивление, которое определяется, как сопротивление неосвещенного фоторезистора. Для большинства фоторезисторов указывается именно нижний предел темнового сопротивления, величина которого находится в пределах от десятков килоом до нескольких мегаом.
Фоторезистор состоит из диэлектрической подложки, выполненной из стеклянной или керамической пластины, на поверхность которой нанесен тонкий слой металла из золота, серебра или платины. На поверхность металлов нанесен тонкий слой из специального полупроводника, например, из сульфидов свинца, висмута, кадмия и др., свойства которого и определяют параметры фоторезистора. Подложка и полупроводник образуют светочувствительный элемент, который снабжен гибкими выводами для включения в электрическую цепь и расположен так, чтобы на него мог падать свет.
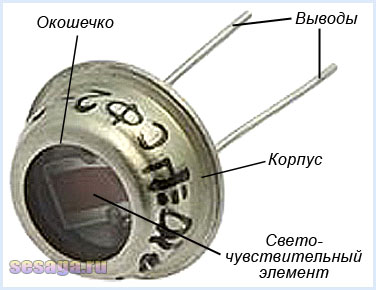
От внешних воздействий фоторезистор защищает слой лака или эпоксидной смолы, пропускающий свет лишь нужной области спектра, а также пластмассовый или металлический корпус. Свет проникает через окошечко в корпусе, расположенное над полупроводниковым слоем.
Отечественная промышленность выпускает фоторезисторы ФСК, ФСД, ФСА, СФ.
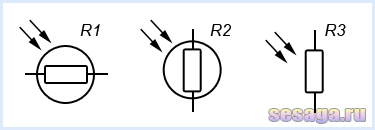
На электрических схемах фоторезисторы обозначаются символом резистора, помещенного в круг, к которому направлены две наклонные параллельные стрелки, символизирующие фотоэлектрический эффект. На некоторых современных отечественных и зарубежных схемах круг указывают не всегда.
К основным параметрам фоторезисторов относятся:
1. Темновое сопротивление, Rт – сопротивление фоторезистора в отсутствии падающего на него излучения в диапазоне его спектральной чувствительности.
2. Световое сопротивление, Rc – сопротивление фоторезистора, измеренное через определенный интервал времени после начала воздействия излучения, создающего на нем освещенность заданного значения.
3. Рабочее напряжение, Uраб – постоянное напряжение, приложенное к фоторезистору, при котором обеспечиваются номинальные параметры при длительной его работе в заданных эксплуатационных условиях (гарантирующее продолжительную работу фоторезистора).
4. Удельная чувствительность – отношение фототока к произведению величины падающего на фоторезистор светового потока и приложенного к нему напряжения.
5. Интегральная чувствительность – определяется как отношение разности токов при освещении и темнового к световому потоку, падающего на резистор при номинальном значении напряжения. Ее величина лежит в пределах от 1000 до 5000 мкА/(лм•В).
Кроме указанных параметров, фоторезистор характеризуется также максимальным рабочим напряжением, номинальной мощностью, относительным изменением сопротивления, временем спада фототока при затемнении, а также спектральными характеристиками, показывающими, в какой части спектра фоторезистор имеет наибольшую чувствительность.
Вот и все, что хотел коротко рассказать о нелинейных резисторах.
Удачи!
Литература:
1. В. А. Волгов – «Детали и узлы радио-электронной аппаратуры», Энергия, Москва 1977 г.
2. Ю. А. Овечкин – «Полупроводниковые приборы», Москва «Высшая школа» 1979 г.
3. В. В. Фролов – «Язык радиосхем», Москва «Радио и связь», 1988 г.
4. И. Б. Бондаренко – «Электрорадиоэлементы. 1 часть. Резисторы», Санкт-Петербург 2012 г.
5. Б. А. Глаговский, И. Д. Пивен – «Электротензометры сопротивления», Энергия, Москва 1964 Ленинград.
6. Е. С. Полищук – «Измерительные преобразователи», Киев, Головное издательство издательского объединения «Вища школа», 1981 г.
7. В. А. Мехеда – «Тензометрический метод измерения деформаций», Самара, Издательство СГАУ, 2011 г.
Виды резисторов
Определение 1
Резистор — пассивный элемент электрических цепей, который обладает определённым или переменным значением электрического сопротивления, предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока и др.
Резисторы являются одними из наиболее распространенных компонентов в электрических цепях, большинство электронных устройств содержат их в большом количестве. Практические резисторы как дискретные компоненты могут состоять из различных соединений и форм. Резисторы также реализованы в интегральных схемах. Они изготовлены из различных химических веществ в виде компактных элементов, или в некоторых случаях — из витого проводника с большим удельным сопротивлением.
Замечание 1
Единица измерения электрического сопротивления резистора Ом, названная в честь немецкого физика Георга Симона Ома.
Типы резисторов
Существуют два основных типа резисторов.
- Линейные резисторы
- Нелинейные резисторы
Линейные резисторы.
Эти резисторы, у которых значения изменяются с приложенным напряжением и температурой, называются линейными резисторами. Другими словами, резистор, значение тока, которого прямо пропорционально приложенному напряжению известен как линейный резистор.
Замечание 2
Линейные резисторы делятся на фиксированные резисторы и переменные резисторы.
Фиксированные резисторы
Фиксированные резисторы на сегодняшний день, наиболее широко используемый тип резисторов. Они используются в схемах электроники, чтобы поставить правильные условия в цепи. Их значения определяются на этапе проектирования схемы, и они никогда не изменяются.
Фиксированные типы резисторов
Есть целый ряд различных типов фиксированных резисторов. На основе состава резисторы могут быть классифицированы следующим образом:
Углеродные композиционные резисторы
Типичный фиксированный резистор выполнен из смеси гранулированного или измельченного углерода или графита, изоляционного наполнителя, или смоляного связующего. Отношение изоляционного материала определяет фактическое сопротивление резистора. Изолирующий порошок, выполнен в виде стержней, и есть две металлические крышки на обоих концах стержня.
Есть два проводника на обоих концах резистора для соединения устройств в цепи с помощью пайки. Пластиковый слой покрывает стержни с различными цветовыми кодами (печатными буквами), которые обозначают величину сопротивления.
Проволочный резистор
Проволочный резистор выполнен из изоляционного сердечника или стержня, обернутый вокруг резистивной проволоки. Сопротивление проволоки представляет собой, как правило, вольфрам, манганин, нихром или хромовый сплав никеля или никель и изолирующий сердечник выполнен из фарфора, бакелита или керамического материала глины.
Тонкопленочные резисторы
В основном, все тонкие пленочные резисторы выполнены из высококачественного керамического стержня и резистивного материала. Очень тонкий проводящий слой материала накладывается на изолирующий стержень, пластину или трубку, которая сделана из высококачественного керамического материала или стекла.
Переменные резисторы
Как видно из названия, эти резисторы, значения которых могут быть изменены с помощью ручки, винта или вручную с помощью правильного метода. В этих типах резисторов, есть подвижная ручка, которая соединена с валом, и значение сопротивления можно изменить путем поворота рычага. Они используются в радиоприемниках для управления громкостью звука.
Примеры таких резисторов:
- Потенциометры
- Реостаты
- Триммеры
Нелинейные резисторы
Известно, что нелинейные резисторы это резисторы, где ток, протекающий, через них не изменяется в соответствии с законом Ома, но, изменяется при изменении температуры или приложенного напряжения.
- Варисторы — сопротивление зависит от приложенного напряжения;
- Терморезисторы — сопротивление зависит от температуры;
- Фоторезисторы — сопротивление зависит от освещённости;
- Тензорезисторы — сопротивление зависит от деформации резистора;
- Магниторезисторы — сопротивление зависит от величины магнитного поля.
10.1. Параметры нелинейных резисторов
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления.
Если нелинейный элемент является безынерционным, то он характеризуется первыми двумя из перечисленных параметров.
Статическое сопротивление равно отношению напряжения на резистивном элементе к протекающему через него току. В частности для точки 1 ВАХ на рис. 1
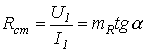 .
.
Под дифференциальным сопротивлениемпонимается отношение бесконечно малого приращения напряжения к соответствующему приращению тока
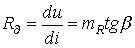 .
.
Следует отметить, что у неуправляемого
нелинейного резистора 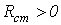 всегда,
а
всегда,
а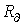 может
принимать и отрицательные значения
(участок 2-3 ВАХ на рис. 1).
может
принимать и отрицательные значения
(участок 2-3 ВАХ на рис. 1).
В случае инерционного нелинейного резистора вводится понятие динамического сопротивления
,
определяемого по динамической ВАХ. В
зависимости от скорости изменения
переменной, например тока, может меняться
не только величина, но и знак 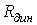 .
.
10.2. Методы расчета нелинейных электрических цепей постоянного тока
Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприменим. В этой связи методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.
Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения. В общем случае при анализе нелинейной цепи описывающая ее система нелинейных уравнений может быть решена следующими методами:
графическими;
аналитическими;
графо-аналитическими;
итерационными.
10.2.1. Графические методы расчета
При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.
а) Цепи с последовательным соединением резистивных элементов.
П
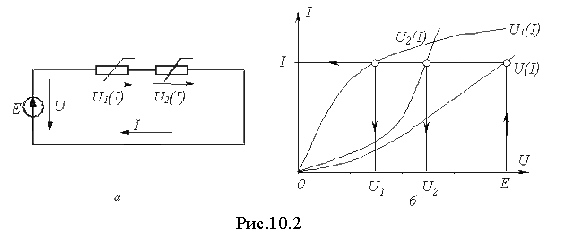 ри
последовательном соединении нелинейных
резисторов в качестве общего аргумента
принимается ток, протекающий через
последовательно соединенные элементы.
Расчет проводится в следующей
последовательности. По заданным ВАХ
ри
последовательном соединении нелинейных
резисторов в качестве общего аргумента
принимается ток, протекающий через
последовательно соединенные элементы.
Расчет проводится в следующей
последовательности. По заданным ВАХ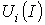 отдельных
резисторов в системе декартовых координат
отдельных
резисторов в системе декартовых координат строится
результирующая зависимость
строится
результирующая зависимость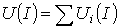 .
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью
.
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью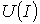 .
Из точки пересечения перпендикуляра с
кривой
.
Из точки пересечения перпендикуляра с
кривой опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей
опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей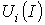 определяются
напряжения
определяются
напряжения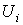 на
отдельных резистивных элементах.
на
отдельных резистивных элементах.
Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис.10. 2,а.
Графическое решение для последовательной
нелинейной цепи с двумя резистивными
элементами может быть проведено и другим
методом – методом пересечений. В
этом случае один из нелинейных резисторов,
например, с ВАХ на
рис.10.2,а, считается внутренним
сопротивлением источника с ЭДС Е, а
другой – нагрузкой. Тогда на основании
соотношения
на
рис.10.2,а, считается внутренним
сопротивлением источника с ЭДС Е, а
другой – нагрузкой. Тогда на основании
соотношения точка
а (см. рис.10.3) пересечения кривых
точка
а (см. рис.10.3) пересечения кривых и
и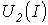 определяет
режим работы цепи. Кривая
определяет
режим работы цепи. Кривая строится
путем вычитания абсцисс ВАХ
строится
путем вычитания абсцисс ВАХ из
ЭДС Е для различных значений тока.
из
ЭДС Е для различных значений тока.
Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением резистивных элементов.
При параллельном соединении нелинейных
резисторов в качестве общего аргумента
принимается напряжение, приложенное к
параллельно соединенным элементам.
Расчет проводится в следующей
последовательности. По заданным ВАХ 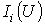 отдельных
резисторов в системе декартовых координат
отдельных
резисторов в системе декартовых координат строится
результирующая зависимость
строится
результирующая зависимость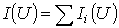 .
Затем на оси токов откладывается точка,
соответствующая в выбранном масштабе
заданной величине тока источника на
входе цепи (при наличии на входе цепи
источника напряжения задача решается
сразу путем восстановления перпендикуляра
из точки, соответствующей заданному
напряжению источника, до пересечения
с ВАХ
.
Затем на оси токов откладывается точка,
соответствующая в выбранном масштабе
заданной величине тока источника на
входе цепи (при наличии на входе цепи
источника напряжения задача решается
сразу путем восстановления перпендикуляра
из точки, соответствующей заданному
напряжению источника, до пересечения
с ВАХ ),
из которой восстанавливается перпендикуляр
до пересечения с зависимостью
),
из которой восстанавливается перпендикуляр
до пересечения с зависимостью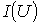 .
Из точки пересечения перпендикуляра с
кривой
.
Из точки пересечения перпендикуляра с
кривой опускается
ортогональ на ось напряжений – полученная
точка соответствует напряжению на
нелинейных резисторах, по найденному
значению которого с использованием
зависимостей
опускается
ортогональ на ось напряжений – полученная
точка соответствует напряжению на
нелинейных резисторах, по найденному
значению которого с использованием
зависимостей определяются
токи
определяются
токи в
ветвях с отдельными резистивными
элементами.
в
ветвях с отдельными резистивными
элементами.
Использование данной методики иллюстрируют графические построения на рис.10. 4,б, соответствующие цепи на рис.10. 4,а.

в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.
1. Расчет таких цепей производится в следующей последовательности:
Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).
2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.
2.2. Нелинейные резистивные элементы
Мгновенный ток через безинерционный элемент зависит лишь от значения напряжения на нем в тот же момент времени. Вольт-амперная характеристика (ВАХ) такого элемента
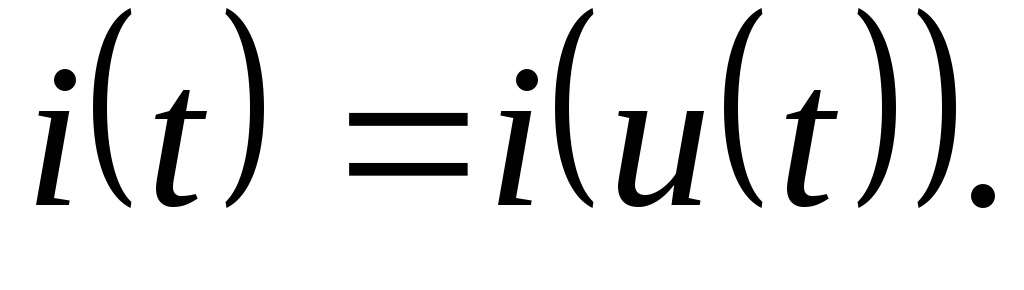 (2.2)
(2.2)
В таких элементах нет сдвига по фазе в колебаниях тока и напряжения, что характерно для резистивных сопротивлений. Соответственно, их называют резистивными элементами. На рис. 2.1 показаны типичные примеры ВАХ нелинейных двухполюсников: а) однозначная характеристика полупроводникового диода; б) характеристика туннельного диода, отличающаяся тем, что одному и тому же значению тока могут соответствовать три разных значения напряжения.


а)
б)
Рис. 2.1
Приложим
к двухполюснику постоянное напряжение  .
Ток через него равен
.
Ток через него равен .
Отношение
.
Отношение
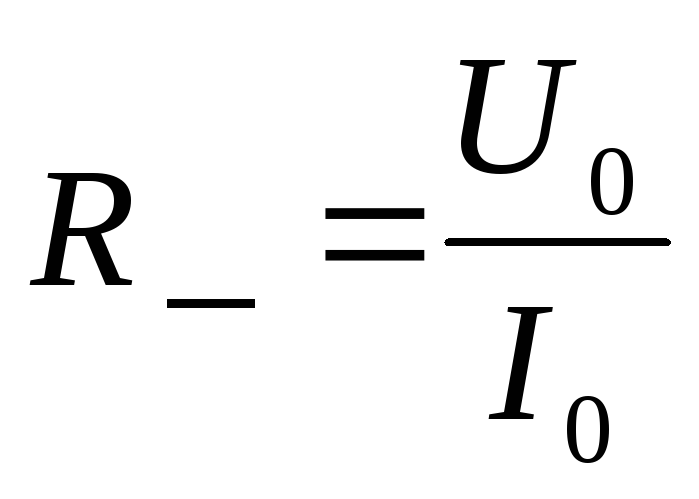 (2.3)
(2.3)
называется сопротивлением
элемента постоянному току.
В отличие от сопротивления линейного
резистора значение 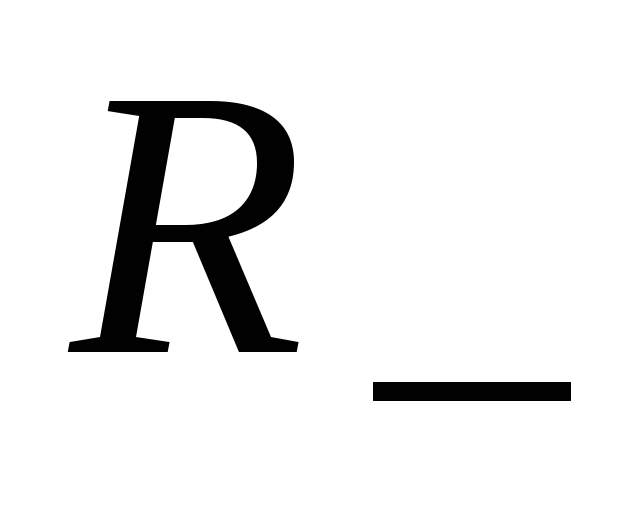 зависит от
зависит от .
.
Приложим
к двухполюснику напряжение 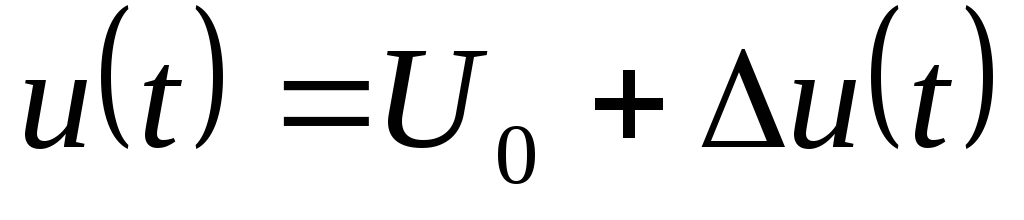 ,
где
,
где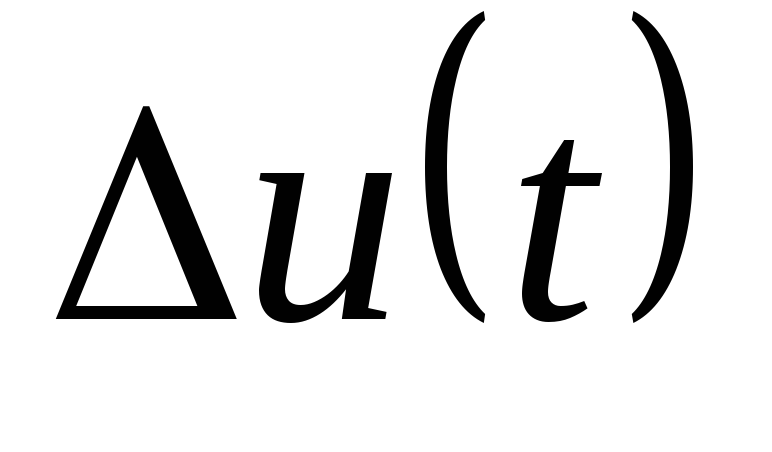 — периодически изменяющееся напряжение
с нулевым средним, например, — гармоническое,
с малой амплитудой колебаний
— периодически изменяющееся напряжение
с нулевым средним, например, — гармоническое,
с малой амплитудой колебаний ,
, .
Аппроксимируем ВАХ (2.2) в окрестности
рабочей точки
.
Аппроксимируем ВАХ (2.2) в окрестности
рабочей точки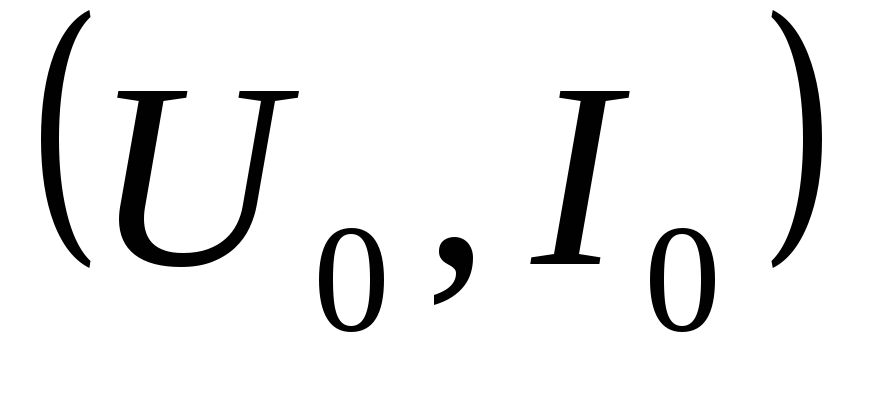 в линейном приближении:
в линейном приближении: .Сопротивление
элемента переменному
току с малой амплитудой колебаний в
окрестности рабочей точки
.Сопротивление
элемента переменному
току с малой амплитудой колебаний в
окрестности рабочей точки 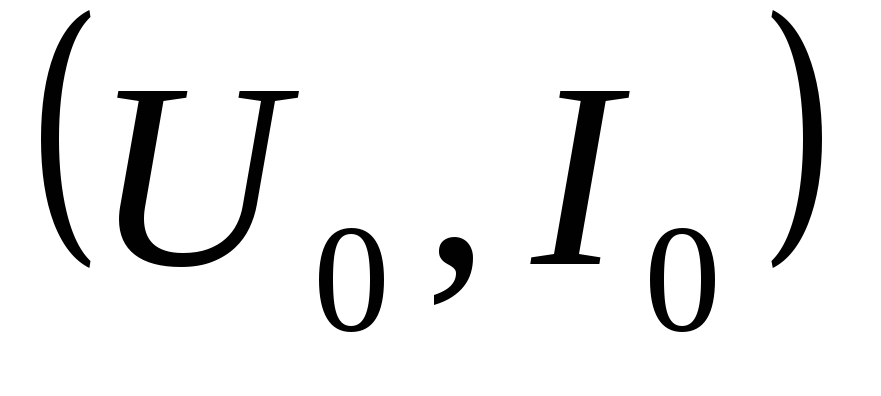 ,
измеряется дифференциальным сопротивлением
,
измеряется дифференциальным сопротивлением
 (2.4)
(2.4)
Оба
сопротивления 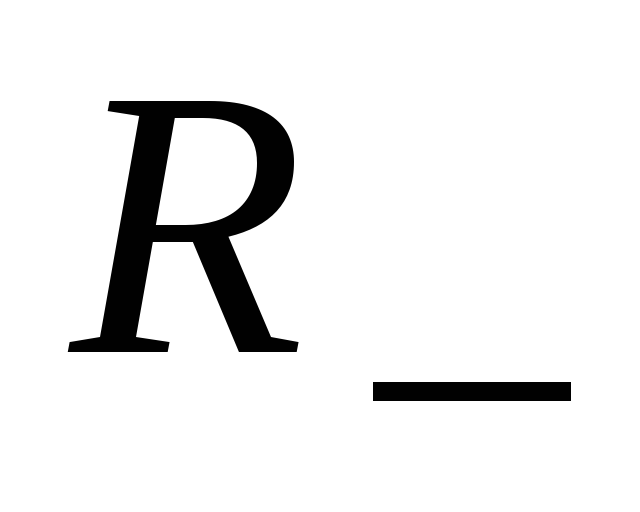 и
и могут быть как положительными, так и
отрицательными или нулевыми. Случай
могут быть как положительными, так и
отрицательными или нулевыми. Случай ()
соответствует элементу, потребляющему
мощность
()
соответствует элементу, потребляющему
мощность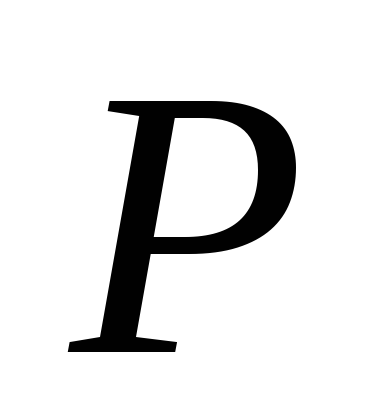 постоянного тока (источнику энергии
постоянного тока). Действительно, в
соответствии с законом Джоуля-Ленца
постоянного тока (источнику энергии
постоянного тока). Действительно, в
соответствии с законом Джоуля-Ленца .
Например, внутреннему сопротивлению
источника постоянного тока отрицательно,
если считать электрическую мощность,
вырабатываемую источником, отрицательной.
Электрическая мощность, потребляемая
резистором в цепи, напротив, будет
положительна. Теперь возьмем цепь
переменного, например, — гармонического
тока. Пусть
.
Например, внутреннему сопротивлению
источника постоянного тока отрицательно,
если считать электрическую мощность,
вырабатываемую источником, отрицательной.
Электрическая мощность, потребляемая
резистором в цепи, напротив, будет
положительна. Теперь возьмем цепь
переменного, например, — гармонического
тока. Пусть и
и — комплексные амплитуды падения напряжения
и тока на резистивном сопротивлении.
Средняя за период колебаний электрическая
мощность на сопротивлении
— комплексные амплитуды падения напряжения
и тока на резистивном сопротивлении.
Средняя за период колебаний электрическая
мощность на сопротивлении .
На участке цепи с резистивным
сопротивлением, где электрическая
мощность потребляется (генерируется),
напряжение и ток колеблются синфазно
(противофазно). Поэтому участок цепи,
где дифференциальное сопротивление
.
На участке цепи с резистивным
сопротивлением, где электрическая
мощность потребляется (генерируется),
напряжение и ток колеблются синфазно
(противофазно). Поэтому участок цепи,
где дифференциальное сопротивление является потребителем электрической
энергии, а участок, где
является потребителем электрической
энергии, а участок, где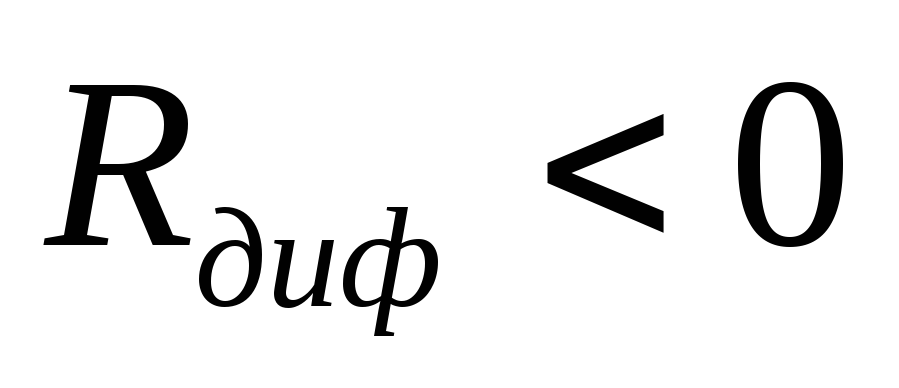 — источником той же энергии.
— источником той же энергии.
ВАХ
линейного резистивного элемента  ,
где
,
где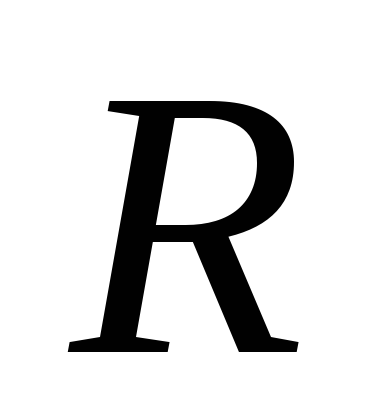 — постоянное сопротивление. Для линейного
элемента
— постоянное сопротивление. Для линейного
элемента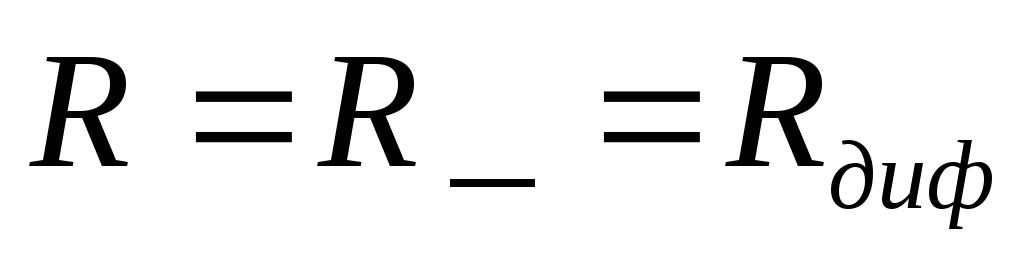 .
.
Проводимость
нелинейного элемента для постоянного
тока  .
Дифференциальная проводимость того же
элемента равна крутизне ВАХ в рабочей
точке:
.
Дифференциальная проводимость того же
элемента равна крутизне ВАХ в рабочей
точке: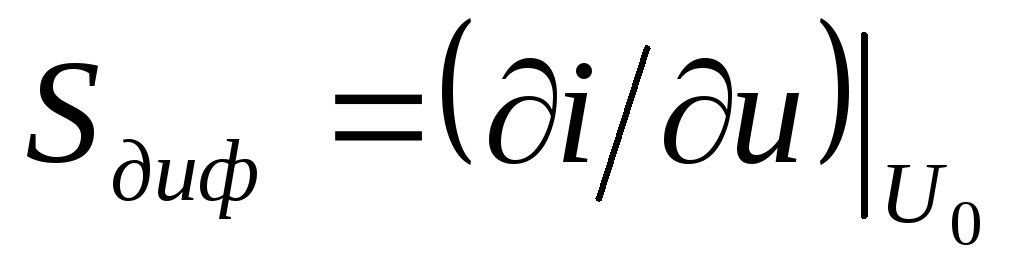 .
.
Для
расчета многих схем, находящихся под
действием гармонических колебаний
большой амплитуды, используют средние
по первой гармонике параметры (среднюю крутизну  ,
среднюю проводимость
,
среднюю проводимость ,
среднюю емкость
,
среднюю емкость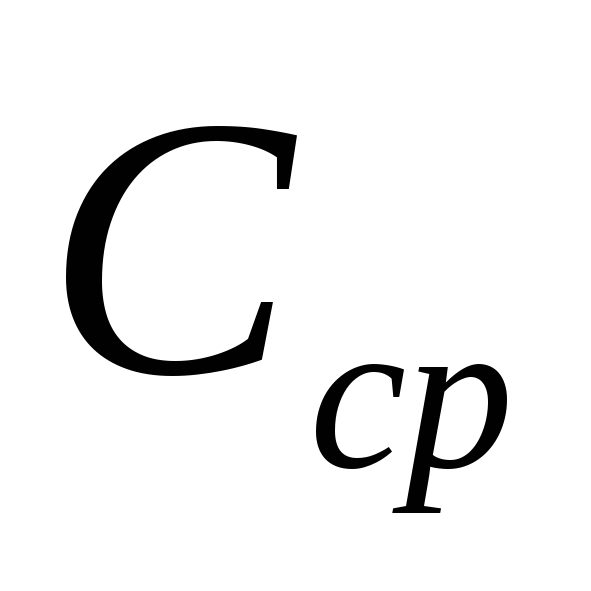 и т.д.). Они определяются отношением
амплитуд первых гармоник. Эти параметры
связывают друг с другом амплитуды первых
гармоник тока и напряжения на
соответствующих участках цепи.
и т.д.). Они определяются отношением
амплитуд первых гармоник. Эти параметры
связывают друг с другом амплитуды первых
гармоник тока и напряжения на
соответствующих участках цепи.
Пример. Рассмотрим
резонансный усилитель на ламповом
триоде (см. рис. 2.2). Пусть на сетку лампы
подано гармоническое напряжение большой
амплитуды 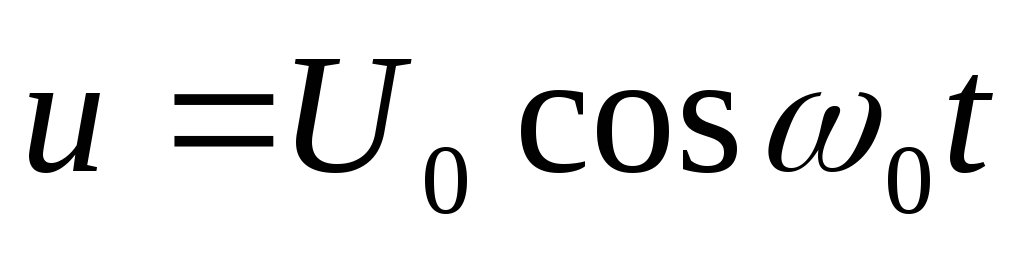 .
Лампа работает в нелинейном режиме
из-за большой амплитуды входного сигнала.
Поэтому ток через лампу не является
гармоническим. Считаем, что параллельный
колебательный контур, служащий нагрузкой
усилителя, настроен на частоту входного
сигнала. Так как контур высокодобротный,
то амплитуда колебаний напряжения на
контуре практически полностью определяется
амплитудой колебаний
.
Лампа работает в нелинейном режиме
из-за большой амплитуды входного сигнала.
Поэтому ток через лампу не является
гармоническим. Считаем, что параллельный
колебательный контур, служащий нагрузкой
усилителя, настроен на частоту входного
сигнала. Так как контур высокодобротный,
то амплитуда колебаний напряжения на
контуре практически полностью определяется
амплитудой колебаний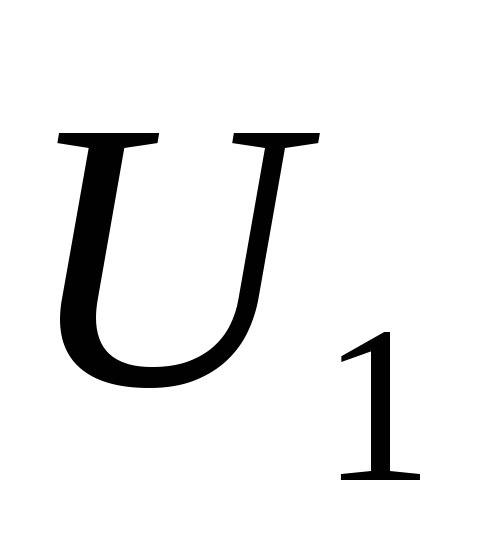 его первой гармоники частоты
его первой гармоники частоты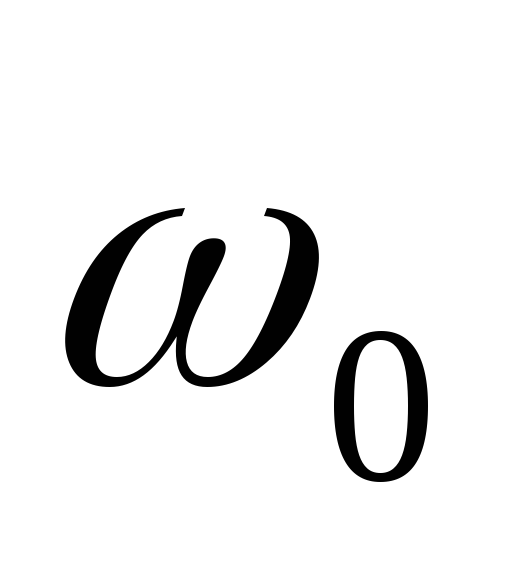 .
Поэтому коэффициент усиления усилителя
можно оценить как
.
Поэтому коэффициент усиления усилителя
можно оценить как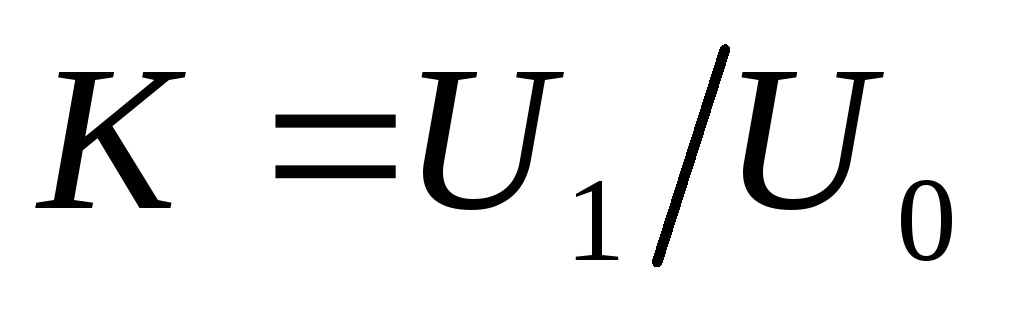 .
Если
.
Если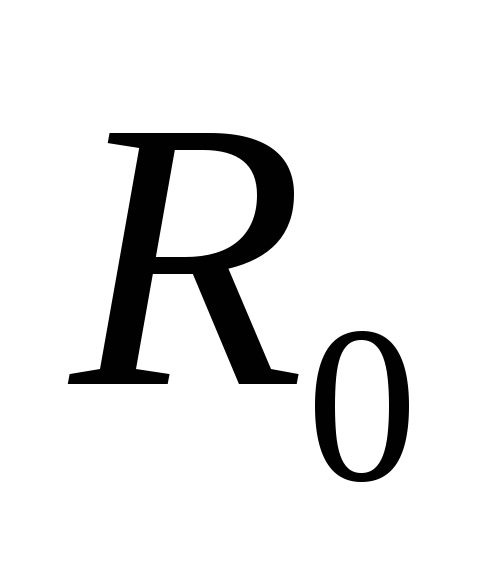 — эквивалентное сопротивление настроенного
контура, то
— эквивалентное сопротивление настроенного
контура, то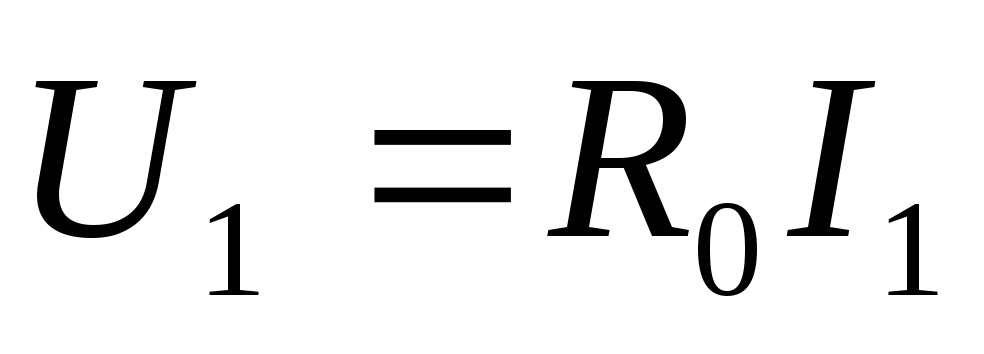 ,
где
,
где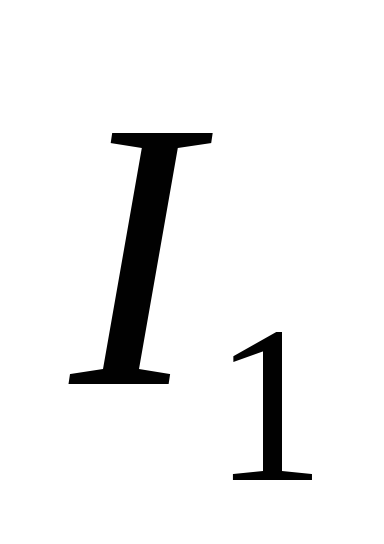 — амплитуда первой гармоники тока в
анодной цепи лампы. Введем среднюю
крутизну анодно-сеточной характеристики
лампы какотношение
амплитуды первой гармоники анодного
тока к амплитуде напряжения на сетке:
— амплитуда первой гармоники тока в
анодной цепи лампы. Введем среднюю
крутизну анодно-сеточной характеристики
лампы какотношение
амплитуды первой гармоники анодного
тока к амплитуде напряжения на сетке: 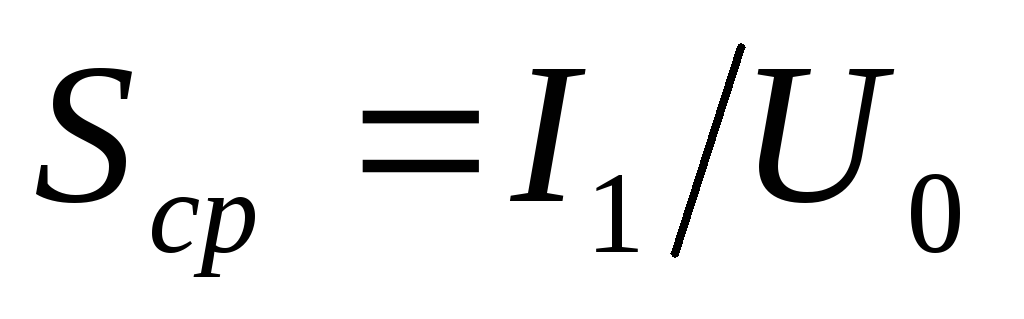 .
Тогда
.
Тогда .
Из построений следует, что средняя
крутизна зависит от амплитуды напряжения
.
Из построений следует, что средняя
крутизна зависит от амплитуды напряжения .
Действительно, изменение
.
Действительно, изменение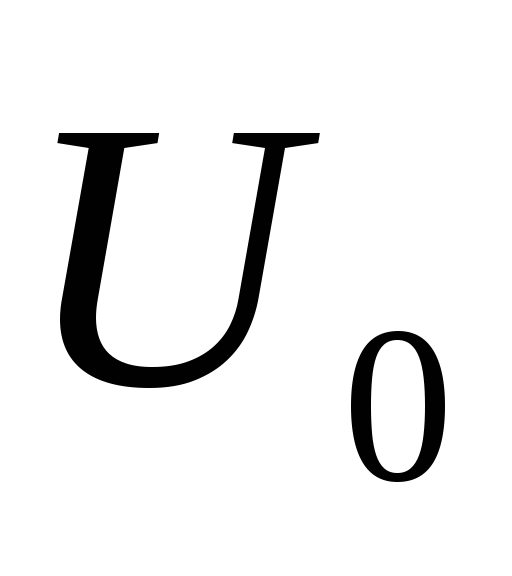 вызывает непропорциональное изменение
вызывает непропорциональное изменение в нелинейном элементе – лампе.
в нелинейном элементе – лампе.
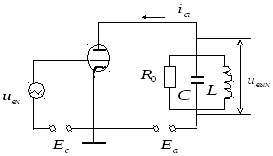

Рис. 2.2
Нелинейные
двухполюсники характеризуются средней
проводимостью – отношением амплитуды
первой гармоники тока 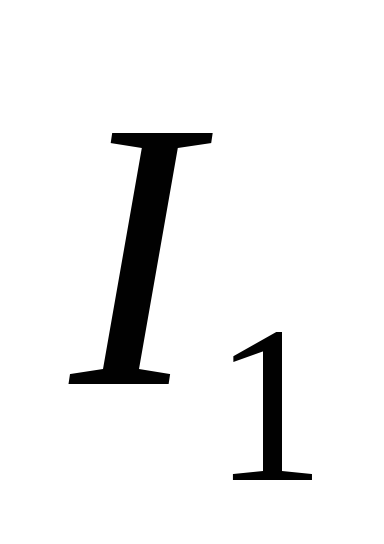 к амплитуде первой гармоники напряжения
к амплитуде первой гармоники напряжения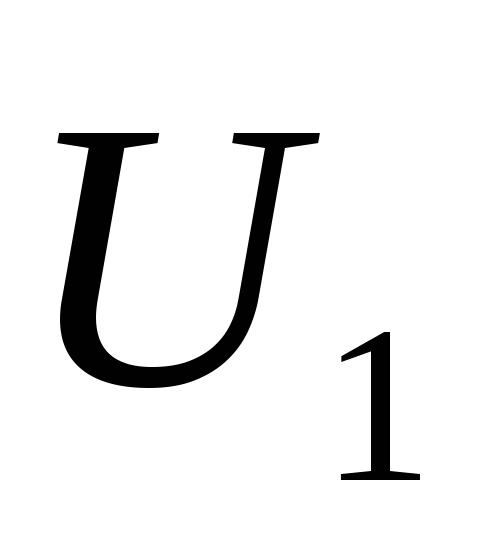 на нем:
на нем: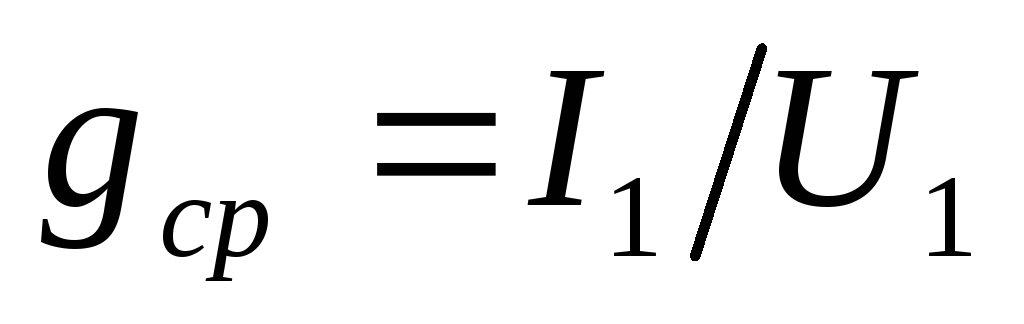 ,
или обратной к ней величиной – средним
сопротивлением
,
или обратной к ней величиной – средним
сопротивлением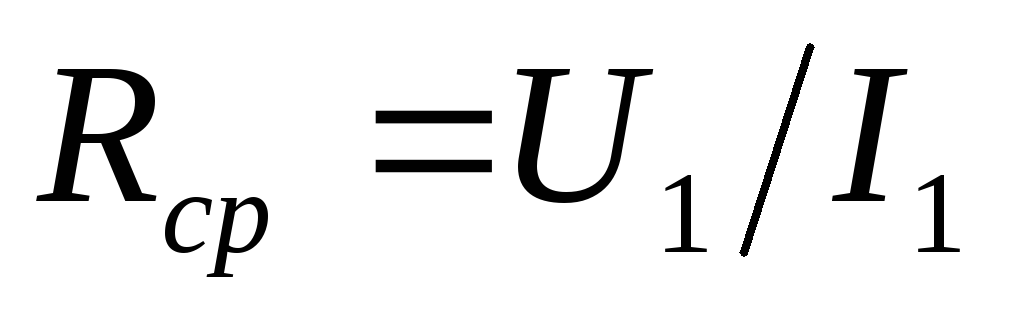 .
Для нелинейных элементов эти величины
зависят от
.
Для нелинейных элементов эти величины
зависят от .
.
Рассмотрим способы описания характеристик нелинейных элементов. Большинство характеристик получают экспериментально, реже – теоретически. Табличное представление особенно удобно для анализа процессов в цепях с помощью ЭВМ. Аргумент и функция образуют двумерный массив в памяти ЭВМ. Чем больше размерность массива и выше точность данных, тем точнее результаты анализа, но сложнее алгоритм и больше временные затраты. Аналитическое представление ВАХ требует подбора аппроксимирующей функции, относительно простой по форме, но отражающей главные свойства ВАХ. В радиотехнике часто используют следующие способы аппроксимации ВАХ нелинейных двухполюсников.
Кусочно-линейная аппроксимация основана на приближенной замене реальной характеристики отрезками прямых линий с различными наклонами.
Пример. На рис. 2.3 показана входная характеристика транзистора КТ306, аппроксимированная двумя отрезками прямых линий.
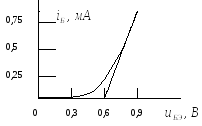
Рис. 2.3
Аппроксимация
определяется двумя параметрами –
напряжением начала 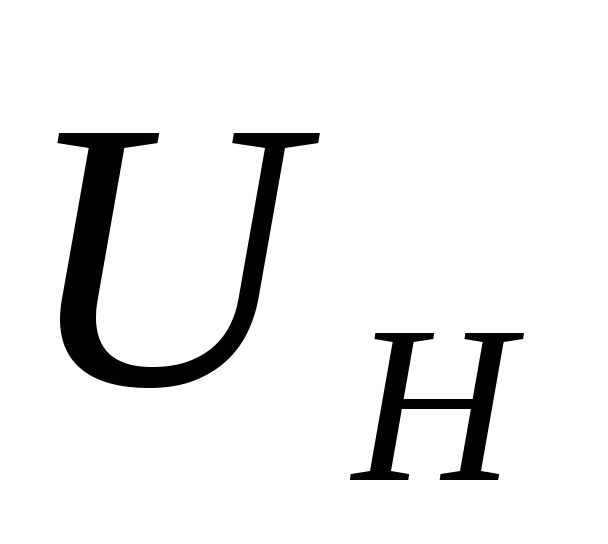 и крутизной
и крутизной .
Аналитически аппроксимация выражается
как
.
Аналитически аппроксимация выражается
как
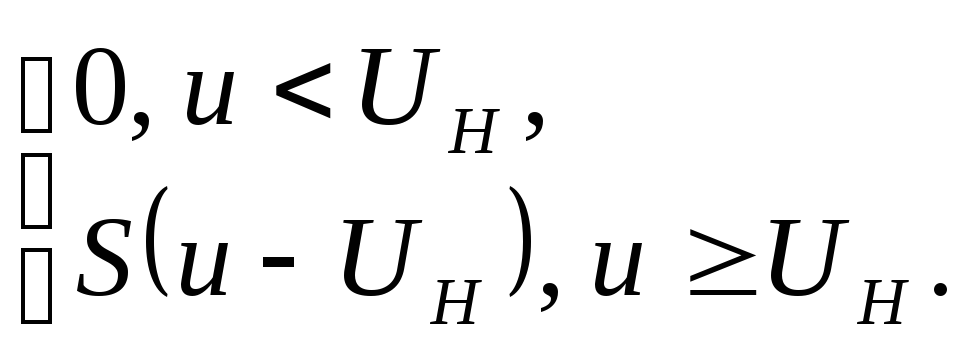 (2.5)
(2.5)
Степенная
аппроксимация основана
на разложении нелинейной ВАХ в ряд
Тейлора в окрестности рабочей точки 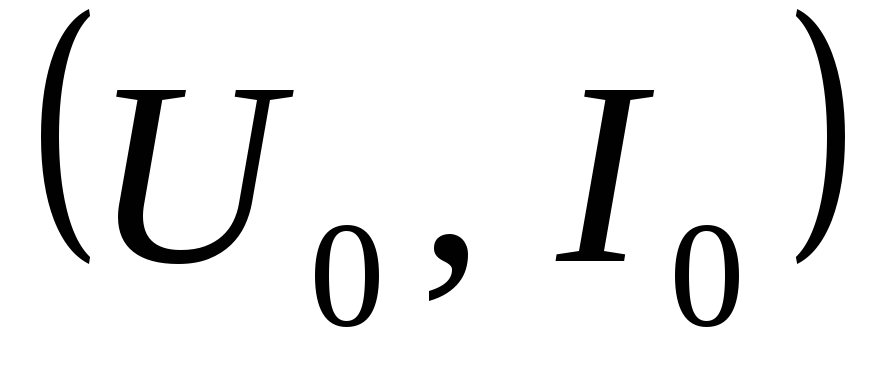 .
При разумных вычислительных затратах
разложение ограничивают несколькими
первыми членами:
.
При разумных вычислительных затратах
разложение ограничивают несколькими
первыми членами:
 (2.6)
(2.6)
что
ограничивает применимость (2.6) лишь
некоторой окрестностью рабочей точки.
Коэффициенты 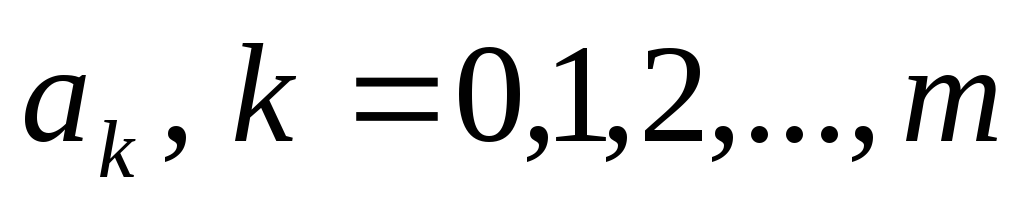 ,
разложения (2.6) находят из решения системы
,
разложения (2.6) находят из решения системы линейных уравнений (
линейных уравнений ( ):
):
 (2.7)
(2.7)
где 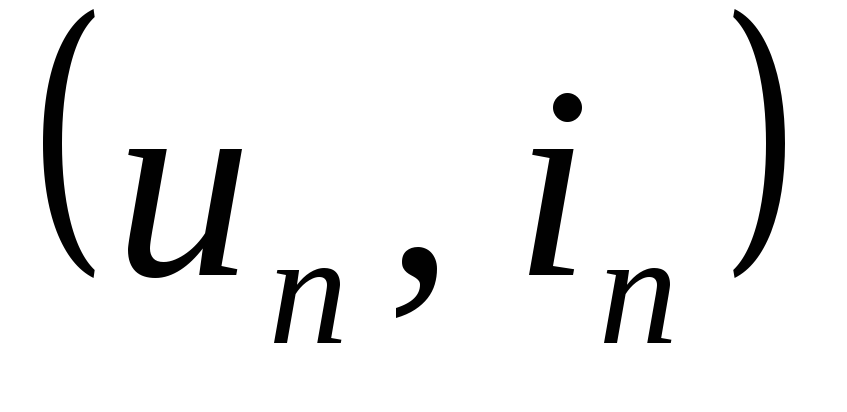 — координаты точки с номером
— координаты точки с номером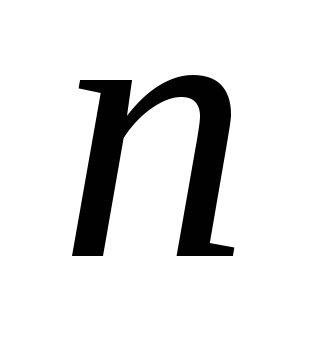 ,
выбранной в окрестности рабочей точки
на аппроксимируемой ВАХ.
,
выбранной в окрестности рабочей точки
на аппроксимируемой ВАХ.
Степенную аппроксимацию используют при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия.
Показательная аппроксимация основана на использовании показательной функции.
Пример. Из теории
работы 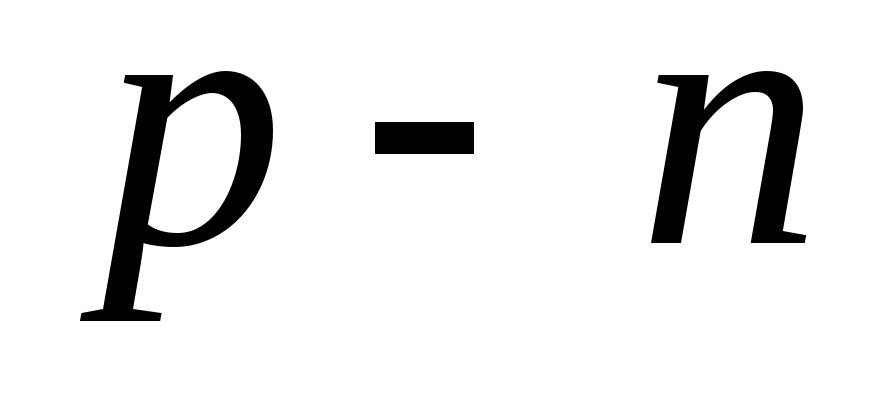 переходов следует, что ВАХ полупроводникового
диода в области
переходов следует, что ВАХ полупроводникового
диода в области описывается выражением
описывается выражением
 (2.8)
(2.8)
где  — обратный ток насыщения, значение
которого обычно мало и составляет
несколько пА,
— обратный ток насыщения, значение
которого обычно мало и составляет
несколько пА,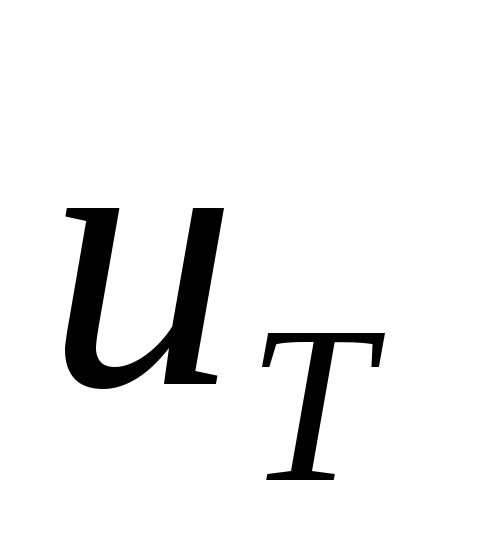 — температурный потенциал,
— температурный потенциал,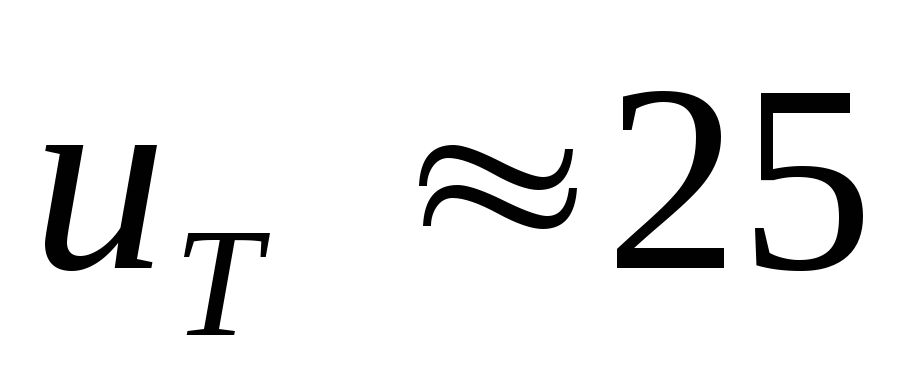 мВ для кремниевых приборов при температуре
мВ для кремниевых приборов при температуре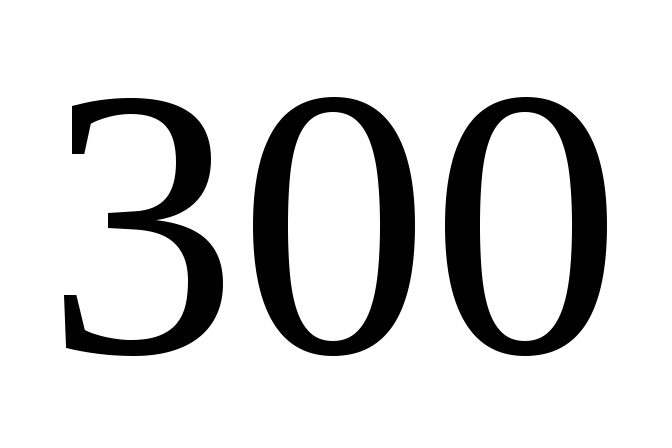 К.
К.
Показательную зависимость (2.8) часто используют при изучении нелинейных явлений в цепях с полупроводниковыми приборами. Аппроксимация (2.8) вполне точна при токах, не превышающих несколько мА. При больших токах характеристика (2.8) плавно переходит в линейную зависимость из-за влияния объемного сопротивления полупроводникового материала.
Извините такой страницы Wp-content Uploads 2014 03 Nelinejnye-soprotivleniya-na-ladoni Pdf не существует!
Выбор статьи по меткам03 (1)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 ноября (2)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)16 профильного ЕГЭ (1)16 января Статград (1)18 (С5) (2)18 задача ЕГЭ (2)23 марта (1)31 января (1)2016 (2)140319 (1)14032019 (1)C5 (1)RC-цепь (1)А9 (1)Александрова (2)Ампера (2)Архимед (1)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (2)ГИА физика задания 5 (1)Герона (1)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (25)ЕГЭ по физике (49)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (6)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (9)Каллисто (1)Кельвин (1)Кирхгоф (1)Кирхгофа (1)Койпера (1)Колебания (1)Коши (1)Коэффициенты поверхностного натяжения жидкостей (1)Кулона-Амонтона (1)Ломоносов (2)Лоренца (1)Луна (1)МГУ (1)МКТ (7)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (3)Менелая (3)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)Нансен (1)НеИСО (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (12)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Плюк (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Сиена (1)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (2)СпБ ГУ вступительный (1)Средняя кинетическая энергия молекул (1)Статград физика (3)Таблица Менделеева (1)Текстовые задачи (8)Тьерри Даксу (1)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Фобос (1)Френеля (1)Цельсий (1)ЭДС (6)ЭДС индукции (2)Эйлера (1)Электрохимические эквиваленты (1)Эрастофен (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (3)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (2)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)апериодический переходной процесс (2)аргумент (1)арифметическая прогрессия (5)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (3)асинхронный (1)атмосферное (2)атмосферном (1)атомная масса (2)афелий (2)база (1)балка (1)банк (1)без калькулятора (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (4)биссектрисы (2)благоприятный исход (1)блеск (4)блок (2)боковой поверхности (1)большая полуось (1)большем давлении (1)бревно (2)бригада (2)бросили вертикально (1)бросили под углом (3)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)бруски (1)брусок (3)брусок распилили (1)бусинка (1)быстрый способ извлечения (1)вариант (3)вариант ЕГЭ (12)вариант ЕГЭ по физике (18)вариант по физике (1)варианты ЕГЭ (6)вариент по физике (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (1)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)весов (1)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видеоразбор (2)видеоразбор варианта (1)видимая звездная величина (2)виртуальная работа (1)виртуальный банк (1)виртуальных перемещений (1)витка (1)витков (1)виток (1)вклад (1)влажность (3)влажность воздуха (1)влетает (2)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (8)вода течет (1)воды (1)возведение в квадрат (1)возвратное уравнение (1)возвратность (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная (1)вписанная окружность (3)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращение (1)времени (2)время (24)время в минутах (1)время выполнения (1)время движения (2)время минимально (1)время падения (1)всесибирская олимпиада (1)в стоячей воде (1)встретились (1)встретятся (1)вступительный (1)вступительный экзамен (1)вторая половина пути (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон Ньютона (4)выбор двигателя (1)выборка корней (4)выколотая точка (1)выплаты (2)выразить вектор (1)высота (5)высота Солнца (1)высота столба (1)высота столба жидкости (1)высота столбика (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (2)газ (3)газа (1)газов (1)газовая атмосфера (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (4)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (7)гигрометр (1)гидродинамика (1)гидростатика (3)гимназия при ВШЭ (1)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)гонщик (1)горизонтальная сила (1)горизонтальной спицы (1)горизонтальную силу (1)горка (1)гравитационная постоянная (1)градус (1)грани (2)график (2)графики функций (5)графически (1)графический способ (1)графическое решение (2)груз (2)грузик (2)группа (1)давление (28)давление жидкости (3)давление пара (1)дальность полета (1)двигатель с активным ротором (1)движение под углом (1)движение под углом к горизонту (4)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)двойное неравенство (1)двойной фокус (1)двугранный угол при вершине (1)девальвация (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (15)делимость чисел (1)делители (1)делитель (2)делится (3)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)диаметру (1)динамика (4)диод (1)диск (1)дискриминант (4)дифракционная решетка (2)дифференцированный платеж (1)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (4)длина вектора (1)длина волны (7)длина отрезка (2)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)долг (1)доля (1)дополнительный угол (1)досок (1)досрочный (2)досрочный вариант (1)дптр (1)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)желоб (2)жесткость (6)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 9 (1)задача 13 профиль (1)задача 14 профиль (3)задача 16 (1)задача 16 ЕГЭ (1)задача 16 профиль (3)задача 17 (1)задача 18 (1)задача 26 ОГЭ (2)задача с параметром (6)задачи (1)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задачи с фантазией (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Бернулли (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закона сохранения (1)закон движения (1)закон кулона (7)закон палочки (3)закон сложения классических скоростей (1)закон сохранения импульса (6)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)законы сохранения (1)закрытым концом (1)замена переменной (2)замкнутая система (2)зануление (1)запаянная (2)заряд (9)заряда (1)заряд конденсатора (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (2)знак неравенства (1)знаменатель (1)знаменатель прогрессии (4)значение выражения (1)идеальный блок (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (3)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермически (1)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (9)импульса (1)импульс силы (1)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)инвариантность (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (8)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)камешек (1)капилляр (1)карлик (2)касательная (4)касательного (1)касательные (1)касаются (1)катер (2)катет (3)катушка (4)качаний (2)квадлратичная зависимость (1)квадрант (1)квадрат (3)квадратичная функция (3)квадратное (1)квадратное уравнение (4)квадратную рамку (1)квазар (1)квант (1)квантов (1)кинематика (2)кинематическая связь (1)кинематические связи (4)кинетическая (12)кинетическая энергия (4)кинетической (1)кинетической энергии (1)кинетическую энегрию (1)классический метод (3)классический метод расчета (1)клин (2)ключ (1)кодификатор (1)колебаний (1)колене (1)количество вещества (1)количество теплоты (9)коллектор (1)кольцо (2)комбинаторика (1)комбинированное (1)коммутация (1)комплексное сопротивление (1)комплексное число (1)комплексные числа (1)компонент (1)конвекция (3)конденсатор (10)конденсаторы (1)конденсации (1)конечная скорость (1)конечная температура (1)конечная температура смеси (1)конечный предел (1)консоль (1)контрольная (1)контрольные (1)контур (5)конус (4)концентрация (7)концентрическим (1)координата (5)координаты (3)координаты вектора (2)координаты середины отрезка (1)координаты точки (1)корабля (1)корень (2)корень квадратный (1)корень кубический (1)корни (2)корни иррациональные (1)корни квадратного уравнения (3)корни уравнения (1)корпоративных (1)косинус (2)косинусы (1)котангенс (1)коэффициент (1)коэффициент жесткости (1)коэффициент наклона (3)коэффициент поверхностного натяжения (3)коэффициент подобия (5)коэффициент трансформации (1)коэффициент трения (5)коэффициенты (1)красное смещение (1)красной границы (1)красный (1)кратковременный режим (1)кратные звезды (1)кредит (11)кредитная ставка (4)кредиты (1)криволинейная трапеция (2)кристаллизация (1)критерии оценки (1)круговая частота (1)круговой контур (1)кружок (1)кубическая парабола (1)кулонова сила (1)кульминация (1)кусочная функция (1)левом колене (1)лед (2)лет (1)линейная скорость (2)линейное напряжение (1)линейное уравнение (2)линейный размер (1)линза (2)линзы (2)линии излома (1)линиями поля (1)линия отвеса (1)литров (1)лифт (1)лифта (1)лифте (1)логарифм (10)логарифмические неравенства (3)логарифмические уравнения (1)логарифмическое неравенство (3)логарифмы (1)лунка (1)лучевая (1)льда (1)магнитное поле (2)магнитном поле (2)магнитные цепи (1)максимальная высота (1)максимальная скорость (1)максимум (1)малых колебаний (1)масса (23)масса воздуха (1)массе (1)массивная звезда (1)массовое содержание (1)массой (1)массу (1)математика (4)математический маятник (1)математического маятника (1)маятник (4)мгновенный центр вращения (1)медиана (2)меридиан (1)мертвая вода (1)мертвая петля (1)метод виртуальных (1)метод внутреннего проецирования (1)метод замены переменной (4)метод интервалов (3)метод комплексных амплитуд (3)метод контурных токов (1)метод координат (1)метод линий (1)методом внутреннего проецирования (1)метод переброски (1)метод переменных состояния (1)метод подстановки (4)метод рационализации (4)метод решетки (1)метод следов (5)метод сложения (4)метод телескопирования (1)метод узловых напряжений (1)методы расчета цепей (2)методы расчета цепей постоянного тока (1)метод эквивалентного генератора (2)механика (1)механическая характеристика (1)механическое напряжение (1)миля (1)минимальная скорость (1)минимальное (1)минимальной высоты (1)минимальной скоростью (1)минимум (2)мишени (1)мнимая единица (1)мнимая часть (1)многоугольник (1)многочлены (1)мода (2)модули (1)модуль (13)модуль Юнга (1)модуль средней скорости (1)молекулярно-кинетическая теория (2)моль (2)молярная масса (5)момент (7)момент инерции (1)момент инерции двигателя (1)момент нагрузки (1)момент сил (1)монета (1)монотонная (1)монотонность функции (1)монохроматического (1)мощности силы тяжести (1)мощность (9)мощностью (1)мяч (1)наблюдатель (1)нагревание (1)нагреватель (1)нагревателя (1)нагрели (1)наибольшее (1)наивысшая точка (1)наименьшее (1)наименьшее общее кратное (1)наклон (1)наклонная плоскость (2)налог (1)на направление (2)на подумать (2)направление (1)направление обхода (3)направлении (1)направляющий вектор (1)напряжение (9)напряжение на зажимах (1)напряжение смещения нейтрали (2)напряженность (4)напряженность поля (6)насос (2)насоса (1)насыщенный пар (4)натуральное (7)натуральные (7)натуральных (1)натяжение нити (5)натяжения (1)находился в полете (2)начальная температура (1)начальной скоростью (1)недовозбуждение (1)незамкнутая система (2)нелинейное сопротивление (1)неопределенность типа бесконечность на бесконечность (1)неопределенность типа ноль на ноль (1)непериодическая дробь (1)неравенства (8)неравенство (22)неразрывности струи (1)нерастяжимой (1)нерастяжимой нити (1)нерастянутой резинки (1)несимметричная нагрузка (1)несинусоидальный ток (3)нестандартные задачи (1)нестрогое (1)неупругим (1)нецентральный (1)нечетная функция (2)нечетное (1)нечетность (1)неявнополюсный (1)нити (2)нити паутины (1)нить (2)нить нерастяжима (1)новости (1)нормаль (1)нормальное ускорение (11)нулевой ток (2)обкладками (1)обкладках (1)обкладки (1)область допустимых значений (9)область значений (1)область определения (8)область определения функции (4)оборот (1)обратные тригонометрические функции (1)обратные функции (1)общая хорда (1)общее сопротивление (1)общее сопротивление цепи (1)объем (36)объемный расход (1)объемом (1)объем пара (1)объем параллелепипеда (1)объем пирамиды (1)одинаковые части (1)одновременно (1)одновременно из одной точки (1)окружность (13)окружность описанная (1)олимпиада (2)олимпиады по физике (2)они встретятся (1)операторный метод (4)описанная (1)оптика (1)оптимальный выбор (1)оптимизация (1)оптическая разность хода (1)оптический центр (1)орбитам (1)орбитой (1)оригинал (1)осевое сечение (1)оси (1)основание (2)основание логарифма (2)основания трапеции (1)основное тригонометрическое тождество (1)основное уравнение МКТ (2)основной газовый закон (1)основной период (1)основной уровень (1)основные углы (1)остаток (1)ось (1)отбор корней (5)ответ (1)отданное (1)относительная (1)относительная влажность (3)относительная скорость (1)относительно (2)относительность движениия (1)относительность движения (2)относительность скоростей (1)отношение (5)отношение времен (1)отношение длин (1)отношение площадей (3)отношение скоростей (2)отрезок (1)отсечение невидимых граней (1)очки (1)падает (1)падает луч (1)падает под углом (1)падение (3)падение напряжения (2)падения (1)пар (3)парабола (5)параболы (1)параллакс (5)параллелепепед (2)параллелепипед (3)параллелограмм (4)параллелограмм Виньера (1)параллельно (2)параллельно двум векторам (1)параллельное соединение (3)параллельные прямые (1)параллельными граням (1)параметр (30)параметры (1)парообразование (1)парсек (1)парциальное (1)парциальное давление (1)паскаль (1)первая треть (1)первичная (1)переброски (1)перевозбуждение (1)перегородка (1)перегрузок (1)перелетит (1)переливания (1)переменное магнитное поле (1)переменное основание (2)перемещение (6)перемычка (5)перемычке (1)перемычку (1)переносная скорость (1)пересекает (1)пересечение (1)пересечения (1)переходная проводимость (1)переходное сопротивление (1)переходной процесс (1)переходные процессы (9)перигелий (2)периметр (3)период (15)периодическая дробь (1)период колебаний (2)период малых колебаний (1)период обращения (2)период функции (1)периоды (1)перпендикулярно (1)песок (1)пион (1)пипетка (1)пирамида (7)пирамида шестиугольная (1)пирамиды (2)пирсона (1)плавание (1)плавкие предохранители (1)плавление (1)план (1)планете (1)планеты (3)планиметрия (13)планиметрия профиль (1)пластинами (1)пластинка (1)платеж (8)плечо (2)плоского зеркала (1)плоскопараллельная (1)плоскость (4)плоскость сечения (1)плотности веществ (1)плотность (22)плотность пара (3)плотность сосуда (1)плотность энергии (1)площади (2)площади фигур на клетчатой бумаге (1)площадь (30)площадь круга (1)площадь пластин (1)площадь поверхности (1)площадь под кривой (2)площадь проекции (1)площадь проекции сечения (1)площадь сектора (1)площадь сечения (5)площадь треугольника (1)поверхностная плотность заряда (1)поворот (1)повторно-кратковременный режим (1)погрешность (1)погружено (1)подвесили (1)подготовка к контрольным (3)под каким углом (1)подмодульное (1)подмодульных выражений (1)подобен (1)подобие (7)подобия треугольников (1)подобны (1)подпереть (1)под углом (2)под углом к горизонту (3)показателем преломления (1)показательное (1)показатель преломления (4)поле (1)полезной работы (1)полезную мощность (1)полигон частот (1)по линиям сетки (1)полное ускорение (1)половина времени (1)половинный угол (1)положительный знаменатель (1)полония (1)полость (1)полуокружность (1)полупроводник (1)полученное (1)понижение горизонта (1)по окружности (1)по переменному основанию (1)поправка часов (1)по прямой (1)поршень (4)поршня (1)порядок решетки (2)последовательно (1)последовательное соединение (3)последовательность (3)по сторонам клеток (1)посторонние корни (4)постоянная Авогадро (1)постоянная Хаббла (1)постоянная времени (1)постоянная скорость (1)постоянная составляющая (2)постоянный ток (5)построение (2)построение графика функции (1)потенциал (5)потенциал шара (1)потенциальная (13)потенциальная энергия (3)потенциальной (1)потери в стали (2)потеря корней (4)поток (5)по физике (1)правило левой (1)правило моментов (3)правильную пирамиду (1)правильный многоугольник (1)правом колене (1)предел функции (1)преломляющий угол (1)преобразование графиков функций (1)преобразования (3)преподаватели (2)пресс (2)призма (6)призмы (3)признаки подобия (4)признаки равенства треугольников (3)пробн (1)пробник (171)пробник по физике (8)пробниук (1)пробный (1)пробный ЕГЭ (2)пробный ЕГЭ по физике (3)пробный вариант (25)пробный вариант ЕГЭ (17)пробный вариант ЕГЭ по физике (111)пробный вариант по физике (1)провода (1)проводник (1)проводник с током (1)проводящего шара (1)проволока (1)проволоки (1)прогрессия (5)проекции скоростей (1)проекции ускорения (2)проекция (7)проекция перемещения (1)проекция скорости (6)проекция ускорения (2)производительность (2)производная (3)промежутка времени (1)промежуток (1)промежуток знакопостоянства (1)пропорциональны (1)проскальзывает (1)проскальзывания (1)противоположное событие (1)противостояние (1)протона (1)прототипы (1)профиль (2)профильный ЕГЭ (1)процент (5)процентная ставка (6)процентное отношение (1)процентное содержание (2)проценты (3)пружин (1)пружина (6)пружинный маятник (1)пружины (1)прямая (6)прямое восхождение (2)прямой (1)прямой АВ (1)прямоугольник (1)пузырек (1)пульсар (1)пуля (1)пути (1)путь (27)пять корней (1)работа (15)работа газа (5)работа тока (1)работу выхода (2)рабочее тело (1)рабочие (1)равнобедренный (1)равновеликий (1)равновесие (4)равновесия (1)равновесное (1)равнодействующая (1)равномерно (1)равноускоренно (2)равноускоренное (3)равные (1)равные фигуры (1)радиальную ось (1)радикал (1)радиус (11)радиус колеса (1)радиус кривизны (2)радиус описанной сферы (1)радиус темного кольца в отраженном свете (1)разбор (1)разбор Статграда по физике (1)разложение на множители (2)размах (1)разности температур (1)разность (2)разность потенциалов (2)разность прогрессии (3)разность хода (1)разрежьте (2)разрезание (5)разрешающая сила (1)разрыв функции (1)рамка (8)рамка с током (1)раскрытие модуля (1)расписание (1)расположение корней квадратного трехчлена (1)распределение частот (1)рассеивающая (1)расстояние (21)расстояние между зарядами (1)расстояние на карте (1)расстояние от точки (1)расстояния (2)раствор (2)растяжение (2)расходуется (1)расцепители (1)расчеты по формулам (1)рационализация (4)рациональные неравенства (1)реактивные элементы (1)реактивный двигатель (1)реакция опоры (4)реакция якоря (1)ребра (1)ребус (2)резервуар (1)резистор (1)рейки (1)рельса (1)рентгеновскую трубку (1)репетитор (1)решебник (1)решение тригонометрических уравнений (1)решение уравнений (2)решение уравнений больших степеней (1)решить в натуральных (1)решить в целых (1)розетка (1)ромб (1)ряд Фурье (1)сарай с покатой крышей (1)сближаются (1)сближения (1)сбрасывают с высоты (1)сверхгигант (2)сверхновая (1)светимость (3)свободно (1)свободного падения (1)свободно падает (2)свойства (2)свойства отрезков (1)свойства степени (1)свойства функции (1)свойства функций (2)свойства чисел (1)свойство биссектрисы (2)свойству биссектрисы (1)сдвинуть (1)сегмент (1)сектор (1)секущая (2)серия решений (1)сертификация (6)сессия (1)сечение (14)сечение наклонной плоскостью (1)сидерический (1)сила (7)сила Архимеда (5)сила Лоренца (4)сила ампера (9)сила взаимодействия (4)сила давления (1)сила на дно (1)сила натяжения (7)сила натяжения нити (4)сила поверхностного натяжения (3)сила реакции опоры (1)сила трения (3)сила тяготения (1)сила тяжести (5)сила упругости (2)силой (2)силу (1)силу натяжения (1)силы трения (2)символический метод (3)симметричная нагрузка (1)симметрия (3)синодический (1)синус (4)синусоида (1)синусоидальный закон (1)синусоидальный ток (5)синусы (1)синхронный компенсатор (1)система (3)система неравенств (7)система отсчета (3)система счисления (1)система уравнений (3)системы уравнений (3)скалярное произведение (3)склонение (1)скольжение (2)скользит (1)скользит равномерно (1)скоросмть (1)скоростей (1)скорости (3)скорости течения (1)скорость (43)скорость реки (1)скорость сближения (3)скорость света (1)скорость теплохода (1)скорость удаления (1)скорость частицы (1)скоростью (1)с лестницы (1)сложение векторов (1)сложная функция (1)смежные углы (1)смекалка (2)смеси (1)смешанное число (1)смещение (2)снаряд (1)собирающая (2)событие (1)соединение звездой (1)соединение треугольником (1)сокращение (1)сокращение дробей (1)соленоид (1)солнечная постоянная (3)солнечная система (1)сообразительность (1)сообщающиеся сосуды (2)соприкосновения (1)сопротивление (13)сопротивления (1)сопряженное (3)составить квадрат (1)составляет с направлением (1)составляющая скорости (2)составляющие (1)составляющие скорости (3)сосуд (1)сосудах (1)сосуде (1)сохранение энергии (1)спектра (2)спектральный класс (2)спецификация (1)спирт (1)сплава (1)сплавы (1)справочные данные (3)справочные материалы (12)спрос (1)сравнение чисел (2)среднее (1)среднее значение (1)среднеквадратичная скорость (1)среднюю линию (1)средняя квадратичная скорость (1)средняя скорость (6)срок (1)срок кредитования (1)стадии (1)стакан (2)статград (17)статика (2)стенка (1)степенная функция (1)степенные уравнения (1)степень (2)стереометрия (4)стержень (3)стержня (1)столб жидкости (3)столбик (3)столбик жидкости (2)столбик ртути (1)столбчатая диаграмма (1)стрелки поравняются (1)строгое (1)струю (1)студенты (2)ступеньку (1)сумма косинусов (1)сумма прогрессии (1)суммарный импульс (1)сумма ряда (1)сумма синусов (1)сумма углов (2)суммирование (2)сумму (1)суперпозиция (1)сутки (1)сфера (5)сферы (2)таблица (1)таблица частот (1)тангенс (3)тангенс разности (1)тангенс суммы (1)тангенциальная (1)тангенциальное ускорение (1)твердое тело (1)тела вращения (1)тележка (2)телескоп (1)телескопирование (1)тело (1)температура (21)температурный коэффициент сопротивления (1)температуры (2)тени (1)тень (1)теорема Пифагора (3)теорема Штейнера (1)теорема виета (5)теорема косинусов (4)теорема синусов (2)теореме косинусов (1)теоремы (1)теоретическое разрешение (1)теория вероятности (1)теплового двигателя (1)тепловое действие (1)тепловое равновесие (2)тепловой баланс (1)тепловой двигатель (1)теплоемкость (1)теплообмен (1)теплопередача (4)теплопроводность (2)теплота (1)теплота сгорания (1)теплоты (5)техника быстрого счета (1)товар (1)ток (11)ток насыщения (1)топливо (1)точечный источник (1)точка касания (1)точка росы (1)точки перемены знака (1)траектории (1)траекторию (1)траектория (1)транзистор (1)трансформатор (1)трапеция (4)трение (1)тренировочная работа (1)тренировочная статград (3)тренировочные работы (1)тренировочный вариант (23)тренировочный вариант ЕГЭ (57)тренировочный вариант ЕГЭ по физике (60)трения (2)трения покоя (1)трения скольжения (1)треугольная пирамида (1)треугольник (4)треугольник Паскаля (1)треугольника (1)треугольники (2)треугольник перемещений (1)трехфазные цепи (2)тригонометрические выражения (2)тригонометрические уравнения (1)тригонометрия (10)троса (1)трубка (5)трубы (1)увеличение (1)угловая скорость (2)угловая частота (2)угловой скоростью (3)углом (1)углы (4)угол между боковыми ребрами (1)угол между векторами (1)угол между плоскостями (2)угол между прямой и плоскостью (1)угол между прямыми (1)угол наклона (1)уголь (12)удар (1)удельная (1)удельная теплоемкость (2)удельная теплота (1)удельная теплота парообразования (2)удельное сопротивление (1)удержать (1)удлинение (3)узел (2)узкую трубку (1)умножение (1)умножение вектора на число (1)умножение на пальцах (1)упростить (1)упрощение (3)упрощение выражений (1)упругий удар (1)уравнение (5)уравнение Менделеева-Клапейрона (8)уравнение окружности (2)уравнение плоскости (3)уравнение теплового баланса (1)уравнению (1)уравнения (2)уравнения высоких степеней (1)уравнения высших степеней (1)урана (1)усеченный конус (1)ускорение (29)ускорением (1)ускорение свободного падения (4)ускорений (1)ускоряющая разность потенциалов (1)условие плавания (2)условие равновесия (1)условия возврата (1)фазное напряжение (1)фигуры (2)физика (29)физика статград (1)фиолетовый (1)фирмы (1)фокальная плоскость (1)фокус (5)фокусное расстояние (1)фонтан (1)формула (1)формула Герона (1)формула Пика (1)формулы сокращенного умножения (2)фотон (4)фотонов (1)функции (1)функция (1)холодильник (1)холодильнику (1)хорда (3)целое (10)целые (8)целые числа (1)целых (1)цель (1)центральный угол (4)центр вращения (1)центр масс (1)центр масс системы (1)центробежная сила (1)центростремительное ускорение (1)центр тяжести (1)центр тяжести системы (1)цепи постоянного тока (13)цепь второго порядка (1)цепь первого порядка (4)цикл Карно (1)циклическая частота (3)цилиндр (2)часовой угол (1)части (4)частица (2)частных клиентов (1)частота (10)частота излучения (1)часть объема (1)человека (1)черная дыра (1)четная функция (3)четное (7)четность (3)чисел (1)числовая пряма%D (1)число витков (1)член (1)шайбы (1)шар (2)шарик (2)шарик на нитке (1)шарик прыгает (1)шарнир (2)шестерня (1)шесть различных
5. Статические и дифференциальный сопротивления.

Статическое
сопротивление пропорционально tgα
образованной секущей проведенной из
начала координат в рассматриваемую
точку характеристики. 

Дифференциальное
сопротивление пропорционально tgβ
образованного касательной в рассматриваемой
точки с осью I: 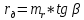
При этом k=v/a,
где v
и а – масштабы напряжений и тока.
Соответственно, 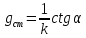 ;
; ;
;
Для так называемых
пассивных элементов, т. е, не содержащих
источников энергии, всегда rст > 0 и gст > 0, но  и
и положительны, только когда данная точка
характеристики лежит на ее восходящей
части, и отрицательные, если данная
точка лежит на падающей части
характеристики.
положительны, только когда данная точка
характеристики лежит на ее восходящей
части, и отрицательные, если данная
точка лежит на падающей части
характеристики.
6. Замена нелинейного элемента линейным сопротивлением и эдс.
Предположим, что область работы нелинейного элемента не выходит за пределы участка вольтамперной характеристики, который с достаточной степенью точности можно представить в виде прямой линии (рис. 2.29-Замена нелинейных элементов динамическими сопротивлениями и ЭДС)
Если продолжить линейные участки характеристик нелинейных элементов, то они пересекут ось абсцисс в точках E1 и E2.
Полученные две
ломаные линии могут быть, в соответствии
с ранее рассмотренным методом расчета
нелинейной электрической цепи,
представлены последовательным
соединением источника ЭДС E и динамического
сопротивления 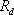 (рис.
2.30,б)
(рис.
2.30,б)

Рис. 2.30. Представление двух типов нелинейности (1 и 2, рис. 2.29) в виде двух линейных цепей (а и б).
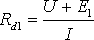 ;
;  ;
;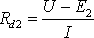 ;
; .
(2.36)
.
(2.36)
После замены нелинейного элемента линейным сопротивлением и ЭДС электрическая цепь рассчитывается как линейная. При этом обязательно должно соблюдаться условие: рабочая точка должна находиться на линейном участке характеристики нелинейного элемента.
VI. Магнитные цепи.
1. Магнитные цепи при постоянных магнитных потоках.
Магнитная цепь- совокупность феррамагнитных тел и воздушных сред,по которым замыкается магнитный поток.
Магнитные цепи являются частью электротехнического устройства и предназначены для создания в заданном объеме магнитного поля нужной интенсивности.
В неразветвленных магнитных цепях поток сечений каждого участка один и тот же.
2. Закон Ома и законы Кирхгофа для магнитных цепей.
 ,
,  ,
, –
индукция
–
индукция
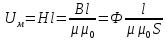 ,
,  -закон Ома для магнитной цепи,
-закон Ома для магнитной цепи, 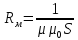 — магнитное сопротивление ,
— магнитное сопротивление , ,
,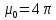 *
* гнитная
постоянная
гнитная
постоянная
Ф= ,
В
замкнутом контуре : Ф=
,
В
замкнутом контуре : Ф=
1 закон Кирхгофа вытекает из принципа непрерывности
линий магнитной индукции: В любом узле
сложной магнитной цепи алгебраическая
сумма магнитных потоков равна 0. 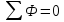
Магнитные потоки направленные к узлу берут со знаком “+”, а выходящие из узла со знаком “-”.
Сумма приходящих к узлу магнитных потоков равна сумме выходящих из узла магнитных потоков.
2 закон Кирхгофа
:В любом
разомкнутом контуре сложной магнитной
цепи алгебраическая сумма магнитных
U
равна сумме 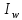 действующих в этом контуре.
действующих в этом контуре.
 ,
,
Достоинство этих законов в том, что они помогают провести аналогию между электрическими и магнитными цепями,которая позволяет применять для расчета магнитных цепей те же методы,что и для расчета н.э.ц.
Электрическая цепь | Магнитная цепь |
|
|
Вывод: возможно использование схем замещения для магнитных цепей постоянного магнитного потока в виде графического изображения элементов магнитной цепи подобных элементам электрической цепи.
Нелинейные цепи постоянного тока. Графические методы расчета (Лекция №30)
Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.
Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.
Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи. Характерной особенностью многополюсных элементов является то, что в общем случае их свойства определяются семейством характеристик, представляющих зависимости выходных характеристик от входных переменных и наоборот: входные характеристики строят для ряда фиксированных значений одного из выходных параметров, выходные – для ряда фиксированных значений одного из входных.
По другому признаку классификации нелинейные элементы можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают.
Понятия инерционных и безынерционных элементов относительны: элемент может рассматриваться как безынерционный в допустимом (ограниченном сверху) диапазоне частот, при выходе за пределы которого он переходит в разряд инерционных.
В зависимости от вида характеристик различают нелинейные элементы с симметричными и несимметричными характеристиками. Симметричной называется характеристика, не зависящая от направления определяющих ее величин, т.е. имеющая симметрию относительно начала системы координат: . Для несимметричной характеристики это условие не выполняется, т.е. . Наличие у нелинейного элемента симметричной характеристики позволяет в целом ряде случаев упростить анализ схемы, осуществляя его в пределах одного квадранта.
По типу характеристики можно также разделить все нелинейные элементы на элементы с однозначной и неоднозначной характеристиками. Однозначной называется характеристика , у которой каждому значению х соответствует единственное значение y и наоборот. В случае неоднозначной характеристики каким-то значениям х может соответствовать два или более значения y или наоборот. У нелинейных резисторов неоднозначность характеристики обычно связана с наличием падающего участка, для которого , а у нелинейных индуктивных и емкостных элементов – с гистерезисом.
Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.
Нелинейные электрические цепи постоянного тока
Нелинейные свойства таких цепей определяет наличие в них нелинейных резисторов.
В связи с отсутствием у нелинейных резисторов прямой пропорциональности между напряжением и током их нельзя охарактеризовать одним параметром (одним значением ). Соотношение между этими величинами в общем случае зависит не только от их мгновенных значений, но и от производных и интегралов по времени.
Параметры нелинейных резисторов
В зависимости от условий работы нелинейного резистора и характера задачи различают статическое, дифференциальное и динамическое сопротивления.
Если нелинейный элемент является безынерционным, то он характеризуется первыми двумя из перечисленных параметров.
Статическое сопротивление равно отношению напряжения на резистивном элементе к протекающему через него току. В частности для точки 1 ВАХ на рис. 1
.
Под дифференциальным сопротивлением понимается отношение бесконечно малого приращения напряжения к соответствующему приращению тока
.
Следует отметить, что у неуправляемого нелинейного резистора всегда, а может принимать и отрицательные значения (участок 2-3 ВАХ на рис. 1).
В случае инерционного нелинейного резистора вводится понятие динамического сопротивления
,
определяемого по динамической ВАХ. В зависимости от скорости изменения переменной, например тока, может меняться не только величина, но и знак .
Методы расчета нелинейных электрических цепей постоянного тока
Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприменим. В этой связи методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.
Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения. В общем случае при анализе нелинейной цепи описывающая ее система нелинейных уравнений может быть решена следующими методами:
- графическими;
- аналитическими;
- графо-аналитическими;
- итерационными.
Графические методы расчета
При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.
а) Цепи с последовательным соединением резистивных элементов.
При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ отдельных резисторов в системе декартовых координат строится результирующая зависимость . Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей определяются напряжения на отдельных резистивных элементах.
Применение указанной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.
Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом – методом пересечений. В этом случае один из нелинейных резисторов, например, с ВАХ на рис.2,а, считается внутренним сопротивлением источника с ЭДС Е, а другой – нагрузкой. Тогда на основании соотношения точка а (см. рис. 3) пересечения кривых и определяет режим работы цепи. Кривая строится путем вычитания абсцисс ВАХ из ЭДС Е для различных значений тока.
Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением резистивных элементов.
При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ отдельных резисторов в системе декартовых координат строится результирующая зависимость . Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ ), из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей определяются токи в ветвях с отдельными резистивными элементами.
Использование данной методики иллюстрируют графические построения на рис. 4,б, соответствующие цепи на рис. 4,а.
в) Цепи с последовательно-параллельным (смешанным) соединением резистивных элементов.
1. Расчет таких цепей производится в следующей последовательности:
Исходная схема сводится к цепи с последовательным соединением резисторов, для чего строится результирующая ВАХ параллельно соединенных элементов, как это показано в пункте б).
2. Проводится расчет полученной схемы с последовательным соединением резистивных элементов (см. пункт а), на основании которого затем определяются токи в исходных параллельных ветвях.
Метод двух узлов
Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем:
Строятся графики зависимостей токов во всех i-х ветвях в функции общей величины – напряжения между узлами m и n, для чего каждая из исходных кривых смещается вдоль оси напряжений параллельно самой себе, чтобы ее начало находилось в точке, соответствующей ЭДС в i-й ветви, а затем зеркально отражается относительно перпендикуляра, восстановленного в этой точке.
Определяется, в какой точке графически реализуется первый закон Кирхгофа . Соответствующие данной точке токи являются решением задачи.
Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.
В качестве примера рассмотрим цепь на рис. 5. Для нее выражаем напряжения на резистивных элементах в функции :
| ; | (1) |
| ; | (2) |
| . | (3) |
Далее задаемся током, протекающим через один из резисторов, например во второй ветви , и рассчитываем , а затем по с использованием (1) и (3) находим и и по зависимостям и — соответствующие им токи и и т.д. Результаты вычислений сводим в табл. 1, в последней колонке которой определяем сумму токов
.
Таблица 1. Таблица результатов расчета методом двух узлов
Алгебраическая сумма токов в соответствии с первым законом Кирхгофа должна равнять нулю, поэтому получающаяся в последней колонке табл. 1 величина указывает, каким значением следует задаваться на следующем шаге.
В осях строим кривую зависимости и по точке ее пересечения с осью напряжений определяем напряжение между точками m и n. Для найденного значения по (1)…(3) рассчитываем напряжения на резисторах, после чего по заданным зависимостям определяем токи в ветвях схемы.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
Контрольные вопросы и задачи
- Почему метод наложения неприменим к нелинейным цепям?
- Какие параметры характеризуют нелинейный резистор?
- Почему статическое сопротивление всегда больше нуля, а дифференциальное и динамическое могут иметь любой знак?
- Какие методы используют для анализа нелинейных резистивных цепей постоянного тока?
- Какая последовательность расчета графическим методом нелинейной цепи с последовательным соединением резисторов?
- Какая последовательность расчета графическим методом нелинейной цепи с параллельным соединением резисторов?
- Какой алгоритм анализа цепи со смешанным соединением нелинейных резисторов?
- В чем сущность метода двух узлов?
- В цепи на рис. 2,а ВАХ нелинейных резисторов и , где напряжение – в вольтах, а ток – в амперах; . Графическим методом определить напряжения на резисторах.
- В цепи на рис. 4,а ВАХ нелинейных резисторов и , где ток – в амперах, а напряжение – в вольтах; . Графическим методом определить токи и .
- В цепи на рис. 5 , где ток – в амперах, а напряжение – в вольтах; третий резистор линейный с . Определить токи в ветвях методом двух узлов, если .
Ответ: .
Ответ: .
Ответ: .




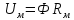
 имеет вебер-амперную
хар-ку
имеет вебер-амперную
хар-ку