1.3.1. Активные элементы
Идеальный источник напряжения(э.д.с.)
В любом источнике электрической энергии существует электрическое поле за счет разделения зарядов внешними силами неэлектрического происхождения.
Источники электрической энергии делятся на источники напряжения и источники тока.
Источник напряжения– напряжение на зажимах практически не зависит от тока, идущего от источника в приемник, и внутреннее сопротивлениеRiкоторых мало, так что напряжение на зажимах источника сравнительно мало и изменяется при изменении протекающего через него тока.
Источник напряжения характеризуется внешней характеристикой U=f(I).
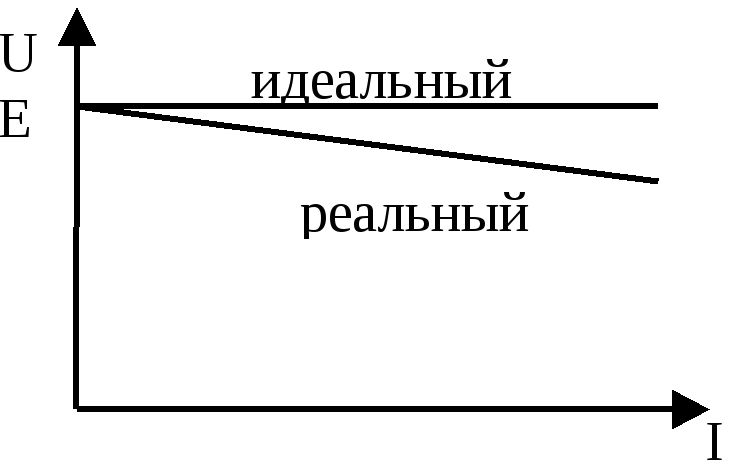
Идеальный источник напряжения(источник э.д.с.) –
Ri=0, E=const, U=E=const.

Изображение источника э.д.с. и его схема замещения
Идеальный источник тока
Источник тока–источник электрической энергии, в котором ток практически не зависит от напряжения, которое создается источником на зажимах приемника.
Источник тока имеет большое внутреннее сопротивление Ri(малую проводимостьGi), так что ток, поступающий в приемник, мало изменяется при изменении напряжения на зажимах источника.
Источник тока характеризуется внешней характеристикой I=f(U).
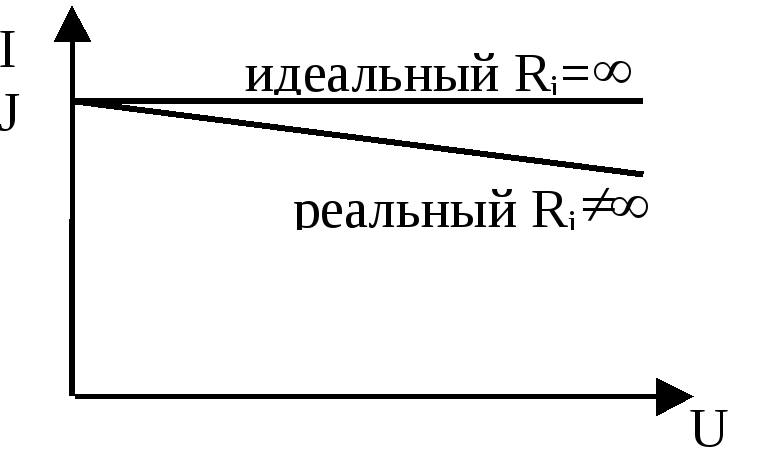
Вольт-амперная характеристика источника тока
Идеальный источник тока–Ri= (Gi=0),J=const,I=J=const.
(Gi=0),J=const,I=J=const.
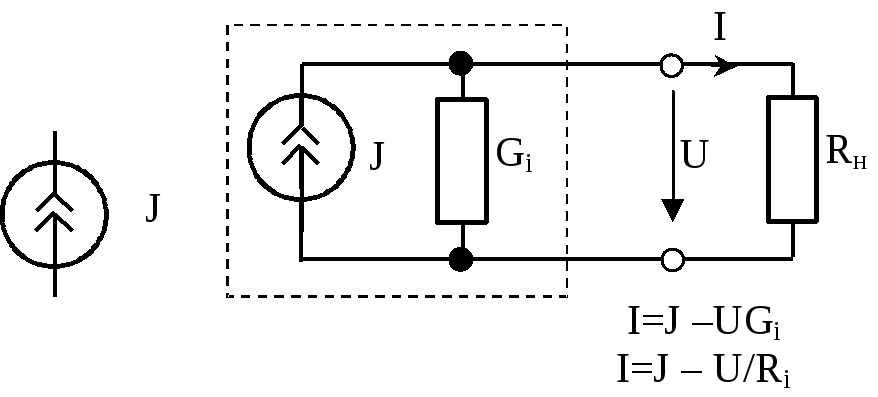
Изображение источника тока и его схема замещения
1.3.2. Пассивные элементы Идеальный резистивный элемент
Идеальный резистивный элемент–элемент схемы замещения электротехнического устройства, отображающий имеющий место в этом устройстве необратимый процесс преобразования электрической энергии источника в другие виды энергии (в большинстве случаев в тепловую энергию).
Природа ИРЭ в большинстве случаев (в цепях постоянного тока всегда) обусловлена столкновением заряженных частиц с атомами кристаллической решетки проводника и необратимым преобразованием электрической энергии источника через посредство кинетической энергии движущихся электронов во внутреннюю (тепловую) энергию проводника.
Параметр ИРЭ– сопротивление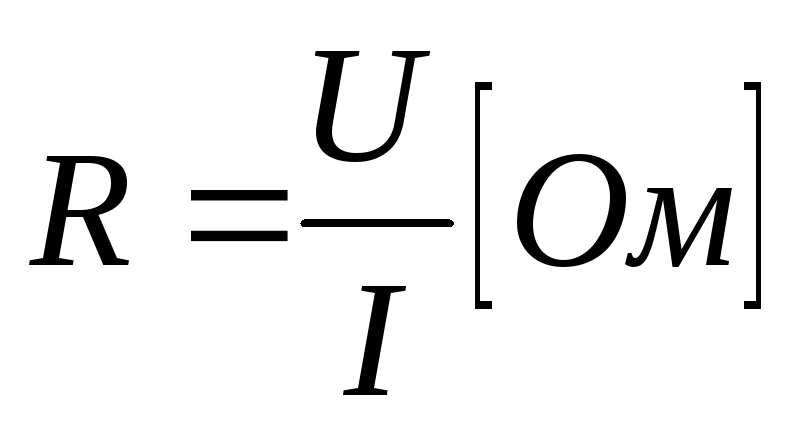 или проводимость
или проводимость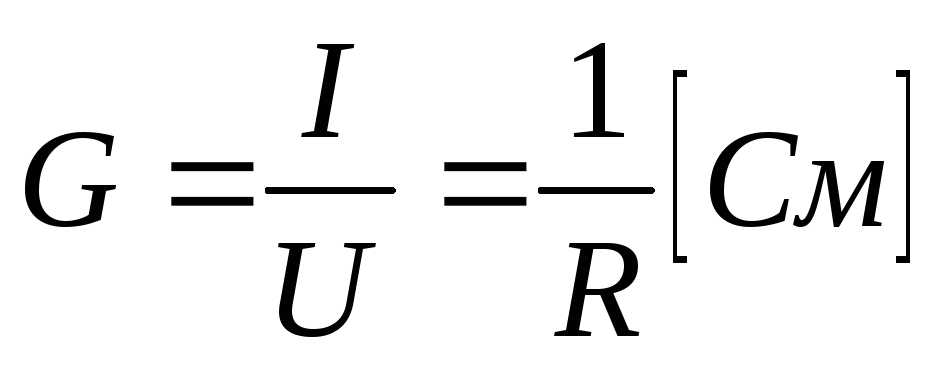 – определяется отношением:
– определяется отношением:
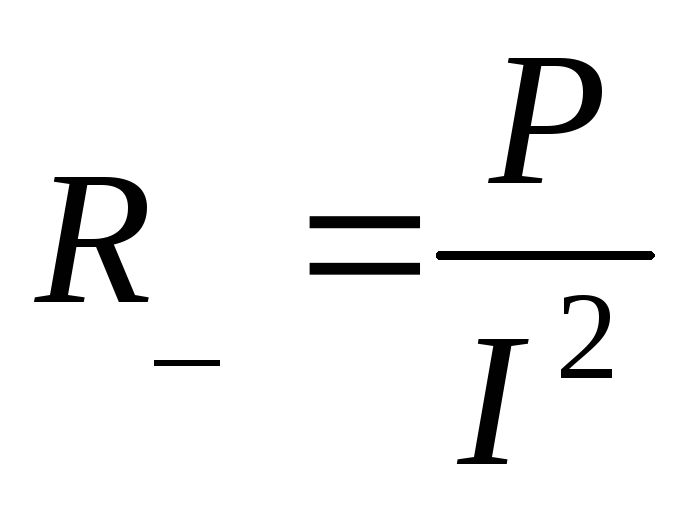 – для постоянного тока;
– для постоянного тока;
 – для переменного тока.
– для переменного тока.
Напряжение и ток на ИРЭ: 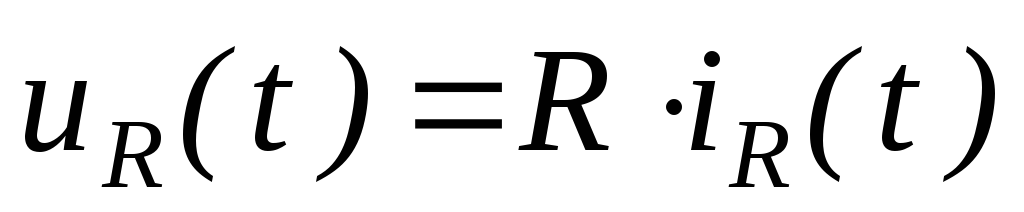
 .
.Электротехнический прибор, специально изготовленный реальный элемент электрической цепи, единственным свойством которого является необратимый процесс преобразования электрической энергии источника в тепловую – резистор.
Условное обозначение на схемах резистора такое же, как и ИРЭ:
Зависимость тока от напряжения на зажимах ИРЭ называют вольтамперной характеристикой элемента (ВАХ).

Если ВАХ линейна, то элемент линейный и электрическая цепь линейна.
Если ВАХ нелинейна, то элемент нелинейный и электрическая цепь нелинейна.
Идеальный индуктивный элемент (ииэ)

Идеальный индуктивный элемент–элемент схемы замещения электротехнического устройства, отображающий имеющий место в этом устройстве процесс преобразования электрической энергии источника в энергию магнитного поля.
Этот процесс обратим.
Параметр ИИЭ–индуктивность L, характеризует способность электротехнического устройства к созданию магнитного поля при протекании через него электрического тока(коэффициент самоиндукции).
Lопределяется соотношением для катушек индуктивности:
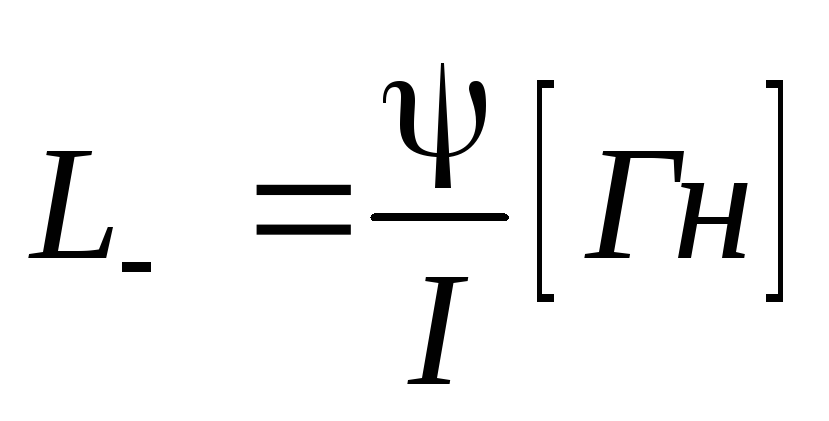 ;
;
 .
.
Напряжение и ток на ИИЭ: 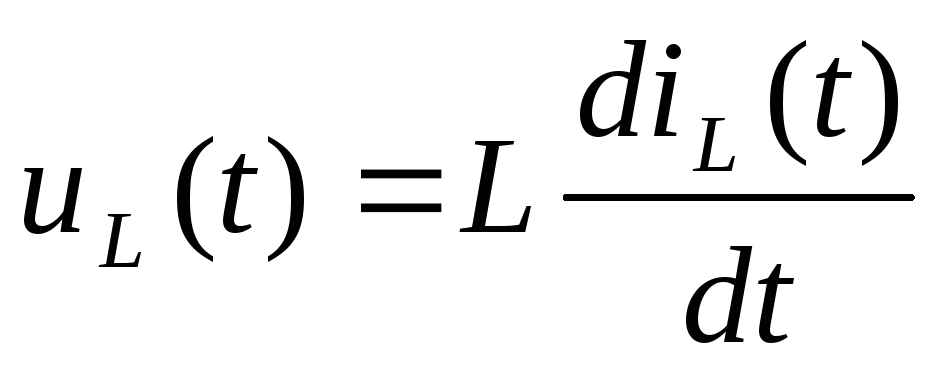 ;
;
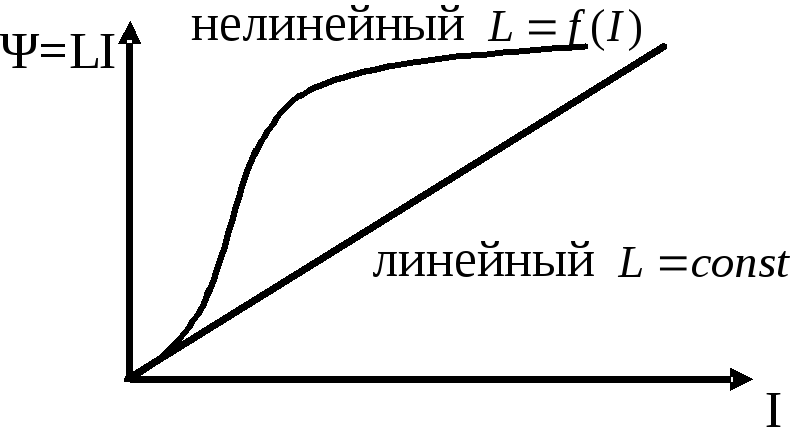
Зависимость потокосцепления элемента или участка цепи от тока в ней называют вебер-амперной характеристикой. Реальный элемент, близкий к ИИЭ – индуктивная катушка.
1.4. Резистивные элементы
Столкновения свободных электронов в проводниках с атомами кристаллической решетки тормозят их поступательное (дрейфовое) движение. Это противодействие направленному движению свободных электронов, т. е. постоянному току, составляет физическую сущность
Для участка цепи с сопротивлением r (рис. 1.5) ток и напряжение связаны простым соотношением — законом Ома:
Uab = rIabилиU=rI— (1.1)
Величина, обратная сопротивлению, называется проводимостью:
g = 1/r.
Основная единица сопротивления в системе СИ — ом (Ом), проводимости —
Проводящие свойства материала определяют его объемное удельное сопротивление rV, равное сопротивлению между противоположными сторонами куба с ребром 1 м, изготовленного из данного материала. Величина, обратная объемному удельному сопротивлению, называется объемной удельной проводимостью: V=1/V.
Единицей объемного сопротивления служит 1 Ом • м, объемной удельной проводимости — 1 См/м.
Сопротивление проводника постоянному току зависит от температуры. В общем случае наблюдается достаточно сложная зависимость. Но при изменениях температуры в относительно узких пределах (примерно 200 °С) ее можно выразить формулой
r2 = r1[1+ a(Q2-Q1)],
где r1 и r2 — сопротивления соответственно при температурах Q1 и Q2; a — температурный коэффициент сопротивления, равный относительному изменению сопротивления при изменении температуры на 1 °С.
В табл. 1.1 приведены значения объемного удельного сопротивления и температурного коэффициента сопротивления некоторых материалов, где 1 мкОм = 10–6 Ом.
Электротехническое устройство, обладающее сопротивлением и применяемое для ограничения тока, называется резистором. Регулируемый резистор называется реостатом. Условные обозначения различных типов резисторов даны в табл. 1.2.
ТАБЛИЦА В ОТДЕЛЬНОМ ФАЙЛЕ
Резистивными элементами называются идеализированные модели резисторов и любых других электротехнических устройств или их частей, оказывающих сопротивление постоянному току независимо от физической природы этого явления. Они применяются при составлении схем замещения цепей и расчетах их режимов. При идеализации пренебрегают токами через изолирующие покрытия резисторов, каркасы проволочных реостатов и т. п.
Линейный резистивный элемент является схемой замещения любой части электротехнического устройства, в которой ток пропорционален напряжению. Его параметром служит сопротивление
Если зависимость тока от напряжения нелинейна, то схема замещения содержит нелинейный резистивный элемент, который задается нелинейной вольт-амперной характеристикой I(U). На рис. 1.6 приведены вольт-амперные характеристики (ВАХ) линейного и нелинейного резистивных элементов (линии а, б), а также условные обозначения их на схемах замещения.
1.5. Источники электрической энергии постоянного тока
Рассмотрим источник энергии на примере гальванического элемента. Один из типов гальванических элементов (рис. 1.7, а) представляет собой две пластины — из меди Cu и из цинка Zn, помещенные в раствор серной кислоты H2SO4 — 2H+ + SO—4.
Вследствие химических процессов положительные ионы цинка Zn++ переходят в раствор серной кислоты, оставляя на цинковой пластине избыток отрицательных свободных зарядов. Одновременно в растворе серной кислоты тяжелые и малоподвижные положительные ионы цинка Zn++ оттесняют легкие и подвижные положительные ионы водорода Н+ к медной пластине, на поверхности которой происходит восстановление нейтральных атомов водорода. При этом медная пластина теряет свободные отрицательные заряды, т. е. заряжается положительно. Между разноименно заряженными пластинами возникает однородное электрическое поле с напряженностью E, которое препятствует направленному движению ионов в растворе. При некотором значении напряженности поля E = E0 накопление зарядов на пластинах прекращается. Напряжение или разность потенциалов между пластинами, при которой накопление зарядов прекращается, служит количественной мерой сторонней силы (в данном случае химической природы), стремящейся к накоплению заряда.
Количественную меру сторонней силы принято называть электродвижущей силой (ЭДС). Для гальванического элемента ЭДС Е = Eod = Uabx, где d — расстояние между пластинами; Uabx = jax — jbx — напряжение, равное разности потенциалов между выводами пластин в режиме холостого хода, т. е. при отсутствии тока в гальваническом элементе.
Если к выводам гальванического элемента подключить приемник, например резистор, то в замкнутой цепи возникнет ток. Направленное движение ионов в растворе кислоты сопровождается их взаимными столкновениями, что создает внутреннее сопротивление гальванического элемента постоянному току.
Таким образом, гальванический элемент, эскизное изображение которого дано на рис. 1.7, а, а изображение на принципиальных схемах — на рис. 1.7, б, можно представить схемой замещения (рис. 1.7, в), состоящей из последовательно включенных источника ЭДС Е и резистивного элемента с сопротивлением rвт, равным его внутреннему сопротивлению. Стрелка ЭДС указывает направление движения положительных зарядов внутри источника под действием сторонних сил. Стрелка напряжения Uab указывает направление движения положительных зарядов в приемнике, если его подключить к источнику энергии.
Схема замещения на рис. 1.7, в справедлива для любых других источников электрической энергии постоянного тока, которые отличаются от гальванического элемента физической природой ЭДС и внутреннего сопротивления.
9. Идеальные элементы (резистивный, индуктивный и емкостный) в цепи переменного тока. Определения, основные соотношения и особенности цепи. Понятие об активной, реактивной и полной мощностях.
Резистивный элемент в цепи переменного тока
Резистивный элемент R , обладающий активным сопротивлением R [Ом], включен в сеть переменного тока i = Im Sin ωt на напряжение uR и потребляет от питающей сети некоторую мощность Р [Вт], которая преобразуется в другие виды энергии, т.е. в некоторую работу.
Поскольку в резистивном элементе по определению отсутствуют переменные электромагнитные поля то по закону Ома для участка цепи сила тока i = uR / R .
Тогда: 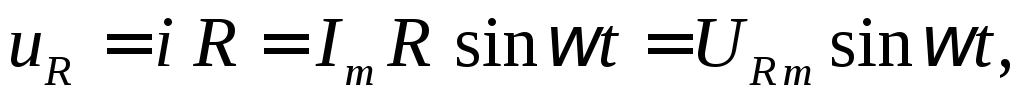 где
где 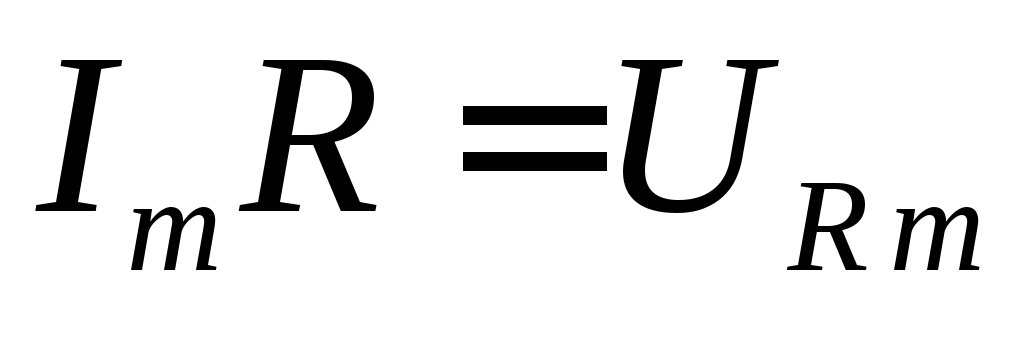 — амплитуда активного напряжения. Отсюда
получаем
выражение закона Ома для амплитудных
значений:
— амплитуда активного напряжения. Отсюда
получаем
выражение закона Ома для амплитудных
значений:
Разделив
обе части этого выражения на  получим выражение закона Ома для
действующих значений:
получим выражение закона Ома для
действующих значений:  или
в комплексной форме:
или
в комплексной форме:  .
.
Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей резистивный элемент (или другими словами – в резистивном элементе), сдвиг фаз φR = Ψи — Ψi= 0, т.е. напряжение и ток в резистивном (активном) элементе совпадают по фазе или синфазны.


В резистивной цепи коэффициент мощности Cos φ R = 1, поэтому среднее значение электрической мощности за период или активная мощность в резистивной цепи равна полной мощности: Р = P cp = I U Cos φ R = I U = S — резистивная цепь потребляет от сети только активную мощность P = S.
Реактивная (обменная) мощность в резистивной цепи: Q = I U Sin φ R = 0 — в резистивной цепи отсутствует обмен реактивной энергией Q = 0.
2. Индуктивный элемент в цепи переменного тока
Индуктивный элемент L [Гн] (идеальная катушка) включен в сеть переменного тока i = Im Sin ωt на напряжение uL и участвует в обмене реактивной энергией Q L [ВАр] с питающей сетью.
Идеальная катушка (по определению) не имеет активного сопротивления R = 0 и в ней не происходит преобразования электрической энергии Р = 0. При этом такая катушка обладает свойством периодически запасать электрическую энергию в виде энергии переменного магнитного поля Q L и обмениваться ею с источником. Поскольку магнитное поле является переменным, то при его изменении в обмотке катушки будет наводиться переменная ЭДС самоиндукции: eL = — dd t = — L di /d t [В], где L = ddi [Гн] — индуктивность катушки.
По второму правилу Кирхгофа для такой цепи можно записать:
uL + eL ) = iR = 0 uL + eLuL = — eL = L di /d t .
После
подстановки получаем выражение для
мгновенного значения индуктивного
напряжения uL :  ,
,
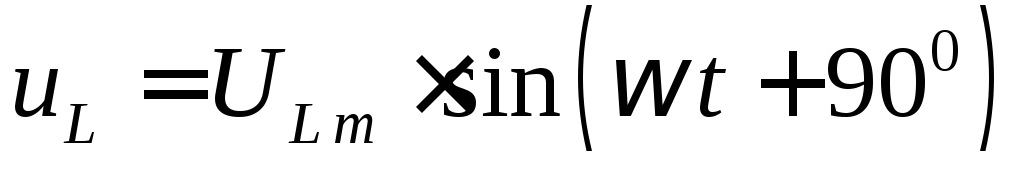 ,где
,где  — амплитуда индуктивного напряжения.
— амплитуда индуктивного напряжения.
Отсюда
получаем
выражение закона Ома для амплитудных
значений: 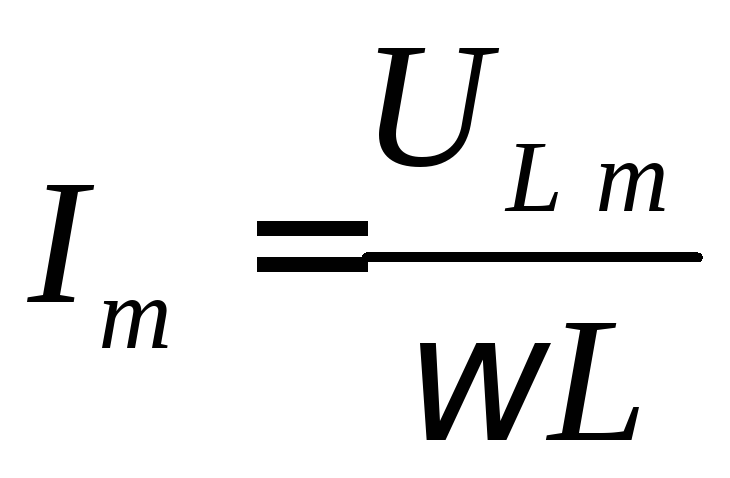
Разделив
обе части этого выражения на  получим выражение закона Ома для
действующих значений:
получим выражение закона Ома для
действующих значений:  ,здесь ωL — имеет размерность сопротивления [Ом]
и называется индуктивным
сопротивлением X L = ωL .
,здесь ωL — имеет размерность сопротивления [Ом]
и называется индуктивным
сопротивлением X L = ωL .
В таком случае закон Ома для индуктивной цепи можно записать:
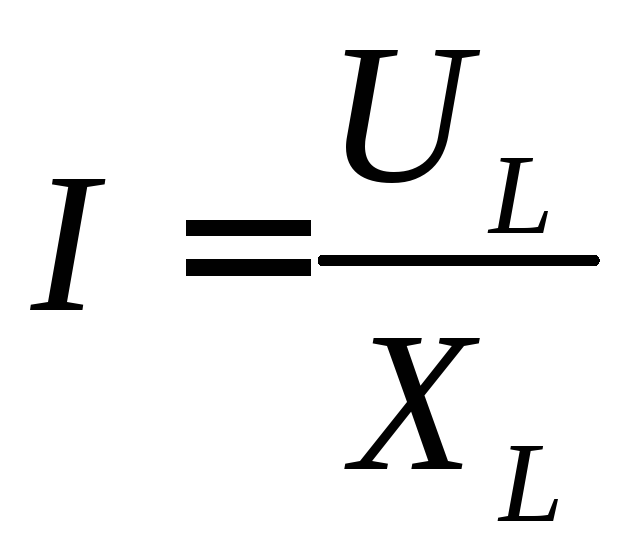
Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей индуктивный элемент (или другими словами – в индуктивном элементе), сдвиг фаз φL = Ψи — Ψi= + 90 O, т.е. напряжение в индуктивном элементе опережает по фазе ток на четверть периода ( + /2 или + 90 O), а ЭДС находится в противофазе с индуктивным напряжением.

В индуктивной цепи коэффициент мощности Cos φ L = 0 , поэтому среднее значение электрической мощности за период или активная мощность равна нулю: Р = I U Cos φ L =0- индуктивная цепь не потребляет от сети активную мощность, следовательно, в ней не происходит преобразования электрической энергии в работу.
Реактивная (обменная) мощность в индуктивной цепи (индуктивная мощность) равна полной мощности: Q L = I U Sin φ L = I U = S — индуктивная цепь потребляет от сети только реактивную мощность Q L = S.
Ёмкостный элемент в цепи переменного тока Ёмкостный элемент С [Ф] (идеальный конденсатор) включен в сеть переменного тока i = Im Sin ωt на напряжение uС и участвует в обмене реактивной энергией Q С [ВАр] с питающей
 сетью.
сетью.
Идеальный
конденсатор (по определению) не имеет
активного сопротивления R
= 0 и в нем не происходит преобразования
электрической энергии Р = 0. При этом
такой конденсатор обладает свойством периодически
запасать электрическую энергию в виде
энергии переменного электрического
поля Q C и
обмениваться ею с источником. Из
выражения для ёмкости 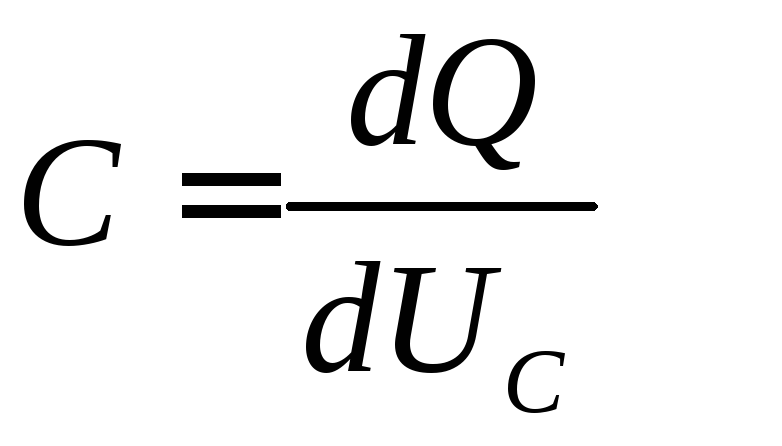 можно
записать:
можно
записать:
 ,откуда
после интегрирования получаем:
,откуда
после интегрирования получаем:
 ,
,
где  — амплитуда ёмкостного
напряжения.
— амплитуда ёмкостного
напряжения.
Отсюда получаем выражение закона Ома для амплитудных значений: .
Разделив
обе части этого выражения на  получим выражение закона Ома для
действующих значений:
получим выражение закона Ома для
действующих значений: 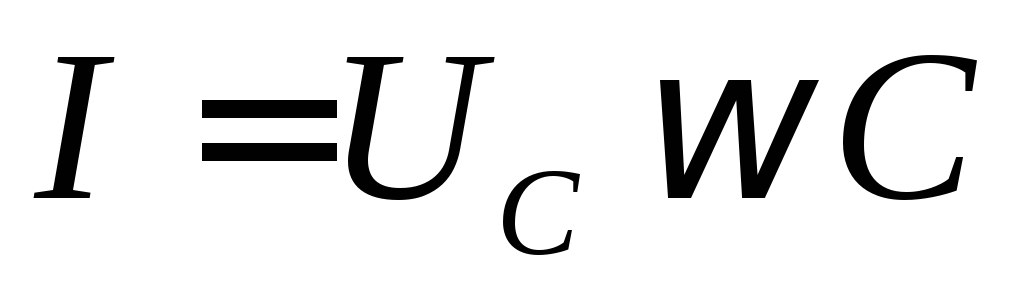 ,
здесь
,
здесь  — имеет размерность сопротивления [Ом]
и называется ёмкостным
сопротивлением.
— имеет размерность сопротивления [Ом]
и называется ёмкостным
сопротивлением.
В
таком случае закон Ома для ёмкостной
цепи можно записать: 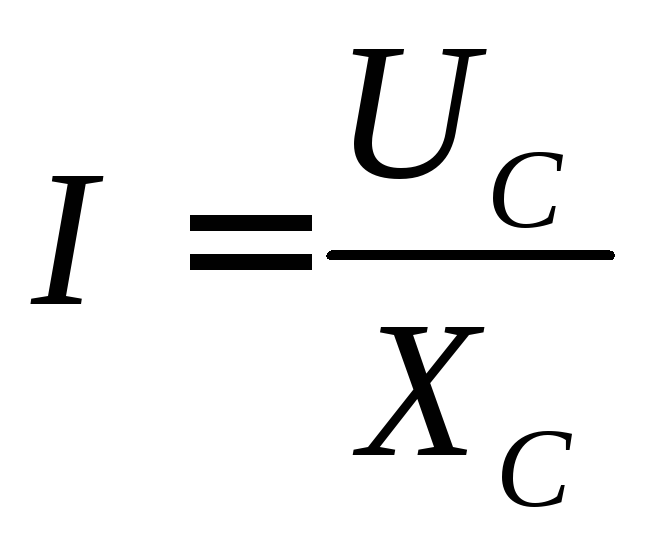
Из сравнения выражений для мгновенных значений напряжения и тока следует, что в цепи, содержащей ёмкостный элемент (или другими словами – в ёмкостном элементе), сдвиг фаз φС = Ψи — Ψi= — 90 O, т.е. напряжение в ёмкостном элементе отстает по фазе от тока на четверть периода ( -пи /2 или — 90 O).

В ёмкостной цепи коэффициент мощности Cos φ С = 0 , поэтому среднее значение электрической мощности за период или активная мощность равна нулю: Р = I U Cos φ С = 0 —ёмкостная цепь не потребляет от сети активную мощность, следовательно, в ней не происходит преобразования электрической энергии в работу.
Реактивная (обменная) мощность в ёмкостной цепи (ёмкостная мощность) равна полной мощности: Q С = I U Sin φ С = I U = S — ёмкостная цепь потребляет от сети только реактивную мощность Q С = S.
Понятие об активной, реактивной и полной мощностях.
В цепях переменного тока в связи с периодическим изменением электрического тока энергия электрических и магнитных полей периодически изменяется и между этими полями и источником электрической энергии происходит обратимый периодический процесс обмена электрической энергией. Скорость такого обратимого процесса обмена электрической энергией между источником и электрической цепью характеризуется понятием реактивная мощность Q [ ВАр], (Вольт-Ампер реактивный).
Одновременно в электрической цепи переменного тока происходит необратимый процесс преобразования электрической энергии в тепло, свет и другие виды энергии, т.е. в работу. Скорость такого необратимого процесса преобразования электрической энергии характеризуется понятием активная мощность Р [Вт], (Ватт).
Таким образом, в общем случае в цепи переменного тока одновременно происходят два процесса: процесс преобразования электрической энергии в другие виды (в работу) и процесс обратимого периодического обмена энергией между источником и цепью. Эти два одновременно протекающих процесса, накладываясь друг на друга, создают в цепи сложный единый энергетический процесс, для характеристики которого вводится понятие полная мощность S [ВА], (Вольт-Ампер).
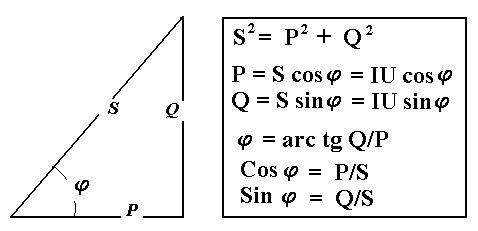 Полученные
энергетические соотношения могут быть
условно представлены на плоскости в
геометрической форме — в виде прямоугольного
треугольника — треугольника
мощностей, из
которого могут быть получены дополнительные
формулы, необходимые для выполнения
электротехнических расчетов.
Полученные
энергетические соотношения могут быть
условно представлены на плоскости в
геометрической форме — в виде прямоугольного
треугольника — треугольника
мощностей, из
которого могут быть получены дополнительные
формулы, необходимые для выполнения
электротехнических расчетов.
Идеализированный резистивный элемент (активное сопротивление) в цепи переменного тока
Рассмотрим
резистор, подключенный к источнику
синусоидального напряжения 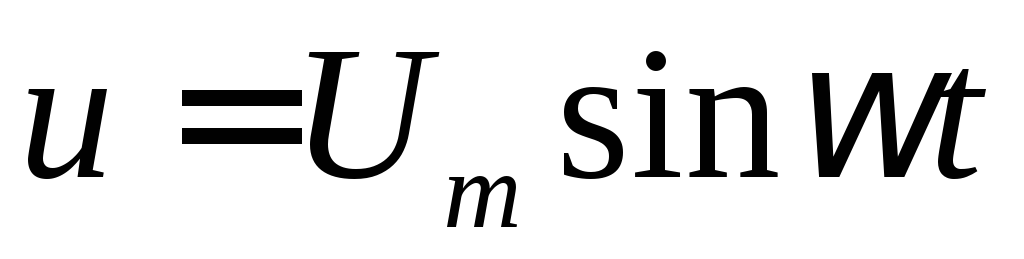 .
.

Укажем на схеме стрелками условно направление токов, напряжений и ЭДС. При этом считают направление тока и напряжения на пассивных участках цепей совпадают, направление ЭДС источника совпадает с направлением тока, направление напряжения источника противоположно направлению ЭДС источника. Согласно закону ОМА, мгновенный ток

Из
данного выражения видно, что ток и
напряжение на резисторе совпадают по
фазе (начальные токи одинаковы и равны
нулю), а их амплитуды связаны законом
Ома 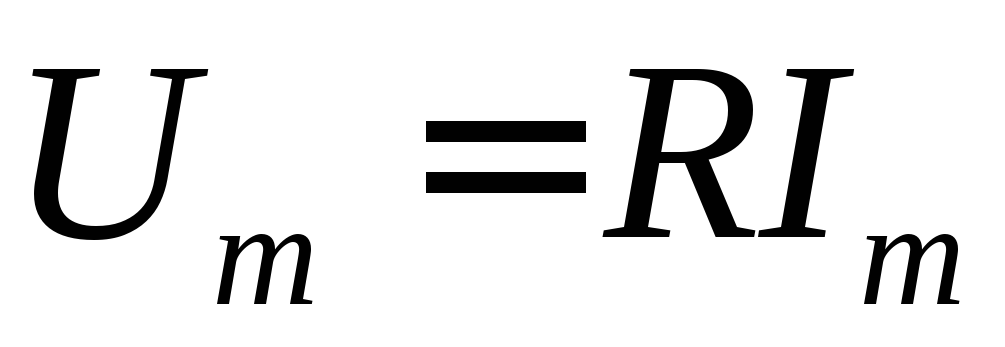 ,
что справедливо и для действующих
значений. Приведем соответственно
временную и векторную диаграммы
напряжения и тока.
,
что справедливо и для действующих
значений. Приведем соответственно
временную и векторную диаграммы
напряжения и тока.
Напряжение и ток в комплексной форме выражают в виде
 ,
,  .
.
Тогда комплексное сопротивление цепи
 ,
,
где  –
фазовый сдвиг.
–
фазовый сдвиг.
Учитывая,
что начальные фазы напряжения и тока
равны  ,
получают.
Активное сопротивление является
положительным действительным числом.
,
получают.
Активное сопротивление является
положительным действительным числом.
Закон Ома в комплексной форме для действующих значений имеет вид
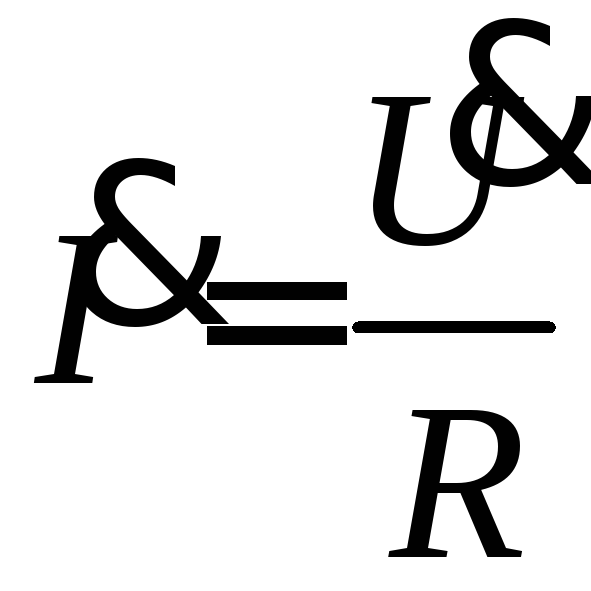 .
.
Мгновенное напряжение на сопротивлении R
 .
.
Мгновенная мощность p определяется как произведение мгновенных значений напряжения и тока:

Т.к. направления тока и напряжения совпадают (по знаку) в любой момент времени, мгновенная мощность остается все время положительной. На практике пользуются средним значением мощности за период, которое называют активной мощностью
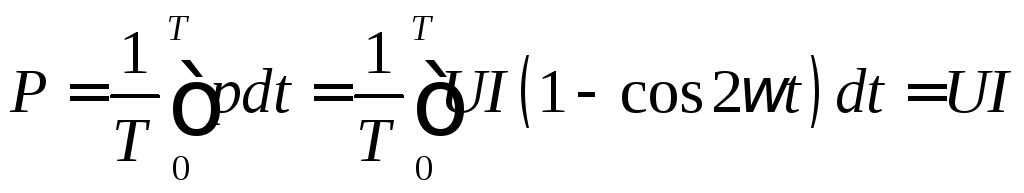
Активная мощность выражается в ваттах (Вт).
Тогда
можно записать  .
.
Идеализированный индуктивный элемент (катушка индуктивности) в цепи переменного тока
При
подключении катушки индуктивности (L – элемент) к источнику синусоидального
напряжения в катушке возникает
синусоидальный ток  ,
начальная фаза которого
,
начальная фаза которого принята равной нулю. Этот ток создает
магнитное поле катушки, а следовательно,
образуется потокосцепление, которое
индуцирует в катушке ЭДС самоиндукции
принята равной нулю. Этот ток создает
магнитное поле катушки, а следовательно,
образуется потокосцепление, которое
индуцирует в катушке ЭДС самоиндукции .
.

или  где
где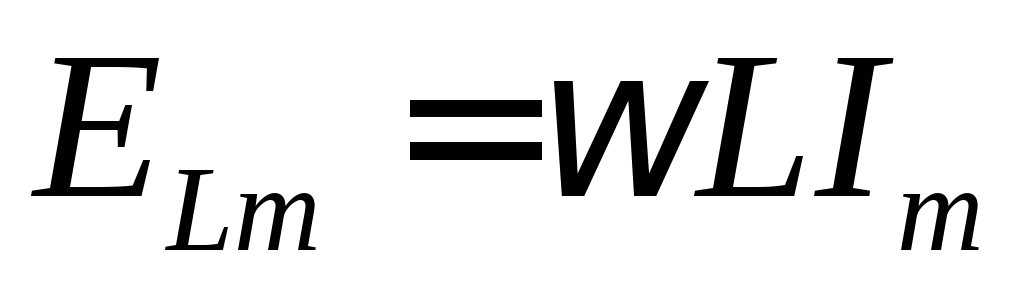 – амплитуда ЭДС самоиндукции.
– амплитуда ЭДС самоиндукции.
Из
полученного выражения видно, что
начальная фаза ЭДС  ,
это указывает на отставание по фазе ЭДС
от тока на четверть периода.
,
это указывает на отставание по фазе ЭДС
от тока на четверть периода.
Напряжение
на катушке индуктивности, которым
источник уравновешивает ЭДС самоиндукции 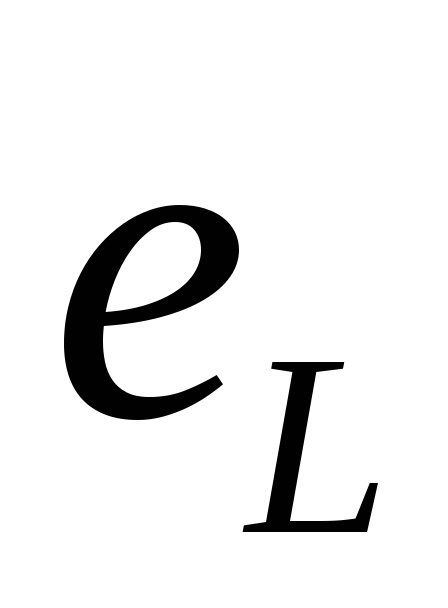 ,
, .
.
Поэтому для цепи содержащей только одну катушку индуктивности
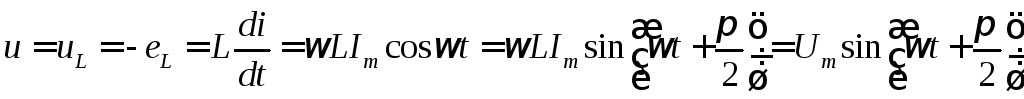 ,
,
т.е. питающее напряжение u полностью расходуется на уравновешение ЭДС.
Как
видно из данного выражения, начальная
фаза напряжения  и, следовательно, напряжение на катушке
индуктивности опережает по фазе ток на
четверть периода. Учитывая, что
и, следовательно, напряжение на катушке
индуктивности опережает по фазе ток на
четверть периода. Учитывая, что ,
сдвиг фаз в цепи, содержащей индуктивный
элемент, равен
,
сдвиг фаз в цепи, содержащей индуктивный
элемент, равен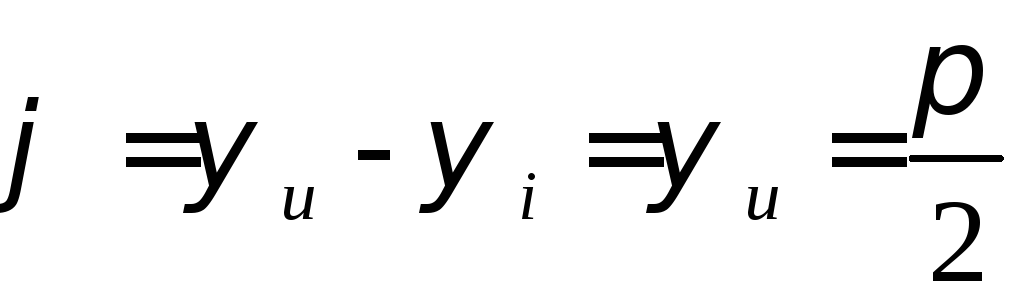 .
График мгновенных значенийu, i и e,
и векторная диаграмма цепи представлена
на рис.
.
График мгновенных значенийu, i и e,
и векторная диаграмма цепи представлена
на рис.
Вставить рис. Схема и диаграмма
Амплитуда
напряжения  ,
откуда
,
откуда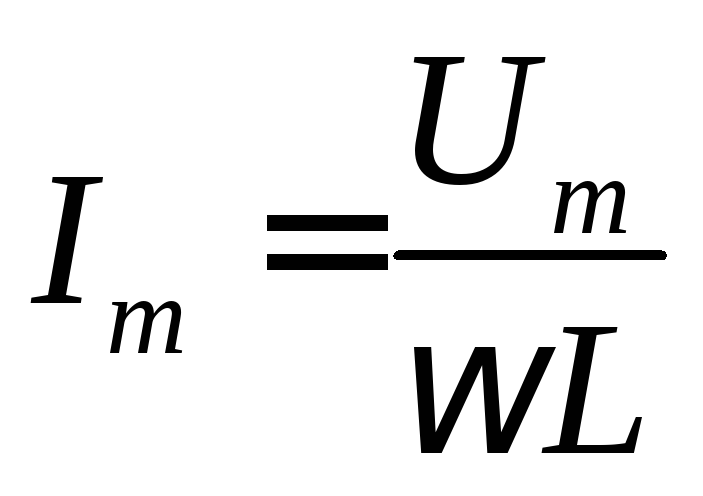 ,
это выражение представляет закон Ома
для цепи, в которую включена индуктивная
катушка.
,
это выражение представляет закон Ома
для цепи, в которую включена индуктивная
катушка.
Индуктивное
сопротивление ,
выражается в Омах (Ом) и обозначается
через
,
выражается в Омах (Ом) и обозначается
через ,
т.е..Чем
больше частотаf,
тем больше
,
т.е..Чем
больше частотаf,
тем больше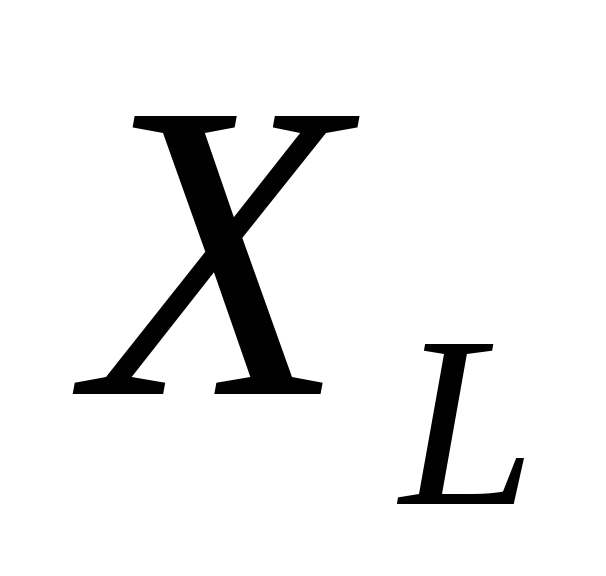 При постоянном токе
При постоянном токе .
.
Напряжение и ток в комплексной форме
 ,
,  ,
,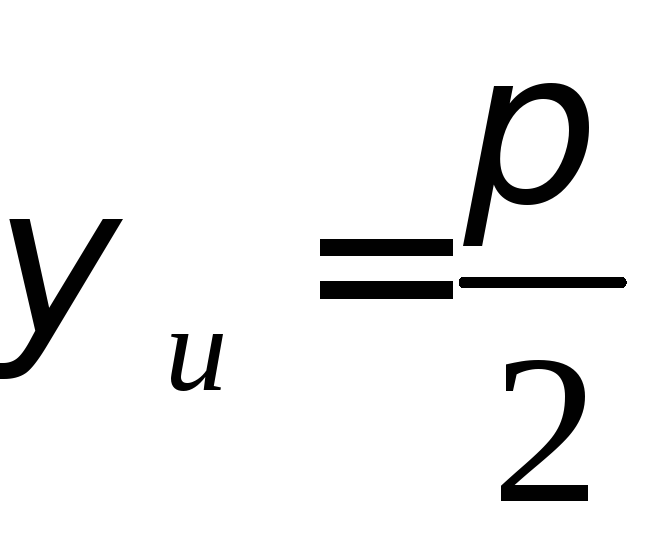 ,
, .
.
Комплексное сопротивление цепи
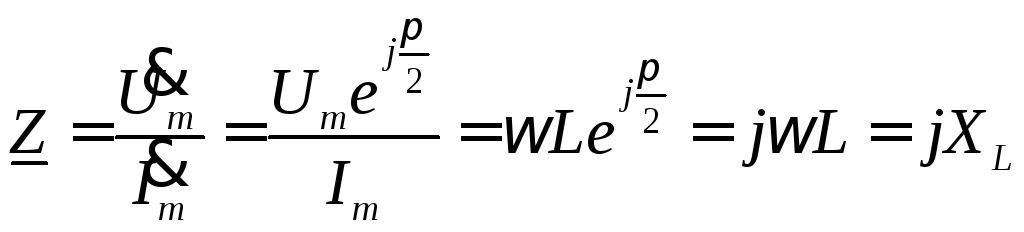 .
.
Индуктивное сопротивление является положительным мнимым числом. Закон Ома в комплексной форме для действующих значений тока и напряжения
 .
.
Мгновенная мощность в индуктивном элементе

где  – амплитудное значение мгновенной
мощности, которую называют реактивной
мощностью индуктивного элемента и
обозначают
– амплитудное значение мгновенной
мощности, которую называют реактивной
мощностью индуктивного элемента и
обозначают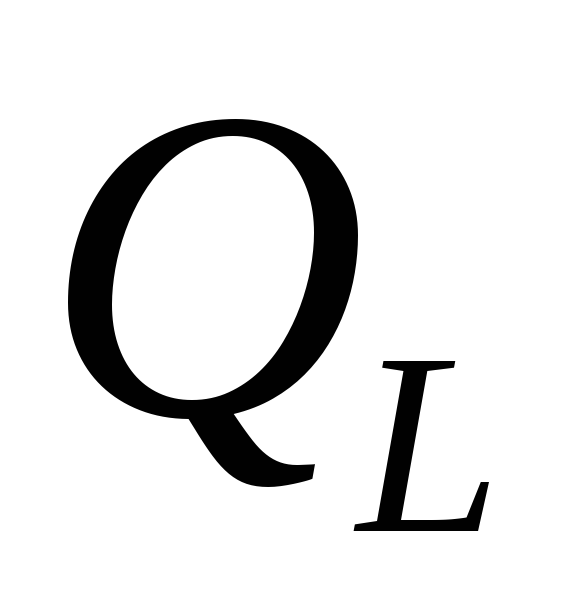 .
Учитывая, что
.
Учитывая, что ,
, .
Реактивная мощность имеет размерность
вольт–ампер реактивный (ВАР).
.
Реактивная мощность имеет размерность
вольт–ампер реактивный (ВАР).
Активная мощность, определяемая средним значением мгновенной мощности за период
 .
.
Следовательно, такая цепь не потребляет электрической энергии. Т.е. в цепи переменного тока, содержащей в качестве приемника идеальную катушку индуктивности, происходит непрерывный обмен энергией между источником и приемником. При этом энергия приемником не расходуется.
Лекция 6.
2.4. Пассивные элементы электрической цепи.
Резистор r , индуктивность L и емкость C являются пассивными элементами электрической цепи. Резистор r или активное сопротивление цепи – это элемент, в котором происходит рассеивание энергии в виде тепла или превращение электрической энергии в другой вид энергии: в световую, химическую или механическую.
Индуктивность L и емкость C называются реактивными элементами цепи, в них происходят накапливание энергии в виде магнитного или электрического поля. Рассеивание энергии в таких элементах отсутствует. Идеальные элементы r, L, C на схеме обозначаются так, как это показано на рис. 2.3а.
Реальные
катушки индуктивности и конденсаторы
рассеивают часть энергии. Этот факт
учитывается с помощью добавочных
сопротивлений 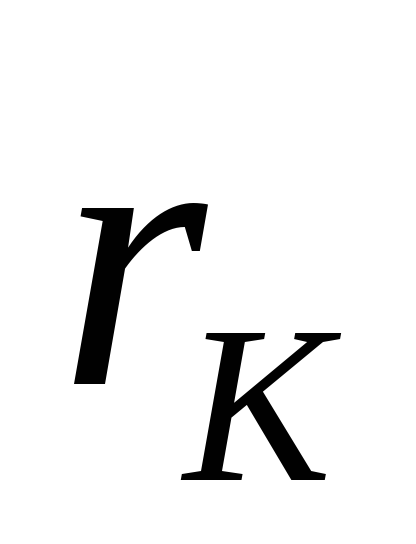 для катушки и
для катушки и для конденсаторов, рис. 2.3б. В проволочных
сопротивлениях и катушках индуктивности
учитывают также межвитковую емкость
для конденсаторов, рис. 2.3б. В проволочных
сопротивлениях и катушках индуктивности
учитывают также межвитковую емкость ,
рис 2.3б.; в реальном конденсаторе можно
учесть паразитную индуктивность
подводящих контактов
,
рис 2.3б.; в реальном конденсаторе можно
учесть паразитную индуктивность
подводящих контактов ,
рис. 2.3б.
,
рис. 2.3б.
 Рассматривая
пассивные элементы цепи r , L, C ответим на следующие вопросы:
Рассматривая
пассивные элементы цепи r , L, C ответим на следующие вопросы:
Каково соотношение между мгновенным значением тока и напряжения на каждом элементе? Каков вид векторов тока и напряжения?
Каковы мгновенная мощность p(t) и накопленная энергия магнитного или электрического полей?
Каково соотношение тока и напряжения на элементе в комплексной форме, как изображаются вектора тока и напряжения на комплексной плоскости.
Под мгновенным значением мощности p(t) понимают произведение мгновенного значения напряжения u(t) на элементе цепи на мгновенное значение протекающего по элементу тока i(t):
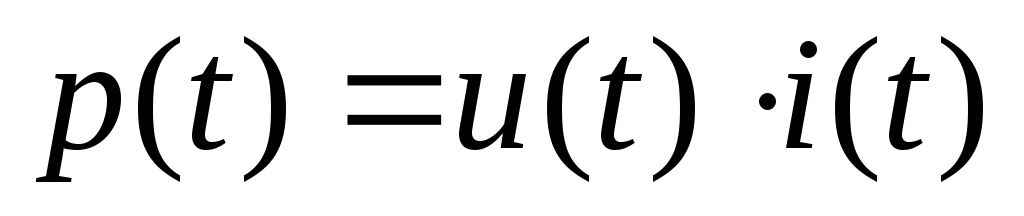 .
.
2.5. Резистивный элемент.
2.5.1. Пусть ток в резисторе:
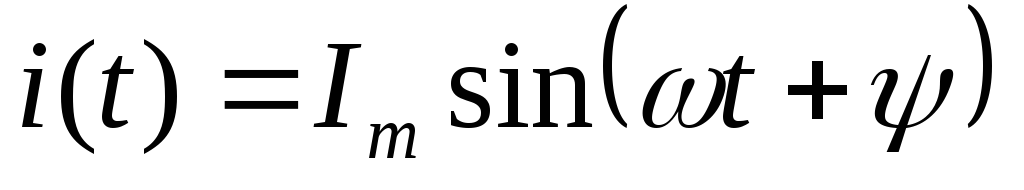 .
.
Мгновенное значение напряжения на резисторе:
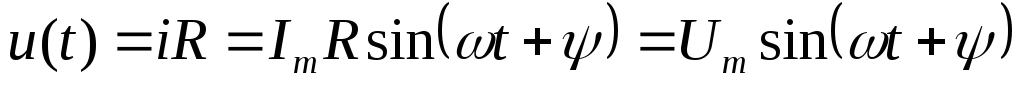
 Векторы
тока и напряжения на резисторе приведены
на рис. 2.4б. Закон Ома для резистора имеет
вид:
Векторы
тока и напряжения на резисторе приведены
на рис. 2.4б. Закон Ома для резистора имеет
вид:
 или
или 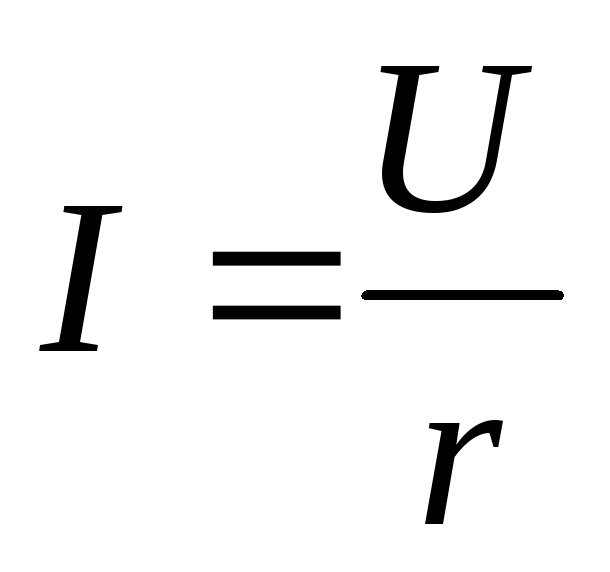 .
.
2.5.2. Мгновенная мощность p(t) равна:

Временные диаграммы i(t), u(t), p(t) приведены на рис.2.4в. Мощность р(t) имеет постоянную составляющую или среднее значение, называемое активной мощностью Р:

Активная мощность Р измеряется в ваттах (Вт).
2.5.3. В комплексной форме напряжение на резисторе записывается в виде
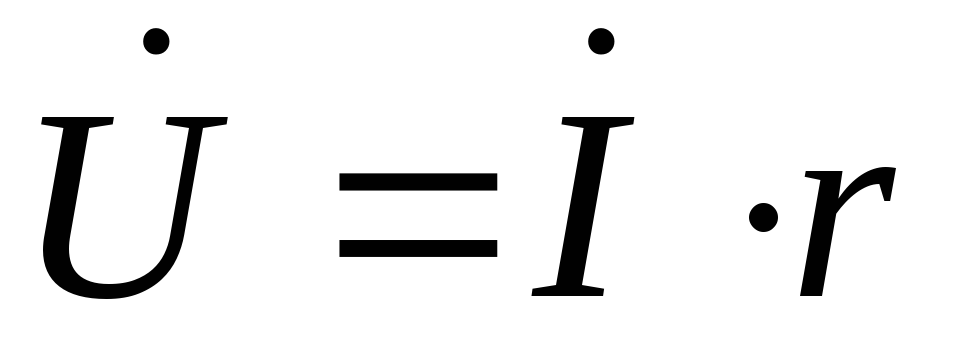
Векторы тока и напряжения на комплексной плоскости приведены на рис. 2.4г.
2.6. Индуктивный элемент в цепи синусоидального тока.
Индуктивный
элемент учитывает явления накапливания
энергии магнитного поля и характеризуется
зависимостью потокосцепления  от токаi:
от токаi:
 ,
измеряется в генри (Гн).
,
измеряется в генри (Гн).
2.6.1. Мгновенное значение напряжения на индуктивности:
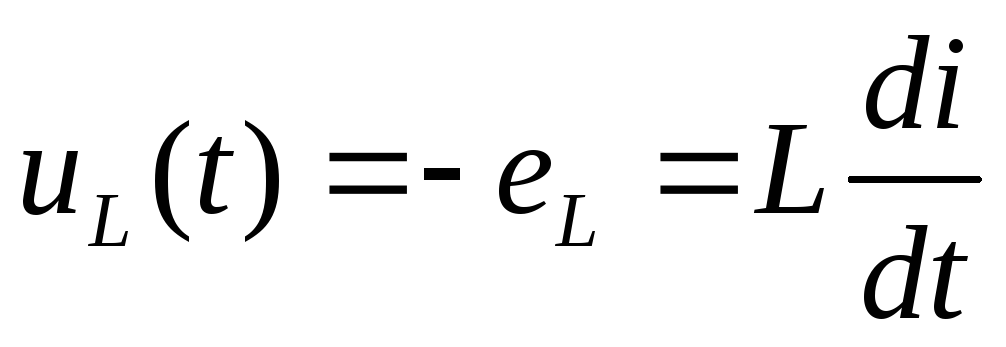
Здесь  — ЭДС, наводимая изменяющимся во времени
магнитным потоком.
— ЭДС, наводимая изменяющимся во времени
магнитным потоком.
Если
принять ток в катушке 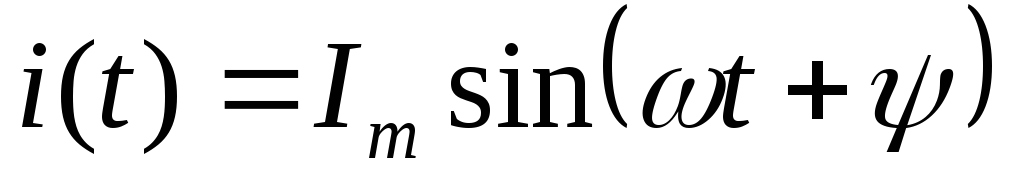 ,
то напряжение запишется в виде:
,
то напряжение запишется в виде:
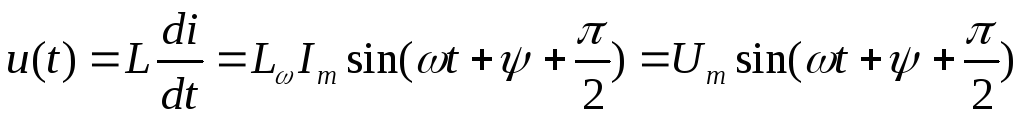 .
.
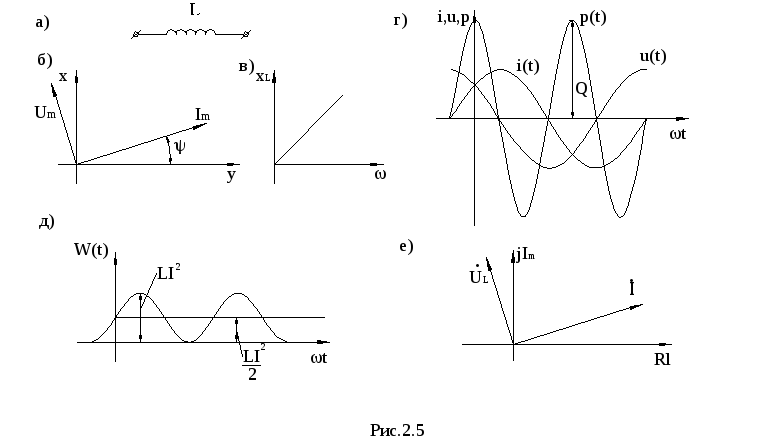
Векторы
тока и напряжения показаны на рис. 2.5б.
Напряжение опережает ток в катушке на
угол 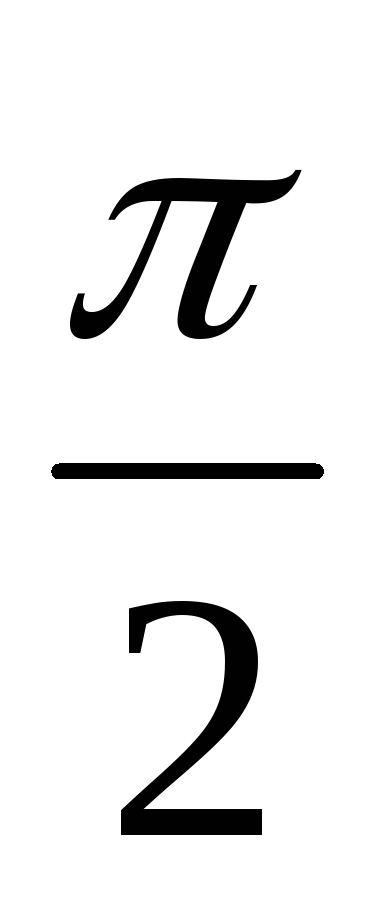 .
Закон Ома для индуктивности:
.
Закон Ома для индуктивности:
 или
или 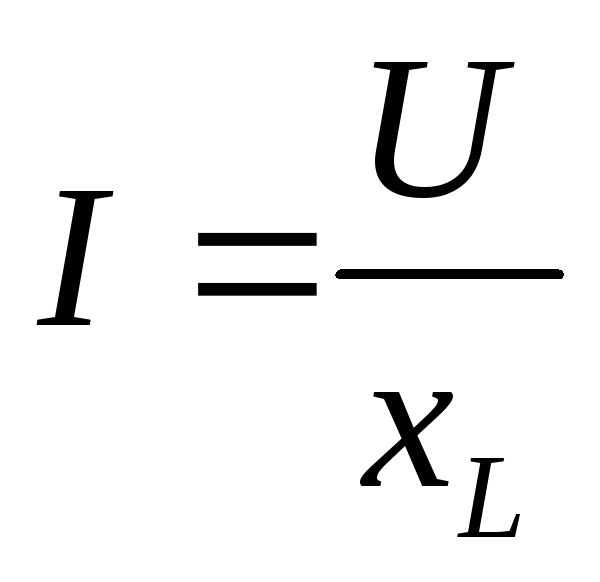 ,
,
где  — индуктивное сопротивление катушки,
измеряется в Омах (Ом). Сопротивление
— индуктивное сопротивление катушки,
измеряется в Омах (Ом). Сопротивление — частично зависимая величина, увеличивается
с ростом частоты, рис. 2.5в.
— частично зависимая величина, увеличивается
с ростом частоты, рис. 2.5в.
2.6.2. Мгновенная мощность:
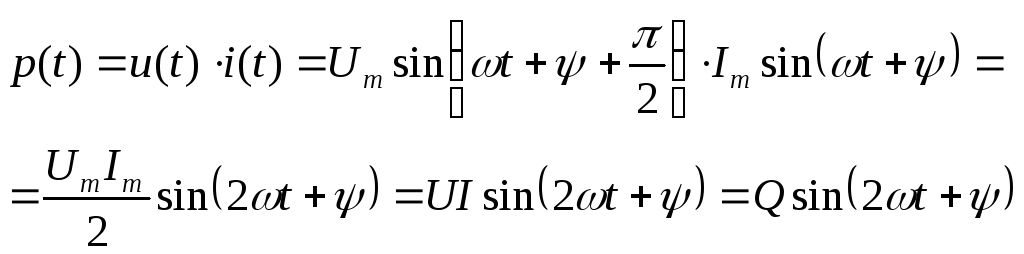
Мощность  называется реактивной и измеряется в
вольт-амперах реактивных (ВАр). Временные
диаграммыw(t),
i(t) и p(t) для катушки приведены на рис. 2.5г. Средняя
мощность равна нулю, т.е. рассеивание
мощности или потери отсутствуют. Энергия
магнитного поля катушки равна:
называется реактивной и измеряется в
вольт-амперах реактивных (ВАр). Временные
диаграммыw(t),
i(t) и p(t) для катушки приведены на рис. 2.5г. Средняя
мощность равна нулю, т.е. рассеивание
мощности или потери отсутствуют. Энергия
магнитного поля катушки равна:
 Временная
диаграмма W(t),
приведена на рис. 2.5д. Максимальная
энергия магнитного поля катушки:
Временная
диаграмма W(t),
приведена на рис. 2.5д. Максимальная
энергия магнитного поля катушки:
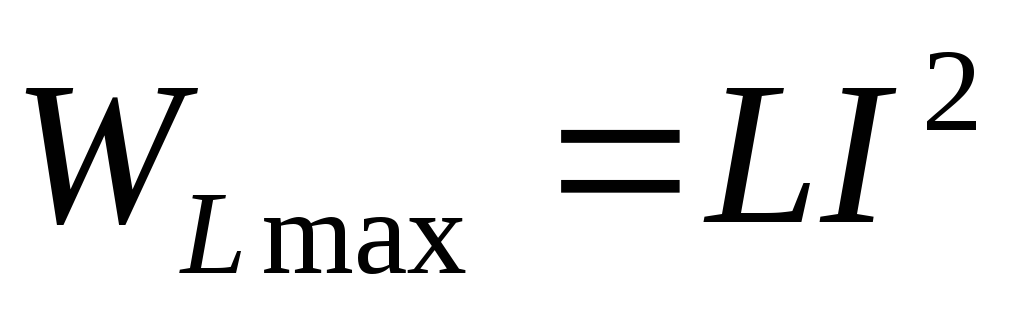 .
.
2.6.3. Напряжение на индуктивности в комплексной форме.
Так как напряжение на катушке:
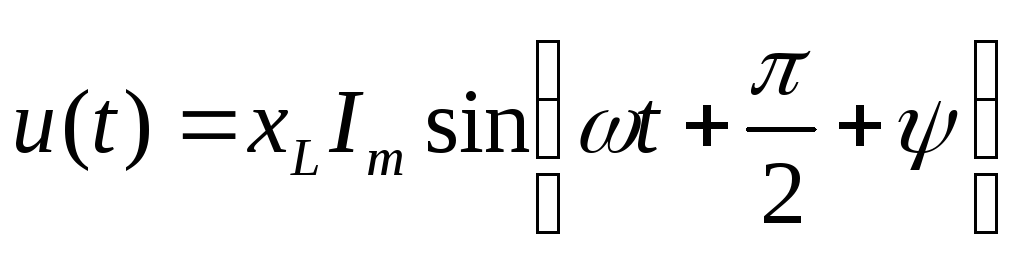 ,
,
то 
Здесь  — индуктивное сопротивление в комплексной
форме.
— индуктивное сопротивление в комплексной
форме.
Оператор 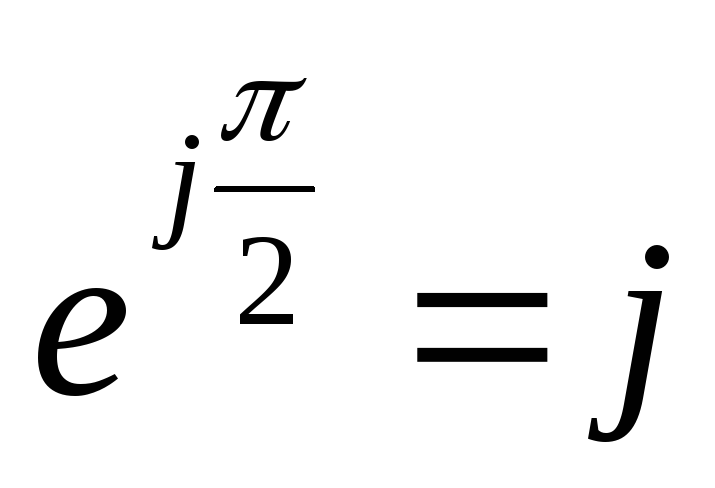 отражает дифференцирование напряжения
на индуктивности.
отражает дифференцирование напряжения
на индуктивности.
Закон Ома в комплексной форме:
 или
или 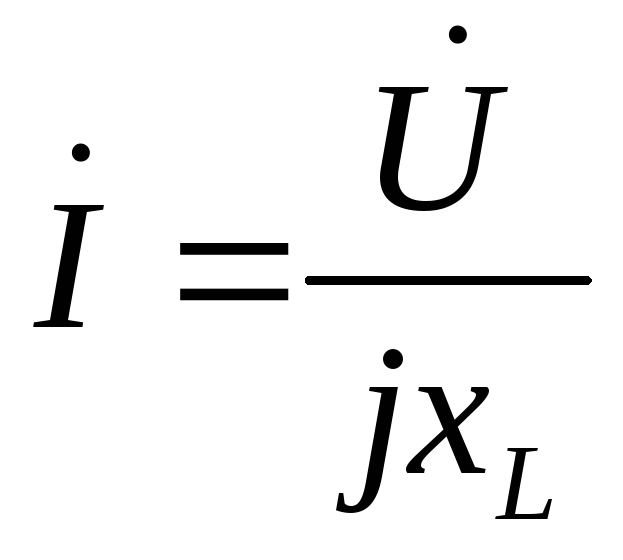
Вектора тока и напряжения на комплексной плоскости приведены на рис. 2.5е.
2.7. Емкостный элемент в цепи синусоидального тока.
Емкость
отражает явление накапливания
электрического поля и характеризуется
зависимостью заряда q от напряжения u : 

2.7.1. Мгновенное значение напряжения на конденсаторе:

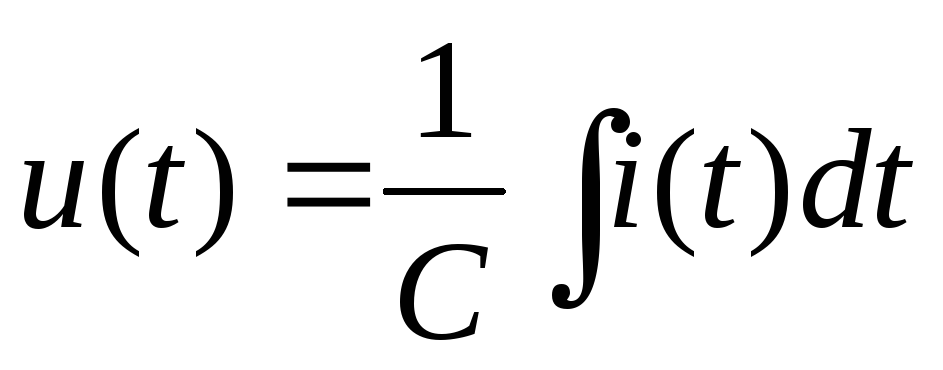
Пусть  , тогда напряжение на конденсаторе:
, тогда напряжение на конденсаторе:
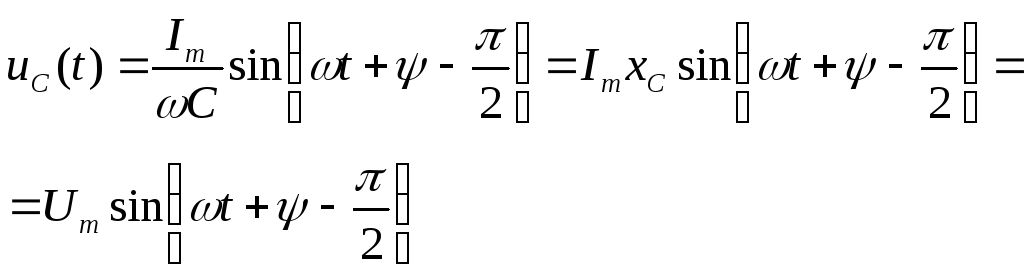
Это
напряжение отстает от тока на угол 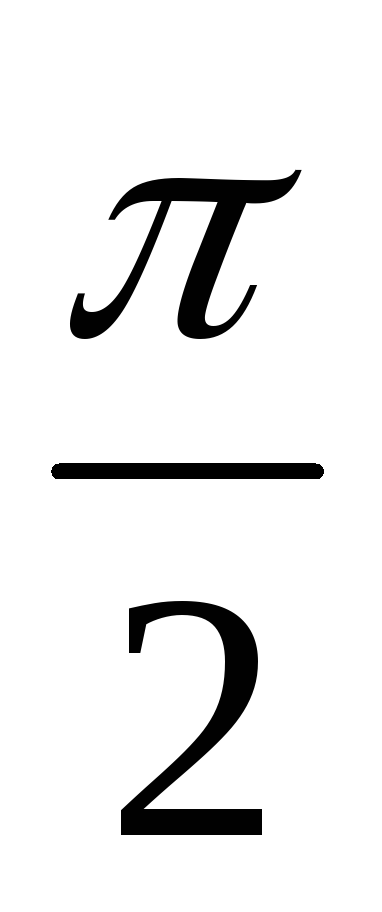 .
.
Векторы тока и напряжения приведены на рис.2.6б.
Закон Ома для емкости:
 или
или  ,
,
где  — емкостное сопротивление, измеряется
в омах (Ом).
— емкостное сопротивление, измеряется
в омах (Ом).
Емкостное
сопротивление уменьшается с ростом
частоты. Зависимость  от частоты приведена на рис. 2.6.в.
от частоты приведена на рис. 2.6.в.
2.7.2. Мгновенная мощность на конденсаторе:

Q
– реактивная мощность конденсатора.
Временные диаграммы 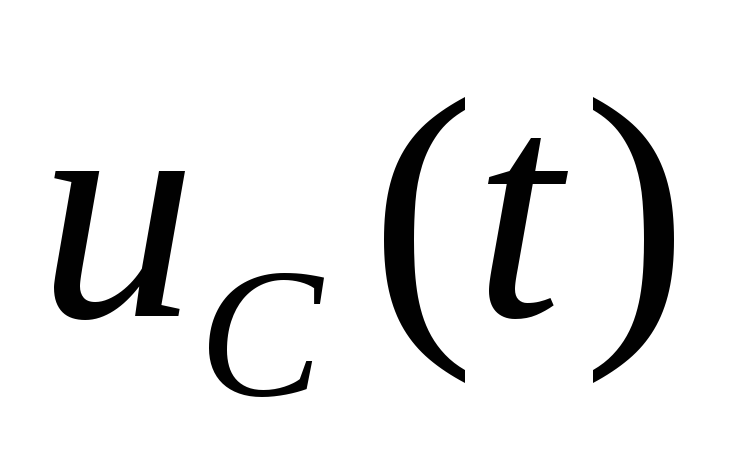 ,i (t), p (t) приведены
на рис. 2.6г.
,i (t), p (t) приведены
на рис. 2.6г.
Среднее значение мощности равно нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия электрического поля в конденсаторе равна:

График  приведен на рис. 2.6д.
приведен на рис. 2.6д.
Максимальная энергия электрического поля равна:

2.7.3. Напряжение на емкости в комплексной форме.
Так
как 
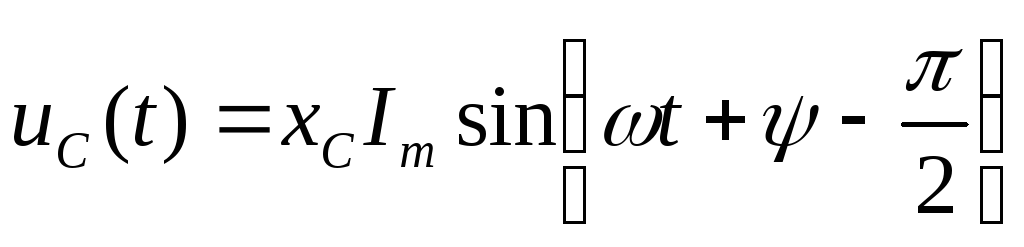 ,
,
То 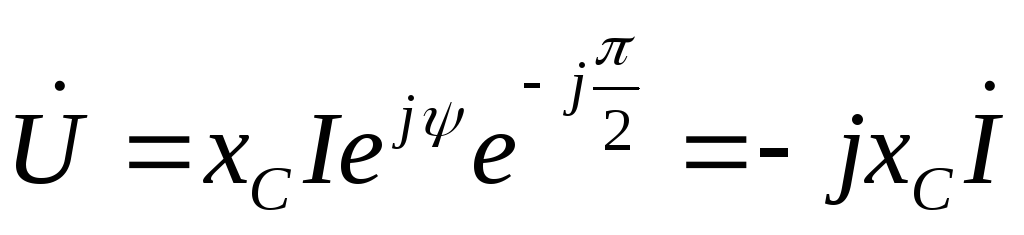 .
.
Здесь 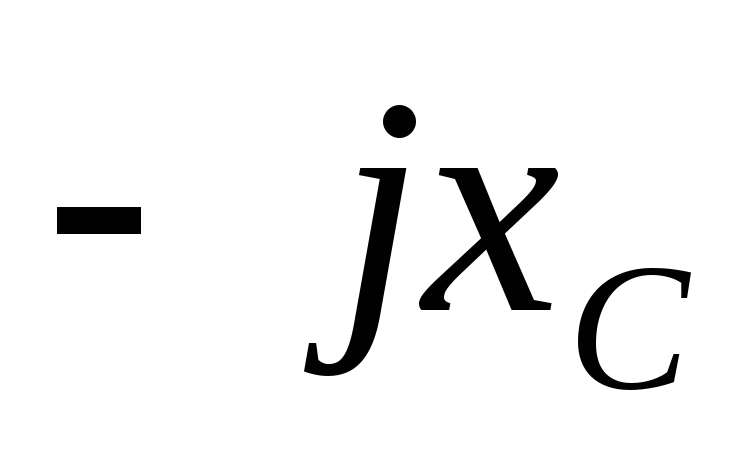 — емкостное сопротивление в комплексной
форме.
— емкостное сопротивление в комплексной
форме.
Оператор 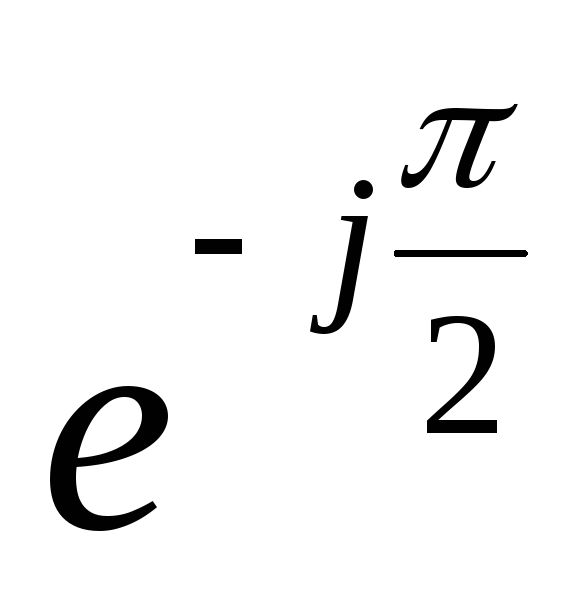 отражает интегрирование тока в формуле
напряжения на емкости.
отражает интегрирование тока в формуле
напряжения на емкости.
Закон
Ома в комплексной форме  или
или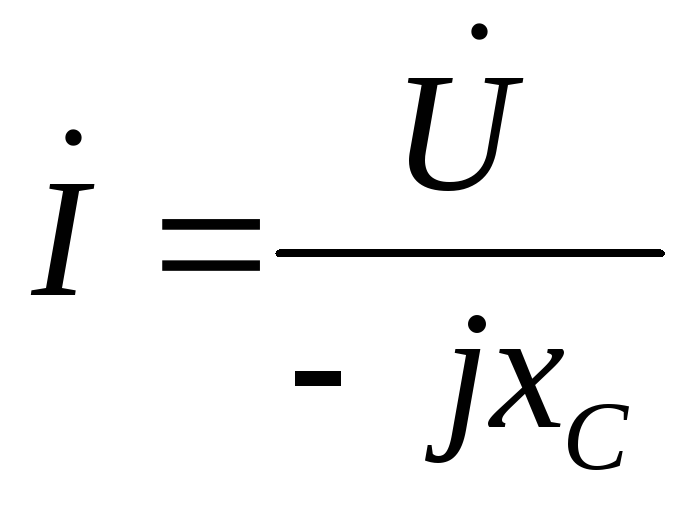 .
Векторы
.
Векторы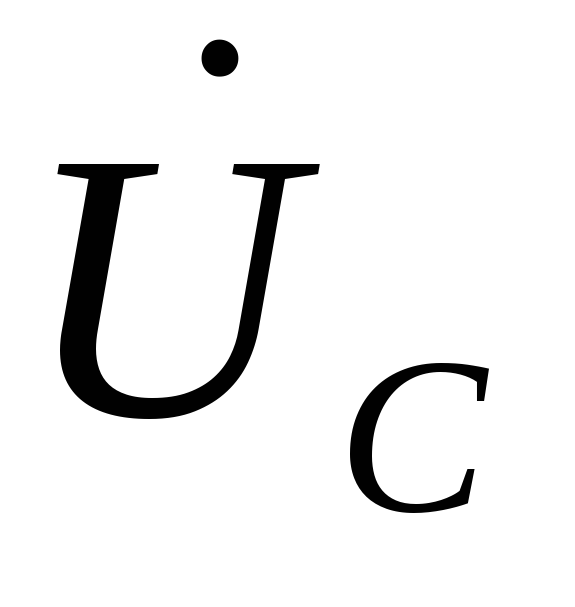 и
и приведены
на рис. 2.6е.
приведены
на рис. 2.6е.
2.8. Последовательное соединение элементов r, L, C.

Для схемы рис. 2.7. уравнение по второму закону Кирхгофа для мгновенных значений запишем в виде:
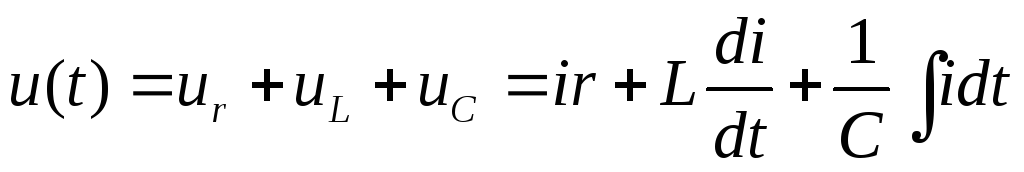 (7)
(7)
Пусть  ,
тогда:
,
тогда:
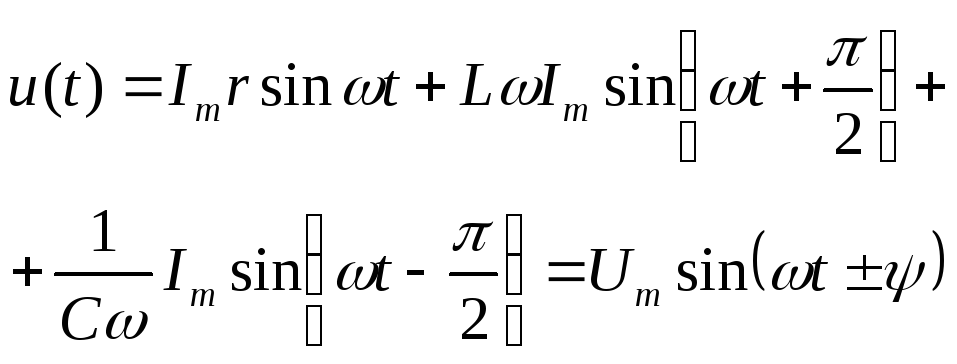 (8)
(8)
Вектор
тока и векторная диаграмма напряжений
приведены на рис. 2.8. Векторы напряжений
на активном и реактивном элементах
ортогональны, а векторы напряжений на L и C смещены на  .
.

В комплексной форме уравнение (8) примет вид:
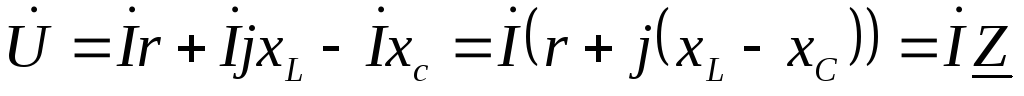 (9)
(9)
Здесь
 — комплексное
сопротивление,
— комплексное
сопротивление,
 — модуль комплексного
сопротивления
— модуль комплексного
сопротивления
 —
фаза комплексного сопротивления.
—
фаза комплексного сопротивления.
На
комплексной плоскости сопротивления  — образуют треугольник сопротивления,
рис. 2.10.
— образуют треугольник сопротивления,
рис. 2.10.

Если
сопротивления умножить на 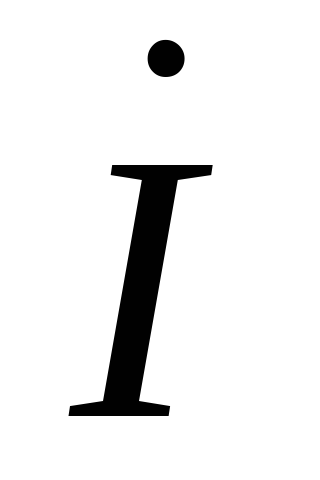 ,
получим диаграмму напряжений, рис. 2.9.
,
получим диаграмму напряжений, рис. 2.9.
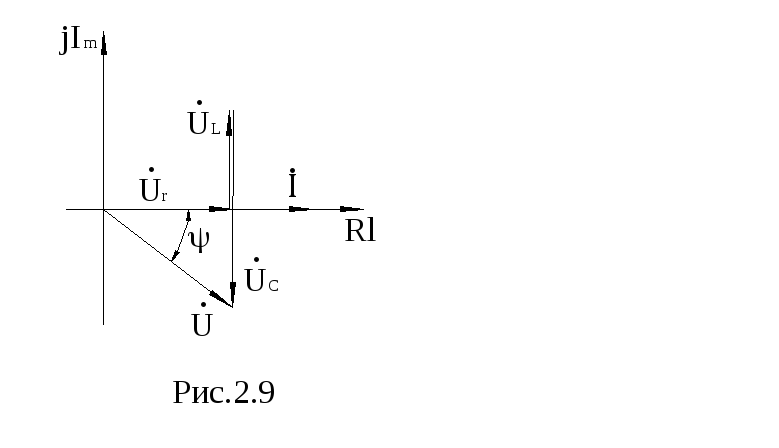
Сравнивания уравнения (8) и (9), отметим, что дифференциальные уравнения (8) после замены мгновенных значений их комплексными символами переводится в уравнение алгебраическое (9). Это одно из преимуществ комплексного метода расчета.
Введение
понятия комплексного сопротивления,
позволяет написать закон Ома для всей
цепи в комплексной форме  или для модулей комплексов
или для модулей комплексов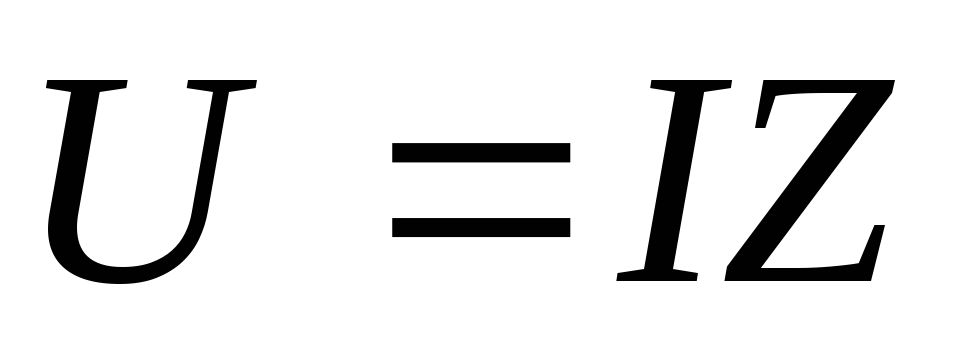
Таким образом, для целей переменного тока можно составлять уравнения, по структуре сходной с уравнениями для цепей постоянного тока.
Цепь переменного тока с резистивным элементом
В резистивном элементе происходит преобразование электрической энергии в тепловую.
Если приложено синусоидально изменяющееся напряжение
u = Um sin ωt,
То, по закону Ома, мгновенное значение тока в цепи:
i = u/R = (Um/R) sin ωt = Im sin ωt
Продолжить
Цепь переменного тока с резистивным элементом URm=R Im
UR=R I
Напряжение и ток совпадают по фазе и в любой момент времени значения тока и напряжения пропорциональны друг другу.
Продолжить
Цепь переменного тока с индуктивным элементом
Индуктивный элемент создает магнитное поле.
Если ток синусоидальный i = Im sin ωt, то тогда
u = — e = L (d i/d t)= ULm cos ωt = ULm sin (ωt+π/2) ULm=ωL Im
Величина ХL =ωL – индуктивное сопротивление, Ом.
Напряжение на индуктивном элементе по фазе опережает ток на угол φ= π/2.
Продолжить
Цепь с емкостным элементом
Емкостный элемент создает электрическое поле.
Если в цепи проходит ток i=Imsin(ωt), i=dq/dt=C(duC/dt) , то тогда напряжение
1 | 1 |
| π | |||
uC |
| idt |
| Imsin( t |
| ) |
C | ωC | 2 | ||||
то есть напряжение отстает от тока на угол π/2. Действующее значение тока в цепи: I=U/XC, где ХС=1/(ωС) – емкостное сопротивление, Ом.
Продолжить
Неразветвленная цепь переменного тока с резистивным и емкостным элементами
Напряжение на зажимах цепи U UR UC
Действующее значение напряжения U IR2 Xc2 IZ
Разность фаз arctg | — XC |
R |
Продолжить
Неразветвленная цепь переменного тока с резистивным, индуктивным и емкостным элементами
Значение напряжения на зажимах этой цепи равно сумме значений трех составляющих:
U UR UL UC
Действующее значение U UR (UL UC )2
Продолжить
Неразветвленная цепь переменного тока с резистивным, индуктивным и емкостным элементами
Сдвиг фаз между напряжением и током:
arctg UL UC arctg X UR R
Х=XL-XC – реактивное сопротивление
Продолжить
Мощности цепи
Активная мощность, Вт:
P = U I cosφ = URI = I2R
Реактивная мощность, вар:
Q = U I sinφ = (UL – UC)I= I2X
Полная мощность, ВА: |
|
| |
P2 | Q2 | ||
S = U I = I2Z = | |||
|
|
Продолжить
резистивный элемент — это… Что такое резистивный элемент?
- резистивный фотоэлемент
- резистная маска
Смотреть что такое «резистивный элемент» в других словарях:
Резистивный элемент резистора — 32. Резистивный элемент резистора Резистивный элемент D. Widerstandselement E. Resistive element F. Element resistant Токопроводящий элемент резистора, определяющий его электрическое сопротивление Источник: ГОСТ 21414 75: Резисторы. Термины и… … Словарь-справочник терминов нормативно-технической документации
резистивиый элемент резистора — резистивный элемент Токопроводящий элемент резистора, определяющий его электрическое сопротивление. [ГОСТ 21414 75] Тематики резисторы Синонимы резистивный элемент EN resistive element DE Widerstandselement FR element resistant … Справочник технического переводчика
термочувствительный элемент — 3.5 термочувствительный элемент: Устройство, разрушающееся или меняющее свою первоначальную форму при заданной температуре. Источник: ГОСТ Р 52316 2005: Техника пожарная. Клапаны термозапорные. Общие технические требования. Методы испытаний … Словарь-справочник терминов нормативно-технической документации
термочувствительный элемент терморезистора — термочувствительный элемент Резистивный элемент терморезистора, сопротивление которого изменяется при изменении его температуры. [ГОСТ 21414 75] Тематики резисторы Синонимы термочувствительный элемент EN thermally sensitive element FR l element… … Справочник технического переводчика
Термочувствительный элемент терморезистора — 33. Термочувствительный элемент терморезистора Термочувствительный элемент E. Thermally sensitive element F. L’element thermosensible Резистивный элемент терморезистора, сопротивление которого изменяется при изменении его температуры Источник:… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 21414-75: Резисторы. Термины и определения — Терминология ГОСТ 21414 75: Резисторы. Термины и определения оригинал документа: 39a. Электрическое сопротивление резистора Электрическое сопротивление Е. Electrical resistance Параметр, характеризующий способность резистора ограничивать… … Словарь-справочник терминов нормативно-технической документации
Тёплый пол — Тёплый пол система отопления, обеспечивающая подогрев полов в помещении. Наиболее распространены электрические … Википедия
РЕОСТАТ — (от греч. rheos течение, поток и …стат) перем. резистор, служащий для регулирования и ограничения силы тока или напряжения в электрич. цепи; осн. части проводящий (резистивный) элемент и подвижный контакт, при помощи к рого регулируют (плавно… … Большой энциклопедический политехнический словарь
композиционный резистор — Резистор, резистивный элемент которого представляет собой композицию из проводящих и диэлектрических материалов [ГОСТ 21414 75] Тематики резисторы EN composition resistor DE Gemischwiderstand FR résistance aglomérée … Справочник технического переводчика
объемный резистор — Резистор, резистивный элемент которого выполнен в виде объемного тела [ГОСТ 21414 75] Тематики резисторы EN carbon composition resistor DE Massewiderstand … Справочник технического переводчика
пленочный резистор — Резистор, резистивный элемент которого представляет собой пленку, нанесенную на электроизоляционное основание. Примечания 1. По материалу резистивного элемента пленочные резисторы подразделяются на: углеродистые, керметные, металлоокисные,… … Справочник технического переводчика




 сетью.
сетью.