Rэкв формула — kak.radiomoon.ru
Формула (от лат. formula – форма, правило, предписание) (математическая) , комбинация математических знаков, выражающая какое-либо предложение.
В более широком смысле формула — всякая чисто символьная запись.
Математическая формула (от лат. formula — уменьшительное от forma — образ, вид) — принятая в математике (а также физике и прикладных науках) символическая запись законченного логического суждения (определения величины, уравнения, неравенства или тождества) .
Как правило, в формулу входят переменные (одна или более) , причём сама формула представляет из себя не просто выражение, а некое суждение. Такое суждение может утверждать что-то о переменных, а может — о применяемых операциях. Точный смысл формулы зачастую подразумевается из контекста и его невозможно понять непосредственно из её вида. Можно выделить три распространённых случая:
1) Формула должна сообщить, как искать значения переменной (уравнения и т. п.) ;
2) Формула (записываемая как «искомое = выражение» ) определяет величину через свои параметры (аналогично присваиванию в программировании и иногда записывается через диграф «:=» как в языке Pascal, но в принципе может считаться вырожденным частным случаем уравнения) ;
Хими́ческая фо́рмула — отражение информации о составе и структуре веществ с помощью химических знаков, чисел и разделяющих знаков — скобок.
Эпическая формула — мнемотехнический прием, связанный с устным характером бытования эпоса и достаточно свободно используемый сказителем.
Формула в эпосе — это выразительная заготовка, обусловленная тремя факторами: ритмом, синтаксической схемой, лексической детерминантой.
Формула служит микроединицей действия, способной комбинироваться с другими формулами, образуя речевой отрезок.
Магическая формула — какая-либо определённая последовательность слов (или звуков) , имеющая магическую силу.
Источник: otvet.mail.ru
Читайте также
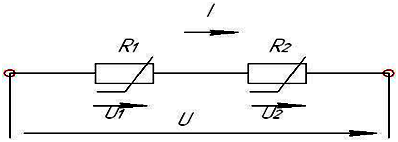
2. Закон Ома для участка и полной цепи
Формула
закона: I=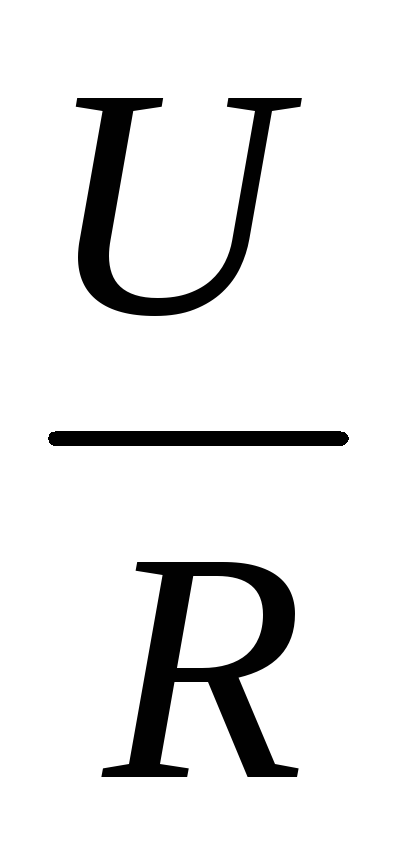 .
Отсюда запишем формулыU= IR и R
=
.
Отсюда запишем формулыU= IR и R
=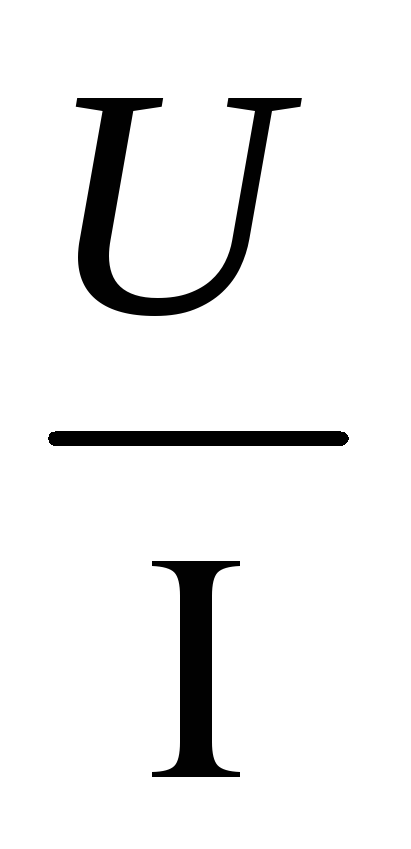
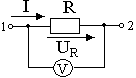 Рис.1.Участок
цепи
Рис.1.Участок
цепи 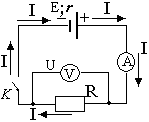 Рис.2.Полная
цепь
Рис.2.Полная
цепь
Закон Ома для полной цепи: сила тока I полной электрической цепи равна ЭДС (электродвижущей силе) источника тока Е, деленной на полное сопротивление цепи (R + r). Полное сопротивление цепи равно сумме сопротивлений внешней цепи
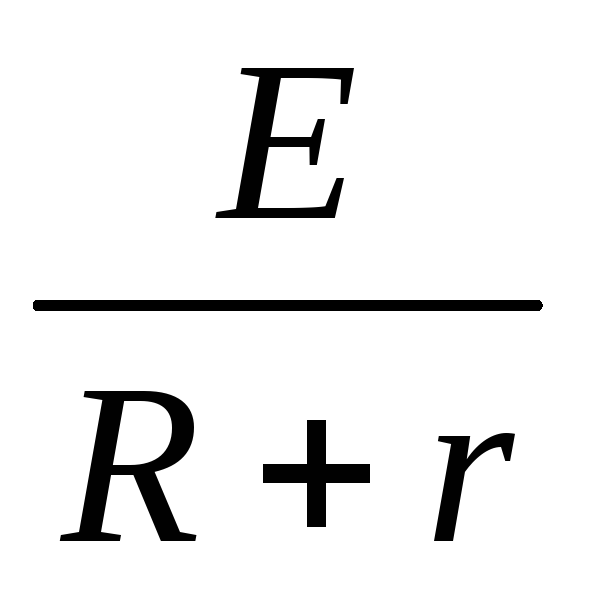 . На
рис. 1 и 2 приведены схемы электрических
цепей.
. На
рис. 1 и 2 приведены схемы электрических
цепей.3. Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно. Смешанное соединение сочетает оба эти соединения.
Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением
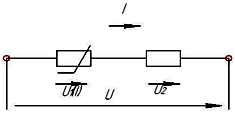
Последовательное соединение
Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.
Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).
1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I1 = I2 = I
Рис. 1. Последовательное соединение двух проводников.
2. Согласно закону Ома, напряжения U1 и U2 на проводниках равны U1 = IR1, U2 = IR2, U3 = IR3.
Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.
U = U1 + U2 + U3
По закону Ома, напряжения U1,U2на проводниках равны U1 = IR1, U2 = IR2, В соответствии вторым правилом Кирхгофа напряжение на всем участке:
U = U1
Общее напряжение U на проводниках равно сумме напряжений U1, U2 ,U3 равно: U
где RЭКВ – эквивалентное сопротивление всей цепи. Отсюда: RЭКВ = R1 + R2 +
При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R ЭКВ= R1 + R2 + R3+…
Этот результат справедлив для любого числа последовательно соединенных проводников.
Из закона Ома следует: при равенстве сил тока при последовательном соединении:
I = 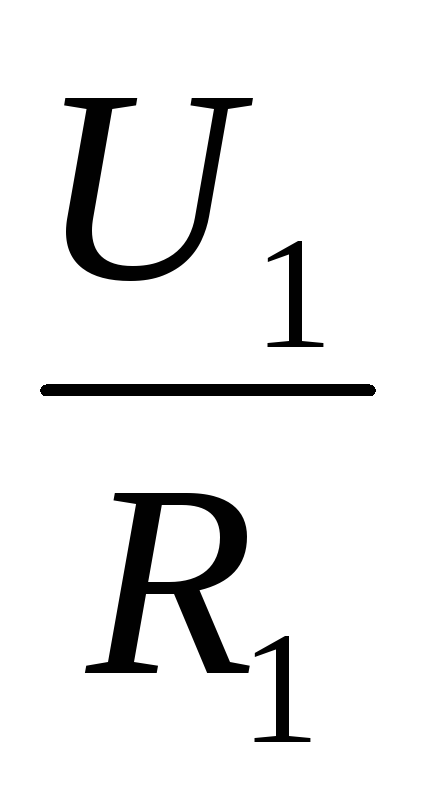
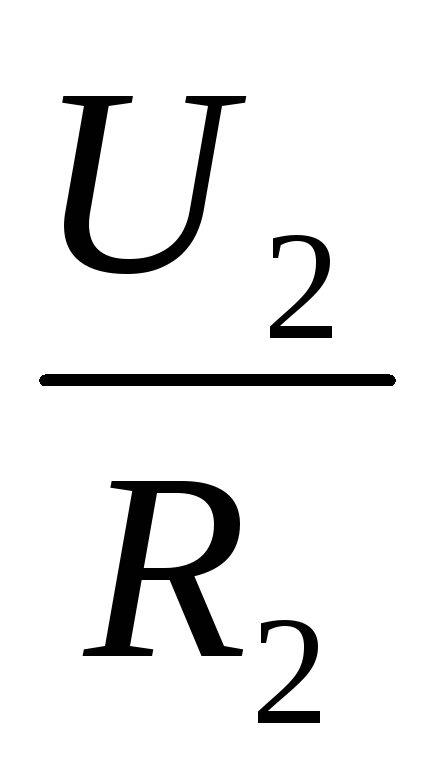 .
Отсюда
.
Отсюда 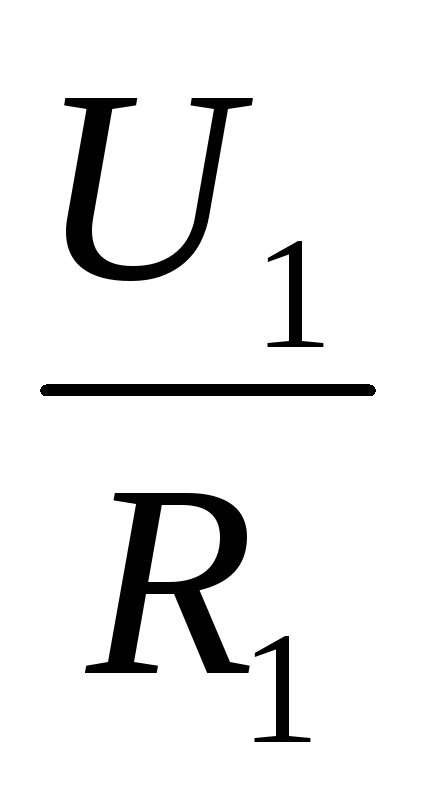 =
= 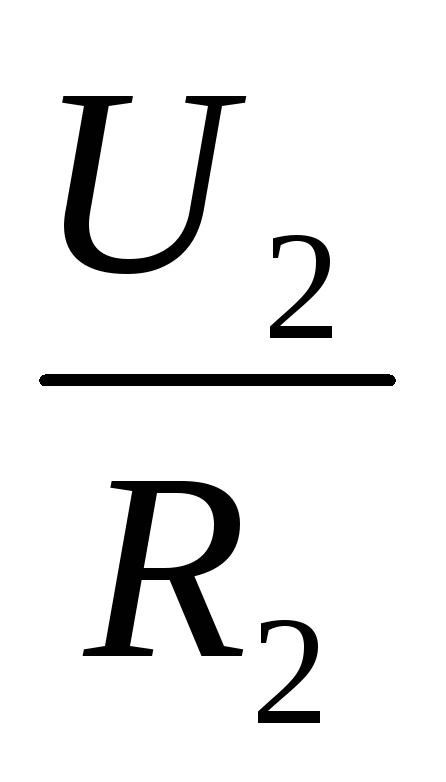 или
или 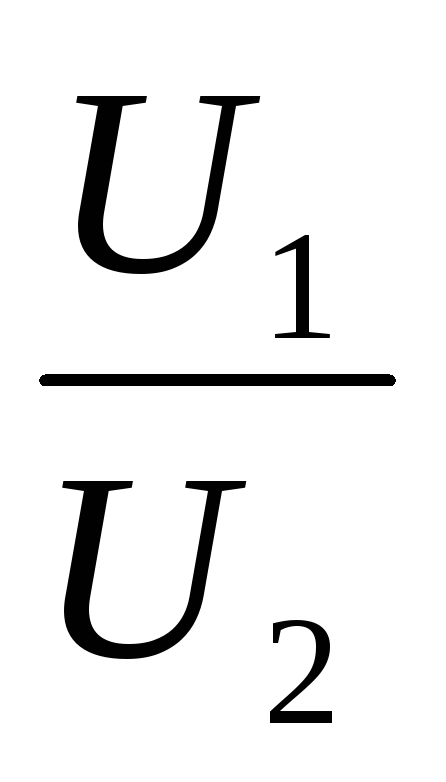 =
=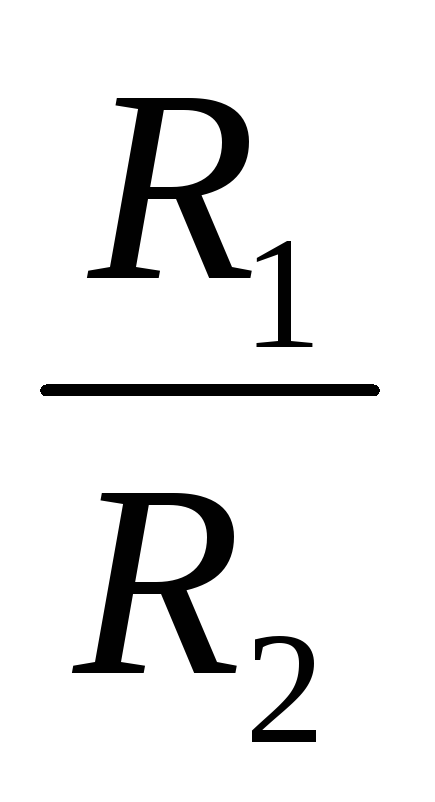 ,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.
,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U1 на их количество n:
UПОСЛЕД= n ·U1. Аналогично для сопротивлений: RПОСЛЕД = n· R1
При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.
Метод эквивалентного источника напряжения (генератора)
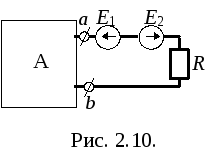
Согласно II закону Кирхгофа ток не изменится, если в цепь, образованную активным двухполюсником и потребителем, включить последовательно два идеализированных встречно направленных источника с одинаковыми ЭДС (рис. 2.10). Величину каждой из них выбираем совпадающей с напряжением UХХ на зажимах активного двухполюсника в режиме холостого хода, который имеет место при отключенном потребителе.
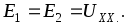 (2.16)
(2.16)
Ток I в цепи с двумя источниками определим методом наложения. С этой целью источники разбиваем на две группы (рис. 211 и 2.12):
1. Источники активного двухполюсника и Е1, которые сохраняются в подсхеме рис. 2.11.
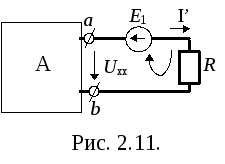
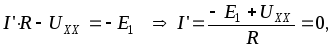 поскольку
поскольку 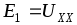 .
.
2. все потребители активного двухполюсника и Е2, сохраняются в подсхеме на рис. 2.12.
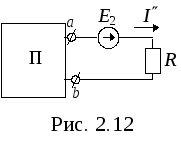
Если эквивалентное сопротивление пассивного двухполюсника, образованного коротким замыканием источников ЭДС и обрывом ветвей, содержащих источники тока, обозначить через Rвх, получим простую одноконтурную схему (рис. 2.13), которую можно рассчитать по закону Ома:
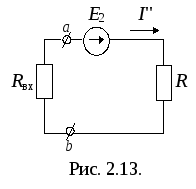
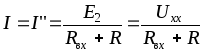 (2.17)
(2.17)Эта формула отражает теорему об активном двухполюснике или об эквивалентном источнике напряжения: относительно любой ветви разветвленной электрической цепи вся остальная часть схемы может быть представлена как источник напряжения, ЭДС которого равна UXX, а внутренне сопротивление равно Rэкв.
При коротком замыкании ветви с нагрузкой R = 0ток превращается в ток короткого замыкания:
 (2.18)
(2.18)
Параметры активного
двухполюсника можно определить опытным
путем. Для этого необходимо разомкнуть
i-ую
ветвь и измерить 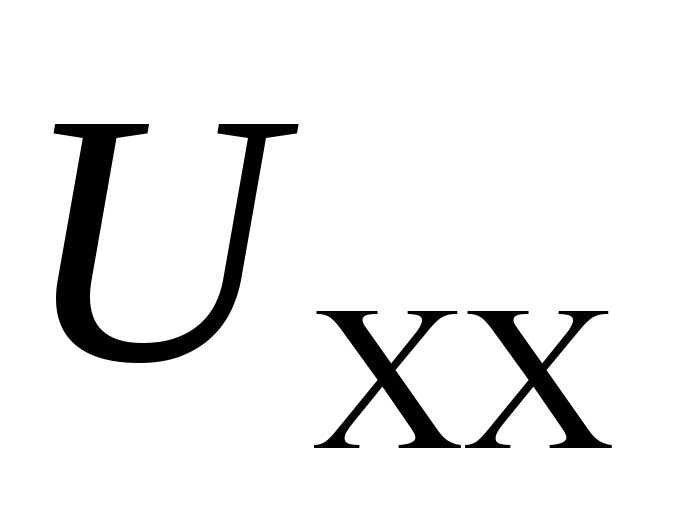 ,
затем замкнуть накороткоRi и измерить IКЗ :
,
затем замкнуть накороткоRi и измерить IКЗ :
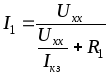 (2.19)
(2.19)
Rвх можно найти расчетным путем, если известна конфигурация цепи и величины сопротивлений.
Методика расчета линейной электрической цепи методом эквивалентного генератора:
Отключается потребитель в ветви с искомым током и на зажимах обозначается UXX по направлению тока.
В образовавшейся более простой цепи находится Uõõ с помощью II закона Кирхгофа, записанного для любого контура, содержащего Uхх. Токи в ветвях упрощенной схемы определяются любым известным методом.
Определяется Rвх на зажимах разомкнутой ветви при условии E=0 и J=0. В полученной пассивной цепи пользуются правилами эквивалентных преобразований для потребителей.
По найденным Uõõ и Rвх определяется ток в искомой ветви, значение которого может быть и отрицательным.
Замечание 1: Rвх можно найти по формуле 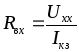 IКЗ при условии Ri=0 любым
известным методом.
IКЗ при условии Ri=0 любым
известным методом.
Замечание 2: если ветвь, в которой определяется ток, содержит источник ЭДС, следует данный источник отнести к активному двухполюснику, отключив только сопротивление Ri. Тогда величина E войдет в расчет UXX .
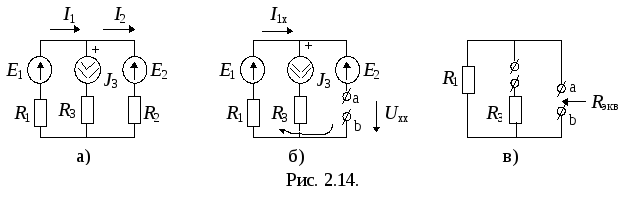
Запишем II закон Кирхгофа для цепи, в которой отключен потребитель R2 (рис. 2.14.,б):
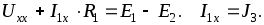
Следовательно, 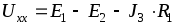 .
.
Rвх определим
по цепи (рис. 2.14., в), из которой
исключены все источники, как 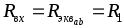 .
.
Тогда искомый ток
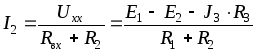
uroki_kroyki_i_shitya
ПОСТОЯННЫЙ ТОК
Единицей измерения проводимости электрической ветви является …
Сименс
Выражение для мощности Р выделяющейся в нагрузке с сопротивлением R, имеет вид…
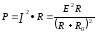
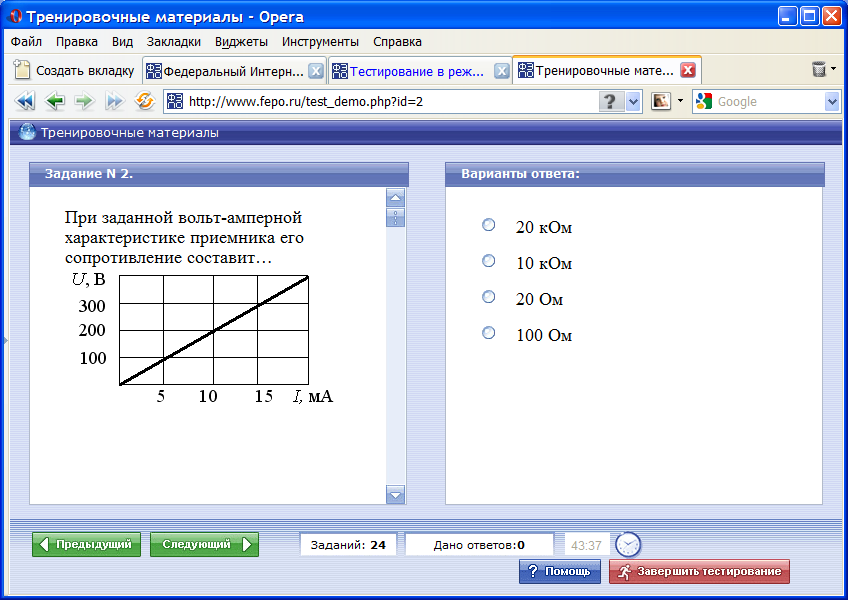
При заданной вольт-амперной характеристике приемника его сопротивление составит…
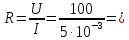 20 кОм
20 кОм
При заданной вольт-амперной характеристике приемника его проводимость равна…
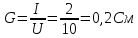
Если
напряжение 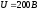 ,
а ток
,
а ток 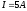 ,
то сопротивление R равно…
,
то сопротивление R равно…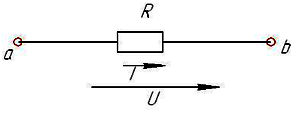
40 Ом
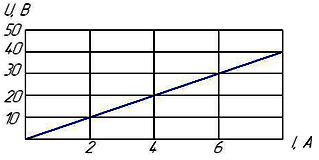
Закон Ома графически выражается в виде…
прямой, проходящей через начало координат
Если показание вольтметра pV составляет 40 В, то амперметр рА при этом будет показывать…
2
А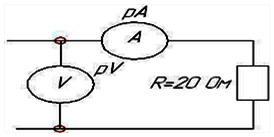
При последовательном соединении нелинейных сопротивлений с характеристиками R1 и R2, если характеристика эквивалентного сопротивления RЭ…

пройдет выше характеристики R1
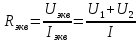 ,
сл-но, для построения графика Rэкв
надо при одной определенной величине
тока сложить напряжения, т.е. ординаты,
поэтому график пойдет выше графиков R1
и R2.
,
сл-но, для построения графика Rэкв
надо при одной определенной величине
тока сложить напряжения, т.е. ординаты,
поэтому график пойдет выше графиков R1
и R2.
При последовательном соединении линейного и нелинейного сопротивлений с характеристиками а и б характеристика эквивалентного сопротивления…
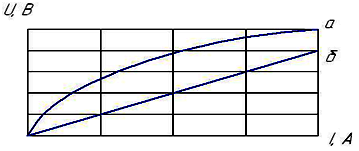
пройдет выше характеристики а
Источники ЭДС работают в следующих режимах…

Е1 – генератор, Е2 – потребитель
Если стрелка тока в ветви совпадает по направлению со стрелкой внутри источника ЭДС, то источник работает в режиме генератора, если наоборот, то потребителя.
Источники ЭДС работают в следующих режимах…
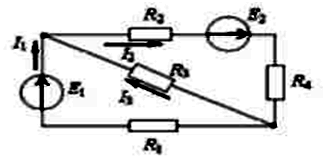
Оба в генераторном режиме
Уравнение баланса мощностей представлено выражением …
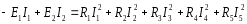
В левой части, если ток в ветви с источником ЭДС совпадает с направлением ЭДС внутри кружочка , то перед ЭДС стоит знак плюс, если наоборот, то минус. В правой части баланса перед произведением тока и сопротивления всегда должен стоять знак плюс.
Уравнение баланса мощностей представлено выражением…
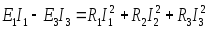
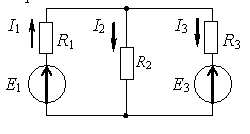
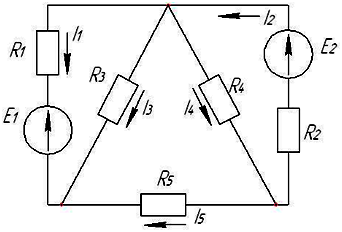
Если
токи в ветвях составляют I1=2 A, I5=3 A,
то ток I2 будет равен…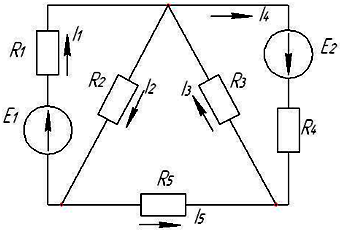
5 А
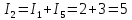
Если токи в ветвях составляют I3=10 A, I4=3 A, то ток I5 будет равен…
7
А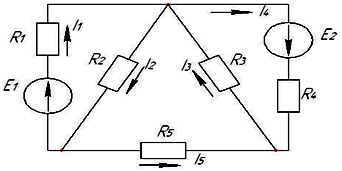
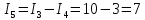
Если
токи в ветвях составляют, 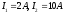 то ток будет равен…
то ток будет равен…
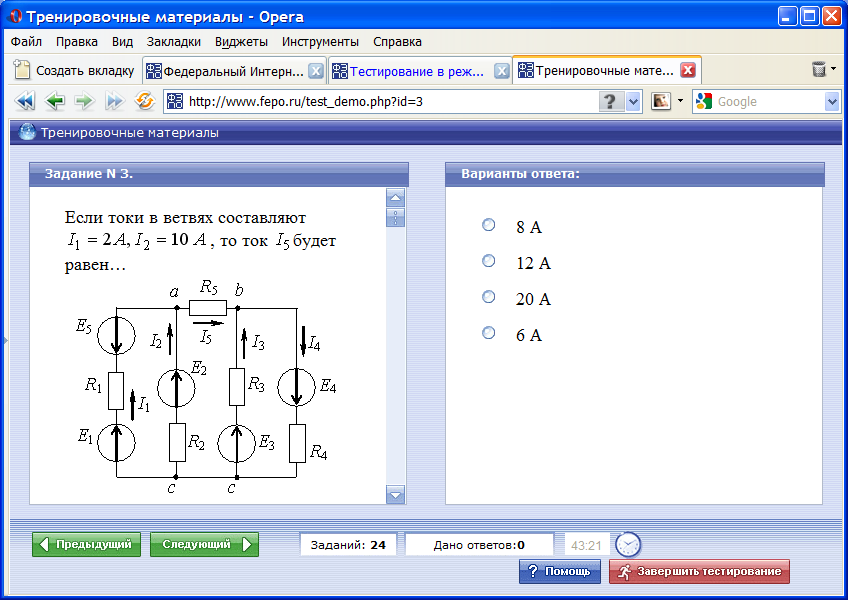
12 А=2+10
Для узла «а» справедливо следующее уравнение по первому закону Кирхгофа…
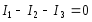
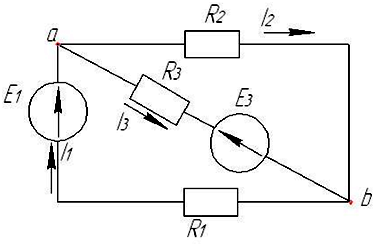
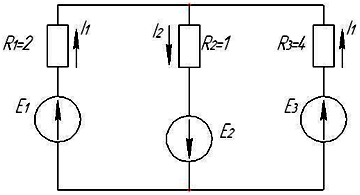
Если сопротивление цепи заданы в Омах, а токи в ветвях составляют I1=1 A, I2=2 A, I3=1 A то потребляемая мощность имеет величину…
10 Вт
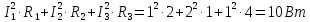
Электрическая цепь, у которой электрические напряжения и электрические токи связны друг с другом линейными зависимостями, называются…
линейной электрической цепью
Электрическая цепь, у которой электрические напряжения и электрические токи связны друг с другом нелинейными зависимостями, называются…
нелинейной электрической цепью
Для
контура, содержащего ветви с 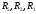 справедливо уравнение по второму закону
Кирхгофа…
справедливо уравнение по второму закону
Кирхгофа…
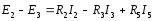
Если
сопротивления  ,
то в ветвях будут наблюдаться следующие
токи …
,
то в ветвях будут наблюдаться следующие
токи …
в
R2→max,
вR3→min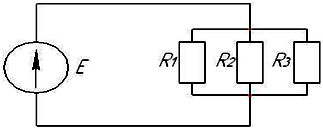
В самом большом сопротивлении ток самый маленький, в самом маленьком сопротивлении ток самый большой
Если
сопротивления 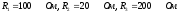 ,
то на резисторах будут наблюдаться
следующие напряжения …
,
то на резисторах будут наблюдаться
следующие напряжения …
в
R3→max,
вR2→min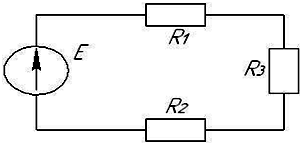
На самом большом сопротивлении напряжение самое большое, на самом маленьком сопротивлении напряжение самое маленькое
Если
сопротивления 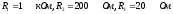 ,
то на резисторах будут наблюдаться
следующие напряжения …
,
то на резисторах будут наблюдаться
следующие напряжения …
в
R1→max,
вR3→min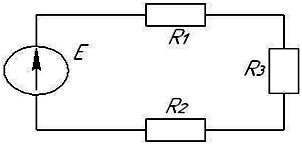
Если статическое сопротивление нелинейного элемента при напряжении U1=200 В равно 5 Ом, то сила тока I1 составит…
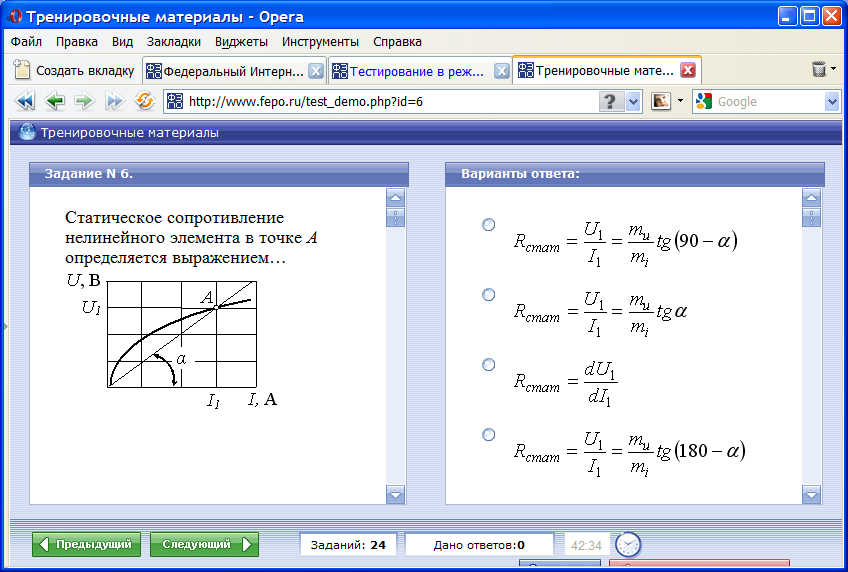
40 А
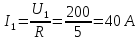
Статическое сопротивление нелинейного элемента при токе 2 А составит…
15
Ом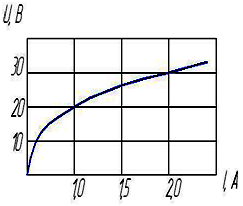
Идеальному источнику ЭДС соответствует внешняя характеристика под номером …
один
4
1
2
3
Источник электрической энергии, напряжение, на выводах которого не зависит от электрического тока в нем, это…
идеальный источник напряжения
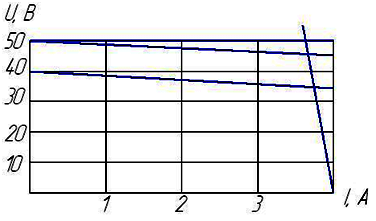
Полярность на вольтметре показывает направление напряжения. Если показание вольтметра pV=50 B, то показание амперметра рА равно…
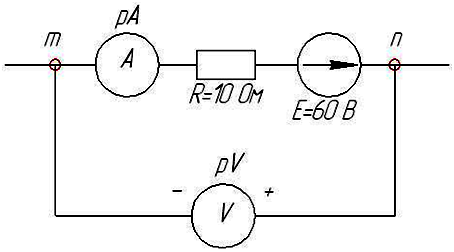
1 А
Эквивалентное
сопротивление цепи относительно
источника ЭДС составит …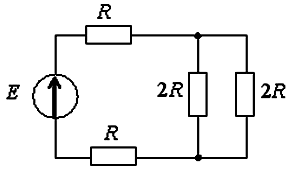
3R
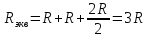
Показание амперметра рА составит…
2 А
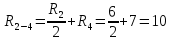
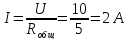
Найти показания амперметра А.
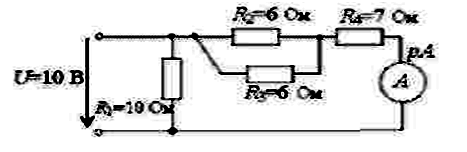
1 А.
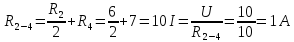
Статическое сопротивление нелинейного элемента в точке А определяется выражением …
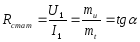
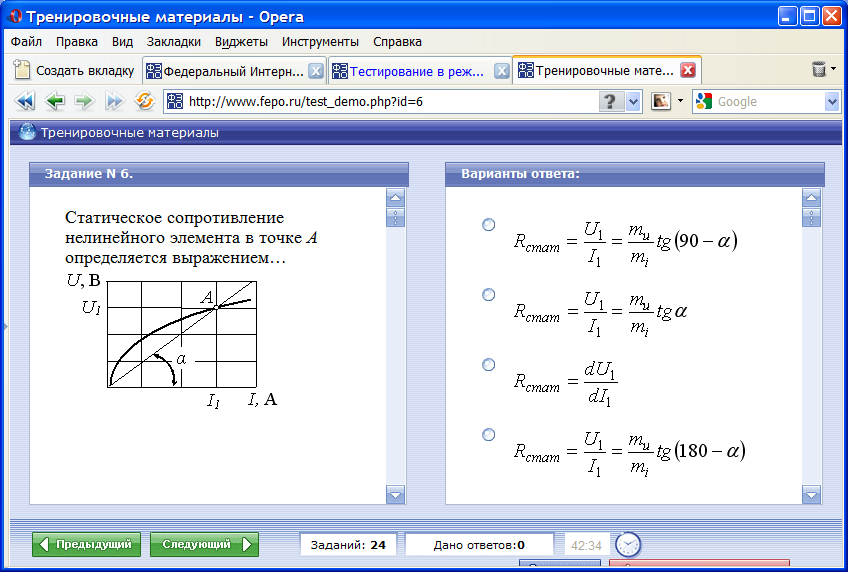
Статическое
сопротивление нелинейного элемента
при токе 2 А составит…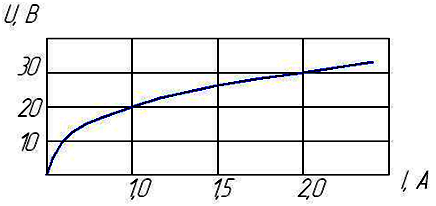
15 Ом
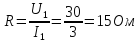
ЭЛЕКТРОМАГНЕТИЗМ
Зависимость магнитной индукции В от напряженности магнитного поля Н, описываемая замкнутой кривой а-б-в-г-а, называется…
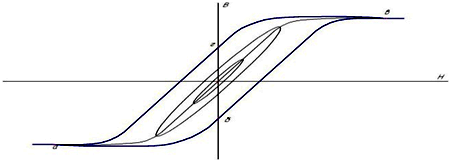
предельной петлей гистерезиса
Если площадь 1 – потери на гистерезис за один цикл перемагничивания, а площади 2 – потери на вихревые токи за один цикл перемагничивания, то замкнутая кривая «в» представляет…
динамической петлей гистерезиса
Приведенная магнитная цепь классифицируется как…
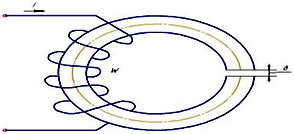
неразветвленная неоднородная
Неразветвленная неоднородная, т.к. есть воздушный зазор
Если при неизменном токе I, числе витков w, площади S поперечного сечения и длине l магнитопровода (сердечник не насыщен), увеличить воздушный зазор δ, то магнитный поток Ф…

уменьшится
Воздушный зазор препятствие для магнитного потока
Если при неизменном токе I, площади S поперечного сечения и длине l магнитопровода (сердечник не насыщен), увеличить число витков w, то магнитный поток Ф…

увеличится
Чем больше число витков, тем больше Ф
Если
при неизменном токе I,
числе витков w,
площади S поперечного сечения и длине l магнитопровода
(сердечник не насыщен), уменьшить
воздушный зазор δ,
то магнитный поток Ф…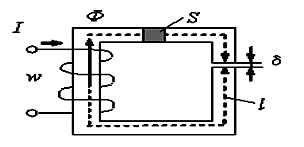
увеличится
Если при неизменном токе I, числе витков w, площади S поперечного сечения уменьшить длину l магнитопровода (сердечник не насыщен), то магнитный поток Ф…
увеличится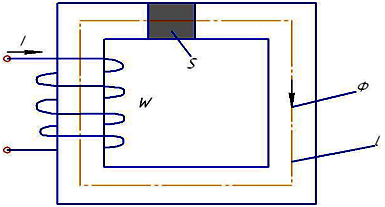
Чем меньше длина магнитопровода, тем больше Ф
Если
потери мощности в активном сопротивлении
провода катушки со стальным сердечником 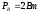 ,
потери мощности на гистерезис
,
потери мощности на гистерезис 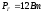 ,
на вихревые токи
,
на вихревые токи 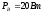 ,то
показание ваттметра составляет…
,то
показание ваттметра составляет…
34
Вт=2+12+20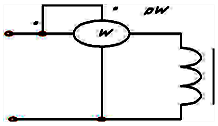
Если
при неизменной амплитуде 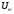 увеличить частоту синусоидального
напряжения, питающего катушку со стальным
сердечником, то потери мощности в
магнитопроводе…
увеличить частоту синусоидального
напряжения, питающего катушку со стальным
сердечником, то потери мощности в
магнитопроводе…
увеличатся
Увеличиваются потери на перемагничивание стали магнитопровода
Фундаментальные уравнения, описывающие электромагнитное поле, это — …
уравнения Максвелла
При описании магнитного поля используется величина…
напряженности магнитного поля Н
Здесь правильный ответ тот, где единственный раз встречается слово «магнитное» и он касается напряженности магнитного поля!!!
Законом Ома для магнитной цепи называется уравнение…
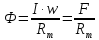
Проведите
ассоциацию с законом
ОМА для цепи постоянного тока 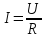 . Правильный тот ответ, где в формуле в знаменателе
стоит сопротивление Rm
. Правильный тот ответ, где в формуле в знаменателе
стоит сопротивление Rm
Соотношение между воздушными зазорами для трех магнитных характеристик Ф=f(Iw) магнитной цепи…
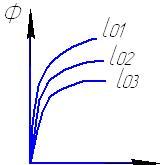
1. 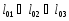
Чем меньше воздушный зазор, тем больше магнитный поток.
Величиной, имеющей размерность А/м, является…
напряженность магнитного поля Н
Величиной, имеющей размерность Гн/м, является…
магнитная проницаемость μ
Если
к катушке с ферромагнитным сердечником
приложено синусоидальное напряжение 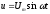 ,
то, пренебрегая рассеянием и активным
сопротивлением катушки, можно принять…
,
то, пренебрегая рассеянием и активным
сопротивлением катушки, можно принять…

Величиной, имеющей размерность Вб, является…
магнитный поток Ф
К ферромагнитным материалам относится…
электротехническая сталь
Если действующее значение ЭДС в катушке со стальным сердечником равно Е, то пренебрегая рассеянием и активным сопротивлением катушки, амплитуда магнитной индукции Вm равна…
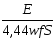 ответ исходит из формулы трансформаторной
ЭДС
ответ исходит из формулы трансформаторной
ЭДС 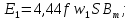
В ферромагнитных веществах магнитная индукция В и напряженность магнитного поля Н связаны соотношением…

Напряженность магнитного поля связана с индукцией магнитного поля соотношением …
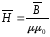
Отрезок в-г основной кривой намагничивания В(Н) соответствует …
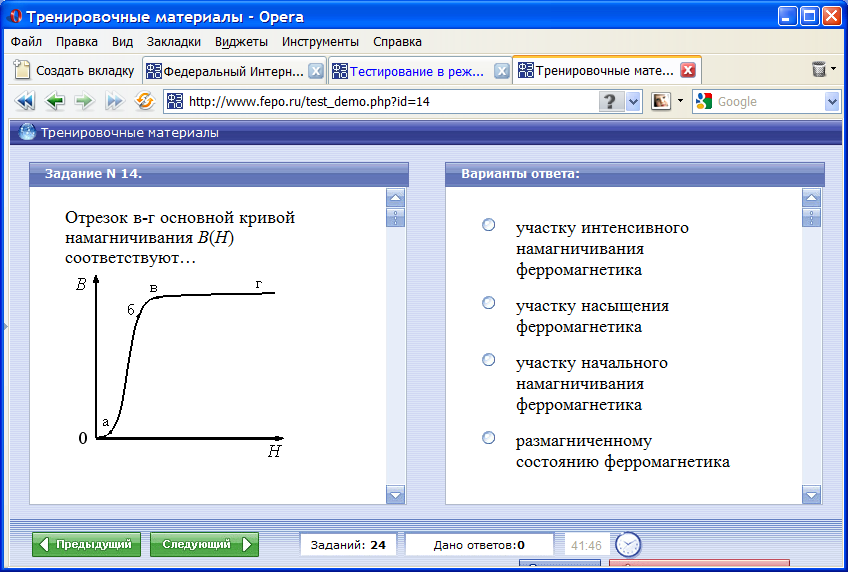
участки насыщения ферромагнетика
Участок в-г – прямая, если Вы насытились едой, то сколько бы еще не ели ощущения голода уже не появится.
Если
напряжение, приложенное к катушке с
ферромагниным сердечником 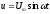 ,
число витков катушки w,
то, пренебрегая рассеянием и активным
сопротивлением катушки, можно принять,
что амплитуда магнитного потока в
сердечнике Фт равна…
,
число витков катушки w,
то, пренебрегая рассеянием и активным
сопротивлением катушки, можно принять,
что амплитуда магнитного потока в
сердечнике Фт равна…
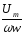
ПЕРЕМЕННЫЙ ТОК
 периодом
является …
периодом
является …

Если период синусоидального тока Т составляет 0,001 с, то частота f составит…
1000 Гц |
|
Угловая частота ω при частоте синусоидального тока f, равной 50 Гц, составит…
314 с-1 |
|
Индуктивное
сопротивление XL при частоте f=50
Гц и величине L=0,318
Гн равно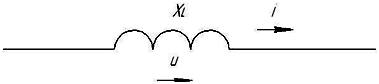
100 Ом XL=2πfL=2·3,14·0,318=100 Ом
Емкостное сопротивление Хс при величине С=100 мкФ и частоте f=50 Гц равно …
31,84
Ом
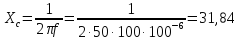
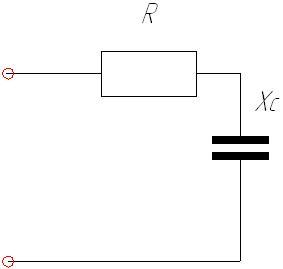
Комплексное
сопротивление приведенной цепи 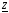 в
алгебраической форме записи при R=8
Ом, XL=7
Ом, XC=13
Ом составляет …
в
алгебраической форме записи при R=8
Ом, XL=7
Ом, XC=13
Ом составляет …
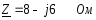
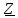 =R+jXL—jXc=8+j7-j13=8-j13
=R+jXL—jXc=8+j7-j13=8-j13
При увеличении частоты f полное сопротивление Z
Уменьшится
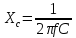 Если f увеличивается, то Xc уменьшается, следовательно,
Если f увеличивается, то Xc уменьшается, следовательно, 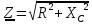 уменьшится
уменьшится
Полное
сопротивление Z приведенной цепи при 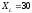 Ом
и
Ом
и 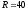 Ом
составляет…
Ом
составляет…

50 Ом
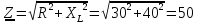
Полное
сопротивление Z приведенной цепи при  Ом
и
Ом
и 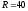 Ом
составляет…
Ом
составляет…
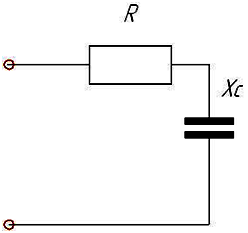
50 Ом
Если P и S активная и полная мощности пассивной электрической цепи синусоидального тока, то отношение P к S равно…
 формула P=UIcosφ=Scosφ
формула P=UIcosφ=Scosφ
Активную мощность Р цепи синусоидального тока можно определить по формуле…
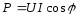
Коэффициент мощности электрической цепи синусоидального тока называется …
отношение активной мощности Р к полной мощности S
Если Q и S – реактивная и полная мощности пассивной электрической цепи синусоидального тока, то отношение Q к S равно…
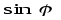 формула Q=UIsinφ
формула Q=UIsinφ
Реактивную
мощность Q цепи, имеющей входное комплексное
сопротивление 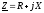 ,
можно определить по формуле…
,
можно определить по формуле…
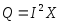
Единица измерения реактивной мощности Q
Вар или расшифровывается вольт-ампер реактивный
Коэффициент мощности пассивной электрической цепи синусоидального тока равен…
cos φ проведите ассоциацию КОСинус — КОЭффициент
Резонансная частота f0 для данной цепи определяется выражением …
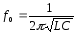
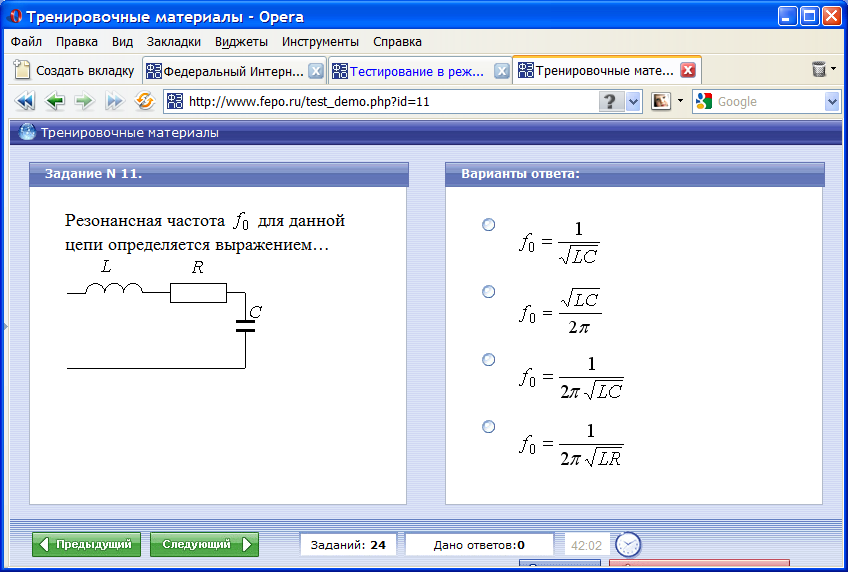
Критерием возникновения резонансного явления в цепи, содержащей индуктивные и емкостные элементы, является…
равенство нулю угла сдвига фаз φ между напряжением и током на входе цепи (при
К возникновению режима резонанса напряжений ведет выполнение условия…
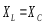

Режим резонанса напряжений может быть установлен в цепи…
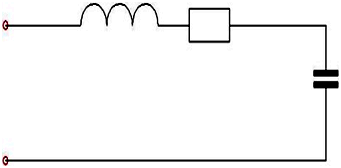 Для
создания резонанса необходимо одновременное
присутствие в цепи и конденсатора и
катушки индуктивности. Резонанс
напряжений
наступает при последовательном соединении
этих элементов (т.к. при таком соединении
ток в них одинаковый)
Для
создания резонанса необходимо одновременное
присутствие в цепи и конденсатора и
катушки индуктивности. Резонанс
напряжений
наступает при последовательном соединении
этих элементов (т.к. при таком соединении
ток в них одинаковый)
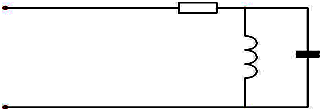
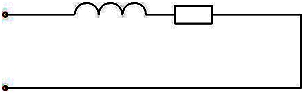
При неизменной амплитуде приложенного напряжения изменение частоты позволяет добиться …
возникновение
режима резонанса токов (резонанс
токов возникает только при параллельном
соединении элементов, т.к. только в этом
случае токи в элементах разные)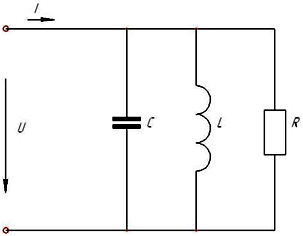
Частотные свойства электрической цепи синусоидального тока обусловлены зависимостью от
Индуктивного XL и емкостного Хс сопротивлений
В трехфазной цепи при соединении по схеме «звезда-звезда с нейтральным проводом» ток в нейтральном проводе отсутствует, если нагрузка …
Симметричная (т.к. при симметричной нагрузке токи всех трех фаз одинаковы по величине и сдвинуты на одинаковый угол 120 градусов, их сумма дает 0 и тока в нейтральном проводе нет)
В трехфазной цепи при соединении по схеме «звезда – звезда с нейтральным проводом» при симметричной нагрузке ток IN в нейтральном проводе равен…
0
В трехфазной цепи при соединении по схеме «звезда – звезда с нейтральным проводом» при симметричной нагрузке ток IN в нейтральном проводе равен…
0
В трехфазной цепи при соединении по схеме «звезда – звезда с нейтральным проводом» при симметричной нагрузке ток IN в нейтральном проводе равен…
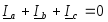
В трехфазной цепи амперметром был замерен ток – 5 А, фазный ток Iа равен…
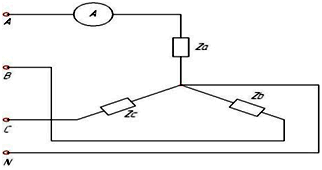
5 А Iф=Iл=5
В
трехфазной цепи был замерен фазный ток 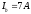 ,
линейный ток равен…
,
линейный ток равен…
7
А Iф=Iл=7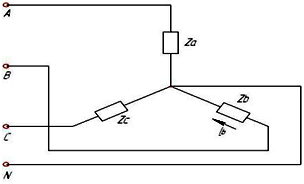
В
симметричной трехфазной системе
напряжений прямой последовательности
вектор напряжения 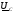 сдвинут
относительно вектора
сдвинут
относительно вектора 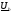 на
угол, равный…
на
угол, равный…
— 120° 2π/3
Действующее значение электрической величины (ток, ЭДС, напряжение) изменяется во времени по синусоидальному закону а(t)=Amsin(ωt+ψа) определяется как
Аm / √2
Комплексное
ДЕЙСТВУЮЩЕЕ значение тока 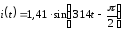 А
составляет…
А
составляет…
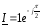 А
А 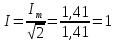 и т.к. это комплекс необходимо учесть
угол
и т.к. это комплекс необходимо учесть
угол 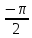 Действующее
значение синусоидального электрического
тока
Действующее
значение синусоидального электрического
тока  А
составляет…
А
составляет…
1
А 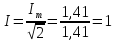
Действующее
значение тока в индуктивном элементе 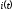 ,
при напряжении
,
при напряжении 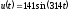 В и величине
В и величине 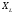 ,
равной 100 Ом составит…
,
равной 100 Ом составит…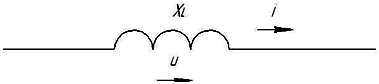
1 А
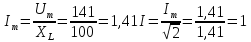
Комплексная
АМПЛИТУДА тока 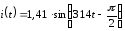 А
составляет…
А
составляет…
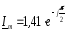 А амплитудное значение это первая цифра в записи мгновенного значения, его
делить на 1,41 не надо!!!!
А амплитудное значение это первая цифра в записи мгновенного значения, его
делить на 1,41 не надо!!!!
Амплитудное
значение тока 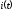 ,
при напряжении
,
при напряжении 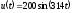 В и величине
В и величине 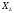 ,
равной 100 Ом, составит…
,
равной 100 Ом, составит…
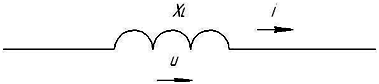
2 А
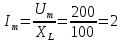
При
токе 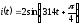 А
и величине R,
равной 50 Ом, амплитудное значение
напряжения
А
и величине R,
равной 50 Ом, амплитудное значение
напряжения 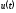 равно…
равно…
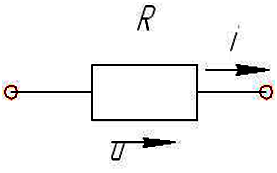
100 В
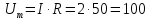
Полное
сопротивление пассивного двухполюсника Z при действующем значении напряжения В и действующем значении тока I1=2 A составит…
В и действующем значении тока I1=2 A составит…
50 Ом

6.3.Расчет согласующих цепей.
1.При расчете согласующей цепи выходного каскада необходимо определить коэффициент фильтрации, исходя из заданной выходной мощности в антенне РА и мощности второй гармоники Р2= 25 мВт.
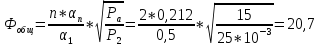
где n = 2 – номер гармоники
α1, αn – коэффициенты разложения последовательности косинусоидальных импульсов выходного тока.
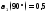 ;
; 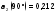
Если коэффициент фильтрации задан в децибелах, то его надо пересчитать.
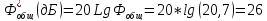
2.Полученный коэффициент фильтрации необходимо распределить между фильтром согласующей цепи выходного каскада Ф и антенным контуром ФА.
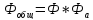
Для этого определим параметры антенного контура.
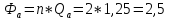
Q – добротность антенного контура.
Определим добротность антенного контура, имеющего сопротивление.
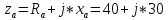
где RA– активное сопротивление антенны.
ХА – реактивное сопротивление антенны.
При 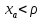 :
:
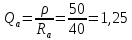
При 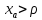 :
:
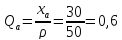
Волновое сопротивление ρ выбираем равным:
50 [Ом] или 75 [Ом], если антенны подключаются к выходному каскаду с помощью коаксиального кабеля,
или (200…400) [Ом] при подключении антенны с помощью двухпроводной линии.
3. Определим коэффициент фильтрации согласующей цепи выходного каскада.
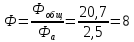
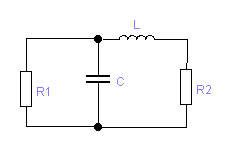
4. Исходя из требуемого коэффициента Ф, рассчитаем параметры согласующей цепи. Рассмотрим два варианта согласующей цепи. (RЭКВ =9 Ом)
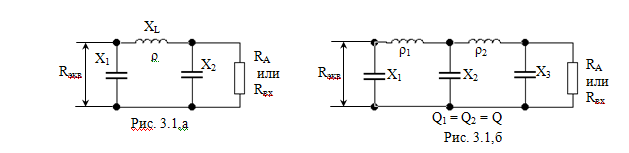
Исходным для расчета является выбор добротности колебательных контуров.
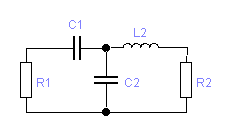
4.1. Для одиночного П-контура:
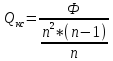 , при n=2
, при n=2 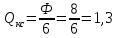
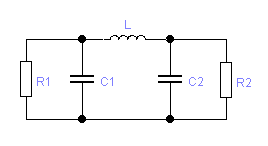
4.2.для сдвоенного П-контура:
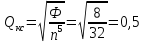
Далее задаемся
добротностью, величиной более рассчитанного
по формулам в п.4.4.1 или 4.4.2., но менее пяти
: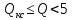
Если значения по формулам в п.4.4.1 или 4.4.2. меньше единицы, то задаются добротностью:
В дальнейших формулах подставляем величину добротности Q, которой задались для одиночного П-контура Q = 2, для сдвоенного – Q = 1,5.
При
расчетах промежуточных каскадов обычно
ограничиваются однозвенными фильтрами
(рис.3.1,а) или схемами (табл.3.1 ), т.к. не
целесообразно применять сложные фильтры,
поскольку последующие каскады работают
в режиме с отсечкой. Расчет фильтра
промежуточного каскада начинают с
п.4.4.3., далее по приведенной методике,
но вместо RА подставляется входное сопротивление
следующего каскада 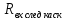 .
.
Таблица 3.1
Параметр контура | Значения параметра для П-контура | |
одного | двух | |
Полоса пропускаемых частот |
|
|
КПД системы контуров |
|
|
где Qx.x— добротность ненагруженного контура, Qx.x= 100
Прежде чем приступить к расчету параметров фильтра, необходимо убедиться также в том, что заданное сопротивление нагрузки (фидера или антенны) больше минимально допустимого.
. Для одного П-контура.
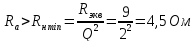
Для системы двух П-контуров.
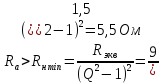
Сначала рассчитываются параметры схемы (рис.3.1,а) по формулам таблицы 3.2.
Таблица 3.2.
Этапы расчета | Формулы для расчета схем | |
Рис. 3.1,а | Рис. 3.1,б | |
1. |
| |
2. |
|
|
3. |
|
|
4. |
|
|
5. |
=9,9i |
|
6. |
|
|
4.5.
Проверяем добротность: 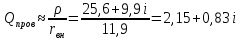
Если 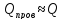 ,
то расчет фильтра верен.
,
то расчет фильтра верен.
Если в ф.5 (табл. 3.2) при определении реактивного сопротивления Х1 под корнем получается отрицательное число, то одиночный П-контур не реализуется. В этом случае необходимо задаться другой величиной добротности или рассчитать схему (рис.3.1,б). После расчета параметров двухзвенного фильтра (рис.3.1,б) также необходимо определить добротность:
4.6.
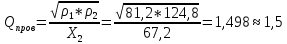
Полученная Qпров должна совпадать с выбранной добротностью Q (Qпров ≈Q, Q= 1.5 ).
Элементы фильтров определяются по формулам:
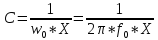 и
и 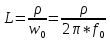
4.7.Рассчитаем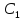 .
.
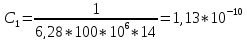 Ф
Ф
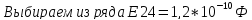
 .
.
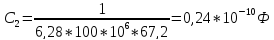
Выбираем
из ряда Е24
=
0,3*
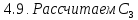 .
.
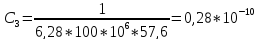 Ф
Ф
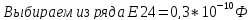
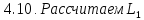 .
.
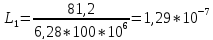 Гн
Гн
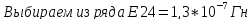
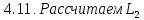 .
.
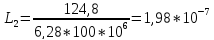 Гн
Гн
Выбираем из ряда
Е24=2*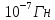
Причем надо иметь в виду, что в умеренном диапазоне частот (до 100 МГц) полученная индуктивность должна быть L> 50 нГн.
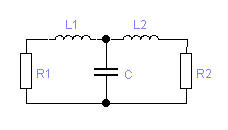
Если расчет рассмотренных вариантов согласующей цепи не получается, то можно рассмотреть другие виды фильтров: Г-, Т-, П-образных цепочек. В таблице 3.3 приведены схемы и расчетные формулы, в которых в качестве R1 используется эквивалентное сопротивление коллекторной нагрузки, в качестве R2 – активное сопротивление антенны или входное сопротивление следующего каскада. В цепях табл. 3.3 сопротивление R2 трансформируется в некоторое сопротивление R0 , а затем R0 — в R1. При этом чем меньше или больше R0 по отношению к R1, R2,тем лучшую фильтрацию будет обеспечивать П- и Т-цепочка, но тем ниже будет её КПД и уже полоса пропускания. Поэтому R0 выбирают в пределах 1,5…10 раз меньше или больше, чем R1 и R2.
Рассчитав емкости фильтров, необходимо номиналы конденсаторов выбирать по стандартному ряду, учитывая паразитные емкости транзистора (рис. 3.1,а).
4.12.Для одиночного:
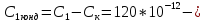
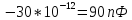
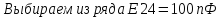
4.13.Для сдвоенного: 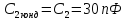
Выбираем из ряда Е24=30 пФ
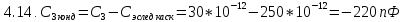
Для оконечного
каскада: 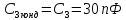
Выбираем из ряда Е24=30 пФ
Поскольку конденсатор с отрицательным номиналом не имеет смысла, рассчитываем фильтры другого типа, см. Табл. 3.3.
Аналогично подбираются конденсаторы для других вариантов схем.
Таблица 3.3
Схема | Расчетные соотношения | КПД
|
Общий случай | ||
Г-цепочка
| при R1>R2 7 < 40, т.е. данный фильтр не подходит для рассчитываемого усилителя мощности
|
|
П-цепочка
| R0<R1,R0<R2,R1 >R2 илиR1 <R2 7 < 40 фильтр подходит. Задаемся R0= 6 Ом
|
|
Т1-цепочка
| R0>R1,R0>R2,R1 >R2 илиR1 <R2 7 < 40 фильтр подходит. Задаемся R0= 180 Ом
|
|
Т2-цепочка
| R0>R1>R2 7 < 40 условие не выполняется
|
|
Элементы фильтров определяются по формулам:
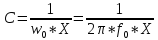 и
и 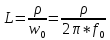
Рассчитаем П-цепочку.
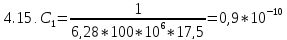 Ф
Ф
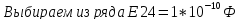
 Ф
Ф
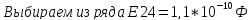
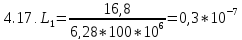 Гн
Гн
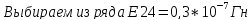
Причем надо иметь в виду, что в умеренном диапазоне частот (до 100 МГц) полученная индуктивность должна быть L> 50 нГн.
1.2. Расчеты факторов эквивалентности и эквивалентных масс
Следует учитывать, что эквивалент одного и того же вещества может меняться в зависимости от того, в какую реакцию оно вступает. Эквивалент элемента также может быть различным в зависимости от вида соединения, в состав которого он входит. Эквивалентом может являться как сама молекула или какая-либо другая формульная единица вещества, так и ее часть.
Рассмотрим реакцию, протекающую по уравнению:
H3PO4 + 2KOH = K2HPO4 + 2H2O.
В ходе этой реакции только два атома водорода замещаются на атомы калия (кислота проявляет основность, равную 2). С другой стороны, на взаимодействие с одной молекулой ортофосфорной кислотой расходуется два иона ОН– щелочи, следовательно, на взаимодействие с ½ молекулы кислоты потребуется один ион ОН–. Эквивалентом кислоты является ½Н3РО4, а эквивалентом щелочи частица КОН.
Число, показывающее, какая часть молекулы или другой частицы вещества соответствует эквиваленту, называется фактором эквивалентности (fЭ).Фактор эквивалентности – это безразмерная величина, которая меньше, либо равна 1. Формулы расчета фактора эквивалентности приведены в таблице 2.
Таким образом, сочетая фактор эквивалентности и формульную единицу вещества, можно составить формулу эквивалента какой-либо частицы, где фактор эквивалентности записывается как химический коэффициент перед формулой частицы:
Эквивалент = fЭ ∙ (формульная единица вещества) (1.7)
В примере, рассмотренном выше, фактор эквивалентности для кислоты, соответственно, равен ½, а для щелочи КОН – 1.
Между H3PO4и КОН также могут происходить и другие реакции. При этом кислота будет иметь разные значения фактора эквивалентности:
H3PO4 + 3KOH = K3PO4 + 3H2O fЭ(H3PO4) = 1/3
H3PO4 + KOH = KН2PO4 + H2O fЭ(H3PO4) = 1.
Эквивалент, как частица, может быть охарактеризован молярной массой (молярным объемом) и определенным количеством веществаэ.
Молярная масса эквивалента(МЭ) – это масса одного моля эквивалентов, г/моль. Она равна произведению молярной массы вещества на фактор эквивалентности:
МЭ = М · fЭ. (1.8)
Молярная масса эквивалента сложного вещества равна сумме молярных масс эквивалентов образующих его составных частей, например:
МЭ(оксида) = МЭ(элемента) + МЭ(О),
МЭ(кислоты) = МЭ(Н) + МЭ(кислотного остатка),
МЭ(основания) = МЭ(Ме) + МЭ(ОН),
МЭ(соли) = МЭ(Ме) + МЭ(кислотного остатка).
Газообразные вещества, кроме молярной массы эквивалента, имеют молярный объем эквивалента(другой термин – эквивалентный объем,VЭ) – объем, занимаемый молярной массой эквивалента или объем одного моля эквивалентов (размерность – дм3/моль). При н.у. получаем:
 (1.9)
(1.9)
Эквивалентный объем водорода при н.у. равен Voэ(Н2) = 22,4/2 = = 11,2 дм3/моль (объем 1 г газа при н.у.), соответственно Voэ(О2) = 22,4/4 = = 5,6 дм3/моль.
Пример. Определить фактор эквивалентности и эквивалент у солей: а) ZnCl2, б) КНСО3, в) (MgOH)2SO4.
Решение: Согласно формулам, приведенным в таблице 1.2:
Таблица 1.2
Расчет фактора эквивалентности
Частица | Фактор эквивалентности | Пример | |
В реакциях обмена | Элемент |
где В(Э) – валентность элемента |
|
Простое вещество |
где n(Э) – число атомов элемента,В(Э) – валентность элемента | fЭ(H2) = 1/(2∙1) = 1/2; fЭ(O2) = 1/(2∙2) = 1/4; fЭ(O3) = 1/(3∙2) = 1/6 | |
Оксид |
где n(Э) – число атомов элемента,В(Э) – валентность элемента | fЭ(Cr2O3) = 1/(2∙3) = 1/6; fЭ(H2O) = 1/(2∙1) = 1/2; fЭ(P2O5) = 1/(2∙5) = 1/10 | |
Кислота | где n(H+) – число отданных в ходе реакции ионов Н+(основность кислоты) | fЭ(H2SO4) = 1/2 (если основность кислоты в реакции равна 2), или fЭ(H2SO4) = 1/1 = 1 (если основность кислоты равна 1) | |
Основа-ние |
где n(ОH–) – число отданных в ходе реакции гидроксид-ионов (кислотность основания) | fЭ(Cu(OH)2) = 1/2(если кислотность основания в реакции равна 2)или fЭ(Cu(OH)2) = 1/1 = 1 (если кислотность основания равна 1) | |
Соль |
где n(Ме) – число атомов металла,В(Ме) – валентность металла;n(А) – число кислотных остатков,В(А) – валентность кислотного остатка | fЭ(Cr2(SO4)3) = 1/(2∙3) = 1/6(расчет по металлу) или fЭ(Cr2(SO4)3) = 1/(3∙2) = 1/6 (расчет поаниону) | |
В ОВР |
где ne– число электронов, участвующих в процессе | MnO4– + 8H+ + 5ē = Mn2+ + 4H2O fЭ(MnO4–) = 1/5 | |
а) ZnCl2(средняя соль)
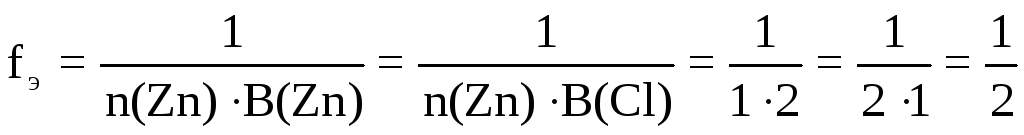 .
.
fЭ(ZnCl2) = 1/2, поэтому эквивалентомZnCl2является частица 1/2ZnCl2;
б) КНСО3(кислая соль)
 ,
,
fЭ(КНСО3) = 1, поэтому эквивалентом КНСО3является частица КНСО3;
в) (MgOH)2SO4(основная соль)
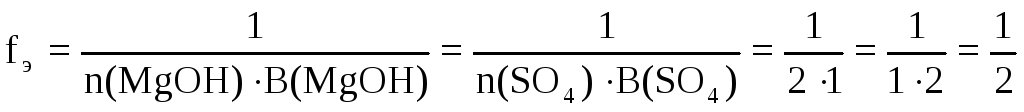 .
.
fЭ( (MgOH)2SO4 ) = 1/2, поэтому эквивалентом(MgOH)2SO4является частица 1/2(MgOH)2SO4.
Из закона эквивалентов следует, что массы (или объемы) реагирующих и образующихся веществ пропорциональны молярным массам (молярным объемам) их эквивалентов. Для любых двух веществ, связанных законом эквивалентов, можно записать:
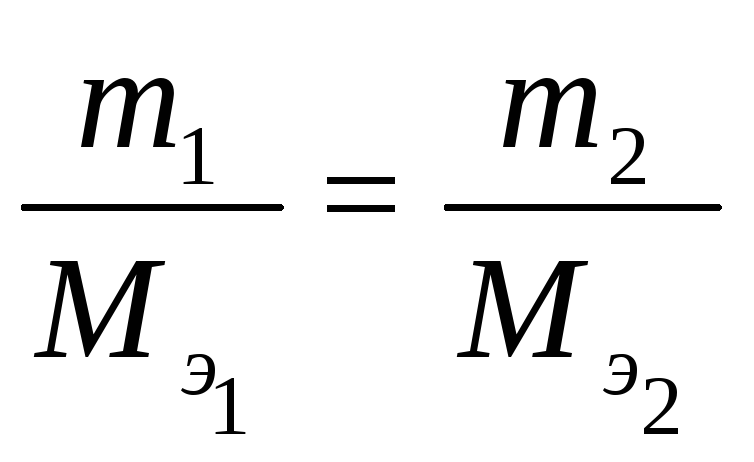 ,
,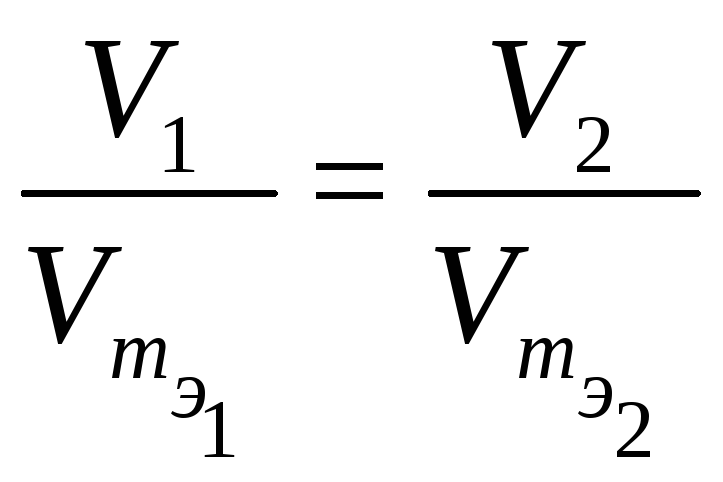 ,
,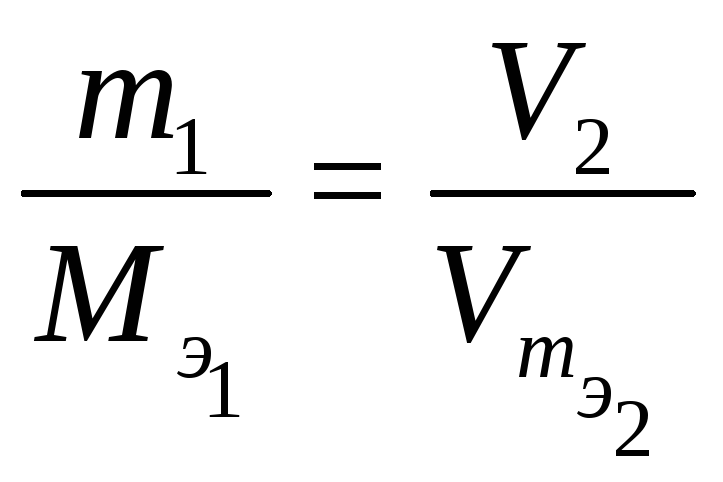 ,
(1.10)
,
(1.10)
где m1иm2 – массы реагентов и (или) продуктов реакции, г;
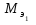 и
и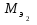 –
молярные массы эквивалентов реагентов
и (или) продуктов реакции,
г/моль;V1,V2– объемы
реагентов и (или) продуктов реакции,
дм3;
–
молярные массы эквивалентов реагентов
и (или) продуктов реакции,
г/моль;V1,V2– объемы
реагентов и (или) продуктов реакции,
дм3;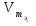 ,
, –
молярные объемы эквивалентов реагентов
и (или) продуктов реакции,
дм3/моль.
–
молярные объемы эквивалентов реагентов
и (или) продуктов реакции,
дм3/моль.
При определенных условиях тела электризуются, т.е. приобретают некоторый заряд. Существуют заряды только двух видов: отрицательные и положительные, причем это деление чисто условное. Одноименные заряды отталкиваются, а разноименные притягиваются. Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А. Перечислим свойства зарядов. 1. Существуют заряды двух видов; отрицательные и положительные. Разноименные заряды притягиваются, одноименные отталкиваются. Носителем элементарного, т.е. наименьшего, отрицательного заряда является электрон, заряд которого qe=-1,6*10-19Кл, а масса mе=9,1*10-31кг. Носителем элементарного положительного заряда является протон qр=+1,6*10-19Кл, масса mр=1,67*10-27кг. 2. Электрический заряд имеет дискретную природу. Это означает, что заряд любого тела кратен заряду электрона q=Nqe, где N – целое число. Однако мы, как правило, не замечаем дискретности заряда, так как элементарный заряд очень мал. 3.В изолированной системе, т.е. в системе, тела которой не обмениваются зарядами с внешними по отношению к ней телами, алгебраическая сумма зарядов сохраняется (закон сохранения заряда). Закон Кулона. Ш. Кулон установил, что сила взаимодействия двух точечных электрических зарядов, находящихся в вакууме, прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояний между ними и направлена вдоль прямой, соединяющей заряды. Заряженное тело, размером и формой которого можно пренебречь по сравнению с расстоянием до других заряженных тел, называется точечным зарядом. Закон Кулона справедлив только для точечных зарядов и выражается следующей формулой: F=k|q1||q2|/r2, где q1 и q2 – величины взаимодействующих зарядов, r – расстояние между ними, k – коэффициент, зависящий от выбора системы единиц. В СИ имеем k=1/40 = 9*109Н*м2/Кл2, где 0 –электрическая постоянная, равная 0 =8,85*10-12Ф/м [Ф/м=Кл2/Н*м2]. Если заряды находятся в идеально однородной среде, то сила взаимодействия между ними уменьшается в раз, — относительная диэлектрическая проницаемость среды. Тогда закон Кулона в СИ имеет вид F=(1/40)*(|q1||q2|)/r2. Если имеется система точечных зарядов, то сила, действующая на каждый из них, определяется как векторная сумма сил, действующих на данный заряд со стороны всех других зарядов системы. При этом сила взаимодействия данного заряда с каким-то конкретным зарядом рассчитывается так, как будто других зарядов нет (принцип суперпозиции). | Электрическое поле точечного заряда. Пусть в точке О находиться точечный заряд q. Вокруг него существует электрическое поле. Для исследования этого поля поместим пробный заряд qпр на расстоянии r от него. Сила кулона, действующая на заряд qпр равна F=k*(|q|* |qпр|)/r2. Напряженность электрического поля Е равна E=F/ qпр, откуда E=k*(|q|/r2)=(1/40)* (|q|/r2). Напряженность поля точечного заряда прямо пропорциональна величине заряда и обратно пропорциональна квадрату расстояний от точечного заряда до исследуемой точки. Если поле создается несколькими зарядами, то напряженность электрического поля в данной точке определяется векторной суммой напряженности полей, создаваемых в этой точке каждым зарядом в отдельности. Причем поле каждого источника считается так, как будто других источников поля нет (принцип суперпозиции полей): Е=Е1+Е2+Е3+…. Поле, создаваемое непрерывно разделенным зарядом, сложно определить, используя только принцип суперпозиции. Напряженность электрического поля. Заряды, находясь на некотором расстоянии один от другого, взаимодействуют. Это взаимодействие осуществляется посредством электрического поля. Наличие электрического поля можно обнаружить, помещая в различные точки пространства электрические заряды. Если на заряд в данной точке действует электрическая сила, то это означает, что в данной точке пространства существует электрическое поле. Силовой характеристикой электрического поля служит напряженность E. Если на находящийся в некоторой точке заряд q0 действует сила F, то напряженность электрического поля Е равна: Е=F/q0. Графически силовые поля изображают силовыми линиями. Силовая линия – это линия, касательная, в каждой точке которой совпадает с вектором напряженности электрического поля в этой точке. Если поля симметричны, то напряженность поля определяется с помощью теоремы Остроградского – Гаусса. Формулы для определения напряженности электрических полей в следующих случаях: 1. Поле равномерно заряженной бесконечной плоскости: E=2/0, где — поверхностная плотность заряда, равная =q/S, а q –заряд площадки S. 2. Поле проводящей сферы радиуса r0. Заряд q равномерно распределен по поверхности сферы. Внутри сферы при r<r0 E=0. Вне сферы при r>r0 E=|q|/40r2. | Диполь представляет собой совокупность равных по модулю и разноименных зарядов, находящихся на малом расстоянии друг от друга. При наложении внешнего электрического поля диполи ориентируются таким образом, что поле, создаваемое поляризованным зарядом, направлено в сторону, противоположную внешнему электрическому полю. Напряженность электрического поля в диэлектрике равна разности напряжений внешнего поля Е0 и поля создаваемого поляризованным зарядом Eп: Е=Ео – Еп. В неполярных диэлектриках в отсутствие внешнего поля молекулы не являются диполями, так как центры положительных и отрицательных зарядов совпадают. При наложении внешнего электрического поля молекулы растягиваются и становятся диполями, при этом поле поляризованного заряда направлено против внешнего поля. Независимо от природы диэлектрика напряженность внешнего поля в нем всегда ослаблена в раз: = Ео/Е. Относительная диэлектрическая проницаемость показывает, во сколько раз напряженность электрического поля в диэлектрики меньше, чем в вакууме. Потенциал — это энергетическая характеристика электрического поля, тогда как напряженность E – это его силовая характеристика, потому что потенциал равен потенциальной энергии, которой обладает единичный заряд в данной точке поля, а напряженность равна силе, с которой поле действует на этот единичный заряд. =Wпот/q, Здесь Wпот – потенциальная энергия заряда q в данной точке поля. Потенциал поля, созданного точечным зарядом — источником q или заряженным шаром с зарядом q, определяется формулой =q/40r. Здесь r –расстояние от точки поля с потенциалом до точечного заряда или до центра шара. Если r=R, где R – радиус шара, то по этой формуле можно определить потенциал шара на его поверхности. Работа перемещения заряда А в электрическом поле определяется выражением A=q(1-2) или А=qU. Здесь 1-2 разность потенциалов (или падение потенциала , или напряжение U) между точками с потенциалами, 1 и 2. Очевидно, что если заряд перемещают между точками с одинаковыми потенциалом, то работа перемещения заряда равна нулю. Точно так же как равна нулю и работа перемещения заряда по замкнутой траектории, т.е. когда он возвращается в исходную точку с прежним потенциалом. Действительно в этом случае А=q(1-2)=0. в однородном электростатическом поле работа перемещения заряда q может быть определена по формуле A=Eqd, (d=Scos), где E – напряженность этого поля, а d – проекция перемещения заряда q на силовую линию этого поля, угол между направлением перемещения S и вектором Е. | Ток – это направленное движение заряженных частиц. Для возникновения и существования тока необходимо, с одной стороны, наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно, а с другой – наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. В металлах носителями тока являются свободные электроны, в электролитах – отрицательные и положительные ионы, в полупроводниках – электроны и дырки, в газах – ионы и электроны. Количественной характеристикой тока является сила тока. Сила тока I определяется количеством электричества, притекающего через поперечное сечение проводника за 1 с. Если I – постоянная величина, то I=q/t, откуда следует, что за промежуток времени t через поперечное сечение проводника протекает количество электричества, равное q=It. Плотность тока – физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока: j=dI/dS. Закон Ома для однородного участка цепи. Если к проводнику приложить разность потенциалов 1-2, то по проводнику потечет электрический ток. Сила тока прямо пропорциональна разности потенциалов (напряжению) на концах проводника, т.е. (1-2)/I=const, 1-2=U, U/I=R, где R – омическое (активное) сопротивление. Сопротивление R зависит от свойств проводника и от его геометрических размеров: R=l/S, где — удельное сопротивление, т.е. сопротивление проводника длинной 1м с единичной площадью поперечного сечения, l – длинна проводника, S – площадь поперечного сечения. Последовательное и параллельное соединение сопротивлений. Сила тока, текущего через последовательно соединенные сопротивления, одинакова. Разность потенциалов А-В равна сумме падений напряжений на сопротивлениях: А-В=IR1+IR2+IR3+…+IRn, следовательно Rэкв= R1+R2+R3+…+Rn. При параллельном соединении все сопротивления находятся под одной разностью потенциалов, но токи, текущие через сопротивления будут различны. Ток, текущий через эквивалентное сопротивление, должен быть равен сумме токов, текущих через сопротивления: I1+I2+I3+…+In, следовательно (А-В)/ Rэкв=(А-В)/ R1+(А-В)/ R2+(А-В)/ R3+…+(А-В)/Rn, или 1/ Rэкв=1/ R1+1/ R2+1/ R3+…+1/ Rn. | Электродвижущая сила. Закон Ома для полной цепи. Для поддержания постоянного электрического тока в цепи необходимо подключить источник. При этом очевидно, что кулоновские силы не могут поддерживать ток, так как работа этих сил по замкнутому контуру равна нулю, а известно, что когда по цепи течет ток, выделяется тепло. Следовательно, в цепи должны действовать цепи некулоновского происхождения, работа которых по замкнутому контуру не равна нулю. Устройство, в котором такие силы возникают, называется источником. Это могут быть химические силы (гальванические элементы), силы со стороны магнитного поля и т.д. Источники тока характеризуются электродвижущей силой (эдс). Эдс – физическая величина, равная работе сторонних сил Аст по перемещению единичного положительного заряда по замкнутой цепи: E=Аст/q0. Последовательное и параллельное соединение источников тока. При последовательном соединении нескольких источников тока полная эдс батареи равна алгебраической сумме эдс всех источников, а суммарное сопротивление равно сумме сопротивлений. При параллельном подключении n источников с одинаковыми эдс и внутренними сопротивлениями суммарная эдс равна эдс одного источника, а внутреннее сопротивление rв=r/n. Если эдс источников различна, то для расчетов значения сил токов в различных участках цепи удобно пользоваться правилами Кирхгофа. Правила Кирхгофа. Первое правило Кирхгофа. Точка соединения нескольких проводников называется узлом. Алгебраическая сумма токов в узле равна нулю: I1 — I2 + I3 = 0. Токи, идущие к узлу, будем считать положительными, от узла отрицательными. Второе правило Кирхгофа. Алгебраическая сумма падений напряжений на замкнутом контуре разветвленной цепи равна алгебраической сумме эдс: I1R1 – I2R2 + I3R3 = E1 – E2 + E3. | (Закон Джоуля – Ленца). Мощность тока – работа, совершаемая за единицу времени и равная P=A/t=IU=I2R=U2/R. Полная мощность P0, развиваемая источником, идет на выделение тепла во внешнем и внутреннем сопротивлениях и равна P0=I2(R+r)=IE=E2(R+r). Мощность, выделяемая во внешнем сопротивлении, называется полезной мощностью и равна Pполез= E2R/(R+r)2. Мощность, выделяемая во внутреннем сопротивлении, использована быть не может и называется теряемой мощностью Ртер=I2r= E2 r /(R+r)2. Тепловое действие тока. Если через сопротивление R течет ток I, то кулоновские силы совершают положительную работу: A=qU=IUt, где q – количества электричества, протекшее через поперечное сечение проводника за промежуток времени t: q=It. При этом происходит выделение тепла Q. Очевидно, что Q=A, или Q=IUt=I2Rt=(U2/R)/t. Магнитное поле. Вокруг проводников с током и постоянных магнитов существует магнитное поле. Оно возникает вокруг любого направленно движущегося электрического заряда, а также при наличии переменного во времени электрического поля. Магнитное поле можно обнаружить, помещая в него магнитные стрелки или проводники с током, так как оно оказывает на них ориентированное действие. Магнитное поле можно исследовать с помощью замкнутого контура с током. Геометрические размеры контура должны быть настолько малы, чтобы в его пределах поле не изменялось. На контур в магнитном поле действует механический вращательный момент. Отношение максимального вращательного момента Ммах к произведению силы тока I, текущего по контуру, и площади поверхности S, охватываемой этим контуром, величина постоянная: Ммах/IS=const. Этим отношением определяется основная силовая характеристика магнитного поля – вектор магнитной индукции В. Произведение IS называется магнитным моментом контура с током Pм=IS. Направление магнитного момента совпадает с направлением индукции магнитного поля, создаваемого в центре контура текущим по нему током. Направление вектора В определяется по правилу: если направление вращение винта совпадает с направлением тока в контуре, то его поступательное движение укажет направление индукции магнитного поля и, соответственно, магнитного момента (следствие правила правого винта). Итак, вектор магнитной индукции определяется максимальным вращательным моментом, действующим на контур с током, магнитный момент которого равен единице: B= Ммах/Pм. Магнитная индукция измеряется в теслах. Индукция магнитного поля – экспериментально измеряемая величина, зависящая от токов, создающих поле, и свойств среды, в которой, в которой оно создано. | Закон Ампера. Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsin, где — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера FА IBlsin. Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для FА, получим FА= qnvSBlsin, где nsl=N – общее число частиц, создающих ток. Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде dB = µ0µ / 4 * I [dl, r] / r3, где dl – вектор, по модулю равный длине элемента проводника и совпадающий по направлению с током, r – радиус-вектор. Направление dB перпендикулярно dl и r. Оно может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе. Наряду с вектором магнитной индукции В вводится еще одна силовая характеристика магнитного поля – напряженность магнитного поля Н. Вектор В и Н связаны соотношением B=0Н. Напряженность магнитного поля измеряется в амперах на метр (А/м), 0 — магнитная постоянная, равная 4*10-7Гн/м, — относительная магнитная проницаемость среды, показывающая, во сколько раз индукция магнитного поля в данной среде больше или меньше, чем в вакууме. Напряженность магнитного поля определяется только конфигурацией проводников, создающих поле, и токами, текущими по этим проводникам, т.е. макроисточниками поля, и не зависит от магнитных свойств среды, в которой поле создается. | Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной µ0 на алгебраическую сумму токов, охватываемых этим контуром: B dl = B1 dl = µ0 lk, где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Выражение выше справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи. Магнитный поток. Магнитным потоком Ф через некоторую поверхность S называется скалярная величина, равная произведению модуля вектора магнитной индукции на площадь этой поверхности и косинус угла между нормалью n к ней и направлением вектора магнитной индукции B: Ф=|B|Scos. Если магнитное поле неоднородно, то поверхность S разбивается на элементарные площадки S в пределах каждой из которых поле можно считать однородным. Тогда полный поток через эту поверхность равен сумме потоков вектора магнитной индукции через элементарные площадки. В СИ единицей магнитного потока является 1 вебер (Вб) – магнитный поток через поверхность 1 м2, расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл: 1Вб=1В*с. Теорема Гаусса для магнитного поля: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: B dS = Bn dS = 0. Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Сила Лоренца. Как показывают опыты, магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой F = Q [vB], где B – индукция магнитного поля, в котором заряд движется. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор B, а четыре вытянутых пальца направить вдоль вектора v, то большой палец укажет направление силы. Магнитное поле не действует на покоящийся заряд а только на движущийся. Сила Лоренца изменяет только направление скорости, не меняя ее модуля. | Электромагнитная индукция. Возникновение эдс в замкнутом проводящем контуре при изменении магнитного потока через эту поверхность, ограниченную этим контуром, называется электромагнитной индукцией. Также эдс индукции, а, следовательно, разность потенциалов возникает на концах разомкнутого проводника, движущегося в магнитном поле и пересекающего силовые линии поля. Опыт показывает, что Эдс индукции не зависит от причин изменения магнитного потока, а определяется скоростью его изменения. Согласно закону Фарадея, эдс индукции определяется как предел отношения изменения магнитного потока Ф к промежутку времени t к нулю, или производной по времени магнитного потока Eинд=limt—>0 Ф/t= -Ф’. Явление самоиндукции. Ток, текущий по проводящему контуру, создает вокруг него магнитное поле. Магнитный поток Ф, сцепленный с контуром, прямопропорционален силе тока в этом контуре: Ф=LI, где L – индуктивность контура. Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс – эдс самоиндукции. Самоиндукция является частным случаем явления электромагнитной индукции. Если I изменяется со временем по линейному закону, то Ecи = — (Ф/t)= — L(I/t), где I/t – скорость изменения силы тока. Эта формула справедлива только при L=const. Индуктивность – величина, численно равная эдс самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении тока на 1А за 1с возникает эдс самоиндукции 1В. Эта единица называется Генри (Гн): 1Гн=1В*с/А. Энергия магнитного поля, созданного током, по закону сохранения энергии равна энергии, затраченной источником на создание тока. При замыкании цепи ток в цепи вследствие самоиндукции не сразу достигнет максимального значения I0, а постепенно. При размыкании цепи ток также исчезает не сразу, а постепенно, при этом в проводнике выделяется тепло. Так как цепь разомкнута, то это тепло не может выделятся за счет работы источника, а может быть только следствием энергии, накопленной в соленоиде, энергии магнитного поля. Энергия магнитного поля соленоида, когда ток полностью прекратиться, переходит в джоулево тепло. Выражение для магнитного поля соленоида имеет вид: Wм=LI2/2. |




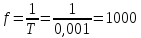
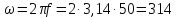
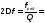
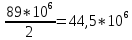
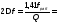
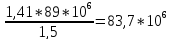
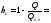
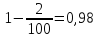
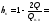
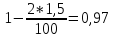
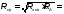
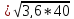 =12
Ом
=12
Ом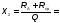
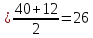
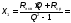


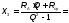
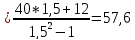
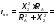

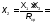
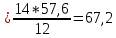
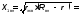
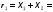
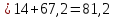
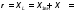
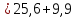 i
i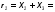
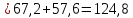
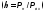

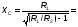
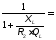

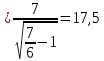
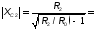
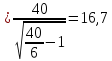
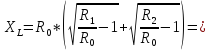
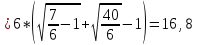
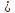
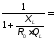
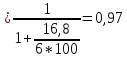
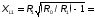
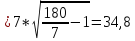
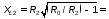
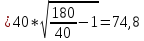
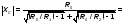
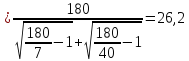
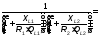
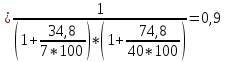
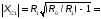
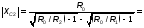
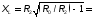
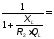
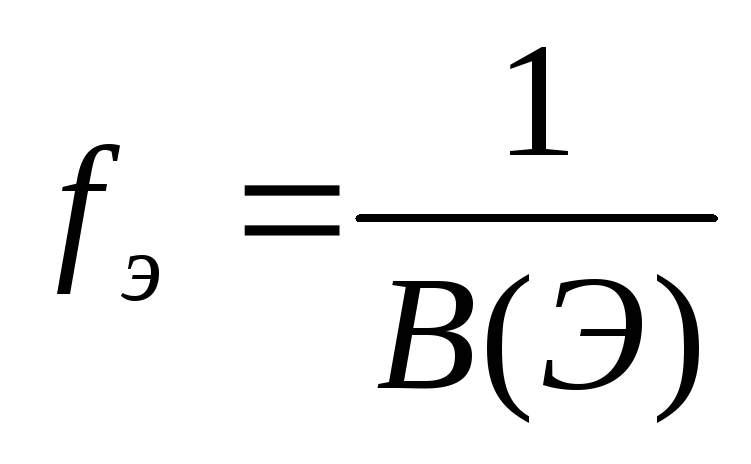 ,
,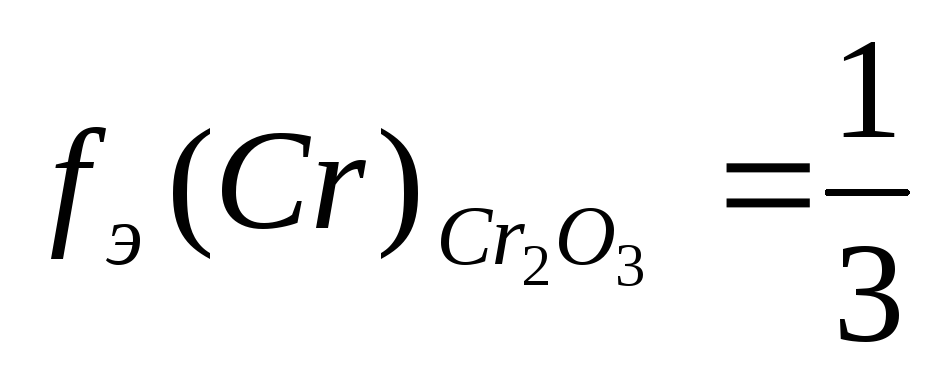
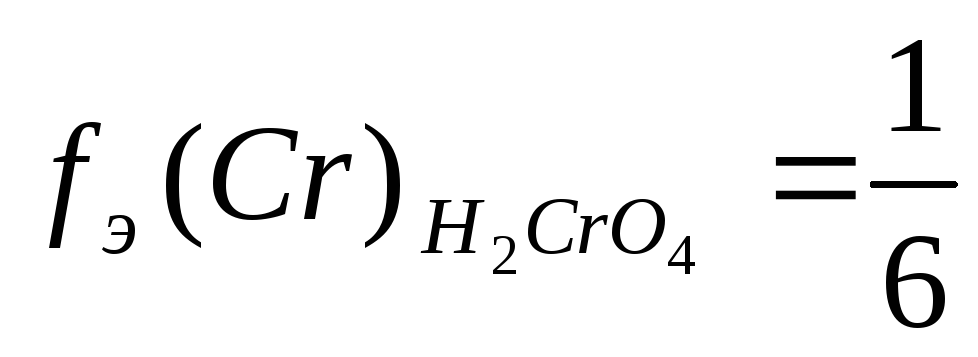
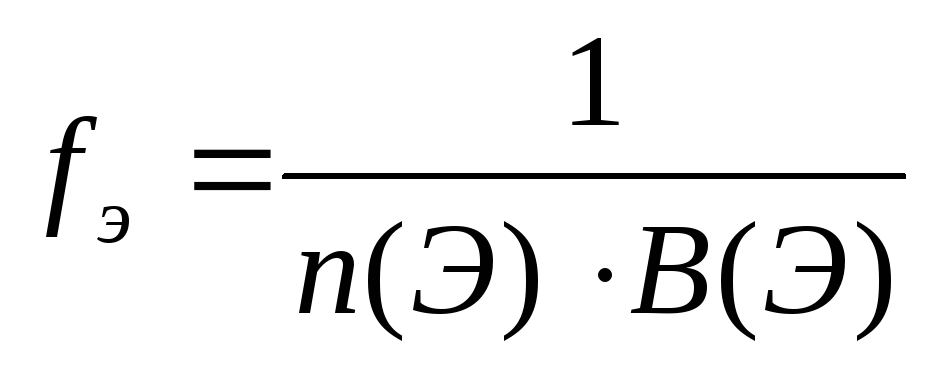 ,
,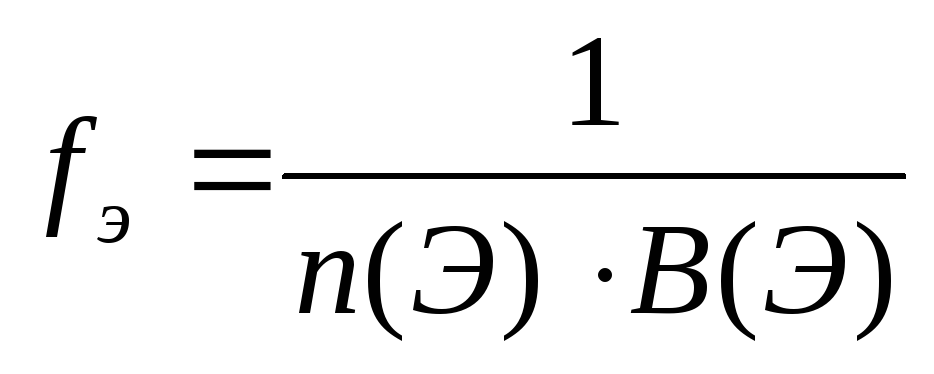 ,
,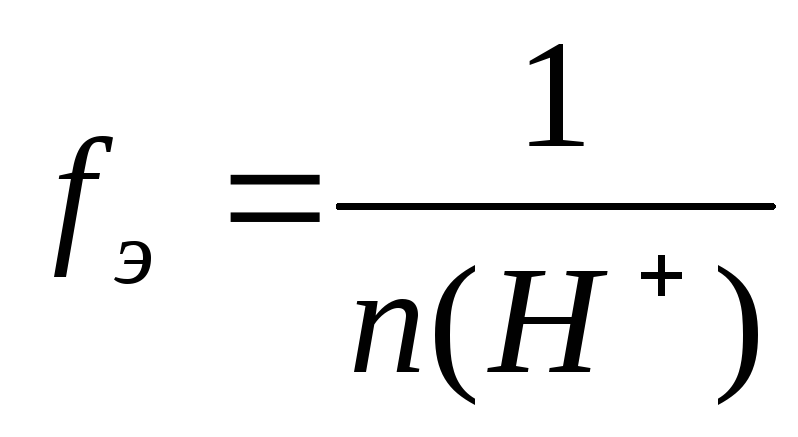 ,
,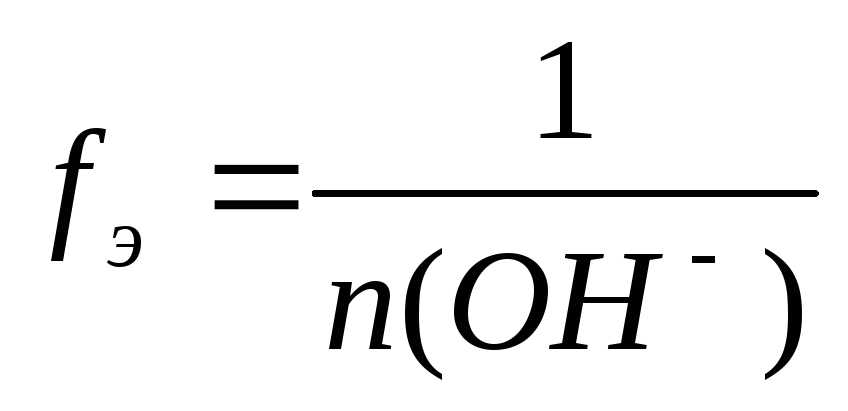 ,
,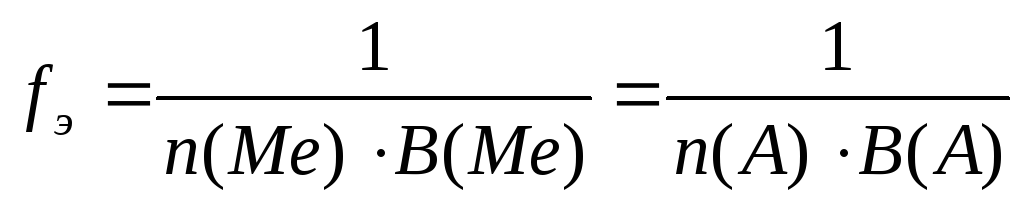 ,
,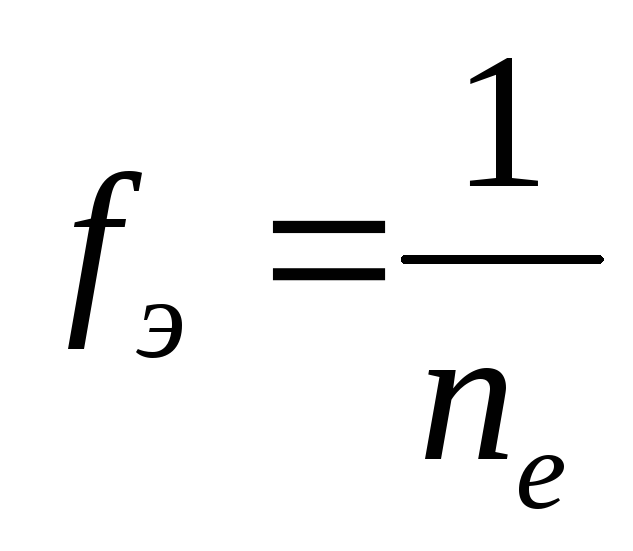 ,
,