Решение задач на потенциалы — Учебник по электродинамике

Задача 1. При перемещении заряда между точками с разностью потенциалов 1 кВ электрическое поле совершило работу 40 мкДж. Чему равен заряд?

Решение: решаем устно. Из формулы A₁₂ = q(φ₂ − φ₁) получаем, что q = A / (φ₂ − φ₁) = 40 · 10 ^{− 6} / 10³ = 4 · 10 ^{− 8} Кл.

Ответ: 4 · 10 ^{− 8} Кл.

Задача 2. В однородном электрическом поле напряженностью 60 кВ/м переместили заряд 5 нКл. Перемещение, равное по модулю 20 см, образует угол 60⁰ с направлением силовой линии. Найти работу поля, изменение потенциальной энергии взаимодействия заряда и поля и напряжение между начальной и конечной точками перемещения. Дать ответы на те же вопросы для случая перемещения отрицательного заряда.

Решение: работу поля по перемещению заряда можно вычислить по формуле 

A = Eqlcos α = 60 · 10³ · 5 · 10 ^{− 9} · 0. 2 · cos 60⁰ = 3 · 10 ^{− 5} Дж. Изменение потенциальной энергии в данном случае равно совершенной работе, следовательно: ΔW = —A = —3 · 10 ^{− 5} Дж (потенциальная энергия уменьшилась). Напряжение определяется через напряженность поля по формуле: U = Ed = Elcos α, поскольку в данном случае в заряд перемещали под углом к направлению силовых линий. Итак, U = 60 · 10³ · 0.2 · cos 60⁰ = 6000 В. В случае с отрицательным зарядом значения 

A и ΔW просто изменят знак.

Ответ: 3 · 10 ^{− 5} Дж, —3 · 10 ^{− 5} Дж, 6000 В, -3 · 10 ^{− 5} Дж, 3 · 10 ^{− 5} Дж, 6000 В.

Задача 3. Электрон переместился в ускоряющем электрическом поле из точки с потенциалом 200 В в точку с потенциалом 300 В. Найти кинетическую энергию электрона, изменение его потенциальной энергии и приобретенную скорость. Начальную скорость электрона считать равной нулю.

Решение: работу, которую совершило поле при перемещении электрона, находим следующим образом: 

A₁₂ = q(φ₂ − φ₁) = 1.6 · 10^-19 · (300 — 200) = 1.6 · 10^-17 Дж. Значит изменение потенциальной энергии электрона в поле равно: ΔW = —A = —1.6 · 10 ^{− 17} Дж. Это уменьшение компенсируется увеличением его кинетической энергии на такое же значение, что следует из закона сохранения энергии: E = 1.6 · 10 ^{− 17} Дж. Поскольку E = mυ² / 2, то υ = √(2E / m) = √(2 · 1.6 · 10 ^{− 17}/9.1 · 10 ^{− 31}) = 6 Мм/с.

Ответ: 1.6 · 10 ^{− 5} Дж, —1.6 · 10 

− 5 Дж, 6 Мм/с.

Задача 4. Какую разность потенциалов должен пройти электрон, чтобы его скорость увеличилась от 10 до 30 Мм/с?

Решение: изменение кинетической энергии электрона при прохождении такой разности потенциалов можно найти из соотношения: ΔE = mυ₂² / 2 — mυ₁² / 2 = 8 / 18  · 9.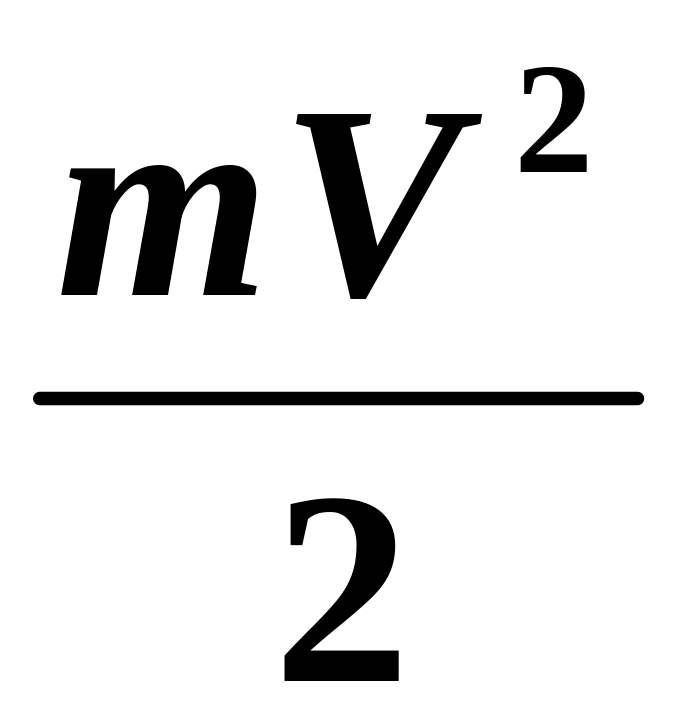 1 · 10 ^{− 31} · (30 · 10 ⁶)² = 3.6 · 10 ^{− 16} Дж. Это же изменение по закону сохранения энергии равняется работе, которую совершило при этом электрическое поле:

E = —A = -3.6 · 10 ^{− 16} Дж. Используя соотношение, записанное в самом начале, получаем: φ₂ − φ₁ = A / q = -3.6 · 10 ^{− 16}/ 1.6 · 10^-19 = -2250 В.

Ответ: -2250 В.

Электричество и магнетизм

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

(5.6)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле 

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

(5.7)

из которого легко получить выражение для угловой скорости частицы

(5.8)

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

(5. 9)

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

(5.10)

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками 

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно. 

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью  и вращения по окружности с угловой скоростью  . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

(5.11)

 

Конспект и презентация «Потенциал и разность потенциалов электростатического поля.

Решение задач»

Тема: «Потенциал и разность потенциалов. Решение задач»

Цели урока:

Дидактическая: обучить навыкам нахождения работы по перемещению заряда в электрическом поле, показать взаимосвязь между напряжённостью и разностью потенциалов, добиться овладения и закрепления качества знаний, дать практику в решении задач.

Развивающая: развивать у учащихся логику мышления при решении задач различного типа, организованность, умение владеть собой и преодолевать трудности.

Воспитательная: сформировать устойчивое осознанное отношение к изучаемому материалу, формировать привычку оказывать помощь товарищам в учении, умения ставить цели и стремления добиваться их.
Тип урока:

закрепление новых знаний

Ход урока

1. Организационный момент

2. Актуализация опорных знаний

— Заблудившиеся величины (соединить стрелками название физических величин с соответствующими формулами). Приложение1

— Выполнить и описать опыт (Электрофорная машина, султанчик и гильза).

— Подумай! Сообрази! (Устный ответ.) Какого знака будут заряды на электрометрах, если убрать металлическую спицу?

Останется ли электроскоп заряжённым, если из-под колокола выкачать воздух?

Объявление темы урока и постановка целей урока учениками самостоятельно.

(Д/з§ 94, тест стр.313)

Видеофрагмент о разности потенциалов.

Для начала вспомним характеристику поля – энергетическую.  Потенциал – физическая величина, показывающая отношение потенциальной энергии заряда в некоторой точке пространства к величине этого заряда:

Так как потенциальная энергия заряда прямо пропорциональна величине заряда, то потенциал от величины заряда не зависит:

Единица измерения потенциала – вольт:

Потенциал некоторой точки пространства можно определить как работу электрического поля по переносу единичного заряда из бесконечности в эту точку. В общем же виде связь потенциала с работой можно задать через ввод электрического напряжения:

Полученная зависимость справедлива вдоль некоторой силовой линии, и здесь – расстояние между двумя точками на одной силовой линии.

Зависимость потенциала поля точечного заряда от расстояния имеет похожий вид с аналогичной зависимостью для напряженности, однако убывает медленнее – не пропорционально квадрату, а пропорционально первой степени:

Так как при перемещении положительного заряда в направлении напряженности электростатическое поле совершает положительную работу, то φ₁ больше φ₂. При перемещении заряда под углом 90⁰ к силовым линиям электрическое поле не совершает работы, т.к. сила перпендикулярна перемещению.

Нам уже известно, что графически напряженность изображается в виде силовых линий, направленных от положительных зарядов к отрицательным. Потенциалы можно также графически отобразить в виде эквипотенциальных поверхностей.

 Эквипотенциальная поверхность – поверхность, каждая точка которой имеет одинаковый потенциал.

Как следует из связи работы и потенциалов:

при переносе заряда вдоль эквипотенциальных поверхностей электрическое поле работы не совершает, так как .

Работа при ненулевой силе равна нулю только в том случае, если вектор силы перпендикулярен вектору перемещения. Из этого следует, что линии напряженности перпендикулярны эквипотенциальным поверхностям. Примерами эквипотенциальных поверхностей служат сферы для поля точечного заряда и параллельные плоскости для однородных полей (рис. 3).

3.Закрепление изученного материала

Решение задач на уроке:

1. .Какую работу совершит поле при перемещении заряда 20 нКл из точки с потенциалом 700 В в точку с потенциалом 200 В?

2. Какую скорость приобретает электрон, пролетевший ускоряющую разность потенциалов 10 кВ?

3 Два заряда по 6 нКл находятся на расстоянии 100 см друг от друга. Какую работу надо совершить, чтобы сблизить их до расстояния 50 см?

4.Физкультминутка (Для шеи, и рук)

5.Самостоятельая работа.(Приложение 2)

Уровень А.

1.Электрон перемещается в поле, силовые линии которого показаны на рис. Выберите правильное утверждение.

А. При перемещении электрона из точки 2 в точку 3 электрическое поле совершает положительную работу.

Б. При перемещении электрона из точки 1 в точку 2 электрическое поле совершает отрицательную работу.

В. При перемещении электрона по траектории 1 -2-3-1 электрическое поле совершает отрицательную работу.

2. Положительно заряженный шарик перемещают из точки 1 в точку 2 в поле заряда Q. Выберите правильное утверждение.

А. Потенциальная энергия взаимодействия шарика с зарядом Q остается неизменной.

Б.При перемещении шарика электрическое поле совершает положительную работу.

В. Шарик притягивается к заряду Q.

Уровень В.

1.Какую работу совершает поле при перемещении заряда 5нКл из точки с потенциалом 300 В в точку с потенциалом 100В?(1 мкДж)

2. Заряд ядра атома цинка равен 4,8*10^-18 Кл. Определите потенциал электрического поля, созданного ядром атома цинка, на расстоянии 10 нм.(4,2В)

Уровень С.

1.Из ядра атома радия со скоростью 2*10⁷ м/с вылетает α-частица массой 6,67*10^-27 кг. Определите энергию частицы и разность потециалов, которая бы обеспечила частице такую энергию. Заряд частицы 3,2*10^-19 Кл.(1.33*10^-12 Дж, 4*10⁶ В)

2. Электрон вылетает из точки, потенциал которой 450В, со скоростью 190м/с. Какую скорость он будет иметь в точке с потенциалом 475В?(3*10⁶ м/с)

6.Подведение итогов

Учащиеся заполяют таблицу(Самооценка)

Актуализация

(1б)

Уровень А

(1б)

Уровень В

(по 1б)

Уровень С (по 2б)

7. Рефлексия. На ладошках учащиеся пишут

Что было понятно? Что не понятно? Что понравилось?

8. Домашнее задание: § 94, тест стр.313

5} \; {\ rm {м / с}} {/ экв}.

Электрическое поле между параллельными пластинами составляет,

{eq} \ begin {align *} E & = \ dfrac {{V ‘}} {d} \\ E & = \ dfrac {{250 \; {\ rm {V}}}} {d} \ end {выровнять *} {/ eq}

а.

Сила, действующая на протон за счет электрического поля, равна,

{eq} \ begin {align *} {F_E} & = eE \\ & = e \ left ({\ dfrac {{250 \; {\ rm {V}}}} {d}} \ right) \ end {выровнять *} {/ eq}

Подставьте значение заряда в приведенное выше уравнение.{- 17}} \; {\ rm {N}}}} \\ d & = 0,0999 \; {\ rm {m}} \\ d & \ приблизительно 0,10 \; {\ rm {m}} \ end {выровнять *} {/ eq}

Здесь мы берем расстояние в метрах, потому что все единицы измерения стандартные.

Таким образом, расстояние между пластинами равно {eq} d \ приблизительно 0,10 \; {\ rm {m}} {/ экв}.

г.

Если убрать электрическое поле, протон будет двигаться по круговой траектории за счет магнитного поля. Радиус круговой орбиты задается как

{eq} R = \ dfrac {{{m_p} v}} {{eB}} {/ eq}

Подставьте указанные значения в приведенное выше уравнение.{- 22}} \; {\ rm {C}} \ cdot {\ rm {T}}}} \\ R & = 2.395 \; {\ rm {m}} \\ R & \ приблизительно 2,4 \; {\ rm {m}} \ end {выровнять *} {/ eq}

Таким образом, в отсутствие электрического поля протон движется по круговой орбите с радиусом кривизны {eq} R \ приблизительно 2,4 \; {\ rm {m}} {/ экв}.

3.2.3. Скорость и энергия в электрических полях

К концу этого раздела вы должны уметь …

• Рассчитывать работу, проделанную в электрическом поле.
• Используйте закон сохранения энергии, чтобы найти скорость частиц, движущихся в электрическом поле.
• Объясните в терминах сил, почему частица ускоряется или замедляется в электрическом поле.

Скорость и энергия в электрических полях

Ранее мы видели, что заряженная частица испытывает несбалансированную силу, если ее поместить в электрическое поле.

Пример:

Если отрицательный заряд помещен в точку A, электрическое поле заставит его ускоряться к точке B.

В позиции A энергия частицы равна ее электрической потенциальной энергии.

В позиции B частица прошла через всю разность потенциалов 2 кВ. В этот момент вся его энергия превратилась в кинетическую энергию.

За счет сохранения энергии полученная кинетическая энергия равна потерянной потенциальной энергии. Это дает;

Отсюда мы можем вычислить скорость известной частицы массы m и заряда Q, движущейся в электрическом поле с разностью потенциалов V.

Скорость не зависит от расстояния между пластинами.Если расстояние уменьшится вдвое или вдвое, конечная скорость останется прежней.

Пример:

На схеме ниже показаны основные характеристики протонного ускорителя. Он заключен в откачанный контейнер.

Протоны, выпущенные из источника протонов, начинаются из состояния покоя в точке P. Между P и Q поддерживается разность потенциалов 200 кВ.

Вычислить: работу, совершаемую при перемещении протона из точки P в Q, и скорость протона в точке Q :

Н.B.

Частица будет испытывать силу только в том случае, если у нее есть электрический заряд. Следовательно, нейтроны и все лептоны не будут взаимодействовать с электрическим полем.

Теперь вы закончили этот раздел, проверьте себя. Можете ли вы …

• Рассчитать работу, проделанную в электрическом поле?
• Использовать сохранение энергии, чтобы найти скорость частиц, движущихся в электрическом поле?
• Объясните в терминах сил, почему частица ускоряется или замедляется в электрическом поле?

Движение электрона в электрическом поле

Пример 5.2: Движение электрона в электрическом поле
Далее: Пример 5.3: Требуемый электрический потенциал Up: Электрический потенциал Предыдущий: Пример 5.1: Начисление в Вопрос: Электрон в телевизоре ускоряется от катода к экран через разность потенциалов +1000 В. Экран находится на расстоянии 35 мм от катод. Каково чистое изменение потенциальной энергии электрона? в процессе разгона? Сколько работы совершает электрическое поле для ускорения электрон? Какова скорость электрона при ударе экран?

Решение: Давай назовем катодную точку и экранную точку.Мы говорят, что разность потенциалов между точками и составляет +1000 В, так

По определению, разница в электрической потенциальной энергии некоторого заряда при баллов и является произведением заряда и разница в электрическом потенциале между этими точками. Таким образом,

поскольку для электрона. Обратите внимание, что потенциальная энергия электрона уменьшается поскольку он ускоряется к экрану. Как мы видели, электрический потенциальная энергия заряда фактически удерживается в окружающем электрическом поле.Таким образом, уменьшение потенциальной энергии заряда соответствует уменьшению энергия поля. В этом случае энергия поле уменьшается, потому что оно действительно работает на заряде. Понятно, что проделанная работа (, т.е. , потеря энергии) полем равняется уменьшению потенциальной энергии заряда,

Таким образом,

Полная энергия электрона состоит из двух компонентов — электрического потенциальная энергия и кинетическая энергия.Таким образом,

Конечно,

где кг — масса электрона, а его скорость. По закону сохранения энергии является константой движения, поэтому

Другими словами, уменьшение электрической потенциальной энергии электрона, как он ускоряется по направлению к экрану, компенсируется соответствующим увеличением его кинетической энергия. Если предположить, что электрон стартует из состояния покоя (, т. е. ), отсюда следует, что

или

Обратите внимание, что расстояние между катодом и экраном в этом случае несущественно. проблема.Конечная скорость электрона полностью определяется его заряд, его начальная скорость, и разность потенциалов, через которую он ускоряется.

---

Далее: Пример 5.3: Требуемый электрический потенциал Up: Электрический потенциал Предыдущий: Пример 5.1: Начисление в

Ричард Фицпатрик 2007-07-14

Какова скорость электрона с длиной волны «0,1 нм»? Если бы этот электрон был доведен до этой скорости из состояния покоя, какая разность потенциалов была необходима?

#v = 7.(-) #.

Теперь представьте, что # «1 В» cdot «C» = «1 Дж» #, это единица энергии , а электрон-вольт (# «эВ» #, также единица энергии ) определение выполненной работы в # «J» #, необходимое для проталкивания одного электрона через разность потенциалов # «1 В» #.

Работа выполнена , # W #, на массе на (не на) расстоянии # Deltavecx #:

#W = vecFDeltavecx #

Отсюда следует (отчасти) аналогично соотношение:

#W = нижняя скоба (верхняя скоба ((1.(-19) отменить «J») #

# = ## ul «150,43 эВ» #

И по определению, мы, таким образом, имеем, что величина разности потенциалов была:

# цвет (синий) (| V | = ul «150,43 В») #.

Физика для науки и техники II

6.13 Возможная разница между двумя точками в цепи от Office of Academic Technologies на Vimeo.

6.13 Разница потенциалов между двумя точками в цепи

Рассмотрим простую схему, которая состоит из источника питания, электромагнитной силы, скажем, батареи, так что разность потенциалов между ее выводами равна 10 вольт. Давайте подключим это к резистору с сопротивлением 5 Ом. А еще давайте воспользуемся амперметром, который измеряет ток в цепи. Как только мы включим переключатель, конечно, по закону Ома, поскольку R равно ε по сравнению с i , мы будем ожидать ток в 10 вольт, разделенных на 5 Ом, что равно 2 амперам, для протекания цепи.

Но на самом деле значение амперметра, которое мы собираемся считывать, будет немного меньше 2 ампер, что указывает на наличие другого сопротивления в цепи.Это сопротивление в основном возникает через то, что мы называем внутренним сопротивлением батареи. И он, как правило, представлен этим символом. И поэтому наш блок ЭДС будет состоять из этого внутреннего сопротивления.

Теперь, когда ток не течет через источник питания, другими словами, когда ЭДС источника питания не накачивает заряды, тогда разность потенциалов между его выводами составляет 10 вольт. Но всякий раз, когда мы вводим батарею в схему, подключая ее к концам сопротивления, R , тогда мы будем вводить внутреннее сопротивление батареи, подключенной последовательно, к сопротивлению R . Другими словами, эквивалент R ( R eq ) в этой схеме будет равен маленькому r плюс большому R .

Итак, в идеальной схеме или в случае идеальной батареи, всякий раз, когда мы включаем переключатель, мы будем иметь ток ε через R , протекающий по цепи. Но в этом случае i ‘ снова будет равно разности потенциалов на резисторе, равной ε , деленной на общее сопротивление цепи, и это будет R плюс . r .Поскольку знаменатель становится больше, ток, потребляемый от источника питания или от электродвижущей силы, будет относительно меньше по сравнению с идеальным корпусом батареи. Итак, если текущий i проходит через эту систему, то i ‘ будет проходить через эту систему.

Отсюда, допустим, мы хотим определить разность потенциалов между любыми двумя точками в данной электрической цепи. Допустим, нас интересует разность потенциалов между этими двумя точками.Чтобы сделать это, мы начнем с первой точки и проследим изменение потенциала по мере продвижения к другой точке по любой из возможных ветвей, другими словами, пройдя этот путь или пройдя через этот путь. филиал.

Допустим, мы начинаем с точки a , поэтому она имеет потенциал V a . А затем сначала пройдите по этому пути, и ток течет от положительного к отрицательному концу. Итак, проходя через эту ветвь, мы пересечем сопротивление R в том же направлении, что и направление тока.Следовательно, потенциал уменьшится на минус и раз на R . Затем мы, в конце концов, придем к другому вопросу, который нас интересует.

Следовательно, этот общий потенциал должен быть равен потенциалу в точке b . Итак, отсюда мы можем сказать, что точка разности потенциалов a и точка b , V a минус V b , будет равна i умножить на R . Или мы можем выразить это как V a минус V b равно i в явной форме.Фактически, в этом случае мы называем это i ′, ε более R плюс r умноженное на R .

Теперь, если мы выберем другой путь, допустим, это путь 1, который следует через эту ветвь, и если мы выберем другой путь, идущий от a к b вдоль второй доступной ветви, тогда мы можем запишите наши уравнения как — скажем, это путь 2. Для пути 2, начиная с первой точки, у нас есть V a , и теперь мы движемся в направлении, противоположном направлению потока тока. .Следовательно, потенциал увеличится в – раз внутреннего сопротивления –.

А теперь пересечем ЭДС в направлении, противоположном направлению стрелки ЭДС, от положительного к отрицательному. Следовательно, потенциал уменьшится на ε вольт. Теперь мы подошли к другому пункту. Следовательно, некоторые изменения потенциала должны быть равны потенциалу в точке b . Переставив это выражение, мы получим V a минус V b будет равно ε минус i умноженное на r .

Опять же, если вы запишете ток в его явной форме, у нас будет ε минус ε на R плюс r умножить на r . Общий знаменатель в правой части даст нам ε умножить на R плюс ε умножить на r минус ε умножить на r , разделенное на R плюс r . ε раз меньше r отменит, и это даст нам ε умножить на R по сравнению с R плюс r .Таким образом, вы можете легко увидеть, что мы имеем точно такой же результат, как разность потенциалов между точкой a и точкой b , перейдя от точки a к точке b двумя разными способами. И это общая процедура, которую мы применяем, чтобы иметь возможность вычислить разность потенциалов между любыми двумя точками в данной электрической цепи.

Итак, если мы сформулируем здесь процедуру, мы можем сказать, что найти разность потенциалов между любыми двумя точками в цепи, начать с одной точки и пройти по цепи к другой точке, следуя любому пути, и добавить, алгебраически, изменения в потенциале, с которым вы столкнетесь.

Давайте вернемся к нашей цепи и разрежем ее прямо перед батареей здесь, в точке b . Если мы это сделаем, это будет выглядеть так. Начнем с точки b , и вот батарея, место действия ЭДС или электродвижущей силы. Его внутреннее сопротивление, r , затем движется дальше, сопротивление R и вот точка a . И в конечном итоге мы снова получим точку b прямо здесь.

Что ж, если мы посмотрим на изменение потенциала по мере того, как мы начнем от этого конца к другому концу этой цепи, я помечу каждый компонент вдоль этой ветви.В точке b у нас есть потенциал V b , и этот потенциал не меняется, пока мы не закончим с электродвижущей силой. И этот электродвигатель, перекачивая свои заряды с отрицательной клеммы на положительную, приведет к увеличению потенциала до и вольт. И тогда потенциал будет оставаться на этом уровне, пока заряды не пройдут через внутреннее сопротивление электродвижущей силы. Это внутреннее сопротивление вызовет уменьшение потенциала в – раз, –.

Итак, вы знаете, что ток течет от положительного конца к отрицательному по этой ветви. Как только заряды выходят из части внутреннего сопротивления, потенциал остается на этом уровне, который имеет тот же потенциал, что и эта точка a здесь. Затем, когда заряды входят в это сопротивление, R , тогда потенциал уменьшается еще дальше — i раз R , i раз больше R , вплоть до потенциала V b .Вот как будет изменяться потенциал, когда мы будем двигаться в направлении тока по этой цепи. Опять же, единицы здесь представляют собой настоящую батарею. А если пренебречь внутренним сопротивлением батареи, то мы называем эту батарею «идеальной батареей».

Резистивный электрический поток — закон Ома

Движущийся заряд ощущает сопротивление

Когда электрический заряд движется через материал, он обычно испытывает сопротивление, которое имеет тенденцию противодействовать движению, возникающее из-за их взаимодействия с другими зарядами в материале, движущемся термически.*

Исходя из нашего опыта работы с силами сопротивления, мы не можем быть уверены в том, что сопротивление, которое испытывает движущийся заряд, не зависит от скорости (например, трение), пропорционально скорости (например, вязкости) или пропорционально квадрату скорости (например, сопротивление ). Во многих ситуациях кажется, что сила сопротивления, которую ощущает движущийся заряд, более вязкоподобна — пропорциональна скорости. Мы увидим, что предположение о том, на что похоже сопротивление, эквивалентно закону Ома — соотношению, которое очень хорошо выполняется для многих систем.{резистивный} = -bv $$

Знак минус означает, что сила направлена ​​в противоположном направлении от скорости.

Что поддерживает это?

Чтобы заряд двигался через резистивную среду, нам нужна сила, уравновешивающая сопротивление. Поскольку мы хотим перемещать заряды, наиболее естественно рассматривать электрическую силу как силу, проталкивающую их через резистивную среду.

Чтобы заряд $ q $ двигался с постоянной скоростью через резистивную среду, нам нужна электрическая сила $ qE $.{net} = qE — bv = 0 $$

или

$$ qE = bv. $$

Закон Ома

Теперь рассмотрим цилиндр, состоящий, скажем, из ионов и электронов, на который мы помещаем электрическое поле. Ионы будут реагировать, возможно, в 120000 раз меньше, чем электроны (отношение массы иона меди к массе электрона), поэтому мы можем игнорировать движение ионов.

Рассмотрим цилиндр заряда с площадью поперечного сечения A и длиной $ L $ с носителями заряда $ q $, имеющими плотность $ n $.Чтобы получить поле E в объеме, наложим разность потенциалов $ ΔV $. Это даст среднее поле E

$$ E = ΔV / L. $$

Уравновешивание наших сил дает

$$ qE = bv $$

$$ qΔV / L = bv $$

Теперь мы хотим избавиться от $ v $ в пользу текущего, $ I $ . Напомним, что ток определяется как (см. Страницу, количественное определение электрического тока) количеством заряда, пересекающего область в секунду, или

$$ I = \ frac {\ mathrm {количество \; из \; заряда \; пересечение \; площадь \; в \; a \; время} Δt} {Δt} $$

Поскольку $ I $ = (заряд на одном носителе) (количество носителей на единицу объема) x
(площадь пересечения объема во времени $ Δt $), деленное на $ Δt $

$$ I = \ frac {qn (AvΔt)} {Δt} = qnvA $$

Таким образом, мы можем решить для $ v $ в $ I $ как

$$ v = \ frac {I} {qnA} $$

Подводя это к нашему уравнению баланса сил, получаем

$$ \ frac {qΔV} {L} = \ frac {bI} {qnA} $$

Решение для $ \ Delta V $ дает

$$ ΔV = \ bigg (\ frac {bL} {q ^ 2nA} \ bigg) I $$

Комбинация $ bL / q ^ 2nA $ — это свойство конкретного цилиндра, на который мы смотрим — его материал (который определяет, что такое $ q $ , $ n $ , и $ b $) и его форма ( что определяет $ L $ и $ A $). 2nA}. $$

Результатом является мощное уравнение Закон Ома ,

$$ ΔV = IR. $$

Что это значит?

В принципе, из вывода мы видим, откуда исходит закон Ома. Все начинается с утверждения, что толчок (исходящий от поля E) уравновешивается сопротивлением (пропорциональным v), поэтому мы поддерживаем постоянную скорость (согласно 2-му закону Ньютона).

Поскольку мы не можем легко создать поля E количественно, но можем легко манипулировать потенциалом, мы выражаем это через разность потенциалов на цилиндре (резисторе).Поскольку мы не можем легко измерить скорость наших носителей тока, но у нас есть устройства (амперметры) для прямого измерения токов, удобно выражать скорость через ток.

Результат интуитивно понятен: больше толчка означает больше потока; большее сопротивление для того же толчка приводит к меньшему потоку. Это стандартное уравнение потока, управляемое градиентом, где изменение некоторого скалярного поля в пространстве приводит к движению чего-то. Другие примеры включают уравнение H-P, тепловой поток за счет теплопроводности и закон диффузии Фика.

Чтобы понять, каковы последствия этого, нам придется рассмотреть множество моделей и установить некоторые принципы использования этого закона, чтобы помочь выяснить, какие потоки куда.

Биолог против закона Ома инженера-электрика

Поскольку электрические резисторы в основном пассивны, инженеры-электрики очень довольны идеей сопротивления — это вещество сопротивляется протеканию тока. Но в биологических системах система часто регулирует свое сопротивление, чтобы активно управлять током.2nA} {bL} $$

$$ I = GΔV $$

Это равнозначные формы закона Ома. (Это ничем не отличается от описания движения в терминах скорости — мили / час или его обратной скорости — минут / мили. Что проще использовать, зависит от того, что вы вычисляете, и формально они полностью эквивалентны.)

Resistivity: Плотность сопротивления

Когда у нас были свойства материи, которые зависят как от того, что это за материя, так и от ее формы, мы сочли полезным создать плотность . 2 $, а не от $ 1 / A $.Можете ли вы увидеть из выводов, что является источником этой разницы?

Откуда разница в напряжении?

Поскольку мы знали, что у нас есть постоянный ток, и поскольку мы знали, что у нас есть некоторое сопротивление, Ньютон 2 сказал нам, что нам нужна толкающая сила, чтобы уравновесить силу сопротивления. Мы предположили, что это вызвано E-полем, связанным с разностью потенциалов. Но откуда взялась эта разница потенциалов?

Давайте рассмотрим идеализированную модель, в которой у нас есть батарея (которая создает разность напряжений и, следовательно, поле E), подталкивающая некоторые заряды вниз по проводу.Если провод практически не имеет сопротивления (и большинство проводов имеют очень низкое сопротивление), любые заряды, которые начинают двигаться, не замедляются. Они продолжают двигаться с постоянной скоростью. Но предположим, что теперь происходит попадание в резистивную область, как показано на рисунке ниже.

Когда движущиеся заряды (синий или + на этой диаграмме) ударяют по резистору, они чувствуют сопротивление и начинают замедляться, накапливая некоторый избыточный + заряд на переднем конце резистора. Эти избыточные заряды создают в резисторе поле E, которое вытесняет положительные заряды, оставляя дефицит +, который является избытком — зарядов.

Как только это стабилизируется (примерно за наносекунду в типичной макроскопической схеме), у нас есть лист + на одной стороне резистора и лист — на другой стороне. Это похоже на конденсатор, устанавливающий между ними электрическое поле, достаточное для поддержания постоянной скорости прохождения зарядов. (В этом нет никакой магии. Если бы не было достаточно зарядов, чтобы удерживать их от замедления, больше зарядов накапливались бы, увеличивая поле E, пока их не будет достаточно. Тогда оно больше не будет увеличиваться, и будет устойчивое состояние. учредил.)

Мы можем измерить разницу напряжений на концах резистора. Если бы поле E было постоянным внутри, то его величина была бы равна

.

$$ E = \ frac {\ Delta V} {\ Delta x} = \ frac {\ Delta V} {L} $$

Хотя $ E $, вероятно, не является постоянным, это все равно будет среднее поле E, $ \ langle E \ rangle $.

Шт.

Из закона Ома ясно, что подходящей единицей измерения сопротивления является «вольт / ампер». Эта комбинация распаковывается —

• В = Джоуль / Кулон,
• Ампер = Кулон / сек,

, поэтому единица сопротивления —

• Вольт / Ампер = Джоуль * сек / Кулон ² = кг-м ² / C ² -с.

Поскольку «b» должно иметь единицы измерения в кг / с, чтобы bv создавала силу (кг-м / с ² ), это соответствует нашей подробной формуле для $ R $.

Эта запутанная комбинация получила обозначение « Ом » и написано с греческой заглавной буквы омега (Ω). Единицей измерения проводимости является (конечно, что это еще может быть?) «Mho». **

* За исключением очень особых обстоятельств — таких как металлы и некоторые другие материалы при очень, очень низких температурах — в этот момент сопротивление потоку может исчезнуть.Это называется сверхпроводимостью.

** Увы, это уже не так. Официальный термин был изменен, так что 1 инверсный Ом официально называется Siemens.

Джо Редиш 27.02.12

2.1 Электрическая потенциальная энергия: разница потенциалов

Цели обучения

По окончании этого раздела вы сможете делать следующее:

• Определить электрический потенциал и электрическую потенциальную энергию
• Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией
• Объяснить электрон-вольт и его использование в субмикроскопических процессах
• Определить электрическую потенциальную энергию с учетом разности потенциалов и количества заряда

Информация, представленная в этом разделе, поддерживает следующие цели обучения AP® и научные практики:

• 2.C.1.1 Учащийся может предсказать направление и величину силы, действующей на объект с электрическим зарядом q , помещенным в электрическое поле E , используя математическую модель связи между электрической силой и электрическое поле: F = q E ; векторное отношение. (С.П. 6.4, 7.2)
• 2.C.1.2 Учащийся может вычислить любую из переменных — электрическую силу, электрический заряд и электрическое поле — в точке, учитывая значения и знак или направление двух других величин. (С.П. 2.2)
• 5.B.2.1 Учащийся может рассчитать ожидаемое поведение системы, используя объектную модель (т. Е. Игнорируя изменения во внутренней структуре) для анализа ситуации. Затем, когда модель не работает, студент может обосновать использование принципов сохранения энергии для расчета изменения внутренней энергии из-за изменений внутренней структуры, потому что объект на самом деле является системой. (С.П. 1.4, 2.1)
• 5.B.3.1 Учащийся может описывать и делать качественные и / или количественные прогнозы на повседневных примерах систем с внутренней потенциальной энергией. (С.П. 2.2, 6.4, 7.2)
• 5.B.3.2 Учащийся может производить количественные вычисления внутренней потенциальной энергии системы на основе описания или диаграммы этой системы. (С.П. 1.4, 2.2)
• 5.B.3.3 Учащийся может применять математические рассуждения для создания описания внутренней потенциальной энергии системы на основе описания или диаграммы объектов и взаимодействий в этой системе. (С.П. 1.4, 2.2)
• 5.B.4.1 Учащийся может описывать и делать прогнозы относительно внутренней энергии систем. (С.П. 6.4, 7.2)
• 5.B.4.2 Учащийся может рассчитывать изменения кинетической энергии и потенциальной энергии системы, используя информацию из представлений этой системы. (С.П. 1.4, 2.1, 2.2)

Когда свободный положительный заряд qq size 12 {q} {} ускоряется электрическим полем, как показано на рисунке 2.2 дана кинетическая энергия. Этот процесс аналогичен ускорению объекта гравитационным полем. Это как если бы заряд спускался с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую. Давайте исследуем работу, совершаемую электрическим полем над зарядом qq размером 12 {q} {} в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.

Рис. 2.2. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма.В обоих случаях потенциальная энергия преобразуется в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем записать W = –ΔPE.W = –ΔPE. размер 12 {W = -? «PE»} {}

Электростатическая или кулоновская сила консервативна, что означает, что работа, выполняемая на qq размером 12 {q} {} , не зависит от пройденного пути. Это в точности аналогично силе гравитации в отсутствие диссипативных сил, таких как трение. Когда сила является консервативной, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией — потому что она зависит только от положения — чем вычислять работу напрямую.

Мы используем буквы PE для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии ΔPE, ΔPE, размер 12 {? «PE»} {} имеет решающее значение, поскольку работа, выполняемая консервативной силой, является отрицательной по отношению к изменению потенциальной энергии; то есть W = –ΔPE.W = –ΔPE. size 12 {W «= -«? «PE»} {} Например, работа WW, выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери в PE или отрицательного ΔPE.ΔPE. размер 12 {? «PE»} {} Перед ΔPEΔPE size 12 {? «PE»} {} должен стоять знак минус, чтобы WW было положительным.PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Потенциальная энергия

W = –ΔPE.W = –ΔPE. size 12 {W «= -«? «PE»} {} Например, работа WW, выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери в PE или отрицательного ΔPE.ΔPE. Перед ΔPEΔPE должен стоять знак минус, чтобы WW было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное понимание энергии и преобразования энергии без необходимости иметь дело с силой напрямую. Например, гораздо более распространено использование концепции напряжения, связанного с электрической потенциальной энергией, чем непосредственное рассмотрение кулоновской силы.

Непосредственный расчет работы обычно затруднен, поскольку W = FdcosθW = Fdcosθ, а направление и величина F F размером 12 {F} {} могут быть сложными для нескольких зарядов, для объектов нечетной формы и вдоль произвольных траекторий. Но мы знаем, что, поскольку F = qE, F = qE, размер 12 {F = ital «qE»} {}, работа и, следовательно, ΔPE, ΔPE, пропорциональны испытательному заряду q.q. размер 12 {q} {} Чтобы получить физическую величину, не зависящую от испытательного заряда, мы определяем электрический потенциал VV размером 12 {V} {} (или просто потенциал, поскольку понимается электрический) как потенциальную энергию на единицу заряда

2.1 V = PEq. V = PEq. размер 12 {V = {{«PE»} поверх {q}} «.» } {}

Электропотенциал

Это электрическая потенциальная энергия на единицу заряда

2.2 V = PEq. V = PEq. размер 12 {V = {{«PE»} поверх {q}}} {}

Поскольку PE пропорционален qq размеру 12 {q} {} , зависимость от qq size 12 {q} {} отменяется. Таким образом, размер VV 12 {V} {} не зависит от кв. размер 12 {q} {} Изменение потенциальной энергии ΔPEΔPE размер 12 {? «PE»} {} имеет решающее значение, поэтому мы обеспокоены разницей в потенциале или разностью потенциалов ΔVΔV размером 12 {? V} {} между две точки, где

2,3 ΔV = VB − VA = ΔPEq. ΔV = VB − VA = ΔPEq. размер 12 {ΔV = V rSub {размер 8 {B}} — V rSub {размер 8 {A}} = {{Δ «PE»} над {q}} «.»} {}

Таким образом определяется разность потенциалов между точками A и B, VB – VA, VB – VA, размер 12 {V rSub {размер 8 {B}} -V rSub {size 8 {A}}} {}. — изменение потенциальной энергии заряда qq размером 12 {q} {} , перемещенного из A в B, деленное на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта

2,4 1 В = 1 J C 1 В = 1 J C размер 12 {1 «V = 1» {{J} больше {C}}} {}

Возможная разница

Разность потенциалов между точками A и B, VB – VA, VB – VA, размер 12 {V rSub {размер 8 {B}} -V rSub {размер 8 {A}}} {} определяется как изменение потенциальная энергия заряда qq перемещается от A к B, деленная на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

Знакомый термин «напряжение» — это общее название разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, а ее напряжение — это разность потенциалов между ними. По сути, точка, которую вы выбираете как ноль вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например уровень моря или, возможно, пол лекционного зала.

Таким образом, взаимосвязь между разностью потенциалов — или напряжением — и электрической потенциальной энергией определяется формулой

2,6 ΔV = ΔPEq, ΔPE = qΔV.ΔV = ΔPEq и ΔPE = qΔV. размер 12 {? V = {{? «PE»} над {q}} «и» D «PE =» q? V «.» } {}

разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением

2.7 ΔV = ΔPEq и ΔPE = qΔV.ΔV = ΔPEqand ΔPE = qΔV. размер 12 {? V = {{? «PE»} над {q}} «и» D «PE =» q? V «. «} {}

Второе уравнение эквивалентно первому.

Соединения в реальном мире: электрический потенциал в электронных устройствах

Вероятно, вы ежедневно используете устройства с накопленным электрическим потенциалом. У вас есть или используете какие-либо электронные устройства, которые не нужно подключать к розетке? Что произойдет, если вы будете использовать эти предметы достаточно долго? Они перестают функционировать? Что делать в таком случае? Выберите один из этих типов электронных устройств и определите, какой электрический потенциал, измеренный в вольтах, требуется устройству для правильного функционирования.Затем оцените количество времени между пополнениями потенциала. Опишите, как время между пополнениями потенциала зависит от использования.

Ответ

Готовые примеры включают калькуляторы и сотовые телефоны. Первый будет либо питаться от солнечной батареи, либо иметь сменные батареи, вероятно, четыре 1,5 В, всего 6 В. Второе потребуется заряжать с помощью специального зарядного устройства, которое, вероятно, выдает 5 В. Время между пополнениями будет сильно зависеть. на какой элемент используется, но должно быть меньше при более интенсивном использовании.

Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение — точнее, одинаковую разность потенциалов между выводами аккумулятора, но при этом один хранит гораздо больше энергии, чем другой, поскольку ΔPE = qΔV.ΔPE = qΔV. Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора — 12 В.

Пример 2.1 Расчет энергии

Предположим, у вас есть мотоциклетный аккумулятор с напряжением 12 В, который может заряжать 5000 градусов Цельсия, и аккумулятор на 12 В.Автомобильный аккумулятор с напряжением 0 В, который может заряжать 60 000 градусов Цельсия. Сколько энергии дает каждый? Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.

Стратегия

Сказать, что у нас батарея на 12,0 В, означает, что на ее выводах разность потенциалов составляет 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное ΔPE = qΔV.ΔPE = qΔV.

Итак, чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов.

Решение

Для аккумулятора мотоцикла q = 5000 Cq = 5000 C и ΔV = 12,0 В. ΔV = 12,0 В. Общая энергия, отдаваемая аккумулятором мотоцикла, составляет

2,8 ΔPEcycle = 5000 C 12,0 В = 5000 C 12,0 Дж / C = 6,00 × 104 Дж. ΔPEcycle = 5,000 C12,0 В = 5,000 C12,0 Дж / C = 6,00 × 104 Дж.

Аналогично, для автомобильного аккумулятора q = 60,000 Cq = 60,000C, размер 12 {q = «60» , «000» «C»} {} и

2,9 ΔPEcar = 60 000 C12,0 V = 7,20 × 105 Дж. ΔPEcar = 60 000 C12,0 V = 7,20 × 105 Дж

Обсуждение

Хотя напряжение и энергия связаны, это не одно и то же.Напряжения батарей одинаковы, но энергия, подаваемая каждым из них, совершенно разная. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию.Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны. Батареи отталкивают электроны от своих отрицательных выводов (A) через любую задействованную схему и притягивают их к своим положительным выводам (B), как показано на рисунке 2.3. Изменение потенциала составляет ΔV = VB – VA = + 12 VΔV = VB – VA = + 12 В, а заряд qq отрицательный, так что ΔPE = qΔVΔPE = qΔV является отрицательным, что означает, что потенциальная энергия батареи уменьшилась, когда qq перемещен из пункта A в пункт B.

Рис. 2.3 Аккумулятор перемещает отрицательный заряд от отрицательной клеммы через фару к положительной клемме. Соответствующие комбинации химических веществ в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. С точки зрения потенциала положительный вывод находится под более высоким напряжением, чем отрицательный. Внутри аккумулятора движутся как положительные, так и отрицательные заряды.

Подключение: потенциальная энергия в батарее

В предыдущем примере говорилось, что потенциальная энергия батареи уменьшается с каждым электроном, который она выталкивает. Однако не должна ли эта уменьшенная внутренняя энергия также снижать потенциал? Да, должно. Так почему мы этого не замечаем?

Частично ответ заключается в том, что количество энергии, потребляемой любым электроном, чрезвычайно мало, и поэтому оно не сильно снижает потенциал. Но главная причина в том, что энергия хранится в батарее в виде ожидаемой химической реакции, а не в виде электрического потенциала. Эта реакция происходит только при подключении нагрузки к обоим клеммам батареи. Любой набор химических реагентов имеет определенный максимальный потенциал, который он может обеспечить; Вот почему более крупные батареи состоят из последовательно соединенных ячеек, так что общий потенциал увеличивается аддитивно. По мере того, как эти реагенты расходуются, каждая ячейка дает меньше потенциала электронам, которые она перемещает; в конечном итоге этот потенциал падает ниже полезного порога. Затем батарею необходимо либо зарядить, что полностью изменить химическую реакцию и восстановить исходные реагенты, либо заменить ее.

Пример 2.2. Сколько электронов проходит через фару каждую секунду?

Когда автомобильный аккумулятор на 12,0 В работает от одной фары мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещаемый заряд связан с напряжением и энергией через уравнение ΔPE = qΔV.ΔPE = qΔV. Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, мы имеем ΔPE = –30.0 JΔPE = –30,0 Дж и, поскольку электроны переходят от отрицательного вывода к положительному, мы видим, что ΔV = + 12,0 В. ΔV = + 12,0 В.

Решение

Чтобы найти перемещенный заряд q q размером 12 {q} {} , мы решаем уравнение ΔPE = qΔV.ΔPE = qΔV.

Вводя значения для ΔPEΔPE размера 12 {? «PE»} {} и ΔV, ΔV, получаем

2,11 q = –30,0 Дж + 12,0 В = –30,0 Дж + 12,0 Дж / C = –2,50 Cq = –30,0 J + 12,0 В = –30,0 Дж + 12,0 Дж / Кл = –2,50 C.

Число электронов nene размером 12 {n rSub {size 8 {e}}} {} — это общий заряд, деленный на заряд одного электрона.То есть

2,12 ne = –2,50 C – 1,60 × 10–19C / e– = 1,56 × 1019 электронов. Ne = –2,50 C – 1,60 × 10–19C / e– = 1,56 × 1019 электронов.

Обсуждение

Это очень большое количество. Неудивительно, что мы обычно не наблюдаем отдельные электроны, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.

Применение научных практик: работа и потенциальная энергия в точечных зарядах

Рассмотрим систему, состоящую из двух положительных точечных зарядов, каждый по 2,0 мкКл, расположенных на расстоянии 1,0 м друг от друга. Мы можем вычислить потенциал, то есть внутреннюю энергию этой конфигурации, вычислив потенциал, связанный с одним из зарядов, а затем вычислив потенциальную энергию второго заряда в потенциале первого. Применение уравнений (19.38) и (19.2) дает нам потенциальную энергию 3.6 × 10 ^–2 Дж. Если переместить заряды ближе друг к другу, скажем, на расстояние 0,50 м, потенциальная энергия удвоится. Обратите внимание, что для создания этого второго случая некоторая внешняя сила должна была бы провести работу в этой системе, чтобы изменить конфигурацию, и, следовательно, это не была закрытая система. Однако, поскольку электрическая сила консервативна, мы можем использовать теорему работы-энергии, чтобы утверждать, что, поскольку не было изменения кинетической энергии, вся проделанная работа пошла на увеличение внутренней энергии системы.Также обратите внимание, что если бы точечные заряды имели разные знаки, они бы были привлечены друг к другу, поэтому они могли бы выполнять работу во внешней системе, когда расстояние между ними уменьшалось. По мере того, как работа выполняется во внешней системе, внутренняя энергия в двухзарядной системе уменьшается.

Рис. 2.4 Работа выполняется путем перемещения двух зарядов одного знака ближе друг к другу, что увеличивает внутреннюю энергию двухзарядной системы.