Электричество и магнетизм
Индукционные токи возникают не только в проволочных витках, но и в толще массивных проводников. В этом случае их называют вихревыми токами или токами Фуко. Из–за малого сопротивления проводников они могут достигать большой силы. По правилу Ленца вихревые токи также действуют против причины, их вызывающей. На этом основана идея электромагнитных демпферов, успокаивающих колеблющиеся части приборов (стрелки гальванометров и т. п.). На подвижной части прибора укрепляется металлическая полоска, находящаяся в поле сильного магнита. При движении системы токи Ж. Фуко (рис. 8.23) тормозят ее, но они отсутствуют при покоящейся стрелке и не препятствуют её остановке в нужном месте, согласно значению измеряемой величины (в отличие от сил трения).
Рис. 8.23. Леон Фуко (1819–1868) — французский физик и астроном
Итогом проведенных рассуждений может быть такая формулировка правила Ленца: индукционный ток всегда направлен так, чтобы препятствовать той причине, которая его породила. Вне зависимости от того, что это за причина.
Например, если проволочное кольцо падает в неоднородном магнитном поле под действием силы тяжести, то в нем течет индукционный ток. Соответственно на кольцо действует сила Ампера. Ничего не вычисляя, можно быть уверенным в том, что эта сила Ампера будет направлена вверх, чтобы — согласно правилу Ленца — мешать силе тяжести, которая является причиной падения кольца, что влечет за собой изменение магнитного потока, а это приводит к появлению индукционного тока, на который действует сила Ампера, тормозящая падение…
Ниже рассматриваются опыты, в которых изучаются свойства токов Фуко.
На рис. 8.24 показан опыт, демонстрирующий падение тел в неоднородном магнитном поле. Неоднородное магнитное поле тормозит движение проводящих предметов из-за токов Фуко, возникающих в проводниках при изменении магнитного потока через них. Демонстрируется беспрепятственное падение диэлектрического деревянного диска между полюсами сильного электромагнита и медленное падение медного и алюминиевого дисков в магнитном поле, напоминающее движение тел в среде с большой вязкостью.
Рис. 8.24. Падение тел в неоднородном магнитном поле
Видео 8.9. Электромагнитное торможение: падение медных и алюминиевых дисков («монет») в магнитном поле.
При падении сильного постоянного магнита внутри вертикальной проводящей трубки в ее стенках возникают токи Фуко, тормозящие это падение. В опыте (рис. 8.25) демонстрируется свободное падение немагнитного алюминиевого цилиндра в разных трубках, а также маленького магнита в стеклянной трубке. Затем показывают замедление падения этого магнита в алюминиевой трубке и его очень медленное падение в толстостенной медной трубке.
Рис. 8.25. Падение магнита в трубках
На рис. 8.26 показано демпфирование колебаний маятника. Толстая сплошная медная пластина, прикрепленная на конце физического маятника, движется при его колебаниях между полюсами сильного электромагнита. Слабо затухающие колебания маятника после включения магнитного поля начинают быстро затухать, превращаясь практически в апериодические колебания. Если на конце маятника закрепить медную пластинку, разрезанную в виде гребенки, то сильное затухание колебаний маятника исчезает, поскольку токи Фуко уже не могут замыкаться в объеме проводника.
Рис. 8.26. Демпфирование колебаний маятника
Видео 8.10. Электромагнитное торможение: маятник.
В опыте на рис. 8.27 показана левитация сплошного проводящего кольца. Токи Фуко могут возникать не только в проводниках при их перемещении в неоднородном магнитном поле, но и при быстром изменении этого поля. сплошное кольцо из алюминия, надетое на вертикальный сердечник электромагнита, питаемого переменным током частотой 50 Гц, висит в воздухе. в то время как такое же, но разрезанное кольцо свободно падает на обмотку.
Рис. 8.27. Левитация сплошного проводящего кольца
На рис. 8.28 показано взаимодействие проводника и электромагнита. Толстый медный диск укреплен в подшипниках на оси с ручкой. Вблизи него на такой же оси закреплен электромагнит. Если вращать за ручку включенный электромагнит, то диск начинает вращаться в ту же сторону. Если же, наоборот, вращать за ручку диск вблизи электромагнита, то последний также начинает вращаться. Силы взаимодействия диска и электромагнита, похожие по характеру на силы вязкого трения, обусловлены возникновением токов Фуко в диске.
11. Разность потенциалов, электродвижущая сила, напряжение.
Электродвижущая
сила – физ. величина, численно равная
работе, совершаемой сторонними силами
при перемещении единичного положительного
заряда. Сторонние силы – силы не
электрического происхождения (например,
в батарейке- сила химической природы). 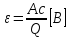
Напряжение на участке цепи — есть физ.величина, определяющаяся работой сторонних и электростатических сил при перемещении единичного положительного заряда на данном участке цепи.
Напряжение — есть обобщённое понятие разности потенциалов, равно разности потенциалов на данном участке, если участок не содержит источник тока.
12. Закон Джоуля-Ленца
При прохождении эл. тока по проводнику в нем выделяется количество теплоты равное:
Q=I²RT=IUt=(U²/R)t, гдеI – ток, R – сопротивление, U–напряжение, t – время
Если за время dt по проводнику протекает заряд Q, то величина заряда dQ=Idt
A=IUt.
По закону сохранения энергии вся работа идет на нагревание проводника.
13. Закон Видемана-Франса
Соотношение,
связывающее между собой теплопроводность
и электрическую проводимость металлов.
В 1853 Г. на основании экспериментальных
данных установили, что для всех металлов
отношение теплопроводности c к
электрической проводимости s при
постоянной температуре одинаково:  В 1882 датский физик Л. Лоренц показал,
что отношение
В 1882 датский физик Л. Лоренц показал,
что отношение 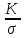 изменяется
прямо пропорционально абсолютной
температуре T:
изменяется
прямо пропорционально абсолютной
температуре T: 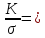
Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов обусловлены в основном движением электронов. В. — Ф. з. впервые был объяснён немецким физиком П. Друде, который рассматривал электроны в металле как газ и применил к ним методы классической кинетической теории газов.
14. Индукция магнитного поля. Магнитное поле. Принцип суперпозиции
Магнитное поле-это поле в пространстве, окружающее токи и постоянные магниты.
Магнитное поле создается только движущимися зарядами, и действуют только на движущиеся заряды.
Микротоки – это связи между орбитами атомов и молекул.
Характер воздействия магнитного поля на ток зависит от :1)формы проводника 2)расположения проводника 3)направления тока
Чтобы охарактеризовать воздействие магнитного поля, рассматривать его надо на определенный ток. Поэтому при исследовании магнитного поля используется плоский замкнутый контур с током, при этом размеры ее, значительно малы, по сравнению с расстоянием до токов, образующих магнитное поле.
Ориентация контура в пространстве определяется нормалью к контуру. За положительное направление нормального контура, принимают направление совпадающее с направлением поступательного движения правого винта, при его вращении по направлению тока в контуре. За направление магнитного поля в точке пространства – принимаем направление вдоль которого устанавливается свободно-подвижная рамка с током
Направление
магнитного поля совпадает с направлением
силы, действующую на стрелку севера
компаса  (Ммах при 90) ( M – вращающий момент;
(Ммах при 90) ( M – вращающий момент; —
магнитный момент контура с током
—
магнитный момент контура с током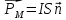 (
( —
направление положительной нормали)
—
направление положительной нормали)
Т.е
магнитная индукция в данной точке
однородного магнитного поля определяется
максимальным вращающим моментом,
действующим на рамку с магнитным
моментом =1, нормаль которой перпендикулярная
полю.  (B – вектор индукции – характеризует
магнитное поле, образованной всеми
макро-и микротоками; H – вектор
напряженности магнитного поля;
(B – вектор индукции – характеризует
магнитное поле, образованной всеми
макро-и микротоками; H – вектор
напряженности магнитного поля; =4π*10-7)
=4π*10-7)
Принцип суперпозиции: Магнитная индукция создаваемая несколькими токами или движущимися зарядами равна векторной сумме магнитных индукций создаваемых током или движущимися зарядами
§ 59. Электродвижущая сила и разность потенциалов. Закон электродвижущей силы.
Рассмотрим в некотором электрическом поле две точки, А иВ. Линейный интеграл электрической силы вдоль некоторого пути перехода от точкиА к точкеВ, т. е.:
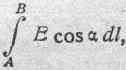
численно равен работе электрических сил поля при перенесении единицы положительного электричества из точки А в точкуВ. Максвелл назвал эту величинуполной электродвижущей силой, действующей вдоль данногопути АВ.
Если линия, вдоль которой берется интеграл, образует замкнутый контур и если полная электродвижущая сила e, действующая в этом контуре, не равна нулю, т. е.

в таком случае система не находится в равновесии, и в ней могут возникнуть электрические токи. Эта полная ЭДС, действующая в замкнутом контуре, есть не что иное, как меравнутренней ЭДС, генерируемой в этом контуре. Если рассматриваемый замкнутый контур интегрирования расположен целиком в диэлектрике, внутренняя ЭДС может в нем возникнуть, по Максвеллу, только за счет явления электромагнитной индукции. Из опытов Фарадея с полной отчетливостью следует, что величина индуктируемой ЭДС совершенно не зависит от сопротивления цепи. Максвелл, распространивший представление о токе и на электрокинетические процессы в диэлектриках (см. главуIII), по существу предположил, что для любого замкнутого контура, даже если он находится полностью в диэлектрике и является непроводящим в обычном смысле, сохраняет силу основное выражение, определяющее величину индуктированной ЭДС, т. е.

где Ф есть поток, сцепляющийся с данным контуром. В этом утверждении заключается одно из главных положений Максвелла,
200
касающихся электромагнитного поля. Это соотношение (45), понимаемое в вышеуказанном общем смысле, мы будем называть законом электродвижущей силы.
В электростатическом поле полная ЭДС внутри какого угодно замкнутого контура равна нулю, т. е.
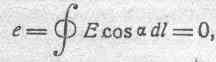
так что, если А иВ суть две точки на этом контуре, полная ЭДС, действующая между этими точками, будет одна и та же вдоль любого из двух путей, на которые разбивается контур. Так как далее каждый из этих путей может быть изменяем независимо от другого, полная ЭДС между точкамиА иВ остается неизменною для всех путей перехода отА кВ. В рассматриваемом случае полная ЭДС называетсяразностью потенциалов между точкамиА к В, т. е

Соотношение (46), определяющее разность потенциалов между точками А к В, как линейный интеграл электрической силы, взятый вдоль любого пути между этими точками, находится в полном соответствии с определением потенциала, данным в пункте„д» предыдущего параграфа 58. Действительно,
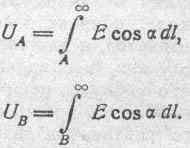
Принимая во внимание, что в данном случае величина линейного интеграла не зависит от пути перехода, можем написать:

Тело, заряженное положительно, стремится двигаться от мест большего положительного к местам меньшего положительного потенциала или к местам с отрицательным потенциалом. Всякое же тело, заряженное отрицательно, стремится двигаться в обратном направлении.
В проводнике электричество может свободно перемещаться относительно проводника. Если, следовательно, две части проводника
201
обладают разными потенциалами, положительное электричество будет двигаться из мест, имеющих высший потенциал, в места низшего потенциала до тех пор, пока существует разность потенциалов. Таким образом, проводник может быть в электрическом равновесии только в том случае, когда все части его имеют один и тот же потенциал, называемый потенциалом проводника.
Итак, в электростатическом поле, т. е. в условиях электрического равновесия, имеем для всех точек проводника:
U=const.
Отсюда следует, во-первых, что в этом случае поверхность проводника является поверхностью уровня, и силовые линии поля нормальны к поверхности проводника. Во-вторых, для всех точек внутри рассматриваемого проводника будет удовлетворяться теорема Лапласа (44):

и потому на основании Теоремы Пуассона (42) получаем:
=0,
иными словами, внутри проводника, находящегося в состоянии электрического равновесия, не может быть объемного распределения электричества.
Как это явствует из всего, что было сказано в пункте „д» :§ 58, в случае многозначности линейного интеграла электрической силы, т. е. в случае, когда величина этого линейного интеграла зависит от пути перехода, понятие о потенциале точки и о разности потенциалов осложняется, и для того, чтобы им пользоваться хотя бы в некоторых случаях, необходимы специальные оговорки. Остановимся прежде всего на случае цепи постоянного тока. Возьмем какие-нибудь точкиА иВ вдоль проводника. Обычно, в цепях постоянного тока принято считать за разность потенциалов между точками цепиА иВ то значение интеграла

которое соответствует случаю, когда линия интегрирования ни разу не проходит через генератор ЭДС. В таком случае при вычислении
величины:

для некоторого участка цепи постоянного тока линия интегрирования вся лежит в пространстве, удовлетворяющем условию:

202
Условию этому именно удовлетворяет вся область установившегося электромагнитного поля вокруг проводника, по которому течет постоянный ток. В этом отношении нет никакой разницы между так называемым „электростатическим» полем и электромагнитным полем вне проводника с постоянным током. Из этого, конечно, не следует, что названные два поля и по существу тождественны.
Придерживаясь максвелловской терминологии, мы можем называть электродвижущей силой ту разность потенциалов, которая действует между какими-либо двумя точками цепи постоянного тока. Это соответствует существу дела, так как данная разность потенциалов, вообще говоря, является причиной, вызывающей ток на данном участке проводника. Для большей точности можно называть разность потенциалов внешней электродвижущей силой, действующей на данном участке проводника. Мы должны при этом строго отличать эту внешнюю электродвижущую силу отвнутренних электродвижущих сил, которые могут генерироваться в различных частях цепи тока и которые являются основной причиной возникновения злектрокинетического процесса в проводящем контуре. Разность потенциалов, действующая на некотором участке цепи постоянного тока, называемая такие иногдаэлектрическим напряжением или простонапряжением, представляет собою не что иное, как часть основной ЭДС, расходуемую на преодоление сопротивлений данного участка. Эти сопротивления могут быть разного рода. Они могут представлять собою обычные электрические сопротивления проводников, входящих в состав цепи. В известных случаях мы встречаемся собратными ЭДС, действующими внутри данного участка цепи навстречу внешней ЭДС, которая возбуждает электрический ток, преодолевая обратные ЭДС, как некоторое „сопротивление». В частном случае напряжение на зажимах конденсатора, заряжаемого в какой-либо цепи от внешней ЭДС, имеет характер обратной ЭДС. На основании всего вышеизложенного очевидно, что физическая размерность разности потенциалов и ЭДС одна и та же. Поэтому обе эти величины измеряются одними и теми же единицами, именно, в практической электромагнитной системе — вольтами.
В случае цепи переменного тока, благодаря наличию изменяющегося магнитного поля вокруг проводника, нет, вообще говоря, такой области, где величина линейного интеграла электрической силы не зависела бы от выбора пути перехода. Ввиду изложенного представление о разности потенциалов, строго говоря, не может применяться при описании явлений, происходящих в цепях переменного тока, и в этом случае следует пользоваться только понятием об ЭДС. Можно говорить об основной переменной ЭДС, генерируемой в альтернаторе или трансформаторе, и об ЭДС, действующей на некотором участке цепи переменного тока, т. е. о напряжении, преодолевающем все сопротивления, какие оказывает цепь на этом участке. Сказанное необходимо иметь в виду, между прочим, во время измерений при помощи вольтметра ЭДС, действующих в различных частях цепи переменного тока. Так как в
203
поле такого тока линейный интеграл электрической силы зависит от выбора пути перехода, то ясно, что вспомогательные проводники, при помощи которых вольтметр присоединяется к соответствующим точкам цепи, могут нечто привнести в измеряемую величину и изменить показания вольтметра, причем эти изменения будут зависеть от общего расположения проводов. В случае низких частот, применяемых в технике сильных токов, описываемое явление столь слабо выражено, что практически оно не имеет существенного значения, и на него обычно не обращают какого-либо внимания. Но в технике высоких частот дело обстоит совсем иначе, и соединительные проводники своим влиянием могут так исказить показания вольтметра, что вопрос о непосредственном измерении ЭДС в высокочастотных цепях в общей форме надо считать практически неразрешимым. Такого рода измерения осуществимы только в отдельных частных случаях и с принятием ряда предосторожностей.
1. Раскройте физ. Смысл эдс, разности потенциалов и напряжёния.
Для
участка цепи: 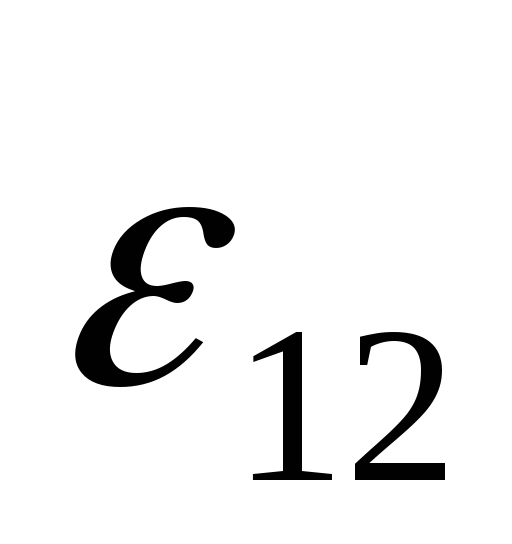 равна работе сторонних сил над единичным
зарядом, работе полож-ым. Сил при
прохождении единичного полож-го заряда
ч/з источник тока.
равна работе сторонних сил над единичным
зарядом, работе полож-ым. Сил при
прохождении единичного полож-го заряда
ч/з источник тока.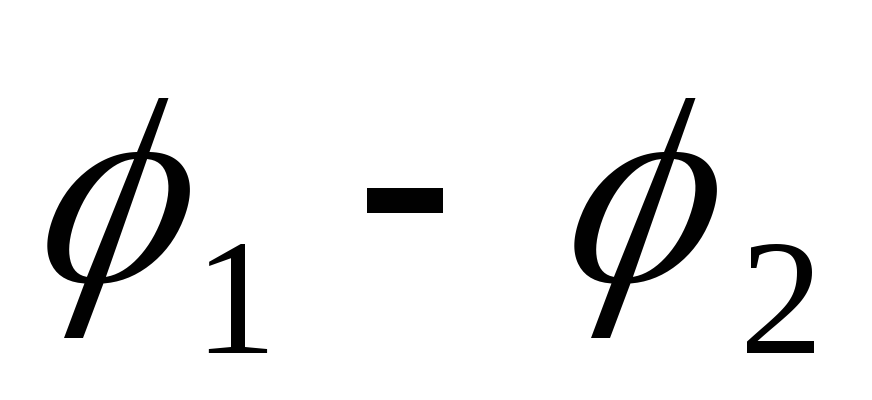 = работе при прохождении единичного
положительного заряда ч/з участки цепи,
не содержащие ЭДС. Напряжение = работе
сил, совершаемой при перемещении
положительного единичного заряда на
участке цепи. При записи закона Ома для
неоднородного участка цепи направление
перемещения заряда выбирается произвольно,
если направление тока совпадает с
выбранным, то ток берётся со знаком “+”,
иначе ”-”. Если направления ЭДС и тока
совпадают, то ЭДС берётся со знаком “+”,
иначе ”-”.
= работе при прохождении единичного
положительного заряда ч/з участки цепи,
не содержащие ЭДС. Напряжение = работе
сил, совершаемой при перемещении
положительного единичного заряда на
участке цепи. При записи закона Ома для
неоднородного участка цепи направление
перемещения заряда выбирается произвольно,
если направление тока совпадает с
выбранным, то ток берётся со знаком “+”,
иначе ”-”. Если направления ЭДС и тока
совпадают, то ЭДС берётся со знаком “+”,
иначе ”-”. .
.
2. Что вы понимаете под током смещения? Запишите второе уравнение Максвелла в интегральной и дифф. Формах. Раскройте его физ. Смысл.
Ток смещения – физическая величина, устанавливающая количественное соотношение между изменяющимся электрическим полем и вызываемым магнитным полем.
По
Максвеллу, переменное электрическое
поле в конденсаторе в каждый момент
времени создаёт такое магнитное поле,
как если бы между обкладками конденсатора
существует ток проводимости, равный
току проводящих проводах.  ,
,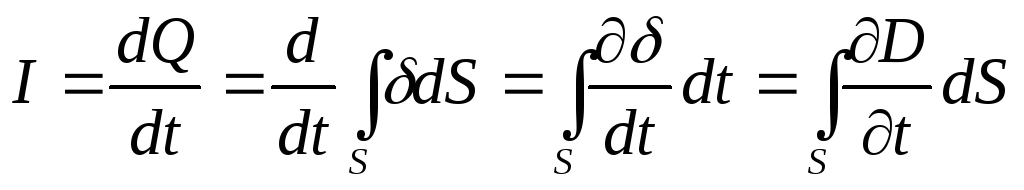 ,
, ,
,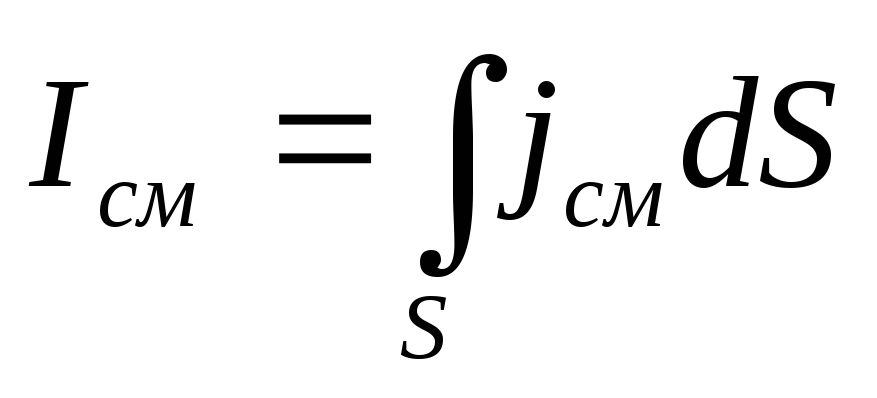 ,
, -плотность
тока смещения.
-плотность
тока смещения.
В
интегральной форме:  ,
,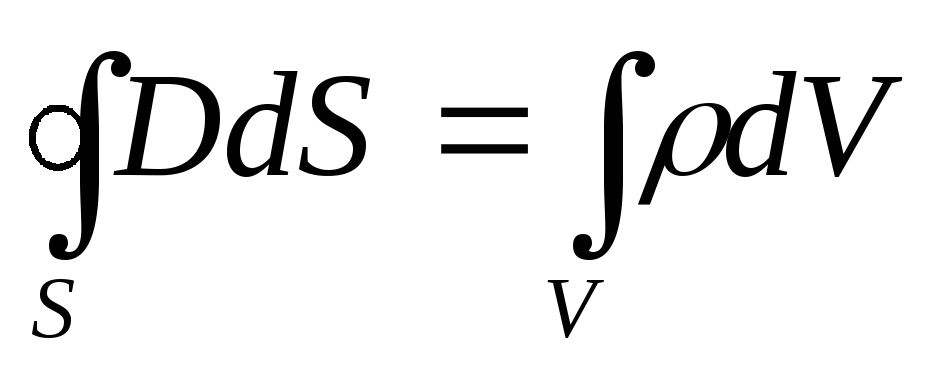 ,
, ,
, ,
, —
объёмная плотность заряда. В дифференциальной
форме:
—
объёмная плотность заряда. В дифференциальной
форме: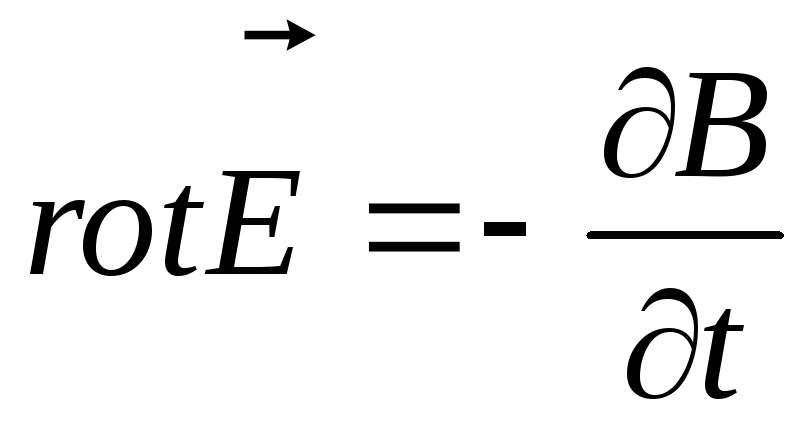 ,
,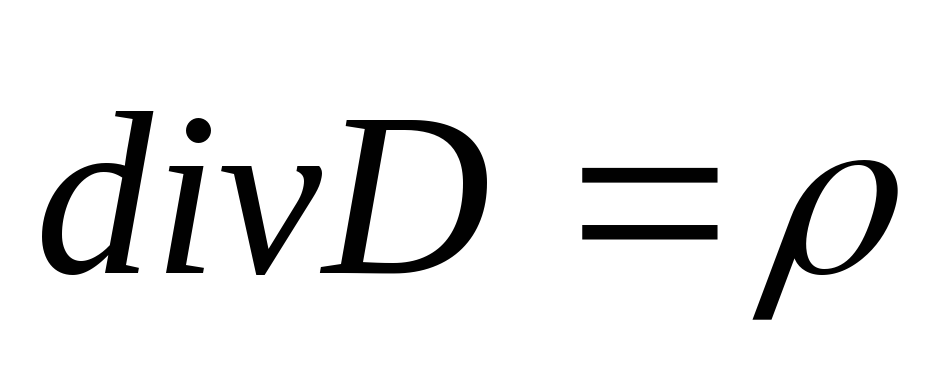 ,
, ,
, .
Из уравнений Максвелла вытекает, что
источниками электрического поля могут
быть либо электрические заряды, либо
изменяющиеся во времени магнитные поля,
а магнитные поля могут возбуждаться
либо электрическими зарядами, либо
переменными электрическими полями.
Уравнения Максвелла не симметричны
относительно электрических и магнитных
полей. Это связано с тем, что в природе
сущ-ют электрические заряды. Электрические
и магнитные поля неразрывно связаны
друг с другом.
.
Из уравнений Максвелла вытекает, что
источниками электрического поля могут
быть либо электрические заряды, либо
изменяющиеся во времени магнитные поля,
а магнитные поля могут возбуждаться
либо электрическими зарядами, либо
переменными электрическими полями.
Уравнения Максвелла не симметричны
относительно электрических и магнитных
полей. Это связано с тем, что в природе
сущ-ют электрические заряды. Электрические
и магнитные поля неразрывно связаны
друг с другом.
Билет №39
1. Какие типы конденсаторов Вам известны? Какова роль конденсатора в эл. Цепи? Выведите формулу ёмкости плоского конденсатора.
Устройство
обладающее способностью при небольших
размерах накапливать заряд, область
большой ёмкости. Если к заряжённому
проводнику приближать др.тела, то на
них возникают индуцированные (на
проводнике) или связанные (на диэлектрике)
заряды, эти заряды ослабляют поле,
создаваемое зарядом Q
=> повышают емкость проводника. На
ёмкость конденсатора не должны оказывать
влияние другие тела, поэтому проводникам
придают такую форму, чтобы поле было
сосредоточено между обкладками
конденсатора. В зависимости от формы
обкладок конденсаторы делятся на:1)
плоские (2 плоские пластины)  —
ёмкость конденсатора.
—
ёмкость конденсатора. ,
, .
2) цилиндрические (2 коаксиальных
цилиндра)
.
2) цилиндрические (2 коаксиальных
цилиндра)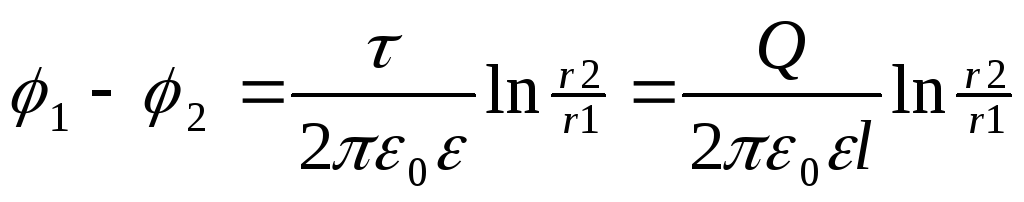 ,
,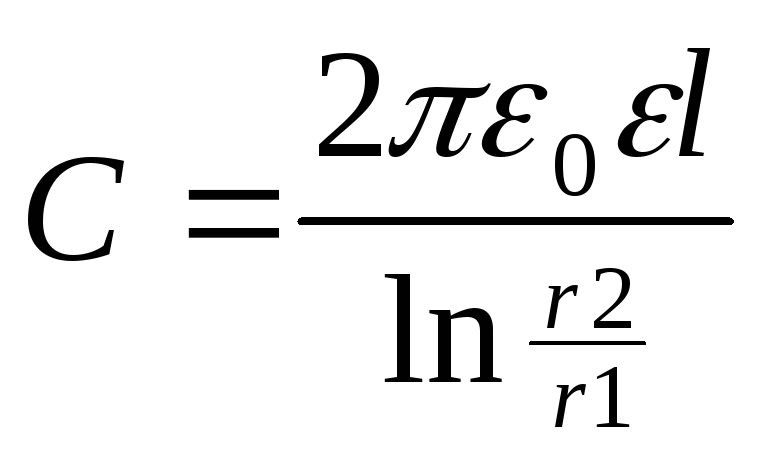 .
3) сферические (2 конц. сферы)
.
3) сферические (2 конц. сферы)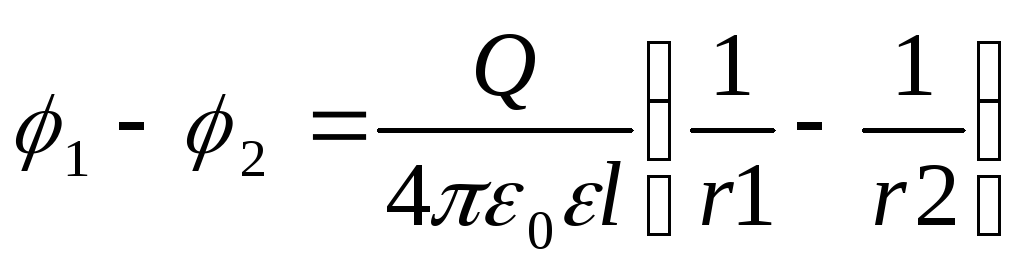 ,
, .
.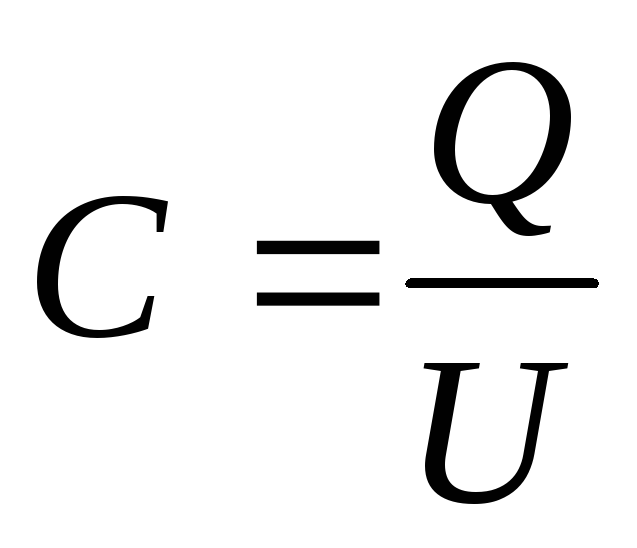 ,
,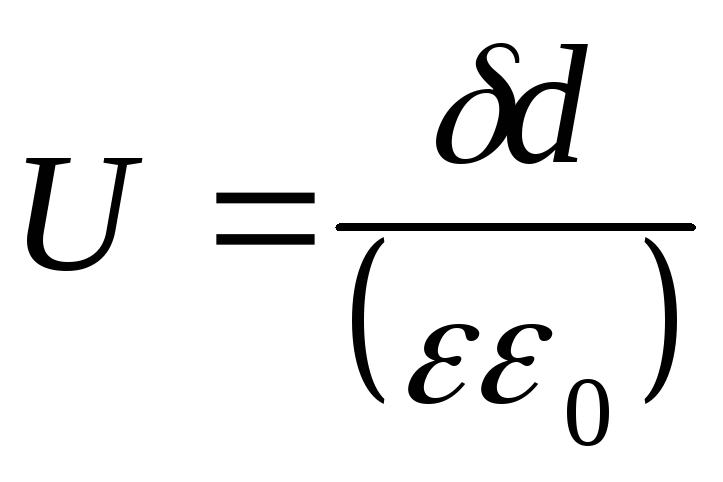 ,
, =>
=>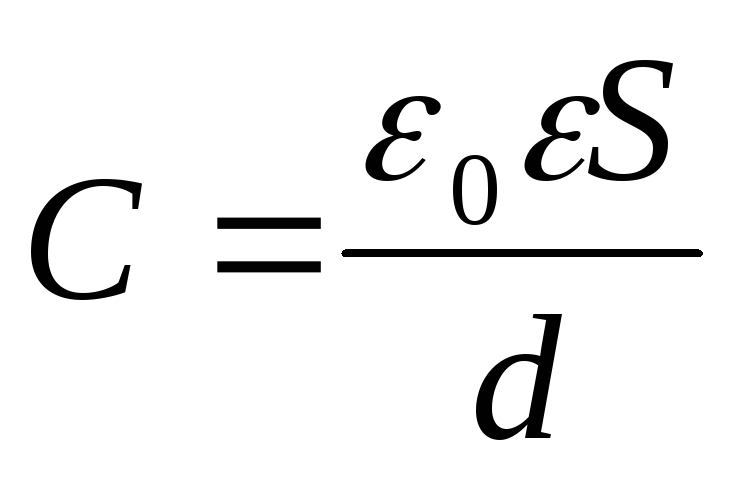 .
.
2. Каковы условия резонанса в эл. Колебательном контуре? Приведите резонансные кривые для тока и напряжения. В чем сходство и различия этих кривых?
Условия
резонанса:
Явление резкого возрастания амплитуды
вынужденных колеб. при приближённой
частоте вынужденных колебаний к частоте
вынуждающего напряжения наз-ся электрическим
резонансом.  .
1) Максимум при резонансе тем выше и
острее, чем меньше
.
1) Максимум при резонансе тем выше и
острее, чем меньше ,
т.е. чем меньше активное сопротивление
и чем больше индуктивность контура. 2)
Амплитуда силы тока имеет максим.
значение при
,
т.е. чем меньше активное сопротивление
и чем больше индуктивность контура. 2)
Амплитуда силы тока имеет максим.
значение при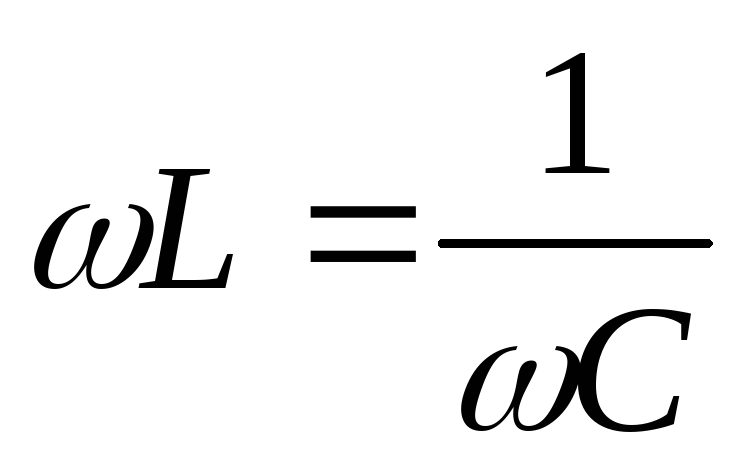 ,
,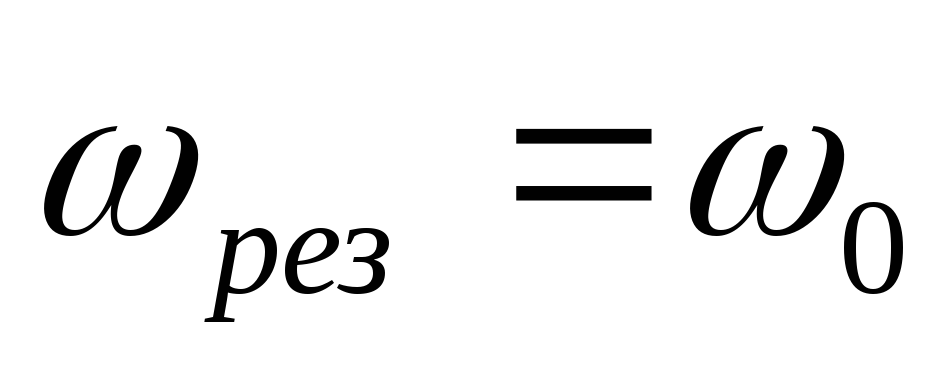 .
3)Q
(добротность) показывает, во сколько
раз напряжение на конденсаторе может
превышать приложенное направление.
.
3)Q
(добротность) показывает, во сколько
раз напряжение на конденсаторе может
превышать приложенное направление.
При  все кривые сх-ся в одной точке. Максимум
тем выше и острее, чем меньше активное
сопротивление и больше индуктивность
контур.
все кривые сх-ся в одной точке. Максимум
тем выше и острее, чем меньше активное
сопротивление и больше индуктивность
контур.
Амплитуда
имеет максимальное значение при  .
Отрезок отсекаемый от оси
.
Отрезок отсекаемый от оси .
.
Билет №40
Про разность потенциалов, электродвижущую силу и напряжение — Статьи
Разность потенциалов
Известно, что одно тело можно нагреть больше, а другое меньше. Степень нагрева тела называется его температурой. Подобно этому, одно тело можно наэлектризовать больше другого. Степень электризации тела характеризует величину, называемую электрическим потенциалом или просто потенциалом тела.
Что значит наэлектризовать тело? Это значит сообщить ему электрический заряд, т. е. прибавить к нему некоторое количество электронов, если мы тело заряжаем отрицательно, или отнять их от него, если мы тело заряжаем положительно. В том и другом случае тело будет обладать определенной степенью электризации, т. е. тем или иным потенциалом, причем тело, заряженное положительно, обладает положительным потенциалом, а тело, заряженное отрицательно, — отрицательным потенциалом.
Разность уровней электрических зарядов двух тел принято называть разностью электрических потенциалов или просто разностью потенциалов.
Следует иметь в виду, что если два одинаковых тела заряжены одноименными зарядами, но одно больше, чем другое, то между ними также будет существовать разность потенциалов.
Кроме того, разность потенциалов существует между двумя такими телами, одно из которых заряжено, а другое не имеет заряда. Так, например, если какое-либо тело, изолированное от земли, имеет некоторый потенциал, то разность потенциалов между ним и землей (потенциал которой принято считать равным нулю) численно равна потенциалу этого тела.
Итак, если два тела заряжены таким образом, что потенциалы их неодинаковы, между ними неизбежно существует разность потенциалов.
Всем известное явление электризации расчески при трении ее о волосы есть не что иное, как создание разности потенциалов между расческой и волосами человека.
Действительно, при трении расчески о волосы часть электронов переходит на расческу, заряжая ее отрицательно, волосы же, потеряв часть электронов, заряжаются в той же степени, что и расческа, но положительно. Созданная таким образом разность потенциалов может быть сведена к нулю прикосновением расчески к волосам. Этот обратный переход электронов легко обнаруживается на слух, если наэлектризованную расческу приблизить к уху. Характерное потрескивание будет свидетельствовать о происходящем разряде.
Говоря выше о разности потенциалов, мы имели в виду два заряженных тела, однако разность потенциалов можно получить и между различными частями (точками) одного и того же тела.
Так, например, рассмотрим, что произойдет в куске медной проволоки, если под действием какой-либо внешней силы нам удастся свободные электроны, находящиеся в проволоке, переместить к одному концу ее. Очевидно, на другом конце проволоки получится недостаток электронов, и тогда между концами проволоки возникнет разность потенциалов.
Стоит нам прекратить действие внешней силы, как электроны тотчас же, в силу притяжения разноименных зарядов, устремятся к концу проволоки, заряженному положительно, т. е. к месту, где их недостает, и в проволоке вновь наступит электрическое равновесие.
Электродвижущая сила и напряжение
Для поддержания электрического тока в проводнике необходим какой-то внешний источник энергии, который все время поддерживал бы разность потенциалов на концах этого проводника.
Такими источниками энергии служат так называемые источники электрического тока, обладающие определенной электродвижущей силой, которая создает и длительное время поддерживает разность потенциалов на концах проводника.
Электродвижущая сила (сокращенно ЭДС) обозначается, буквой Е. Единицей измерения ЭДС служит вольт. У нас в стране вольт сокращенно обозначается буквой «В», а в международном обозначении — буквой «V».
Итак, чтобы получить непрерывное течение электрического тока, нужна электродвижущая сила, т. е. нужен источник электрического тока.
Первым таким источником тока был так называемый «вольтов столб», который состоял из ряда медных и цинковых кружков, проложенных кожей, смоченной в подкисленной воде. Таким образом, одним из способов получения электродвижущей силы является химическое взаимодействие некоторых веществ, в результате чего химическая энергия превращается в энергию электрическую. Источники тока, в которых таким путем создается электродвижущая сила, называются химическими источниками тока.
В настоящее время химические источники тока — гальванические элементы и аккумуляторы — широко применяются в электротехнике и электроэнергетике.
Другим основным источником тока, получившим широкое распространение во всех областях электротехники и электроэнергетики, являются генераторы.
Генераторы устанавливаются на электрических станциях и служат единственным источником тока для питания электроэнергией промышленных предприятий, электрического освещения городов, электрических железных дорог, трамвая, метро, троллейбусов и т. д.
Как у химических источников электрического тока (элементов и аккумуляторов), так и у генераторов действие электродвижущей силы совершенно одинаково. Оно заключается в том, что ЭДС создает на зажимах источника тока разность потенциалов и поддерживает ее длительное время.
Эти зажимы называются полюсами источника тока. Один полюс источника тока испытывает всегда недостаток электронов и, следовательно, обладает положительным зарядом, другой полюс испытывает избыток электронов и, следовательно, обладает отрицательным зарядом.
Соответственно этому один полюс источника тока называется положительным (+), другой — отрицательным (—).
Источники тока служат для питания электрическим током различных приборов — потребителей тока. Потребители тока при помощи проводников соединяются с полюсами источника тока, образуя замкнутую электрическую цепь. Разность потенциалов, которая устанавливается между полюсами источника тока при замкнутой электрической цепи, называется напряжением и обозначается буквой U.
Единицей измерения напряжения, так же как и ЭДС, служит вольт.
Если, например, надо записать, что напряжение источника тока равно 12 вольтам, то пишут: U — 12 В.
Для измерения ЭДС или напряжения применяется прибор, называемый вольтметром.
Чтобы измерить ЭДС или напряжение источника тока, надо вольтметр подключить непосредственно к его полюсам. При этом, если электрическая цепь разомкнута, то вольтметр покажет ЭДС источника тока. Если же замкнуть цепь, то вольтметр уже покажет не ЭДС, а напряжение на зажимах источника тока.
ЭДС, развиваемая источником тока, всегда больше напряжения на его зажимах.
ЭДС, напряжение и разность потенциалов. Закон Ома для неоднородного участка цепи.
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю. Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
|
|
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на определенные участки. Те участки, на которых не действуют сторонние силы (то есть участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе  12, действующей на данном участке. Поэтому полная работа равна
12, действующей на данном участке. Поэтому полная работа равна
|
Величину U12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
|
Это соотношение принято называть обобщенным законом Ома.
Закон Ома для полной цепи:

сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.





 12.
12. = Δφ12 +
= Δφ12 +  .
.