19. Эдс, разность потенциалов и напряжение.

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (н епотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил (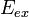). В замкнутом контуре () тогда ЭДС будет равна:

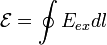, где 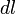— элемент длины контура.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

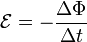
где — поток магнитного поля через замкнутую поверхность 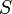, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

Электрическое напряжение между двумя точками электрической цепи или электрического поля, равно работе электрического поля по перемещению единичного положительного заряда из одной точки в другую. В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд; в этом случае Э. н. между двумя точками совпадает с разностью потенциалов между ними.

Если поле непотенциально, то напряжение зависит от того пути, по которому перемещается заряд между точками. Непотенциальные силы, называются сторонними, действуют внутри любого источника постоянного тока (генератора, аккумулятора, гальванического элемента и др.). Под напряжением на зажимах источника тока всегда понимают работу электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника; в этом случае Э. н. равно разности потенциалов на зажимах источника и определяется законом Ома: U = IR—E, где I — сила тока, R — внутреннее сопротивление источника, а E — его электродвижущая сила (эдс). При разомкнутой цепи (I = 0) напряжение по модулю равно эдс источника. Поэтому эдс источника часто определяют как Э. н. на его зажимах при разомкнутой цепи.

В случае переменного тока Э. н. обычно характеризуется действующим (эффективным) значением, которое представляет собой среднеквадратичное за период значение напряжения. Напряжение на зажимах источника переменного тока или катушки индуктивности измеряется работой электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника или катушки. Вихревое (непотенциальное) электрическое поле на этом пути практически отсутствует, и напряжение равно разности потенциалов.

Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

Наименование и обозначение производной единицы СИ:

международное – volt, V

русское – 

вольт, В

Выражение через основные и производные единицы СИ:

1 V = 1 W / A

5.3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока (ЭДС) :

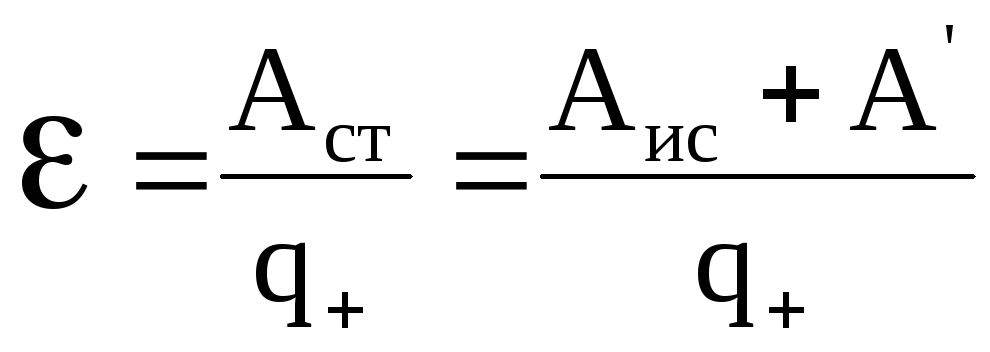. (5.15)

Работа сторонних сил вдоль замкнутой цепи

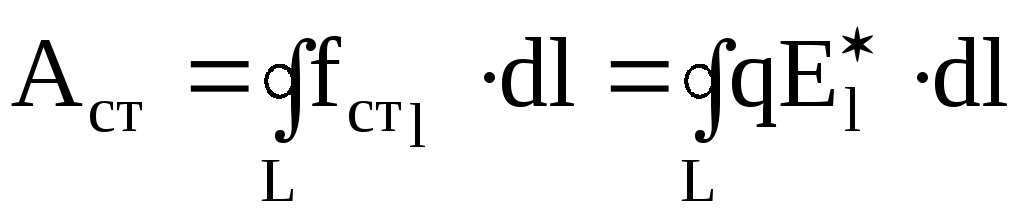, (5.16)

где E^* – напряженность поля сторонних сил.

Тогда

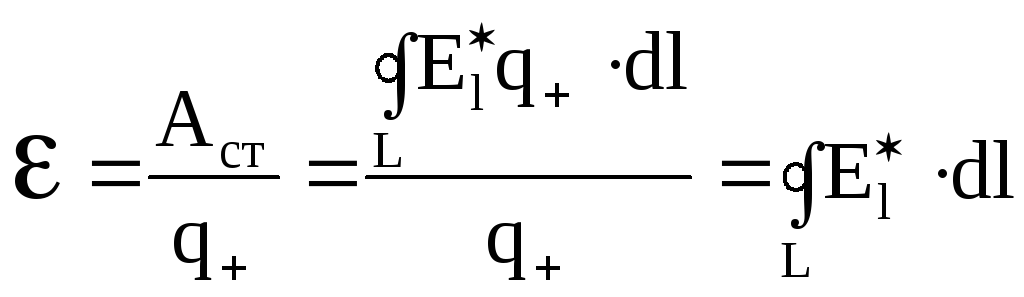. (5.17)

При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля (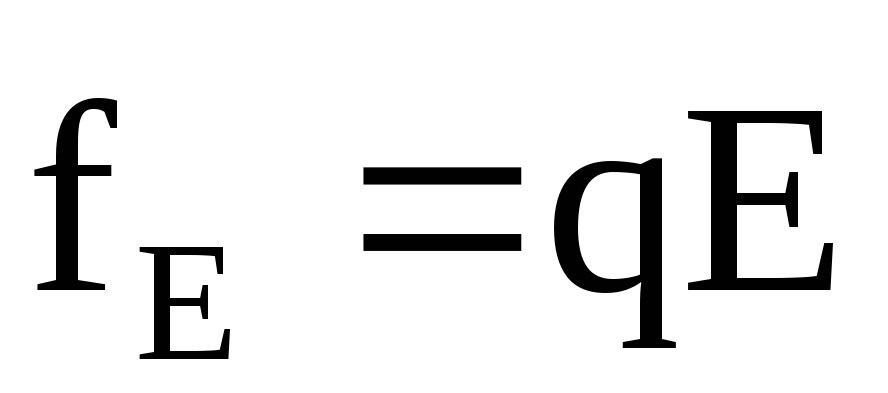). Следовательно, в любой точке цепи на заряд q действует результирующая сила:

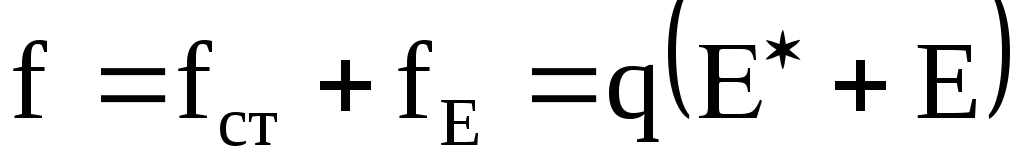. (5.18)

Работа, совершаемая этой силой на участке 1 – 2,

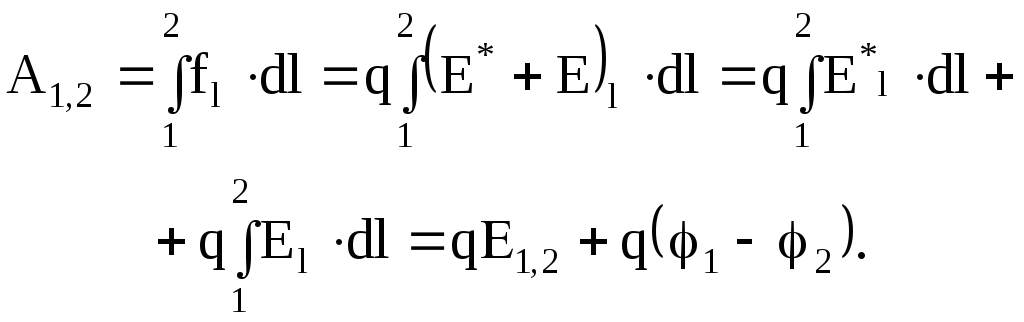(5.19)

Физическая величина, численно равная работе сторонних и электрических сил по перемещению положительного единичного заряда на данном участке цепи, называется падением напряжения или напряжением на данном участке цепи:

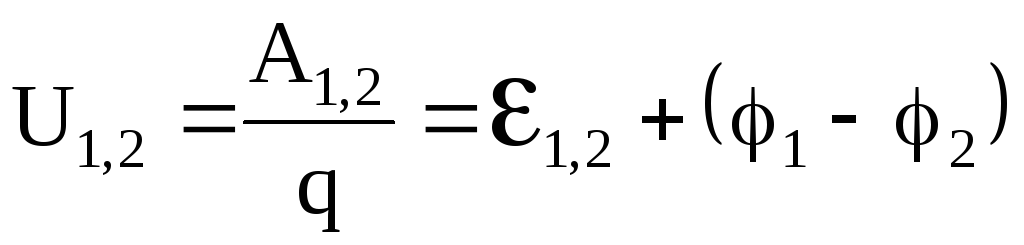. (5.20)

Если на участке цепи отсутствует ЭДС (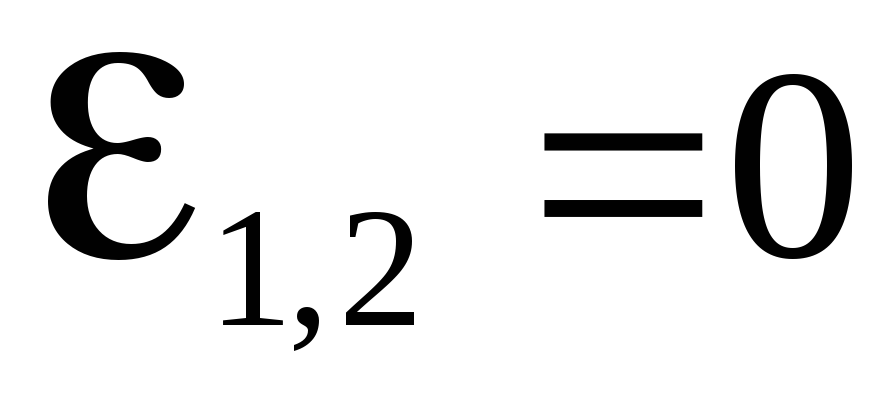

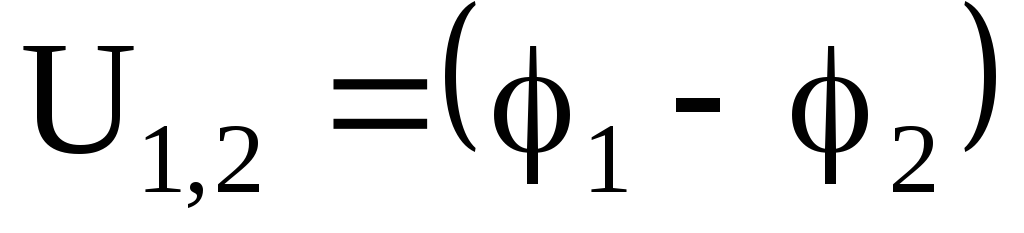), то

. (5.21)

При ₁ — ₂ = 0,

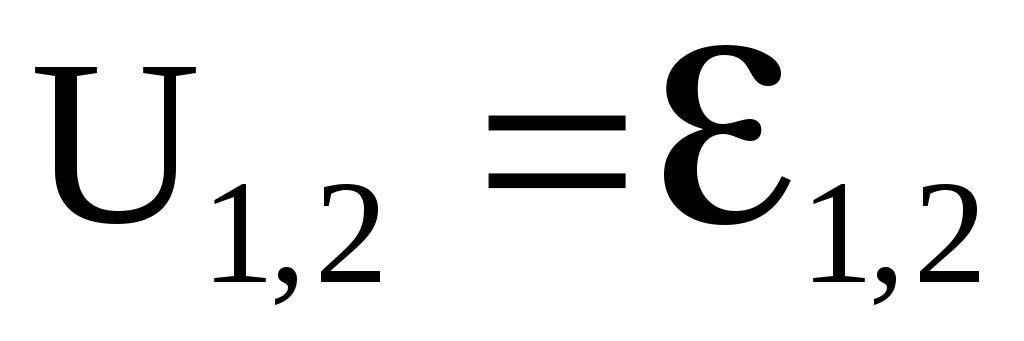. (5.22)

Измеряются , U, (₁ — ₂) в системе СИ в вольтах (1 В).

Лекция 6. Классическая электронная теория проводимости металлов. Законы постоянного тока

Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах.

Электрическое сопротивление проводников. Изменение сопротивления проводников от температуры и давления. Сверхпроводимость. Соединения сопротивлений: последовательное, параллельное, смешанное. Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам. Правила (законы) Кирхгофа и их применение к расчету простейших электрических цепей. Закон Джоуля-Ленца в дифференциальной и интегральной формах. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД) источника постоянного тока.

6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах

Классическая электронная теория проводимости металлов объясняет различные электрические свойства веществ существованием и движением в них так называемых квазисвободных электронов проводимости. Электроны проводимости при этом рассматриваются как электронный газ, подобный идеальному газу молекулярной физики.

До открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускали электрический ток. После чего исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу различных металлов не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Опыты доказали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.

Прямым доказательством, что электрический ток в металлах обусловливается движением электронов, были опыты Толмена и Стюарда, проведенные в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.

Представим себе проводящую катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжают движение по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

Обозначим линейное ускорение катушки при торможении – a. Оно направлено по касательной к поверхности катушки. При достаточно плотной намотке и тонких проводах можно считать, что ускорение направлено вдоль проводов. При торможении катушки к каждому свободному электрону приложена сила инерции F_ин = m_ea, направленная противоположно ускорению. Под ее действием электрон ведет себя в металле так, как если бы на него действовало эффективное электрическое поле с напряженностью

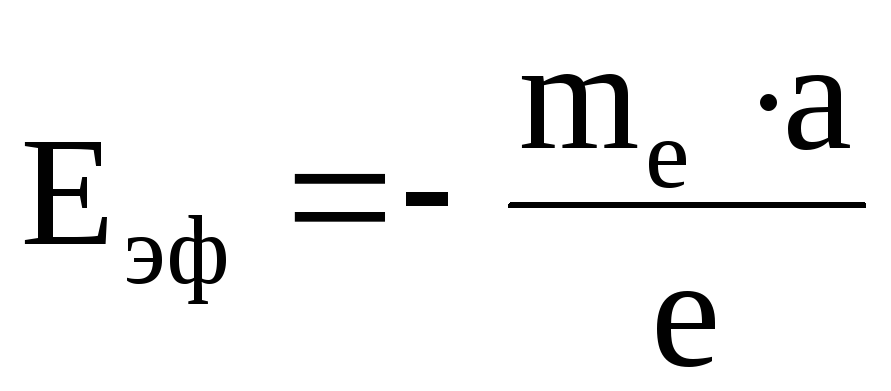. 6.1)

Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов,

, (6.2)

где L – длина провода на катушке.

Все точки провода тормозятся с одинаковым ускорением, и поэтому ускорение вынесено за знак интеграла.

С учетом формулы (6.2) запишем закон Ома для замкнутой цепи в виде

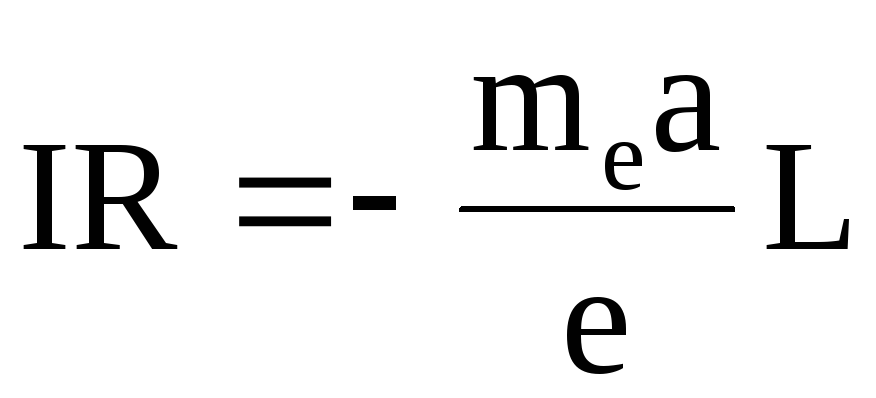, (6.3)

где I – сила тока в замкнутой цепи;

R – сопротивление всей цепи, включая сопротивление проводов катушки, проводов внешней цепи и гальванометра.

Количество электричества, протекшее через поперечное сечение проводника в течение времени dt при силе тока I,

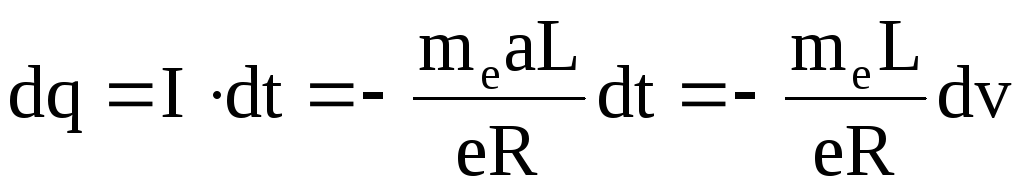. (6.4)

Поэтому в течение времени торможения катушки от начальной линейной скорости v_o до полной остановки через гальванометр пройдет количество электричества

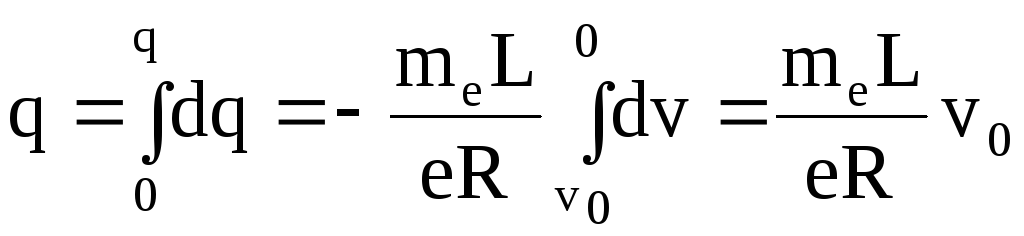. (6.5)

Значение q определяется по гальванометру, а значения L, R, v_o известны. Поэтому можно найти как знак, так и абсолютное значение e/m_e. Эксперименты показали, что e/m_e соответствует отношению заряда электрона к его массе. Таким образом, было доказано, что наблюдаемый с помощью гальванометра ток обусловлен движением электронов.

В отсутствие электрического поля в проводниках электроны проводимости движутся хаотично, в произвольных направлениях со скоростями, обусловленными температурой, т.е. с так называемой тепловой скоростью u.

Через определенный промежуток времени t = , двигаясь по прямой, электрон проводимости может провзаимодействовать с ионом кристаллической решетки или с другим электроном проводимости. В результате такого взаимодействия, а оно считается в классической теории проводимости абсолютно упругим, сохраняются полные импульс и энергия, а величина и направление скорости движения могут измениться. Предельным является случай, когда через время, равное  (время свободного пробега), направление скорости теплового движения электрона проводимости изменяется на противоположное. Время свободного пробега зависит от природы вещества и тем меньше, чем чаще происходят взаимодействия. Между соударениями (взаимодействиями) со скоростью u ничего не происходит.

П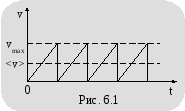ри наложении электричес-кого поля с напряженностьюE под действием силы F = eE эле-ктроны проводимости приобре-тают некоторое ускорение a и направленное движение с изме-няющейся скоростью от v_o = 0 до v = v_max за время t = .

Изменение скорости направленного движения электрона проводимости происходит до его взаимодействия (рис. 6.1). В результате взаимодействия эта скорость так же может измениться как по величине, так и по направлению.

Если в единице объема проводника n электронов проводимости, которые в некоторый момент времени t обладают скоростью v, то можно определить заряд, прошедший через некоторую площадку S, расположенную перпендикулярно направлению скорости движения электронов проводимости:

, (6.6)

где <v> — средняя скорость упорядоченного движения электронов проводимости.

Сила (величина) тока в проводнике в этом случае

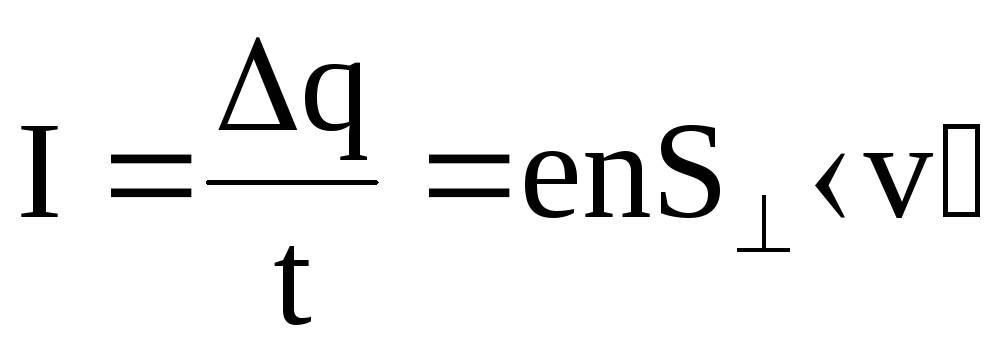. (6.7)

Плотность тока проводимости

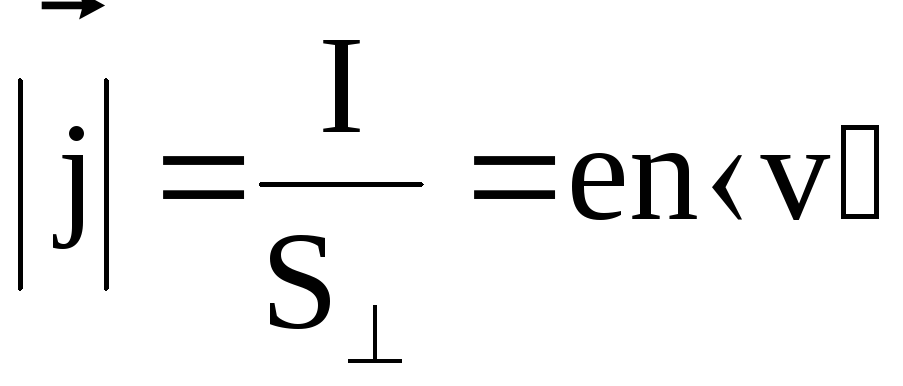. (6.8)

В векторной форме

. (6.9)

Согласно (6.8) для определения плотности электрического тока в проводнике необходимо определить среднюю скорость упорядоченного движения электронов проводимости.

Средняя скорость упорядоченного движения в данном случае может быть определена по формуле

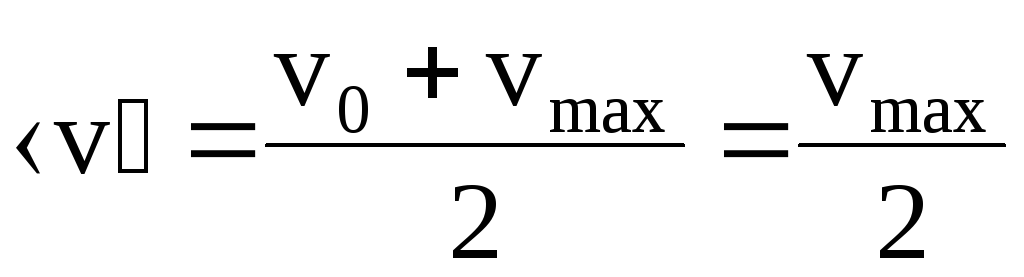, (6.10)

т.к. в начальный момент времени t=0, когда отсутствует электрическое поле, v_o=0.

Максимальная скорость упорядоченного движения, которую приобретает электрон под действием электрического поля за время свободного пробега,

,

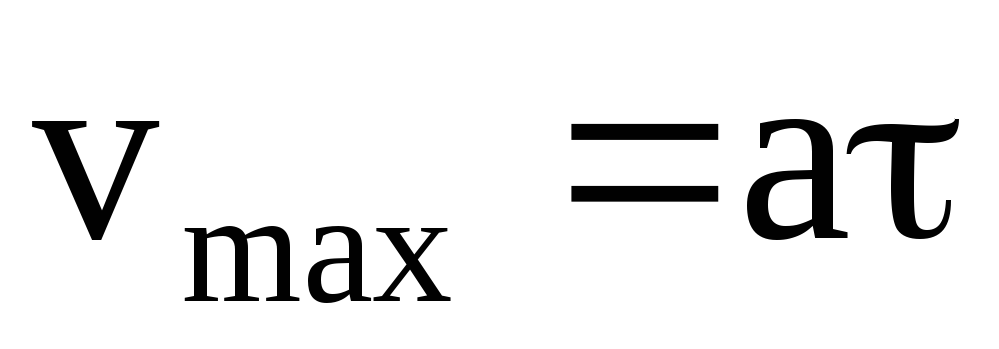где a – ускорение, приобретаемое электроном проводимости под действием электрического поля;

 – время пробега электрона проводимости от взаимодействия до взаимодействия.

На основании второго закона Ньютона F = ma, где F — кулоновская сила,

F = eE.

Имеем:

;

;

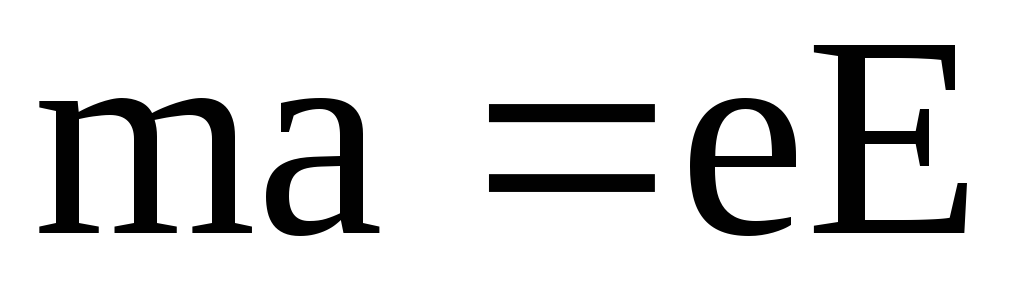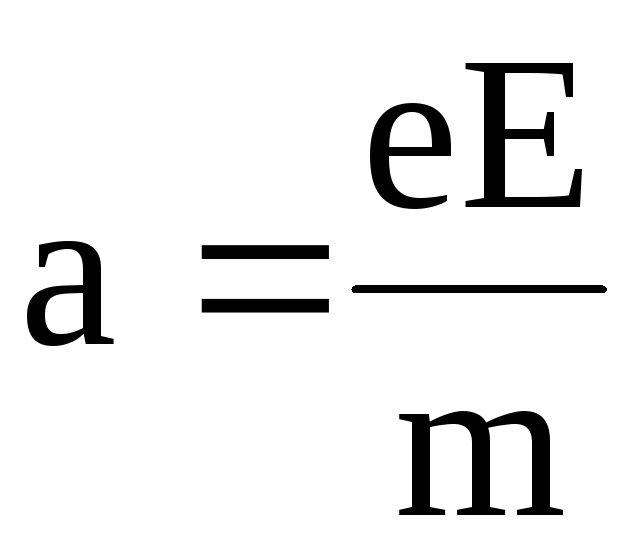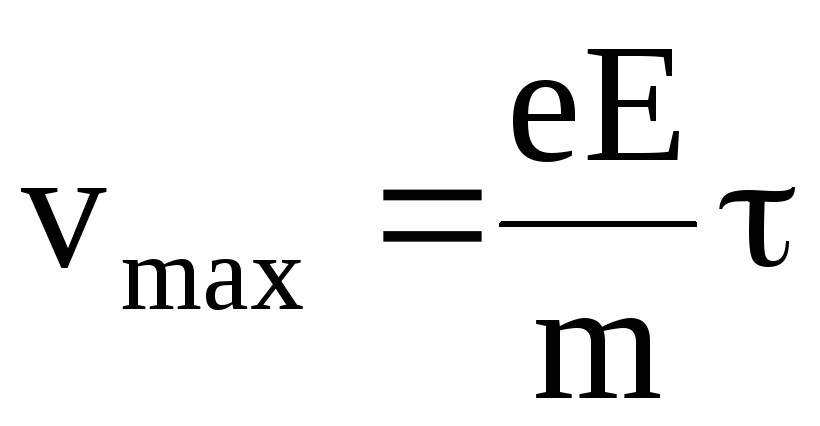. (6.11)

Для средней скорости упорядоченного движения электронов проводимости получим

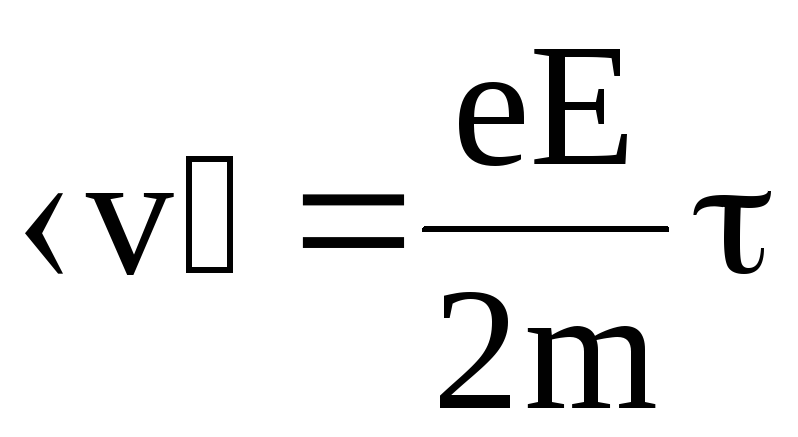. (6.12)

Зная среднюю скорость теплового движения электронов проводимости и среднее расстояние, проходимое ими от взаимодействия до взаимодействия, можно определить время между двумя последующими взаимодействиями:

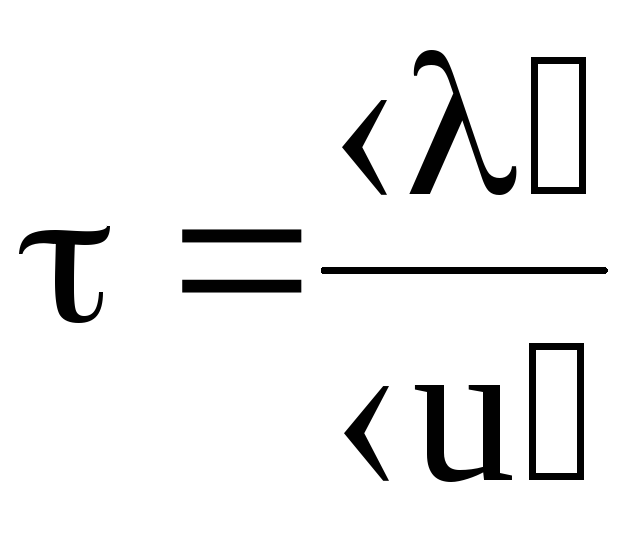. (6.13)

Сделав подстановку и необходимые преобразования, для плотности тока проводимости будем иметь

, (6.14)

где 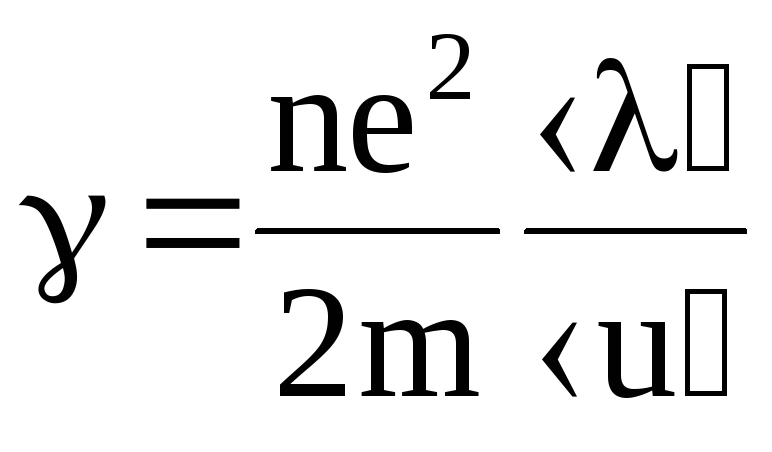— удельная электропроводность металла проводника.

В векторной форме

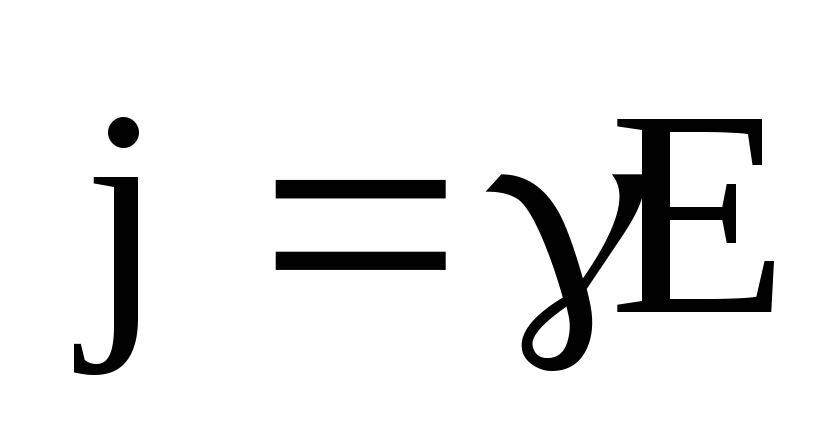. (6.15)

Выражения (6.14) и (6.15) являются математической формой записи закона Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любых проводников, любых токов, характеризует плотность тока проводимости в любой точке проводника.

Из закона Ома в дифференциальной форме можно получить закон Ома в интегральной форме для замкнутой (или полной) цепи. Для чего выражение (6.15) умножим на величину элементарного участка цепи dl:

,

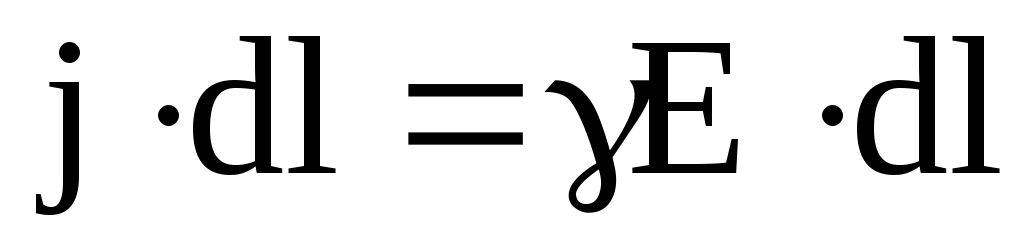где ;;.

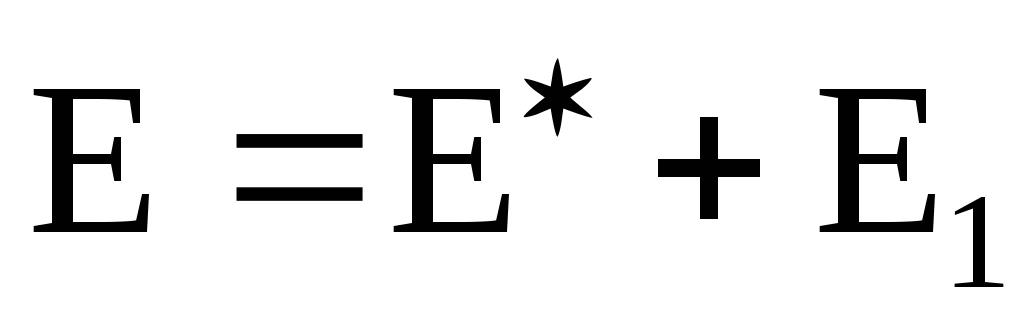Таким образом, имеем

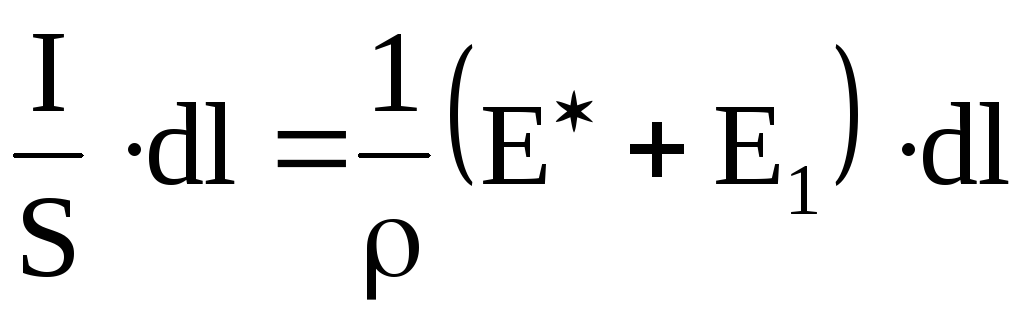
или

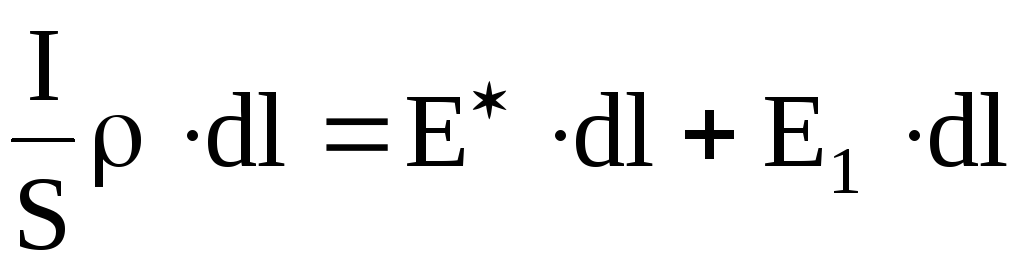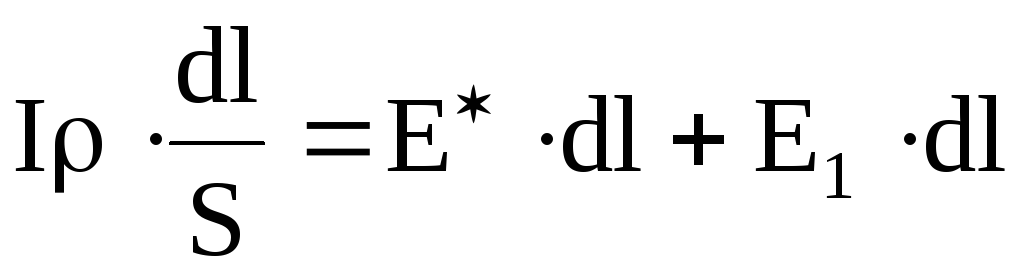; . (6.16)

Проинтегрировав выражение (6.16) по замкнутому контуру L, получим

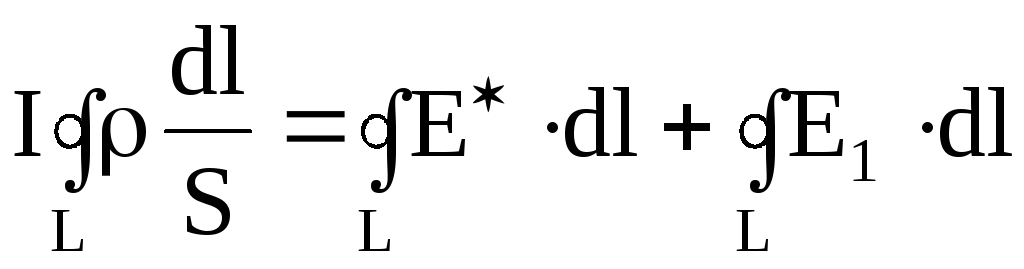, (6.17)

где 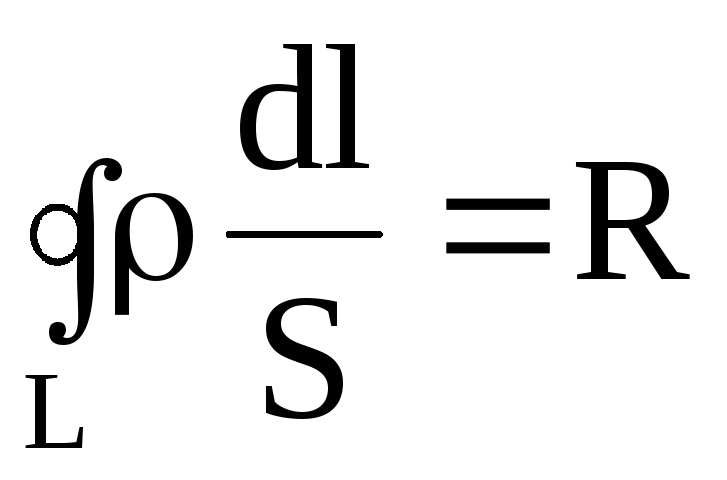– сопротивление внешнего и внутреннего участков цепи;

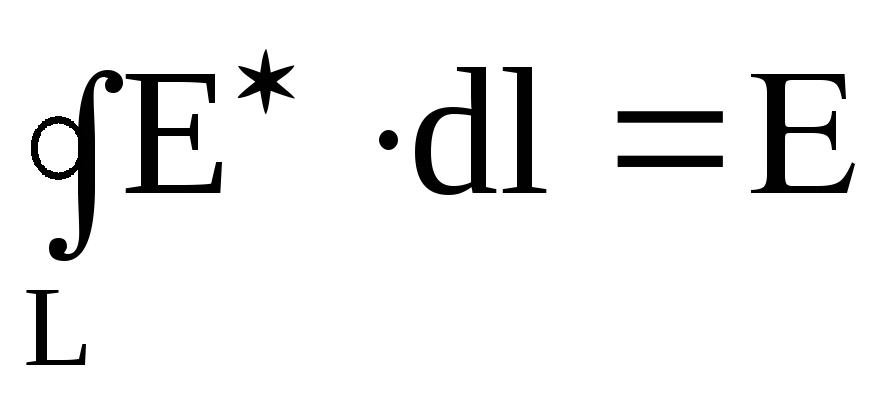–ЭДС, действующая в замкнутой цепи, численно равная циркуляции вектора напряженности поля сторонних сил;

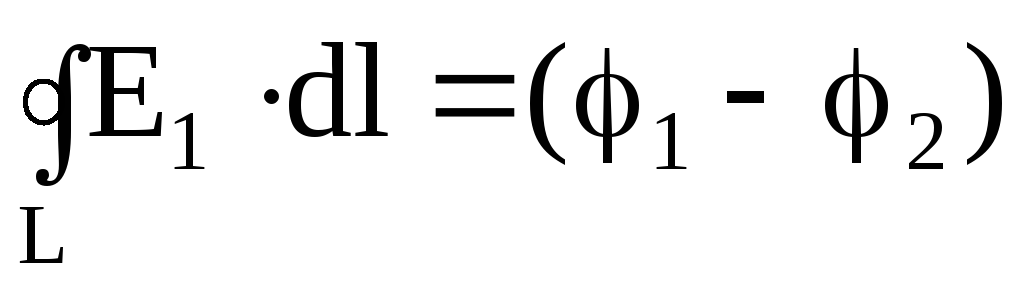–разность потенциалов между двумя рассматриваемыми точками замкнутой цепи.

Для замкнутой цепи

(₁ — ₂) = 0; .

Таким образом, имеем

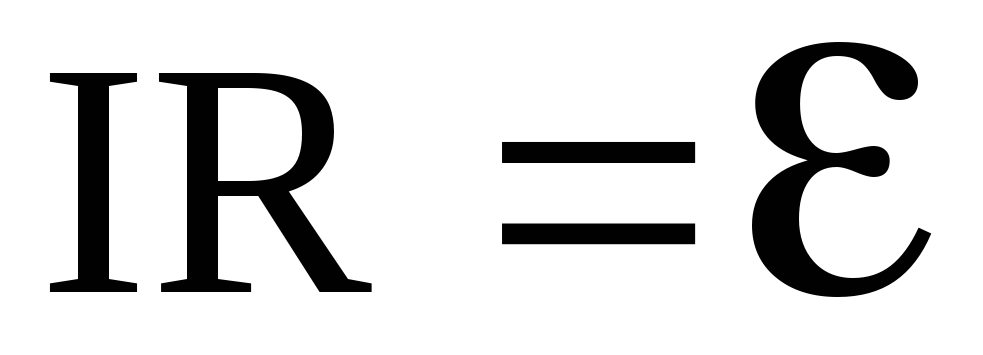или , (6.18)

где R₁ – сопротивление внешнего участка цепи;

r – внутреннее сопротивление источника тока.

Из формулы (6.18)

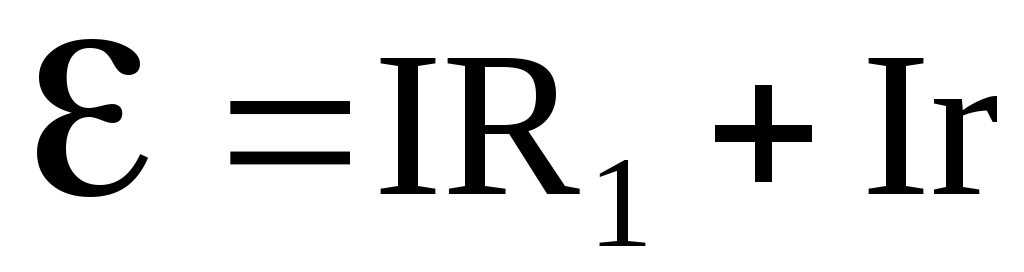. (6.19)

Следовательно, ЭДС уравновешивает падение напряжения во внешней и внутренней цепи и тем самым обеспечивает непрерывное движение электронов проводимости.

Если цепь не замкнута и в ней отсутствует ЭДС, то

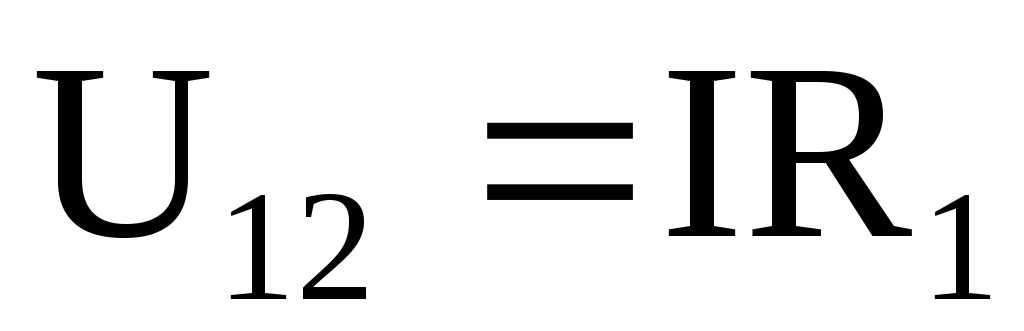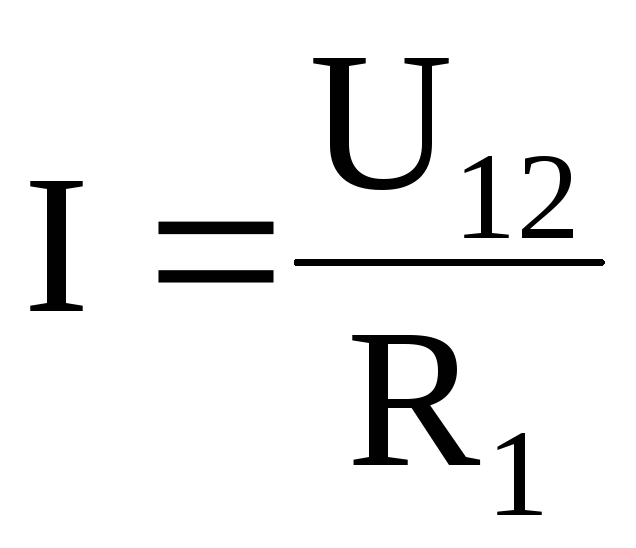, а . (6.20)

Выражения (6.18) и (6.20) являются математической формой записи закона Ома, соответственно, для полной (замкнутой) цепи и участка цепи, который был открыт им экспериментально. Сила тока в цепи прямопропорциональна ЭДС (напряжению на участке цепи) и обратно пропорциональна сопротивлению цепи.

Понятие силы тока, ЭДС и разности потенциалов?

Электрическим током называют упорядоченное движение заряженных частиц (тел). За направление движение электрического тока условно принимают направление движения положительных зарядов. Проходящий через какую-то поверхность электрический ток характеризуется силой тока I. Сила тока является скалярной величиной, численно равная количеству электричества, проходящего через площадь S за единицу времени:

Если за любые равные промежутки времени через любое сечение проводника проходит одинаковое количество электричества с неизменным направлением зарядов, то такой ток называется постоянным:

Сила тока в Международной системе единиц (СИ) является основной и носит название Ампер. Из уравнения (1а) следует определение единицы заряда:

В системе СГС сила тока измеряется в СГС_I, согласно (1а) получим:

Распределение электрического тока по сечению проводника характеризуют плотностью тока, которую можно выразить формулой:

В случае постоянного тока его плотность будет одинакова и равна:

Плотность тока j является векторной величиной, направленной вдоль тока и численно  равная количеству электричества, протекающему через единицу площади, ориентированной перпендикулярно направлению протекания тока, за единицу времени, в системе СИ плотность тока измеряют в А/м².

Важно отметить, что различают несколько видов электрического тока. Предположим, что в пространстве перемещается какое-то заряженное макроскопическое тело (шар, например). Поскольку вместе с этим телом будут перемещаться и заряды, то возникнет направленное движение электрических зарядов – электрический ток. Электрический ток, связанный с движением заряженных макроскопических тел называют конвекционным.

Если огромное количество заряженных частиц упорядоченно перемещаются внутри какого-нибудь тела вследствие того, что в нем создано электрическое поле, то данное явление будет носить название ток проводимости. Для его получения необходимо наличие источника тока и  замкнутой цепи. Вектор напряженности поля Е имеет направление от положительного заряда к отрицательному. Отсюда следует, что находящиеся внутри проводника отрицательные заряженные частицы будут двигаться против поля, а положительные – по полю.

Если электрические заряды движутся под влиянием внешнего поля в вакууме, то данное явление называют электрический ток в вакууме.

Более детально остановимся на отдельных закономерностях, которые больше характерны для тока проводимости.

Представим, что на концах определенного проводника длиной l существует разность потенциалов Δφ = φ₁ – φ₂, которая создает внутри этого проводника электрическое поле Е, направленное в сторону падения потенциала (рисунок ниже):

Согласно формуле:

При этом в проводнике возникнет электрический ток, который будет идти от большего потенциала (φ₁) к меньшему (φ₂).

Движение зарядов от φ₁ к φ₂ приводит к выравниванию потенциалов во всех точках. При этом в проводнике исчезает электрическое поле, и протекание электрического тока прекращается. Отсюда следует, что обязательным условием существования электрического тока является наличие разности потенциалов Δφ = φ₁ – φ₂ ≠ 0, а для его поддержания необходимо специальное устройство, которое будет поддерживать данную разницу потенциалов. Это устройство называют источник тока.

В качестве источников тока могут использовать электрические генераторы, аккумуляторы, термоэлементы и гальванические элементы. Источник тока также выполняет еще одну задачу – замыкает электрическую цепь, по которой и осуществляется непрерывное движение заряженных частиц. Электрический ток протекает по внутренней части – источнику тока, и внешней – проводнику. В источнике тока имеется два полюса – положительный с более высоким потенциалом и отрицательный с более низким потенциалом. При разомкнутой внешней цепи на положительном полюсе источника образуется недостаток электронов, а на отрицательном наоборот – переизбыток. В источнике тока разделение зарядов производят с помощью сторонних сил – направленных против кулоновских сил, действующих на разноименные заряды в проводниках самого источника тока. Сторонние силы могут иметь самое различное происхождение – химическое, биологическое, тепловое, механическое и другое.

Если электрическая цепь замкнута, то по ней протекает электрический ток и при этом совершается работа сторонних сил. Данная работа складывается из работы, совершаемой внутри самого источника тока против сил электрического поля (А_ист), и работы, совершаемой против механических сил сопротивления среды источника (А^/), то есть:

Электродвижущая сила источника тока – это величина, которая равна отношению работы, совершаемой сторонними силами при перемещении положительного точечного заряда вдоль всей электрической цепи, включая и источник тока, к заряду:

По определению работа против сил электрического поля равна:

А^/ = 0 если полюсы источника разомкнуты, и тогда из формулы (5) следует:

Отсюда следует, что электродвижущая сила источника тока при разомкнутой внешней цепи будет равна разности потенциалов на его полюсах.

Потенциал. Разность потенциалов.

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду: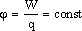

  — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

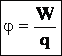
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.

— следствие принци­па суперпозиции полей (потенциалы складываются алгебраически).

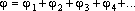
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

В СИ потенциал измеряется в вольтах: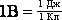

 Разность потенциалов

 

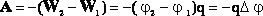
Напряжение — разность значений потенциала в начальной и конечной точках траектории.

Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.

Разность потенциалов (напряжение) не зависит от выбора

системы координат!

Единица разности потенциалов

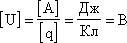
напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

Из этого соотношения видно:

1. Вектор напряженности направлен в сторону уменьшения потенциала.

2. Электрическое поле существует, если существует разность потенциалов.

3. Единица напряженности: —Напряженность поля равна

Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величи­на, равная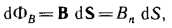

Поток вектора магнитной индук­ции Ф_в через произвольную поверхность S равен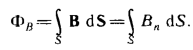

Теорема Гаусса для поля В: поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю:

полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

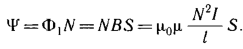
Проводники в электростатическом поле. Электроемкость уединенного проводника.

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действо­вать электростатическое поле, в результа­те чего они начнут перемещаться. Переме­щение зарядов (ток) продолжается до тех пор, пока не установится равновесное рас­пределение зарядов, при котором электро­статическое поле внутри проводника обра­щается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напря­женность поля во всех точках внутри проводника равна нулю:

Е = 0.

По гауссу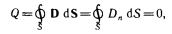

Величину

С = Q/ф

называют электроемкостью (или просто емкостью) уединенного проводника. Ем­кость уединенного проводника определяет­ся зарядом, сообщение которого провод­нику изменяет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от мате­риала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциа­ла. Сказанное не противоречит формуле, так как она лишь показывает, что емкость уединенного проводника прямо пропорциональна его заряду и обратно пропорциональна потенциалу.

Единица электроемкости — фарад (Ф): 1Ф

ЭДС

Разность потенциалов и электродвижущая сила

Тело можно наэлектризовать (т. е. прибавить к нему некоторое количество электронов или отнять их), тогда оно станет обладать  электрическим потенциалом или просто потенциалом тела. В результате, тело, заряженное положительно, станет обладать положительным потенциалом, а тело, заряженное отрицательно, — отрицательным потенциалом.

Разность уровней электрических зарядов двух тел принято называть разностью электрических потенциалов или просто разностью потенциалов. Следует иметь в виду, что если два одинаковых тела заряжены одноименными зарядами, но одно больше, чем другое, то между ними также будет существовать разность потенциалов. Кроме того, разность потенциалов существует между двумя такими телами, одно из которых заряжено, а другое не имеет заряда. Итак, если два тела заряжены таким образом, что потенциалы их неодинаковы, между ними неизбежно существует разность потенциалов.

Говоря о разности потенциалов, мы имеем в виду два заряженных тела, однако разность потенциалов можно получить и между различными частями (точками) одного и того же тела. Так, например, приложим внешнюю силу к  куску медной проволоки,  под действием которой свободные электроны, находящиеся в проволоке, переместятся к одному ее концу. Очевидно, на другом конце проволоки получится недостаток электронов, и тогда между концами проволоки возникнет разность потенциалов. Стоит нам прекратить действие внешней силы, как электроны тотчас же, в силу притяжения разноименных зарядов, устремятся к концу проволоки, заряженному положительно, т. е. к месту, где их недостает, и в проволоке вновь наступит электрическое равновесие.

Для поддержания электрического тока в проводнике необходим внешний источник энергии, который все время поддерживал бы разность потенциалов на концах этого проводника. Протекание электрического тока сопровождается непрерывным расходованием энергии на преодоление сопротивления. Эту энергию доставляет источник электрической энергии, в котором происходит процесс преобразования механической, химической, тепловой или других видов энергии в электрическую. Способность источника электрической энергии создавать и поддерживать на своих зажимах определенную разность потенциалов называется электродвижущей силой, сокращенно э. д. с.

Численно электродвижущая сила измеряется работой, совершаемой источником электрической энергии при переносе единичного положительного заряда по всей замкнутой цепи. Если источник энергии, совершая работу A, обеспечивает перенос по всей замкнутой цепи заряда q, то его электродвижущая сила (Е) будет равна

E=A/q

За единицу измерения электродвижущей силы в системе СИ принимается вольт (в). Источник электрической энергии обладает эдс в 1 вольт, если при перемещении по всей замкнутой цепи заряда в 1 кулон совершается работа, равная 1 джоулю. Физическая природа электродвижущих сил в разных источниках весьма различна.

Самоиндукция — возникновение ЭДС индукции  в замкнутом проводящем контуре при изменении тока, протекающего по контуру. 

При изменении тока I в контуре пропорционально меняется и магнитный поток B через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС E. Это явление и называется самоиндукцией. 

Понятие родственно понятию взаимоиндукции, являясь его частным случаем.

 

Источники:  

http://electricalschool.info/main/osnovy/390-pro-raznost-potencialov.html

http://jamshyt.ru/wnopa/f/?p=21

 http://ru.wikipedia.org/

7.2. Разность потенциалов, электродвижущая сила, напряжение.

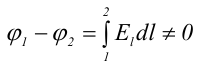
Величина, равная работе сторонних сил по переносу единичного положительного заряда по данному участку цепи называется электродвижущей силой (ЭДС), на данном участке

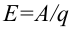
Падение напряжения (или просто напряжение) на данном участке цепи называется величина, численно равная работе, совершаемой электрическими и сторонними силами при перемещении по данному участку единичного положительного заряда

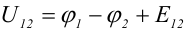
7.3. Закон Ома.

Сила тока на однородном участке цепи пропорциональна падению напряжения на участке

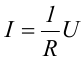
здесь R − электрическое сопротивление проводника, которое зависит от его формы, размеров и свойств материала, из которого изготовлен проводник.

Для однородного цилиндрического проводника

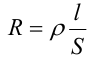
7.4. Работа, мощность и тепловое действие тока. Закон Джоуля-Ленца.

Мощность, развиваемая током на этом участке

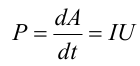
Форма выделяемой при этом энергии зависит от природы физических факторов, обуславливающих падение потенциала.

Это может быть и механическая работа (электродвигатель), и магнитная энергия, и тепловая энергия.

Если падение потенциала происходит на оммическом сопротивлении проводника, то вся энергия выделяется в виде тепла с мощностью

Это выражение называется закон Джоуля−Ленца.

8.1. Законов Ома и Джоуля-Ленца в дифференциальной форме (вывод).

Закон Ома в дифференциальной форме

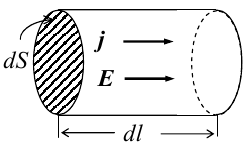В изотропном проводнике направление векторов j и E совпадают. Выделим в проводнике трубкутока (поверхность, образованную линиями тока) в проводнике. Пусть площадь сечения ее dS а длина dl.

Ток через площадку dS будет

С другой стороны

или в векторном виде получаем соотношение, называемое законом Ома в дифференциальной форме

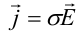
Дифференциальная форма закона Джоуля−Ленца

Применим закон Джоуля−Ленца к малому цилиндру длиной dl и площадью сечения dS, тогда получим

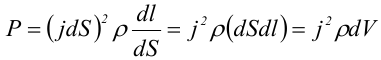
Введем удельную мощность тока, равную количеству тепла, выделившемуся в единице объема в единицу времени

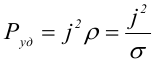
Отсюда, используя закон Ома , получаем закон Джоуля−Ленца в дифференциальной форме

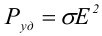
Можно также записать этот закон несколько в ином виде

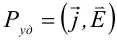
9.1. Магнитное поле. Вектор магнитной индукции.

По аналогии с полевой трактовкой кулоновского взаимодействия, возникновение силы Ампера можно представить следующим образом: ток I1 рождает в окружающем пространстве магнитное поле; это магнитное поле действует на постоянные магниты или движущиеся заряды (ток I2).

Существование магнитного поля убедительно доказал в серии своих опытов по ориентирующему действию поля тока на магнитные стрелки Эрстед (1820 г.). Из опытов Эрстеда следует, что магнитное поле имеет направленный характер и, следовательно, должно характеризоваться векторной величиной. Эту величину называют магнитной индукцией и обозначают символом B.

Опыт показывает, что для магнитного поля, так же как и для электрического, справедлив принцип суперпозиции.

Вектор магнитной индукции B в данной точке поля совпадает по направлению с силой, которая действует на северный полюс бесконечно малой магнитной стрелки, помещенной в эту точку.

5.3. Электродвижущая сила (эдс), напряжение и разность потенциалов. Их физический смысл. Связь между эдс, напряжением и разностью потенциалов

Физическая величина, равная работе сторонних сил по перемещению положительного единичного заряда вдоль всей цепи, включая источник тока, называется электродвижущей силой источника тока (ЭДС) :

. (5.15)

Работа сторонних сил вдоль замкнутой цепи

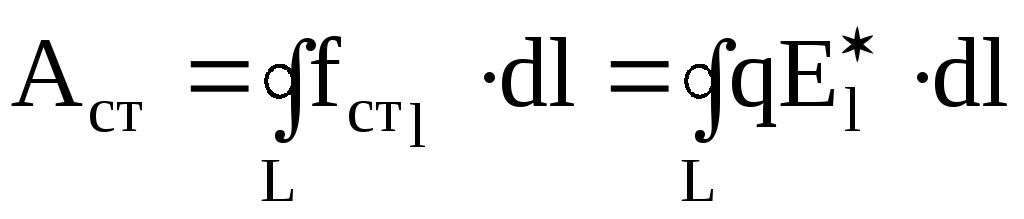, (5.16)

где E^* – напряженность поля сторонних сил.

Тогда

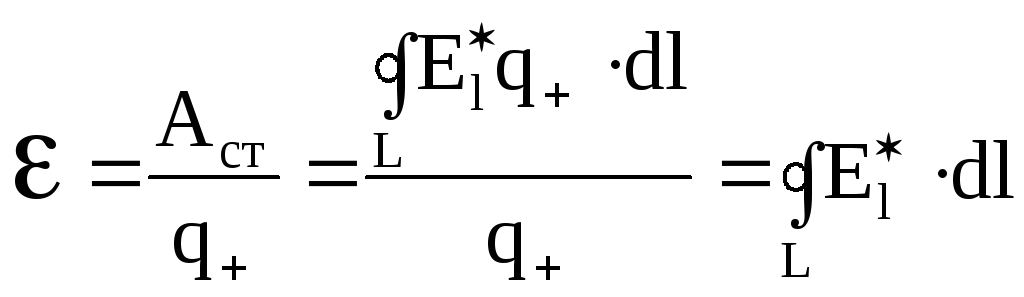. (5.17)

При движении зарядов в проводнике кроме сторонних сил на них действуют силы электростатического поля (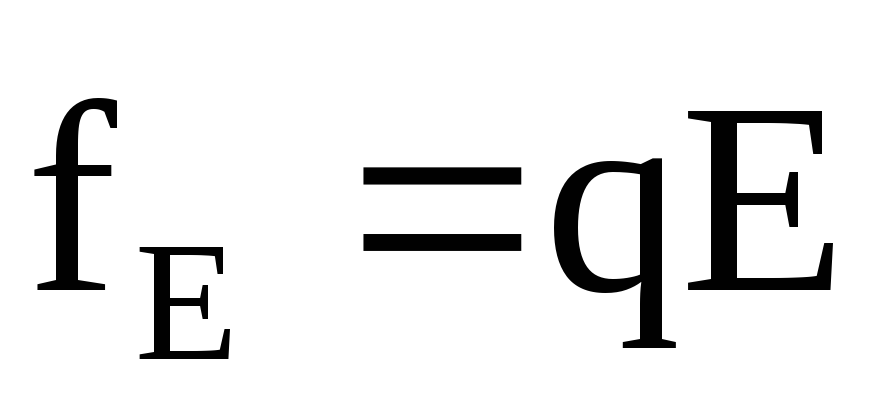). Следовательно, в любой точке цепи на заряд q действует результирующая сила:

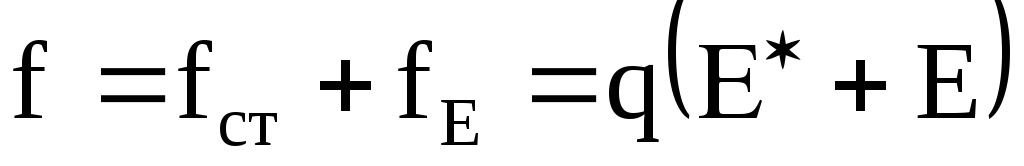. (5.18)

Работа, совершаемая этой силой на участке 1 – 2,

(5.19)

Физическая величина, численно равная работе сторонних и электрических сил по перемещению положительного единичного заряда на данном участке цепи, называется падением напряжения или напряжением на данном участке цепи:

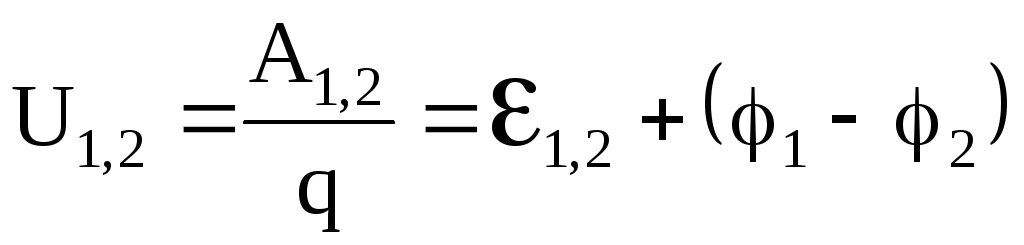. (5.20)

Если на участке цепи отсутствует ЭДС (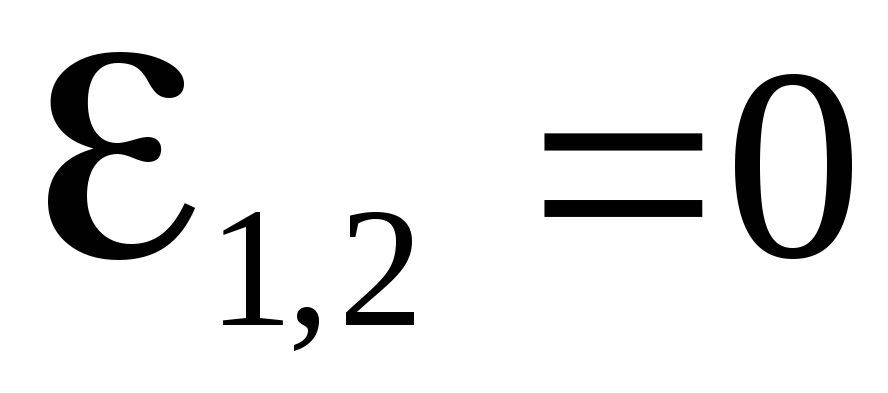), то

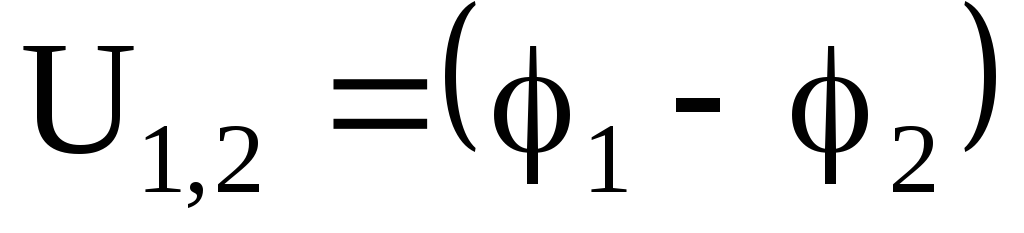. (5.21)

При ₁ — ₂ = 0,

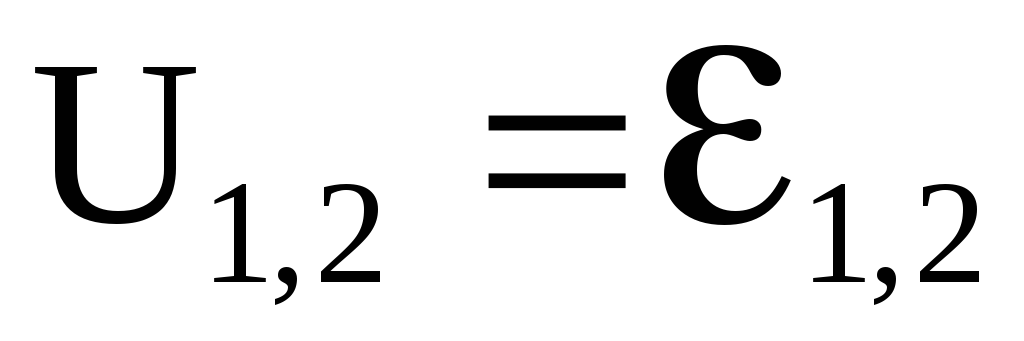. (5.22)

Измеряются , U, (₁ — ₂) в системе СИ в вольтах (1 В).

Лекция 6. Классическая электронная теория проводимости металлов. Законы постоянного тока

Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах. Электрическое сопротивление проводников. Изменение сопротивления проводников от температуры и давления. Сверхпроводимость. Соединения сопротивлений: последовательное, параллельное, смешанное. Шунтирование электроизмерительных приборов. Добавочные сопротивления к электроизмерительным приборам. Правила (законы) Кирхгофа и их применение к расчету простейших электрических цепей. Закон Джоуля-Ленца в дифференциальной и интегральной формах. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (КПД) источника постоянного тока.

6.1. Классическая электронная теория электропроводности металлов и ее опытные обоснования. Закон Ома в дифференциальной и интегральной формах

Классическая электронная теория проводимости металлов объясняет различные электрические свойства веществ существованием и движением в них так называемых квазисвободных электронов проводимости. Электроны проводимости при этом рассматриваются как электронный газ, подобный идеальному газу молекулярной физики.

До открытия электронов было экспериментально показано, что прохождение тока в металлах не связано, в отличие от тока в жидких электролитах, с переносом вещества металла. Опыт состоял в том, что через контакт двух различных металлов, например золота и серебра, в течение времени, исчисляемого многими месяцами, пропускали электрический ток. После чего исследовался материал вблизи контактов. Было показано, что никакого переноса вещества через границу различных металлов не наблюдается и вещество по различные стороны границы раздела имеет тот же состав, что и до пропускания тока. Опыты доказали, что атомы и молекулы металлов не принимают участия в переносе электрического тока, но они не ответили на вопрос о природе носителей заряда в металлах.

Прямым доказательством, что электрический ток в металлах обусловливается движением электронов, были опыты Толмена и Стюарда, проведенные в 1916 г. Идея этих опытов была высказана Мандельштамом и Папалекси в 1913 г.

Представим себе проводящую катушку, которая может вращаться вокруг своей оси. Концы катушки с помощью скользящих контактов замкнуты на гальванометр. Если находящуюся в быстром вращении катушку резко затормозить, то свободные электроны в проволоке продолжают движение по инерции, в результате чего гальванометр должен зарегистрировать импульс тока.

Обозначим линейное ускорение катушки при торможении – a. Оно направлено по касательной к поверхности катушки. При достаточно плотной намотке и тонких проводах можно считать, что ускорение направлено вдоль проводов. При торможении катушки к каждому свободному электрону приложена сила инерции F_ин = m_ea, направленная противоположно ускорению. Под ее действием электрон ведет себя в металле так, как если бы на него действовало эффективное электрическое поле с напряженностью

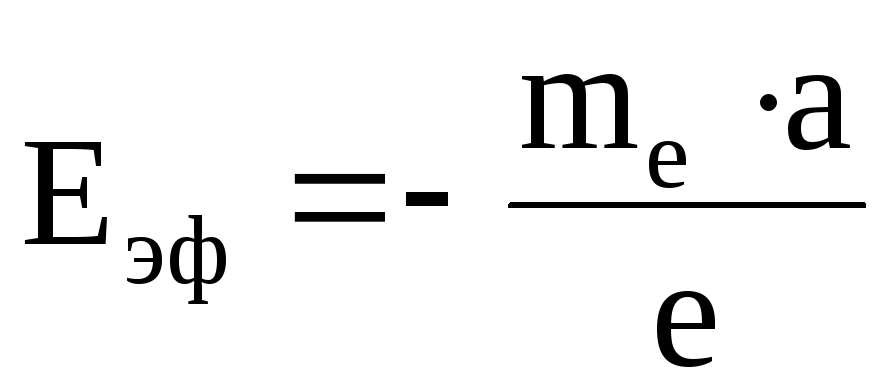. 6.1)

Поэтому эффективная электродвижущая сила в катушке, обусловленная инерцией свободных электронов,

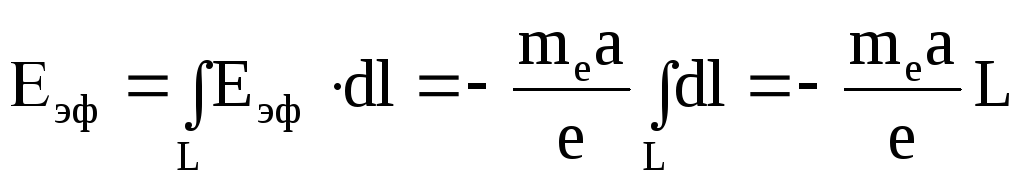, (6.2)

где L – длина провода на катушке.

Все точки провода тормозятся с одинаковым ускорением, и поэтому ускорение вынесено за знак интеграла.

С учетом формулы (6.2) запишем закон Ома для замкнутой цепи в виде

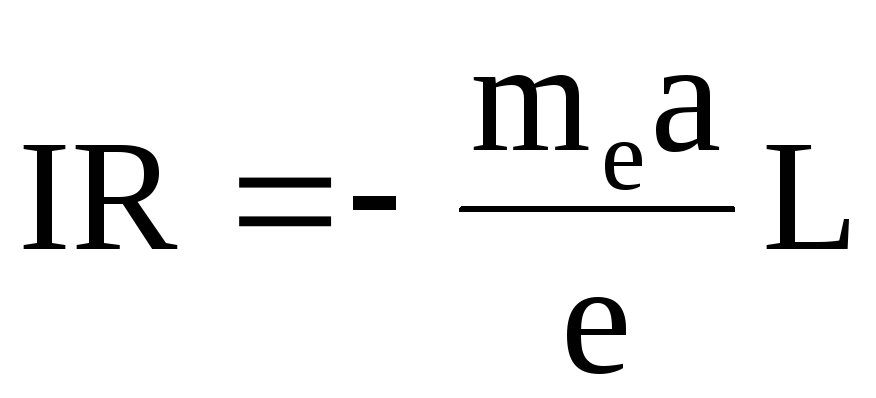, (6.3)

где I – сила тока в замкнутой цепи;

R – сопротивление всей цепи, включая сопротивление проводов катушки, проводов внешней цепи и гальванометра.

Количество электричества, протекшее через поперечное сечение проводника в течение времени dt при силе тока I,

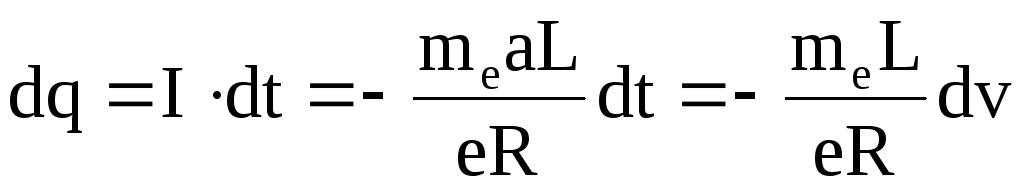. (6.4)

Поэтому в течение времени торможения катушки от начальной линейной скорости v_o до полной остановки через гальванометр пройдет количество электричества

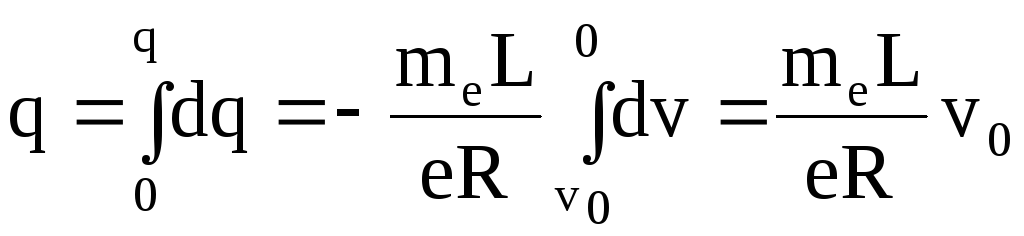. (6.5)

Значение q определяется по гальванометру, а значения L, R, v_o известны. Поэтому можно найти как знак, так и абсолютное значение e/m_e. Эксперименты показали, что e/m_e соответствует отношению заряда электрона к его массе. Таким образом, было доказано, что наблюдаемый с помощью гальванометра ток обусловлен движением электронов.

В отсутствие электрического поля в проводниках электроны проводимости движутся хаотично, в произвольных направлениях со скоростями, обусловленными температурой, т.е. с так называемой тепловой скоростью u.

Через определенный промежуток времени t = , двигаясь по прямой, электрон проводимости может провзаимодействовать с ионом кристаллической решетки или с другим электроном проводимости. В результате такого взаимодействия, а оно считается в классической теории проводимости абсолютно упругим, сохраняются полные импульс и энергия, а величина и направление скорости движения могут измениться. Предельным является случай, когда через время, равное  (время свободного пробега), направление скорости теплового движения электрона проводимости изменяется на противоположное. Время свободного пробега зависит от природы вещества и тем меньше, чем чаще происходят взаимодействия. Между соударениями (взаимодействиями) со скоростью u ничего не происходит.

П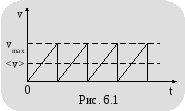ри наложении электричес-кого поля с напряженностьюE под действием силы F = eE эле-ктроны проводимости приобре-тают некоторое ускорение a и направленное движение с изме-няющейся скоростью от v_o = 0 до v = v_max за время t = .

Изменение скорости направленного движения электрона проводимости происходит до его взаимодействия (рис. 6.1). В результате взаимодействия эта скорость так же может измениться как по величине, так и по направлению.

Если в единице объема проводника n электронов проводимости, которые в некоторый момент времени t обладают скоростью v, то можно определить заряд, прошедший через некоторую площадку S, расположенную перпендикулярно направлению скорости движения электронов проводимости:

, (6.6)

где <v> — средняя скорость упорядоченного движения электронов проводимости.

Сила (величина) тока в проводнике в этом случае

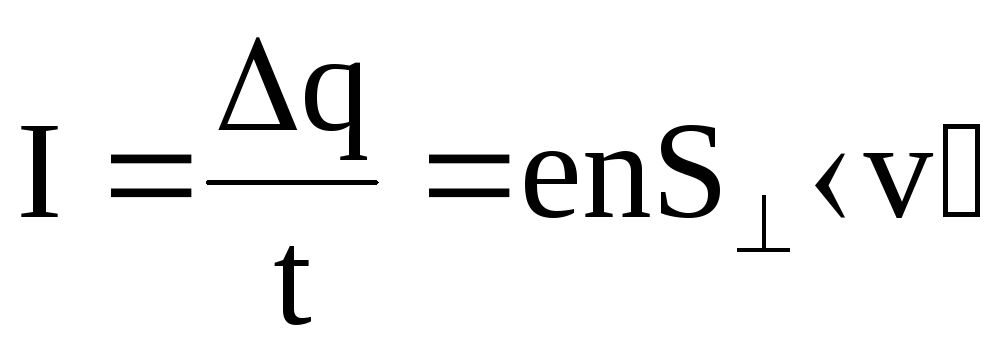. (6.7)

Плотность тока проводимости

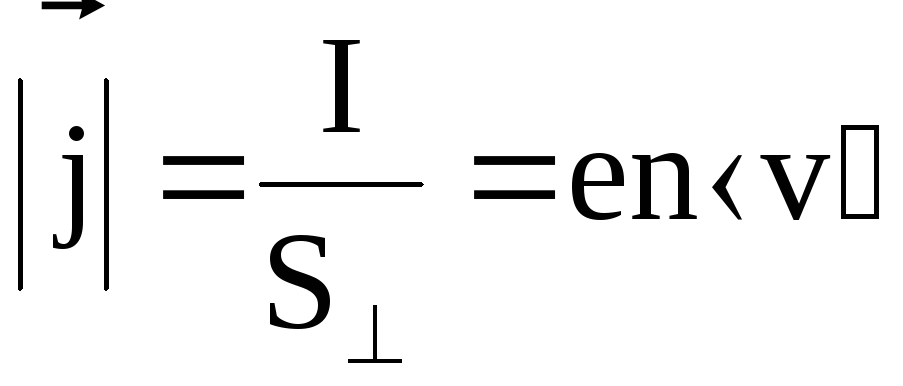. (6.8)

В векторной форме

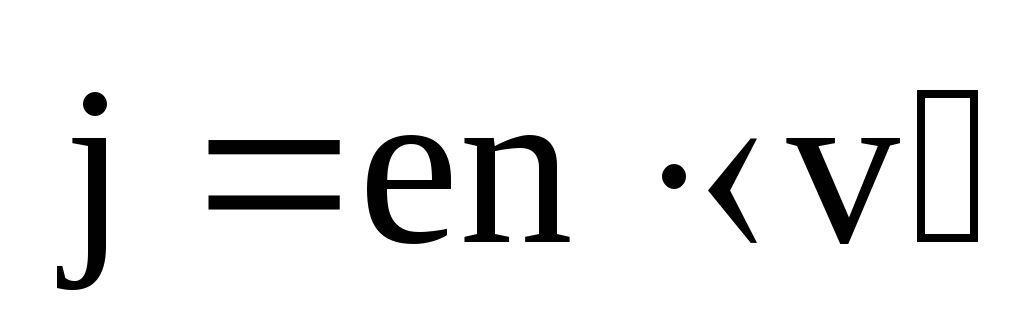. (6.9)

Согласно (6.8) для определения плотности электрического тока в проводнике необходимо определить среднюю скорость упорядоченного движения электронов проводимости.

Средняя скорость упорядоченного движения в данном случае может быть определена по формуле

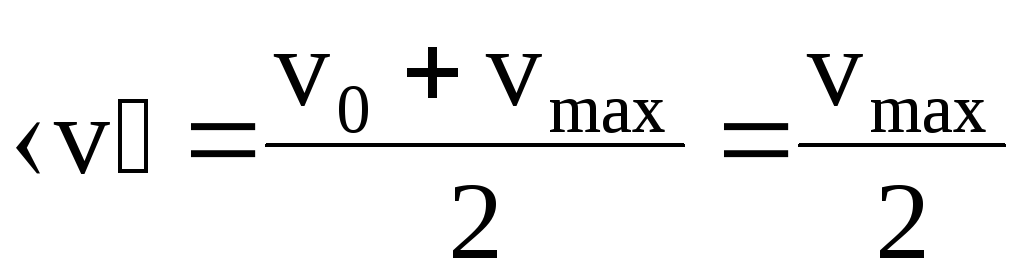, (6.10)

т.к. в начальный момент времени t=0, когда отсутствует электрическое поле, v_o=0.

Максимальная скорость упорядоченного движения, которую приобретает электрон под действием электрического поля за время свободного пробега,

,

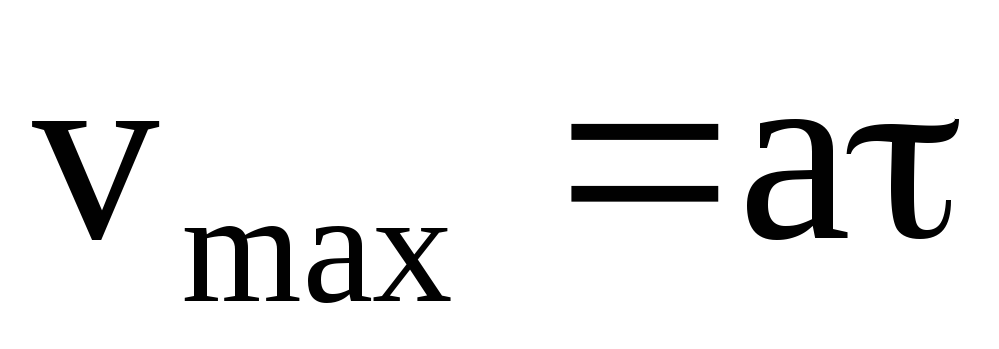где a – ускорение, приобретаемое электроном проводимости под действием электрического поля;

 – время пробега электрона проводимости от взаимодействия до взаимодействия.

На основании второго закона Ньютона F = ma, где F — кулоновская сила,

F = eE.

Имеем:

;

;

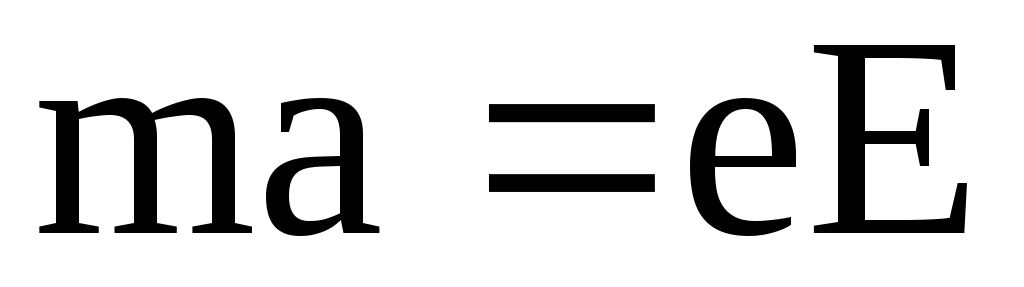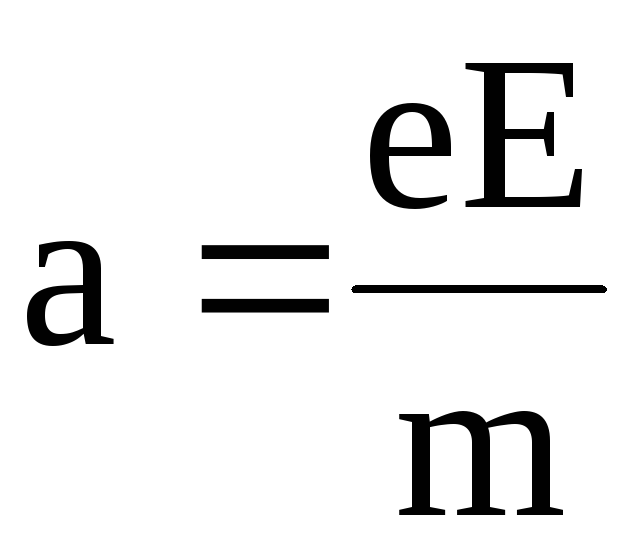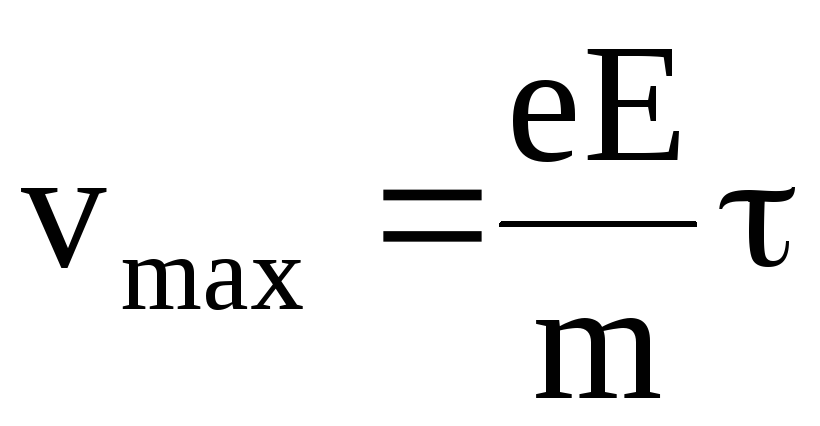. (6.11)

Для средней скорости упорядоченного движения электронов проводимости получим

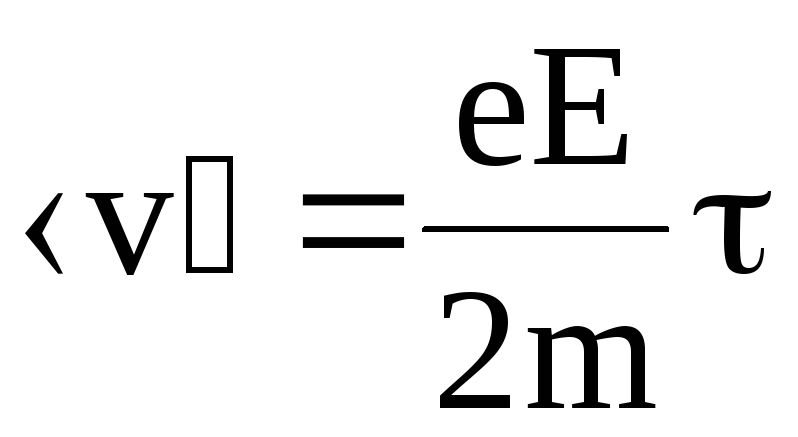. (6.12)

Зная среднюю скорость теплового движения электронов проводимости и среднее расстояние, проходимое ими от взаимодействия до взаимодействия, можно определить время между двумя последующими взаимодействиями:

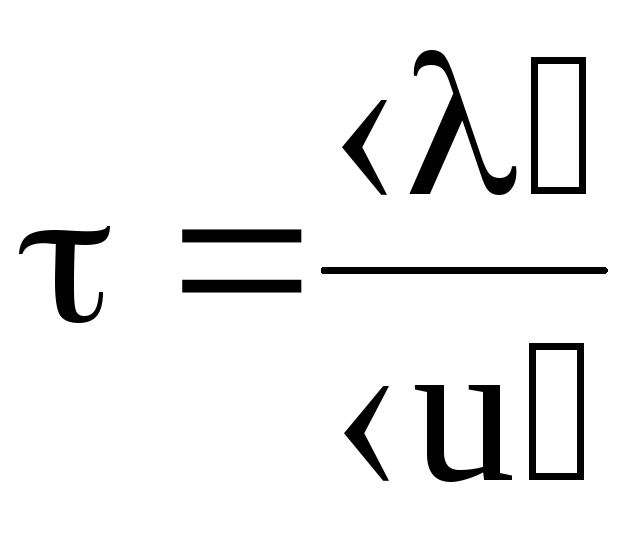. (6.13)

Сделав подстановку и необходимые преобразования, для плотности тока проводимости будем иметь

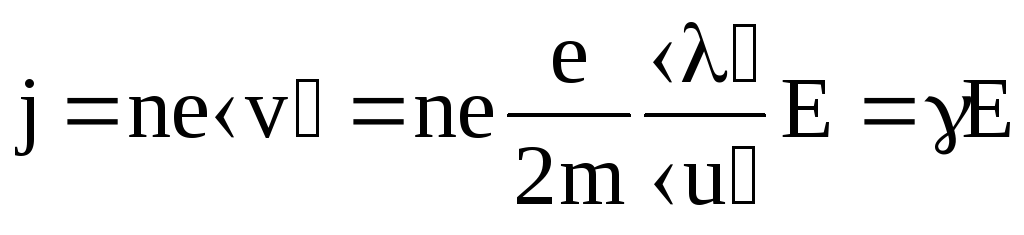, (6.14)

где 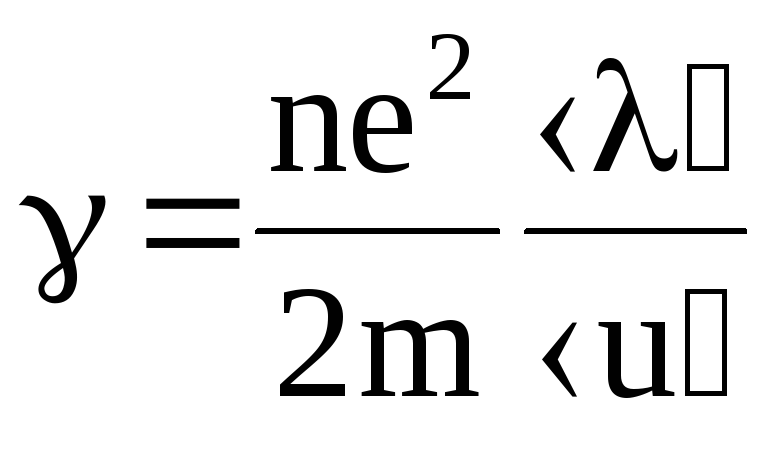— удельная электропроводность металла проводника.

В векторной форме

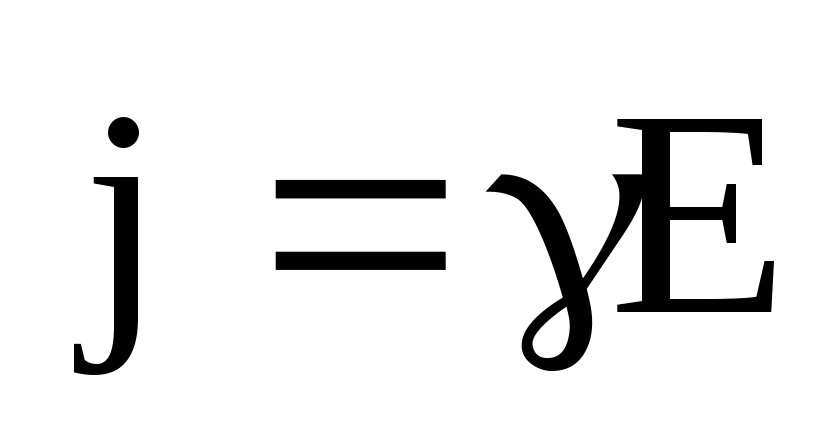. (6.15)

Выражения (6.14) и (6.15) являются математической формой записи закона Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любых проводников, любых токов, характеризует плотность тока проводимости в любой точке проводника.

Из закона Ома в дифференциальной форме можно получить закон Ома в интегральной форме для замкнутой (или полной) цепи. Для чего выражение (6.15) умножим на величину элементарного участка цепи dl:

,

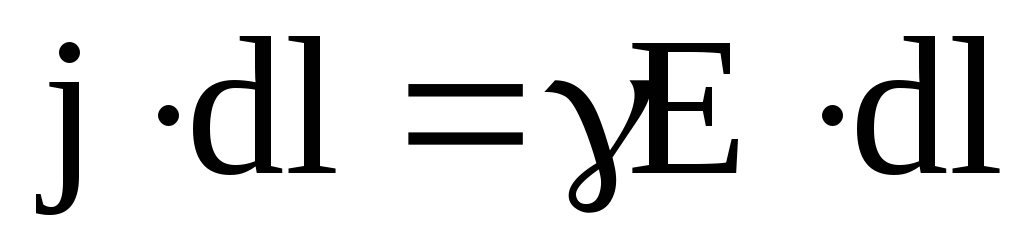где ;;.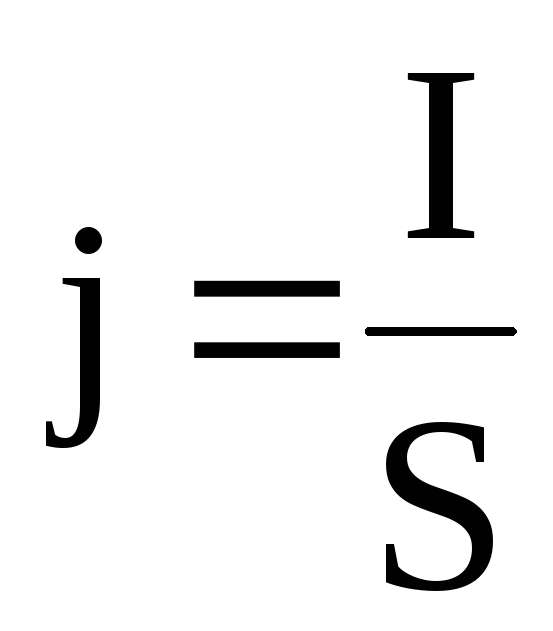

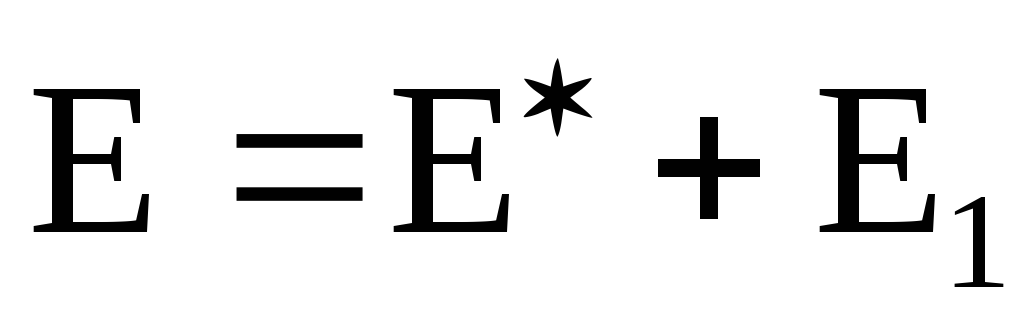Таким образом, имеем

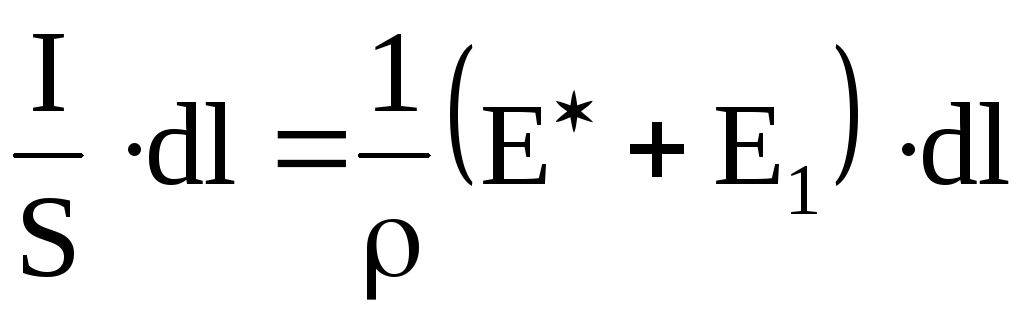
или

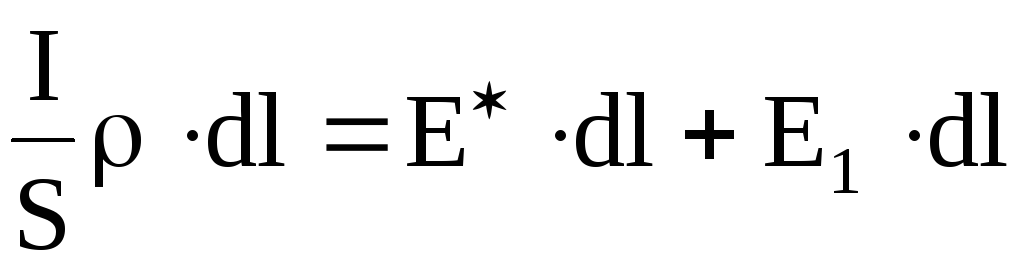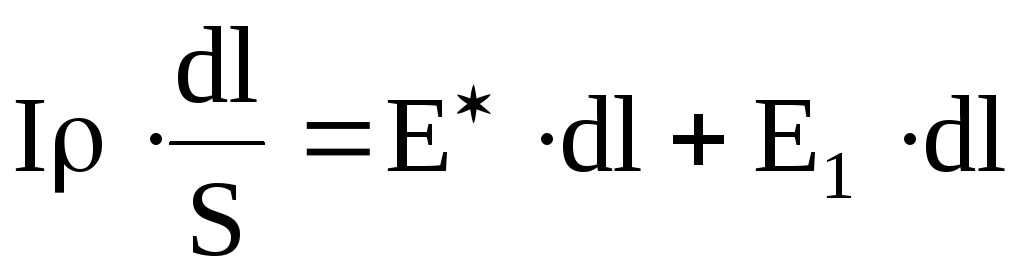; . (6.16)

Проинтегрировав выражение (6.16) по замкнутому контуру L, получим

, (6.17)

где – сопротивление внешнего и внутреннего участков цепи;

–ЭДС, действующая в замкнутой цепи, численно равная циркуляции вектора напряженности поля сторонних сил;

–разность потенциалов между двумя рассматриваемыми точками замкнутой цепи.

Для замкнутой цепи

(₁ — ₂) = 0; .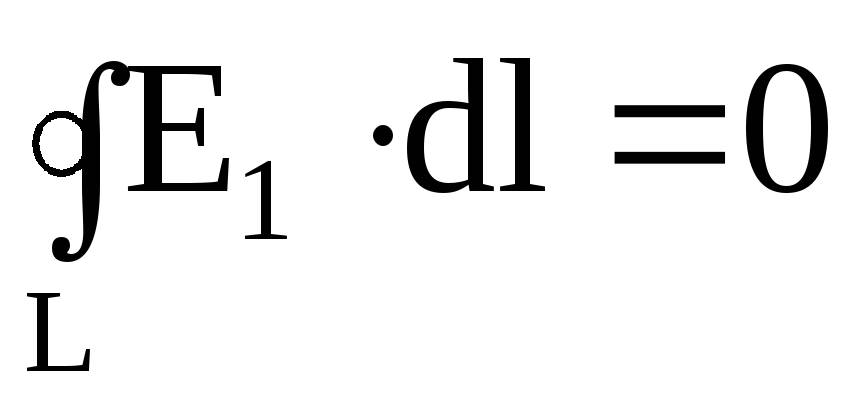

Таким образом, имеем

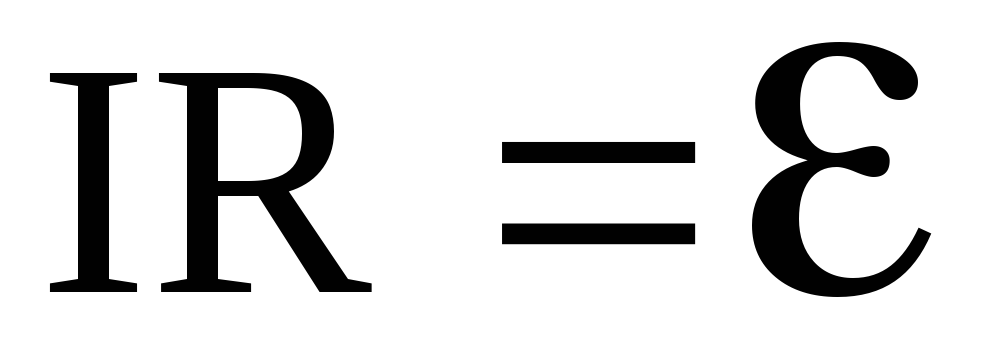или , (6.18)

где R₁ – сопротивление внешнего участка цепи;

r – внутреннее сопротивление источника тока.

Из формулы (6.18)

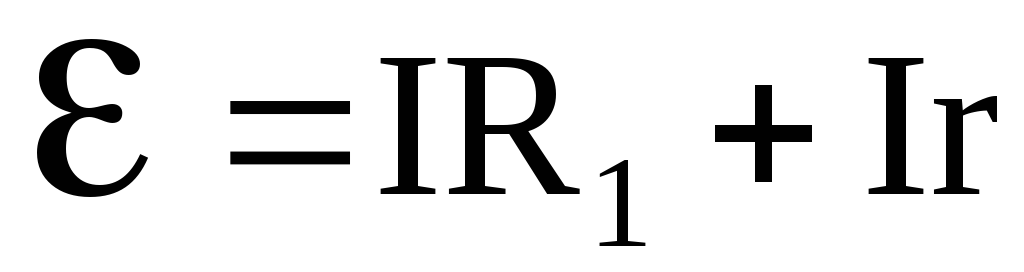. (6.19)

Следовательно, ЭДС уравновешивает падение напряжения во внешней и внутренней цепи и тем самым обеспечивает непрерывное движение электронов проводимости.

Если цепь не замкнута и в ней отсутствует ЭДС, то

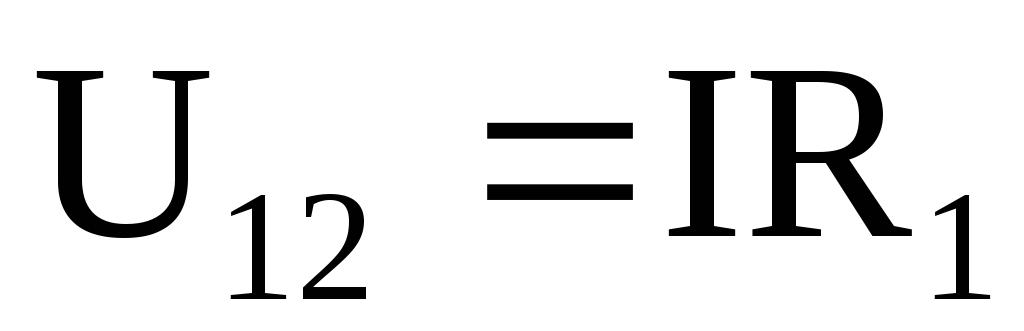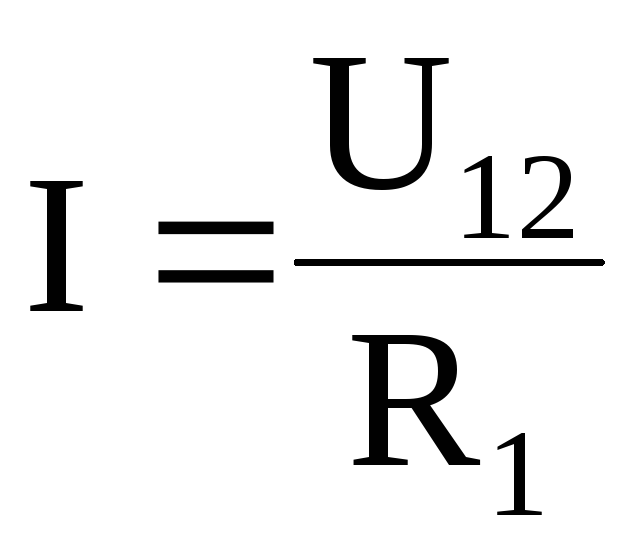, а . (6.20)

Выражения (6.18) и (6.20) являются математической формой записи закона Ома, соответственно, для полной (замкнутой) цепи и участка цепи, который был открыт им экспериментально. Сила тока в цепи прямопропорциональна ЭДС (напряжению на участке цепи) и обратно пропорциональна сопротивлению цепи.