3.Работа и разность потенциалов.

Задача 5. Электрон переместился в ускоряющем поле из точки с потенциалом 200В в точку с потенциалом 300В. Найти кинетическую энергию электрона, изменение потенциальной энергии взаимодействия с полем и приобретенную скорость. Начальная скорость электрона равна нулю.

РЕШЕНИЕ

При перемещении электрона с зарядом е силами электростатического поля совершается работа:

A = —e (φ₁ – φ_2).

Эта работа численно равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

A = —ΔW_p или ΔW_p

= e (φ₁ – φ₂)_.

По теореме о кинетической энергии работа сил электрического поля численно равна приобретенной электроном кинетической энергии W_K:

A = W_K или — e (φ₁ – φ₂) =.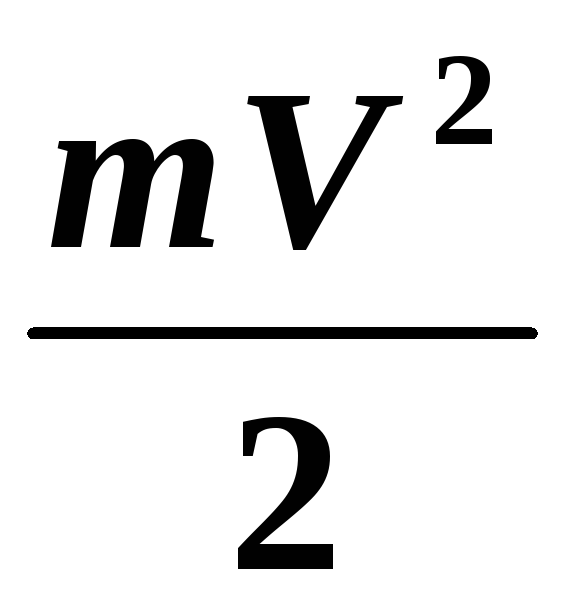

Отсюда скорость электрона, прошедшего разность потенциалов φ₁ – φ

2_:



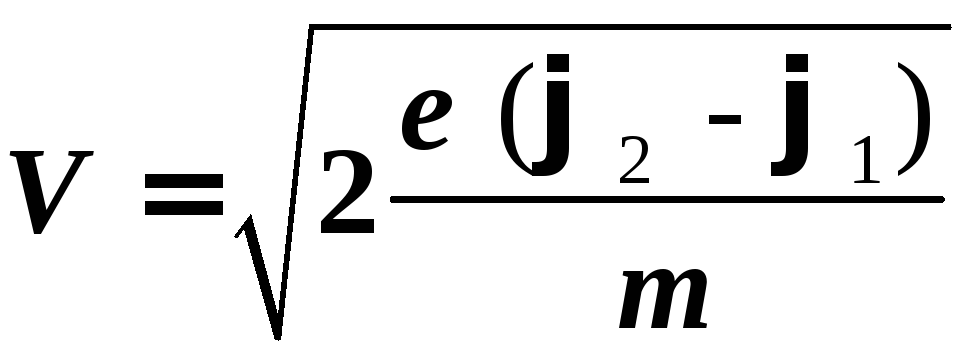
где е = 1,610^-19 Кл, m = 9,110^-31кг — заряд и масса электрона.

Вычисления: W_Р = -1,610^-19 (300 — 200) = -1,6

10^-17 Дж.

Потенциальная энергия электрона уменьшилась.

W_K = 1,610^-17 Дж.

Кинетическая энергия электрона увеличилась.

.

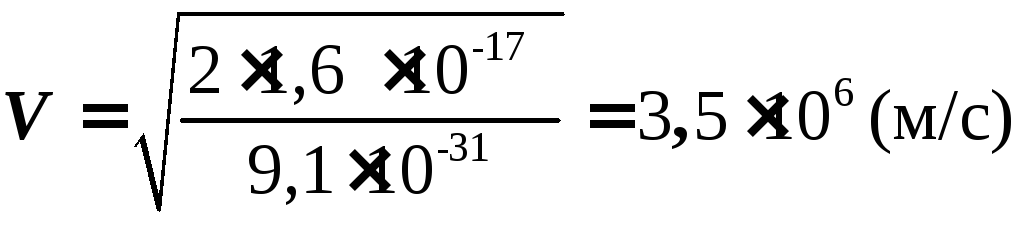4.Движенне заряженных частиц в электростатическом поле

Задача 6. Какова максимальная сила взаимодействия между двумя про­тонами, каждый с энергией 10⁶ эВ, летящих во встречных пучках?

РЕШЕНИЕ

Выберем систему отсчета связанную с одним из протонов, тогда скорость второго протона увеличиться в два раза, а его кинетическая энергия — в четыре раза.По мере сближения протонов кинетическая энергия движущегося протона уменьшается, переходя в потенциальную энергию

W_P взаимодействия двух протонов. Условие остановки протонов:

W_К = W_P.

Учитывая, что Wp = q φ получаем:

W_К= q φ (1)

где q — заряд движущегося протона и

(2)

— потенциал поля неподвижного протона, r — расстояние между протонами. Из формул (1-2) находим расстояние r, на которое сблизятся протоны:

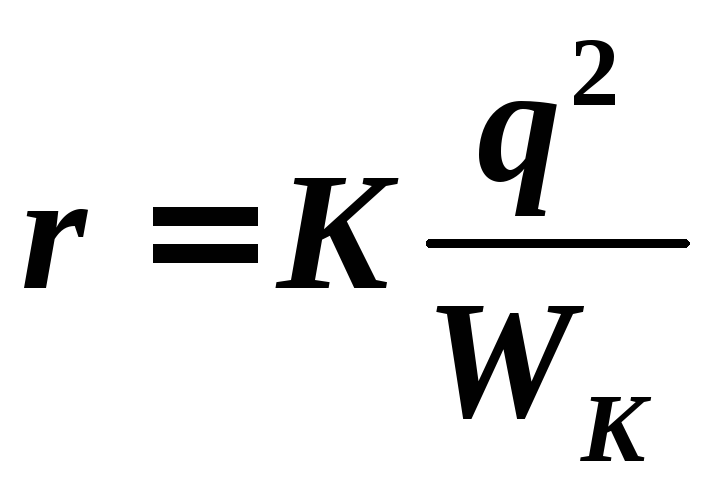. (3)

Зная расстояние r , найдем максимальную силу F взаимодействия протонов. По закону Кулона:

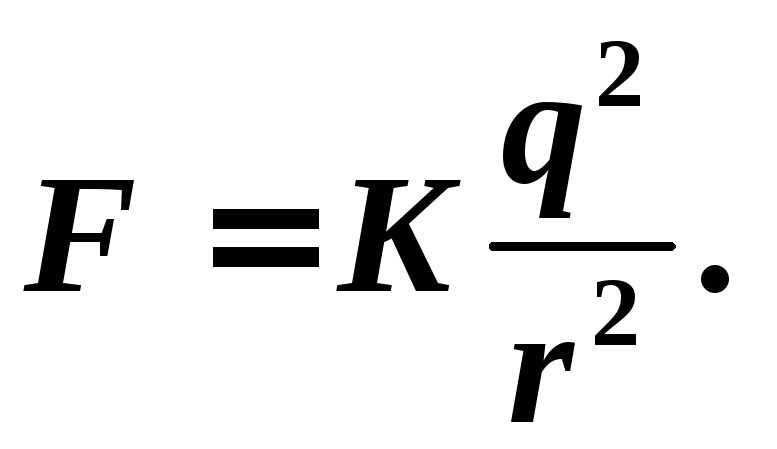
С учетом (3): .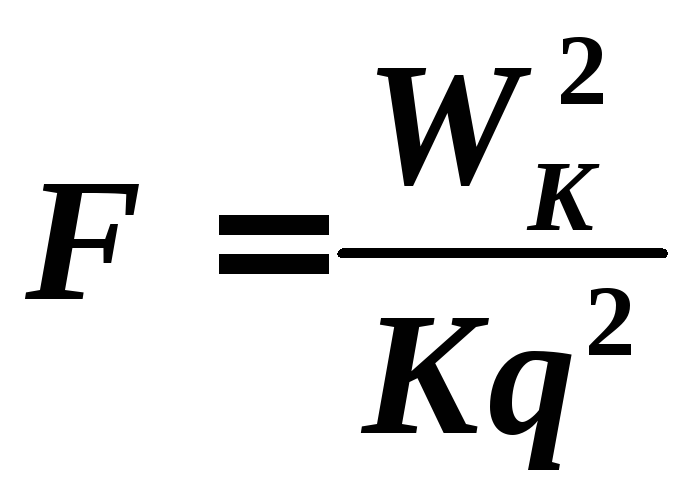

Проверка размерности: .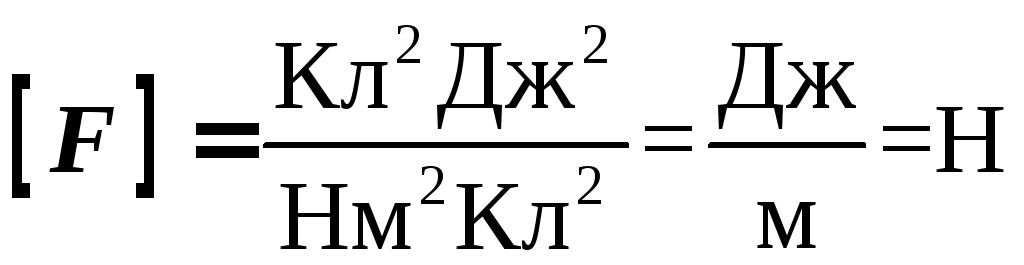

q = 1,610^-19 Кл,

W_K = 410 ⁶ 1,610^-19 = 6,4

10^-13 Дж.

.

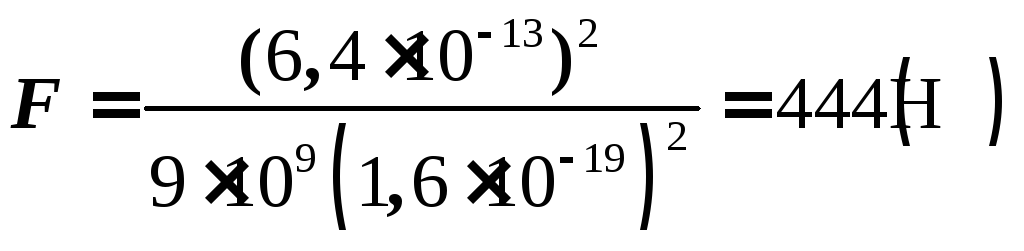Задача 7. Электрон испускается верхней пластиной конденсатора с нулевой скоростью. Напряженность поля между пластинами 6 10⁵ В/м, расстояние ─ 5 мм. Найти: 1) силу, действующую на электрон; 2) ускорение электрона; 3) скорость, с которой электрон подлетает ко второй пластине; 4) плотность заряда на пластинах.

ДАНО: E = 6 10⁵ В/м, V₀ = 0, d

= 0,05 м.

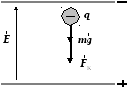ОПРЕДЕЛИТЬ:F_К , a , V, .

РЕШЕНИЕ

1. На частицу с зарядом q в электрическом поле горизонтально расположенного конденсатора действуют две силы: mg — сила тяжести и F_К = q E — кулоновская сила со стороны поля.

Рис. 5

Результирующая этих сил равна: F = mg + q E.

2. Из второго закона Ньютона, определяем ускорение электрона:

.

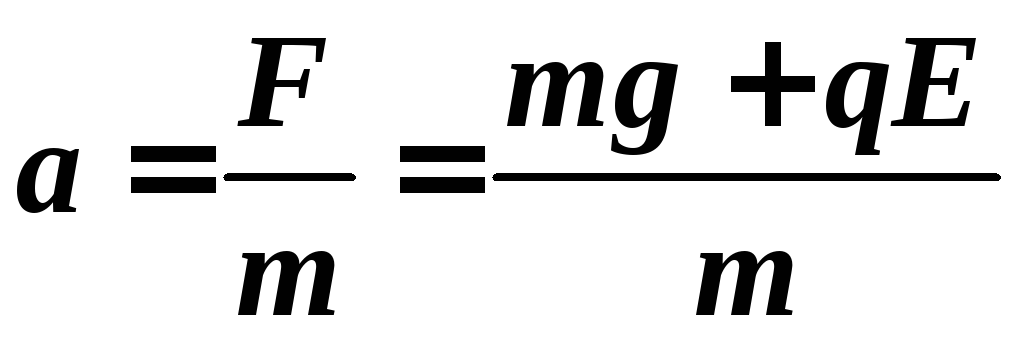2. Движение электрона — равноускоренное с ускорением а и начальной скоростью, равной нулю. Поэтому:

,

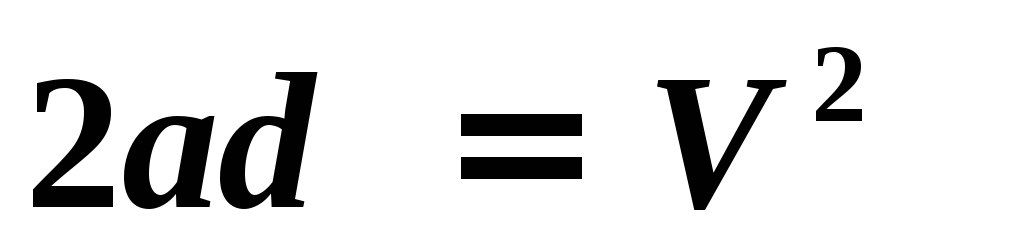
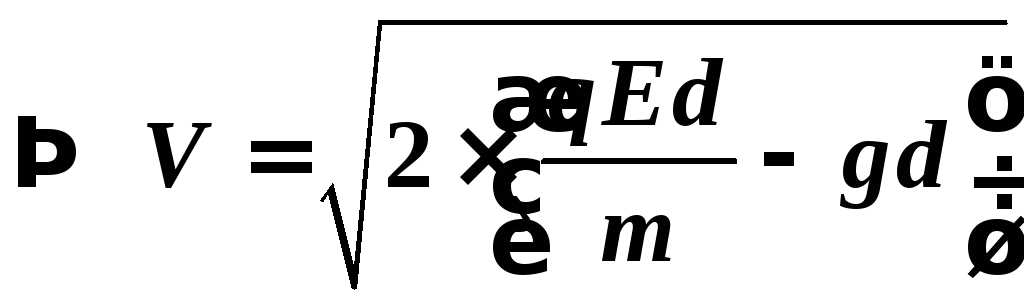
где d — расстояние между пластинами.

4. Плотность заряда на пластине конденсатора найдем из формулы напряженности поля плоского конденсатора:

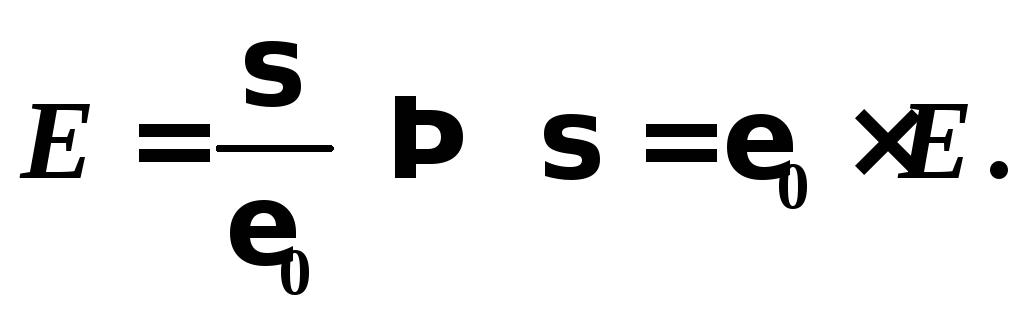
Вычисления: Силой тяжести mg вследствие её малости можно пренебречь.

F = 1,610^-196

10⁵ = 9,610^-14 (Н).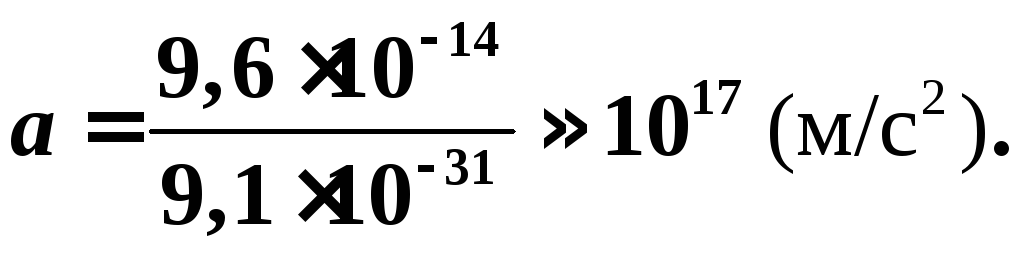

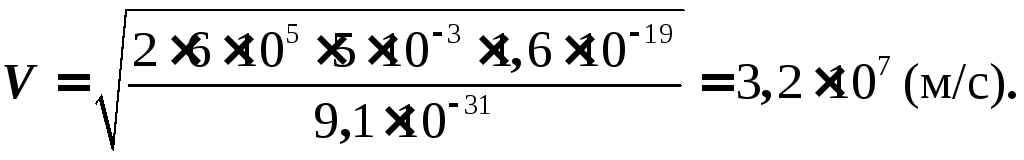
Задана 8. В пространство между двумя параллельными заряженными пластинами, помещенными в вакуум, параллельно им влетает электрон со скоростью V₀ . На расстоянии L скорость электрона отклоняется на угол α от первоначального направления. Найти напряженность поля конденсатора.

РЕШЕНИЕ

На заряд действует сила Кулона

F = q E,

поэтому электрон приобретает ускорение вдоль оси OY :

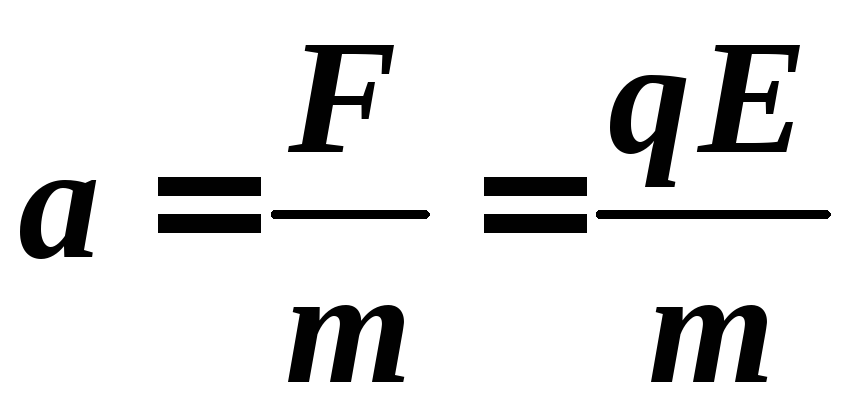. (1)

Рис.6

Рис.6

Скорость электрона вдоль оси Y :

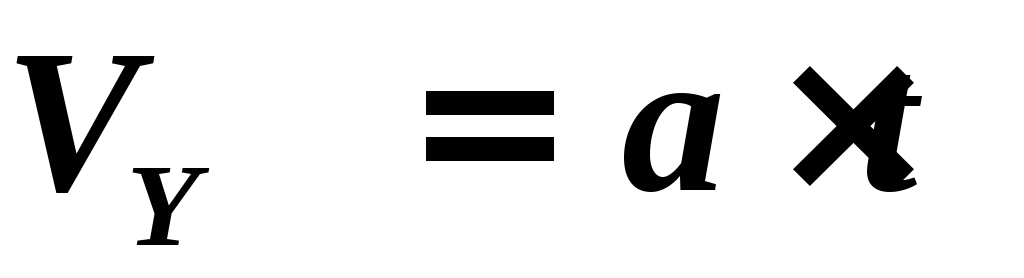. (2)

Вдоль оси X электрон движется с постоянной скоростью V₀. Время t , за которое электрон пройдет расстояние L: 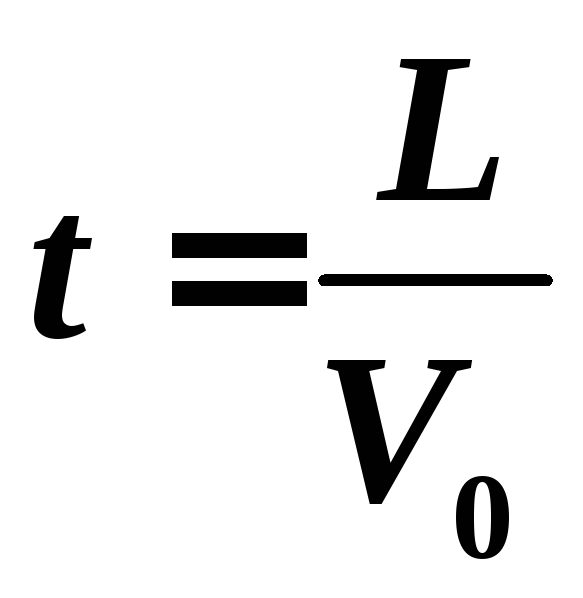. (3)

Подставив (3) в (2), получим: 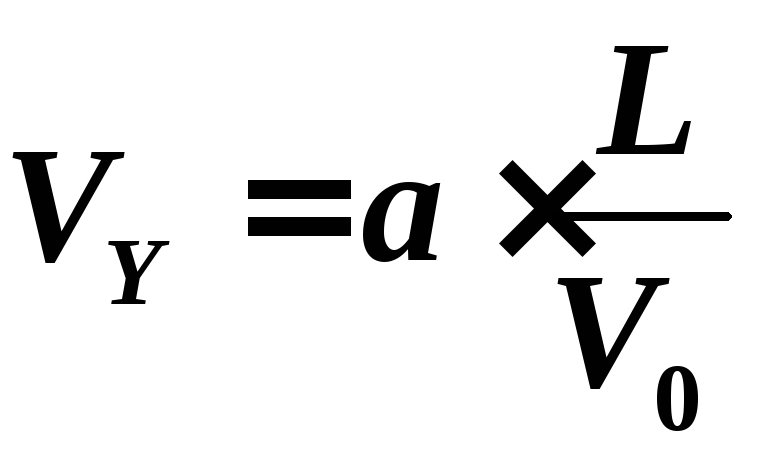. (4)

С другой стороны, 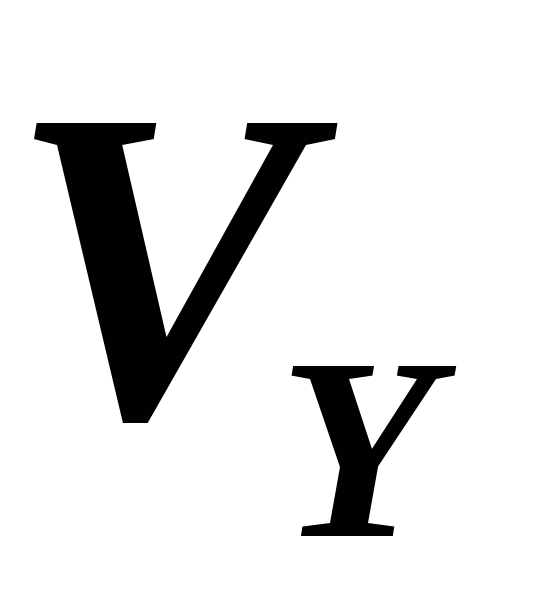можно выразить из треугольника скоростей (см. рис.6):

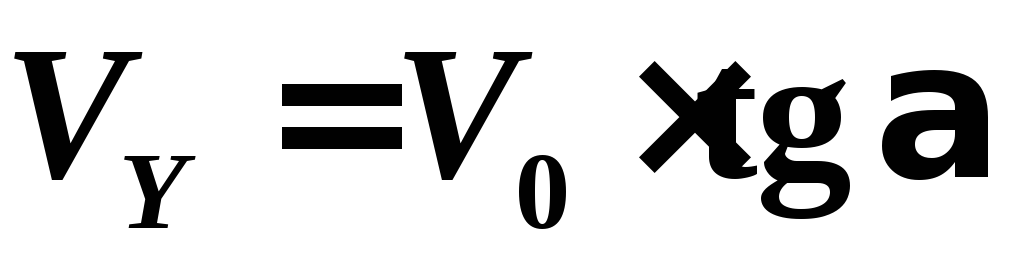. (5)

Из формул (4) и (5) находим:

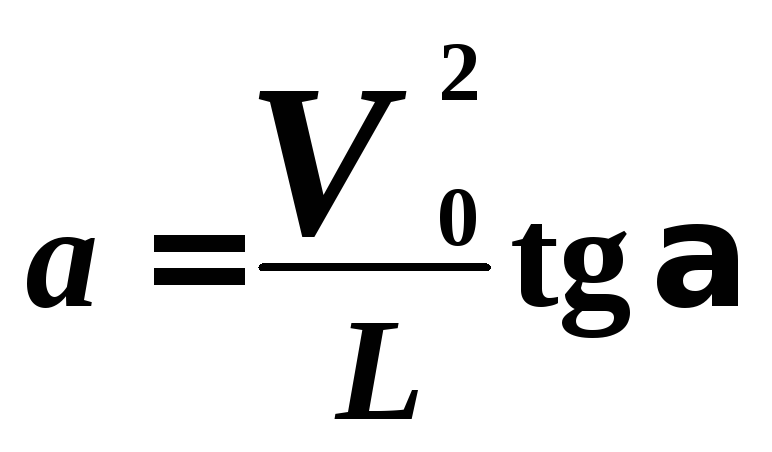. (6)

Напряженность электростатического поля конденсатора E выразим из соотношения (1) с учетом (6):

.

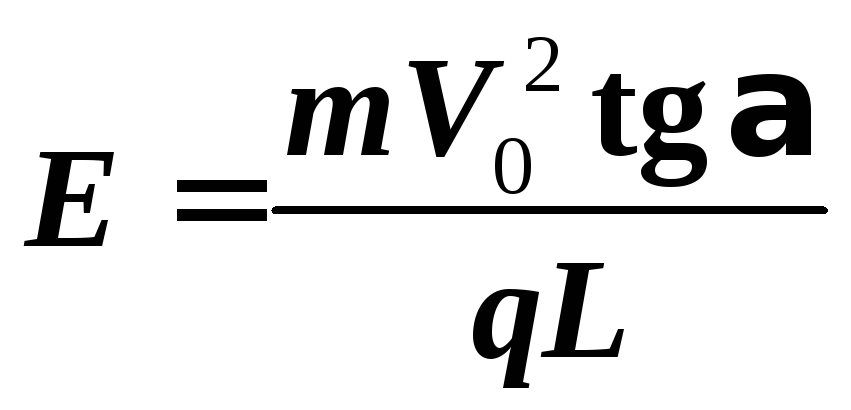Проверка размерности: :

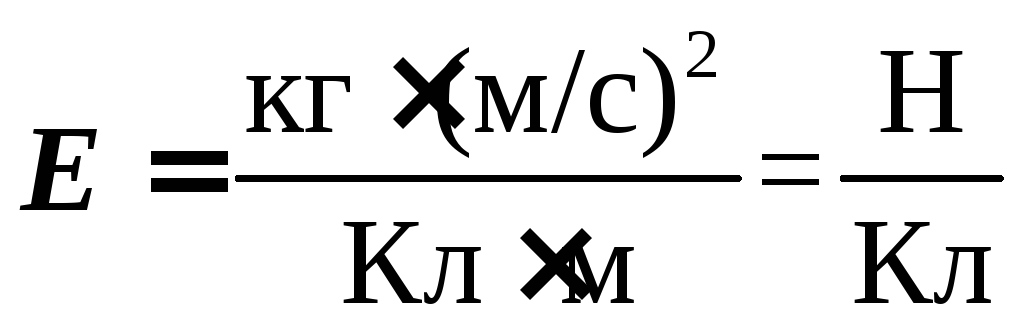
4. Электроемкость

Задача 9. Тысяча одинаковых наэлектризованных капель сливаются в одну, причем их общий заряд сохраняется. Как изменится общая электрическая энергия капель, если считать, что капли сферические и маленькие капли находились на большом расстоянии друг от друга?

РЕШЕНИЕ:

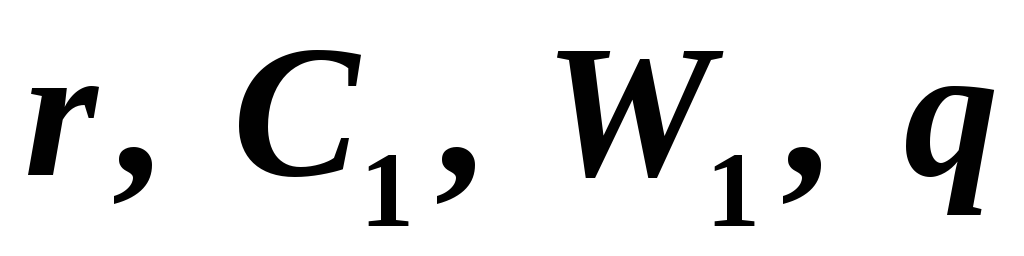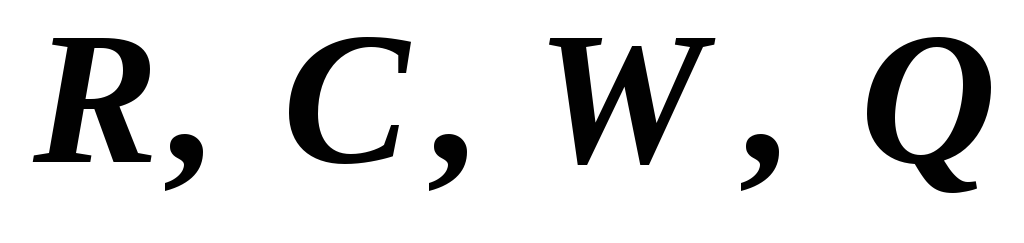Обозначим через радиус, емкость, энергию и заряд одной капли до слияния; радиус, емкость, энергию и заряд большой капли. Приравняем объем капель после и до слияния:

,

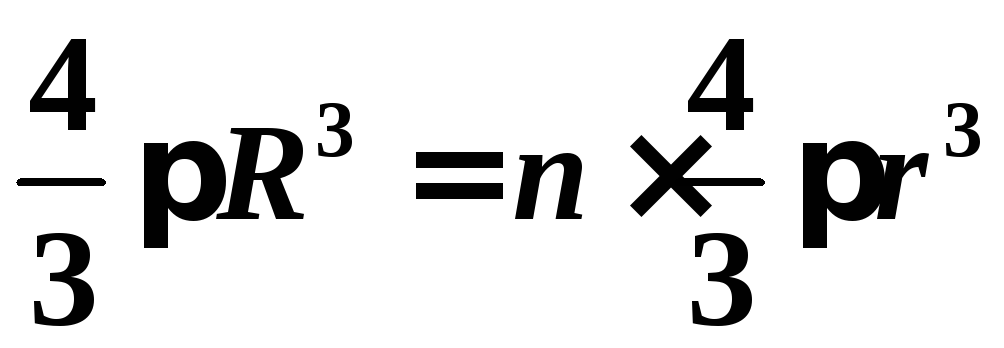откуда ,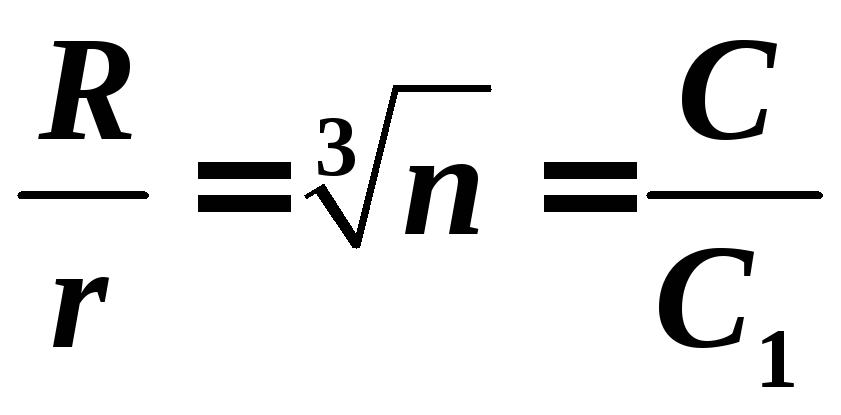

где n — число маленьких капель, — емкость шара.

Электрическая энергия одной капли до слияния .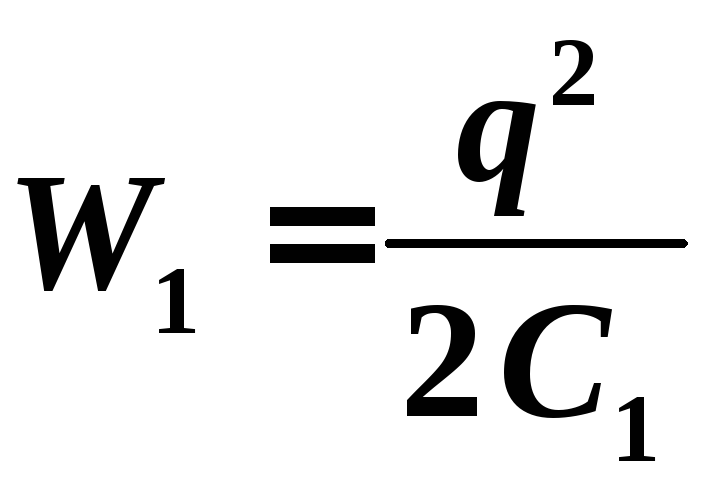

Энергия n капель в n раз больше и равна .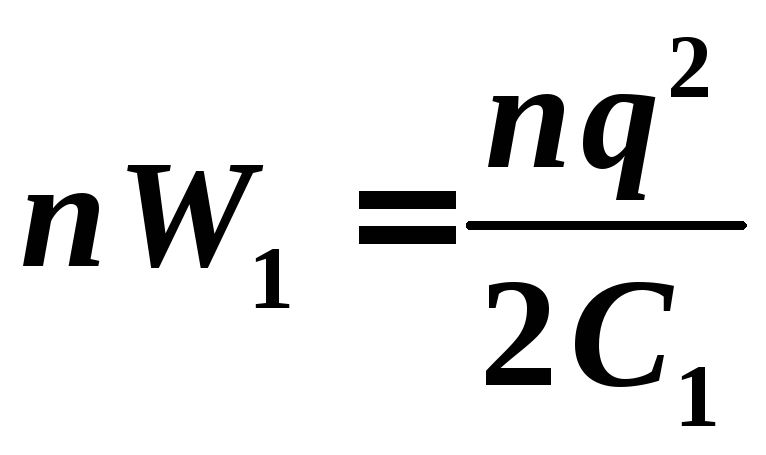

Энергия капели после слияния равна .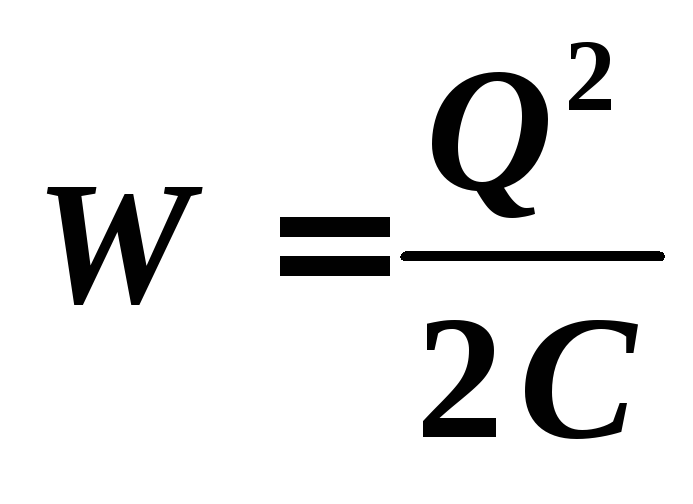

Отношение .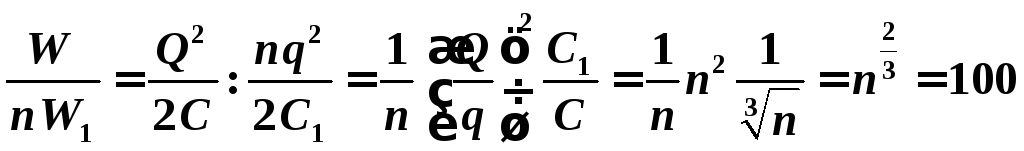

Энергия увеличилась в 100 раз.

Задача 10. Батарея конденсаторов сделана из четырех слюдяных пласти­нок толщиной d = 0,1 мм и площадью S = 100 см² каждая из пластинок станиоля (проводник). Сколько понадобилось пластинок станиоля (n) при параллельном соединении батареи? Начертить схему соединения. Опре­делить емкость батареи. Определить запас электрической энергии, если батарея подключена к источнику на­пряжения U = 220 В. Диэлектрическая проницаемость слюды ε = 7.

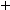
Станиоль

Рис. 7

РЕШЕНИЕ

При параллельном соединении конденсаторов между собой соединяются все положительные и все отрицательно заряженные пластинки станиоля. Каждая пластинка станиоля может служить обкладкой двух соседних конденсаторов, как показано на втором рисунке. Количество пластинок станиоля n = 5. Общая емкость C = nC₁ , где C₁ — емкость одного конденсатора: 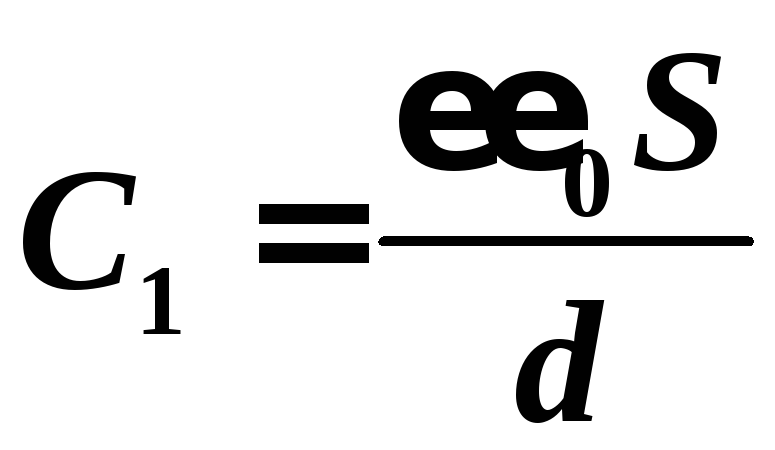. Общая емкость.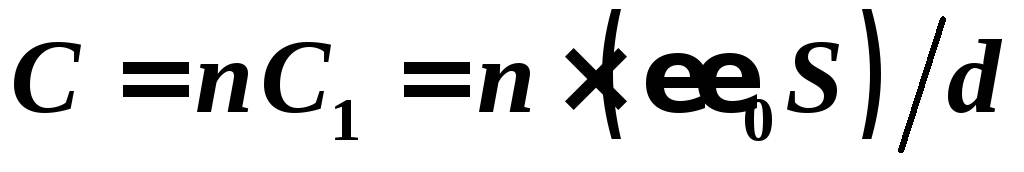

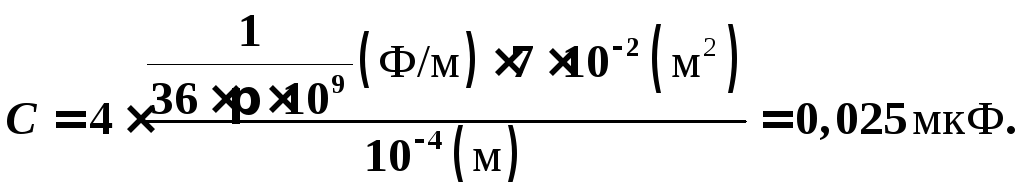
Энергия батареи конденсаторов: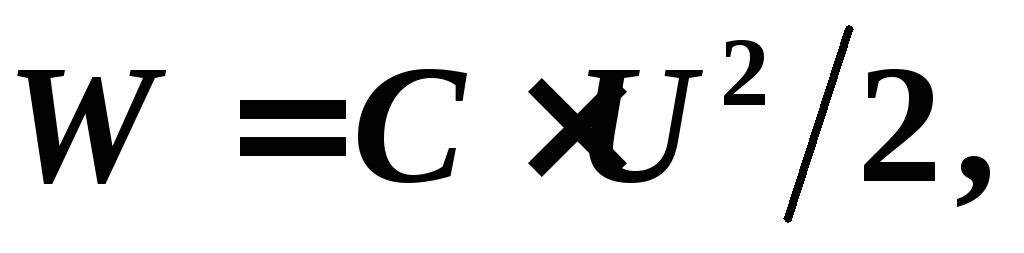

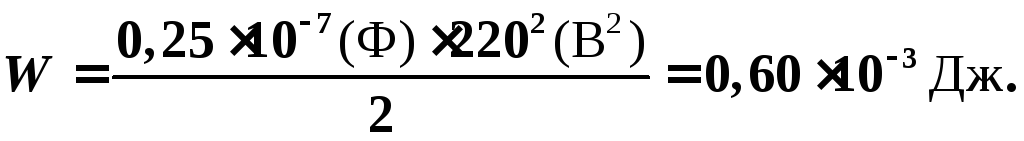
3.Работа и разность потенциалов.

Задача 5. Электрон переместился в ускоряющем поле из точки с потенциалом 200В в точку с потенциалом 300В. Найти кинетическую энергию электрона, изменение потенциальной энергии взаимодействия с полем и приобретенную скорость. Начальная скорость электрона равна нулю.

РЕШЕНИЕ

При перемещении электрона с зарядом е силами электростатического поля совершается работа:

A = —e (φ₁ – φ_2).

Эта работа численно равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:

A = —ΔW_p или ΔW_p = e (φ₁ – φ₂)_.

По теореме о кинетической энергии работа сил электрического поля численно равна приобретенной электроном кинетической энергии W_K:

A = W_K или — e (φ₁ – φ₂) =.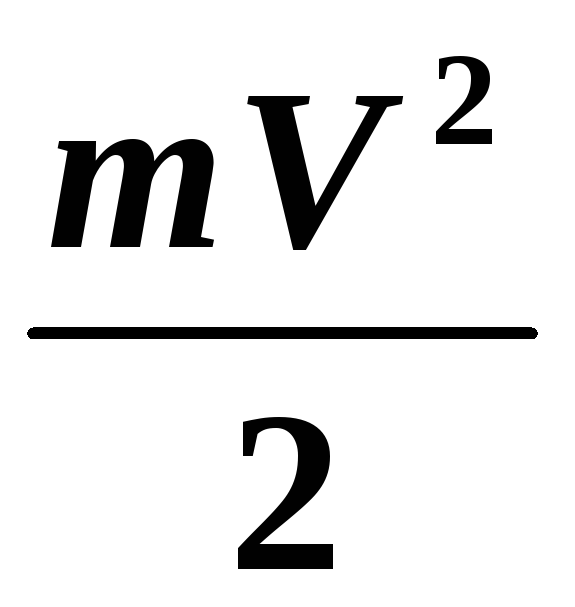

Отсюда скорость электрона, прошедшего разность потенциалов φ₁ – φ_2:



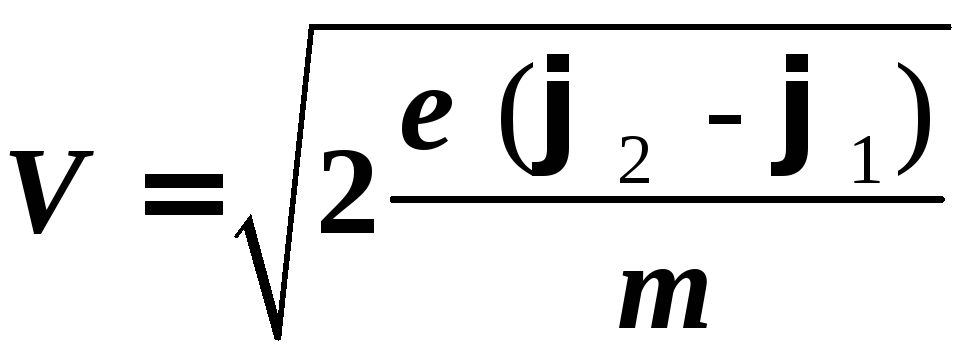
где е = 1,610^-19 Кл, m = 9,110^-31кг — заряд и масса электрона.

Вычисления: W_Р = -1,610^-19 (300 — 200) = -1,610^-17 Дж.

Потенциальная энергия электрона уменьшилась.

W_K = 1,610^-17 Дж.

Кинетическая энергия электрона увеличилась.

.

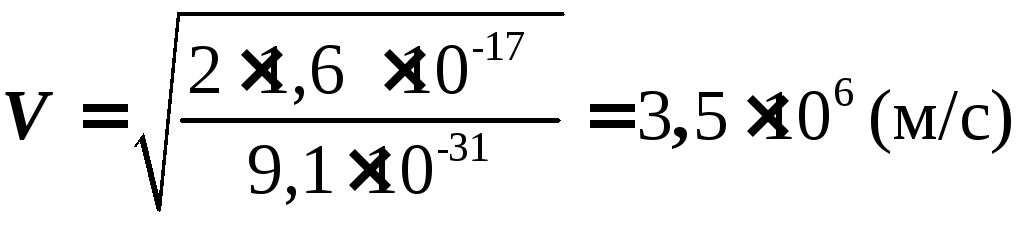4.Движенне заряженных частиц в электростатическом поле

Задача 6. Какова максимальная сила взаимодействия между двумя про­тонами, каждый с энергией 10⁶ эВ, летящих во встречных пучках?

РЕШЕНИЕ

Выберем систему отсчета связанную с одним из протонов, тогда скорость второго протона увеличиться в два раза, а его кинетическая энергия — в четыре раза.По мере сближения протонов кинетическая энергия движущегося протона уменьшается, переходя в потенциальную энергию W_P взаимодействия двух протонов. Условие остановки протонов:

W_К = W_P.

Учитывая, что Wp = q φ получаем:

W_К= q φ (1)

где q — заряд движущегося протона и

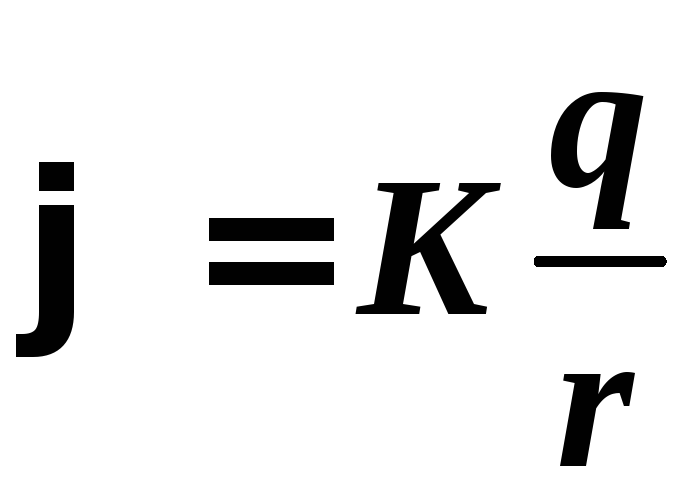(2)

— потенциал поля неподвижного протона, r — расстояние между протонами. Из формул (1-2) находим расстояние r, на которое сблизятся протоны:

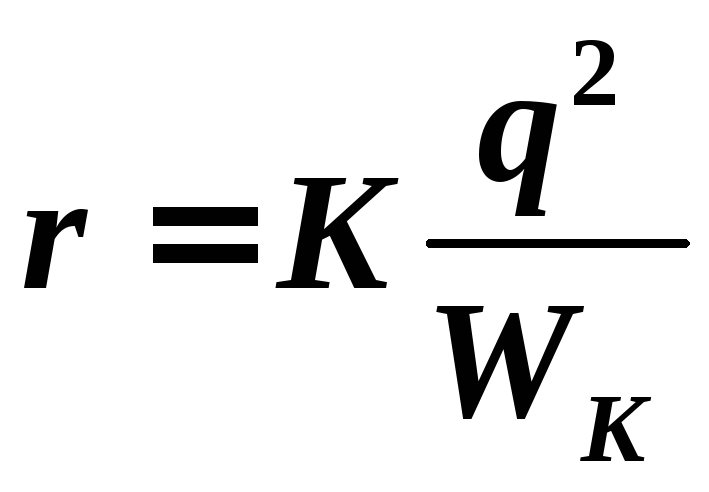. (3)

Зная расстояние r , найдем максимальную силу F взаимодействия протонов. По закону Кулона:

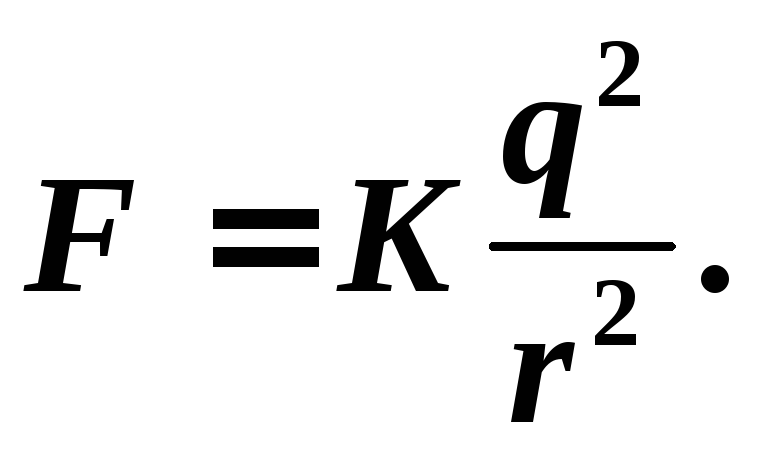
С учетом (3): .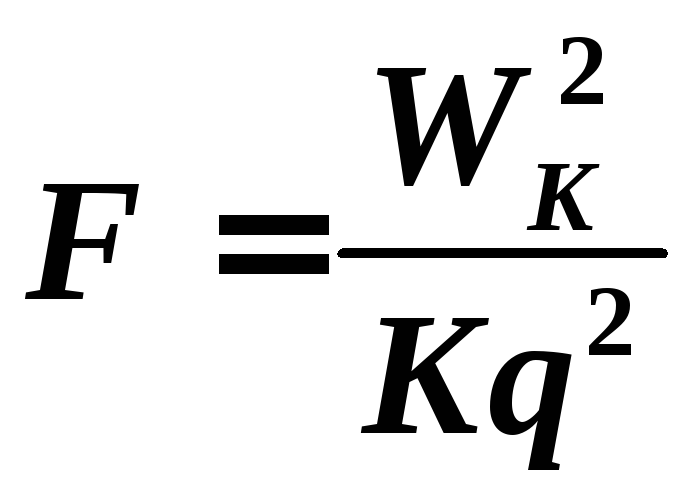

Проверка размерности: .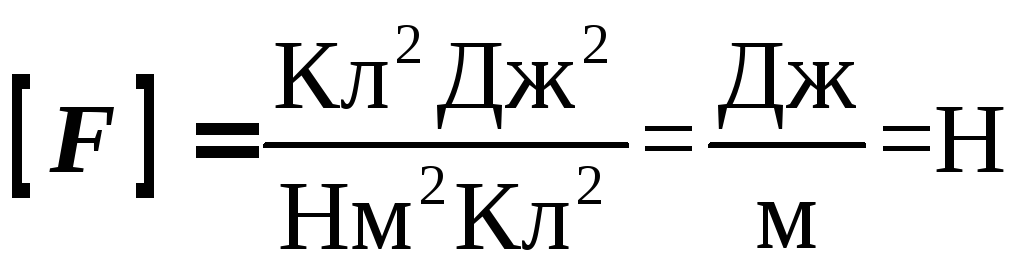

q = 1,610^-19 Кл,

W_K = 410 ⁶ 1,610^-19 = 6,410^-13 Дж.

.

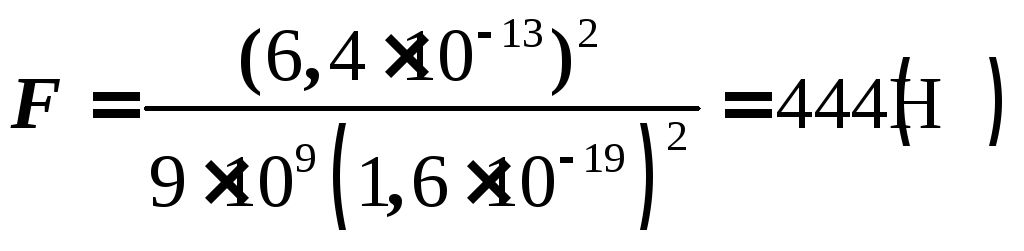Задача 7. Электрон испускается верхней пластиной конденсатора с нулевой скоростью. Напряженность поля между пластинами 6 10⁵ В/м, расстояние ─ 5 мм. Найти: 1) силу, действующую на электрон; 2) ускорение электрона; 3) скорость, с которой электрон подлетает ко второй пластине; 4) плотность заряда на пластинах.

ДАНО: E = 6 10⁵ В/м, V₀ = 0, d = 0,05 м.

О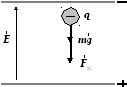ПРЕДЕЛИТЬ:F_К , a , V, .

РЕШЕНИЕ

1. На частицу с зарядом q в электрическом поле горизонтально расположенного конденсатора действуют две силы: mg — сила тяжести и F_К = q E — кулоновская сила со стороны поля.

Рис. 5

Результирующая этих сил равна: F = mg + q E.

2. Из второго закона Ньютона, определяем ускорение электрона:

.

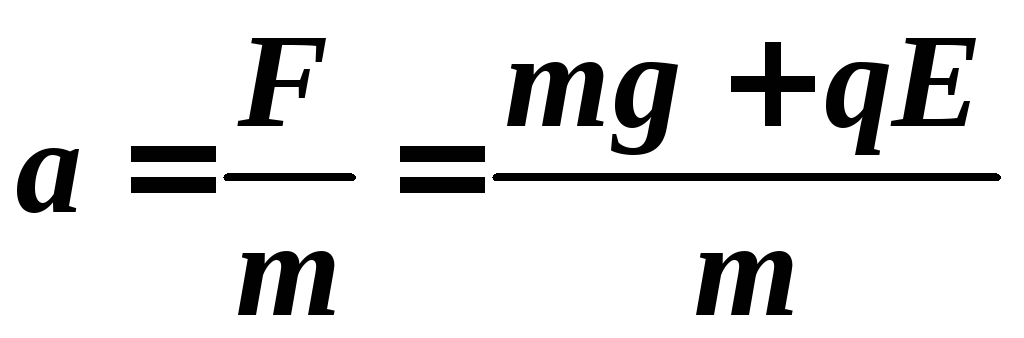2. Движение электрона — равноускоренное с ускорением а и начальной скоростью, равной нулю. Поэтому:

,

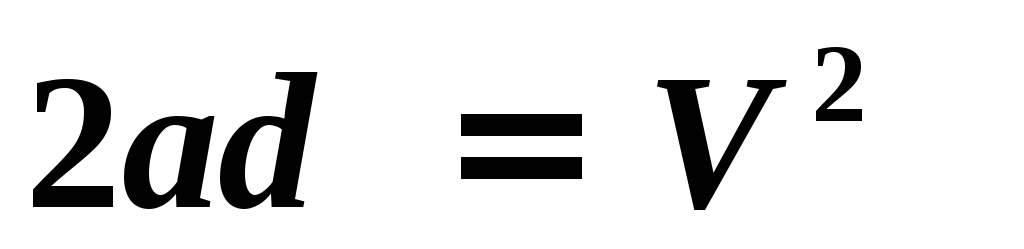
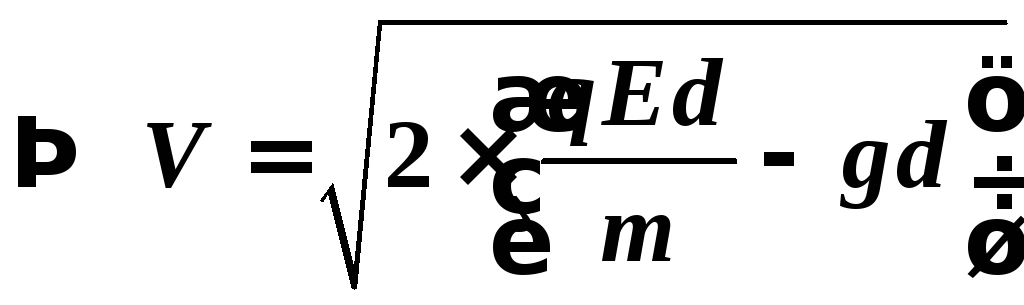где d — расстояние между пластинами.

4. Плотность заряда на пластине конденсатора найдем из формулы напряженности поля плоского конденсатора:

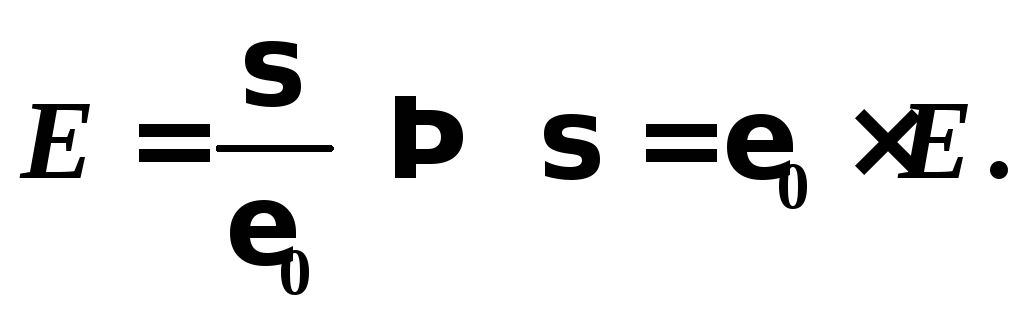
Вычисления: Силой тяжести mg вследствие её малости можно пренебречь.

F = 1,610^-19610⁵ = 9,610^-14 (Н).

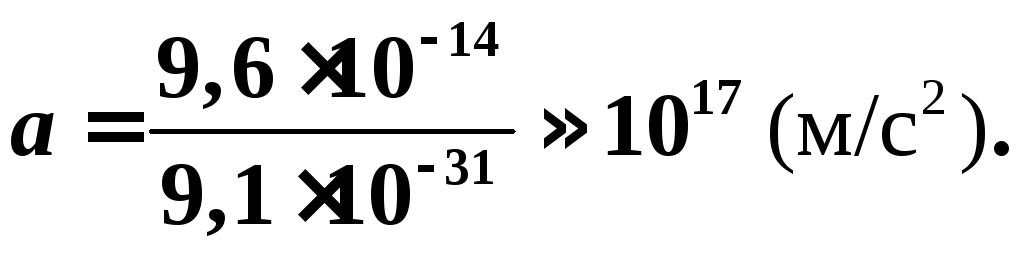
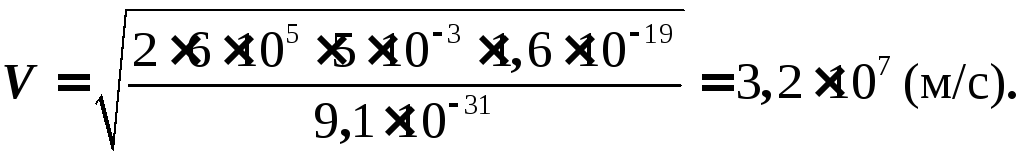
Задана 8. В пространство между двумя параллельными заряженными пластинами, помещенными в вакуум, параллельно им влетает электрон со скоростью V₀ . На расстоянии L скорость электрона отклоняется на угол α от первоначального направления. Найти напряженность поля конденсатора.

РЕШЕНИЕ

На заряд действует сила Кулона

F = q E,

поэтому электрон приобретает ускорение вдоль оси OY :

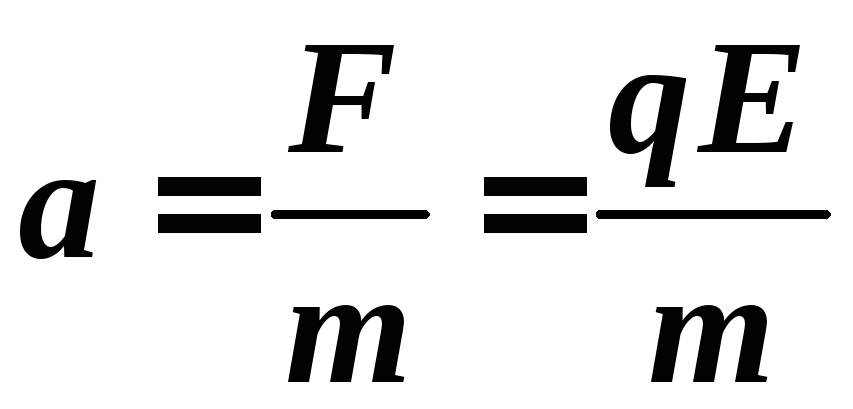. (1)

Рис.6

Рис.6

Скорость электрона вдоль оси Y :

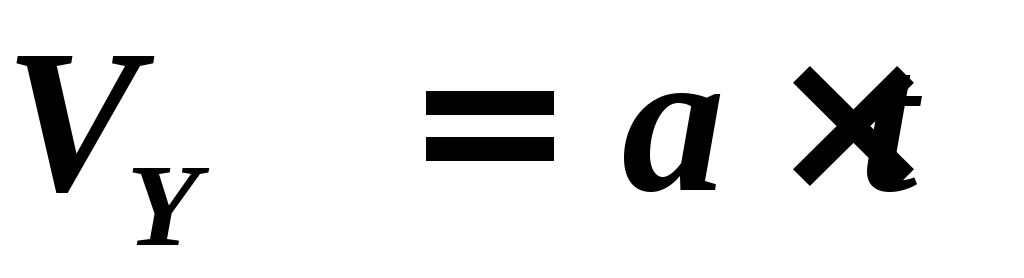. (2)

Вдоль оси X электрон движется с постоянной скоростью V₀. Время t , за которое электрон пройдет расстояние L: 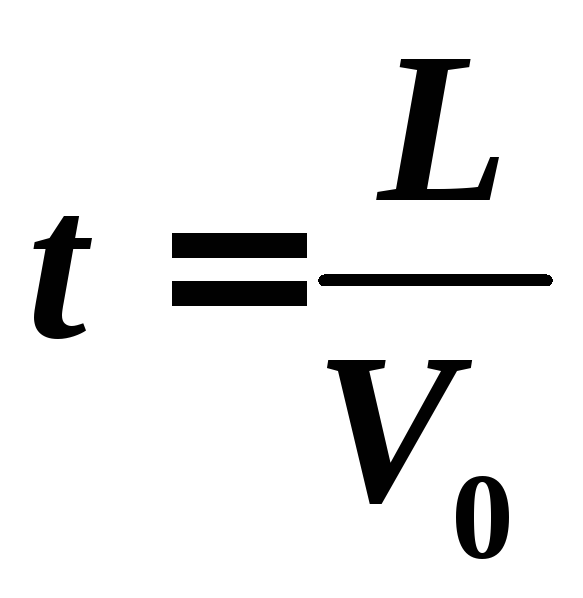. (3)

Подставив (3) в (2), получим: 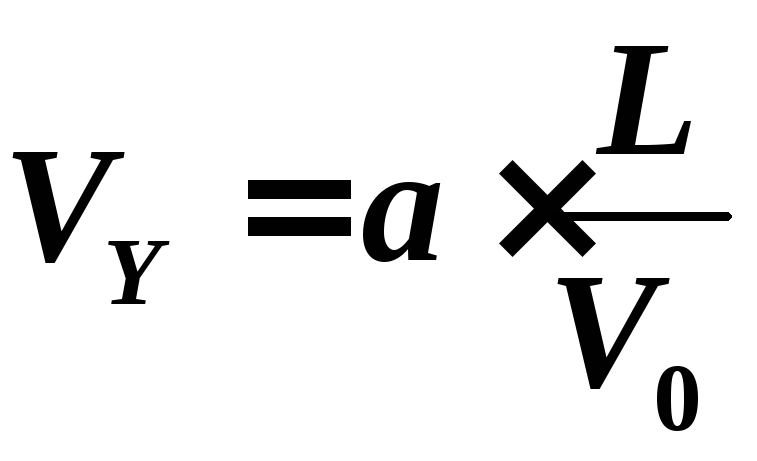. (4)

С другой стороны, 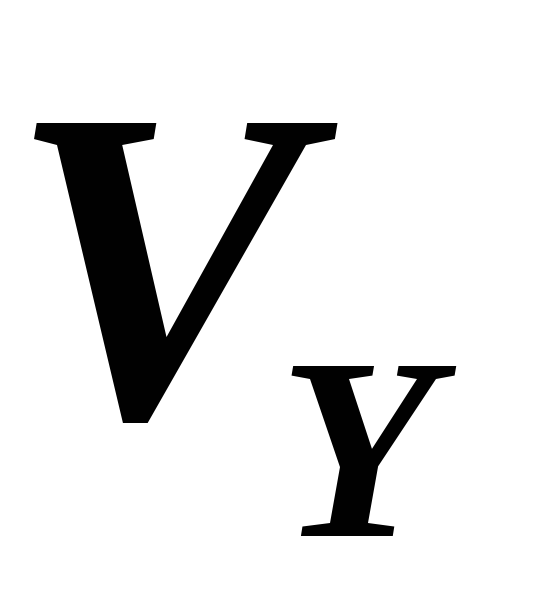можно выразить из треугольника скоростей (см. рис.6):

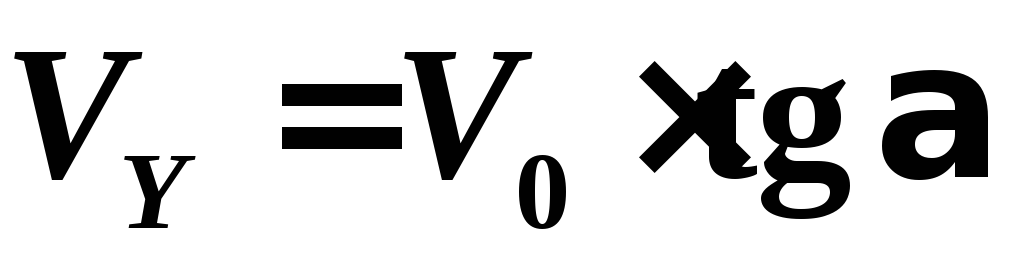. (5)

Из формул (4) и (5) находим:

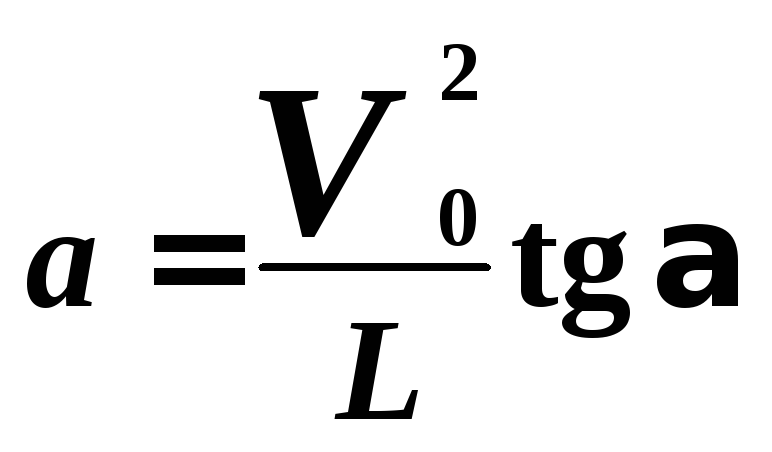. (6)

Напряженность электростатического поля конденсатора E выразим из соотношения (1) с учетом (6):

.

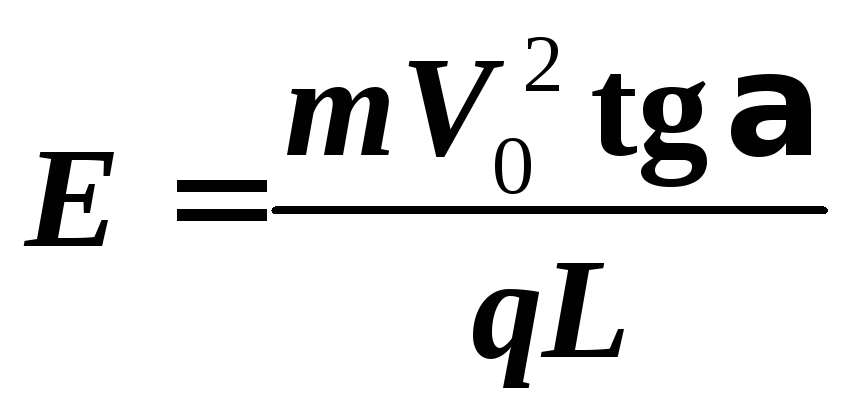Проверка размерности: :

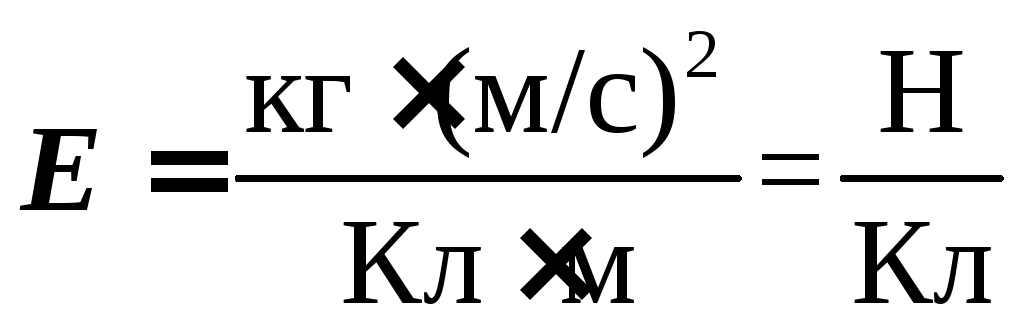
4. Электроемкость

Задача 9. Тысяча одинаковых наэлектризованных капель сливаются в одну, причем их общий заряд сохраняется. Как изменится общая электрическая энергия капель, если считать, что капли сферические и маленькие капли находились на большом расстоянии друг от друга?

РЕШЕНИЕ:

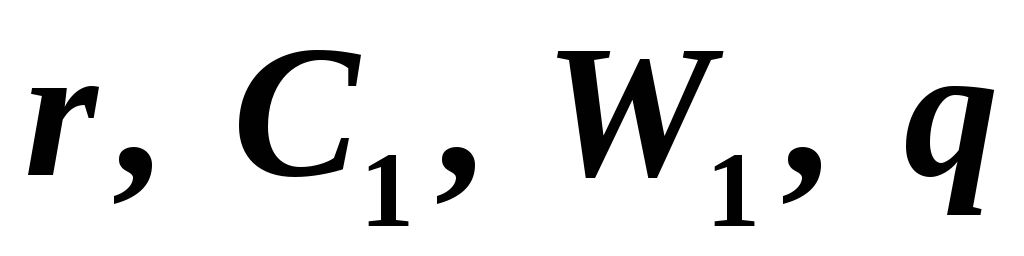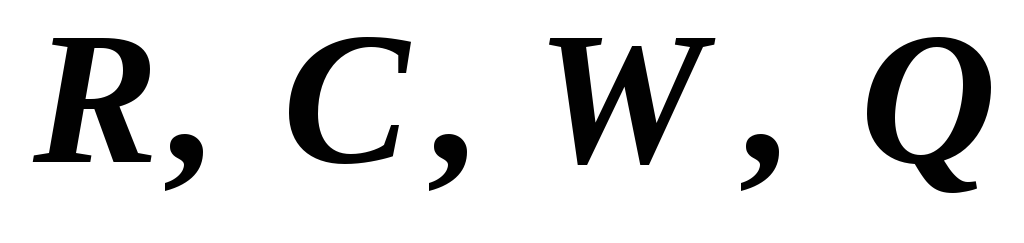Обозначим через радиус, емкость, энергию и заряд одной капли до слияния; радиус, емкость, энергию и заряд большой капли. Приравняем объем капель после и до слияния:

,

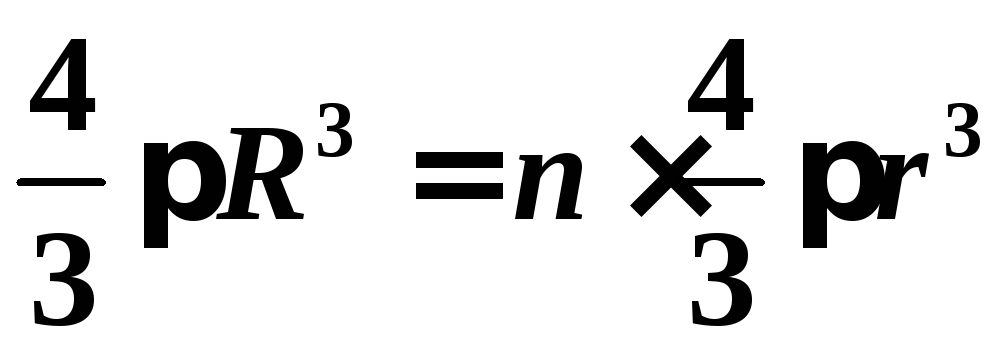откуда ,

где n — число маленьких капель, — емкость шара.

Электрическая энергия одной капли до слияния .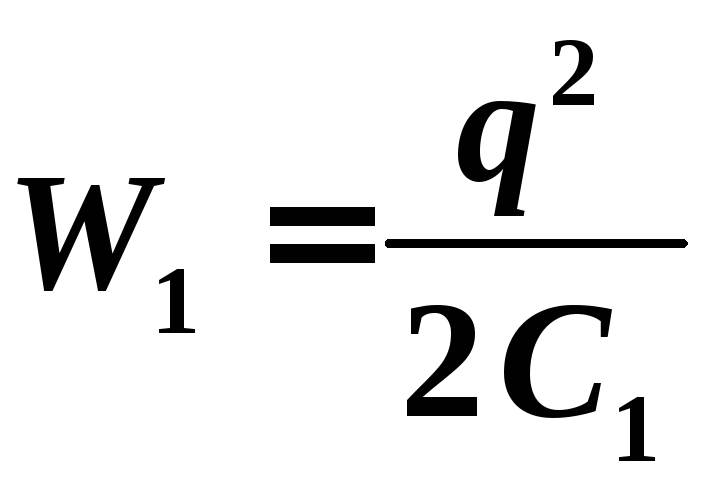

Энергия n капель в n раз больше и равна .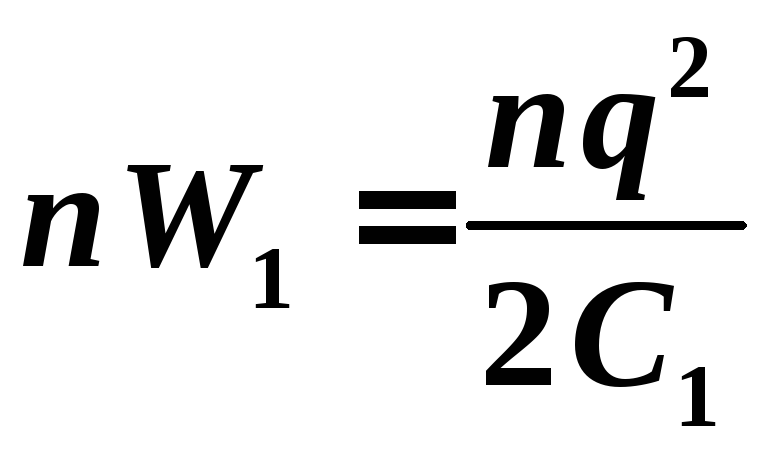

Энергия капели после слияния равна .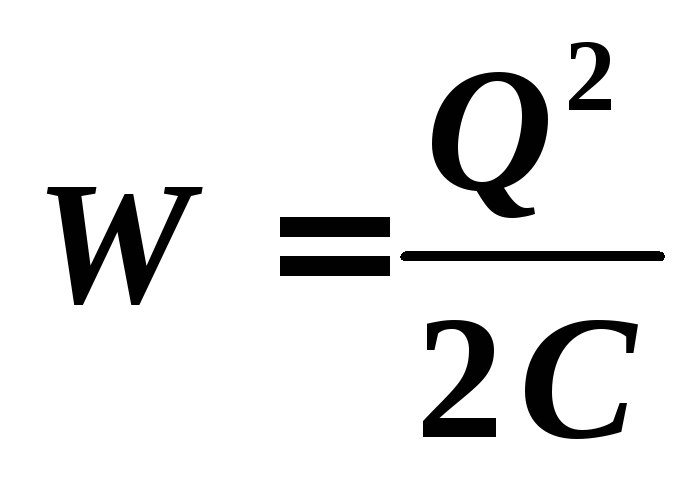

Отношение .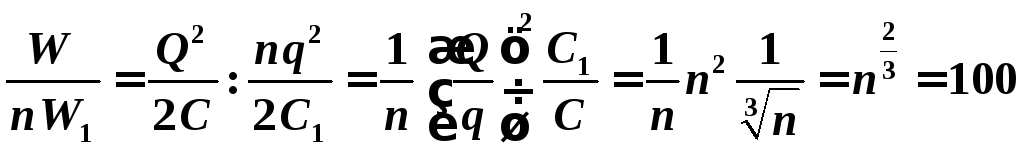

Энергия увеличилась в 100 раз.

Задача 10. Батарея конденсаторов сделана из четырех слюдяных пласти­нок толщиной d = 0,1 мм и площадью S = 100 см² каждая из пластинок станиоля (проводник). Сколько понадобилось пластинок станиоля (n) при параллельном соединении батареи? Начертить схему соединения. Опре­делить емкость батареи. Определить запас электрической энергии, если батарея подключена к источнику на­пряжения U = 220 В. Диэлектрическая проницаемость слюды ε = 7.

Станиоль

Рис. 7

РЕШЕНИЕ

При параллельном соединении конденсаторов между собой соединяются все положительные и все отрицательно заряженные пластинки станиоля. Каждая пластинка станиоля может служить обкладкой двух соседних конденсаторов, как показано на втором рисунке. Количество пластинок станиоля n = 5. Общая емкость C = nC₁ , где C₁ — емкость одного конденсатора: 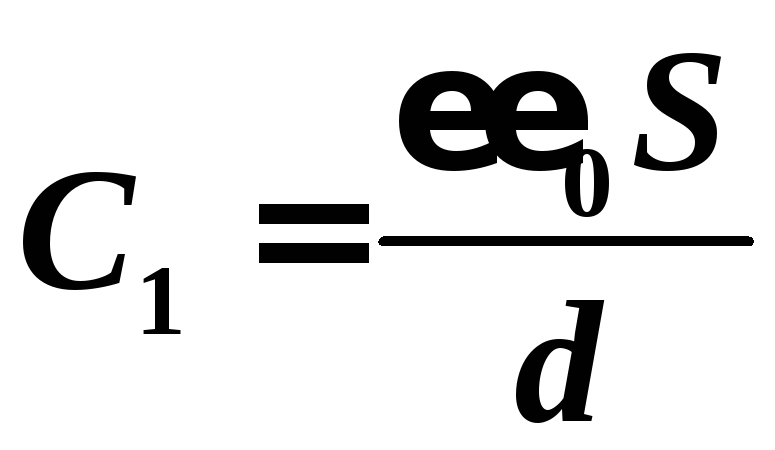. Общая емкость.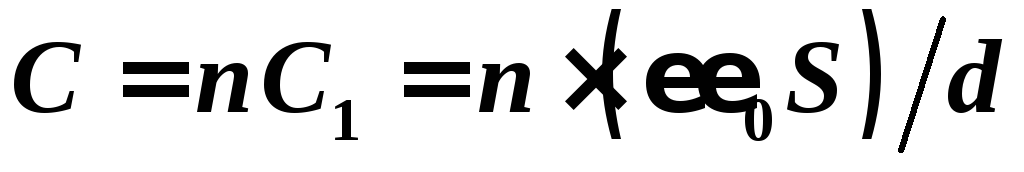

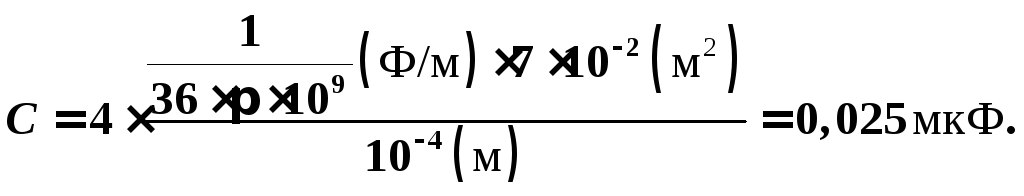
Энергия батареи конденсаторов: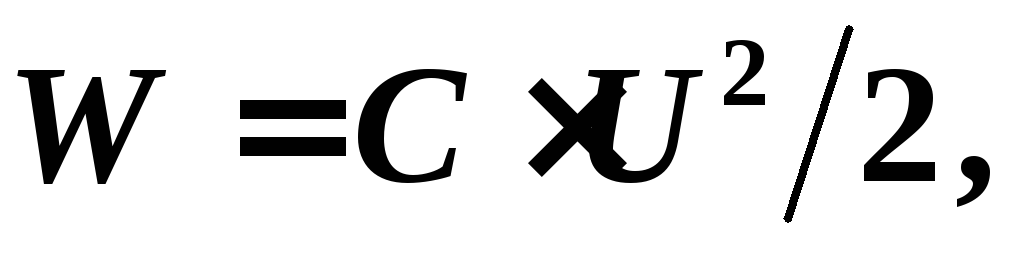

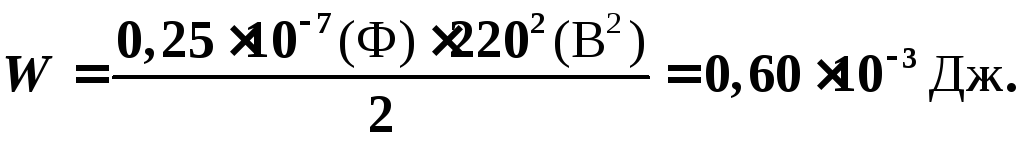
3.3. Потенциал. Разность потенциалов.

Сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на заряд каждый из зарядов системы в отдельности (принцип суперпозиции).

Тогда

A = ∑Ai

Здесь каждое слагаемое не зависит от формы пути и, следовательно не зависит от формы пути и сумма.

Итак электростатическое поле потенциально.

Работу сил электростатического поля можно выразить через убыль

	потенциальной энергии – разность двух функций состояния:
	A12 = Eп1 – Eп2								(3.2.2)
	Тогда выражение (3.2.2) можно переписать в виде:
	A12 =		qq’		−	qq’			(3.2.3)
			4πεε r			4πεε r
		0		1		0	2
	Сопоставляя формулу (3.2.2) и (3.2.3) получим выражение для потенциальной
	энергии заряда q’ в поле заряда q:	1		qq’
	En =					+const			(3.2.4)
		4πεε0			r

Потенциальную энергию определяют с точностью до постоянной интегрирования. Значение константы в выражении Eпот. выбирают таким образом, чтобы при удалении заряда на бесконечность (т. е. при r = ∞), потенциальная энергия обращалась

в нуль. Выражение (3.2.4.) – для одного заряда. Для системы зарядов
EnΣ = ∑Eni	(3.2.5)

Разные пробные заряды q’,q»,… будут обладать в одной и той же точке поля разными энергиями En’, En» и так далее. Однако отношение En/q’пр. будет для всех зарядов одним и тем же. Поэтому ввели скалярную величину, являющуюся

	энергетической характеристикой собственно поля – потенциал.
	φ=	En		(3.3.1)
		q’

Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Подставив в (3.3.1.) значение потенциальной энергии (3.2.3), получим для

	потенциала точечного заряда следующее выражение:
	φ=	1	q	(3.3.2)
		4πεε0	r

Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Договорились считать, что потенциал точки удаленной в бесконечность равен нулю. Поэтому когда говорят «потенциал такой-то точки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала:

φ = Aq∞ или A∞ = qφ,

т.е. потенциал числено равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность

dA = Fl dl = El qdl

(наоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.

Если поле создается системой зарядов, то, используя принцип суперпозиции, получим:

		1		N	qi q’
	En =			∑=					(3.3.3)
		4πεε			r
	0			i 1	i
	Тогда:			1				qi
	φ= ∑φi φ=					∑			(3.3.4)
				4πεε				r
					0			i

т.е. потенциал поля, создаваемый системой зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности, как вы помните, складываются при наложении полей – векторно.

По этой причине потенциалы полей считать проще, чем напряженности.

Вернемся к работе сил электростатического поля над зарядом q’. Выразим работу

через разность потенциалов:
A12 = En1 − En2 = φ1q′−φ2 q′ = q′(φ1 −φ2 )	(3.3.5)
Т.о., работа над зарядом q’ равна произведению заряда на убыль потенциала. То
есть:
A = q'(φ1 −φ2 )= q’U ,
A = qU ,	(3.3.6)

где U – разность потенциалов или еще называют напряжение. Между прочим, хорошая аналогия:

A12 = mgh2 −mgh3 = m(gh2 − gh3 )

gh – имеет смысл потенциала гравитационного поля, а m – заряд.

Итак потенциал – скалярная величина, поэтому пользоваться и вычислять φ

проще, чем E . Приборы для измерения разности потенциалов широко распространены. Формулу A∞=qφ можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из ∞ единичного положительного заряда необходимо совершить работу равную единице.

Так в СИ – единица потенциала 1В = 1Дж/1Кл, в СГСЭ 1ед.пот. = 300В.

В физике часто используется единица энергии и работы, называемой эВ – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1В, то есть:

1эВ =1,6 10−19 Кл В =1,6 10−19 Дж

3.4. Связь между напряженностью и потенциалом.

Итак электростатическое поле можно описать либо с помощью векторной

величины E , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:

Изобразим перемещение заряда q по произвольному пути l.

Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl можно найти так:

(3.4.1)

El – проекция E на drl ; dl – произвольное направление перемещения заряда.

С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl.

	dA = −qdφ; El qdl = −qdφ			(3.4.2)
	El = −	dφ		(3.4.3)
		dl

Вот отсюда размерность напряженности поля В/м.

Для ориентации dl – (направление перемещения) в пространстве, надо знать проекции E на оси координат:

Ex = −

∂φ

; Ey = − ∂φ

; Ez = −

∂φ

;

(3.4.4)

∂x

∂y

∂z

r

∂φr

−

∂φr

∂φ r

(3.4.5)

E = −

∂x

i

∂y

j −

∂z

k

где i, j,k – орты осей – единичные вектора.

По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть:

gradφ = ∂∂φx ri + ∂∂φy rj + ∂∂φz kr

Тогда коротко записывается так:
E = −gradφ	(3.4.6)
gradφ – вектор, показывающий направление наибыстрейшего	увеличения

функции. Знак минус говорит о том, что E направлен в сторону уменьшения потенциала электрического поля.

3.5. Силовые линии и эквипотенциальные поверхности.

Как мы с вами уже знаем, направление силовой линии (линии напряженности) в

каждой точке совпадает с направлением E . Отсюда следует, что напряженность E

равна разности потенциалов на единицу длины силовой линии.

Именно вдоль силовой линии происходит максимальное изменение потенциала.

Поэтому всегда можно определить E между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые

линии – прямые. Поэтому здесь определение E наиболее просто:

E =	U		В
					(3.5.1)
	l
			м

Теперь запишем определение эквипотенциальной поверхности. Воображаемая поверхность все точки, которой имеют одинаковый потенциал, называют

эквипотенциальной поверхностью. Уравнение этой поверхности
φ =φ (x,y,z) = const.	(3.5.2)

Рис. 3.4

При перемещении по этой поверхности на dl, потенциал не изменится: dφ = 0. Следовательно, проекция вектора E на dl равна 0, то есть El = 0. Отсюда

следует, что E в каждой точке направлена по нормали к эквипотенциальной поверхности.

Эквипотенциальных поверхностей можно провести сколько угодно много. По

густоте эквипотенциальных поверхностей можно судить о величине E , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине. На одной из лабораторных работах мы с вами будем моделировать электрическое поле и находить эквипотенциальные поверхности и силовые линии от электродов различной формы – очень наглядно вы увидите как могут располагаться эквипотенциальные поверхности.

Формула E = −gradφ – выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и

обратную задачу, т.е. по известным значениям E в каждой точке поля найти разность φ между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:

2 r r

A12 = ∫qEdl

1

С другой стороны работу можно представить в виде:

A12 = q(φ1 −φ2 )

тогда

2	r r
φ1 −φ2 = ∫Edl		(3.5.3)
1

Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру φ1 = φ2 получим:

т.е. пришли к известной нам теореме о циркуляции вектора напряженности.

Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее этим

свойством, называется потенциальным. Из обращения в нуль циркуляции вектора E ,

следует, что линии E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах и на отрицательных зарядах заканчиваются или уходят в бесконечность.

31

Как обьяснть разность потенциалов простыми словами?!

С детства высокий потенциал ассоциируется с высокой горкой, низкий — с ямкой в земле.

Это напряжение, которое показывает, какую работу совершает суммарное поле сторонних и кулоновских сил при перемещении единичного положительного заряда из одной точки в другую.

Ответ заимствован с сайта electrikpro.ru Сам искал объяснение для ребенка, и практически везде ответы ни о чем. Аналогия с потенциалом в гравитационном поле хоть и близка по сути, но не объясняет откуда разница берется. Ребенок спросил «Это нужно один провод выше другого поставить?» Хоть вопрос и старый, но выходит при запросе о потенциалах в первую десятку, поэтому и ответил, вдруг кому — нибудь поможет Стоит вспомнить о том, что электрические заряды существуют 2-х видов — положительные «+» и отрицательные «-». Они обладают одним простым и полезным свойством, отталкивания и притягивания друг друга в зависимости одинаковости и разноимённости своих видов. То есть, если начать приближать друг к другу одни плюсы или только минусы, то они будут взаимно отталкиваться. Если же приблизить плюс и минус, то они попытаются притянуться друг к другу. Помимо этого, сила взаимного притяжения и отталкивания будет напрямую зависеть от количества самих зарядов. Проще говоря, чем больше «плюса» в одном месте и «минуса» в другом, тем сильнее они будут притягиваться друг к другу. Или наоборот, отталкиваться при одинаковом заряде (+ и + либо — и -). Теперь давайте вообразим, что у нас имеются 2 железных шарика. Каждый из них внутри содержит большое количество элементарных частичек, которые находятся друг от друга на некотором расстоянии и неспособны к свободному перемещению. Это ядра атомов вещества. Вокруг этих частичек с огромной скоростью бегают более мелкие частички — электроны. Они способны оторваться от одних атомов и перейти к другим. Если общее количество электронов будет равно количеству протонов в ядре, шарики нейтральны. Если отобрать некоторое количество электронов у железного шарика, то он перестанет быть нейтральным. Он будет стремиться притянуть к себе недостающее количество электронов, в результате чего образуя вокруг себя поле со знаком «+». Чем больше электронов не хватает, тем сильней поле. В другом шарике сделаем избыток электронов. В результате образуется электрическое поле, но со знаком «-». Вот мы и создали 2 разноимённых потенциала, один из которых стремится приобрести электроны, а второй от них избавится. В железном шарике, где избыток электронов имеется теснота и частицы, вокруг которых имеется поле, выталкивают друг друга. А в том шарике, где недостаток электронов, происходит что-то вроде вакуума, который стремится всосать в себя электроны. Это образует разность потенциалов или электрическое напряжение. Но, как только мы эти шары соединим, так сразу произойдёт взаимный обмен, и электрическое напряжение исчезнет из-за скомпенсированности. Упрощённо говоря, разность потенциалов или электрическое напряжение — эта наличие стремления заряженных частиц, находящихся между двумя точками, притянуть или перейти от более заряженных мест к менее заряженным. Допустим, у нас есть провода подключенные к обычной электрической батарейки. Внутри неё происходит химическая реакция, которая способствует выталкиванию электронов из положительной области батарейки в отрицательную. Избыток электронов находящийся в отрицательной области подходит к отрицательной клемме батарейки. Электроны стремятся вернуться на то место, откуда их вытолкали. Сделать это внутри самой батареи не выходит. Остаётся ждать, когда им проложат мостик в виде металлического электронопроводящего проводника, по которому они перейдут на положительную клемму батареи.

Кто не знает, что Фарадей двести лет назад получил ток с отрицательными и положительными зарядами, который распространяется в прилегающем к проводнику слое эфира, тому теорией электричества заниматься не стоит. Разность электрических потенциалов формируется между нулевым потенциалом и положительным потенциалом, которая рождает в цепи силу движения позитронов, или формируется между нулевым потенциалом и отрицательным потенциалом, которая рождает в цепи силу движения электронов. Нулевой потенциал это как бы нулевой трамплин, откуда берёт своё развитие сила движения разноимённых зарядов. В однофазной системе постоянный ток это движение позитронного тока от плюсовой фазы к нулю или электронного тока от нуля к минусовой фазе. Осциллограммы демонстрирует эту точку зрения Переменный ток формируется точно также, только с соблюдением заданной генератором тока очерёдности протекания разноимённых зарядов, называемой частотой переменного тока. В трёхфазной системе нулевой потенциал переменного тока формируется, когда фазы имеют максимальный положительный или отрицательный потенциалы. А предыдущая и последующая фазы в своих синусоидах в это самое время имеют одноимённые заряды, но с противоположными векторами их движения, которые в сумме рождает нулевой потенциал. Таким образом, в трёхфазной системе нулевой потенциал может формироваться без нулевого провода, исключительно потому, что заряды рассматриваемой фазы текут: позитроны от плюсовой фазы к нулю или электроны от нуля к минусовой фазе. И текут они исключительно в эфире, окружающем проводники. Фиксируемое приборами протекание токов вокруг проводников доказывает существование всепроникающего мирового эфира. <img src=»//otvet.imgsmail.ru/download/264598902_4ef21a466ca262dc5093e05bf42de1f3_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/264598902_4ef21a466ca262dc5093e05bf42de1f3_120x120.jpg» data-big=»1″>

В современной теории электричества сложилось мнение, что кулоновские силы действуют только между зарядами. На самом же деле, в металлических проводниках существует нулевой потенциал проводника. И именно этот нулевой потенциал является центральным элементом электричества, без которого никакой ток никуда не побежит потому, что разность электрических потенциалов между нулевым потенциалом проводника и отрицательным (или положительным) потенциалом источника тока рождает в цепи силу движения зарядов – ЭДС. И эта сила равна алгебраической разности величины перемещаемого заряда и нулём. ЭДС = +q или –q минус 0. То есть ЭДС и напряжение источника – это одно и то же явление. А сторонняя сила это выдумка мыслителей, не разобравшихся в электричестве. В предыдущем ответе в трёхфазной системе я перемудрил. Заряды движутся по общему закону. Геннадий Твердохлебов <img src=»https://otvet.imgsmail.ru/download/272766473_c99c5108d834ca79866f7886d7cf9a40_800.jpg» data-big=»1″ data-lsrc=»//otvet.imgsmail.ru/download/272766473_c99c5108d834ca79866f7886d7cf9a40_120x120.jpg»>

Разность потенциалов между нулевым потенциалом проводника и отрицательным, или положительным потенциалом источника тока рождает ЭДС. <img src=»//otvet.imgsmail.ru/download/265070448_4b41ac82fa4bb04125cb375ecbacd5f4_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/265070448_4b41ac82fa4bb04125cb375ecbacd5f4_120x120.jpg» data-big=»1″>

Ольг­а, спа­си­бо, ч­то по­со­ве­т­ова­л­а <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&amp;st.cmd=logExternal&amp;st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&amp;https://mail.ru &amp;st.name=externalLinkRedirect&amp;st» target=»_blank»>fond2019.ru</a> Вып­л­а­т­или 28 т­ы­сяч за 20 м­и­ну­т как т­ы и на­п­и­с­ала. Ж­а­ль что ра­н­ьш­е не зн­а­л­а про т­а­ки­е ф­о­н­ды, на ра­б­о­ту бы х­оди­т­ь не приш­л­о­с­ь:)

Электрон, прошедший некоторую разность потенциалов, влетает в однородное магнитное

Условие задачи:

Электрон, прошедший некоторую разность потенциалов, влетает в однородное магнитное поле с индукцией 0,01 Тл перпендикулярно магнитным силовым линиям. В магнитном поле он движется по окружности, радиус которой 100 мм. Определить разность потенциалов, которую прошел электрон.

Задача №8.2.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(B=0,01\) Тл, \(\alpha=90^\circ\), \(R=100\) мм, \(U-?\)

Решение задачи:

Чтобы найти какой разностью потенциалов \(U\) был ускорен электрон, запишем закон сохранения энергии:

\[eU = \frac{{{m_e}{\upsilon ^2}}}{2}\]

Откуда:

\[U = \frac{{{m_e}{\upsilon ^2}}}{{2e}} \;\;\;\;(1)\]

Масса электрона \(m_e\) равна 9,1·10^-31 кг, а модуль его заряда \(e\) равен 1,6·10^-19 Кл.

На электрон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:

\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(2)\]

Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость электрона, \(e\) — модуль заряда электрона, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена влево.

Сила Лоренца \(F_Л\) сообщает электрону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:

\[{F_Л} = {m_e}{a_ц}\;\;\;\;(3)\]

Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(4)\]

Подставим (4) в (3), тогда:

\[{F_Л} = \frac{{{m_e}{\upsilon ^2}}}{R}\;\;\;\;(5)\]

Приравняем правые части (2) и (5):

\[B\upsilon e\sin \alpha = \frac{{{m_e}{\upsilon ^2}}}{R}\]

Имеем:

\[Be\sin \alpha = \frac{{{m_e}\upsilon }}{R}\]

Откуда скорость электрона \(\upsilon\) равна:

\[\upsilon = \frac{{BeR\sin \alpha }}{{{m_e}}}\]

Полученное выражение подставим в формулу (1):

\[U = \frac{{{m_e}}}{{2e}} \cdot \frac{{{B^2}{e^2}{R^2}{{\sin }^2}\alpha }}{{m_e^2}}\]

\[U = \frac{{{B^2}e{R^2}{{\sin }^2}\alpha }}{{2{m_e}}}\]

Задача решена в общем виде, посчитаем численный ответ задачи:

\[U = \frac{{{{0,01}^2} \cdot 1,6 \cdot {{10}^{ — 19}} \cdot {{0,1}^2} \cdot {{\sin }^2}90^\circ }}{{2 \cdot 9,1 \cdot {{10}^{ — 31}}}} = 87912,1\;В \approx 87,9\;кВ\]

Ответ: 87,9 кВ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.