Джоуль — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Джо́уль (Дж, J) — одиниця вимірювання роботи і енергії в системі СІ.
Джоуль дорівнює роботі, яка виконується при переміщенні матеріальної точки, до якої прикладена сила 1 Н, на відстань 1 м в напрямку дії сили:
- 1 Дж = 1 Н·м = 1 (кг·м²)/с²
В термінах електрики джоуль дорівнює енергії, яка виділяється за 1 c струмом із силою 1 А на ділянці електричного кола з падінням напруги 1 В. 1 Дж також дорівнює енергії, яку потрібно надати заряду в 1 Кл, щоб збільшити його електричний потенціал на 1 В:
- 1 Дж = 1 В·с·А.
Кратні і частинні одиниці[ред. | ред. код]
| Кратні | Частинні | ||||||
|---|---|---|---|---|---|---|---|
| величина | назва | позначення | величина | назва | позначення | ||
| 101 Дж | декаджоуль | даДж | daJ | 10−1 Дж | дециджоуль | дДж | dJ |
| 102 Дж | гектоджоуль | гДж | hJ | 10−2 Дж | сантиджоуль | сДж | cJ |
| 103 Дж | кілоджоуль | кДж | kJ | 10−3 Дж | міліджоуль | мДж | mJ |
| 106 Дж | мегаджоуль | МДж | MJ | 10−6 Дж | мікроджоуль | мкДж | µJ |
| 109 Дж | гігаджоуль | ГДж | GJ | 10−9 Дж | наноджоуль | нДж | nJ |
| тераджоуль | ТДж | TJ | 10−12 Дж | пікоджоуль | пДж | pJ | |
| 1015 Дж | петаджоуль | ПДж | PJ | 10−15 Дж | фемтоджоуль | фДж | fJ |
| 1018 Дж | ексаджоуль | ЕДж | EJ | 10−18 Дж | атоджоуль | аДж | aJ |
| 1021 Дж | зетаджоуль | ЗДж | ZJ | 10−21 Дж | зептоджоуль | зДж | zJ |
| 1024 Дж | йотаджоуль | ЙДж | 10−24 Дж | йоктоджоуль | йДж | yJ | |
Одиниця отримала свою назву на честь англійського фізика Джеймса Прескотта Джоуля.
В інших системах одиниць[ред. | ред. код]
- 1 Дж = 1 кг·м²/с² = 1 Н·м = 1 Вт·с.
- 1 Дж ≈ 6,2415×1018еВ.
- 1 000 000 Дж ≈ 0,277(7) кВт·год.
- 1 кВт·год = 3 600 000 Дж ≈ 859 845 калорій.
- 1 кВт·с = 1 000 Дж.
- 1 Дж ≈ 0,238846 калорій.
- 1 калорія = 4,1868 Дж.[1]
- 1 термохімічна калорія = 4,1840 Дж.[1]
- ↑ а
- Біленко І. І. Фізичний словник. — К.: Вища школа, Головне видав. 1979. — 336 с.
Джоуль — Википедия
Джо́уль (ингилизча: Joule; белгиленнгени: Дж, J) — иш бла энергияны ЁС-де ёлчем биримиди. Джоуль, ньютоннга тенг кючню салыныу нохтасыны, бир метр аралыкъгъа кёчюрген ишге тенгди. Электричествода 1 ампер электрика токну 1 секундну ичинде, 1 Ом къаршчыланыуну юсю бла ётюуде ишге тенгди[1].
Джоуль биринчи кере, Джеймс Джоулну ёлген джылында бардырылгъан (1889) Электриклени экинчи халкъла арасы конгрессинде джюрютюлюб башланнганды
Электрика биримле бла эталонланы юсюнден халкъла арасы конференция (Лондон, 1908) «халкъла арасы» электрика биримлени, аны ичиндеда «халкъла арасы Джоульну» бегитгенди. 1948 джылны 1-чи янаврындан башлаб абсолют электрика биримлеге къайтыудан сора: 1 халкъла арасы Джоуль = 1,00020 абсолют Джоулгъа марда бегитилгенди[3].
- 1 Дж = кг·м²/с² = Н·м = Вт·с.
- 1 Дж ≈ 6,2415eэВ.
- 1 000 000 Дж ≈ 0,277(7) кВт·сгъ.
- 1 кВт·сгъ = 3 600 000 Дж ≈ 859 845 калория.
- 1 кВт·с = 1 000 Дж.
- 1 Дж ≈ 0,238846 калория.
- 1 калория = 4,1868 Дж.[4]
- 1 термохимиялыкъ калория = 4,1840 Дж.
Онлукъ къат эмда юлюш биримлени ЁС-ни стандарт индекслерини болушлугъу бла къурайдыла.
| Къат | Юлюш | ||||||
|---|---|---|---|---|---|---|---|
| ёлчеми | аты | белгилениую | ёлчеми | аты | белгилениую | ||
| 101 Дж | декаджоуль | даДж | daJ | 10−1 Дж | дециджоуль | дДж | dJ |
| 102 Дж | гектоджоуль | гДж | hJ | 10−2 Дж | сантиджоуль | сДж | cJ |
| 103 Дж | килоджоуль | кДж | kJ | 10−3 Дж | миллиджоуль | мДж | mJ |
| 106 Дж | мегаджоуль | МДж | MJ | 10−6 Дж | микроджоуль | мкДж | µJ |
| 109 Дж | гигаджоуль | ГДж | GJ | 10−9 Дж | наноджоуль | нДж | nJ |
| 1012 Дж | тераджоуль | ТДж | TJ | 10−12 Дж | пикоджоуль | пДж | pJ |
| 1015 Дж | петаджоуль | ПДж | PJ | 10−15 Дж | фемтоджоуль | фДж | fJ |
| 1018 Дж | эксаджоуль | ЭДж | EJ | 10−18 Дж | аттоджоуль | аДж | aJ |
| 1021 Дж | зеттаджоуль | ЗДж | ZJ | 10−21 Дж | зептоджоуль | зДж | zJ |
| 1024 Дж | йоттаджоуль | ИДж | YJ | 10−24 Дж | йоктоджоуль | иДж | yJ |
| хайырланыргъы рекомендация берилмейди | |||||||
- ↑ http://dic.academic.ru/dic.nsf/medic/2109
- ↑ Джоуль
- ↑ БСЭ
- ↑ 4,04,1 Физический энциклопедический словарь, М., 1983, стр. 241 (статья «Калория»)
ДЖОУЛЬ — это… Что такое ДЖОУЛЬ?
ДЖОУЛЬ — (по имени англ. физика 1818 89). Работа в течение одной секунды такого электрического тока, электродвижущая сила которого равна 1 вольту, а сила = 1 амперу. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. джоуль… … Словарь иностранных слов русского языка
ДЖОУЛЬ — (Joule) Джеймс Прескотт (1818 89), английский физик, экспериментально обосновавший закон сохранения энергии. Владелец пивоваренных заводов. Показал, что теплоту можно получить за счет работы и вычислил механический эквивалент теплоты. Установил… … Современная энциклопедия
ДЖОУЛЬ — единица энергии, работы и количества теплоты СИ. Названа по имени Дж. П. Джоуля. Обозначается Дж. 1 Дж = 107 эрг = 0,2388 кал = 6,24 . 1018 эВ … Большой Энциклопедический словарь
ДЖОУЛЬ — ДЖОУЛЬ, я, муж. Единица энергии, работы и количества теплоты. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ДЖОУЛЬ — (Дж, J), единица СИ работы, энергии и кол ва теплоты. Названа в честь англ. физика Дж. П. Джоуля (J. P. Joule). 1 Дж равен работе силы 1 Н при перемещении точки приложения силы на расстояние 1 м в направлении действия силы. 1 Дж=1Н•м=107… … Физическая энциклопедия
ДЖОУЛЬ — одна ватт секунда (Joule) единица работы в абсолютной системе мер, равная 107 эргам. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
ДЖОУЛЬ — единица электр. работы или энергии, равная 10 000 000 эргов (э), или 0,102 килограммометра (кгм), или 0,24 кал. Сокращенное обозначение J, или дж. 1 дж = 1 вт с; 3 600 дж = 1 вт ч; 360 000 дж = 1 гвт ч; 3 600 000 дж =1 квт ч. Технический… … Технический железнодорожный словарь
джоуль — сущ., кол во синонимов: 1 • единица (830) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Джоуль — (James Prescott Joule) известный англ. физик (1818 89). До15 лет Д. воспитывался в семье отца своего, богатого пивовара; затемработал на заводе, изучая в то же время математику, химию и физику подруководством Дальтона. Первые работы Д.,… … Энциклопедия Брокгауза и Ефрона
Джоуль — (Дж) единица измерения энергии по Международной системе единиц (СИ), заменившая калорию. 1 Дж=0,2388 кал. Экологический словарь. Алма Ата: «Наука». Б.А. Быков. 1983 … Экологический словарь
Джоуль — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Джо́уль (англ. Joule
В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы джоуль пишется со строчной буквы, а её обозначение — с заглавной. Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием джоуля. Например, обозначение единицы молярной внутренней энергии «джоуль на моль» записывается как Дж/моль.
Джоуль был введён в абсолютные практические электрические единицы в качестве единицы работы и энергии электрического тока на Втором международном конгрессе электриков, проходившем в год смерти Джеймса Джоуля (1889). Международная конференция по электрическим единицам и эталонам (Лондон, 1908) установила «международные» электрические единицы, в том числе «международный джоуль». После возвращения с 1 января 1948 к абсолютным электрическим единицам было принято соотношение: 1 международный джоуль = 1,00020 абсолютного джоуля[3]. В Международную систему единиц (СИ) джоуль введён решением XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом[4].
Перевод в другие единицы
Кратные и дольные единицы
В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы джоуля образуются с помощью стандартных приставок СИ[6]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в РФ тех же приставок[7].
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Дж | декаджоуль | даДж | daJ | 10−1 Дж | дециджоуль | дДж | dJ |
| 102 Дж | гектоджоуль | гДж | hJ | 10−2 Дж | сантиджоуль | сДж | cJ |
| 103 Дж | килоджоуль | кДж | kJ | 10−3 Дж | миллиджоуль | мДж | mJ |
| 106 Дж | мегаджоуль | МДж | MJ | 10−6 Дж | микроджоуль | мкДж | µJ |
| 109 Дж | гигаджоуль | ГДж | GJ | 10−9 Дж | наноджоуль | нДж | nJ |
| 1012 Дж | тераджоуль | ТДж | TJ | 10−12 Дж | пикоджоуль | пДж | pJ |
| 1015 Дж | петаджоуль | ПДж | PJ | 10−15 Дж | фемтоджоуль | фДж | fJ |
| 1018 Дж | эксаджоуль | ЭДж | EJ | 10−18 Дж | аттоджоуль | аДж | aJ |
| 1021 Дж | зеттаджоуль | ЗДж | ZJ | 10−21 Дж | зептоджоуль | зДж | zJ |
| 1024 Дж | иоттаджоуль | ИДж | YJ | 10−24 Дж | иоктоджоуль | иДж | yJ |
| применять не рекомендуется | |||||||
Примеры
- Средняя энергия теплового движения, приходящаяся на одну степень свободы молекул при температуре 1 К: 0,690·10−23 Дж.
- Энергия фотона красного видимого света: 2,61·10−19 Дж.
- Энергия Ферми металлического золота: 8,8·10−19 Дж[8].
- Атомная единица энергии (энергия Хартри), <math>E_h = m_\mathrm{e} c^2\alpha^2 </math>: 4.360·10−18 Дж.
- Дульная энергия пули при выстреле из АКМ: 2,3·103 Дж.
- Энергия, необходимая для нагрева 1 литра воды от 20 до 100 °C: 3,35·105 Дж.
- Энергия, выделяемая при взрыве 1 тонны тринитротолуола (тротиловый эквивалент): 4,184·109 Дж.
- Энергия, выделенная при атомной бомбардировке Хиросимы: около 6·1013 Дж.
См. также
Напишите отзыв о статье «Джоуль»
Примечания
Отрывок, характеризующий Джоуль
и 8 орудий дивизии Фриана и Дессе,Всего – 62 орудия.
Начальник артиллерии 3 го корпуса, генерал Фуше, поставит все гаубицы 3 го и 8 го корпусов, всего 16, по флангам батареи, которая назначена обстреливать левое укрепление, что составит против него вообще 40 орудий.
Генерал Сорбье должен быть готов по первому приказанию вынестись со всеми гаубицами гвардейской артиллерии против одного либо другого укрепления.
В продолжение канонады князь Понятовский направится на деревню, в лес и обойдет неприятельскую позицию.
Генерал Компан двинется чрез лес, чтобы овладеть первым укреплением.
По вступлении таким образом в бой будут даны приказания соответственно действиям неприятеля.
Канонада на левом фланге начнется, как только будет услышана канонада правого крыла. Стрелки дивизии Морана и дивизии вице короля откроют сильный огонь, увидя начало атаки правого крыла.
Вице король овладеет деревней [Бородиным] и перейдет по своим трем мостам, следуя на одной высоте с дивизиями Морана и Жерара, которые, под его предводительством, направятся к редуту и войдут в линию с прочими войсками армии.
Все это должно быть исполнено в порядке (le tout se fera avec ordre et methode), сохраняя по возможности войска в резерве.
В императорском лагере, близ Можайска, 6 го сентября, 1812 года».
Диспозиция эта, весьма неясно и спутанно написанная, – ежели позволить себе без религиозного ужаса к гениальности Наполеона относиться к распоряжениям его, – заключала в себе четыре пункта – четыре распоряжения. Ни одно из этих распоряжений не могло быть и не было исполнено.
В диспозиции сказано, первое: чтобы устроенные на выбранном Наполеоном месте батареи с имеющими выравняться с ними орудиями Пернетти и Фуше, всего сто два орудия, открыли огонь и засыпали русские флеши и редут снарядами. Это не могло быть сделано, так как с назначенных Наполеоном мест снаряды не долетали до русских работ, и эти сто два орудия стреляли по пустому до тех пор, пока ближайший начальник, противно приказанию Наполеона, не выдвинул их вперед.
Второе распоряжение состояло в том, чтобы Понятовский, направясь на деревню в лес, обошел левое крыло русских. Это не могло быть и не было сделано потому, что Понятовский, направясь на деревню в лес, встретил там загораживающего ему дорогу Тучкова и не мог обойти и не обошел русской позиции.
Третье распоряжение: Генерал Компан двинется в лес, чтоб овладеть первым укреплением. Дивизия Компана не овладела первым укреплением, а была отбита, потому что, выходя из леса, она должна была строиться под картечным огнем, чего не знал Наполеон.
Четвертое: Вице король овладеет деревнею (Бородиным) и перейдет по своим трем мостам, следуя на одной высоте с дивизиями Марана и Фриана (о которых не сказано: куда и когда они будут двигаться), которые под его предводительством направятся к редуту и войдут в линию с прочими войсками.
Сколько можно понять – если не из бестолкового периода этого, то из тех попыток, которые деланы были вице королем исполнить данные ему приказания, – он должен был двинуться через Бородино слева на редут, дивизии же Морана и Фриана должны были двинуться одновременно с фронта.
Все это, так же как и другие пункты диспозиции, не было и не могло быть исполнено. Пройдя Бородино, вице король был отбит на Колоче и не мог пройти дальше; дивизии же Морана и Фриана не взяли редута, а были отбиты, и редут уже в конце сражения был захвачен кавалерией (вероятно, непредвиденное дело для Наполеона и неслыханное). Итак, ни одно из распоряжений диспозиции не было и не могло быть исполнено. Но в диспозиции сказано, что по вступлении таким образом в бой будут даны приказания, соответственные действиям неприятеля, и потому могло бы казаться, что во время сражения будут сделаны Наполеоном все нужные распоряжения; но этого не было и не могло быть потому, что во все время сражения Наполеон находился так далеко от него, что (как это и оказалось впоследствии) ход сражения ему не мог быть известен и ни одно распоряжение его во время сражения не могло быть исполнено.
Многие историки говорят, что Бородинское сражение не выиграно французами потому, что у Наполеона был насморк, что ежели бы у него не было насморка, то распоряжения его до и во время сражения были бы еще гениальнее, и Россия бы погибла, et la face du monde eut ete changee. [и облик мира изменился бы.] Для историков, признающих то, что Россия образовалась по воле одного человека – Петра Великого, и Франция из республики сложилась в империю, и французские войска пошли в Россию по воле одного человека – Наполеона, такое рассуждение, что Россия осталась могущественна потому, что у Наполеона был большой насморк 26 го числа, такое рассуждение для таких историков неизбежно последовательно.
Ежели от воли Наполеона зависело дать или не дать Бородинское сражение и от его воли зависело сделать такое или другое распоряжение, то очевидно, что насморк, имевший влияние на проявление его воли, мог быть причиной спасения России и что поэтому тот камердинер, который забыл подать Наполеону 24 го числа непромокаемые сапоги, был спасителем России. На этом пути мысли вывод этот несомненен, – так же несомненен, как тот вывод, который, шутя (сам не зная над чем), делал Вольтер, говоря, что Варфоломеевская ночь произошла от расстройства желудка Карла IX. Но для людей, не допускающих того, чтобы Россия образовалась по воле одного человека – Петра I, и чтобы Французская империя сложилась и война с Россией началась по воле одного человека – Наполеона, рассуждение это не только представляется неверным, неразумным, но и противным всему существу человеческому. На вопрос о том, что составляет причину исторических событий, представляется другой ответ, заключающийся в том, что ход мировых событий предопределен свыше, зависит от совпадения всех произволов людей, участвующих в этих событиях, и что влияние Наполеонов на ход этих событий есть только внешнее и фиктивное.
Джоуль — это… Что такое Джоуль?
ДЖОУЛЬ — • ДЖОУЛЬ (Joule) Джеймс Прескотт (1818 89), британский физик. Сформулировал закон Джоуля (1841), гласящий, что прохождение тока по проводнику является причиной потери им тепла, и заложил основы для последующей формулировки ЗАКОНА СОХРАНЕНИЯ… … Научно-технический энциклопедический словарь
ДЖОУЛЬ — (по имени англ. физика 1818 89). Работа в течение одной секунды такого электрического тока, электродвижущая сила которого равна 1 вольту, а сила = 1 амперу. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. джоуль… … Словарь иностранных слов русского языка
ДЖОУЛЬ — (Joule) Джеймс Прескотт (1818 89), английский физик, экспериментально обосновавший закон сохранения энергии. Владелец пивоваренных заводов. Показал, что теплоту можно получить за счет работы и вычислил механический эквивалент теплоты. Установил… … Современная энциклопедия
ДЖОУЛЬ — единица энергии, работы и количества теплоты СИ. Названа по имени Дж. П. Джоуля. Обозначается Дж. 1 Дж = 107 эрг = 0,2388 кал = 6,24 . 1018 эВ … Большой Энциклопедический словарь
ДЖОУЛЬ — ДЖОУЛЬ, я, муж. Единица энергии, работы и количества теплоты. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ДЖОУЛЬ — (Дж, J), единица СИ работы, энергии и кол ва теплоты. Названа в честь англ. физика Дж. П. Джоуля (J. P. Joule). 1 Дж равен работе силы 1 Н при перемещении точки приложения силы на расстояние 1 м в направлении действия силы. 1 Дж=1Н•м=107… … Физическая энциклопедия
ДЖОУЛЬ — одна ватт секунда (Joule) единица работы в абсолютной системе мер, равная 107 эргам. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
ДЖОУЛЬ — единица электр. работы или энергии, равная 10 000 000 эргов (э), или 0,102 килограммометра (кгм), или 0,24 кал. Сокращенное обозначение J, или дж. 1 дж = 1 вт с; 3 600 дж = 1 вт ч; 360 000 дж = 1 гвт ч; 3 600 000 дж =1 квт ч. Технический… … Технический железнодорожный словарь
джоуль — сущ., кол во синонимов: 1 • единица (830) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Джоуль — (James Prescott Joule) известный англ. физик (1818 89). До15 лет Д. воспитывался в семье отца своего, богатого пивовара; затемработал на заводе, изучая в то же время математику, химию и физику подруководством Дальтона. Первые работы Д.,… … Энциклопедия Брокгауза и Ефрона
Джоуль — (Дж) единица измерения энергии по Международной системе единиц (СИ), заменившая калорию. 1 Дж=0,2388 кал. Экологический словарь. Алма Ата: «Наука». Б.А. Быков. 1983 … Экологический словарь
Джоуль единица измерения — Справочник химика 21
Количество теплоты, подводимой (или отводимой) к произвольной массе вещества, обозначают Qt, а удельное количество теплоты, отнесенное к единице массы вещества, — (/. Теплоту в системе СИ измеряют в джоулях (Дж), килоджоулях (кДж) допускаются и такие единицы измерения, как калория и килокалория (ккал). [c.25]Единицами измерения количества теплоты служат джоуль и калория (ГОСТ 8550—57). В практике расчетов необходимо различать малые калории (кал) и большие калории, или килокалории (ккал). Одна малая калория представляет собой количество тепла, которое необходимо для нагревания 1 г, а ккал — 1 кг воды на 1 (с 19,5 до 20,5° С) при нормальном атмосферном давлении. [c.21]
Джоуль (Дж)—единица измерения всех видов энергии и работы в Международной системе единиц СИ. Он равен работе силы в 1 Н на пути в 1 м. [c.23]
Необходимо условиться относительно единицы измерения количества теплоты. В настоящее время за единицу количества теплоты принят джоуль, который равен работе, производимой силой в 1 ньютон при перемещении точки ее приложения на 1 -метр по направлению этой силы. С другой стороны, джоуль можно охарактеризовать как работу, совершаемую электрическим током мощностью в 1 ватт в течение 1 с. Наконец, следует отметить, еще одно определение джоуля, связанное непосредственно с представлением о количестве теплоты. Джоуль — это такое количество теплоты, которое необходимо для нагревания 1/4,186 г воды на ГС в интервале температур от 14,65 до 15,65°С. Последнее определение иллюстрирует взаимосвязь джоуля с калорией, которая в настоящее время для определения количества теплоты не рекомендуется. Следовательно, единицей теплоемкости для принятой единицы количества вещества является Дж/К. [c.29]
Соотношения между единицами энергии. При вычислении термодинамических свойств веществ на основании использования экспериментальных результатов спектроскопических, калориметрических, масс-спектрометрических и иных исследований приходится иметь дело с количествами энергии, выраженными в различных единицах. Традиционной единицей измерения энергии при калориметрических исследованиях является калория, в то время как традиционными единицами энергии при спектроскопических исследованиях — обратный сантиметр, а при масс-спектрометрических исследованиях — электрон-вольт. В механике издавна укоренились в качестве основных единиц энергии эрг и джоуль = 10 эрг. Однако если соотношения между обратным сантиметром и эргом и электронвольтом и эргом определяются лишь значениями основных физических постоянных, так как [c.956]
В данной книге в качестве единицы измерения теплоты используется только джоуль, однако следует знать и о калории, поскольку в старой литературе повсеместно используется именно калория. Калория приблизительно вчетверо больше джоуля 1 кал = 4,184 Дж. Теплоты реакций для молярных количеств веществ обычно имеют порядок килоджоулей (кДж) или килокалорий (ккал) 1 кДж = 1000 Дж и 1 ккал = 1000 кал. [c.89]
Обозначения единиц, происходящих от имен собственных, начинаются с прописной буквы. Например, А — ампер, К — кельвин, Дж — джоуль. Единицы измерения, выражающие произведение двух других единиц, представляют знаком умножения, например Н м, Дж с. Единицы измерения, как частное от деления двух другах единиц, могут быть представлены любым из способов м/с, [c.6]
Ранее вы уже встречались с единицей измерения под названием джоуль при измерении количества энергии. При рассмотрении энергоемкости пищевых продуктов мы используем понятие калория вовсе не для того, чтобы сбить вас с толку. Энергию измеряли в калориях во всех случаях до тех пор, пока не была введена метрическая систсма мер СИ. В принципе энергоемкость продуктов питания можно считать и в джоулях, поскольку [c.240]
В СИ предусматривается одна и та же единица — джоуль для измерения всех видов анергии, в том числе тепловой. Это устраняет необходимость введения в расчетные формулы дополнительных множителей для пересчета единиц измерения различных видов энергии. Если же тепловая энергия измеряется в ккал, то для перехода к единицам СИ или МКГСС в расчетные формулы вводится делитель А (термический эквивалент работы), равитга количеству тепла, которое соответствует данной единице работы (дж или кгс-м) [c.34]
Джоуль является очень удобной единицей измерения теплоты, так как с его помощью легко понять связь между теплотой, работой-и энергией. До введения системы СИ в химии было принято пользоваться в качестве единицы измерения теплоты калорией. Одна калория (кал) определяется как количество теплоты, необходимое для повышения температуры 1 г чистой воды на 1″С (точнее от 14,5 до 15,5″»С). Это определение основано на измерениях теплоты и непосредственно не связано с работой. Дело в том, что калория была введена в XIX столетии, когда еще не было известно, что теплота и работа являются различными формами энергии. [c.88]
Работу также измеряют в джоулях (система СИ) применяется и другая единица измерения — килограмм-сила-метр (кгс-м) [c.25]
Этот переход происходит в строго эквивалентной (равной) мере, хотя исторически сложилось так, что каждой форме энергии соответствуют свои единицы измерения. В настоящее время за общую единицу энергии принят джоуль. В этих единицах измеряется также работа теплоту чаще принято измерять в калориях. [c.13]
Чтобы получить представление о величине джоуля, укажем, что бейсбольный мяч массой около 150 г, летящий после подачи со скоростью около 150 км ч (40 м с ), обладает кинетической энергией в 120 Дж. Широко распространенная в прошлом единица измерения тепла-калория (кал)-приблизительно в четыре раза больше джоуля (точнее, 1 кал = = 4,184 Дж). [c.101]
Единица измерения работы — Джоуль (1 Дж=1 Н-м). Энергию и работу измеряют в одних и тех же единицах. [c.212]
Стандартная энтропия чистых веществ относится к 1 моль вещества при р=101 кПа и определенной температуре, чаще 298 К. Она обозначается 5 . Единица измерения энтропии — джоуль на моль-кельвин (Дж/(моль-К). [c.98]
Традиционной единицей измерения теплоты, работы и энергии является калория, которая вводится эмпирически как количество теплоты, необходимое для повышения температуры одного грамма воды на один градус Ке
Идеальный газ — Википедия
Идеа́льный газ — теоретическая модель, широко применяемая для описания свойств и поведения реальных газов при умеренных давлениях и температурах. В этой модели, во-первых, предполагается, что составляющие газ частицы не взаимодействуют друг с другом, то есть их размеры пренебрежимо малы, поэтому в объёме, занятом идеальным газом, нет взаимных столкновений частиц. Частицы идеального газа претерпевают столкновения только со стенками сосуда. Второе предположение: между частицами газа нет дальнодействующего взаимодействия, например, электростатического или гравитационного. Дополнительное условие упругих столкновений между молекулами и стенками сосуда в рамках молекулярно-кинетической теории приводит к термодинамике идеального газа 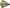 .
.
В различных расширенных моделях идеального газа предполагается, что частицы имеют внутреннюю структуру и протяженные размеры, что можно представить частицы в виде эллипсоидов или сфер, соединённых упругими связями (например, двухатомные молекулы). Представление частиц газа в виде многоатомных молекул приводит к возникновению дополнительных степеней свободы, что побуждает учитывать энергию не только поступательного, но и вращательно-колебательного движения частиц, а также не только центральные, но и нецентральные столкновения частиц[1].
Модель широко применяется для решения задач термодинамики газов и аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с достаточной для практических расчётов точностью хорошо описывается моделью идеального газа.
В случае очень больших давлений требуется применение более точных уравнений состояния реальных газов, например, полуэмпирического уравнения Ван-дер-Ваальса, в котором учитывается притяжение между молекулами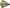 и их конечные размеры. При очень высоких температурах молекулы реальных газов могут диссоциировать на составляющие их атомы, или атомы могут ионизироваться с отщеплением электронов. Поэтому в случаях высоких давлений и/или температур уравнения состояния идеального газа применимы только с некоторыми допущениями, либо неприменимы совсем.
и их конечные размеры. При очень высоких температурах молекулы реальных газов могут диссоциировать на составляющие их атомы, или атомы могут ионизироваться с отщеплением электронов. Поэтому в случаях высоких давлений и/или температур уравнения состояния идеального газа применимы только с некоторыми допущениями, либо неприменимы совсем.
Различают классический идеальный газ (его свойства выводятся из законов классической механики и подчиняются статистике Максвелла — Больцмана)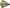 , квазиклассический идеальный газ[2] (для которого — в отличие от классического идеального газа — не выполняется закон равномерного распределения энергии по степеням свободы[3][4]) и квантовый идеальный газ (его свойства определяются законами квантовой механики и описываются статистиками Ферми — Дирака или Бозе — Эйнштейна)
, квазиклассический идеальный газ[2] (для которого — в отличие от классического идеального газа — не выполняется закон равномерного распределения энергии по степеням свободы[3][4]) и квантовый идеальный газ (его свойства определяются законами квантовой механики и описываются статистиками Ферми — Дирака или Бозе — Эйнштейна)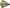 .
.
С термодинамической точки зрения различие между классическим и квазиклассическим идеальными газами состоит в следующем. Теплоёмкость классического идеального газа не зависит от температуры и однозначно задана геометрией молекулы газа[5], которая тем самым определяет вид калорического уравнения состояния газа. Классические идеальные газы с одинаковой геометрией молекул подчиняются одному и тому же калорическому уравнению состояния. Теплоёмкость квазиклассического идеального газа зависит от температуры[6][K 1], причём эта зависимость индивидуальна для каждого газа; соответственно каждый квазиклассический идеальный газ описывается своим собственным калорическим уравнением состояния. Очень часто — в том числе и в данной статье, — когда различия между классическим и квазиклассическим приближениями не играют роли, термин «классический идеальный газ» рассматривают как синоним выражения «неквантовый идеальный газ». При макроскопическом подходе идеальными классическими и квазиклассическими газами называют гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона[11][12] (Клапейрона — Менделеева[13][12]). Иногда дополнительно указывают, что для классического идеального газа справедлив закон Джоуля[14][15][16][17]. Термодинамика утверждает, что закон Джоуля выполняется для любого флюида с уравнением состояния вида pT=f(V){\displaystyle {\frac {p}{T}}=f(V)} или pV=f(T){\displaystyle pV=f(T)}, где p{\displaystyle p} — давление, T{\displaystyle T} — абсолютная температура и V{\displaystyle V} — объём (см. [18][19][20]). Поэтому, давая дефиницию классическому идеальному газу, упоминать о законе Джоуля необязательно. С другой стороны, если рассматривать данный закон как обобщение экспериментальных данных, то изложение макроскопической теории классического идеального газа требует привлечения только самых элементарных сведений из термодинамики.
Популярность модели «идеальный газ» в учебных курсах термодинамики обусловлена тем обстоятельством, что результаты, получаемые с помощью уравнения Клапейрона, представляют собой не слишком сложные математические выражения и обычно допускают простой аналитический и/или графический анализ поведения входящих в них величин. Квазиклассическое приближение используют для вычисления термодинамических функций газов по их молекулярным данным[21][22][23].
 Бенуа Клапейрон
Бенуа КлапейронИстория возникновения понятия идеальный газ восходит к успехам экспериментальной физики, начало которым было положено в XVII веке. В 1643 г. Эванджелиста Торричелли впервые доказал, что воздух имеет вес (массу), и, совместно с В. Вивиани, провёл опыт по измерению атмосферного давления с помощью запаянной с одного конца стеклянной трубки, заполненной ртутью. Так появился на свет первый ртутный барометр. В 1650 г. немецкий физик Отто фон Герике изобрёл воздушный насос и провёл в 1654 году знаменитый эксперимент с магдебургскими полушариями, наглядно подтвердивший существование атмосферного давления. Эксперименты английского физика Роберта Бойля по уравновешиванию ртутного столба давлением сжатого воздуха привели в 1662 году к выводу газового закона, названного впоследствии законом Бойля — Мариотта[24], в связи с тем, что французский физик Эдм Мариотт в 1679 г. провёл аналогичное независимое исследование.
В 1802 году французский физик Гей-Люссак опубликовал в открытой печати закон объёмов (называемый в русскоязычной литературе законом Гей-Люссака)[25], однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них этот закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно он был описан французским учёным Гийомом Амонтоном в конце XVII века. Гей-Люссак также установил, что коэффициент объёмного расширения одинаков для всех газов, несмотря на общепринятое мнение, что разные газы расширяются при нагревании различным образом.
Гей-Люссак (1822)[26][27][28] и Сади Карно (1824)[29][30][28] были первыми, кто объединил в едином уравнении законы Бойля — Мариотта и Шарля — Дальтона — Гей-Люссака. Поскольку, однако, Гей-Люссак найденным им уравнением не пользовался, а с полученными Карно результатами знакомились не по его ставшей библиографической редкостью[31] книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу»[32], а по изложению идей Карно в работе Бенуа Клапейрона «Мемуар о движущей силе огня»[33], то и вывод термического уравнения состояния идеального газа приписали Клапейрону[34][30], а уравнение стали называть уравнением Клапейрона, хотя сам этот учёный никогда не претендовал на авторство обсуждаемого уравнения[28]. Не вызывает, между тем, сомнения, что именно Клапейрон первый понял плодотворность применения уравнения состояния, существенно упрощавшего все связанные с газами расчёты.
Экспериментальные исследования физических свойств реальных газов в те годы были не вполне точны и проводились в условиях не сильно отличавшихся от нормальных (температура 0 ℃, давление 760 мм рт. ст.). Предполагалось также, что газ, в отличие от пара, представляет собой субстанцию, неизменную в любых физических условиях. Первый удар по этим представлениям нанесло сжижение хлора в 1823 г. В дальнейшем выяснилось, что реальные газы представляют собой перегретые пары, достаточно удалённые от областей конденсации и критического состояния. Любой реальный газ может быть превращён в жидкость путём конденсации, либо путём непрерывных изменений однофазового состояния. Таким образом выяснилось, что реальные газы представляют одно из агрегатных состояний соответствующих простых тел, а точным уравнением состояния газа может быть уравнение состояния простого тела. Несмотря на это, газовые законы сохранились в термодинамике и в её технических приложениях как законы идеальных газов — предельных (практически недостижимых) состояний реальных газов[35]. Уравнение Клапейрона было выведено при некоторых допущениях на основе молекулярно-кинетической теории газов (Августом Крёнигом в 1856 г.[36] и Рудольфом Клаузиусом в 1857 г.)[37]. Клаузиусом было введено и само понятие «идеальный газ»[38] (в отечественной литературе конца XIX — начала XX веков вместо названия «идеальный газ» использовали термин «совершенный газ»[39]).
Следующий важный шаг в формулировке термического уравнения состояния идеального газа — переход от индивидуальной для каждого газа постоянной к универсальной газовой постоянной — сделал русский инженер Илья Алымов[40][30][41], работа которого, опубликованная в малоизвестном среди физиков и химиков издании, не обратила на себя внимание. Этот же результат был получен Менделеевым в 1874 году[39][30][41]. Независимо от работ русских ученых Густав Цейнер[en] (1866)[42], Като Гульдберг (1867)[43] и Август Горстман[de] (1873)[44] пришли к выводу, что произведение индивидуальной для каждого газа постоянной в уравнении Клапейрона на молекулярный вес газа должно быть постоянной для всех газов величиной.
В 1912 году при выводе постоянной Нернста был впервые применён принцип разделения фазового пространства на равновеликие ячейки. Впоследствии в 1925 году Ш. Бозе опубликовал статью «Закон Планка и гипотеза о световых квантах», в которой развил эту идею применительно к фотонному газу. Эйнштейн сказал о данной статье, что «использованный здесь метод позволяет получить квантовую теорию идеального газа» [45]. В декабре того же года Энрико Ферми разработал статистику частиц с полуцелым спином, подчиняющихся принципу Паули, которые позднее назвали фермионами[46][47].
В отечественной литературе, изданной до конца 1940-х годов, термическое уравнение состояния идеального газа называли уравнением Клапейрона[48][49][50][51][52][53] или уравнением Клапейрона для 1 моля[54]. В фундаментальной отечественной монографии 1948 года, посвящённой различным уравнениям состояния газов[55], Менделеев — в отличие от Клапейрона — вообще не упоминается. Фамилия Менделеева в названии рассматриваемого нами уравнения появилась после начала «борьбы с низкопоклонством перед Западом» и поиска «русских приоритетов». Тогда-то и стали в научной и учебной литературе использовать такие варианты названия, как уравнение Менделеева[39][56], уравнение Менделеева — Клапейрона[57][58][59] и уравнение Клапейрона — Менделеева[56][60][61][62].
Молекулярно-кинетическая теория идеального газа[править | править код]
Объём идеального газа линейно зависит от температуры при постоянном давленииСвойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:
- Размеры молекул пренебрежимо малы по сравнению со средним расстоянием между ними, так что суммарный объём, занимаемый молекулами, много меньше объёма сосуда[63][64][65];
- импульс передаётся только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях[65];
- соударения частиц между собой и со стенками сосуда абсолютно упруги[65];
- количество молекул в газе велико и фиксированно, что позволяет вычислять средние величины по малому (по сравнению с размерами системы) объёму, система является эргодической, для того чтобы средние по ансамблю были равны средним по времени;
- газ находится в термодинамическом равновесии со стенками сосуда и дополнительно отсутствуют макроскопические потоки вещества. Тут следует уточнить, что градиенты термодинамических величин могут иметь место, как например при включении внешнего поля, к примеру гравитационного.
В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно полному импульсу, передаваемому при столкновении частиц с участком стенки единичной площади в единицу времени[65], внутренняя энергия — сумме энергий частиц газа[66].
По эквивалентной макроскопической формулировке идеальный газ — такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака[64][67], то есть:
- pV=const⋅T,{\displaystyle pV=\mathrm {const} \cdot T,}
где p{\displaystyle p} — давление, V{\displaystyle V} — объём, T{\displaystyle T} — абсолютная температура.
Термическое уравнение состояния и термические коэффициенты идеального газа[править | править код]
Изотермы идеального газа нa p—V—T диаграммеТермические свойства классического и квазиклассического идеального газа описываются уравнением Клапейрона[68][69][58]:
- pV=mMRT,{\displaystyle pV={\frac {m}{M}}RT,}
где R — универсальная газовая постоянная (8.3144598 Дж⁄(моль∙К)), m — масса газа, M — его молярная масса, или
- pV=νRT,{\displaystyle pV=\nu RT,}
где ν — количество газа в молях.
В формулах статистической физики принято использовать постоянную Больцмана k (1.3806·10−23Дж⁄К), массу частицы m´{\displaystyle {\acute {m}}} и число частиц N. Статистические и термодинамически величины связаны соотношениями:
- m=m´N, ν=NNA, R=kNA, kN=νR,{\displaystyle m={\acute {m}}N,~~~\nu ={\frac {N}{N_{A}}},~~~R=kN_{A},~~~kN=\nu R,}
где NА — число Авогадро (6.02214·10231⁄моль). С использованием обозначений статистической физики уравнение Клапейрона принимает вид
- pV=NkT,{\displaystyle pV=NkT,}
или
- p=nkT,{\displaystyle p=nkT,}
где n — концентрация частиц.
Материал, касающийся термических коэффициентов идеального газа, изложен в статье Уравнение состояния.
Смесь идеальных газов[править | править код]
Смесь идеальных газов тоже идеальный газ. Каждой компоненте газа соответствует своё парциальное давление и общее давление смеси есть сумма парциальных давлений компонент смеси p=p1+p2+p3{\displaystyle p=p_{1}+p_{2}+p_{3}}… Также можно получить общее количество молей в смеси газов как сумму ν=ν1+ν2+ν3{\displaystyle \nu =\nu _{1}+\nu _{2}+\nu _{3}}… Тогда уравнение состояния для смеси идеальных газов[70]
- pV=νRT.{\displaystyle pV=\nu RT.}
Совершенный газ (гидроаэромеханика)[править | править код]
В отличие от термодинамики в гидроаэромеханике газ, подчиняющийся уравнению Клапейрона, называют совершенным. У совершенного газа молярные изохорная CV{\displaystyle C_{V}} и изобарная CP{\displaystyle C_{P}} теплоёмкости постоянны. В то же время идеальным в гидроаэромеханике называют газ, у которого отсутствуют вязкость и теплопроводность. Модель совершенного газа широко применяют при исследовании течения газов[71].
Теплоёмкость[править | править код]
Определим теплоёмкость при постоянном объёме для идеального газа как
- c^V=1νRT(∂S∂T)V=1νR(∂U∂T)V,{\displaystyle {\hat {c}}_{V}={\frac {1}{\nu R}}T\left({\frac {\partial S}{\partial T}}\right)_{V}={\frac {1}{\nu R}}\left({\frac {\partial U}{\partial T}}\right)_{V},}
где S — энтропия. Это безразмерная теплоёмкость при постоянном объёме, которая обычно зависит от температуры из-за межмолекулярных сил. При умеренных температурах это константа: для одноатомного газа ĉV = 3/2, для двухатомного газа и многоатомных газов с линейными молекулами это ĉV = 5/2, а для многоатомного газа с нелинейными молекулами ĉV = 6/2=3. Видно, что макроскопические измерения теплоемкости могут дать информацию о микроскопической структуре молекул. В отечественной учебной литературе, где понятие безразмерной теплоёмкости не получило распространения, для классического идеального газа его теплоёмкость при постоянном объёме CV полагают не зависящей от температуры и, согласно теореме о равнораспределении, равной[72]: 3Rν/2 для всех одноатомных газов, 5Rν/2 для всех двухатомных газов и многоатомных газов с линейными молекулами, 3Rν для всех многоатомных газов с нелинейными молекулами. Отличие квазиклассического идеального газа от классического состоит в ином виде зависимости внутренней энергии газа от его температуры[73]. Для классического идеального газа его теплоёмкость при постоянном объёме CV не зависит от температуры (она составляет), то есть внутренняя энергия газа всегда пропорциональна его температуре; для квазиклассического идеального газа его теплоёмкость CV{\displaystyle C_{V}} зависит от химического состава газа и температуры, то есть имеет место нелинейная зависимость внутренней энергии газа от температуры[74].
Теплоёмкость при постоянном давлении 1/R моль идеального газа:
- c^P=1νRT(∂S∂T)P=1νR(∂H∂T)P=c^V+1,{\displaystyle {\hat {c}}_{P}={\frac {1}{\nu R}}T\left({\frac {\partial S}{\partial T}}\right)_{P}={\frac {1}{\nu R}}\left({\frac {\partial H}{\partial T}}\right)_{P}={\hat {c}}_{V}+1,}
где H = U + PV — энтальпия газа.
Иногда проводится различие между классическим идеальным газом, где ĉV и ĉP могут меняться с температурой и квазиклассическим идеальным газом, для которого это не так.
Для любого классического и квазиклассического идеального газа справедливо соотношение Майера[75]:
- CP−CV=R,{\displaystyle C_{P}-C_{V}=R,}
где CP{\displaystyle C_{P}} — молярная теплоёмкость при постоянном давлении.
Соотношение теплоёмкостей при постоянном объёме и постоянном давлении
- γ=cPcV{\displaystyle \gamma ={\frac {c_{P}}{c_{V}}}}
называется показателем адиабаты. Для воздуха, представляющего собой смесь газов, это соотношение составляет 1,4. Для показателя адиабаты справедлива теорема Реша[76]:
| CPCV=(∂P∂V)S(∂P∂V)T.{\displaystyle {\frac {C_{P}}{C_{V}}}={\frac {\left({\frac {\partial P}{\partial V}}\right)_{S}}{\left({\frac {\partial P}{\partial V}}\right)_{T}}}.} | (Теорема Реша) |
Энтропия и термодинамические потенциалы[править | править код]
Выражая CV в терминах ĉV как было показано в предыдущем разделе, дифференцируя уравнение состояния идеального газа и интегрируя можно получить выражение энтропии[77]:
- ΔS=c^VNkln(TT0)+Nkln(VV0),{\displaystyle \Delta S={\hat {c}}_{V}Nk\ln \left({\frac {T}{T_{0}}}\right)+Nk\ln \left({\frac {V}{V_{0}}}\right),}
Данное выражение, после ряда преобразований позволяет получить термодинамические потенциалы для идеального газа как функции T, V, и N в виде[78]:
U{\displaystyle U\,} =c^VNkT{\displaystyle ={\hat {c}}_{V}NkT\,} A{\displaystyle A\,} =U−TS{\displaystyle =U-TS\,} =μN−NkT{\displaystyle =\mu N-NkT\,} H{\displaystyle H\,} =U+PV{\displaystyle =U+PV\,} =c^PNkT{\displaystyle ={\hat {c}}_{P}NkT\,} G{\displaystyle G\,} =U+PV−TS{\displaystyle =U+PV-TS\,} =μN{\displaystyle =\mu N\,}
где, как и раньше,
- c^P=c^V+1.{\displaystyle {\hat {c}}_{P}={\hat {c}}_{V}+1.}
Физический смысл температуры газа[править | править код]
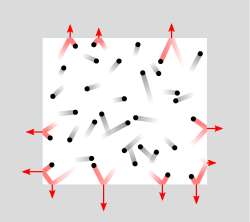 Давление, как процесс передачи импульса молекул газа стенкам сосуда
Давление, как процесс передачи импульса молекул газа стенкам сосудаВ рамках молекулярно-кинетической теории давление молекул газа на стенку сосуда p=FS{\displaystyle p={\frac {F}{S}}} равно отношению силы F{\displaystyle F}, действующей на стенку со стороны молекул, к площади стенки S{\displaystyle S}. Силу можно вычислить как отношение суммарного импульса K{\displaystyle K}, переданного стенке при столкновениях молекул за время Δt{\displaystyle \Delta t}, к длительности этого интервала:
- p=KSΔt.{\displaystyle p={\frac {K}{S\Delta t}}.\qquad \qquad }(1)
При упругом соударении молекула массы



