Расчетное значение — ток — Большая Энциклопедия Нефти и Газа, статья, страница 1
Расчетное значение — ток
Cтраница 1
Расчетные значения токов и напряжений изображают в виде векторов на комплексной плоскости. [2]
Расчетное значение тока, протекающего при несинхронном включении по генераторам и трансформаторам, определенное по формуле ( 1 — 12), несколько превышает действительную величину, так как в расчете не учтено влияние нагрузки, подключенной параллельно генераторам. Электродвигатели, составляющие обычно значительную часть нагрузки, за счет накопленной, энергии, представляют как бы дополнительную генерирующую мощность, и в момент несинхронного включения через них проходит часть тока. [3]
Расчетные значения токов д напряжений изображают в виде векторов на комплексной плоскости. [4]
Расчетные значения тока
Расчетные значения тока и постоянной времени цени должны быть определены без учета сопротивления выключателя и сопротивления дуги в месте КЗ. Номинальные значения постоянной времени указываются в информационных материалах заводов-изготовителей. [6]
Расчетные значения токов замыкания на землю должны быть определены для той из возможных в эксплуатации схемы сети, при которой токи замыкания на землю имеют наибольшее значение. [7]
Расчетное значение тока покоя коллектора / Ок применяемого транзистора должно обеспечить с достаточным запасом как по линейным искажениям, так и с точки зрения изменения положения точки покоя при колебаниях температуры окружающей среды и замене транзистора, максимальную расчетную амплитуду переменной составляющей входного тока транзистора следующего каскада / вхтсл. [8]
За расчетное значение тока срабатывания защиты 1С з расч принимается большее из двух полученных. [9]
По расчетному значению тока в соответствии с табл. 4.4 может быть выбран трехжильный медный кабель 3 х 70 мм2, допускающий при прокладке в траншее ( земле) ток, равный 285 А. [10]
Надежность срабатывания автоматического выключателя проверяется по расчетному значению тока короткого замыкания в конце защищаемого участка. [11]
Таким образом, размеры электродвигателя определяются расчетными значениями тока и магнитного потока. Эти же значения определяют величину момента всякой электрической машины. [12]
Подзарядное устройство ( ПЗУ) выбирают по
Для определения параметров элементов систем электроснабжения необходимо знать расчетные значения токов и мощностей. [15]
Страницы: 1 2 3 4
7. Рассчитать действующие значения силы тока в конденсаторе, используя данные;
Ростовский государственный экономический университет (РИНХ)
Елизаров Ю.Д
Электротехника
Методические указания по выполнению практических работ
Ростов-на-Дону
2014 год
Практическая работа №1
Электрические цепи постоянного тока
Цель работы:
-Исследование последовательного и параллельного соединения резисторов;
-Эквивалентная замена двух последовательно включенных источников ЭДС;
-Эквивалентная замена двух параллельно включенных источников ЭДС; -Исследование делителя напряжения;
-Исследование делителя тока.
Краткие сведения из теории
Электрическая цепь обычно состоит из соединительных определенным образом элементов и соединительных проводников. Такими элементами могут быть сопротивления (резисторы), электрические емкости (конденсаторы), индуктивности (катушки индуктивности, реле, обмотки трансформатора и др.) В цепях переменного тока любой элемент цепи обладает сопротивлением, индуктивностью и емкостью, а в цепях постоянного тока имеет значение только сопротивление потребителя энергии, подводящих проводов и измерительных приборов. Поэтому электрическую цепь удобно представить схемой замещения, где каждый из элементов представлен своим сопротивлением.
Закон Ома для замкнутой цепи
I
=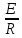
Где I – сила тока в цепи, Е-ЭДС источника, R – сопротивление внешней цепи (нагрузки) и внутренней цепи источника.
Напряжение на выходах источника U=E-IRвнутр.
Эквивалентное преобразование участка цепи. Замена является эквивалентной, если ток через заменяемый участок цепи и напряжение на его выводах не изменяется при замене.
Эквивалентная замена двух последовательно включенных сопротивлений одним Rэ:
Rэ=
Эквивалентная замена двух параллельно включенных сопротивлений одним Rэ:
Rэ
= 
Замена последовательно включенных источников ЭДС:
Еэ
=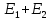
Делители напряжения предназначены для уменьшения напряжения, подаваемого на участок цепи. Простейший делитель состоит их двух, соединённых последовательно, резисторов; выходное напряжение подают на оба резистора, выходное снимают с одного из них как показано на рисунке 1.1
 Рис
1.1 Схема делителя напряжения
Рис
1.1 Схема делителя напряжения
Формула для вычисления снимаемого напряжения с плеча делителя
U
Такие делители используются, например, в приборах с несколькими диапазонами измерения. При измерении большего напряжения включается дополнительное сопротивление , а на показывающий прибор подается меньшее, пропорциональное подаваемому, напряжение. Делители тока предназначены для уменьшения тока в цепи. В этом случае два резистора включаются параллельно, и ток измеряется в цепи одного из них (рис 1.2) Так, например, осуществляется шунтирование в измерительных приборах приборов – амперметрах.
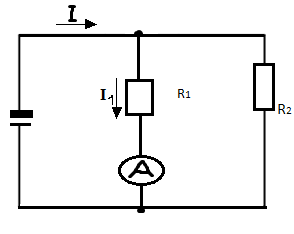 Рис
1.2 Схема делителя тока
Рис
1.2 Схема делителя тока
Формула
для вычисления тока через одно из плеч
делителя тока (резистор R1)
I
= 
Порядок выполнения работы
Изучить основные положения теорем электрических цепей постоянного тока.
Рассчитать эквивалентное сопротивление участка электрической цепи из двух последовательно соединённых резисторов
 .
.Ознакомиться с вводной частью практикума по «Электротехника». Запустить программу. Найти в «Меню» «Правка» «Описание работ», открыть и выбрать лабораторную работу №1.
Открыть файл c1_001 с электрической схемой. Включить мультиметр и измерить сопротивление с заданного участка цепи. Записать полученную величину и сравнить с рассчитанным значением сопротивления.
Рассчитать эквивалентное сопротивление участка электрической цепи, состоящего из двух параллельно соединенных резисторов
 = 12 Ом
= 12 Ом
Открыть файл c1_002. Включить мультиметр и измерить сопротивление заданного участка цепи. Записать полученную величину и сравнить с расчётным значение.
Рассчитать значение эквивалентной ЭДС для последовательного соединения двух источников ЭДС

Отрыть файл с_003, подключить вольт метр к точкам А и В и проверить условие эквивалентности.
Рассчитать напряжение на каждом резисторе делителя напряжения
 =
50 Ом
=
50 Ом  = 100 Ом
= 100 Ом 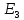 = 15 B
= 15 B
Открыть файл с_007. Подключая вольтметр параллельно каждому резистору, проверить правильность расчета.
Рассчитать токи через каждый резистор делителя тока —
 = 5 Ом
= 5 Ом = 10 ОмI
= 6A
= 10 ОмI
= 6AОткройте файл с_008. Подключая амперметр последовательно с каждым резистором, проверить правильность расчетов.
Оформить результат работы отчетом.
Содержание отчета
Название. Цель работы.
Название эксперимента и исходные данные для расчета.
Расчетные формулы, алгоритм вычислений и результаты расчета.
Электрическая схема измерений для каждого эксперимента, результаты измерений.
Выводы о соответствии расчетных и измерительных электрических величин по каждому эксперименту.
Контрольные вопросы:
Сформулируйте закон Ома для замкнутой цепи и для ее участка.
В каких единицах выражают ЭДС, напряжение, силу тока, сопротивление.
От чего зависит сопротивление однородного металлического проводника?
Каково соотношения между ЭДС и напряжением на выводах источника электрической энергии?
Как определяется ток при коротком замыкании выводов источника электрической энергии?
Почему желательно, чтобы внутреннее сопротивление мощного источника электрической энергии было возможно меньшим?
Сформулируйте первый и второй законы Кирхгофа, а также правило знаков для токов и ЭДС.
Как определяется общее сопротивление при последовательном, параллельном и смешанном соединении потребителей энергии.
Как определяется напряжение в делителе напряжения?
Как определяется токи в делителе тока?
Литература, пособия, инструкции:
Касаткин А.С., Немцов М.В. «Электротехника». 2008 г, -522е.
Синявский Г.П. и др. «Электротехника» Практикум РГЭУ(РИНХ) Ростов-на-Дону 2007г-76с.
Практическая работа №2
Цепи однофазного синусоидального тока.
Цель работы: Исследование амплитудно-фазовых соотношений и мощности для переменного тока и напряжения в резисторе, конденсаторе и катушке индуктивности.
Краткие сведения из теории:
Переменный ток промышленной частоты (f = 50 Гц) имеет синусоидальную форму i – мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) тока, (wt – φi) где i — мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) , (wt – φi) – фаза тока. В выражение для фазы тока входит w – циклическая частота переменного тока, связанные с обычной частатой соотношением w = 2 πf, а так же φ – начальная фаза (в момент времени t = 0).
Соответственно и напряжение в цепи переменного тока имеет синусоидальную форму u = Um sin(wt+ φi), где все величины имеют аналогичный току смысл. Мгновения значения токаи напряжения можно определить амплитудные значения токаи напряжения. Обычно на практике ток и напряжение характеризуют их действующими значениями I и U, которые указывают в паспортах на приборы, на электрической арматуре и т.д. Действующие значения тока и амплитудными значениями соотношениями
I
=  = 0,707
= 0,707 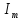 ;
U =
;
U =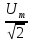 = 0,707
= 0,707 .
.
В
цепи переменного тока с резистором закон Ома выполняется как для амплитудных
значений тока напряжения 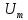 =
= R,
так и для их действующих значений U
= IR. Конденсатор в
цепи переменного тока имеет
емкостное сопротивление
R,
так и для их действующих значений U
= IR. Конденсатор в
цепи переменного тока имеет
емкостное сопротивление 
C
– величина емкости конденсатора, ƒ –
частота переменного тока. Мгновенные
значение силы тока в конденсаторе i
= 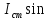 (wt
– φi),
мгновенное значение напряжения на
конденсаторе u
=
(wt
– φi),
мгновенное значение напряжения на
конденсаторе u
=  (wt
– φi).
(wt
– φi).
Начальные
фазы связаны соотношением 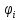 =
=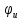 +
+ 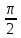 ,
то есть ток опережает по фазе напряжение
на
,
то есть ток опережает по фазе напряжение
на .
Закон Ома связывает амплитудные значения
тока и напряжения на конденсаторе
соотношением
.
Закон Ома связывает амплитудные значения
тока и напряжения на конденсаторе
соотношением =
=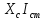 .
.
Полная
мощность двухполюсника определяется
произведением действующих значений
тока и напряжения (измеряется в ВА) S
=  =UI
Связь полной, активной и реактивной
мощностей
=UI
Связь полной, активной и реактивной
мощностей  =
= +
+ Активную мощность измеряет ваттметрами
разного принципа действия. Обычно
ваттметр имеет две измерительные цепи,
как показано на рис 2.1
Активную мощность измеряет ваттметрами
разного принципа действия. Обычно
ваттметр имеет две измерительные цепи,
как показано на рис 2.1
рис 2.1
нагрузка
Одна цепь ваттметра включена последовательно нагрузке, ток в ней i равен току нагрузки. Другая цепь включается параллельно и напряжение в ней равно напряжению u нагрузки. В лабораторной работе роль ваттметра выполняет умножитель напряжений.
Порядок выполнения работы:
Изучить основные положения теории электрических цепей однофазного синусоидального тока.
Ознакомиться с вводной частью работы практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка» «Описание работ», открыть и выбрать лабораторную работу 2.
Рассчитать действующее значение тока в резисторе, используя данные U = 120B, R = 120B, r = 0,01 Oм
Открыть файл с2_01.ewb. Подключить амперметр и проверить правильность отчета.
Определить фазовые соотношения тока и напряжения.
(Есть ли фазовый сдвиг колебаний тока относительно колебаний подаваемого на резистор напряжения?) Подключить осциллограф и проверить соответствие теории данных эксперимента. Для этого измерить и сравнить периоды колебаний тока и напряжения на осциллограмме, а также сдвиг ∆T.
Определить мощность резистора.
Подать сигналы, пропорциональные току и цепи резистора (снимается в виде падения напряжения на вспомогательном резисторе 0,01 Ом) и напряжению на резисторе (снимается с источника ЭДС) на два входа умножителя. Подключить к выходу умножителя осциллограф в соответствие с электрической схемой рис. 2.1., по осциллограмме определить минимальную и максимальную активную мощность резистора.
Подключив на выход умножителя вольтметр постоянного напряжения, убедиться, что с точностью до некоторого коэффициента он измеряет активную мощность. Определить на опыте этот коэффициент.
u=120 B, f=50 Гц, с=53ϻФ, r=0,01 Oм
8. Открыть файл c2_02.ewb. Подключить амперметр и проверить правильность расчета.
9. Определить фазовые соотношения тока и напряжения на конденсаторе. (Совпадают ли по фазе колебания тока и напряжения в цепи конденсатора?) проверить экспериментально выводы теории. Подключить осциллограф, сравнить осциллограммы тока и напряжения, измерить периоды Т колебаний и сдвиг ∆T. Рассчитать фазовый сдвиг, зная, что периоду соответствует фаза 2π.
10. Измерить мощность конденсатора.
Подать сигналы, пропорциональные току и напряжению, на два входа умножителя подключите на выход умножителя осциллограф. По осциллограмме мощности определить минимальные и максимальные значения реактивной мощности конденсатора.
11. Рассчитать действующую значение тока в катушке индуктивности по данным: u = 120В ƒ =5кГц L = 955,4 Мн r = 0,1Ом
12. Открыть файл с2_03.ewb. Подключить амперметр и проверить правильность расчета.
13. Определить фазовые соотношения тока и напряжения в цепи катушки индуктивности. Подключить осциллограф и проверить соответствие теории экспериментально наблюдаемых соотношений фаз тока и напряжения в цепи катушки индуктивности.
14. Измерение мощности катушки индуктивности. Подайте сигналы, пропорциональные току и напряжению, на два входа умножителя и по осциллограмме мощности. Определить минимальное и максимальное значения реактивной мощности катушки индуктивности.
15. Оформить результаты работы отчётом.
Содержание отчёта:
1.Название, цель работы.
2.Название эксперимента и исходные данные расчета.
3. Расчетные формулы, алгоритм вычислений для расчета.
4. Электрическая схема измерений для каждого эксперимента, результаты измерений.
5. Выводы с соответствием расчетных и измененных электрических величин, а также о соответствии результатов экспериментов теории.
Контрольные вопросы:
1. Каковы основные характеристики синусоидального тока?
2. Какова связь между частотой, периодом и циклической частотой колебаний?
3. Какова связь между действующим, средним и амплитудным значениями синусоидального тока?
4. Как изображаются синусоидальные токи и напряжения с помощью вектора на комплексной плоскости?
5. Как сдвинуты друг относительно друга векторы тока и напряжения резистора, конденсатора, конденсатора, катушки индуктивности?
6. Как преобразуется электрическая энергия источника ЭДС в резисторе, конденсаторе и катушке индуктивности?
Литература, пособия, инструкции:
Касаткин А.С., Немцов М.В. «Электротехника». М.А. «Академия», -2008, 544е.
Синявский Г.П. и др. «Электротехника» Практикум – РГЭУ(РИНХ) г. Ростов-на-Дону, 2007г.,-76с.
Практическая работа №3
Цепи однофазного тока при последовательном включении электроприемников.
Цель работы: Исследование физических процессов, происходящих в установившимся режиме в цепи, содержащий последовательно соединенные активное, индуктивное и емкостное сопротивление.
Краткие сведения из теории.
При последовательном включении элементов схемы силы тока в них одинакова по закону Ома для участка цепи, падение напряжения на резисторе, катушке индуктивности и конденсаторе соответственно пропорционально величине активного тока R, индуктивного Х.
 =
= (1)
(1)
 =
= =
= (2)
(2)
Полное сопротивление цепи Z определяется по формуле:
Z
=  (3)
(3)
Действующие значение силы тока I, в цепи рассчитывается из выражения
Z
=  (4)
(4)
Где U-напряжение, снимаемое с источника ЭДС.
Полная мощность, потребляемая цепью:
 =
U
=
U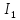 ;
;  =
= Z,
Z,
Коэффициент
мощности можно определить как  =
=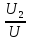 ,
,
Цепь
потребляет от источника активную
мощность
: =
=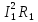 или
или =U
=U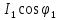
Реактивная
мощность равна разности индуктивной и
емкостной мощностей: 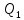 =
=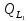 —
— ,
,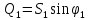
Отметим
здесь еще раз смысл коэффициента
мощности. Коэффициент мощности равен:
=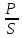
Полную
мощность S
можно представить в виде S= ,
а для цепи содержащей конденсатор и
катушку индуктивности,S=
,
а для цепи содержащей конденсатор и
катушку индуктивности,S=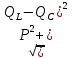 .
.
Тогда для коэффициента мощностей такой цепи справедливо выражение
 =
= 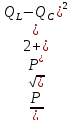
Таким образом, коэффициент мощности представляет собой величину, которая показывает долю активной мощности в общем балансе мощностей, потребляемых электроприемником.
Из анализа последнего выражения можно сделать важные для теории и практики выводы:
1) Если реактивная мощность катушки больше реактивной мощности конденсатора, то цепь потребляет от источника и активную, и реактивную мощность;
2) Если реактивные мощности катушки больше реактивной мощности и конденсатора, то цепь потребляет от источника и активную, реактивную мощность;
3) Если реактивная мощность конденсатора больше реактивной мощности катушки, то цепь потребляет от источника активную мощность и отдает в сеть избыточную реактивную.
Порядок выполнения работы:
1. Изучить основные положения теории электрических цепей однофазного синусоидального тока.
2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка», «Описание работ», открыть и выбрать в папке Лаб 5 файл 51.ewb.
3.
Рассчитать индуктивное, емкостное и
полное сопротивление цепи (Ом), используя
формулы (1,2,3), при U=
70, 71В., R=10
Ом, 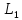 =50mГн,
=50mГн, 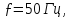 С=1mФ;
С=1mФ;
4.
Рассчитать действующее значение силы
тока в цепи и падение напряжения в
резисторе 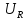 ,
катушке индуктивности
,
катушке индуктивности и конденсаторе
и конденсаторе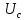 .
.
5. Открыть файл 51.ewb в папке Лаб5. Измерить падение напряжения в резисторе, катушке индуктивности и конденсаторе.
6. Рассчитать катушки, потребляемые цепью: полную, активную и реактивную. Коэффициент катушки.
7. Оформить результаты работы отчетом.
Содержание отчета:
1. Название, цель работы.
2. Исходные данные для расчета.
3. Расчетные формулы, алгоритм вычислений и результаты расчета.
4. Электрическая схема измерений, рисуемых осциллограммы напряжения сети и тока цепи, результаты измерений.
5. Выводы о соответствии расчетный и измерительных электрических величин.
Контрольные вопросы:
1. Как изображается гармоническое колебание с помощью вектора?
2. Как сдвинуты друг относительно друга векторы тока и напряжения для резистора, конденсатора и катушки индуктивности?
3. Как строится векторная диаграмма для последовательного включённых R,L и С?
4. Что такое резонанс напряжений?
5. Какими мощностями характеризуются цепи синусоидального тока?
6. По каким формулам можно рассчитать полную, активную и реактивную мощности?
7. Как измерить активную мощность?
8. Что такое коэффициент мощности, каков смысл?
Литература, пособия, инструкции:
1. Касаткин А.С., Немцов М.В. Электротехника. М: «Академия», 2008г-544с.
2.Синявский Г.П. и др. Электротехника: Практикум-РГЭУ(РИНХ) 2007г.-76с.
Практическая работа №4
Цепи трехфазного тока при соединении электроприемников звездой.
Цель работы: Исследование цепи трехфазного переменного тока в симметрическом режиме и влияния нейтрального провода на величину фазных напряжений электроприемников.
Краткие сведения из теории
В
практике передачи и распределения
электрической энергии соединяют в одну
цепь три цепи синусоидального тока с
независимыми источниками энергии.
Источником электрической энергии служат
три фазных обмотки статора трехфазного
генератора переменного тока. При вращении
магнитного поля ротора в этих обмотках
последовательного тока. При вращении
магнитного поля ротора в этих обмотках
последовательно индуцируются
синусоидальные ЭДС. Сдвинутые на фазный
угол  (треть
периода) относительно друг друга. Цепь
каждой обмотки генератора – фазным
напряжением источника.
(треть
периода) относительно друг друга. Цепь
каждой обмотки генератора – фазным
напряжением источника.
Трехфазную
систему получают, соединяя фазы источника
энергии и приемники звездой или
треугольником. При соединении звездой
все концы фазных обмоток генератора
соединяются в общий узел, концы фаз
приемника тоже образуют узел, а три
провода между ними объединяются в один
общий нейтральный провод(нейтраль).
Начала трех фаз генератора соединяются
с фазами приемника тремя линейными
проводами. Напряжение между линейными
проводами называется линейным напряжением.
Действующие значения линейных и фазных
напряжений связаны с соотношением
UЛ=2UФ*cos30=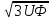 .
Действующие линейные токи равны фазным.
.
Действующие линейные токи равны фазным.
При
симметричном режиме цепи, все напряжения
источника равны между собой и одинаковы
все три сопротивления электроприемника.
При соединении в звезду фазные токи
равны линейным, а линейные напряжения
в 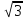 раз больше фазных:
раз больше фазных:  =
=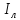
 =
= .
.
Когда электроприемник представляет собой активную нагрузку, то угол сдвига между токами и напряжениями каждой фазной цепи равен 0, а полная мощность электроприемника равна активной, которая складывается из активных мощностей фаз, Вт:
S=P=3 =3
=3 R.
R.
В общем случае трехфазный электроприемник потребляет от источника активную и реактивную мощность.
Рассчитываются активные мощности каждой фазы, Вт:
 =
=  cos
φ,
cos
φ,
 =
= 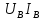 cosφ,
cosφ,
 =
= 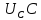 cosφ,
cosφ,
Активная мощность электроприемника:
Р=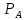 +
+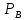 +
+ ;
при симметрии Р=3
;
при симметрии Р=3 .
.
Рассчитываются реактивные мощности каждой фазы,, вар:
 =
=  φ,
φ,
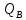 =
= 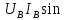 φ,
φ,
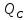 =
=  φ,
φ,
Q
= 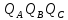 .
при симметрииQ
= 3
.
при симметрииQ
= 3 .
.
Коэффициент мощности можно определить:
 =
= =
=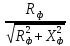
Полная мощность электроприемника, В*А,
S=
Порядок выполнения работы
1. Изучить основные положения теории электрических цепей трехфазного тока.
2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню « Правка» — «Описание работ», открыть и выбрать в папке Лаб8 фаул81.ewb.
3.
Рассчитать фазные токи и напряжение в
симметрическом режиме, при  =50Гц,
=50Гц, =100
Ом,
=100
Ом,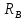 =100
Ом,
=100
Ом, =100
Ом.
=100
Ом.
4. Открыть файл 81.ewb в папке Лаб8. Измерить замещение фазных токов и напряжений тока, в контрольном проводе. Изменить характер осциллограмм
фазных напряжений.
5. Рассчитать активную, реактивную и полную мощность трехфазной цепи.
6. Оформить результаты работы отчетом.
Содержание отчета:
1. Название, цель работы.
2. Исходные данные для расчета.
3. Расчетные формулы, алгоритм вычислений и результаты расчета.
4.Электрическая схема измерений, рисунок осциллограмм фазных напряжений, результаты измерений.
5. Выводы о соответствии расчетных и измеримых электрических величин.
Контрольные вопросы
1. Что такое трехфазный переменный ток и почему он так называется?
2. Что называется фазой цепи трехфазного тока?
3. Какое соединение обмоток генератора называется соединением «звездой»?
4. При каких условиях можно производить соединение фаз «звездой» без нулевого провода?
5. Что называется линейным напряжением и фазовым напряжением?
6. Каково соотношение между фазовым и линейным напряжениями при соединении «звездой»?
7. К чему приведет обрыв нулевого провода при несимметричной нагрузке?
8. Как измеряют мощность и энергию трехфазной системы при симметричной и несимметричной нагрузках?
Литература, пособия, инструкции:
1. Касаткин А.С., Немцов М.В. Электротехника. М. «Академия»,-2008-544с.
2.Синяковский Г.П. и др. Электротехника: Практикум – РГЭУ(РИНХ) 2007г.76с.
Глава 5 Методы определения расчетных электрических нагрузок
Одним из основных этапов проектирования систем электроснабжения объекта, является правильное определение ожидаемых электрических нагрузок, как отдельных ЭП, так и узлов нагрузки на всех уровнях системы электроснабжения.
Расчетные значения
нагрузок — это нагрузки, соответствующие
такой неизменной токовой нагрузке ( ),
которая эквивалентна фактической
изменяющейся во времени нагрузке по
наибольшему тепловому воздействию (не
превышая допустимых значений) на элемент
системы электроснабжения.
),
которая эквивалентна фактической
изменяющейся во времени нагрузке по
наибольшему тепловому воздействию (не
превышая допустимых значений) на элемент
системы электроснабжения.
Зная электрические нагрузки, можно выбрать нужную мощность силовых трансформаторов, мощность и место подключения компенсирующих устройств, выбрать и проверить токоведущие части по условию допустимого нагрева, рассчитать потери и колебания напряжения, выбрать виды защит.
Существуют различные методы расчета электрических нагрузок, которые в свою очередь делятся на:
— основные;
— вспомогательные.
5.1 Основные методы расчета электрических нагрузок
— По номинальной мощности и коэффициенту использования;
— По номинальной мощности и коэффициенту спроса;
— По средней мощности и расчетному коэффициенту;
— По средней мощности и отклонению расчетной нагрузки от средней;
— По средней мощности и коэффициенту формы графика нагрузки.
Применение того или иного метода определяется допустимой погрешностью расчетов и наличия исходных данных.
По номинальной мощности и коэффициенту использования
Метод определения расчетных нагрузок по номинальной мощности и коэффициенту использования применяется, как правило, для индивидуальных ЭП напряжением до 1 кВ, работающих в длительном режиме (ПВ=1).
По данному методу расчетные нагрузки принимаются равными средним значениям нагрузок за наиболее загруженную смену:
— расчетная активная мощность, потребляемая одним ЭП, при наличии графика нагрузки по активной мощности
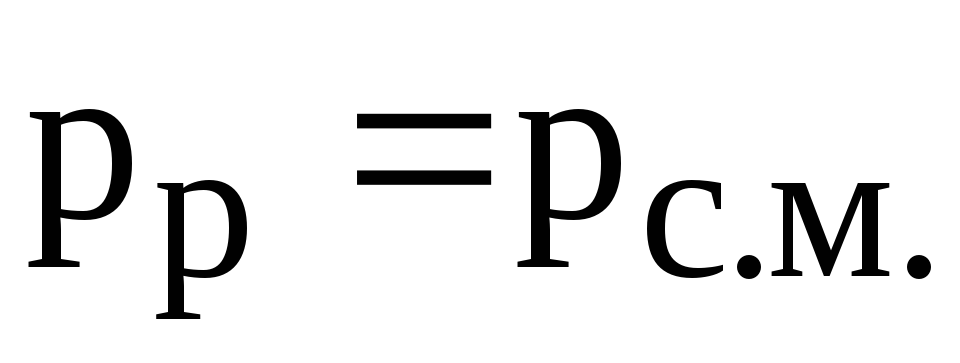 ,
(5.1)
,
(5.1)
где  – расчетная активная мощность, кВт;
– расчетная активная мощность, кВт;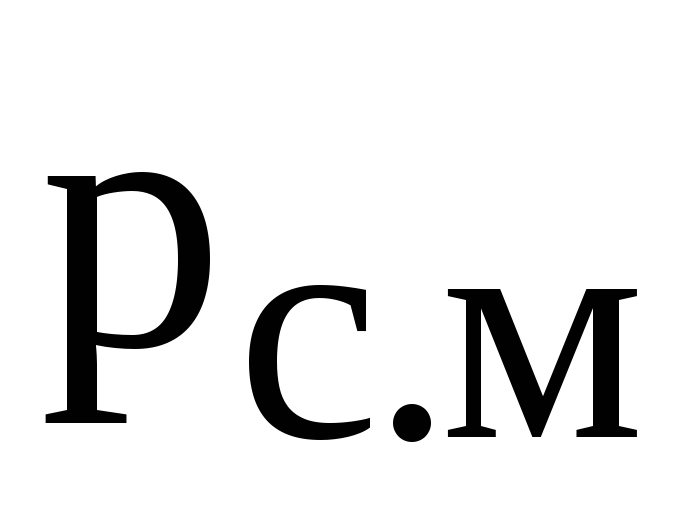 — среднее значение активной мощности
ЭП за наиболее загруженную смену, кВт;
— среднее значение активной мощности
ЭП за наиболее загруженную смену, кВт;
— расчетная активная мощность, потребляемая одним ЭП, при отсутствии графика нагрузки по активной мощности
 ,
(5.2)
,
(5.2)
где  — коэффициент использования активной
мощности электроприемником за
рассматриваемый промежуток времени
(технологический параметр), о.е.;
— коэффициент использования активной
мощности электроприемником за
рассматриваемый промежуток времени
(технологический параметр), о.е.; — номинальная активная мощность ЭП, кВт;
— номинальная активная мощность ЭП, кВт;
— расчетная реактивная мощность, потребляемая одним ЭП, при наличии графика нагрузки по реактивной мощности
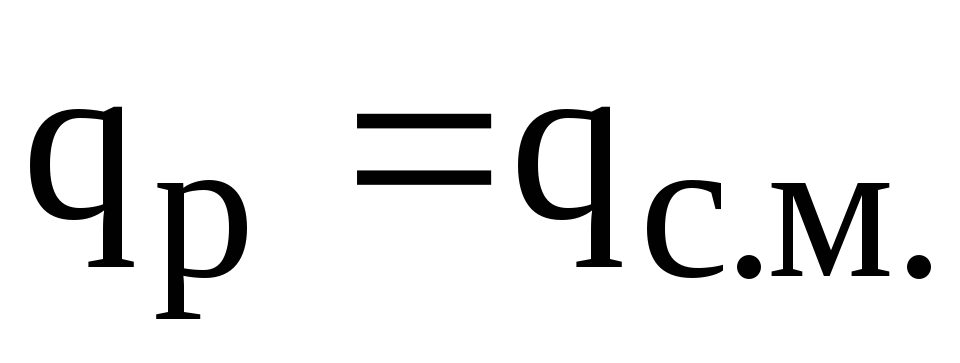 ,
(5.3)
,
(5.3)
где  – расчетная реактивная мощность, кВ·Ар;
– расчетная реактивная мощность, кВ·Ар; — среднее значение реактивной мощности
ЭП за наиболее загруженную смену, кВ·Ар;
— среднее значение реактивной мощности
ЭП за наиболее загруженную смену, кВ·Ар;
— расчетная реактивная мощность, потребляемая одним ЭП, при отсутствии графика нагрузки по реактивной мощности
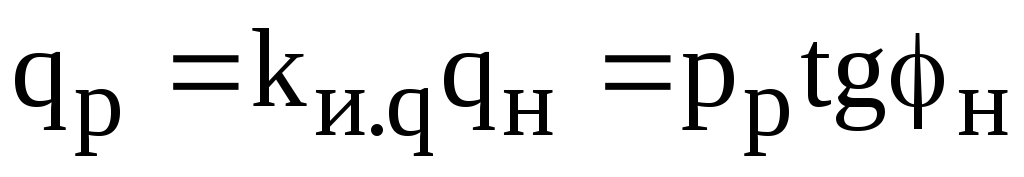 ,
(5.4)
,
(5.4)
где 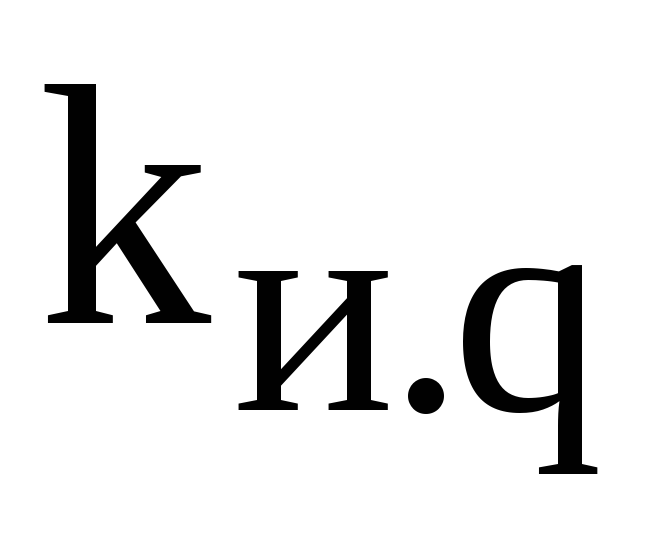 — коэффициент использования реактивной
мощности ЭП за рассматриваемый промежуток
времени (технологический параметр),
о.е.;
— коэффициент использования реактивной
мощности ЭП за рассматриваемый промежуток
времени (технологический параметр),
о.е.;
 — номинальная
реактивная мощность ЭП, кВт; tg
— номинальная
реактивная мощность ЭП, кВт; tg — номинальное значение коэффициента
реактивной мощности, соответствующий
cos
— номинальное значение коэффициента
реактивной мощности, соответствующий
cos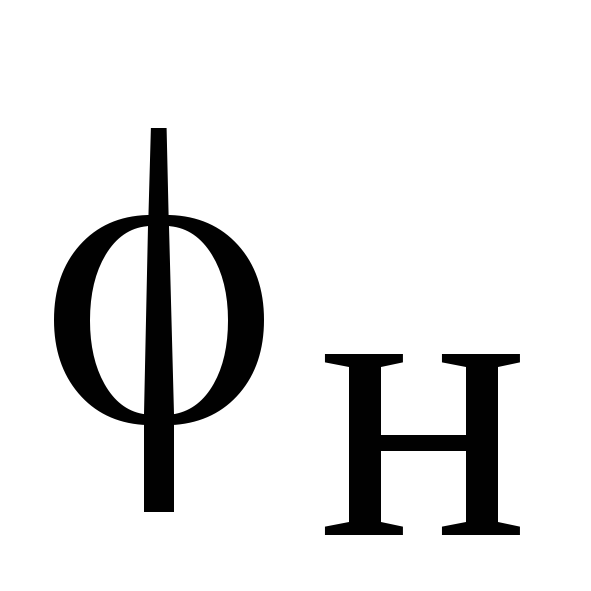 ЭП;
ЭП;
— расчетная полная мощность, потребляемая одним ЭП
 ,
(5.5)
,
(5.5)
где  — расчетное значение полной мощности
ЭП, кВ·А;
— расчетное значение полной мощности
ЭП, кВ·А;
— расчетное значение тока ЭП
 ,
(5.6)
,
(5.6)
где  – расчетный ток ЭП, А;
– расчетный ток ЭП, А; – напряжение питания ЭП, кВ.
– напряжение питания ЭП, кВ.
По данному методу допускается определение расчетных нагрузок группы ЭП напряжением до 1 кВ, связанных технологическим процессом, (например, многодвигательные приводы), а их число, как правило, не более трех-четырех. Режим работы электроприемников данной группы должен быть приведен к длительному режиму (ПВ=1).
Расчетные нагрузки группы ЭП, определяемые по данному методу:
— расчетная активная мощность, потребляемая группой ЭП, при наличии группового графика узла нагрузки по активной мощности
 ,
(5.7)
,
(5.7)
где 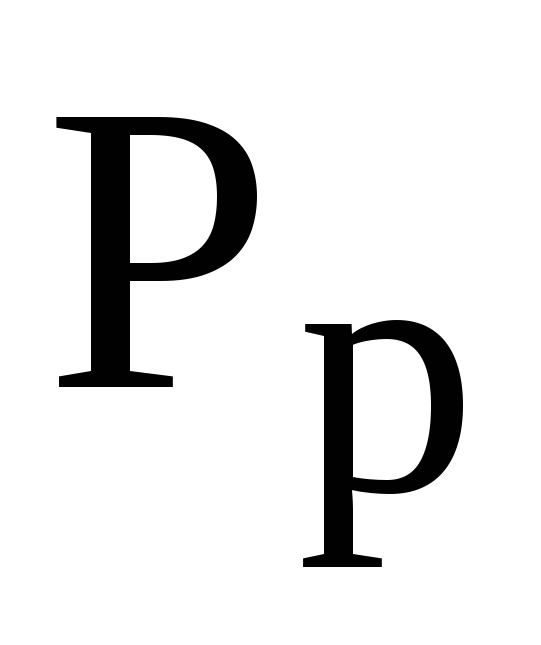 — расчетная активная мощность, потребляемая
группой ЭП, кВт;
— расчетная активная мощность, потребляемая
группой ЭП, кВт;
 — средняя активная
мощность, потребляемая группой ЭП, за
наиболее загруженную смену, кВт;
— средняя активная
мощность, потребляемая группой ЭП, за
наиболее загруженную смену, кВт;
— расчетная активная мощность, потребляемая группой ЭП, при отсутствии группового графика узла нагрузки по активной мощности
 ,
(5.8)
,
(5.8)
где  — коэффициент использования по активной
мощности индивидуального ЭП, входящего
в группу; n
– число ЭП в группе;
— коэффициент использования по активной
мощности индивидуального ЭП, входящего
в группу; n
– число ЭП в группе;
— расчетная реактивная мощность, потребляемая группой ЭП, при наличии группового графика узла нагрузки по реактивной мощности
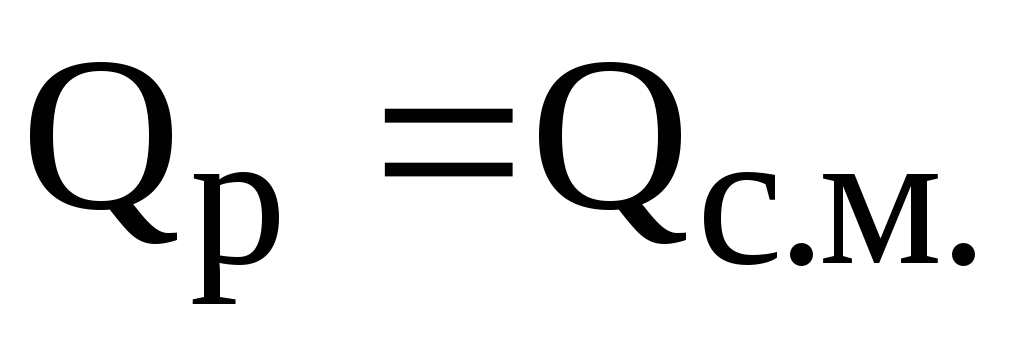 ,
(5.9)
,
(5.9)
где  — расчетная реактивная мощность группы
ЭП, кВ·Ар;
— расчетная реактивная мощность группы
ЭП, кВ·Ар;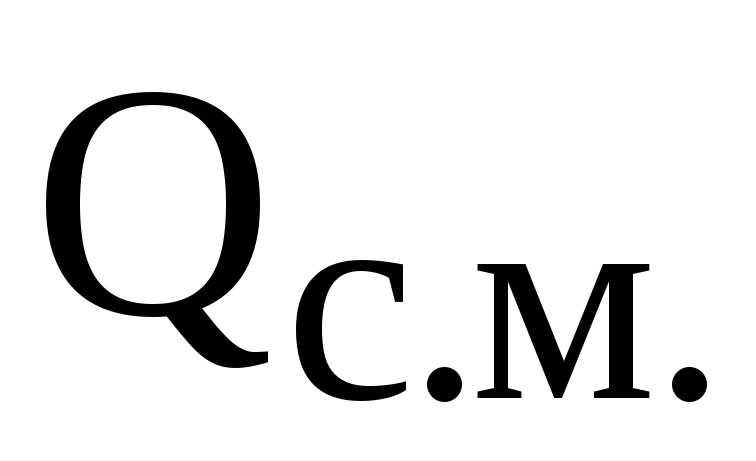 — среднее значение реактивной мощности
группы ЭП, кВ·Ар;
— среднее значение реактивной мощности
группы ЭП, кВ·Ар;
— расчетная реактивная мощность, потребляемая группой ЭП, при отсутствии группового графика узла нагрузки по реактивной мощности
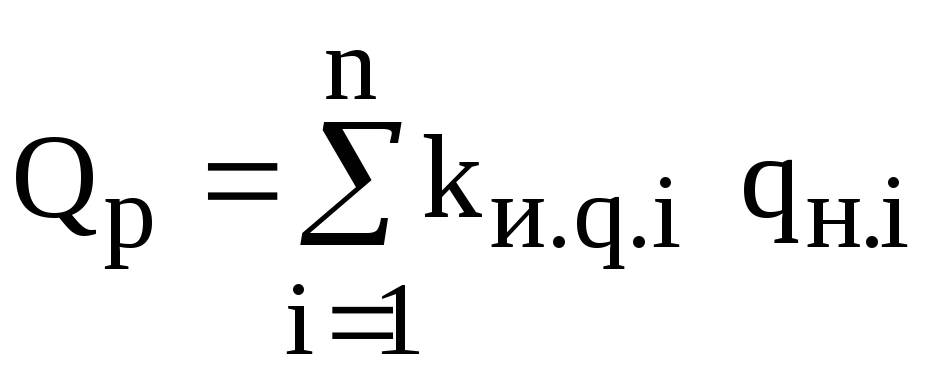 или
или  ,
(5.10)
,
(5.10)
где  — коэффициент использования по реактивной
мощности индивидуального ЭП, входящего
в группу;
— коэффициент использования по реактивной
мощности индивидуального ЭП, входящего
в группу;  — средневзвешенный коэффициент реактивной
мощности, соответствующий средневзвешенному
значению
— средневзвешенный коэффициент реактивной
мощности, соответствующий средневзвешенному
значению 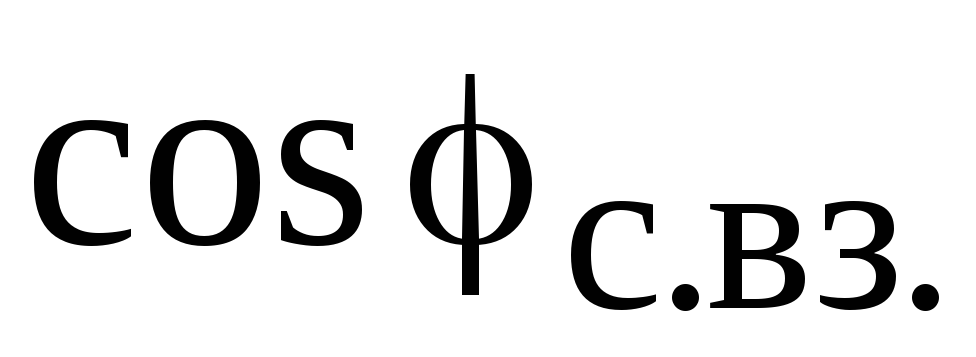 данной группы ЭП;
данной группы ЭП;
— расчетная полная мощность, потребляемая группой ЭП
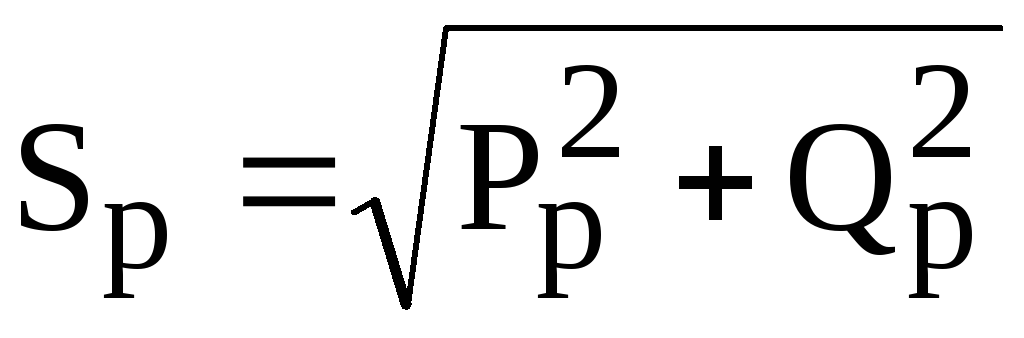 (5.11)
(5.11)
где  — расчетная полная мощность узла нагрузки,
кВ·А.
— расчетная полная мощность узла нагрузки,
кВ·А.
— Расчетное значение тока группы ЭП:
 (5.12)
(5.12)
где Iр – суммарный расчетный узла нагрузки, А; Uн – напряжение питания узла нагрузки, кВ.
Расчет среднего и среднеквадратичного значений тока/напряжения
..
Вот здесь есть расширенный и углубленный вариант данной заметки
.
.
Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:
Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока
Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.
Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.
В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.
Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник
и треугольник
А уж на основе этих базовых сигналов можно сляпать и пилу
и даже то, что творится на вторичке пушпула:
И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.
Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!
Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]
Содержание архива (также прилеплен к заметке):
AVG_RMS.zip:
Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel;
Среднее и среднеквадратичное.pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.
Переменный ток
Переменный ток все время изменяет свое направление в отличие от постоянного, который протекает только в одном направлении. Постоянный ток вырабатывают батареи и источники постоянного тока, а переменный – генераторы сигналов и государственные энергетические системы.
Синусоидальные колебания
Форма переменного тока или напряжения может принимать самые различные виды. Наиболее распространенной является синусоидальная форма переменного напряжения или тока (рис. 2.1). Синусоидальное колебание имеет два максимальных значения, или пика: положительный пик и отрицательный. Пиковое значение называется также амплитуде синусоиды. Значение синусоидального напряжения, измеренное от пика до пика (размах), является разностью потенциалов между положительным пиком и отрицательным.
Размах = Положительная амплитуда + Отрицательная амплитуда = Удвоенная амплитуда.

Рис. 2.1. Синусоидальные колебания переменного тока
Среднеквадратическое значение
Постоянный ток имеет постоянное значение, и это значение можно использовать во всех вычислениях. Значение же переменного тока изменяется во времени. Чтобы преодолеть эту трудность, за «постоянное» значение переменного тока приняли и используют его среднеквадратическое значение.
Среднеквадратическое значение переменного тока является эквивалентом значения постоянного тока, при котором вырабатывается такая же мощность, что и при исходном значении переменного тока. Если известно среднеквадратическое значение переменного тока, то его можно использовать для вычисления мощности так же, как если бы это было постоянное напряжение или ток. Например:
Мощность пост. тока = Постоянный ток х Постоянное напряжение;
Мощность перем. Тока = Среднеквадр. значение тока х Среднеквадр. значение напряжения.
Значения переменного тока и напряжения всегда задают в виде среднеквадратической величины, за исключением специально оговоренных случаев.
Пример 1
Какое сопротивление имеет домашний электрический обогреватель мощностью 1 кВт?
Решение
Домашние обогреватели работают от сетевого напряжения, имеющего среднеквадратическое значение 240 В (в России 220 В. — Прим. перев.). Мощность, потребляемая обогревателем, составляет 1 кВт = 1000 Вт. Из формулы P = V2/R определяем
P = V2/R = 240*240/1000 = 57, б Ом.
Соотношение между пиковыми и среднеквадратическими значениями
Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Заметим, что это справедливо только для синусоидального сигнала. Например, если амплитуда синусоидального сигнала Vр = 10 В, то его среднеквадратическое значение составит Vср.кв. = 0,707 * Vр = 0,707 * 10 = 7,07 В (см. рис. 2.2). Из соотношения Vср.кв. = 0,707 * Vр следует, что
Vр = 1/0,707 * Vср.кв. = 1,414 * Vср.кв.

Рис. 2.2. Среднеквадратическое значение синусоидального сигнала.

Рис. 2.3. Постоянная составляющая сигнала переменного тока.
Постоянная составляющая в сигнале переменного тока
До сих пор мы имели дело с сигналами переменного тока, которые не содержали постоянной составляющей. Рассмотрим два синусоидальных сигнала, изображенных на рис. 2.3. Левый сигнал не имеет постоянной составляющей, и его положительный пик равен отрицательному. Правый же сигнал содержит составляющую постоянного тока величиной 5 В.
Постоянная составляющая переменного тока называется также средним, или усредненным значением сигнала переменного тока.
Определим постоянную составляющую сигнала, имеющего прямоугольную форму (рис. 2.4).

Рис. 2.4.
1. Сначала определим положение нулевого уровня.
2. Вычислим площадь А1, лежащую выше нулевого уровня:
А1 = 4*1 = 4.
3. Вычислим площадь А2, лежащую ниже нулевого уровня:
А2 = 2*1 = 2.
4. Вычислим суммарную площадь:
А1 – А2 = 4 – 2 = 2.
5. Отсюда среднее значение напряжения за период равно
Суммарная площадь/Время периода = 2/3 = 0,67 В.
Среднеквадратическое значение сложных сигналов
Как уже говорилось, соотношение
Среднеквадратическое значение = 0,707 амплитуды
справедливо только для синусоидальных сигналов. Среднеквадратическое значение сигналов, имеющих другую форму, может быть определено следующим образом.
1. Определить площадь сигнала за один период. Заметим, что при определении площади отрицательное значение превращается в положительное.
2. Определить среднее значение площади сигнала за период.
3. Вычислить квадратный корень из средней площади сигнала за период.
Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5(а)). Площадь положительного полупериода этого сигнала равна 3 * 3 = 9. Площадь отрицательного полупериода составля¬ет (-3) * (-3) = 9. Среднее значение площади за период, следовательно, равно 9. Отсюда среднеквадратическое значение напряжения будет корень из 9 = 3 В.

Рис. 2.5. Сравнение среднеквадратических значений
прямоугольного и синусоидального сигналов.
Для сравнения определим среднеквадратическое значение синусоидального напряжения, имеющего значение положительной и отрицательной амплитуды +3 В и –3 В соответственно (рис. 2.5(б)): 0,707 * 3 В = 2,12 В.
Как видим, прямоугольный сигнал имеет большее среднеквадратическое значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.
На рис. 2.6 изображен прямоугольный сигнал, имеющий только положительные значения. Среднеквадратическое значение этого сигнала меньше его пикового значения.
При однополупериодном выпрямлении среднеквадратическое значение напряжения равно половине его амплитуды.
При двухполупериодном выпрямлении среднеквадратическое значение такое же, как у полной синусоиды, т. е. 0,707 амплитуды (рис. 2.7), поскольку при вычислении среднеквадратического значения положительная полуволна сигнала идентична отрицательной, положительный полупериод идентичен отрицательному.
Заметим, что постоянная составляющая, или среднее значение сигнала, это просто усредненное значение напряжения за один период, не имеющее никакого отношения к среднеквадратическому значению.

Рис. 2.6. Среднеквадратическое значение прямоугольного сигнала, имеющего только положительную полярность.


Рис. 2.7. (а) При однополупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,5 амплитуды.
(б) При двухполупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,707 амплитуды.
В этом видео наглядно рассказывается о типах тока, в том числе о переменном токе:
Добавить комментарий
Действующее значение тока и напряжения
Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как говорят, по действующей, эффективной его величине.
Действующее или эффективное значение переменного тока равно силе такого постоянного тока, который, протекая по данному проводнику, выделяет в нем ежесекундно то же количество энергии в виде тепла, что и переменный ток.
Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых достигает переменный ток, но и от формы тока.
Вообще говоря, в электротехнике, и особенно в радиотехнике, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы нескольких синусоидальных токов с различными частотами, амплитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.
Если известна амплитуда переменного синусоидального тока, то действующее или эффективное его значение определяется по формуле:
то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.
Аналогичная формула применяется и для вычисления эффективного значения синусоидального напряжения:
Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эффективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!




 .
. = 12 Ом
= 12 Ом

 = 5 Ом
= 5 Ом = 10 ОмI
= 6A
= 10 ОмI
= 6A