Расчет трехфазных цепей
6. Расчёт трёхфазных цепей.
Многофазной системой электрических цепей называют совокупность электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе, создаваемые общими источником энергии (ГОСТ 19880-74).
Многофазной цепью называют многофазную систему электрических цепей в которой отдельные фазы электрически соединены друг с другом (ГОСТ 19880-74). В частности при числе фаз многофазной системы равной 3 будем иметь трехфазную цепь.
Различают симметричную и несимметричную многофазную систему. Симметричной многофазной системой токов называют многофазную систему электрических токов в которой отдельные электрические токи равны по амплитуде и отстают по фазе относительно друг друга на уг
 ,
где m – число фаз. (ГОСТ 19880-74).
,
где m – число фаз. (ГОСТ 19880-74).Несимметричной многофазной системой электрических токов называют систему не удовлетворяющую любому из вышеуказанных признаков (ГОСТ 19880-74).
6.1. Трехфазная система ЭДС.
Под трёхфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе относительно друг друга на 120°.

 ,
,  ,
, 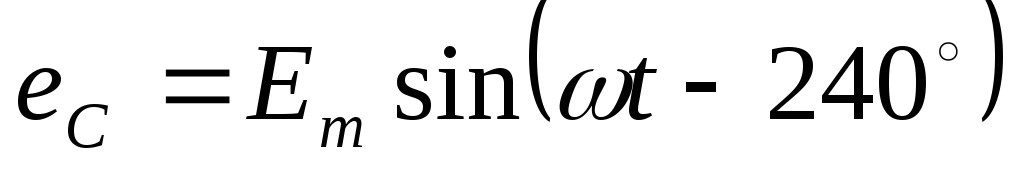 .
.
Соответственно, для действующих ЭДС в комплексной форме можно записать
 ,
, 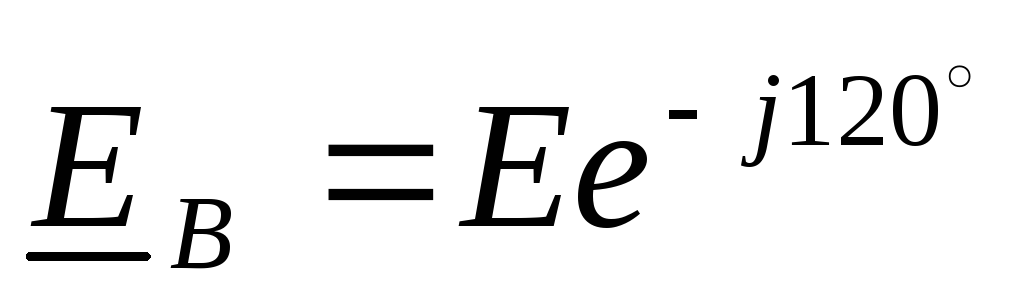 ,
, 
и изобразить на комплексной плоскости

6.2. Общие положения и допущения при расчете трехфазных цепей.
Трехфазные цепи являются разновидностью цепей синусоидального тока и поэтому их расчет производится теми же методами и приёмами, которые присущи цепям однофазного синусоидального тока. Для анализа трехфазных цепей применим комплексный (символический) метод расчета, могут строиться векторные и топографические диаграммы.
Для анализа трехфазных цепей введем два допущения, которые сводятся к тому, что синусоидальное напряжение на зажимах трехфазного генератора симметричны при любой нагрузке:
система ЭДС трехфазного генератора, симметрична;
все источники ЭДС имеют бесконечно большую мощность.
6.3.Расчет соединения звезда-звезда с нулевым проводом.
П редположим
сейчас и в дальнейшем, что сопротивление
проводов, соединяющих источник с
нагрузкой, равно нулю. В этом случае в
схеме образуются три обособленных
контура. Токи в них
редположим
сейчас и в дальнейшем, что сопротивление
проводов, соединяющих источник с
нагрузкой, равно нулю. В этом случае в
схеме образуются три обособленных
контура. Токи в них
 ,
,  ,
, 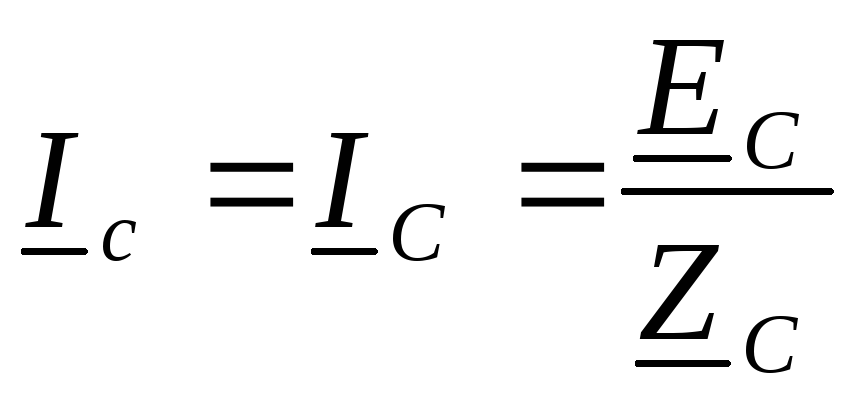 ,
,
где  ,
,  и
и  — линейные токи, а
— линейные токи, а 
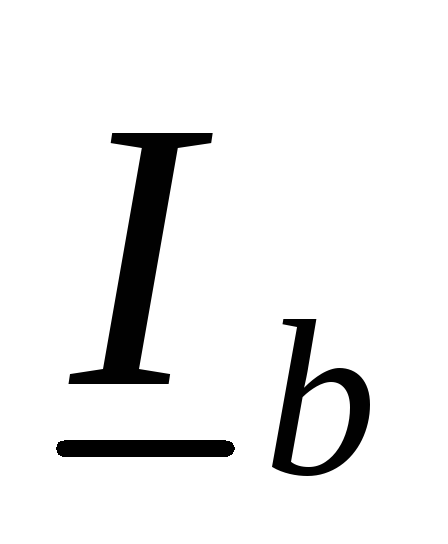 и
и  — фазные токи, токи в нагрузке,
соответственно, фазы a,
b,
c.
— фазные токи, токи в нагрузке,
соответственно, фазы a,
b,
c. Ток
в нулевом проводе равен  .
Напряжение между линейным проводом и
нулевым узлом
.
Напряжение между линейным проводом и
нулевым узлом  — фазное напряжение:
— фазное напряжение:  ,
, 
 .
Напряжение между линейными проводами
.
Напряжение между линейными проводами 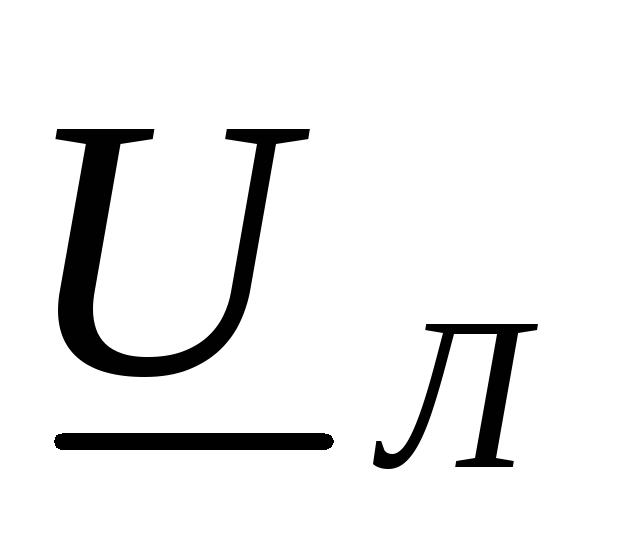 — линейное напряжение:
— линейное напряжение: 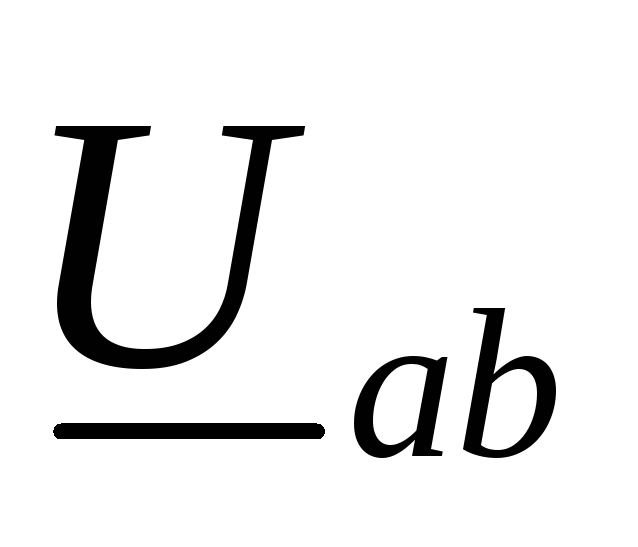 ,
,  и
и  .
. При
соединении звезда-звезда с нулевым
проводом, справедливы следующие
соотношения для токов: 
 и
и  ;
или для модулей:
;
или для модулей:  ;
для напряжений:
;
для напряжений: 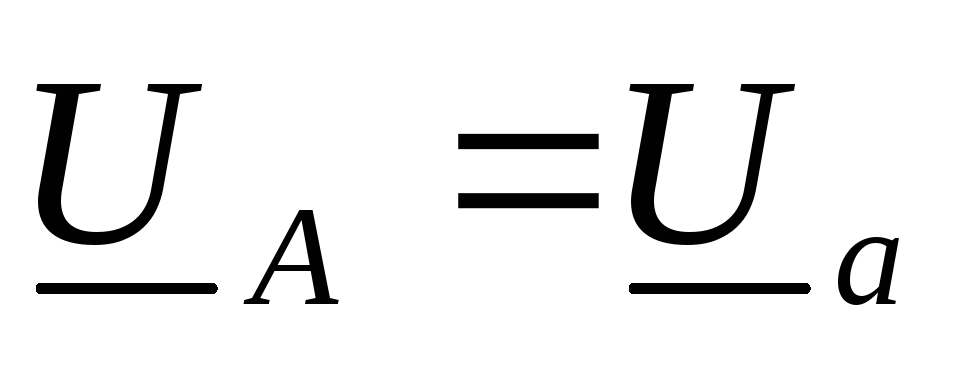 ,
, 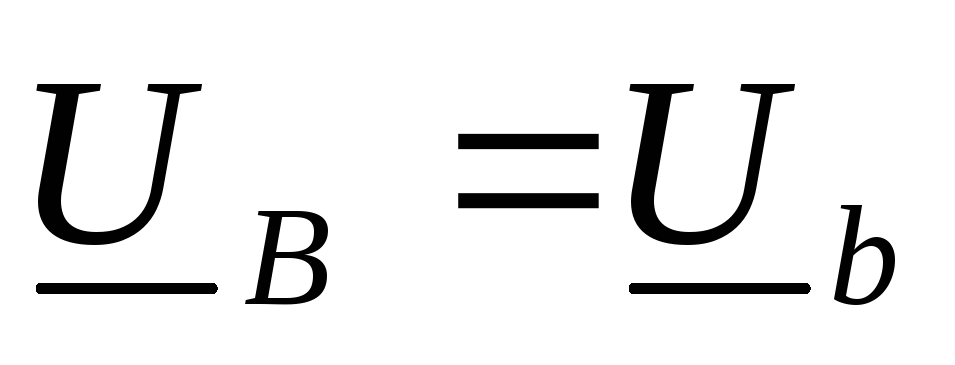 ,
, 
 ,
, 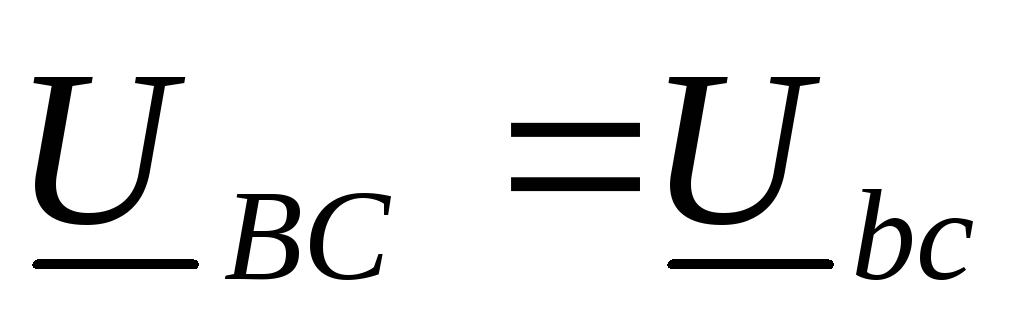 ,
,  ;
или для модулей:
.
;
или для модулей:
.Симметричная цепь (нагрузка).
С имметричная
многофазная (трёхфазная) цепь
– это цепь, в которой комплексные
сопротивления, составляющих её фаз,
одинаковы (ГОСТ 19880-74). На рисунке представлена
векторная диаграмма напряжений на
источнике и нагрузке. Векторная диаграмма
токов построена для симметричной цепи
ак-тивного характера. При этом
имметричная
многофазная (трёхфазная) цепь
– это цепь, в которой комплексные
сопротивления, составляющих её фаз,
одинаковы (ГОСТ 19880-74). На рисунке представлена
векторная диаграмма напряжений на
источнике и нагрузке. Векторная диаграмма
токов построена для симметричной цепи
ак-тивного характера. При этом 
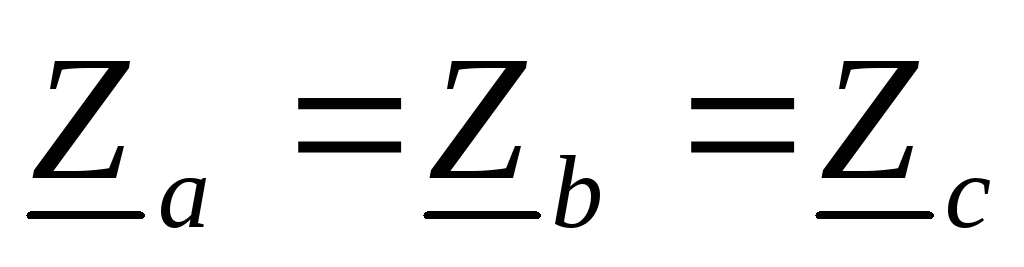 .
.Несимметричная цепь (нагрузка).
Если
нагрузка несимметрична, то есть  ,
то появляется ток в нулевом проводе:
,
то появляется ток в нулевом проводе: 
Как
это, например, показано на векторной
диаграмме, когда сопротивления фаз
равны по величине, но имеют различный
характер: в фазе  — активная нагрузка, в фазе
— активная нагрузка, в фазе  — индуктивная нагрузка, а в фазе
— индуктивная нагрузка, а в фазе  — емкостная нагрузка.
— емкостная нагрузка.

6.4. Расчет соединения звезда-звезда без нулевого провода.
Симметричная цепь (нагрузка).
В случае симметричной цепи расчет токов
в фазах нагрузки сводится к расчету
соединения звезда-звезда с нулевым
проводом, как это было показано в пункте
6.3.
случае симметричной цепи расчет токов
в фазах нагрузки сводится к расчету
соединения звезда-звезда с нулевым
проводом, как это было показано в пункте
6.3.
 ,
, 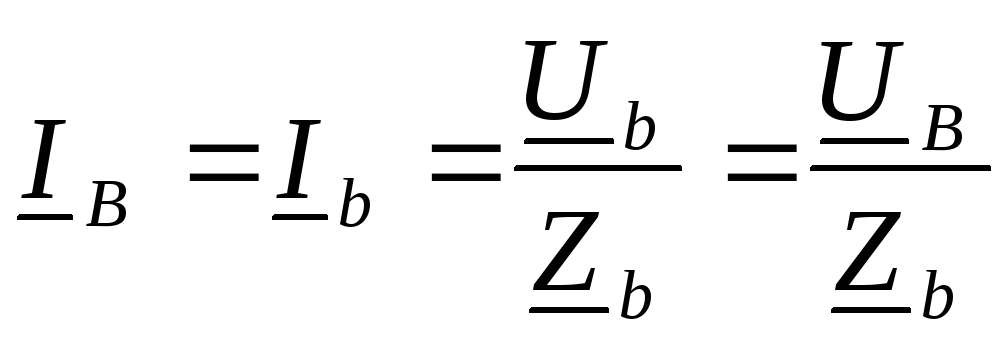 ,
, 
Несимметричная нагрузка.
В случае несимметричной
цепи напряжение на фазе нагрузки не
равно соответствующему напряжению
источника. Для определения искомого
тока  ,
,  и
и  необходимо отыскать фазное напряжение
на нагрузке.
необходимо отыскать фазное напряжение
на нагрузке.
Для этого следует
записать уравнение по второму закону
Кирхгофа для контуров, образованных
источником ЭДС, сопротивлением нагрузки
и напряжением холостого хода между
узлами  :
:  ,
откуда
,
откуда 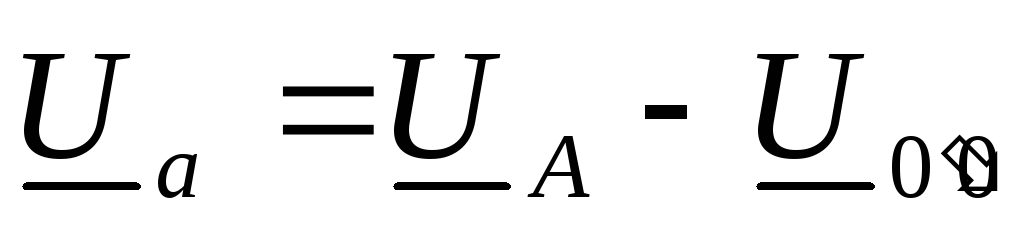 .
.
О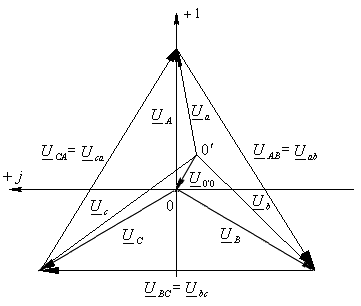 пределение
пределение  ,
,  и
и  в
последних трёх выражениях возможно в
случае, когда известно
в
последних трёх выражениях возможно в
случае, когда известно  — напряжение смещения нейтрали.
— напряжение смещения нейтрали.
Напряжение смещения
нейтрали можно определить по методу
двух узлов, представляя  или
или 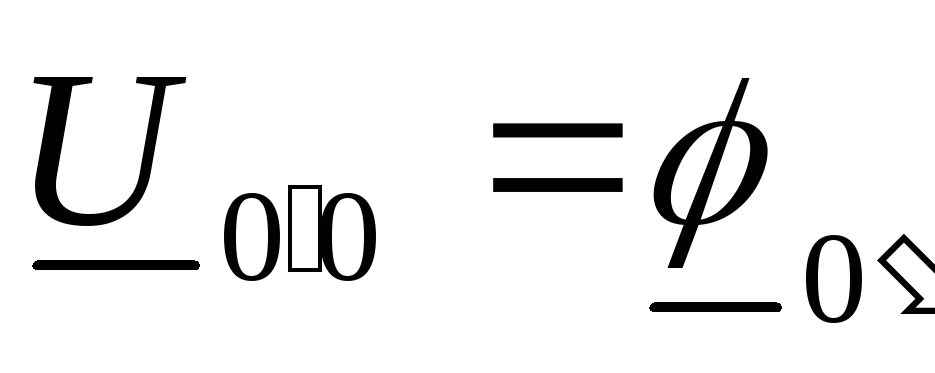 при условии, что потенциал узла
при условии, что потенциал узла  принять равным нулю,
принять равным нулю,
тогда:  .
.
Если по условию проектирования нулевой провод обладает некоторой проводимостью, то последнее выражение можно переписать в виде:
 .
.
При этом расчете
было предположено, что сопротивления
фазных обмоток генератора и сопротивления
линейных проводов равны нулю. Если эти
условия не соблюдаются, то эти сопротивления
могут быть учтены путем их введения в
сопротивления соответствующих фаз  ,
,  и
и  .
При отсутствии сопротивлений обмоток
генератора их ЭДС равны фазным напряжениям
на его зажимах
.
При отсутствии сопротивлений обмоток
генератора их ЭДС равны фазным напряжениям
на его зажимах  ,
,  ,
,  и
тогда полученную формулу для определения
смещения нейтрали можно записать в
виде:
и
тогда полученную формулу для определения
смещения нейтрали можно записать в
виде:
 .
.
6 .5.
Расчет соединения треугольник-треугольник.
.5.
Расчет соединения треугольник-треугольник.
Пусть сопротивление
фазных обмоток генератора и сопротивления
линейных проводов равны нулю, тогда: 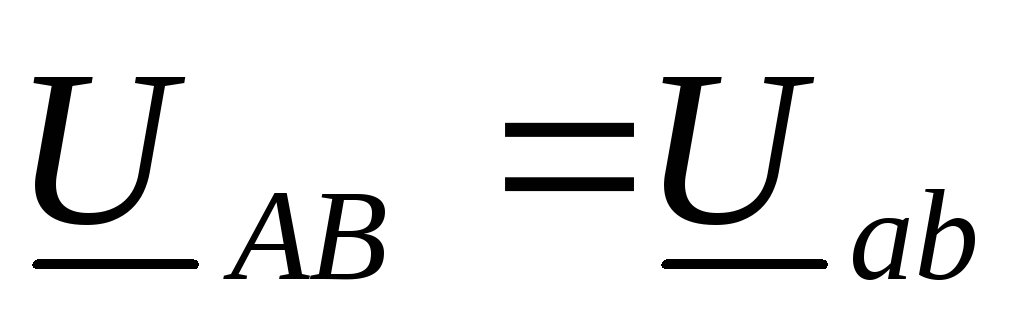 ,
,  ,
,  .
.
Ток в фазах нагрузки – фазный ток:
 ,
,  ,
,  .
.
Линейные токи в общем случае, то есть для несимметричной цепи можно определить по первому закону Кирхгофа:
 ,
,  ,
,  .
.
Для симметричной
цепи линейные токи в  раз больше фазных токов.
раз больше фазных токов.
6.6. Активная, реактивная и полная мощности трёхфазной цепи.
Под активной и
реактивной мощностями понимают: 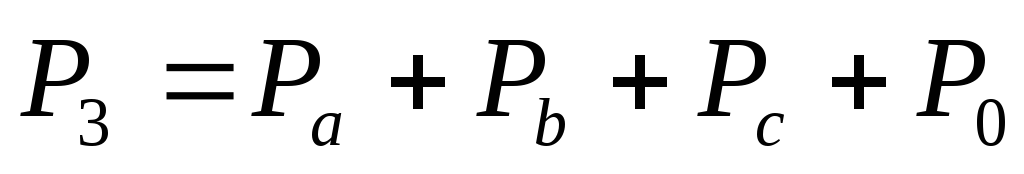 и
и  .
Полная мощность:
.
Полная мощность:  .
.
Если нагрузка
симметричная, то 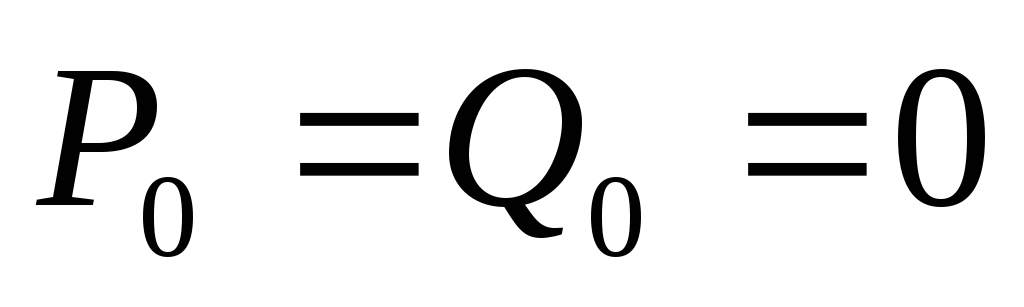 ,
, 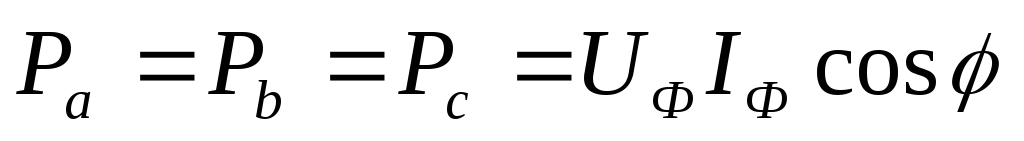 ,
,  и тогда мощность трёхфазной цепи, через
фазные токи и напряжения:
и тогда мощность трёхфазной цепи, через
фазные токи и напряжения:  ,
,  ,
,  или через линейные токи и напряжения
независимо от способа её соединения в
звезду или треугольник
или через линейные токи и напряжения
независимо от способа её соединения в
звезду или треугольник  ,
, 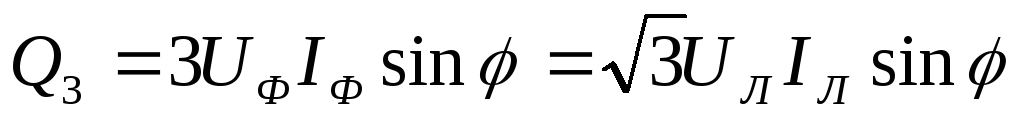 и
и 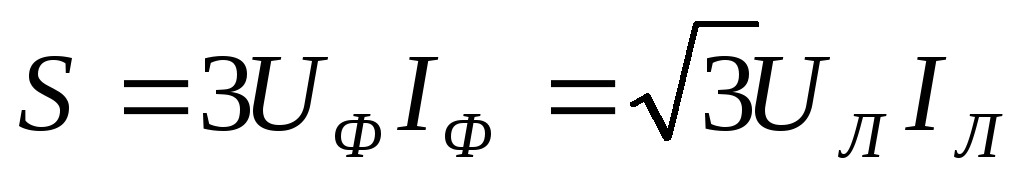 .
.
6.7. Измерение активной мощности в трёхфазной цепи.
Метод трёх ваттметров используют для измерения активной мощности трёхфазной цепи в случае несимметричной нагрузки. Активная мощность всей цепи равна сумме показаний всех ваттметров.
П ри
симметричной нагрузке достаточно
измерить мощность одной из фаз и результат
утроить – это, так называемый, метод
одного ваттметра.
ри
симметричной нагрузке достаточно
измерить мощность одной из фаз и результат
утроить – это, так называемый, метод
одного ваттметра.
В случае, если узел 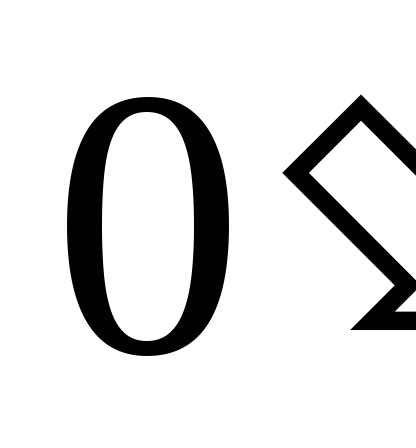 недоступен, то измерение мощности можно
произвести двумя ваттметрами.
недоступен, то измерение мощности можно
произвести двумя ваттметрами.
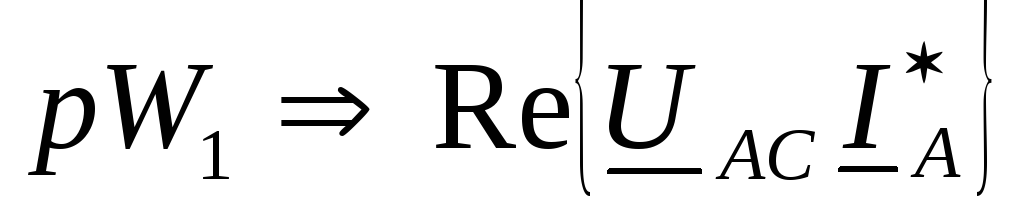
 и
и 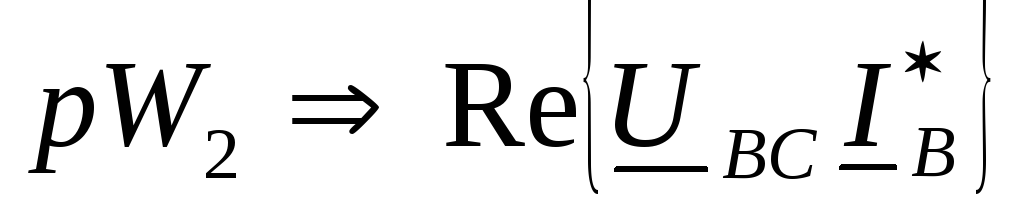 .
.
Докажем, что сумма показаний двух ваттметров представляет собой активную мощность трехфазной цепи.
Составим уравнение
по второму закону Кирхгофа для контура,
образованного фазными напряжениями  и
и  и линейным напряжением
и линейным напряжением  :
:  ,
откуда
,
откуда  ;
аналогично
;
аналогично  .
.
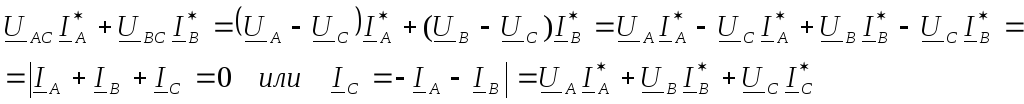
Сумма реальных частей каждого слагаемого соответствует активной мощности трехфазной цепи.
Лекция n17 Расчет трехфазных цепей
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
фаза как аргумент синусоидально изменяющейся величины;
фаза как составная часть многофазной электрической системы.
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.
Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.

Источником
трехфазного напряжения является
трехфазный генератор, на статоре
которого (см. рис. 1) размещена трехфазная
обмотка. Фазы этой обмотки располагаются
таким образом, чтобы их магнитные оси
были сдвинуты в пространстве друг
относительно друга на  эл.
рад. На рис. 1 каждая фаза статора
условно показана в виде одного витка.
Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы-
соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора
индуцируются в результате пересечения
их витков магнитным полем, создаваемым
током обмотки возбуждения вращающегося
ротора (на рис. 1 ротор условно изображен
в виде постоянного магнита, что
используется на практике при
относительно небольших мощностях).
При вращении ротора с равномерной
скоростью в обмотках фаз статора
индуцируются периодически изменяющиеся
синусоидальные ЭДС одинаковой частоты
и амплитуды, но отличающиеся вследствие
пространственного сдвига друг от
друга по фазе на
эл.
рад. На рис. 1 каждая фаза статора
условно показана в виде одного витка.
Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы-
соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора
индуцируются в результате пересечения
их витков магнитным полем, создаваемым
током обмотки возбуждения вращающегося
ротора (на рис. 1 ротор условно изображен
в виде постоянного магнита, что
используется на практике при
относительно небольших мощностях).
При вращении ротора с равномерной
скоростью в обмотках фаз статора
индуцируются периодически изменяющиеся
синусоидальные ЭДС одинаковой частоты
и амплитуды, но отличающиеся вследствие
пространственного сдвига друг от
друга по фазе на рад.
(см. рис. 2).
рад.
(см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
— экономичность передачи электроэнергии на большие расстояния;
— самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
— возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
— уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
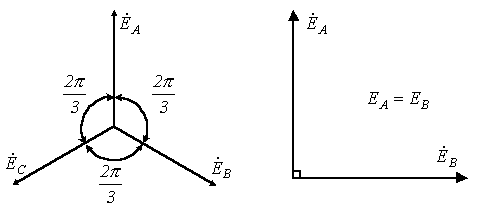
Система
ЭДС (напряжений, токов и т.д.) называется симметричной, если
она состоит из m одинаковых по модулю
векторов ЭДС (напряжений, токов и
т.д.), сдвинутых по фазе друг относительно
друга на одинаковый угол  .
В частности векторная диаграмма для
симметричной системы ЭДС, соответствующей
трехфазной системе синусоид на рис.
2, представлена на рис. 3.
.
В частности векторная диаграмма для
симметричной системы ЭДС, соответствующей
трехфазной системе синусоид на рис.
2, представлена на рис. 3.
| |
Рис.3 | Рис.4 |
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).
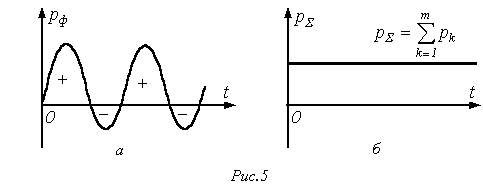
Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).
Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
Схемы соединения трехфазных систем
Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 1200. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
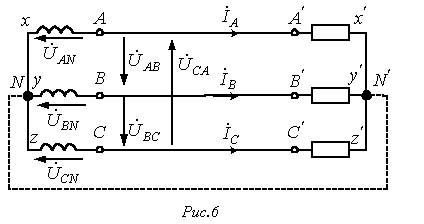
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все
величины, относящиеся к фазам, носят
название фазных
переменных, к
линии — линейных. Как
видно из схемы на рис. 6, при соединении
в звезду линейные токи 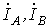 и
и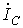 равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе
равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе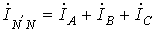 .
Если система фазных токов симметрична,
то
.
Если система фазных токов симметрична,
то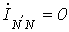 .
Следовательно, если бы симметрия
токов была гарантирована, то нейтральный
провод был бы не нужен. Как будет
показано далее, нейтральный провод
обеспечивает поддержание симметрии
напряжений на нагрузке при несимметрии
самой нагрузки.
.
Следовательно, если бы симметрия
токов была гарантирована, то нейтральный
провод был бы не нужен. Как будет
показано далее, нейтральный провод
обеспечивает поддержание симметрии
напряжений на нагрузке при несимметрии
самой нагрузки.
Поскольку
напряжение на источнике противоположно
направлению его ЭДС, фазные напряжения
генератора (см. рис. 6) действуют от
точек А,В и С к нейтральной точке N;  —
фазные напряжения нагрузки.
—
фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
| (1) |
| (2) |
| (3) |
О тметим,
что всегда
тметим,
что всегда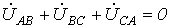 —
как сумма напряжений по замкнутому
контуру.
—
как сумма напряжений по замкнутому
контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае
| (4) |
Обычно
при расчетах принимается 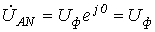 .
Тогда для случаяпрямого
чередования фаз
.
Тогда для случаяпрямого
чередования фаз 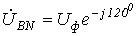 ,
,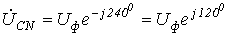 (приобратном
чередовании фаз фазовые
сдвиги у
(приобратном
чередовании фаз фазовые
сдвиги у  и
и меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7.
Направляя вещественную ось системы
координат по вектору
меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7.
Направляя вещественную ось системы
координат по вектору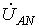 (его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений
по отношению к этой оси, а их модули
определяем в соответствии с (4). Так
для линейных напряжений
(его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений
по отношению к этой оси, а их модули
определяем в соответствии с (4). Так
для линейных напряжений и
и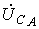 получаем:
получаем: ;
;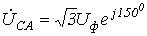 .
.
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
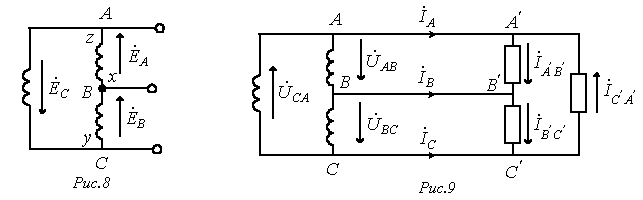
Для симметричной системы ЭДС имеем
 .
.
Таким
образом, при отсутствии нагрузки в
фазах генератора в схеме на рис. 8 токи
будут равны нулю. Однако, если поменять
местами начало и конец любой из фаз,
то 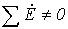 и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями

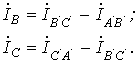
А налогично
можно выразить линейные токи через
фазные токи генератора.
налогично
можно выразить линейные токи через
фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Литература
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
Какой принцип действия у трехфазного генератора?
В чем заключаются основные преимущества трехфазных систем?
Какие системы обладают свойством уравновешенности, в чем оно выражается?
Какие существуют схемы соединения в трехфазных цепях?
Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
На диаграмме на рис. 10 (трехфазная система токов симметрична)
 .
Определить комплексы остальных
фазных и линейных токов.
.
Определить комплексы остальных
фазных и линейных токов.Какие схемы соединения обеспечивают автономность работы фаз нагрузки?
Методы расчета трёхфазных цепей
Соединение звездой
Нагрузка в трёхфазной цепи может быть:
1) симметричной, если сопротивления фаз нагрузки одинаковы по характеру и значению;
2) несимметричной, если сопротивления фаз нагрузки различны.
Рассмотрим наиболее общий случай расчёта цепи с нулевым проводом, сопротивление которого ZN
Если нужно учесть сопротивления линейных проводов и фаз источника их можно отнести к нагрузке, прибавив к сопротивлениям последнего по правилам сложения комплексных чисел. Наиболее удобным методом расчёта в данном случае является метод узлового напряжения:

Напряжения на фазах нагрузки:
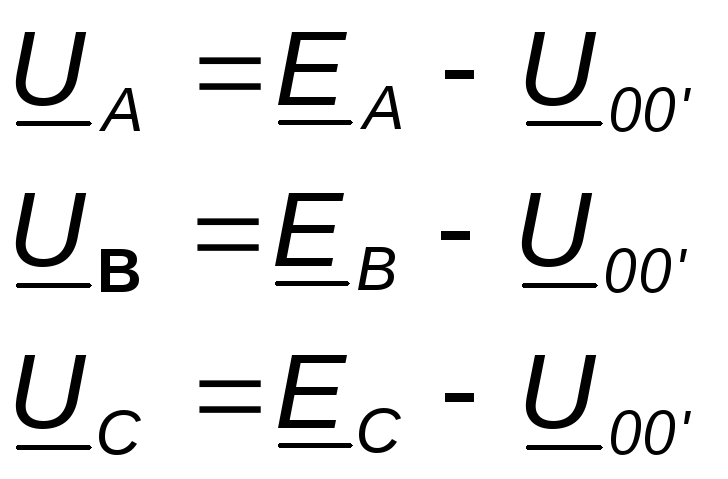
Методы расчета трёхфазных цепей Соединение треугольником
Трёхфазная цепь при соединении источника и приёмника треугольником имеет разветвлённую многоконтурную схему.
Расчёт этой сложной цепи значительно упрощается, если не принимать во внимание сопротивление проводов.
В этом случае напряжения на фазах приёмника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
Если трёхфазная система напряжений, приложенных к приёмнику, известна, то фазные токи в симметричном приёмнике определяются порознь по известным формулам:

Токи в линейных проводах:
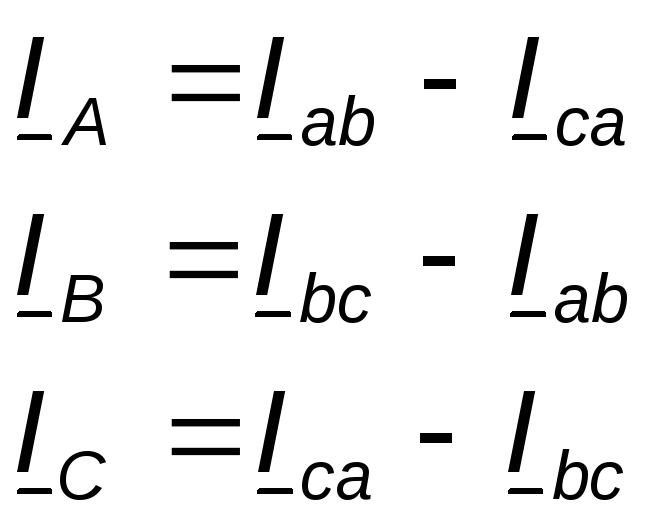
Если же сопротивления линейных проводов необходимо учитывать, то для расчёта цепи следует преобразовать треугольник сопротивления нагрузки в звезду, определить токи в линейных проводах с учётом формулы и затем найти напряжения и токи фаз нагрузки. При симметричной нагрузке фаз достаточно провести расчёт одной фазы.
Измерение мощности в трёхфазных цепях
Активной мощностью трехфазной системы называют сумму активных мощностей ее отдельных фаз:
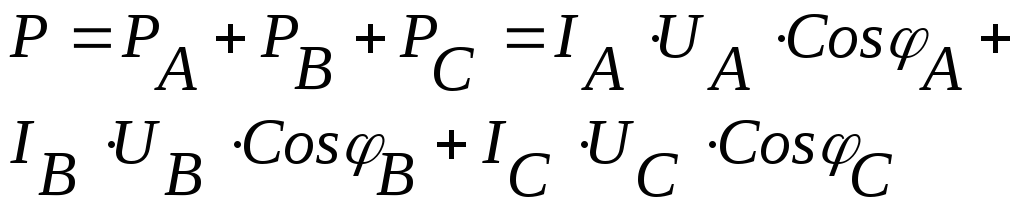
При симметричной нагрузке мощности отдельных фаз равны между собой, а общая мощность определяется как

На практике мощность трехфазной системы чаще выражают через линейные, а не через фазные токи и напряжения.
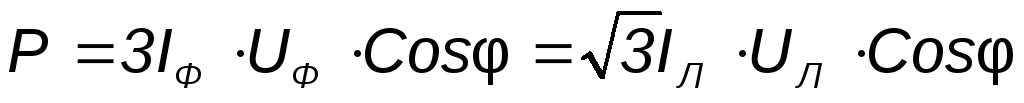 Для трехфазной
системы также справедливы следующие
соотношения для полной, активной и
реактивной мощностей, соответственно:
Для трехфазной
системы также справедливы следующие
соотношения для полной, активной и
реактивной мощностей, соответственно:
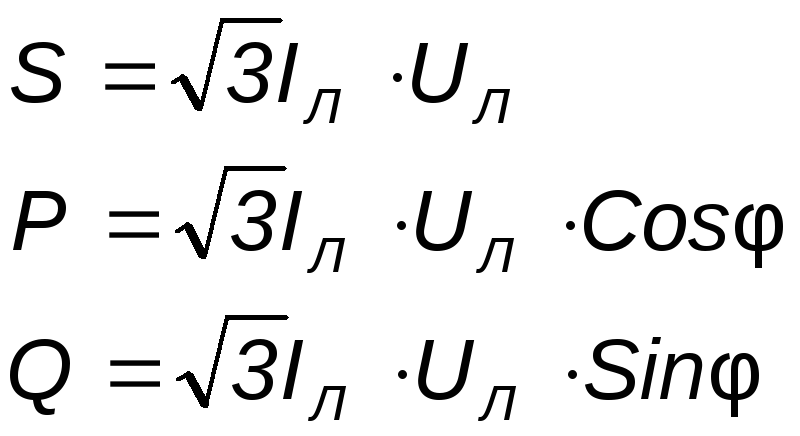
Существуют несколько методов измерения мощности трехфазной системы, у каждого из них своя область применения.
Способ одного ваттметра.
Используют для измерения мощности при симметричной нагрузке, соединенной звездой с доступной нулевой точкой
В этом случае общая мощность трехфазной системы равна утроенному показанию ваттметра:

2) Определить показания вольтметра pV и указать, в каких режимах работают источники эдс (Ri, Ом, Ej, b)
По второму закону Кирхгофа:
E1— E2 = R1I + R2I = (R1+ R2)I,
I =(E1— E2) /(R1+ R2) == (60-10) / (30+20)
Показание вольтметра не зависит от того, какая часть схемы рассматривается с целью его определения. Для определения показания вольтметра составляется уравнение, согласно II закону Кирхгофа
Е1 = R1 I + Uab , Uab = E1 – R1 I
или Е2 = R2 I + Uab , Uab = E2 – R2 I
4.5. Расчет трехфазных цепей соединением треугольник
П
Рис. 3. 11. 3.12.
ри соединении треугольником (рис. 4.11.) каждая фаза приемника подключена к двум линейным проводам, поэтому каждое фазное напряжение равно соответствующему линейному напряжению .
.Таким образом, соединение треугольником следует применять тогда, когда каждая фаза трехфазного приемника рассчитана на напряжение, равное номинальному линейному напряжению сети.

Рис. 4.11.
Фазные токи  ,
, ,
, в общем случае не равны линейным токам
в общем случае не равны линейным токам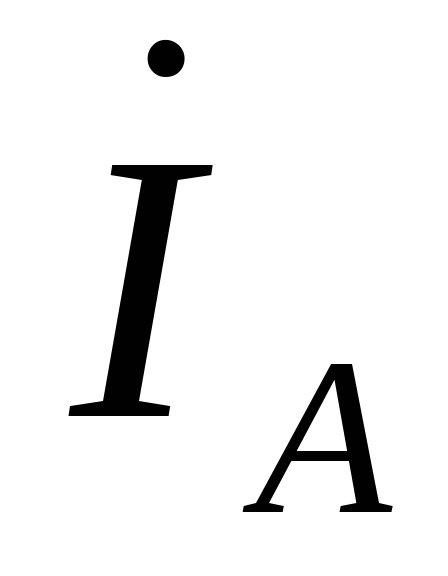 ,
, ,
, и могут быть найдены по следующим
соотношениям:
и могут быть найдены по следующим
соотношениям:
 ,
,  ,
, .
.
Линейные токи  ,
, ,
, могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:
могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:
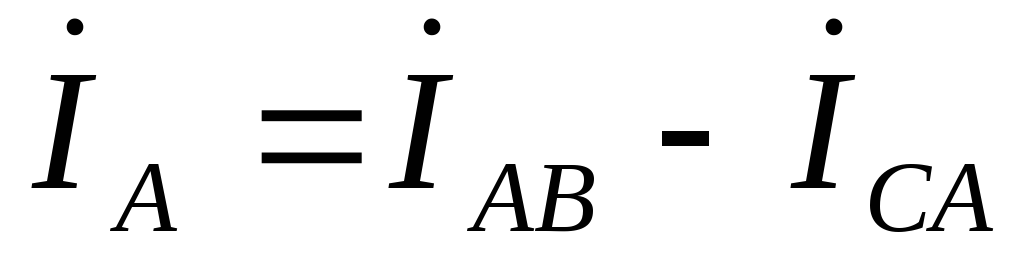 ,
, 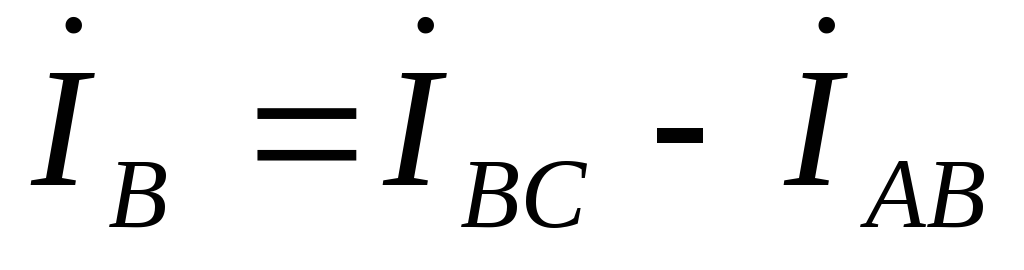 ,
, .
.
Использую указанные соотношения и имея векторы фазных токов, можно построить векторную диаграмму линейных токов (рис. 4.12.).

При симметричной
нагрузке соединением «треугольник»
равны в отдельности активные и полные
реактивные сопротивления всех фаз  ,
,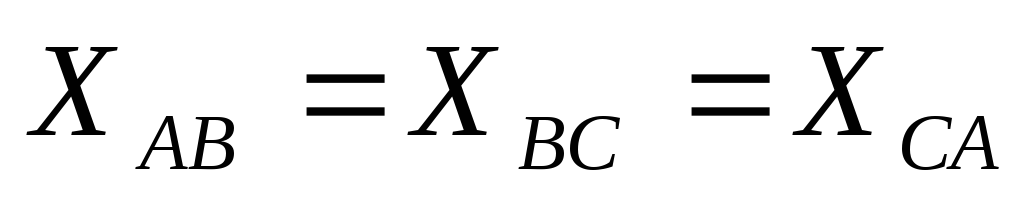
Однако, как правило,
однофазные приемники подключаются не
одновременно. Нагрузку можно считать
симметричной лишь тогда, когда включены
все приемники. Для каждой фазы могут
быть использованы все методы расчета,
рассмотренные ранее применительно к
однофазной цепи с одним источником.
Зная, например, фазные напряжения и
сопротивления, можно по закону Ома найти
фазные токи по формулам  ,
, ,
,
При симметричной
нагрузке,  ,
, -фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.
-фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.
В
Рис. 3. 13.
екторная диаграмма фазных напряжений и токов на рис. 4.13. показывает, что при симметричной нагрузке векторы фазных токов равны по величине и сдвинуты по фазе относительно друг друга на угол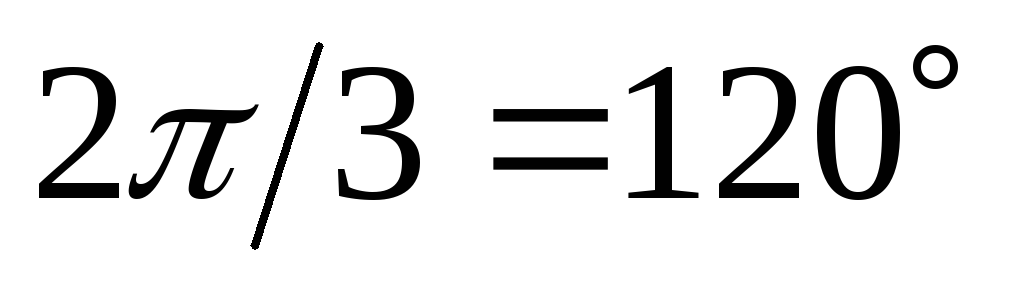 .
. Векторы линейных
токов  изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что
изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что .
.

Рис. 4.13.
Такое же соотношение существует между любыми другими фазными и линейными токами. Поэтому можно написать, что при симметричной нагрузке
 .
.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы АВ будут равны

Таким же путем
находим мощности фаз ВС и СА. В силу
равенства напряжений, токов, углов
сдвига фаз и сопротивлений при симметричной
нагрузке  ,
, ,
, .
.
При симметричной
нагрузке активная Р,
реактивная Q и полная S мощности трехфазного приемника  ,
, ,
,
 .
.
В качестве
номинальных напряжений и токов трехфазных
приемников указываются обычно линейные
напряжения и токи. Учитывая это, мощности
трехфазных приемников желательно также
выражать через линейные напряжения и
токи  ,
, ,
, .
.
4.6. Несимметричные нагрузки при соединении треугольником
Несимметричной нагрузкой считают такую, при которой активное или реактивное сопротивление хотя бы одной из фаз не равно сопротивлениям других фаз (рис. 4.14.) rAB = rBC = rC; XAB=XBC≠X CA. В таком случае при несимметричной нагрузке ZAB ≠ ZBC ≠ ZCA.
Фазные токи, углы сдвига фаз между фазными напряжениями и токами, а также мощности могут быть определены по формулам
 ,
, 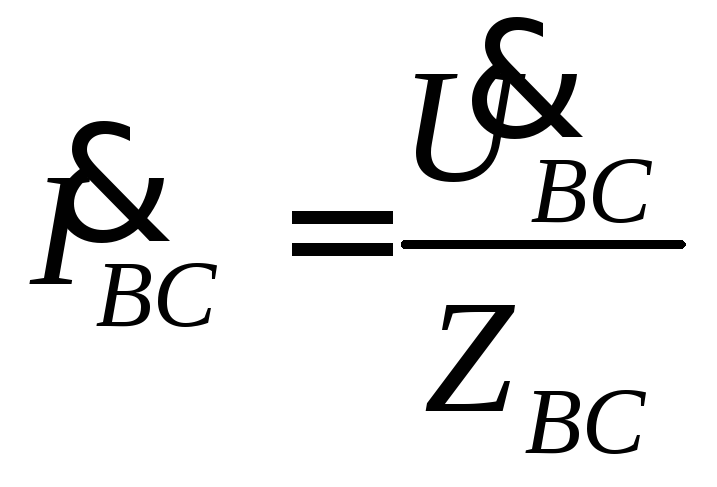 ,
,
Так как ,
а при несимметричной нагрузкеZAB≠ ZBC ≠ ZCA, то
,
а при несимметричной нагрузкеZAB≠ ZBC ≠ ZCA, то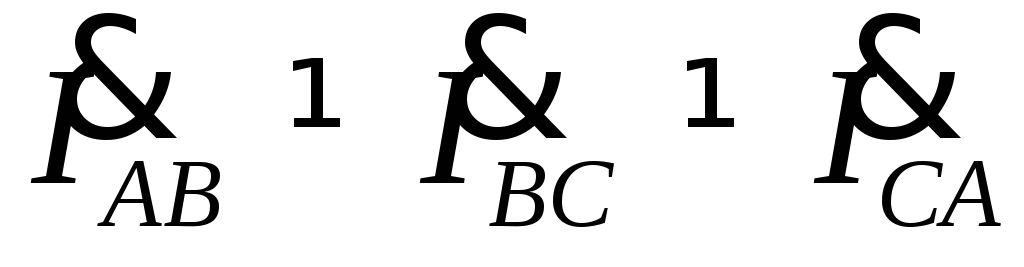 .
.
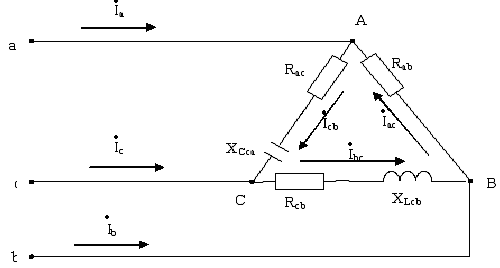
Рис. 4.14.
Углы сдвига фаз
между фазными токами и напряжениями
зависят от величины и характера
сопротивлений фаз и могут быть определены
следующим образом 
 ;
; ;
;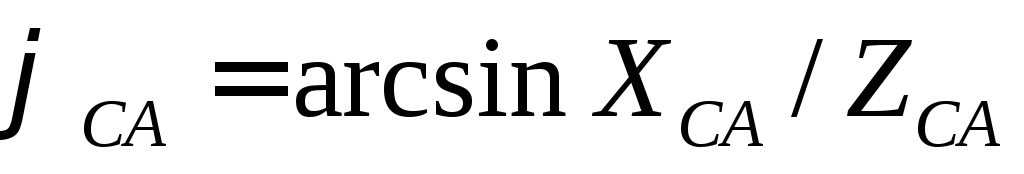 .
.
Т.о., при несимметричной нагрузке фазные токи, углы сдвига фаз и фазные мощности в общем случае различные.
Зная фазные напряжения, токи и углы сдвига фаз между ними, либо токи и сопротивления, можно найти фазные мощности. Например, мощности фазы AB


Активные и реактивные
мощности приемника 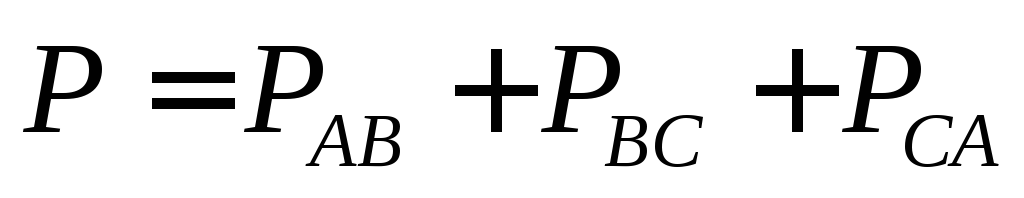 ;
;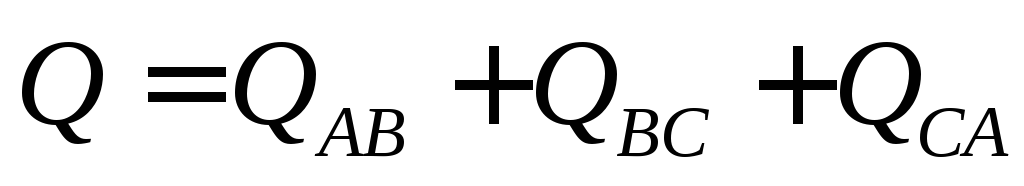 .
.
Векторная диаграмма
при несимметричной нагрузке для случая,
когда в фазе AB
имеется активное сопротивление, в фазе
BC
– активное и индуктивное сопротивления,
фазе CA
– активное и емкостное сопротивления,
приведена на рис. 4.15. Построение векторов
линейных токов произведено в соответствии
с выражениями  ,
,  ,
, .
.
Е сли
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.
сли
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.
Рис. 4.15.
О
Рис. 3. 15.
тключение нагрузки одной из фаз можно считать частным случаем несимметричной нагрузки, при которой сопротивление отключенной фазы равно бесконечности. Так при отключении фазыCA сопротивление Z CA= ∞. При этом, ток ;
фазные токи
;
фазные токи ,
а также углыφAB,φ BC не изменятся, а линейные токи
,
а также углыφAB,φ BC не изменятся, а линейные токи 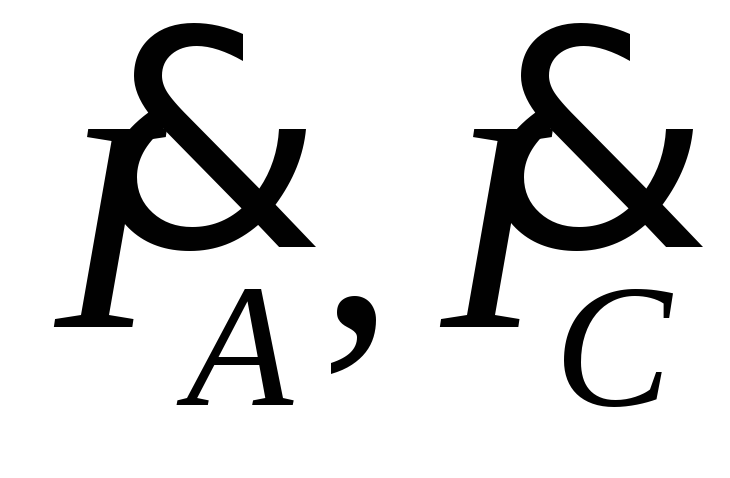 уменьшатся и будут равны
уменьшатся и будут равны  ,
,  .
.Лекция N 17. Расчет трехфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный
приемник и вообще многофазная цепь
называются симметричными, если
в них комплексные сопротивления
соответствующих фаз одинаковы, т.е. если  .
В противном случае они являются несимметричными. Равенство
модулей указанных сопротивлений не
является достаточным условием симметрии
цепи. Так, например трехфазный приемник
на рис. 1,а является симметричным, а на
рис. 1,б – нет даже при условии:
.
В противном случае они являются несимметричными. Равенство
модулей указанных сопротивлений не
является достаточным условием симметрии
цепи. Так, например трехфазный приемник
на рис. 1,а является симметричным, а на
рис. 1,б – нет даже при условии: 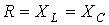 .
.

Если
к симметричной трехфазной цепи приложена
симметричная трехфазная система
напряжений генератора, то в ней будет
иметь место симметричная система токов.
Такой режим работы трехфазной цепи
называется симметричным. В
этом режиме токи и напряжения
соответствующих фаз равны по модулю и
сдвинуты по фазе друг по отношению к
другу на угол 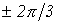 .
Вследствие указанного расчет таких
цепей проводится для одной – базовой – фазы, в качестве которой обычно
принимают фазу А. При этом соответствующие
величины в других фазах получают
формальным добавлением к аргументу
переменной фазы А фазового сдвига
.
Вследствие указанного расчет таких
цепей проводится для одной – базовой – фазы, в качестве которой обычно
принимают фазу А. При этом соответствующие
величины в других фазах получают
формальным добавлением к аргументу
переменной фазы А фазового сдвига 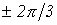 при
сохранении неизменным ее модуля.
при
сохранении неизменным ее модуля.
Так
для симметричного режима работы цепи
на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз 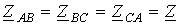 можно
записать
можно
записать
 ,
,
где  определяется
характером нагрузки
определяется
характером нагрузки  .
.
Тогда на основании вышесказанного
 ;
;
 .
.
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все
треугольники заменяются эквивалентными
звездами. Поскольку треугольники
симметричны, то в соответствии с формулами
преобразования «треугольник-звезда»  .
.
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть,
например, при заданном фазном напряжении 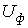 необходимо
определить линейные токи
необходимо
определить линейные токи 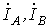 и
и  в
схеме на рис. 3, все сопротивления в
которой известны.
в
схеме на рис. 3, все сопротивления в
которой известны.
В
соответствии с указанной методикой
выделим расчетную фазу А, которая
представлена на рис. 4. Здесь  ,
,  .
.
Тогда
для тока  можно
записать
можно
записать
 ,
,
и
соответственно  .
.
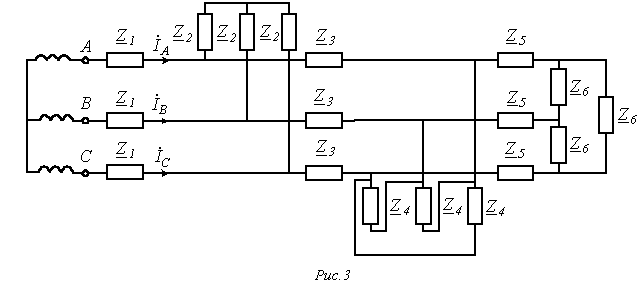
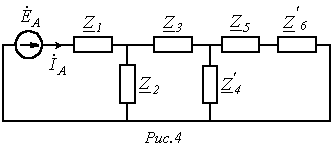
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При
заданных линейных напряжениях наиболее
просто рассчитываются трехфазные цепи
при соединении в треугольник. Пусть в
схеме на рис. 2,а  .
Тогда при известных комплексах линейных
напряжений в соответствии с законом
Ома
.
Тогда при известных комплексах линейных
напряжений в соответствии с законом
Ома
 ;
;  ;
; 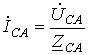 .
.
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:
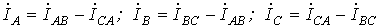 .
.
Обычно
на практике известны не комплексы
линейных напряжений, а их модули. В этом
случае необходимо предварительное
определение начальных фаз этих напряжений,
что можно осуществить, например,
графически. Для этого, приняв 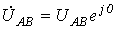 ,
по заданным модулям напряжений, строим
треугольник (см. рис.5), из которого (путем
замера) определяем значения углов a и
b.
,
по заданным модулям напряжений, строим
треугольник (см. рис.5), из которого (путем
замера) определяем значения углов a и
b.
Т огда
огда
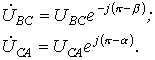
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
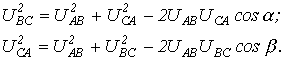
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим
трехфазную цепь на рис. 6,а. При симметричном
питании и несимметричной нагрузке 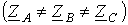 ей
в общем случае будет соответствовать
векторная диаграмма напряжений (см.
рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные
положения, т.е.
ей
в общем случае будет соответствовать
векторная диаграмма напряжений (см.
рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные
положения, т.е.  .
.
Разность
потенциалов нейтральных точек генератора
и нагрузки называется напряжением
смещения нейтральной точки (обычно
принимается, что  )
или просто напряжением
смещения нейтрали. Чем
оно больше, тем сильнее несимметрия
фазных напряжений на нагрузке, что
наглядно иллюстрирует векторная
диаграмма на рис.
6,б.
)
или просто напряжением
смещения нейтрали. Чем
оно больше, тем сильнее несимметрия
фазных напряжений на нагрузке, что
наглядно иллюстрирует векторная
диаграмма на рис.
6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
 .
.

Тогда для искомых токов можно записать:
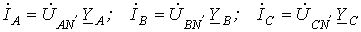 .
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
| (1) |
При
наличии нейтрального провода с нулевым
сопротивлением 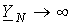 ,
и из (1)
,
и из (1) 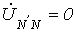 .
В случае отсутствия нейтрального провода
.
В случае отсутствия нейтрального провода 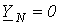 .
При симметричной нагрузке
.
При симметричной нагрузке 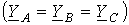 с
учетом того, что
с
учетом того, что 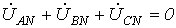 ,
из (1) вытекает
,
из (1) вытекает 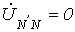 .
.
В качестве примера анализа несимметричного
режима работы цепи с использованием
соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием
фаз источника будет гореть ярче, если
качестве примера анализа несимметричного
режима работы цепи с использованием
соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием
фаз источника будет гореть ярче, если  .
.
Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь
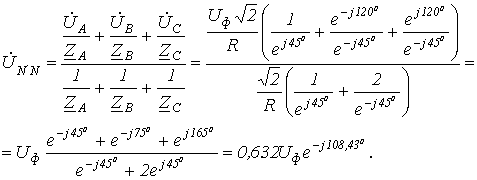
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В
заключение отметим, что если при
соединении в звезду задаются линейные
напряжения (что обычно имеет место на
практике), то с учетом того, что сумма
последних равна нулю, их можно однозначно
задать с помощью двух источников ЭДС,
например,  и
и 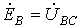 .
Тогда, поскольку при этом
.
Тогда, поскольку при этом  ,
соотношение (1) трансформируется в
формулу
,
соотношение (1) трансформируется в
формулу
| (2) |
Литература
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
Какой многофазный приемник является симметричным?
Какой режим работы трехфазной цепи называется симметричным?
В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
Что такое напряжение смещения нейтрали, как оно определяется?
Как можно определить комплексы линейных напряжений, если заданы их модули?
Что обеспечивает нейтральный провод с нулевым сопротивлением?
В цепи на рис. 6,а
 ;
;  ;
;  ;
;  .
Линейное напряжение равно 380 В.
.
Линейное напряжение равно 380 В.
Определить ток в нейтральном проводе.
Ответ:  .
.
В схеме предыдущей задачи
 ;
;  .
Остальные параметры те же.
.
Остальные параметры те же.
Определить ток в нейтральном проводе.
Ответ:  .
.
В задаче 8 нейтральный провод оборван.
Определить фазные напряжения на нагрузке.
Ответ: 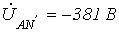 ;
; 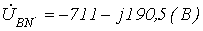 ;
; 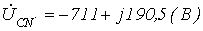 .
.
В задаче 9 нейтральный провод оборван.
Определить фазные напряжения на нагрузке.
Ответ: 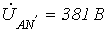 ;
;  ;
;  .
.
ЛЕКЦИЯ 13 РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ

(продолжение)
План лекции
1. Соединение звездой четырехпроводной с нейтральным проводом без сопротивления 2. Мощности трехфазных цепей
3. Способы измерения активной мощности
1. Соединениезвездойчетырехпроводной
снейтральнымпроводомбезсопротивления.
Схема замещения анализируемой цепи приведена на рис. 13.1.
По известным значениям напряжения генератора и сопротивлений фаз приемника нужно вычислить фазные и линейные токи, а также ток в нейтральном проводе, соединяющем нейтральные точки генератора и приемника.
|
|
|
| C |
| IA |
|
|
| C |
|
|
|
|
|
|
| a |
|
|
|
|
| a | Ia |
|
|
|
| CA | A |
|
|
|
| Ca | A |
|
| ||
|
| E | UA |
|
|
| E | Ua |
|
| |||
|
| a |
| Z |
| InN |
|
| a | Z |
|
|
|
E | C | A | N | Z |
|
|
| A | Z | n |
|
| |
| E |
|
|
|
| Cc | E |
| Z b |
| |||
|
|
| E | EB |
|
| E |
|
| ||||
|
| Z |
|
|
|
| a | Z |
|
|
|
| |
C |
| Z | UC |
| UB | B | c | A | Z |
| Ub | Ib | b |
a |
| E |
| IB |
| Ic | Uc |
|
|
| |||
|
|
|
|
| E | E |
|
|
|
| |||
A |
|
|
|
| IC |
|
| Z |
|
|
|
|
|
E |
|
|
|
|
|
| Z |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| ||
Z |
|
|
|
|
| Рис. 13.1 |
| E |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
E
1.Приемник несимметричный Из схемы видно, что при соединении фаз приемника звездой фазные и
линейные токи соответственно равны между собой, например I A = Ia .
Нейтральный провод с нулевым сопротивлением соединяет нейтральные точки генератора и приемника, следовательно, их потенциалы равны
между собой: VN =Vn .
Если сопротивлением линии пренебрегают, то потенциалы начал фаз генератора и приёмника одинаковы: VA =Va;VB =Vb;VC =Vc . Поэтому фазные
Теоретические основы электротехники. Конспект лекций | -84- |

ЛЕКЦИЯ 13. РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
1. Соединение звездой четырехпроводной с нейтральным проводом без сопротивления.
напряжения генератора и приёмника соответственно равны:
U А =Uа;U B =Ub;UC =Uc .
Линейные и фазные токи определяют по закону Ома:
IA = Ia = U A ; IB = Ib = UB ; IC = Ic = UC . | ||
Z a | Zb | Z c |
Ток в нейтральном проводе InN = Ia + Ib + Ic зависит не только от ха-
рактера и величины сопротивлений фаз, но и от схемы их включения. При перемене местами нагрузок двух фаз ток нейтрального провода может измениться в несколько раз.
Топографические диаграммы напряжений генератора и приемника совпадают. Нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Векторы фазных токов ориентируют относительно векторов соответствующих фазных напряжений приемника в зависимости от нагрузки фаз.
Вектор тока в нейтральном проводе InN получают как геометрическую сумму векторов фазных токов.
2. Приемник симметричный Если приемник симметричный, токи в фазах и линиях равны между со-
бой по величине и сдвинуты относительно друг друга по фазе на 120°. Достаточно вычислить только один ток:
IA = Ia = U A . Z a
Тогда IB = Ib = Ia e− j120° = a2 I A ; IC = Ic = I A e j120° = a I A .
Ток в нейтральном проводе InN = Ia + Ib + Ic = 0 .
2.Мощноститрехфазныхцепей
Втрехфазных цепях различают те же мощности, что и в однофазных: мгновенную р, активную Р, реактивную Q и полную S .
Мощности р, Р и Q находят как суммы мощностей трех фаз: р = ∑ рф ;
Р = ∑Рф ; Q = ∑Qф .
Мощности каждой фазы вычисляют по известным формулам. Потребляемой является активная мощность. Активную мощность фазы
проще всего определить по формуле Рф =Uф Iф cos ϕф или Рф = Rф Iф2 . Реактивную мощность фазы ищут следующим образом:
Теоретические основы электротехники. Конспект лекций | -85- |

ЛЕКЦИЯ 13. РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
2. Мощности трехфазных цепей
Qф =Uф Iф sinϕф или Qф = Хф Iф2 .
Полную мощность трехфазной цепи вычисляют как гипотенузу суммарного треугольника мощностей:
S =  P2 +Q2 =
P2 +Q2 =  (∑Pф)2 + (∑Qф)2 .
(∑Pф)2 + (∑Qф)2 .
При симметричной нагрузке мощности фаз одинаковы, поэтому
P = 3Pф = 3Uф Iф cos ϕф; Q = 3Qф = 3Uф Iф sin ϕф .
При соединении звездой Uф = U3л и Iф = Iл, а при соединении тре-
угольником Uф =Uл и Iф = Iл3 . Поэтому независимо от схемы соединения
фаз приемника можно получить одинаковые формулы мощностей, вычисленных через линейные напряжения и токи:
Р =  3Uл Iл cos ϕф; Q = 3Uл Iл sin ϕф ; S =
3Uл Iл cos ϕф; Q = 3Uл Iл sin ϕф ; S =  P2 +Q2 =
P2 +Q2 =  3Uл Iл .
3Uл Iл .
3. Способыизмеренияактивноймощности
Для измерения активной мощности используют ваттметры. Число ваттметров и способ их включения зависят от способа соединения фаз приемника и от их параметров.
Ваттметр показывает активную мощность, которую вычисляют по формуле
P | =U |
| I |
|
|
| ^ |
| или P = Re(S |
|
|
| * |
| , |
W | W | cos U | W | I |
| W | )= Re U | W | I |
| |||||
W |
|
|
|
| W | W |
| W |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где UW и IW – действующие значения напряжения на ваттметре и тока
в нем.
Угол сдвига фаз между ними соответствует одинаковым положительным направлениям UW и IW относительно зажимов, отмеченных звездочка-
ми.
Количество и способ включения ваттметров зависят от нагрузки и характеристики цепи.
Способ одного ваттметра Применяют при симметричной нагрузке. Ваттметр подключают таким
образом, чтобы он измерял фазные напряжение и ток (рис. 13.2, а и б). Чтобы
Теоретические основы электротехники. Конспект лекций | -86- |

ЛЕКЦИЯ 13. РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
3. Способы измерения активной мощности
найти потребляемую трехфазным приемником мощность, показание ваттметра утраивают.
A |
| * | A |
|
|
|
|
| |
|
| W * |
| * |
|
|
|
| |
|
| Z | Z | W * |
N |
| n |
| Z |
Z | Z |
| ||
|
|
| ||
B |
|
| B | Z |
|
|
| ||
C | а |
| C | б |
|
|
| ||
|
|
| Рис. 13.2 |
|
Часто фаза приемника недоступна. В четырехпроводной цепи ваттметр можно подключить так, как показано на рис. 13.3, потому что линейные и фазные токи соответственно одинаковы.
В трехпроводной цепи можно создать искусственную нейтральную точку (рис. 13.4). Добавочное сопротивление Rд должно быть равно сопро-
тивлению обмотки напряжения ваттметра (порядка нескольких кОм).
| * |
| * | * |
A | * W | A | W | |
B | Симметричный | B |
| Симметричный |
|
|
| ||
C | приемник | C |
| приемник |
|
| |||
|
|
| ||
N |
|
| RД | RД |
|
|
|
| |
| Рис. 13.3 |
|
| Рис. 13.4 |
Способ двух ваттметров Применяют в трехпроводной цепи при несимметричной нагрузке. Схе-
ма подключения ваттметров показана на рис. 13.5. Сумма показаний ваттметров равна потребляемой цепью мощности. Проще это можно доказать для комплексной мощности. Активная мощность является действительной составляющей комплексной мощности.
Теоретические основы электротехники. Конспект лекций | -87- |

ЛЕКЦИЯ 13. РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
3. Способы измерения активной мощности
| I A | * |
| |
| * W |
| ||
A | ||||
1 |
| |||
B | IB |
| Z | |
|
| |||
C IC  * W2
* W2
*
Рис. 13.5
Комплексная мощность
|
|
|
|
|
| * |
|
| * |
|
|
|
|
|
|
| * |
| * |
| |
S = SW + SW | =U AB I A | +UCB IC |
| = (U A −U B )I A + (UC | −U B )IC | = | |||||||||||||||
| 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| =U |
| * | +U |
| * |
| * |
|
| * | . |
|
| |||||
|
|
| A | I | A | − I | A | − I |
| +U | C | I | C |
|
| ||||||
|
|
|
|
|
|
| B |
|
| C |
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По | первому | закону |
| Кирхгофа |
| I A + IB + IC = 0 , | следовательно | ||||||||||||||
* * | * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IA + IB + IC = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| * |
| * | * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда IB = −I A − IC . |
|
| * |
|
|
| * |
|
| * |
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Тогда S = SW |
| + SW |
| =U A I A +U B | IB +UC IC | = S A + S B + S C . |
| ||||||||||||||
| 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Этот метод наиболее распространен на практике.
Способ трех ваттметров Применяют в четырехпроводной цепи при несимметричной нагрузке.
Каждый ваттметр измеряет активную мощность одной фазы (см. рис. 13.2, а, б). Мощность системы определяют как сумму показаний ваттметров. Метод громоздкий и неудобный.
Измерение трехфазным ваттметром Представляет из себя конструктивное сочетание трех однофазных
ваттметров. Суммирование их показаний происходит автоматически.
Применение измерительных комплексов
Теоретические основы электротехники. Конспект лекций | -88- |

ЛЕКЦИЯ 13. РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
3. Способы измерения активной мощности
Представляется наиболее удобным. Измерительные комплексы снабжены амперметром, вольтметром и ваттметром. При переключении тумблера происходит подключение измерительных приборов на разные фазы.
Вопросыдлясамопроверки
1.Чему равно напряжение на фазе приемника при соединении звездой четырехпроводной с нейтральным проводом без сопротивления?
2.Как вычислить ток в нейтральном проводе?
3.Каков алгоритм построения векторно-топографической диаграммы при соединении звездой четырехпроводной с нейтральным проводом без сопротивления?
4.Какие мощности различают в трехфазных цепях?
5.Какие способы измерения активной мощности вы знаете?
6.В каких цепях для измерения активной мощности применяют метод двух ваттметров?
Теоретические основы электротехники. Конспект лекций | -89- |
Лекция n17 Расчет трехфазных цепей
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
фаза как аргумент синусоидально изменяющейся величины;
фаза как составная часть многофазной электрической системы.
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.
Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.

Источником
трехфазного напряжения является
трехфазный генератор, на статоре
которого (см. рис. 1) размещена трехфазная
обмотка. Фазы этой обмотки располагаются
таким образом, чтобы их магнитные оси
были сдвинуты в пространстве друг
относительно друга на 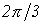 эл.
рад. На рис. 1 каждая фаза статора
условно показана в виде одного витка.
Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы-
соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора
индуцируются в результате пересечения
их витков магнитным полем, создаваемым
током обмотки возбуждения вращающегося
ротора (на рис. 1 ротор условно изображен
в виде постоянного магнита, что
используется на практике при
относительно небольших мощностях).
При вращении ротора с равномерной
скоростью в обмотках фаз статора
индуцируются периодически изменяющиеся
синусоидальные ЭДС одинаковой частоты
и амплитуды, но отличающиеся вследствие
пространственного сдвига друг от
друга по фазе на
эл.
рад. На рис. 1 каждая фаза статора
условно показана в виде одного витка.
Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы-
соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора
индуцируются в результате пересечения
их витков магнитным полем, создаваемым
током обмотки возбуждения вращающегося
ротора (на рис. 1 ротор условно изображен
в виде постоянного магнита, что
используется на практике при
относительно небольших мощностях).
При вращении ротора с равномерной
скоростью в обмотках фаз статора
индуцируются периодически изменяющиеся
синусоидальные ЭДС одинаковой частоты
и амплитуды, но отличающиеся вследствие
пространственного сдвига друг от
друга по фазе на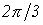 рад.
(см. рис. 2).
рад.
(см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
— экономичность передачи электроэнергии на большие расстояния;
— самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
— возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
— уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система
ЭДС (напряжений, токов и т.д.) называется симметричной, если
она состоит из m одинаковых по модулю
векторов ЭДС (напряжений, токов и
т.д.), сдвинутых по фазе друг относительно
друга на одинаковый угол  .
В частности векторная диаграмма для
симметричной системы ЭДС, соответствующей
трехфазной системе синусоид на рис.
2, представлена на рис. 3.
.
В частности векторная диаграмма для
симметричной системы ЭДС, соответствующей
трехфазной системе синусоид на рис.
2, представлена на рис. 3.
| |
Рис.3 | Рис.4 |
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).
Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).
Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.

Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
Схемы соединения трехфазных систем
Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 1200. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной.
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
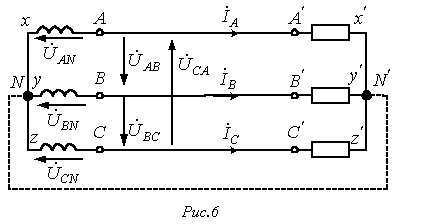
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все
величины, относящиеся к фазам, носят
название фазных
переменных, к
линии — линейных. Как
видно из схемы на рис. 6, при соединении
в звезду линейные токи 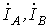 и
и равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе
равны
соответствующим фазным токам. При
наличии нейтрального провода ток в
нейтральном проводе .
Если система фазных токов симметрична,
то
.
Если система фазных токов симметрична,
то .
Следовательно, если бы симметрия
токов была гарантирована, то нейтральный
провод был бы не нужен. Как будет
показано далее, нейтральный провод
обеспечивает поддержание симметрии
напряжений на нагрузке при несимметрии
самой нагрузки.
.
Следовательно, если бы симметрия
токов была гарантирована, то нейтральный
провод был бы не нужен. Как будет
показано далее, нейтральный провод
обеспечивает поддержание симметрии
напряжений на нагрузке при несимметрии
самой нагрузки.
Поскольку
напряжение на источнике противоположно
направлению его ЭДС, фазные напряжения
генератора (см. рис. 6) действуют от
точек А,В и С к нейтральной точке N; 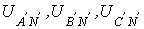 —
фазные напряжения нагрузки.
—
фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
| (1) |
| (2) |
| (3) |
О тметим,
что всегда
тметим,
что всегда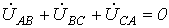 —
как сумма напряжений по замкнутому
контуру.
—
как сумма напряжений по замкнутому
контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при осно. вании, равными 300), в этом случае
| (4) |
Обычно
при расчетах принимается 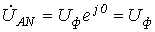 .
Тогда для случаяпрямого
чередования фаз
.
Тогда для случаяпрямого
чередования фаз  ,
,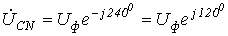 (приобратном
чередовании фаз фазовые
сдвиги у
(приобратном
чередовании фаз фазовые
сдвиги у 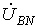 и
и меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7.
Направляя вещественную ось системы
координат по вектору
меняются
местами). С учетом этого на основании
соотношений (1) …(3) могут быть определены
комплексы линейных напряжений. Однако
при симметрии напряжений эти величины
легко определяются непосредственно
из векторной диаграммы на рис. 7.
Направляя вещественную ось системы
координат по вектору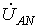 (его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений
по отношению к этой оси, а их модули
определяем в соответствии с (4). Так
для линейных напряжений
(его
начальная фаза равна нулю), отсчитываем
фазовые сдвиги линейных напряжений
по отношению к этой оси, а их модули
определяем в соответствии с (4). Так
для линейных напряжений и
и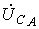 получаем:
получаем: ;
; .
.
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
 .
.
Таким
образом, при отсутствии нагрузки в
фазах генератора в схеме на рис. 8 токи
будут равны нулю. Однако, если поменять
местами начало и конец любой из фаз,
то 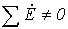 и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
и
в треугольнике будет протекать ток
короткого замыкания. Следовательно,
для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной
фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
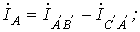

А налогично
можно выразить линейные токи через
фазные токи генератора.
налогично
можно выразить линейные токи через
фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Литература
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
Какой принцип действия у трехфазного генератора?
В чем заключаются основные преимущества трехфазных систем?
Какие системы обладают свойством уравновешенности, в чем оно выражается?
Какие существуют схемы соединения в трехфазных цепях?
Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
На диаграмме на рис. 10 (трехфазная система токов симметрична)
 .
Определить комплексы остальных
фазных и линейных токов.
.
Определить комплексы остальных
фазных и линейных токов.Какие схемы соединения обеспечивают автономность работы фаз нагрузки?




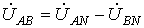 ;
; 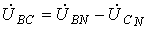 ;
; .
.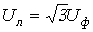
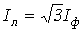 .
. 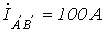 .
Определить комплексы остальных
фазных и линейных токов.
.
Определить комплексы остальных
фазных и линейных токов. .
. 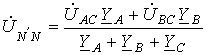 .
. 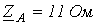 ;
;  ;
; 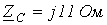 ;
;  .
Линейное напряжение равно 380 В.
.
Линейное напряжение равно 380 В. ;
;  .
Остальные параметры те же.
.
Остальные параметры те же.
 ;
; 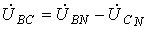 ;
; .
.
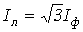 .
.  .
Определить комплексы остальных
фазных и линейных токов.
.
Определить комплексы остальных
фазных и линейных токов.