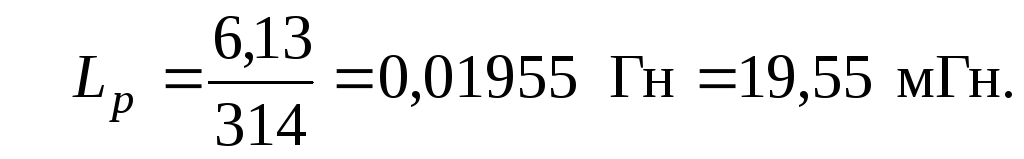3.2. Методика расчета трехфазных электрических цепей переменного тока
3.2.1. Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездой
В цепи, изображенной на схеме (рис. 3.1), потребители трехфазного тока соединены звездой.
Известно
линейное напряжение 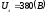 и сопротивления фаз:
и сопротивления фаз:
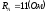 ,
, 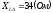 ,
,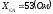 ,
, ,
, ,
, .
.
Определить
полные сопротивления фаз, фазные токи
и ток в нейтральном проводе, активную,
реактивную и полную мощности каждой
фазы и всей цепи.
Дано:  ,
, 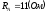 ,
, ,
,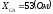 ,
, ,
,
 .
.Определить: 
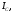
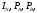


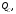

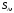
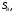


Рис. 3.1
Графоаналитический метод расчета
(расчет с применением векторных диаграмм)
При соединении звездой


Так
как есть нейтральный провод, то
Вычисляем сопротивление фаз и углы φ определяем по диаграммам сопротивлений.

 ;
;
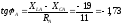
 -в
фазе А напряжение отстает от тока на
60°.
-в
фазе А напряжение отстает от тока на
60°.
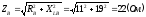 ;
;
 ;
;
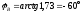 —
в фазе В напряжение опережает ток на
60°
—
в фазе В напряжение опережает ток на
60°
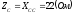 ;
;

Фазные токи можно определить следующим образом:
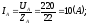
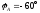 ;
;

 ;
;
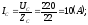

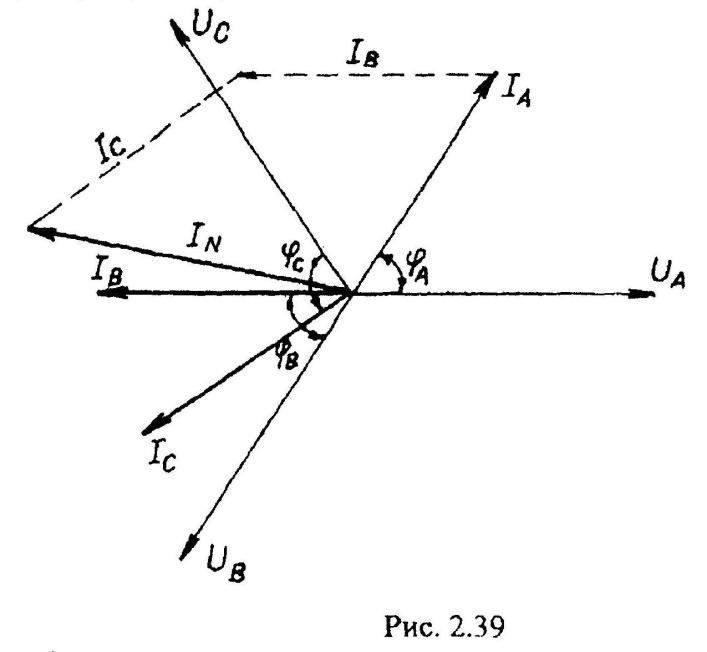
Чтобы вычислить ток в нейтральном проводе, нужно построить векторную диаграмму цепи.
На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины.
Векторы
фазных токов строятся в масштабе под
вычисленными углами φ по отношению к фазным напряжениям. В
фазе А нагрузка носит емкостный характер,
значит, ток  опережает напряжениена
угол
опережает напряжениена
угол .
.
В
фазе В нагрузка носит индуктивный характер,
следовательно, ток 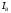
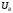 нa
угол
нa
угол 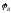 .
. В
фазе С нагрузка емкостная, следовательно, ток 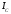 опережает напряжение
опережает напряжение на угол
на угол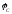 .
.
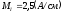 —
масштаб.
—
масштаб.



Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов: Рис. 3.2
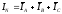
Измерив
длину вектора  ,
находим
ток
,
находим
ток

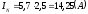
Определим активные мощности фаз:


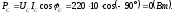
Активная мощность трехфазной цепи:

Определяем реактивные мощности фаз:
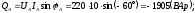


Реактивная мощность трехфазной цепи:
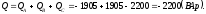
Вычисляем полную мощность каждой фазы и всей цепи:



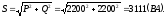
Символический метод расчета
Строгий аналитический расчет трехфазных цепей производится символическим методом, т. е. в комплексной форме.
Выразим в комплексной форме фазные напряжения:
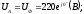
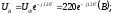

Выразим сопротивления фаз в комплексной форме:
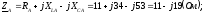
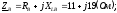
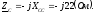
Переведем комплексные сопротивления фаз из алгебраической формы в показательную:

где 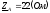 — полное сопротивление фазыА;
— полное сопротивление фазыА;
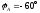 —
угол сдвига фаз между током и напряжением
в фазе А.
—
угол сдвига фаз между током и напряжением
в фазе А.
Аналогично определяем:

где  ,
, .
.
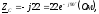
где 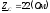 ,
,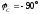 .
.
Находим комплексы фазных токов:

модуль 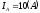 ,
аргумент
,
аргумент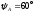 ,
,

модуль  ,
аргумент
,
аргумент ,
,
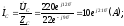
модуль 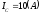 ,
аргумент
,
аргумент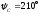 .
.
Находим алгебраическую форму записи комплексов фазных токов:


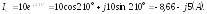
Вычисляем ток в нейтральном проводе:
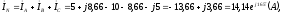
модуль  ,
аргумент
,
аргумент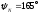 .
.
Вычисляем мощности фаз и всей цепи:
 где
где 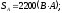


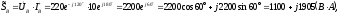 где
где 
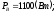
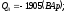
 где
где 


тогда

где 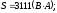


3.2.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником
В
цепи, изображенной на схеме (рис.
3.3),
потребители соединены треугольником.
Известно линейное напряжение  и сопротивления фаз
и сопротивления фаз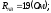



 .Определить
фазные, линейные токи, мощности активные,
реактивные, полные мощности каждой фазы
и всей цепи. Построить векторную диаграмму
цепи.
.Определить
фазные, линейные токи, мощности активные,
реактивные, полные мощности каждой фазы
и всей цепи. Построить векторную диаграмму
цепи.

Дано:  ,
,



 .
.
Определить:  ,
, ,
, ,
, ,
,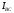 ,
, ,
,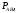


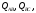

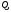
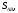


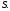
При соединении трехфазной цепи треугольником расчет будем вести
Рис. 3.3 символическим метолом.
Модули фазных напряжений при соединении треугольником равны линейным напряжениям
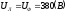 ,
то есть
,
то есть  .
.
Комплексы
данных напряжений запишем из условия,
что вектор 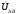 совмещен
с действительной осью комплексной
плоскости
совмещен
с действительной осью комплексной
плоскости


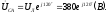
Вычислим комплексы фазных сопротивлений:

где 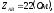
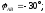

где 
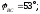

где 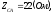
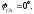
Определяем фазные токи:

модуль 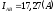 ,
, ;
;
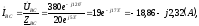
модуль  ,
,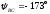 ;
;
модуль 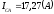 ,
, .
.
Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов В, А, С (рис. 3.3).
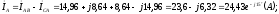
модуль 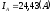 ,
аргумент
,
аргумент ;
;
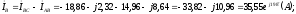
модуль 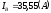 ,
аргумент
,
аргумент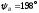 ;
;
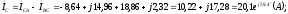
модуль  ,
аргумент
,
аргумент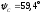 .
.
Вычисляем мощности каждой фазы и всей цепи:
 ,
,
где 
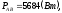
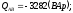
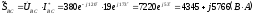 ,
,
где 

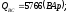
 ,
,
где 
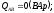
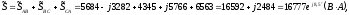 где
где 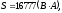

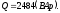
Строим в масштабе векторную диаграмму напряжений и токов.
Векторы
фазных токов 
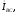
 строятся под углами
строятся под углами
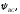
 к
действительной оси. К концам векторов
к
действительной оси. К концам векторов 

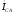 пристраиваются отрицательные фазные
токи согласно уравнениям:
пристраиваются отрицательные фазные
токи согласно уравнениям:
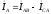 ;
;
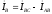 ;
;
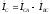 .
.
Замыкающие
векторные треугольники векторов 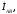
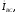
 представляют в выбранном масштабе
линейные токи.
представляют в выбранном масштабе
линейные токи.
Выбираем
масштаб: 
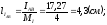


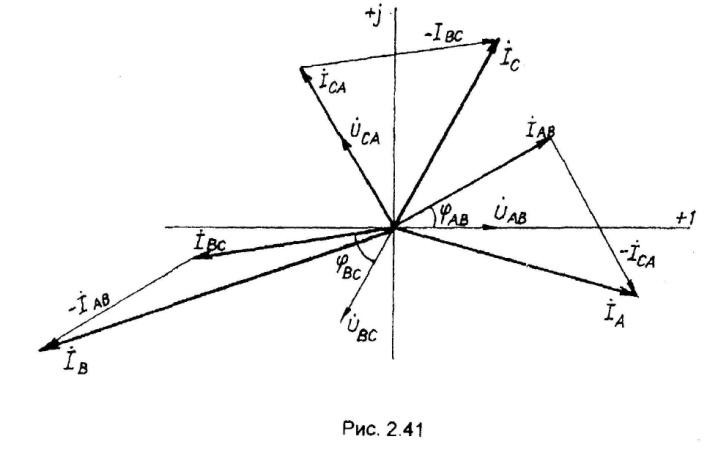
Рис. 3.4
Результаты расчетов занесем в соответствующие таблицы
Результаты расчета токов
Фазные и линейные токи | Алгебраическая форма, А | Показательная форма, А | Действующее значение, А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет трехфазных цепей (Лекция №17)
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если . В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: .
Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол . Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз можно записать
,
где определяется характером нагрузки .
Тогда на основании вышесказанного
;
.
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» .
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении необходимо определить линейные токи и в схеме на рис. 3, все сопротивления в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь , .
Тогда для тока можно записать
,
и соответственно .
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома
; ; .
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:
.
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b.
Тогда
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е. .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
.
Тогда для искомых токов можно записать:
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
| . | (1) |
При наличии нейтрального провода с нулевым сопротивлением , и из (1) . В случае отсутствия нейтрального провода . При симметричной нагрузке с учетом того, что , из (1) вытекает .
В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если .
Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, и . Тогда, поскольку при этом , соотношение (1) трансформируется в формулу
| . | (2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
- С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
- Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а ; ; ; . Линейное напряжение равно 380 В.
- В схеме предыдущей задачи ; . Остальные параметры те же.
- В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: .
Определить ток в нейтральном проводе.
Ответ: .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
Расчет трехфазных цепей
6. Расчёт трёхфазных цепей.
Многофазной системой электрических цепей называют совокупность электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе, создаваемые общими источником энергии (ГОСТ 19880-74).
Многофазной цепью называют многофазную систему электрических цепей в которой отдельные фазы электрически соединены друг с другом (ГОСТ 19880-74). В частности при числе фаз многофазной системы равной 3 будем иметь трехфазную цепь.
Различают
симметричную и несимметричную многофазную
систему. Симметричной
многофазной системой токов называют
многофазную
систему электрических токов в которой
отдельные электрические токи
равны по амплитуде и отстают по фазе
относительно друг друга на углы
равные 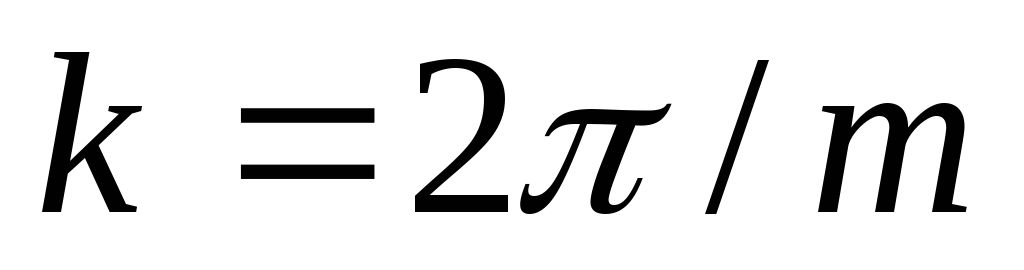 ,
где m – число фаз. (ГОСТ 19880-74).
,
где m – число фаз. (ГОСТ 19880-74).
Несимметричной многофазной системой электрических токов называют систему не удовлетворяющую любому из вышеуказанных признаков (ГОСТ 19880-74).
6.1. Трехфазная система ЭДС.
Под трёхфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе относительно друг друга на 120°.

 ,
, 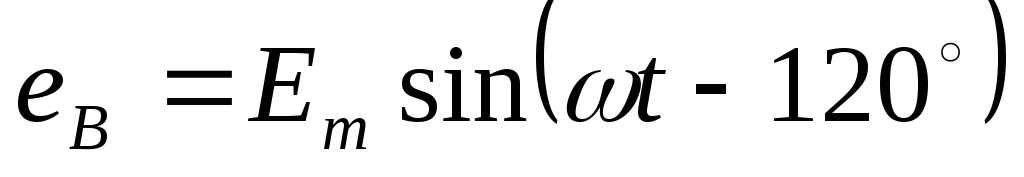 ,
, 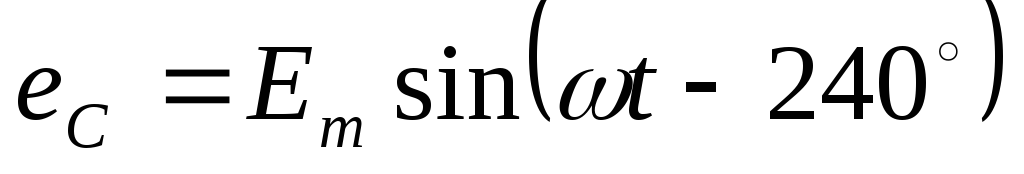 .
.
Соответственно, для действующих ЭДС в комплексной форме можно записать
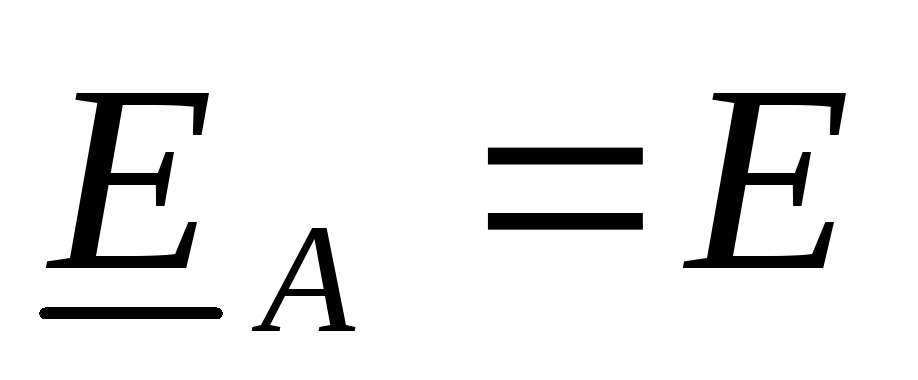 ,
,  ,
, 
и изобразить на комплексной плоскости

6.2. Общие положения и допущения при расчете трехфазных цепей.
Трехфазные цепи являются разновидностью цепей синусоидального тока и поэтому их расчет производится теми же методами и приёмами, которые присущи цепям однофазного синусоидального тока. Для анализа трехфазных цепей применим комплексный (символический) метод расчета, могут строиться векторные и топографические диаграммы.
Для анализа трехфазных цепей введем два допущения, которые сводятся к тому, что синусоидальное напряжение на зажимах трехфазного генератора симметричны при любой нагрузке:
система ЭДС трехфазного генератора, симметрична;
все источники ЭДС имеют бесконечно большую мощность.
6.3.Расчет соединения звезда-звезда с нулевым проводом.
П редположим
сейчас и в дальнейшем, что сопротивление
проводов, соединяющих источник с
нагрузкой, равно нулю. В этом случае в
схеме образуются три обособленных
контура. Токи в них
редположим
сейчас и в дальнейшем, что сопротивление
проводов, соединяющих источник с
нагрузкой, равно нулю. В этом случае в
схеме образуются три обособленных
контура. Токи в них
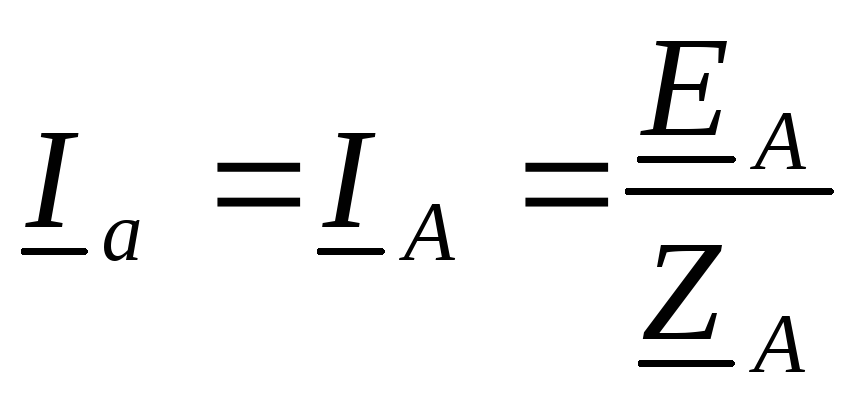 ,
, 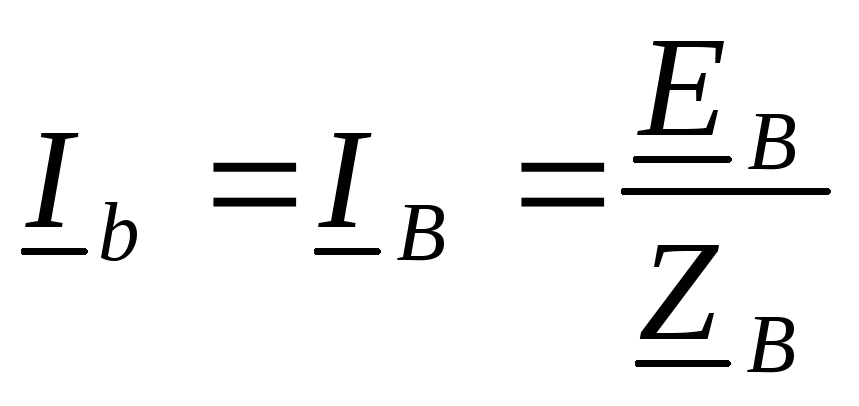 ,
,  ,
,
где  ,
, 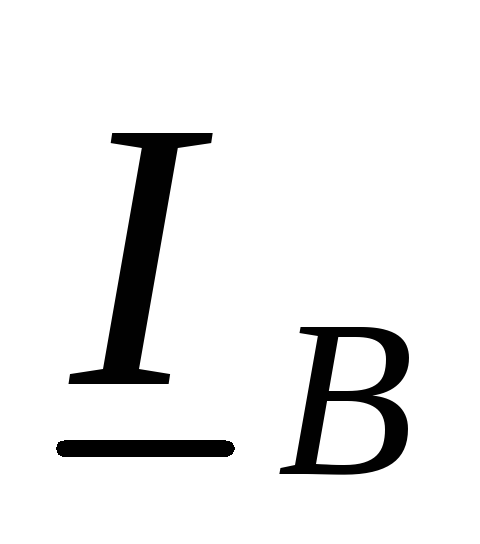 и
и  — линейные токи, а
— линейные токи, а  ,
,  и
и 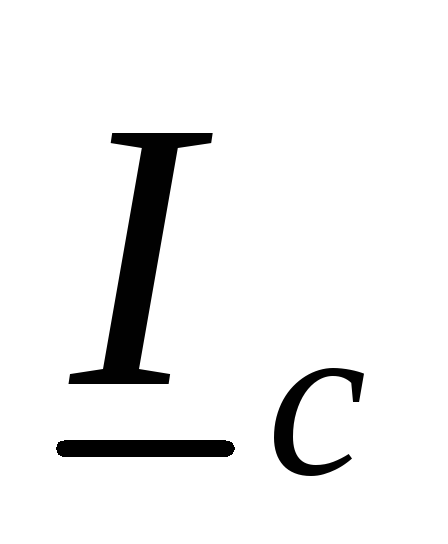 — фазные токи, токи в нагрузке,
соответственно, фазы a,
b,
c.
— фазные токи, токи в нагрузке,
соответственно, фазы a,
b,
c.
Ток
в нулевом проводе равен 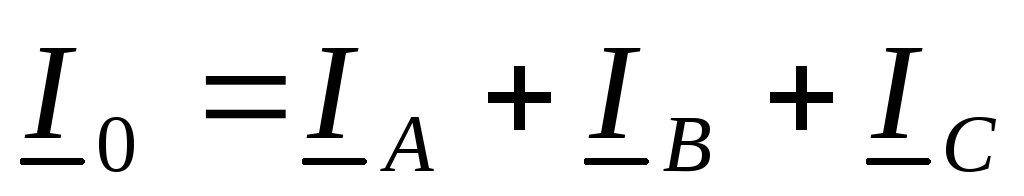 .
Напряжение между линейным проводом и
нулевым узлом
.
Напряжение между линейным проводом и
нулевым узлом 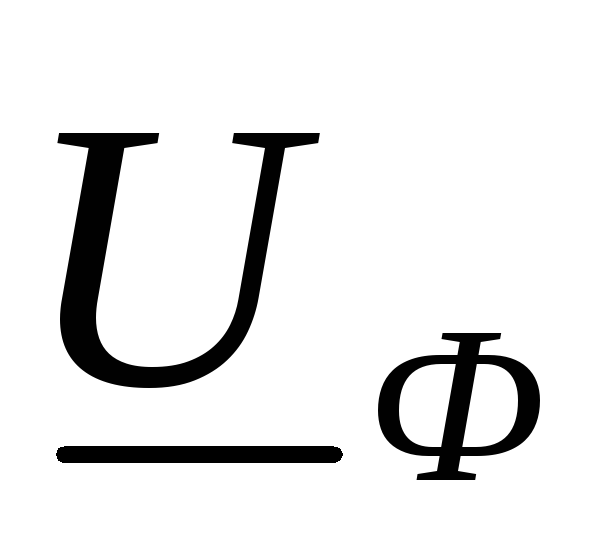 — фазное напряжение:
— фазное напряжение:  ,
,  и
и  .
Напряжение между линейными проводами
.
Напряжение между линейными проводами 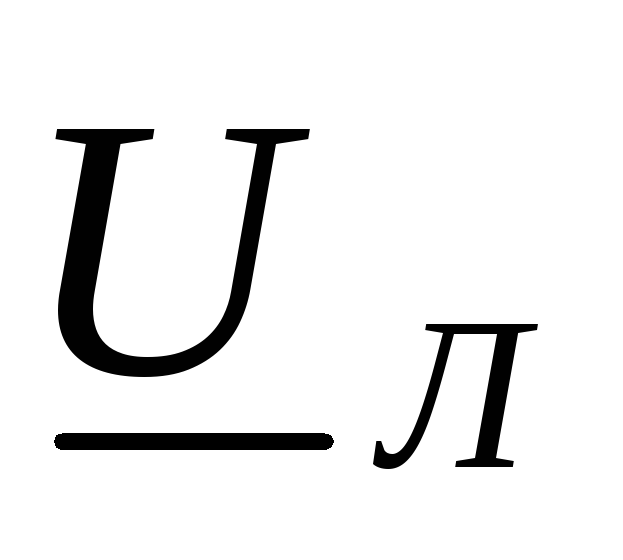 — линейное напряжение:
— линейное напряжение:  ,
,  и
и  .
.
При
соединении звезда-звезда с нулевым
проводом, справедливы следующие
соотношения для токов:  ,
,  и
и 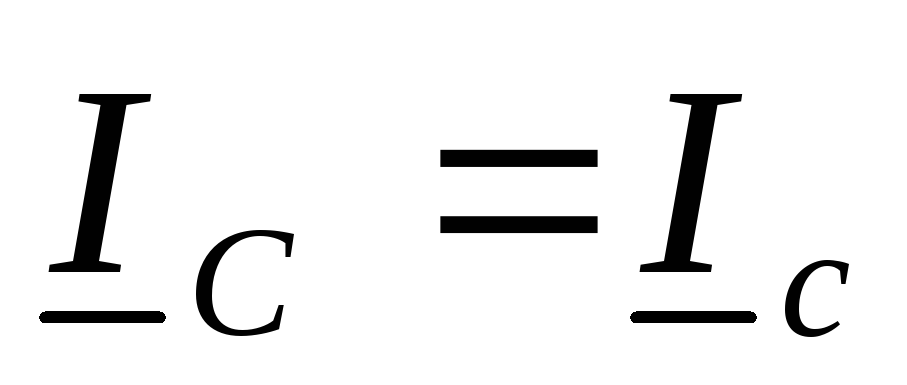 ;
или для модулей:
;
или для модулей:  ;
для напряжений:
;
для напряжений:  ,
,  ,
, 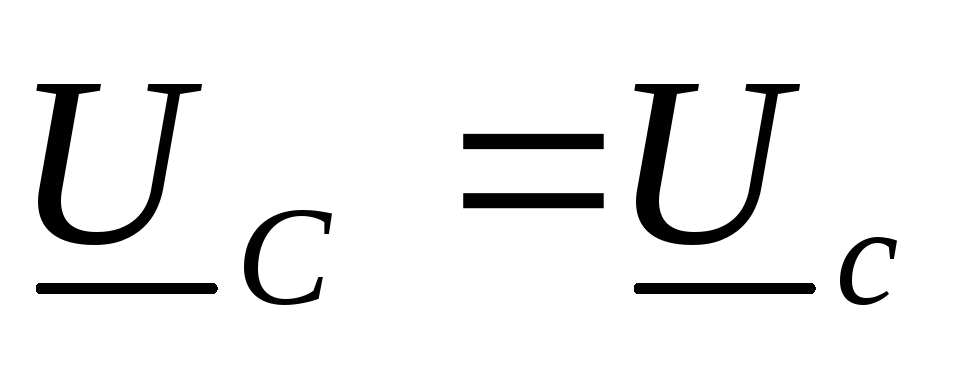 и
и  ,
,  ,
,  ;
или для модулей:
;
или для модулей: 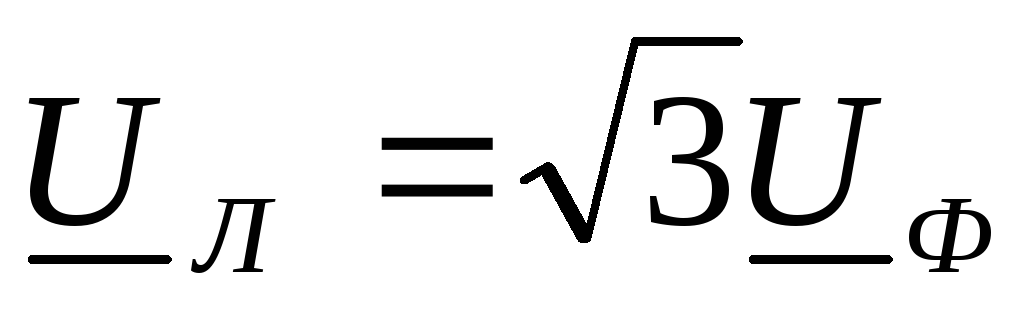 .
.
Симметричная цепь (нагрузка).
С имметричная
многофазная (трёхфазная) цепь
– это цепь, в которой комплексные
сопротивления, составляющих её фаз,
одинаковы (ГОСТ 19880-74). На рисунке представлена
векторная диаграмма напряжений на
источнике и нагрузке. Векторная диаграмма
токов построена для симметричной цепи
ак-тивного характера. При этом
имметричная
многофазная (трёхфазная) цепь
– это цепь, в которой комплексные
сопротивления, составляющих её фаз,
одинаковы (ГОСТ 19880-74). На рисунке представлена
векторная диаграмма напряжений на
источнике и нагрузке. Векторная диаграмма
токов построена для симметричной цепи
ак-тивного характера. При этом  и, следовательно, нулевой провод может
быть устранён из цепи без изме-нения
режима её работы. Аннало-гичная ситуация
наблюдается и для симметрич-ной цепи с
ак-тивно-реактивной нагрузкой, когда
и, следовательно, нулевой провод может
быть устранён из цепи без изме-нения
режима её работы. Аннало-гичная ситуация
наблюдается и для симметрич-ной цепи с
ак-тивно-реактивной нагрузкой, когда  .
.
Несимметричная цепь (нагрузка).
Если
нагрузка несимметрична, то есть  ,
то появляется ток в нулевом проводе:
,
то появляется ток в нулевом проводе: 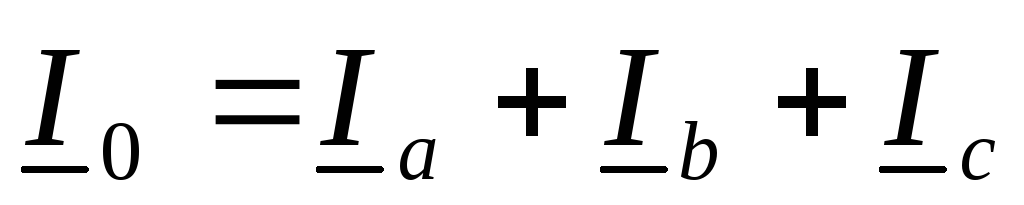 .
.
Как
это, например, показано на векторной
диаграмме, когда сопротивления фаз
равны по величине, но имеют различный
характер: в фазе  — активная нагрузка, в фазе
— активная нагрузка, в фазе  — индуктивная нагрузка, а в фазе
— индуктивная нагрузка, а в фазе  — емкостная нагрузка.
— емкостная нагрузка.

6.4. Расчет соединения звезда-звезда без нулевого провода.
Симметричная цепь (нагрузка).
В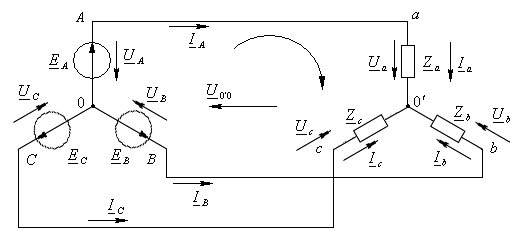 случае симметричной цепи расчет токов
в фазах нагрузки сводится к расчету
соединения звезда-звезда с нулевым
проводом, как это было показано в пункте
6.3.
случае симметричной цепи расчет токов
в фазах нагрузки сводится к расчету
соединения звезда-звезда с нулевым
проводом, как это было показано в пункте
6.3.
 ,
, 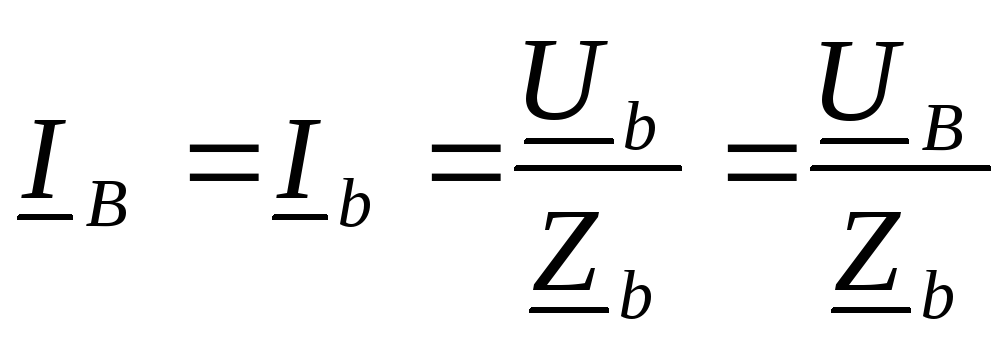 ,
,  .
.
Несимметричная нагрузка.
В случае несимметричной
цепи напряжение на фазе нагрузки не
равно соответствующему напряжению
источника. Для определения искомого
тока  ,
,  и
и  необходимо отыскать фазное напряжение
на нагрузке.
необходимо отыскать фазное напряжение
на нагрузке.
Для этого следует
записать уравнение по второму закону
Кирхгофа для контуров, образованных
источником ЭДС, сопротивлением нагрузки
и напряжением холостого хода между
узлами  :
,
откуда
:
,
откуда 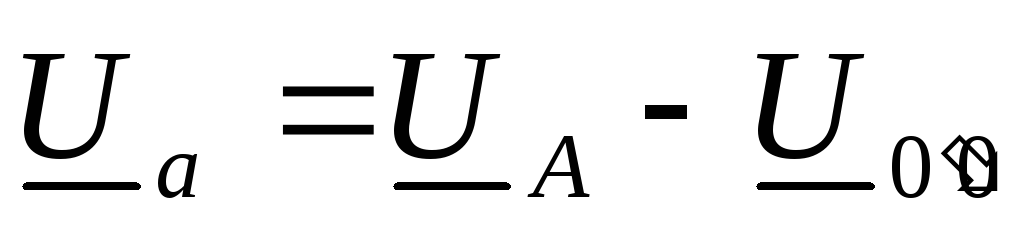 .
.
О пределение
пределение 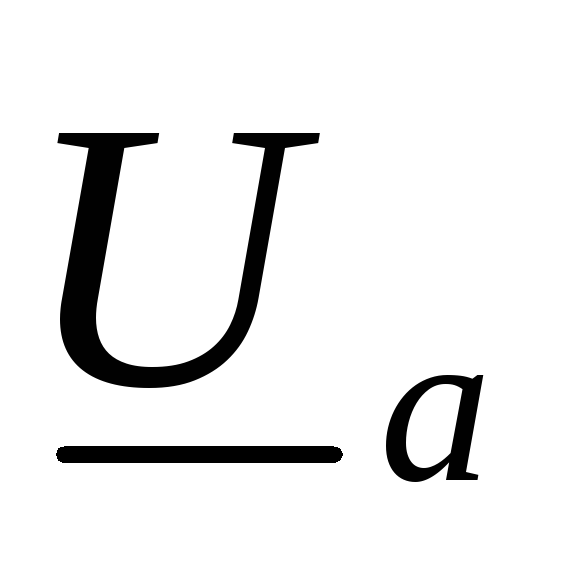 ,
,  и
и  в
последних трёх выражениях возможно в
случае, когда известно
в
последних трёх выражениях возможно в
случае, когда известно  — напряжение смещения нейтрали.
— напряжение смещения нейтрали.
Напряжение смещения
нейтрали можно определить по методу
двух узлов, представляя 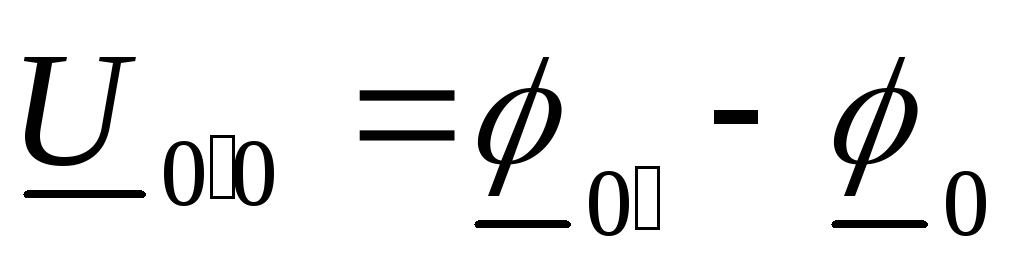 или
или  при условии, что потенциал узла
при условии, что потенциал узла  принять равным нулю,
принять равным нулю,
тогда: 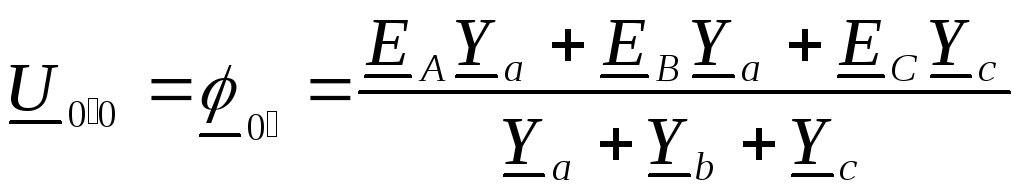 .
.
Если по условию проектирования нулевой провод обладает некоторой проводимостью, то последнее выражение можно переписать в виде:
 .
.
При этом расчете
было предположено, что сопротивления
фазных обмоток генератора и сопротивления
линейных проводов равны нулю. Если эти
условия не соблюдаются, то эти сопротивления
могут быть учтены путем их введения в
сопротивления соответствующих фаз  ,
,  и
и  .
При отсутствии сопротивлений обмоток
генератора их ЭДС равны фазным напряжениям
на его зажимах
.
При отсутствии сопротивлений обмоток
генератора их ЭДС равны фазным напряжениям
на его зажимах  ,
, 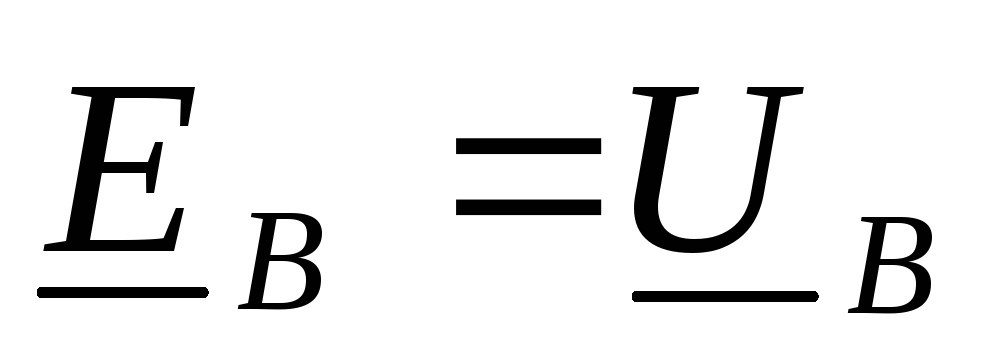 ,
, 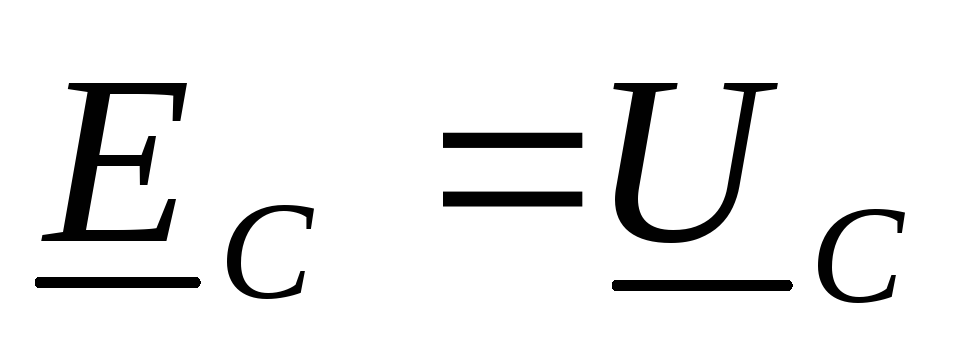 и
тогда полученную формулу для определения
смещения нейтрали можно записать в
виде:
и
тогда полученную формулу для определения
смещения нейтрали можно записать в
виде:
 .
.
6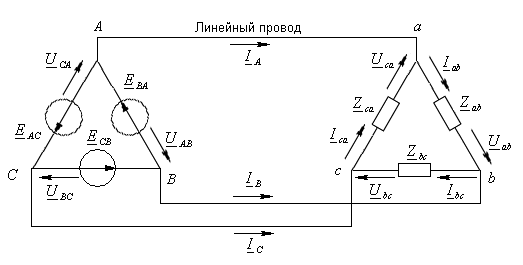 .5.
Расчет соединения треугольник-треугольник.
.5.
Расчет соединения треугольник-треугольник.
Пусть сопротивление
фазных обмоток генератора и сопротивления
линейных проводов равны нулю, тогда:  ,
, 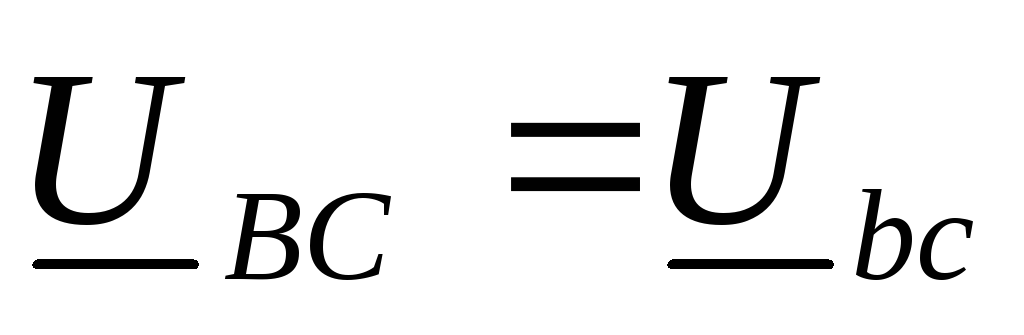 ,
,  .
.
Ток в фазах нагрузки – фазный ток:
 ,
,  ,
, 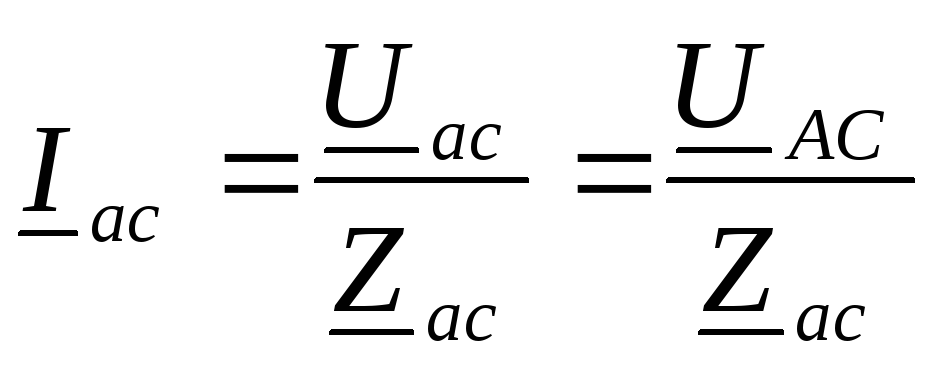 .
.
Линейные токи в общем случае, то есть для несимметричной цепи можно определить по первому закону Кирхгофа:
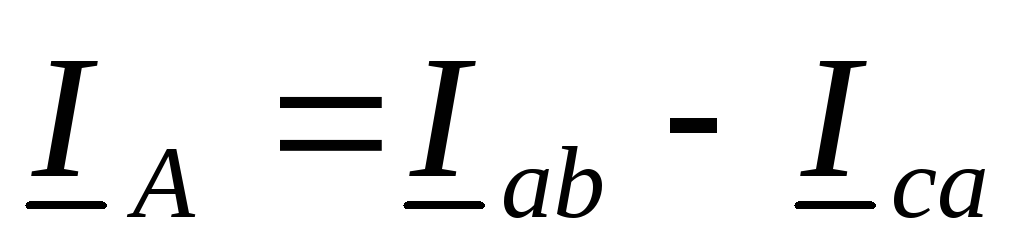 ,
,  ,
,  .
.
Для симметричной
цепи линейные токи в  раз больше фазных токов.
раз больше фазных токов.
6.6. Активная, реактивная и полная мощности трёхфазной цепи.
Под активной и
реактивной мощностями понимают:  и
и  .
Полная мощность:
.
Полная мощность: 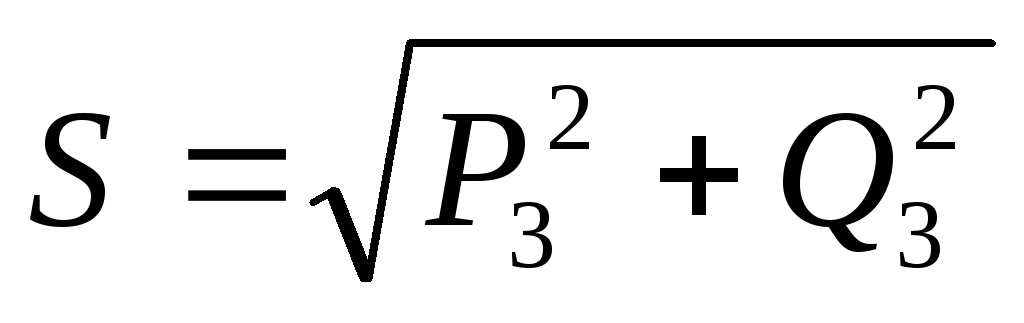 .
.
Если нагрузка
симметричная, то  ,
,  ,
,  и тогда мощность трёхфазной цепи, через
фазные токи и напряжения:
и тогда мощность трёхфазной цепи, через
фазные токи и напряжения:  ,
, 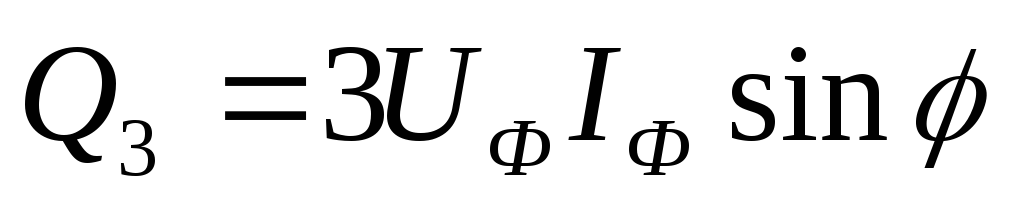 ,
,  или через линейные токи и напряжения
независимо от способа её соединения в
звезду или треугольник
или через линейные токи и напряжения
независимо от способа её соединения в
звезду или треугольник  ,
,  и
и 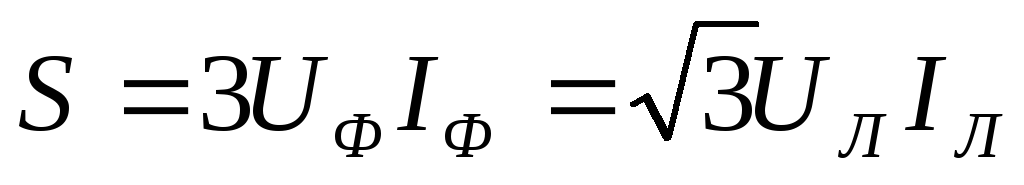 .
.
6.7. Измерение активной мощности в трёхфазной цепи.
Метод трёх ваттметров используют для измерения активной мощности трёхфазной цепи в случае несимметричной нагрузки. Активная мощность всей цепи равна сумме показаний всех ваттметров.
П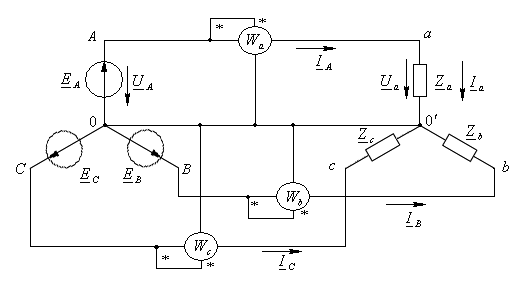 ри
симметричной нагрузке достаточно
измерить мощность одной из фаз и результат
утроить – это, так называемый, метод
одного ваттметра.
ри
симметричной нагрузке достаточно
измерить мощность одной из фаз и результат
утроить – это, так называемый, метод
одного ваттметра.
В случае, если узел 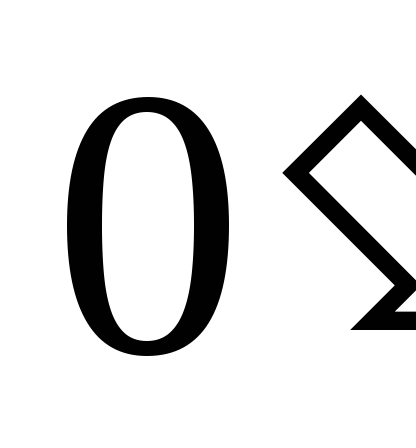 недоступен, то измерение мощности можно
произвести двумя ваттметрами.
недоступен, то измерение мощности можно
произвести двумя ваттметрами.

 и
и 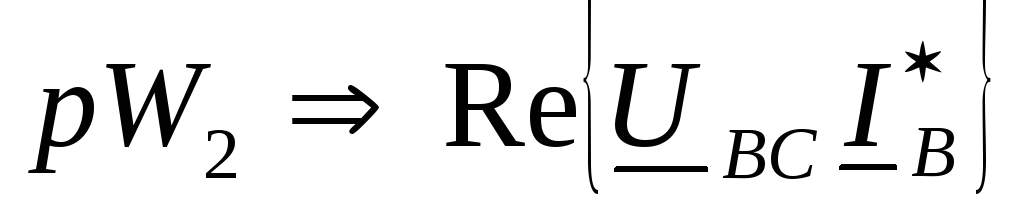 .
.
Докажем, что сумма показаний двух ваттметров представляет собой активную мощность трехфазной цепи.
Составим уравнение
по второму закону Кирхгофа для контура,
образованного фазными напряжениями  и
и 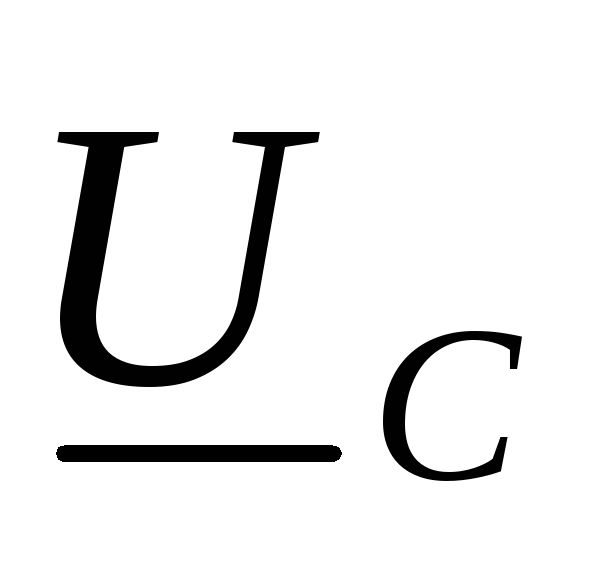 и линейным напряжением
и линейным напряжением 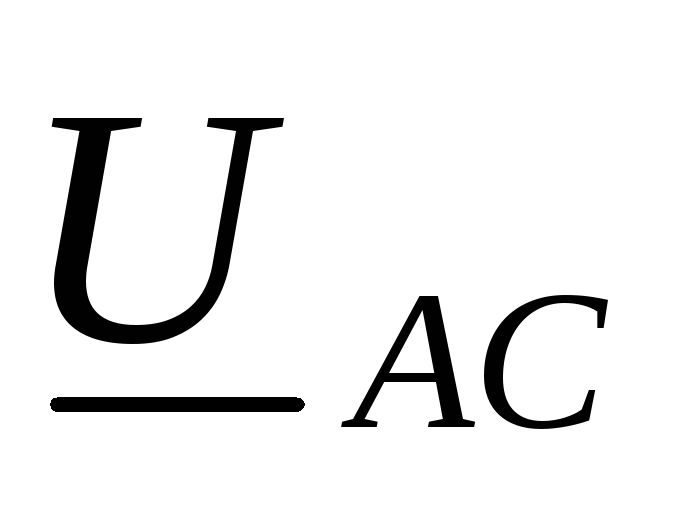 :
:  ,
откуда
,
откуда 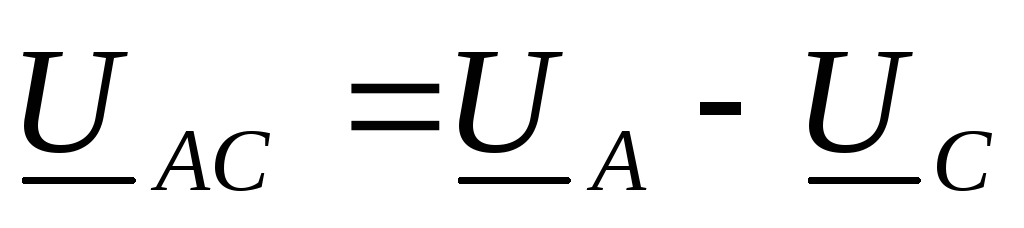 ;
аналогично
;
аналогично  .
.
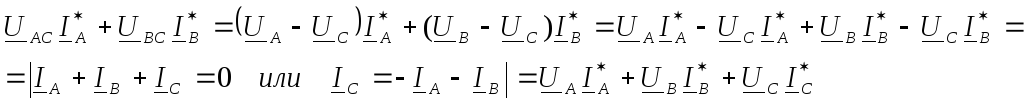
Сумма реальных частей каждого слагаемого соответствует активной мощности трехфазной цепи.
1. Расчет трехфазной цепи при соединении потребителей звездой.
Так как в схеме есть нейтральный провод, то напряжение на фазах нагрузки равно соответствующему фазному напряжению источника питания (обмотки генератора считаем соединенными звездой, а сопротивлением нейтрального провода пренебрегаем):
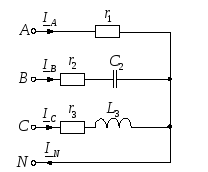
Рисунок 9 – Схема трёхфазной цепи при соединении потребителей звездой
 ,
,  ,
,  ;
;
в численном виде:
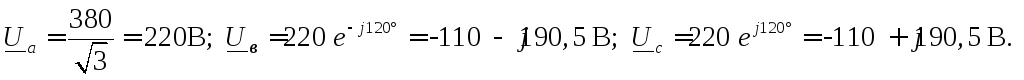
Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
ω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с .
Реактивное индуктивное сопротивление
xL3 = ω L3 = 314 ∙ 31,8 ∙ 10–3 = 10 Ом.
Реактивное емкостное сопротивление
xС2 =1/(ω С2) = 1/(314 ∙ 159 ∙ 10–6) = 20 Ом.
В общем случае полное сопротивление каждой из фаз в комплексной форме определяют с помощью выражения, которое использовалось в однофазных цепях,
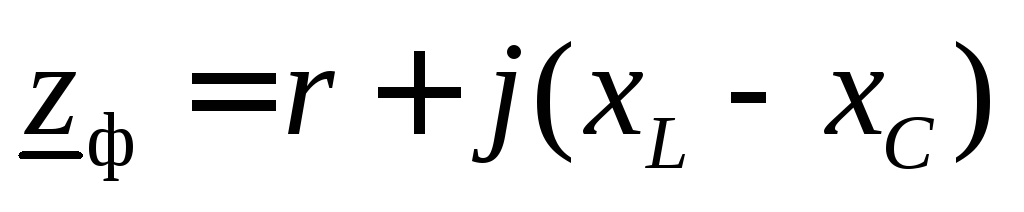 .
.
Применяем эту формулу для нашего конкретного случая и получаем полные сопротивления фаз в следующем виде:

Комплексные сопротивления фаз различны, следовательно, нагрузка несимметричная.
Токи в линейных проводах (фазные токи нагрузки) определяем с помощью закона Ома:
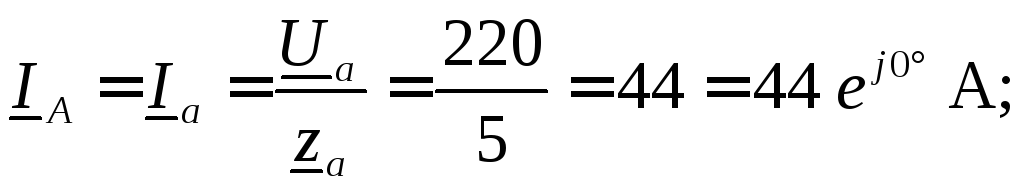


Ток в нейтральном проводе находим по первому закону Кирхгофа

Полные мощности фаз:


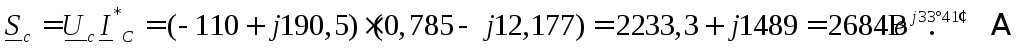
Так как вещественная часть полной мощности есть активная мощность цепи, а мнимая часть – реактивная, то, просуммировав отдельно вещественные, а затем мнимые части мощностей трех фаз, определяем трехфазную активную и реактивную мощности.
Активная трехфазная мощность

Реактивная трехфазная мощность

Полная мощность
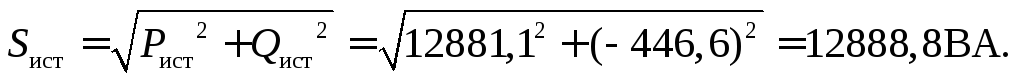
Активная трехфазная мощность нагрузки может быть определена суммой активных мощностей потребителей каждой из фаз
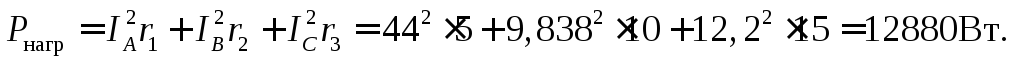
Относительная ошибка вычислений для активной мощности

Реактивная трехфазная мощность нагрузки также определяется суммой реактивных мощностей потребителей каждой из фаз
Суммарная реактивная мощность всех потребителей

Относительная ошибка вычислений для активной мощности

Ошибка менее одного процента допускается. Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно.
Векторную диаграмму размещаем на комплексной плоскости с осями +1 и + j, рисунок 3.21. Выбираем масштаб векторов тока равным 10 А/деление, а векторов напряжения – 40 В/деление. Строим векторы фазных напряжений, а затем векторы токов. Длина вектора соответствует в масштабе модулю показательной формы соответствующего выражения тока или напряжения, а угол, под которым этот вектор строится к вещественной оси, равен аргументу комплексного значения величины.
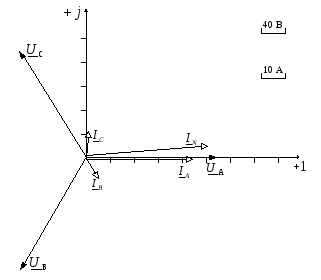
Рисунок 10 – Векторная диаграмма при соединении
потребителей звездой с нейтральным проводом
2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем схему трёхфазной цепи, причем элементы из фазы A, B, C соединения потребителей звездой подключим соответственно между точками ab, bc, ca при соединении потребителей треугольником (рисунок 11).
В комплексной форме записи линейные напряжения на нагрузке:



Рисунок 11 – Схема трёхфазной цепи при соединении потребителей
треугольником
Сопротивления фаз нагрузки в комплексной форме:
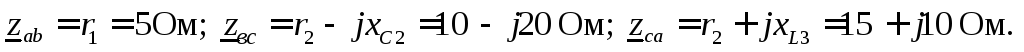
Фазные токи определяем по закону Ома:
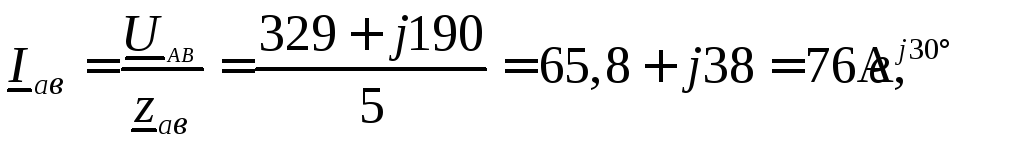


Для определения линейных токов используем первый закон Кирхгофа для точек a,в,cсхемы (рисунок 11)
 А,
А,
 А,
А,
 А.
А.
Полные комплексные мощности



Трехфазная активная мощность
 Вт.
Вт.
Трехфазная реактивная мощность
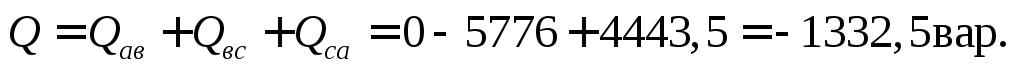
Трехфазная полная мощность
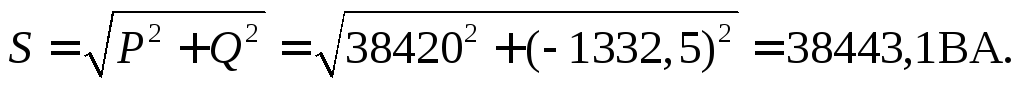
Векторную диаграмму токов для нагрузки, соединенной треугольником,строим в масштабе на комплексной плоскости относительно осей +1 и + j (рисунок12).На векторной диаграмме линейные токи получены на основании первого закона Кирхгофа, путем вычитания одного вектора фазного тока из соответствующего другого.
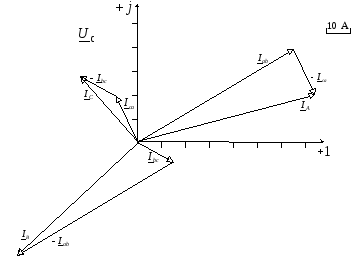
Рисунок 12 – Векторная диаграмма токов для
нагрузки, соединённой треугольником
ЗАДАЧА 1
РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА
Для цепи, изображенной на рисунке 13, известны ЭДС Е1, Е2 и внутренние сопротивления r01, r02 источников питания, а также сопротивления r1–r6. Необходимо:
1. Составить систему уравнений для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи ветвей методом контурных токов.
3. Составить баланс мощностей.
4. Построить потенциальную диаграмму для контура, включающего две ЭДС.
Значения параметров элементов цепи приведены в таблице 1. Теоретический материал и пример расчета даны во втором разделе пособия, а также в учебниках [1 – 4, 10].
Таблица 1 – Числовые значения исходных данных к задаче № 3
Вариант
E1
E2
r01
r02
r1
r2
r3
r4
r5
r6
B
Ом
1
2
3
4
5
6
7
8
9
0
27
12
127
127
36
220
127
220
127
36
12
127
110
12
127
36
220
380
36
220
0,1
0,3
0,1
0,4
0,5
0,3
0,6
0,5
0,7
1,8
0,8
0,6
1,0
1,2
0,7
0,8
1,2
1,5
1,2
2,8
5
3
9
4
6
6
7
9
5
9
3
8
4
7
3
8
4
3
3
6
7
5
5
2
9
3
1
6
7
3
6
3
5
2
3
6
2
5
5
8
3
4
6
4
5
4
5
3
8
6
7
5
7
5
3
6
8
8
9
3
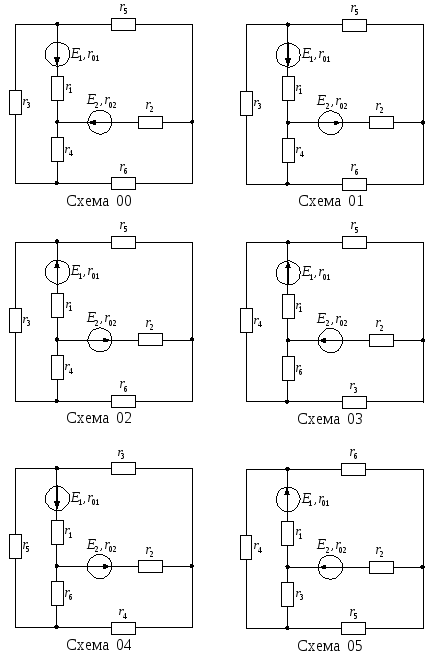
Рисунок 13 – Варианты электрических цепей к задаче № 1

Продолжение рисунка 13

Продолжение рисунка 13

Продолжение рисунка 13

Продолжение рисунка 13
Продолжение рисунка 13
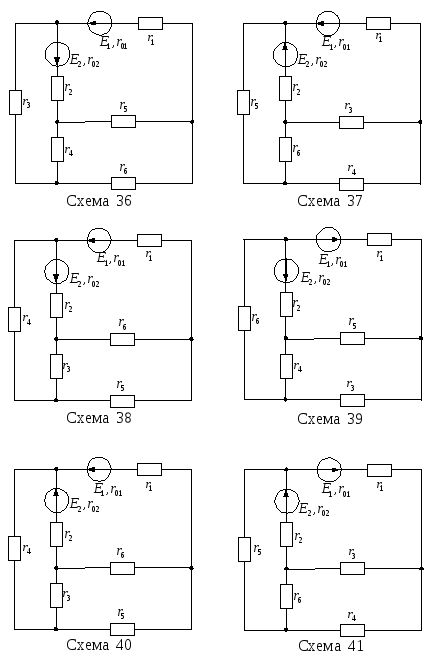
Продолжение рисунка 13
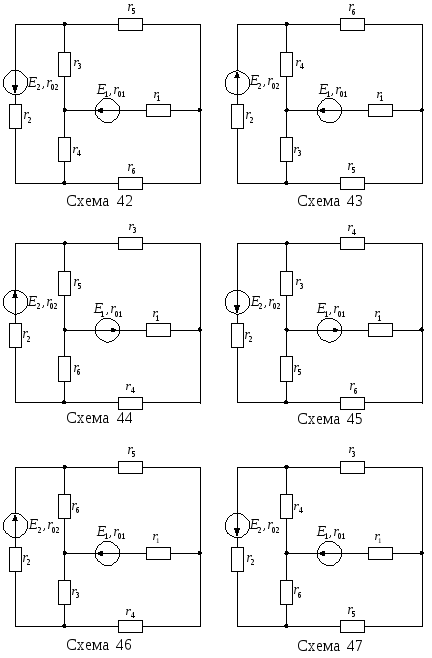
Продолжение рисунка 13

Продолжение рисунка 13
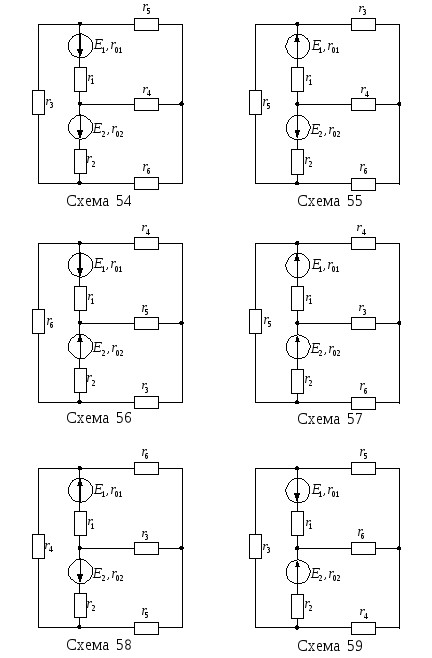
Продолжение рисунка 13
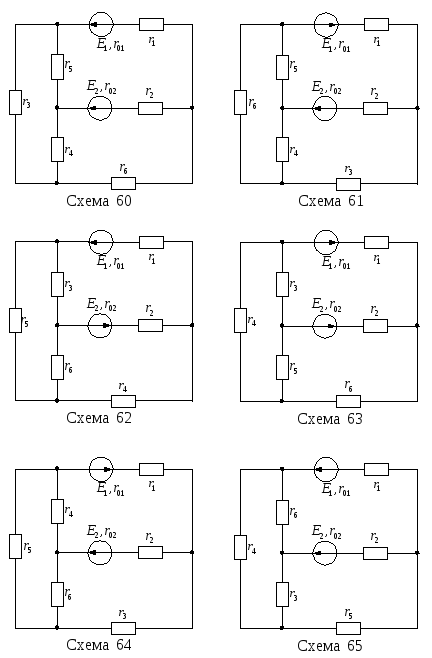
Продолжение рисунка 13
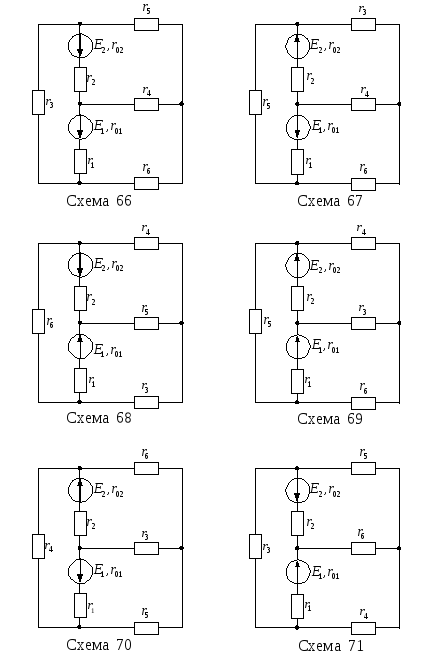
Продолжение рисунка 13
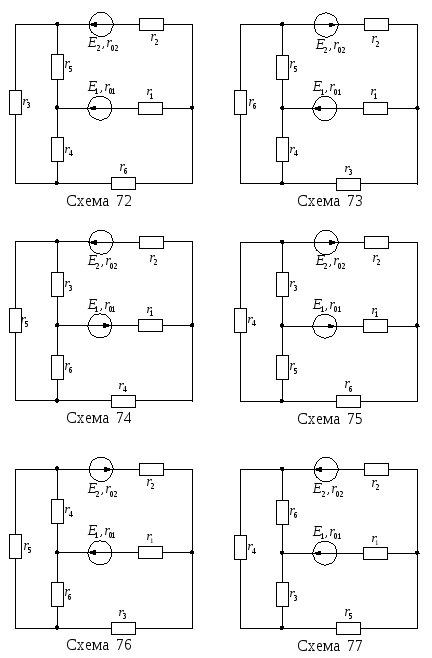
Продолжение рисунка 13
Продолжение рисунка 13
 Продолжение рисунка
13
Продолжение рисунка
13

Продолжение рисунка 13

Продолжение рисунка 13
Расчет трехфазных цепей
Расчет трехфазных трехпроводных электрических цепей в несимметричном режиме производится комплексным методом, так как в этом режиме токи и напряжения фаз не равны между собой и основные соотношения между линейными и фазными величинами не выполняются.
Пример расчета трехфазной цепи при соединении нагрузки звездой:
Заданна схема трехфазной трехпроводной цепи (рис. 2.7), с соединением нагрузки звездой и сопротивления фаз нагрузки:
|
|
|
|
|
|
50 | 60 | 100 | 100 | 50 | 50 |
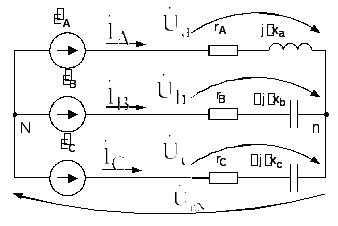
Рис. 2.7. Схема трехфазной цепи с нагрузкой, соединенной звездой
Нагрузка
несимметричная, ЭДС трехфазного
идеального источника равны:  В,
В, ,
,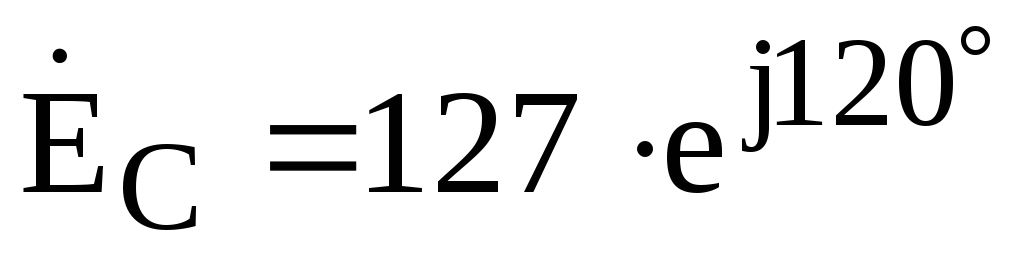 В.
В.
По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, напряжение смещения нейтрали, активную, реактивную, полную мощность.
Решение:
В
несимметричном режиме работы трехпроводной
трехфазной цепи, с нагрузкой, соединенной
звездой, возникает напряжение смещения
нейтрали  .
Величину этого напряжения можно
определить по методу двух узлов. При
известных комплексных сопротивлениях
и проводимостях фаз нагрузки:
.
Величину этого напряжения можно
определить по методу двух узлов. При
известных комплексных сопротивлениях
и проводимостях фаз нагрузки:
 См,
См,
 Ом;
Ом;
 См;
См;
 Ом;
Ом;
 См;
См;
 Ом.
Ом.
Напряжение смещения нейтрали определяется по формуле:

Фазные напряжения на нагрузке в несимметричном режиме определяются по второму закону Кирхгофа:
 В;
В;


Фазные токи нагрузки равны линейным токам и определяются по формулам:
 А;
А;
 А;
А;
 А.
А.
Сумма фазных токов, по первому закону Кирхгофа, должна быть равна нулю:
 .
.
Комплекс полной мощности трехфазной нагрузки, соединенной звездой:
 где:
где: — сопряженные комплексы фазных токов.
— сопряженные комплексы фазных токов.
Активная мощность Р = 476.426 Вт, а реактивная мощность Q= 59.553 ВА.
Пример расчета трехфазной цепи при соединении нагрузки треугольником:
Заданна схема трехфазной трехпроводной цепи (рис. 2.8), с соединением нагрузки треугольником и сопротивления фаз нагрузки:
|
|
|
|
|
|
100 | 50 | 100 | 200 | 150 | 300 |
Нагрузка
несимметричная, ЭДС трехфазного
идеального источника равны: 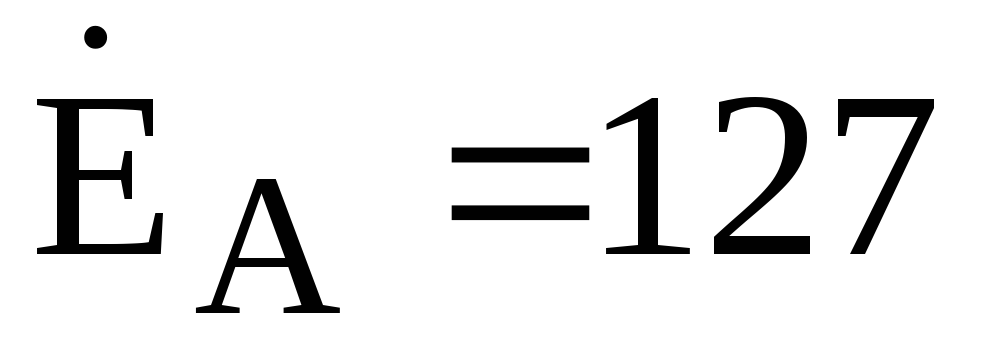 В,
В, ,
,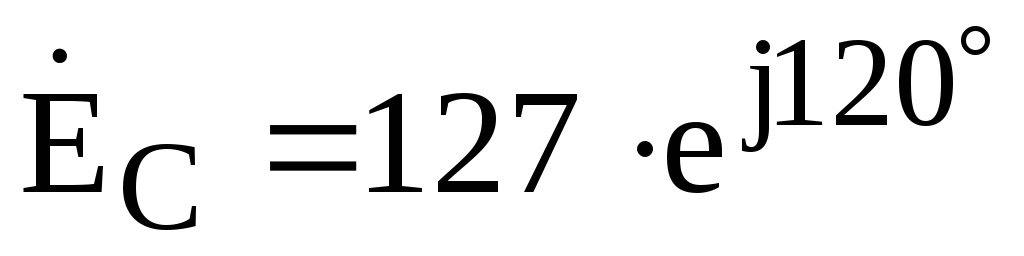 В.
В.
По заданным значениям активных и реактивных сопротивлений фаз нагрузки определить: фазные токи и напряжения на нагрузке, фазные напряжения на нагрузке, активную, реактивную, полную мощность.

Рис. 2.8. Схема трехфазной цепи при соединении нагрузки треугольником
Решение:
В несимметричном режиме работы трехпроводной трехфазной цепи, с нагрузкой, соединенной треугольником, фазные напряжения на нагрузке равны линейным напряжениям источника питания. Величины этих напряжений можно определить по второму закону Кирхгофа:
 В;
В;
 В;
В;
 В.
В.
При известных комплексных сопротивлениях фаз нагрузки:
 Ом;
Ом;
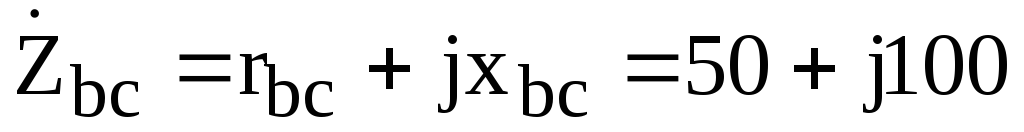 Ом;
Ом;
 Ом.
Ом.
Фазные токи рассчитываются по закону Ома:
 А;
А;
 А;
А;
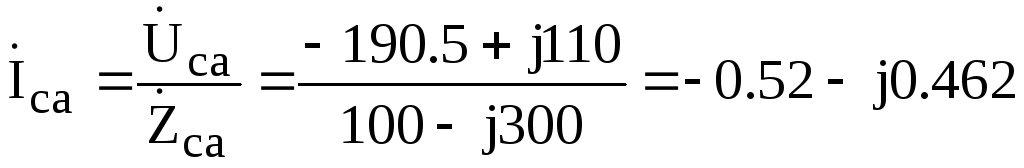 А.
А.
Линейные токи определяются по первому закону Кирхгофа:
 А;
А;
 А;
А;
 А.
А.
Сумма
линейных токов, по первому закону
Кирхгофа, должна быть равна нулю:  .
.
Комплекс полной мощности трехфазной нагрузки, соединенной треугольником:

где:  — сопряженные комплексы фазных токов.
— сопряженные комплексы фазных токов.
Активная мощность Р = 338.709 Вт, а реактивная мощность Q= 435.483 ВА.
3 расчет трехфазной цепи
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УО «МИНСКИЙ ГОСУДАСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ »
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Методические указания
по выполнению курсового проекта по теме
«Трехфазные электрические цепи»
для учащихся заочной формы обучения
для специальностей
2-36 03 31-01 «Монтаж и эксплуатация электрооборудования»
(производственная деятельность)
2-37 01 05 «Городской электрический транспорт»
Разработчики Т.С. Шмакова
Р. П.Скойбеда
Рецензент
Методические указания рассмотрены и рекомендованы для внедрения в учебный процесс на: заседании цикловой комиссии электротехнических дисциплин
Протокол № _____ от «____»______________2011 г.
Председатель комиссии Т.С.Шмакова
-заседании экспертного методического совета Заседание №_____ от «____»______________2
2011
1 Расчет трехфазной цепи переменного тока при соединении фаз приемника треугольником
Для данных приведенных в таблице 1 выполнить следующее:
Рассчитать сопротивления элементов схемы замещения приемников;
Начертить схему включения приемников в трехфазную сеть.
Определить фазные и линейные токи каждого приемника;
Рассчитать мощности;
Построить векторную топографическую диаграмму.
Таблица1- Исходные данные
Приемники | Номинальные данные | ||||
Uном В | Рном, кВт | Qном, квар | cosφ | Род нагрузки | |
№1 | 127 | 6 | 0,6 | индукт. | |
№2 | 127 | 10 | 0,8 | емкость | |
№3 | 127 | 5 | 0 | индукт. | |
Линейное напряжение сети Uл=127В.
1.1 Расчет сопротивлений элементов схемы, замещения приемников
Полное сопротивление Z, Ом, однофазного приемника определяется по формуле.
| (1) |
| (2) |
где Uном— номинальное напряжение, В;
Pном— номинальная активная мощность, Вт;
Qном— номинальная реактивная мощность, вар.
Активное сопротивление R, Ом, определяется по формуле
| (3) |
Реактивное сопротивление Х, Ом, определяется по формуле
| (4) |
Комплексное сопротивление определяется по формуле
| (5) |
Таким образом, для однофазных приемников:
№1


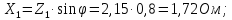

№2

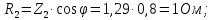

 ,так как род нагрузки
емкостный.
,так как род нагрузки
емкостный.

№3
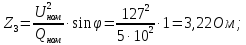
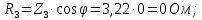


сosφ=0, следовательно Pном=0.
1.2 Чертим схему включения приемников в трехфазную сеть.

Рисунок 1. Схема включения
1.3 Определяем фазные и линейные токи
Комплексные действующие значения фазных напряжений



Находим фазные токи
|
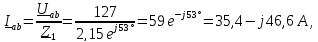


Действующие значения токов в фазах
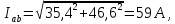


Находим линейные токи
|
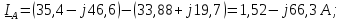
|
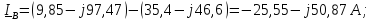
|
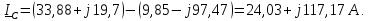
Действующие значения токов в линии



1.4 Определяем активную, реактивную и полную мощности
Активная мощность
| |
Где |
где
|

|

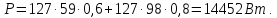
Реактивная мощность
|
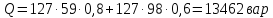
Полная мощность S рассчитывается по формуле.
|

1.5 Построение векторной топографической диаграммы токов и напряжений.
Зададим масштаб: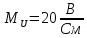 ;
; .
.

Рисунок 2. Топографическая векторная диаграмма токов и напряжений.
2 Расчет трехфазной цепи переменного тока при соединении фаз приемника звездой
Для данных приведенных в таблице 2 выполнить следующее:
1. Рассчитать сопротивления элементов схемы замещения приемников;
2.Начертить схему включения приемников в трехфазную сеть;
3.Определить фазные и линейные токи каждого приемника;
4.Рассчитать мощности;
5.Построить векторную топографическую диаграмму.
Таблица 2- Исходные данные
Приемники | Номинальные данные | ||||
Uном В | Рном, кВт | Qном, квар | cosφ | Род нагрузки | |
№1 | 127 | 10 | 0 | 1 | |
№2 | 127 | 0 | 10 | 0 | емкость |
№3 | 127 | 0 | 10 | 0 | индукт. |
Линейное напряжение сети Uл=220В.
2.1 Расчет сопротивлений элементов схемы, замещения приемников
Полное сопротивление Z, Ом, однофазного приемника определяется по формуле.
| (1) |
| (2) |
где
Uном— номинальное напряжение, В;
Pном— номинальная активная мощность, Вт;
Qном— номинальная реактивная мощность, вар.
Активное сопротивление R, Ом, определяется по формуле
| (3) |
Реактивное сопротивление Х, Ом, определяется по формуле
| (4) |
Комплексное сопротивление определяется по формуле
| (5) |
Таким образом, для однофазных приемников:
№1

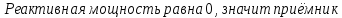 активный,
активный,
cosφ=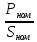 =
=
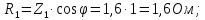


№2
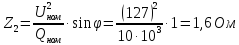

cos ,
,
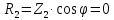


№3

 (
(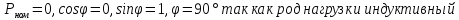


 Ом.
Ом.
2.2 Чертим схему включения приемников в трехфазную сеть
Так как по условию задачи:


то для включения приёмников используется соединение звездой риунок-3. А поскольку приёмники не симметричны
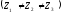
,то необходим нейтральный провод, который обеспечивает равенство по величине фазных напряжений приёмников:


Рисунок3. Схема включения приёмников звездой.
2.3 Определяем фазные, линейные токи каждого приёмника и ток в нулевом проводе
Запишем
комплексные значение фазных напряжений
сети, совместив вектор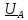 c
осью действительных величин.
c
осью действительных величин.
 ;
;
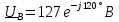 ;
;
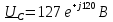 .
.
Тогда линейные напряжения сети запишем в виде
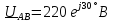 ;
;

 .
.
Фазные токи однофазных приёмников
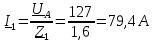 ;4
;4

 ;
;

Ток нейтрального провода
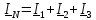

2.4 Определяем активную, реактивную и полную мощности
Активная мощность
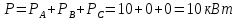
Реактивная мощность

Полная мощность
 =
=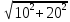 =22
∙
=22
∙ 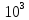 ВA
ВA
2.5 Построение векторной топографической диаграммы токов и напряжений
Для построения векторной топографической диаграммы выбираем масштаб по току и напряжению
 ;
; .
.
Векторы фазных
напряжений  ,,
,,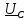 размещаем на комплексной
размещаем на комплексной
плоскости. Векторы
токов 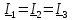 откладываем от начала координат
откладываем от начала координат
комплексной
плоскости в соответствии с расчётными
значениями. Вектор  совпадает с
совпадает с  ,
так как приёмник №1-активный. Вектор
,
так как приёмник №1-активный. Вектор  опережает
опережает  на
на 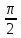 , так как приёмник №2-ёмкастной. Вектор
, так как приёмник №2-ёмкастной. Вектор  отстаёт от
отстаёт от  на
на  ,
так как приёмник №3-индуктивный. Вектор
,
так как приёмник №3-индуктивный. Вектор согласно уравнению:
согласно уравнению:


Рисунок 4. Векторная топографическая диаграмма.
Литература
Евдокимов Ф. Е. Теоретические основы электротехники. — М., 2004.
Попов В. С. Теоретическая электротехника. — М., 1990.
ЛотерейчукЕ.А. Теоретические основы электротехники. — М., 2010.
ГилицкаяЛ.Н. Теоретическая электротехника. Курсовое проектирование. — Мн., 1992.
Зайчик М. Ю. Сборник задач и упражнений по теоретической электротехнике. — М., 1988.
Липатов Д. Н. Вопросы и задачи по электротехнике для программированного обучения. — М., 1977.
Усc Л. В. Лабораторный практикум по общей электротехнике с основами электроники. — Мн., 1993.
Касаткин А. С, Немцов М. В. Электротехника. — М., 2000.
Китунович Р: Г. Электротехника. — Мн., 1999.
Синдеев Ю. Г., Граховский В. Г. Электротехника. — Ростов-н/Д., 1999.
ГОСТ 19431-84. Энергетика и электрификация. Термины и определения.
ГОСТ 8417-81. Единицы физических величин.
3. Расчет однофазной цепи переменного тока
3.1. Задание для самостоятельной работы
Для цепи синусоидального тока заданы параметры (табл. 8) включенных в нее элементов (рис. 10) и действующее значение напряжения на ее зажимах; частота питающего напряжения f = 50 Гц. Необходимо:
1) определить действующие значения тока в ветвях и неразветвленной части цепи символическим методом;
2) по полученным комплексным изображениям записать выражения для мгновенных значений тока в ветвях и напряжения на участке цепи с параллельным соединением;
3) построить упрощенную векторную диаграмму;
4) составить баланс мощности;
5) определить характер (индуктивность или емкость) и параметры элемента, который нужно добавить в неразветвленную часть схемы, чтобы в цепи имел место резонанс напряжений;
6) выполнить моделирование режима работы цепи при заданных параметрах и в режиме резонанса напряжений с помощью системы схемотехнического моделирования Electronics Workbench.
3.2. Методические указания к выполнению аналитического расчета
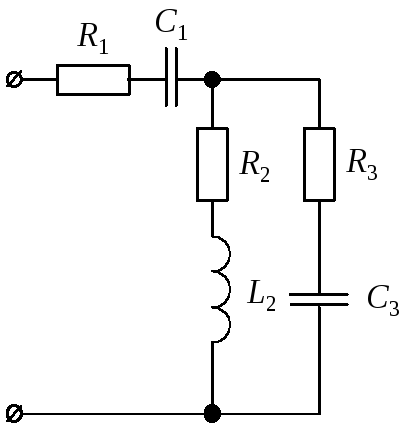
3.2.1. Рассмотрим порядок расчета однофазной цепи переменного тока на примере анализа схемы, представленной на рис. 11, а. Числовые значения параметров указаны в табл. 9.
Расчет однофазной цепи с одним источником выполняют методом эквивалентных преобразований («сворачиванием» – «разворачиванием») схемы, который рассмотрен в разд. 1.
Перед выполнением расчетов необходимо значения всех параметров привести к международной системе единиц СИ (1 мГн = 10-3 Гн; 1 мкФ = 10-6 Ф). Расчет ведется символическим методом с помощью аппарата комплексных чисел.

 1
2
1
2 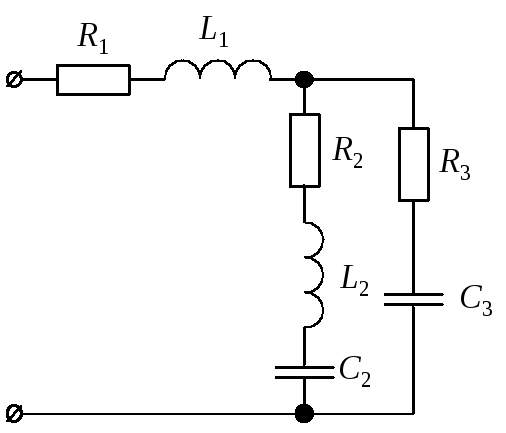


3 4 5

6 7
 EMBED Word.Picture.8
EMBED Word.Picture.8  EMBED Word.Picture.8
EMBED Word.Picture.8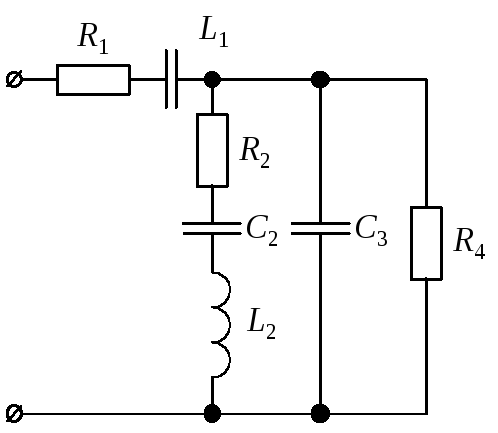
8 9 0
Рис. 10
Таблица 8
Числовые значения параметров элементов схемы
Вариант | Напряжение, В | Параметры элементов цепи | ||||||||
R1, Ом | L1, мГн | С1, мкФ | R2, Ом | L2, мГн | С2, мкФ | R3, Ом | L3, мГн | С3, мкФ | ||
0 | 220 | 9 | 15 | 800 | 9 | 17 | 1000 | 5 | 14 | 800 |
1 | 127 | 6 | 20 | 200 | 8 | 18 | 800 | 6 | 10 | 700 |
2 | 380 | 8 | 25 | 400 | 7 | 20 | 600 | 7 | 8 | 450 |
3 | 380 | 5 | 16 | 600 | 6 | 48 | 400 | 8 | 13 | 600 |
4 | 127 | 7 | 10 | 500 | 5 | 13 | 500 | 9 | 11 | 500 |
5 | 220 | 4 | 14 | 1000 | 12 | 31 | 700 | 10 | 9 | 400 |
6 | 220 | 3 | 18 | 700 | 6 | 20 | 900 | 7 | 21 | 300 |
7 | 127 | 6 | 12 | 300 | 7 | 16 | 450 | 8 | 18 | 200 |
8 | 380 | 5 | 26 | 650 | 6 | 18 | 650 | 6 | 15 | 900 |
9 | 127 | 8 | 24 | 480 | 8 | 26 | 800 | 4 | 12 | 600 |
Таблица 9
Числовые значения параметров элементов схемы для примера расчета
Вариант | Напряжение, В | Параметры элементов цепи | ||||
R1, Ом | R2, Ом | L2, мГн | С2, мкФ | С3, мкФ | ||
– | 127 | 5 | 10 | 20 | 200 | 300 |
Для расчета полных
комплексных сопротивлений ветвей
определим реактивные составляющие
сопротивлений (рис. 11, б), которые создают
реактивные элементы, находящиеся в
ветвях. Реактивное сопротивление
индуктивного элемента  ,
емкостного –
,
емкостного –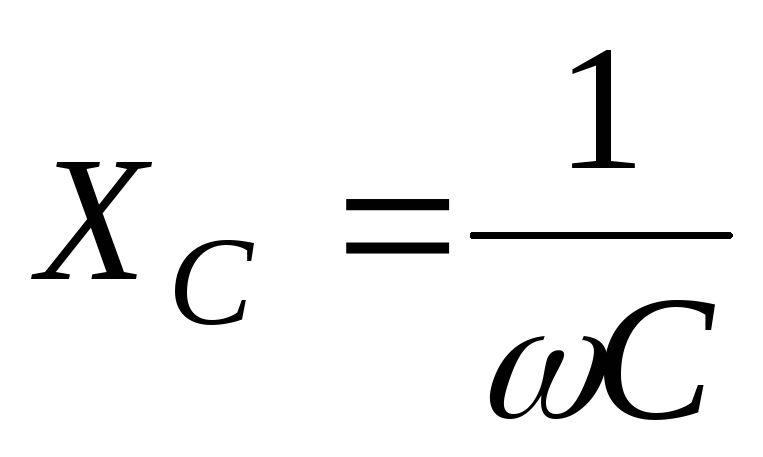 ,
общее сопротивление ветви, содержащей
индуктивный и емкостный элементы, –
,
общее сопротивление ветви, содержащей
индуктивный и емкостный элементы, – ,
где
,
где рад; f = 50 Гц – частота питающего
напряжения.
рад; f = 50 Гц – частота питающего
напряжения.
Первая ветвь цепи
не содержит реактивного элемента,
поэтому реактивная составляющая
сопротивления ветви будет равна нулю: 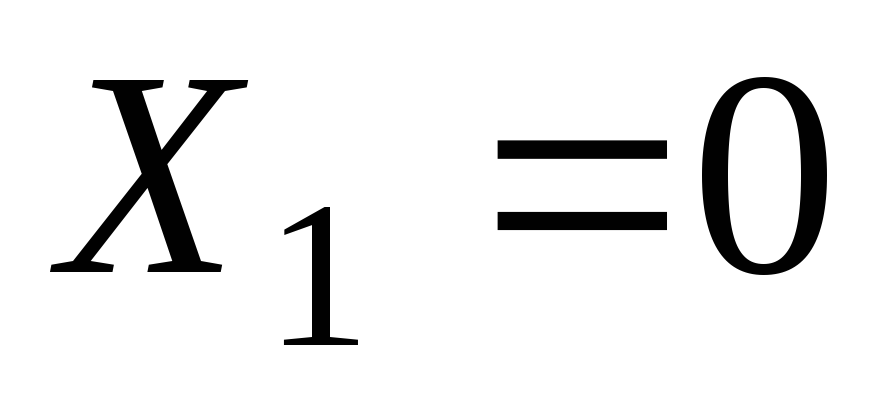 Ом.
Ом.
Вторая ветвь содержит два реактивных элемента. Общее реактивное сопротивление ветви равно алгебраической сумме индуктивного и емкостного сопротивлений. Знак «плюс» ставится у индуктивного сопротивления, «минус» – у емкостного:
 ;
;(55)
 Ом;
Ом; ;
;(56)
 Ом;
Ом; ;
;(57)
 Ом.
Ом.
Знак «минус» перед общим реактивным сопротивлением ветви указывает на его емкостный характер. Этот знак сохраняется и при записи полного комплексного сопротивления (см. ниже).


а б


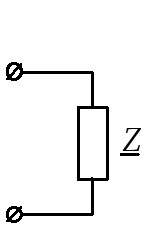
в г д
Рис. 11
Реактивное сопротивление третьей ветви
 ;
;(58)
 Ом.
Ом.
Полные комплексные сопротивления ветвей в алгебраической, показательной и тригонометрической форме (см. рис. 11) имеют вид:
 ,
(59)
,
(59)
где R – действительная составляющая комплексного сопротивления;
Х – мнимая составляющая комплексного сопротивления;
 –модуль комплексного
сопротивления;
–модуль комплексного
сопротивления;
 –аргумент
комплексного сопротивления, знак
аргумента зависит от знака реактивного
сопротивления ветви.
–аргумент
комплексного сопротивления, знак
аргумента зависит от знака реактивного
сопротивления ветви.
Для ветвей рассматриваемой электрической цепи
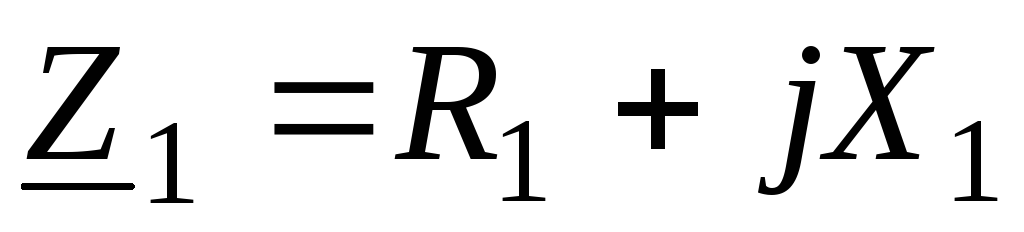 ;
(60)
;
(60)
 Ом;
Ом;
 ;
(61)
;
(61)
 Ом;
Ом;
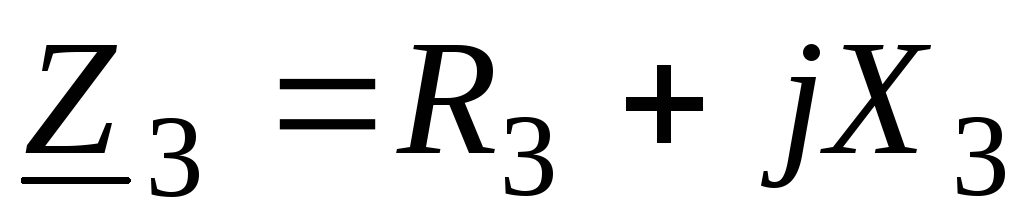 ;
(62)
;
(62)
 Ом.
Ом.
Эквивалентная схема с учетом выполненных расчетов представлена на рис. 11, в.
Последующие операции «сворачивания» электрической схемы основаны на рассмотренных в первом разделе свойствах параллельного и последовательного соединений. Нужно помнить, что сложение и вычитание комплексных чисел выполняется в алгебраической форме записи, а умножение и сложение – в показательной, если расчеты ведутся на калькуляторе.
Заменим параллельный участок на эквивалентное сопротивление (рис. 11, г):
 ;
(63)
;
(63)

Последовательное соединение двух сопротивлений преобразуем в простейшую цепь (рис. 11, д):
 ;
(64)
;
(64)
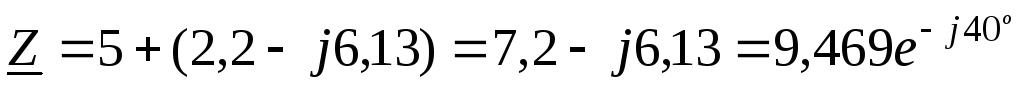 Ом.
Ом.
Полученная элементарная цепь рассчитывается по закону Ома для цепей переменного тока:
Напряжение на параллельном участке
 ;
;(66)
 В.
В.
Токи в параллельных ветвях рассчитываются по выражениям:
Для построения векторной диаграммы необходимо также определить напряжение на неразветвленной части цепи:
 ;
;(69)
 В.
В.
Расчет однофазной цепи с помощью математического редактора Mathсad представлен в прил. 3. Нужно заметить, что в Mathсad операции с комплексными числами выполняют в алгебраической форме записи. Для определения модулей и аргументов комплексных чисел нужно выполнить дополнительные команды. Углы в Mathсad вычисляются в радианах. Для перехода в градусную меру измерения углов необходимо дополнительно указать оператор: «deg» (см. прил. 3).
Результаты расчетов занесите в графу «Расчет» табл. 10.
Таблица 10
Полученные значения токов и напряжений для рассматриваемой цепи
Параметр | Действующие значения для исходной схемы | Моделирование резонанса | |
расчет | моделирование | ||
I1, А | 13,44 | 13,46 | 17,57 |
I2, А | 6,32 | 6,352 | 8,290 |
I3, А | 8,26 | 8,300 | 10,83 |
U23, В | 87,62 | 86,96 | 113,5 |
φ, градус | 40,41 | 40,05 | 0 |
3.2.2. Мгновенные
значения тока в ветвях и напряжения
можно записать с учетом того, что
амплитудное значение тока в  раз больше действующего значения,
которое равно модулю полученного
комплексного числа:
раз больше действующего значения,
которое равно модулю полученного
комплексного числа:
| (70) |
|
| (71) |
|
| (72) |
|
| (73) |
|
| (74) |
|
3
Рис. 12
.2.3. Для проверки правильности расчетов строят векторную диаграмму токов и напряжений электрической цепи. Необходимо выбрать масштаб по току ,
А/мм, и по напряжению
,
А/мм, и по напряжению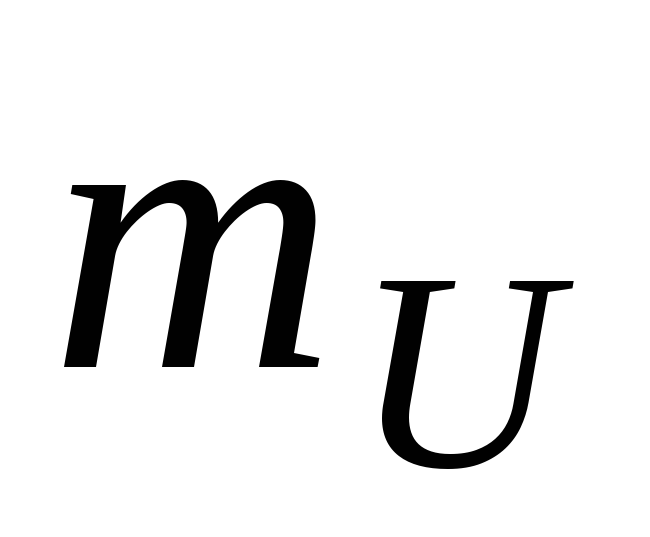 ,
В/мм, построить систему ортогональных
осей комплексной плоскости (+1, +j). Векторы
тока и напряжения строят из начала
координат так, чтобы длина вектора была
равна модулю комплексного числа
(действующему значению) с учетом масштаба,
а угол наклона к действительной оси
(+1) – аргументу комплексного числа
(начальной фазе), причем положительные
углы откладываются против часовой
стрелки, отрицательные – по часовой.
Векторная диаграмма для рассматриваемого
примера приведена на рис. 12.
,
В/мм, построить систему ортогональных
осей комплексной плоскости (+1, +j). Векторы
тока и напряжения строят из начала
координат так, чтобы длина вектора была
равна модулю комплексного числа
(действующему значению) с учетом масштаба,
а угол наклона к действительной оси
(+1) – аргументу комплексного числа
(начальной фазе), причем положительные
углы откладываются против часовой
стрелки, отрицательные – по часовой.
Векторная диаграмма для рассматриваемого
примера приведена на рис. 12.Если на векторной диаграмме сумма векторов токов параллельных ветвей равна вектору тока в неразветвленной части цепи в соответствии с первым законом Кирхгофа для узловой точки, а сумма векторов напряжения – напряжению источника, то считается, что диаграмма сходится, и это обязательное, но не достаточное условие для вывода о правильности расчетов.
3.2.4. Окончательно о правильности полученных результатов можно судить по балансу мощности, который для цепей переменного тока может быть составлен для комплексов полной мощности источника и потребителей:
 ,
(75)
,
(75)
или для активной и реактивной мощностей как составляющих. Выполним проверку по балансу активной и реактивной мощностей:
где  ,
, – угол сдвига фаз между приложенным
напряжением и током в неразветвленной
части цепи, он зависит от нагрузки цепи
и равен аргументу полного комплексного
сопротивления
– угол сдвига фаз между приложенным
напряжением и током в неразветвленной
части цепи, он зависит от нагрузки цепи
и равен аргументу полного комплексного
сопротивления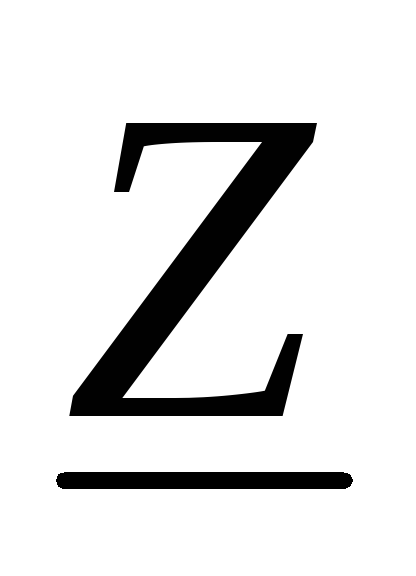 ;
;
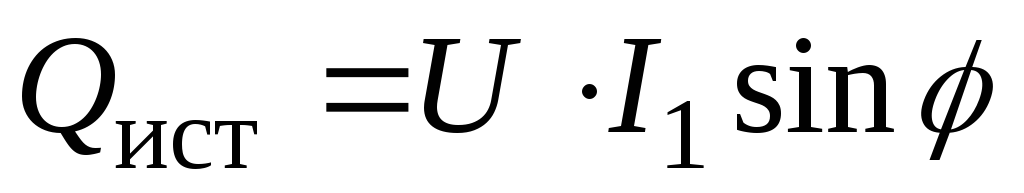 ;
;
 ,
где
,
где  – действующие значения токов, т. е.
модули комплексных чисел, изображающих
соответствующие токи;
– действующие значения токов, т. е.
модули комплексных чисел, изображающих
соответствующие токи;
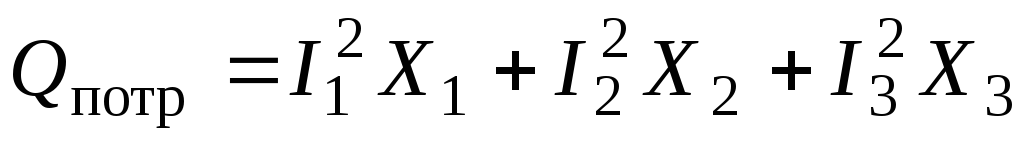 ,
реактивное сопротивление берется с
учетом знака.
,
реактивное сопротивление берется с
учетом знака.
Активная мощность всегда положительна, реактивная может быть и отрицательной. Знак «минус» указывает на то, что реактивная мощность отдается цепью в сеть, а не потребляется из сети.
Для рассматриваемого примера:
 Вт;
Вт;
 Вт;
Вт;
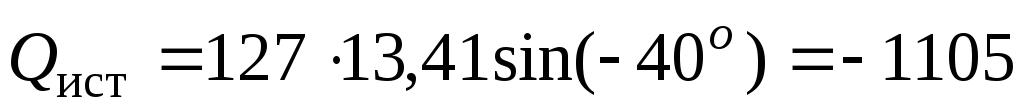 вар;
вар;

В результате баланс активной мощности:
1297 Вт = 1297 Вт,
а реактивной:
– 1105 вар = – 1105 вар.
Баланс активной и реактивной мощности выполняется, следовательно, расчет однофазной цепи выполнен верно.
3.2.5. Резонанс
напряжений в цепи наступает тогда, когда
реактивное сопротивление цепи равно
нулю. Если реактивное сопротивление
цепи носит индуктивный характер ( ),
то необходимо в неразветвленную часть
цепи добавить емкостное сопротивление,
значение которого равно индуктивной
составляющей сопротивления:
),
то необходимо в неразветвленную часть
цепи добавить емкостное сопротивление,
значение которого равно индуктивной
составляющей сопротивления:
 (77)
(77)
 .
(78)
.
(78)
Если реактивное
сопротивление цепи носит емкостный
характер (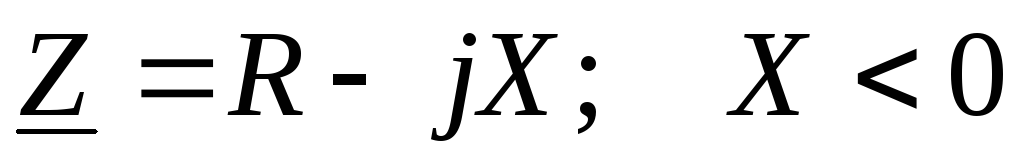 ),
то необходимо в неразветвленную часть
цепи добавить индуктивное сопротивление:
),
то необходимо в неразветвленную часть
цепи добавить индуктивное сопротивление:
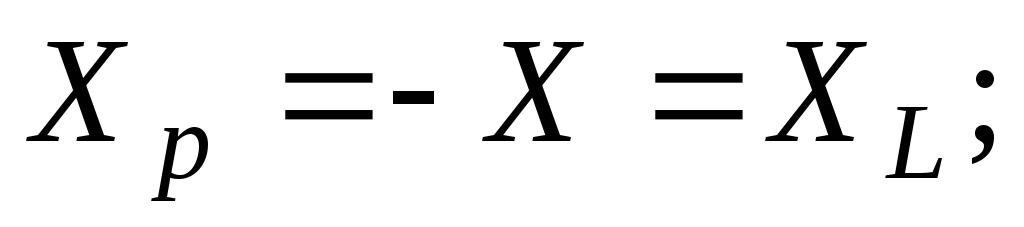 (79)
(79)
 .
(80)
.
(80)
В рассматриваемом
примере  ;
реактивная составляющая сопротивления
– емкостная. Рассчитаем индуктивное
сопротивление, которое обеспечит в цепи
резонанс напряжений:
;
реактивная составляющая сопротивления
– емкостная. Рассчитаем индуктивное
сопротивление, которое обеспечит в цепи
резонанс напряжений:
 Ом;
Ом;






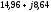
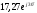
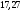


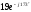


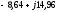


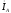




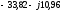
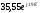


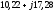

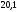
 ,
Ом
,
Ом ,
Ом
,
Ом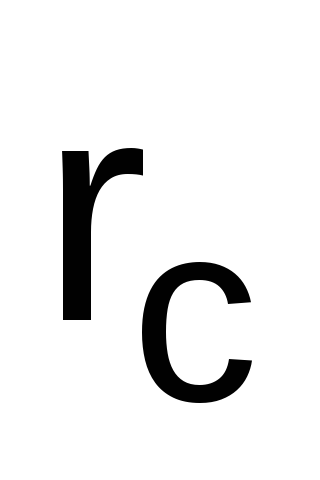 ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом ,
Ом
,
Ом
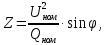
 .
.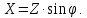

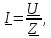
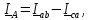



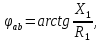
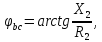
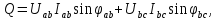

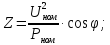
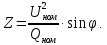
 .
.

 ;
;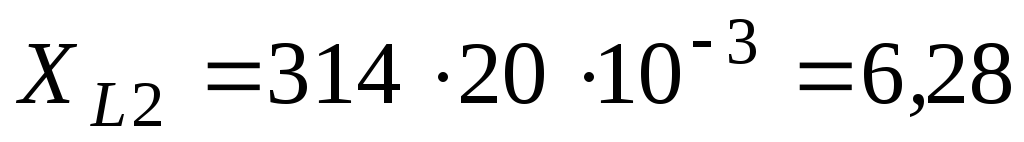 Ом;
Ом; ;
; Ом;
Ом; ;
;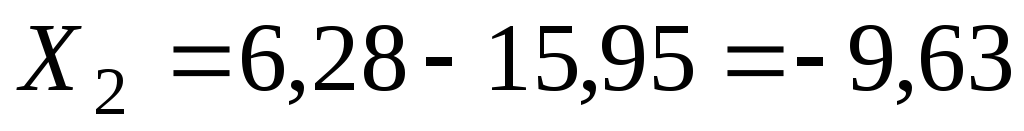 Ом.
Ом. ;
; Ом.
Ом. ;
; В.
В.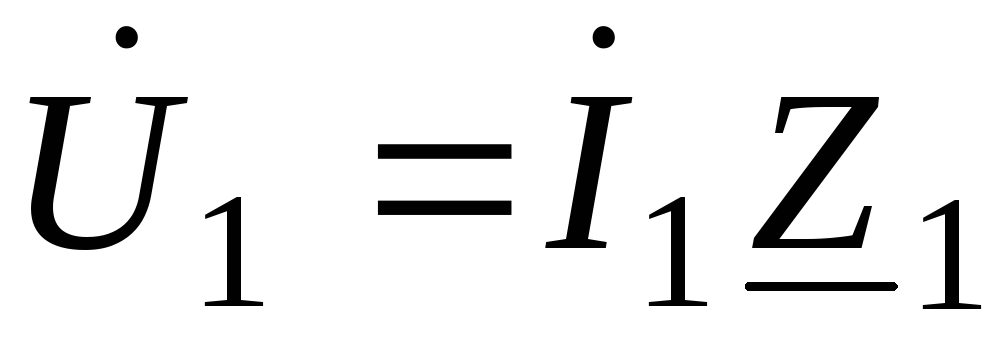 ;
;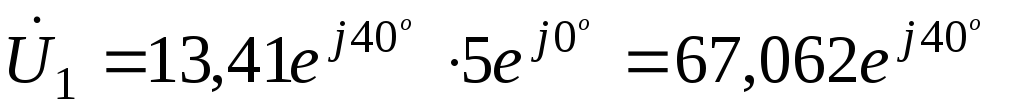 В.
В. ;
; ;
; ;
;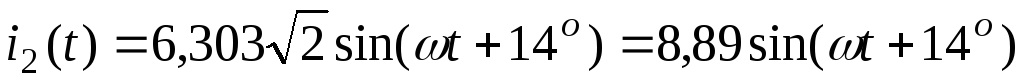 ;
;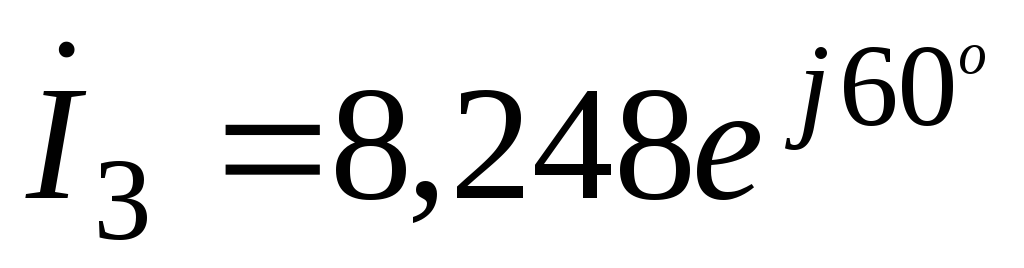 ;
; ;
; ;
; ;
; ;
;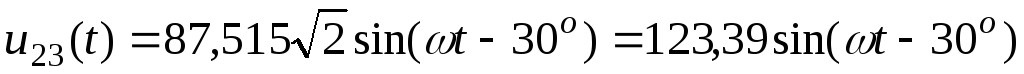 .
. Ом;
Ом;