Сопротивление при параллельном соединении: формула расчета расчета

На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при параллельном соединении проводников и некоторые другие технические вопросы.

Сопротивление проводника

Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.

Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм². Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.

При расчёте сопротивления используется известная из школьного курса физики формула:

R = ρ · l/S, S – площадь сечения; l – длина.

Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.

Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм², она вычисляется по формуле:

δ = I/S, I – ток, S – сечение.

Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в ПУЭ (Правилах Устройства Электроустановок). Для проводников нагревательных устройств существуют свои нормы плотности тока.

Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.

Правилами регламентируется производить расчёт проводников на нагрев.

Способы соединения проводников

Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.

На фото видно, что полное сопротивление равно: R = R₁ + R₂ + R₃.

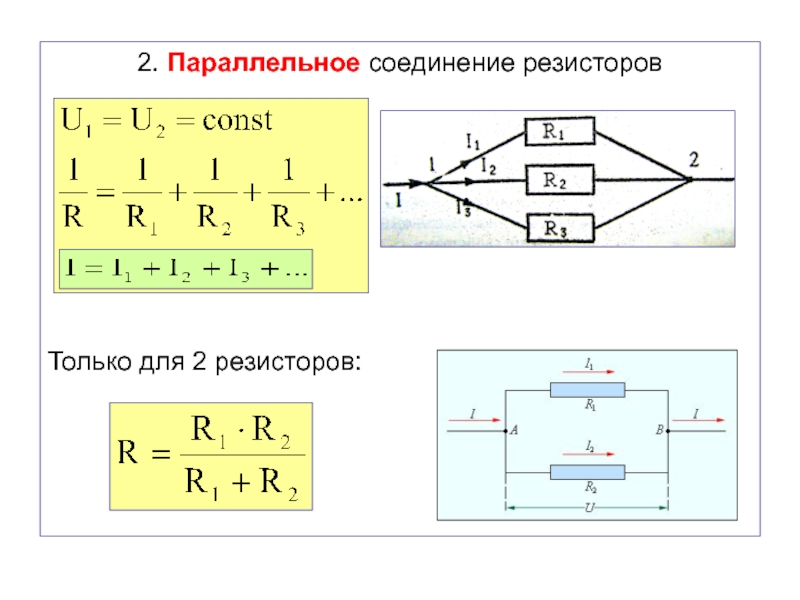
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.

Можно поступить и по-другому, прежде рассчитать общее сопротивление при параллельном соединении резисторов R1 и R2, после этого повторить операцию и найти R.

Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.

Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.

Теперь можно рассчитать сопротивление при параллельном соединении, формула которого имеет вид:

R2,3,4 = R2,3 · R4/(R2,3 + R4).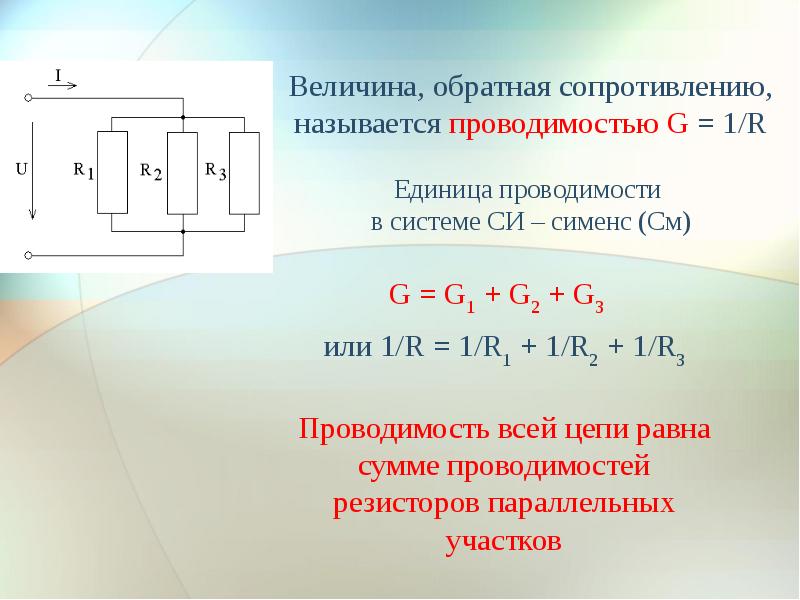

Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.

Виды проводников

В электронной технике, при производстве печатных плат, проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.

Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров — от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.

Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения.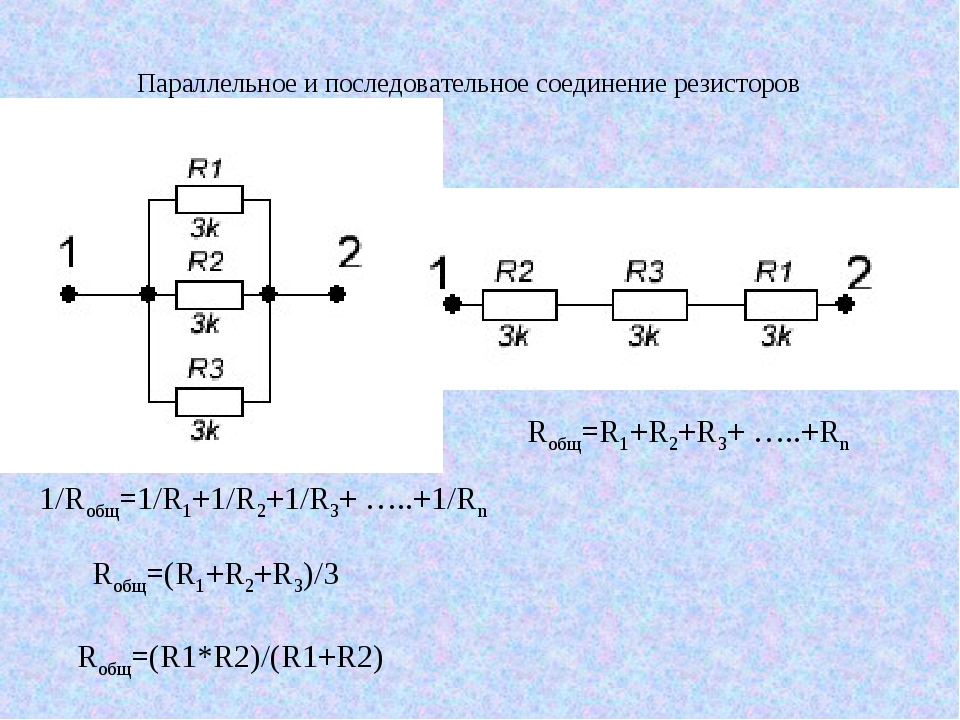 Причины этого бывают самые различные, например, кабель сечением 240 мм² очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм²,^{и проблема решена.}

Расчёт проводов на нагрев

Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника сечение (провода или кабеля).

На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.

Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.

Расчёт проводников на потерю напряжения

При расположении потребителя R_н на большом расстоянии L от источника энергии U₁ возникает довольно большое падение напряжения на проводах линии. К потребителю R_н поступает напряжение U₂ значительно ниже начального U₁. Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.

Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R_н. Далее следует определить сопротивление проводов линии.

R_л = ρ · 2L/S,

Здесь S – сечение провода линии, мм².

Далее определяется ток в линии: I = U₁/(R_л + R_н). Теперь, зная ток, определяют падение напряжения на проводах линии: U = I · R_л. Удобнее находить его в процентном отношении к U₁.

U% = (I · R_л/U₁) · 100%

Рекомендуемое значение U% — не более 15%. Приведённые расчёты применимы для любого рода тока.

Расчет результирующего сопротивления при последовательно-параллельном соединении

Последовательно-параллельное,
или смешанное, соединение представляет собой сложное соединение трех и
более сопротивлений.
Результирующее сопротивление при смешанном соединении рассчитывается
поэтапно с применением формул расчета сопротивлений при последовательном
и параллельном соединениях. Рассчитать последовательно-параллельное соединение трех сопротивлений по схеме на рисунке. Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивление …

Понятия и формулы

Последовательно-параллельное, или смешанное, соединение представляет собой сложное соединение трех и более сопротивлений. Результирующее сопротивление при смешанном соединении рассчитывается поэтапно с применением формул расчета сопротивлений при последовательном и параллельном соединениях.

Примеры

1. Рассчитать последовательно-параллельное соединение трех сопротивлений по схеме на рис. 1.

Сначала заменим параллельно соединенные сопротивления r2 и r3 результирующим сопротивлением r(2-3):

r(2-3)=(r2r3)/(r2+r3 )=(1020)/30=6,6 Ом.

Результирующее сопротивление всей схемы r=r1+r(2-3)=5+6,6=11,6 Ом.

Рис. 1.

2. Какой ток протекает по цепи (рис. 2) в случаях разомкнутого и замкнутого рубильника P? Как изменяется напряжение на сопротивлении r2 в обоих случаях?

Рис. 2.

а) Рубильник разомкнут. Результирующее сопротивление последовательно включенных сопротивлений r1 и r2

r(1-2)=r1+r2=25 Ом.

Ток I(1-2)=U/r(1-2) =100/25=4 А.

Падение напряжения на сопротивлении r2

U2=I(1-2)r2=45=20 В.

б) Рубильник замкнут. Результирующее сопротивление параллельно включенных сопротивлений r1 и r3

r(1-3)=(r1r3)/(r1+r3 )=(2010)/(20+10)=200/30=6,6 Ом.

Общее сопротивление всей схемы r=r(1-3)+r2=6,6+5=11,6 Ом.

Ток I=U/r=100/11,6=8,62 А.

Падение напряжения на сопротивлении r2 в этом случае равно: U2=Ir2=8,625=43,25 В.

Во втором случае ток увеличился в результате подключения параллельного сопротивления R3. Больший ток создает большее падение напряжения на сопротивлении r2.

3. Каким должно быть добавочное сопротивление rд, чтобы две параллельно соединенные лампы на напряжение 120 В и ток 0,2 А могли быть включены в сеть напряжением U=220 В (рис. 3)?

Рис. 3.

Напряжение на лампах должно быть равно 120 В. Остальное напряжение (100 В) падает на дополнительном сопротивлении rд. Через сопротивление rд проходит ток двух ламп I=0,4 А.

По закону Ома rд=Uд/I=100/0,4=250 Ом.

4. Электронные лампы с напряжением накала 1,2 В и током накала 0,025 и 0,05 А подключены последовательно к источнику постоянного тока напряжением 4,5 В. Какими должны быть добавочное сопротивление rд и параллельное сопротивление (шунт) к лампе, имеющей меньший ток накала (рис. 4)?

Рис. 4.

Сопротивления в схеме должны быть подобраны так, чтобы протекал ток накала второй лампы I=0,05 А. Напряжение на нитях накаливания электронных ламп будет равно 1,2+1,2=2,4 В. Вычтя эту величину из напряжения батареи, получим величину падения напряжения на добавочном сопротивлении rд: Uд=4,5-2,4=2,1 В.

10.12.2016 Без рубрики

Проверка формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном соединении

СОДЕРЖАНИЕ

1.   Цель работы                                                                                                           2

2.  Приборы и оборудование                                                                                        2

3.  Техника безопасности                                                                                             2

4.  Порядок выполнения работы                                                                                  2

5.  Содержание отчета                                                                                                4

6.  Контрольные вопросы                                                                                             4

7.  Рекомендуемая литература                                                                                    4

Приложение 1. Теоретические сведения                                                            5

Приложение 2. Задание для домашней подготовки к работе.                             7

1.   цель работы

1.1  Приобрести навыки выполнения различных видов соединений резисторов.

1.2  Произвести опытную проверку формул для расчёта эквивалентных сопротивлений при последовательном, параллельном и смешанном их соединениях.

2.   приборы и оборудование

Таблица 1

№ п/п	Наименование прибора	Услов. обозн.	Тип	Завод. номер	Измерительная система		Класс точно-сти	Род тока	Пре-делы измер.	Цена дел.
					название	Усл. обозн.
1	Амперметр	РА1
2	Амперметр	РА2
3	Вольтметр	PV

3.    техника безопасности

3.1  Сборку схем и переключения в них, производить только при отключенной от источника цепи.

3.2  Электрическую цепь или стенд включать только с разрешения преподавателя.

3.3  При сборке схем использовать только соединительные провода с исправной изоляцией.

3.4  По окончании работы отключить цепь от источника, показать преподавателю результаты измерений и расчета для проверки, привести рабочее место в порядок.

4.   порядок выпонения работы

4.1  Измерение тока и напряжения. Расчёт сопротивлений резисторов R1, R2, R3.

4.1.1  На базе стенда ЛЭС-4 собрать электрическую цепь (рис. 1) и показать ее преподавателю для проверки.

4.1.2  Начертить схему замещения электрической цепи (рис.1).

4.1.3  Поочерёдно подключая к зажимам 1, 2 используемые в опыте резисторы произвести замеры тока и напряжения. Используя закон Ома рассчитайте их сопротивления. Результаты измерений и расчёта занесите в табл.2.

Таблица 2

Резистор	Измерено		Вычислено
	U, B	I, A	R, Oм
R1
R2
R3

4. 2.  Последовательное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.2.1.  Соединить последовательно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).

4.2.2.   Включить стенд, измерить ток и напряжение. Показания вольтметра и амперметра записать в табл.3.

4.2.3.  Начертить схему замещения  цепи с последовательно соединёнными резисторами R1, R2, R3.

Таблица 3

Вид соединения резисторов	Измерено		Вычислено
	U, B	I, A	По закону Ома RЭ	По формуле RЭ
Последовательное
Параллельное
Смешанное

4. 2.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.3.  Параллельное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.3.1. Соединить параллельно резисторы R1, R2, R3 и подключить к зажимам 1, 2 электрической цепи (рис.1).

4.3.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.

4.3.3.Начертить схему замещения цепи с параллельно соединёнными резисторами R1, R2, R3.

4.3.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.4.  Смешанное соединение резисторов R1, R2, R3. Измерение тока и напряжения.

4.4.1. Соединить резисторы  R2, R3 параллельно и подключить их к резистору R1 последовательно. Смешанное соединение резистора R1, R2, R3 подключить к зажимам 1, 2 электрической цепи (рис. 1).

4.4.2. Включить стенд , измерить ток и напряжение. Показания вольтметра и амперметра записать в таблицу 3.

4.4.3. Начертить схему замещения цепи с смешанным соединением резисторов R1, R2, R3.

4.4.4. Произвести расчёт эквивалентного сорпотивления по закону Ома и, исходя из вида соединения резисторов по формуле. Результаты расчёта записать в табл.3.

4.5.  По результатам работы сделать вывод, отвечающий на вопросы цели работы.

5.   СОДЕРЖАНИЕ ОТЧЕТА

5.1  Цель работы.

5.2  Приборы и оборудование.

5.3  Выполнение рабочего задания.

5.3.1. Наименование задания.

5.3.2. Схемы электрических цепей.

5.3.3. Схема замещения.

5.3.4. Таблицы результатов измерений и вычислений.

5.3.5. Основные расчетные формулы.

5.4  Выводы по работе.

6.  контрольные вопросы

6.1  Что называют последовательным и параллельным соединением?

6. 2  Запишите формулы для расчёта эквивалентного сопротивления при последовательном и параллельном соединении.

6.3  На каком из 2-х последовательно соединённых разных по величине резисторов будет больше падение напряжения?

6.4  В какой из 2-х параллельных ветвей, имеющих разное сопротивление будет больше ток?

6.5  Как рассчитать проводимость ветвей?

7.  рекомендуемая литература

7.1  Евдокимов Ф.Е. «Теоретические основы электротехники», М. «Высшая школа», 1975.

приложение 1

Теоретические сведения

Последовательное соединение резисторов – это такое соединение, когда к концу одного резистора присоединяется начало второго, к концу второго начало третьего и т.д. и при этом образуется неразветвлённая цепь или участок цепи. При последовательном соединении ток во всех резисторах одинаков.

                                                                                                   Рис.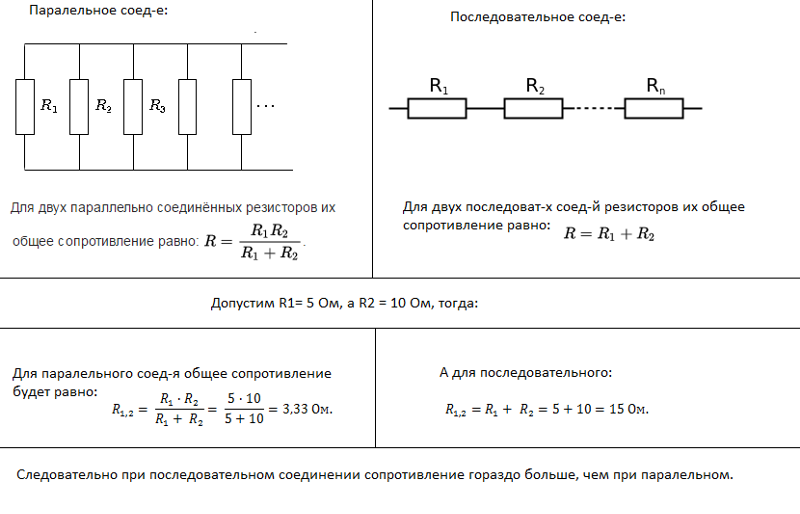 5

Для последовательного соединения выполняется:

                                                                      (1)

                                                                     (2)

                                                                     (3)

                                                          (4)

                                                        (5)

                                                                      (6)

                                                                     (7)

                                                                     (8)

                                                        (9)

Параллельное соединение резисторов – это такое соединение, когда начала всех резисторов соединены в одну точку, а их концы в другую.

Рис.6

Для параллельного соединения характерно одинаковое падение напряжения на каждом резисторе и всём участке:   U = U1 = U2 = U3

При параллельном соединении резисторов выполняется:

                                                               (10)

                                                     (11)

                                                         (12)

                                             (13)

                                        (14)

                                          (15)

                                                            (16)

На рис.7 изображено смешанное соединение резисторов.

 

                                                                                 Рис.

7

Резисторы R2, R3, R4 соединены параллельно, для них выполняются закономерности параллельного соединения, а резисторы R1, R2,3,4 и  R5 соединены последовательно.

приложение 2

задание для домашней подготовки к работе

Ознакомиться по учебнику, конспекту с материалом о последовательном

Расчёт сопротивления нескольких динамиков.

Последовательное соединение динамиков

При последовательном соединении ( рис. 1) динамики подключаются последовательно, один за другим. Очень важно правильно фазировать динамики, подключая плюс одного динамика к минусу другого. При последовательном подключении общее сопротивление возрастает, а выходная мощность уменьшается. Этот метод можно использовать для уменьшения выходной мощности канала, который поддерживает звучание других — например, тыловой или центральный каналы. Последовательно лучше соединять не более двух динамиков, поскольку большее их количество сильно уменьшит выходную мощность. Нельзя соединять динамики с разным сопротивлением, например, четырех- и восьмиомный, так как в этом случае каждый из них будет иметь разную громкость. Последовательным способом можно подключать только совершенно одинаковые динамики, ведь у разных динамиков может также различаться сопротивление в диапазоне 0.5 Ом.

 

При последовательном соединении сопротивление динамиков рассчитывается по формуле:

R = R1 + R2,

где R — сопротивление, которое мы получим в результате такого соединения, а R1 и R2 — сопротивление динамиков 1 и 2. Сопротивление большего количества динамиков рассчитывается аналогично: R = R1 + R2 + R3 + … + Rn, т.е. сопротивления суммируются.

Уменьшение мощности из-за увеличенной нагрузки рассчитывается по формуле:

P = Preal  (Rreal/Rcurrent),

где P — мощность при измененной нагрузке, Preal — паспортная мощность усилителя при стандартном сопротивлении, Rreal — сопротивление нагрузки, при котором проводились измерения реальной мощности усилителя (паспортное сопротивление нагрузки), Rcurrent — суммарное сопротивление динамиков, которое мы получили.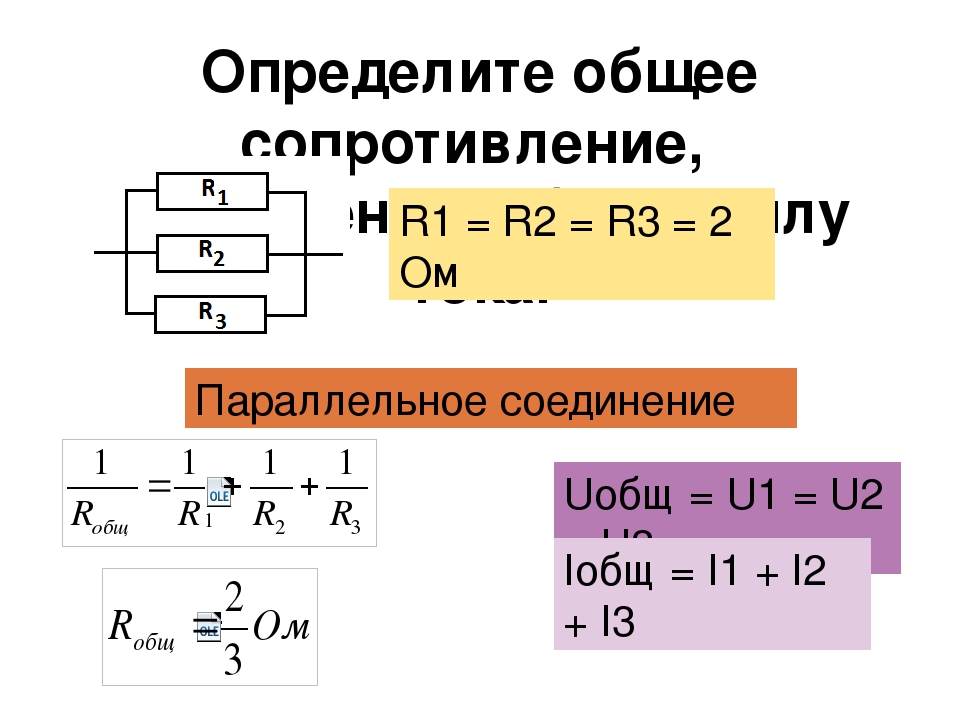 Эту формулу можно использовать при любом из трех описанных видов подключения, и с ее помощью легко рассчитывается увеличение или уменьшение мощности усилителя из-за нестандартной нагрузки.

Параллельное соединение динамиков

При параллельном подключении динамиков ( рис. 2) растет выходная мощность, а сопротивление уменьшается. При подключении двух четырехомных динамиков таким способом их совместное сопротивление станет равным 2 Ом, и необходимо узнать, сможет ли усилитель работать на такой низкой нагрузке. Значительно чаще попадаются усилители, которые могут нормально работать при сопротивлении в 2 Ом, чем на 1 или 0.5 Ом — последние уже большая редкость.

 

При подключении к усилителю более низкого сопротивления нагрузки, чем его паспортное значение, может привести к повреждению устройства. Но если усилитель раньше работал с сопротивлением в четыре Ом, и может работать на два Ом, то теперь на такую нагрузку он будет давать намного больше мощности и, возможно, ему потребуется более мощный блок питания! Например, если раньше усилителю вполне хватало четырех ампер для питания, то теперь для повышения мощности в два раза ему потребуется около восьми ампер (т. е. в два раза больше).

Вычислить сопротивление, которое будет после параллельного соединения динамиков, можно по формуле:

R = (R1  R2) / (R1 + R2),

где R — сопротивление нагрузки при параллельном соединении, которое мы ищем, а R1 и R2 — сопротивления динамиков, которые соединены данным способом. Например, сопротивление при параллельном соединении двух восьмиомных динамиков составит 4 Ом [(88)/(8+8) = 4 Ом]. При параллельном подключении двух динамиков выходная мощность усилителя на такую нагрузку будет в два раза больше.

Комбинированное соединение динамиков

Эту схему подключения ( рис. 3) используют для того, чтобы получить нужное сопротивление для усилителя. Например, для того, чтобы подключить четыре динамика с общим сопротивлением 4 Ом. Для вычисления сопротивления нагрузки по этому способу подключения используется формула:

R = (R1+2  R3+4) / (R1+2 + R3+4),

 

где R12 — общее сопротивление динамиков 1 и 2, которые подключены последовательно, а R34 — аналогично для динамиков 3 и 4. Если у вас есть четыре 30-ваттных 4-Омных динамика, то по такой схеме подключения общая мощность составит 120 Вт и сопротивление будет все тех же 4 Ом. А мощность, подводимая от усилителя, будет поровну делиться на четыре динамика.

Для большего количества динамиков используем формулу

1/Rпар=1/ R1+1/R2+1/R3+1/R4+1/R5……. для параллельного соединения динамиков с одинаковым сопротивлением  можно посчитать по ф.

Rпар= Rном./ n  , где n- количество динамиков

Пример расчета: Надо подключить 2 динамика имеющие по две катушки в 2 Ом

1 вариант, (самый хороший) подключаем обе катушки одного динамика параллельно получаем 2/2= 1Ом , соединяем последовательно со вторым динамиком у которого также подключены параллельно катушки и получаем 2Ом .      2/2+2/2= 2Ом

2вариант: подключаем все катушки и динамики последовательно 2+2+2+2=8 Ом,

3 вариант: катушки подключаем последовательно а сами динамики параллельно, (2+2)/2= 2Ом.

4 вариант: все катушки обоих динамиков параллельно ,2/4= 0,5Ом, тут уже сами думайте, чтобы так подключить, необходимо очень хорошее питание усилителя.

Рекомендации : 

не используйте разные динамики в таких подключениях, тем более с разным сопротивлением!

Простой расчет сопротивления нескольких динамиков.xlsx

последовательно соединенных резисторов — Расчет сопротивления — CCEA — Редакция GCSE Physics (Single Science) — CCEA

Ток

При последовательном подключении резисторов ток через каждый резистор одинаков.

Ток одинаков во всех точках последовательной цепи.

В схеме ниже: I _S = I ₁ = I _{0.0.0.1:0.1.0.$0.$1.$3.$5″> 2} = I ₃

Напряжение В (или разность потенциалов)

При последовательном соединении резисторов сумма всех напряжение (иногда называемое разностью потенциалов) на каждом компоненте равно напряжению на источнике питания.

В приведенной выше схеме:

V _S = V ₁ + V ₂ + V ₃

Это просто форма xdovx3wl3u.0.0.0.1:0.1.0.$0.$1.$10.$1″> закона сохранения энергии .

Напряжение питания — это мера энергии, подводимой к каждому электрону.

Напряжение на каждом компоненте — это электрическая энергия, преобразованная каждым компонентом.

Следовательно, поданная энергия равна преобразованной энергии — энергия не была создана или разрушена в цепи.

В последовательной цепи напряжение на источнике питания равно сумме напряжений на каждом компоненте.

Сопротивление

Общее сопротивление R двух или более последовательно соединенных резисторов является суммой отдельных сопротивлений резисторов.

Для схемы выше общее сопротивление R определяется по формуле:

xdovx3wl3u.0.0.0.1:0.1.0.$0.$2.$4″> R = R ₁ + R ₂ + R ₃

Пример

Найдите полное сопротивление схемы выше.

Ответ

Это последовательная цепь, поэтому полное сопротивление определяется по формуле:

R = R ₁ + R ₂ + R ₃ + R ₄

0.0.0.1:0.1.0.$0.$4.$3″> R = \ ({ 4} \ Omega + {8} \ Omega + {2} \ Omega + {12} \ Omega \)

R = \ ({26} \ Omega \)

Общее сопротивление цепи резисторов равно \ ( {26} \ Omega \). Это означает, что четыре отдельных резистора можно заменить одним резистором из \ ({26} \ Omega \).

Последовательное добавление резисторов всегда увеличивает общее сопротивление.

Ток должен проходить через каждый резистор по очереди, поэтому добавление дополнительного резистора увеличивает уже встреченное сопротивление.

Параллельные резисторы

Ток

При параллельном подключении резисторов ток от источника питания равен сумме токов, протекающих через каждую ветвь цепи.

Другими словами, токи в ветвях параллельной цепи складываются с током питания.

В приведенной выше схеме:

I _S = I ₁ + I ₂ + I ₃

Это соотношение выражает закон сохранения заряда.

Все электроны, вышедшие из источника, должны вернуться в источник, и каждый электрон может пройти только через одну параллельную ветвь.

В параллельной цепи ток от источника питания равен сумме токов в каждой ветви цепи.

0.0.1:0.1.0.$0.$7.$0″> Напряжение

В параллельной цепи напряжение на каждой ветви схемы равно напряжению питания.

Для схемы выше:

В _S = В ₁ = В ₂ = В ₃

В параллельной цепи напряжение на каждой ветви равно напряжению питания.

Сопротивление

При параллельном подключении резисторов общее сопротивление R рассчитывается по формуле:

\ [\ frac {1} {R} = \ frac {1} {R} _ {1} + \ frac {1} {R} _ {2} + \ frac {1} {R} _ {3} \]

Как рассчитать эквивалентное сопротивление в параллельной цепи | Физика

Как рассчитать эквивалентное сопротивление в параллельной цепи

Шаг 1: Определите количество резисторов в параллельной цепи и сопротивления каждого резистора.

Шаг 2: Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно в Шаге 1 .

Что такое эквивалентное сопротивление в параллельной цепи?

Эквивалентное сопротивление в параллельной цепи: Эквивалентное сопротивление в параллельной цепи рассчитывается как обратная сумма всех резисторов, включенных параллельно. Эквивалентное сопротивление всегда будет меньше, чем у любого из резисторов, образующих параллельную цепь.

$$ \ frac {1} {R_t} = \ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n} $$

Где {eq} R_t {/ eq} — полное или эквивалентное сопротивление, {eq} R_1 {/ eq}, {eq} R_2 {/ eq} и {eq} R_n {/ eq} — сопротивления резисторов, включенных параллельно. Сумма продолжает увеличиваться до тех пор, пока не будет {eq} R_n {/ eq}, где n — количество резисторов, включенных параллельно.

Используя это уравнение, давайте попрактикуемся в вычислении эквивалентного сопротивления резисторов параллельно с двумя примерами задач, решаемых шаг за шагом.

Примеры расчета эквивалентного сопротивления в параллельной цепи

Пример 1

Четыре резистора включены параллельно, сопротивление резисторов следующее: 10 Ом, 5 Ом, 2 Ом и 1 Ом. Какое эквивалентное сопротивление параллельных резисторов?

Шаг 1: Определите количество резисторов в параллельной цепи и сопротивления каждого резистора.

Есть четыре резистора, их сопротивления 10 Ом, 5 Ом, 2 Ом и 1 Ом.

Шаг 2: Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно в Шаге 1 .

$$ \ frac {1} {R_t} = \ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n} $$$$ \ frac {1} {R_t} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ frac {1} {R_4} $$$$ \ frac {1} {R_t} = \ frac {1} {10} + \ frac {1} {5} + \ frac {1} {2} + \ frac {1} {1} $$$$ \ frac {1} {R_t} = 1,8 $$$$ R_t \ приблизительно0,56 \ \ mathrm {ohms} $$

Эквивалентное сопротивление в цепи равно {eq} \ mathbf {0,56 \ \ mathrm {ohms}} {/ eq} исправьте до двух значащих цифр, обратите внимание на то, что сопротивление меньше, чем у любого из резисторов, составляющих схему.

Пример 2

Три параллельно включенных резистора имеют сопротивление 1000 Ом, 200 Ом и 500 Ом. Какое эквивалентное сопротивление в цепи?

Шаг 1: Определите количество резисторов в параллельной цепи и сопротивления каждого резистора.

Есть три резистора, их сопротивления 1000 Ом, 200 Ом и 500 Ом.

Шаг 2: Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно в Шаге 1 .

$$ \ frac {1} {R_t} = \ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n} $$$$ \ frac {1} {R_t} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$$$ \ frac {1} {R_t} = \ frac {1} {1000} + \ frac {1} {200} + \ frac {1} {500} $$$$ \ frac {1} {R_t} = 0,008 $$$$ R_t = 125 \ \ mathrm {ohms} $$

Эквивалентное сопротивление цепи равно {eq} \ mathbf {125 \ \ mathrm {ohms}} {/ eq}, снова обратите внимание, что сопротивление меньше, чем у любого из резисторов в цепи.

Получите доступ к тысячам практических вопросов и объяснений!

21.

1 Последовательные и параллельные резисторы — College Physics chapters 1-17

На рисунке 3 показаны резисторы , подключенные параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.

Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рис. 3 (b).)

Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс] \ boldsymbol {R _ {\ textbf {p}}} [/ latex], давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что полный ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:

[латекс] \ boldsymbol {I =} [/ латекс] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {= V} [/ latex] [латекс] \ boldsymbol {(\ frac { 1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {R_3})}.[/ latex]

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {= V} [/ латекс ] [latex] \ boldsymbol {(\ frac {1} {R_p})}. [/ latex]

Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление [латекс] \ boldsymbol {R_p} [/ latex] параллельного соединения связано с отдельными сопротивлениями соотношением

[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots} [/ latex]

Это соотношение приводит к общему сопротивлению [латекс] \ boldsymbol {R_p} [/ latex], которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) Когда резисторы подключаются параллельно, от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.

Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: [latex] \ boldsymbol {V = 12.0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает

[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {R_3}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [latex] \ boldsymbol {\ frac {1} {1.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]

Таким образом,

[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.00} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.1667} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.07692} {\ Omega}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.2436} {\ Omega}} [/ латекс]

(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)

Мы должны перевернуть это, чтобы найти полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает

[латекс] \ boldsymbol {R_p =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]

Общее сопротивление с правильным количеством значащих цифр составляет [латекс] \ boldsymbol {R_p = 0.804 \; \ Omega} [/ latex]

Обсуждение для (а)

[латекс] \ boldsymbol {R_p} [/ latex], как и предполагалось, меньше минимального индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, заменив полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {0.8041 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 14.92 \; \ textbf {A}} [/ latex]

Обсуждение для (б)

Ток [latex] \ boldsymbol {I} [/ latex] для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,

[латекс] \ boldsymbol {I_1 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {1.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 12.0 \; \ textbf {A}}. [/ Latex]

Аналогично

[латекс] \ boldsymbol {I_2 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {6.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 2.00 \; \ textbf {A}} [/ latex]

и

[латекс] \ boldsymbol {I_3 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]

Обсуждение для (c)

Общий ток складывается из отдельных токов:

[латекс] \ boldsymbol {I_1 + I_2 + I_3 = 14.92 \; \ textbf {A}}. [/ Latex]

Это соответствует сохранению заряда.

Стратегия и решение для (d)

Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 11.1 \; \ textbf {W}}. [/ Latex]

Обсуждение для (д)

Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.

Стратегия и решение для (e)

Общую мощность также можно рассчитать несколькими способами. Выбрав [латекс] \ boldsymbol {P = IV} [/ latex] и введя общий ток, получим

[латекс] \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]

Обсуждение для (e)

Суммарная мощность, рассеиваемая резисторами, также 179 Вт:

[латекс] \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. [/ латекс]

Это соответствует закону сохранения энергии.

Общее обсуждение

Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.

Резисторы в параллельной формуле

В электрических цепях часто можно заменить группу резисторов одним эквивалентным резистором. Эквивалентное сопротивление ряда резисторов, включенных параллельно, можно найти, используя обратное сопротивление, 1 / R. Обратная величина эквивалентного сопротивления равна сумме обратных величин каждого сопротивления. Единицей измерения сопротивления является Ом (Ом), который равен Вольт на Ампер (1 Ом = 1 В / А). Также распространены более крупные резисторы с сопротивлением килоом (1 кОм = 10 ³ Ом) или мегаом (1 МОм = 10 ⁶ Ом).

R _eq = эквивалентное сопротивление (Ом или более единицы)

R ₁ = сопротивление первого резистора (Ом)

R ₂ = сопротивление второго резистора (Ом)

R ₃ = сопротивление третьего резистора (Ом)

Параллельные резисторы Вопросы по формуле:

1) Какое эквивалентное сопротивление резистора 1000 кОм и резистора 250,0 кОм, подключенных параллельно?

Ответ: Оба сопротивления выражены в килоомах, поэтому менять их единицы измерения не нужно.Эквивалентное сопротивление можно найти в кОм по формуле:

.

Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:

R _экв = 200,0 кОм

Эквивалентное сопротивление резисторов 1000 кОм и 250,0 кОм, включенных параллельно, составляет 200,0 кОм.

2) Три резистора включены в электрическую цепь параллельно.Их сопротивления составляют 400 Ом, 40,0 кОм и 4,00 МОм. Какое эквивалентное сопротивление?

Ответ: Три значения сопротивления выражены в разных единицах измерения. Первый шаг к нахождению эквивалентного сопротивления — преобразовать их в общую единицу. Два значения можно преобразовать в ту же единицу, что и третье. В этом решении все значения будут преобразованы в Ом.

Если R ₁ = 400 Ом, R ₂ = 40,0 кОм и R ₃ = 4,00 МОм, то:

R ₂ = 40.0 кОм

R ₂ = 40 000 Ом

Стоимость ₃ рэнд составляет:

R ₃ = 4,00 МОм

R ₃ = 4000000 Ом

Эквивалентное сопротивление можно найти в Ом по формуле:

.

Последний шаг — инвертировать значения с обеих сторон формулы, чтобы найти эквивалентное сопротивление:

Эквивалентное сопротивление 400 Ом, 40.Сопротивление резисторов 0 кОм и 4,00 МОм, включенных параллельно, составляет примерно 396 Ом.

Основное электрическое оборудование | Сопротивление в параллельном соединении

Параллельные цепи

Параллельная цепь определяется как цепь, имеющая более одного пути тока, подключенного к общему источнику напряжения. Следовательно, параллельные цепи должны иметь два или более сопротивления нагрузки, которые не соединены последовательно. Каждый путь имеет отдельные резисторы (нагрузки) и может работать независимо от других путей. Различные пути прохождения тока обычно называют ветвями параллельной цепи.

Параллельная комбинация резисторов

Два или более резистора считаются подключенными параллельно, если один конец резистора подключен к одному концу другого резистора, а второй конец первого резистора подключен ко второму концу резистора. другой резистор таким образом, чтобы разность потенциалов на каждом резисторе была одинаковой.

Одним из преимуществ параллельной схемы является то, что в случае обрыва одной ветви это не повлияет на работу компонентов в других ветвях, поскольку они все еще подключены к источнику питания.В параллельной цепи напряжение одинаково на всех компонентах цепи.

• Устройства подключаются параллельно, когда они образуют петлю, не охватывающую никакие другие элементы.
• Устройства подключаются параллельно, если у них есть два общих узла.

Эквивалентное сопротивление параллельной цепи

Суммарное сопротивление (или результирующее сопротивление) ряда сопротивлений или резисторов, соединенных параллельно, можно рассчитать, используя закон комбинации сопротивлений, включенных параллельно.По закону сочетания сопротивлений параллельно. Сумма, обратная суммарному сопротивлению ряда параллельно включенных сопротивлений, равна сумме обратных величин всех отдельных сопротивлений . Например, если несколько сопротивлений, R ₁ , R ₂ , R _3, и т. Д. Подключены параллельно, то их общее сопротивление R определяется по формуле:

1 / R _экв. = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

Предположим, что сопротивление R ₁ составляет 4 Ом R ₂ составляет 6 Ом и третье сопротивление R ₃ = 12 соединены параллельно, и мы хотим узнать их суммарное сопротивление R.

Мы знаем, что

1 / R _eq = 1/4 + 1/6 + 1/12

1 / R _eq = 6/12

R _eq = 2 Ом

Это означает, что если мы соединим три сопротивления 4 Ом, 6 Ом и 12 Ом параллельно, то их общее сопротивление составит всего 2 Ом, что меньше, чем любое из трех отдельных сопротивлений (4 Ом, 6 Ом и 12 Ом). Таким образом, когда несколько сопротивлений соединены параллельно, их суммарное сопротивление меньше наименьшего индивидуального сопротивления. Это связано с тем, что когда у нас есть два или более сопротивлений, соединенных параллельно друг другу, то один и тот же ток получает дополнительные пути для протекания, и общее сопротивление уменьшается.

Примечание: — Если в параллельной цепи всего два пути, можно использовать следующую формулу:

R _eq = ( ₁ × R ₂ ) ⁄ ( ₁ + R ₂ )

Два сопротивления умножаются, а затем складываются.При использовании этой формулы нет необходимости находить значения, обратные значениям сопротивления. Эта формула может использоваться только при наличии двух сопротивлений в параллельной цепи. Если имеется более двух сопротивлений, необходимо использовать формулу обратного.

Другой простой метод определения полного сопротивления в параллельной цепи — это когда все значения сопротивления одинаковы. Примером параллельной цепи со всеми одинаковыми сопротивлениями является гирлянда, соединенная параллельно. Каждая лампа имеет одинаковое сопротивление.Когда все сопротивления равны, чтобы найти общее сопротивление, разделите значение сопротивления каждого резистора на количество путей, пять резисторов 10 Ом подключены параллельно, общее сопротивление равно 10, разделенному на 5, или 2 Ом.

Напряжение в параллельной цепи резистора

Любое количество резисторов (компонентов) может быть подключено параллельно. Рассмотрим параллельную схему с тремя резисторами, каждый из которых имеет обозначения сопротивления: R ₁ , R _2, и R ₃ .

Предположим, что разность потенциалов между точками A и B равна V. Разность потенциалов между любыми двумя точками не зависит от пути, пройденного между точками. Разность потенциалов между любыми двумя точками — это единственная фиксированная скалярная величина. Работа, выполняемая между этими двумя точками, не зависит от пути, пройденного испытательным зарядом. Технический способ сказать это — «электрическое поле консервативно», что также известно как закон напряжения Кирхгофа.

Поскольку каждое сопротивление подключено между одними и теми же двумя точками A и B, следовательно, разность потенциалов на каждом сопротивлении будет одинаковой и будет равна приложенной разности потенциалов V.Следовательно, напряжение на всех трех сопротивлениях, то есть R ₁ , R ₂ и R ₃ , будет равно напряжению питания (В).

Это главное преимущество параллельной схемы и причина того, почему большинство повседневных схем подключаются параллельно. Это гарантирует, что на все компоненты подается одинаковое напряжение. Например, каждая цепь в доме подключена параллельно, обеспечивая подачу 230 В (или 120 В в Северной Америке) на каждый компонент.Лампа на 230 В может быть подключена параллельно к пылесосу на 230 В и электрокамину на 230 В, все к источнику питания 230 В, и все они имеют одинаковое напряжение питания.

Ток в параллельной цепи резистора

Если мы поместим амперметры в параллельную цепь, как показано на рисунке, мы обнаружим, что сумма показаний тока в каждой ветви будет равна току, потребляемому от источника питания.

Компоненты параллельной цепи работают независимо друг от друга.Когда два или более блока соединены параллельно, на каждый блок будет приходиться часть общего протекания тока в цепи. То есть полный ток схемы делится в одной или нескольких точках, и часть проходит через каждое сопротивление цепи. Обычно, когда мы анализируем схему этого типа, мы предполагаем, что сопротивление провода незначительно, а источник питания не имеет внутреннего сопротивления. Полный ток в параллельной цепи равен сумме токов в отдельных компонентах.Уравнение, выражающее это утверждение, следующее:

I _T = I ₁ + I ₂ + I ₃ + ——– I _N

Обычно, когда мы анализируем параллельную цепь, мы предполагаем, что сопротивление провода незначительно и источник питания не имеет внутреннего сопротивления. Параллельная цепь всегда содержит более одного пути для прохождения тока; следовательно, ток может «выбирать», через какую единицу нагрузки проходить. В соответствии с природой физики (и законом Ома) больше электронов будет идти по пути более низкого сопротивления, а меньшее количество электронов — по пути с более высоким сопротивлением.Таким образом, в параллельной цепи любой путь с более высоким сопротивлением, естественно, получает меньше тока, а цепи с низким сопротивлением будут получать больший ток.

Согласно закону Кирхгофа, сумма токов, приближающихся к любому переходу в цепи, равна сумме токов, выходящих из того же перехода, и может быть выражена следующим образом:

I = I ₁ + I ₂ + I ₃

Из закона Ома

I = E / R

Подставляя значение I, мы получаем

E / R _T = E / R ₁ + E / R ₂ + E / R ₃

Поскольку напряжение питания E является общим для каждого сопротивления, мы можем разделить приведенное выше уравнение на E:

E / R _T = E / E.R ₁ + E / ER ₂ + E / ER ₃

1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

Где R _T — полное сопротивление цепи

Обзор параллельных цепей

1. При разделении цепи на ветви напряжение не падает; следовательно, на каждую ветвь цепи подается одинаковое напряжение.
2. Полный ток в цепи равен сумме токов в ее параллельных ветвях.
3. Обратное эквивалентное сопротивление равно сумме обратных величин отдельных сопротивлений.
4. Общее сопротивление параллельной цепи всегда меньше, чем сопротивление ветви с наименьшим сопротивлением.
5. Если один из параллельных путей разорван, ток будет продолжать течь по всем другим путям.

Преимущества параллельных цепей в бытовой электропроводке

Расположение светильников и различных других электроприборов в параллельных цепях используется в бытовой электропроводке из-за следующих преимуществ:

1. В параллельных цепях, если один электроприбор останавливается работает из-за какого-либо дефекта, тогда все остальные приборы продолжают работать нормально. Например, если несколько лампочек подключены в параллельные цепи и одна лампочка перегорела (или перегорела), то все остальные лампочки будут продолжать светиться.
2. В параллельных цепях каждый электроприбор имеет собственный выключатель, благодаря которому его можно включать и выключать независимо, не влияя на работу других электроприборов. Например, все лампы, включенные в параллельную цепь в доме, имеют отдельные выключатели, благодаря которым мы можем включать или выключать любую лампочку по мере необходимости, не затрагивая другие лампы в доме.
3. В параллельных цепях каждый электроприбор получает такое же напряжение (220 В), что и линия электропитания. Благодаря этому вся бытовая техника будет работать исправно. Например, все лампочки, включенные в параллельные цепи, получают одинаковое напряжение 220 вольт линии питания и поэтому светятся очень ярко.
4. При параллельном включении электроприборов общее сопротивление бытовой цепи снижается, из-за чего ток от источника питания велик. Таким образом, каждое устройство может потреблять необходимое количество тока. Например, в параллельных цепях даже приборы с высокой мощностью, такие как электрические утюги, водонагреватели, кондиционеры и т. Д., Могут потреблять большой ток, необходимый для их правильного функционирования.

Решенный пример параллельной схемы резистора

Вопрос 1. Цепь состоит из трех параллельно включенных резисторов, каждый из которых имеет сопротивление 2 Ом, 4 Ом, 16 Ом соответственно.Если цепь подключена к источнику питания 120 В, рассчитайте:

(1). Ток через каждую ветку

(2). Ток питания

(3). Полное сопротивление.

Sol: — Принципиальная схема вышеуказанного вопроса показана на рисунке

1). Ток через каждую ветвь

⇒ I ₁ = E / R ₁ = 120/6

I ₁ = 20 A

⇒ I ₂ = E / R ₂ = 120 / 12

I ₂ = 10 A

⇒ I ₃ = E / R ₃ = 120/16

I ₂ = 7.5 A

2.) Ток питания

I _T = I ₁ + I ₂ + I ₃

I _T = 20 + 10 + 7,5

I _Т = 37,5 А

(3) . Общее сопротивление

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃

1 / R _экв = 1/6 + 1/12 + 1 / 16

1 / R _экв = 15/48

R _экв = 48/15 = 3.2 Ом

---

Для Последовательное сопротивление | Последовательная схема Нажмите здесь

Для фундаментальной электротехники Нажмите здесь

Чтобы узнать о влиянии температуры на сопротивление, нажмите здесь

Чтобы ознакомиться с концепцией сопротивления и законом Ома, нажмите здесь

Для фундаментальных -quantities-and-units Щелкните здесь

сообщите об этом объявлении

Расчет параллельного сопротивления — Pi My Life Up

В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления .

Параллельное сопротивление — полезная часть электроники, но его может быть трудно рассчитать, когда вы начинаете иметь дело с более чем двумя резисторами.

Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Это удобно, когда вам нужно определенное сопротивление, но нет резистора, который соответствует требуемому значению.

Уменьшение сопротивления вызвано тем, что у тока больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больше тока через цепь и, следовательно, снижает общее сопротивление, с которым сталкивается ваша цепь.

Например, в цепи с двумя резисторами равного номинала, включенными параллельно, сопротивление будет уменьшено ровно наполовину. Математика немного отличается для разных сопротивлений и наличия большего количества резисторов. Мы углубимся в это позже в руководстве.

Если вы хотите увеличить сопротивление вашей цепи, а не уменьшать его, вы можете вместо этого использовать резисторы последовательно.

Чтобы помочь вычислить общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает процесс.

Если вас смущают цвета на резисторе, обязательно ознакомьтесь с руководством по цветовым кодам резистора, поскольку оно научит вас всему, что вам нужно знать.

Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление. Затем введите значение для каждого резистора.

Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.

Расчет общего сопротивления параллельно

Если вы предпочитаете учиться, вы можете вручную рассчитать сопротивление резисторов, подключенных параллельно.Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами параллельно.

Существует три различных уравнения, которые можно использовать для расчета полного сопротивления при параллельном подключении.

Суммарное сопротивление двух одинаковых резисторов

Первое уравнение может использоваться только в том случае, если у вас есть два параллельно подключенных резистора с одинаковым сопротивлением.

Если у вас параллельно установлены два резистора с одинаковым сопротивлением, то общее сопротивление равно половине одного резистора.

Пример использования уравнения

Для этого примера предположим, что у нас есть два резистора 200 Ом , включенных параллельно, как показано на схеме ниже.

Зная, что параллельно подключено только два резистора и что они имеют одинаковое значение, мы можем использовать наше уравнение.

Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).

Чтобы получить общее сопротивление, все, что нам нужно сделать, это разделить наше значение 200 Ом на 2 .

Ответ очень легко найти: 100 .

После этого у вас должно быть представление о том, как поступить в простейшем случае, когда два резистора одинакового номинала включены параллельно.

Суммарное сопротивление двух разных резисторов

Второе уравнение — это упрощенная версия основного уравнения, которое мы будем использовать позже.Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.

Есть еще несколько процессов, которые вам нужно выполнить для расчета сопротивления двух резисторов, включенных параллельно, но это не намного сложнее.

Пример использования уравнения

В этом примере мы будем предполагать, что у нас есть цепь с двумя параллельными резисторами разных значений.

В этой схеме у нас есть резистор на 600 Ом и резистор на 250 Ом , включенные параллельно.Теперь мы хотим вычислить общее сопротивление, обеспечиваемое этими резисторами.

Для начала нам нужно заполнить наше уравнение, где R1 будет нашим резистором 600 Ом, а значение R2 будет резистором 250 Ом.

Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение перед тем, как продолжить.

Умножение 600 (R1) на 250 (R2) даст результат 150 000 .Добавление 600 (R1) к 250 (R2) даст вам ответ 850 .

Когда оба значения определены, все, что нам нужно сделать, это разделить верхнее число на нижнее число. Таким образом, мы можем определить полное сопротивление двух параллельно включенных резисторов.

Вы должны выполнить математические вычисления в этом примере: 150 000 разделить на 850 . Отсюда вы должны получить результат 176,47 . Будут лишние десятичные точки, но мы округлим их до ближайших двух.

После этого вы должны иметь представление о том, как рассчитать полное сопротивление двух резисторов, включенных параллельно.

Далее мы покажем вам, как обращаться с тремя и более резисторами. Это уравнение — немного более сложный процесс, поскольку он включает в себя много делений, которые приводят к большим десятичным числам.

Общее сопротивление нескольких резисторов

Третье и последнее уравнение, с которым мы будем иметь дело, — это уравнение, которое вы будете использовать для трех или более резисторов, включенных параллельно.

Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.

Единственным недостатком этого уравнения является то, что на него требуется больше времени, чем больше резисторов вы добавляете.

Простым решением является использование параллельного вычислителя резисторов, как мы включили выше.

Пример использования уравнения

В этом примере мы покажем, как использовать более сложное уравнение параллельного резистора.

Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1 кОм (R4) .

Для начала нам нужно заполнить уравнение всеми нашими значениями.

Каждое из наших значений резистора будет делителем для 1 , и вы можете добавить столько резисторов, сколько вам нужно в это уравнение. В этом примере мы обрабатываем только четыре.

Наш следующий шаг — разделить 1 на каждое из значений резистора . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.

Например, в наших расчетах мы делим 1 на 100 , что дает нам результат 0.01 .

После того, как вы закончили делить каждый набор значений, теперь нам нужно сложить каждое значение вместе.

Для схемы нашего примера это будет означать: 0,01 + 0,004 + 0,005 + 0,001 . К счастью для нас, это складывается довольно гладко и дает нам хорошее круглое число 0,02 .

Затем нам нужно переместить делитель из левой части уравнения вправо.

Этот ход будет означать, что наше вычисленное значение станет делителем 1 и должно выглядеть так, как показано ниже.

Наконец, разделите 1 на ваш делитель, и в нашем случае будет 0,02 . Это уравнение рассчитает окончательное полное сопротивление ваших параллельных резисторов.

Резюме

Надеюсь, теперь вы накопили достаточно знаний о том, как рассчитать полное сопротивление резисторов, включенных параллельно. Вам будет удобно, если вы планируете делать какие-то проекты схем Raspberry Pi или любой другой проект электроники.

Если у вас есть отзывы или вопросы по этому руководству, пожалуйста, оставьте комментарий ниже.

резисторов последовательно и параллельно

резисторов последовательно и параллельно
следующий: Правила Кирхгофа Up: Electric Current (Электрический ток) Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах. Практические схемы часто содержат очень сложные комбинации резисторов. Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторой общей схемы резисторов.Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правила. Эти правила относятся к резисторам, включенным последовательно, и в параллели.

Рисунок 18: Два резистора, соединенных последовательно.

Рассмотрим два резистора, включенных в серию , как показано на рис. 18. Понятно, что через оба резистора протекает одинаковый ток.Ибо, если бы это было не так, заряд накапливался бы в одном или другом резисторов, которые не соответствовали бы установившаяся ситуация (таким образом нарушая основное предположение этого раздела). Предположим, что падение потенциала от точки к точке есть. Это падение представляет собой сумму потенциальных падает и на двух резисторах и соответственно. Таким образом,

(135)

Согласно закону Ома, эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,

(136)

давая

(137)

Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правило

Эквивалентное сопротивление двух последовательно соединенных резисторов равно сумма индивидуальных сопротивлений.

Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .

Рисунок 19: Два резистора, включенных параллельно.

Рассмотрим два резистора, соединенных параллельно , как показано на рис. 19. Это Из рисунка видно, что падение потенциала на двух резисторах равно тем же. В общем, однако, токи и которые протекают через резисторы и соответственно разные. По закону Ома эквивалентное сопротивление между и — отношение падения потенциала через эти точки и текущий которая течет между ними.Этот ток должен равняться сумме токи и протекающие через два резистора, в противном случае заряд будет накапливаться на одном или обоих переходах в цепи. Таким образом,

(138)

Следует, что

(139)

давая

(140)

Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов.Ясно, что правило

Обратное эквивалентное сопротивление двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.

Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .

---

следующий: Правила Кирхгофа Up: Electric Current (Электрический ток) Предыдущее: ЭДС и внутреннее сопротивление

Ричард Фицпатрик 2007-07-14

.