Расчет сложной электрической цепи постоянного тока: Расчёт сложной цепи постоянного тока » СтудИзба – НТБ МАЛИ :: Ошибка 404 — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Расчёт сложных электрических цепей постоянного и синусоидального токов

РОССИЙСКАЯ ФЕДЕРАЦИЯ

МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ

ГОУ ВПО «Дальневосточный государственный университет путей сообщения МПС России»

Кафедра «Электротехника, электроника и электромеханика»

В.С. Матющенко

Рекомендовано методическим советом ДВГУПС в качестве учебного пособия

Хабаровск

Издательство ДВГУПС

2004

Рецензенты:

Кафедра «Теория электросвязи, электроники и метрологии» Хабаровского филиала Сибирского государственного университета телекоммуникаций и информатики, (заведующий кафедрой профессор В.А. Константинов)

Начальник отдела ОАО «Дальэлектропроект» А.П. Сукачев

М 353 Матющенко, В.C. Расчёт сложных электрических цепей постоянного и синусоидального токов. Учеб. пособие / В.C. Матющенко. – Хабаровск: Изд-во ДВГУПС, 2004. – 69 с.: ил.

Учебное пособие соответствует государственным образовательным стандартам высшего профессионального образования направлений: 657700 «Системы обеспечения движения поездов», 650900 «Электроэнергетика», 654500 «Электротехника, электромеханика и электротехнологии», 657600 «Подвижной состав железных дорог», 654400 «Телекоммуникации».

Содержит методические рекомендации по составлению расчётных схем и уравнений, необходимые сведения о правилах приближенных вычислений и действиях с комплексными числами, правила построения графиков и векторных диаграмм, примеры конкретных вычислений, задания для расчётно-графических работ.

Предназначено для студентов всех форм обучения, изучающих «Теоретические основы электротехники».

ГОУ ВПО «Дальневосточный государственный университет путей сообщения МПС России» (ДВГУПС), 2004

Тема 3 Методы анализа сложных электрических цепей Расчет сложных электрических цепей постоянного тока.

Метод узловых и контурных уравнений. Метод контурных токов.

а) Метод наложения (суперпозиции).

Метод наложения может быть применен ко всем электрическим процессам, описываемым линейными уравнениями.

Рисунок 4

Суть метода заключается в определении токов при действии источников ЭДС раздельно, а затем алгебраическом сложении полученных значений. После исключения Е₂ получается смешанное соединение резистивных элементов. Тогда

;

Затем исключается Е₁ и рассчитываются токи

; ;.

По методу наложения

;

Если у источников имеются внутренние сопротивления, то при расчете источники заменяются соответствующим резистивными элементами.

в) Метод контурных токов.

Метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа.

Независимые контуры выбираются для сложной электрической цепи так же, как и при составлении уравнений по второму закону Кирхгофа (I, II, III). Затем в каждом из контуров произвольно выбирается положительное направление контурного тока (I

11; I₂₂; I₃₃). Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих токов.

Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС (Е_КК), т.е.

; ;

Рисунок 5

Арифметическая сумма сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением (r_КК).

; ;

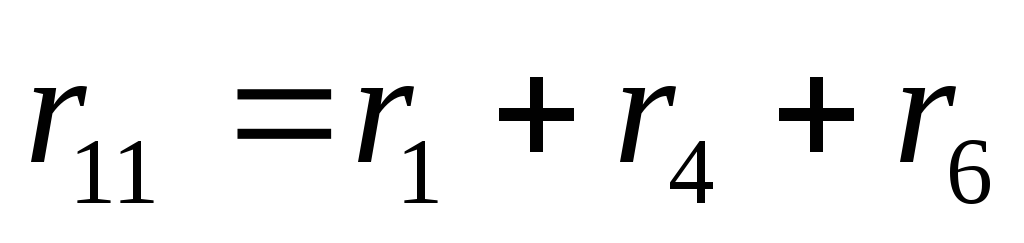Арифметическая сумма сопротивлений резистивных элементов, находящихся в общих ветвях двух контуров m и l называется общим сопротивлением этих контуров (r_ml= r_lm).

; ;.

Для контурных токов должен выполняться второй закон Кирхгофа. Тогда

Решение полученной системы уравнений может быть записано для контурных токов в общей форме с введением определителей

В рассматриваемом примере

Определитель системы

— алгебраические дополнения, получаемые из определителя Δ посредством вычеркивания К-й строки и Р-го столбца и умножением полученного определителя на (-1)^К+Р.

Вычислив значение контурных токов, определим по первому закону Кирхгофа токи во всех ветвях цепи:

, , ,,,

Метод контурных токов применим и для расчета цепи, если ее схема содержит источники тока. В этом случае ток каждого контура, который содержит источник тока, известен и равен току источника. Поэтому для таких контуров составлять уравнения не нужно.

Электрические цепи трехфазного тока.

Три синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые по фазе на ,образуют трёхфазную симметричную систему. Аналогично получаются трёхфазные системы напряжений и токов.

В настоящее время трёхфазные системы получили широкое распространение, что объясняется главным образом следующими причинами: 1) при одинаковых условиях питание трёхфазным током позволяет получить значительную экономию материала проводов по сравнению с тремя однофазными линиями; 2) при прочих равных условиях трёхфазный генератор дешевле, легче и экономичнее, чем три однофазных генератора такой же общей мощности; то же относится к трёхфазным двигателям и трансформаторам; 3) трёхфазная система токов позволяет получить вращающееся магнитное поле с помощью трёх неподвижных катушек, что существенно упрощает производство и эксплуатацию трехфазных двигателей; при равномерной нагрузке трёхфазный генератор создаёт на валу приводного двигателя постоянный момент в отличие от однофазного генератора, у которого мощность и момент на валу пульсируют с двойной частотой.

При симметричной нагрузке, когда все три нагрузочных сопротивления равны по значению и имеют одинаковый характер, синусоиды напряжений и токов изображаются графиками, аналогичными графику ЭДС. При этом начальные фазы токов определяются характером нагрузки, токи I_A,I_B ,I_C равны по амплитуде и сдвинуты по фазе на один относительно другого.

Трёхфазный генератор, соединённый проводами с трёхфазным потребителем, образуют трёхфазную цепь.

В трёхфазной цепи протекает трёхфазная система токов, т.е. синусоидальные токи с тремя различными фазами. Участок цепи, по которому протекает один из токов, называют фазой трёхфазной цепи.

Алгоритм расчета сложной электрической цепи постоянного тока.

⇐ ПредыдущаяСтр 5 из 18Следующая ⇒

Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системылинейных уравнений c lнеизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)

Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.

Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:

1. Выбирают положительные направления токов в ветвях электрической цепи.

2. Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.

3. Выбирают (l—k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.

4. Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.

5. Решают систему из (l—m) линейных уравнений любым удобным способом.

Более наглядно методика составления системы уравнений для данного способа расчета сложных электрических цепей показана на рисунке ниже.

На рисунке изображена схема сложной электрической цепи, содержащей 4 узла и 6 ветвей (k=4, l=6). Для расчета цепи необходимо составить систему из 6 линейных уравнений. Предварительно выберем направления токов в каждой из ветвей. По первому закону Кирхгофа (формула 1.20) составляем 3 уравнения (k-1=4-1=3), например для узлов A, B и C. Вместо любого из этих узлов для составления уравнения можно взять узел D, на результат расчетов это не повлияет. Оставшиеся 3 уравнения (l—k+1-m=6-4+1-0=3) придется составлять по второму закону Кирхгофа.

Для этого выбираем 3 независимых контура электрической цепи и для каждого из них выберем направление обхода. Составляем для каждого выбранного контура уравнение по второму закону Кирхгофа (формула 1.21). Получаем систему из 6 линейных уравнений с 6 неизвестными, которую и решаем любым удобным способом.

Магнитное поле. Сила Лоренца.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментамиэлектронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции (вектор индукции магнитного поля)^[3]^[4]. С математической точки зрения —векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Сила Лоренца

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,

может быть выражена через силы, действующие на отдельные носители заряда.

Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:

Выражение для силы Ампера можно записать в виде:

F = q n S Δl υB sin α.

Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна

Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или поправилу буравчика. Взаимное расположение векторов , и для положительно заряженной частицы показано на рис. 1.18.1.

Сила Лоренца направлена перпендикулярно векторам и

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса

Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).

Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле

Период обращения частицы в однородном магнитном поле равен

Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.

Угловая скорость движения заряженной частицы по круговой траектории

называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.

Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона

Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.

Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, ²⁰Ne и ²²Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источникаS, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся вскрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и

На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условииE = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.

Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q₁ = q₂) масс-спектрометр позволяет разделить частицы с разными массами.

Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10^–4.

Рисунок 1.18.4. Селектор скоростей и масс-спектрометр

Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ_┴ вектора а шаг спирали p – от модуля продольной составляющей υ_|| (рис. 1.18.5).

Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле

Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 10⁶ K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).

Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током

Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемыерадиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.

Расчет сложных электрических цепей

Законы Кирхгофа

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I₁— ток, втекающий в узел , а токи I₂ и I₃ — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:

I₁ = I₂ + I₃ (1)

Что бы подтвердить справедливость формулировки №2, перенесем токи I₂ и I₃ в левую часть выражения (1), тем самым получим:

I₁ — I₂ — I₃ = 0 (2)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

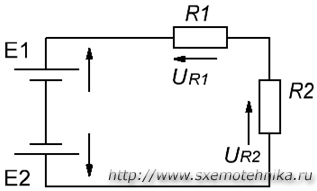
Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

E₁— Е₂ = -UR₁ — UR₂ или E₁ = Е₂ — UR₁ — UR₂ (3)

Расчет сложной цепи постоянного тока

2. Расчет сложной цепи постоянного тока

2.1. Задание для самостоятельной работы

Для сложной цепи постоянного тока (рис. 5), числовые значения параметров которой заданы в табл. 5, необходимо следующее:

1) рассчитать значения тока во всех ветвях

при помощи непосредственного применения законов Кирхгофа;

методом контурных токов;

2) проверить правильность расчета, составив баланс мощности, и сделать вывод по его результатам;

3) определить значения тока в ветвях, содержащих ЭДС, по методу межузлового напряжения, предварительно преобразовав исходную схему в схему с двумя узлами, заменив пассивный «треугольник» сопротивлений эквивалентной «звездой»;

4) выполнить моделирование заданной электрической цепи с помощью системы схемотехнического моделирования Electronics Workbench. Сравнить полученные результаты с расчетными.

Таблица 5

Числовые значения параметров элементов схемы

Вариант	ЭДС, В			Сопротивление, Ом
Вариант	Е₁	Е₂	Е₃	R₁	R₂	R₃	R₄	R₅	R₆
0	22	24	10	2	1	8	4	10	6
1	55	18	4	8	4	3	2	4	4
2	36	10	25	4	8	3	1	2	7
3	16	5	32	9	3	2	4	1	5
4	14	25	28	5	2	8	2	2	6
5	20	22	9	1	2	6	3	8	4
6	5	16	30	6	4	3	2	5	3
7	10	6	24	3	5	6	6	3	1
8	6	20	4	4	6	4	4	3	3
9	21	4	10	5	7	2	8	1	1

2.2. Методические указания к выполнению аналитического расчета

При анализе режима работы сложной электрической цепи неизвестными являются значения тока в ветвях, для их определения необходимо составить систему алгебраических уравнений и решить ее. Система должна содержать столько уравнений, сколько имеется неизвестных значений тока, т. е. ветвей в электрической цепи. Рассмотрим применение названных в задании методов расчета на примере схемы, приведенной на рис. 6, значения параметров которой даны в табл. 6.

Таблица 6

Параметры элементов схемы, приведенной в примере

Вариант	ЭДС, В			Сопротивление, Ом
Вариант	Е₁	Е₂	Е₃	R₁	R₂	R₃	R₄	R₅	R₆
—	5	16	30	6	4	3	2	5	3

2.2.1. Расчет схемы по законам Кирхгофа подразумевает составление системы уравнений, позволяющих определить значения тока в ветвях непосредственно по первому и второму законам Кирхгофа.

По первому закону Кирхгофа алгебраическая сумма значений тока в узле электрической цепи равна нулю:

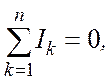(21)

т. е. уравнения по первому закону Кирхгофа составляются относительно узла.

Знак тока зависит от его направления относительно узла. Можно принять, что токи, направленные к узлу, будут записываться со знаком «плюс», а направленные от узла – со знаком «минус», либо наоборот.

Уравнения по второму закону Кирхгофа составляются для независимых контуров электрической цепи. По второму закону Кирхгофа алгебраическая сумма падения напряжения на приемниках электрической энергии в контуре равна алгебраической сумме ЭДС, действующих в этом контуре:

. (22)


1		2	3

4	5			6

7		8			9

		0
		Рис. 5

Если направление напряжения (тока) и ЭДС совпадают с направлением обхода контура, перед слагаемым в сумме ставится знак «плюс», в противном случае – «минус».

Для выполнения задания можно рекомендовать следующий порядок решения.

1) Для исходной цепи произвольно выбираем направления токов в ветвях и указываем их на схеме (рис. 6).

2) Количество неизвестных токов определяет порядок сложности цепи N и равно количеству ветвей. В рассматриваемом примере количестве ветвей в = N = 6. Следовательно, необходимо составить систему из шести уравнений.

Расчет сложной электрической цепи постоянного тока: Расчёт сложной цепи постоянного тока » СтудИзба – НТБ МАЛИ :: Ошибка 404