Калькулятор резонанса колебательного контура — MOREREMONTA
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью
 .
. Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = 
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит
 .
. В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты внешнего воздействия с некоторыми значениями (резонансными частотами), определяемыми свойствами системы.
F=1/(2π×√L×C), где
F — Резонансная частота, Гц)
L — Индуктивность, (Гн)
C — Ёмкость, (Ф)
Сайт для радиолюбителей
 Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Резонансная частота контура определяется так называемой формулой Томсона:
При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо. Также на настройку контура будет влиять емкость монтажа, ведь она соизмерима со значением С. Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как 100000 : 1 в абсолютном значении, что подходит для большинства контуров.
Например, для частоты 10,7 МГц оптимальным будет С=47 пФ и L= 4,7 мкГн, а для частоты 465 кГц оптимальные С=1000пФ и L=117мкГн.
Исходя из всего выше сказанного, онлайн калькулятор позволяет подобрать значения емкости и индуктивности в пределах ±20% от оптимального значения.
Для расчета частоты резонанса колебательного контура LC заполните предложенную форму:
Расчёт ёмкости для колебательного контура LC
Расчёт индуктивности для колебательного контура LC
Coil32 — Расчет резонансного контура
- Подробности
- Просмотров: 11950
Расчет колебательного контура
 Во вкладке «контур» программа Coil32 рассчитывает значения емкости, индуктивности и частоты для резонансного колебательного контура. Расчет ведется по формуле Томсона, выведенной в 1853 году и которая известна всем еще со школьного курса физики:
Во вкладке «контур» программа Coil32 рассчитывает значения емкости, индуктивности и частоты для резонансного колебательного контура. Расчет ведется по формуле Томсона, выведенной в 1853 году и которая известна всем еще со школьного курса физики:


, где:
- f — частота (Гц)
- L — индуктивность (Гн)
- C— емкость (Ф)
Программа позволяет рассчитать:
- Резонансную частоту контура при известных емкости и индуктивности
- Емкость контура при известной резонансной частоте и индуктивности
- Индуктивность контура при известной емкости и резонансной частоте
Подобный расчет также реализован в онлайн-калькуляторе
Во вкладке «катушка» при выборе однослойных катушек программа выдает дополнительные результаты для параллельного контура, в состав которого входит катушка:
- Емкость на резонансной частоте.
- Характеристическое сопротивление контура:

- Эквивалентное сопротивление контура:
 По умолчанию эти расчеты не выводятся. Для включения вывода дополнительных расчетов в текстовое поле нужно нажать крайнюю кнопку в панели инструментов над ним.
По умолчанию эти расчеты не выводятся. Для включения вывода дополнительных расчетов в текстовое поле нужно нажать крайнюю кнопку в панели инструментов над ним.
Расчеты верны конечно только для ненагруженного контура
Добротность контурного конденсатора принимается равной 1000.
Собственная емкость катушки учитывается при расчете величины емкости контурного конденсатора.
Эти расчеты имеют смысл на частотах много меньших частоты собственного резонанса катушки.
Добавить комментарийРасчет колебательного контура
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители!
Сегодня мы с вами рассмотрим порядок расчета LC контура.
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:
На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F)2/C где:
L – индуктивность катушки в мкГн;
С – емкость конденсатора в пФ;
F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1)2 /1000 = 25 мкГн
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.
Рассчитать число витков для катушки без сердечника можно по такой формуле:
N=32 *√(L/D) где:
N – требуемое число витков;
L – заданная индуктивность в мкГн;
D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
Расчёт LC — фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд
напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной.
И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и
электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
И начнём мы с расчёта самого простого LC-фильтра — колебательного контура.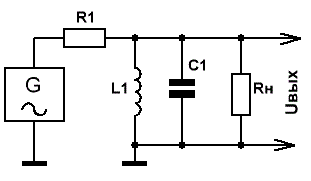
Включённый по приведённой на рис.1 схеме, он представляет собой узкополосный полосовой фильтр, настроенный на частоту
fо= 1/2π√LС.
На резонансной частоте сопротивление контура равно:
Rо = pQ, где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора.
Оно в свою очередь рассчитывается по формуле р = √L/C.
Рис.1
На низких (звуковых) частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить тестером. Если эта попытка удалась, то Q=2πfL/R, где R – активное сопротивление катушки индуктивности.
На радиочастотах значение активного сопротивления катушки может составлять доли ома, поэтому для расчёта добротности надо — либо
найти сопротивление в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в
метрах, d — диаметр провода в мм, либо вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким
внутренним сопротивлением, и определить добротность экспериментально.
К тому же на высоких частотах возможно проявление влияния добротности конденсатора, особенно если он окажется варикапом, хотя
современные недорогие керамические изделия (например, фирмы Murata) имеют значение параметра добротности — не менее 800.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 200 омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядок меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
К тому же я добавлю сюда
параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора — 1000, а для
испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу
ссылка на страницу .
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
Рис.2
Крутизна спада АЧХ этих фильтров в полосе подавления — 12 дБ/октаву, коэффициент передачи в полосе пропускания К=1 при R1
Однако наилучшие параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются
при R1=Rн=ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
Ну да ладно, ближе к делу.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
А если надо рассчитать L и C при известных значениях Fср и ρ ? Не вопрос,
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Данные ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.
Рис.3
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками.
Широкополосные полосовые LC — фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.


Фильтры RC. Частота среза. Расчёт онлайн.
Фильтр нижних частот (ФНЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.
Фильтр высших частот (ФВЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.
Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.

Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить исходя из коэффициента деления с импедансом Z.
Импеданс — комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ; Z = √(R² + X²) , где Х — реактивное сопротивление.
Тогда на выводах резистора напряжение UR будет составлять:

XC – реактивное сопротивление конденсатора, равное 1/2πfC
При равенстве R = XC на частоте f, выражение упростится сокращением R и примет вид:

Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:

τ — постоянная времени цепи RC равна произведению RC
Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.
Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).
Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ) спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.

Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) — красная линия на рисунке, или фильтр высших частот (ФВЧ) — синяя линия.
Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.


Частоту f = 1/(2π τ) называют граничной частотой fгр или частотой среза fср фильтра.
Частоту среза фильтра можно посчитать с помощью онлайн калькулятора
Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Пост. времени τ RC и частота среза RC-фильтра |
Похожие страницы с расчётами:
Расчёт импеданса.
Расчёт резонансной частоты колебательного контура.
Расчёт компенсации реактивной мощности.
Замечания и предложения принимаются и приветствуются!
Coil32 — Начинающим о колебательном контуре
 Для начинающих радиолюбителей хотелось бы привести немного информации о параметрах колебательных контуров. Ведь катушки индуктивности в основном являются их составной частью. Контур, как известно, состоит из катушки индуктивности и конденсатора. Рассмотрим параллельный контур, как наиболее часто встречающиийся.
Для начинающих радиолюбителей хотелось бы привести немного информации о параметрах колебательных контуров. Ведь катушки индуктивности в основном являются их составной частью. Контур, как известно, состоит из катушки индуктивности и конденсатора. Рассмотрим параллельный контур, как наиболее часто встречающиийся.
Основными характеристиками контура являются: 
- Резонансная частота контура
- Добротность контура
- Эквивалентное сопротивление контура
- Полоса пропускания
Рис1.
Резонансная частота контура определяется по формуле:

| Где L и C в Генри и Фарадах соответственно. |
Однако, необходимо помнить об одном очень важном моменте. C — это не номинальная емкость конденсатора контура. Она слагается из суммы емкостей — этого конденсатора, паразитной емкости катушки, емкости внешних цепей, подключенных к контуру (например выходная и входная емкость транзисторного каскада), паразитной емкости монтажа. Эти привнесенные емкости имеют достаточно существенную величину, особенно на высоких частотах, где они соизмеримы с емкостью самого контурного конденсатора. Их необходимо учитывать! Иногда на форумах можно прочесть сообщения типа: » Я рассчитал катушку, пользуясь такой-то программой, собрал конструкцию, а потом оказалось, что витки пришлось подбирать методом » научного тыка «, зачем такая программа, если она неправильно считает «. Программа считает правильно. Просто она считает «голый» контур, а на схему и конструкцию устройства надо, как говорил персонаж известного фильма, смотреть «ширше и глубже».
Теоретически, все вышесказанное относится и к индуктивности L, однако в реальности, привнесенные в контур индуктивности на порядок меньше и их в большинстве случаев можно не учитывать.
Добротность «голого» ненагруженного контура Q определяется добротностями катушки QL и конденсатора QC. QLзависит от сопротивления rL (см. рис1.), эквивалентного потерям электрической энергии в проводе, в изоляции провода, каркасе, экране, сердечнике катушки индуктивности. QL = 2πƒL /rL. Обычно в зависимости от качества конструкции катушки индуктивности и применяемых материалов QL≈50÷250.
Добротность конденсатора QC Зависит от сопротивления RC, эквивалентного потерям диалектической энергии в конденсаторе. QC = 1/(2πƒСRC). Обычно QC≈400÷1000.
Всевозможные сопротивления потерь (rL,RC) можно, для удобства расчетов заменить одним сопротивлением Rэ, подключенным параллельно идеальному контуру без потерь, которое называется эквивалентным сопротивлением контура. Оно характеризует все потери реального контура и равно сопротивлению контура на резонансной частоте. Попутно замечу, что на резонансной частоте реактивные сопротивления катушки и конденсатора равны и противоположны по знаку и компенсируют друг друга, в результате общее сопротивление контура чисто активно.
Величина Rэ связана с другими параметрами контура следующими соотношениями:
Rэ = 2πf0LQ = Q/(2πf0C) , f0 – резонансная частота.
Здесь опять существует важный момент. При подключении к контуру внешних цепей параллельно Rэ подключаются дополнительные сопротивления, вносимые внешними цепями. При этом Rэ и Q уменьшаются. Причем для высокодобротных контуров, это уменьшение может быть существенным. Чтобы минимизировать влияние внешних цепей на контур, применяют частичное включение через емкостный делитель, отвод катушки, либо применяют катушку связи.
Полоса пропускания равна полосе частот, где коэффициент передачи контура равен 70,7% от коэффициента передачи на резонансной частоте.

Справедливо соотношение: Q = f/Δf , которое можно использовать для измерения добротности реального контура.
Имеет какое-либо значение отношение индуктивности к емкости конденсатора? Как выбрать оптимальное?
Колебательный контур характеризуется параметром ρ = √L/C, называемым характеристическим сопротивлением. Этот параметр и ,соответственно, оптимальное соотношение L/C, зависят от импедансов схемы в которую включен колебательный контур. Ориентировочно в транзисторных схемах ρ ≈ 500-2000 ом на частотах КВ и 70-200 ом на частотах УКВ. С ростом частоты ρ стараются понижать для уменьшения влияния наводок и паразитных емкостей схемы и для избежания самовозбуждения.
Подводя итог, отмечу, что колебательный контур широко используется в радиотехнических устройствах для фильтрации электрических колебаний, для поворота фазы, для согласования сопротивлений и для других целей. При расчете контура обязательно необходимо учитывать параметры внешних цепей, подключенных к контуру и качественные характеристики самих деталей контура, особенно катушки индуктивности.
Coil32 — Последовательный колебательный контур
Здесь будет немного теории колебательного контура с отступлениями и комментариями. Надеюсь, что эта информация будет полезна не только студентам и школьникам, но и поможет радиолюбителям, дополнив практику теорией, может быть забытой кем-то, может для кого-то новой.
Последовательный колебательный контур – это цепь, составленная из последовательно соединенных индуктивности и ёмкости.(рис1)  рис 1
рис 1
R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах. При этом сами L и C, можно представить как идеальные без потерь.
È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов
Ζ = R + (jωL + 1 / jωC) = R + jωX
Или, что тоже самое:
Ζ = ¦Ζ¦ejφ,
где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC)
Активную составляющую входного сопротивления R можно приближенно считать не зависящей от частоты генератора, хотя реально это совсем не так. Здесь работают факторы скин-эффекта, эффекта близости другие эффекты от которых зависит добротность. Но для получения представления как меняется реактивное сопротивление контура от частоты пока этими тонкостями можно пренебречь. Реактивная составляющая является функцией частоты и в зависимости от величины L, C, и ω изменяется по величине и знаку (рис2).
 рис 2
рис 2
В точке ω0 контур попадает в режим, при котором
XC= — XL, X=0. Этот режим называется резонансом напряжений, при этом ω0L — 1/ω0C = 0, откуда
ω0 = 1/√LC или ƒ0 = 1/(2π√LC),
формула резонансной частоты контура, впервые выведенная сэром Вильямом Томсоном (1824 – 1907), великим английским физиком, более известным как лорд Кельвин, в честь которого названа шкала абсолютных температур.
В точке резонанса Ζ = R. Ток в цепи: Ì0 = È/R, напряжения на емкости и индуктивности равны и противоположны по знаку
UC = UL = ω0LÌ0 = (1/ω0C)Ì0
При этом
UL/Ì0 = UC/Ì0 = ω0L = 1/ω0C = √L/C = ρ
ρ–характеристическое или волновое сопротивление контура.
Очевидно, что ρ » R, поэтому UC = UL » E, откуда и произошло название – резонанс напряжений. Т.е. амплитуда напряжения на реактивных элементах на резонансной частоте в десятки и сотни раз превышает амплитуду напряжения источника. Подобное явление наблюдается в механике, например маятник в часах, качели и носит общее название явление резонанса.
Это возрастание амплитуды характеризуется следующими соотношениями
UL/E = UC/E = ρ/R = Q
Q – безразмерная величина, носящая название добротности контура.
Обратим внимание на выражение Q = ρ/R = √L/C/R, из которого следует, что добротность должна расти при увеличении соотношения L/C. Однако, это не совсем так. Дело в том, что при увеличении L одновременно растет и R, ведь число витков и размеры катушки увеличиваются и, грубо говоря, увеличивается длина провода катушки и его омическое сопротивление. Поэтому зависимость величины добротности контура от соотношения индуктивности и емкости носит более сложный характер и простыми формулами не описывается. В начале мы пренебрегли «тонкостями» зависимости активного сопротивления контура от частоты, но здесь уже так легкомысленно поступать нельзя.
Вообще, конструкция контура для разных областей его применения разрабатывалась в основном энтузиастами радиолюбителями с паяльником в руках, интуицией и минимумом расчетов. Так было на заре развития радио. Тогда в результате экспериментов было установлено, что добиться хорошей чувствительности и избирательности приемника, например, можно применив контур с катушкой внушительных размеров. Потом уже с появлением малошумящих полупроводников и высокочастотных ферритов размеры перестали играть такое значение. Но и сегодня практический опыт нельзя оставлять без внимания, советую ознакомится с ним на этом форуме
Амплитудно-частотая характеристика тока в цепи колебательного контура описывается уравнением:
I/I0 = 1/√1+Q2(ƒ/ƒ0-ƒ0/ƒ)2
Фазочастотная характеристика определяется выражением:
φ = arctg[Q(ƒ/ƒ0-ƒ0/ƒ)]
Эти характеристики относительно нормированной частоты ω/ω0 приведены на следующем рисунке: Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазо-сдвигаюшую цепь.
Из этих графиков видно, что колебательный контур можно использовать как частотно-избирательную или фазо-сдвигаюшую цепь.





