Расчет колебательного контура
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители!
Сегодня мы с вами рассмотрим порядок расчета LC контура.
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:
На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F)2/C где:
L – индуктивность катушки в мкГн;
С – емкость конденсатора в пФ;
F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1)
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.
Рассчитать число витков для катушки без сердечника можно по такой формуле:
N=32 *√(L/D) где:
N – требуемое число витков;
L – заданная индуктивность в мкГн;
D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
РЕЗОНАНСНЫЕ СХЕМЫ
Схемы, содержащие R, L, C элементы часто имеют специальные характеристики, полезные во многих приложениях. Поскольку их частотные характеристики (сопротивление, напряжение или ток в зависимости от частоты) могут иметь резкий максимум или минимум на определенных частотах, эти схемы очень важны для работы телевизионных приемников, радиоприемников и передатчиков. В этой главе мы представим различные типы, модели и формулы типичных резонансных цепей.
В этой главе мы представим различные типы, модели и формулы типичных резонансных цепей.
Типичный последовательный резонансный контур показан на рисунке ниже.
Общее сопротивление:Во многих случаях R представляет собой сопротивление потерь индуктивности, которое в случае катушек с воздушным сердечником просто означает сопротивление обмотки. Сопротивления, связанные с конденсатором, часто пренебрежимо малы.
Полные сопротивления конденсатора и индуктора являются воображаемыми и имеют противоположный знак. На частоте w0 L = 1 /w0C, общая мнимая часть равна нулю, и, следовательно, полное сопротивление равно R, имея минимум на w0частота. Эта частота называется Последовательность резонансной частоты.
Типичная характеристика полного сопротивления цепи показана на рисунке ниже.
Из w0L = 1 /w0Коррекция, угловая частота последовательного резонанса: или для частоты в Гц:
f0
Это так называемый Формула Томсона.
Если R мало по сравнению с XL, ИКСC реактивное сопротивление вокруг резонансной частоты, сопротивление резко меняется на последовательная резонансная частотаВ этом случае мы говорим, что схема имеет хорошее избирательность.
Селективность может быть измерена добротность Q Если угловая частота в формуле равна угловой частоте резонанса, мы получим резонансный добротность Eсть Более общее определение показателя качества:
напряжение через индуктор или конденсатор может быть намного выше, чем напряжение от общей схемы. На резонансной частоте полное сопротивление цепи составляет:Z = R
Предполагая, что ток в цепи равен I, общее напряжение в цепи равно
Vкарапуз= I * R
Однако напряжение на индуктивности и конденсаторе
Поэтому
Это означает, что на резонансной частоте напряжения на индуктивности и конденсаторе равны Q0 раз больше, чем общее напряжение резонансного контура.
Типичный пробег VL, VC Напряжение показано на рисунке ниже.
Продемонстрируем это на конкретном примере.
Пример 1
Найти частоту резонанса (f0) и резонансный добротность (Q0) в последовательной цепи ниже, если C = 200 нФ, L = 0.2H, R = 200 Ом и R = 5 Ом. Нарисуйте векторную диаграмму и частотную характеристику напряжений.
Для R = 200 Ом
Это довольно низкое значение для практических резонансных контуров, которые обычно имеют качественные коэффициенты более 100. Мы использовали низкое значение, чтобы легче продемонстрировать работу на векторной диаграмме.
Ток на резонансной частоте I = Vs/ R = 5m>
Напряжения при токе 5mA: VR V =s = 1 V
между тем: VL V =C = Я *w0L = 5 * 10-3 *5000 * 0. 2 = 5V
2 = 5V
Теперь давайте посмотрим на векторную диаграмму, вызвав ее из меню анализа переменного тока TINA.
Мы использовали инструмент Auto Label окна диаграммы, чтобы комментировать изображение.
Фазовая диаграмма хорошо показывает, как напряжения конденсатора и катушки индуктивности компенсируют друг друга на резонансной частоте.
Теперь посмотрим VLи VCпо сравнению с частотой.
Обратите внимание, что VL начинается с нулевого напряжения (потому что его реактивное сопротивление равно нулю при нулевой частоте), а VC начинается с 1 V (потому что его реактивное сопротивление бесконечно при нулевой частоте). Точно так же VL стремится к 1V и VCв 0V на высоких частотах.
Теперь для R = 5 Ом коэффициент качества намного выше:
Это относительно высокий показатель качества, близкий к практическим достижимым значениям.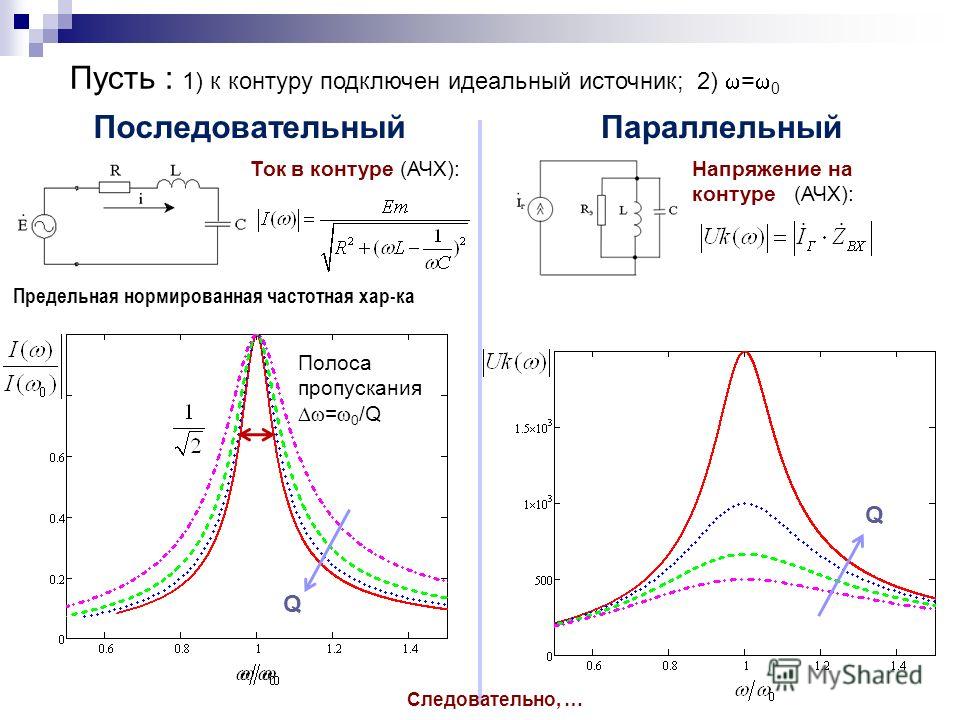
Ток на резонансной частоте I = Vs/ R = 0.2A
между тем: VL V =C = Я *w0L = 0.2 * 5000 * 0.2 = 200
Опять же соотношение между напряжениями равно качеству!
Теперь нарисуем просто VL и VC напряжение против частоты. На векторной диаграмме VR будет слишком маленьким по сравнению с VLи VC
Как мы видим, кривая очень четкая, и нам нужно было построить 10,000 точек, чтобы точно получить максимальное значение. Используя более узкую полосу пропускания на линейной шкале на оси частот, мы получим более подробную кривую ниже.
Наконец, давайте посмотрим на характеристику импеданса схемы: для разных добротностей.
Рисунок ниже был создан с использованием TINA путем замены генератора напряжения на измеритель импеданса. Кроме того, настройте пошаговый список параметров для R = 5, 200 и 1000 Ом. Чтобы настроить пошаговое изменение параметров, выберите «Объект управления» в меню «Анализ», переместите курсор (который превратился в символ резистора) в резистор на схеме и щелкните левой кнопкой мыши. Чтобы установить логарифмическую шкалу на оси импеданса, мы дважды щелкнули по вертикальной оси и установили Scale на Logarithmic и пределы 1 и 10k.
Чтобы установить логарифмическую шкалу на оси импеданса, мы дважды щелкнули по вертикальной оси и установили Scale на Logarithmic и пределы 1 и 10k.
ПАРАЛЛЕЛЬНЫЙ РЕЗОНАНС
Чисто параллельный резонансный контур показан на рисунке ниже.
Если пренебречь сопротивлением потерь индуктивности, R представляет сопротивление утечки конденсатора. Однако, как мы увидим ниже, сопротивление потерь индуктивности может быть преобразовано в этот резистор.
Общий вход:
Допуски (так называемые восприимчивости) конденсатора и индуктора являются воображаемыми и имеют противоположный знак. На частоте w0C = 1 /w0L полная мнимая часть равна нулю, поэтому полная проводимость равна 1 / R — ее минимальное значение и полное сопротивление имеет максимальное значение, Эта частота называется параллельная резонансная частота.
Общая характеристика полного сопротивления чистого параллельного резонансного контура показана на рисунке ниже:
Обратите внимание, что сопротивление изменяется очень быстро вокруг резонансной частоты, хотя мы использовали логарифмическую ось импеданса для лучшего разрешения. Та же самая кривая с линейной осью полного сопротивления показана ниже. Обратите внимание, что при взгляде на эту ось импеданс, по-видимому, меняется еще быстрее вблизи резонанса.
Подверженности индуктивности и емкости равны, но имеют противоположный знак при резонансе: BL = BC, 1 /w0L = w0С, отсюда угловая частота параллельного резонанса:
определяется снова Формула Томсона.
Решение для резонансной частоты в Гц:
На этой частоте допуск Y = 1 / R = G и находится на минимуме (т. Е. Полное сопротивление максимально). течения через индуктивность и емкость может быть намного выше, чем текущий от общей схемы. Если R относительно велико, напряжение и адмитанс резко изменяются вокруг резонансной частоты. В этом случае мы говорим, что схема имеет хорошее избирательность.
Если R относительно велико, напряжение и адмитанс резко изменяются вокруг резонансной частоты. В этом случае мы говорим, что схема имеет хорошее избирательность.
Селективность может быть измерена добротность Q
Когда угловая частота равна угловой частоте резонанса, мы получаем резонансный добротность
Существует также более общее определение показателя качества:
Другим важным свойством параллельного резонансного контура является его трафик, Пропускная способность — это разница между двумя частоты среза, где полное сопротивление падает от своего максимального значения до
максимум.Можно показать, что Δf Пропускная способность определяется по следующей простой формуле:
Эта формула также применима для последовательных резонансных цепей.
Давайте продемонстрируем теорию на нескольких примерах.
Пример 2
Найти резонансную частоту и резонансный фактор качества в чисто параллельном резонансном контуре, где R = 5 кОм, L = 0. 2 H, C = 200 нФ.
2 H, C = 200 нФ.
Резонансная частота:
и резонансный добротность:
Кстати, этот добротность равна IL /IR на резонансной частоте.
Теперь нарисуем диаграмму сопротивления цепи:
Самый простой способ — заменить источник тока измерителем импеданса и выполнить анализ передачи переменного тока.
Вышеупомянутую «чистую» параллельную схему было очень легко исследовать, поскольку все компоненты были включены параллельно. Это особенно важно, когда цепь подключена к другим частям.
Однако в этой схеме сопротивление последовательных потерь катушки не учитывалось.
Теперь давайте рассмотрим следующий так называемый «реальный параллельный резонансный контур» с последовательным сопротивлением потерь катушки и узнаем, как мы можем преобразовать его в «чистую» параллельную цепь.
Эквивалентное сопротивление:
Давайте рассмотрим этот импеданс на резонансной частоте, где 1-w02LC = 0
Также будем предполагать, что добротность Qo = woL / RL>> 1.
На резонансной частоте
Так как на резонансной частотеw0L = 1 /w0C
Zeq=Qo2 RL
Так как в чисто параллельном резонансном контуре на резонансной частоте Zeq = R, реальный параллельный резонансный контур может быть заменен чисто параллельным резонансным контуром, где:
R = Qo2 RL
Пример 3
Сравните диаграммы импеданса реальной параллельной и ее эквивалентной чисто параллельной резонансной схемы.
Резонансная (томсоновская) частота:
Диаграмма импеданса следующая:
Эквивалентное параллельное сопротивление: Req = Qo2 RL = 625 Ом
Эквивалентная параллельная схема:
Диаграмма импеданса:
Наконец, если мы используем копирование и вставку, чтобы увидеть обе кривые на одной диаграмме, мы получим следующую картинку, где две кривые совпадают.
Наконец, давайте исследуем пропускную способность этой схемы.
Расчетное значение:
Давайте подтвердим это графически, используя диаграмму.
ZМакс = 625 ом. Пределы сопротивления, которые определяют частоты среза:
Разница курсоров AB составляет 63.44 Гц, что очень хорошо согласуется с теоретическим результатом 63.8 Гц даже с учетом неточности графической процедуры.
Методы измерения электрического колебательного контура
Эффект резонанса находит своё применение в решении различных технических задач. Одной из таких задач была симуляция резонанса вибростенда электрическим колебательным контуром. Подбор элементов для колебательного контура осуществляется с целью добиться резонанса на заданной частоте с заданной добротностью. Резонансная частота и добротность определяются по нижеприведённым формулам. Для подтверждения расчетной частоты резонанса или добротности требуются практические методы с использованием измерительных приборов. Преимущество виртуальной лаборатории ZETLab в том, что она содержит в себе широкий спектр программ для различных измерений, которые можно использовать для проверки теоретических расчетов.
Преимущество виртуальной лаборатории ZETLab в том, что она содержит в себе широкий спектр программ для различных измерений, которые можно использовать для проверки теоретических расчетов.
Принципиальная схема последовательного колебательного контура
Параметры схемы, приведённой на рисунке 1, вычисляются по следующим формулам:
Резонансная частота электрического колебательного контура
Добротность электрического колебательного контура
Примечание: в формулы для расчета подставляются не паспортные данные элементов (по которым их возможно выбирали), а реальные, которые были измерены с помощью соответствующих измерительных приборов.
Теоретический расчет
R=16 Ом,
L=18 мГн,
C=1,75 мкФ
Резонансная частота
Добротность
Программа «Измерение АЧХ (8 каналов)»
График АЧХ электрического резонансного контура
Измерение добротности по графику АЧХ
По графику АЧХ колебательного контура определяем частоту резонанса курсорными измерениями: f0 = 847 Гц.
Добротность электрического колебательного контура обратно пропорциональна разности относительных частот, соответствующих значениям относительного напряжения 1/√2 (относительно резонансной частоты и резонансного напряжения):
Кроме того добротность может быть вычислена как отношение напряжения в пике резонанса к входному напряжению.
На частоте менее 10% от резонансной частоты напряжение на конденсаторе будет составлять более 99% от входного напряжения. Соответственно ошибка, которую внесёт метод вычисления добротности, составит менее 1%.
Программа «Измерение АЧХ-ФЧХ (4 канала)»
Как известно из радиотехники, полосу пропускания колебательного контура можно найти из частотных характеристик, отмечая граничные частоты, по уровню 1/v2 от максимума модуля амплитудной характеристики для последовательного колебательного контура или максимума сопротивления для параллельного контура. Можно также измерить полосу пропускания резонатора по фазово-частотной характеристике электрического импеданса как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Отношение резонансной частоты к ширине полосы пропускания есть добротность колебательной системы.
Гафики измеренных АЧХ и ФЧХ
f0 = 845,3 Гц
Измерение добротности по АЧХ
АЧХ: f2=898,5 Гц ФЧХ: f2=903,3 Гц
АЧХ: f1=739 Гц ФЧХ: f1=738 Гц
Измерение добротности по ФЧХ
Модальный анализ
Измерение резонанса с помощью программы «Модальный анализ»
Затухающие колебания на выходе электрического колебательного контура
Если на вход системы подать дельта-импульс, то на выходе будет импульсная характеристика системы. Дельта-импульс эмулируется радио-импульсом высокой частоты с 0 периодов (полуволна).
Характеристики колебательного контура:
τ — время релаксации колебаний — время, в течение которого амплитуда колебаний уменьшится в e раз.
λ — логарифмический декремент затухания — логарифм отношения двух последовательных амплитуд колебаний.
Q — добротность контура — отношение энергии запасённой в контуре к убыли энергии за один период колебаний умноженное на 2π.
Взаимный узкополосный спектр, передаточная функция h2
Вычисления по взаимному узкополосному спектру:
Вычисления по переходной характеристике:
Взаимный узкополосный спектр генератора и измерительного канала
Корреляционная функция (белый шум и радиоимпульс)
Корреляционная функция сигнала генератора и выхода колебательного контура
U1=48,922 мВ·g
U2=24,297 мВ·g
U3=12,513 мВ·g
U4=6,498 мВ·g
Узкополосный спектр
Применяя те же самые формулы, что и для АЧХ находим характеристики системы:
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Проведение виброиспытаний на системе с резонансом
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Результаты, полученные в ходе испытаний:
5 Последовательный колебательный контур — СтудИзба
4. Последовательный колебательный контур
4.1. Схема последовательного колебательного контура
Последовательным колебательным контуром называют электрическую цепь, представляющую собой последовательное соединение катушки индуктивности и конденсатора. Его возможные варианты включения как четырехполюсника показа- ны на рис. 4.1 (выход-
ное напряжение сни- Рис. 4.1
мается с конденсатора
или с катушки индуктивности).
Конденсатор и катушка индуктивности имеют внутренние потери энергии, которые учитываются последовательно соединенными с ними эквивалентными сопротивлениями потерь и соответственно. На практике в керамических конденсаторах всегда и потерями в них пренебрегают, тогда эквивалентные схемы последовательных колебательных контуров рис. 4.1 примут вид, показанный на рис. 4.2.
Рекомендуемые файлы
Техническое задание
Инженерия требований и спецификация программного обеспечения
FREE
Маран Программная инженерия
Программаня инженерия
FREE
Заполненные лабы 2,3,5,6,7,8,9,10,14,15
Материаловедение
FREE
ДЗ 2 (ангем) вариант 25
Аналитическая геометрия
Вариант 10 — ЛР №2, 3, 7, 8, 11, 12, 15
Безопасность жизнедеятельности (БЖД и ГРОБ)
FREE
Рис. 4.2
В дальнейшем будем рассматривать схему на рис. 4.2а, в которой выходное напряжение снимается с емкости, а схему
71
на рис. 4.2б аналогично рассмотрите самостоятельно.
4.2. Входное сопротивление последовательного
колебательного контура
Определим входное сопротивление последовательного колебательного контура показанного на рис. 4.3. Полное комплексное сопротивление равно
. (4.1)
Рис. 4.3 Его модуль , аргумент , активная
и реактивная составляющие соответственно равны:
Зависимости этих функций от частоты сигнала при Ом, мГн, нФ показаны на рис. 4.4. На частоте
(4.2)
реактивное сопротивление и принимает минималь-
72
ное значение, равное ,
. (4.3)
Рис. 4.4
При отклонении частоты от модуль сопротивления контура резко возрастает. В области реактивное сопротивление положительно, то есть контур имеет индуктивный характер сопротивления, сдвиг фаз между напряжением и током . В области реактивное сопротивление отрицательно и сопротивление контура имеет емкостный характер .
4.3. Ток и напряжения в контуре, резонансные явления
Подключим к контуру рис. 4.2а идеальный источник гармонического напряжения, получим схему на рис. 4.5.
73
Комплексная амплитуда ЭДС источника равна , тогда для комплексной амплитуды тока в контуре получим
Рис. 4.5 , (4.4)
а для его амплитуды и начальной фазы соответственно
, (4.5)
. (4.6)
Зависимости амплитуды и начальной фазы тока от частоты при Ом, мГн, нФ, В и представлены на рис. 4.6.
Рис. 4.6
74
Ток в контуре резко нарастает при приближении частоты источника к частоте (4.3), его максимальное значение равно
. (4.7)
Однако резонанс тока в последовательном колебательном контуре отсутствует, так как ток в контуре равен току источника, а не возрастает по сравнению с ним.
Так как изменения тока происходят в малой окрестности около частоты , то целесообразно строить графики в координатах абсолютной расстройки, равной
, (4.8)
то есть производится смещение начала координат в точку .
Те же графики, что и на рис. 4.6, но в координатах , показаны на рис. 4.7.
Рис.4.7
Как видно, координаты абсолютной расстройки удобны для построения графиков частотных характеристик колебательного контура.
75
Определим комплексные амплитуды напряжений на элементах контура:
, (4.9)
, (4.10)
. (4.11)
Тогда для амплитуд этих напряжений получим:
, (4.12)
, (4.13)
. (4.14)
76
а их начальные фазы равны
, (4.15)
, (4.16)
. (4.17)
На рис. 4.8 показаны зависимости амплитуд напряжений на элементах контура при Ом, мГн, нФ, В и (обратите внимание, что сопротивление потерь в 10 раз больше, чем в предыдущем примере)
Рис. 4.8
77
На рис. 4.8а кривые представлены в широком диапазоне частот, а на рис. 4.8б – в координатах абсолютной расстройки и узком частотном интервале в окрестности .
Как видно на частоте напряжения на индуктивности и емкости резко возрастают по сравнению с напряжением (ЭДС) источника (становятся много больше ), то есть в последовательном колебательном контуре имеет место резонанс напряжений на реактивных элементах. Напряжение на сопротивлении не превышает входной ЭДС, поэтому о его резонансе говорить не приходится.
Частоты, на которых напряжения и максимальны, примерно равны , поэтому частоту (4.2)
называют резонансной.
Точные значения резонансных частот нетрудно найти, определив производные и по частоте и приравняв результат нулю (проделайте это самостоятельно). Как видно из кривых рис. 4.8б, эти частоты отличаются от весьма незначительно (резонансная частота напряжения емкости меньше , а индуктивности – больше) и тем сильнее, чем больше сопротивление (для того, чтобы это увидеть графически и было выбрано Ом).
Принимая резонансную частоту равной , определим резонансные амплитуды напряжений,
, (4.18)
, (4.19)
78
. (4.20)
Подстановкой нетрудно убедиться, что
, (4.21)
тогда резонансные напряжения на реактивных элементах одинаковы и равны
. (4.22)
Величину
(4.23)
называют добротностью колебательного контура. Согласно (4.22) добротность является важнейшей характеристикой резонансных явлений.
На рис. 4.9 приведены зависимости от частоты сдвигов фаз напряжений на элементах контура относительно фазы ЭДС источника,
,
, (4.24)
,
начальные фазы напряжений определяются из (4.15)-(4.17). Как видно, напряжение на индуктивности опережает по фазе
79
напряжение на сопротивлении на , а на емкости – отстает от него на . Напряжение на индуктивности опережает по фазе напряжение на емкости на , то есть эти напряжения противофазны.
Рис. 4.9
4.4. Вторичные параметры колебательного контура
Последовательный колебательный контур полностью описывается своими первичными параметрами , и . Однако их численные значения малоинформативны, и на практике широко используются дополнительные (вторичные) параметры.
Резонансная частота контура
(4.25)
измеряется в радианах делить на секунду, или
, (4.26)
80
которая измеряется в герцах. Ее значение сразу определяет частоту настройки колебательного контура.
Характеристическое сопротивление контура
(4.27)
измеряется в Омах и численно равно модулю реактивного сопротивления индуктивности или емкости (отдельно) на резонансной частоте .
Добротность контура
(4.28)
— величина безразмерная, характеризует резонансные свойства колебательного контура. Физический смысл добротности – это отношение максимальной энергии, накапливаемой в реактивных элементах, к энергии потерь в контуре за период колебаний на резонансной частоте.
Как видно из (2.28), добротность возрастает с уменьшением сопротивления потерь контура, которое практически полностью определяется потерями мощности сигнала в катушке индуктивности. На практике добротность . В большинстве случаев добротность составляет 70-100. Для получения высоких добротностей 150-300 используют специальный провод (покрытый тонким слоем серебра – «серебрянку»), вжигание серебряного проводника в керамический каркас и ряд других инженерных решений. Более высокие значения добротности LC колебательных контуров получить не удается.
Явление резонанса и понятие добротности используются и в механических колебательных системах. Например,
81
в кристаллах кварца (горного хрусталя) очень малы потери энергии механических колебаний, то есть они имеют высокую добротность. Поэтому изготовленные из него бокалы при слабом ударе издают продолжительный звон. В железе, алюминии или пластмассе эти потери велики, поэтому сделанные их них бокалы не обладают соответствующим звучанием.
Помимо малых потерь энергии механических колебаний монокристаллы кварца характеризуются явлением пьезоэффекта (повторите материал по физике): при возникновении в кварцевой пластине механических колебаний на ее гранях возникает переменное напряжение и наоборот, приложенное к кристаллу переменное напряжение вызывает механические колебания кристалла. Из кварцевых пластин изготавливают электронные устройства — кварцевые резонаторы. С электрической точки зрения они эквивалентны последовательному колебательному контуру с очень высокой добротностью .
4.5. Частотные характеристики контура
Под частотными характеристиками последовательного колебательного контура (рис. 4.2) понимают зависимость от частоты характеристик комплексного коэффициента передачи по напряжению вида
(4.29)
или
, (4.30)
где — комплексная амплитуда напряжения на емкости (обычно полагают, что потери в емкости отсутствуют), — комплексная амплитуда напряжения на последовательном со-
82
единении индуктивности с ее сопротивлением потерь (напряжение на реальной катушке индуктивности).
Рассмотрим комплексный коэффициент передачи напряжения емкости (аналогичный анализ проведите самостоятельно). Из (4.29) с учетом (4.11) получим
. (4.31)
Из (4.31) АЧХ и ФЧХ контура имеют вид
, (4.32)
. (4.33)
Частотные характеристики последовательного колебательного контура при мГн, нФ для двух значений Ом (сплошные линии) и Ом (пунктир) в различных масштабах показаны на рис. 4.10 в координатах абсолютной расстройки. Кривые резко возрастает при приближении частоты сигнала к резонансной частоте контура (4.25). Максимум коэффициента передачи имеет место приближенно
83
на частоте и равен добротности контура,
. (4.34)
Рис. 4.10
На рис. 4.10а приведены АЧХ в абсолютном, а на рис. 4.10б в относительном масштабах по оси ординат. На рис. 4.11 показаны ФЧХ этих контуров.
Рис. 4.11.
Как видно, с ростом сопротивления потерь в колеба-
84
тельном контуре максимум АЧХ падает (так как уменьшается добротность) и кривая АЧХ становится «шире», а ФЧХ – более пологой.
По форме АЧХ видно, что последовательный колебательный контур является узкополосным частотным фильтром.
4.6. Обобщенная расстройка
Исследование частотных характеристик колебательного контура удобнее всего проводить в координатах обобщенной расстройки , равной
. (4.35)
Как видно, она зависит от частоты сигнала и параметров контура. Проведем преобразования
. (4.36)
Обозначая абсолютную расстройку
, (4.37)
85
и приближенно полагая в первой дроби , получим
. (4.38)
Из (4.38) видно, что обобщенная расстройка прямо пропорциональна абсолютной расстройке, то есть частоте сигнала (начало координат смещено в точку ).
4.7. Частотные характеристики в координатах обобщенной
расстройки
Комплексное входное сопротивление контура (4.1) в координатах можно записать в виде
, (4.39)
а его модуль, аргумент, активную и реактивную составляющие соответственно
(4.40)
Эти характеристики как функции обобщенной расстройки показаны на рис. 4.12. Сплошной линией показаны точные, а пунктирной – приближенные значения, полученные из (4.40).
86
Рис. 4.12
Проведем расчет комплексного коэффициента передачи, приближенно заменив в числителе (4.31) на ,
. (4.41)
Частотные характеристики последовательного колебательного контура в координатах обобщенной расстройки имеют вид
, (4.42)
(4.43)
Зависимости АЧХ и ФЧХ показаны на рис. 4.13 пунктирными линиями. Их точные значения показаны сплошными кривыми.
Как видно, расчеты частотных характеристик в координатах обобщенной расстройки имеют вполне удовлетворитель-
87
ную точность в достаточно широкой окрестности резонансной частоты, то есть там, где они и представляют практический интерес.
Рис. 4.13
С помощью обобщенной расстройки можно проводить расчеты токов и напряжений в контуре:
, (4.44)
, (4.45)
, (4.46)
, (4.47)
Выражения и вычисления существенно упрощаются.
Запишите самостоятельно выражения для амплитуд и начальных фаз тока и напряжений на элементах контура. Постройте их зависимости от частоты и обобщенной расстройки, оцените погрешность вычислений в координатах .
88
4.8. Полоса пропускания и коэффициент
прямоугольности
Определим полосу пропускания контура, расчет проведем в координатах обобщенной расстройки (рис. 4.14).
Максмум АЧХ контура равен добротности , тогда полоса пропускания определяется на уровне
.
С учетом (4.42) урав-
нение имеет
вид Рис. 4.14
(4.48)
и его решения равны
Интервал обобщенной расстройки в полосе пропускания
,
с другой стороны из (4.38)
,
89
тогда получим уравнение
,
а полоса пропускания будет равна
. (4.49)
Как видно, полоса пропускания контура с заданной частотой настройки определяется только его добротностью. Высокодобротный контур позволяет реализовать узкополосный частотный фильтр. Как уже отмечалось, большие значения обеспечить достаточно сложно.
Для определения коэффициента прямоугольности необходимо найти полосу пропускания контура на уровне 1/10 от максимума. Для этого составим уравнение в координатах ,
, (4.50)
решения которого равны
90
Интервал величин обобщенной расстройки в полосе пропускания на уровне 1/10 от максимума равен
,
тогда получим уравнение
,
а полоса пропускания будет равна
. (4.51)
В результате коэффициент прямоугольности колебательного контура оказывается равным
.
Как видно, последовательный колебательный контур является полосовым частотным фильтром с низкой избирательностью.
4.9. Влияние внутреннего сопротивления источника
сигнала и нагрузки на резонансные свойства контура
Рассмотрим контур с подключенным реальным источником напряжения (- его внутреннее сопротивление) и сопротивлением нагрузки (рис. 4.15). Можно провести анализ этой цепи отдельно, однако целесообразнее преобразовать
91
ее к уже рассмотренной цепи вида рис. 4.5 (с идеальным источником напряжения и без нагрузки) и воспользоваться уже полученными результатами анализа.
Рис. 4.15
Как видно, сопротивление источника просто складывается с , увеличивая сопротивление потерь контура. Нагрузка же подключена параллельно емкости, и тогда параллельное соединение необходимо эквивалентно преобразовать в последовательное соединение элементов (как по-
Рис. 4.16 казано на рис. 4.16). Эти
цепи эквивалентны, если равны их полные комплексные сопротивления, тогда получим
.
Преобразуя дроби и приводя обе части равенства к алгебраической форме записи комплексных чисел, можно записать
.
92
Комплексные числа равны тогда и только тогда, когда равны отдельно их действительные и мнимые части, поэтому после алгебраических преобразований получим два уравнения для неизвестных ,
, (4.52)
. (4.53)
Проделайте необходимые преобразования самостоятельно.
Как видно, эквивалентные параметры последовательной цепи зависят от частоты и, строго говоря, такое преобразование возможно только на фиксированной частоте. При анализе колебательного контура интерес представляет окрестность его резонансной частоты , поэтому в (4.52) и (4.53), приняв и условие
, (4.54)
получим
, (4.55)
. (4.56)
Эти равенства является точными на частоте и приближенными в ее окрестности. На рис. 4.17 показаны зависимости эквивалентных сопротивления и емкости от абсолютной
93
расстройки при нФ и рад/с и различных значениях сопротивления нагрузки . Как видно, при больших , и особенно при выполнении условия (4.54), величины и практически постоянны в широкой окрестности резонансной частоты.
Рис. 4.17
Таким образом эквивалентная схема последовательного колебательного контура с реальным источником сигнала и нагрузкой имеет вид, показанный на рис. 4.18, где — эквивалентное сопротивление потерь, рав-
Рис. 4.18 ное
. (4.56)
Контур рис. 4.18 уже изучен, его резонансные свойства определяются эквивалентной добротностью ,
94
. (4.57)
Как видно, внутреннее сопротивление источника сигнала снижает эквивалентную добротность, его влияние будет мало, если
или , (4.58)
Собственное сопротивление потерь достаточно мало (доли Ома — единицы Ом), поэтому источник сигнала для последовательного колебательного контура должен быть практически идеальным.
Нагрузка контура также снижает его добротность, чем больше , тем меньше падает . Для того, чтобы влияние нагрузки было невелико, необходимо выполнение условия
или . (4.59)
На практике величина характеристического сопротивления составляет сотни Ом – килоОмы, добротность лежит в пределах от нескольких десятков до 150, тогда произведение составляет десятки — сотни килоОм. С учетом сделанных оценок необходимое сопротивление нагрузки при условии (4.59) оказывается достаточно большим, например, 1 МОм, что крайне сложно обеспечить на практике.
Для ослабления влияния нагрузки на добротность контура используют ее неполное включение, один из вариантов схемы показан на рис. 4.19.
95
Рис. 4.19
Проведите самостоятельно анализ этой цепи аналогично предыдущей, преобразовав параллельное соединение в последовательное, получите выражение для эквивалентной добротности, в результате можно записать
, (4.60)
где — коэффициент включения нагрузки в контур, равный
. (4.61)
Требования к сопротивлению нагрузки определяются неравенством
, (4.62)
что значительно слабее (4.59). Например, при кОм и (типичное значение) необходимо выполнение условия кОм, что вполне приемлемо на практике.
96
4.10. Расчеты цепей с последовательными
колебательными контурами
Расчет гармонических токов и напряжений в электрических цепях с колебательными контурами проводится методом комплексных амплитуд чаще всего в координатах обобщенной расстройки.
Рассмотрим пример, показанный на рис. 4.20, в котором на заданной частоте рад/с при Ом, мГн, нФ, Ом и В необходимо определить комплексную амплитуду напряжения на нагрузке . Расчет в координатах частоты будет достаточно громоздким (проведите его самостоятельно, чтобы убедиться в этом). Рис. 4.20
Резонансная частота
контура равна
,
а добротность соответственно
.
В координатах обобщенной расстройки , равной
,
97
сопротивление последовательного колебательного контура равно Ом.
Сопротивление параллельного соединения контура с нагрузкой определяется выражением
Ом.
Вычислим общее сопротивление цепи,
,
в результате получим
Ом.
Комплексная амплитуда тока в цепи равна
а напряжения на нагрузке соответственно
В.
Переход к координатам обобщенной расстройки существенно упрощает расчеты цепей с колебательными контурами. При расчетах широко используют известные выражения для коэффициента передачи и других характеристик контура.
98
Рассмотрим пример, показанный на рис.4.21 при В рад/с, Ом, мГн и нФ. Необходимо рассчитать мгновенные значения напряжения на емкости последовательного колебательного контура .
Резонансная частота и добротность равны Рис. 4.21
, ,
тогда для обобщенной расстройки получим
.
Комплексный коэффициент передачи определяется выражением
,
тогда комплексная амплитуда напряжения на емкости равна
В,
а для его мгновенных значений получим
В.
99
4.11. Моделирование последовательного колебательного
контура
На рис. 4.22 показана модель последовательного колебательного контура Ом, мГн и пФ с нагрузкой МОм в пакете программ MicroCAP7. На рис. 4.23 приведены результаты моделирования в АЧХ и ФЧХ режиме «Stepping» при изменении сопротивления потерь от 50 Ом (верхние кривые) до 150 Ом (нижние
кривые) с шагом 50 Ом.
Рис.4.22 На рис. 4.24 пока-
заны аналогичные зависимости при Ом и изменении сопротивления нагрузки от МОм (нижние кривые) до МОм верхние кривые) с шагом 1МОм .
Как видно по результатам моделирования, максимум АЧХ снижается с ростом сопротивления потерь и уменьшением сопротивления нагрузки, причем даже при большом МОм добротность контура существенно уменьшается. При этих условиях АЧХ и ФЧХ становятся более пологими.
На рис. 4.25 представлены результаты моделирования контура при изменении его емкости от 100пФ (правая кривая) до 200пФ (левая кривая) с шагом 50 пФ для Ом. Такие изменения происходят при настройке колебательного контура в радиоприемнике с помощью конденсатора переменной емкости.
Проведите расчеты, подтверждающие результаты моделирования, например, вычислите максимальные значения АЧХ при соответствующих параметрах цепи.
100
101
102
103
4.12. Применение последовательного колебательного
контура
Последовательный колебательный контур широко используется как узкополосный частотный фильтр. Таким фильтром является преселектор (предварительный селектор), который присутствует в любом супергетеродинном радиоприемнике (факультативно поинтересуйтесь у преподавателя, как работает супергетеродинный радиоприемник), его условная схема показана на рис. 4.26. Антенна приемника включена в контур как источник сигнала, а напряжение с емкости подается на вход усилителя высокочастотного сигнала (УВЧ), входное сопротивление которого является нагрузкой колебательного контура. Так как транзисторный УВЧ имеет невысо-
Рис. 4.26 кое входное сопротивление,
то используется неполное включение нагрузки. Задача преселектора – фильтрация «зеркального канала» приема в супергетеродинном приемнике.
На базе последовательного колебательного контура можно реализовать режекторный фильтр, пример которого показан на рис. 4.27. На рис 4.28 показана его модель при мГн, нФ и Ом, сопротив-
лении потерь катушки ин-
дуктивности Ом и сопротивлении нагрузки
Рис. 4.27 кОм, а на рис. 4.29 –
АЧХ и ФЧХ.
104
Рис. 4.28
Рис. 4.29
Как видно, фильтр подавляет сигнал в окрестности частоты 160 кГц. Нетрудно спроектировать такой фильтр на частоту 50 или 100 Гц, что часто необходимо в биомедицинской аппаратуре, питающейся от силовой сети переменного тока 220В с частотой 50 Гц (проведите необходимые расчеты и схемотехническое моделирование).
105
4.13. Задания для самостоятельного решения
Задание 4.1. Определите сопротивление потерь колебательного контура при , рад/с и мГн.
Задание 4.2. Определите сопротивление потерь колебательного контура при полосе пропускания рад/с и мГн.
Задание 4.4. Определите полосу пропускания колебательного контура при рад/с, нФ и сопротивлении потерь Ом.
Задание 4.4. Определите добротность колебательного контура при рад/с и полосе пропускания рад/с.
Задание 4.5. Определите напряжение на катушке индуктивности контура рис. 4.30 при мГн, пФ,
Ом, В, Ом и рад/с. Расчет проведите обычным методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки, сравните результаты.
Рис. 4.30
Задание 4.6. Определите напряжение на емкости контура рис. 4.31 при мГн, нФ, Ом, В, Ом и рад/с. Расчет проведите обычным
106
методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки
сравните результаты. Рис. 4.31
Задание 4.7. Вычислите резонансные значения тока и напряжение на емкости контура при мГн, нФ, Ом и ЭДС идеального источника напряжения В.
Задание 4.8. В координатах обобщенной расстройки вычислите напряжение на нагрузке в цепи на рис. 4.32 при В, мГн, нФ, Ом, Рис. 4.32
Ом, кОм и рад/с.
Рекомендуем посмотреть лекцию «9. Районирование в экономической и социальной географии».
Задание 4.9. Получите выражение для АЧХ цепи, показанной на рис. 4.33, постройте ее график. Проанализируйте влияние нагрузки и сопротивлений и на форму АЧХ.
Рис. 4.33
«Резонансный трансформатор» — Анапский Индустриальный Техникум
В рамках работы кружка «Электротехника и электроника» силами участников кружка был изготовлен маломощный резонансный трансформатор (трансформатор Теслы) для демонстрации электрических разрядов в атмосфере (корона).
Работу резонансного трансформатора можно объяснить на примере обыкновенных качелей. Если их раскачивать в режиме принудительных колебаний, то максимально достигаемая амплитуда будет пропорциональна прилагаемому усилию. Если раскачивать в режиме свободных колебаний, то при тех же усилиях максимальная амплитуда вырастает многократно. Так и с трансформатором Теслы — в роли качелей выступает вторичный колебательный контур, а в роли прилагаемого усилия — генератор. Их согласованность («подталкивание» строго в нужные моменты времени) обеспечивает первичный контур или задающий генератор (в зависимости от устройства).
К изготовлению в рамке работы кружка принята следующая можификация трансформатора Теслы
SSTC (Solid State Tesla Coil) — генератор выполнен на полупроводниках. Она включает в себя задающий генератор (с регулируемой частотой, формой, длительностью импульсов) и силовые ключи (мощные полевые MOSFETтранзисторы). Данный вид катушек Тесла является самым интересным по нескольким причинам: изменяя тип сигнала на ключах, можно кардинально изменять внешний вид разряда. Также ВЧ сигнал генератора можно промодулировать звуковым сигналом, например музыкой — звук будет исходить из самого разряда. Впрочем, аудиомодуляция возможна (с небольшими доработками) и в VTTC. К прочим достоинствам можно отнести низкое питающее напряжение и отсутствие шумного искрового разрядника, как в SGTC.
Принципиальная схема устройства приведена на рисунке ниже:
Рис. 1. Принципиальная схема резонансного трансформатора.
Первичная обмотка трансформатора изготовлена из медной трубки диаметром 9 мм и насчитывает 2,5 витка. Для изготовления вторичной обмотки применен провод диаметром 0,14 мм витков во вторичной обмотке 1250.
В качестве корпуса прибора был использован корпус от устаревшего ПК, то же касается и источника питания 12В.
Рис. 2. Внешний вид резонансного трансформатора.
В ходе экспериментов с трансформатором Теслы по демонстрации коронного разряда в атмосфере к антенне была прикреплена игла для обеспечения наилучших условий возникновения разряда.
Рис. 3. Внешний вид антенны трансформатора с закрепленной иглой
Рис. 4. Коронный разряд в атмосфере.
Как известно, под воздействие электрического поля высокой напряженности газ может ионизироваться и превращаться в плазму, которая, в свою очередь, проводит электрический ток. В следующем эксперименте наблюдалось свечение ионизированного газа в колбе обычной лампы накаливания:
Рис. 5. Свечение газа в колбе лампы накаливания, помещенной в электрическое поле резонансного трансформатора
Показать еще
(PDF) Comparison of power losses in switch of boost qrpc with parallel and series resonant circuits
46 ISSN 1607-7970. Техн. електродинаміка. 2016.№ 4
аналогично предыдущим. Исследова-
лись КРИП-ПНТ с мощностью до 250
Вт, частотой коммутации до 500 кГц,
при экспериментальном исследовании
использовался ключевой карбидо-
кремниевый транзистор SPW17N80C3.
Мощность (P) и энергия (Q) потерь в
транзисторных ключах повышающих
КРИП-ПНТ приведены в таблице.
Проведённые исследования потерь мощности на транзисторе КРИП-ПНТ в процессе переключения позво-
ляют сделать следующие выводы. Статические потери являются основными (82%) в КРИП с параллельным
резонансным контуром, а в КРИП с последовательным контуром преобладают динамические потери (более
82%). Динамические потери можно уменьшить, если устранить влияние паразитного колебательного контура
между Lr и Cds на время выключения. Статические потери уменьшаются при увеличении индуктивности и умень-
шении ёмкости резонансного контура.
1. Войтенко В.П. Этапы алгоритма квазиоптимального регулирования в системе с импульсным преобразователем
// Технічна електродинаміка.. – 2012. – № 3. – С. 125–126.
2. Городний А.Н. Анализ мощности рассеивания транзисторным ключом в последовательных импульсном и квази-
резонансном преобразователях // Технічна електродинаміка.. – 2012. – № 3. – С. 75–76.
3. Шидловський А.К., Жаркін А.Ф., Пазєєв А.Г. Безперервні наближені моделі перетворювачів змінної напруги в
постійну з активною корекцією коефіцієнта потужності // Технічна електродинаміка. – 2011. – № 6. – С. 11–17.
4. Denisov Y., Gorodny A., Gordienko V., Yershov R., Stepenko S., Kostyrieva О., Prokhorova A. Switch operation power
losses of quasi-resonant pulse converter with parallel resonant circuit // Proceedings of the IEEE 36th International Conference on
Electronics and Nanotechnology (ELNANO-2016), April 19-21, 2016, Kyiv, Ukraine. – 2016. – Pp. 327–332.
УДК 621.316.721
ПОРІВНЯННЯ ВТРАТ ПОТУЖНОСТІ В КЛЮЧАХ ПІДВИЩУЮЧИХ КРІП З ПАРАЛЕЛЬНИМ І ПОСЛІДОВ-
НИМ РЕЗОНАНСНИМИ КОНТУРАМИ
Ю.О.Денисов, докт.техн.наук, О.М.Городній, канд.техн.наук, В.В.Гордіенко, канд.техн.наук,
С.А.Степенко, канд.техн.наук, Р.Д.Єршов, Т.М.Тепла
Чернігівський національний технологічний університет,
вул. Шевченка, 95, Чернігів, 14027, Україна. e-mail: [email protected]
У роботі виконано розрахунок енергетичних показників електромагнітних процесів в транзисторних ключах підвищуючих
квазірезонансних імпульсних перетворювачів (КРІП) з паралельним і послідовнним резонансними контурами. Розрахунки
виконано з використанням операторного методу і методу припасовування. Для кожного інтервалу комутації отримано
аналітичні вирази, які дозволили оцінити енергетичні втрати на кожному інтервалі, а також загальні втрати. Результа-
ти дослідження дозволили порівняти два перетворювача з однаковими параметрами живлення, силової частини і наван-
таження в залежності від способу підключення резонансного контуру. Бібл. 4, табл. 1, рис. 4.
Ключові слова: резонансний контур, квазірезонансний імпульсний перетворювач, транзисторний ключ
COMPARISON OF POWER LOSSES IN SWITCH OF BOOST QRPC WITH PARALLEL
AND SERIES RESONANT CIRCUITS
Yu.О.Denysov, О.М.Gorodniy, V.V.Gordienko, S.A.Stepenko, R.D.Yershov, Т.М.Tepla
Chernihiv National University of Technology,
Shevchenka str., 95, Chernihiv, 14027, Ukraine. e-mail: [email protected]
In this work the calculation of energy indicators of electromagnetic processes in power switches of boost quasi-resonant pulse con-
verters (QRPC) with parallel and series resonant circuits is performed. The calculations were performed using the operator method
and the method of stitching the results of change of transistor switch current and voltage. For each switching interval the analytical
expressions were obtained, which allow to estimate the energy losses at each interval, as well as total losses. The findings made it
possible to compare two converters with the same parameters of supply, power stage and load depending on the connection of the
resonant circuit. References 4, table 1, figures 4.
Key words: resonant circuit, quasi-resonant pulse converter, transistor switch
1. Voitenko V.P Algorithm stages of quasi-optimal regulation in system with a pulse converter // Tekhnichna elektrodynamika. –
2012. – No 3. – Pp. 125–126 (Rus.).
2. Gorodnyi A.N. Analyzing of transistor switch dissipation power in sequential type switched-mode and quasi-resonant zero current
switch converters // Tekhnichna elektrodynamika. – 2012. – No 3. – Pp. 75–76 (Rus.).
3. Shydlovskyi A.K., Zharkin A.F., Pazieiev A.G. Continuous approximate model of AC/DC converters with active power factor cor-
rection // Tekhnichna elektrodynamika. – 2011. – No 6. – Pp. 11–17 (Ukr.).
4. Denisov Y., Gorodny A., Gordienko V., Yershov R., Stepenko S., Kostyrieva О., Prokhorova A. Switch operation power losses of
quasi-resonant pulse converter with parallel resonant circuit // Proceedings of the IEEE 36th International Conference on Electronics
and Nanotechnology (ELNANO-2016), April 19-21, 2016, Kyiv, Ukraine. – 2016. – Pp. 327–332.
Надійшла 22.01.2016
Остаточний варіант 26.05.2016
КРИП-ПНТ с параллельным
контуром
КРИП-ПНТ с последова-
тельным контуром
Интервалы P, Вт Q, мкДж Q, % P, Вт Q, мкДж Q, %
Включения 0.360 0.002 0.20 0.120 0.001 0.07
Открытого состояния 5.888 0.650 64.48 1.010 0.257 17.15
Открытого состояния
транзистора и диода 1.753 0.180 17.86 0.045 0.007 0.46
Выключения 0.641 0.176 17.46 0.880 1.234 82.32
Всего 2.061 1,008 100 0.670 1.499 100
Сводка методов расчета емкости нагрузки и отклонения частоты кварцевого генератора
Метод расчета емкости нагрузки
При проектировании схемы многие инженеры не знают, как рассчитать нагрузочную емкость кварцевого генератора. При проектировании многие люди используют свой опыт для добавления 20 ПФ, или 22 ПФ, 18 ПФ.
Два контакта кварцевого генератора соединяются с инвертором внутри микросхемы (например, однокристальным микрокомпьютером), а затем объединяются с внешними согласующими конденсаторами CL1, CL2, R1, R2 для формирования генератора Пирса. Как показано ниже:
На приведенном выше рисунке U1 — это инвертирующий усилитель с большим коэффициентом усиления, CL1 и CL2 — согласующие конденсаторы, которые являются конденсаторами деления напряжения в трехточечной конденсаторной цепи, и точкой заземления. — точка разделения напряжения. Принимая точку заземления или точку делителя напряжения в качестве контрольной точки, вход и выход находятся в противоположных фазах, но с точки зрения параллельного резонансного контура, то есть двух концов кристалла кварца, положительная обратная связь формируется для убедитесь, что цепь продолжает колебаться. Они немного повлияют на частоту колебаний. Используйте и настройте частоту и форму волны, а также повлияйте на амплитуду. X1 представляет собой кристалл, который эквивалентен индуктивности в трехточечном типе. R1 — сопротивление обратной связи (обычно ≥1 МОм), которое превращает инвертор в линейную рабочую зону в начале колебаний. R2 и согласующий конденсатор сформировать сеть, обеспечивающую сдвиг фазы на 180 градусов, чтобы ограничить амплитуду колебаний и предотвратить перегрузку кварцевого генератора на выходе инвертора и его повреждение.
Здесь задействован очень важный параметр кварцевого генератора, а именно емкость нагрузки CL (емкость нагрузки), которая представляет собой общую эффективную емкость на двух концах кристалла в цепи (не согласующая емкость, внешняя по отношению к кварцевому генератору)), которая в основном влияет на резонансную частоту нагрузки и эквивалентное резонансное сопротивление нагрузки. Вместе с кварцевым резонатором она определяет рабочую частоту контура генератора. Регулируя емкость нагрузки, рабочую частоту генератора может быть настроен на номинальное значение.
Формула емкости нагрузки выглядит следующим образом:
C_L=C_S+(C_D×C_G)/(C_D+C_G )
где CS — паразитная емкость между двумя выводами кристалла (шунтирующая емкость)
CD представляет собой общую емкость от выходного контакта схемы кварцевого генератора до земли, включая емкость следа печатной платы CPCB, паразитную емкость вывода микросхемы CO и внешнюю согласующую емкость CL2, то есть CD = CPCB.6=1.67。
Как правило, при выборе кварцевого генератора точность лучше. Чипы, такие как STM32, в основном приемлемы, когда ppm меньше 30.
, онлайн-калькулятор
Калькулятор и формулы для последовательной цепи, состоящей из катушки, конденсатора и резистора
Вычислитель серии RCL
Этот калькулятор возвращает наиболее важные значения последовательного резонансного контура, состоящего из резистора, катушки и конденсатора.
Омическое сопротивление R представляет собой внешний демпфирующий резистор или сопротивление потерь катушки.
Вычислитель резонансного контура серии |
Формулы для резонансного контура серии RLC
Последовательный колебательный контур представляет собой решетчатый или фильтрующий контур. Допускаются частоты, близкие к резонансной.
Сила тока одинакова во всех точках измерения.
Ток и напряжение синфазны на омическом сопротивлении.
При индуктивном сопротивлении катушки напряжение опережает ток на + 90 °.
При емкостном сопротивлении конденсатора напряжение отстает от тока на -90 °.
Следовательно, U L и U C сдвинуты по фазе на 180 °, т.е. не совпадают по фазе.
Полное сопротивление резонансного контура называется импедансом Z. Закон Ома применим ко всей цепи. 2} \)
В резонансе X L = X C .Фаза напряжения противоположная; два значения компенсируют друг друга, и применяется следующее:
\ (\ Displaystyle Z = R \)
Ток и напряжение
Ток наибольший при резонансе
\ (\ Displaystyle I_0 = \ гидроразрыва {U} {Z_0} = \ гидроразрыва {U} {R} \)
Если есть резонанс, значит напряжение увеличивается.Напряжение на L и C может быть больше, чем приложенное напряжение
Качество Q и демпфирование d
Качество Q указывает на увеличение напряжения
\ (\ Displaystyle Q = \ гидроразрыва {U_L} {U} = \ гидроразрыва {U_C} {U} = \ гидроразрыва {X_L} {R} = \ гидроразрыва {X_C} {R} \)
Демпфирование: \ (\ displaystyle d = \ frac {1} {Q} \)
Пропускная способность
Полоса пропускания определяет частотный диапазон между верхней и нижней частотой среза.Чем выше качество Q, тем уже резонансный контур.
\ (\ displaystyle b = \ frac {f_0} {Q} = f_0 · d = \ frac {f_0 · R} {X_L} = \ frac {f_0 · U} {U_L} \)
Частоты среза
Верхняя частота отсечки: \ (\ displaystyle f_ {go} = f_0 + \ frac {b} {2} \)
Нижняя частота отсечки: \ (\ displaystyle f_ {go} = f_0- \ frac {b} {2} \)
Следующее относится к частоте среза:
\ (\ Displaystyle f = f_ {go} \) или \ (\ displaystyle f = f_ {gu} \)
\ (\ Displaystyle φ = 45 ° \)
\ (\ Displaystyle I_g = \ гидроразрыва {I_0} {\ sqrt {2}} \)
\ (\ Displaystyle U_R = \ гидроразрыва {U} {\ sqrt {2}} \)
\ (\ Displaystyle Z_g = \ sqrt {2} · Z_0 \)
|
Калькулятор импеданса LC-цепи серии
• Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц
Этот последовательный калькулятор импеданса LC-цепи определяет импеданс и угол разности фаз идеального индуктора и идеального конденсатора, подключенных последовательно для заданной частоты синусоидальный сигнал.Также определяется угловая частота.
Пример: Рассчитайте полное сопротивление катушки индуктивности 100 мГн и конденсатора 800 нФ на частоте 562 Гц. Этот пример показывает очень низкий импеданс, близкий к резонансному, около 0,9 Ом. Если вы хотите проверить импеданс почти при точном резонансе, введите 562,6977 Гц вместо 562 Гц. На этой частоте сопротивление слегка индуктивное. Если вы введете немного более низкую частоту 562,6976 Гц, импеданс изменится на слегка емкостный, и вы заметите, что угол разности фаз изменился с 90 ° на –90 °.
Входной
Индуктивность, л
генри (H) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH)
Емкость, C
фарад (F) микрофарад (нанофарад) (нанофарад) (нФ) пикофарад (пФ)
Частота, f
герц (Гц) миллигерц (МГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)
Выходной сигнал
35 Угловая частота рад / ωЕмкостное реактивное сопротивление X C = Ом
Индуктивное реактивное сопротивление X L = Ом
Общее полное сопротивление LC | Z LC | = Ом
Разность фаз φ = ° = рад
Резонансная частота
f 0 = Гц ω 0 = рад / сВведите значения емкости, индуктивности и частоты, выберите единиц и нажмите или коснитесь кнопки Calculate .Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Для расчета используются следующие формулы:
φ = 90 °, если 1/2 πfC <2 πfL
30 = –– φ если 1/2 πfC > 2 πfL
φ = 0 °, если 1/2 πfC = 2 πfL
где
Z — это сопротивление цепи в омах (Ом),
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
L — индуктивность в генри (H ),
C — емкость в фарадах (F),
ω 0 = резонансная угловая частота в радианах в секунду (рад / с),
f 0 = резонансная частота в герц (Г),
X C i s реактивное сопротивление конденсатора в Ом (Ом),
X L — реактивное сопротивление катушки индуктивности в Ом (Ом),
φ — фазовый сдвиг между общим напряжением В, T и общим ток I T , а
j — мнимая единица.
Для расчета введите индуктивность, емкость и частоту, выберите единицы измерения, и результат для полного сопротивления LC будет показан в омах, а для разности фаз — в градусах. Также будут рассчитаны реактивные сопротивления C и L, а также резонансная частота. Щелкните или коснитесь Расчет на резонансной частоте , чтобы увидеть, что произойдет при резонансе.
Последовательная LC-цепь состоит из последовательно соединенных катушек индуктивности L и конденсатора C. Контур LC может резонировать на резонансной частоте.Резонанс возникает на частоте, на которой полное сопротивление цепи минимально, то есть, если в цепи нет реактивного сопротивления. Это явление возникает, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за их противоположных знаков они компенсируют друг друга (подавление можно увидеть на правой векторной диаграмме ниже).
Несколько графиков полного сопротивления последовательного LC-контура Z LC в зависимости от частоты f для заданной индуктивности и емкости показывают нулевое сопротивление на резонансных частотах.Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако, если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности. При нулевой частоте последовательный LC-контур действует как разомкнутый контур. Обратите внимание, что импеданс является индуктивным справа от резонанса и емкостным слева от резонанса.
Калькулятор определяет резонансную частоту LC-контура, и вы можете ввести эту частоту или значение немного выше или ниже, чтобы посмотрите, что произойдет с другими расчетными значениями при резонансе.
Векторная диаграмма теоретически идеальной последовательной LC-цепи. Слева — емкостное реактивное сопротивление, то есть схема выполняет роль конденсатора; в центре — индуктивное реактивное сопротивление, то есть цепь действует как индуктор; справа — нулевое реактивное сопротивление при резонансе, и цепь действует как короткое замыкание.
В последовательной цепи через катушку индуктивности и конденсатор протекает один и тот же ток, но отдельные напряжения на конденсаторе и на катушке индуктивности различаются. На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения.Из-за отсутствия сопротивления на резисторе нет падения напряжения в фазе с током, протекающим по цепи. Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90 °, поэтому он нарисован под + 90 °. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90 ° и проходит под углом –90 °. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе.
На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | выше, мы увидим, что эффективный импеданс равен нулю, потому что два противоположных напряжения просто компенсируют друг друга. Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, на резонансной частоте ток, потребляемый от источника, становится теоретически бесконечным, и идеальный последовательный LC-контур на резонансной частоте, подключенный к источнику напряжения, действует как короткое замыкание.В реальной жизни индукторы всегда имеют сопротивление, ограничивающее ток. Настоящие источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания.
Резонансная частота последовательного LC-контура определяется с учетом того, что
Умножая обе части уравнения на частоту f , мы получим
Разделив обе части на 2 πL , взяв квадратный корень из обеих частей уравнения и упрощая, мы получим резонансную частоту:
Катушки индуктивности в радиочастотном модуле телевизионного приемника
Режимы отказа
Что, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткое замыкание
Обрыв цепи
Чисто емкостная цепь
Резонансная цепь
Чисто индуктивная цепь
Индуктивная цепь
Примечания
- В наших объяснениях поведения этой цепи нулевая частота означает постоянный ток.Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
- При нулевой частоте мы считаем реактивное сопротивление конденсатора равным нулю, если его емкость бесконечно велика. Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор.
- При нулевой частоте мы считаем реактивное сопротивление идеальной катушки индуктивности бесконечно большим, если ее индуктивность бесконечно велика.Если катушка индуктивности имеет конечную индуктивность, ее реактивное сопротивление при нулевой частоте равно нулю, а для источника постоянного напряжения оно представляет собой короткое замыкание.
Эта статья написана Анатолием Золотковым.
Калькулятор импеданса параллельной RLC-цепи • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц
Этот калькулятор импеданса параллельной RLC-цепи определяет импеданс и угол разности фаз резистора, индуктора , и конденсатор, включенный параллельно для заданной частоты синусоидального сигнала.Также определяется угловая частота.
Пример: Рассчитайте полное сопротивление резистора 300 Ом, катушки индуктивности 100 мГн и конденсатора 10 мкФ на частоте 159 Гц. В этом примере показано высокое сопротивление, близкое к резонансному, около 299,99 Ом. Если вы хотите проверить импеданс при почти точном резонансе, введите 159,1549 Гц вместо 159 Гц. Схема немного индуктивна, а индуктивное сопротивление меньше емкостного. Если ввести чуть более высокую частоту 159.1550 Гц, схема изменится на слегка емкостную, ее индуктивное реактивное сопротивление станет выше емкостного, и вы заметите, что угол разности фаз, который был немного больше нуля, стал отрицательным.
Вход
Сопротивление, R
миллиом (мОм) Ом (Ом) килоом (кОм) мегом (МОм)
Индуктивность, л
генри (H) миллигенри (мГн) микрогенри (мкГн) ) пикогенри (pH)
Емкость, C
фарад (F) микрофарад (мкФ, мкФ) нанофарад (нФ) пикофарад (пФ)
Частота, f
герц (Гц) миллигерц (мГц) килогерц (мГц) кГц (МГц) гигагерцы (ГГц)
Выход
Угловая частота ω = рад / с
Емкостное реактивное сопротивление X C = Ом
Индуктивное реактивное сопротивление X L
= Общее индуктивное сопротивление X L = Ом Сопротивление RLC | Z RLC | = ОмРазность фаз φ = ° = рад
Коэффициент качества Q =
Резонансная частота
f 0 = Гц ω 0 = рад / сВведите сопротивление, значений емкости, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки Calculate .Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.
Для расчета используются следующие формулы:
Здесь
Z RLC сопротивление цепи RLC Ом ,
ω = 2πf — угловая частота в рад / с,
f — частота в герцах (Гц),
R — сопротивление в Ом (Ом),
L — индуктивность в генри (Гн),
C — емкость в фарадах (Ф),
Q — добротность параллельной RLC-цепи (безразмерная),
ω 0 — резонансная угловая частота в радианах в секунду (рад / с),
f 0 — резонансная частота в герцах (Г),
φ — фазовый сдвиг между общим напряжением В T и полный ток I T в градусах (°).
Для расчета введите сопротивление, индуктивность, емкость и частоту, выберите единицы измерения, и результат для импеданса RLC будет показан в омах, а для разности фаз — в градусах. Также будут рассчитаны добротность, реактивное сопротивление C и L и резонансная частота. Щелкните или коснитесь Расчет на резонансной частоте , чтобы увидеть, что произойдет при резонансе.
Параллельная цепь RLC состоит из резистора R, катушки индуктивности L и конденсатора C, соединенных параллельно.На английском языке последовательность букв в названии цепи может быть разной: RLC, RCL, LCR и т. Д. Как и в чисто параллельном LC-контуре, RLC-контур может резонировать на резонансной частоте, и резистор увеличивает затухание колебаний на этой частоте. частота.
Слева: график импеданса Z RLC параллельной цепи RLC в зависимости от частоты f для заданного сопротивления, индуктивности и емкости. Значения сопротивления, индуктивности и емкости подбираются так, чтобы резонансная частота была одинаковой для всех графиков.
Справа: график полного сопротивления параллельной цепи RLC Z RLC и фазового сдвига между полным напряжением и полным током φ в зависимости от частоты f
Резонанс возникает на частоте, на которой сопротивление цепь находится на максимуме, то есть, если в цепи нет реактивного сопротивления. Другими словами, если сопротивление чисто резистивное (или реальное). Это явление возникает, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за их противоположных знаков они компенсируют друг друга (подавление можно увидеть на правой векторной диаграмме ниже).
Калькулятор определяет резонансную частоту контура RLC, и вы можете ввести эту частоту или значение немного выше или ниже, чтобы увидеть, что произойдет с другими расчетными значениями при резонансе.
Калькулятор также определяет Q-фактор RLC-контура, параметр, который используется для характеристики резонансных контуров и не только электрических, но и механических резонаторов. Цепи RLC с демпфированием и потерями с низким сопротивлением имеют низкий коэффициент добротности и широкополосный диапазон, тогда как схемы с низким сопротивлением имеют высокий коэффициент добротности.Для параллельной RLC-цепи коэффициент добротности можно рассчитать по приведенной выше формуле.
Векторная диаграмма для параллельной цепи RLC. 1 — индуктивное реактивное сопротивление, то есть цепь действует как индуктор, 2 — емкостное реактивное сопротивление, то есть цепь действует как конденсатор, и 3 — полное сопротивление при резонансе определяется только сопротивлением, а цепь является чисто резистивной на резонансной частоте.
В параллельной цепи RLC приложенное напряжение одинаково для резистора, катушки индуктивности и конденсатора, но отдельные токи во всех ветвях цепи разные.На векторной диаграмме показано напряжение V T идеального источника напряжения. Из-за сопротивления вектор тока резистора появляется в фазе с приложенным напряжением. Вектор тока индуктивности I L отстает от вектора напряжения на 90 °, поэтому он нарисован под углом –90 °. Вектор емкостного тока I C опережает вектор напряжения на 90 ° и вычерчивается под углом + 90 °. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от тока, протекающего через индуктивность и емкость.Вектор полного тока I T получается с помощью теоремы Пифагора.
На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | Выше мы увидим, что эффективное сопротивление равно сопротивлению и является максимальным. Токи, протекающие через катушку индуктивности и конденсатор, равны, потому что их реактивные сопротивления равны. Итак, на резонансной частоте ток, потребляемый от источника, определяется только резистором.Из-за этого параллельный контур RLC на резонансной частоте, подключенный к источнику напряжения, действует как чистый резистор.
В то же время мы можем видеть, что ток циркулирует через катушку индуктивности и конденсатор взад и вперед. Это можно сравнить с качелями, которые могут колебаться с уменьшающейся амплитудой без приложения к ним какой-либо внешней силы.
На английском языке параллельная цепь RLC часто называется цепью резервуара, потому что она может накапливать энергию в форме электрического поля, а магнитное поле с циркулирующим током, как резервуар, может хранить жидкость, не выпуская ее.Величина этого циркулирующего тока зависит от импеданса конденсатора и катушки индуктивности. Если индуктивность высокая, а емкость низкая, их реактивные сопротивления будут высокими, а ток будет небольшим. И наоборот, если индуктивность низкая, а емкость высокая, их реактивные сопротивления будут низкими, а ток будет высоким.
Индукторы с воздушным сердечником в радиочастотном модуле телевизионного приемника
Режимы отказа
Что делать, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:
Специальные режимы
Неисправный электролитический конденсатор
Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:
Различные режимы постоянного тока
Короткие цепь
Обрыв цепи
Чисто емкостная цепь
Цепь в резонансе
Чисто индуктивная цепь
Индуктивная цепь
Примечания
- В наших объяснениях поведения этой цепи нулевая частота означает постоянный ток.Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения.
- При нулевой частоте мы считаем реактивное сопротивление конденсатора равным нулю, если его емкость бесконечно велика. Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор.
- При нулевой частоте мы считаем реактивное сопротивление идеальной катушки индуктивности бесконечно большим, если ее индуктивность бесконечно велика.Если катушка индуктивности имеет конечную индуктивность, ее реактивное сопротивление при нулевой частоте равно нулю, а для источника постоянного напряжения оно представляет собой короткое замыкание.
Эту статью написал Анатолий Золотков.
RLC Resonance Frequency Calculator [Series / Parallel] • Электрические калькуляторы Org
Вычислитель резонансной частотыRLC используется для расчета резонансной частоты последовательных / параллельных цепей. Он также вычисляет последовательный и параллельный коэффициент демпфирования.
RLC Резонансная частота Формула
RLC Резонанс — это особая частота, на которой резонирует электрическая цепь.Значение частоты RLC определяется индуктивностью и емкостью цепи. Резонанс возникает как в последовательной, так и в параллельной цепях. Хотя основная формула для расчета серий и резонансной частоты одинакова, тем не менее, существуют определенные различия, которые определяют резонансную частоту.
Резонансная частота серииРезонанс последовательной цепи возникает, когда индуктивное реактивное сопротивление в точности равно емкостному реактивному сопротивлению. Однако необходимым условием является разность фаз в 180 градусов, при которой они должны компенсировать друг друга. Последовательный резонансный контур имеет минимальное сопротивление при резонансе. Последовательный резонансный контур и его формула:
Частота параллельного резонанса
Параллельная резонансная частота чаще встречается в электронных схемах, но не менее сложна. Мы можем определить параллельный резонанс как условие нулевой разности фаз или единичного коэффициента мощности. Параллельный резонансный контур имеет максимальное сопротивление.
Коэффициент демпфирования
Коэффициент демпфирования цепи определяется как отношение ширины полосы пропускания к центральной частоте.Коэффициент демпфирования схемы определяет частоту полосы пропускания. Более высокий коэффициент демпфирования означает более широкую полосу пропускания, а более низкий коэффициент демпфирования означает, что полоса пропускания будет ниже. Коэффициент демпфирования последовательной цепи напрямую связан с сопротивлением по формуле:
В то время как коэффициент параллельного демпфирования обратно пропорционален сопротивлению:
Практическое применение
Практически последовательные и параллельные RLC и LC резонансные цепи используются в приложениях электронного проектирования и моделирования цепей.
Проектирование схем фильтров
Частотные фильтры, такие как фильтры нижних и верхних частот, полосовые и полосовые фильтры, используют в своей конструкции концепции полосовой и резонансной частоты.
Настройка аналоговой магнитолы
Настройка аналогового радиоприемника выполняется с помощью переменного конденсатора с параллельными пластинами, значение которого изменяется для настройки радиоприемника на частоты, поступающие от радиоприемника.
Пример числовых задач
Пример № 1: Последовательный резонансный контур имеет индуктивность 50 мГн и емкость 20 мкФ, которые подключаются к резистору 10 кОм.Найдите резонансную частоту и коэффициент затухания.
Решение:
Приведенные значения: L = 50 мГн и C = 20 мкФ
Из формулы:
= 1 / (50 * 0,001 * 20 * 0,000001) = 1000 Гц или 1 кГц
Коэффициент демпфирования серииможно рассчитать по формуле:
= (5 кОм) √ ((20 * 0,000001) / (50 * 0,001) = 100
Пример № 2: Параллельный резонансный контур имеет резистор 1 МОм, конденсатор 20 пФ и катушку индуктивности 500 мкГн. Найдите резонансную частоту и коэффициент параллельного демпфирования.
Решение:
Приведенные значения: L = 500 мкГн, C = 20 пФ
из
= 1 / √ (500 мкГн * 20 пФ) = 10 МГц
Для расчета параллельного демпфирования используйте уравнение:
= 1 / (2 * 1 МОм) √ (500 мкГн / 20 пФ)
Импеданс R, C и L параллельно Калькулятор
- Цель использования
- Схема
[1] 2021/10/08 18:25 Уровень 30 лет / Инженер / Очень /
- Цель использования
- Полезно для выполнения расчетов, которые помогают мне понять мою домашнюю работу
[2 ] 2021/09/17 04:50 До 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- помог с заданием
[3] 2021 / 08/23 23:35 20 лет уровень / старшая школа / университет / аспирант / очень /
- Цель использования
- Предварительные знания
- Комментарий / запрос
- параллельная цепь RCL.Две формулы для фазового угла дают одинаковую величину, но противоположный знак для угла.
[4] 2021/08/15 13:45 60 лет старый уровень или выше / пенсионер / очень /
- Цель использования
- помогает проверить мои ответы на мои задания
[5] 2021.01.22 01:59 Уровень 20 лет / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- цель двойной проверки моих ответов и лучшего понимания импеданса
[6] 2020/12/07 21:02 Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Понимание работы в колледже
- Комментарий / Запрос
- Довольно полезно, как и я изучаю инженерное дело и изо всех сил пытаюсь учиться на дому из-за текущих ограничений Covid-19.Если бы шаги были включены, это тоже было бы очень полезно.
[7] 2020/11/18 16:27 До 20 лет / Старшая школа / Университет / Аспирант / Полезно /
- Цель использования
- Двойная проверка ответов
- Комментарий / запрос
- Очень полезно использовать.
[8] 2020/10/26 08:08 До 20 лет / Старшая школа / Университет / аспирант / Полезно /
- Цель использования
- проверка ответов на практические задачи
[9] 2020/10/23 03:22 Уровень 50 лет / Учитель / Исследователь / Полезный /
- Цель использования
- хобби
[10] 2020/07 / 25 16:54 Уровень 60 и старше / Инженер / Полезный /
Калькулятор резонанса контура резервуара-Apogeeweb
Что такое контур резервуара?LC-контур также называется резонансным контуром, резервуарным контуром или настроенным контуром.
В цепи переменного тока с элементами сопротивления R, индуктивности L и емкости C фаза напряжения в цепи и ток в ней обычно различаются. Если вы отрегулируете параметры компонентов схемы (L или C) или частоту источника питания, вы можете сделать их одной и той же фазой, и вся цепь будет выглядеть чисто резистивной. Цепь, достигающая этого состояния, называется резонансной.
Как работает контур резервуара?LC-контур может накапливать энергию, колеблющуюся на своей резонансной частоте.Накопитель энергии поля пластины электрода конденсатора, в зависимости от напряжения и изменений. Электрическая энергия, запасенная катушкой в магнитном поле, изменяется в соответствии с током, протекающим через катушку. Когда катушка, в которой накапливается энергия, подключена к катушке, через катушку начинает течь ток, в ней формируется магнитное поле и напряжение, приложенное к конденсатору, уменьшается.
В конце концов, вся энергия, накопленная в конденсаторе, высвобождается. Однако ток продолжает течь.Это связано с тем, что функция катушки — предотвращать изменения тока, извлекать энергию из магнитного поля и пытаться заставить ток течь постоянно. Ток постепенно накапливается в конденсаторе, и напряжение подается с полярностью, противоположной предыдущей. Когда магнитное поле исчезает, ток прекращается, и конденсатор получает питание с противоположной полярностью и возвращается в исходное состояние. На этот раз ток начал течь в обратном направлении.
Контур резервуара
Заряд проходит между электродами конденсатора через катушку.Поскольку на самом деле существует внутреннее сопротивление, если энергия не поступает извне, колебания энергии между конденсатором и катушкой будут ослаблены. Эта операция математически называется гармоническим осциллятором и аналогична случаю качания маятника. Поскольку накопленная энергия подобна маятнику, в частности, параллельный резонансный контур LC также называют (контуром резервуара).
Явление резонансаРезонанс возникает, когда индуктивное и емкостное сопротивление равны.Контур LC не будет резонировать сам по себе, чтобы предотвратить колебания маятника самостоятельно. Термин «резонанс» относится к явлению, при котором возникновение небольших колебаний оказывает большое влияние на всю систему. Если LC-цепь не имеет источника переменного тока или источника питания, такого как радиоволны, резонанса не будет. Частота, при которой индуктивность и емкостное сопротивление равны, называется резонансной частотой цепи.
Применение резонансного эффекта(1) Наиболее типичное применение — регулировка.Например, при настройке на конкретную радиостанцию, LC-контур резонирует на несущей частоте этой станции.
(2) Последовательный резонансный контур увеличивает напряжение.
(3) Параллельный резонансный контур увеличивает ток.
(4) Параллельный резонансный контур можно использовать в качестве сопротивления нагрузки выходной цепи ВЧ усилителя.
(5) Параллельный резонансный контур можно использовать для индукционного нагрева.
Часто задаваемые вопросы1.Что такое резонансный резервуар?
LC-контур, также называемый резонансным контуром, резервуарным контуром или настроенным контуром, представляет собой электрическую цепь, состоящую из индуктора, обозначенного буквой L, и конденсатора, обозначенного буквой C, соединенных вместе.
2. Что такое резонанс в цепи?
Резонанс — это явление в электрической цепи, при котором выходной сигнал цепи максимален на одной определенной частоте. И эта частота известна как резонансная частота.На резонансной частоте емкостное и индуктивное сопротивление равны.
3. Как определить резонансную частоту LC-контура?
Резонанс в LC-цепи возникает, когда индуктивное сопротивление катушки индуктивности становится равным емкостному сопротивлению конденсатора. Итак: xL = 2 * π * f * L. xC = 1 / (2 * π * f * C)
4. Какая польза от резонансного контура?
Одно из применений резонанса — установить условие стабильной частоты в цепях, предназначенных для генерации сигналов переменного тока.Обычно для этой цели используется параллельная (баковая) цепь, в которой конденсатор и катушка индуктивности напрямую соединены вместе, обмениваясь энергией между собой.
5. Как работает резонансный контур?
Резонансный контур образуется, когда конденсатор и катушка индуктивности включены параллельно или последовательно. Два элемента схемы будут блокировать или пропускать одну конкретную частоту из разнообразного микса. По этой причине резонансные цепи делают возможной передачу и прием радио и телевидения и выполняют множество других полезных задач.
6. Что происходит на резонансной частоте?
Резонансная частота — это колебание системы при естественном или ненасильственном резонансе. Резонанс возникает, когда система способна хранить и легко передавать энергию между различными режимами хранения, такими как кинетическая энергия или потенциальная энергия, как в случае с простым маятником.
7. Какова резонансная частота LC-контура?
На одной конкретной частоте два реактивных сопротивления XL и XC одинаковы по величине, но имеют обратный знак.Таким образом, эта частота называется резонансной частотой, которая обозначается LC-контуром. В конфигурации контура последовательного резонанса LC два резонанса XC и XL компенсируют друг друга.
8. Какова собственная частота LC-контура?
1,25,000 циклов в секунду
Собственная частота LC-контура 1,25 000 циклов в секунду.
9. В чем разница между резонансной частотой и собственной частотой?
Объекты, которые могут свободно вибрировать, будут иметь одну или несколько собственных частот, на которых они вибрируют. Если объект заставляют вибрировать с собственной частотой, возникает резонанс, и вы будете наблюдать колебания большой амплитуды.
10. Что вызывает собственную частоту?
Более легкая масса или более жесткая пружина увеличивает собственную частоту. Более тяжелая масса или более мягкая пружина уменьшают собственную частоту.
ФОРМУЛЫ И КАЛЬКУЛЯТОРЫ
Xtal Set Society, Inc
Формульный индекс:
Обновлено 22.11.13
Формулы на этой странице:
Калькуляторы предназначены для некоторых из перечисленных формул.Эти процессы выполняются с использованием ЦП вашего компьютера в сочетании с JavaScript, загруженным с веб-страницей. В большинстве случаев вы видите форму на веб-странице, она работает с помощью сценария. Большинство браузеров теперь поддерживают сценарии, включая Explorer 4.5 и более поздних версий, Netscape 4.6 и более поздних версий и текущую версию Mozilla Foxfire. Возможно, вам потребуется «включить» сценарии. Посмотрите в меню HELP на панели инструментов вашего браузера.
Калькуляторы, которые мы кодировали до сих пор, просты в использовании и начинаются с отображаемого типового решения. СБРОС вернет вас к типичному исходному решению.Если формула требует N параметров, введите все N или N-1 и щелкните круглую кнопку параметра, который вы хотите рассчитать / обновить. Если к ним проявится интерес, мы добавим еще. Сообщите нам, что бы вы хотели добавить / изменить. Мы ценим и приветствуем конструктивные предложения и комментарии!
Резонансная частота LC-контура — с калькулятором
, где f — частота в герцах, индуктивность L в генри и емкость C в фарадах.
Для диапазона AM-вещания типичные значения индуктивности (катушки) находятся в диапазоне от 250 мкГн. Значения емкости варьируются от десятков до нескольких сотен пфс. Крышки с воздушной переменной мощностью 365 пФ являются общими.
Индуктивное сопротивление катушки
где f — частота в герцах, а L — индуктивность катушки в генри. X — сопротивление катушки по переменному току. Пример: на 1 МГц с L, равным 250 мкГн, X = 2 * 3,14 * 1 * exp (6) * 250 * exp (-6) = 1570 Ом.exp (6) означает 10 в 6-й степени или 1000000.
Емкостное сопротивление конденсатора
где f — частота в герцах, а C — емкость в фарадах. X — полное сопротивление конденсатора по переменному току. Пример: на 1 МГц с C, равным 105 пФ, X = 1 / (2 * 3,14 * 1 * exp (6) * 105 * exp (-12) = 1,516 Ом.
Индуктивность однослойной цилиндрической (катушки) — с вычислителем
, где L в мкГн, N — витки, длина «l» в дюймах, радиус катушки r в дюймах и шаг p в дюймах.Шаг — это расстояние между центром одного поворота и следующего. Np — длина катушки. Калькулятор ниже использует вторую формулу. Первый приписывается Уиллеру; вторая небольшая адаптация. Показанный пример сброса относится к катушке с L = 250 мкГн, радиусом 1,75 дюйма, с 61 витком и расстоянием между обмотками 0,05 дюйма.
Индуктивность катушки паутины (спирали)
Катушка Spider (спиральная) будет производить более сильный сигнал, чем ее собрат, стандартная цилиндрическая катушка с закрытой намоткой.Это достигается путем отделения соседних обмоток друг от друга, тем самым уменьшая эффект близости между проводами, при этом чем ближе они проходят ток в одном, тем выше сопротивление другого. Разделение соседних витков достигается разделением каждого полного витка на нечетное количество сегментов, при этом каждый дополнительный сегмент наматывается на противоположной стороне плоской формы. Это возможно за счет вырезания нечетного числа радиальных прорезей, идущих от внешнего края центральной опоры формы.Обмотки первых нескольких витков показаны на рисунке 1. Обмотка начинается снизу внутреннего кольца формы; следовательно, первый и все нечетные сегменты первого поворота будут отображаться сверху, как отмечено цифрой «1». Последний сегмент поворота 1, сегмент 9, выходит сверху и изгибается зигзагами, чтобы стать поворотом 2, при этом он снова проходит под формой. Следующий сегмент поворота 2 будет наверху, как указано, и так далее. Индуктивность звездообразной катушки определяется ее внутренним и внешним радиусом, а также диаметром и расстоянием между используемыми проводами.Вот уравнение для катушки паутины, полученное из исходной формулы Уиллера для цилиндрических катушек:
Для нашей формулы катушки внутренний диаметр Di — это отверстие в центре катушки, а внешний диаметр измеряет полную длину катушки. Например, при использовании 56 витков провода 150/45 Litz, внутреннего диаметра 1,6 нм и внешнего диаметра 4,2 дюйма, формула говорит, что индуктивность катушки составляет 254 мкГн. Установленный в кристалл, это казалось правильным, учитывая, что крышка 365 пФ настраивала полосу примерно от 550 до 1500 кГц.См. Страницу загрузки файлов для получения более подробной информации.
Q катушки
, где омега — это 2 (пи) f, f — в герцах, L — в генах, а (AC) r — в омах. Пример: на частоте 1 МГц катушка 250 мкГн с сопротивлением 6 Ом переменного тока имеет Q = 2 * 3,14 * 1 * exp (6) * 250 * exp (-6) / 6 = 261. Q пропорционально диаметру формы катушки. и обратно пропорционально сопротивлению переменного тока в катушке. Следовательно, катушка диаметром 3,5 дюйма с лицевым проводом (многопроволочный провод с низкими потерями) будет иметь намного более высокую добротность, чем катушка с соединительным проводом, намотанным на 2-дюймовую форму.Селективность кристалла обратно пропорциональна Q; то есть полоса пропускания параллельно настроенного контура, близкого к резонансу, равна его частоте, деленной на эффективную ширину полосы пропускания, BW.
Измерение собственной емкости катушки — с использованием метода двойной частоты
, где Co — собственная емкость, а C2 и C1 — измеренные значения. Рассматриваемая катушка резонирует на частоте f2, и измеряется емкость C2. (Возможно с помощью измерителя емкости).Затем катушка резонирует на f1, которое устанавливается равным удвоенному значению f2, и измеряется необходимая емкость C1. Затем рассчитывается собственная емкость катушки по приведенной выше формуле. Пример: катушка 90 мкГн резонирует на частоте 909 кГц с конденсатором на 340 пФ. Затем катушка снова резонирует с удвоенной частотой, 1818 кГц с конденсатором 80 пФ. Следовательно, собственная емкость = (340 — 4 * 80) / 3 = 6,6 пФ. Для вывода формулы см. Выпуск XSS Newsletter за сентябрь 2007 г.
Преобразование серии в параллельную цепь — на заданной частоте
, где Rp и Xp — параллельные эквивалентные значения на конкретной частоте, соответствующей последовательной цепи.Подробнее см. Статью 1: Эквивалентные последовательные и параллельные схемы. Пример: резистор 50 Ом, соединенный последовательно с конденсатором 100 пФ на частоте 1 МГц, имеет эквивалентную параллельную цепь на этой частоте резистора 50,7 кОм, включенного параллельно, с емкостью около 100 пФ.
Сопротивление переменного тока / фут провода
где R — сопротивление провода переменному току в Ом / фут, f — в Гц, а D — диаметр провода в дюймах. Пример: Сопротивление переменного тока на фут соединительного провода # 24, если предположить, что медь, на частоте 1 МГц равно = exp (-6) sqrt (exp (6) / 0.02 = 0,05 Ом / фут. Таким образом, полное сопротивление переменному току катушки 250 мкГн с 61 витком и диаметром 3,5 дюйма будет = 0,05 * 2 * 3,14 * 3,5 / 2 * 61/12 = 2,79 Ом!
Глубина скин-слоя для меди
, где толщина скин-слоя (меди) выражена в мил, а f — частота в МГц. Пример: толщина скин-слоя переменного тока на частоте 1 МГц в меди составляет = 2,6 / sqrt (exp (6)) = 2,6exp (-3) мил или 2,6 микродюйма.
Ток диода и динамическое сопротивление — с калькулятором
где iD — ток диода, Io — ток насыщения диода, m — добротность [от 1 до 2, используйте 1.2], vd — напряжение на диоде. Кроме того, rd — прямое динамическое сопротивление диода в рабочей точке Q.
.


