Самостоятельная работа Последовательное соединение проводников. Параллельное соединение проводников 8 класс
Самостоятельная работа Последовательное соединение проводников. Параллельное соединение проводников. Расчет полного сопротивления и силы тока в цепи 8 класс с ответами. Самостоятельная работа представлена в 10 вариантах.
Вариант 1
R1 = 6 Ом
R2 = 12 Ом
R3 = 2 Ом
R4 = 3 Ом
R5 = 6 Ом
UAB = 48 В
R = ?
I = ?
Вариант 2
R1 = 4 Ом
R2 = 5 Ом
R3 = 10 Ом
R4 = 30 Ом
R5 = 3 Ом
UAB = 40 В
R = ?
I = ?
Вариант 3
R1 = 20 Ом
R2 = 20 Ом
R3 = 50 Ом
R4 = 15 Ом
R5 = 10 Ом
UAB
R = ?
I = ?
Вариант 4
R1 = 1 Ом
R2 = 6 Ом
R3 = 6 Ом
R4 = 5 Ом
R5 = 7 Ом
UAB = 42 В
R = ?
I = ?
Вариант 5
R1 = 3 Ом
R2 = 6 Ом
R3 = 2 Ом
R4 = 12 Ом
R5 = 6 Ом
UAB = 18 В
R = ?
I = ?
Вариант 6
R1 = 6 Ом
R2 = 12 Ом
R3 = 10 Ом
R4
R5 = 12 Ом
UAB = 120 В
R = ?
I = ?
Вариант 7
R1 = 6 Ом
R2 = 12 Ом
R3 = 8 Ом
R4 = 8 Ом
R5 = 3 Ом
UAB = 15 В
R = ?
I = ?
Вариант 8
R1 = 8 Ом
R2 = 4 Ом
R3 = 2 Ом
R4 = 10 Ом
R5 = 12 Ом
UAB = 32 В
R = ?
I = ?
Вариант 9
R1 = 5 Ом
R3 = 3 Ом
R4 = 6 Ом
R5 = 2 Ом
UAB = 36 В
R = ?
I = ?
Вариант 10
R1 = 6 Ом
R2 = 8 Ом
R3 = 4 Ом
R4 = 14 Ом
R5 = 12 Ом
UAB = 120 В
R = ?
I = ?
Ответы на самостоятельную работу Последовательное соединение проводников.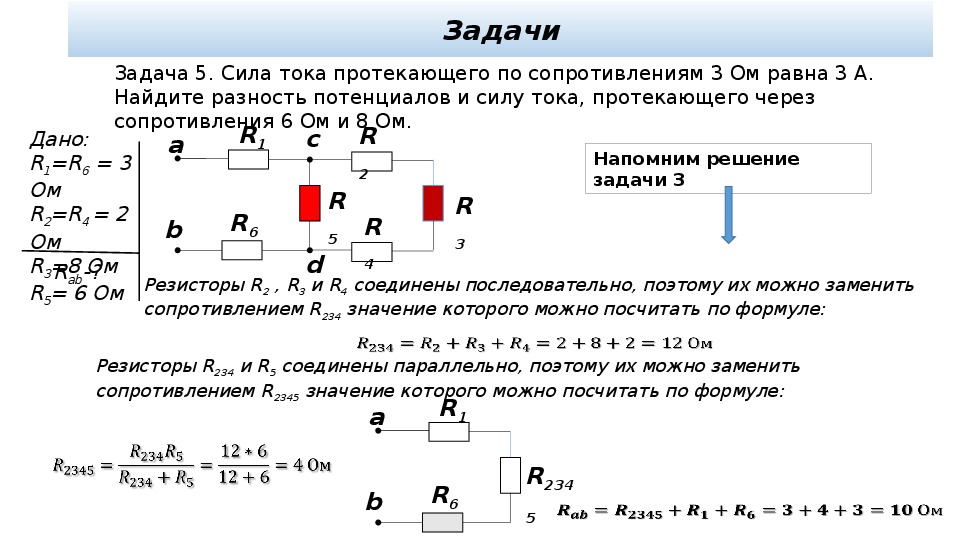 Параллельное соединение проводников. Расчет полного сопротивления и силы тока в цепи 8 класс
Параллельное соединение проводников. Расчет полного сопротивления и силы тока в цепи 8 класс
Вариант 1
R = 8 Ом
I = 6 А
Вариант 2
R = 10 Ом
I = 4 А
Вариант 3
R = 50 Ом
I = 2 А
Вариант 4
R = 7 Ом
I = 6 А
Вариант 5
R = 2 Ом
I = 9 А
Вариант 6
R = 10 Ом
I = 12 А
Вариант 7
R = 5 Ом
I = 3 А
Вариант 8
R = 4 Ом
I = 8 А
R = 6 Ом
I = 6 А
Вариант 10
R = 30 Ом
I = 4 А
Закон Ома. Онлайн расчёт для постоянного и переменного тока.
Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи
с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.
Начнём с терминологии.
Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области
электрической цепи в другую.
Напряжение электрического тока между точками A и B электрической цепи — физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление — это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.
Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы
электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо
пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника
и записана в следующем виде:
I=U/R,
где
I – сила тока в проводнике, измеряемая в амперах [А];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.
Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности,
рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам,
также являющимся производными от основной формулы закона Ома:
Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.
Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:
Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.
Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.
Все наши расчёты проводились при условии, что значение внешнего сопротивления R
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов
определяются исходя из формулы:
1/R
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице
ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше,
остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует
понимать действующее (эффективное) значение амплитуды переменного сигнала.
А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2),
сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает
амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.
Рассчитываем действующее значение напряжение интересующей нас формы:
Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.
С этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости
в цепи переменного тока.
В общем случае смотреться это будет так:
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z,
состоящее из активного, ёмкостного и индуктивного сопротивлений.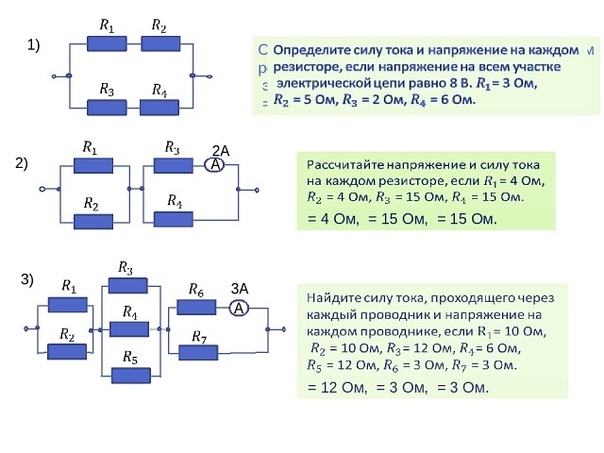
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих
трёх элементов обойтись не удаётся, и формула приобретает вид:
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице
ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока
и описываются формулами:
XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии
индуктивного или емкостного элемента — необходимо указать значение частоты
f !
КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем
простенький бестрансформаторный источник питания.
Токозадающими цепями в данной схеме являются элементы R1 и С1.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока
нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.
Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!
общие сведения, зависимость от других величин и формулы расчета
Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.
Физический смысл
Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.
Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.
Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.
Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.
Зависимость электропроводимости
R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.
Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.
Электрические величины
К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).
Кроме того, необходимо учитывать и тип тока (постоянный или переменный).
Геометрические параметры и тип вещества
Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.
Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.
Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:
Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:
- Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
- Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.
П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.
Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:
- Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
- Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:
- Визуально определить геометрическую фигуру при разрезе П.
- Найти в справочнике формулу S.
- Произвести измерения при помощи ШЦ необходимых величин.
- Подставить в формулу и вычислить S.
Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.
Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.
Температура проводника
Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.
В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:
- для металлов а > 0;
- для электролитов a < 0.
Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.
В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.
Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.
Цепь переменного тока
Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:
- активным;
- индуктивным;
- емкостным;
- полным.
Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).
Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.
Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.
При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:
- w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
- C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.
Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:
- геометрии П;
- типа вещества, из которого сделан П;
- температуры;
- деформации различного вида;
- электрических показателей I, U, f, L, C и R.
Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.
Измерение сопротивления
На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.
Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.
Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.
Расчет полного сопротивления в цепи переменного тока — импеданс
Понятие импеданса используется в разных сферах науки. Существуют разные его формы: гидродинамический, артериальный (медицинский термин, состоит из статического и кинетического компонентов), используемый при измерении гидростатического давления. Есть и электрический импеданс, описывающий полное сопротивление цепного фрагмента. Электрику необходимо знать, от чего зависит и как вычисляется эта величина в однофазных и трехфазных цепях с трансформаторами тока и иными компонентами.
Импеданс описывает сопротивление всей цепи
Что такое импеданс
Это понятие описывает комплексное сопротивление цепи или ее межузлового участка. Оно было введено лондонским инженером и физиком О. Хевисайдом в 1886 году. В состав полного сопротивления цепи входят активная и реактивная компоненты. Фазовый сдвиг и само значение импенданса при электротоке, чья кривая имеет форму синусоиды, могут быть рассчитаны с ориентиром на то, каким образом соединены входящие в цепь компоненты.
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Важно! Выражение для сопротивления резистора можно записать так: R=U/I.
Резисторы – источники активного сопротивления
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.
Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.
Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами.
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.
Расчет эквивалентного сопротивления элементов цепи
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.
Видео
Помогите!!! 4 вариант, Расчёт полного сопротивления и силы тока в цепи CP-31
Tч=60мин/Ск
Тм=1мин/Ск
Тч/Тм=60*1=60
Ответ: в 60 раз
Ответ а) — только не сила тяжОсти , а тяжЕсти!
Ек= mV(кв) /2
m= 245х2:(700х700 )= 0.001
Будем считать, что снег — это лёд, температура которого t₁=-1°C. Следовательно снег сначала нагревается до температуры t₂=0°C, затем плавится при температуре 0°C, а затем вода нагревается до t₃=2°C.
Q₁=c₁·m·(t₂-t₁), Q₂=λ·m, Q₃=c₂·m·(t₃-t₂)
Масса снега, а следовательно масса воды равна m = ρ·S·h, где ρ — плотность льда.
Теплота, которая выделяется при сгорании дров: Q₄= q·m₁, где m₁ = масса дров. При этом КПД установки = 45%
η=((Q₁+Q₂+Q₃)·100%)/Q₄
η=((c₁·m·(t₂-t₁)+λ·m+c₂·m·(t₃-t₂))·100%)/q·m₁ = (ρ·S·h·(c₁·(t₂-t₁)+λ+c₂·(t₃-t₂))·100%)/q·m₁
m₁= (ρ·S·h·(c₁·(t₂-t₁)+λ+c₂·(t₃-t₂))·100%)/q·η
S — площадь снега
h — высота снежного покрова
c₁ — удельная теплоёмкость льда
c₂ — удельная теплоёмкость воды
λ — удельная теплота плавления льда
η — КПД
q — удельная теплота сгорания дров
Осталось подставить и рассчитать
1 700 075 400 г вот такая площадь
Расчет полного сопротивления в цепи коррозионных пар, образованных соприкасающимися электродами
из «Математические методы расчета электрохимической коррозии и защиты металлов »
Целью расчета многоэлектродных систем (МЭС) является определение силы и направления тока в цепи каждого электрода. [c.88]Методика расчета МЭС зависит от соотношения площадей электродов, отношений расстояний между электродами к их характерным размерам, соотношения поляризационного и омического сопротивлений, а также от схемы соединений электродов по внутренней цепи. [c.88]
в частности, один из электродов МЭС значительно (в 10 и более раз) больше по площади, чем все другие электроды той же системы, то расчет МЭС сводится к расчету коррозионных пар, образуемых каждым из электродов этой системы с наибольшим (см. разд. 2.1.2). [c.88]
МЭС общего вида. [c.89]
Аналогично строится суммарная анодная кривая полной поляризации (кривая//на рис. 2.7). [c.89]
Если для данного электрода I/ I I / то этот электрод является анодом, а при 1/ 1 — катодом. В частном случае, когда 1/ 1 = = i n, рассматриваемый электрод является в составе данной МЭС электронейтральным (не потребляет и не отдает тока). [c.90]
Аналитический расчет МЭС указанного типа производится по формулам (2.2) — (2.5), в которых величины Рд/п, Ркт заменяются соответственно величинами рд + г внешн. т+г внутр. ml РКт + г внешн, т + внутр, m J РАп внешн. п внутр, п Л внутр. т внутреннее сопротивление в луче звезды , соединяющемся с т -ья электродом г внешн, т — сопротивление растекания т-го электрода, / внутр. я. г внешн, я — то же для п-го электрода. При этом значения г внешн, т определяются по материалам разд. 2.1, а значения г внутр, т являются заданными параметрами. [c.92]
Расчет МЭС при произвольной схеме внутренней цепи и произвольном расстоянии между электродами производится с использованием эквивалентных электрических схем этих систем. [c.92]
Расчет эквивалентных электрических схем МЭС производится при любой заданной схеме внутренней цепи с помощью общих методов расчета нелинейных электрических цепей (см. например, [96]). [c.93]
Материалы настоящего подраздела позволяют учесть статистический характер стационарных электродных потенциалов металлов при расчете многоэлектродных систем. При этом стационарные электродные потенциалы отдельных электродов предполагаются статистически независимыми, а их средние значения характеризуются нормальным законом распределения вероятностей с параметрами — среднее значение (математическое ожидание) стационарного электродного потенциала /п-го электро-да 0 — среднеквадратичное отклонение стационарного электрода потенциала т-го электрода. [c.93]
Кроме того, принимается, что случайный разброс настолько мал, что не приводит к изменению полярности электродов. [c.93]
Приведенные в дальнейшем материалы для определения величины сопротивлений растекания даны в обобщенном виде, позволяющем использовать их при решении всех указанных задач. [c.94]
Особенности расчета сопротивлений растекания зависят от соотношений геометрических параметров рассматриваемых систем электродов. [c.94]
При непосредственном контакте электродов раздельное определение поляризационного сопротивления и сопротивления растекания невозможно в этом случае находится полное сопротивление между электродами (см. разд. 2.2.4). [c.95]
Все приведенные в настоящем разделе данные получены в предположении, что удельная электрическая проводимость коррозионной среды постоянна по всему ее объему, а поляризационные кривые всех рассматриваемых металлов (как анодные, так и катодные) линейны. [c.95]
Выражения для С, соответственно и для г, могут быть установлены для широкого класса электродных систем с помощью справочных материалов по расчету электрической емкости (например, 140]). Поэтому в настоящем разделе приведены материалы для расчета сопротивлений растекания лишь для уединенных электродов и коррозионных пар наиболее типичной формы. [c.95]
Формулы для расчета сопротивлений растекания уединенных электродов наиболее типичной формы представлены в табл..2.9, где 7 — удельная электропроводимость коррозионной среды. [c.96]
П р имечание. Все приведенные формулы, за исключением 9, 10.16,18. 20. являются приближенными. Относителы ая погрешность расчета по этим формулам ие превышает 10 %. [c.103]
Плоскопараллельные системы являются расчетными моделями таких реальных коррозионных пар, размеры которых в направлении какой-либо оси во много раз превышают размеры их сечений плоскостью, перпенди-кулярной к этой оси. [c.105]
Формулы для расчета величины погонного сопротивления г о/ между электродами наиболее типичной формы представлены в табл. 2.14, где 7 — удельная электропроводимость коррозионной среды К (а), и К (а) — полные эллиптические интегралы первого рода с модулями а и V 1 -соответственно . [c.105]
Вернуться к основной статье
Формула сопротивления тока при параллельном соединении
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему [1] . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
Последовательное соединение проводников
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
Параллельное соединение проводников
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
На практике нередко встречается задача нахождения сопротивления проводников и резисторов при различных способах соединения. В статье рассмотрено, как рассчитывается сопротивление при и некоторые другие технические вопросы.
Сопротивление проводника
Все проводники имеют свойство препятствовать течению электрического тока, его принято называть электрическим сопротивлением R, оно измеряется в омах. Это основное свойство проводниковых материалов.
Для ведения электротехнических расчётов применяется удельное сопротивление – ρ Ом·м/мм 2 . Все металлы – хорошие проводники, наибольшее применение получили медь и алюминий, гораздо реже применяется железо. Лучший проводник – серебро, оно применяется в электротехнической и электронной промышленности. Широко распространены сплавы с высоким значением сопротивления.
При расчёте сопротивления используется известная из школьного курса физики формула:
R = ρ · l/S, S – площадь сечения; l – длина.
Если взять два проводника, то их сопротивление при параллельном соединении станет меньше из-за увеличения общего сечения.
и нагрев проводника
Для практических расчётов режимов работы проводников применяется понятие плотности тока – δ А/мм 2 , она вычисляется по формуле:
δ = I/S, I – ток, S – сечение.
Ток, проходя по проводнику, нагревает его. Чем больше δ, тем сильнее нагревается проводник. Для проводов и кабелей разработаны нормы допустимой плотности, которые приводятся в Для проводников нагревательных устройств существуют свои нормы плотности тока.
Если плотность δ выше допустимой, может произойти разрушение проводника, например, при перегреве кабеля у него разрушается изоляция.
Правилами регламентируется производить расчёт проводников на нагрев.
Способы соединения проводников
Любой проводник гораздо удобнее изображать на схемах как электрическое сопротивление R, тогда их легко читать и анализировать. Существует всего три способа соединения сопротивлений. Первый способ самый простой – последовательное соединение.
На фото видно, что полное сопротивление равно: R = R 1 + R 2 + R 3 .
Второй способ более сложный – параллельное соединение. Расчёт сопротивления при параллельном соединении выполняется поэтапно. Рассчитывается полная проводимость G = 1/R, а затем полное сопротивление R = 1/G.
Можно поступить и по-другому, прежде рассчитать общее сопротивление при R1 и R2, после этого повторить операцию и найти R.
Третий способ соединения наиболее сложный – смешанное соединение, то есть присутствуют все рассмотренные варианты. Схема приведена на фото.
Для расчёта этой схемы её следует упростить, для этого заменяют резисторы R2 и R3 одним R2,3. Получается несложная схема.
R2,3,4 = R2,3 · R4/(R2,3 + R4).
Схема становится ещё проще, в ней остаются резисторы, имеющие последовательное соединение. В более сложных ситуациях используется этот же метод преобразования.
Виды проводников
В электронной технике, при производстве проводники представляют собою тонкие полоски медной фольги. Ввиду малой длины сопротивление у них незначительно, им во многих случаях можно пренебречь. Для этих проводников сопротивление при параллельном соединении уменьшается вследствие увеличения сечения.
Большой раздел проводников представляют обмоточные провода. Они выпускаются разных диаметров – от 0,02 до 5,6 миллиметра. Для мощных трансформаторов и электродвигателей выпускаются медные шинки прямоугольного сечения. Иногда при ремонте заменяют провод большого диаметра на несколько параллельно соединённых меньшего размера.
Особый раздел проводников представляют провода и кабели, промышленность предоставляет широчайший выбор марок для самых различных нужд. Нередко приходится заменять один кабель на несколько, меньшего сечения. Причины этого бывают самые различные, например, кабель сечением 240 мм 2 очень трудно прокладывать по трассе с крутыми изгибами. Его заменяют на 2×120 мм 2 , и проблема решена.
Расчёт проводов на нагрев
Проводник нагревается протекающим током, если его температура превысит допустимую, наступает разрушение изоляции. ПУЭ предусматривает расчёт проводников на нагрев, исходными данными для него являются сила тока и условия внешней среды, в которой проложен проводник. По этим данным из таблиц в ПУЭ выбирается рекомендуемое проводника или кабеля).
На практике встречаются ситуации, когда нагрузка на действующий кабель сильно возросла. Существует два выхода ‒ заменить кабель на другой, это бывает дорого, или параллельно ему проложить ещё один, чтобы разгрузить основной кабель. В этом случае сопротивление проводника при параллельном соединении уменьшается, следовательно падает выделение тепла.
Чтобы правильно выбрать сечение второго кабеля, пользуются таблицами ПУЭ, важно при этом не ошибиться с определением его рабочего тока. В этой ситуации охлаждение кабелей будет даже лучше, чем у одного. Рекомендуется рассчитать сопротивление при параллельном соединении двух кабелей, чтобы точнее определить их тепловыделение.
Расчёт проводников на потерю напряжения
При расположении потребителя R н на большом расстоянии L от источника энергии U 1 возникает довольно большое на проводах линии. К потребителю R н поступает напряжение U 2 значительно ниже начального U 1 . Практически в качестве нагрузки выступает различное электрооборудование, подключаемое к линии параллельно.
Для решения проблемы производят расчет сопротивления при параллельном соединении всего оборудования, так находится сопротивление нагрузки R н. Далее следует определить сопротивление проводов линии.
Здесь S – сечение провода линии, мм 2 .
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома.
С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Виды соединений
Резистор – пассивный элемент , присутствующий в каждой электрической цепи. Он предназначен для того, чтобы сопротивляться электрическому току. Существует два вида резисторов:
Зачем же спаивать проводники друг с другом? Например, если для какой-то электрической цепи нужно определённое сопротивление. А среди номинальных показателей нужного нет. В таком случае необходимо подобрать элементы схемы с определёнными значениями сопротивления и соединить их. В зависимости от вида соединения и сопротивлений пассивных элементов мы получим какое-то определённое сопротивление цепи. Оно называется эквивалентным. Его значение зависит от вида спайки проводников. Существует три вида соединения проводников:
Значение эквивалентного сопротивления в цепи считается достаточно легко. Однако, если резисторов в схеме очень много, то лучше воспользоваться специальным калькулятором, который считает это значение. При ведении расчёта вручную, чтобы не допускать ошибок, необходимо проверять, ту ли формулу вы взяли.
Последовательное соединение проводников
В последовательной спайке резисторы идут как бы друг за другом. Значение эквивалентного сопротивления цепи равно сумме сопротивлений всех резисторов. Особенность схем с такой спайкой заключается в том, что значение тока постоянно . Согласно закону Ома, напряжение в цепи равно произведению тока и сопротивления. Так как ток постоянен, то для вычисления напряжения на каждом резисторе, достаточно перемножить значения. После этого необходимо сложить напряжения всех резисторов, и тогда мы получим значение напряжения во всей цепи.
Расчёт очень простой. Так как с ним имеют дело в основном инженеры-разработчики, то для них не составит труда сосчитать всё вручную. Но если резисторов очень много, то проще воспользоваться специальным калькулятором.
Примером последовательного соединения проводников в быту является ёлочная гирлянда.
Параллельное соединение резисторов
При параллельном соединении проводников эквивалентное сопротивление в цепи считается по-другому. Немного сложнее, чем при последовательном.
Его значение в таких цепях равняется произведению сопротивлений всех резисторов, делённому на их сумму. А также есть и другие варианты этой формулы. Параллельное соединение резисторов всегда снижает эквивалентное сопротивление цепи. То есть, его значение всегда будет меньше, чем наибольшее значение какого-то из проводников.
В таких схемах значение напряжения постоянно . То есть значение напряжения во всей цепи равно значениям напряжений каждого из проводников. Оно задаётся источником напряжения.
Сила тока в цепи равна сумме всех токов, протекающих через все проводники. Значение силы тока, протекающего через проводник. равно отношению напряжения источника к сопротивлению этого проводника.
Примеры параллельного соединения проводников:
- Освещение.
- Розетки в квартире.
- Производственное оборудование.
Для расчёта схем с параллельным соединением проводников лучше пользоваться специальным калькулятором. Если в схеме много резисторов, спаянных параллельно, то гораздо быстрее вы посчитаете эквивалентное сопротивление с помощью этого калькулятора.
Смешанное соединение проводников
Этот вид соединения состоит из каскадов резисторов . Например, у нас есть каскад из 10 проводников, соединённых последовательно, и после него идёт каскад из 10 проводников, соединённых параллельно. Эквивалентное сопротивление этой схемы будет равно сумме эквивалентных сопротивлений этих каскадов. То есть, по сути, здесь последовательное соединение двух каскадов проводников.
Многие инженеры занимаются оптимизацией различных схем. Её целью является уменьшение количества элементов в схеме за счёт подбора других, с подходящими значениями сопротивлений. Сложные схемы разбиваются на несколько небольших каскадов, ведь так гораздо проще вести расчёты.
Сейчас, в двадцать первом веке, инженерам стало гораздо проще работать. Ведь несколько десятилетий назад все расчёты производились вручную. А сейчас программисты разработали специальный калькулятор для расчёта эквивалентного сопротивления цепи. В нём запрограммированы формулы, по которым ведутся расчёты.
В этом калькуляторе можно выбрать вид соединения, и потом ввести в специальные поля значения сопротивлений. Через несколько секунд вы уже увидите это значение.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (), то общее сопротивление цепи составит:
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов и – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором :
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов и одним резистором :
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
ИСКРЫ: Расчет импеданса
Расчет импеданса
В цепях переменного тока Закон Ома принимает более общая форма: E = I⋅Z , где E — напряжение, а I актуален, как и раньше. Новый термин, Z , равен импедансу , комбинация векторов:
- Сопротивление, R (в Ом), при падении напряжения в фазе с электрический ток.
- Индуктивное реактивное сопротивление, X L (в Ом), с напряжением опускает опережающий ток на 90 °.
- Емкостное реактивное сопротивление, X C (в Ом) с напряжением падает с запаздыванием ток на 90 °.
| f = 6,4 кГц R = 120 Ом L = 3,6 мГн C = 0,38 мкФ |
Рисунок 1. Пример цепи RLC |
| Рис. 2. Векторная сумма R и X L — X C дает Z |
Из формул для X L и X C , вы можете видим, что реактивные сопротивления зависят от обоих значений компонентов L и C , а также частота переменного тока, f :
а также
, где f — частота в Герцы (или сек -1 ), L — индуктивность по Генри, а C — это индуктивность. емкость в фарадах.Потому что X L и X C различаются по фазе на 180 °, общее реактивное сопротивление X последовательной цепи X L — X C .
Знакомые применения закона Ома, такие как последовательная и параллельная цепь. расчеты, все еще применяются. Однако теперь вы должны рассмотреть конкурирующий вектор. вклады от сопротивлений и реактивных сопротивлений.
Фазовые углы и векторы
Давайте найдем полное сопротивление цепи на Рисунке 1.Используя формулы выше:
Создавая импеданс Z , резистор вносит вклад в горизонтальную составная часть. Вертикальная составляющая — это разница реактивных сопротивлений: X L — X C . Тогда Z — это векторная сумма R и X L — X C , как показано на рисунке 2.
На рисунке 2 видно, что Z — гипотенуза прямоугольного треугольника, мы можем использовать теорему Пифагора и геометрию прямоугольного треугольника, чтобы вычислить Z .
Итак, в этой схеме мы наблюдаем эффект импеданса 144 Ом, при отставании тока от напряжения питания на фазовый угол 33,5 °.
Как вы могли догадаться из обсуждения выше, вполне возможно, что индуктивное и емкостное сопротивление для точной компенсации при правильных комбинациях из L , C и f ценности.Это очень важное условие, известное как резонанс .
Цепи переменного тока серииRLC | Физика
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом данного раздела. Суть анализа цепи RLC — это частотная зависимость X L и X C , а также их влияние на фазу зависимости напряжения от тока (установлено в предыдущий раздел).Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X L и емкостного реактивного сопротивления X C определяется как полное сопротивление , аналог сопротивления в цепи постоянного тока по переменному току.Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].
Здесь I 0 — пиковый ток, В 0 — пиковое напряжение источника, а Z — полное сопротивление цепи. Единицы импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток.Чтобы получить выражение для Z через R , X L и X C , мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение. Эти напряжения обозначены как В R , В L и В C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны.Но мы знаем из предыдущего раздела, что напряжение на катушке индуктивности В L опережает ток на одну четверть цикла, напряжение на конденсаторе В C следует за током на единицу. -четвертый цикл, и напряжение на резисторе В, R точно совпадает по фазе с током. На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В R + В L + В C , где все четыре напряжения — мгновенные значения.Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как V R находится в фазе с током, V L опережает 90º, а V C следует на 90º. Таким образом, V L и V C сдвинуты по фазе на 180º (от пика до впадины) и имеют тенденцию к аннулированию, хотя и не полностью, если они не имеют одинаковой величины.{2}}} \\ [/ latex],
, где V 0 R , V 0 L и V 0 C — пиковые напряжения на R , L и C , соответственно. {2}} \\ [/ latex],
, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X L = 0; а для тех, у кого нет конденсатора, возьмите X C = 0.
Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы в сумме равняются напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1.Расчет импеданса и тока
Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В среднеквадратичное значение = 120 В, что будет I среднеквадратичное значение на каждой частоте?
СтратегияДля каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)В обоих случаях результат почти такой же, как и наибольшее значение, а импеданс определенно не является суммой отдельных значений. Ясно, что X L доминирует на высокой частоте, а X C доминирует на низкой частоте.
Решение для (b)Текущее значение I среднеквадратичное значение можно найти, используя версию закона Ома по переменному току в уравнении I среднеквадратичное значение = В среднеквадратичное значение / Z :
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц
Наконец, на частоте 10,0 кГц мы находим
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц
Обсуждение для (а)Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от того, который был обнаружен для одной катушки индуктивности в Примере 1 из разделов «Реактивное сопротивление, индуктивность и емкость».{2}}} \\ [/ латекс]
Реактивные сопротивления изменяются в зависимости от частоты: X L большое на высоких частотах и X C большое на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f 0 реактивные сопротивления будут равны и уравновешены, давая Z = R — это минимальное значение для импеданса и максимальное значение для I rms результатов .Мы можем получить выражение для f 0 , взяв
X L = X C .
Замена определений X L и X C ,
[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].
Решение этого выражения для f 0 дает
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],
, где f 0 — резонансная частота последовательной цепи RLC .Это также собственная частота , , при которой цепь будет колебаться, если не будет управляться источником напряжения. При f 0 влияние катушки индуктивности и конденсатора компенсируется, так что Z = R и I среднеквадратичное значение является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызванное источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на ее f 0 . Переменный конденсатор часто используется для настройки f 0 , чтобы получить желаемую частоту и отклонить другие. На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I среднеквадратичное значение при f 0 . Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f 0 , но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В 0 .
Пример 2. Расчет резонансной частоты и тока
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I среднеквадратичное значение при резонансе, если В среднеквадратичное значение равно 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.
Решение для (b)Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].
Обсуждение для (б)В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.
Питание в цепях переменного тока серии
RLCЕсли ток изменяется в зависимости от частоты в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I действующее значение ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В действующее значение 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
Стратегия и решение для (а)Коэффициент мощности при 60,0 Гц находится из
.[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].
Мы знаем Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что
[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].
Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].
Обсуждение для (а)Фазовый угол близок к 90 °, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90 °).
Стратегия и решение для (b)Средняя мощность при 60,0 Гц —
P ср. = I среднеквадратичное значение В среднеквадратичное значение cos ϕ .
I среднеквадратичное значение оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает
P средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.
Стратегия и решение для (c)На резонансной частоте мы знаем, что cos ϕ = 1, и I среднеквадратичное значение оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P средн. = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)
ОбсуждениеКак ток, так и коэффициент мощности больше в резонансе, что дает значительно большую мощность, чем на высоких и низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в схему.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистый контур LC с незначительным сопротивлением колеблется на f 0 , той же резонансной частоте, что и контур RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.
Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Исследование PhET: комплект для конструирования цепей (AC + DC), виртуальная лабораторияСоздавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I o — пиковый ток, а В o — пиковое напряжение источника.{2}} \\ [/ латекс].
- Резонансная частота f 0 , при которой X L = X C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
- В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
- ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.
Концептуальные вопросы
1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.
2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.
Задачи и упражнения
1. Цепь RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.
2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.
3. Цепь LC состоит из индуктора 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?
5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В среднеквадратичное значение = 5,60 В, что будет I среднеквадратичное значение на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I RMS в резонансе?
11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В СКЗ = 408 В, что будет I СКЗ на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I RMS в резонансе?
12. Последовательная цепь RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (a) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.
13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.
14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. На частоте 8000 Гц фазовый угол составляет 45,0 °. {2}} \\ [/ latex]
- резонансная частота:
- — частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]
- фазовый угол:
- обозначается ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- Коэффициент мощности:
- — величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ
Избранные решения проблем и упражнения
1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой — индуктор доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.
5. От 9,30 нФ до 101 нФ
7. 3,17 пФ
9. (а) 1,31 мкГн (б) 1,66 пФ
11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A
13. (а) 0,159 (б) 80,9 ° (в) 26,4 Вт (г) 166 Вт
15. 16.0 Вт
Расчет полного сопротивления
Расчет общего импеданса Z в электрических цепях переменного тока.В коллекции примеров вы можете найти формулы для емкостного реактивного сопротивления X C и индуктивного реактивного сопротивления X L . Импеданс больше, чем сопротивление. Импеданс состоит из трех компонентов: сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления. Импеданс в общем случае вектор. Составляющие импеданса представляют собой геометрическую сумму, потому что они также являются векторами. Комплексные числа используются для расчета импеданса и его составляющих.
Составляющие импеданса
Импеданс состоит из трех компонентов.В общем, импеданс — это вектор, состоящий из комплексных чисел.
Z = R + j · X L -j · X C
где
• R = ρ · l / S — сопротивление [Ом]
• X L = ω · L — индуктивное реактивное сопротивление [ Ω]
• X C = 1 / (ω · C) — емкостное реактивное сопротивление [Ω]
• ω = 2 · Π · f — пульсация [рад / с]
Составляющие импеданса
Определение полного сопротивления — пример 1
Обозначение полного сопротивления и его компонентов для цепи переменного тока.В примере будет вычислено полное сопротивление цепи Z , которое видно с клемм источника питания. Схема построена из двух резисторов R, конденсатора C и индуктивности L. Построим также векторную диаграмму токов и напряжений в цепи.
Полный импеданс — пример 1
Определение полного сопротивления — пример 2
Обозначение полного сопротивления Z для электрической цепи переменного тока. Рассматриваемая электрическая схема построена из трех резисторов R, конденсатора С и индуктивности L.Все части в цепи имеют одинаковое значение импеданса, равное 1 [Ом]. Детали в цепи соединены смешанными способами, потому что есть последовательные соединения и параллельные соединения. Полный импеданс обозначается как импеданс, видимый от силовых клемм. В примере будет применено соотношение между импедансом Z и полным сопротивлением Y → Y = 1/ Z .
• Z = R + j · X → Z = R + j · (X L -X C )
• Y = G + j · B
Полный импеданс — пример 2
Определение полного сопротивления — пример 3
Обозначение полного сопротивления и его компонентов для цепи переменного тока.В примере будет вычислено полное сопротивление цепи, которое видно с клемм источника питания. Схема построена из двух резисторов, двух катушек и одного конденсатора. Также будут написаны формулы для закона Ома в цепи переменного тока.
Полный импеданс — пример 3
Определение полного сопротивления — пример 4
Обозначение полного сопротивления и его компонентов для цепи переменного тока. В примере будет вычислено полное сопротивление цепи, которое видно с клемм источника питания. Схема построена из трех катушек, трех конденсаторов и одного резистора.Также будет записан закон Ома в цепи переменного тока.
Полный импеданс — пример 4
Определение полного сопротивления — пример 5
Обозначение полного сопротивления Z и его компонентов для цепи переменного тока. В примере будет вычислено полное сопротивление цепи, которое видно с клемм источника питания. Схема построена на двух конденсаторах, индуктивности и резисторе. Известны импедансы каждой части цепи. Схема имеет смешанные соединения, параллельные и последовательные.Будет применено соотношение между импедансом Z и проводимостью Y → Y = 1/ Z .
Полный импеданс — пример 5
Определение полного сопротивления — пример 6
Обозначение полного сопротивления Z и его компонентов для цепи переменного тока. В примере будет вычислено полное сопротивление цепи, которое видно с клемм источника питания. Схема построена с двумя индуктивностями, тремя резисторами и конденсатором. Известны импедансы каждой части цепи.Схема имеет смешанные соединения, параллельные и последовательные. Будет применено соотношение между импедансом Z и проводимостью Y → Y = 1/ Z . Проводимость обычно используется для расчета полного сопротивления параллельного соединения между частями.
Полный импеданс — пример 6
Определение полного сопротивления — пример 7
Электрическая цепь состоит из трех пассивных частей, резистора R 1 = 2 [Ом], конденсатора C 1 = 2 [мкФ] и индуктивности L 1 = 100 [мГн].Все части в цепи соединены параллельно. На схему подается напряжение U . Действующее значение напряжения составляет 230 [В переменного тока]. Напряжение имеет частоту f = 50 [Гц]. Примером может служить расчет тока I , протекающего по цепи. В примере будет вычислено полное сопротивление Z . Закон для цепей переменного тока будет применяться для расчета тока I → I = U / Z . Все расчеты в примере производятся с применением комплексных чисел.
Полный импеданс — пример 7
Преобразователь случайных чисел | Онлайн-конвертеры единиц измеренияКонвертер длины и расстоянияКонвертер массыКонвертер объёма сухого воздуха и общих измерений при варкеПреобразователь площадиПреобразователь объёма и общего измерения при варкеПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь силыПреобразователь силыКонвертер времениЛинейный конвертер скорости и скоростиКонвертер угловой эффективностиПреобразователь топливной эффективности, расхода топлива и информации о расходе топливаКонвертер единиц Хранение данныхКурсы обмена валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаПреобразователь момента инерцииПреобразователь момента силыКонвертер крутящего моментаПреобразователь удельной энергии, теплоты сгорания (на единицу температуры на массу) Преобразователь интерваловКонвертер коэффициента теплового расширенияПреобразователь теплового сопротивленияПреобразователь теплопроводности Конвертер удельной теплоемкости ter Конвертер скорости передачиКонвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер яркостиКонвертер яркостиКонвертер разрешения цифрового изображенияПреобразователь частоты и длины волныОптическая мощность (диоптрия) в преобразователь фокусного расстоянияПреобразователь оптической мощности (диоптрий) в увеличение (X) Конвертер электрического заряда Конвертер плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объёмной плотности заряда Конвертер электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь единиц магнитного поля в ваттах и дБм Конвертер плотности потока Конвертер мощности поглощенной дозы излучения, Конвертер мощности дозы полного ионизирующего излученияРадиоактивность.Преобразователь радиоактивного распада Преобразователь радиационного воздействияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксов Конвертер передачи данных Конвертер единиц типографии и цифрового изображения Конвертер единиц измерения объема древесины Калькулятор молярной массыПериодическая таблица Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовывать многие единицы измерения из одной системы в другую. Страница преобразования единиц представляет собой решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеренными в различных единицах. Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрическую, британскую и американскую) в 76 категорий или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и емкость, объемный расход и многое другое. Преобразователи общих единицКонвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, расстояние до Луны (от Земли до Луны), лига , миля, морская миля (международная), сажень, длина кабеля (международная), точка, пиксель, калибр, планковская длина… Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, камень (США), камень (Великобритания), карат, зерно, талант (библейский греческий), драхма (библейский греческий), денарий (библейский римлянин), шекель (библейский иврит), масса Планка, масса протона, атомная единица массы, масса электрона (покой), масса Земли, масса Солнца … Сухой объем и общие измерения при приготовлении пищи : литр, бочка сухой (США), пинта сухой (США), квартовый сухой (США), peck (США), peck (Великобритания), bushel (США), bushel (UK), cor (библейский), homer (библейский), ephah (библейский) ), seah (библейский), omer (библейский), cab (библейский), log (библейский), кубометр. Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круглый дюйм, поселок, роуд, стержень², окунь², усадьба, шест², сабин, арпент, куерда, квадратная верста, квадратный аршин, квадратный фут, квадратный сажень, площадь Планка … Конвертер объёма и общепринятых единиц измерения : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, бочка (масло), бочка (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов… Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ренкина, градус Реомюра, температура Планка. Преобразователь давления, напряжения, модуля Юнга : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, атмосферно-техническая, стандартная атмосфера, ksi, psi, ньютон на метр², бар, миллибар, килограмм-сила / метр², грамм- сила / сантиметр², тонна-сила (короткая) / фут², фунт-сила / фут², миллиметр ртутного столба (0 ° C), дюйм ртутного столба (32 ° F), сантиметр водяного столба (4 ° C), фут водяного столба (4 ° C) , метр морской воды… Конвертер энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектронвольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (IT), калория (пищевая), Британские тепловые единицы (IT), мега Btu (IT), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (взрывчатые вещества), килограмм в тротиловом эквиваленте, дин-сантиметр, грамм-сила-сантиметр, килограмм-сила-метр, килопонд-метр, фут-фунт, дюйм-фунт, энергия Планка … Power Converter : ватт, киловатт, мегаватт, милливатт, лошадиные силы, вольт-ампер, ньютон-метр / секунда, джоуль / секунда, мегаджоуль в секунду, килоджоуль в секунду, миллиджоуль в секунду, джоуль в час, килоджоуль в час, эрг в секунду, британские тепловые единицы (IT) в час, килокалории (IT) в час… Преобразователь силы : ньютон, килоньютон, миллиньютон, дин, джоуль / метр, джоуль / сантиметр, грамм-сила, килограмм-сила, тонна-сила (короткая), кип-сила, килопунт-сила, фунт-сила сила, унция-сила, фунтал, фунт-фут в секунду², pond, sthene, грав-сила, миллиграв-сила … Преобразователь времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, декада, век, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический), год (сидерический), год (григорианский), две недели, встряска… Конвертер линейной скорости и скорости : метр в секунду, километр в час, километр в секунду, миля в час, фут в секунду, миля в секунду, узел, узел (Великобритания), скорость света в вакууме, космический скорость — первая, космическая скорость — вторая, космическая скорость — третья, скорость Земли, скорость звука в чистой воде, Мах (стандарт СИ), Мах (20 ° C и 1 атм), ярд / секунду … Угол Конвертер : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, круг, поворот, квадрант, прямой угол, секстант. Конвертер топливной экономичности, расхода топлива и экономии топлива : метр / литр, километр / литр, миля (США) / литр, морская миля / литр, морская миля / галлон (США), километр / галлон (США), литр / 100 км, галлон (США) / миля, галлон (США) / 100 миль, галлон (Великобритания) / миля, галлон (Великобритания) / 100 миль … Конвертер чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, основание-3, основание-4, основание-5, основание-6, основание-7, основание-9, основание-10, основание-11, основание-12, основание-13, основание-14, основание-15, основание-20, основание-21, основание-22, основание-23, основание-24, основание-28, основание-30, основание-32, основание-34, основание-36… Преобразователь единиц информации и хранения данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит), кибибит, кибибайт, килобайт (10³ байтов), мегабайт (10⁶ байтов), гигабайт (10⁹ байтов), терабайт (10¹² байтов), петабайт (10¹⁵ байтов), эксабайт (10¹⁸ байтов), гибкий диск (3,5 ED), гибкий диск (5,25 HD), Zip 250, Jaz 2 ГБ, CD (74 минут), DVD (2 слоя 1 сторона), диск Blu-ray (однослойный), диск Blu-ray (двухслойный) … Курсы валют : евро, доллар США, канадский доллар, британский фунт стерлингов, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель , Иорданский динар, малайзийский ринггит, мексиканское песо, новозеландский доллар, норвежская крона, пакистанская рупия, филиппинское песо, румынский лей, российский рубль, саудовский риял, сингапурский доллар, Южноафриканский рэнд, южнокорейский вон, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна… Размеры женской одежды и обуви : женские платья, костюмы и свитера, женская обувь, женские купальные костюмы, размер буквы, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Естественная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, континентальный, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея .. Размеры мужской одежды и обуви : мужские рубашки, мужские брюки / брюки, размер мужской обуви, размер букв, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, Рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, континентальный, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика… МеханикаПреобразователь угловой скорости и частоты вращения : радиан / секунда, радиан / день, радиан / час, радиан / минута, градус / день, градус / час, градус / минута, градус / секунда, оборот / день, оборот / час, оборот / минута, оборот / секунда, оборот / год, оборот / месяц, оборот / неделя, градус / год, градус / месяц, градус / неделя, радиан / год, радиан / месяц, радиан / неделя. Преобразователь ускорения : дециметр / секунда², метр / секунда², километр / секунда², гектометр / секунда², декаметр / секунда², сантиметр / секунда², миллиметр / секунда², микрометр / секунда², нанометр / секунда², пикометр / секунда², фемтометр / секунда² , аттометр / секунда², галлон, галилей, миля / секунда², ярд / секунда², фут / секунда², дюйм / секунда², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне… Конвертер плотности : килограмм / метр³, килограмм / сантиметр³, грамм / метр³, грамм / сантиметр³, грамм / миллиметр³, миллиграмм / метр³, миллиграмм / сантиметр³, миллиграмм / миллиметр³, экзаграмма / литр, петаграмм / литр, тераграмма / литр, гигаграмм / литр, мегаграмм / литр, килограмм / литр, гектограмм / литр, декаграмм / литр, грамм / литр, дециграмм / литр, сантиграмм / литр, миллиграмм / литр, микрограмм / литр, нанограмм / литр, пикограмм / литр , фемтограмм / литр, аттограмм / литр, фунт / дюйм³ … Конвертер удельного объема : метр³ / килограмм, сантиметр³ / грамм, литр / килограмм, литр / грамм, фут³ / килограмм, фут³ / фунт, галлон (США ) / фунт, галлон (Великобритания) / фунт. Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметр², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда², фунт-дюйм². , фунт-сила-дюйм-секунда², ударный фут². Конвертер момента силы : метр ньютон, метр килоньютон, метр миллиньютон, метр микроньютон, метр тонна-сила (короткий), метр тонна-сила (длинный), метр тонна-сила (метрический), метр килограмм-сила, грамм-сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм. Гидротрансформатор : ньютон-метр, ньютон-сантиметр, ньютон-миллиметр, килоньютон-метр, дин-сантиметр, дин-сантиметр, дин-миллиметр, килограмм-сила-метр, килограмм-сила-сантиметр, килограмм-сила-миллиметр, грамм-сила-метр, грамм- сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм. Термодинамика — теплоКонвертер удельной энергии, теплоты сгорания (на массу) : джоуль / килограмм, килоджоуль / килограмм, калория (IT) / грамм, калория (th) / грамм, BTU (IT) / фунт, BTU (th) / фунт, килограмм / джоуль, килограмм / килоджоуль, грамм / калория (IT), грамм / калория (th), фунт / BTU (IT), фунт / Btu (th), фунт / лошадиная сила-час, грамм / лошадиная сила (метрическая) -час, грамм / киловатт-час. Конвертер удельной энергии, теплоты сгорания (на объем) : джоуль / метр³, джоуль / литр, мегаджоуль / метр³, килоджоуль / метр³, килокалория (IT) / метр³, калория (IT) / сантиметр³, терм / фут³, терм / галлон (Великобритания), британские тепловые единицы (IT) на фут³, британские тепловые единицы на фут³, CHU / фут³, метр³ / джоуль, литр / джоуль, галлон (США) / лошадиная сила-час, галлон (США) / лошадиная сила (метрическая система) )-час. Конвертер теплопроводности : ватт / метр / K, ватт / сантиметр / ° C, киловатт / метр / K, калория (IT) / секунда / сантиметр / ° C, калория (th) / секунда / сантиметр / ° C , килокалория (IT) / час / метр / ° C, килокалория (th) / час / метр / ° C, BTU (IT) дюйм / секунда / фут² / ° F, BTU (th) дюйм / секунда / фут² / ° F , BTU (IT) фут / час / фут² / ° F, Btu (th) фут / час / фут² / ° F, BTU (IT) дюйм / час / фут² / ° F, BTU (th) дюйм / час / фут² / ° F. Конвертер удельной теплоемкости : джоуль / килограмм / K, джоуль / килограмм / ° C, джоуль / грамм / ° C, килоджоуль / килограмм / K, килоджоуль / килограмм / ° C, калория (IT) / грамм / ° C, калория (IT) / грамм / ° F, калория (th) / грамм / ° C, килокалория (IT) / килограмм / ° C, килокалория (th) / килограмм / ° C, килокалория (IT) / килограмм / K , килокалория (th) / килограмм / K, килограмм-сила-метр / килограмм / K, фунт-сила-фут / фунт / ° R, Btu (IT) / фунт / ° F, Btu (th) / фунт / ° F, Btu (IT) / фунт / ° R, Btu (th) / фунт / ° R, Btu (IT) / фунт / ° C, CHU / фунт / ° C. Конвертер плотности теплового потока : ватт / метр², киловатт / метр², ватт / сантиметр², ватт / дюйм², джоуль / секунда / метр², килокалория (IT) / час / метр², килокалория (IT) / час / фут², калория (IT) / минута / сантиметр², калория (IT) / час / сантиметр², калория (th) / минута / сантиметр², калория (th) / час / сантиметр², дина / час / сантиметр, эрг / час / миллиметр², фут-фунт / минута на фут², лошадиные силы на фут², лошадиные силы (метрические единицы) на фут², британские тепловые единицы (IT) / секунда на фут², британские тепловые единицы (IT) в минуту на фут², британские тепловые единицы (ИТ) на час / фут², британские тепловые единицы (единицы) / секунда на дюйм² , Btu (th) / секунда / фут², Btu (th) / минута / фут², Btu (th) / час / фут², CHU / час / фут². Преобразователь коэффициента теплопередачи : ватт / метр² / K, ватт / метр² / ° C, джоуль / секунда / метр² / K, килокалория (IT) / час / метр² / ° C, килокалория (IT) / час / фут² / ° C, BTU (IT) / секунда / фут² / ° F, Btu (th) / секунда / фут² / ° F, BTU (IT) / час / фут² / ° F, BTU (th) / час / фут² / ° F, CHU / час / фут² / ° C. Гидравлика — жидкостиКонвертер объемного расхода : метр³ / секунда, метр³ / день, метр³ / час, метр³ / минута, сантиметр³ / день, сантиметр³ / час, сантиметр³ / минуту, сантиметр³ / секунда, литр / день, литр в час, литр в минуту, литр в секунду, миллилитр в день, миллилитр в час, миллилитр в минуту, миллилитр в секунду, галлон (США) в день, галлон (США) в час, галлон (США) в минуту, галлон (США) в секунду, галлон (Великобритания) в день, галлон (Великобритания) в час, галлон (Великобритания) в минуту, галлон (Великобритания) в секунду, килобаррель (США) в день, баррель (США) в день… Конвертер массового расхода : килограмм / секунда, грамм / секунда, грамм / минута, грамм / час, грамм / день, миллиграмм / минута, миллиграмм / час, миллиграмм / день, килограмм / минута, килограмм / час , килограмм / день, экзаграмм / секунда, петаграмма / секунда, тераграмма / секунда, гигаграмма / секунда, мегаграмм / секунда, гектограмм / секунда, декаграмма / секунда, дециграмма / секунда, сантиграмма / секунда, миллиграмм / секунда, микрограмм / секунда, тонна (метрическая) / секунда, тонна (метрическая) / минута, тонна (метрическая) / час, тонна (метрическая) / день … Конвертер молярного расхода : моль / секунда, экзамен / секунда, петамоль / секунда, терамоль в секунду, гигамоль в секунду, мегамоль в секунду, киломоль в секунду, гектомоль в секунду, декамоль в секунду, децимоль в секунду, сантимоль в секунду, миллимоль в секунду, микромоль в секунду, наномоль в секунду, пикомоль в секунду, фемтомоль в секунду. секунда, аттомоль в секунду, моль в минуту, моль в час, моль в день, миллимоль в минуту, миллимоль в час, миллимоль в день, километр в минуту, километр в час, километр в день. Преобразователь потока массы : грамм / секунда / метр², килограмм / час / метр², килограмм / час / фут², килограмм / секунда / метр², грамм / секунда / сантиметр², фунт / час / фут², фунт / секунда / фут². Конвертер молярной концентрации : моль / метр³, моль / литр, моль / сантиметр³, моль / миллиметр³, километр / метр³, километр / литр, километр / сантиметр³, километр / миллиметр³, миллимоль / метр³, миллимоль / литр, миллимоль / сантиметр³, миллимоль / миллиметр³, моль / дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный. Конвертер массовой концентрации в растворе : килограмм / литр, грамм / литр, миллиграмм / литр, часть / миллион, гран / галлон (США), гран / галлон (Великобритания), фунт / галлон (США), фунт / галлон (Великобритания), фунт / миллион галлон (США), фунт / миллион галлон (Великобритания), фунт / фут³, килограмм / метр³, грамм / 100 мл. Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила-секунда на метр², ньютон-секунда на метр², миллиньютон-секунда на квадратный метр, дин-секунда на сантиметр², равновесие, экзапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектопуаз, декапуаз, деципуаз, сантипуаз, миллипуаз, микропуаз, наноуаз, пикопуаз, фемтопуаз, аттопуаз, фунт-сила-секунда / дюйм², фунт-сила-секунда / фут², фунт-секунда / фут², грамм / сантиметр / секунда… Конвертер кинематической вязкости : метр² / секунда, метр² / час, сантиметр² / секунда, миллиметр² / секунда, фут² / секунда, фут² / час, дюйм² / секунда, стоксы, экзастоки, петастоки, терастоки, гигастоки, мегастоксы, килостоки, гектостоки, декастоки, децистоки, сантистоки, миллистоки, микростоки, наностоки, пикостоки, фемтостоки, аттостоки. Преобразователь поверхностного натяжения : ньютон на метр, миллиньютон на метр, грамм-сила на сантиметр, дина на сантиметр, эрг / сантиметр², эрг / миллиметр², фунт на дюйм, фунт-сила / дюйм. Акустика — ЗвукПреобразователь чувствительности микрофона : децибел относительно 1 вольт на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольта на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль. Преобразователь уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дин / квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах. Фотометрия — светКонвертер яркости : кандела на метр², кандела на сантиметр², кандела на фут², кандела на дюйм², килокандела на метр², стильб, люмен на метр² / стерадиан, люмен на сантиметр² / стерадиан² / люмен стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостиль, блондель, брил, скот. Конвертер силы света : кандела, свеча (немецкий язык), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица измерения яркости, десятичный буж, люмен / стерадиан, свеча (Международный). Конвертер освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, nox, кандела стерадиан на метр², люмен на метр², люмен на сантиметр², люмен на фут², ватт на сантиметр² (при 555 нм) . Преобразователь частоты и длины волны : герцы, эксагерцы, петагерцы, терагерцы, гигагерцы, мегагерцы, килогерцы, гектогерцы, декагерцы, децигерцы, сантигерцы, миллигерцы, микрогерцы, микрогерцы, секунды, микрогерцы / секунды , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах… Конвертер оптической силы (диоптрия) в фокусное расстояние : Оптическая сила (диоптрическая сила или преломляющая сила) линзы или другой оптической системы — это степень, с которой система сходится или рассеивает свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы, и измеряется в обратных метрах в СИ или, чаще, в диоптриях (1 диоптрия = м⁻¹) ЭлектротехникаКонвертер электрического заряда : кулон, мегакулон , килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, франклин, ампер-час, миллиампер-час, ампер-минута, ампер-секунда, фарадей (на основе углерода 12), элементарный плата. Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭДС тока, статампер, ЭДС тока, СГС э.м. единица, CGS e.s. единица, микроампер, наноампер, ток Планка. Линейный преобразователь плотности тока : ампер / метр, ампер / сантиметр, ампер / дюйм, абампер / метр, абампер / сантиметр, абампер / дюйм, эрстед, гильберт / сантиметр, ампер / миллиметр, миллиампер / метр, миллиампер / метр , миллиампер / сантиметр, миллиампер / миллиметр, микроампер / метр, микроампер / дециметр, микроампер / сантиметр, микроампер / миллиметр. Преобразователь поверхностной плотности тока : ампер / метр², ампер / сантиметр², ампер / дюйм², ампер / мил², ампер / круговой мил, абампер / сантиметр², ампер / миллиметр², миллиампер / миллиметр², микроампер / миллиметр², миллиампер / миллиметр², километр » миллиампер / сантиметр², микроампер / сантиметр², килоампер / сантиметр², ампер / дециметр², миллиампер / дециметр², микроампер / дециметр², килоампер / дециметр². Преобразователь напряженности электрического поля : вольт на метр, киловольт на метр, киловольт на сантиметр, вольт на сантиметр, милливольт на метр, микровольт на метр, киловольт на дюйм, вольт на дюйм, вольт на мил, абвольт на сантиметр, статвольт / сантиметр, статвольт / дюйм, ньютон / кулон, вольт / микрон. Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт / ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковское напряжение. Преобразователь электрического сопротивления : Ом, мегаом, мкОм, вольт / ампер, обратный сименс, abohm, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, кОм. Преобразователь удельного электрического сопротивления : омметр, ом-сантиметр, ом-дюйм, микром-сантиметр, микром-дюйм, ом-сантиметр, статом-сантиметр, круговой мил-ом / фут, ом-кв.миллиметр на метр. Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер / вольт, mho, gemmho, micromho, abmho, statmho, квантованная проводимость Холла. Конвертер электропроводности : сименс / метр, пикосименс / метр, mho / метр, mho / сантиметр, abmho / метр, abmho / сантиметр, статмо / метр, статмо / сантиметр, сименс / сантиметр, миллисименс / метр, миллисименс / сантиметр, микросименс / метр, микросименс / сантиметр, единица электропроводности, коэффициент проводимости, доли на миллион, шкала 700, шкала частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, части на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700. Преобразователь емкости : фарад, эксафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сентифарад, миллифарад, микрофарад, емкость, нанофарад, аттофарад, эм. , статфарад, ЭСУ емкости. Преобразователь индуктивности : генри, экзагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, амберогенри, энтогенри, энтогенри, энтиогенри, энтогенри , статенри, ЭСУ индуктивности. Преобразователь реактивной мощности переменного тока : реактивный вольт-ампер, реактивный милливольт-ампер, реактивный киловольт-ампер, реактивный мегавольт-ампер, реактивный гигавольт-ампер. Американский преобразователь калибра проволоки : Американский калибр проволоки (AWG) — это стандартизированная система калибра проволоки, используемая в Соединенных Штатах и Канаде для измерения диаметров цветных электропроводящих проводов, включая медь и алюминий. Чем больше площадь поперечного сечения провода, тем выше его допустимая нагрузка по току.Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Самый большой размер AWG — 0000 (4/0), а самый маленький — 40. В этой таблице перечислены размеры и сопротивление AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике. Магнитостатика, магнетизм и электромагнетизмПреобразователь магнитного потока : Вебер, милливебер, микровебер, вольт-секунда, единичный полюс, мегалин, килолин, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока. Конвертер плотности магнитного потока : тесла, Вебер / метр², Вебер / сантиметр², Вебер / дюйм², Максвелл / метр², Максвелл / сантиметр², Максвелл / дюйм², Гаусс, линия / сантиметр², линия / дюйм², гамма. Radiation and RadiologyКонвертер мощности поглощенной дозы излучения, суммарной мощности дозы ионизирующего излучения : серый цвет в секунду, эксагрей в секунду, петагрей в секунду, тераграрей в секунду, гигаграй в секунду, мегагрей в секунду, килограмм в секунду, гектограмм / секунда, декаграй / секунда, дециграй / секунда, сантигрей / секунда, миллиграй / секунда, микрогрей / секунда, наногрей / секунда, пикграй / секунда, фемтогрей / секунда, аттогрей / секунда, рад / секунда, джоуль / килограмм / секунда, ватт на килограмм, зиверт в секунду, миллизиверт в год, миллизиверт в час, микрозиверт в час, бэр в секунду, рентген в час… Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одна / секунда, дезинтеграция. Конвертер облучения : кулон на килограмм, милликулон на килограмм, микрокулон на килограмм, рентген, миллирентген, микрорентген, тканевый рентген, Паркер, респ. Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль на килограмм, джоуль на грамм, джоуль на сантиграм, джоуль на миллиграмм, грей, эксагрей, петагрей, терагрей, гигагрей, мегагрей, килограмм, гектагрей, декагрей, децигрей, сантигрей, микрогрей, миллиграм , наногрей, пикограй, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт … Прочие преобразователиКонвертер метрических префиксов : нет, йотта, дзетта, экса, пета, тера, гига, мега, килограмм, гектодека, дека , деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто. Конвертер передачи данных : бит / секунда, байт / секунда, килобит / секунда (SI по умолчанию), килобайт / секунда (SI по умолчанию), кибибит / секунда, кибибайт / секунда, мегабит / секунда (SI по умолчанию) , мегабайт в секунду (SI по умолчанию), мебибит в секунду, мебибайт в секунду, гигабит в секунду (SI по умолчанию), гигабайт в секунду (SI по умолчанию), гибибит в секунду, гибибит в секунду, терабит в секунду (SI по умолчанию). .), терабайт в секунду (по умолчанию SI), тебибит в секунду, тебибайт в секунду, Ethernet, Ethernet (быстрый), Ethernet (гигабит), OC1, OC3, OC12, OC24, OC48 … Типографика и цифровой Конвертер единиц изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер), точка (DTP / PostScript) ), point (компьютер), point (принтер), en, cicero, em, Didot point. Конвертер единиц измерения объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, футы для досок, тысяча футов для досок, шнур, шнур (80 фут3), футы для шнура, культ, поддон, поперечина, стяжка. Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на количество вещества в молях. Другими словами, это масса одного моля определенного вещества. Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, расположенных слева направо и сверху вниз по их атомным номерам, электронным конфигурациям и повторяющимся химическим свойствам, расположенным в форме таблицы таким образом, чтобы элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами.У некоторых групп есть имена, а также номера. Например, все элементы группы 1, кроме водорода, являются щелочными металлами, а элементы группы 18 — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что это расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек. У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Задайте свой вопрос в TCTerms , и вы получите ответ от опытных технических переводчиков в считанные минуты. |
Последовательный калькулятор импеданса R, C и L
- Цель использования
- Проверить закупки
[1] 2021/04/07 00:32 Уровень 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Проверка ответов на упражнения, разработанные для использования в классе в качестве инструктора по программа по электронике
[2] 2019/11/19 21:17 Уровень 50 лет / Учитель / Исследователь / Очень /
- Цель использования
- Глядя на Z входных цепей на старых передатчиках
- Комментарий / запрос
- Очень полезно.Спасибо
[3] 2019/03/27 21:26 Уровень 60 и старше / Инженер / Очень /
- Цель использования
- Точная настройка значений компонентов для электрической испытательной цепи.
[4] 2019/01/09 18:17 Уровень 30 лет / Инженер / Очень /
- Цель использования
- Помогать мне подготовиться к экзамену, очень полезно!
[5] 2018/11/29 22:57 Уровень 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Проверка
[6] 2018/11/20 01:21 Уровень 50 лет / Учитель / Исследователь / Очень /
- Цель использования
- Расчет импеданса антенны для дизайн-проекта
[7] 29.04.2018 20: 13 Уровень 50 лет / Средняя школа / Университет / аспирант / Very /
- Назначение
- для подготовки к экзаменам…
- Комментарий / запрос
- пожалуйста, скажите мне, как решить импеданс от нормали к импедансу n угол … ???
[8] 2017/11/08 06:15 Моложе 20 лет / Высшая школа / Вуз / Аспирант / Немного /
- Цель использования
- Рассчитать импеданс последовательного RC (без L) для демпфирования катушки реле, когда катушка отключена. под напряжением.
[9] 2017/10/19 00:58 Уровень 50 лет / Инженер / Очень /
- Комментарий / запрос
- Это обычная «простая схема RLC» Но что, если мне нужны 2 или 3 индуктора последовательно в цепи? Что, если 2 или 3 катушки индуктивности связаны магнитным полем?
[10] 2017/07/17 08:35 40-летний уровень / Другое / Немного /
РЕАКТИВНАЯ МОЩНОСТЬ — прикладное промышленное электричество
Рисунок 6.1 Чисто резистивная цепь переменного тока: напряжение и ток резистора совпадают по фазе.Если бы мы изобразили ток и напряжение для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)
Рисунок 6.2 Напряжение и ток «синфазны» для резистивной цепи.Поскольку резистор просто и напрямую сопротивляется протеканию тока во все периоды времени, форма волны падения напряжения на резисторе точно совпадает по фазе с формой волны тока через него.Мы можем посмотреть в любой момент времени вдоль горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «снимок», показывающий значения волны, называется мгновенными значениями , что означает значения при этом момент времени ). Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Аналогичным образом, в момент времени, когда ток через резистор достигает своего положительного пика, напряжение на резисторе также находится на своем положительном пике, и так далее.В любой момент времени на волнах закон Ома справедлив для мгновенных значений напряжения и тока.
Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)
Рисунок 6.3 Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительная.Резисторы и индуктивности
Катушки индуктивности ведут себя иначе, чем резисторы. В то время как резисторы просто противодействуют протеканию тока через них (снижая напряжение, прямо пропорциональное току), индукторы противодействуют изменениям тока через них, снижая напряжение, прямо пропорциональное скорости изменения тока.В соответствии с законом Ленца , это индуцированное напряжение всегда имеет такую полярность, чтобы поддерживать ток на его текущем значении. То есть, если ток увеличивается по величине, индуцированное напряжение будет «противодействовать» протеканию тока; если ток уменьшается, полярность изменится на противоположную и «подтолкнет» ток, чтобы противодействовать уменьшению. Это противодействие изменению тока называется реактивным сопротивлением , а не сопротивлением . Выражаясь математически, соотношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:
[латекс] e = L \ frac {d_i} {d_t} [/ латекс]
Переменный ток в простой индуктивной цепи
Выражение di / dt — это выражение из расчетов, означающее скорость изменения мгновенного тока (i) во времени в амперах в секунду.Индуктивность (L) измеряется в Генри, а мгновенное напряжение (е), конечно, выражается в вольтах. Иногда вы можете встретить скорость мгновенного напряжения, выраженную как «v» вместо «e» (v = L di / dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктора:
Рисунок 6.4 Чистая индуктивная цепь: ток индуктора отстает от напряжения индуктора на 90 °.Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее на . Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток достигает пика (нулевое изменение или наклон уровня на синусоидальной волне тока), а мгновенное напряжение находится на пике везде, где мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, сдвинутой по фазе на 90 ° с волной тока. Глядя на график, кажется, что волна напряжения имеет «фору» по сравнению с волной тока; напряжение «опережает» ток, а ток «отстает» от напряжения.
Ток отстает от напряжения на 90 ° в чисто индуктивной цепи.
Все становится еще интереснее, когда мы строим график мощности для этой цепи:
Рисунок 6.6 В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p = ie), мощность равна нулю, когда мгновенный ток или напряжение равно нулю. Если мгновенный ток и напряжение положительные (над линией), мощность положительная. Как и в примере с резистором, мощность также положительна, когда мгновенный ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90 °, бывают моменты, когда одна из них положительна, а другая — отрицательна, что приводит к одинаково частым возникновению отрицательной мгновенной мощности .
Что такое отрицательная сила?
Но что означает отрицательная мощность ? Это означает, что катушка индуктивности возвращает мощность в цепь, в то время как положительная мощность означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности с течением времени, индуктор возвращает обратно в цепь столько же мощности, сколько потребляет в течение полного цикла. В практическом смысле это означает, что реактивное сопротивление катушки индуктивности рассеивает нулевую полезную энергию, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, у которых нет сопротивления провода.
Реактивное сопротивление в зависимости от сопротивления
Противодействие катушки индуктивности изменению тока означает противодействие переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току аналогично сопротивлению, но отличается тем, что всегда приводит к сдвигу фаз между током и напряжением и рассеивает нулевую мощность. Из-за различий он имеет другое название: реактивное сопротивление .Реактивное сопротивление по переменному току выражается в омах, как и сопротивление, за исключением того, что его математический символ — X вместо R. Чтобы быть конкретным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X L .
Так как напряжение на катушках индуктивности падает пропорционально скорости изменения тока, они будут снижать большее напряжение при более быстром изменении тока и меньшее напряжение при более медленном изменении тока. Это означает, что реактивное сопротивление в Ом для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула для определения реактивного сопротивления выглядит следующим образом:
[латекс] X_L = 2πfL [/ латекс]
Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, он проявит реактивные сопротивления, указанные в таблице ниже.
Реактивное сопротивление индуктора 10 мГн:
| Частота (Герцы) | Реактивное сопротивление (Ом) |
| 60 | 3.7699 |
| 120 | 7,5398 |
| 2500 | 157.0796 |
В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение. Это количество радиан в секунду, на которое «вращается» переменный ток, если вы представите себе один цикл переменного тока, представляющий вращение полного круга. радиан — это единица измерения угла: в одном полном круге 2π радиана, так же как в полном круге 360 °.Если генератор переменного тока является двухполюсным, он будет производить один цикл на каждый полный оборот вала, что составляет каждые 2π радиан или 360 °. Если эту константу 2π умножить на частоту в герцах (циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.
Угловая скорость в системах переменного тока
Угловая скорость может быть представлена выражением 2πf или ее собственным символом — строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формулу реактивного сопротивления X L = 2πfL можно также записать как X L = ωL.
Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро колеблются колебания переменного тока, полный цикл равен 2π радиан. Это не обязательно отражает фактическую скорость вала генератора переменного тока. Если генератор имеет более двух полюсов, угловая скорость будет кратной скорости вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.
Как бы мы ни выразили угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в катушке индуктивности. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока катушка индуктивности будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Пример схемы показан здесь:
Индуктивное сопротивление(Индуктивное сопротивление индуктора 10 мГн при 60 Гц)
[латекс] X_L = 3,7600 Ом [/ латекс]
[латекс] I_ {X_ {L}} = \ frac {E} {X} [/ latex]
[латекс] = \ frac {10 В} {3,7600 Ом} [/ латекс]
[латекс] \ mathbf {= 2.6526A} [/ латекс]
Фазовые углы
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг + 90 ° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что сопротивление катушки индуктивности току также имеет фазовый угол:
[латекс] \ text {Opposition} = \ frac {\ text {Voltage}} {\ text {Current}} [/ latex]
[латекс] \ text {Opposition} = \ frac {10 V \ angle \ text {90 °}} {2.6526A \ angle \ text {90 °}} [/ латекс]
[латекс] \ begin {align} \ text {Opposition} = & 3.7699 \ Omega \ angle \ text {90 °} \\ \ text {or} & 0 + j3.7699 \ Omega \ end {align} [/ latex]
Математически мы говорим, что фазовый угол сопротивления катушки индуктивности току равен 90 °, что означает, что сопротивление катушки индуктивности току является положительной мнимой величиной. Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют. Будет полезно представить любую оппозицию компонента току в терминах комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.
- Индуктивное реактивное сопротивление — это противодействие, которое индуктор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
- Индуктивное реактивное сопротивление можно рассчитать по следующей формуле: X L = 2πfL
- Угловая скорость цепи переменного тока — это еще один способ выразить ее частоту в единицах электрических радиан в секунду вместо циклов в секунду.Его символизирует строчная греческая буква «омега» или ω.
- Индуктивное реактивное сопротивление увеличивается с увеличением частоты . Другими словами, чем выше частота, тем сильнее он противодействует потоку электронов переменного тока.
Возьмем эту схему в качестве примера для работы:
Цепь последовательного резистора индуктивности: ток отстает от приложенного напряжения от 0 ° до 90 °.
Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а катушка индуктивности — 3.Реактивное сопротивление 7699 Ом на переменный ток при 60 Гц.
Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности — мнимым числом (3,7699 Ом ∠ 90 ° или 0 + j3,7699 Ом), комбинированный эффект двух компонентов будет противодействовать току, равному комплексной сумме двух чисел.
Это комбинированное противодействие будет векторной комбинацией сопротивления и реактивного сопротивления. Чтобы выразить это противопоставление лаконично, нам нужен более полный термин для обозначения сопротивления току, чем просто сопротивление или реактивное сопротивление.
Этот термин называется импедансом , его символ — Z, и он также выражается в единицах Ом, точно так же, как сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:
Сопротивление по закону Ома
Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:
На самом деле, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E = IR), так же как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление, отдельно или в комбинации (последовательно / параллельно), могут и должны быть представлены как единый импеданс в цепи переменного тока.
Чтобы рассчитать ток в приведенной выше схеме, нам сначала нужно задать опорный фазовый угол для источника напряжения, который обычно считается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0 ° и + 90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока).
Как и в чисто индуктивной схеме, волна тока отстает от волны напряжения (источника), хотя на этот раз запаздывание не так велико: всего 37,016 ° по сравнению с полными 90 °, как в случае чисто индуктивного схема.
Ток отстает от напряжения в последовательной цепи L-R.
Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось.Напряжение на резисторе синфазно (сдвиг 0 °) с током через него, а напряжение на катушке индуктивности на + 90 ° не совпадает по фазе с током, проходящим через него. Мы можем проверить это математически:
Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора).
Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через катушку индуктивности имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °. Это говорит нам о том, что E и I все еще не совпадают по фазе на 90 ° (только для катушки индуктивности).
Используйте закон Кирхгофа о напряжении
Мы также можем математически доказать, что эти комплексные значения в сумме составляют общее напряжение, как и предсказывает Закон Кирхгофа о напряжении:
Давайте возьмем те же компоненты для нашей схемы последовательного примера и соединим их параллельно:
Рисунок 6.7 Параллельная цепь R-L.Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.2 Таблица анализа импеданса 1Единственная разница в нашей методике анализа на этот раз состоит в том, что мы будем применять правила для параллельных цепей вместо правил для последовательных цепей.Принцип такой же, как и для DC. Мы знаем, что напряжение распределяется равномерно между всеми компонентами в параллельной цепи, поэтому мы можем передать значение общего напряжения (10 вольт 0 °) на все столбцы компонентов:
Таблица 6.3. Таблица анализа импеданса 2Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:
Таблица 6.4. Таблица анализа импеданса 3Так же, как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току все еще сохраняется для переменного тока, как и для постоянного тока):
Таблица 6.5 Таблица анализа импеданса 4Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Между прочим, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений.
[латекс] \ tag {6.1} Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [ / латекс]
Единственная проблема с использованием этой формулы состоит в том, что она обычно требует большого количества нажатий клавиш калькулятора.И если вы полны решимости использовать такую формулу, как эта «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается. Независимо от того, каким способом вы рассчитываете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:
Таблица 6.6 Таблица анализа импеданса 5- Импедансом (Z) управляют так же, как сопротивлением (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме!
[латекс] Z_ {parallel} = \ frac {1} {(\ frac {1} {Z1} + \ frac {1} {Z2} +… \ Frac {1} {Zn})} [/ латекс]
- Закон Ома для цепей переменного тока:
[латекс] E = {I} {Z} [/ латекс]; [латекс] I = \ frac {E} {Z} [/ latex]; [латекс] Z = \ frac {E} {I} [/ latex]
- Когда резисторы и катушки индуктивности смешаны вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и + 90 °.Ток в цепи будет иметь фазовый угол от 0 ° до -90 °.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противодействие переменному току строго основано на индуктивной реакции на изменения тока, а не на трении электронов, как в случае с резистивными компонентами.Однако индукторы не так чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, и мы знаем, что все проволоки обладают некоторой измеримой величиной сопротивления (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было подключено последовательно с идеальной индуктивностью катушки, например:
Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.
Следовательно, полное сопротивление любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и индуктивного реактивного сопротивления.
Эту проблему усугубляет то, что называется скин-эффектом , который представляет собой тенденцию переменного тока проходить через внешние области поперечного сечения проводника, а не через середину. Когда электроны движутся в одном направлении (постоянный ток), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, меняющие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения. Скин-эффект становится более выраженным с увеличением частоты.
Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается к катушке индуктивности и поэтому проявляется в виде сопротивления (рассеяния мощности) в цепи.
Помимо резистивных потерь в проводе и излучения, в индукторах с железным сердечником действуют и другие эффекты, которые проявляются как дополнительное сопротивление между выводами.Когда на катушку индуктивности подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи в железном сердечнике, известные как вихревые токи , . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление, обеспечиваемое железом, который не так хорош в качестве проводника, как медь. Вихретоковым потерям в первую очередь противодействуют, разделив железный сердечник на множество тонких листов (пластин), каждый из которых отделен от другого тонким слоем электроизоляционного лака.Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого не будет (или будет очень мало) резистивных потерь.
Как и следовало ожидать, потери на вихревые токи в металлических сердечниках индуктора проявляются в виде тепла. Эффект более выражен на высоких частотах и может быть настолько сильным, что иногда его используют в производственных процессах для нагрева металлических предметов! Фактически, этот процесс «индукционного нагрева» часто используется в процессах литья металлов высокой чистоты, где металлические элементы и сплавы должны нагреваться в вакууме, чтобы избежать загрязнения воздухом, и, таким образом, там, где стандартная технология нагрева сжиганием была бы бесполезной.Это «бесконтактная» технология, когда нагретое вещество не должно касаться катушки (катушек), создающей магнитное поле.
В высокочастотной среде вихревые токи могут возникать даже в поперечном сечении самого провода, что способствует дополнительным резистивным эффектам. Чтобы противодействовать этой тенденции, можно использовать специальный провод, сделанный из очень тонких, индивидуально изолированных жил, который называется Litz wire (сокращенно от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.
Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля индуктора, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействовать этому эффекту лучше всего за счет правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, генерируемой в каждом цикле.
В целом паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:
Рисунок 6.9 Эквивалентная схема реального индуктора с потерями на скин-эффект, излучение, вихревые токи и гистерезис.
Следует отметить, что скин-эффект и потери на излучение применимы к прямым отрезкам провода в цепи переменного тока так же хорошо, как и к спиральному проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах они могут быть довольно большими. Например, антенна радиопередатчика спроектирована специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.
Конденсаторы Vs. Резисторы
Конденсаторы не ведут себя так же, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения является другой формой реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.
Характеристики цепи конденсатора
Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе выглядит следующим образом:
[латекс] i = C \ frac {d_e} {d_t} [/ латекс]
Выражение de / dt — это выражение из расчетов, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду. Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.Иногда скорость мгновенного изменения напряжения с течением времени выражается как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:
Рисунок 6.10 Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °
Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Рисунок 6.11 Формы сигналов чисто емкостной цепи.
Помните, что ток через конденсатор — это реакция на изменение напряжения на нем. Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение находится на пике (нулевое изменение или наклон уровня на синусоидальной волне напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение имеет максимальное изменение (точки самый крутой наклон на волне напряжения, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, которая на -90 ° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Рисунок 6.12 Напряжение отстает от тока на 90 ° в чисто емкостной цепи.
Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:
Рисунок 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой схемой индуктивности, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительной и отрицательной полярностью. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения означает сопротивление переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой данной величины переменного напряжения на данной частоте конденсатор данного размера будет «проводить» определенную величину переменного тока. Так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , обеспечиваемого конденсатором. Как и в случае с индукторами, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или X C , чтобы быть более точным).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. . Это означает, что реактивное сопротивление в Ом для любого конденсатора равно , обратно пропорционально частоте переменного тока.
[латекс] X_C = \ frac {1} {2πfC} [/ латекс]
Реактивное сопротивление конденсатора 100 мкФ:| Частота (Герцы) | Реактивное сопротивление (Ом) |
| 60 | 26.5258 |
| 120 | 13,2629 |
| 2500 | 0,6366 |
Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления. Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Индукторы противодействуют более быстрому изменению токов, создавая большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения, допуская большие токи.
Как и в случае с индукторами, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение X C = 1 / (2πfC) также может быть записано как X C = 1 / (ωC), где ω приведено в единицах радиан в секунду .
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
[латекс] X_C = 26,5258 Ом [/ латекс]
[латекс] I = \ frac {E} {X} [/ латекс]
[латекс] I = \ frac {10} {26,5258 Ом} [/ латекс]
[латекс] I = 0,3770A [/ латекс]
Однако нужно иметь в виду, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению.Если мы математически представим эти фазовые углы напряжения и тока, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
Напряжение в конденсаторе отстает от тока на 90 °.
Математически мы говорим, что фазовый угол сопротивления конденсатора току составляет -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют.Будет полезно представить любую оппозицию компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
- Емкостное реактивное сопротивление — это противодействие, которое конденсатор предлагает переменному току из-за его сдвинутого по фазе накопления и высвобождения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
- Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
- Емкостное реактивное сопротивление уменьшается с увеличением частоты .Другими словами, чем выше частота, тем меньше он противодействует (тем больше «проводит») переменному току.
Используя компоненты с одинаковыми значениями в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:
Рисунок 6.14 Параллельная цепь RC.
Параллельный резистор и конденсатор
Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:
Таблица 6.7Теперь это параллельная схема, и мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт 0 °) во все столбцы:
Таблица 6.8 Расчетс использованием закона Ома
Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам в таблице, рассчитав ток через резистор и ток через конденсатор:
Таблица 6.9Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа о токе):
Таблица 6.10Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле. И снова формула параллельного импеданса выглядит так:
[латекс] Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [/ латекс]
Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:
- Импедансом (Z) управляют так же, как сопротивлением (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы. Только не забудьте
- выполнять все вычисления в комплексной (не скалярной) форме! ZTotal = 1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
- Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
- Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
- Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.
(Следующий раздел был адаптирован из: Уроки электрических цепей, Том II, Глава 5 — Реактивное сопротивление и импеданс — R, L и C)
Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.
Сопротивление
Это по сути трение против потока тока. В той или иной степени он присутствует во всех проводниках (кроме проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).
Реактивное сопротивление
По сути, это инерция , против потока тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).
Импеданс
Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° не в фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.
Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.
Рис. 6.15. Идеальный резистор, катушка индуктивности и конденсатор.Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток всегда находятся в фазе , поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.
Полное сопротивление переменного тока ведет себя аналогично сопротивлению в цепях постоянного тока: они складываются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:
Закон Ома для цепи переменного тока
[латекс] \ begin {align} \ tag {6.2} \ text {E} & = {I} {Z} \\ \ text {I} & = \ frac {E} {Z} \\ \ text {Z } & = \ frac {E} {I} \ end {align} [/ latex]
Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:
Рисунок 6.16 Пример параллельной схемы R, L и C.Импеданс в параллельных компонентах
Тот факт, что эти компоненты соединены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.
Рисунок 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими значения компонентов.Со всеми значениями компонентов, выраженными как импедансы (Z), мы можем настроить таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательного.
Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем перенести значение общего напряжения во все столбцы компонентов в таблице:
Значения компонентов в таблице 6.11 выражаются как изображение импеданса 2Теперь мы можем применить закон Ома (I = E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:
Таблица 6.12. Значения компонентов выражаются как изображение импеданса 3Расчет полного тока и полного импеданса
Существует две стратегии расчета полного тока и полного сопротивления.Во-первых, мы можем рассчитать общий импеданс из всех отдельных параллельных сопротивлений (Z Total = 1 / (1 / Z R + 1 / Z L + 1 / Z C ), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I = E / Z).
Тем не менее, работа с уравнением параллельного импеданса с комплексными числами — непростая задача, учитывая все взаимные колебания (1 / Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать индивидуальные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).Второй способ рассчитать общий ток и полное сопротивление — сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи — переменный или постоянный — равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z = E / I).
Таблица 6.13 Расчет полного тока и полного импедансаЛюбой из методов, выполненный должным образом, даст правильные ответы.
За заметным исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты для цепей постоянного тока.Единственное существенное отличие состоит в том, что в расчетах переменного тока используются комплексные величины, в то время как в расчетах постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, остаются верными для переменного тока, когда напряжение, ток и импеданс выражаются комплексными числами. Те же стратегии поиска и устранения неисправностей, которые применяются в цепях постоянного тока, справедливы и для переменного тока, хотя с переменным током, безусловно, труднее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.
Power — это отдельная тема, которая будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и высвобождается, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.
При анализе цепи переменного тока первым шагом в анализе является преобразование всех значений компонентов резистора, катушки индуктивности и конденсатора в импедансы (Z) в зависимости от частоты источника питания.После этого выполните те же шаги и стратегии, которые были изучены для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I = E / Z; и Z = E / I
Помните, что только рассчитанные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольные обозначения — это просто полезный инструмент для сложения и вычитания сложных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеряемого напряжения или тока, а угол напрямую связан с фазовым сдвигом в градусах, является наиболее практичным способом выражения сложных величин для анализа схем.
Мощность в цепи переменного тока — Университетская физика, том 2
Цели обучения
К концу раздела вы сможете:
- Опишите, как можно записать среднюю мощность от цепи переменного тока в терминах пикового тока и напряжения, а также среднеквадратичных значений тока и напряжения
- Определите соотношение между фазовым углом тока и напряжения и средней мощностью, известное как коэффициент мощности
Элемент схемы рассеивает или вырабатывает мощность в зависимости от того, где I — ток через элемент, а В — напряжение на нем.Поскольку ток и напряжение в цепи переменного тока зависят от времени, мгновенная мощность также зависит от времени. График p ( t ) для различных элементов схемы показан на (Рисунок). Для резистора i ( t ) и v ( t ) синфазны и поэтому всегда имеют один и тот же знак (см. (Рисунок)). Для конденсатора или катушки индуктивности относительные знаки i ( t ) и v ( t ) меняются в течение цикла из-за разницы фаз (см. (Рисунок) и (Рисунок)).Следовательно, p ( t ) в некоторые моменты бывает положительным, а в другие — отрицательным, что указывает на то, что емкостные и индуктивные элементы вырабатывают энергию в одни моменты и поглощают ее в другие.
Поскольку мгновенная мощность изменяется как по величине, так и по знаку в течение цикла, она редко имеет какое-либо практическое значение. То, что нас почти всегда интересует, — это усредненная по времени мощность, которую мы называем средней мощностью. Он определяется средним по времени мгновенной мощностью за один цикл:
где — период колебаний.С заменами и этот интеграл становится
Используя тригонометрическое соотношение, получаем
Вычисление этих двух интегралов дает
и
Следовательно, средняя мощность, связанная с элементом схемы, равна
В технических приложениях известен как коэффициент мощности, который представляет собой величину, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе.Для резистора, поэтому средняя рассеиваемая мощность составляет
Сравнение p ( t ) и показано на (Рисунок) (d). Чтобы выглядеть как его аналог постоянного тока, мы используем среднеквадратичные значения тока и напряжения. По определению это
где
С получаем
Затем мы можем написать для средней мощности, рассеиваемой резистором,
Это уравнение дополнительно подчеркивает, почему при обсуждении выбирается среднеквадратичное значение, а не пиковые значения.Оба уравнения для средней мощности верны для (Рисунок), но среднеквадратичные значения в формуле дают более четкое представление, поэтому дополнительный коэффициент 1/2 не требуется.
Переменные напряжения и токи обычно описываются их действующими значениями. Например, напряжение 110 В от бытовой розетки является среднеквадратичным значением. Амплитуда этого источника равна. Поскольку большинство измерителей переменного тока откалиброваны по среднеквадратичным значениям, обычный вольтметр переменного тока, помещенный в бытовую розетку, будет показывать 110 В.
Для конденсатора и катушки индуктивности соответственно. Поскольку мы находим из (Рисунок), что средняя мощность, рассеиваемая любым из этих элементов, равна Конденсаторам, а катушки индуктивности поглощают энергию из цепи в течение одного полупериода, а затем разряжают ее обратно в цепь в течение другого полупериода. Это поведение проиллюстрировано на графиках (Рисунок), (b) и (c), которые показывают, что p ( t) колеблется синусоидально около нуля.
Фазовый угол генератора переменного тока может иметь любое значение.Если генератор выдает мощность; если он поглощает энергию. В терминах среднеквадратичных значений средняя мощность генератора переменного тока записывается как
Для генератора в цепи RLC ,
и
Отсюда средняя мощность генератора
Это также можно записать как
, который означает, что мощность, производимая генератором, рассеивается в резисторе. Как мы видим, закон Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на импеданс.
Проверьте свое понимание Вольтметр переменного тока, подключенный к клеммам генератора переменного тока 45 Гц, показывает 7,07 В. Напишите выражение для ЭДС генератора.
Проверьте свое понимание Покажите, что действующие значения напряжения на резисторе, конденсаторе и катушке индуктивности в цепи переменного тока, где среднеквадратичный ток выражается соответственно. Определите эти значения для компонентов цепи RLC (рисунок).
Сводка
- Средняя мощность переменного тока определяется путем умножения среднеквадратичных значений тока и напряжения. Закон
- Ома для среднеквадратичного значения переменного тока находится делением среднеквадратичного напряжения на полное сопротивление.
- В цепи переменного тока существует фазовый угол между напряжением источника и током, который можно найти, разделив сопротивление на полное сопротивление.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла.
- Коэффициент мощности находится в диапазоне от –1 до 1.
Концептуальные вопросы
При каком значении фазового угла между выходным напряжением источника переменного тока и током средняя выходная мощность источника является максимальной?
Обсудите разницу между средней мощностью и мгновенной мощностью.
Мгновенная мощность — это мощность в данный момент. Средняя мощность — это мощность, усредненная за цикл или количество циклов.
Средний переменный ток, подаваемый в цепь, равен нулю.Несмотря на это, мощность в цепи рассеивается. Объяснять.
Может ли мгновенная выходная мощность источника переменного тока быть отрицательной? Может ли средняя выходная мощность быть отрицательной?
Мгновенная мощность может быть отрицательной, но выходная мощность не может быть отрицательной.
Номинальная мощность резистора, используемого в цепях переменного тока, относится к максимальной средней мощности, рассеиваемой в резисторе. Как это соотносится с максимальной мгновенной мощностью, рассеиваемой на резисторе?
Глоссарий
- средняя мощность
- среднее время мгновенной мощности за один цикл
- Коэффициент мощности
- величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе




