Вычисление синуса, косинуса, тангенса и котангенса онлайн
Определения синуса, косинуса, тангенса и котангенса
 Синус угла
Синус угла 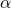 (обозначается
(обозначается  ) – ордината точки
) – ордината точки 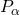 , полученной поворотом точки
, полученной поворотом точки 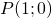 вокруг начала координат на угол
вокруг начала координат на угол 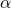 .
.
Косинус угла 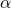
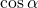 ) – абсцисса точки
) – абсцисса точки 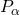 , полученной поворотом точки
, полученной поворотом точки 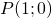 вокруг начала координат на угол
вокруг начала координат на угол 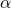 .
.Тангенс угла 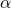
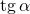 ) – отношение синуса угла
) – отношение синуса угла 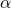 к его косинусу, т.е.
к его косинусу, т.е. ![\[\operatorname{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f3cba66971d7fd1d95998220eb211676_l3.png)
Котангенс угла 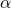
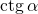 ) – отношение косинуса угла
) – отношение косинуса угла 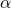 к его синусу, т.е.
к его синусу, т.е. ![\[\operatorname{ctg}\alpha = \frac{\cos\alpha}{\sin\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f6efc9004c51766c5c3efc271d310896_l3.png)
Таблица значений синуса, косинуса, тангенса и котангенса
Калькулятор синусов, косинусов, тангенсов и котангенсов
Данный калькулятор поможет легко вычислить значения этих тригонометрических функций от углов, заданных в градусах, радианах или градах.
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
Таблица косинусов от 0° — 360°
|
|
|
|
|
|
|
|
|
|
Смотрите также
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (
Основные формулы тригонометрии | umath.ru
1. Определения синуса, косинуса, тангенса и котангенса угла.
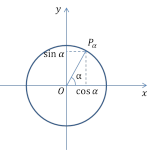 Синус угла
Синус угла 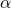 (обозначается
(обозначается  ) – ордината точки
) – ордината точки 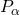 , полученной поворотом точки
, полученной поворотом точки 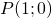 вокруг начала координат на угол
вокруг начала координат на угол 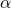 .
.
Косинус угла 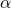 (обозначается
(обозначается 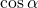 ) – абсцисса точки
) – абсцисса точки 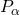 , полученной поворотом точки
, полученной поворотом точки 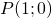 вокруг начала координат на угол
вокруг начала координат на угол 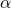 .
.
Тангенс угла 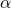 (обозначается
(обозначается 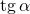 ) – отношение синуса угла
) – отношение синуса угла 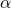 к его косинусу, т.е.
к его косинусу, т.е.
Котангенс угла
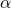 (обозначается
(обозначается 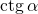 ) – отношение косинуса угла
) – отношение косинуса угла 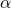 к его синусу, т.е.
к его синусу, т.е. 2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента 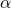 :
:
Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом
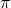 функции:
Число
функции:
Число 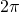 является наименьшим положительным периодом синуса и косинуса, а число
является наименьшим положительным периодом синуса и косинуса, а число 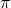 – наименьшим положительным периодом тангенса и котангенса.
– наименьшим положительным периодом тангенса и котангенса.Для любого целого
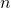 справедливы равенства
справедливы равенства 5. Формулы сложения:
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10. Формулы суммы и разности косинусов:
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:
Онлайн калькулятор синуса, косинуса, тангенса и котангенса
- ГЛАВНАЯ
- расчеты
- мониторинг
- консалтинг
- ОБЪЕКТЫ
- сосуды и аппараты
- здания и сооружения
- трубопроводы
- прочие
- ОНЛАЙН
- сосуды и аппараты
- трубопроводы
- прочие
- математика
- МАТЕРИАЛЫ
- статьи
- презентации
- отчеты
- log-files
- прочие
- ЛИТЕРАТУРА
- сосуды и аппараты
- здания и сооружения
- трубопроводы
Функция косинуса: онлайн калькулятор, формулы, график
Косинус — тригонометрическая функция, которая геометрически определяется как соотношение прилежащего катета к гипотенузе. Как и все тригонометрические функции, косинус нашел широчайшее применение в науке.
История вопроса
Тригонометрия как наука возникла еще в Древней Индии, когда ученые разработали таблицу соотношений катетов и гипотенуз и их численных значений для основных углов. Термин «косинус» — сравнительно молодой, так как изначально ученые пользовались только синусом и тангенсом угла. Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Геометрически косинус — это соотношение прилежащего катета к гипотенузе. Прилежащий катет — это сторона прямоугольного треугольника, которая вместе с гипотенузой образует рассматриваемый угол. Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Определение косинуса
Итак, есть прямоугольный треугольник, катеты которого обозначаются как A и B, а гипотенуза как C. Из определения косинуса мы получаем, что для заданного угла AC его соотношение прилежащего катета и гипотенузы будет равно cosAC = A/C. Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники.
Теорема косинусов
Для любого треугольника справедливо равенство:
a2 = b2 + c2 — 2b × c × cosA,
где угол A — это угол, противолежащий стороне a.
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
a2 = b2 + c2,
где a — гипотенуза.
Использование косинусов
В повседневной жизни тригонометрические функции не находят применения. Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности.
Наша программа представляет собой онлайн-калькулятор, который позволяет рассчитывать значения основных тригонометрических функций углов, выраженных в градусах или радианах. Для использования калькулятора требуется выбрать в меню программы требуемую функцию и ввести величину угла в градусах. Калькулятор вычисляет и обратную функцию арккосинуса. Если требуется определить угол по известному значению косинуса, введите значение функции в ячейку «Косинус» и выполните расчет. Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора.
Примеры из жизни
Вычисление углов
Пусть в задаче по геометрии дан треугольник со сторонами A = 3 см, B = 4 см и C = 5 см. Требуется найти значения всех углов. На первый взгляд это сложная задача, однако мы знаем, что 3, 4 и 5 — это классическая пифагорова тройка, следовательно, известны значения катетов и гипотенуз. Очевидно, что угол AB = 90 градусов, так как катеты всегда образуют прямой угол. Теперь мы можем найти углы AC и BC. Косинус угла численно равен дроби, в числителе которой стоит прилежащий катет, а в знаменателе — гипотенуза. Прилежащие катеты — это образующие угол катеты, следовательно, cosAC = A/C и cosBC = B/C. Подсчитаем численные значения:
- cosAC = A/C = 3/5 = 0,6;
- cosBC = B/C = 4/5 = 0,8.
Теперь определим соответствующие углы при помощи нашего калькулятора. Углы с такими значениями косинусов равны соответственно 53,13 и 36,87 градуса. Правильность решения легко проверить, сложив величины углов:
90 + 53,13 + 36,87 = 180.
Расчет косинусов
Прямая задача определения численных значений функций — это вычисление косинуса в зависимости от величины угла. Для такой задачи можно использовать таблицу Брадиса — четырехзначные таблицы значений тригонометрических функций для целочисленных величин углов. Вычислим значения косинусов для основных углов. Для этого введем значения в ячейки «Косинус»:
- cos30 = 0,866;
- cos45 = 0,707;
- cos60 = 0,5;
- cos90 = 0;
- cos120 = –0,5;
- cos150 = — 0,866;
- cos180 = — 1.
Это основные значения косинусов для стандартных величин углов треугольника. В целом значения тригонометрических функций периодически повторяются каждые 360 градусов.
Заключение
Тригонометрия — определенно важный раздел математики, функции которого повсеместно используются в современных технологиях. Наши калькуляторы прекрасно подходят для элементарных расчетов по геометрии и тригонометрии.
Функция COS — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Описание
Возвращает косинус заданного угла.
Синтаксис
COS(число)
Аргументы функции COS описаны ниже.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=COS(1,047) |
Косинус 1,047 радиан |
0,5001711 |
|
=COS(60*ПИ()/180) |
Косинус 60 градусов |
0,5 |
|
=COS(РАДИАНЫ(60)) |
Косинус 60 градусов |
0,5 |



