Простые устройства — Расчёт индуктивности дросселя из порошкового материала

Многие сталкиваются с необходимостью рассчитать индуктивность дросселя, намотанного на порошковом торике, или определить необходимое количество витков для получения нужной индуктивности… Статья о том, как просто это сделать.

Нам понадобится каталог Power Conversion & Line Filter Applications компании Micrometals, документ в формате PDF весит 6,7Мб.

Итак, качаем, открываем страницу 1.

{ads2}Сверху вы видите таблицу, в который показано, какой из 12 материалов каким цветом маркируется. Допустим, вы вынули из убитого

БП АТХ, пущенного на запчасти, дроссель, намотанный на торике жёлтого цвета, у которого одна грань белого цвета. По таблице это 26-й материал, самый распространённый и дешёвый. Дроссель имеет 32 витка. Замеряем размеры, допустим у нас это внешний диаметр 27мм, внутренний 14мм, и высота торика 12мм (точно замерять нет необходимости, т.к. ближайшие «соседи» в таблице врядли совпадут по размерам). Ищем эти размеры в таблице и находим на 9-й странице: это, оказывается, Т106-26, число 26 обозначает тип материала.

Для расчёта индуктивности нам нужен параметр AL:

для Т106-26 AL=93nH/N2, т.е. 93 нГ·виток², соответственно считаем индкутивность  нашего дросселя:

(32*32)*93=95232нГн = 95 мкГн

Витки считаем соответственно по формуле:

w=√(L/AL), где L — индкутивность в нГн,

AL из таблицы для данного сердечника.

 Например, нам нужно получить 250 мкГн, и у нас имеется торик Т68-52. Находим, что у него AL равно 40, значит:

√(250000\40) = 79 витков дадут нам 250мкГн.

Надеюсь эта информация поможет вам.

{ads1}

Простые устройства — Расчёт индуктивности дросселя из порошкового материала

Многие сталкиваются с необходимостью рассчитать индуктивность дросселя, намотанного на порошковом торике, или определить необходимое количество витков для получения нужной индуктивности… Статья о том, как просто это сделать.

Нам понадобится каталог Power Conversion & Line Filter Applications компании Micrometals, документ в формате PDF весит 6,7Мб.

Итак, качаем, открываем страницу 1.

{ads2}Сверху вы видите таблицу, в который показано, какой из 12 материалов каким цветом маркируется. Допустим, вы вынули из убитого БП АТХ, пущенного на запчасти, дроссель, намотанный на торике жёлтого цвета, у которого одна грань белого цвета. По таблице это 26-й материал, самый распространённый и дешёвый. Дроссель имеет 32 витка. Замеряем размеры, допустим у нас это внешний диаметр 27мм, внутренний 14мм, и высота торика 12мм (точно замерять нет необходимости, т.к. ближайшие «соседи» в таблице врядли совпадут по размерам). Ищем эти размеры в таблице и находим на 9-й странице: это, оказывается, Т106-26, число 26 обозначает тип материала.

Для расчёта индуктивности нам нужен параметр AL:

для Т106-26 AL=93nH/N2, т.е. 93 нГ·виток², соответственно считаем индкутивность  нашего дросселя:

(32*32)*93=95232нГн = 95 мкГн

Витки считаем соответственно по формуле:

w=√(L/AL), где L — индкутивность в нГн, AL из таблицы для данного сердечника.

 Например, нам нужно получить 250 мкГн, и у нас имеется торик Т68-52. Находим, что у него AL равно 40, значит:

√(250000\40) = 79 витков дадут нам 250мкГн.

Надеюсь эта информация поможет вам.

{ads1}

Простые устройства — Расчёт индуктивности дросселя из порошкового материала

Многие сталкиваются с необходимостью рассчитать индуктивность дросселя, намотанного на порошковом торике, или определить необходимое количество витков для получения нужной индуктивности… Статья о том, как просто это сделать.

Нам понадобится каталог Power Conversion & Line Filter Applications компании Micrometals, документ в формате PDF весит 6,7Мб.

Итак, качаем, открываем страницу 1.

{ads2}Сверху вы видите таблицу, в который показано, какой из 12 материалов каким цветом маркируется. Допустим, вы вынули из убитого БП АТХ, пущенного на запчасти, дроссель, намотанный на торике жёлтого цвета, у которого одна грань белого цвета. По таблице это 26-й материал, самый распространённый и дешёвый. Дроссель имеет 32 витка. Замеряем размеры, допустим у нас это внешний диаметр 27мм, внутренний 14мм, и высота торика 12мм (точно замерять нет необходимости, т.к. ближайшие «соседи» в таблице врядли совпадут по размерам). Ищем эти размеры в таблице и находим на 9-й странице: это, оказывается, Т106-26, число 26 обозначает тип материала.

Для расчёта индуктивности нам нужен параметр AL:

для Т106-26 AL=93nH/N2, т.е. 93 нГ·виток², соответственно считаем индкутивность  нашего дросселя:

(32*32)*93=95232нГн = 95 мкГн

Витки считаем соответственно по формуле:

w=√(L/AL), где L — индкутивность в нГн, AL из таблицы для данного сердечника.

 Например, нам нужно получить 250 мкГн, и у нас имеется торик Т68-52. Находим, что у него AL равно 40, значит:

√(250000\40) = 79 витков дадут нам 250мкГн.

Надеюсь эта информация поможет вам.

{ads1}

Расчет индуктивности на ферритовом стержне.

Плагин Ferrite:
Расчет индуктивности на ферритовом стержне

В отличии от тороидальной индуктивности на ферритовом кольце, магнитный поток катушки на ферритовом стержне не замкнут целиком внутри феррита и каждая силовая линия проходит и по ферритовому стержню и по воздуху, поэтому расчет такой катушки представляет довольно сложную задачу. Индуктивность зависит от:

• магнитной проницаемости ферритового стержня и его размеров;
• размеров самой катушки;
• взаимного соотношения размеров катушки и стержня;
• положения катушки относительно центра стержня.

 

Расчет индуктивности катушки на ферритовом стержне основан на определении относительной эффективной проницаемости стержня. Другими словами, нам нужно определить насколько возрастет индуктивность катушки с «воздушным сердечником» если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:

μe = Lf / Lair = (1 + x) / (1 / k + x / μfe )

[1]

,где L_f / L_air — отношение индуктивности катушки с ферритом к индуктивности той же катушки без феррита, а коэффициенты x, k и μ_fe вычисляются по следующему алгоритму:

1. l’ = l_c + 0.45 d_c;
2. φ_φmax ≈ 1 / [ 1 + { ( ( l_f — l_c ) / d_f )^1.4 } / ( 5 μ ) ];
3. C_anf = 0.5 π ε₀ ( l_f — l_c ) / [ ln { 2 ( l_f + d_f) / d_f } — 1 ];
4. k = [ (φ_φmax C_anf / ε₀ ) + 2 d_f ] / 2 d_c
5. x = 5.1 [ l’ / d_c ] / [1+ 2.8 ( d_c / l’ )];
6. μ_fe = ( μ -1) ( d_f /d_c)² +1;

где ε₀ = 8,8542*10^-12 Ф/м — электрическая постоянная, μ — начальная магнитная проницаемость материала стержня. Основные размеры в метрах, обозначения понятны из рисунка:

Немного теории обосновывающей этот алгоритм.

• Можно считать что воздушная катушка имеет магнитную цепь состоящую из двух частей. Снаружи катушки и внутри нее. Они отличаются плотностью силовых линий и магнитным сопротивлением. Если магнитное сопротивление внутренней части магнитной цепи выше, чем наружной части (а это так, поскольку ее площадь поперечного сечения намного меньше), тогда применение феррита уменьшает это сопротивление и имеет эффект увеличения индуктивности. Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма.
• Параметр μ_fe учитывает случай, когда обмотка не плотно прилегает к стержню, т.е. между стержнем и обмоткой существует радиальный зазор.
• Параметр C_anf учитывает влияние частей стержня, которые выступают за пределы катушки. Эти части уменьшают магнитное сопротивление внешней части магнитной цепи и также увеличивают индуктивность.
• Параметр φ_φmax учитывает конечное магнитное сопротивление феррита. Этот параметр, наряду с параметром C_anf используется для расчета коэффициента k из основного уравнения [1]

При смещении катушки относительно стержня индуктивность катушки уменьшается, это обстоятельство учитывается с помощью поправочного коэффициента K:

K = -440.9943706*sh8+1318.707293*sh7 -1604.5491034*sh6+1021.078226*sh5 -363.8218957*sh4+71.6178135*sh3 -7.6027344*sh2+0.3013663*sh+0.995

[2]

,где

• s_h — относительное смещение = смещение s деленное на половину длины сердечника [s_h = s / ( l_f / 2 )].

Эта формула получена методом регрессионного анализа и справедлива при s = 0,05 — 0,75

---

В итоге индуктивность катушки на ферритовом стержне определяется по следующей формуле:

L(мкГн) = μe Lair*K

[3]

Индуктивность катушки  «воздушным» сердечником L_air рассчитывается по алгоритму расчета однослойной катушки с учетом шага намотки. Длину намотки можно определить по следующей формуле:

,где

• N — число витков.
• d_w — диаметр провода.
• p — шаг намотки.

Алгоритм имеет следующие ограничения в расчетах:

• шаг намотки не может превышать удвоенного диаметра провода;
• диаметр катушки не может быть больше удвоенного диаметра стержня;
• длина намотки должна быть меньше 3/4 длины стержня;
• длина стержня должна быть не менее чем в 12 раз больше его диаметра;
• при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
• начальная магнитная проницаемость стержня должна быть больше 100;

Также как и в дросселе на ферритовом кольце с немагнитным зазором, при больших значениях начальной магнитной проницаемости стержня его эффективная магнитная проницаемость слабо зависит от начальной и составляет величину не более нескольких десятков.

В версиях плагина ferrite.coi ниже 0.3 использовалась методика расчета, предложенная В.И. Хомичем в книге «Ферритовые антенны МБР-721 1989г.» Как оказалось, эта методика дает ошибочный результат расчета. В плагине версии от 0.3 до 11.2 применялась методика по ссылке [2]. Эта методика также не согласуется с реальными измерениями. Расчет изложенный в этой статье основан на работе Алана Пейна G3RBJ (см ссылку [1]). Расчет идет по формулам [1],[2], [3] и [4] методом итераций. Расчет реализован в плагине версии 12.2 и выше.

Кроме того, вы можете воспользоваться онлайн-калькулятором катушки на ферритовом стержне.

---

Источник:

1. http://g3rbj.co.uk/wp-content/uploads/2014/06/Web-The-Inductance-of-Ferrite-Rod-Antennas-issue-3.pdf
2. http://makearadio.com/tech/files/Ferrite_Rod_Inductance.pdf

---

Особая благодарность Андрею Васильевичу Каинову за конструктивную помощь и соавторство в разработке методики расчета.

Как рассчитать дроссель? – Программа для расчета BoosterRing

Для начала, хотелось бы отметить, что новичку, который столкнулся с расчетом дросселя повышающего или понижающего преобразователя есть, где поломать голову и допустить ошибку. Программа для расчета дросселей BoosterRing входит в список программ созданных Владимиром Денисенко. Она имеет статус свободно распространяющейся, скачать ее можно и на нашем сайте, ищем ссылку на нее в конце статьи. С помощью данного ПО, проблема, как рассчитать дроссель отпадает сама собой.

Как рассчитать дроссель? – Программа для расчета BoosterRing

Для того, что бы провести расчет дросселя онлайн, можно использовать этот сервис. Для некоторых радиолюбителей вполне будет достаточно и его.

При использовании BoosterRing можно увидеть более подробные расчетные данные. Программа для расчета дросселей имеет простой и понятный интерфей, не требует никакой инсталляции. Работать с программой не сложно, достаточно ввести свои параметры и можно сразу увидеть результаты расчета. При наведении курсора на некоторые поля, всплывают подсказки. Так выглядит интерфейс работы с программой.

В общем, данное ПО можно смело использовать в своих самодельных схемах и поделках для расчета дросселя. Тем, кто хочет отблагодарить разработчика, может в разделе «о программе» увидеть все его реквизиты.

Как и обещали, мы прикрепляем ссылку для скачивания. В архиве также есть и другие не менее полезные и популярные программы от этого разработчика.

Вконтакте

Facebook

Twitter

Одноклассники

comments powered by HyperComments

Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2.

Всем доброго времени суток. В первой части я рассказал, как рассчитать индуктивность катушек с замкнутыми сердечниками тороидального и П-образного типа. Данная статья продолжает тему индуктивности катушек с замкнутыми сердечниками, здесь я расскажу о расчёте катушек с Ш-образными и броневыми сердечниками.

Расчёт катушки с Ш – образным сердечником прямоугольного сечения

Ш-образные сердечники также как и П-образные выполняются разборными. Существует несколько видов таких сердечников, я рассмотрю два типа: с прямоугольным сечением и круговым сечением среднего керна.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Данные типы сердечников применяются в трансформаторах преобразователей с частотой работы до 100 кГц. Их применение обеспечивает наибольшее полное сопротивление при минимальном количестве витков в обмотке, что позволяет уменьшить потери и индуктивность рассеяния.

Вначале рассмотрим Ш-образные сердечники прямоугольного сечения, они могут состоять из двух Ш-образных половинок или из Ш-образной части с замыкающей пластиной.

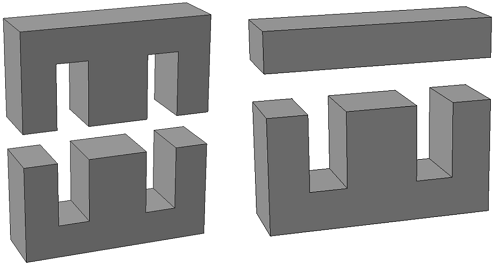
Ш – образный сердечник прямоугольного сечения: из двух Ш-образных половинок (слева) и Ш-образной части и замыкающей пластины (справа).

Для того чтобы рассчитать параметры такого сердечника рассмотрим его сечения.

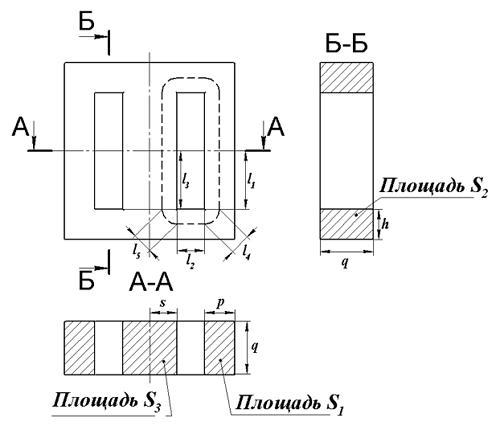
Расчёт параметров Ш – образного сердечника прямоугольного сечения.

Силовую линию магнитного поля в данном сердечнике можно разложить на несколько участков l₁, l₂, l₃, l₄, l₅ с различным сечением S₁, S₂, S₃, S₄, S₅. Исходя из этого постоянные сердечника можно рассчитать по следующим выражениям

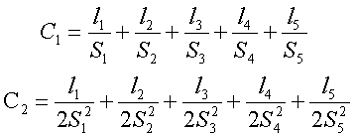
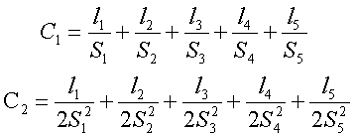
Некоторые величины можно найти измерением, а остальные по приведённым ниже выражениям. Так средняя длина магнитной линии и средняя площадь поперечного сечения на угловых участках составит

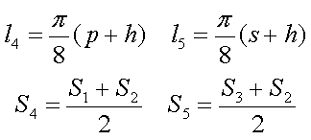
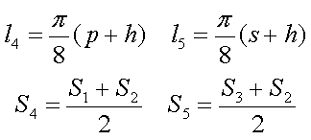
Пример. Рассчитаем индуктивность катушки намотанной на замкнутом Ш-образном сердечнике состоящего из двух половинок типа Ш20х28, выполненных из материала M2000НМ (μ_r = 2000), обмотка выполнена из ω = 200 витков.

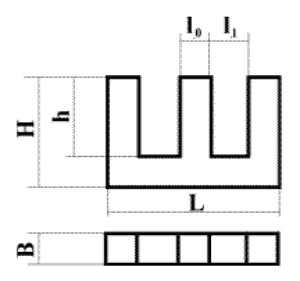
Сердечник типа Ш20х28, где L = 65, B = 28, H = 32,5, h = 22, l₀ = 20, l_l = 12.

Определим размеры и площади необходимых участков

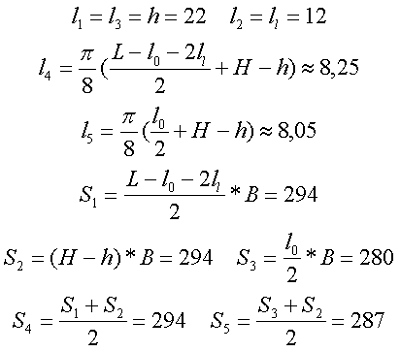
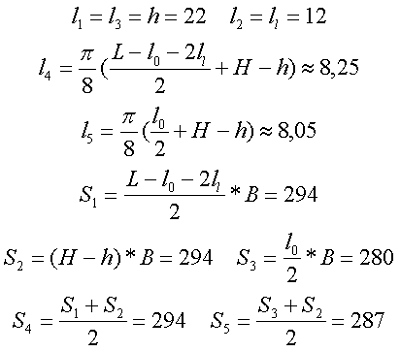
Из полученных значений вычислим коэффициент C1 и индуктивность L, полученной катушки

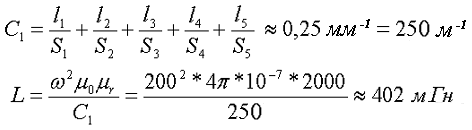
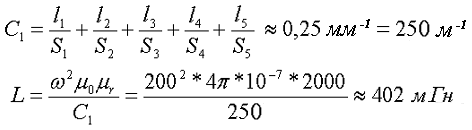
Расчёт катушки с Ш – образным сердечником круглого сечения

Теперь рассмотрим Ш-образные сердечники с круговым сечением центрального керна. Они также выполняются разборными, состоящими из двух одинаковых половинок.

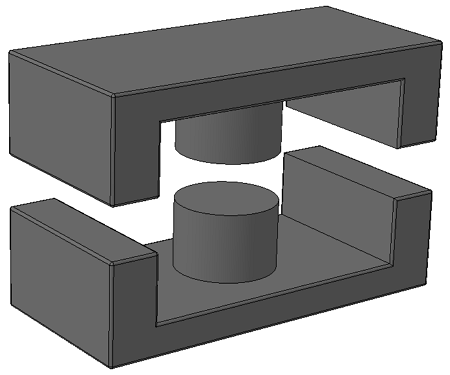
Ш – образный сердечник с центральным керном круглого сечения.

Для расчёта его параметров рассмотрим его сечение

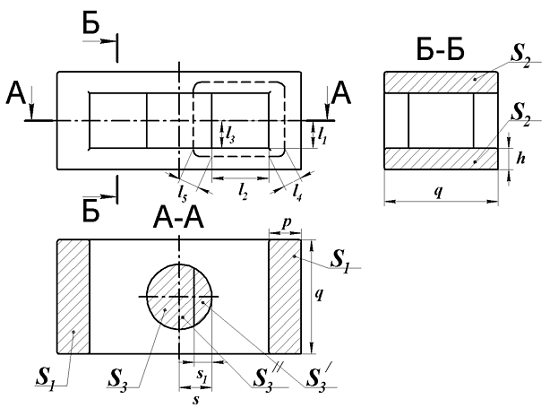
Расчёт параметров Ш – образного сердечника с центральным керном кругового сечения.

Аналогично предыдущим типам сердечников, разделим силовую линию магнитного поля на следующие части: линейные – l₁, l₂, l₃ и угловые – l₄, l₅, так же выделим соответствующие им поперечные сечения: S₁, S₂, S₃, S₄, S₅. Размеры линейных участков достаточно легко посчитать или измерить, а угловые размеры участков могут быть вычислены по следующим выражениям

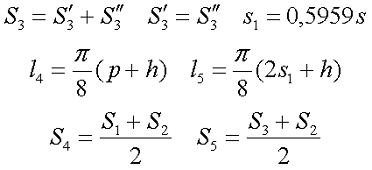
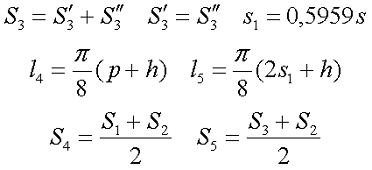
Исходя из этого, коэффициенты сердечника можно рассчитать по следующим выражениям

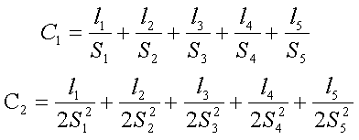
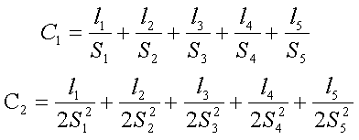
Пример. В качестве примера, рассчитаем индуктивность дросселя намотанного на сердечнике Epcos, состоящем из двух половинок ER 14.5/6 выполненных их материала N87 (μ_r = 2200), количество витков ω = 30

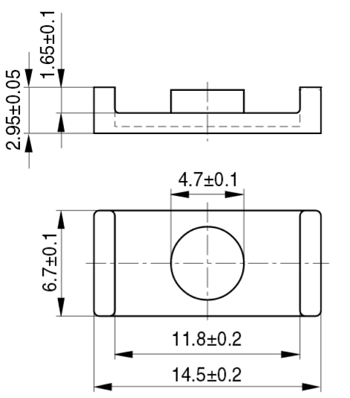
Сердечник Epcos типа ER 14.5/6.

Рассчитаем длину и сечение участков магнитной силовой линии

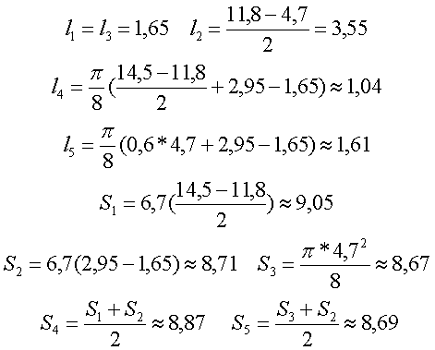
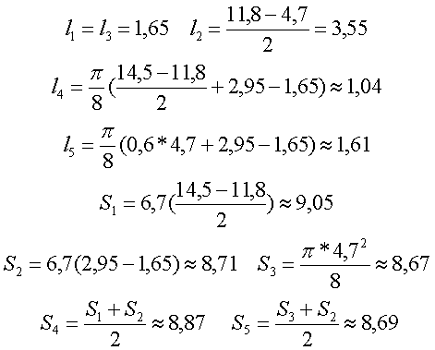
Таким образом, индуктивность данного дросселя составит

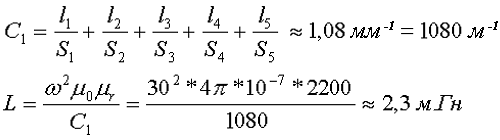
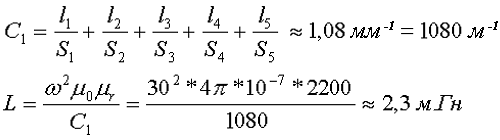
Существует большое количество различных типов Ш-образных сердечников, различающиеся теми или иными конструктивными особенностями, но расчёт их постоянных коэффициентов (С₁ и С₂) и эффективных параметров (l_e, S_e(A_e) и V_e) сводится к разделению полной длины магнитной силовой линии на простейшие линейные или угловые участки и вычисление постоянных коэффициентов.

Расчёт катушки с броневым сердечником

Броневые сердечники представляют собой сборную конструкцию, состоящую из двух чашеобразных частей. В центре каждой чашки имеется центральный керн, в большинстве случаев имеющий осевое отверстие, используемое для подстройки величины индуктивности.

Такие сердечники имеют универсальное применение благодаря высокой добротности в заданной полосе частот, низким искажениям, отсутствие полей рассеяния и небольшими габаритами.

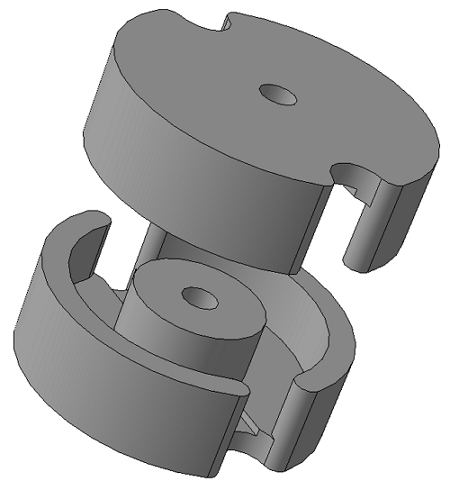
Броневой сердечник.

Расчёт постоянных С₁ и С₂ данного типа сердечника выполняется по аналогии с предыдущими типами, но в связи с формой броневого сердечника имеются свои особенности. Рассмотрим сечение броневого сердечника

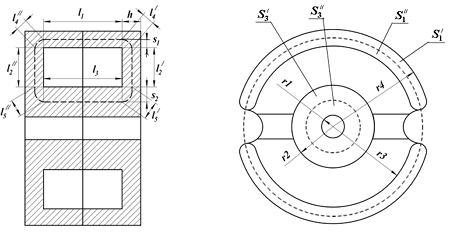
Расчёт параметров броневого сердечника.

Разделим данный сердечник на простейшие линейные и угловые участки с различным сечением: линейные – l₁, l₂, l₃ и угловые – l₄, l₅, так же выделим соответствующие им поперечные сечения: S₁, S₂, S₃, S₄, S₅. Длины линейных участков достаточно просто определить, для нахождения длины угловых участков и сечений на всех участках можно используя следующие выражения

Таким образом, вычислив длину и площадь поперечного сечения отдельных участков, можно вычислить постоянные для данного типа сердечников

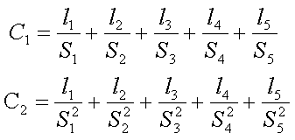
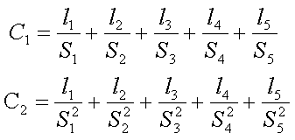
Данные выражения определяют параметры сердечника без технологических пазов и вырезов. При желании их учитывать необходимо, внести следующие поправки

где n – число пазов,

g – ширина паза.

Пример. В качестве примера рассчитаем индуктивность дросселя выполненного на броневом сердечнике, состоящем из двух чашек типа Ч22 из феррита марки 50ВН (μ_r = 50), количество витков ω = 100.

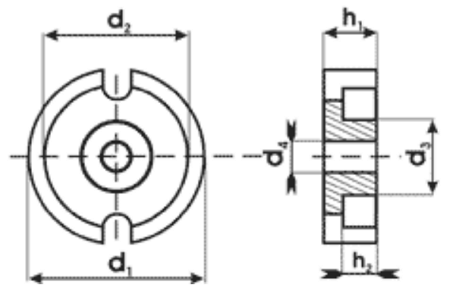
Сердечник типа Ч22: d₁ = 22, d₂ = 17,9, d₃ = 9,4, d₄ = 4,4, h₁ = 6,8, h₂ = 4,6.

С учётом конструктивных особенностей выразим величины заложенные в требуемые нам выражения:

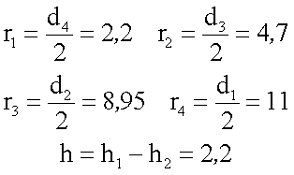
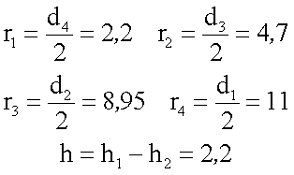
Найдем длины и сечение участков магнитопровода. Расчёт будем вести без учёта технологических пазов и вырезов.

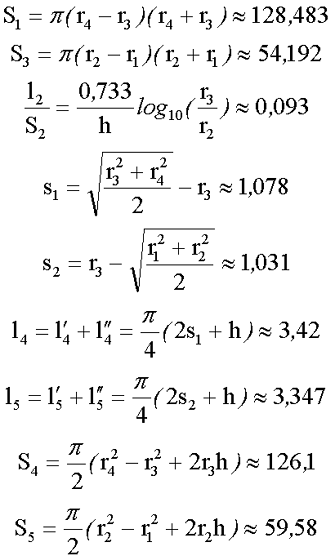
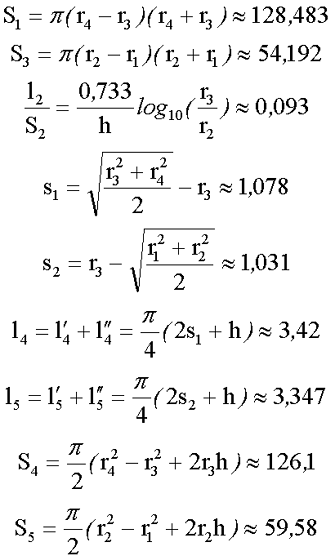
С учётом рассчитанных выше значений определим индуктивность исходного дросселя

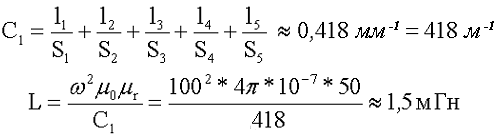
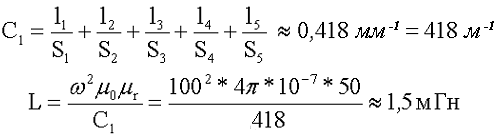
На этом можно и остановиться с расчётами индуктивных элементов с замкнутыми сердечниками. В следующей статье я рассмотрю индуктивные элементы на разомкнутых сердечниках.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.