1.4.2 Методика расчета цепи методом контурных токов
В данном методе за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи. Расчет токов ветвей выполняют в следующем порядке:
1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2 Определяем все независимые контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11,I22,I33и т. д.) или римские цифры.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5 Решаем любым методом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (
7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Пример 1.3. Расчёт сложной цепи методом контурных токов
В цепи, изображённой на рисунке 1.4, рассчитать все токи методом контурных токов. Параметры цепи:
Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаемI11иI22(см. рисунок 1.4).
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
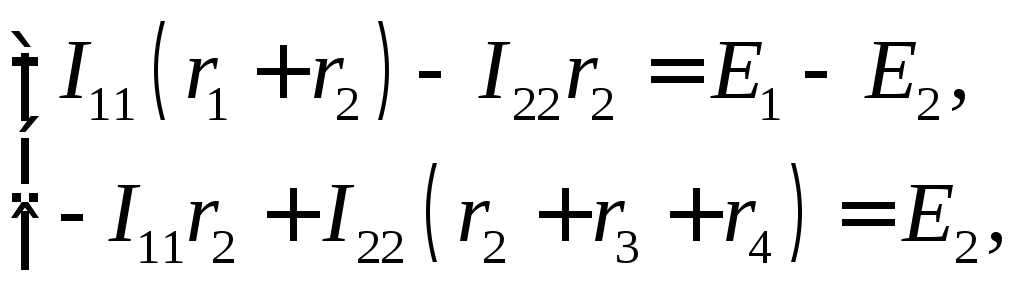

Решаем систему и получаем контурные токи I11=I22= 3 А.
Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1.4 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.
Переходим от контурных токов к реальным.
В первой ветви протекает только один
контурный ток I
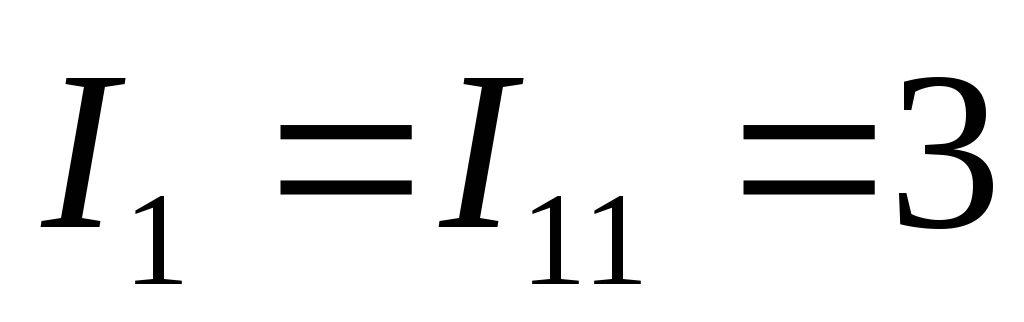 А.
А.
Реальный ток второй ветви формируется двумя контурными I11,иI22. ТокI22совпадает по направлению с реальным, аI11направлен навстречу реальному. В результате
 А.
А.
В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для
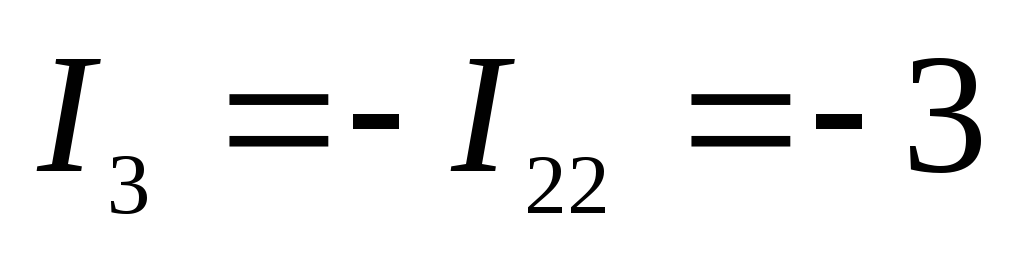 А.
А.
Результаты расчёта цепи методом контурных токов совпадают с результатами, полученными при определении токов с помощью законов Кирхгофа. Следует отметить, как положительный факт, что в методе контурных токов пришлось решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.
7. Метод контурных токов.
В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.
Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:
1. Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2. Определяем все независимые контуры.
3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.
4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5. Решаем любым методом полученную систему относительно контурных токов и определяем их.
6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).
7. Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
8. Использование метода узлового напряжения в расчете сложных цепей.
Порядок расчета цепей методом узлового напряжения:
1. Если по условию задачи задан реальный источник ЭДС, обязательно указываем на схеме его внутреннее сопротивление.
2. Расставляем направления токов в ветвях: все токи либо вытекают из узла, либо втекают в него.
3. Рассчитываем электрическую проводимость каждой ветви: g = 1/R (См).
4.
Рассчитываем напряжение между узловыми
точками по формуле: 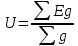 .
В этой формуле ЭДС берется со знаком
“+”, если ее направление совпадает с
направлением тока в ветви.
.
В этой формуле ЭДС берется со знаком
“+”, если ее направление совпадает с
направлением тока в ветви.
5. Рассчитываем значения токов в ветвях по формуле: Ii = (Ei – U)× gi. В этой формуле ЭДС берется со знаком “+”, если ее направление совпадает с направлением тока в ветви.
6. Т.к. направления токов в ветвях были выбраны произвольно, то при расчете токи получаются алгебраическими величинами (либо положительными, либо отрицательными). Если какой-то ток получился отрицательным, это значит, что модуль его равен полученному значению, а действительное направление на схеме в противоположную сторону.
9. Работа и мощность постоянного тока. Нагрев проводов током. Выбор сечения проводов на нагрев.
РАБОТА ПОСТОЯННОГО ТОКА
Работа тока — это работа электрического поля по переносу электрических зарядов вдоль проводника. Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.
Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:
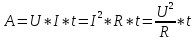
По закону сохранения энергии работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока.
ЗАКОН ДЖОУЛЯ -ЛЕНЦА
При прохождении тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
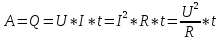
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.
МОЩНОСТЬ ПОСТОЯННОГО ТОКА
— отношение работы тока за время t к этому интервалу времени.
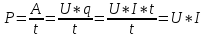
Основным показателем, по которому рассчитывают провод, является его длительно допустимая токовая нагрузка. Проще говоря, это такая величина тока, которую он способен пропускать на протяжении длительного времени.
Чтобы найти величину номинального тока, необходимо подсчитать мощность всех подключаемых электроприборов в доме. Рассмотрим пример расчета сечения провода для обычной двухкомнатной квартиры.
После того как мощность будет известна, найти силу тока можно по формуле:
— для однофазной сети 220 В:
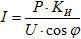
где Р — суммарная мощность всех электроприборов, Вт;
U — напряжение сети, В;
КИ= 0.75 — коэффициент одновременности;
 —
для бытовых электроприборов.
—
для бытовых электроприборов.
—
для трехфазной сети 380 В: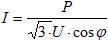
Зная величину тока, сечение провода находят по таблице. Если окажется что расчетное и табличное значения токов не совпадают, то в этом случае выбирают ближайшее большее значение.
3. Метод контурных токов для анализа электрической цепи синусоидального тока
Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи.
Число
уравнений  (р
– число контуров, m – число узлов ,n –
число неизвестных токов) равно числу
независимых контуров (каждый новый
контур содержал хотя бы одну ветвь, не
входящую в предыдущие). Первый закон
Кирхгофа выполняется автоматически.
(р
– число контуров, m – число узлов ,n –
число неизвестных токов) равно числу
независимых контуров (каждый новый
контур содержал хотя бы одну ветвь, не
входящую в предыдущие). Первый закон
Кирхгофа выполняется автоматически.
Метод основывается на том свойстве, что ток в любой ветви цепи может быть представлен в виде алгебраической суммы независимых контурных токов, протекающих по этой ветви. При использовании данного метода вначале выбирают и обозначают независимые контурные токи (по любой ветви цепи должен протекать хотя бы один контурный ток).
Алгоритмом метода контурных токов:
1. Задаются направлением токов ветвей и обозначают их на схеме.
2. Определяют независимые контуры и их нумеруют. При наличии в схеме источников тока независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока.
3. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока должен проходить только один контурный ток!).
4. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.
5. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.
Рекомендуется
выбирать количество ветвей с источниками
тока так, чтобы каждый из них проходил
через один источник тока (эти контурные
токи можно считать совпадающими с
соответствующими токами источников
тока:  ,
они обычно являются заданными по условию
задачи.
,
они обычно являются заданными по условию
задачи.
Для определения контурных токов составляют по второму закону Кирхгофа для этих контуров р уравнений в виде:

где Zkk – сумма сопротивлений всех ветвей, входящих в контур k всегда положительное собственное сопротивление контура; , RlkRkl– сумма сопротивлений элементов, общих для контуров k и l , причём если направления контурных токов в общей для контуров k и l ветви совпадают, то значение Rkl положительно, в противном случае оно отрицательно; Ekk – алгебраическая сумма ЭДС источников, включенных в ветви, образующие контур k; Rk(k+m) — общее сопротивление k контура с контуром, содержащим источник тока Jm.


Обойдя контур aeda, по второму закону Кирхгофа имеем:
 ,
подставим значения токов.
,
подставим значения токов.

Cоставим уравнения для других контуров и сведем в систему уравнений:

Систему уравнений можно записать в виде:



4. Метод узловых потенциалов для анализа электрической цепи синусоидального тока
Данный
метод вытекает из первого закона
Кирхгофа. В качестве неизвестных
принимаются потенциалы узлов, по
найденным значениям которых с помощью
закона Ома для участка цепи с источником
ЭДС затем находят токи в ветвях. Поскольку
потенциал – величина относительная,
потенциал одного из узлов (любого)
принимается равным нулю. Таким образом,
число неизвестных потенциалов, а
следовательно, и число уравнений равно  , т.е. числу ветвей.
, т.е. числу ветвей.
Метод узловых потенциалов, как и метод контурных токов является одним из основных расчетных приемов. В тех случаях, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.
Если схема имеет п узлов, то ей соответствует система из (n — 1) уравнений вида:

Проводимость
в узле определяется как сумма проводимостей
сходящихся ветвей: 
 —
сумма проводимостей сходящихся в узле
k.
—
сумма проводимостей сходящихся в узле
k.  —
сумма проводимостей ветвей, соединяющих
узлы k и m, взятая со знаком минус.
—
сумма проводимостей ветвей, соединяющих
узлы k и m, взятая со знаком минус. есть узловой ток k узла. Если к k узлу
подтекает ток от источника тока, то он
должен быть включен в ток Ikk со знаком
плюс, если утекает, то со знаком минус.
Если между какими-либо двумя узлами нет
ветви, то соответствующая проводимость
равна нулю.
есть узловой ток k узла. Если к k узлу
подтекает ток от источника тока, то он
должен быть включен в ток Ikk со знаком
плюс, если утекает, то со знаком минус.
Если между какими-либо двумя узлами нет
ветви, то соответствующая проводимость
равна нулю.
После решения системы (1) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС.
Алгоритм
Заменить источники напряжения, включенные последовательно с сопротивлениями, на эквивалентные источники тока, включенные параллельно сопротивлениям.
Заменить сопротивления резисторов на проводимости.
Выбирать опорный узел (U0).
Назначить неизвестные напряжения (U1), (U2) … (UN) оставшимся узлам.
Сформировать уравнения Первого Закона Кирхгофа для каждого из узлов. Сумма проводимостей, связанных с первым узлом схемы, будет положительным коэффициентом первого напряжения в уравнении 1. Сумма проводимостей, связанных со вторым узлом схемы, будет положительным коэффициентом второго напряжения в уравнении 2, и так далее, в зависимости от количества узлов. В результате у вас должна получиться диагональ положительных значений.
Все остальные коэффициенты уравнений будут иметь отрицательный знак, так как они представляют проводимости, расположенные между узлами.
Правые части уравнений представляют собой значения источников тока, подключенных к соответствующим узлам.
Решитm систему уравнений, чтобы найти неизвестные напряжения.


Для узла а.

Подставим значения токов.

Сгруппируем соответствующие члены выражения.

Аналогично для узла b.

1.
В левой части i-го уравнения записывается
со знаком “+”потенциал i-го узла, для которого составляется
данное i-е уравнение, умноженный на сумму
проводимостей
i-го узла, для которого составляется
данное i-е уравнение, умноженный на сумму
проводимостей ветвей, присоединенных к данному i-му
узлу, и со знаком “-”потенциал
ветвей, присоединенных к данному i-му
узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен
на сумму проводимостей
соседних узлов, каждый из которых умножен
на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
ветвей, присоединенных к i-му и k-му узлам.
Из
сказанного следует, что все члены  ,
стоящие на главной диагонали в левой
части системы уравнений, записываются
со знаком “+”, а все остальные – со
знаком “-”, причем
,
стоящие на главной диагонали в левой
части системы уравнений, записываются
со знаком “+”, а все остальные – со
знаком “-”, причем .
Последнее равенство по аналогии с
методом контурных токов обеспечивает
симметрию коэффициентов уравнений
относительно главной диагонали.
.
Последнее равенство по аналогии с
методом контурных токов обеспечивает
симметрию коэффициентов уравнений
относительно главной диагонали.
2.
В правой части i-го уравнения записывается
так называемый узловой ток  ,
равный сумме произведений ЭДС ветвей,
подходящих к i-му узлу, и проводимостей
этих ветвей. При этом член суммы
записывается со знаком “+”, если
соответствующая ЭДС направлена к i-му
узлу, в противном случае ставится знак
“-”. Если в подходящих к i-му узлу ветвях
содержатся источники тока, то знаки
токов источников токов, входящих в
узловой ток простыми слагаемыми,
определяются аналогично.
,
равный сумме произведений ЭДС ветвей,
подходящих к i-му узлу, и проводимостей
этих ветвей. При этом член суммы
записывается со знаком “+”, если
соответствующая ЭДС направлена к i-му
узлу, в противном случае ставится знак
“-”. Если в подходящих к i-му узлу ветвях
содержатся источники тока, то знаки
токов источников токов, входящих в
узловой ток простыми слагаемыми,
определяются аналогично.
В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
4.2 Метод контурных токов
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11и I22- контурные токи.
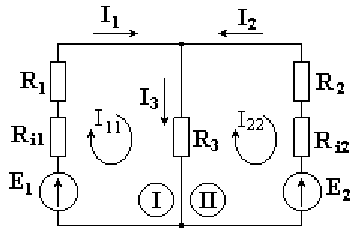 Рис.
4.2
Рис.
4.2
Токи в сопротивлениях R1и R2равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11и I22, так как эти токи направлены в ветви с R3встречно.
Порядок расчета
Выбираются независимые контуры, и задаются произвольные направления контурных токов. В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
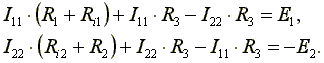
Перегруппируем слагаемые в уравнениях
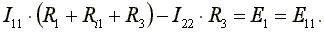 (4.4)
(4.4)
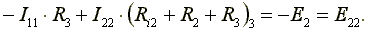 (4.5)
(4.5)
Суммарное сопротивление данного контура называется собственным сопротивлением контура. Собственные сопротивления контуров схемы
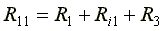 ,
, .
.
Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.
 ,
,
где R12- общее сопротивление между первым и вторым контурами; R21- общее сопротивление между вторым и первым контурами. E11= E1и E22= E2- контурные ЭДС. В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
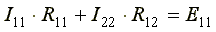 ,
,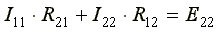 .
.
Собственные сопротивления всегда имеют знак «плюс». Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению. Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11и I22, затем от контурных токов переходим к токам в ветвях. Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. В схеме нарис. 4.2
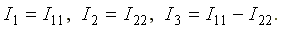 .
.
Рекомендации
Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам. Контурные токи желательно направлять одинаково (по часовой стрелке или против). Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным. Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.
4.3. Метод узловых потенциалов
Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла.
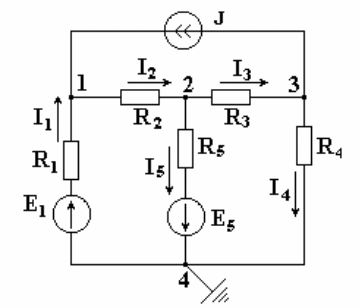
Рис. 4.3
Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов.
Примем для схемы ᵠ4 = 0.
Запишем уравнение по первому закону Кирхгофа для узла 1.
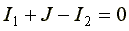 (4.6)
(4.6)
В соответствии с законами Ома для активной и пассивной ветви
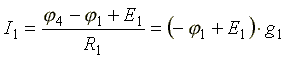 ,
,
Где 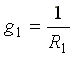 — проводимость первой ветви.
— проводимость первой ветви.
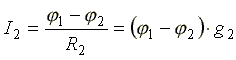 ,
,
Где 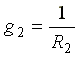 — проводимость второй ветви.
— проводимость второй ветви.
Подставим выражения токов в уравнение (4.6).
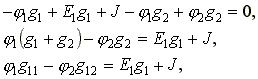 (4.7)
(4.7)
где g11= g1+ g2- собственная проводимость узла 1.
Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле. g12= g2- общая проводимость между узлами 1 и 2. Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
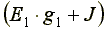 —
сумма токов источников, находящихся в
ветвях, сходящихся в узле 1.
Если ток
источника направлен к узлу, величина
его записывается в правую часть уравнения
со знаком «плюс», если от узла — со
знаком «минус».
По аналогии запишем
для узла 2:
—
сумма токов источников, находящихся в
ветвях, сходящихся в узле 1.
Если ток
источника направлен к узлу, величина
его записывается в правую часть уравнения
со знаком «плюс», если от узла — со
знаком «минус».
По аналогии запишем
для узла 2:
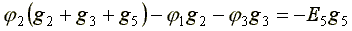 (4.8)
(4.8)
для узла 3:
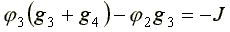 (4.9)
(4.9)
Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы φ 1,φ2,φ3, а затем по закону Ома для активной или пассивной ветви найдем токи. Если число узлов схемы — n, количество уравнений по методу узловых потенциалов — (n — 1).
Рассчитать токи в заданной схеме методом контурных токов
 Рассчитать
токи в заданной схеме методом контурных
токов, методом узловых потенциалов и
неизвестный ток в одной из ветвей методом
эквивалентного источника.
Рассчитать
токи в заданной схеме методом контурных
токов, методом узловых потенциалов и
неизвестный ток в одной из ветвей методом
эквивалентного источника.
Построить векторные диаграммы токов для одного из узлов и напряжений для одного из контуров, не содержащего источники тока.
Проверку правильности выполненного расчета осуществить методом сравнения результатов расчета различными методами.
Определить показания вольтметра, измеряющего действующее значение.
В ответе указать значения токов в комплексной форме и во временной для тока, расс
читанного методом эквивалентного источника, показание прибора.етырьмя витками в измерения: e [В], i [А], R [Ом], L [мГн], С [мкФ].






Домашнее задание №1
Выполнил
Проверил
Гр. ИУ3-32
Вар. 16 б
Николаев С.С.


МГТУ
им. Н. Э. Баумана
Условие задачи.
Рассчитать токи в заданной схеме методом контурных токов, методом узловых потенциалов и неизвестный ток в одной из ветвей методом эквивалентного источника.
Построить векторные диаграммы токов для одного из узлов и напряжений для одного из контуров, не содержащего источники тока.
Проверку правильности выполненного расчета осуществить методом сравнения результатов расчета различными методами.
Определить показания вольтметра, измеряющего действующее значение.
В ответе указать значения токов в комплексной форме и во временной для тока, рассчитанного методом эквивалентного источника, показание прибора.
Пронумеровать узлы, индуктивность рисовать четырьмя витками в соответствии с ГОСТ.
Единицы измерения: e [В], i [А], R [Ом], L [мГн], С [мкФ].
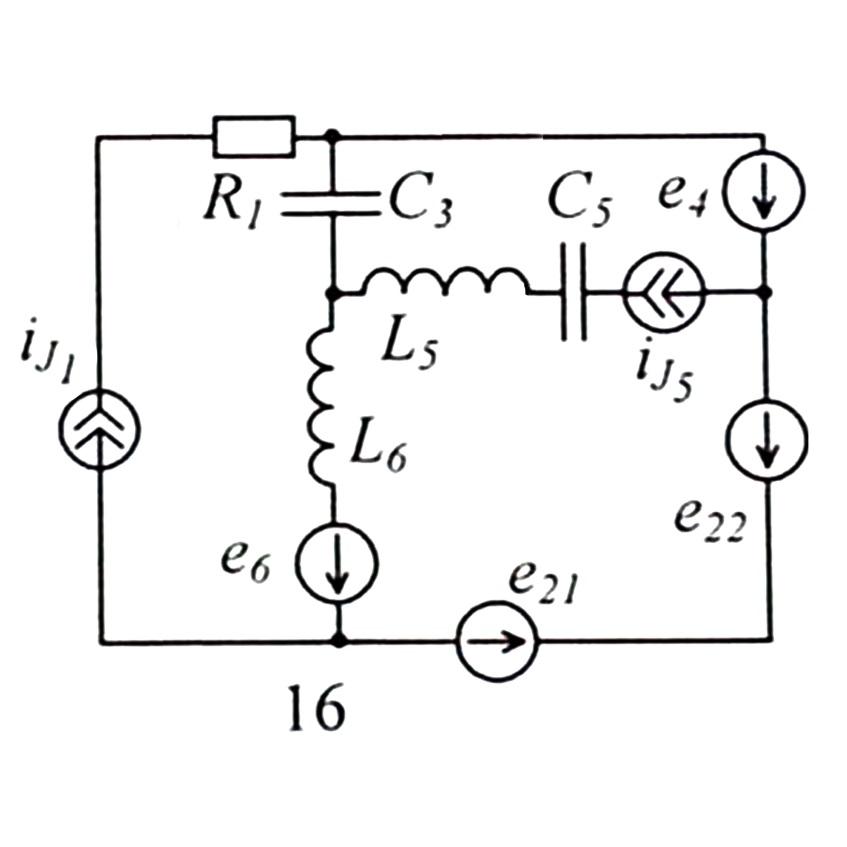
Дано: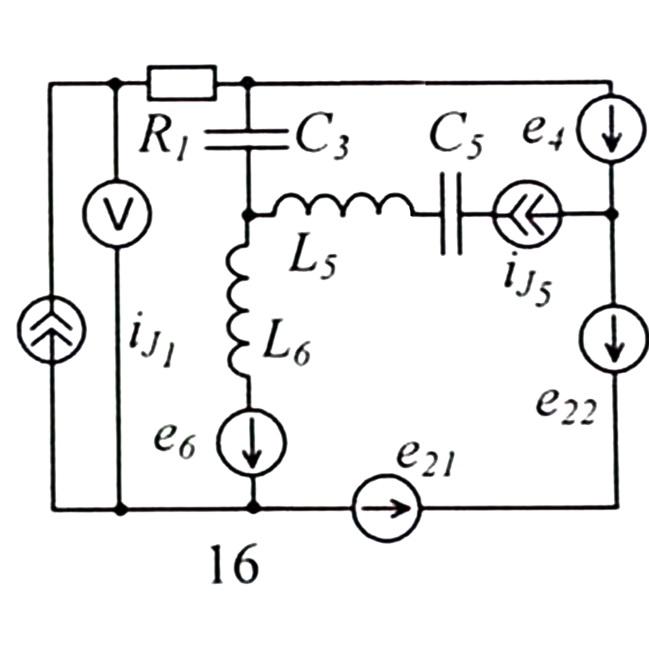
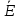 21 =
-100+200j
21 =
-100+200j
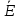 4 = 100j
4 = 100j
e6 =50 sin(103t-270°)[В]
sin(103t-270°)[В]
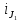 =
=  sin(103t-90°)[A]
sin(103t-90°)[A]
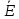 22 = -100+100j
22 = -100+100j
L3 = 300 [мГн]
L6 = 50 [мГн]
 5 = 1 [A]
5 = 1 [A]
C3 = 10 [мкФ]
C5 = 5 [мкФ]
R1 = 100 [Ом]
Перевод данных в комплексную форму записи.
e6 =50sin(103t-270°) [В]
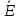 6 =
6 = 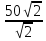 cos(-270°)+
j
cos(-270°)+
j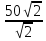 sin(-270°)=
50j
sin(-270°)=
50j
 =
= 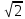 sin(103t-90°)
[A]
sin(103t-90°)
[A]
 1 =
1 = 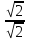 cos(-90°)+
j
cos(-90°)+
j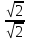 sin(-90°)=
-j
sin(-90°)=
-j
I4
I1
Метод контурных токов
I33




I3


I5


I22
I11
I6



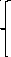
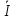 11 = J1
11 = J1
I2

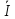 22 = J5
22 = J5
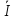 11 Z13 +
11 Z13 + 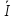 22 Z23 +
22 Z23 + 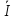 33 Z33 =
33 Z33 = 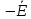 4
4 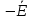 22+
22+ 21+
21+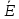 6
6
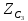 =
= 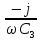 =
= 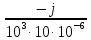 =
= 
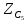 =
= 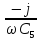 =
=  =
= 
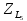 =
=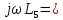
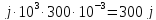
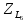 =
=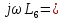
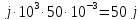
 33 =
33 =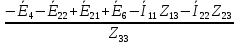 =
= 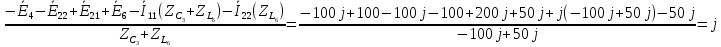
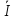 1 =
1 =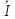 11 =
11 =  1=
1= 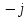
 2 =
2 = 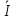 22
22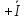 33 =
1
33 =
1
 3 =
3 = 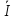 11
11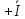 33 =
33 = 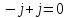
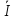 4 =
4 = 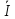 33 =
33 = 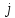
 5 =
5 =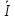 22 =
22 = 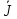 5
5 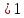
 6 =
6 =  22
22 33 =
33 = 
Метод узловых потенциалов
1
I4
I1




2

0
I3
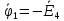
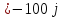

I5
I6
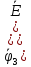
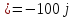

I2
3
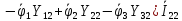
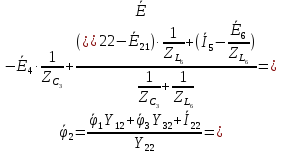

Найдём значение токов в цепи:
 1 =
1 = 
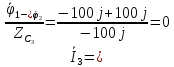
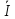 5
5 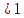
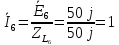
По первому закону Кирхгофа:
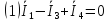 ;
; 
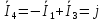
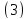
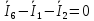 ;
;

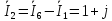
Получили:
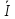 1 =
1 =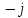
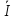 2 =
1
2 =
1
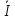 3
3
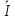 4 =
4 = 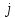
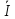 5 =
5 =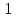
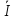 6 =
6 =
Метод эквивалентного генератора.
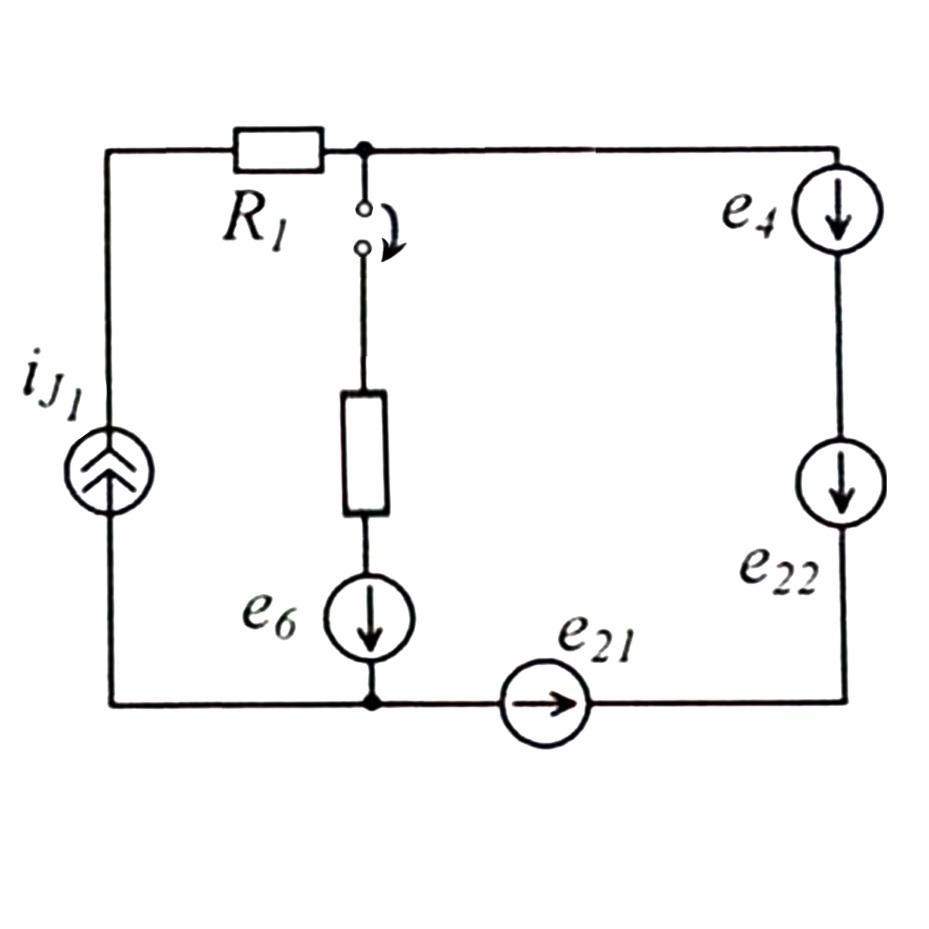

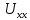
Еэкв.
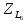

I3
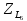
Zвх = Zэкв = 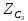 =
= 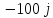
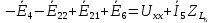
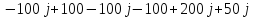 =
= 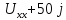
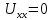
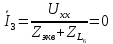
Векторные диаграммы.
 Векторная
диаграмма токов.
Векторная
диаграмма токов.
j
 По
первому закону Кирхгофа, для узла 1:
По
первому закону Кирхгофа, для узла 1: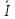 4
4
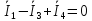

0

 1
1
 1 =
1 =
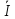 3
3 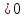
-j
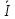 4 =
4 = 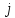
Векторная диаграмма напряжений.
По второму закону Кирхгофа, для контура без источника тока:

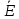 21 =
-100+200j
21 =
-100+200j
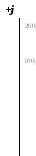
 4 = 100j
4 = 100j



 21
21
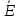 6
6
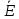 22 = -100+100j
22 = -100+100j

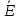 6 =
50j
6 =
50j

50j













50
100
200
-100

 4
4
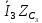
0
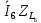 =
50j
=
50j

-100j

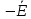 22
22
Показания вольтметра.
1
4
 Выше
нашли, что:
Выше
нашли, что:
0
2
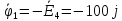
I5
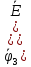
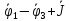 1 R1
1 R1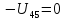
3
5
Отсюда найдём искомую величину:
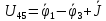 1 R1
1 R1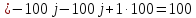 В
В
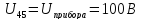
Ответ:
 1 =
1 =
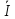 2 =
1
2 =
1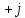
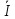 3
3 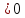
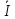 4 =
4 = 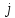
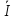 5 =
5 =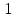
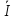 6 =
6 =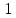
12
Методы анализа электрических цепей

В связи с широким развитием вычислительных устройств задача расчета и моделирования электрических схем заметно упростилась. Наиболее подходящим программным обеспечением для данных целей является продукт National instruments – Multisim (Electronic Workbench ).
В данной статье рассмотрим простейшие примеры моделирования электрических схем с помощью Multisim.
Читать дальше →

Метод узловых потенциалов – один из методов анализа электрической цепи, который целесообразно использовать, когда количество узлов в цепи меньше или равно числу независимых контуров. Данный метод основан на составлении уравнений по первому закону Кирхгофа. При этом, потенциал одного из узлов цепи принимается равным нулю, что позволяет сократить число уравнений до n-1.
Читать дальше →

Одним из распространенных методов расчета электрических цепей является метод двух узлов. Этот метод применяется в случае, когда в цепи всего два узла.
Читать дальше →

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.
Читать дальше →


Наряду с методом контурных токов для анализа электрических цепей используется другой метод – метод наложения. Этот метод основан на принципе наложения, который применяется только к линейным системам.
Метод наложения относительно прост, и в основном применяется для не сложных электрических цепей.
Читать дальше →


При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Читать дальше →


При решении задач по электротехнике, зачастую требуется знать режим работы не всей цепи, а только одной определённой ветви. Для определения параметров такой ветви существует метод эквивалентного генератора.
Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется эквивалентным ЭДС Еэкв, с её внутренним сопротивлением rэкв. При этом часть цепи, в которую входит источник ЭДС называют эквивалентным генератором или активным двухполюсником, откуда и название метода.
Читать дальше →
Основы электротехники и электроники: Курс лекций, страница 5
 .
.
Тогда по закону Ома
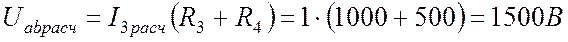 .
.
Но, с другой стороны, по закону Ома
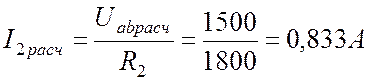 .
.
По первому закону Кирхгофа
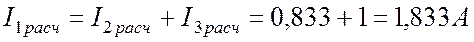 .
.
Но по закону Ома для участка с ЭДС
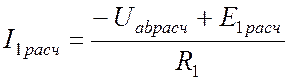 .
.
Откуда выражаем расчетную ЭДС:
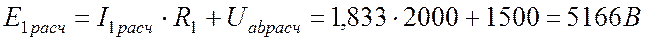 .
.
Находим коэффициент пересчета:
 .
.
Находим реальные токи:
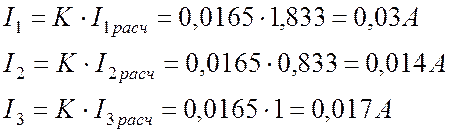 .
.
Замечание: Так как исходные данные заданы с точностью до двух значащих цифр, окончательные результаты расчетов округляем также до двух значащих цифр, а в промежуточных расчетах оставляем три значащие цифры.
Проверяем расчет при помощи баланса мощности.
Мощность источников
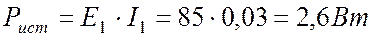 .
.
Мощность потребителей
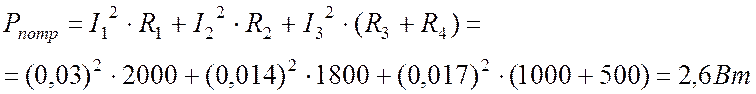 .
.
 .
.
8. МЕТОД КОНТУРНЫХ ТОКОВ
При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют реальные токи ветвей.
Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить по второму закону Кирхгофа для независимых контуров. Следовательно, метод контурных токов более экономен, чем метод на основе законов Кирхгофа (в нем меньше уравнений).
Вывод основных расчетных уравнений покажем на примере схемы с двумя независимыми контурами (Рис. 8.1).
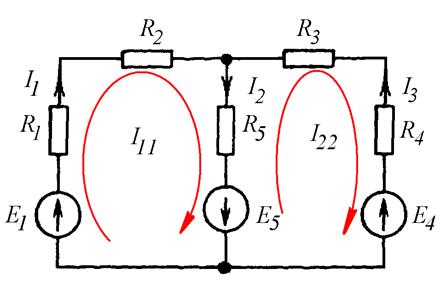
Рис. 8.1
Пусть в левом контуре по часовой стрелке течет контурный ток I11, а в правом (также по часовой стрелке) – контурный ток I22.
Прежде всего, запишем соотношения между контурными и реальными токами. В схеме два контура. Они имеют одну общую ветвь (последовательно соединенные ЭДС E5 и сопротивление R5). Следовательно, в этой ветви течет как контурный ток первого контура (I11), так и контурный ток второго контура (I22). Но если контурный ток I11 течет сверху вниз, то контурный ток I22 течет снизу вверх.
Алгебраическая сумма контурных токов будет равна реальному току ветви, то есть току I2. С учетом направления реального тока имеем:
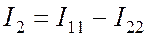 . (8.1)
. (8.1)
Очевидно, что в остальных ветвях с учетом направления реальных токов:
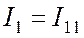 , (8.2)
, (8.2)
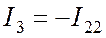 . (8.3)
. (8.3)
Запишем уравнения по второму закону Кирхгофа для реальных токов:
 . (8.4)
. (8.4)
Подставим в (8.4) соотношения (8.1-8.3):
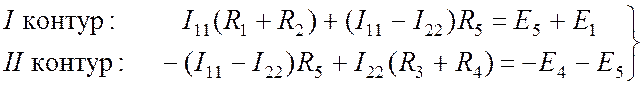 . (8.5)
. (8.5)
Перегруппируем слагаемые в (8.5) и получим систему линейных алгебраических уравнений относительно контурных токов:
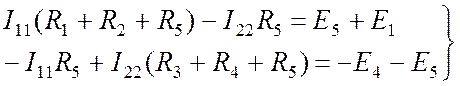 . (8.6)
. (8.6)
Алгоритм расчета цепи методом контурных токов
- Выбирается произвольное направление контурных токов в каждом из независимых контуров.
- По второму закону Кирхгофа составляются уравнения для каждого из независимых контуров с использованием контурных токов. При этом первый закон Кирхгофа выполняется автоматически. В правильно составленной системе уравнений главный определитель симметричен относительно главной диагонали.
- После расчета полученной системы уравнений для контурных токов определяются реальные токи ветвей как алгебраическая сумма контурных токов. Если по ветви протекает один контурный ток, то реальный ток равен контурному.
- Правильность расчета можно проверить либо с помощью баланса мощности, либо по второму закону Кирхгофа (но не по первому закону Кирхгофа!).
Пример 8.1:
Найти неизвестные токи методом контурных токов (Рис. 8.2).
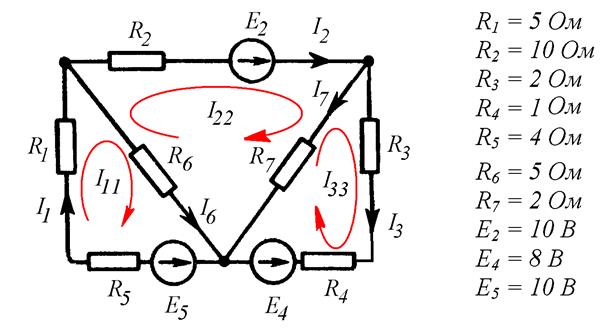
Рис. 8.2
Выбираем независимые контуры по ячейкам схемы. Задаем направления контурных токов. В данном случае направим все контурные токи по часовой стрелке.
Составляем уравнения по второму закону Кирхгофа для контурных токов.
Для I контура. Собственное сопротивление контура состоит из R1, R6 и R5. По ветви с R6 текут два контурных тока I11 и I22 в противоположных направлениях. Значит, в уравнение по второму закону Кирхгофа для контура I ток I22 войдет с минусом:
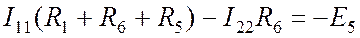 . (Пр. 8.1.1)
. (Пр. 8.1.1)
Для II контура. Собственное сопротивление контура состоит из R2, R7 и R6. По ветви с R6 ток I11 течет противоположно току I22. А ток I33 течет по ветви с R7 противоположно току I22. Значит, в уравнение по второму закону Кирхгофа для контура II токи I11 и I33 войдут с минусом:
 . (Пр.
8.1.2)
. (Пр.
8.1.2)
Для III контура. Собственное сопротивление контура состоит из R3, R4 и R7. По ветви с R7 течет ток I22 противоположно току I33. Значит, в уравнение по второму закону Кирхгофа для контура III ток I22 войдет с минусом:
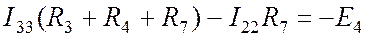 . (Пр. 8.1.3)
. (Пр. 8.1.3)
Объединяем уравнения (Пр. 8.1.1-Пр. 8.1.3) в систему, следя за тем, чтобы в уравнениях присутствовали все неизвестные токи и располагались они руг под другом. В уравнении (Пр. 8.1.1) нет тока I33. Значит, запишем его, умноженным на ноль. Аналогично поступим с током I11 в уравнении (Пр. 8.1.3):
 . (Пр.
8.1.4)
. (Пр.
8.1.4)
В числах система (Пр. 8.1.4) будет выглядеть так:
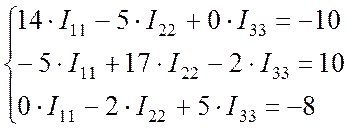 . (Пр. 8.1.5)
. (Пр. 8.1.5)
Заметим, что система (Пр. 8.1.5) имеет главный определитель, симметричный относительно главной диагонали.
Систему (Пр. 8.1.5) решим методом Крамера.
Главный определитель системы:
 .
.
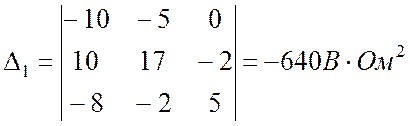 .
.
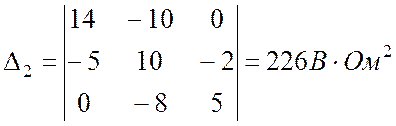 .
.
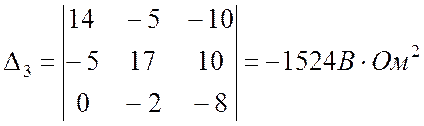 .
.
Контурные токи:
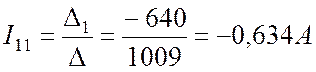 .
.
 .
.
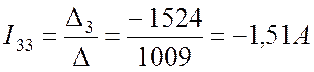 .
.
Определяем реальные токи (См. Рис. 8.2):
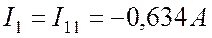 .
.
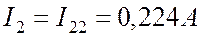 .
.
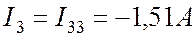 .
.
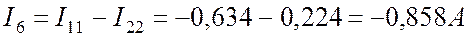 .
.
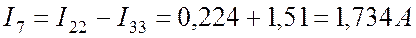




 —
для бытовых электроприборов.
—
для бытовых электроприборов.