Вопрос 20. Расчёт сложных электрических цепей методом контурных токов.

Метод контурных токовпозволяет решать меньшее количество уравнений, чем при расчёте сложных электрических цепей методом уравнений Кирхгофа.

Порядок расчёта:

1. Выбираем произвольное направление контурного (расчётного) тока.

2. Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от контурного (собственного) тока и контурных токов соседних контуров.

3. Решаем полученную систему уравнений и рассчитываем контурные токи.

4. Рассчитываем действительные токи ветвей по правилу:

Если в ветви течёт один контурный ток, то действительный ток равен контурному току. Если два и более — то действительный равен их алгебраической сумме и направлен в сторону большего.

Задача

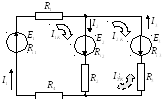
Найти и направить все токи в электрической цепи методом контурных токов.

Используя алгоритм, составляется система уравнений:

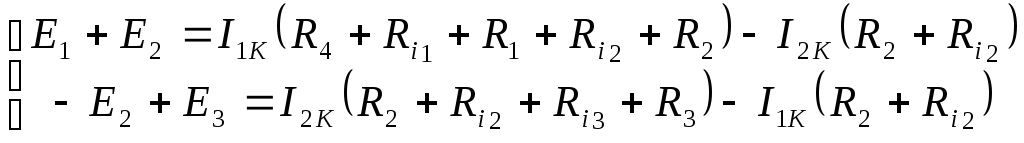
Пусть при решении получили контурные токи:

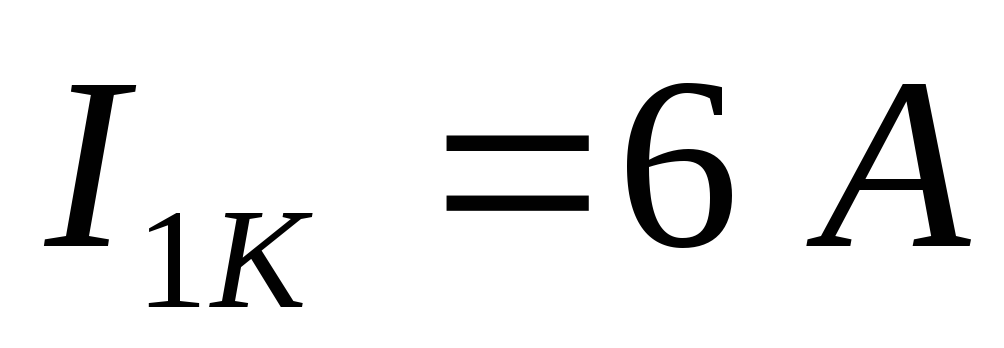
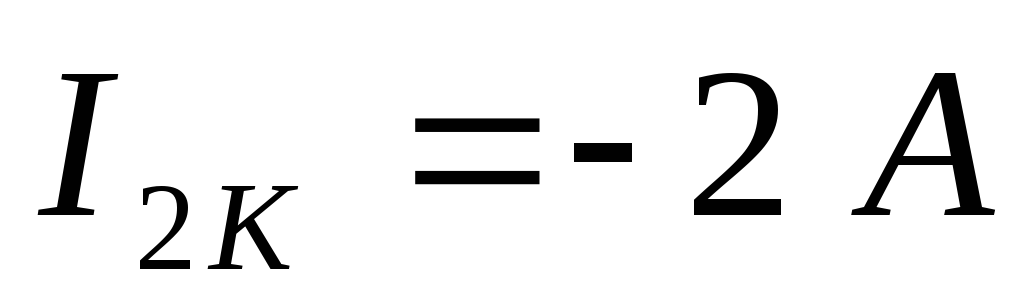
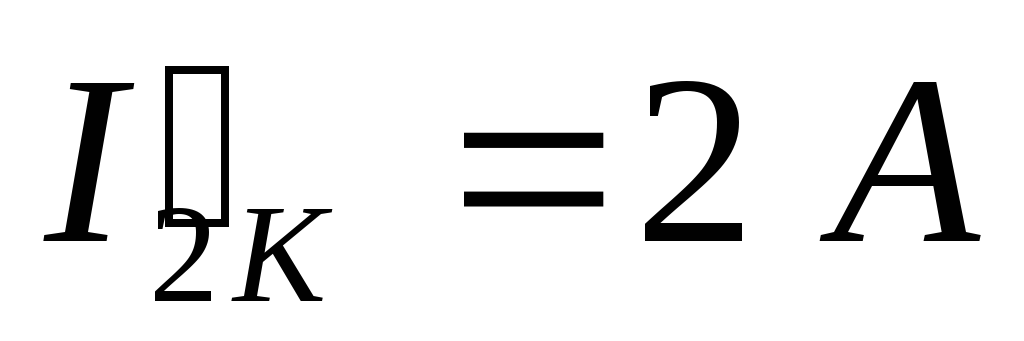
Тогда можно рассчитать действительные токи:

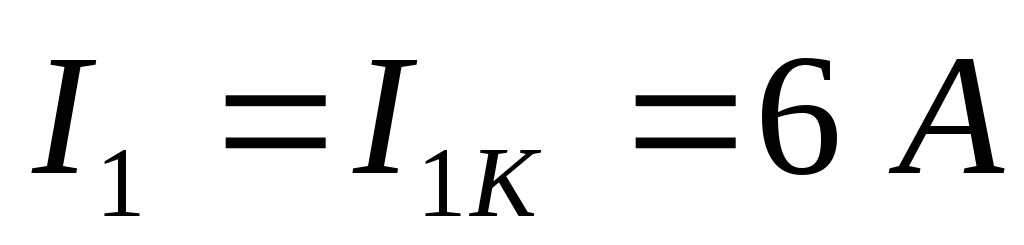
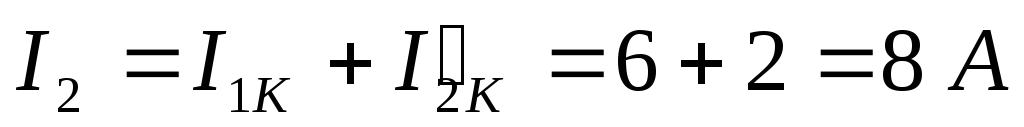
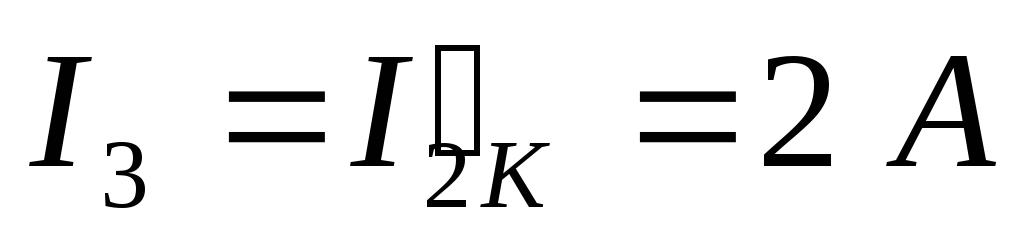
Вопрос 21. Расчёт сложных электрических цепей методом двух узлов.

Рассмотрим метод узловых напряжений(двух узлов) на примере.

Задача

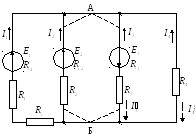
Определить токи ветвей и направить их.

Порядок расчёта:

1. обозначаем узлы А и Б: под узлом А обозначаем узел, к которому направлена большая ЭДС;

2. все токи направляем к узлу А;

3. рассчитываем проводимость каждой ветви по формуле

:

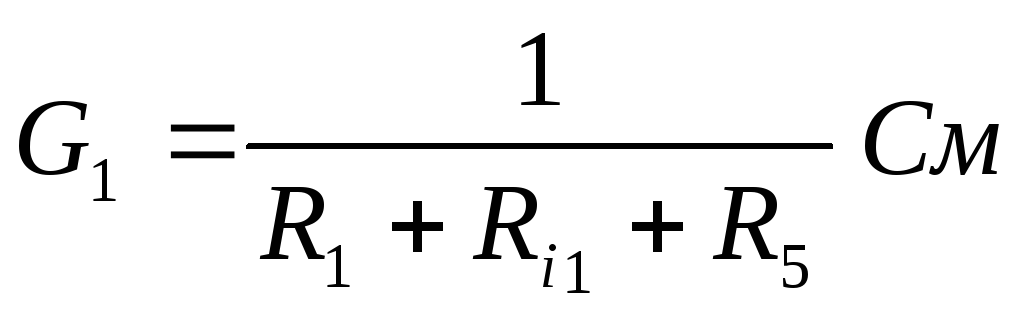
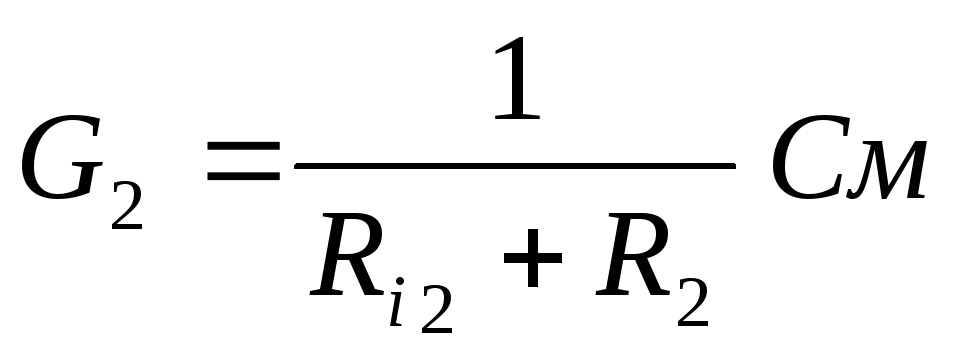
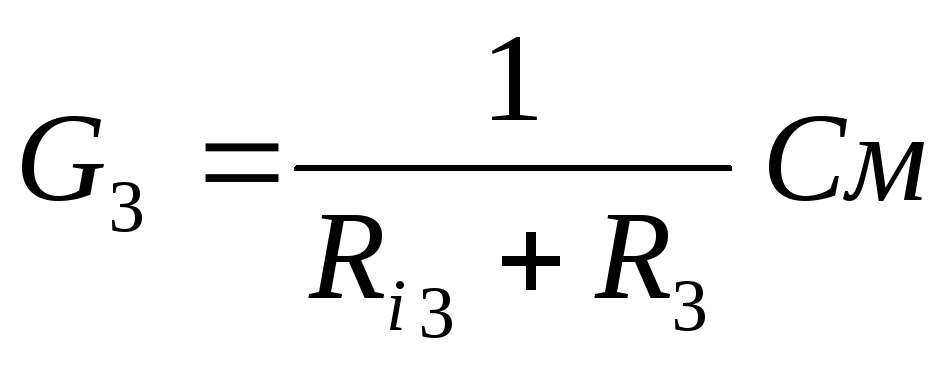
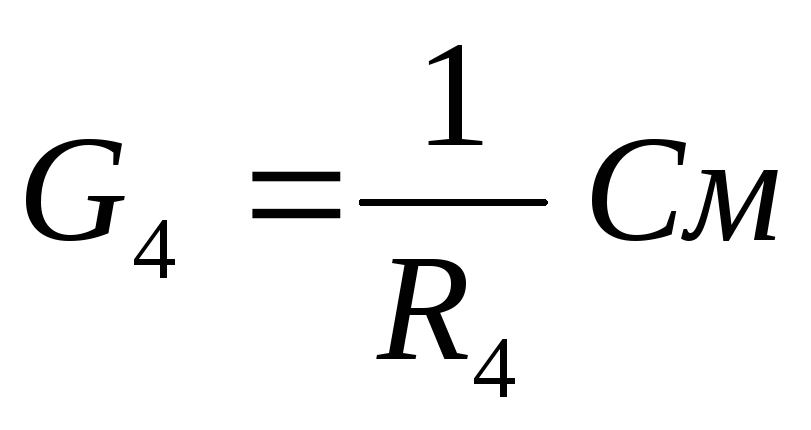
4. Рассчитываем напряжение между двумя узлами по формуле:

В формулу Eвходит со знаком “+”, если она направлена к узлу А; если от узла — то со знаком “–”.

5. Находим токи ветвей:

6. Изменяем направление отрицательных токов.

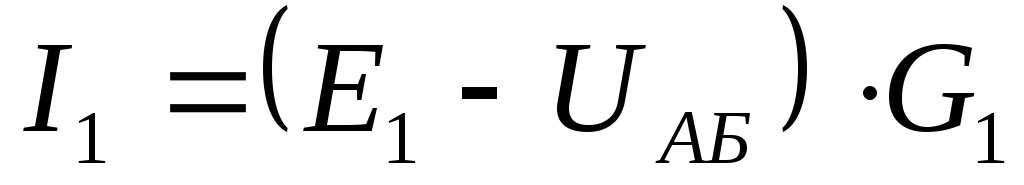
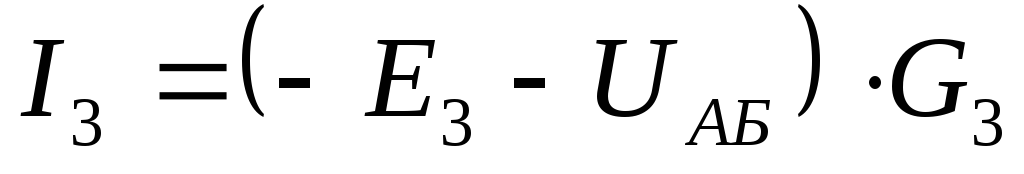
Вопрос 22. Расчёт сложных электрических цепей методом эквивалентного генератора.

Методом эквивалентного генераторанаходят ток в одной ветви. Особенно удобно, если сопротивление этой ветви изменяется.

Согласно теореме об эквивалентном генераторе, любой активный двухполюсник можно заменить эквивалентной ЭДС (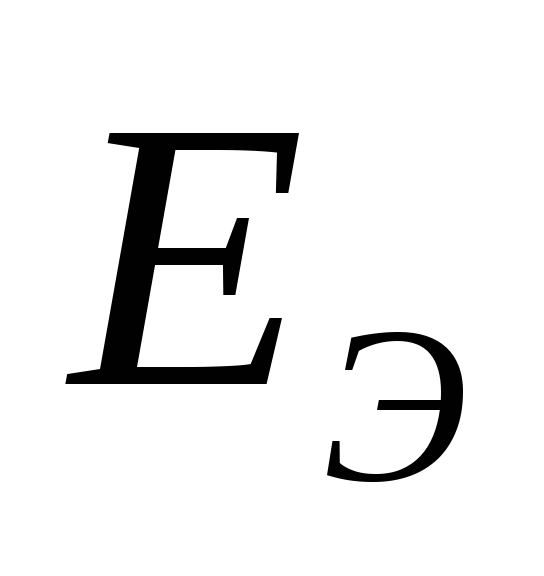) и эквивалентным внутренним сопротивлением (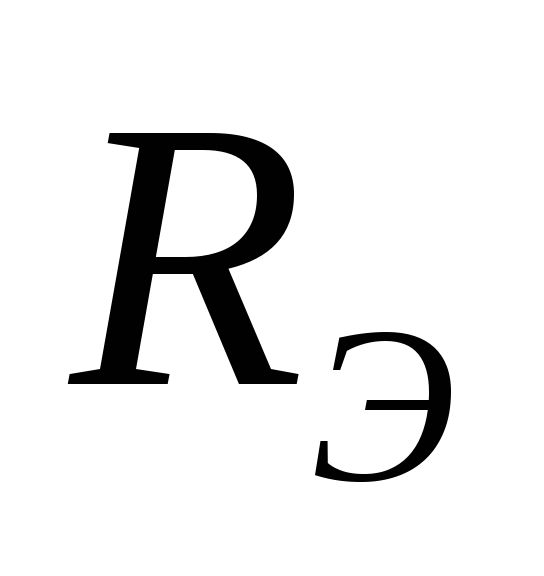). То, что обведено пунктиром на схеме 1, — активный двухполюсник:

Схема 1А

Схема 1Б

Чтобы найти 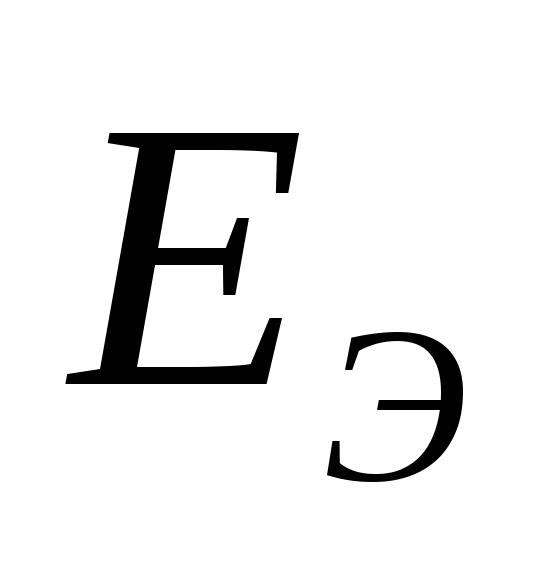, надо разомкнуть ветвь АБ и найти напряжение на зажимах разомкнутой ветви. Оно будет равно: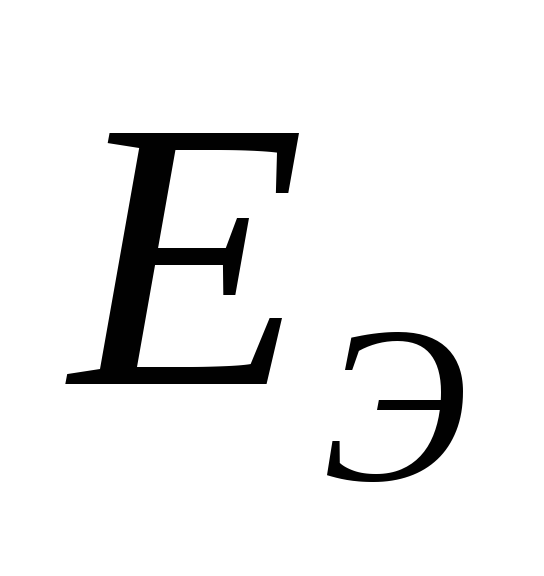

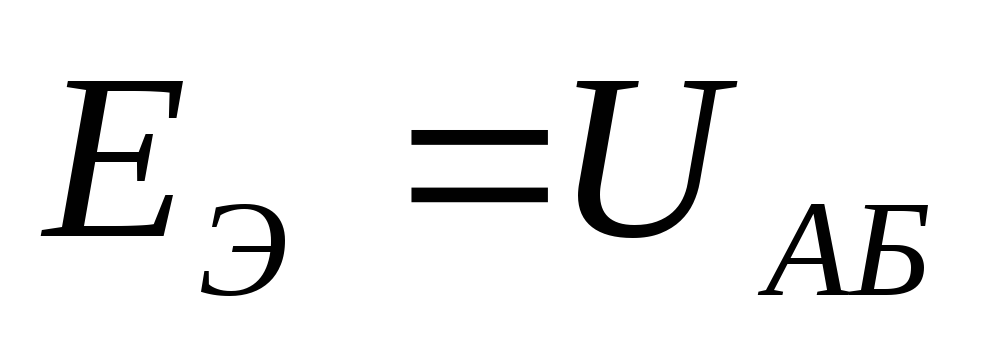
Чтобы найти 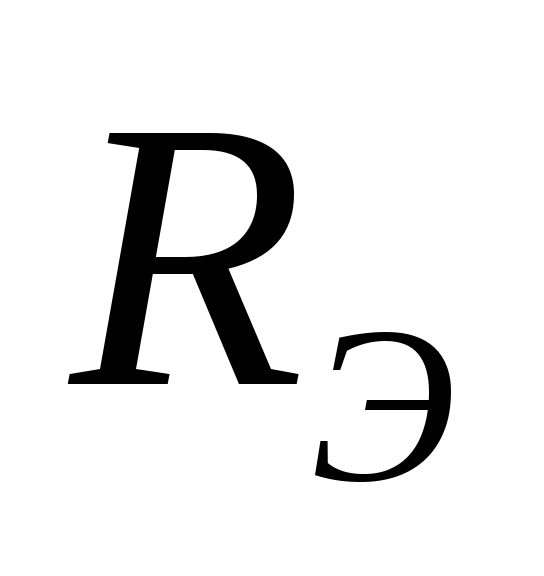, надо разомкнуть ветвь АБ, убрать все источники, оставив их внутренние сопротивления. Далее необходимо рассчитать сопротивление цепи по отношению к зажимам АБ. Это и будет.

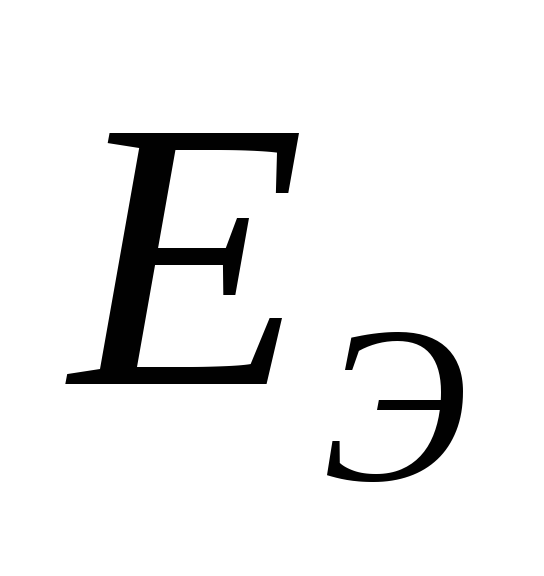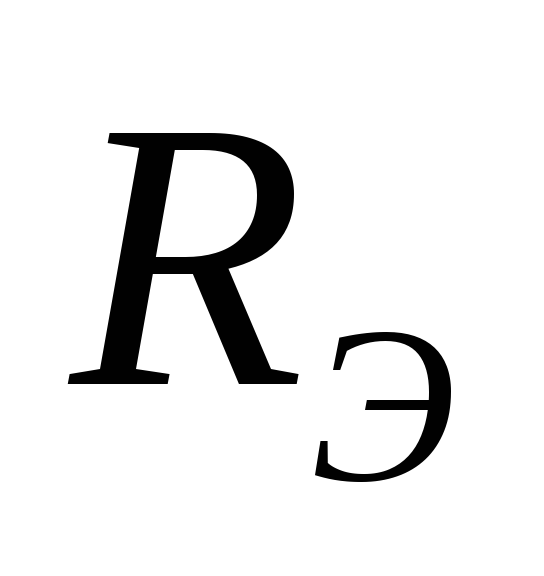Если известны и, то:

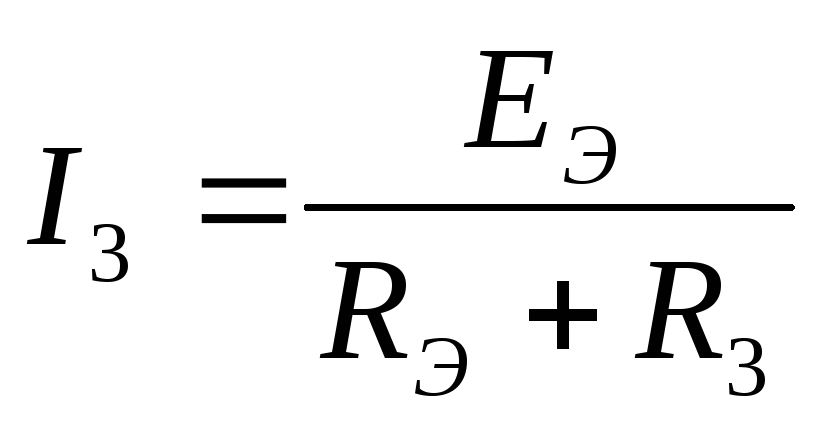
Задача

Дано (для схемы 1А):

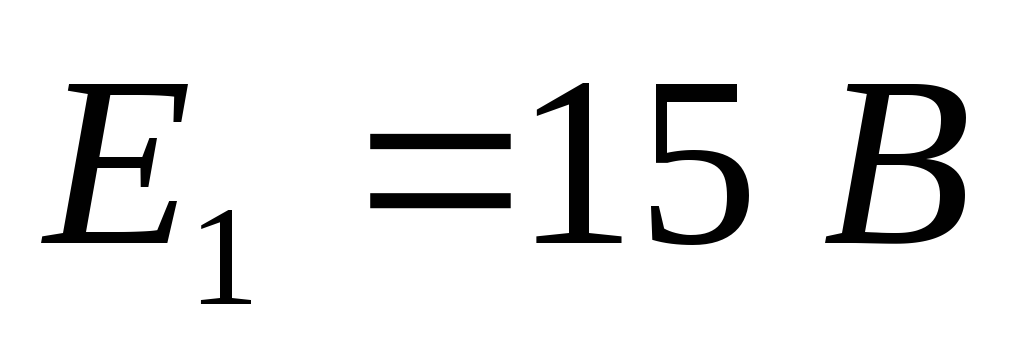
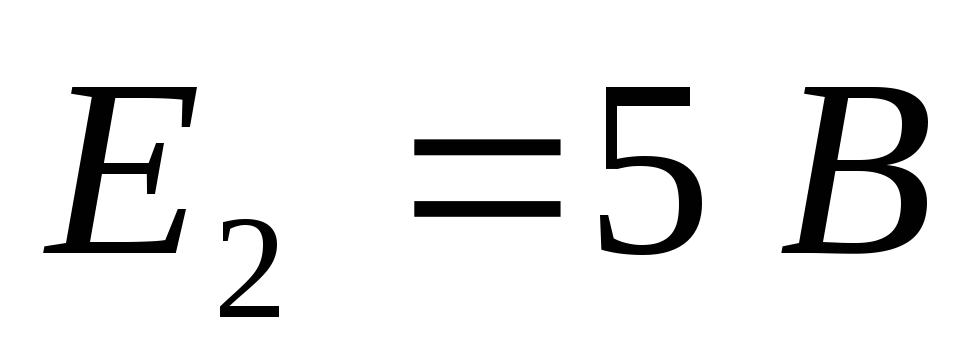
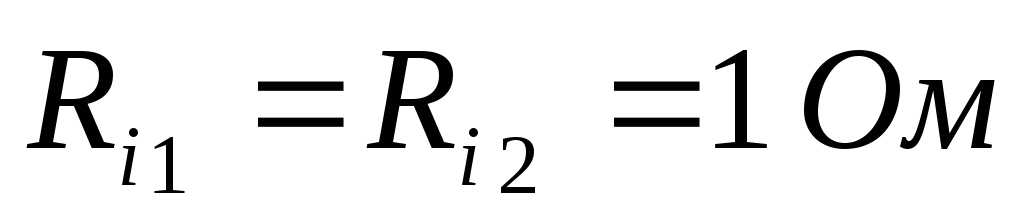
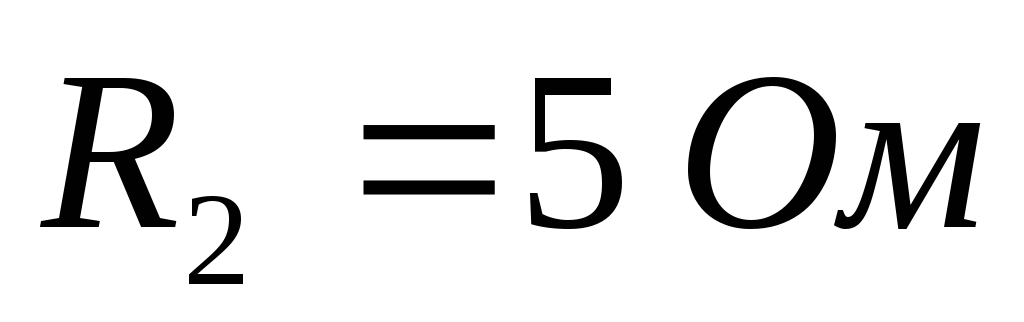
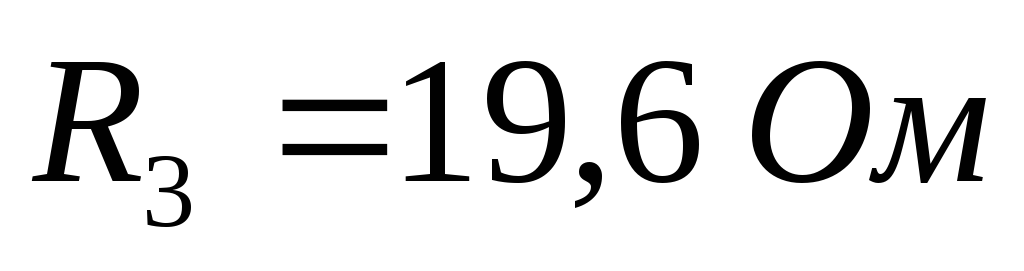
Найти ток 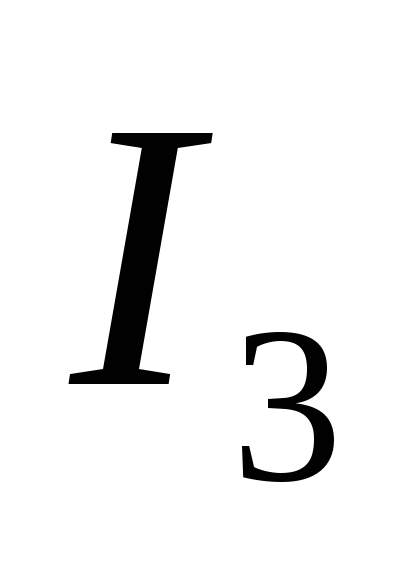в цепи (методом эквивалентного генератора).

Разомкнутая цепь приведена на схеме:

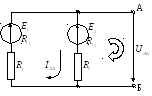
Находим ток холостого хода:

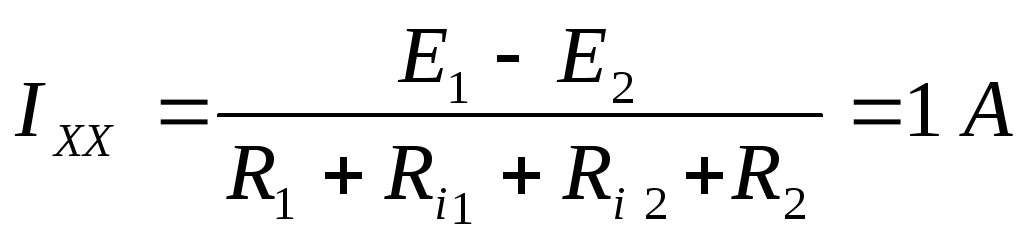
Найдём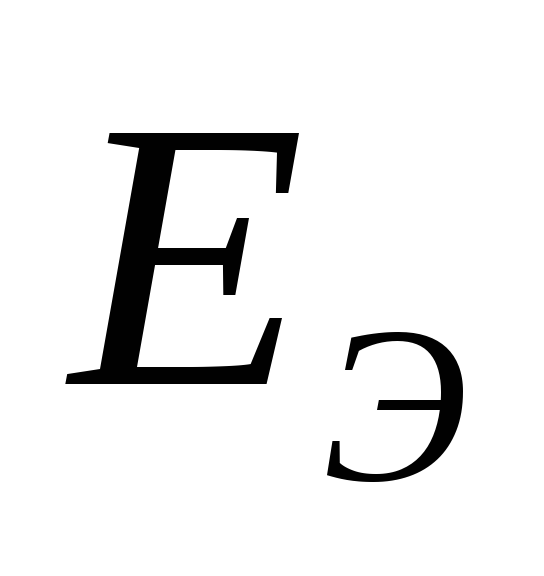

:

Обходим контур по второму закону Кирхгофа так, чтобы он замкнулся через напряжение 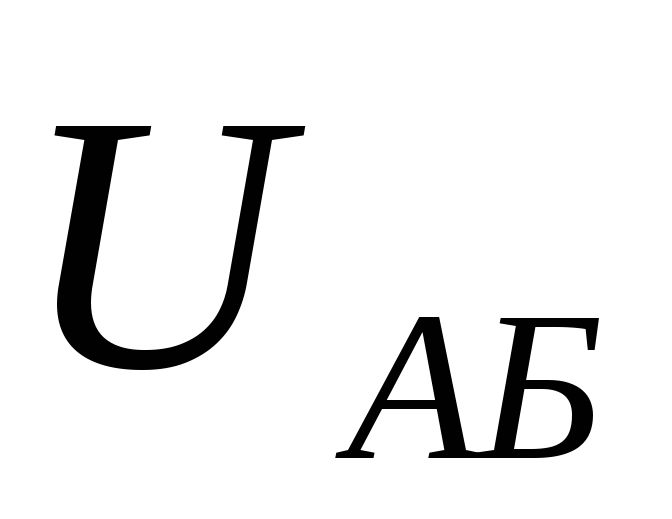(лучше взять такой контур, где меньше элементов):

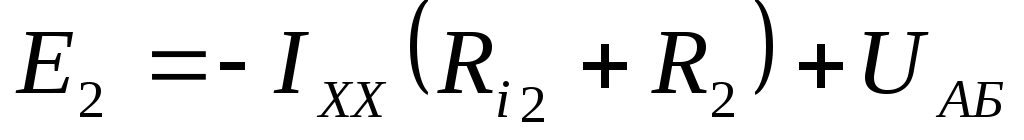
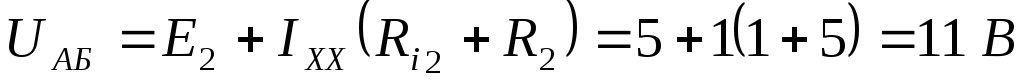
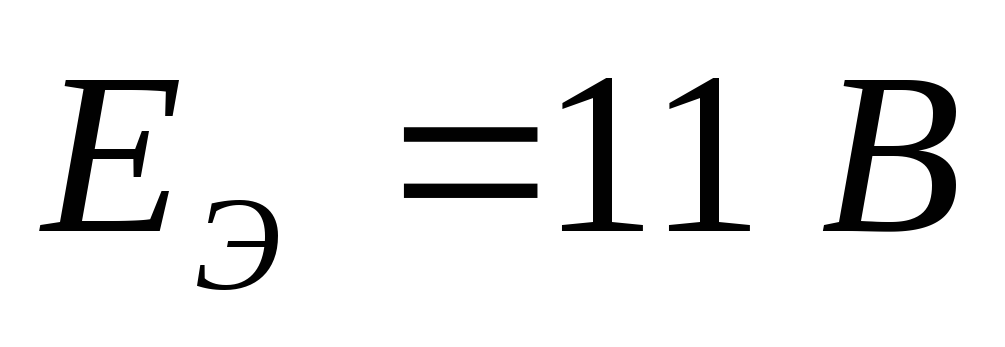
Находим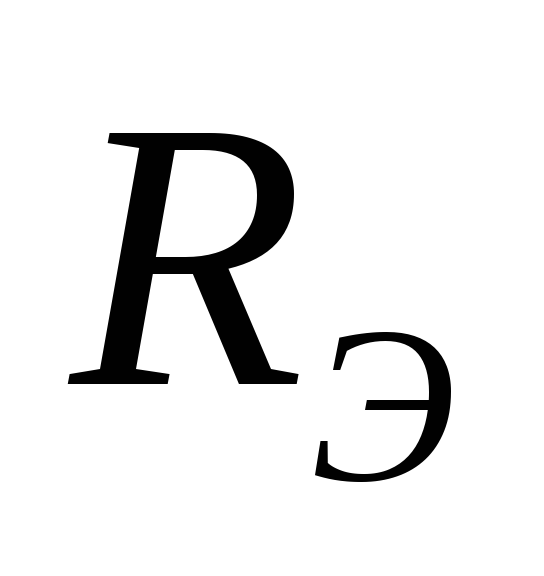

:

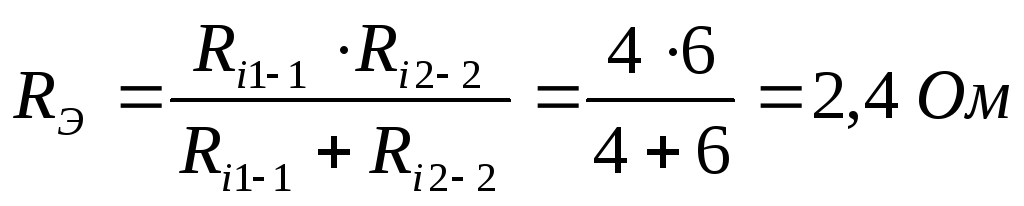
Далее можно выразить искомый ток:

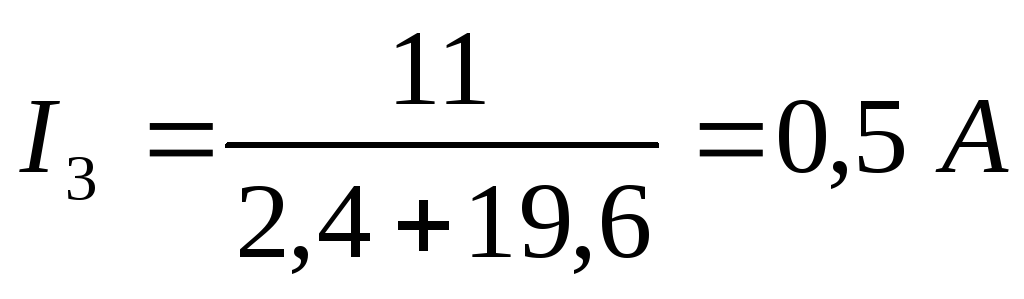
Вопрос 23. Метод наложения.

Метод наложенияоснован напринципе наложения, согласно которому ток в каждой ветви может быть найден как алгебраическая сумма токов от действия каждой ЭДС в отдельности.

Порядок расчёта:

1. Поочерёдно оставляем в схеме по одному источнику, внутреннее сопротивление исключаемых источников также остаётся.

2. Расставляем частичные токи (обозначаем их со штрихом).

3. Находим действительный ток, как алгебраическую сумму частичных токов. Действительный ток направляем в сторону большего частичного.

Например:

Пусть , тогда.

Расчет электрической цепи методом контурных токов

При расчете цепи методом контурных токов выдвигаются два предположения:

• в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;
• ток каждой ветви равен алгебраической сумме контурных токов, протекающих через эту ветвь.

Рассмотрим схему, представленную на рис. 5

При расчете рекомендуется следующая последовательность действий:

• находят в цепи ветви, узлы и контуры;
• указывают произвольные направления токов в ветвях и направления обхода контуров;
• произвольно выбирают направления контурных токов, обычно совпадающие с направлениями обхода контура;
• для независимых контуров составляют уравнения по второму закону Кирхгофа относительно неизвестных контурных токов I₁, I₁₁, I₁₁₁.

Для рассчитываемой электрической цепи система уравнений будет иметь вид:

• для контура acef: (R_I + r₀₁ + R₃) I_I – R₃ I_II =E₁
• для контура abc: -R₃ I_I + (R₂ + R₃ +R₄) I_II — R₂ I_III = -E₂
• для контура bdc: -R₃ I_II + (R₂ + R₅ +R₆) I_III = E₂

В рассматриваемом примере при составлении уравнений принято во внимание то, что вторая (R₂, E₂) и третья (R_з) ветви электрической цепи являются смежными и по ним протекают два контурных тока, каждый из которых обусловливает на резисторе смежной ветви падение напряжения, например, R₂I_II и R₂I_III (для токов второй ветви).

r₀₁ – внутреннее сопротивление источника ЭДС Е₁.

Токи в ветвях определяют алгебраическим суммированием контурных токов, протекающих через ту или иную ветвь. Контурный ток берется со знаком «плюс», если его направление совпадает с направлением тока ветви, и со знаком «минус» — при встречном направлении.

1.8. Расчет цепей методом контурных токов.

Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.

Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.

При расчете рекомендуется придерживаться следующей последовательности:

– выделить все независимые контуры

– указать направления обхода контуров (желательно одно и то же для всех контуров)

– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)

– для всех независимых контуров составить уравнения второго закона Кирхгофа

– решить полученную систему уравнений любым известным методом

– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.

Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E₁R₃R₁E₁и R₃E₂R₂R₃. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R₃, которая принадлежит двум контурам сразу, протекают два контурных тока I_K1и I_K2, но в противоположных направлениях.

E₁ = I_K1 (R₁ + R₃) – I_K2R₃

– E₂= –I_K1R₃+I_K2(R₂+R₃)

Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.

Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: I_K1=7 A, I_K2= – 5 A. Тогда I₁= I_K1= 7 = 7 A и протекает в резисторе R₁так же, как контурный ток I_K1по схеме сверху вниз. Ток I₂= – I_K2= – 5 А и протекает в резисторе R₂по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R₃ , цепи представленной на рис. 1.10, протекают контурный ток I_K1= 7 А по схеме сверху вниз и контурный ток I₂= – 5 А по схеме снизу вверх. I_K1> I_K2и I₃= I_K1– I_K2= 7 – (–5) = 12 А. Ток I₃имеет такое же направление, что и ток I_K1 , т.е. по схеме сверху вниз.

1.9. Расчет цепей методом эквивалентного преобразования.

Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.

По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.

Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)

Например, в цепи представленной на рис. 1.11а приемники R₃и R₄соединены последовательно и их можно заменить одним эквивалентным с сопротивлением

R₃₄= R₃+ R₄.

После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R₂ и эквивалентный приемник R₃₄включены параллельно. Параллельный участок R₂– R₃₄также можно заменить одним эквивалентным с сопротивлением

после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.

Входное сопротивление этой цепи R₁₂₃₄= R₁+ R₂₃₄

позволяет найти ток I₁исходной цепи рис. 1.11а, пользуясь законом Ома

.

Напряжение на участке R₂₃₄легко найти по закону Ома для пассивного участка цепи

U₂₃₄= I₁R₂₃₄.

Токи в ветвях R₂и R₃₄также находятся по закону Ома

.

Токи I₃= I₄, т.к. приемники R₃и R₄включены последовательно, они равны току I₃₄.

Практическая работа «Расчет сложных цепей постоянного тока методом контурных токов»

Практическая работа

«Расчет сложных цепей постоянного тока методом контурных токов»

1. Определить токи в ветвях схемы методом контурных токов.

2. Составить уравнение баланса мощностей.

рис.

Е₁, В

Е₂, В

Е₃, В

R₁, В

R₂, В

R₃, В

R₄, В

R₅, В

R₆, В

1.

рис.1.

200

100

180

10

15

10

18

25

23

2.

рис.2.

100

200

50

25

10

15

10

18

22

3.

рис.3.

120

220

200

23

25

10

15

10

18

4.

рис.4.

200

50

80

22

25

18

10

15

10

5.

рис.1.

100

200

120

23

18

25

22

10

15

6.

рис.2.

80

180

200

18

23

25

20

15

10

7.

рис.3.

200

100

80

10

18

20

15

25

22

8.

рис.4.

220

200

50

20

10

15

18

22

25

9.

рис.1.

80

180

200

20

15

10

25

18

22

10.

рис.2.

200

120

100

15

20

25

10

22

18

11.

рис.3.

50

200

220

25

15

20

22

10

18

12.

рис.4.

80

80

200

22

25

15

20

18

10

13.

рис.1.

120

180

100

22

25

18

15

10

20

14.

рис.2.

100

150

50

23

18

25

10

15

22

15.

рис.3.

220

180

80

18

22

10

25

23

15

Методика решения:

Рис.1

Дано:

Е₁=100 В; R₂=5 Ом;

Е₂=120 В; R₃=16 Ом;

Е₃=200 В; R₄=21 Ом;

R₁=4 Ом; R₅=15 Ом;

R₆=23 Ом;

1. Определить токи в ветвях схемы методом контурных токов,

2. Составить уравнение баланса мощностей.

Решение:

1. Составим уравнение для каждого контура по 2 закону Кирхгофа.

2. Подставим исходные данные в полученную систему уравнений и решим ее относительно неизвестных I_к1, I_к2, I _к3:

Главный определитель:

= 40·36·49 + (-15) · (-5) · (-21) + (-15) · (-5) · (-21) — (-21) · 36· (-21) —

— (-15) · (-15) · 49 — (-5) · (-5) ·40 = 70560-1575-1575-15876-11025-1000 = 39509

Определитель по первому неизвестному:

= 100·36·49 + (-15) · (-5) · (-120) + (-80) · (-5) · (-21) — (-21) · 36· (-120)- (-15) · (-80) ·49 — (-5) · (-5) ·100 = 176400 – 9000 – 8400 – 90720 – 58800 – 1225 = 8255

А

Определитель по второму неизвестному:

= 40· (-80) · 49 + 100· (-5) · (-21) + (-15) · (-120) · (-21) — (-21) · (-80) · (-21) — 100· (-15) · 49 — (-5) · (-120) · 40 = -156800+10500-37800+35280+73500-24000 = -99320

А=-2,51 А

Определитель по третьему неизвестному:

= 40·36·(-120) + (-15) · (-80)·(-21) + (-15)·(-5)·100 — 100·36·(-21) —

— (-15)·(-15)·(-120) — (-80)·(-5)·40 = -172800 – 25200 + 7500 + 75600 + 27000 — 16000=-103900

А=-2,63А

3.Определим реальные токи в ветвях:

I₁ = I_к1 = 0,21 A

I₂ = I_к2 — I_к3 = -2,52 — (-2,63) = 0,11 A

I₃ = I_к2 = -2,52 A (Ток I₃ направлен встречно I_к2)

I₄ = I_к1-I_к3 = 0,18 — (-2,63) = 2,81 A

I₅ = I_к1— I_к2 = 0,18 — (-2,51)=2,69 A

I₆ = I_к3 = -2,63 A (Ток I₆ направлен встречно I_к3)

4. Составим уравнение баланса мощностей:

ΣР_ИСТ=ΣР_ПОТР

ΣР_ИСТ = Е₁I₁+Е₂I₂+Е₃I₃ =100·0,21+120·0,11+200·2,52=21+13,2+504=538,2 Вт;

ΣР_ПОТР = I₁²R ₁+ I₂²R₂+ I₃²R₃+ I₄²R₄+ I₅²R₅+ I₆²R₆ = 0,21²·4 + 0,11²·5 + 2,52²·16 +

+2,81²·21+ 2,69²·15++2,63²·23 = 0,18 + 0,061+101,61 +165,82 +108,54+159,09=538,3 Вт

538,2 Вт ≈ 538,3 Вт

Таким образом, баланс мощностей выполняется.

3.Расчёт электрической цепи постоянного тока методом контурных токов.

1. Основные законы и методы расчета цепей постоянного тока.

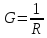, См (Сименс) проводимость

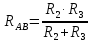
Закон Ома

IR=U (1)

Закон Ома в форме ур-я (1) справедлив для участка цеп, не сод источников ЭДС. При наличии таких источников закон Ома принимает форму: IR=U+E (2)

E – ЭДС всех источников, вкл-ных в рассматр участок цепи.

Первый закон Кирхгофа: Алгебраическая сумма сил токов, сход-ся в любой точке разветвления проводников (или в узле) равна нулю.

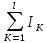=0

l- число токов, сх-ся в данном узле.

Причем токи, протекающие к узлу счит-ся +, токи вытекающие из узла –

Второй закон Кирхгофа: В любом замкнутом контуре произвольно выделяют в сложной сети проводников алгебр сумма падений напря-ий на отдеьны участках контура равна сумме ЭДС в этом контуре: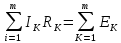

Где m – число участков в замкнутом контуре.

Основан на применении 2 закона Кирхгофа. Метод позволяет уменш число совместно решаемых уравнений до числа независимых контуров.

B – число ветвей в схеме цепи

BI – число ветвей, содержащие источники тока

Y – число узлов в схеме

Метод заключается в:

1. Выбираются независимые контуры и положительные направления контурных токов в них, каждый из которых протекает по всем элементам соответствующего контура.

Для схем, допускающих изображение на плоскости без пересечения ветвей дост условием выделением числа K незав контуров будет являться наличие в каждом из них хотя бы ветви, принадл-щей только этому контуру.

2. Для незав контуров сост-ся ур-я по по 2,3 Кирхгофа совместное решение которых опр-ет все контурные токи.

3. Ток каждой ветви опред-ся по 1,3 Кирхгофа, как алгебр сумма контурных токов соотв ветви.

К=6-0-4+1=3

В левой части уравнений коэффициент при контурном токе рассматриваемого контура положителен и равен сумме сопротивлений его ветвей. Коэффициенты при контурных токах в контурах, имеющих общие ветви с рассматриваемым контуром, равны сумме сопротивлений общих ветвей со знаком плюс (минус), если направления контурных токов в общих ветвях совпадают (противоположны).

Правая часть уравнений содержит алгебраическую сумму ЭДС ветвей рассматриваемого контура, причем слагаемое записывается со знаком плюс (минус), если направления ЭДС и положительное направление контурного тока совпадают (противоположны).

1: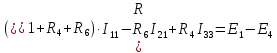

2:

3: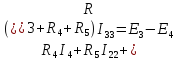

.

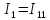
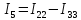
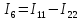5.Цепь переменного тока с активным и индуктивным сопротивлениями.

Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Рассмотрим электрическую цепь, в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток I = Im∙sinωt

Через катушку и резистор протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем строить вектор напряжения, приложенного к этой цепи. Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе.

U = UL + UR (4.17)

Напряжение на резисторе будет совпадать по фазе с током:

UR = UmR∙sinωt (4.18), а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму закону Кирхгофа).

UL = L∙ = Im∙ω∙L∙cosωt = UmL∙sin(ωt + π/2) (4.19)

Мы видим, что напряжение на индуктивности опережает ток на угол π/2. Построив векторы I, UR и UL и, воспользовавшись формулой (4.17), найдём вектор U. Векторная диаграмма показана на следующем рисунке.

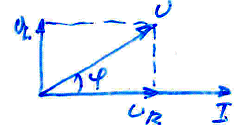
В рассматриваемой цепи ток I отстаёт по фазе от приложенного напряжения U, но не на

π / 2, как в случае с чистой индуктивностью, а на некоторый угол φ. Этот угол может принимать любые значения от 0 до π / 2 и при заданной индуктивности зависит от активного сопротивления. С увеличением R угол φ уменьшается. Как видно из диаграммы, модуль вектора U равен:

U == I∙= I∙ZL (4.20), где

ZL = (4.21) называется полным сопротивлением цепи с индуктивностью и активным сопротивлением. Сдвиг по фазе между током и напряжением в данной цепи также определяется из векторной диаграммы:

tg φ = UR / UL = ωL / R (4.22)

1.8. Расчет цепей методом контурных токов.

Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.

Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.

При расчете рекомендуется придерживаться следующей последовательности:

– выделить все независимые контуры

– указать направления обхода контуров (желательно одно и то же для всех контуров)

– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)

– для всех независимых контуров составить уравнения второго закона Кирхгофа

– решить полученную систему уравнений любым известным методом

– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.

Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E₁R₃R₁E₁и R₃E₂R₂R₃. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R₃, которая принадлежит двум контурам сразу, протекают два контурных тока I_K1и I_K2, но в противоположных направлениях.

E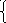₁ = I_K1 (R₁ + R₃) – I_K2R₃

– E₂= –I_K1R₃+I_K2(R₂+R₃)

Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.

Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: I_K1=7 A, I_K2= – 5 A. Тогда I₁= I_K1= 7 = 7 A и протекает в резисторе R₁так же, как контурный ток I_K1по схеме сверху вниз. Ток I₂= – I_K2= – 5 А и протекает в резисторе R₂по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R₃ , цепи представленной на рис. 1.10, протекают контурный ток I_K1= 7 А по схеме сверху вниз и контурный ток I₂= – 5 А по схеме снизу вверх. I_K1> I_K2и I₃= I_K1– I_K2= 7 – (–5) = 12 А. Ток I₃имеет такое же направление, что и ток I_K1 , т.е. по схеме сверху вниз.

1.9. Расчет цепей методом эквивалентного преобразования.

Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.

По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.

Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)

Например, в цепи представленной на рис. 1.11а приемники R₃и R₄соединены последовательно и их можно заменить одним эквивалентным с сопротивлением

R₃₄= R₃+ R₄.

После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R₂ и эквивалентный приемник R₃₄включены параллельно. Параллельный участок R₂– R₃₄также можно заменить одним эквивалентным с сопротивлением

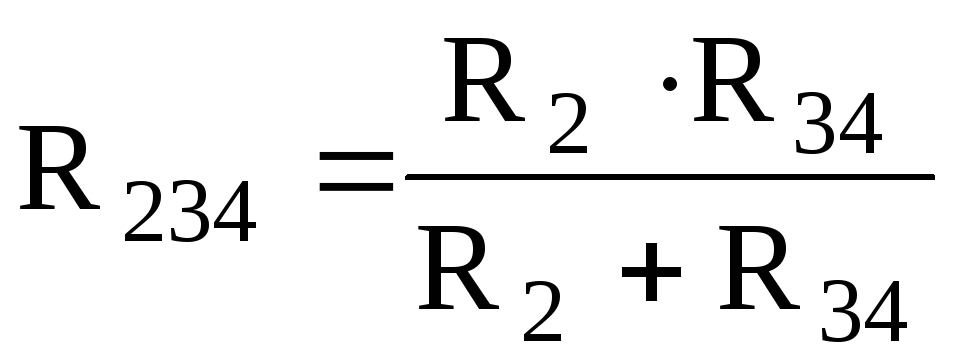
после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.

Входное сопротивление этой цепи R₁₂₃₄= R₁+ R₂₃₄

позволяет найти ток I₁исходной цепи рис. 1.11а, пользуясь законом Ома

.

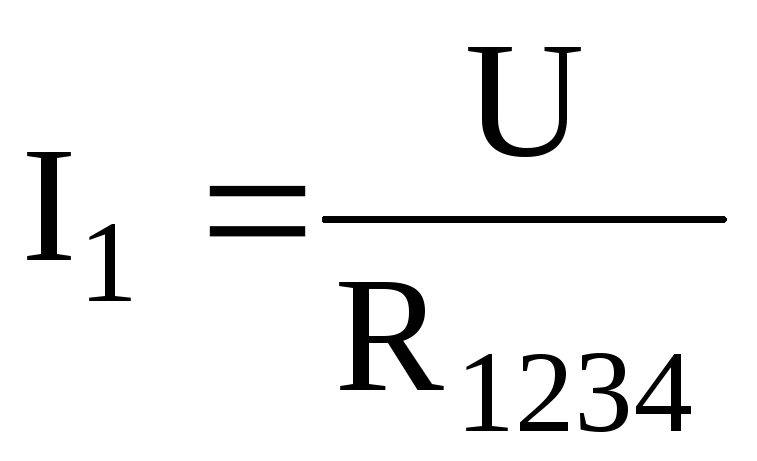Напряжение на участке R₂₃₄легко найти по закону Ома для пассивного участка цепи

U₂₃₄= I₁R₂₃₄.

Токи в ветвях R₂и R₃₄также находятся по закону Ома

.

Токи I₃= I₄, т.к. приемники R₃и R₄включены последовательно, они равны току I₃₄.

2. Расчет линейных электрических цепей постоянного тока методом контурных (фиктивных) токов

Данный метод базируется на законах Кирхгофа и наиболее удобен при расчетах электрических цепей, где число независимых контуров меньше числа электрических узлов.

При решении задач предполагается, что в независимых контурах электрической цепи протекают свои контурные токи, которые будем в дальнейшем обозначать для первого, второго и т.д. контуров соответственно I₁₁, I₂₂ и т.д.

Затем составляются линейные уравнения относительно выбранных неизвестных контурных (фиктивных) токов, согласно второму закону Кирхгофа. Количество составленных независимых линейных уравнений должно соответствовать количеству неизвестных контурных токов. Решая полученную систему уравнений относительно неизвестных контурных токов, определяем неизвестные (реальные) токи I₁, I₂ и т.д.

Применение метода контурных токов рассмотрим на конкретном числовом примере.

Пример №12.

Дано: Е₁=150 В, Е₂=50 В, Е₃=120 В, Е₄=20 В, Е₅=150 В, R₁=9 Ом, R₂=4 Ом, R₃=7 Ом, R₄=1 Ом, R₅=3 Ом, R₆=3 Ом, R₇=2 Ом. (Рис. 14)

О

E₂

R₄

R₁

пределить: токи в цепи, построить потенциальную диаграмму для внешнего контура.

Е₁

R₁

R₆

R₇

I₁₁

I₂₂

I₁

I₂

I₃

1

2

3

4

5

6

7

8

9

10

11

E₃

E₅

R₂

E₄

R₃

R₅

Рис. 14.

Решение.

Направим произвольным образом реальные неизвестные токи I₁, I₂, I₃. Поскольку в расчетной схеме два независимых контура (1,11,10,2,3,4,5,6,1) и (1,7,8,9,2,10,11,1), то контурных токов должно быть тоже два, соответственно I₁₁, I₂₂. Выберем произвольным образом направление контурных токов, например, по часовой стрелке (см. рис. 14).

Составим два линейных уравнения относительно неизвестных контурных токов I₁₁, I₂₂, используя второй закон Кирхгофа.

Вначале определяем все падения напряжения в первом контуре от протекающего в нем контурного тока I₁₁ со знаком «+»:

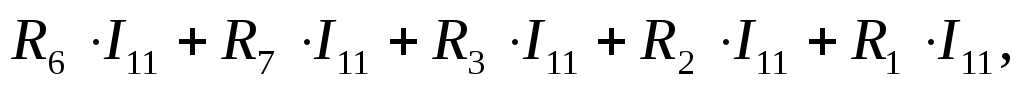
а затем все падения напряжения от контурного тока I₂₂, протекающего через участок 2,10,11,1 этого же контура, но со знаком «-»: , так как контурные токиI₁₁ и I₂₂ на резисторах R₆ и R₇ направлены относительно друг друга в противоположные стороны.

Таким же образом определяются падения напряжения для второго контура.

Следовательно:

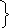
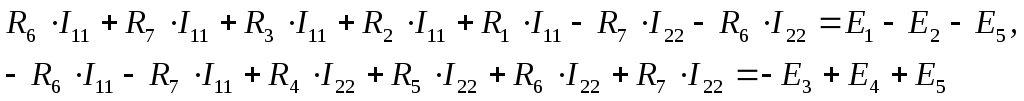
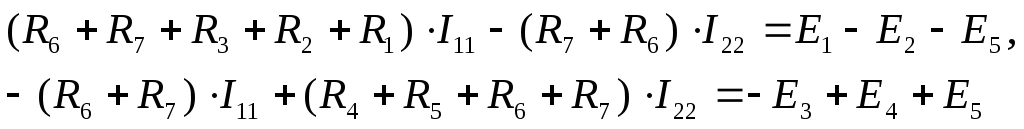
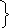
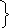
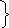
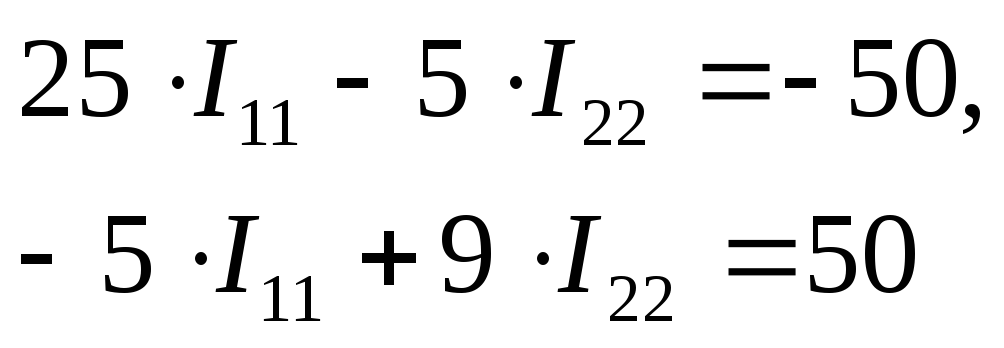
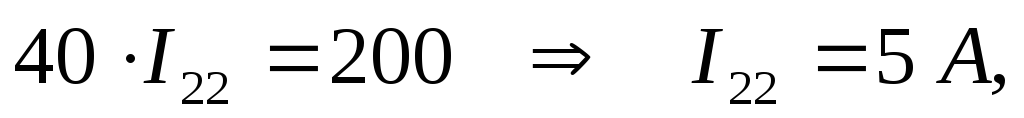
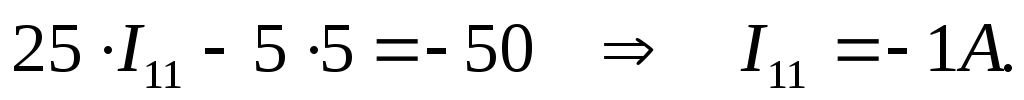
Согласно данному методу величина и направление выбранных контурных токов I₁₁ и I₂₂ соответствует искомым физическим токам соответственно I₁ и I₂ (см. рис. 14).

Следовательно, I₁= I₁₁=-1 А, а I₂=I₂₂=5 А.

Знак «-» тока I₁ означает, что истинное направление тока должно быть противоположно рассчитанному. На схеме истинное направление тока I₁ показано пунктиром.

Ток I₃ определим по первому закону Кирхгофа для узла 1:

Правильность проведенных расчетов проверим по балансу мощностей:

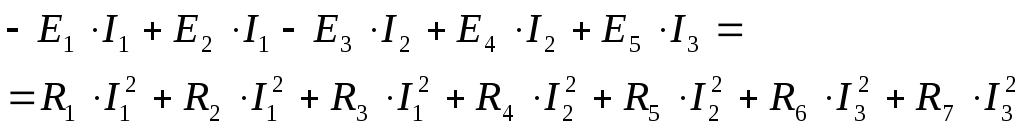
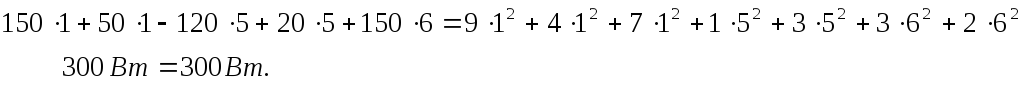
Построим потенциальную диаграмму для замкнутого контура 3456178923 .

Пусть потенциал φ₃=0, тогда φ₄= φ₃+R₂ ·I₁ = 0+4·1=4 В,

φ₅= φ₄+Е₁ = 4+150=154 В,

φ₆= φ₅+R₁ ·I₁ = 154+9·1=163 В,

φ₁= φ₆ – Е₂ = 163 – 50=113 В,

φ₇= φ₁ – R₄ ·I₂ = 113 – 1·5=108 В,

φ₈= φ₇ – Е₃ = 108 – 120= –12 В,

φ₉= φ₈ – R₅ ·I₂ = –12 – 3·5= –27 В,

φ₂= φ₉+Е₄ = –27+20= –7 В,

φ₃= φ₂+R₃ ·I₁ = –7+7·1=0 В.

Графически потенциальная диаграмма выглядит следующим образом (рис. 15):

В 

163

₆

154

₅

140

120

₁

₇

113

100

108

80

60

40

20

R

Ом

₄

R₂

R₃

R₄

R₅

R₁

₃

4

₃

0

-7

24

17

13

14

4

-12

₂

₈

-27

₉

В, (-  )

Рис. 15