Методы расчета электрических цепей при постоянных токах и напряжениях
Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряженияхОсновными законами электрического состояния любой цепи являются законы Ома и Кирхгофа, Если цепь содержит один активный элемент (источник электрической энергии), то, в ряде случаев, расчет исходной схемы наиболее рационально вести с помощью метода преобразований и формулы «разброса». При этом нужно помнить, что во всех преобразованиях замена одних схем другими, им эквивалентными, не должна приводить к изменению токов или напряжений на участках цепи, которые не подверглись преобразованиям (замена последовательно или параллельно соединенных сопротивлений эквивалентными, преобразование треугольника сопротивлений в звезду, или наоборот). Для быстрого и правильного расчета электрических цепей с помощью законов Кирхгофа необходимо приобрести навыки в составлении уравнений на основании этих законов.
Линейную электрическую цепь любого вида можно также рассчитать методом контурных токов или методом узловых потенциалов. Если число взаимно независимых контуров nк и число узлов nу схемы связаны между собой неравенством nк < nу, то для расчета такой цепи пользуются методом контурных токов. В случаях, когда выполняется неравенство nк > nу, для расчета цепей рекомендуется применять метод узловых потенциалов.
Расчет линейных электрических цепей можно значительно упростить с помощью принципа наложения
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.1 Методы анализа, основанные на законах Ома и Кирхгофа
1.2 Метод наложения
1.3 Метод контурных токов
1.4
1.5 Метод эквивалентного генератора (источника ЭДС)
1.6 Методы расчета нелинейных электрических цепей постоянного тока
Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях
1 2 Ctrl →
RSSЭлектрические цепи постоянного тока и методы их расчета
1.1. Электрическая цепь и ее элементы
Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.
Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 1.1.
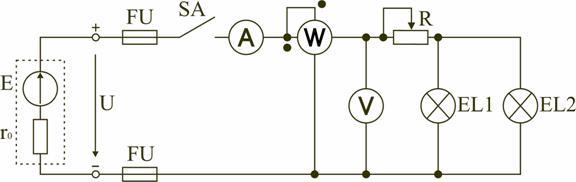
Рис. 1.1
Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы:
1) Источники электрической энергии (питания).
Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).
2) Потребители электрической энергии.
Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой.
3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.
Все элементы цепи охвачены одним электромагнитным процессом.
В электрической схеме на рис. 1.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r0, с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL1 и EL2.
1.2. Основные понятия и определения для электрической цепи
Для
расчета и анализа реальная электрическая
цепь представляется графически в виде
расчетной электрической схемы (схемы
замещения). В этой схеме реальные элементы
цепи изображаются условными обозначениями,
причем вспомогательные элементы цепи
обычно не изображаются, а если сопротивление
соединительных проводов намного меньше
сопротивления других элементов цепи,
его не учитывают. Источник питания
показывается как источник ЭДС E с
внутренним сопротивлением r
При этих условиях схема на рис. 1.1 может быть представлена в виде расчетной электрической схемы (рис. 1.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r0
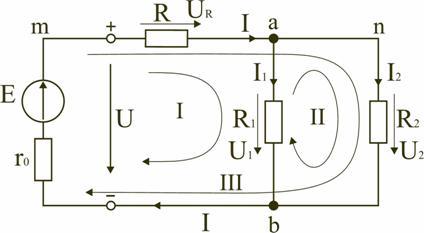
Рис. 1.2
Источник ЭДС на электрической схеме (рис. 1.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.
При расчете в схеме электрической цепи выделяют несколько основных элементов.
Ветвь
электрической цепи (схемы) – участок
цепи с одним и тем же током. Ветвь может
состоять из одного или нескольких
последовательно соединенных элементов.
Схема на рис. 1.2 имеет три ветви: ветвь
bma, в которую включены элементы r
Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R1 и R2 (рис. 1.2) находятся в параллельных ветвях.
Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.
Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.2) стрелками укажем положительные направления ЭДС, напряжений и токов:
а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;
б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;
в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.
Все электрические цепи делятся на линейные и нелинейные.
Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.
Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.
Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.
Расчет линейных электрических цепей постоянного тока
Расчет неразветвленных цепей
Основой расчета одноконтурных (неразветвленных) электрических цепей, содержащих источники обоих видов и потребители, служат рассмотренные ранее законы Ома и Кирхгофа.
Если в цепи нет источников тока, а параметры потребителей (R) и источников напряжения (Е) заданы, то задача обычно состоит в определении тока контура. Положительное направление искомого тока выбирается произвольно и составляется уравнение:
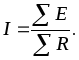 (2.1)
(2.1)
При этом необходимо помнить, что со знаком «+» берутся ЭДС источников, которые действуют в направлении выбранного тока. Истинное направление совпадает с выбранным, если в результате расчета ток оказывается положительной величиной, и противоположно выбранному, если ток оказывается отрицательным.
Если в цепи, кроме
потребителе (R)
и источников ЭДС (E),
имеется источник тока (J),
то задача обычно сводится к определению
напряжения на источнике тока UJ,
т.к. ток контура I совпадает
с заданным током источника J. Положительная полярность UJ выбирается
произвольно, но предпочтительно у острия
стрелки ставить знак «+» (такой полярности
соответствует формула: 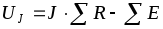 ).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле
).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле 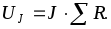 .
.
Расчет разветвленных цепей с одним источником
Разветвленную цепь с одним источником обычно упрощают, преобразуя в неразветвленную (рис. 2.1.), и решают методами, изложенными выше. Основная проблема состоит в нахождении токов и напряжений ветвей исходной схемы, поскольку в результате преобразования такие ветви не сохраняются.
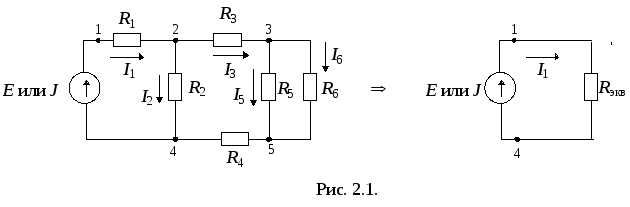
Для определения токов и напряжений в схеме рис. 2.1. сначала определяется Rэкв смешанного соединения потребителей относительно зажимов источника (точки 1 и 4 на рис. 2.1.). Затем, если цепь питается источником напряжения, то определяется ток по формуле:
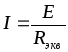
Если цепь питается источником тока, то определяется напряжение
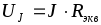
Порядок дальнейшего расчета одинаков для обоих случаев, т.к. известны E или UJ и I или J неразветвленной части схемы. Рассмотрим порядок расчета для представленной на рис. 2.1 цепи.
Ток в потребителе R1 совпадает с найденным током неразветвленной
части I, а напряжение 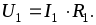
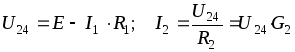 .
.
Ток I3 определяется
по закону Кирхгофа: 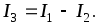
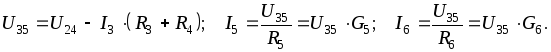
Указанный прием используется и в тех случаях, когда для упрощения цепи приходится прибегать к преобразованию «треугольник звезда» или «звезда треугольник». Недостаток заключается в том, что цепь приходится рассчитывать дважды – преобразованную и исходную.
При расчетах удобно
пользоваться формулой
о токах в двух параллельных пассивных ветвях.
Выведем ее на примере схемы рис. 2.1.
Напряжение 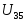 по закону Ома определяется по формуле
по закону Ома определяется по формуле
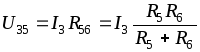
Тогда ток 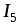 можно определить
можно определить
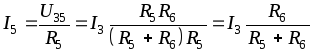 (2.2)
(2.2)
Аналогично можно определить ток
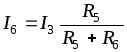 (2.3)
(2.3)
Таким образом, ток в одной из двух параллельных ветвей равен току неразветвленной части (общей ветви), умноженному на сопротивление противоположной ветви, деленному на сумму сопротивлений обеих ветвей.
Известен еще один метод расчета таких цепей – метод пропорциональных величин. Он применим к «удлиненным» цепям (цепным соединениям).
Суть этого метода
состоит в следующем: в ветви наиболее
удаленной от источника (R6)
задаются
некоторым значением тока или напряжения.
Для удобства расчетов обычно это 1А или
1В. Затем перемещаясь к началу цепи
определяют поочередно токи и напряжения
всех ветвей вплоть до ветви, содержащей
источник. Тем самым определяют какие
напряжение Uвх и ток Iвх. должен
иметь источник для того, чтобы вызвать
во всех ветвях токи и напряжения
вычисленных значений. Если ЭДС (Е)
или задающий ток (J)
с этими значениями не совпадают, то
необходимо пропорционально изменить
вычисленные значения токов и напряжений
ветвей путем умножениях их на отношение 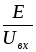 или
или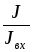 .
.
Для схемы на рис.
2.1. пусть I6 =
1. Тогда 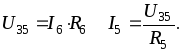
I3 можно
определить по I
закону Кирхгофа: 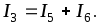
U24 определяем по II
закону Кирхгофа: 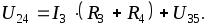
По закону Ома: 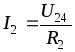 ,
поI
закону
Кирхгофа:
,
поI
закону
Кирхгофа: 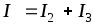 .
.
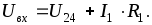
Коэффициент
пересчета определяется следующим
образом: 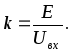 Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
Расчет цепей переменного тока
Расчет электрических цепей переменного синусоидального тока производится в комплексной форме. При этом величины синусоидальных ЭДС и токов представляются в виде комплексных амплитуд или комплексных действующих значений, а все элементы в схеме – в виде комплексных сопротивлений.
Например,
если ЭДС источника равна 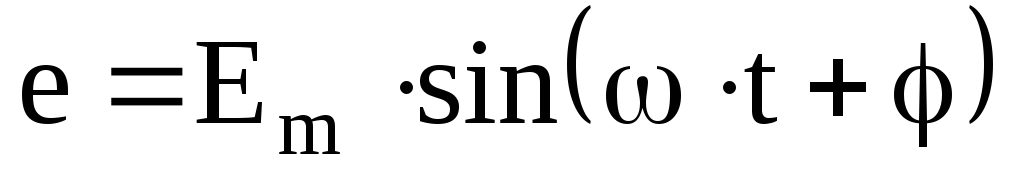 ,
то комплексная амплитуда запишется в
виде
,
то комплексная амплитуда запишется в
виде — в показательной форме записи, или
— в показательной форме записи, или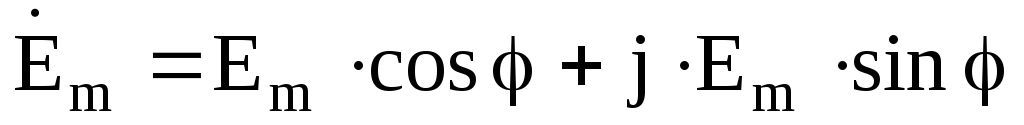 — в алгебраической форме. Комплексное
действующее значение синусоидальной
ЭДС:
— в алгебраической форме. Комплексное
действующее значение синусоидальной
ЭДС: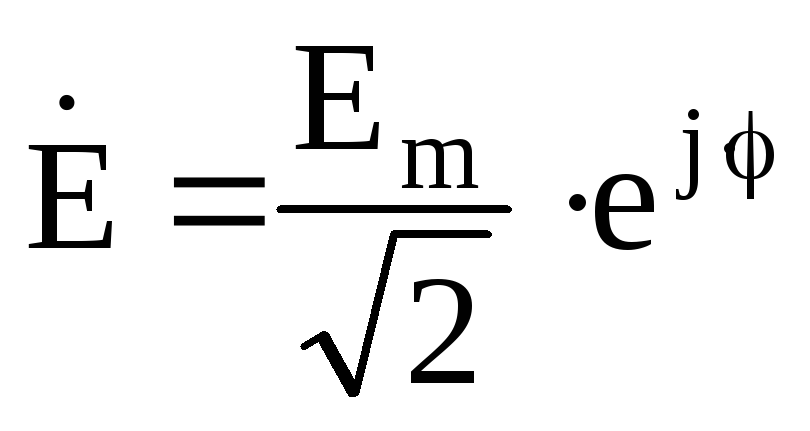 — в показательной форме записи, или
— в показательной форме записи, или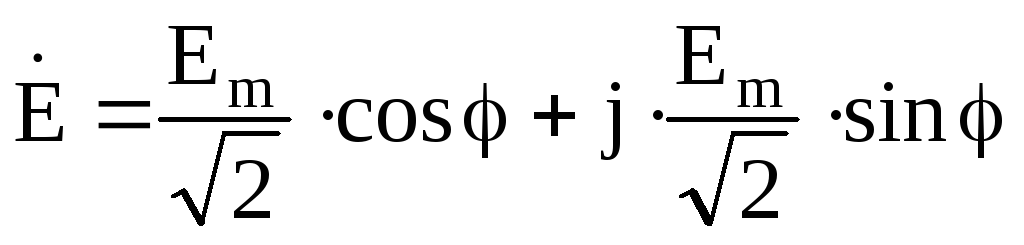 — в алгебраической форме.
— в алгебраической форме.
Комплексные сопротивления элементов электрической цепи переменного тока:
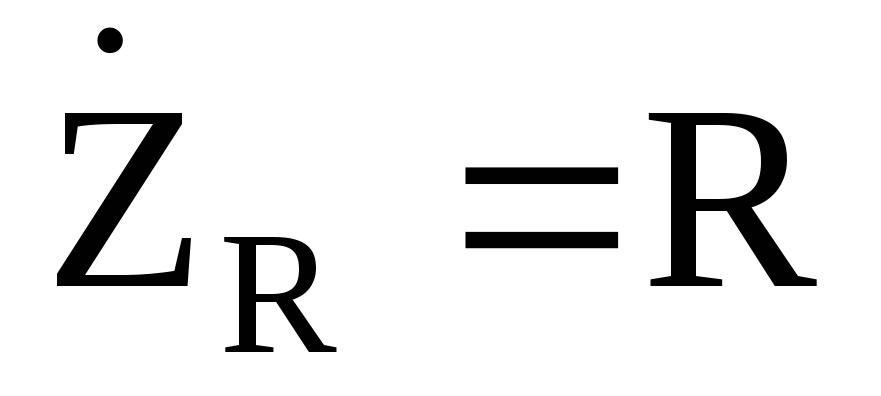 — для идеального сопротивления,
— для идеального сопротивления,
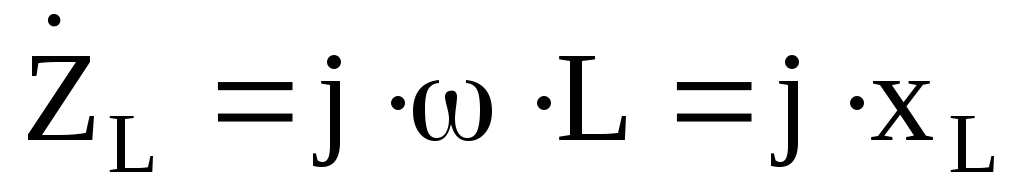 — для идеальной индуктивности,
— для идеальной индуктивности,
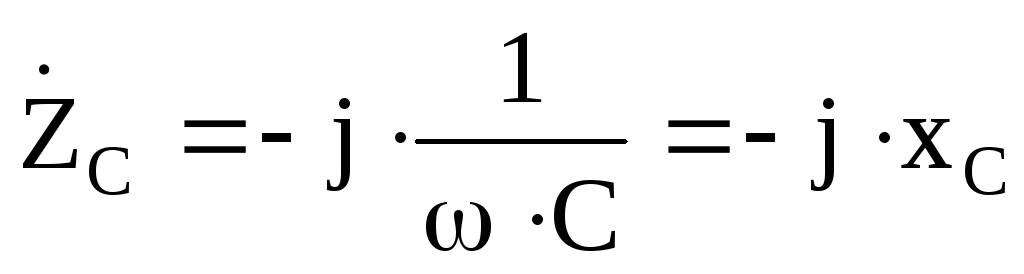 — для идеальной емкости.
— для идеальной емкости.
Далее расчет электрической цепи переменного тока можно вести любым методом, известным из раздела – «электрические цепи постоянного тока». При этом используется математический аппарат, разработанный для операций с комплексными числами.
Применяются три формы записи комплексного значения синусоидальной величины:
 — показательная форма,
— показательная форма,
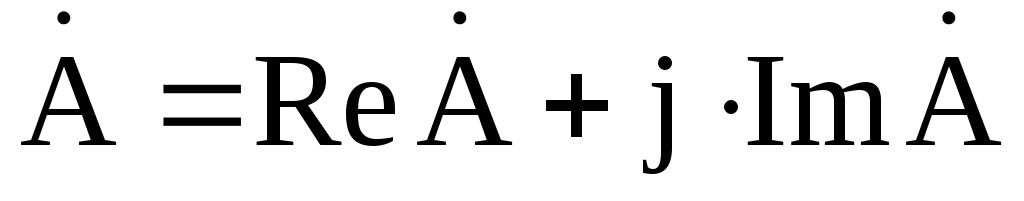 — алгебраическая форма,
— алгебраическая форма,
где 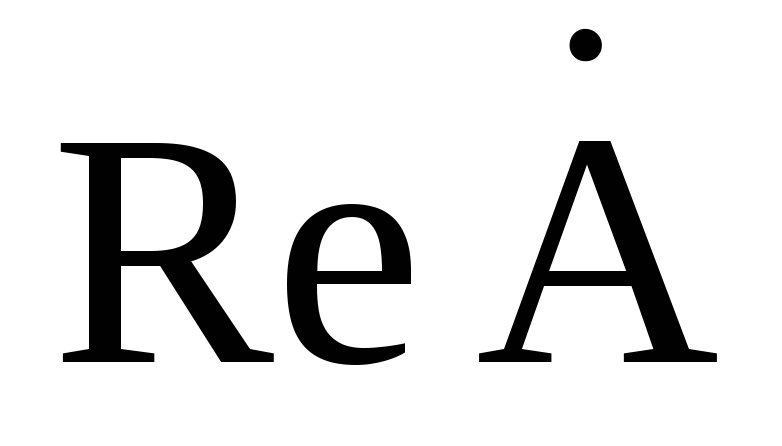 и
и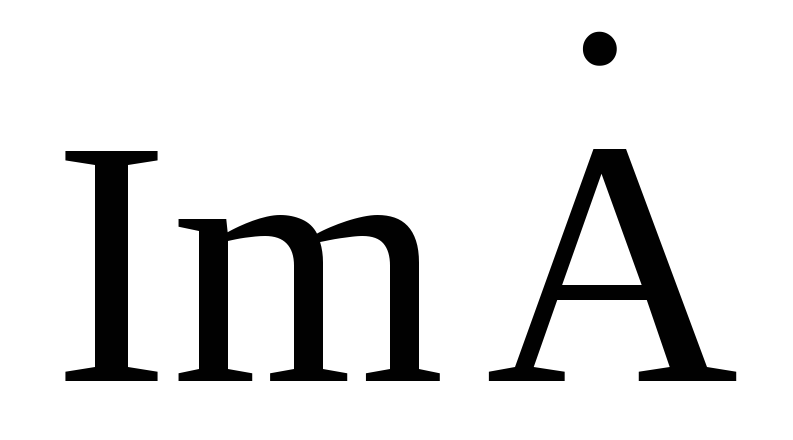 — действительная и мнимая часть
комплексного значения синусоидальной
величины. Переход от алгебраической
формы к показательной осуществляется
по формулам:
— действительная и мнимая часть
комплексного значения синусоидальной
величины. Переход от алгебраической
формы к показательной осуществляется
по формулам:
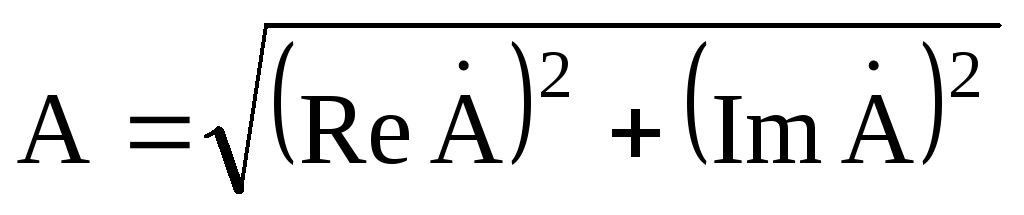 ;
;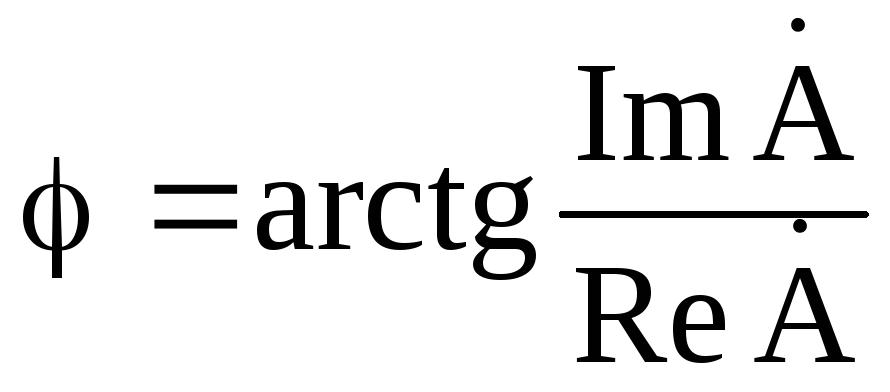 .
.
Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:
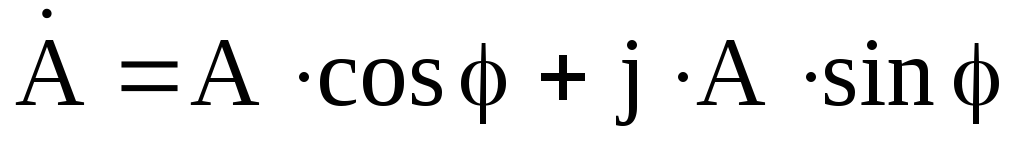 .
.
Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной.
При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.
Расчет однофазных цепей
Р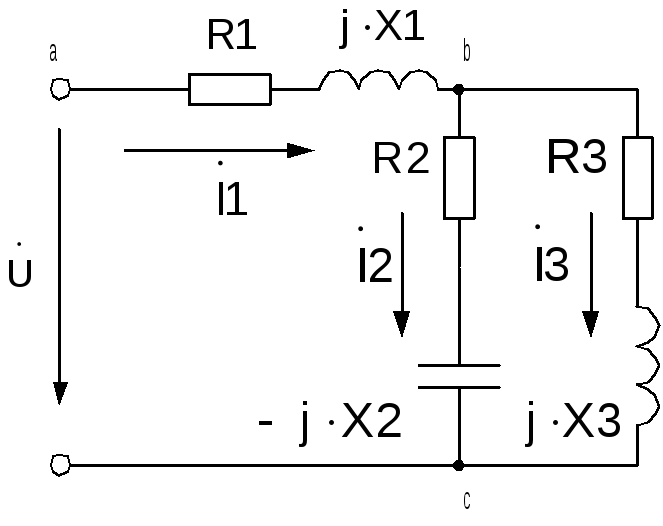 асчет
однофазных цепей переменного тока при
наличии одного источника синусоидальной
ЭДС производится методом эквивалентных
преобразований. Рассмотрим пример
расчета однофазной цепи приведенной
на рис.
асчет
однофазных цепей переменного тока при
наличии одного источника синусоидальной
ЭДС производится методом эквивалентных
преобразований. Рассмотрим пример
расчета однофазной цепи приведенной
на рис.
Рис. 2.4. Схема электрической цепи к примеру расчета
Пример расчета однофазной цепи
По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей. Исходные данные для расчета приведены в таблице.
U, В | R1, Ом | R2, Ом | R3, Ом | X1, Ом | X2, Ом | X3, Ом |
100 | 50 | 100 | 100 | 50 | 50 | 100 |
Решение:
Электрическая
цепь на рис. 2.4 состоит из трех ветвей,
определим комплексные сопротивления
ветвей. Сопротивление первой ветви,
состоящей из сопротивления R1
и идеальной катушки индуктивности с
комплексным сопротивлением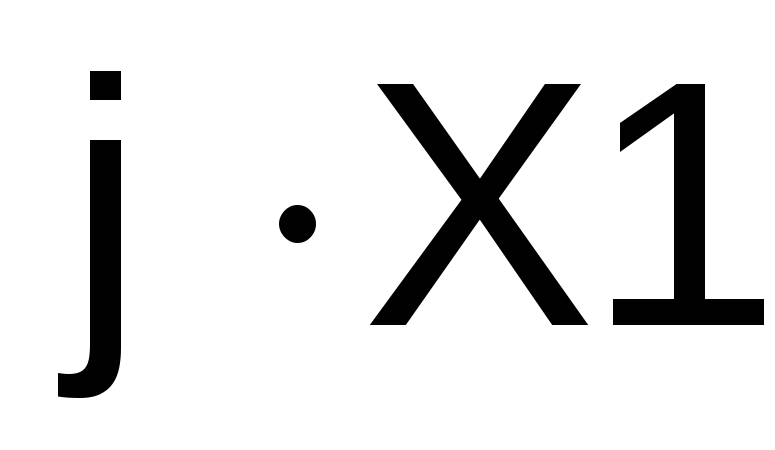 :
:
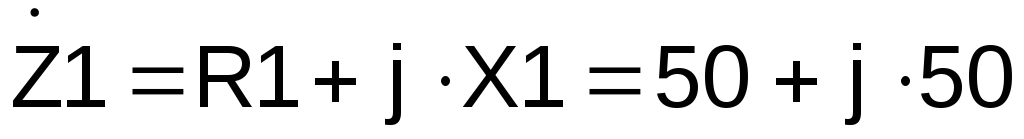 Ом.
Ом.
Сопротивление
второй ветви, состоящей из сопротивления
R2 и идеальной емкости с
комплексным сопротивлением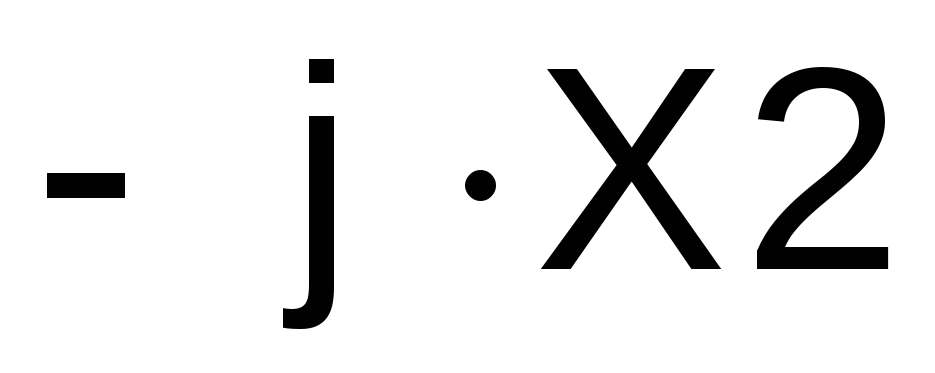 :
:
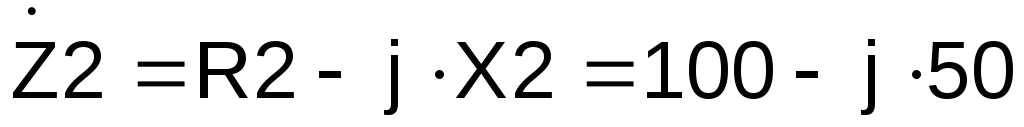 Ом.
Ом.
Сопротивление
третьей ветви, состоящей из сопротивления
R3 и идеальной катушки
индуктивности с комплексным сопротивлением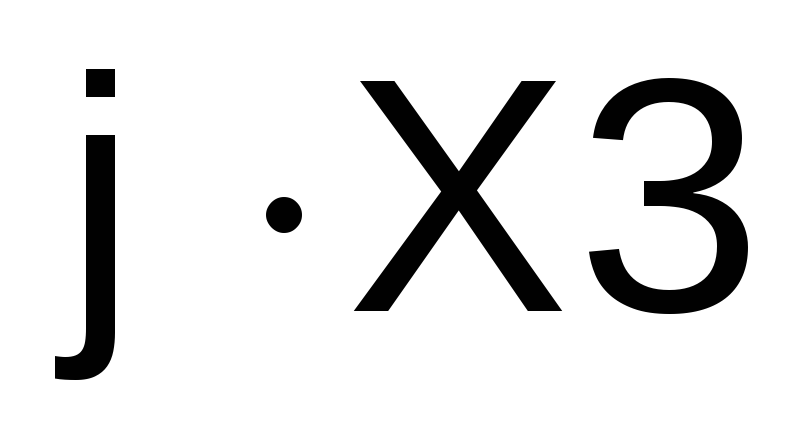 :
:
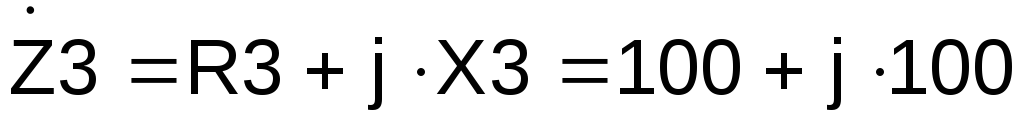 Ом.
Ом.
Вторая и третья ветвь соединены параллельно, поэтому их эквивалентное сопротивление
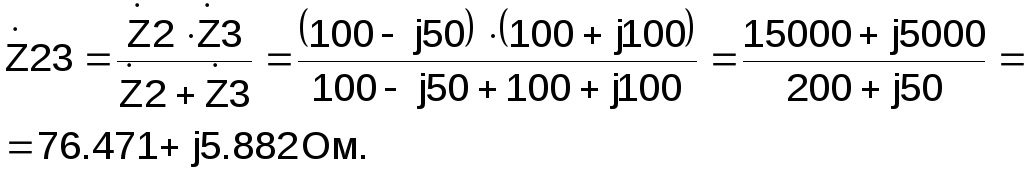
Эквивалентное сопротивление всей схемы:
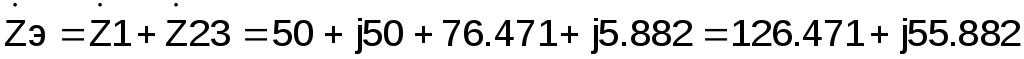 Ом.
Ом.
Зная эквивалентное сопротивление, можно определить ток в первой ветви:
 А.
А.
Затем можно определить напряжения на участках цепи:
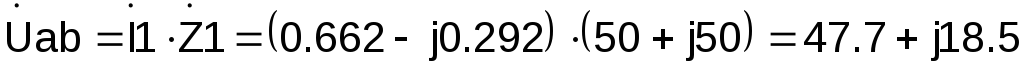 В,
В,
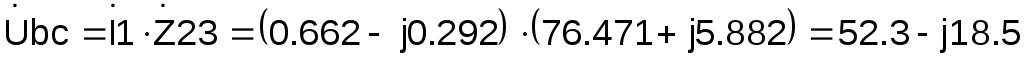 В.
В.
Зная напряжение на участке bc можно рассчитать токи
 А,
А,
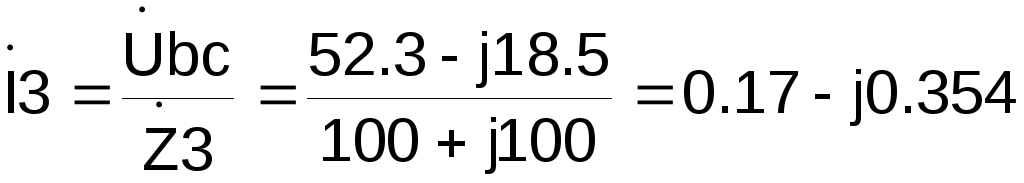 А.
А.
Проверку правильности расчета токов можно выполнить по первому закону Кирхгофа в комплексной форме:
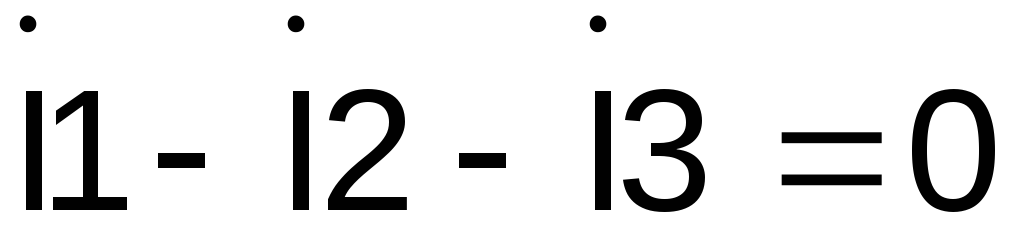 ,
или
,
или
 .
.
Так как первый закон Кирхгофа выполняется, значит, расчет токов выполнен верно.
Комплекс полной мощности:
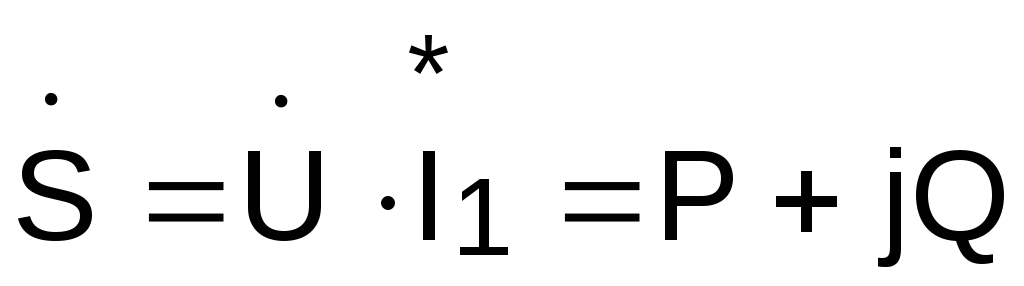 ,
,
где 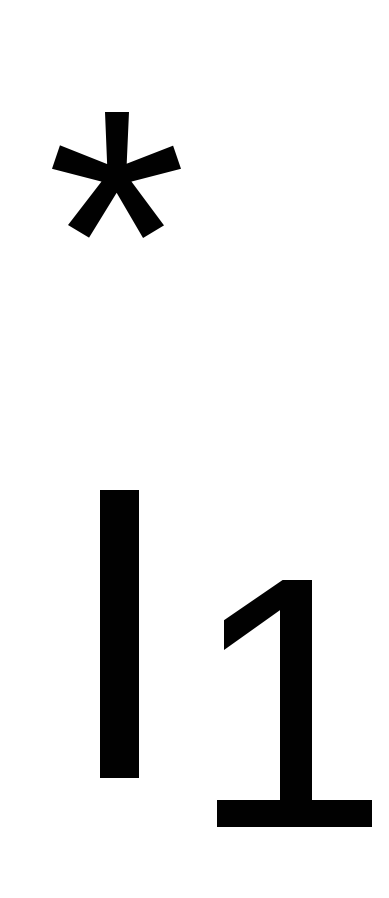 —
сопряженный комплекс тока
—
сопряженный комплекс тока .
Если
.
Если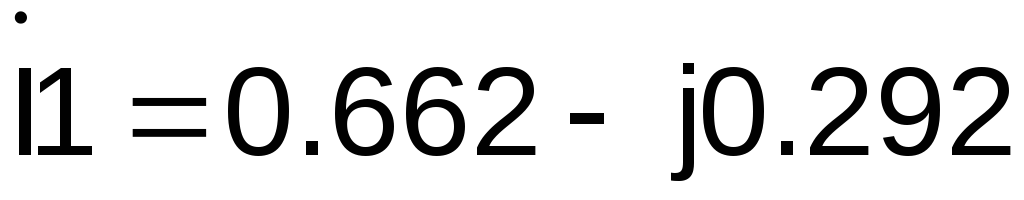 А, то сопряженный комплексА.
Таким образом, комплекс полной мощности
равен
А, то сопряженный комплексА.
Таким образом, комплекс полной мощности
равен
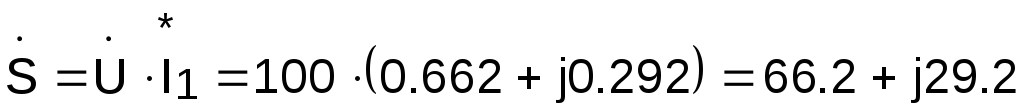 ВА.
ВА.
При этом действительная часть комплекса полной мощности равна активной мощности потребляемой схемой
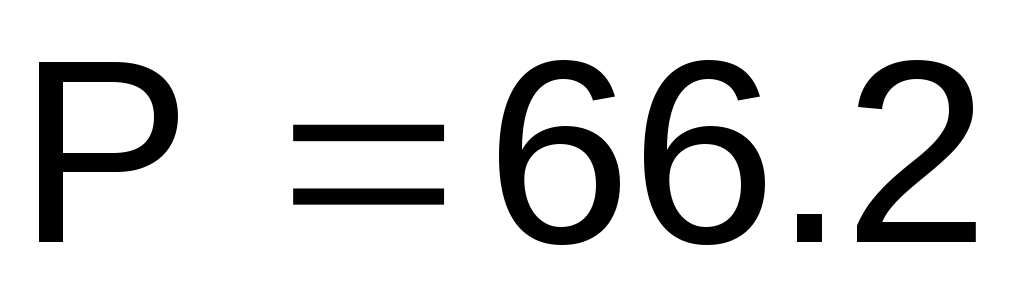 Вт,
Вт,
а мнимая часть комплекса полной мощности равна реактивной мощности схемы
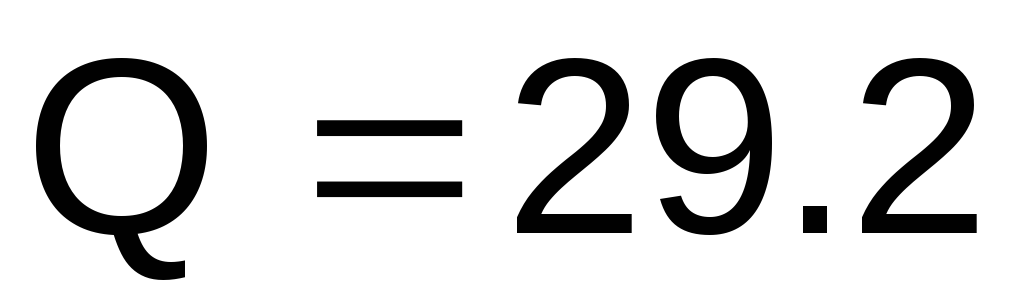 ВА.
ВА.
В екторная
диаграмма токов и напряжений строиться
на комплексной плоскости по координатам,
полученным при расчете в комплексной
форме. Токи и напряжения строятся в
одних координатных осях, но для них
выбираются разные масштабы. Диаграмма
для рассчитанной схемы показана на рис.
2.5.
екторная
диаграмма токов и напряжений строиться
на комплексной плоскости по координатам,
полученным при расчете в комплексной
форме. Токи и напряжения строятся в
одних координатных осях, но для них
выбираются разные масштабы. Диаграмма
для рассчитанной схемы показана на рис.
2.5.
Рис. 2.5. Векторная диаграмма токов и напряжений
Выражения для мгновенных значений токов можно получить из комплексных значений записанных в показательной форме:
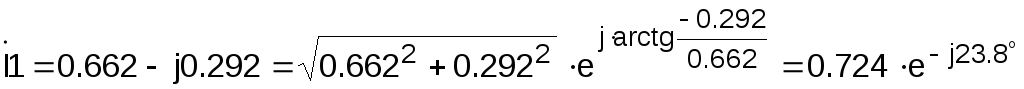 А.
А.
Действующее
значение тока I1 = 0.724 А, а
фазовый сдвиг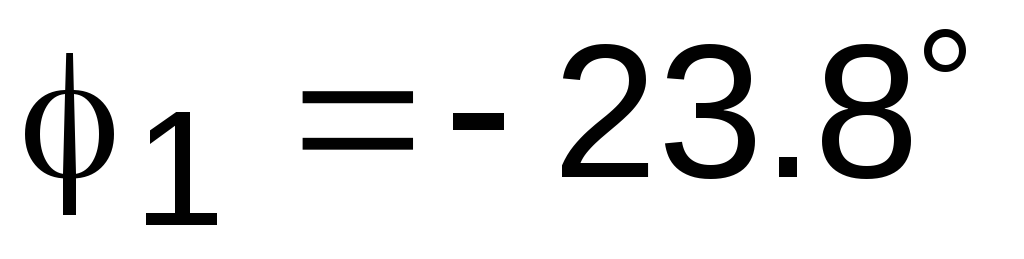 ,
таким образом мгновенное значение тока
равно
,
таким образом мгновенное значение тока
равно
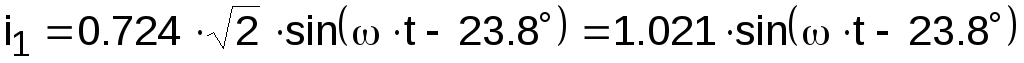 А.
А.
Аналогично для остальных токов:
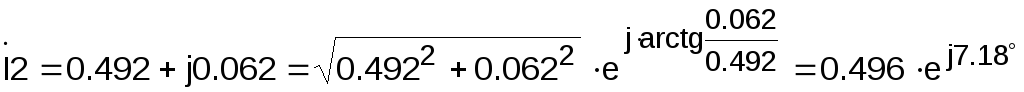 А.
А.
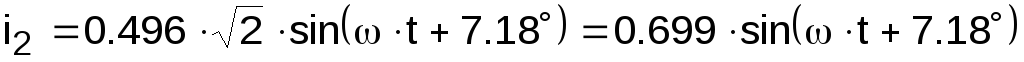 А.
А.
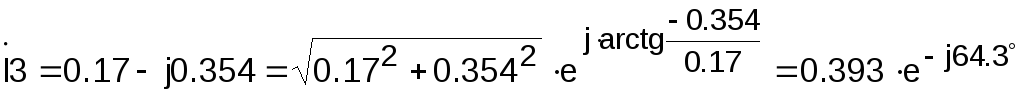 А.
А.
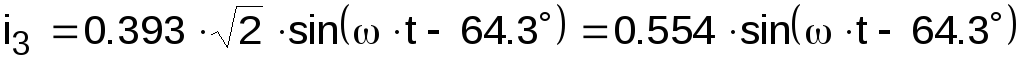
 А.
А.
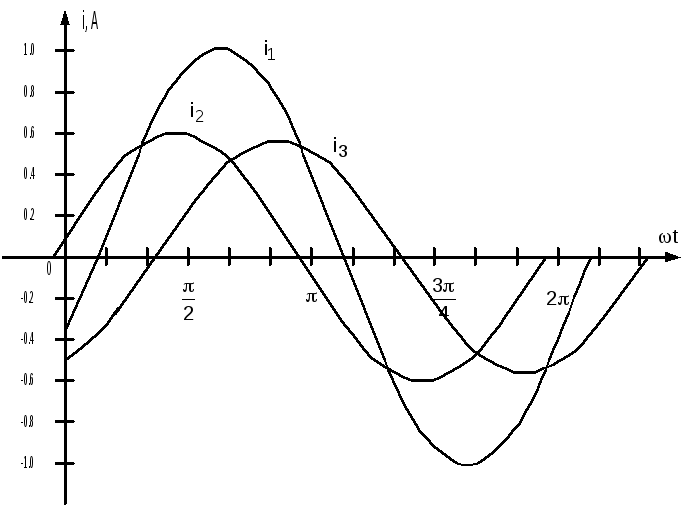
Графики мгновенных значений токов приведены на рис. 2.6.
Рис. 2.6. Мгновенные значения токов



