Радиус — Википедия

Материал из Википедии — свободной энциклопедии

Радиус окружности обозначен красным цветом

Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или сфере), а также длина этого отрезка. Радиус составляет половину диаметра.

Слово «радиус» впервые встречается в 1569 г. у французского учёного П. Ромуса, несколько позже у Ф. Виета. Становится общепринятым лишь в конце XVII века. Происходит от лат. radius, означающего «луч, спица колеса».

Радиусом множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y))/2{\displaystyle (\sup _{x,y\in M}\rho (x,y))/2}. Например, радиус n-размерного гиперкуба со стороной s равен

r=s2n.{\displaystyle r={\frac {s}{2}}{\sqrt {n}}.}

В чем измеряется диаметр в системе СИ

Все расстояния в системе си в метрах.

В метрической системе .

Проскакала на майданах и спрашиваешь почему сало сало

В тех же, что и радиус.

Окружность, радиус, диаметр, число Пи, сектор, касательная

Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.

Центр окръжности

Радиус: расстояние от центра окружности до его границы.

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.

$d = 2\cdot r$

Периметр (длина окружности): длина границы окружности.

Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$

---

$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.

Дуга: изогнутая линия, которая является частью окружности.

Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ — четверть круга,
180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$

Хорда: отрезок прямой, соединяющей две точки на окружности.

Сектор: похож на часть пирога (клин).

Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.

Формулы

Длина окружности $=\pi \cdot \text{диаметр} = 2\cdot \pi \cdot \text{радиус}$

Площадь круга

$= \pi \cdot$ радиус²

Радиус обозначается как r, диаметр как d, длина окружности как P и площадь как S.

$P = \pi \cdot d = 2\cdot \pi \cdot r$
$S = \pi \cdot r^2$

Площадь сектора круга

Площадь сектора круга K: (с центральным углом $\theta$ и радиусом $r$).
Если угол $\theta$ в градусах, тогда площадь = $\frac{\theta}{360} \pi r^2$
Если угол $\theta$ в радианах, тогда площадь, тогда площадь = $\frac{\theta}{2} r^2$

Углы

Центральный угол

Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).

Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:

$\theta = 360 \cdot \frac{l}{P} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r}$

$l$ — длина дуги.

Вписанный угол

Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.

Величина вписанного угла равна половине дуги, на которую он опирается.

Пример:
$\widehat{AB} = 84^\circ$
$\angle APB = \frac{84}{2} = 42^\circ$

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$

Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

$\angle ABC =\frac{1}{2}(x — y)$

На рисунке дуга AB=80° и дуги CD=30°.
$\angle ABC = \frac{1}{2}(80 — 30) = \frac{1}{2} \cdot 50 = 25^\circ$

Хорды

Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:

$AX \cdot XB = CX \cdot XD$

Диаметр — Википедия

Материал из Википедии — свободной энциклопедии

Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символы со сходным начертанием: Ø · ø · ∅

Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. В Word работает ALT+8960. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.

Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.

Сопряжённые диаметры эллипса и гиперболы[править | править код]

Сопряжённые диаметры эллипса[править | править код]

Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм

• Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).

• Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
• Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле r=abb2cos2⁡φ+a2sin2⁡φ=b1−e2cos2⁡φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиус-вектором данной точки и осью абсцисс.

Сопряжённые диаметры гиперболы[править | править код]

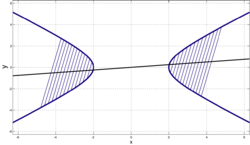Диаметры гиперболы

• Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
• Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением

k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}

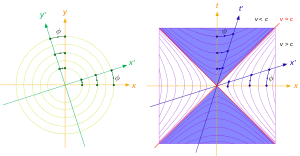
Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.

• Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
• Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
• В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.

Диаметром множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y)){\displaystyle (\sup _{x,y\in M}\rho (x,y))}.

Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.

• В частности:
  • Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
  • Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние измеренное в количестве рёбер между двумя вершинами графа, максимально удалёнными друг от друга.
  • Максимальное расстояние Хэмминга между двумя словами равной в символах длины n{\displaystyle n} равно n{\displaystyle n}, другими словами диаметр множества слов в метрике Хэмминга равен n{\displaystyle n}.
  • Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.

Например, диаметр n-размерного гиперкуба со стороной s равен

d=s⋅n{\displaystyle d=s\cdot {\sqrt {n}}}.

Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре[править | править код]

Что такое диаметр, радиус и как измерить окружность

Начнём по порядку. Диаметр это длина отрезка, проходящего через центр окружности и соединяющего две точки окружности. Радиус это длина отрезка соединяющего центр окружности с любой точкой окружности. Измерить окружность легко. Проводятся две касательные, к измеряемой окружности, прямые. В зависимости от масштаба и для достижения наибольшей точности, предпочтительно, чтобы угол между этими касательными был около 90 градусов (поймёте с опытом). Затем, через точки касания, проводятся нормали (линии, перпендикулярные касательным). Точка пересечения этих нормалей и есть центр измеряемой окружности. Затем, например линейкой, измеряем радиус и (или) диаметр. Затем можно вычислить периметр окружности, умножив диаметр на Пи (примерно равно 3,14159) или радиус умножить на 2Пи… Теперь о других ответах. Круг это не окружность, так как он имеет площадь. Окружность же её не имеет, так как это линия! И штангенциркулем не измеряется ни окружность, ни круг! Из похожего на окружность и на круг штангенциркулем измеряется диаметры цилиндрических поверхностей, как наружных, так и внутренних…

Рано тебе еще это знать, вот перейдешь в 4 класс тогда и поймешь

Круг=2 радиусам, измеряется штангенциркулем

В чём измеряется длина дуги окружности?

Смотря в каком измеряется радиус. По формуле градусы сокращаются L=((пR)/180)m, m — градусная мера дуги внутри окружности, но если очень надо могу потом нарисовать.

В градусах, в радианах! 360 градусов = 6,28 радиан!…

в килограммах по-моему длина измеряется в метрах (СИ)

Длина дуги окружности L радиуса R с центральным углом a, измеренным в радианах, вычисляется по формуле: L = R*A . (где a угол

Длина дуги измеряется в метрических мерах. А поверхность внутри радиусов и дуги называется сектор и меряется градусами.

Радиус инерции, теория и примеры

Осевые моменты инерции для твердых тел в некоторых случаях задают при помощи массы и радиуса инерции такого тела. Обычно радиус инерции обозначают буквой , но могут встречаться и другие обозначения. Для того чтобы не путать радиус инерции с плотностью вещества радиус инерции идентифицируют при помощи индекса, например пишут: . Особенно часто радиус инерции применяют для выражения осевых моментов инерции тел, имеющих сложную форму.

Определения радиуса инерции

Выражение (1) означает, что равен расстоянию от оси до места в пространстве, в котором следует сосредоточить всю массу тела для того, чтобы момент инерции данной материальной точки был равен моменту инерции тела по отношению к той же оси.

Так, например, момент инерции однородного шара массы радиуса R относительно оси X, проходящей через его центр, равен:

   

Момент инерции материальной точки, имеющей массу , находящейся на расстоянии от этой же оси равен:

   

Приравнивая правые части выражений (2) и (3), выразим радиус инерции и для шара получим:

   

Используя радиус инерции, можно используя формулу (1) найти момент инерции тела и наоборот.

Радиусом инерции сечения (плоской фигуры) () относительно оси X, называют величину равную:

   

Из выражения, определяющего радиус инерции сечения (4), следует, что он равен расстоянию от оси X до точки, в которой необходимо сосредоточить всю площадь рассматриваемого сечения (S), при этом момент инерции этой точки будет равен моменту инерции всего сечения.

Радиусы инерции, которые соответствуют главным осям, называют главными радиусами инерции. Их определяют при помощи выражений:

   

Радиусы инерции измеряются в метрах в международной системе единиц (СИ).

Примеры решения задач