Стерадиан — Википедия
Материал из Википедии — свободной энциклопедии
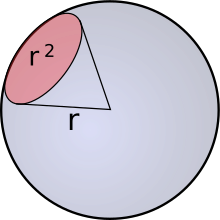 Графическое изображение телесного угла в 1 стерадиан
Графическое изображение телесного угла в 1 стерадиан 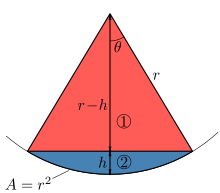 Угол раскрытия кругового конуса 2θ{\displaystyle 2\theta } с телесным углом 1 стерадиан
Угол раскрытия кругового конуса 2θ{\displaystyle 2\theta } с телесным углом 1 стерадианСтерадиа́н (русское обозначение: ср, международное: sr; от др.-греч. στέρεος — твёрдый, объёмный, пространственный, и лат. radius — луч) — единица измерения телесных углов.
Телесный угол в 1 стерадиан с вершиной в центре сферы радиусом r вырезает из этой сферы поверхность площадью r2. Если такой телесный угол имеет вид кругового конуса, то угол его раскрытия ϕ{\displaystyle \phi } составит:
- ϕ=2θ=2arccos(1−12π)≈1.144rad,{\displaystyle \phi =2\theta =2\arccos \left(1-{\frac {1}{2\pi }}\right)\approx 1.144\,{\text{rad}},}
(приблизительно 65,541° или 65°32′28″).
Поверхность сферы, наблюдаемая из её центра образует телесный угол 4π{\displaystyle {4\pi }} стерадиан; соответственно, 1 ср = 1⁄4π ≈ 0,0796 полного телесного угла (сферы), или (180⁄π)² ≈ 3282,8 квадратного градуса[en]*.
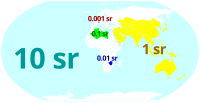 Телесные углы, под которыми различные территории видны из центра Земли
Телесные углы, под которыми различные территории видны из центра ЗемлиСтерадиан входит в Международную систему единиц (СИ). В соответствии с решением XX Генеральной конференции по мерам и весам, принятым в 1995 году, стерадиан является безразмерной производной единицей СИ, имеющей специальное наименование и обозначение, которые могут быть использованы или не использованы в выражениях для других производных единиц СИ (по необходимости)
Формула для определения телесного угла Ω{\displaystyle \Omega }, если известен угол ϕ{\displaystyle \phi } при вершине кругового конуса:
- Ω=2π[(1−cos(ϕ/2)].{\displaystyle \Omega =2\pi [(1-\cos(\phi /2)].}
Термин «стерадиан» (англ. steradian) был впервые введён Дж. Холстедом[en] в его книге «Метрическая геометрия» (англ. Metrical geometry. An elementary treatise on mensuration, Boston: Ginn, Heath & co., 1881)
Радиан — Циклопедия
Что такое радиан? // LifeTensor [9:27] Градусы и радианы // KhanAcademyRussian [10:06]Радиан (в математике и физике) — это единица измерения плоскостных углов, принятая в Международной системе единиц СИ.
Один радиан — это плоскостной угол, образованный двумя радиусами, так, что длина дуги между ними точно равна радиусу окружности. То есть, измерение угла в радианах показывает во сколько раз длина дуги окружности, опирающейся на этот угол, отличается от его радиуса.
Радиан является безразмерной единицей измерения и имеет обозначение
Полная длина окружности равна 2πr, где r — радиус окружности. Поэтому полный круг является углом в 2π≈6,28319 радиан. Преобразование радианов в градусы и наоборот осуществляется следующим образом:
- 2π рад = 360°,
- 1 рад = 360°/(2π) = 180°/π ≈ 57,29578°.
- 360° = 2π рад,
- 1° = 2π/360 рад = π/180 рад.
Широкое применение радианов в математическом анализе обусловлено тем, что выражения с тригонометрическими функциями, аргументы которых измеряются в радианах, приобретают максимально простой вид (без числовых коэффициентов). Например, используя радианы, получим простое тождество
- [math]\lim_{h\rightarrow 0}\frac{\sin h}{h}=1,[/math]
что лежит в основе многих элегантных формул в математике.
При малых углах синус и тангенс угла, выраженного в радианах, равен самому углу, что удобно при приближенных вычислениях.
Косинус малого угла, выраженного в радианах, приблизительно равен:
- [math]\cos(x) \approx 1 — \frac{x^2}{2}[/math]
Радиан есть безразмерной единицей измерения. То есть числовое значение угла, измеренного в радианах, лишено размерности. Это легко видеть из самого определения радиана, как отношения длины окружности к радиусу. Согласно рекомендациям Международного бюро мер и весов радиан интерпретируется как единица с размерностью 1 = м·м−1 (м/м, то есть метр на метр — числитель и знаменатель возможно сократить, то есть оно не имеет размерности).
Иначе, безразмерность радиана можно видеть по выражению ряда Тейлора для тригонометрической функции sin(x):
- [math]\sin(x) = x — \frac{x^3}{3!} + \frac{x^5}{5!}-\cdots.[/math]
Если бы x имел размерность, тогда эта сумма была бы лишена смысла — линейное слагаемое x нельзя было бы добавить к кубическому x3/3!, как величины разных размерностей. Итак, x должен быть безразмерным.
Радиус атома — Википедия
 Изображение атома гелия, где плотность вероятности нахождения электрона представлена серым цветом, более тёмные области соответствуют большей плотности.
Изображение атома гелия, где плотность вероятности нахождения электрона представлена серым цветом, более тёмные области соответствуют большей плотности. 
Радиус атома — расстояние между атомным ядром и самой дальней из стабильных орбит электронов в электронной оболочке этого атома. Поскольку, согласно квантовой механике, атомы не имеют четких границ, а вероятность найти электрон, связанный с ядром данного атома, на определённом расстоянии от этого ядра быстро убывает с увеличением расстояния, атому приписывают некоторый определённый радиус, полагая, что в шаре этого радиуса заключена подавляющая часть электронной плотности (порядка 90 процентов). Существуют различные определения радиуса атома[⇨], три наиболее широко используемых: радиус Ван-дер-Ваальса, ионный радиус и ковалентный радиус.
В зависимости от определения термин «радиус атома» может применяться либо только к изолированным атомам, либо также к атомам в конденсированной среде, ковалентно связанным в молекулах или в ионизированном и возбужденном состояниях; его значение может быть получено путем экспериментальных измерений или вычислено из теоретических моделей. Значение радиуса может зависеть от состояния атома и окружающей среды[1].
Электроны не имеют четко определённых орбит или границ. Скорее, их положения могут быть описаны как распределения вероятностей, которые постепенно сужаются по мере удаления от ядра без резкого сокращения. Кроме того, в конденсированном веществе и молекулах электронные облака атомов обычно в некоторой степени перекрываются, и некоторые из электронов могут перемещаться в области, охватывающей два или более атомов («принадлежать» нескольким атомам одновременно).
Согласно большинству определений, радиусы изолированных нейтральных атомов колеблются в диапазоне от 30 до 300 пм (триллионных долей метра) или от 0,3 до 3 ангстрем. Следовательно, радиус атома более чем в 10 тысяч раз больше радиуса его ядра (1-10 фм)[2] и составляет менее 1/1000 длины волны видимого света (400—700 нм).
Во многих случаях форма атома может быть аппроксимирована сферой. Это лишь грубое приближение, но оно может дать количественные представления и выступить в качестве базовой модели для описания для многих явлений, таких как плотность жидкостей и твердых веществ, диффузия жидкостей через молекулярные сита, расположение атомов и ионов в кристаллах, а также размер и форма молекул.
Радиусы атомов изменяются, подчиняясь определённым закономерностям периодической таблицы химических элементов. Например, радиусы атомов обычно уменьшаются при перемещении слева направо вдоль каждого периода (строки) таблицы, от щелочных металлов до благородных газов, и возрастают по мере продвижения сверху вниз в каждой группе (столбце). Радиусы атомов резко возрастают при переходе между благородным газом в конце каждого периода и щелочным металлом в начале следующего периода. Эти тенденции изменения радиусов атомов (наряду с другими химическими и физическими свойствами элементов) могут быть объяснены с точки зрения теории электронной оболочки атома, а также представляют доказательства подтверждения квантовой теории. Радиусы атомов уменьшаются в периодической таблице, потому что с увеличением атомного номера увеличивается число протонов в атоме, а дополнительные электроны добавляются в одну и ту же квантовую оболочку. Следовательно, эффективный заряд атомного ядра по отношению к внешним электронам увеличивается, притягивая внешние электроны. В результате электронное облако сжимается и атомный радиус уменьшается.
В 1920 году, вскоре после того, как стало возможным определять размеры атомов с помощью рентгеноструктурного анализа, было высказано предположение, что все атомы одного и того же элемента имеют одинаковые радиусы[3]. Однако в 1923 году, когда было получено больше данных о кристаллах, было обнаружено, что аппроксимация атома сферой не всегда корректна при сравнении атомов одного и того же элемента в разных кристаллических структурах[4].
Широко используемые определения радиуса атома включают:
- Радиус Ван-дер-Ваальса, Вандерваальсовы радиусы[5] — эта величина соответствует половине межъядерного расстояния между ближайшими одноимёнными атомами, не связанными между собой химической связью и принадлежащими разным молекулам (например, в молекулярных кристаллах).[6].
- Ионный радиус: номинальный радиус ионов элемента в определённом состоянии ионизации, выведенный из расстояния между атомными ядрами в кристаллических солях, которые включают эти ионы. В принципе, расстояние между двумя соседними противоположно заряженными ионами (длина ионной связи между ними) должно равняться сумме их ионных радиусов[6].
- Ковалентный радиус: номинальный радиус атомов элемента, когда они ковалентно связаны с другими атомами, выводится из расстояния между атомными ядрами в молекулах. В принципе, расстояние между двумя атомами, которые связаны друг с другом в молекуле (длина этой ковалентной связи), должно равняться сумме их ковалентных радиусов[6].
- Металлический радиус: номинальный радиус атомов элемента, когда они соединены с другими атомами металлическими связями.
- Боровский радиус: радиус орбиты электрона с наименьшей энергией, предсказанный Боровской моделью атома (1913)[7][8]. Он применим только к атомам и ионам с одним электроном, таким как водород, однократно ионизованный гелий и позитроний. Хотя сама модель в настоящее время устарела, радиус Бора для атома водорода считается одной из фундаментальных физических постоянных.
Измерение радиуса атома опытным путём[править | править код]
В таблице приведены измеренные опытным путём ковалентные радиусы для элементов, опубликованные американским химиком Д.Слейтером в 1964 году[9]. Значения приведены в пикометрах (пм или 1 × 10-12 м) с точностью около 5 пм. Оттенки цвета ячеек варьируются от красного до жёлтого по мере увеличения радиуса; серый цвет — отсутствие данных.
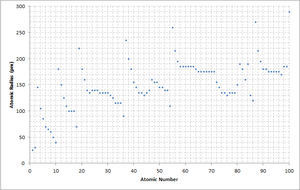
Изменение радиуса атома с увеличением зарядового числа можно объяснить расположением электронов в оболочках с постоянной ёмкостью. Оболочки обычно заполнены в порядке увеличения радиуса, поскольку отрицательно заряженные электроны притягиваются положительно заряженными протонами атомного ядра. Поскольку зарядовое число увеличивается вдоль каждой строки периодической таблицы, дополнительные электроны входят в ту же самую внешнюю оболочку, а её радиус постепенно сжимается из-за увеличения заряда ядра. В атомах инертных газов внешняя оболочка полностью заполнена; следовательно, дополнительный электрон следующего элемента — щелочного металла — перейдет в следующую внешнюю оболочку, что объясняет внезапное увеличение атомного радиуса.
Увеличивающийся заряд ядра частично уравновешивается ростом числа электронов, это явление известно как экранирование[en]; он объясняет, почему размер атомов обычно увеличивается в каждом столбце периодической таблицы. Из этой закономерности есть важное исключение, известное как лантаноидное сжатие: меньшие, по сравнению с ожидаемыми, величины ионных радиусов химических элементов, входящих в группу лантаноидов (атомный номер 58—71), которое происходит из-за недостаточного экранирования заряда ядра электронами 4f-орбитали.
По существу, атомный радиус уменьшается на протяжении периодов из-за увеличения количества протонов в ядре. Соответственно, большее количество протонов создает более сильный заряд и сильнее притягивает электроны, уменьшая размер радиуса атома. При движении сверху вниз по столбцам (группам) периодической таблицы атомный радиус увеличивается, поскольку есть больше энергетических уровней и, следовательно, больше расстояние между протонами и электронами. Кроме того, электронное экранирование ослабляет притяжение протонов, поэтому оставшиеся электроны могут удаляться от положительно заряженного ядра. Таким образом, размер (радиус атома) увеличивается.
В следующей таблице приведены основные факторы, влияющие радиус атома:
| Фактор | Закон | Возрастает с… | как правило | Влияние на радиус атома |
|---|---|---|---|---|
| Электронные оболочки | Квантовая механика | Главным и азимутальным квантовым числом | Увеличивает радиус атома | Возрастает сверху вниз в каждой колонке |
| Атомный заряд | Притяжение электронов протонами ядра атома | Зарядовым числом | Сокращает радиус атома | Сокращается в течение всего периода |
| Экранирование | Отталкивание внешних электронов внутренними электронами | Количеством электронов во внутренних оболочках | Увеличивает радиус атома | Снижает эффект второго фактора |
У химических элементов группы лантаноидов электроны в 4f-подоболочке, которая постепенно заполняется от церия (Z = 58) до лютеция (Z = 71), не особенно эффективны для экранирования увеличивающегося заряда ядра. Элементы, следующие непосредственно за лантаноидами, имеют радиусы атомов, которые меньше, чем можно было бы ожидать, и которые почти идентичны атомным радиусам элементов, находящихся непосредственно над ними
Лантаноидное сжатие даёт 5 следующих эффектов:
- Размер ионов Ln3 + регулярно уменьшается с атомным номером. Согласно правилам Фаянса[en], уменьшение размера ионов Ln3+ увеличивает ковалентную связь и уменьшает основную связь между ионами Ln
La3+ > Ce3+ > …, … > Lu3+. - Наблюдается регулярное уменьшение ионных радиусов.
- Наблюдается регулярное снижение способности монов действовать в качестве восстановителя с увеличением атомного номера.
- Второй и третий ряды переходных элементов d-блока довольно близки по свойствам.
- Эти элементы встречаются вместе в природных минералах и их трудно разделить.
d-сжатие[en] менее выражено, чем лантаноидное сжатие, но возникает по той же причине. В этом случае плохая экранирующая способность 3d-электронов влияет на атомные радиусы и химические свойства элементов, следующих непосредственно за первым рядом переходных металлов, от галлия (Z = 31) до брома (Z = 35)
В таблице приведены значения радиусов атомов, рассчитанные по теоретическим моделям, опубликованные итальянским химиком Энрико Клементи[en] и другими в 1967 году[11]. Значения даны в пикометрах (пм).
- ↑ Cotton, F. A.; Wilkinson, G. Advanced Inorganic Chemistry (неопр.). — 5th. — Wiley, 1988. — С. 1385. — ISBN 978-0-471-84997-1.
- ↑ Basdevant, J.-L.; Rich, J.; Spiro, M. Fundamentals in Nuclear Physics (неопр.). — Springer, 2005. — С. 13, fig 1.1. — ISBN 978-0-387-01672-6.
- ↑ Bragg, W. L. The arrangement of atoms in crystals (англ.) // Philosophical Magazine : journal. — 1920. — Vol. 6, no. 236. — P. 169—189. — DOI:10.1080/14786440808636111.
- ↑ Wyckoff, R. W. G. On the Hypothesis of Constant Atomic Radii (англ.) // Proceedings of the National Academy of Sciences of the United States of America : journal. — 1923. — Vol. 9, no. 2. — P. 33—38. — DOI:10.1073/pnas.9.2.33. — Bibcode: 1923PNAS….9…33W. — PMID 16576657.
- ↑ Такое написание даёт «Русский орфографический словарь: около 200 000 слов / Российская академия наук. Институт русскоrо языка им. В. В. Виноградова / Под ред. В. В. Лопатина, О. Е. Ивановой. — Изд. 4-е, испр. и доп. — М.: АСТ-ПРЕСС КНИГА, 2013. — 896 с. — (Фундаментальные словари русскою языка). — с. 68. — ISBN 978-5-462-01272-3».
- ↑ 1 2 3 L.; Pauling. The Nature of the Chemical Bond (неопр.). — 2nd. — Cornell University Press (англ.)русск., 1945.
- ↑ Bohr, N. On the Constitution of Atoms and Molecules, Part I. – Binding of Electrons by Positive Nuclei (англ.) // Philosophical Magazine : journal. — 1913. — Vol. 26, no. 151. — P. 1—24. — DOI:10.1080/14786441308634955.
- ↑ Bohr, N. On the Constitution of Atoms and Molecules, Part II. – Systems containing only a Single Nucleus (англ.) // Philosophical Magazine : journal. — 1913. — Vol. 26, no. 153. — P. 476—502. — DOI:10.1080/14786441308634993.
- ↑ Slater, J. C. Atomic Radii in Crystals (англ.) // Journal of Chemical Physics : journal. — 1964. — Vol. 41, no. 10. — P. 3199—3205. — DOI:10.1063/1.1725697. — Bibcode: 1964JChPh..41.3199S.
- ↑ 1 2 W. L.; Jolly. Modern Inorganic Chemistry (неопр.). — 2nd. — McGraw-Hill Education, 1991. — С. 22. — ISBN 978-0-07-112651-9.
- ↑ Clementi, E.; Raimond, D. L.; Reinhardt, W. P. Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons (англ.) // Journal of Chemical Physics : journal. — 1967. — Vol. 47, no. 4. — P. 1300—1307. — DOI:10.1063/1.1712084. — Bibcode: 1967JChPh..47.1300C.
- Рабинович В. А., Хавин З.Я. Краткий химический справочник. Изд. 2-е, испр. и доп. — Л.: Химия, 1978. — 392 с.
Радиус инерции сечения — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2013; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2013; проверки требуют 6 правок.Радиус инерции сечения — геометрическая характеристика сечения, связывающая геометрический момент инерции фигуры J{\displaystyle J} с её площадью F{\displaystyle F} следующими формулами:
- Jy=iy2F{\displaystyle J_{y}=i_{y}^{2}F}
- Jz=iz2F{\displaystyle J_{z}=i_{z}^{2}F}
Отсюда, формула радиуса инерции:
- iy=JyF{\displaystyle i_{y}={\sqrt[{}]{\frac {J_{y}}{F}}}}
- iz=JzF{\displaystyle i_{z}={\sqrt[{}]{\frac {J_{z}}{F}}}}
Таким образом, радиус инерции отражает отношение жесткости стержня на изгиб (EJ{\displaystyle EJ}) и на сжатие (EF{\displaystyle EF}).
В сопротивлении стержней продольному изгибу (потере устойчивости прямолинейной формы при сжатии) основную роль играет гибкость стержня, а значит и величина наименьшего радиуса инерции сечения. Таким образом, большую экономичность будут иметь те сечения, у которых наименьший радиус инерции равен наибольшему, то есть сечения у которых все центральные моменты инерции равны, а эллипс инерции обратился бы в круг.
Единица измерения СИ — м. В строительной литературе чаще записывается в миллиметрах или сантиметрах, ввиду небольшой величины на практике.
Если моменты инерции Jy{\displaystyle J_{y}} и Jz{\displaystyle J_{z}} являются главными моментами инерции, то iy{\displaystyle i_{y}} и iz{\displaystyle i_{z}} — также являются главными радиусами инерции.
В некоторой литературе радиус инерции обозначается просто r{\displaystyle r}.
- Беляев Н. М. Сопротивление материалов. — 15-е изд., перераб. — М.: Наука, 1976. — 607 с. — 200 000 экз.
Единицы измерения расстояния — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 апреля 2017; проверки требуют 12 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 апреля 2017; проверки требуют 12 правок.Единицы измерения расстояния[править | править код]
Метрическая система[править | править код]
Единицей измерения расстояния и одной из основных единиц в Международной системе единиц (СИ) является метр. Метр также является единицей измерения расстояния и относится к числу основных единиц в метрических системах МКС, МКСА, МКСК, МКСГ, МСК, МКСЛ, МСС, МКГСС и МТС[1].
В системе СГС единицей измерения расстояния служит сантиметр.
На практике применяются также кратные и дольные единицы метра, образуемые с помощью стандартных приставок СИ:
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 м | декаметр | дам | dam | 10−1 м | дециметр | дм | dm |
| 102 м | гектометр | гм | hm | 10−2 м | сантиметр | см | cm |
| 103 м | километр | км | km | 10−3 м | миллиметр | мм | mm |
| 106 м | мегаметр | Мм | Mm | 10−6 м | микрометр | мкм | µm |
| 109 м | гигаметр | Гм | Gm | 10−9 м | нанометр | нм | nm |
| 1012 м | тераметр | Тм | Tm | 10−12 м | пикометр | пм | pm |
| 1015 м | петаметр | Пм | Pm | 10−15 м | фемтометр | фм | fm |
| 1018 м | эксаметр | Эм | Em | 10−18 м | аттометр | ам | am |
| 1021 м | зеттаметр | Зм | Zm | 10−21 м | зептометр | зм | zm |
| 1024 м | иоттаметр | Им | Ym | 10−24 м | иоктометр | им | ym |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Британская/американская система[править | править код]
- Лига (лье) = 4,828032 км
- Миля = 1,609344 км
- Фурлонг = 201,16 м
- Чейн = 20,1168 м
- Род = 5,0292 м
- Ярд = 91,44 см
- Инспекционный фут = 1,000002 фута = 30,48006096 см
- Фут = 30,48 см
- Линк = 20,1168 см
- Хэнд = 10,16 см
- Дюйм = 2,54 см
- Линия большая = 0,254 см
- Линия малая = 0,2116 см
- Мил = 0,0254 мм
Старорусская система[править | править код]
- 1 пядь = 17,78 см
- 2 пяди = 1 стопа (35,56 см)
- 3 пяди = 1 локоть (53,34 см)
- 4 пяди = 1 аршин (71,12 см)
- 5 пядей = 1 шаг (88,9 см)
- 6 пядей = 1 мера или полсаженя (106,68 см)
- 7 пядей = 1 лоб (124,46см) (7 пядей во лбу)
- 8 пядей = 1 столбец (142,24 см)
- 9 пядей = 1 посох (160,02 см)
- 10 пядей = 1 витой посох (177,8 см)
- 12 пядей = 1 сажень (213,36 см) (катет)
- 16 пядей = 1 круг (284,48 см)
- 17 пядей = 1 косая сажень (302,26 см) (гипотенуза)
- 1/2 пяди = 1 пясть (8,89 см)
- 1/4 пяди = 1 вершок (4,445 см)
- 1/16 пяди = 1 нокоть (1,11125 см)
- 1/256 пяди (1/16 ноктя) = 1 линия (0,069453 см)
- 1/4096 пяди (1/16 линии) = 1 волос (0,00434 см)
- 1/65536 пяди (1/16 волоса) = 1 волосок (0,00027 см)
- 1 верста = 6000 пядей (1066,8 метров)
- 1 столбовая верста = 1517,41632 метра
- 1 мерная верста = 1000 саженей (2133,6 метра)
- 1 миля = 7 вёрст (7,4676 км)
- Великая сажень ≈ 244,0 см
- Городовая сажень ≈ 284,8 см
- Греческая сажень ≈ 230,4 см позже приравняли аттический стадий = 6 английских футов 1 дюйм = 185,42 см
- Казённая (мерная, трёхаршинная) сажень. В XVI веке сажень была приравнена к 3 аршинам и стала называться казённой, или трёхаршинной (213,36 см)
- Кладочная сажень ≈ 159,7 см
- Косая сажень — расстояние от пальцев ноги до конца пальцев руки, вытянутой над головой по диагонали ≈ 248 см
- Малая сажень — расстояние от поднятой на уровень плеча руки до пола ≈ 142,4 см
- Маховая сажень — расстояние между вытянутыми пальцами раскинутых (размахнутых) рук. В таких маховых саженях, которые легко отсчитывать, выражена, например, высота колокольни Ивана Великого в Кремле. Эта наиболее древняя мера, начиная с XVI века, перешла в разряд неофициальных, бытовых. = 2,5 аршина = 152—177,8 см
- Морская сажень = 6 английским футам = 182,88 см
- Народная сажень ≈ 176,0 см
- Простая сажень ≈ 150,8 см
- Сажень без чети — наибольшее расстояние между подошвой левой ноги и концом большого пальца поднятой вверх правой руки ≈ 197,2 см
- Трубная сажень — мерили только длину труб на соляных промыслах ≈ 187 см
- Царская сажень ≈ 197,4 см
- Церковная сажень ≈ 186,4 см
- Четырёхаршинная сажень = 4 аршина = 284,48 см
Японская система[править | править код]
- Мо = 0,003030303 см
- Рин = 0,03030303 см
- Бу = 0,3030303 см
- Сун = 3,030303 см
- Сяку = 30,30303 см
- Кэн = 181,8182 см
- Хиро = 181,8182 см
- Дзё = 303,0303 см
- Тё = 10909,09 см
- Ри = 392727.3 см
Древнегреческая система[править | править код]
- Палайста = 7 см
- Плетр = 31 м
- Миля = 1,388 км
- Стадий = 185,136 м
- Плетр = 30,856 м
- Амма = 18,514 м
- Акена (декапод) = 3,086 м
- Оргия (гексапод) = 1,851 м
- Бема (шаг) = 77,14 см
- Пехис (локоть) греческий = 61,712 см
- Пехис (локоть) короткий = 46,284 см
- Пус (фут) = 30,856 см
- Спитам = 23,142 см
- Дихас = 15,428 см
- Палестра (ладонь) = 7,714 см
- Кондиль = 3,857 см
- Дактиль (палец) = 1,928 см
- Стадий олимпийский = 192,27 м
- Стадий аттический = 184,98 м
- Стадий птолемеевский = 185 м
Типографическая система[править | править код]
- твип = 1/20 пункта
- пункт = 0,352777… мм (пункт Adobe) или 0,3759 мм (пункт Дидо) или 0,3515 мм (пункт Хоукса) или 0,375 мм (метрический пункт) или 0,3473 мм (пункт Фурнье)
- цицеро = 12 пунктам (= 4,2333… мм в системе Adobe)
- нонпарель = 5,708 пунктов
Флотская система[править | править код]
Единицы, применяемые в астрономии[править | править код]
Единицы, набранные малым шрифтом, практически не используются или устарели.
Единицы, применяемые в физике[править | править код]
Единицы, применяемые в технике[править | править код]
- юнит = 44,45 мм = 1,75 дюйма;
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Согласно новому определению астрономической единицы, принятому МАС в сентябре 2012 г.
- ↑ WolframAlpha (неопр.). Архивировано 10 апреля 2013 года.
- ↑ В скобках указано стандартное отклонение. Таким образом, значение планковской длины можно представить в следующих формах:
ℓP{\displaystyle \ell _{P}} ≈ 1,616199(97) · 10−35 м =
= (1,616199 ± 0,000097) · 10−35 м =
= [1,616102 ÷ 1,616296] · 10−35 м - ↑ NIST, «Planck length» (англ.), NIST’s published CODATA constants
- ↑ Fundamental Physical Constants — Complete Listing
РАДИАН — Физический энциклопедический словарь
(от лат. radius — луч, радиус) (рад, rad), единица плоского угла; 1 рад равен углу между двумя радиусами окружности, длина дуги между к-рыми равна радиусу. 1 рад=57°17’44,8″»3,44•103 угл. минут»2,06•105 угл. секунд»63,7g (см. ГРАД).
Источник: Физический энциклопедический словарь на Gufo.me
Значения в других словарях
- Радиан — Единица плоского угла, угловой координаты в СИ. Словарь мер и весов
- радиан — Радиана, м. [от латин. radius – луч] (мат.). Единица измерения углов, представляющая собою угол, у к-рого дуга равна радиусу окружности. Большой словарь иностранных слов
- радиан — радиан , -а Орфографический словарь. Одно Н или два?
- Радиан — (от лат. radius — луч, радиус) угол, соответствующий дуге, длина которой равна её радиусу; содержит приблизительно 57°17 ‘44,8’’. Р. принимается за единицу измерения углов при т. н. круговом, или радианном, измерении углов. Большая советская энциклопедия
- радиан — РАДИАН а, м. radian m., нем. Radian <�лат. лат. radius луч. Угол, соответствующий дуге, длина которой равна ее радиусу. БАС-1. — Лекс. Гранат: радиан; СИС 1937: радиан. Словарь галлицизмов русского языка
- радиан — радиан м. Единица измерения плоских углов. Толковый словарь Ефремовой
- радиан — РАДИАН -а; м. [от лат. radius — радиус] Матем. Угол, соответствующий дуге, длина которой равна её радиусу. ◁ Радианный, -ая, -ое. Р-ое измерение углов. Толковый словарь Кузнецова
- РАДИАН — РАДИАН (от лат. radius — радиус) — центральный угол, соответствующий дуге, длина которой равна ее радиусу. Содержит приблизительно 57 °17?45?. Принимается за единицу измерения углов. Углы в 30 °, 45 °, 60 °, 90 °содержат соответственно ?/6, ?/4, ?/3, ?… Большой энциклопедический словарь
- РАДИАН — РАДИАН, угол, образованный пересечением двух радиусов из центра ОКРУЖНОСТИ, при этом длина дуги, ограниченной этими радиусами, равна длине радиуса. Таким образом радиан — единица измерения УГЛА, приблизительно равный 57,296°, а углу 360° соответствует 2p радиан. Научно-технический словарь
- радиан — Единица измерения углов. Радиан представляет собой угол, стягиваемый дугой окружности, длина которой равна радиусу этой окружности. Таким образом, 2? радиан эквивалентны 360°, а радиан равен примерно 57,30°. Большой астрономический словарь
- радиан — орф. радиан, -а, р. мн. -ов, счетн. ф. -иан (ед. измер.) Орфографический словарь Лопатина
- Радиан — Угол, соответствующий дуге, длина к-рой равна ее радиусу; содержит приблизительно 57°17’44», 80625. Р. принимается за единицу измерения углов при т. н. круговом, или радианном, измерении углов. Если круговая мера угла равна аР. Математическая энциклопедия
- радиан — Радиан, радианы, радиана, радианов, радиану, радианам, радиан, радианы, радианом, радианами, радиане, радианах Грамматический словарь Зализняка
- радиан — сущ., кол-во синонимов: 3 единица 830 рад 7 угол 27 Словарь синонимов русского языка
- радиан — РАДИ’АН, радиана, ·муж. (от ·лат. radius — луч) (мат.). Единица измерения углов, представляющая собою угол, у которого дуга равна радиусу окружности. Толковый словарь Ушакова
- радиан — Ради/а́н/ [от ра́ди(ус)]. Морфемно-орфографический словарь

Телесный угол — Википедия
Материал из Википедии — свободной энциклопедии
Телесный уголТеле́сный у́гол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность. Обозначается телесный угол обычно буквой Ω.
Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы:
- Ω=SR2.{\displaystyle \Omega \,=\,{S \over R^{2}}.}

Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса r поверхность с площадью r2. Полная сфера образует телесный угол, равный 4π стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла.
Телесный угол имеет нулевую физическую размерность.
Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол.
Коэффициенты пересчёта единиц телесного угла.
| Ω{\displaystyle \Omega } | Стерадиан | Кв. градус | Кв. минута | Кв. секунда | Полный угол |
|---|---|---|---|---|---|
| 1 стерадиан = | 1 | (180/π)² ≈ ≈ 3282,806 кв. градусов | (180×60/π)² ≈ ≈ 1,1818103⋅107 кв. минут | (180×60×60/π)² ≈ ≈ 4,254517⋅1010 кв. секунд | 1/4π ≈ ≈ 0,07957747 полного угла |
| 1 кв. градус = | (π/180)² ≈ ≈ 3,0461742⋅10−4 стерадиан | 1 | 60² = = 3600 кв. минут | (60×60)² = = 12 960 000 кв. секунд | π/(2×180)² ≈ ≈ 2,424068⋅10−5 полного угла |
| 1 кв. минута = | (π/(180×60))² ≈ ≈ 8,461595⋅10−8 стерадиан | 1/60² ≈ ≈ 2,7777778⋅10−4 кв. градусов | 1 | 60² = = 3600 кв. секунд | π/(2×180×60)² ≈ ≈ 6,73352335⋅10−9 полного угла |
| 1 кв. секунда = | (π/(180×60×60))² ≈ ≈ 2,35044305⋅10−11 стерадиан | 1/(60×60)² ≈ ≈ 7,71604938⋅10−8 кв. градусов | 1/60² ≈ ≈ 2,7777778⋅10−4 кв. минут | 1 | π/(2×180×60×60)² ≈ ≈ 1,87042315⋅10−12 полного угла |
| Полный угол = | 4π ≈ ≈ 12,5663706 стерадиан | (2×180)²/π ≈ ≈ 41252,96125 кв. градусов | (2×180×60)²/π ≈ ≈ 1,48511066⋅108 кв. минут | (2×180×60×60)²/π ≈ ≈ 5,34638378⋅1011 кв. секунд | 1 |
Для произвольной стягивающей поверхности S телесный угол Ω, под которым она видна из начала координат, равен
- Ω=∫SdΩ=∬Ssinϑdφdϑ=∫S(r/r)⋅ndSr2,{\displaystyle \Omega =\int \limits _{S}d\Omega =\iint \limits _{S}\sin \vartheta \,d\varphi \,d\vartheta =\int \limits _{S}{\frac {(\mathbf {r} /r)\cdot \mathbf {n} dS}{r^{2}}},}
где r,ϑ,φ{\displaystyle r,\vartheta ,\varphi } — сферические координаты элемента поверхности dS,{\displaystyle dS,} r{\displaystyle \mathbf {r} } — его радиус-вектор, n{\displaystyle \mathbf {n} } — единичный вектор, нормальный к dS.{\displaystyle dS.}
- Полный телесный угол (полная сфера) равен 4π стерадиан.
- Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.
- Треугольник с координатами вершин r1{\displaystyle \mathbf {r} _{1}}, r2{\displaystyle \mathbf {r} _{2}}, r3{\displaystyle \mathbf {r} _{3}} виден из начала координат под телесным углом
- Ω=2arctg(r1r2r3)r1r2r3+(r1⋅r2)r3+(r2⋅r3)r1+(r3⋅r1)r2,{\displaystyle \Omega =2\,\mathrm {arctg} \,{\frac {(\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})}{r_{1}r_{2}r_{3}+(\mathbf {r} _{1}\cdot \mathbf {r} _{2})r_{3}+(\mathbf {r} _{2}\cdot \mathbf {r} _{3})r_{1}+(\mathbf {r} _{3}\cdot \mathbf {r} _{1})r_{2}}},}
- где (r1r2r3){\displaystyle (\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})} — смешанное произведение данных векторов, (ri⋅rj){\displaystyle (\mathbf {r} _{i}\cdot \mathbf {r} _{j})} — скалярные произведения соответствующих векторов, полужирным шрифтом обозначены векторы, нормальным шрифтом — их длины. Используя эту формулу, можно вычислять телесные углы, стянутые произвольными многоугольниками с известными координатами вершин (для этого достаточно разбить многоугольник на непересекающиеся треугольники).
- Телесный угол при вершине прямого кругового конуса с углом раствора α равен Ω=2π(1−cosα2).{\displaystyle \Omega =2\pi \left(1-\cos {\frac {\alpha }{2}}\right).} Если известны радиус основания R{\displaystyle R} и высота H{\displaystyle H} конуса, то Ω=2π(1−HR2+h3).{\displaystyle \Omega =2\pi \left(1-{\frac {H}{\sqrt {R^{2}+H^{2}}}}\right).} Когда угол раствора конуса мал, Ω≈πα24{\displaystyle \Omega \approx {\frac {\pi \alpha ^{2}}{4}}} (угол α{\displaystyle \alpha } выражен в радианах), или Ω≈0,000239α2{\displaystyle \Omega \approx 0{,}000239\alpha ^{2}} (угол α{\displaystyle \alpha } выражен в градусах). Так, телесный угол, под которым с Земли видны Луна и Солнце (их угловой диаметр примерно равен 0,5°), составляет около 6⋅10−5 стерадиан, или ≈0,0005 % площади небесной сферы (то есть полного телесного угла).
- Телесный угол двугранного угла в стерадианах равен удвоенному значению двугранного угла в радианах.
- Ω=4arctgtg(θs2)tg(θs−θa2)tg(θs−θb2)tg(θs−θc2),{\displaystyle \Omega =4\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}},} где θs=θa+θb+θc2{\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}} — полупериметр.
- Через двугранные углы α,β,γ{\displaystyle \alpha ,\beta ,\gamma } телесный угол выражается как:
- Ω=α+β+γ−π.{\displaystyle \Omega =\alpha +\beta +\gamma -\pi .}
- Телесный угол, под которым видна грань правильного N-гранника из его центра, равна 1N{\displaystyle {\frac {1}{N}}} полного телесного угла, или 4πN{\displaystyle {\frac {4\pi }{N}}} стерадиан.
 Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода[1]:
Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода[1]:
- Ω=2π+2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega =2\pi +{\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r≤R,{\displaystyle r\leq R,}
- Ω=2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega ={\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r>R,{\displaystyle r>R,}
- где K(k){\displaystyle K(k)} и Π(α2,k){\displaystyle \Pi (\alpha ^{2},k)} — полные нормальные эллиптические интегралы Лежандра 1-го и 3-го рода, соответственно;
- r{\displaystyle r} — расстояние от центра основания конуса до проекции вершины конуса на плоскость основания;
- H{\displaystyle H} — высота конуса;
- L=h3+(r+R)2{\displaystyle L={\sqrt {H^{2}+(r+R)^{2}}}} — длина максимальной образующей конуса;
- k=4rRL;{\displaystyle k={\frac {\sqrt {4rR}}{L}};}
- α=4rRr+R.{\displaystyle \alpha ={\frac {\sqrt {4rR}}{r+R}}.}
- где K(k){\displaystyle K(k)} и Π(α2,k){\displaystyle \Pi (\alpha ^{2},k)} — полные нормальные эллиптические интегралы Лежандра 1-го и 3-го рода, соответственно;




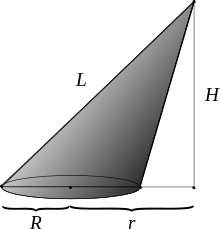 Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода[1]:
Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода[1]: