Механическая работа: определение и формула

 

Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?

Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.

Механическая работа в физике

Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть.

В каком случае совершается механическая работа?

Определение механической работы

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

A=Fs,

где A – работа,
F – сила,
s – пройденный путь.

Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние,  на которое мы передвинули тело.

Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения, то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.

Нужна помощь в учебе?

Предыдущая тема: Воздухоплавание в физике
Следующая тема:&nbsp&nbsp&nbspМощность: формула и применение в физике

Физическая работа — урок. Физика, 8 класс.

Совершённая работа равна изменению энергии, потраченной на совершение работы.

Величину работы можно определить, вычитая из конечного значения энергии начальное значение энергии.

 

A=Eконеч.−Eнач.,или A=ΔE, где A — работа (Дж); E — энергия (Дж).

 

Работу, как и энергию, измеряют в джоулях (Дж).

 

Если энергия тела увеличивается, тогда общая совершённая работа является положительной.

Пример:

Когда автомобиль начинает двигаться, его кинетическая энергия увеличивается. Значит, двигатель автомобиля совершает положительную работу.

Если энергия тела уменьшается, тогда общая совершённая работа является отрицательной.

Пример:

Когда автомобиль свободно катится по горизонтальной поверхности, его скорость и кинетическая энергия уменьшаются. Значит, сила сопротивления совершает отрицательную работу.

 

В физике рассматривают физическую работу, которая связана с перемещением тел.

Если при прямолинейном движении на тело действует неизменная сила, направленная в сторону движения тела, тогда работа, произведённая приложенной силой, равна произведению величины силы на величину проделанного перемещения.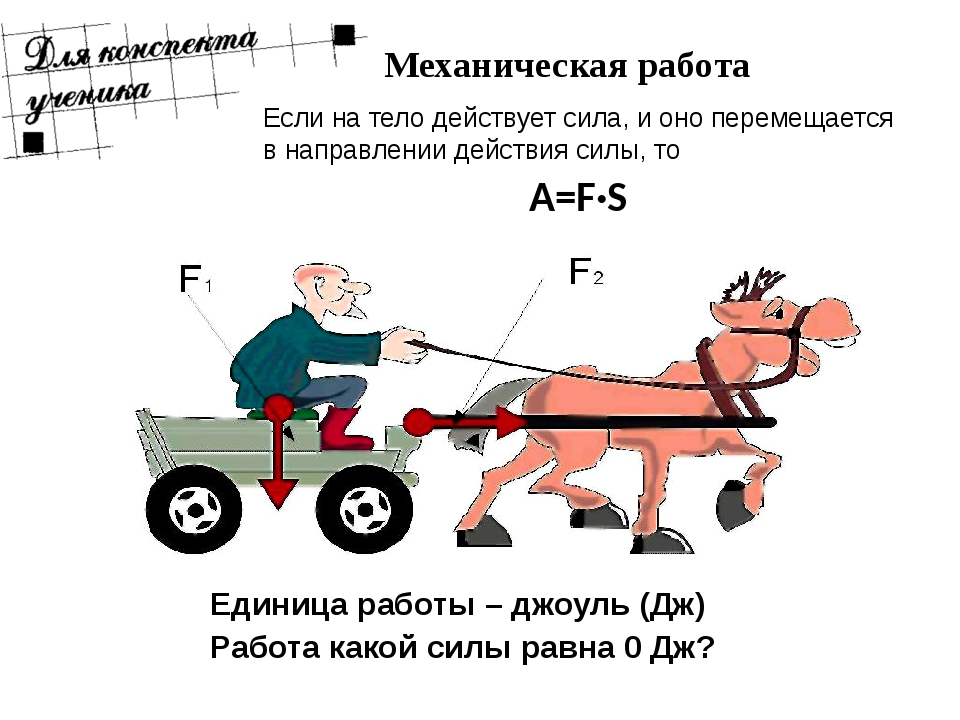

Если к телу приложена сила под вертикальным углом к направлению движения тела, как это показано на рисунке, тогда величина совершённой работы зависит от:

1) величины приложенной силы (F), которая совершает работу;

2) расстояния (l), на которое перемещается тело;

3) угла \(α\) между направлением действия силы и направлением движения тела.

Работа определяется по формуле: A=F⋅l⋅cosα.

  

  

Обрати внимание!

Если сила направлена параллельно направлению перемещения, тогда угол \(α = 0\), а \(косинус\) угла \(α\) равен \(1\). В этом случае формула упрощается: A=F⋅l.

Если проделанный путь является прямолинейным, тогда вместо пути \(l\) можно использовать перемещение (s). 

В этом случае формула для расчёта работы приобретает такой вид: A=F⋅s.

На трёх рисунках изображены случаи, когда направление силы и направление движения тела совпадают.

1) Действие силы и направление движения тела направлены горизонтально. Например, автомобиль едет по прямому пути, и сила тяги автомобиля приложена в том же направлении.

 

 

2) Действие силы и направление движения тела направлены под одинаковым углом наклона по отношению к горизонту. Например, автомобиль едет в гору.

  

  

3) Действие силы и направление движения тела направлены вертикально. Например, груз поднимается вверх, и сила упругости троса тоже направлена вверх. В этом случае величину совершённой работы можно рассчитать также по формуле A=m⋅g⋅h, где

(m) — масса тела, (g) — ускорение свободного падения,

(h) — высота подъёма тела над поверхностью земли.

 

 

Обрати внимание!

Если направление действия силы противоположно направлению движения, тогда совершаемая этой силой работа отрицательна.

Работа отрицательна, так как функция \(косинус\) в интервале значений угла \(90° — 180°\) является отрицательной.

Таким образом, любая работа, совершённая силой трения или сопротивления, является отрицательной.

Пример:

Когда автомобиль едет с равномерной скоростью по прямой дороге, как это показано на рисунке, работа силы тяги автомобиля является положительной, а работа силы сопротивления равна по величине, но является отрицательной. В результате этого кинетическая и потенциальная энергия автомобиля остаются неизменными. 

Если сила направлена прямо противоположно направлению движения, тогда работу вычисляют по формуле: A=−F⋅l.

 

Источники:

Работа, мощность, энергия — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Механическая работа

К оглавлению…

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Работой, совершаемой постоянной силой F, называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S:

Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.

Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:

Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F_упр = kx).

 

Мощность

К оглавлению…

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P (иногда обозначают буквой N) – физическая величина, равная отношению работы A

к промежутку времени t, в течение которого совершена эта работа:

По этой формуле рассчитывается средняя мощность, т. е. мощность обобщенно характеризующая процесс. Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:

По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.

КПД – коэффициент полезного действия, равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:

Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.

Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).

В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:

 

Кинетическая энергия

К оглавлению…

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения):

То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е_к = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.

Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.

Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью

v, то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.

Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:

Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения. Применять данную теорему удобно в задачах на разгон и торможение тела.

 

Потенциальная энергия

К оглавлению…

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:

Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.

Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

Потенциальная энергия растянутой пружины рассчитывается по формуле:

где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x₁, тогда при переходе в новое состояние с удлинением x₂ сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы). Понятие потенциальной энергии для силы трения вводить нельзя.

 

Коэффициент полезного действия

К оглавлению…

Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).

КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.

В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.

В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.

Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т.п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.

Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.

 

Закон сохранения механической энергии

К оглавлению…

Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):

Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:

Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах. Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.

Алгоритм решения задач на закон сохранения энергии:

1. Найти точки начального и конечного положения тела.
2. Записать какой или какими энергиями обладает тело в данных точках.
3. Приравнять начальную и конечную энергию тела.
4. Добавить другие необходимые уравнения из предыдущих тем по физике.
5. Решить полученное уравнение или систему уравнений математическими методами.

Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.

 

Разные задачи на работу

К оглавлению…

Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:

1. Работу можно найти по формуле: A = FS∙cosα. Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
2. Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
3. Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
4. Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt.
5. Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.

 

Закон сохранения энергии и динамика вращательного движения

К оглавлению…

Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:

1. Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).
2. Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
3. Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
4. В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
5. Провести остальные необходимые математические операции для получения окончательного результата.

При решении задач надо помнить, что:

• Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
• При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
• Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.

 

Неупругие соударения

К оглавлению…

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц). В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).

 

Абсолютно упругий удар

К оглавлению…

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.  Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.

 

Законы сохранения. Сложные задачи

К оглавлению…

Несколько тел

В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.

Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:

1. выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
2. записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
3. учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
4. при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда

В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.

Столкновения с тяжёлой плитой

Пусть навстречу тяжёлой плите, которая движется со скоростью v, движется лёгкий шарик массой m со скоростью u_н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты. В таком случае, для конечной скорости шарика получим:

Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:

Задачи о максимальных и минимальных значениях энергии сталкивающихся шаров

В задачах такого типа главное понять, что потенциальная энергия упругой деформации шаров максимальна, если кинетическая энергия их движения минимальна – это следует из закона сохранения механической энергии. Сумма кинетических энергий шаров минимальна в тот момент, когда скорости шаров будут одинаковы по величине и направлены в одном направлении. В этот момент относительная скорость шаров равна нулю, а деформация и связанная с ней потенциальная энергия максимальна.

Механическая работа и мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа — мера воздействия силы.

Определение механической работы

Определение 1

Работа А, совершаемая постоянной силой F→, — это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

A=Fs cos α.

Работа – это скалярная величина. Единица измерения работы по системе СИ — Джоуль (Дж).

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F→: A=Fs cos α=Fss

При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsiсуммируется и производится по формуле:

A=∑∆Ai=∑Fsi∆si.

Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.

Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.

F→упр=-F→

Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.

Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.

Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид

A=kx22.

Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.

Определение 2

Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.

Мощность

Определение 3

Мощностью называют работу силы, совершаемую в единицу времени.

Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:

N=At.

Определение 4

Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт — это мощность, которую совершает работу в 1 Дж за время 1 с.

Помимо Ватта, существуют и внесистемные единицы измерения мощности.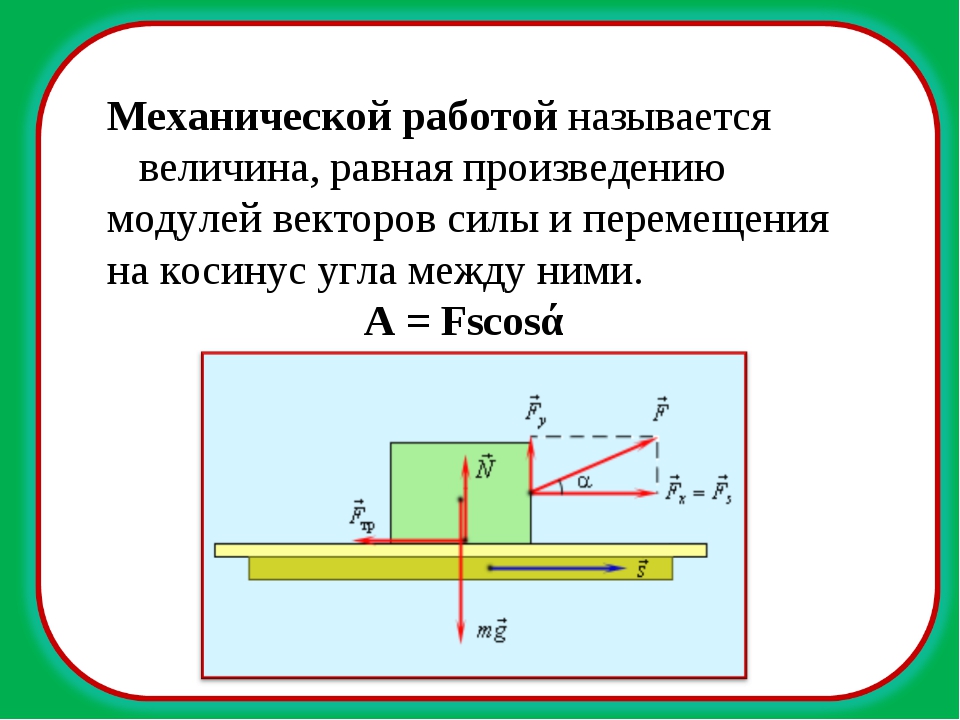 Например, 1 лошадиная сила примерна равна 745 Ваттам.  

Работа равнодействующей силы, тяжести, трения, упругости. Мощность, коэффициент полезного действия. Примеры, формулы

Тестирование онлайн

Работа

Работа — это скалярная величина, которая определяется по формуле

Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.

Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.

Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.

Угол между вектором силы и перемещением

1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.

На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.

Работа силы тяжести

Работа реакции опоры

Работа силы трения

Работа силы натяжения веревки

Работа равнодействующей силы

Работу равнодействующей силы можно найти двумя способами: 1 способ — как сумму работ (с учетом знаков «+» или «-«) всех действующих на тело сил, в нашем примере
2 способ — в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок

Работа силы упругости

Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.

Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу

Мощность

Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле

Коэффициент полезного действия

КПД — это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время

Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.

КПД наклонной плоскости — это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.

Главное запомнить

1) Формулы и единицы измерения;
2) Работу выполняет сила;
3) Уметь определять угол между векторами силы и перемещения

Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными.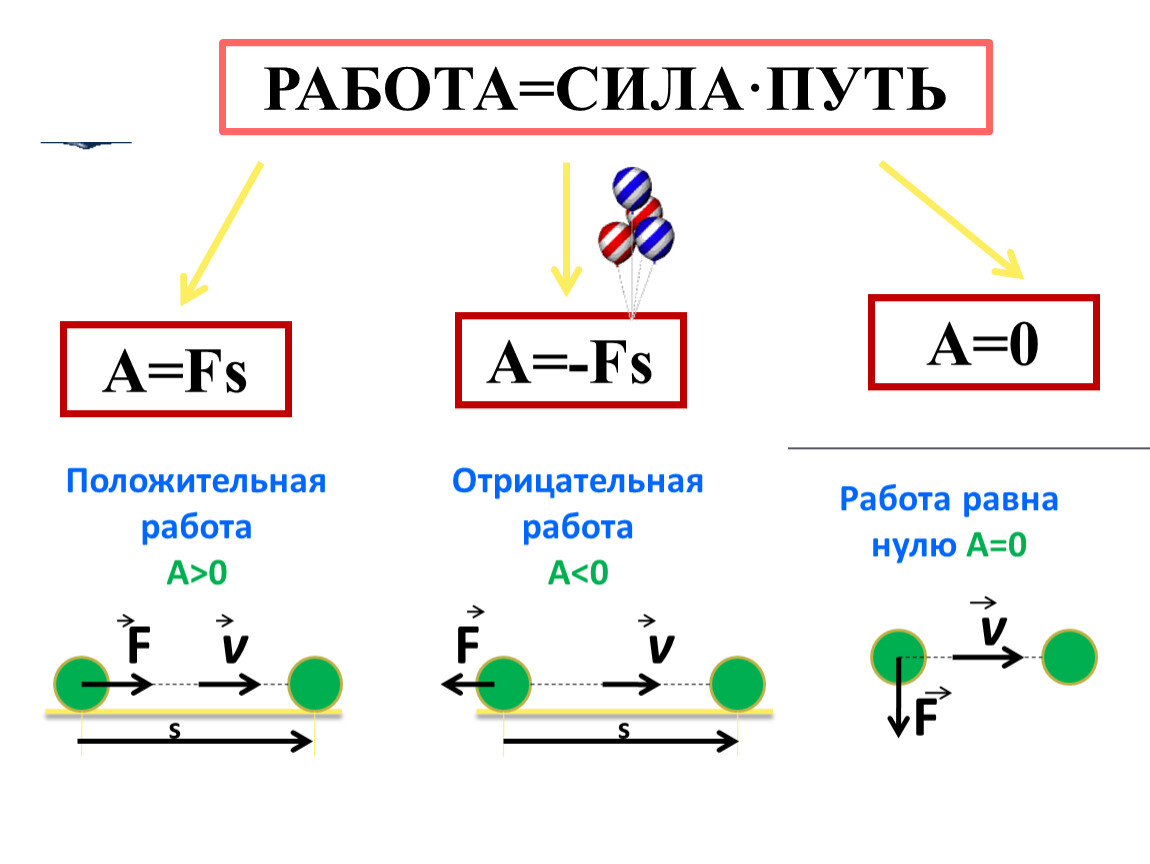 Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной.

Есть условия, при которых нельзя использовать формулу
Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:

Значение работы некоторой силы зависит от выбора системы отсчета.

Механическая работа. Мощность | Физика

1. Определение работы

С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.

Если сила направлена так же, как перемещение тела, то работа силы

A = Fs     (1)

В этом случае работа силы положительна.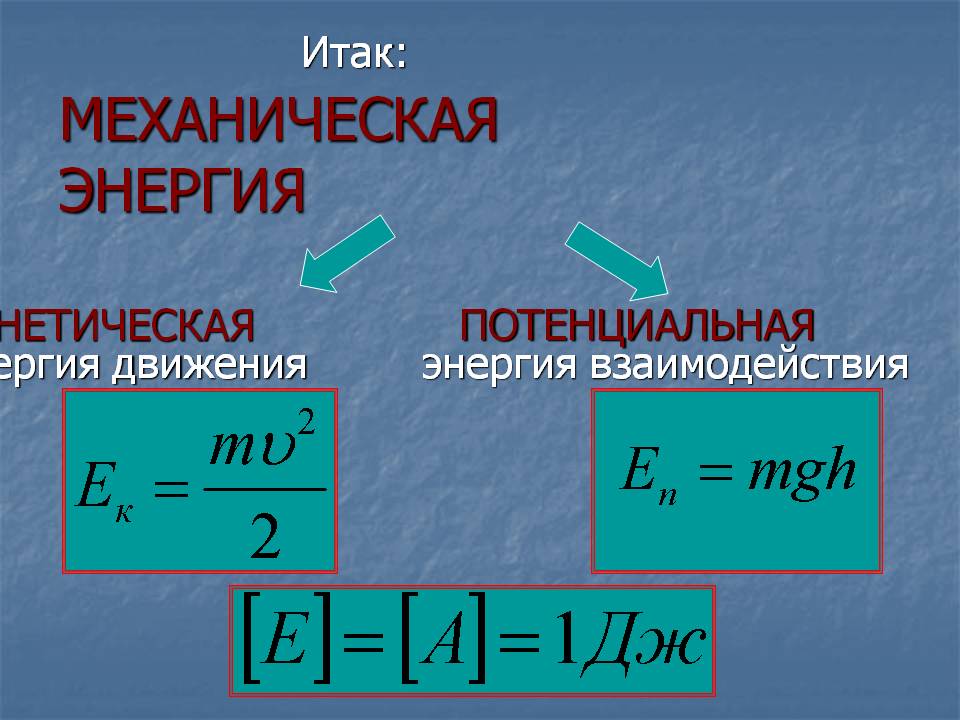

Если сила направлена противоположно перемещению тела, то работа силы

A = –Fs     (2)

В этом случае работа силы отрицательна.

Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:

A = 0      (3)

Работа – скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:

1 Дж = 1 Н * м.

? 1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском и столом равен 0,2. Чему равна работа действующей на брусок:
а) силы тяжести m?
б) силы нормальной реакции ?
в) силы упругости ?
г) силы трения скольжения _тр?

Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами:
1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.

Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.

? 2. Чему равна:
а) сумма работ всех действующих на брусок сил?
б) равнодействующая всех действующих на брусок сил?
в) работа равнодействующей? В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.

Работа A постоянной силы равна произведению модуля силы F на модуль перемещения s и на косинус угла α между направлением силы и направлением перемещения:

A = Fs cos α     (4)

? 3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.

? 4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) –3 Дж; в) –3 Дж; г) –6 Дж? Сделайте пояснительные чертежи.

2. Работа силы тяжести

Пусть тело массой m движется вертикально от начальной высоты h_н до конечной высоты h_к.

Если тело движется вниз (h_н > h_к, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (h_н < h_к, рис. 28.2, б), то работа силы тяжести отрицательна.

В обоих случаях работа силы тяжести

A = mg(h_н – h_к).     (5)

Найдем теперь работу силы тяжести при движении под углом к вертикали.

? 5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.

а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж.
б) Выразите работу силы тяжести через m, g, s, α.
в) Выразите s через h и α.
г) Выразите работу силы тяжести через m, g, h.
д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?

Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали – как вниз, так и вверх.

Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).

Таким образом,
работа силы тяжести при движении но любой траектории выражается формулой

A_т = mg(h_н – h_к),

где h_н – начальная высота тела, h_к – его конечная высота.
Работа силы тяжести не зависит от формы траектории.

Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.

? 6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?

3. Работа силы упругости

Когда пружина возвращается в недеформированное состояние, сила упругости совершает всегда положительную работу: ее направление совпадает с направлением перемещения (рис. 28.7).

Найдем работу силы упругости .
Модуль этой силы связан с модулем деформации x соотношением (см. § 15)

F = kx.     (6)

Работу такой силы можно найти графически.

Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).

На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.

Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.

Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).

? 7. Используя рисунок 28.10, докажите, что

работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой

A = (kx₂)/2.     (7)

? 8. Используя график на рисунке 28.11, докажите, что при изменении деформации пружины от x_н до x_к работа силы упругости выражается формулой

Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.

? 9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см.
а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?

? 10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?

4. Работа силы трения

Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).

Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.

? 11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см.
а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.

5. Мощность

Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.

Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:

P = A/t.      (9)

(Иногда мощность в механике обозначают буквой N, а в электродинамике – буквой P. Мы считаем более удобным одинаковое обозначение мощности.)

Единица мощности – ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что

1 Вт = 1 Дж/c.

? 12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?

Часто мощность удобно выражать не через работу и время, а через силу и скорость.

Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:

P = (Fs)/t = F(s/t) = Fv.     (10)

? 13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?

Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.

? 14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?

Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.

Дополнительные вопросы и задания

15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю.
а) Чему равна работа силы тяжести при подъеме мяча?
б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча?
г) Есть ли в условии лишние данные?

16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия?
в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?

17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.

а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности?
б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м?
в) Чему равен модуль силы трения при движении санок по горе?
г) Чему равна работа силы трения при спуске санок?
д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?

18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м₃, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.

Физика. Механическая работа | 7 класс Онлайн

Конспект по физике для 7 класса «Механическая работа». ВЫ УЗНАЕТЕ: Что такое механическая работа. Как рассчитать механическую работу. Когда механическая работа положительна, когда отрицательна и когда равна нулю. ВСПОМНИТЕ: Что такое сила? Каковы единицы силы?

Конспекты по физике    Учебник физики    Тесты по физике

---

Механическая работа

В обыденной жизни словом «работа» мы называем различные действия человека или технического устройства. Например, мы говорим: работает учитель, работает врач, работает грузчик, работает холодильник, pa6oтaeт компьютер. Хотя мы прекрасно понимаем, что речь идёт о разных вещах, и не стремимся сравнить результаты работы грузчика с результатами работы компьютера.

Если обозначить величины: работа — А, сила, действующая на тело, — F и пройденный путь – s, то работу рассчитывают по формуле A = Fs, если направление силы совпадает с направлением движения тела. В старших классах вы узнаете, как вычислять работу силы, направлен ной под углом к направлению движения тела.

ПРИМЕРЫ МЕХАНИЧЕСКОЙ РАБОТЫ

В физике термин «работа» или «механическая работа» — это определённая физическая величина, которую можно измерить.

Автомобиль движется по автомагистрали благодаря силе тяги работающего двигателя. Мяч под действием силы тяжести падает на поверхность Земли. В этих примерах на тела действуют силы, изменяется их скорость и положение в пространстве — совершается механическая работа.

Во всех технических устройствах, от самых простых до крайне сложных, всегда действуют силы, которые совершают работу при движении механизма или отдельных его частей. Так, например, в старинных паровых машинах сила давления пара на поршень совершает работу при движении поршня. А в современных электрических двигателях силы взаимодействия электрических токов совершают работу при вращении мотора.

ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКОЙ РАБОТЫ

Считается, что механическая работа совершается, когда тело движется под действием силы. Таким образом, в физике понятие работы напрямую связано с силой (нет силы — нет работы). Поэтому принято говорить о работе некоторой силы.

Механической работой называют физическую величину, зависящую от численного значения и направления силы и от перемещения точки се приложения. Механическая работа совершается только тогда, когда на тело действует сила и тело перемещается под действием этой силы. Следовательно, механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пути.

Таким образом, в самом простом случае работа равна произведению силы, действующей на тело, на путь, пройденный телом под действием этой силы: работа = сила х путь.

Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Например, мы везём по снегу санки, и направление приложенной нами силы совпадает с направлением движения.

В этом случае сила совершает положительную работу, которую определяют по формуле А = Fs.

Если движение тела происходит в направлении, противоположном направлению приложенной силы, то данная сила совершает отрицательную работу. Отрицательная работа, например, совершается силой трения скольжения в случае, когда сапки, скатившись с горы, движутся по снегу вплоть до полной остановки. В данном случае работа будет определяться по формуле А = –Fs.

Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю.

ЕДИНИЦА РАБОТЫ

За единицу работы принимают работу, совершаемую силой в 1 Н, на пути, равном 1 м. Единица работы — джоуль (Дж) названа в честь английского ученого Джеймса Джоуля.

1 Дж = 1 Н•м.

Также часто используют килоджоули и миллиджоули: 1 кДж = 1000 Дж, 1 мДж = 0,001 Дж.

СИТУАЦИИ, В КОТОРЫХ МЕХАНИЧЕСКАЯ РАБОТА НЕ СОВЕРШАЕТСЯ

Мы уже знаем, что если сила действует перпендикулярно направлению движения тела, то работа этой силы равна нулю. А в каких ещё случаях работа может быть равна нулю? Очевидно, что в случае, когда равны нулю либо силы, действующие на тело, либо под действием сил тело не перемещается.

Например, после выключения двигателя ракета, летящая в открытом космосе, продолжает движение по инерции. В этом случае нет действующей на тело силы и механическая работа не совершается.

Если мы стараемся сдвинуть с места тяжёлый предмет, но сила, с которой мы на него действуем, меньше максимально возможной в этом случае силы трения покоя, то предмет останется на месте. Поэтому, несмотря на нашу усталость, механической работы не совершалось, так как не было перемещения тела.

Как бы ни было тяжело мифологическому герою Атланту, держащему на плечах небесный свод, механической работы при этом он не совершал, так как небесный свод в этом случае не двигался.

ДЛЯ СПРАВКИ:

Джеймс Прескотт Джоуль (1818–1889). Английский физик, член Лондонского королевского общества.

---

Вы смотрели Конспект по физике для 7 класса «Механическая работа»: Что такое механическая работа. Как рассчитать механическую работу. Когда механическая работа положительна, когда отрицательна и когда равна нулю.
Вернуться к Списку конспектов по физике (В оглавление).

Пройти онлайн-тест «»

Определение и математика работы

В первых трех разделах «Класса физики» мы использовали законы Ньютона для анализа движения объектов. Информация о силе и массе использовалась для определения ускорения объекта. Информация об ускорении впоследствии использовалась для определения информации о скорости или смещении объекта по прошествии заданного периода времени. Таким образом, законы Ньютона служат полезной моделью для анализа движения и прогнозирования конечного состояния движения объекта.В этом модуле будет использоваться совершенно другая модель для анализа движения объектов. Движение будет рассматриваться с точки зрения работы и энергии. Будет исследовано влияние работы на энергию объекта (или системы объектов); итоговая скорость и / или высота объекта могут быть затем спрогнозированы на основе информации об энергии. Чтобы понять этот подход к анализу движения, основанный на работе и энергии, важно сначала получить твердое понимание нескольких основных терминов.Таким образом, Урок 1 этого раздела будет посвящен определениям и значениям таких терминов, как работа, механическая энергия, потенциальная энергия, кинетическая энергия и мощность.

Когда на объект действует сила, вызывающая смещение объекта, говорят, что над объектом было выполнено работы . Есть три ключевых ингредиента для работы — сила, смещение и причина. Чтобы сила квалифицировалась как выполнившая работы над объектом, должно быть смещение, и сила должна вызывать смещение .Есть несколько хороших примеров работы, которые можно наблюдать в повседневной жизни: лошадь, тащащая плуг по полю, отец, толкающий тележку с продуктами по проходу продуктового магазина, первокурсник, поднимающий на плечо рюкзак, полный книг, тяжелоатлет, поднимающий штангу над головой, олимпиец, запускающий толкание ядра, и т. д. В каждом описанном здесь случае на объект действует сила, заставляющая этот объект смещаться.

Прочтите следующие пять утверждений и определите, представляют ли они примеры работы.Затем нажмите кнопку «Просмотреть ответ», чтобы просмотреть ответ.

Заявление	Ответ с объяснением
Учитель применяет силу к стене и истощается.
Книга падает со стола и падает на землю.
Официант переносит поднос с едой над головой за одну руку прямо через комнату с постоянной скоростью. (Осторожно! Это очень сложный вопрос, который будет обсуждаться более подробно позже.)
Ракета летит в космосе.

Рабочее уравнение

Математически работу можно выразить следующим уравнением.

W = F • d • cos Θ

, где F — сила, d — смещение, а угол ( тета ) определяется как угол между силой и вектором смещения.Возможно, самый сложный аспект приведенного выше уравнения — это угол «тета». Угол — это не просто любой угол , а, скорее, очень специфический угол. Угловая мера определяется как угол между силой и смещением. Чтобы понять его значение, рассмотрите следующие три сценария.

• Сценарий А. Сила действует на объект вправо, когда он смещается вправо. В таком случае вектор силы и вектор смещения находятся в одном направлении.Таким образом, угол между F и d равен 0 градусов.

• Сценарий B: Сила действует влево на объект, смещенный вправо. В таком случае вектор силы и вектор смещения имеют противоположное направление. Таким образом, угол между F и d составляет 180 градусов.

• Сценарий C: Сила действует вверх на объект, когда он смещается вправо. В таком случае вектор силы и вектор смещения расположены под прямым углом друг к другу.Таким образом, угол между F и d составляет 90 градусов.

Для работы, силы должны Вызвать Смещения

Рассмотрим сценарий C более подробно. Сценарий C включает ситуацию, аналогичную ситуации, когда официант несет поднос с едой над головой за одну руку прямо через комнату с постоянной скоростью. Ранее упоминалось, что официант не работает с подносом , поскольку он переносит его через комнату.Сила, прикладываемая официантом к подносу, направлена ​​вверх, а смещение подноса — это горизонтальное смещение. Таким образом, угол между силой и смещением составляет 90 градусов. Если рассчитать работу официанта на подносе, то результат будет 0. Независимо от величины силы и смещения, F * d * косинус 90 градусов равен 0 (поскольку косинус 90 градусов равен 0 ). Вертикальная сила никогда не может вызвать горизонтальное смещение; таким образом, вертикальная сила не действует на горизонтально смещенный объект !!

Можно точно отметить, что рука официанта на короткое время толкала поднос вперед, чтобы ускорить его от состояния покоя до конечной скорости ходьбы.Но как только достигает скорости , лоток будет продолжать движение по прямой с постоянной скоростью без поступающей силы. И если единственная сила, действующая на лоток во время стадии его движения с постоянной скоростью, направлена ​​вверх, то с лотком не выполняется никаких действий. Опять же, вертикальная сила не действует на горизонтально смещенный объект.

Уравнение для работы содержит три переменных — каждая переменная связана с одним из трех ключевых слов, упомянутых в определении работы (сила, смещение и причина).Угол тета в уравнении связан с величиной силы, вызывающей смещение. Как упоминалось в предыдущем разделе, когда на объект действует сила под углом к ​​горизонтали, только часть силы способствует (или вызывает) горизонтальное смещение. Давайте рассмотрим силу цепи, тянущей вверх и вправо на Фидо, чтобы тянуть Фидо вправо. Только горизонтальная составляющая силы натяжения в цепи заставляет Фидо смещаться вправо.Горизонтальная составляющая находится путем умножения силы F на косинус угла между F и d. В этом смысле тета-косинус в уравнении работы относится к коэффициенту , вызывающему причину, — он выбирает часть силы, которая фактически вызывает смещение.

Значение теты

При определении меры угла в уравнении работы важно понимать, что угол имеет точное определение — это угол между силой и вектором смещения.Обязательно избегайте бездумного использования в уравнении любого олеугольного угла . Обычная физическая лаборатория включает приложение силы, чтобы переместить тележку по пандусу к вершине стула или ящика. К тележке прилагается усилие , чтобы сместить ее на вверх по склону с постоянной скоростью. Обычно используются несколько углов наклона; тем не менее, сила всегда применяется параллельно уклону. Перемещение тележки также параллельно уклону. Поскольку F и d находятся в одном направлении, угол theta в уравнении работы равен 0 градусов.Тем не менее, большинство студентов испытали сильное искушение измерить угол наклона и использовать его в уравнении. Не забывайте: угол в уравнении — это не просто , любой угол равен . Он определяется как угол между силой и вектором смещения.

Значение отрицательной работы

Иногда на движущийся объект действует сила, препятствующая перемещению.Примеры могут включать в себя автомобиль, заносящий до остановки на проезжей части, или бегущий по бейсболу, который останавливается по грязи на приусадебном участке. В таких случаях сила действует в направлении, противоположном движению объектов, чтобы замедлить его. Сила не вызывает смещения, а скорее препятствует . Эти ситуации включают то, что обычно называют отрицательной работой . отрицательный отрицательной работы относится к числовому значению, которое получается, когда значения F, d и тета подставляются в уравнение работы.Поскольку вектор силы прямо противоположен вектору смещения, тета составляет 180 градусов. Косинус (180 градусов) равен -1, поэтому количество работы, проделанной с объектом, будет отрицательным. Негативная работа станет важной (и более значимой) в Уроке 2, когда мы начнем обсуждать взаимосвязь между работой и энергией.

Единицы работы

Каждый раз, когда в физику вводится новая величина, обсуждаются стандартные метрические единицы, связанные с этой величиной.В случае работы (а также энергии) стандартной метрической единицей является Джоуль (сокращенно Дж ). Один Джоуль эквивалентен одному Ньютону силы, вызывающей смещение на один метр. Другими словами,

Джоуль — это единица работы.
1 Джоуль = 1 Ньютон * 1 метр
1 Дж = 1 Н * м

Фактически, любая единица силы, умноженная на любую единицу смещения, эквивалентна единице работы.Ниже показаны некоторые нестандартные агрегаты для работы. Обратите внимание, что при анализе каждый набор единиц эквивалентен единице силы, умноженной на единицу смещения.

Нестандартные единицы работы:

фут • фунт

кг • (м / с 2 ) • м

кг • (м 2 / с 2 )

Таким образом, работа выполняется, когда на объект действует сила, вызывающая смещение.Чтобы рассчитать объем работы, необходимо знать три величины. Эти три величины — сила, смещение и угол между силой и смещением.

Расследовать!

Работаем каждый день. Работа, которую мы делаем, требует калорий … эээээ, следует сказать Джоулей. Но сколько джоулей (или калорий) было бы израсходовано на различные виды деятельности? Используйте виджет Daily Work , чтобы исследовать объем работы, который необходимо выполнить для бега, ходьбы или езды на велосипеде в течение заданного времени в заданном темпе.

Нажмите, чтобы продолжить урок по работе

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного интерактивного приложения It’s All Uphill. Вы можете найти его в разделе Physics Interactives на нашем сайте.Интерактивная программа It’s All Uphill Interactive позволяет учащемуся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.

Работа — Гипертекст по физике

Обсуждение

что такое работа?

Целевая аудитория этой книги — люди с некоторым образованием. Это не детская книга; и под детьми я не имею в виду противоположность взрослых.Я считаю подростков (или подростков, если хотите) прото-взрослыми. Если это относится к вам, значит, у вас было формальное научное образование (хорошее, плохое или уродливое). Где-то по ходу дела вы должны были познакомиться с концепцией энергии. Если нет, то перестаньте читать это и найдите себе образование (или хотя бы какой-то жизненный опыт).

Те из вас, у кого было небольшое формальное образование, вероятно, получили урок энергии в какой-то момент своей жизни. Если это так, то велики шансы, что вам дали определение энергии как «способность выполнять работу».Если вы были хорошим учеником или просто хотели доставить удовольствие своему учителю, вы, вероятно, слышали это и сказали себе: «Хорошо, энергия — это способность выполнять работу». Если бы вы были действительно хорошим учеником с желанием учиться или очень плохим учеником с желанием указать на интеллектуальные недостатки вашего учителя, тогда вам следовало бы задать следующий логичный вопрос. Что такое работа?

Надеюсь, вам дали правильный ответ, но шансы пятьдесят на пятьдесят, что вы проигнорировали.Не потому, что правильный ответ так сложно узнать, а потому, что правильный ответ так сложно объяснить или, по крайней мере, трудно объяснить так, чтобы его можно было быстро уловить. Я думаю, это в основном связано с тем, что слово «работа» имеет два значения: обычное для повседневной жизни и техническое — для физики.

Технически, работа — произведение силы-смещения (для тех из вас, кто предпочитает алгебру)

W = F ∆ с cos θ

или интеграл по траектории сила-смещение (для тех из вас, кто предпочитает исчисление).

Я понимаю, что для многих из вас это бессмысленное определение. Так много слов и так мало сказано, не так ли? На самом деле, как раз наоборот. Это определение настолько компактно, что похоже на поэзию. Он говорит как можно больше, используя как можно меньше слов. Оно настолько компактно, что объяснение его на обычном языке приводит к тому, что полдюжины слов технического определения расширяются до почти сотни слов так называемого «естественного языка». Позвольте мне объяснить, что такое работа, с помощью серии мысленных образов. Каждый раз, когда приводится пример, помните, что работа выполняется всякий раз, когда сила вызывает смещение.

Представьте себе, что учитель физики неподвижно стоит перед классом учеников. Поскольку он не прилагает никаких сил, которые могли бы сместить что-либо за пределами его тела, он не выполняет никакой работы. Очевидно. Но выполнение этого в течение любого промежутка времени, безусловно, истощит его энергию, как если бы он весь день толкал бумаги по столу (пример, когда сила приводит к тому, что сила приводит к смещению). Конечно, теперь вы могли бы убедить его, что его определение работы должно быть неправильным. Может быть, под давлением уступит меньший учитель, но не учитель физики.

Безусловно, учитель физики или любой другой человек, стоящий , — это , выполняющий работу, но выполняемую работу не так-то легко увидеть. Внутри тела сердце перекачивает кровь, пищеварительная система переваривает завтрак, рецепторы перемещают молекулы через клеточные мембраны. Мы работаем, даже когда спим. Силы, вызывающие смещения, происходят повсюду у нас под кожей. Человеческое тело — это занятое место.

Если система в целом воздействует на свое окружение и происходит смещение, то выполненная работа называется внешней работой .Учитель физики, толкая бумаги через стол, выполняет внешнюю работу. Стоящий неподвижно учитель физики не выполняет значительной внешней работы.

Если часть системы воздействует на другую часть той же системы и происходит смещение, выполненная работа называется внутренней работой . Учитель физики глубоко мыслящий или лежащий в коме выполняет внутреннюю работу. (Дополнительный балл, если вы можете отличить их.) Учитель физики, который что-то делает — или ничего не делает — выполняет внутреннюю работу.Умерший учитель физики не выполняет никакой работы, внутренней или внешней. В механике, когда мы говорим, что работа сделана, мы часто имеем в виду внешнюю работу.

Теперь, когда мы решили, что учитель, стоящий на месте, не выполняет никакой работы, давайте представим, что учитель двигается и спрашивает, была ли работа выполнена. Хм, хорошо, когда руки и ноги начинают двигаться, ситуация умеренно сложная. Это затрудняет определение того, что в движении требует работы, а что нет. Нам нужно еще немного упростить.Дайте учителю книгу (например, учебник физики) и попросите его переместить книгу несколькими простыми способами. Теперь возникает вопрос: «Выполнил ли учитель какую-нибудь работу над книгой ?» Это гораздо уже, чем спрашивать, выполнял ли учитель какую-либо работу, а это означает, что на него легче ответить и лучше подходит для ознакомления с концепцией.

Для учителя, держащего книгу или любую другую систему в этом отношении, работа выполняется всякий раз, когда сила вызывает смещение. Рассмотрим следующие шесть примеров, представленных по три за раз.

Никакая работа не выполняется с учебником, когда он находится в состоянии покоя. Положительная работа выполняется с учебником, когда он поднимается вертикально с постоянной скоростью. Положительная работа также выполняется с учебником, когда он поднимается по диагонали с постоянной скоростью.

Первый пример имеет очевидный смысл. Если держать книгу, не перемещая ее, работа с книгой не выполняется. Замени учителя на стол или пол. На полу лежит книга. Какую работу выполняет пол? Ничего никуда не денется.Ничего не происходит. Ничего не делается — даже не работает.

Второй и третий примеры тоже имеют смысл. Учитель толкает книгу, и она движется. Сила привела к смещению. Работа была сделана. Это согласуется с нашим повседневным представлением о работе. Все в порядке с миром.

Рассмотрим еще три примера.

Работа с учебником не выполняется, если его переносят горизонтально с постоянной скоростью. Отрицательная работа выполняется с учебником, когда его опускают по диагонали с постоянной скоростью.Отрицательная работа также выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

Первый в этом наборе надоедливый. Это нелогично. По сути, это говорит о том, что не нужно переносить книгу по ровной поверхности. Это настолько очевидно глупо, что должно быть неправильно, верно? Неправильный! Это верно. (Вы должны прочитать этот последний бит как внутренний диалог, чтобы он имел смысл.) Работа над объектом выполняется всякий раз, когда сила вызывает смещение. В этом примере приложенная сила вертикальна, но смещение горизонтально.Как вертикальная сила влияет на горизонтальное движение? Короткий ответ: «Это не так».

Вертикальные силы влияют на вертикальное движение. Горизонтальные силы влияют на горизонтальное движение. Когда движение и сила параллельны, жизнь проста. Когда движение и сила , а не параллельны, жизнь , а не просто. Ангелы уходят, и демоны вступают во владение. Под демонами я подразумеваю векторы, в частности, векторные компоненты. Работа выполняется всякий раз, когда сила или составляющая силы приводит к смещению.Никакая составляющая силы не действует в направлении движения, когда книга перемещается горизонтально с постоянной скоростью. Сила и смещение независимы. Ручная работа над книгой не выполняется.

Взгляните на последние два примера в этом наборе из шести. Здесь мы видим, что ведется негативная работа. Учитывая то, что я сказал о компонентах, это может иметь или не иметь для вас смысла. И снова, когда сила и смещение параллельны, жизнь проста.

Приложите силу → Переместите объект → Выполните работу

Когда сила не совсем параллельна смещению, это похоже на то, что для выполнения работы используется меньшая сила.

Приложите меньшее усилие → Сделайте меньше работы

Это тоже довольно просто. Когда угол между силой и смещением достигает 90 °, составляющая силы, параллельная смещению, уменьшается до нуля.

Не прилагать усилия → Не работать

Хорошо, сначала это было нелогично, но теперь в этом есть смысл.

Чем дальше два вектора удаляются от параллели, тем меньше работы выполняется. Увеличьте угол до 90 °. Сила и смещение начинают двигаться в противоположных направлениях.При 90 ° никаких работ не производилось. Если угол превышает 90 °, работа не должна выполняться. Это отрицательная работа.

Приложите меньшее усилие → Работайте меньше, чем не работайте

Есть еще одна причина принять негативную работу. Знак работы указывает направление изменения. Отрицательный знак указывает на потерю чего-либо. В случае опускания книги это означает снижение ее способности выполнять работу — снижение ее энергии.

Следуйте этой цепочке рассуждений. Чтобы поднять книгу, нужно потрудиться.Поднятие книги повышает ее энергию. Теперь я могу использовать энергию, хранящуюся в книге, для работы — и под «работой» я имею в виду физический труд, а не обучение американской молодежи. Я могу толкать им разные вещи — грецкие орехи, насекомых, квадратные колышки в круглые отверстия. Я делаю эту работу, опуская книгу. Это также снижает его энергию. Он больше не может работать, когда снова лежит на столе. Поднятие книги действительно работает. Его опускание отменяет работу над ним. С точки зрения работы или энергии книга вернулась в исходное состояние.В числовом выражении положительная работа, проделанная при ее повышении, была отменена отрицательной работой, сделанной при ее понижении, что привело к нулю выполненной работы в целом по книге . (Ситуация иная для разбитого грецкого ореха, насекомого или квадратного колышка.)

алгебра

Работа выполняется всякий раз, когда сила вызывает смещение. При прочих равных условиях применение большей силы должно приводить к выполнению большего объема работы. Точно так же приложение заданной силы на большем расстоянии должно привести к выполнению большего количества работы.И, как мы обсуждали в дюжине параграфов, предшествующих этому, важна составляющая силы, параллельная смещению. Работа прямо пропорциональна первым двум факторам: силе и перемещению. Направление обрабатывается функцией косинуса. Косинус наибольший, когда угол равен нулю (угол между двумя векторами, указывающими в одном направлении, равен нулю), ноль при девяноста градусах (силы, перпендикулярные смещению, не действуют), и отрицательный для тупых углов (силы, действующие в противоположном направлении смещения, отменяют работу). .

Работа лучше всего определяется уравнением. Вот одна распространенная версия…

W = F ∆ с cos θ

где…

Вт =	работ выполнено
F =	среднее приложенное усилие
∆ с =	смещение, вызванное силой
θ =	Угол усилие-смещение

Это уравнение предполагает, что сила постоянна как по величине, так и по направлению относительно смещения во все времена.Для многих задач это предположение разумно, поэтому оно написано здесь.

исчисление

Для тех случаев, когда изменения в величине или направлении значительны, мы представляем наше знакомое исчисление. При некотором конечном смещении сила может изменяться по величине и направлению. При меньшем смещении он наверняка изменится меньше. Разрежьте смещение на серию небольших смещений, вычислите работу, проделанную на каждом шаге, и сложите результаты вместе. Для достижения наилучших результатов позвольте ступенькам приблизиться к бесконечно малому размеру.

Пока мы занимаемся этим, давайте также заменим функцию косинуса более компактной нотацией скалярного произведения. Есть два способа умножения векторов — скалярное произведение · и перекрестное произведение ×. Скалярное произведение — это скалярный продукт, который увеличивается с увеличением сходства направления. Триггерная функция, которая делает это, — косинус. Перекрестное произведение — это векторное произведение, которое увеличивается с увеличением перпендикулярности и выходит за пределы плоскости, содержащей два вектора.Триггерная функция, которая это делает, — синус. Поскольку мы ранее определили косинус как правильную функцию, мы будем использовать скалярное произведение.

В пределе конечное ∆ s становится бесконечно малым d s , а конечное ∑ становится бесконечным ∫. Конечная сумма конечных величин всегда конечна. Бесконечный интеграл бесконечно малых дифференциалов также может быть конечным. Магия исчисления в том, что последнее вообще может быть правдой.

Работа лучше всего определяется уравнением.Вот еще одна распространенная версия…

Это уравнение является примером интеграла по путям (или линейного интеграла ). Когда большинство студентов знакомятся с интеграцией, им говорят, что интеграция — это способ найти площадь под кривой. Это делается путем математического разбиения кривой на бесконечно малые сегменты одинаковой ширины, измерения площади прямоугольной полосы, которая помещается между каждым сегментом кривой и горизонтальной осью, а затем сложения площадей сегментов вместе.Нет ничего плохого в том, что это введение в интеграцию, но иногда студенты зацикливаются на понятии, что интеграция — это просто «поиск области». Интеграция — это действительно соединение частей в единое целое. Это основное значение слова на английском языке и — основное значение слова в исчислении. Интегрирование можно использовать, чтобы найти площадь под кривой (я назову это традиционным интегралом ), но его также можно использовать, чтобы найти количество некоторой величины, накопленной на пути (интеграл по пути ), чтобы найти количество некоторого количества, захваченного поверхностью (интеграл поверхности ), или количество некоторого количества, содержащегося в объеме (интеграл объема ).

Квартир

Единица работы СИ — джоуль .

[J = Н · м = кг · м ² / с ² ]

Работа и энергия могут быть выражены в одних и тех же единицах. К сожалению, помимо джоуля есть много единиц для энергии. (Это обсуждается в другом разделе этой книги.) Наиболее часто встречающиеся в США в начале 21 века, вероятно, калории (диета и питание), британские тепловые единицы (отопление и охлаждение), киловатт-час (счета за электроэнергию), тепловая энергия ( счета за природный газ), квадроцикл (макроэкономика), тонна тротила (ядерное оружие), эрг (ученые старшего возраста) и фут-фунт (инженеры старшего возраста).Первые два в этом списке, калорийность и британская тепловая единица, были впервые введены учеными XIX века, изучающими калориметрию. (Французы дали нам калорию, а англичане дали британские тепловые единицы или британские тепловые единицы.) Последний в списке фунт-фут был введен учеными 19 века, изучающими механику. В XIX веке калориметрия и механика были отдельными дисциплинами. Калориметрия — это исследование тепла. Механика — это изучение движения и сил. Образованный джентльмен (а в то время обычно это были мужчины) мог изучать и то, и другое, но он, вероятно, не связывал их сколько-нибудь значительным образом.То есть, если только его не звали Джоуль.

Джеймс Джоуль (1818–1889) был богатым английским пивоваром, который занимался различными аспектами науки и экономики. Иногда эти усилия совпадали. Он изобрел фут-фунт как единицу работы: фут является единицей перемещения, а фунт — единицей силы. Это позволило ему количественно сравнить «экономичность» различных механических систем. В то время паровые двигатели, работающие на угле, были основным источником промышленной мощи, но тогда на горизонте высоких технологий появилась электроэнергия.Джоуль понял, что механическая работа, тепло и электрическая энергия каким-то образом взаимозаменяемы. Тепло может работать. Работа может вызвать тепло. Работа может производить электричество, Электричество может производить работу, Электричество может производить тепло. Тепло может производить электричество. Энергия — актер разносторонний.

Наиболее известным экспериментом

Джоуля, вероятно, является определение механического эквивалента тепла (я надеюсь, что он будет обсуждаться более подробно в другом месте этой книги). Теплота измерялась в британских тепловых единицах (по крайней мере, британцами), а работа — в фут-фунтах (что изобрел Джоуль).Джоуль установил, что одна британская тепловая единица тепла эквивалентна примерно 770 фут-фунтам механической работы — очень близко к сегодняшнему значению 778 фут-фунт / британских тепловых единиц. Этот результат был важен для осознания того, что, несмотря на то, что она проявляется во множестве форм, энергия — это одно.

Международная система единиц, которая начала доминировать в научном мире в середине 20 века, имела французское происхождение. Фут-фунтам и британским тепловым единицам не место в этой гораздо более логичной системе.12 дюймов в футе. 16 унций в фунте. 128 унций в галлоне в США и неизвестно сколько в Великобритании. Математика была слишком сложной. Parlez-vous les unités métriques ? СИ был французским по происхождению, но международным по своему характеру. Когда прозвучал призыв назвать единицу энергии, ответ был громким: Джоуль! Отпущение грехов!

Некоторые примечания к агрегатам.

• Джоуль эквивалентен ньютон-метру , но он никогда не должен называться таковым.Эта единица зарезервирована для крутящего момента. Крутящий момент также является произведением силы-смещения, но другого вида. Крутящий момент максимизируется, когда сила и смещение перпендикулярны, что означает, что он использует синус вместо косинуса для согласования направления (или для более продвинутых читателей он использует перекрестное произведение вместо скалярного произведения). Крутящий момент не измеряется в джоулях, и работу никогда не следует измерять в ньютон-метрах.
• Гауссовская единица работы — эрг [эрг = дин см = г см ² / с ² ].10 000 000 эрг = 1 джоуль. Слово эрг происходит от классического греческого слова, обозначающего работу: εργον ( ergon ). ERG также было названием спортивного напитка, появившегося в США в конце 1960-х или начале 1970-х годов. ERG расшифровывалось как «замена электролита глюкозой».
• Англо-американская единица работы — фут-фунт (когда фунт является единицей силы) или фут-фунтал (когда фунт является единицей массы). Первое встречается чаще, чем второе. Путаницы с единицами крутящего момента можно избежать, изменив порядок.Англо-американская единица крутящего момента — фунт-фут или фунт-фут в зависимости от вашего определения фунта. Опять же, первое встречается чаще, чем второе. Джеймс Джоуль изобрел фут-фунт.

консервативные против неконсервативных сил

текст

Положительная работа выполняется, когда учебник перемещается вправо по поверхности стола уровня с постоянной скоростью. Положительная работа также выполняется, когда учебник перемещается влево по поверхности стола уровня с постоянной скоростью.

текст

Положительная работа выполняется над учебником, когда он поднимается вертикально с постоянной скоростью. Отрицательная работа выполняется над учебником, когда он опускается вертикально с постоянной скоростью.

текст

теорема об энергии работы

текст

W = ∆ E

• работа вызывает изменение энергии
• работа переносит энергию из одной системы в другую

Условные обозначения:

• Когда система работает в своей среде, W <0; то есть полная энергия системы уменьшается.Работа выполняется по системе.
• Когда среда работает в системе, W > 0; то есть полная энергия системы увеличивается. Работа ведется по системе .

Томас Янг (1773–1829) был первым, кто использовал эту формулу. ← Это правда?

Определение работы по физике

В физике работа определяется как сила, вызывающая движение или смещение объекта. В случае постоянной силы работа — это скалярное произведение силы, действующей на объект, и смещения, вызванного этой силой.Хотя и сила, и смещение являются векторными величинами, работа не имеет направления из-за природы скалярного произведения (или скалярного произведения) в векторной математике. Это определение согласуется с правильным определением, потому что постоянная сила интегрируется просто как произведение силы и расстояния.

Читайте дальше, чтобы узнать о некоторых реальных примерах работы, а также о том, как рассчитать объем выполняемой работы.

Примеры работ

Примеров работы в повседневной жизни много.В классе физики есть несколько заметок: лошадь, тащащая плуг по полю; отец толкает тележку с продуктами по проходу продуктового магазина; студентка поднимает на плечо рюкзак, полный книг; штангист поднимает над головой штангу; и олимпиец запускает толкание ядра.

В общем, для того, чтобы работа произошла, к объекту должна быть приложена сила, заставляющая его двигаться. Итак, разочарованный человек, толкающийся о стену только для того, чтобы истощить себя, не выполняет никакой работы, потому что стена не двигается.Но если книга упадет со стола и ударится о землю, это будет считаться работой, по крайней мере, с точки зрения физики, потому что сила (гравитация) действует на книгу, заставляя ее смещаться вниз.

Что не работает

Интересно, что официант, несущий поднос высоко над его головой и поддерживаемый одной рукой, когда он идет равномерным шагом через комнату, может подумать, что он много работает. (Он может даже вспотеть.) Но, по определению, он не выполняет никакой работы .Правда, официант силой толкает поднос над головой, и правда, поднос движется по комнате, пока официант идет. Но сила — поднятие подноса официантом — не заставляет поднос двигаться. «Чтобы вызвать смещение, должна быть компонента силы в направлении смещения», — отмечает The Physics Classroom.

Расчет работы

Базовый расчет работы на самом деле довольно прост:

W = Fd

Здесь «W» означает работу, «F» — силу, а «d» — смещение (или расстояние, на которое перемещается объект).Physics for Kids дает следующий пример задачи:

Бейсболист бросает мяч с силой 10 ньютонов. Мяч летит на 20 метров. Какая общая работа?

Чтобы решить эту проблему, вам сначала нужно знать, что Ньютон определяется как сила, необходимая для обеспечения массы в 1 килограмм (2,2 фунта) с ускорением 1 метр (1,1 ярда) в секунду. Ньютон обычно обозначается сокращенно как «Н.» Итак, воспользуйтесь формулой:

Вт = Fd

Таким образом:

Вт = 10 Н * 20 метров (где символ «*» обозначает время)

Так:

Работа = 200 джоулей

Джоуль, термин, используемый в физике, равен кинетической энергии 1 килограмма, движущегося со скоростью 1 метр в секунду.

Работа: Научное определение | Физика

Цели обучения

К концу этого раздела вы сможете:

• Объясните, как объект должен перемещаться, чтобы сила, действующая на него, выполняла работу.
• Объясните, как относительные направления силы и смещения определяют, является ли выполненная работа положительной, отрицательной или нулевой.

Что значит работать

Научное определение труда несколько отличается от его повседневного значения.Некоторые вещи, которые мы считаем тяжелой работой, например написание экзамена или ношение тяжелой ноши на ровной поверхности, не являются работой, как это определено ученым. Научное определение работы показывает ее связь с энергией — когда работа выполняется, энергия передается.

Для выполнения работы в научном смысле необходимо приложить силу и должно быть движение или смещение в направлении силы.

Формально, работа , выполняемая в системе с помощью постоянной силы, определяется как произведение составляющей силы в направлении движения на расстояние, на которое действует сила .Для одностороннего движения в одном измерении это выражается в форме уравнения как W = | F | (cos θ ) | d |, где W — работа, d — смещение системы, а θ — угол между вектором силы F и вектором смещения d , как на рисунке 1. Мы также можно записать это как W = Fd cos θ .

Чтобы найти работу, проделанную в системе, которая претерпевает движение, которое не является односторонним или которое находится в двух или трех измерениях, мы делим движение на односторонние одномерные сегменты и складываем работу, выполненную по каждому сегменту.

Что такое работа?

Работа, совершаемая в системе постоянной силой, равна произведению составляющей силы в направлении движения на расстояние, на которое действует сила . Для одностороннего движения в одном измерении это выражается в форме уравнения как W = Fd cos θ , где W — работа, F — величина силы, действующей на систему, d. — величина смещения системы, а θ — угол между вектором силы F и вектором смещения d .

Рисунок 1. Примеры работы. (a) Работа, выполняемая силой F на этой газонокосилке, составляет Fd cos θ . Обратите внимание, что F cos θ — это составляющая силы в направлении движения. (б) Человек, держащий портфель, не работает с ним, потому что нет движения. Никакая энергия не передается в портфель или из него. (c) Человек, перемещающий портфель в горизонтальном направлении с постоянной скоростью, не работает с ним и не передает ему энергию.(d) Работа с портфелем выполняется путем его подъема по лестнице с постоянной скоростью, поскольку обязательно присутствует составляющая силы F в направлении движения. Энергия передается в портфель и, в свою очередь, может использоваться для работы. e) когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, выполняемая генератором с портфелем, является отрицательной, что приводит к отведению энергии из портфеля, потому что F и d находятся в противоположных направлениях.

Чтобы изучить, что означает определение работы, давайте рассмотрим другие ситуации, показанные на рисунке 1. Например, человек, держащий портфель на рисунке 1b, не работает. Здесь d = 0, значит W = 0. Почему вы устаете просто держать груз? Ответ заключается в том, что ваши мышцы работают друг против друга, , но они не работают в интересующей системе («система портфель-Земля» — см. Подробнее «Энергия гравитационного потенциала»).Для выполнения работы должно быть движение, и должна быть составляющая силы в направлении движения. Например, человек, несущий портфель на ровной поверхности на рисунке 1c, не работает с ним, потому что сила перпендикулярна движению. То есть cos 90º = 0, и поэтому W = 0.

Напротив, когда сила, действующая на систему, имеет компонент в направлении движения, как на рис. 1d, работа выполняется на — энергия передается портфелю.Наконец, на рисунке 1e энергия передается от портфеля к генератору. Есть два хороших способа интерпретировать эту передачу энергии. Одно из объяснений состоит в том, что вес портфеля действительно воздействует на генератор, давая ему энергию. Другая интерпретация заключается в том, что генератор отрицательно воздействует на портфель, тем самым забирая из него энергию. На чертеже показано последнее, где сила от генератора направлена ​​вверх на портфель, а смещение — вниз. Это составляет θ = 180º, а cos 180º = -1; следовательно, W отрицательно.

Расчет работы

Работа и энергия имеют одинаковые единицы. Из определения работы мы видим, что эти единицы — это сила, умноженная на расстояние. Таким образом, в единицах СИ работа и энергия измеряются в ньютон-метров . Ньютон-метр получает специальное название джоуль (Дж), а 1Дж = 1Н · м = 1 кг · м ² / с ² . Один джоуль — это не большое количество энергии; он поднимет небольшое 100-граммовое яблоко на расстояние около 1 метра.

Пример 1.Расчет работы, которую вы выполняете, чтобы протолкнуть газонокосилку по большой лужайке

Сколько работы проделывает с газонокосилкой человек, изображенный на Рисунке 1a, если он прикладывает постоянную силу 75,0 Н под углом 35º ниже горизонтали и толкает газонокосилку на 25,0 м по ровной поверхности? Преобразуйте объем работы из джоулей в килокалории и сравните его со средним дневным потреблением этого человека 10 000 кДж (около 2400 ккал) пищевой энергии. Одна калорий (1 кал) тепла — это количество, необходимое для нагрева 1 г воды на 1ºC, и эквивалентно 4.184 Дж, а на одну пищевую калорию (1 ккал) эквивалентно 4184 Дж.

.

Стратегия

Мы можем решить эту проблему, подставив указанные значения в определение работы, выполняемой в системе, указанное в уравнении Вт = Fd cos θ . Приведены сила, угол и перемещение, поэтому неизвестна только работа W .

Решение

Уравнение для работы: Вт = Fd cos θ .{-4} \\ [/ латекс]

Обсуждение

Это соотношение — крошечная доля того, что человек потребляет, но это типичное значение. Очень мало энергии, выделяемой при потреблении пищи, используется для работы. Даже когда мы «работаем» весь день, менее 10% потребляемой нами энергии уходит на работу, а более 90% преобразуется в тепловую энергию или сохраняется в виде химической энергии в жире.

Сводка раздела

Работа — это передача энергии силой, действующей на объект при его перемещении.

Работа W , которую сила F производит на объект, является произведением величины F силы, умноженной на величину d смещения, умноженную на косинус угла θ между ними. . В символах Вт = Fd cos θ .

Единицей измерения работы и энергии в системе СИ является джоуль (Дж), где 1 Дж = 1 Н · м = 1 кг · м ² / с ² .

Работа, совершаемая силой, равна нулю, если смещение равно нулю или перпендикулярно силе.

Выполненная работа является положительной, если сила и смещение имеют одинаковое направление, и отрицательной, если они имеют противоположное направление.

Концептуальные вопросы

1. Приведите пример того, что мы считаем работой в повседневных обстоятельствах, что не является работой в научном смысле. В вашем примере энергия передается или изменяется по форме? Если да, объясните, как это достигается без выполнения работы.
2. Приведите пример ситуации, в которой есть сила и смещение, но сила не работает.Объясните, почему это не работает.
3. Опишите ситуацию, в которой сила действует в течение длительного времени, но не работает. Объяснять.

Задачи и упражнения

1. Сколько работы кассир в супермаркете проделывает с банкой с супом, которую он толкает на 0,600 м по горизонтали с силой 5,00 Н? Выразите свой ответ в джоулях и килокалориях.
2. Человек весом 75,0 кг поднимается по лестнице, набирая высоту 2,50 метра. Найдите работу, проделанную для выполнения этой задачи.
3. (а) Рассчитайте работу, проделанную с кабиной лифта массой 1500 кг по тросу, чтобы поднять ее 40.0 м при постоянной скорости, предполагая, что трение в среднем составляет 100 Н. (b) Какую работу совершает в этом процессе сила тяжести на подъемнике? (c) Какова общая работа подъемника?
4. Предположим, автомобиль проезжает 108 км со скоростью 30,0 м / с и использует 2,0 галлона бензина. Только 30% бензина расходуется на полезную работу за счет силы, которая позволяет автомобилю двигаться с постоянной скоростью, несмотря на трение. (В галлоне бензина 1,2 × 10 ⁸ Дж.) (A) Какова величина силы, прилагаемой для поддержания постоянной скорости движения автомобиля? (b) Если требуемая сила прямо пропорциональна скорости, сколько галлонов будет использовано для проезда 108 км со скоростью 28.0 м / с?
5. Рассчитайте работу, проделанную мужчиной весом 85,0 кг, который толкает ящик на 4,00 м по пандусу, образующему угол 20,0 ° с горизонтом. (См. Рис. 2.) Он прилагает силу 500 Н к ящику параллельно рампе и перемещается с постоянной скоростью. Обязательно укажите работу, которую он проделывает с ящиком и телом, чтобы подняться по пандусу.

   Рис. 2. Мужчина толкает ящик по пандусу.

6. Сколько работы выполняет мальчик, тащащий свою сестру 30,0 м в фургоне, как показано на рисунке 3? Предположим, что на вагон не действует трение.

   Рис. 3. Мальчик работает с системой телеги и ребенка, когда тянет их, как показано.

7. Покупатель толкает тележку для продуктов на 20,0 м с постоянной скоростью по ровной поверхности, преодолевая силу трения 35,0 Н. Он толкает в направлении на 25,0 ° ниже горизонтали. а) Какая работа происходит с тележкой за счет трения? б) Какую работу совершает гравитационная сила на тележке? (c) Какую работу проделывает покупатель с тележкой? (d) Найдите силу, которую оказывает покупатель, используя энергетические соображения.(e) Какова общая работа, проделанная с тележкой?
8. Предположим, что лыжный патруль спускает спасательные сани и пострадавшего, общая масса которого составляет 90,0 кг, вниз по склону 60,0 ° с постоянной скоростью, как показано на рисунке 4. Коэффициент трения между санями и снегом составляет 0,100. а) Сколько работы совершает трение, когда сани движутся по холму на 30,0 м? б) Сколько работы на этом расстоянии совершает веревка на санях? (c) Какую работу совершает сила тяжести на салазках? (г) Какова общая проделанная работа?

   Рисунок 4.Спасательные сани и пострадавший спускаются по крутому склону.

Глоссарий

энергия: работоспособность

работа: передача энергии силой, которая заставляет объект перемещаться; произведение составляющей силы в направлении смещения на величину смещения

джоуль: единица работы и энергии в СИ, равная одному ньютон-метру

Избранные решения проблем и упражнения

1.3,00 Дж = 7,17 × 10 ⁻⁴ ккал

3. (а) 5.92 × 10 ⁵ Дж; (б) −5,88 × 10 ⁵ Дж; (c) Чистая сила равна нулю.

5. 3,14 × 10 ³ Дж

7. (а) -700 Дж; (б) 0; (c) 700 Дж; (d) 38,6 N; (д) 0

7.1: Работа — научное определение

Что значит делать работу

Научное определение труда несколько отличается от его повседневного значения. Некоторые вещи, которые мы считаем тяжелой работой, например написание экзамена или ношение тяжелой ноши на ровной поверхности, не являются работой, как это определено ученым.Научное определение работы показывает ее связь с энергией — когда работа выполняется, энергия передается. Для выполнения работы в научном смысле необходимо приложить силу, и должно быть движение или смещение в направлении силы.

Формально работа, совершаемая в системе постоянной силой, определяется как произведение составляющей силы в направлении движения на расстояние, на которое действует сила . Для одностороннего движения в одном измерении это выражается в форме уравнения как

\ [W = | \ vec {F} | \, \ cos \, \ theta | \ vec {d} | \ label {eq1} \]

где \ (W \) — работа, \ (d \) — смещение системы, а \ (\ theta \) — угол между вектором силы \ (\ vec {F} \) и вектором смещения \ (\ vec {d} \), как на рисунке \ (\ PageIndex {1} \).Мы также можем записать уравнение \ ref {eq1} как

\ [W = F \, d \, \ cos \, \ theta \ label {eq2} \]

Чтобы найти работу, проделанную в системе, которая претерпевает движение, которое не является односторонним или которое находится в двух или трех измерениях, мы делим движение на односторонние одномерные сегменты и складываем работу, выполненную по каждому сегменту.

Что такое работа?

Работа, совершаемая в системе постоянной силой, равна произведению составляющей силы в направлении движения на расстояние, на которое действует сила .Для одностороннего движения в одном измерении это выражается в форме уравнения как

\ [W = F \, d \, \ cos \, \ theta \]

где \ (W \) — работа, \ (F \) — величина силы, действующей на систему, \ (d \) — величина смещения системы, а \ (\ theta \) — угол между вектором силы \ (F \) d вектором смещения \ (d \).

Рисунок \ (\ PageIndex {1} \): Примеры работы. (a) Работа, совершаемая силой \ (F \) на этой газонокосилке, равна \ (Fd \, cos \, \ theta \). Обратите внимание, что \ (F \, cos \, \ theta \) — это составляющая силы в направлении движения.(б) Человек, держащий портфель, не работает с ним, потому что нет движения. Никакая энергия не передается в портфель или из него. (c) Человек, перемещающий портфель в горизонтальном направлении с постоянной скоростью, не работает с ним и не передает ему энергию. (d) Работа с портфелем выполняется путем его перетаскивания наверх с постоянной скоростью, потому что обязательно присутствует компонент силы \ (F \) в направлении движения. Энергия передается в портфель и, в свою очередь, может использоваться для работы. e) когда портфель опускается, энергия передается из портфеля в электрический генератор.Здесь работа, выполняемая генератором с портфелем, является отрицательной, что приводит к отведению энергии из портфеля, потому что \ (F \) и \ (d \) находятся в противоположных направлениях.

Чтобы изучить, что означает определение работы, давайте рассмотрим другие ситуации, показанные на рисунке. Например, человек, держащий портфель на рисунке \ (\ PageIndex {1b} \), не работает. Здесь \ (d = 0 \), поэтому \ (W = 0 \). Почему ты устаешь просто держать груз? Ответ заключается в том, что ваши мышцы работают друг против друга, , но они не работают в интересующей системе («система портфель-Земля» — см. Подробнее «Энергия гравитационного потенциала»).o = 0 \), поэтому \ (W = 0 \).

Напротив, когда сила, действующая на систему, имеет компонент в направлении движения, как, например, на рисунке \ (\ PageIndex {1d} \), работа выполняется на — энергия передается портфелю. Наконец, на рисунке \ (\ PageIndex {1e} \) энергия передается от портфеля к генератору. Есть два хороших способа интерпретировать эту передачу энергии. Одно из объяснений состоит в том, что вес портфеля действительно воздействует на генератор, давая ему энергию. Другая интерпретация заключается в том, что генератор отрицательно воздействует на портфель, тем самым забирая из него энергию.o C \) и эквивалентен 4 184 Дж , в то время как одна пищевых калорий ( 1 ккал ) эквивалентна 4 184 Дж .

Стратегия

Мы можем решить эту проблему, подставив заданные значения в определение работы, выполняемой над системой, указанное в уравнении \ (W = Fd \, cos \, \ theta \). Даны сила, угол и перемещение, так что неизвестна только работа \ (W \).

Решение

Уравнение для работы (Equation \ ref {eq2}):

\ [W = Fd \, \ cos \, \ theta \ nonumber \]

Подстановка известных значений дает

\ [\ begin {align *} W & = (75 \, N) (25.{-4}. \ nonumber \]

Обсуждение

Это соотношение — крошечная доля того, что человек потребляет, но это типичное значение. Очень мало энергии, выделяемой при потреблении пищи, используется для работы. Даже когда мы «работаем» весь день, менее 10% потребляемой нами энергии уходит на работу, а более 90% преобразуется в тепловую энергию или сохраняется в виде химической энергии в жире.

7.1 Работа: Научное определение — Физика колледжа

Что значит выполнять работу

Научное определение труда несколько отличается от его повседневного значения.Некоторые вещи, которые мы считаем тяжелой работой, например написание экзамена или ношение тяжелой ноши на ровной поверхности, не являются работой, как это определено ученым. Научное определение работы показывает ее связь с энергией — когда работа выполняется, энергия передается.

Для того, чтобы работа в научном смысле могла быть выполнена, должна быть приложена сила и должно быть смещение в направлении силы.

Формально работа, совершаемая в системе постоянной силой, определяется как произведение составляющей силы в направлении движения на расстояние, на которое действует сила .Для одностороннего движения в одном измерении это выражается в форме уравнения как

W = ∣F∣cosθ∣d∣, W = ∣F∣cosθ∣d∣, размер 12 {W = lline F rline left («cos» θ right) lline d rline} {}

7.1

где размер WW 12 {W} {} — рабочий, размер dd 12 {d} {} — смещение системы, а размер θθ 12 {θ} {} — угол между вектором силы FF размером 12 {F} {} и вектором смещения dd размером 12 {d} {}, как показано на рисунке 7.2. Мы также можем записать это как

W = Fd cosθ.W = Fd cosθ. размер 12 {W = ital «Fd» «cos» θ} {}

7.2

Чтобы найти работу, проделанную над системой, которая претерпевает движение, которое не является односторонним или которое находится в двух или трех измерениях, мы делим движение на односторонние одномерные сегменты и складываем работу, выполненную по каждому сегменту. .

Что такое работа?

Работа, совершаемая в системе постоянной силой, равна произведению составляющей силы в направлении движения на расстояние, на которое действует сила . Для одностороннего движения в одном измерении это выражается в форме уравнения как

W = Fdcosθ, W = Fdcosθ, размер 12 {W = ital «Fd» «cos» θ} {}

7.3

, где размер WW 12 {W} {} — рабочий, размер FF 12 {F} {} — величина силы, действующей на систему, dd размер 12 {d} {} — величина смещения системы , а θθ размер 12 {q} {} — это угол между вектором силы FF размером 12 {F} {} и вектором смещения dd размером 12 {d} {}.

Рисунок 7.2 Примеры работы. (a) Работа, выполняемая силой FF размером 12 {F} {} на этой газонокосилке, равна FdcosθFdcosθ размером 12 {ital «Fd» «cos» θ} {}. Обратите внимание, что FcosθFcosθ размером 12 {F «cos» θ} {} является составляющей силы в направлении движения.(б) Человек, держащий портфель, не работает с ним, потому что нет перемещения. Никакая энергия не передается в портфель или из него. (c) Человек, перемещающий портфель в горизонтальном направлении с постоянной скоростью, не работает с ним и не передает ему энергию. (d) Работа — это работа , выполняемая с портфелем, когда он поднимается по лестнице с постоянной скоростью, потому что обязательно присутствует составляющая силы FF размером 12 {F} {} в направлении движения. Энергия передается в портфель и, в свою очередь, может использоваться для работы.e) когда портфель опускается, энергия передается из портфеля в электрический генератор. Здесь работа, выполняемая генератором с портфелем, является отрицательной, что приводит к потере энергии портфеля, потому что FF размера 12 {F} {} и dd размера 12 {d} {} находятся в противоположных направлениях.

Чтобы изучить, что означает определение работы, давайте рассмотрим другие ситуации, показанные на рис. 7.2. Например, человек, держащий портфель на рис. 7.2 (b), не работает. Здесь d = 0d = 0 размер 12 {d = 0} {}, поэтому W = 0W = 0 размер 12 {W = 0} {}.Почему ты устаешь просто держать груз? Ответ заключается в том, что ваши мышцы работают друг против друга, , но они не работают в интересующей системе («система портфель-Земля» — см. Подробнее «Энергия гравитационного потенциала»). Для выполнения работы должно быть смещение, и должна быть составляющая силы в направлении движения. Например, человек, несущий портфель на ровной поверхности на рис. 7.2 (c), не работает с ним, потому что сила перпендикулярна движению.То есть cos90º = 0cos90º = 0 размер 12 {«cos» «90» «° =» 0} {}, и поэтому W = 0W = 0 размер 12 {W = 0} {}.

Напротив, когда сила, действующая на систему, имеет компонент в направлении движения, как на рис. 7.2 (d), работа выполняется на — энергия передается портфелю. Наконец, на рис. 7.2 (e) энергия передается от портфеля к генератору. Есть два хороших способа интерпретировать эту передачу энергии. Одно из объяснений состоит в том, что вес портфеля действительно воздействует на генератор, давая ему энергию.Другая интерпретация заключается в том, что генератор отрицательно воздействует на портфель, тем самым забирая из него энергию. На чертеже показано последнее, где сила от генератора направлена ​​вверх на портфель, а смещение — вниз. Это составляет θ = 180ºθ = 180º размер 12 {θ = «180» °} {}, а cos 180º = –1cos 180º = –1 размер 12 {«cos 180» ° = + — 1} {}; следовательно, размер WW 12 {W} {} отрицательный.

Расчет работы

Работа и энергия имеют одинаковые единицы. Из определения работы мы видим, что эти единицы — это сила, умноженная на расстояние.Таким образом, в единицах СИ работа и энергия измеряются в ньютон-метрах. Ньютон-метр получает специальное название джоуль (Дж), а 1 Дж = 1 Н · м = 1 кг · м2 / с21 Дж = 1 Н · м = 1 кг · м2 / с2 размер 12 {1 «J» = 1 «N» cdot m = 1 «kg» cdot m rSup {size 8 {2}} «/ s» rSup {size 8 {2}}} {}. Один джоуль — это не большое количество энергии; он поднимет небольшое 100-граммовое яблоко на расстояние около 1 метра.

Пример 7.1

Расчет работы, которую вы выполняете, чтобы протолкнуть газонокосилку по большой лужайке

Сколько работы проделал на газонокосилке человек, изображенный на Рисунке 7.2 (a) если он прилагает постоянную силу 75,0N75,0N размером 12 {«75» «.» 0 «N»} {} под углом 35º35º ниже горизонтали и толкает газонокосилку 25,0м25,0м размером 12 {«25» «.» 0 «m»} {} на ровном месте? Преобразуйте объем работы из джоулей в килокалории и сравните его со средним дневным потреблением этого человека 10 000 кДж 10 000 кДж размером 12 {«10», «000» «кДж»} {} (около 2400 ккал, 2400 ккал, размер 12 {«2400» «ккал «} {}) пищевой энергии. Одна калория (1 кал) тепла — это количество, необходимое для нагрева 1 г воды на 1ºC1ºC размером 12 {1 ° C} {}, и эквивалентно 4.186J4.186J, в то время как одна калорийность пищи (1 ккал) эквивалентна 4186J4186J, размер 12 {«4186» «J»} {}.

Стратегия

Мы можем решить эту проблему, подставив заданные значения в определение работы, выполняемой над системой, указанное в уравнении W = FdcosθW = Fdcosθ size 12 {W = ital «Fd» «cos» θ} {}. Сила, угол и перемещение даны, так что неизвестен только размер WW 12 {W} {}.

Решение

Уравнение для работы

W = Fdcosθ.W = Fdcosθ. размер 12 {W = ital «Fd» «cos» θ} {}

7,4

Подстановка известных значений дает

W = 75.0 N25.0 mcos35.0º = 1536 J = 1.54 × 103J.W = 75.0 N25.0 mcos35.0º = 1536 J = 1.54 × 103J.alignl {stack { размер 12 {W = left («75» «.» «0 N» right) left («25» «.» «0 m» right) «cos» left («35» «.» 0 ° вправо)} { } # размер 12 {«» = «1536» «J» = 1 «.» «54» умножить на «10» rSup {размер 8 {3}} «J» «.» } {} }} {}

7,5

Преобразование работы в джоулях в килокалории дает W = (1536Дж) (1 ккал / 4186Дж) = 0.367 ккалВт = (1536 Дж) (1 ккал / 4186 Дж) = 0,367 ккал, размер 12 {W = \ («1536″ `Дж \) \ (1`» ккал «/» 4186 «` Дж \) = 0 «.» «367» `» ккал «} {}. Отношение проделанной работы к суточному потреблению составляет

Вт 2400 ккал = 1,53 × 10–4. Вт 2400 ккал = 1,53 × 10–4. размер 12 {{{W} больше {«2400″ `» ккал «}} = 1″. » «53» умножить на «10» rSup {размер 8 {- 4}} «.» } {}

7,6

Обсуждение

Это соотношение — крошечная доля того, что человек потребляет, но это типичное значение. Очень мало энергии, выделяемой при потреблении пищи, используется для работы.Даже когда мы «работаем» весь день, менее 10% потребляемой нами энергии уходит на работу, а более 90% преобразуется в тепловую энергию или сохраняется в виде химической энергии в жире.

Работа: определение, характеристики и примеры — видео и стенограмма урока

Что такое работа?

Обычно вы просыпаетесь, одеваетесь, завтракаете и отправляетесь на работу. Проведя весь день на работе, вы идете домой, ужинаете, выгуливаете собаку, может быть, смотрите телевизор, а затем ложитесь спать.В этом смысле работа может быть чем угодно — строительством, набором текста на клавиатуре, вождением автобуса, обучением в классе, приготовлением еды, лечением пациентов и многим другим.

А вот в физике работа более конкретна. Это смещение объекта под действием силы. Объем выполненной работы зависит от расстояния, на которое перемещается объект. Это позволяет легко представить работу в решаемом уравнении: работа = сила * расстояние . Хотя это уравнение довольно простое, следует отметить три важных момента.Во-первых, для выполнения работы объект должен переместиться на некоторое расстояние. Во-вторых, сила и расстояние движения должны быть в одном направлении. И наконец, сила должна быть постоянной.

В работе используются джоули (Дж), названные в честь Джеймса Прескотта Джоуля. Хотя теперь он известен своими научными работами, на самом деле он предпочитал варить пиво … пока не понял, как наука может помочь ему стать лучшим пивоваром!

Джоуль — это комбинация обоих компонентов в правой части нашего рабочего уравнения: силы и расстояния.Проще говоря, джоуль — это ньютон-метр (Н * м), а один джоуль работы выполняется, когда сила 1 Н действует на расстояние 1 м.

Этот объем работы сравним с поднятием яблока над головой.